Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Ingeniería mecánica, tecnología y desarrollo
versión impresa ISSN 1665-7381
Ingenier. mecáni. tecnolog. desarroll vol.3 no.1 México sep. 2008
Artículos
Modeling of Machining Processes for Predictive Analysis of Self-excited Vibrations
Luciano Vela-Martínez1, a, Juan Carlos Jáuregui-Correa1,b, Oscar González-Brambila1,c, Gilberto Herrera-Ruiz2, Alejandro Lozano-Guzmán3
1 CIATEQ, A. C. Unidad Aguascalientes. Circuito Aguascalientes Nte. 135, Parque Industrial del Valle de Aguascalientes; 20355 Aguascalientes, Ags. Correos electrónicos: avela@ciateq.mx, bjcjaur@ciateq.mx, coscarm@ciateq.mx.
2 DEPFI-UAQ. Centro Universitario Cerro de las Campanas, 76010 Querétaro, Qro. dgherrera@uaq.mx.
3 CONCYTEQ. Luis Pasteur Sur 36, Col. Centro; 76000 Querétaro, Qro. Correo electrónico: concyteq@prodigy.net.mx.
Fecha de recepción: 09-01-08
Fecha de aceptación: 20-03-08
Abstract
Chatter is a condition of instability that limits productivity of machining processes. This phenomenon was classified as a self-excited vibration problem; therefore, it has been studied under linear and nonlinear approaches. Even though regeneration theory and linear time delay models are the most widely accepted explanation of chatter, nonlinear effects of the process are disregarded. The nonlinear effects are characterized by the presence of limit cycles, the jump phenomenon, subcritical Hopf and period doubling bifurcations. Experimental results showed that nonlinear behavior can be represented by both structural and regenerative nonlinear terms; even though characterization of these nonlinear terms is under discussion. In this work, a review of the most outstanding models based on both linear and nonlinear approaches is presented. Additionally, predictive analysis of chatter for typical machining operations is also performed. It can be seen that a linear analysis is enough to obtain a good approach of stability conditions; however, nonlinear analysis is necessary to enhance productivity near unstable machining conditions.
Keywords: Chatter, stability analysis, nonlinear dynamics, chaos, bifurcations.
Resumen
Las vibraciones auto-inducidas son una condición de inestabilidad que limita la productividad de los procesos de maquinado. Este fenómeno, comúnmente conocido como chatter, por su término en inglés, ha sido estudiado con métodos lineales y no lineales. Aunque la teoría de regeneración y los modelos lineales con retraso en el tiempo representan la explicación más aceptada del origen de la vibración, los efectos no lineales del proceso no se toman en cuenta. El comportamiento no lineal del fenómeno de vibración auto-inducida está caracterizado por la presencia de ciclos límite, el fenómeno de salto y bifurcaciones subcríticas tipo Hopf y de período duplicado. Resultados experimentales muestran que el comportamiento no lineal se puede representar mediante términos no lineales de tipo estructural y regenerativo, pero la caracterización de esos términos está en discusión. En este trabajo se presenta una revisión de los modelos más representativos del análisis de vibraciones auto-inducidas, basados en métodos lineales y no lineales. También se presenta un análisis predictivo de una operación típica de maquinado. Se concluye que el análisis lineal es suficiente para obtener una buena aproximación de las condiciones críticas de estabilidad; sin embargo, el análisis no lineal es necesario para mejorar la productividad cerca de condiciones inestables de maquinado.

Introducción
Chatter was first identified as a limitation of productivity, by Taylor (1907); however, theoretical explanations for chatter generation were proposed afterward, such as negative damping, by Arnold (1946); the theory of regeneration of chip thickness, by Tobias (1958); structural dynamics, by Tlusty (1963) and Merrit (1965); dry friction and modal coupling, by Wu and Liu (1985a, 1985b). The regeneration theory is still the most comprehensive explanation for chatter, where the destabilizing term was introduced in the cutting force as a function of the current and the previous cut. Tobias (1958) concluded that instability was originated by the auto-excitation of the system from the dynamic variation of chip thickness, because a static chip thickness would not cause instability. It was Merrit (1965) who classified chatter as a kind of self-excited vibrations and presented stability charts in terms of process parameters, such as depth of cut and spindle speed. A first effort on modeling nonlinear behavior of chatter was performed by Hanna and Tobias (1974), who proposed a model with square and cubic terms to represent both structural and regenerative nonlinearities; even though the process of solution was limited, nonlinear behavior as finite amplitude vibrations and the jump phenomenon was found.
More recently, Altintas (2000) developed a comprehensive technology for predictive analysis, based on the regenerative theory and supported by modal and frequency measurements. He applied this method for turning, milling and drilling. In addition, Altintas et al. (1999) proposed a theoretical model to improve dynamic stability through variable pitch cutters. Altintas and Budak (1995, 1998a, 1998b) proposed a two-degree of freedom linear model for the cutting tool in milling, where the cutting force was proportional to the chip section and depended on the instantaneous immersion angle of the j-th tooth on the rotating tool, geometry of tool and number of teeth. The loss of contact between the j-th tooth and the workpiece was modeled by a unit step function; however, this approach is valid for full or half-immersed problems, but not for highly interrupted cutting. Similar models were later used by Insperger and Stépán (2000), and Bayly et al. (2002), where numerical solutions were performed to take into account low radial immersion. Dry friction was identified as a main source of chatter due to its velocity-dependent nature (Wu and Liu; 1985a, 1985b). An extensive research on sources of chatter and theoretical modeling was performed by Wiercigroch and Budak (2001). They identified additional causes of instability that confer the chatter phenomenon a highly nonlinear nature. Among these causes were: hardening and softening by deformation, thermal softening, dependence of deformation rate, variable friction, heat generation and conduction, hysteretic behavior for feed, intermittent cutting of tool, and time delay. Likewise, Wiercigroch and Krivtsov (2001) found a chaotic behavior due to the effect of dry friction in orthogonal metal cutting. Tlusty (2000) found an experimental power law for the cutting force in terms of the chip thickness, called the three-quarter rule, attributed to the friction between the cutting tool and the workpiece during the cutting process.
In contrast with the classical linear theory, Stépán et al. (2003, 2005a, 2005b) included the aforementioned power-law function in the cutting force, for the nonlinear analysis of turning and high speed milling. As a result, period doubling (flip) bifurcations were found. Even though the power-law function was reached from experimental data, its work lacks of theoretical validation. Insperger et al. (2004a) analyzed the stability of the turning process through a single degree of freedom delay differential equation with a variable delay as a parametric excitation. These authors found that variation of spindle speed was highly effective in eliminating chatter at low speeds; whereas improvement was not significant at high speed. Insperger et al. (2003, 2004b) and Mann et al. (2003) also analyzed the stability of models with one or two degrees of freedom for up-milling, down-milling and high speed milling with time dependent parameters. Flexibility in the cutting tool has also been taken into account; thus, the effect of compliance between the cutting tool and the work-piece was investigated by Bravo et al. (2005) for milling and by Vela-Martínez et al. (2008) for turning.
In summary, regenerative chatter is a highly nonlinear vibration problem with chaotic behavior; multiple sources of high nonlinearity are identified and complex models are in good agreement with experimental results. However, neither a unifying model nor an exact solution has been proposed yet. In this work, predictive analyses for typical machining processes are performed by using both linear and nonlinear approaches. From the obtained results, nonlinear behavior can be attributed to structural nonlinearities. Hence, future work to model nonlinearities from both the cutting force and the structural stiffness is under preparation, such that a better understanding of the phenomenon will be obtained.
Modeling of Self-Excited Vibrations
Regeneration theory and linear stability analysis.
The regeneration theory was proposed by Tobias (1958), and it establishes that the onset of chatter is due to an excitation of one of the mode shapes of the system, such that vibration causes a wavy surface on the workpiece and chip thickness varies at the subsequent cutting pass. Thus, current vibrations depend of both dynamics of the system and vibrations from the previous period of revolution. In a condition of severe chatter, vibrations can grow exponentially that the cutting tool can loose contact with the workpiece due to large amplitude vibrations. The first approach to represent the dynamics of the process of metal cutting was also proposed by Tobias through a single degree of freedom model, as shown in Figure 1 for a turning process.

The cutting process originates a motion in the cutting tool, defined by x(t), such that the equation of motion for the cutting tool is defined as follows:
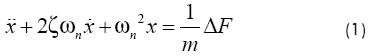
where ωn, k, m, and ζ are the modal parameters, which can be experimentally obtained through an experimental modal analysis based on the impact testing (Altintas, 2000; Vela-Martínez et al., 2007a). According to the theory of regeneration, the dynamic chip thickness is given by the following expression:

If the Merchant model is used for the cutting force (Altintas, 2000), Equation (1) becomes:
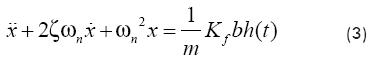
A stability analysis of Equation (3) can be seen in Altintas (2000). Equation (3) is carried to the frequency domain by the Laplace transform with initial conditions set to zero. Afterward, from an expression of the chip thickness in frequency domain, the characteristic equation of the system is obtained by considering a pure imaginary root as condition of critical stability. Finally, the system will perform a chatter-free condition whenever the depth of cut is less than the critical depth of cut, which is given by:
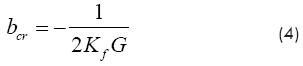
where G is the real part of the transfer function of the system in terms of modal parameters and the ratio of the chatter frequency and the natural frequency 

From Equations (4) and (5) it can be seen that the minimal depth of cut is obtained when G is minimum. The function G behaves as follows: G grows slowly as r approaches 1 from the left and reaches a maximum in the vicinity of r = 1; then, G decays drastically to cross the horizontal axis at r = 1. Then, G keeps decaying and reaches a minimum, after that, it starts growing slow and asymptotically to the horizontal axis. Thus, chatter frequency can be calculated as the frequency ratio, r, ranges from 1 to 1.15.
In addition, the spindle speed associated to the critical depth of cut is calculated as follows:

where n is an integer number that represents a hypothetical number of waves on the machined surface, from which multiple solutions of the system are obtained; whereas ε is the phase shift of the system:

Even though any structure has an infinite number of modes of vibration, chatter analysis is usually performed only around the first mode of vibration, because it is the most flexible. Then, stability lobes from the second or third mode would appear above the corresponding to them of the first mode. Sometimes, any intersection between the upper part of the first mode lobes and the lower part of the second mode lobes occur such that first mode lobes look incomplete. For the purpose of this analysis, only the first mode of vibration will be taken into consideration.
On the other hand, the model of Budak and Altintas (1998a, 1998b) for milling was more refined since the cutting force was time and directional dependant, as well as loss of contact between the j-th tooth and the workpiece was modeled by a unit step function, such that it took a value of 1 during contact time and zero otherwise. Thus, equations of motion, which represents the cutting phenomenon from Figure 2, are expressed as follows:
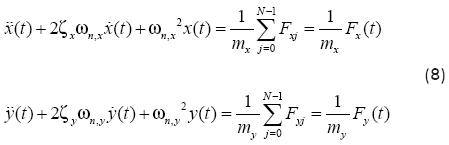

Accordingly, the cutting force is given by:

where the periodic terms A(t) are time and directional dependant, {x(t)-x(t-τ), y(t)-y(t-τ)} is the dynamic load of chip due to the vibration of the current and previous cutting pass, whereas τ = 2π/NΩ is the tooth period at a spindle speed W. Kt and Kr represent the cutting coefficient in thrust and radial direction, respectively.
Periodic terms of A(t) are calculated as a Fourier series:

Summing the cutting forces contributed by all teeth, matrix A(t) can be represented by time-dependant directional dynamic milling force coefficients:
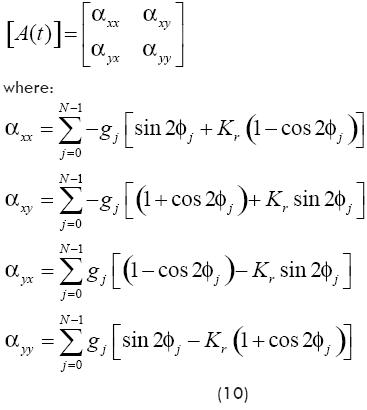
Here, gj(φj) = 1 is the unit step function, and φj = Ωτ.
The number of harmonics, r, of the tooth passing frequency to be considered is reflected in the accuracy of A(t), which depends on both the immersion conditions and the number of engaged teeth. The simplest case corresponds to full immersion and no overlapping in the engagement of teeth, such that no harmonics, r = 0, are included in the analysis. Hence, Equation (10) becomes:

where φst and φex are the entry and exit angle of the j-th tooth.
Linear stability analysis of Equation (8) was performed in order to obtain the characteristic equation in frequency domain, such that the critical depth of cut for a chatter-free machining was given by:

where is obtained from the characteristic equation:

Additionally, the spindle speed can be calculated by Equation (6); however, the phase shift of the system for milling is obtained as follows:

This model is useful to predict stability for a milling process where the cutting tool is totally immersed or half-immersed into the material. However, when the width of cut is very small, the milling force is intermittent such that the average coefficients from the matrix A(t) are limited for the analysis. Low immersion and intermittency of cutting tool is analyzed in the next Section.
Nonlinearities from the structure and the cutting force.
The turning process was modeled by Stépán et al. (2003) through a single degree of freedom model with a chip thickness function in terms of the three-quarter rule, proposed and experimentally proven by Tlusty (2000), as follows:

The cutting force F is approximated by a Taylor series respect to h, such that stability conditions can be represented by the following equations:

and

where  and ωc is the chatter frequency at which stability is lost. Even though, a theoretical validation of coefficients of the Taylor series was not presented.
and ωc is the chatter frequency at which stability is lost. Even though, a theoretical validation of coefficients of the Taylor series was not presented.
Insperger et al. (2002, 2004b) used the semidiscretization method to solve the problem of low immersion milling for 1 and 2 degree of freedom delayed models. The advantage of this method is that only the delayed terms are discretized while the actual domain terms are unchanged, in contrast to full discretization techniques; thus, a finite dimensional discrete map approximation of the delayed differential equation is constructed. Consequently, the stability of the system depended on the nature of the eigenvalues of the Floquet transition matrix. Modeling of a 1 degree of freedom milling process is described below:

where the cutting coefficient is time dependent:

Here, N is the number of teeth, Kt and Kn are the tangential and the normal cutting coefficients, respectively; whereas Φj(t) is the angular position of the j-th tooth, and the function g(Φj(t)) is the unit step function to model contact between the cutting tool and the workpiece, such that it takes a value of 1 or 0 as the j-th tooth is in contact or not with the workpiece, respectively.
The discretization scheme proposed by Insperger et al. (2004b) is applied to Equation (17), which can be transformed to the following linear differential equation:

where:

In addition, A(t + T ) = A(t), B(t + T) = B(t), τ(t + T) = τ(t). First, the time interval discretization [ti, ti+1], i = 0, 1, ... with length Δt, is constructed over a principal period of time T = k Δt, where k is an integer that can be considered as an approximation parameter of the time period.
A series of integers mi, which can be considered as an approximation parameter of the length of the time delay, is introduced:

If ti is denoted by i, Equation (19) can be approximated in the i-th interval as:
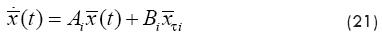
where , , and is the following approximation of the delayed term on [ti, ti+1]:

with weigths:

The solution of Equation (19) for the initial condition 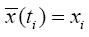
means that:

Thus, a map for x can be expressed as:

where

The discrete map of Equation (26) can be expressed as :

with the (M+1)-dimensional vector
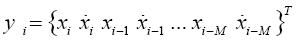
and the coefficient matrix Ci is composed by the submatrices Pi, αiRi, βiRi and the identity matrix I.
The next step is to determine the transition matrix F over the principal period T = kΔt, According to the Floquet theory:

where:

The stability criterion is that if the eigenvalues of Φ are in modulus less than one, then the system is stable.
RESULTS AND DISCUSION.
In this Section, stability analyses for turning, as well as full and partial immersion milling are performed by applying the predictive models described in the last Section. Both linear and nonlinear models are tailored to the machining process through the dynamic parameters of the system, which can be obtained from the impact testing, as mentioned above. The cutting coefficient can be obtained according to the material of the workpiece and geometry in terms of the immersion of the cutting tool. Results from the experimental modal analysis presented by Vela-Martínez et al. (2007a), for a turning process, are used in this work. An AISI 1018 50 mm diameter and 150 mm length steel bar, mounted in the chuck of a CINCINNATI MILACRON CNC HAWK TC-200 11 kW@5000 RPM turning center, was analyzed. Thus, the modal parameters of the systems were estimated as: ωn = 402.83 Hz; ζ= 7.58%; and κ = 2 912 685.27 N/m. In addition, a cutting coefficient of Kf = 1,000X106 N/m^2 for steel was used.
A linear stability analysis of the turning process is shown in Figure 3a, the stability chart is constructed with Equations (4) and (6), where the chatter frequency is swept around the natural frequency of the system. On the other hand, limits of stability from the nonlinear analysis are constructed with Equations (15) and (16) and shown in Figure 3b. A general agreement between stable and unstable zones is obtained, even though some discrepancies are found. An unconditionally stable depth of cut of 0.48 mm is predicted by the linear theory, whereas 0.35 mm is predicted by the nonlinear analysis. This discrepancy can be attributed to the fact that feed ratio is affected by a ¾ power coefficient in the nonlinear analysis; the cutting coefficient can also be a source of discrepancy because the same value was used in both models, however it could be measured in a different way for a proportional or a power-law function for the cutting force. On the other hand, nonlinear lobes look displaced respect to the linear lobes because shift phase between the cutting tool and the workpiece is taken into consideration in the linear analysis. If this shift phase is disregarded, both nonlinear and linear lobes are totally in phase.

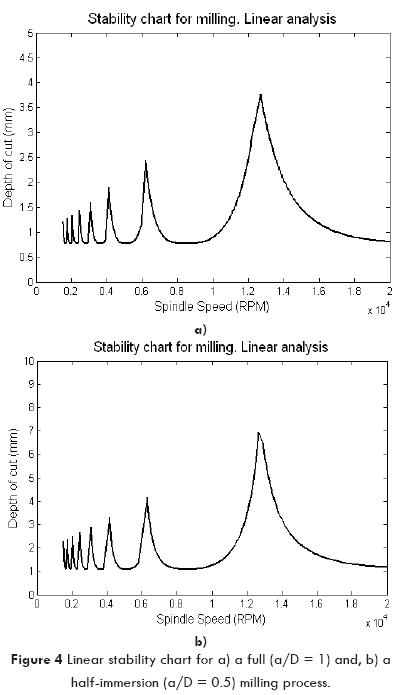
The following modal parameters for a two degree of freedom milling process with a three-flute end mill and a work-piece made of aluminum, are taken from Budak and Altintas (1998a): ωn,x = 603 Hz; ζx = 3.9%; and kx = 5600 kN/m, ωn,y = 666 Hz; ζy = 3.5%; and ky = 5700 kN/m, Kt = 600 X106 N/m^2, Kn = 0.07Kt . Stability charts for full, a/D = 1, and half-immersion milling process, a/D = 0.5, are constructed with Equations (6), and (11) to (13), as shown in Figures 4a and 4b, respectively. The critical depth of cut for full immersion is 0.77 mm, whereas it is raised to 1.08 mm for half-immersion process. In fact, the stability borderline is also raised at the peaks of lobes for half-immersion process.
Even though the discretized map approximation of Equation (27) was derived for the delayed single degree of freedom Equation (17), these results can be used to show the effect of low immersion milling. Stability charts for different immersion rates, such as: a/D = 1, 0.5, 0.2, and 0.05, are shown in Figure 5a-d, respectively. Good agreement with linear stability, in the arrangement of lobes along the spindle speed axis is found; however, stability is dropped when nonlinearities are taken into account; the critical and the maximum depth of cut at every lobe are smaller than in the linear analysis, whether for full or half-immersion process. On the other hand, stability is enhanced as the immersion rate is 0.5; since the cutting tool can remove a heavier chip thickness because the contact time with the workpiece is smaller. However, an interesting result is obtained when the immersion rate is 0.2 and 0.05; isolated instability conditions inside a larger stability zone are found because of the highly interrupted cutting.

From the preceding results, it can be summarized that linear stability analysis shows good accuracy for continuous turning, as well as full or half immersion milling. Models based on the power law-function showed nonlinear behavior as measured experimentally, even though theoretical validation of the nonlinear terms was not presented. On the other hand, solution of the discretized map approximation from the original delay differential equation showed intermittency of the cutting force as an important source of structural nonlinearity, even though the original cutting force of the model was a linear function. Hence, nonlinear behavior can be attributed to discontinuities of the cutting force, such that a nonlinear delayed model with structural nonlinear terms is suitable to represent self-excited vibrations in machining. Future work will be aimed to obtain structural nonlinearities from the experimental measurement of nonlinear behavior, such as the frequency response function.
CONCLUSIONS.
Chatter is a condition of instability related to dynamic characteristics of the machining system, which are defined by its modal parameters such as: natural frequency, damping ratio, mass and stiffness. Chatter is classified as self-excited vibrations with nonlinear behavior characterized by finite amplitude oscillations, limit cycles, as well as subcritical (Hopf) and period doubling (flip) bifurcations. Even though several sources of nonlinearities have been identified, regeneration theory and time delay differential equations are the most accepted explanation for the onset of chatter. Dynamic stability of machining processes has been analyzed under both linear and nonlinear techniques. Linear stability analysis is satisfactory for machining conditions such as: continuous turning or full immersion milling. However, nonlinear analysis is necessary for interrupted turning, high speed and low immersion milling, where loss of contact between the cutting tool and the workpiece has a dominant effect on the stability of the system. Consequently, prediction of stability is enhanced when models with structural and regenerative nonlinear terms are used. Hence, a nonlinear delayed model with structural nonlinear terms is suitable to represent self-excited vibrations in machining. Even though characterization of these nonlinear terms is under discussion, intermittency of cutting seems an important source of nonlinearity, such that they can be obtained from the experimental measurement of nonlinear behavior, such that the frequency response function.
ACKNOWLEDGEMENTS.
Authors gratefully acknowledge the support for this research to The Science and Technology Council of Aguascalientes under Agreement No. 21/56/06.
REFERENCES.
Altintas Y., Budak E., "Analytical Prediction of Stability Lobes in Milling", CIRP Annals, 1995, 44 (1), 357-362. [ Links ]
Altintas Y., Budak E., "Analytical Stability Prediction and Design of Variable Pitch Cutters", Transactions of the ASME Journal of Manufacturing Science and Engineering, 1999, 121, 173-178. [ Links ]
Altintas Y., Manufacturing Automation, Metal Cutting Mechanics, Machine Tool Vibrations, and CNC Design, Cambridge University Press, New York, 2000. [ Links ]
Arnold R. N., "The Mechanism of Tool Vibration in the Cutting of Steel", in: Proceedings of the Institution of Mechanical Engineers, 1946, 154, 261-284. [ Links ]
Bayly P. V., Mann B. P., Stépán G., Insperger T., Effects of Radial Immersion and Cutting Direction on Chatter Instability in End-milling, in: Proceedings of IMECE2002, ASME International Mechanical Engineering Congress & Exposition, 2002, New Orleans, 17-22 Nov., IMECE2002-39116. [ Links ]
Bravo U., Altuzarra O., López de Lacalle L. N., Sánchez J. A., Campa F. J., "Stability Limits of Milling Considering the Flexibility of the Workpiece and the Machine", International Journal of Machine Tools and Manufacture, 2005, 45 (15), 1669-1680. [ Links ]
Budak E., Altintas Y., "Analytical Prediction of Chatter Stability in Milling-Part I: General Formulation", Transactions of the ASME Journal of Dynamic Systems, Measurement and Control,1998, 120, 22-30. [ Links ]
Budak E., Altintas Y., "Analytical Prediction of Chatter Stability in Milling-Part II: Application of the General Formulation to Common Milling Systems", Transactions of the ASME Journal of Dynamic Systems, Measurement and Control, 1998, 120, 31-36. [ Links ]
Hanna N. H., Tobias S. A., "A Theory of Nonlinear Regenerative Chatter", Transactions of the ASME Journal of Engineering for Industry, 1974, 96, 247-255. [ Links ]
Insperger T., Stépán G., "Semi-discretization Method for Delayed Systems", International Journal for Numerical Methods in Engineering, 2002, 55 (5), 503-518. [ Links ]
Insperger T., Mann B. P., Stépán G., Bayly P. V., "Stability of Up-milling and Down-milling, Part 1: Alternative Analytical Methods", International Journal of Machine Tools and Manufacture, 2003, 43 (1), 25-34. [ Links ]
Insperger T., Stépán G., "Stability Analysis of Turning with Periodic Spindle Speed modulation via semidiscretization", Journal of Vibration and Control, 2004, 10, 1835-1855. [ Links ]
Insperger T., Stépán G., "Updated Semi-discretization Method for Periodic Delayed-differential Equations with Discrete Delay"; International Journal for Numerical Methods in Engineering, 2004, 61 (1), 117-141. [ Links ]
Mann B. P., Insperger T., Bayly P. V., Stépán G., "Stability of Up-milling and Down-milling, Part 2: Experimental Verification", International Journal of Machine Tools and Manufacture, 2003, 43 (1), 35-40. [ Links ]
Merrit H. E., "Theory of Self-excited Machine-tool Chatter", Transactions of the ASME Journal of Engineering for Industry, 1965, 87 (4), 447-454. [ Links ]
Pratt J. R., Vibration Control for Chatter Suppression; Doctor of Philosophy in Engineering Mechanics Thesis, Virginia Polytechnic Institute and State University, 1997. [ Links ]
Stépán G., Szalai R., Insperger T., Nonlinear Dynamics of High-speed Milling Subjected to Regenerative Effect, in: G. Radons (Ed.) Nonlinear Dynamics of Production Systems, Wiley-VCH, New York, 2003. [ Links ]
Stépán G., Szalai R., Mann B. P., Bayly P. V., Insperger T., Gradisek J., Govekar E., "Nonlinear Dynamics of High-speed Milling – Analyses, Numerics and Experiments", ASME Journal of Vibration and Acoustics, 2005, 127, 197-203. [ Links ]
Stépán G., Insperger T., Szalai R., "Delay, Parametric Excitation, and the Nonlinear Dynamics of Cutting Processes", International Journal of Bifurcation and Chaos, 2005, 15 (9), 2783-2798. [ Links ]
Taylor F., "On the Art of Cutting Metals", Transactions of the ASME, 1907, 28, 31-350. [ Links ]
Tlusty J., Polacek M., "The Stability of Machine Tools Against Self Excited Vibrations in Machining", International Research in Production Engineering. ASME, 1963, 465-474. [ Links ]
J. Tlusty, Manufacturing Processes and Equipment, Prentice-Hall, Englewood Cliffs, NJ, 2000. [ Links ]
Tobias S. A., Fishwick W., "A Theory of Regenerative Chatter", The Engineer-London, 1958. [ Links ]
Vela-Martínez L., Jáuregui-Correa J. C., Rubio-Cerda, E., Herrera-Ruiz, G., Lozano-Guzmán, A., Validación Experimental de Modelos Predictivos de Vibraciones Auto-excitadas en Torneado, In: Memorias de XIII Congreso Internacional Anual SOMIM 2007, 18-21 Sept. 2007, Durango, Dgo. [ Links ]
Vela-Martínez L., Jáuregui-Correa J. C., Rubio-Cerda, E., Herrera-Ruiz, G., Lozano-Guzmán, A., "Analysis of Compliance Between the Cutting Tool and the Workpiece on the Stability of a Turning Process", International Journal of Machine Tools and Manufacture, 2008, 48, 1054–1062. [ Links ]
Wiercigroch M., Budak E., "Sources of Nonlinearities, Chatter Generation and Suppression in Metal Cutting", Philosophical Transactions of the Royal Society of London, 2001, 359, 663–693. [ Links ]
Wiercigroch M., Krivtsov A.M., "Frictional Chatter in Orthogonal Metal Cutting", Philosophical Transactions of the Royal Society of London, 2001, 359, 713–738. [ Links ]
Wu D. W., Liu C. R., "An Analytical Model of Cutting Dynamics. Part 1: Model Building", Transactions of the ASME Journal of Engineering for Industry, 1985, 107, 107-111. [ Links ]
Wu D. W., Liu C. R., "An Analytical Model of Cutting Dynamics. Part 2: Verification", Transactions of the ASME Journal of Engineering for Industry, 1985, 107, 112-118. [ Links ]














