1. INTRODUCTION
Digital image processing is mainly used for improving or enhancing the pictorial information for human interpretation and processing image data for storage transmission and representation. At present all the images have square shaped pixels and henee all the image processing algorithms are done on the same basis. Processing based on hexagonal grid is a new approach in the field of image processing, because of its various advantages.
Hexagonal image processing is a new developing área of image processing, in which the images are represented by using hexagonal shaped pixels rather than square pixels. Image processing in hexagonal grid is very much advantageous than in the conventional rectangular grid. The advantages include higher angular resolution, consistent connectivity, higher sampling efficiency, etc.
Usually digital images are mapped on square lattice. In hexagonal image processing we change the square lattice to hexagonal lattice by re-sampling the images.
Image denoising is one of the major challenges in the field of image processing and computer visión. Image denoising is the process of estimating the original image by suppressing noise from a noisy image. Usually the noise is introduced in the images during image acquisition (digitization) or during image transmission. Sensor temperature and light levéis are major factors that affect the amount of noise in the images while acquiring images with CCD camera. Also, images are corrupted during transmission. A noisy image can be mathematically expressed as shown in Eq. (1).
where I(x,y) is the original image, N(x,y) is the noise, and I N (x,y) is the resulting noisy image. Typical noises usually present in an image are uniform or quantization noise, salt & pepper noise, Gaussian noise, Gamma noise, Rayleigh distribution noise, etc. (Jaiswal, Upadhyay, & Somkuwar, 2004). In this work we focus on Gaussian noise present in an image.
In Gaussian noise the noise having a probability density function (PDF) equal to that of the normal distribution, which is also known as the Gaussian distribution (i.e., the valúes that the noise can take on are Gaussian-distributed). The probability density function 'p' of a Gaussian random variable 'z' is given by
where µ is the mean valué and o is the standard deviation. In the case of images z represents the grey level. A special case is white Gaussian noise, in which the valúes at any pair of times are identically distributed and statistically independent. A lot of algorithms have been proposed to improve the performance of image denoising scheme. All these works are based on the images on rectangular grid. Wavelet thresholding based image denoising by representing images in hexagonal grid using the modified NeighShrink thresholding is mentioned in this work.
The paper is organized as follows. Section 2 is devoted for literature review which includes brief introduction to discrete wavelet transform, wavelet thresholding, and concepts of hexagonal image processing and related works.
In Section 3 we introduce the proposed methodology of image denoising using JeevKrish (Jeev: first four letters of the ñame of the first author, Krish: first five letters of the ñame of the second author) thresholding in hexagonal domain. Results and discussion, and conclusions are given in sections 4 and 5, respectively.
2. LITERATURE REVIEW
2.1 DISCRETE WAVELET TRANSFORM (DWT)
A wavelet is a waveform of an effectively limited duration that has an average valué of zero. A function ψ (x) can be called a wavelet if it possesses the following properties:
1.- The function intégrate to zero, or equivalently, its Fourier transform denoted as ψ (ω) is zero
2.- It is square integrable, or equivalently, has finite energy
Eq. (3) suggests that the function is either oscillatory or has a wavy appearance and Eq. (4) implies that most of the energy in ψ (x) is confined to a finite interval or in other words ψ (x) has good space localization.
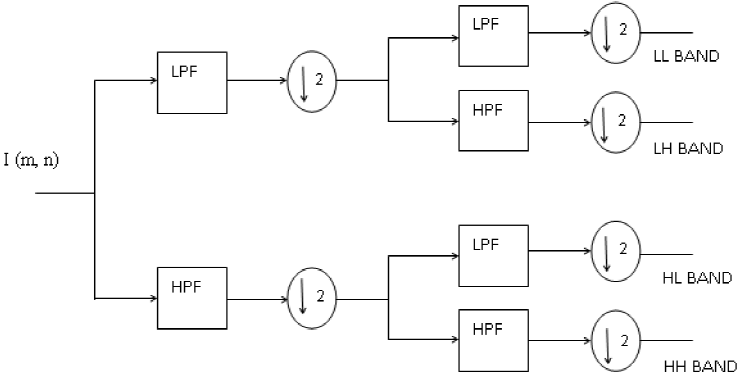
The discrete wavelet transform (DWT) is obtained by filtering the signal through a series of digital filters at different scales. The scaling operation is done by changing the resolution of the signal by the process of subsampling. In the computation of DWT, the input image is decomposed into low-pass and high-pass sub-bands, i.e., each decomposition stage consists of a low-pass filter (LPF) and a high-pass filter (HPF). When the signal passes through these filters, it splits into two bands. The LPF, which corresponds to an averaging operation, extracts the coarse information of the signal. The HPF, which corresponds to a differencing operation, extracts the detailed information of the signal. The output of the filtering operation is then decimated by two. In the case of images (two-dimensional signal), first, the image is filtered along the row and decimated by two.
Then it is followed by filtering the sub-image along the column and decimated by two. This operation splits the image into four bands namely LL (Low frequency or approximation coefficient), LH (vertical details), HL (horizontal details), and HH (diagonal details) as shown in Figure 1.
2.2 WAVELET THRESHOLDING
Denoising by thresholding in wavelet domain was developed by Donoho and Johnstone (1995). In wavelet domain, large coefficients correspond to the signal and small ones represent mostly the noise. The thresholding of wavelet coefficients is done by either 'Hard' or 'Soft' thresholding function.
In hard thresholding (Figure 2(a)) the wavelet coefficients below the threshold 'T' are made zero and coefficients above the threshold are not changed. If 'x' and 'y' represent the input and output respectively, then the hard thresholding is given by the equation
In the case of soft thresholding (Fig. 2(b) ), the wavelet coefficients are shrunk towards zero by a threshold valué 'T'. It can be represented by the equation
Selection of low valué of threshold may produce a result which is near to the input, but the result still may be noisy. Larger valué of threshold produces an output with large number of zero coefficients. The result of this selection is a very smooth signal. The smoothness suppresses the details and edges of the original image and causing blurring and ringing artifaets. Some of the existing methods in the literature for estimating the threshold are described below.
VisuShrink
This technique consists of applying the soft thresholding operator using the universal threshold proposed by Donoho and Johnstone (1995) and this threshold is given by the equation
where
SureShrink
Thresholding method that minimizes the Stein Unbiased Risk Estimator (SURE) developed by Donoho and Johnstone (1995) is known as SureShrink wavelet thresholding technique. This method select distinct threshold for each sub-band of each level of the wavelet tree and henee it is known as an adaptive method for selecting threshold. The SureShrink threshold Tsure is expressed as
where 't' represents the valué that minimize the Stein Unbiased Risk Estimator (SURE),
BayesShrink
The threshold derived in a Bayesian approach is given by the equation
where
NeighShrink
Chen, Bui, and Krzyzak (2004) proposed a new wavelet thresholding method in their paper titled Tmage denoising using neighbouring wavelet coefficients' called NeighShrink. It is the modification of wavelet denoising scheme for ID signal by incorporating neighboring coefficients in the thresholding process proposed by Cai & Silverman (2001). In NeighShrink method, the wavelet coefficients are thresholded according to the valué of the squared sum of all the valúes of wavelet coefficients in the neighborhood window. The window size can be taken as 3X3, 5X5, 7X7, etc. Init is already reported that 3X3 window gives better results. The shrinkage for NeighShrink is expressed as
where
Some other thresholding methods are SmoothShrink method proposed by Mastriani and Giraldez (2007) for images corrupted by speckle noise. Another method called BiShrink, based on non-Gaussian bivariate distributions model proposed by Sendur & Selesnick (2002a, 2002b). Shengqian, Yuanhua, and Daowen (2002) proposed an adaptive shrinkage denoising scheme using neighborhood characteristics and they claimed that their scheme produced better results than the results produced by Donoho (1995) and Donoho et al. (1995).
2.3 HEXAGONAL IMAGE PROCESSING
The photoreceptors (Rods & Cones) of human retina closely resembré to hexagonal structure (Curcio, Sloan. Kalina, & Hendrickson, 1990). Figure 3 shows the arrangement of rods & cones in human retina. Since the cells in human retina have hexagonal structure, the image developed in the retina has hexagonal shaped pixels. In addition, hexagonal geometry has some advantages like higher sampling efficiency, consistent connectivity and higher angular resolution. Due to these reasons many researchers have studied the possibility of representing digital images with hexagonal pixels (Barun, Pooja & Kuldip, 2014; Middleton & Sivaswamy, 2005; Veni & Narayanankutty, 2011). But the non-availability of hardware for capturing and displaying hexagonal based images limits the use of hexagonal image structure for further processing. Since there is no hardware for capturing the hexagonal images, conversión has to be done from square to hexagonal image before hexagonal-based image processing.
There have been several ways to simúlate a hexagonal grid on a regular rectangular grid. The common simulations methods are re-sampling the square lattice to the hexagonal lattice, mimic hexagonal pixels using square pixels, pseudo hexagonal pixel, and virtual hexagonal structure.
One method of representing hexagonal lattice using the simulation method - resampling the square lattice to the hexagonal lattice - is altérnate pixel suppressal method (Sankar, Sanjay & Rajan, 2004). Hexagonal grid image based on altérnate pixel suppressal method can be obtained from the conventional image by alternatively suppressing rows and columns of the existing rectangular grid and sub-sampling it. All the other pixels of the rectangular grid which do not have any correspondence with the hexagonal counterparts are suppressed to zero.
While processing this sub-sampled image the suppressed pixels are not considered in computation. The sub-sampled hexagonal grid is shown in Figure 4.

Fig 4 (a) Rectangular grid an (b) Simulated hexagonal grid obtained using alternate pixel suppression.
Image processing applications like image rotation, edge detection, etc. in hexagonal lattice have already been discussed by many researchers. Middleton and Jayanthi Sivaswamy (2001) proposed an edge detection method in a hexagonal image processing framework. In this work the authors conclude that the hexagonal framework gives better results for edge detection. Veni, and Narayanankutty (2011), Vidya et al. (2009) and Vidya (2011) also analyzed the performance of edge detection on hexagonal sampling grid. Comparisons of image alignment on hexagonal and square lattices were performed by Shima, Sugimoto, & Okutomi (2010). Azam, Anjum, & Javed (2010) proposed discrete cosine transform based method for face recognition in hexagonal images. Wavelet based image compression in hexagonal domain was proposed by Jeevan & Krishnakumar (2014) in the paper titled 'Compression of images represented in hexagonal lattice using wavelet and Gabor filter'. In all these works, the authors confirmed that the hexagonal representation gives better results.
In this paper we propose an image denoising method in hexagonal lattice using wavelet thresholding method. Modified NeighShrink method, which is explained in the next section, is used for thresholding.
3. PROPOSED METHODOLOGY
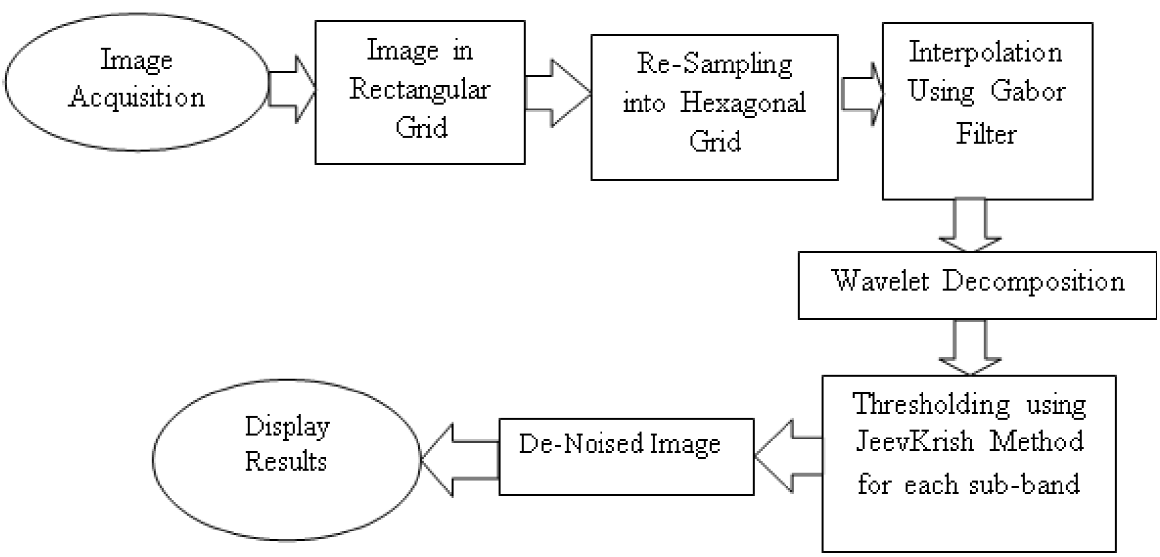
An image denoising method using modified NeighShrink thresholding method named as JeevKrish thresholding is proposed in our work. Although the work proposed is image denoising, we are trying to confirm that the hexagonal representation is better than the normal square pixel representation of images. We consider images corrupted with Gaussian noise. Figure 5 shows the block diagram of the proposed method.
Due to the non-availability of hardware for acquiring hexagonal images, rectangular grid to hexagonal grid conversión has to be done before performing hexagonal image processing. In this work we use altérnate pixel suppressal method, which is explained in Section 2.3 for simulating the hexagonal grid from rectangular grid. During the conversión of images from rectangular lattice to the hexagonal lattice, considerable loss in image quality was observed. So, image reconstruction through interpolation is used. Interpolation using Gabor filter is used in this work.
Gabor filter (Gabor, 1946; Vidya, 2011) is the only filter with orientation selectivity that can be expressed as a sum of two separable filters. In the spatial domain, a 2D Gabor filter is a Gaussian kernel function modulated by a sinusoidal plañe wave. The foliowing equations represent the 2D-Gabor function which was proposed by Daugman (1985). Equations 13 and 14 represent the real and imaginary part of the function, respectively.
where x' = xcosθ + ysinθ and xy' = -xsinθ + ycosθ
The arguments 'x' and 'y' specify the position of 'x' and 'y' coordínate of the image and sigma (σ), gamma (γ), lambda (λ), theta (ɵ), and phi (φ ) are parameters as follows. The standard deviation (σ) of the Gaussian factor determines the size of the receptive field. The parameter gamma (γ) named as aspect ratio, specifies the ellipticity of the Gaussian factor. It has been found to vary in a limited range of 0.23 < γ < 0.92. The parameter lambda (λ) is the wavelength and 1/ λ the spatial frequency of the cosine factor in Eq. (13). The ratio σ / λ determines the spatial frequency bandwidth.
The interpolation is done using Gabor filter in the following manner. Hexagonal sampled grid has directional symmetry in 0o, 60°, and 120° orientations. Due to these three axes of symmetry of hexagonal grid, we select three different orientation of Gabor filter along in 0o, 60°, and 120°, and the filtering is done in these three orientations (Jeevan et al., 2014). The three filtered images in these three orientations are then superimposed to get the interpolated image.
The filtered image is then decomposed using wavelet to get four sub-bands namely LL, LH, HL and HH. LL is the low frequency sub-band and most of the image details are present in this sub-band. LH, HL, and HH contain high frequency components and henee most of the noises are present in these bands. Therefore, thresholding is done on all the coefficients in LH, HL, and HH sub-bands. This thresholding is done using JeevKrish method which is explained below.
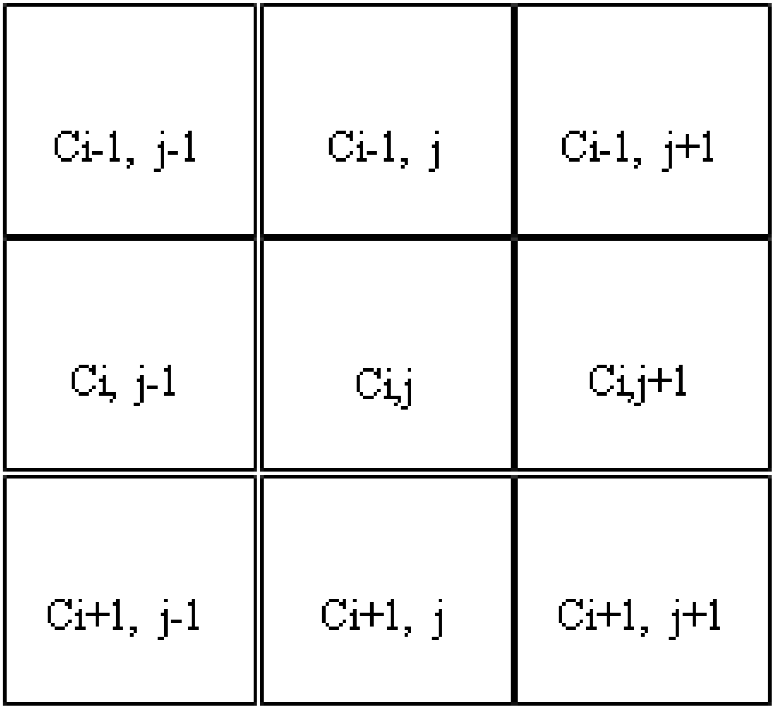
Let Cij be the wavelet coefficients in the sub-band.
Select the neighborhood window as shown in Figure 6 with size 3X3 and C as the center element.
1. Calcúlate
If
else
Where
As explained in Section 2.2 SureShrink is the thresholding method that minimizes the Stein Unbiased Risk Estimator (SURE). This method selects distinct threshold for each sub-band of each level of the wavelet tree and get an optimal threshold valué compared to the universal thresholding. The SureShrink threshold Tsure is expressed as
where 't' represents the valué that minimize the Stein Unbiased Risk Estimator (SURE),
Therefore, the shrinkage rule is; if
The proposed denoising algorithm can be summarized as follows:
Convert the noisy image in rectangular grid to hexagonal grid using altérnate pixel suppressal method.
Perform Gabor filter interpolation on hexagonal grid image.
Perform wavelet decomposition on the image obtained after step 2.
Threshold the wavelet coefficients in the sub-bands LH, HL, and HH using the proposed JeevKrish method choosing 3X3 neighborhood window size.
Perform inverse wavelet transform on the thresholded wavelet coefficient to get the denoised image.
This method gives better results compared to other shrinkage methods like VisuShrink, SureShrink, and NeighShrink and also it is better than the MATLAB denoising function 'wdencmp'.
4. RESULTS AND DISCUSSION
The proposed JeevKrish denoising method is performed on more than hundred images. This paper gives importance for performing denoising using proposed method in hexagonal domain. The hexagonal grid is obtained using altérnate pixel suppressal method and interpolation using Gabor filter. The Gabor filtering is done in three different orientations along in 0", 60", and 120°. This filtering helps to remove noises in high frequency región. The test results for all these images in terms of Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR) indícate that the denoising performance is better in hexagonal domain. In addition to MSE and PSNR, we also used structural similarity (SSIM) for analyzing the performance. SSIM also indícate that the performance is better in hexagonal domain. The performances of proposed method on conventional images are better than the denoising using NeighShrink, VisuShrink and SureShrink_methods. It also performed better than the MATAB de-noising function 'wdencmp' and if we represent the images in hexagonal lattice, the performance of the proposed method again improves and gives better Mean Square Error (MSE) and Peak Signal to Noise Ratio (PSNR). These results confirm that the hexagonal representation is better than the conventional rectangular lattice.
In NeighShrink,
MSE and PSNR, two commonly used measures for quantifying the error between images, are used for the performance analysis. MSE indicate the average difference of the pixel throughout the image. If MSE is higher the difference of the pixel between the original and the processed image is also higher. The MSE between two images P and Q is defined by
where the sum over 'i' and 'j' denotes the sum over all pixels in the images, and 'N' is the total number of pixels in each image. The PSNR between two images is given by
SSIM is another parameter used for the performance analysis. It is used for measuring similarity between two images. "The MSE or PSNR estímate absolute errors on the other hand, SSIM is a perception-based model that considers image degradation as perceived change in structural information, while also incorporating important perceptual phenomena, including both luminance masking and contrast masking terms (Wang Zhou et al, 2004).
The obtained PSNR for five different images are represented in Table 1. Graphical representation of 'MSE vs. σ ' for the image 'elephant.jpg' is shown in Figure 7. Experiments are performed on more than hundred images. Figure 8 (a - f) and Figure 9(a - f) shows the test result for two different images 'car.jpg' with σ = 30 and 'lena.png' with σ = 40. Table 2 gives a comparison of SSIM for conventional square grid images and hexagonal grid images.
Table 1 MSE&PSNR obtained for five different images for different σ
| Noise Level (σ) | Test Images | MATALAB Function (wdencmp | JeevKrish | (Proposed Method) | |||
|---|---|---|---|---|---|---|---|
| Rectangular Grid Image | Rectangular Grid Image | Hexagonal Grid Image | |||||
| MSE | PSNR | MSE | PSNR | MSE | PSNR | ||
| 10 | car.jpg | 17.576 | 35.6816 | 14.7061 | 36.4558 | 2.6659 | 43.8723 |
| elephant.jpg | 30.2087 | 33.3295 | 18.1072 | 35.5523 | 9.6699 | 38.2766 | |
| flower.jpg | 20.141 | 35.09 | 17.6277 | 35.6688 | 2.2797 | 44.5521 | |
| barbara.png | 40.9523 | 32.008 | 25.7547 | 34.0222 | 13.0611 | 36.971 | |
| lena.png | 23.5426 | 34.4123 | 19.979 | 35.1251 | 3.7642 | 42.3741 | |
| 20 | car.jpg | 43.2053 | 31.7754 | 42.5185 | 31.845 | 3.155 | 43.1409 |
| elephant.jpg | 45.6756 | 31.534 | 42.1588 | 31.8819 | 11.7425 | 37.4332 | |
| flower.jpg | 44.7033 | 31.6274 | 44.4646 | 31.6507 | 3.1774 | 43.1101 | |
| barbara.png | 57.7775 | 30.5132 | 52.8348 | 30.9016 | 14.3789 | 36.5536 | |
| Lena.png | 46.6498 | 31.4423 | 46.612 | 31.4458 | 4.6889 | 41.4201 | |
| 30 | car.jpg | 63.6594 | 30.0922 | 63.6157 | 30.0952 | 4.0735 | 42.0311 |
| elephant.jpg | 57.7272 | 30.517 | 55.9205 | 30.6551 | 13.9895 | 36.6728 | |
| flower.jpg | 65.0948 | 29.9943 | 64.7502 | 30.0184 | 5.2854 | 40.9 | |
| barbara.png | 73.0098 | 29.497 | 70.8848 | 29.6253 | 15.7914 | 36.1466 | |
| lena.png | 66.3655 | 29.9114 | 66.0229 | 29.9339 | 5.8342 | 40.471 | |
| 40 | car.jpg | 77.052 | 29.263 | 76.9681 | 29.2677 | 5.9666 | 40.3735 |
| elephant.jpg | 67.7233 | 28.8234 | 65.0718 | 29.9969 | 17.9162 | 35.5983 | |
| flower.jpg | 78.336 | 29.1912 | 78.0755 | 29.2057 | 9.3387 | 38.4279 | |
| barbara.png | 82.6824 | 28.9567 | 81.5699 | 29.0155 | 18.023 | 35.5725 | |
| lena.png | 79.1361 | 29.1471 | 78.3899 | 29.1882 | 7.487 | 39.3877 | |
| 50 | car.jpg | 85.8141 | 28.7952 | 85.8648 | 28.7927 | 6.1066 | 40.2728 |
| elephant.jpg | 73.2895 | 29.4804 | 72.1936 | 29.5458 | 22.0585 | 34.695 | |
| flower.jpg | 86.9257 | 28.7393 | 87.3004 | 28.7206 | 15.3704 | 35.9323 | |
| barbara.png | 90.0086 | 28.588 | 90.0932 | 28.5839 | 22.3416 | 34.6397 | |
| lena.png | 86.9196 | 28.7396 | 87.0679 | 28.7322 | 10.2045 | 38.0429 | |

Fig. 8 (a) Original image (b) Noisy Image a =30, (c) Noisy image in Hexagonal lattice (d) Image after interpolation using Gabor filter (e) De-noised image in Rectangular lattice (f) De-noised image in Hexagonal Lattice.

Fig. 9 (a) Original image (b) Noisy Image a =40, (c) Noisy image in Hexagonal lattice (d) Image after interpolation using Gabor filter (e) De-noised image in Rectangular lattice (f) De-noised image in Hexagonal Lattice.
A statistical analysis is also done for the performance comparison. Analysis of Variance (ANOVA) is used for the analysis of the methods presented in this paper. Data sets used for the statistical analysis and the details of analysis are presented in Table 3, 4 and 5 respectively. between the methods and also it is seen that the average From the table it is clear that the 'F' valué is greater than valué of PSNR is greater for the proposed method. So we 'F-Critical' which indícate there is significant difference can conclude that our method gives better results.
Table 2 SSIM obtained for Square Grid and Hexagonal Grid Images
| Test Images Noise Level (σ) is 20 | SSIM | |
|---|---|---|
| Rectagular Grid Image | Hexagonal Grid Image | |
| Imagel | 0.4869 | 0.6856 |
| Image2 | 0.4771 | 0.585 |
| Image3 | 0.5403 | 0.6496 |
| Image4 | 0.5537 | 0.5818 |
| Image5 | 0.5102 | 0.643 |
| Image6 | 0.5228 | 0.557 |
| Image7 | 0.3889 | 0.6931 |
| Image8 | 0.3855 | 0.673 |
| Image9 | 0.4935 | 0.5865 |
| ImagelO | 0.393 | 0.6008 |
Table 3 Data Sets Used for ANOVA.
| Denoising Using JeevKrish (proposed) Method in Hexagonal Grid Image | Denoising Using JeevKrish (proposed) Method in Rectangular Grid Image | Denoising Using MATLAB Function (wdencmp) | |
|---|---|---|---|
| PSNR for 5 Different test Images (Noise Level σ=10) | 43.8723 | 36.4558 | 35.6816 |
| 38.2766 | 35.5523 | 33.3295 | |
| 44.5521 | 35.6688 | 35.09 | |
| 36.971 | 34.0222 | 32.008 | |
| 42.3741 | 35.1251 | 34.4123 |
Table 4.Analysis of Variance (ANOVA) Summary
| Groups | Count | Sum | Average | Variance |
|---|---|---|---|---|
| Denoising Using JeevKrish (proposed) Method in Hexagonal Grid Image | 5 | 206.0461 | 41.20922 | 11.54664 |
| Denoising Using JeevKrish (proposed) Method in Rectangular Grid Image | 5 | 176.8242 | 35.36484 | 0.794471 |
| Denoising Using MATLAB Function (wdencmp) | 5 | 170.5214 | 34.10428 | 2.137283 |
5. CONCLUSION
We simulated the proposed method and it has been found that the images represented in hexagonal domain gives better results than conventional images. Also the proposed method is better than the denoising function 'wdencmp' used in MATLAB. MSE, PSNR and SSIM are found to be better in hexagonal domain. Combining wavelet and processing of images in hexagonal grid, we achieved a better result than conventional methods, because hexagonal wavelet includes the advantage of hexagonal grid along with the wavelet. Also it gives the missing córner stone of artificial human visual system.
CONFLICT OF INTEREST
The authors have no confliets of interest to declare.











 nueva página del texto (beta)
nueva página del texto (beta)