1. Introduction
Sulfur compounds in diesel fuel can generate SO x during combustion, which would result in health damage and serious environmental problems. Desulfurization of diesel fuel has increasingly gained importance since most of the countries, particularly the developed ones, have implemented more stringent legislation to regulate the sulfur content of transportation fuels (Song & Ma, 2003). Meanwhile, nitrides contained in diesel may produce a significant effect on their stability and have a dominant effect on the color of oil and creation of resins (Sano, Choi, Korai, & Mochida, 2004). Also, organic nitrides in oil product cause air pollution during burning. Refining diesel fuel and improving its stability are of considerable interest currently to meet the increasing needs of higher quality diesel fuel. Therefore, it is urgent to develop the desulfurization and denitrification technologies of diesel fuel. It is therefore particularly meaningful to search for the ideal membrane materials, which can facilitate the diffusion of sulfur compounds and nitric compounds, and restrain the diffusion of non-sulfur compounds and non-nitric compounds.
In this paper, desulfurization and denitrification technologies based on the activated carbon adsorption belong to non-hydrogenation desulfurization and denitrification technologies. In order to improve the activated carbon selective adsorption of sulfur compounds and nitrogen compounds, a layer of polymer film material with high selectivity is coated on the surface of the activated carbon, which ensures the sulfur content and nitrogen content cannot be changed.
However, it is quite difficult and time consuming to explore the proper membranes directly by means of most of the existing experimental techniques. In view of the fact that experimental method of selecting the proper membrane materials is expensive, time consuming and requires a lot of pure samples, the new method using computer simulation technique to screen the optimal membrane materials is presented in this paper. We develop a neural network (NN) pattern recognition (PR) model that can predict polymer membrane diffusion properties directly from adsorbent experimental data.
Pattern recognition is a rapidly evolving and a promising subject in artificial intelligence sciences. In recent years, the theory and method of pattern recognition have been getting more and more attention globally. PR is based on the truth "Birds of a feather flock together" to recognize, discriminate and classify the unknown attribute of things. The basic assumption of pattern recognition is that certain features cause different types of observed things, then they should have some very similar features and similarities make them together in the same pattern space. When the direct connection between the research objective and the influencing factor is unknown, or it is difficult to find out the direct connection with most of the existing theories, pattern recognition is an effective method which can summarize the empirical data and search for the direct and indirect connections between the target and a number of factors and find out the optimized target areas or optimized direction (Jain, Murty, & Flynn, 1999). Pattern recognition technology was firstly used in chemistry and chemical engineering by Kowalski, Bender and Wold in the 1970s (Kowalski & Bender, 1972; Wold & Sjostrom, 1977). With the rapid development of computer technology, pattern recognition produced positive effects in the field of material optimal design. Two main types of statistical pattern recognition methods (nearest neighbor classification and principal component analysis) have been used for material optimal design; however, they have many difficulties in selecting the discriminant function in the multidimensional space (Cardoso, 1999; Chu & Plemmons, 2005; Guan, Tao, Luo, & Yuan, 2012; Kramer, 1991). As a result, the great differences between the classification results and the real experimental data may lead to erroneous conclusions in material optimal design (Kalidindi & Graef, 2015; Panchal, Kalidindi, & McDowell, 2013).
Neural network is an effective modeling method for material optimal design (Kou, Parks, & Tan, 2012; Shabani & Mazahery, 2012; Srinivasan & Saghir, 2013). The neural network for pattern recognition (NN-PR) can get rid of the noise in the sample data, reduce redundant structure, improve the precision and speed of calculation and reduce harm to network error forecasts. Thus, the simulation results will be more accurate and reliable (Chattoraj, Mondal, Das, Roy, & Sadhukhan, 2014; Chen, 2015; Porrazzo, Cipollina, Galluzzo, & Micale, 2013). NN-PR is expected to be a more scientific, advanced and feasible method for material optimal design research. For NN-PR, optimizing and selecting the main parameters are two key factors that effect the recognize results.
The first aim of the present work is to develop a NN-PR model to predict the diffusion behavior of the model diesel components (dibenzothiophene(DBT) and quinoline(QL)) in three different membranes of polyvinyl alcohol (PVA), polyvinyl chloride (PVC) and polymethyl acrylate (PMA) which are coated with active carbon; the second one is to select the effective desulfurization and denitrification agent. Firstly, GA is used to optimize the structure of NN. Then, the NN-PR model is built to get excellent desulfurization and denitrification agent discrimination results. Then, the validity of the NN-PR method is compared and verified with the molecular dynamic (MD) simulation method, which we have done before. Finally, the validity and practicality of the NN-PR method are further determined by comparing the results of the simulating data with the experimental data.
2. Materials and experimental design
2.1. Polymer membrane activated carbon desulfurization and denitrification sorbents
Two main methods for diesel desulfurization are non-hydrodesulfurization (non-HDS) and hydrodesulfurization (HDS). As a non-HDS method, adsorptive desulfurization has the advantages of being low cost, easy to operate and environmentally friendly as well as not reducing the cetane number of diesel fuel, among others.
Also, there are two main methods for diesel denitrification: non-hydrodenitrogenation (non-HDN) and hydrodenitrogenation (HDN). As a non-HDN method, adsorptive denitrogenation has the advantages of being low cost and the simplicity of equipment and operation; however, the capacity of the adsorbent is limited.
In non-HDS and non-HDN, spherical activated carbons are often used as adsorbents. In this study, we mainly improve the selectivity of sulfur compounds and nitrogen compounds under the premise of no changing the activated carbon adsorption sulfur capacity and nitrogen capacity. For this purpose, the surface of activated carbon is coated with a layer of highly selective polymer membrane materials. The diffusion behavior, dynamic selective adsorption and adsorption capacity of DBT and QL are researched in three different polymer membrane systems (PVA, PVC, and PMA). In order to obtain the optimizing desulfurization and denitrification properties, coated active carbon are evaluated by NN-PR model. Meanwhile, the MD method and the adsorption experimental method are discussed and compared.
2.2. Preparation of simulated diesel
Petroleum fractions mainly contain DBT and substituted derivatives under a temperature higher than 300 °C. In this study, DBT was selected as a model diesel sulfur compound component. QL is a toxic, biodegradable organic nitrogen compound and it was selected as nitrogen compound in diesel components. N-octane was selected as the main solvent of the model diesel. In order to make a comparison and take verification tests, two types of model diesel (single-component and two-component) were prepared.
(1) Preparation of the single-component model diesel
Put a certain amount of DBT or QL in a volumetric flask, then add a certain amount of n-octane. The single component solution concentration is 10.0 μmol/g, and then shake the mixture well.
(2) Preparation of the double-component model diesel of the same initial concentration
Weigh a certain amount of DBT and QL and put them in the volumetric flask, then add a certain amount of n-octane. Two of the solution concentrations are 10.0 μmol/g, and then shake the mixture well.
2.3. Single-component and double-component adsorption experimental data
The equilibrium adsorption experiment data including two important parameters of adsorption rate constant and adsorption capacity are shown in Table 1.
Table 1 The equilibrium adsorption data of DBT and QL on the ACStyrene.
| Types | q e,exp (μmol/g) | K (h (μmol/g)−1) |
|---|---|---|
| ACStyrene-DBT | 557.3-588.2 | 0.0527-0.0678 |
| ACStyrene-PVA-DBT | 564.1-592.5 | 0.0638-0.0772 |
| ACStyrene-PMA-DBT | 556.9-590.4 | 0.0636-0.0779 |
| ACStyrene-PVC-DBT | 574.7-593.7 | 0.0634-0.0781 |
| ACStyrene-QL | 317.2-336.4 | 0.0438-0.0512 |
| ACStyrene-PVA-QL | 316.8-359.0 | 0.0457-0.0602 |
| ACStyrene-PMA-QL | 328.4-353.1 | 0.0425-0.0556 |
| ACStyrene-PVC-QL | 312.2-352.6 | 0.0453-0.0581 |
3. Neural network for pattern recognition theoretical methods
3.1. Pattern recognition
In this study, screening technology for desulfurization agent and denitrification agent are based on the intelligent pattern recognition theory. Pattern recognition establishes the perception formed from experience and analyzes the data accumulated by a measurement system. It is a useful method to extract information from data (Nianyi, Wencong, Ruiliang, Chonghe, & Pei, 1999).
Feature selection and extraction are two keys for pattern recognition. In general, the more different types of candidate features we obtain, the better the recognition results should be. Nevertheless, it is difficult to distinguish high dimension features because of the dimension disasters. In this study, the neural network feature extraction method is used for feature selection and extraction, which is a nonlinear filtering characteristic algorithm by calculating contribution ratio of different independent variables forecasting ability.
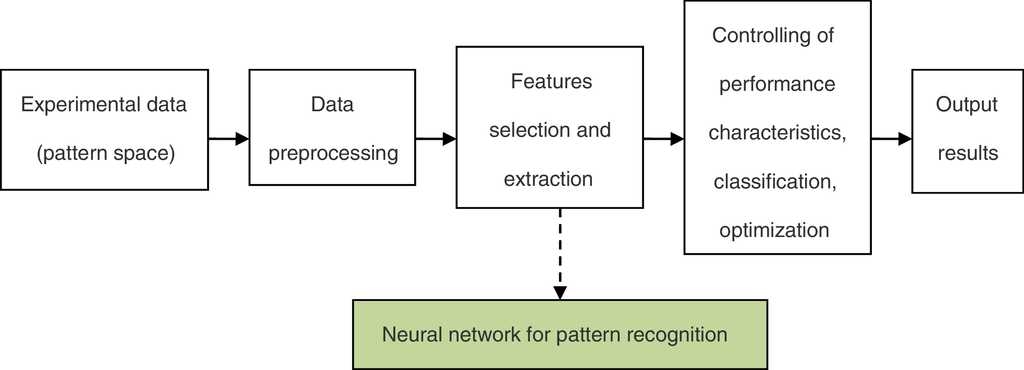
The framework of the neural network for the pattern recognition model is shown in Fig. 1.
3.2. Artificial neural networks
The first artificial neural network was developed by McCulloch and coworkers in the early 1940s (McCulloch & Pitt, 1943). ANN is classified as a non-symbolic artificial intelligence technique, which simulates the human brain and its underlying process is based on graphs and algorithms (Papadopoulos, Beligiannis, & Hela, 2011). In the last few decades, some important researches have been reported in the field of ANNs and their efficiency has been proven in various applications in the fields of engineering. The learning modes of neural networks from the input samples make them very suitable for solving pattern recognition problems, which are one of the successful application areas of neural networks (Christopher, 1995).
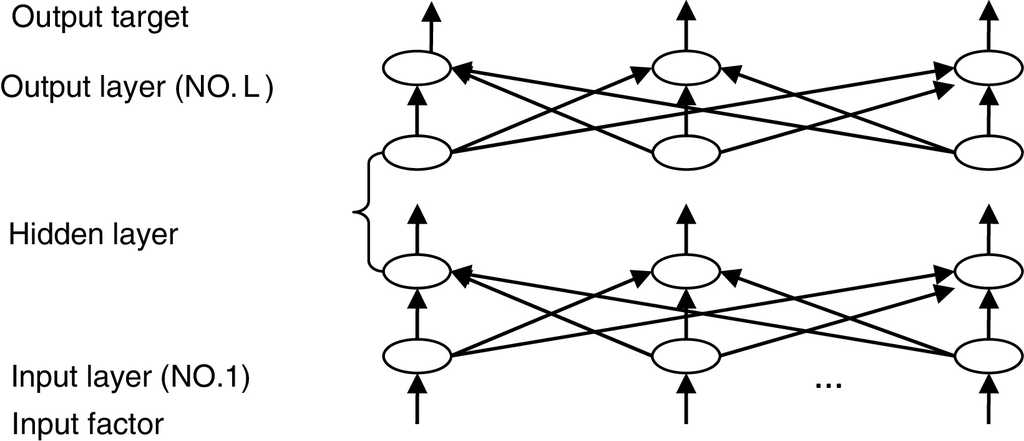
The most widely used training algorithm of NNs is the back-propagation (BP) algorithm, which is a gradient-based method. The basic structure of BPNN is shown in Fig. 2.
Usually, BPNN is represented by the following model:
where pot (l ) (l = 1, 2, ..., L ) is the node number of each layer. Êj is the estimated value of the design objective. The hidden layer error is determined by the back propagating algorithm. The BP algorithm is repeated several times until obtaining the reasonable residual error. The steps of the optimization procedure and the learning algorithm are detailed in Perlovsky (2001).
3.3. Neural network for pattern recognition
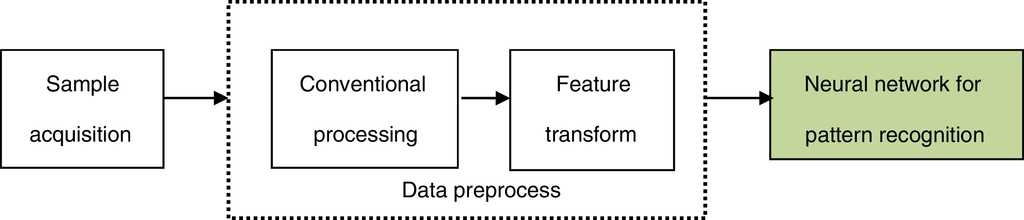
In the neural network for pattern recognition, firstly, known samples are used to train the neural network, which can give different outputs corresponding to different kinds of inputs. Then, the unknown samples can be distinguished by the trained NN-PR model. The flow chart of the neural network for pattern recognition is shown in Fig. 3.
The roles of the main parts of NN-PR are as follows:
(1) Sample acquisition
This step is mainly used to get a certain amount of training and recognizing samples.
(2) Conventional processing
The role of this step is equivalent to the data acquisition and conventional processing of the traditional pattern recognition, namely, by effective observing and quantitative sampling to obtain a series of data, and then the original samples are obtained and simulated by removing noise.
(3) Feature transform
In this step, feature transformation is presented by the neural network based on the original samples. The role of this step is similar to feature selection and extraction of the traditional pattern recognition, but the original samples are processed by neural network.
The above two steps are the data preprocess of the neural network for pattern recognition.
(4) Neural network for pattern recognition
Varying recognized objects and research problems, the neural network is trained by choosing anappropriate network structure and learning algorithm.
After the training process, the network is equivalent to a fixed mapping, and new input samples (test samples) can be mapped to different types according to the different data.
4. Neural network for pattern recognition model
In this study, firstly, the original adsorption experimental data were normalized to [0 1]. Next, the normalized data were trained by BP network to get the predicted data. Then, the predicted data were recognized and classified by pattern recognition. Finally, optimal desulfurization agent and denitrification agent were selected based on NN-PR model.
4.1. Optimizing the neural network for pattern recognition
Any continuous function can be approximated with a single hidden layer BP network. In generally, any mapping mode (from M -dimensional to N -dimensional) can be recognized by a three-layer BP neural network based on Kolmogorov theory (Hanafizadeh, Zavasan, & Khaki, 2010; Kolmogorov, 1963). In this network, the input layer includes two adsorption factors: adsorption rate constant and adsorption capacity, and the output layer is the adsorption comprehensive performance mode. NN is highly sensitive to the number of hidden layer neurons. There are no theoretical formulas used to compute the number of hidden cells, and it is often selected by experiential Eq. (2):
where n is the number of hidden nodes. m and k are the numbers of input nodes and output nodes, respectively; a is a constant between 1 and 10. According to experience, the more hidden nodes in the NN, the better prediction result will be obtained. However, the NN configuration will be more complictated. The number of hidden nodes should be no less than the total number of input and output nodes. According to Eq. (2), the number of hidden nodes is designated as 4.
The optimizing NN-PR model is implemented by using Matlab programming software. The basic parameters are shown in Table 2. The parameters are debugged to improve the accuracy and speed of convergence.
Table 2 Basic parameters of the neural network for pattern recognition.
| Basic parameters | Debugged value |
|---|---|
| Target error | 0.001 |
| Transfer function | Sigmoid |
| Nodes of hidden layer | 4 |
| Activation function | Tansig |
| Weight | 0.5 |
| Bias | 0.5 |
| Momentum factor | 0.92 |
| Number of epochs | 170 |
Fig. 4 is the network training error curve. The network has reached accuracy after 170 times which is set as the number of epochs.
4.2. Denoting two grades
To distinguish different modes based on pattern recognition, a set of input sample data can be mapped to an output vector. By using the adsorption rate constant and adsorption capacity as two criterions (superior class and inferior class) and the comparison standards, we can get the following classifications: For DBT, the data range DBT q > 575 μmol/g and K > 0.0636 h (μmol/g)−1 are superior class points (the output values are set as 1) and denoted as grade I; others are inferior class points (the output values are set as 0) and denoted as grade II. For QL, the data range q > 320 μmol/g and K > 0.0462 h (μmol/g)−1 are superior class points, and denoted as grade I; others are inferior class points and denoted as grade II. There are eight types of ACStyrene (the adsorption performance) date are distinguished for different modes, and each ACStyrene data set include 10 for training and 5 for testing. There are 80 training data and 40 testing data are used for the implementation of the NN (shown as Table 3). For any unknown samples, the grade can be recognized correctly according to what kind of point is close to.
Table 3 Recognize results of activated carbon coating materials adsorption comprehensive performance.
| No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ACStyrene-DBT | II | II | II | I | II | II | I | II | II | I | I | II | II | I | I |
| ACStyrene-PVA-DBT | II | II | II | II | II | II | II | II | II | II | II | II | II | II | II |
| ACStyrene-PMA-DBT | II | II | II | II | II | II | II | II | II | II | II | II | II | II | II |
| ACStyrene-PVC-DBT | I | I | I | I | I | II | II | II | II | I | I | I | II | I | II |
| ACStyrene-QL | I | II | II | II | II | II | I | II | II | I | II | I | II | II | II |
| ACStyrene-PVA-QL | II | I | I | II | I | I | I | II | I | I | II | I | II | I | I |
| ACStyrene-PMA-QL | II | II | II | II | II | II | I | II | II | I | II | II | II | II | II |
| ACStyrene-PVC-QL | II | II | II | II | II | II | II | II | II | II | II | II | II | II | II |
4.3. Recognized results
The recognized results of activated carbon coating materials adsorption comprehensive performance are shown in Table 3.
From Table 3, DBT adsorbability of activated carbon coated with PVC is higher than the original activated carbon. For example, sample No. 1, DBT adsorbability increased from grade II (q is 560 μmol/g and K is 0.0527 h (μmol/g)−1) to grade I (q is 582 μmol/g and K is 0.0639 h (μmol/g)−1), while the adsorption rate of QL decreased from graded I to grade II (q is 555 μmol/g and K is 0.0438 h (μmol/g)−1). The main reason for their changes is that PVC coated on the surface of the spherical activated carbon is good for the diffusion of DBT, while bad for the diffusion of QL, which may be related to the interaction of functional groups, which indicates that PVC film has a better permeability to DBT.
Also, it can be seen from Table 3 that the activated carbon coated with polyvinyl alcohol could increase the adsorption rate of QL and decrease the adsorption rate of DBT, which shows that PVA film has a better permeability to QL.
5. Comparative study of molecular dynamic simulations method
To verify the accuracy and effectiveness of NN-PR, theNN-PR model results were compared and discussed with the results of the MD method.
5.1. Molecular dynamic simulations
Molecular dynamics simulations (Frenkel & Smit, 2001) are widely used for computer simulations of large and complex calculating systems. The basic principle of MD simulation is to set up an appropriate system based on Newton's motion laws, statistical thermodynamics and statistical physics principle, and to calculate the macroscopic physical properties through the trajectory of the system.
In the past 20 years, with the rapid development of the molecular simulation technique, the technique has become an important tool to study the molecular structure of the polymer membrane material and the mechanism of adsorption and diffusion in the polymer membrane. The development of molecular dynamics simulations provided huge impetus for researching the microscopic mechanisms for permeation of molecules dissolved in the polymer film. MD would explain the way in which a variety of factors affected the separation performance on the molecular scale; whilst the molecular simulation technique can provide a feasibility study, process optimization and material properties screening prediction before the experiment (Tamai, Tanaka, & Nakanishi, 1995).
In this study, molecular dynamics simulation was used to investigate the diffusion behavior of the model diesel components in three different membranes. In accordance with the real diesel environment, DBT and QL were selected as representatives of sulfur and nitrogen compounds. The diffusion coefficients of DBT and QL in three different membranes were calculated by Einstein equation. Then, in order to get and verify the most favorable diesel desulfurization and denitrification membrane systems, a comparison of the diffusion selectivity of the three different molecular membranes was performed.
5.2. Results of the molecular dynamics simulations
In the MD method, diffusion coefficients are used to study diffusional adsorption performance of DBT and QL in different PVA, PVC and PMA membrane systems. Mean square displacement (MSD) curves obtained by the MD method are used to analyze and calculate the diffusion coefficients.
Diffusion of molecules in the polymer film system can be calculated by MSD as shown in Eq. (3)
where r i (t ) is the position coordinate of the molecule i at t point, and r i (0) is the initial position coordinate of the molecule i .
The relationship between the diffusion coefficient (D ) and MSD can be expressed as Eq. (4) which is the exponential form of Einstein equation (Konduri & Nair, 2007):
where D is the diffusion coefficient; d is set as 3 and is the dimension of molecules' random motion; α is the exponent; and t is time.
The results for the diffusion coefficients are shown in Table 4. To provide scientifical theoretical support, the single-component system, which DBT and QL exist alone, and the double-component system, which DBT and QL exist together, are studied together.
Table 4 Diffusion coefficients of DBT and QL in different PVA, PVC and PAM membrane systems.
| Membrane systems | D DBT (D × 10−9 m2/s) | D QL (D × 10−9 m2/s) |
|---|---|---|
| PVA (single-component) | 0.068 | 0.182 |
| PVA (double-component) | 0.088 | 0.278 |
| PVC (single-component) | 0.210 | 0.147 |
| PVC (double-component) | 0.223 | 0.190 |
| PAM (single-component) | 0.143 | 0.250 |
| PAM (double-component) | 0.125 | 0.180 |
According to Table 4, when the DBT and QL exist alone, the DBT diffusion coefficients are lower than the QL diffusion coefficients in the PVA and PMA membrane systems; which means that the relative concentration of the DBT is higher than that of QL. They are the same as in the double-component PVA and PMA membrane systems. While in the PVC membrane system, the DBT diffusion coefficients are higher than the QL's both in the PVC single-component or in the PVC double-component. Therefore, it can be concluded that the PVC is advantageous for removing sulfur compounds in diesel fuel, which is the same as the result of the NN-PR method.
Also, according to the diffusion coefficient of the molecules in Table 4, it can be seen that the QL diffusion coefficients are lower than the DBT diffusion coefficients in the PVC membrane systems when the DBT, or QL, exists alone; which are the same as in the double-component PVC membrane systems, while in the PVA and PMA membrane systems, the QL diffusion coefficients are higher than those of the DBTs, whether they are in single-component or in double-component solutions; thus, it can be concluded that the PVA and PMA membranes are advantageous for removing nitrogenous compounds in diesel fuel. But, which one is better than that of the PVA or PMA membrane?; further comparisons of the diffusion selectivity of the different membranes are needed.
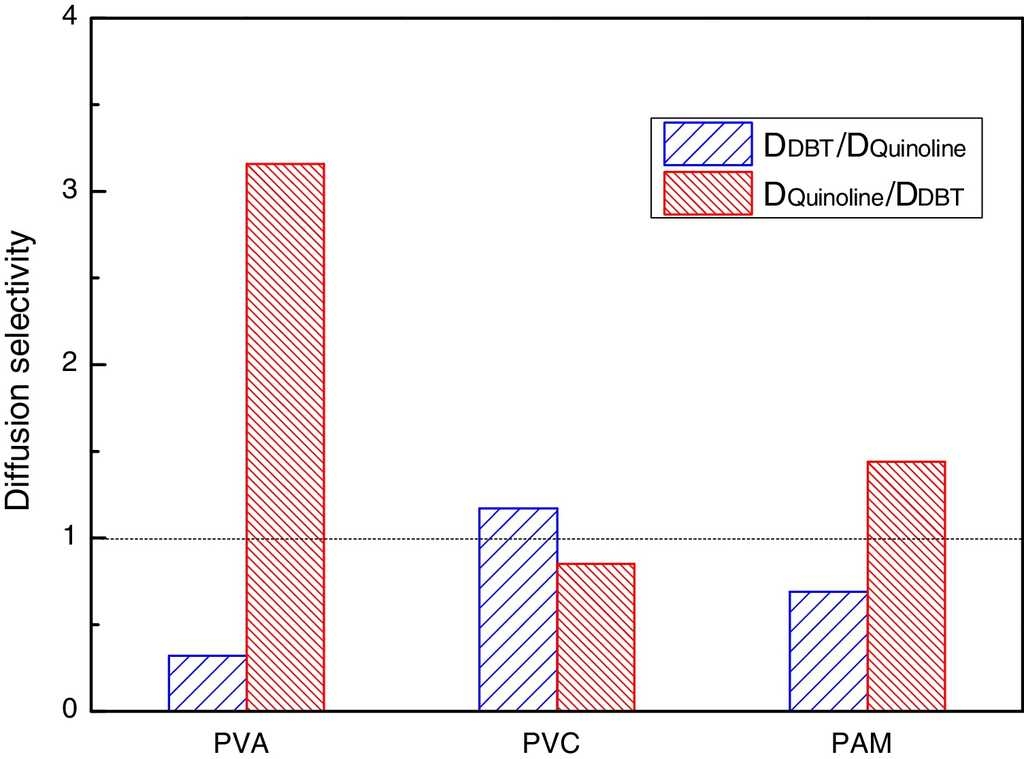
In order to get the optimal denitrification membrane, a comparative study of the diffusion selectivity in the double-component solute systems of different molecular diffusion membranes is done by the MD method. The results of two types of diffusion selectivity are shown in Fig. 5, one is the QL-DBT selectivity D DBT /D QL , and the other one is the DBT-QL selectivity D QL /D DBT .
From Fig. 5, it can be seen that D DBT /D QL is greater than 1 in the PVC; while in PVA and PMA, D DBT /D QL is less than 1. Also, it can be seen that D QL /D DBT is greater than 1 in PVA and PMA membrane systems, especially for the PVA membrane, while for the PVC membrane, D QL /D DBT is less than 1. The results suggest that PVA is advantageous for diesel denitrifying, and hence it was selected as the optimal denitrification membrane. Again, it was verified that the PVC film was advantageous for diesel desulfurizing, which fully agrees with the result of the NN-PR method.
6. Experimental verification
To further validate the results of the NN-PR method, the DBT and QL adsorption behaviors of styrene-based spherical activated carbon coated with PVC and PVA were investigated by experimental research. The breakthrough curve is the main tool to research the adsorption behavior in the experimental method. By analyzing fixed bed dynamics adsorption experiments, the breakthrough curves obtained were as follows:
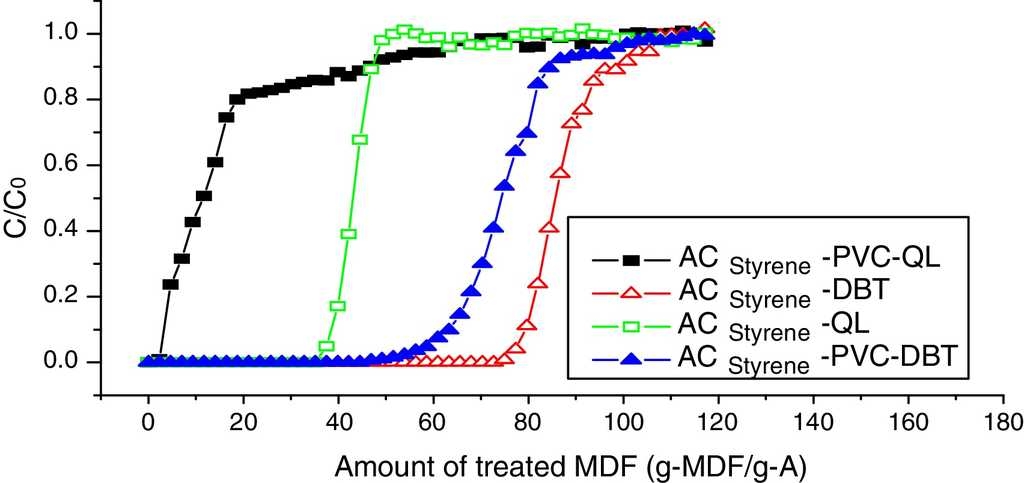
6.1. Breakthrough curves coated with PVC
Dynamic adsorption breakthrough curves of DBT and QL of styrene-based activated carbon spheres coated with PVC are shown in Fig. 6. It can be seen that the adsorption volumes of DBT and QL decreased at the penetrating point after being coated with PVC. DBT is decreased from 77.0 g-MDF/gA to 58.0 g-MDF/gA, and QL is decreased from 38.0 g-MDF/gA to 7.0 g-MDF/gA. Nevertheless, the penetrating time (from the penetrating point to the saturation point) of QL is longer than that of DBT, which indicates that the adsorption rate of DBT will increase, while the adsorption rate of QL will decrease; hence, the PVC membrane can enhance the proliferation of DBT, which also shows that PVC is fit for removing sulfur compounds in diesel fuel.
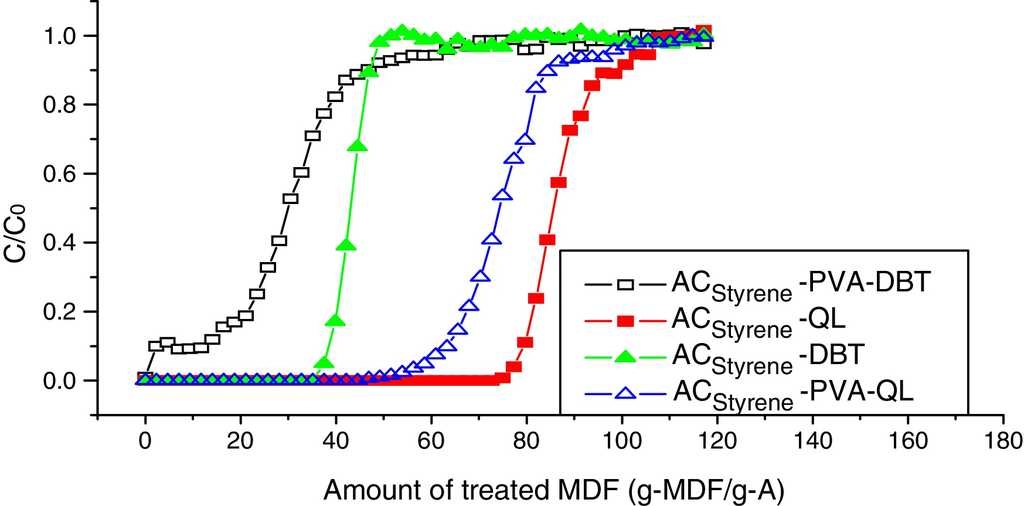
6.2. Dynamic adsorption breakthrough curves coated with PVA
Dynamic adsorption breakthrough curves of DBT and QL of styrene-based activated carbon spheres coated with PVA are shown in Fig. 7. It can be seen that adsorption volumes of DBT and QL have been decreased drastically at the penetrating point after being coated with PVA. Also, the penetrating time of DBT is longer than that of QL, which indicates that the QL adsorption rate is slightly increased, while the DBT adsorption rate is significantly decreased. It was verified that PVA is fit for removing nitrification compounds in diesel fuel.
7. Conclusions
In this paper, the diffusion selectivities of DBT and QL in the three polymer membrane systems (PVA, PVC, and PMA) are investigated based on NN-PR. Adsorption capacity constant and adsorption rate are selected as double criteria and two grades are selected as the comparison standard. The results show that PVC membrane can improve the diffusion selectivity of DBT, which also shows that PVC membrane is advantageous to remove sulfur compounds in diesel fuel, while PVA membrane can increase the diffusion selectivity of QL and it is advantageous for the removal of nitrogen compounds.
Then, MD is used to study the diffusion behavior of DBT and QL, and its influencing factors, in three different polymer membrane systems (PVA, PVC, and PMA). The same conclusion can be drawn by investigating the diffusion coefficient and free volume fraction of diffusion molecules at the molecular level. Though the principle and method of NN-PR and MD are totally different, the same conclusion is reached, which can ensure the high accuracy of NN-PR. Also, NN-PR carries more advantages: it yields more intuitive conclusions and it is not necessary to establish an adsorption kinetics model.
By comparing the NN-PR method with the experimental data, it can be determined that the results of the NN-PR method are consistent with the experimental results, which also confirms that the NN-PR method can be well used to predict and determine the diffusion behavior of the polymer membranes in model diesel. Moreover, this approach can be used as an alternative to the experimental method thereby reducing the related cost.











 nueva página del texto (beta)
nueva página del texto (beta)