1. Introducción
Hasta principios de la década de los años ochenta, las crisis financieras eran consideradas eventos aislados que ocurrían en mercados individuales sin una naturaleza sistémica, razón por la cual la literatura económica y financiera sobre el mecanismo de transmisión de los choques recibió poca atención hasta la década de los años noventas, Boffelli y Urga (2016). Como consecuencia de diversas reformas implementadas en los años noventa en muchas economías emergentes, las cuales promovían una mayor apertura comercial y la eliminación de controles de capitales, se registró una creciente interdependencia económica y financiera. En esta misma década se presentaron diversas crisis financieras ―las crisis de los tipos de cambio europeos en 1992, mexicana de 1994-95, asiática de 1997-98, rusa de 1998 y brasileña de 1999. Las consecuencias negativas asociadas con los periodos de inestabilidad no se limitaron a los países de origen, se transmitieron rápidamente a varios mercados internacionales en todo el mundo.
Es en este contexto que la literatura sobre el contagio financiero comienza a desarrollarse. No hay una definición exacta de contagio financiero. No obstante, una de las más aceptadas es la propuesta por Forbes y Rigobon (2002), quienes definen contagio como un incremento significativo en los vínculos entre los mercados después de un choque a un país o a un grupo de países, otra forma de concebirlo es como un aumento anómalo en la intensidad de las relaciones causales, Gómez y Sosvilla (2016).
El estudio de la transmisión de choques es importante porque tiene diversas implicaciones: i) incide en la administración de portafolios, particularmente en la diversificación del riesgo internacional; ii) adquiere mayor relevancia dada la creciente interdependencia de los mercados financieros internacionales y iii) es crucial para una mejor comprensión de la efectividad de las intervenciones de las instituciones financieras en el contexto de crisis, Boffelli y Urga (2016).
El contagio se ha abordado básicamente desde dos enfoques. El primero de ellos denominado “contagio basado en los factores fundamentales”, el cual tiene lugar si dicho incremento anormal puede explicarse por fundamentos macroeconómicos, vínculos financieros o choques regionales o globales. Mientras que el segundo, “contagio puro” se activa únicamente por un cambio en los sentimientos idiosincrásicos del mercado, Gómez y Sosvilla (2016).
En 2008-2009, Estados Unidos experimentó la peor crisis financiera desde la Gran Depresión. Esta crisis comenzó en Estados Unidos con el estallido del mercado hipotecario subprime y el desvelamiento del proceso de bursatilización en el verano de 2007 que se había construido para financiar esas hipotecas. Pronto quedó claro que esta crisis no solo habría tenido profundas consecuencias en los Estados Unidos, sino que también habría influido en cada región del globo.
En el período previo a la crisis financiera subprime estadounidense, los bancos de los países afectados invirtieron en bonos que ofrecían altos rendimientos pero estaban respaldados por hipotecas de baja calidad. Cuando la crisis comenzó en el país de origen, estos bancos perdieron automáticamente sus inversiones a través de la reducción de precios de los activos, Ueda (2012). Al enfrentar el riesgo de liquidez cubriéndose en un mercado interbancario mundial, la transferencia del riesgo de crédito puede desembocar en una crisis de mayores proporciones, Allen y Carletti (2006).
Tras la crisis de alto riesgo (2007), la crisis financiera mundial (2008-2009) y la gran depresión económica (2009), se observó que varias pérdidas de mercado y quiebras bancarias conllevan un considerable riesgo sistémico, un grave riesgo soberano y grandes crisis de deuda y confianza para varias economías desarrolladas y emergentes. Para limitar los efectos de tales crisis, salvar el sistema bancario y los mercados financieros, mejorar la gestión de riesgos y controlar el crédito y los mercados financieros, Basilea III y la Comisión Europea introdujeron nuevas reformas y medidas de regulación financiera, Hemche, Jawadi, Maliki y Cheffou (2016).
Con el propósito de determinar si la crisis de las hipotecas subprime contagió a los principales mercados accionarios de América Latina: Argentina, Brasil, México y Chile a través del mercado accionario más representativo de los Estados Unidos, empleamos un modelo GARCH multivariado para los residuos de la dinámica de los rendimientos de los mercados accionarios de Argentina (MERVAL), México (IPyC), Brasil (IBOVESPA) y Chile (IPSA) y de Estados Unidos (S P500). Este modelo es apropiado para medir correlaciones condicionales variables en el tiempo siguiendo la propuesta de Chiang, Jeon y Li (2007). Esta metodología tiene la ventaja de que nos permitirá abordar el problema de heterocedasticidad planteado por Forbes y Rigobon (2002) sin dividir arbitrariamente la muestra en dos subperíodos. Además de esta introducción, el artículo contiene una revisión sucinta del estado del arte en lo que concierne al escrutinio empírico, la metodología econométrica utilizada, el análisis de los resultados empíricos y la conclusión a la que nos inducen nuestros hallazgos.
2. Revisión de la literatura empirica
Diversos estudios han empleado el modelo GARCH multivariado con correlaciones dinámicas condicionales (DCC) propuesto por Engle (2002). Por ejemplo, Chiang, Jeon y Li (2007) aplican el modelo de correlaciones dinámicas a los rendimientos diarios de nueve mercados accionarios de 1990 a 2003. Sus resultados muestran evidencia de contagio del mercado accionario de Estados Unidos a los mercados accionarios de Asia (Tailandia, Malasia, Indonesia, Filipinas, Corea del Sur, Taiwan, Hong Kong y Hong Kong). Todos los índices accionarios están medidos en moneda local. Con el analisis de los coeficientes de correlación identifican dos fases de la crisis asiática. La primera muestra un incremento en la correlación (contagio), mientras que la segunda muestra una continua alta correlación (conducta de rebaño). El análisis estadístico de los coeficientes de correlación también encuentra un cambio en la varianza durante el periodo de crisis, lo cual, a decir de los autores, pone en duda los beneficios de la diversificación internacional de portafolios. La evidencia encontrada por estos autores muestra que las agencias calificadores juegan un papel importante en la configuración de la estructura de las correlaciones dinámicas en los mercados asiáticos.
De igual forma, Syllignakis y Kouretas (2011) analizan el contagio entre los mercados bursátiles de Estados Unidos, Alemania, Rusia y un grupo de países de Europa Central y Oriental. Uno de los principales resultados de su estudio es que encuentran un aumento estadísticamente significativo en las correlaciones condicionales entre los rendimientos accionarios de Estados Unidos y de Alemania y los rendimientos de los países de Europa Central y Oriental, en particular durante la crisis financiera de 2007-2009, lo que implica que estos mercados emergentes están expuestos a los choques externos con un cambio sustancial de régimen en sus correlaciones condicionales.
Kenourgios y Samitas (2011) aplican el modelo DCC-GARCH asimétrico generalizado (AG) (1,1) de Cappiello, Engle y Sheppard (2006) para confirmar el aumento de las correlaciones dinámicas entre cinco mercados de valores emergentes de los Balcanes, los Estados Unidos y tres países desarrollados europeos mercados durante la crisis financiera internacional; también consideran las asimetrías en la dinámica de las correlaciones. Ellos concluyen que la mayor interdependencia de los mercados accionarios se debe al comportamiento "de rebaño o de manada" durante el período de crisis. Kenourgios, Samitas y Paltalidis (2011) amplían este trabajo para investigar las correlaciones condicionales de cinco eventos de crisis financiera de 1995 a 2006 para los BRIC, Estados Unidos y el Reino Unido utilizando varios modelos DCC así como el original de Engle (2002) y el AG-DCC. Kenourgios y Padhi (2012), a su vez, estiman modelos AG-DCC para estudiar las correlaciones durante los períodos de crisis entre 1994 y 2008 en nueve mercados emergentes, Estados Unidos y dos índices globales. A través del análisis de cointegración y de corrección de errores los autores encuentran evidencia de relaciones de corto y de largo plazos sólo entre las bolsas emergentes durante las crisis rusa y asiática, tanto para los mercados accionarios como para los de bonos durante la crisis subprime y no encuentran evidencia de impacto alguno de la turbulencia argentina en ninguno de los mercados examinados. El análisis posterior efectuado por los autores en un marco asimétrico multivariable proporciona evidencia sobre el impacto global del incumplimiento de Rusia, los efectos de contagio de la crisis subprime, el aspecto regional de la crisis asiática y de la turbulencia argentina. A partir de estos resultados concluyen que los mercados bursátiles parecen constituir un mecanismo de transmisión más fuerte durante las tres crisis más contagiosas.
Horvath y Poldauf (2012) investigan los co-movimientos de los mercados accionarios de Australia, Brasil, Canadá, China, Alemania, Hong Kong, Japón, Rusia, Sudáfrica, el Reino Unido y Estados Unidos, tanto a nivel agregado como a nivel sectorial en el periodo de 2000 a 2010, utilizando modelos GARCH multivariados. Sus resultados sugieren que la correlación entre los rendimientos accionarios durante la crisis financiera (2008-2010) se incrementó, sugiriendo que la crisis financiera internacional representó un shock común para todos los países. Además, encontraron que el mercado de valores de Estados Unidos es el más correlacionado con los mercados bursátiles de Brasil, Canadá y el Reino Unido. La correlación de los mercados de valores de Estados Unidos y China es en esencia igual a cero antes de la crisis, y se vuelve ligeramente positivo durante la crisis. Los índices sectoriales están menos correlacionados que los índices de mercado durante todo el período, pero, una vez más, las correlaciones aumentan durante la crisis.
Kazi, Guesmi y Kaabia (2011) investigan el efecto de contagio entre los mercados bursátiles de Estados Unidos y dieciséis países de la OCDE debido a la crisis financiera mundial (2007-2009). Para tal fin, estiman las correlaciones condicionales dinámicas a través de un modelo GARCH multivariado con los rendimientos diarios de los precios accionarios. Para identificar el contagio, prueban si la media de los coeficientes de las correlaciones dinámicas en el período de crisis difiere de la del período previo a la crisis, cuyo punto de quiebre de la crisis es identificado por la prueba de Bai-Perron (1998, 2003). Sus resultados muestran un aumento significativo en la media del coeficiente de correlación condicional dinámico entre los mercados bursátiles de Estados Unidos y la mayoría de los países de la OCDE analizados durante el período de crisis. De lo cual concluyen que hay evidencia de contagio entre los mercados bursátiles de Estados Unidos y la OCDE.
Horvath y Poldauf (2012), con datos de 50 mercados accionarios, con el modelo DCC aumentado examinan las correlaciones condicionales e incondicionales en torno a dos eventos bancarios importantes durante la crisis financiera de 2008-09, a saber, la adquisición de Bear Stearns por JP Morgan y el colapso de Lehman Brothers; concluyen que si bien la adquisición de Bear Stearns por parte de JP Morgan tuvo un impacto insignificante en las correlaciones bursátiles en todas las regiones, el efecto sobre la interdependencia del colapso de Lehman Brothers fue considerable, mientras que sus resultados de los análisis de correlación incondicional y condicional sugieren que el impacto de la crisis financiera en los mercados bursátiles es significativo para todas las regiones. Kotkatvuori-Örnberg, Nikkinen y Äijö (2013) también investigan el impacto de estos dos eventos mediante variables ficticias en la ecuación de la varianza incondicional de una GARCH (1,1) multivariado con datos de cincuenta índices bursátiles para el periodo de 2007 a 2009. Posteriormente, estiman el modelo DCC en seis especificaciones multivariadas para cada región y las correlaciones resultantes son utilizadas para estimar GARCH(1,1) multivariados con las mismas dummies para el intercepto en la media y en la varianza. Sus resultados muestran que el impacto de la crisis es significativo en los comovimientos y especialmente el efecto del colapso de Lehman Brothers es prominente en todas las regiones.
Kenourgios y Dimitriou (2015) investigan los efectos de contagio de la crisis financiera mundial (2007-2009) analizando diez sectores en seis regiones emergentes y desarrolladas durante las diferentes fases de la crisis. De esta forma, prueban diferentes canales de contagio financiero en regiones y sectores de economía real con base en las correlaciones condicionales dinámicas del modelo multivariado Fraccionalmente Integrado Asimetrico (FIAPARCH). Sus resultados muestran la región desarrollada del Pacífico; en particular, algunos sectores de bienes de consumo, salud y tecnología en todas las regiones parecen verse menos afectados por la crisis, mientras que los sectores más vulnerables se observan en las regiones emergentes de Asia y Europa. Además, el análisis en el periodo de crisis indica que los efectos de contagio más graves ocurren después del fracaso de Lehman Brothers, lo cual, sostienen, limita la efectividad y los beneficios de la diversificación de los potafolios.
A través de un GARCH Multivariado con correlaciones dinámicas condicionales, Bejarano, Gomez, Melo y Torres (2015) investigan si los mercados accionarios de seis países de América Latina -Argentina, Brasil, Colombia, Chile, México y Perú- se contagiaron en tres periodos de crisis: (i) el de la burbuja de las "empresas punto com" registrada entre el 4 de julio de 2001 y el 27 de septiembre de 2002; (ii) la crisis financiera internacional ubicada del 26 de septiembre de 2008 al 29 de septiembre de 2009 y (iii) la crisis de los bonos soberanos europeos que se presentó del 13 de julio de 2011 al 16 de enero de 2012. Con tal fin, Bejarano et al. (2015) estiman regresiones individuales para las correlaciones dinámicas de los mercados accionarios de cada país con respecto al de Estados Unidos y tres dummies diferentes correspondientes a cada uno de los periodos anteriormente mencionados. Sus resultados muestran evidencia de contagio financiero para Argentina, Chile, México y Perú en el caso de la crisis financiera internacional y para la totalidad de los mercados analizados en el caso de la crisis de los bonos soberanos europeos.
Romero, Bonilla, Benedetti y Serletis (2015) utilizan la prueba de Hinich (1996) de bicorrelación portmanteau para identificar eventos nolineales detectados en los mercados accionarios de América Latina. Esta prueba les permite identificar el inicio, el final, la intensidad y la persistencia de esos episodios no lineales. Los seis episodios identificados en el período comprendido entre enero de 1994 a noviembre de 2012 coinciden con las crisis financieras internacionales, lo que les permite especular que el contagio causado por las crisis financieras induce dependencias no lineales.
Mollah, Quoreshi y Zafirov (2016) muestran evidencia de contagio del mercado accionario de Estados Unidos a los mercados mundiales para las dos crisis mundiales registradas en el periodo 2003-2013. Los autores revelan que la transferencia de riesgo bancario entre Estados Unidos y otros países es el mecanismo de transmisión clave que explica las correlaciones entre países.
Wang, Xie, Lin y Stanley (2017) proponen un estadístico de contagio de correlación multiescala para evaluar el contagio de los mercados de valores durante la crisis financiera mundial de los Estados Unidos a seis paises del G7 y de los BRICS. Sus resultados muestran que las correlaciones cruzadas entre el mercado accionario de Estados Unidos y el de los países seleccionados están condicionadas a la escala de tiempo. Uno de sus principales resultados es que el contagio de Estados Unidos a Japon, China y Brasil ocurre cuando la escala de tiempo es mayor a 50 días o más.
A partir de la metodología propuesta por Hatemi y Hacker (2005), Rodriguez (2018) somete a prueba la hipotesis de contagio financiero de los mercados accionarios más representativos de Estados Unidos a los principales mercados accionarios de América Latina. Sus resultados muestran evidencia de contagio unicamente para los mercados de Argentina y Brasil, y para el caso de México sus resultados no son concluyentes.
Polanco, Fernández y Neumann (2018) efectuan un análisis de los índices bursátiles periféricos de la Unión Europea (España, Grecia, Irlanda, Italia y Portugal) en relación con el índice S P Europe 350 (SPEURO) durante los periodos de pre-crisis (2004-2007) y de la crisis de 2008-2011. Ellos calculan una correlación espectral con ventanas moviles para los rendimientos accionarios y aplican pruebas no lineales de causalidad de Granger a los coeficientes de la descomposición espectral de los rendimientos. Sus resultados muestran que la correlación es más fuerte para el periodo de crisis que para el periodo previo y que los índices bursátiles de Portugal, Italia y España estuvieron más interconectados entre sí durante la crisis que con el SPEURO. Las pruebas de causalidad no lineal indican que en las primeras tres escalas de onduletas (wavelets) (intrasemanal, semanal y quincenal) el número de causalidades unidireccionales y bidireccionales es mayor durante la crisis que en el período previo, lo cual ellos atribuyen al contagio financiero.
3. Metodología Econométrica
La metodología econométrica usada en este trabajo es la propuesta por Chiang, Jeon y Li (2007), quienes sugieren emplear un modelo GARCH multivariado de correlaciones dinámicas condicionales (DCC, por sus siglas en inglés). La metodología consiste en estimar la matriz de correlaciones variables en el tiempo de los residuos estandarizados de un sistema de ecuaciones para los niveles de los rendimientos de un conjunto de activos. Esta es una forma de enfrentar el problema de la heterocedasticidad planteada por Forbes y Rigobon (2002) sin dividir la muestra arbitrariamente en dos subperiodos. Otra ventaja de esta técnica es que no requiere especificar el país donde se originó la crisis debido a que se estiman todos los coeficientes de la matriz de correlación. De esta forma es posible probar contagio puro o financiero como un incremento en las correlaciones entre cada par de países y no sólo entre el país donde inició la crisis y el resto de los países. La propuesta de Chiang, Jeon y Li (2007) se basa en el siguiente sistema de ecuaciones para las trayectorias de los rendimientos de los activos:
Donde
donde la matriz de correlaciones condicionales
los elementos de la matriz
Independientemente del tipo de objetivo de varianza que se elija, es posible adoptar el procedimiento de estimación en dos pasos (Boffelli y Urga, 2016). En el primer paso, se estiman m modelos GARCH univariados para obtener las desviaciones estándar condicionales que componen los elementos diagonales
Algunos trabajos como son los de Caporin y McAleer (2013) y McAleer et al. (2008) han abordado las limitaciones y deficiencias del modelo DCC, o "filtro" como proponen llamarlo ellos, al compararlo con otros estimadores similares, por ejemplo, el modelo BEKK de Engle y Kroner (1995), el modelo VCC de Tse y Tsui (2002) y el GARCC de McAleer et al. (2008). Es importante mencionar que la principal inferencia que se extrae del modelo no recae en la estimación de los parámetros del modelo DCC, ya que a pesar de los inconvenientes que este presenta se recomienda emplearlo para estimar o pronosticar las correlaciones condicionales dinámicas de un conjunto de activos, Caporin y McAleer (2013), además de que este fue el principal propósito para el cual dicho modelo fue desarrollado por Engle (2002).
Gómez y Sosvilla (2016) argumentan que la principal limitación del modelo DCC estándar es la suposición de que las correlaciones condicionales siguen la misma estructura dinámica, lo cual podría no ser realista en el trabajo empírico. Entre otras limitaciones que presenta el modelo DCC se encuentran el decho que representa las covarianzas condicionales dinámicas de los residuos estandarizados y de esta manera no produce correlaciones condicionales dinámicas, Caporin y McAleer (2008). Además, el modelo DCC carece de momentos; de condiciones de regularidad comprobables y propiedades asintóticas, Caporin y McAleer (2013). Sin embargo, el modelo DCC ha sido ampliamente adoptado en la literatura financiera para capturar los comovimientos de los mercados de acciones, bonos y derivados (véase, por ejemplo, Antonakakis et al. (2016) y Cappiello et al. (2006)).
A pesar de los inconvenientes que presenta el modelo DCC, Fresoli y Ruiz (2016) apuntan que no ha habido intentos en la literatura para medir la incertidumbre asociada con las correlaciones condicionales pronosticadas por los modelos DCC.
Una vez estimadas las correlaciones es necesario especificar una prueba para el contagio. Sin embargo, la inspección de la evolución en el tiempo de las correlaciones dinámicas estimadas constituye por si misma una primera aproximación para inferir la presencia o no de contagio financiero, en virtud de que si dichas correlaciones se incrementan en el periodo identificado como de crisis sugieren la posible existencia de contagio financiero.
Una primera prueba formal que empleamos para determinar si las correlaciones dinámicas son mayores en el periodo de crisis que en el periodo previo, y de esta manera contagio financiero, es la prueba de Kolmogorov-Smirnov. Dicha prueba permite probar si las medias de dos funciones de distribución muestrales son diferentes. Específicamente estamos interesados en encontrar evidencia de que la media de las correlaciones dinámicas estimadas para el periodo de crisis es mayor que la media de dichas correlaciones correspondiente al periodo previo a la crisis, si este es el caso lo interpretamos como evidencia de contagio financiero entre los mercados accionarios analizados.
Una segunda herramienta alternativa que es posible utilizar para modelar las correlaciones dinámicas estimadas a través del GARCH Multivariado (DCC) son los modelos de cambio de régimen markovianos desarrollados para capturar cambios en la forma en que se encuentran relacionadas variables económicas o financieras (Boffelli y Urga, 2016). De acuerdo con este tipo de modelos, es posible estimar el siguiente modelo para las correlaciones dinámicas:
donde
Todas las probabilidades así calculadas se pueden recopilar en la matriz de transición:
La matriz de transición está diseñada de tal manera que, para cada fila, la siguiente condición es verdadera:
En este trabajo emplearemos el modelo constante dependiente del estado planteado en la ecuación (5) como una prueba de contagio financiero entre los mercados accionarios de América Latina, en el cual esperamos que la constante estimada para las correlaciones dinámicas en el tiempo del mercado i con respecto del mercado j en el periodo previo a la crisis sea menor a la constante estimada para las mismas correlaciones en el periodo correspondiente al periodo de crisis, si se encuentra evidencia de esta diferencia en las constantes estimadas y si resultan significativas para ambos regímenes entonces hay evidencia de contagio financiero.
4. Resultados econométricos
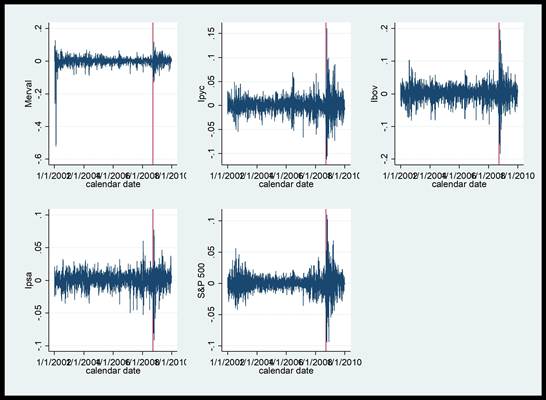
La gráfica 1 muestra los rendimientos de los principales mercados accionarios de América Latina y de Estados Unidos en el periodo comprendido entre el 1 de enero de 2002 y el 31 de diciembre de 2009 para un total de 5,828 observaciones correspondientes a los días hábiles en los cuales operaron los mercados financieros. Los rendimientos se calcularon a partir de los precios de cierre de los índices accionarios denominados en dólares obtenidos de economatica.
Fuente: Elaboración propia
Gráfica 1 Rendimientos de los los mercados accionarios de América Latina y Estados Unidos en el periodo de 2002 a 2009.
Como se puede ver en el gráfico 1, en todos los mercados, incluso en el de Estados Unidos, hay un periodo de relativa estabilidad de los rendimientos accionarios hasta mediados de septiembre de 2018, fecha en que ubicamos el inicio de la crisis, mientras que a partir de esta fecha se registra un periodo turbulencia o un cluster de volatilidad.
Siguiendo la propuesta de Chiang, Jeon y Li (2007) de modelar la media de los rendimientos de cada mercado en función de un término autorregresivo y de los rendimientos accionarios de Estados Unidos también desfasados un periodo, el cuadro 1 reporta las estimaciones de las ecuaciones de los rendimientos (media) y de la varianza condicional. El término AR(1) en la ecuación de la media es significativo y positivo para el IPSA, también es positivo para el IPyC pero no significativo, mientras que resultó negativo y no significativo para el MERVAL y el IBOVESPA, y con este mismo signo y significativo para el S P 500. Estos resultados no son consistentes con la evidencia empírica encontrada para los mercados emergentes en los que para la mayoría se ha encontrado que este término es positivo (Antoniou, Koutmos y Percli, 2005 y Chiang, Jeon y Li (2007).
Cuadro 1 Resultados de la estimación del modelo DCC-GARCH.
| Ecuación de los rendimientos | Ecuación de las varianzas | ||||||
|---|---|---|---|---|---|---|---|
| γ0 | γ1 | γ2 | c | a | b | Persistencia | |
| IPyC | 0.0013*** | 0.0057 | 0.1019*** | 0.0000*** | 0.9166*** | 0.0654*** | 0.9820 |
| (4.6) | (0.29) | (3.2) | (4.49) | (89.45) | (4.49) | ||
| MERVAL | 0.0011*** | -0.0169 | 0.1168*** | 0.0000*** | 0.9265*** | 0.0661*** | 0.9926 |
| (3.15) | (-0.76) | (3.2) | (4.92) | (150.47) | (9.95) | ||
| IBOV | 0.0022*** | -0.005 | 0.117 | 0.0000*** | 0.9173*** | 0.0618*** | 0.9791 |
| (5.06) | (-0.25) | (2.46) | (4.22) | (84.86) | (7.73) | ||
| IPSA | 0.001 | 0.1838*** | 0.1057*** | 0.0000*** | 0.8915*** | 0.0754*** | 0.9670 |
| (4.67) | (8.78) | (5.03) | (4.2) | (59.24) | (7.23) | ||
| S&P 500 | 0.0005*** | -0.1228*** | 0.0000*** | 0.9308*** | 0.0617*** | 0.9925 | |
| (3.04) | (-5.57) | (4.16) | (116.41) | (8.23) | |||
Notas: Los números entre paréntesis son los estadísticos z de cada coeficiente. El nivel de persistencia se calcula como la suma de los coeficientes en la ecuación de la varianza (a + b). ***, ** y * denotan significancia estadística al nivel del 1%, 5% y 10%, respectivamente. La ecuación de la varianza:
Fuente: Elaboración propia.
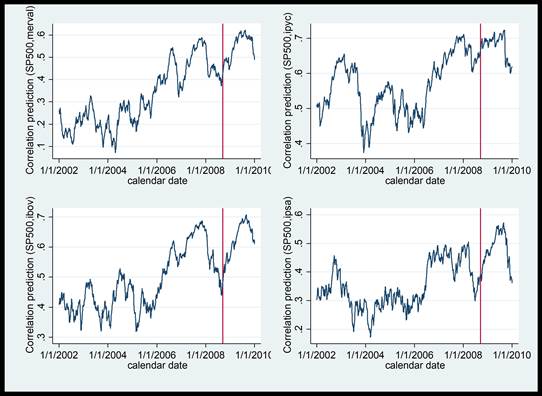
Es preciso destacar que la suma de los coeficientes estimados de la varianza (última columna) es cercano a la unidad en todos los casos, lo cual implica que la volatilidad de los mercados analizados es altamente persistente. Después de ajustar el modelo DCC, obtenemos las correlaciones dinámicas a través del tiempo. La evolución de las correlaciones dinámicas de los mercados accionarios de América Latina con el de Estados Unidos, de los periodos previos a la crisis y posterior a la crisis, se muestran en la gráfica 2. En esa gráfica la línea vertical identifica el colapso de Lehman Brothers, en algunos casos las correlaciones dinámicas de México (IPyC) con respecto a Estados Unidos parecen incrementarse después del colapso, no obstante en algunos otros como el de Brasil (IBOVESPA) éstas parecen ser resultado de una tendencia cíclica natural, por lo que se requiere una prueba formal adicional para determinar si hay o no evidencia de contagio.
Fuente: Elaboración propia
Gráfica 2 Evolución de las correlaciones dinámicas entre los mercados accionarios de América Latina y el de Estados Unidos para los periodos de precrisis y de crisis.
Con el fin de comparar adecuadamente la distribucion de las correlaciones, antes y después del colapso de Lehman Brothers, aplicamos la prueba Kolmogorov-Smirnov.
En cada caso, el primer renglón proporciona los resultados de la prueba de la hipótesis nula de que la distribución de las correlaciones dinámicas en el periodo de crisis es dominada estocásticamente por la distribución de las correlaciones dinámicas del periodo de precrisis, es decir, prueba la hipótesis de que la función de distribución de las correlaciones dinámicas del periodo de crisis contiene valores más pequeños que la función de distribución de las mismas del periodo de precrisis. Mientras que en el segundo renglón se prueba la hipótesis nula de que la distribución de las correlaciones dinámicas del periodo de precrisis es dominada estocásticamente por la distribución de las correlaciones dinámicas del periodo de crisis. En tanto que el renglón correspondiente a la prueba combinada de la prueba Kolmogorov-Smirnov evalúa la igualdad de las dos distribuciones. Los valores p reportados en el cuadro 2 se basan en las distribuciones asintóticas derivadas de Smirnov (1993).
Cuadro 2 Resultados de las pruebas de Kolmogorov-Smirnov de la igualdad de las funciones de distribución.
| MERVAL - S&P 500 | IPyC - S&P 500 | ||||
| Estadístico D | Valor-p | Estadístico D | Valor-p | ||
| 1. | 0.7747 | 0.000 | 1. | 0.689 | 0.000 |
| 2. | 0.0000 | 0.999 | 2. | 0.0000 | 0.999 |
| Combinada | 0.7747 | 0.000 | Combinada | 0.689 | 0.000 |
| IBOVESPA - S&P 500 | IPSA - S&P 500 | ||||
| Estadístico D | Valor-p | Estadístico D | Valor-p | ||
| 1. | 0.6507 | 0.000 | 1. | 0.6478 | 0.000 |
| 2. | 0.0000 | 0.999 | 2. | 0.0000 | 0.999 |
| Combinada | 0.6507 | 0.000 | Combinada | 0.6478 | 0.000 |
Fuente: Elaboración propia.
Los resultados de las pruebas revelan que en los cuatro casos considerados la distribución de las correlaciones dinámicas correspondiente al período de crisis domina de manera estocástica a la distribución de las correlaciones del periodo previo a la crisis. De igual forma, para todos los casos analizados se rechaza la hipótesis nula de la igualdad de las distribuciones de los coeficientes de correlación de los periodos previo y posterior a la crisis. De esta manera, las pruebas de Kolmogorov-Smirnov muestran evidencia de contagio del mercado accionario de Estados Unidos a los mercados accionarios de los países de América Latina analizados.
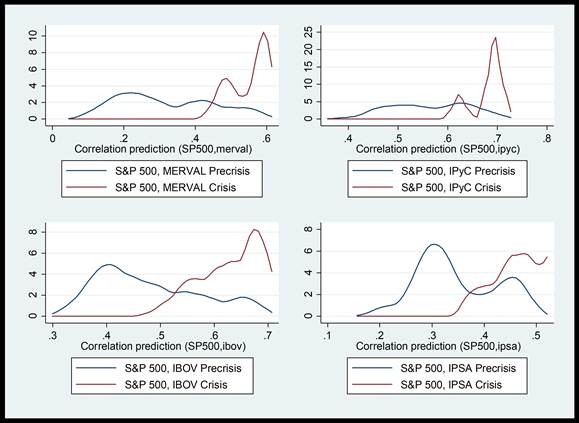
La gráfica 3 ilustra las diferentes distribuciones de las correlaciones dinámicas que caracterizan los periodos de precrisis y de crisis. Como se puede observar, para los cuatro países: Argentina, México y Brasil y Chile, las distribuciones correspondientes a las crisis se encuentran mucho más cargadas a la derecha que las correspondientes a la pre-crisis, lo cual sugiere una correlación mucho mayor con el mercado accionario de Estados Unidos que en periodos normales.
Fuente: Elaboración propia
Gráfica 3 Distribuciones de las correlaciones de los periodos de precrisis y de crisis de los mercados accionarios de América Latina contra el de Estados Unidos.
El cuadro 3 muestra los resultados de las estimaciones del modelo de cambio de régimen para la media y la varianza, con dos regímenes, de las correlaciones dinámicas estimadas a través del modelo GARCH multivariado DCC.
Cuadro 3 Resultados de las estimaciones del modelo Markov Switching para las correlaciones dinámicas con dos regímenes.
| Coeficiente | Error estándar | z | P>|z| | |
|---|---|---|---|---|
| Correlaciones dinámicas S&P 500 - MERVAL | ||||
|
|
0.2182 | 0.0019 | 112.97 | 0 |
|
|
0.059 | 0.0014 | ||
|
|
0.4848 | 0.0025 | 195.06 | 0 |
|
|
0.0792 | 0.0018 | ||
| Probabilidades de |
|
|
|
|
| Transición | 0.9995 | 0.0005 | 0.0005 | 0.9995 |
| Régimen 1 | Régimen 2 | |||
| Duración esperada | 1998.85 | 2071.99 | ||
| Correlaciones dinámicas S&P 500 - IpyC | ||||
|
|
0.4865 | 0.0017 | 293.85 | 0 |
|
|
0.0496 | 0.0012 | ||
|
|
0.6348 | 0.0011 | 601.08 | 0 |
|
|
0.0335 | 0.0008 | ||
| Probabilidades de |
|
|
|
|
| Transición | 0.9974 | 0.0026 | 0.0023 | 0.9977 |
| Régimen 1 | Régimen 2 | |||
| Duración esperada | 385.95 | 427.91 | ||
| Correlaciones dinámicas S&P 500 - IBOVESPA | ||||
|
|
0.4147 | 0.0014 | 303.43 | 0 |
|
|
0.043 | 0.001 | ||
|
|
0.6002 | 0.002 | 301.17 | 0 |
|
|
0.0604 | 0.0014 | ||
| Probabilidades de |
|
|
|
|
| Transición | 0.9976 | 0.0024 | 0.0025 | 0.9975 |
| Régimen 1 | Régimen 2 | |||
| Duración esperada | 420.78 | 392.76 | ||
| Correlaciones dinámicas S&P 500 - IPSA | ||||
|
|
0.298 | 0.0013 | 233.32 | 0 |
|
|
0.0387 | 0.0009 | ||
|
|
0.4552 | 0.0018 | 256.02 | 0 |
|
|
0.0485 | 0.0012 | ||
| Probabilidades de |
|
|
|
|
| Transición | 0.9977 | 0.0023 | 0.0027 | 0.9973 |
| Régimen 1 | Régimen 2 | |||
| Duración esperada | 437.73 | 371.75 | ||
Fuente: Elaboración propia.
Como se puede apreciar en el cuadro 3, en todos los casos analizados la media tiende a incrementarse en el régimen 2,
De igual forma, también es posible inferir que el régimen 1 es muy persistente con
Otro dato relevante que también se reporta en las estimaciones es la duración de los estados o regímenes. De las cuales destaca la duración estimada de los regímenes de las correlaciones dinámicas del S P 500 y el MERVAL, la cual divide la muestra analizada en prácticamente dos periodos, razón por la cual las estimaciones de la duración de ambos regímenes son muy elevadas en relación con los otros tres países analizados. Para los otros tres mercados, la duración estimada de los regímenes es más o menos similar, oscilando alrededor de 400 días en ambos casos.
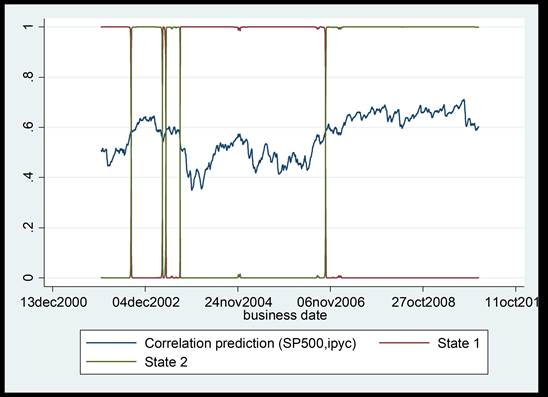
Las gráficas 4 a 7 muestran las probabilidades filtradas de los estados o regímenes para las correlaciones dinámicas del MERVAL, del IPyC, del IBOVESPA y del IPSA, de forma respectiva. En el caso de las probabilidades filtradas de las correlaciones dinámicas del MERVAL y del S P 500 que se presentan en la gráfica 4, muestran que el patrón de las correlaciones se mueve entre dos regímenes, pasando de un régimen de baja correlación a otro de mayor correlación, que comienza a finales de 2005 y sigue hasta el final de la muestra. Un patrón de comportamiento distinto presentan las probabilidades filtradas de los estados o regímenes para el resto de las correlaciones dinámicas analizadas en los cuales hay periodos en los que alternan ambos regímenes a lo largo de todo el periodo analizado.

Fuente: Elaboración propia
Gráfica 4 Probabilidades filtradas de los estados para la correlaciones dinámicas del MERVAL y el S P 500.
Fuente: Elaboración propia
Gráfica 5 Probabilidades filtradas de los estados para la correlaciones dinámicas del IPyC y el S P 500.
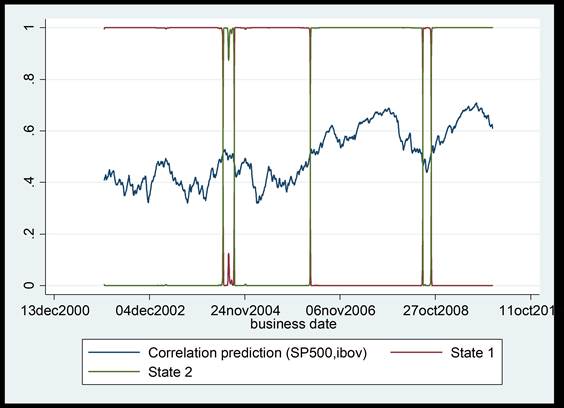
Fuente: Elaboración propia
Gráfica 6 Probabilidades filtradas de los estados para la correlaciones dinámicas del IBOVESPA y el S P 500.
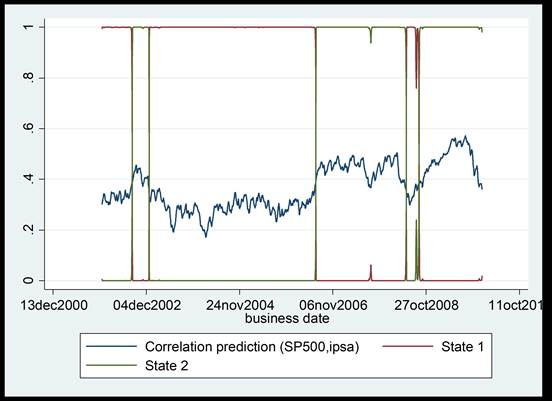
Fuente: Elaboración propia
Gráfica 7 Probabilidades filtradas de los estados para la correlaciones dinámicas del IPSA y el S P 500.
Otro resultado importante a destacar es el hecho de que el estado o régimen 2, correspondiente al patrón de mayor correlación, se registra casi a principios de 2006 para el IPyC, el IBOVESPA y el IPSA, sugiriendo de esta manera que el contagio de la crisis financiera internacional comenzó a registrarse mucho antes de la fecha de inicio en la que suele ubicarse, es decir, a mediados de septiembre de 2008. Quizá por esta razón, diversos estudios y analistas tienden a ubicar en fechas diferentes el inicio de la crisis financiera internacional. Por último, el estimar los patrones de menor y mayor correlación a través de este método estocástico a diferencia del determinista comúnmente empleado, a través de dummies, en los estudios que emplean las correlaciones dinámicas obtenidas a través del GARCH multivariado, permite identificar otros periodos en los que se registra un incremento de las correlaciones dinámicas (contagio financiero) a lo largo del periodo analizado. Por ejemplo, a finales de 2002 y a lo largo de 2003 para México, en 2004 para el IBOVESPA y a finales de 2002 para el IPSA.
Conclusión
En este trabajo empleamos las correlaciones dinámicas condicionales (DCC) estimadas a través de un modelo GARCH multivariado para evaluar el efecto de contagio del mercado accionario de Estados Unidos (S P 500) hacia cuatro de los principales mercados accionarios de América Latina.
El análisis gráfico de las correlaciones dinámicas estimadas sugiere que estas tienden a incrementarse en el periodo posterior a la crisis en comparación con las obtenidas en el periodo previo a la crisis. No obstante, esto no deja de ser una apreciación subjetiva, por lo que es preciso realizar una prueba formal para determinar si las correlaciones dinámicas se incrementan o no en los periodos de crisis comparados con los periodos previos.
Los resultados del modelo GARCH multivariado muestran que la volatilidad estimada de los mercados accionarios de América Latina es persistente. Por otro lado, las pruebas de dominancia estocástica de Kolmogorov-Smirnov aplicadas a las correlaciones dinámicas de las distribuciones de los periodos previo y posterior a las crisis sugieren que la distribución de las correlaciones del periodo de crisis domina a la distribución de las correlaciones del periodo previo a la crisis en todos los casos analizados. De lo cual, se deduce que hay evidencia de contagio financiero del mercado accionario de Estados Unidos (S P 500) hacia los mercados accionarios de América Latina analizados: Argentina (MERVAL), México (IPyC), Brasil (IBOVESPA) y Chile (IPSA).
La mayoría de los estudios que utilizan las correlaciones dinámicas condicionales estimadas con un modelo GARCH multivariado para probar contagio financiero en algunos periodos específicos de tiempo recurren a incorporar variables dummies en el análisis de regresión y a verificar de esta manera si las correlaciones dinámicas se incrementaron. A diferencia de este procedimiento empleado con frecuencia, en este trabajo procedimos de una manera distinta, ya que el análisis de las correlaciones lo efectuamos con modelos Markov-switching. El empleo de esta metodología confirma la existencia de dos regímenes para las correlaciones dinámicas entre el mercado accionario de Estados Unidos y los principales mercados accionarios de América Latina, lo cual es más evidente para el de Argentina (MERVAL), cuyos periodos de precrisis se caracterizan por ser relativamente estables mientras que el segundo, de crisis, se asocia a un mayor nivel de turbulencia y grado de interdependencia entre los mercados accionarios de Latinoamérica y el de Estados Unidos. Una de las principales ventajas de emplear este modelo para analizar las correlaciones dinámicas es que, además de revelar la naturaleza de las fluctuaciones temporales de las correlaciones, también permite identificar los periodos en donde se incrementan la correlaciones dinámicas y no es necesario especificar a priori los periodos en donde se sospecha que éstas se incrementan como en algunos estudios se ha tendido a proceder en la literatura sobre el tema. De esta manera, el análisis de dichas correlaciones puede reflejar las condiciones dinámicas de los mercados. No obstante, es preciso tener en cuenta que nuestros resultados pueden sufrir de algún sesgo debido al modelo GARCH Multivariado empleado para obtener las correlaciones dinámicas a partir de las cuales efectuamos las pruebas de contagio financiero, de acuerdo a lo planteado por Caporin y McAleer (2013), por lo que se requiere una mayor investigación sobre el tema que refuerce o cuestione los anteriores resultados.











 nueva página del texto (beta)
nueva página del texto (beta)


