1. Introduction
The fulfillment of the purchasing power parity (PPP) principle, understood as a long-run equilibrium relationship such that bilateral real exchange rates show a reversion to the mean, has been intensely debated, insofar as it is a fundamental pillar of many open-economy macroeconomic models (Baharumshah, Soon, Fountas, and Mohamad, 2016). Various empirical studies undertaken with a wide range of econometric techniques have tended to show that this principle is fulfilled; nonetheless, paradoxically, real exchange rates have shown great volatility and estimates of the half-life of deviations from equilibrium are relatively large. This is the purchasing-power-parity puzzle, so named by Rogoff (1996), because we would expect a stationary series, such as a real exchange rate fulfillment characterized by high volatility, to return quickly to its mean, i.e., for it to have a short half-life.
In terms of econometric tests, one argument given to explain the puzzle is the lack of robustness of conventional unit root tests, exacerbated by the high persistence of real exchange rates.
The PPP is relevant because it allows us to quantify the equilibrium exchange rate and, thus, measure the magnitude of the disequilibria of the exchange rate, compare income levels among countries, and, further, it is a point of reference that helps forecast the nominal exchange rate (Baharumshah et al., 2016). Fulfillmentof the PPP means that the volatility of the real exchange rate is reduced, thus eliminating the risk associated with this indicator. In addition, the disequilibria in the exchange rate are considereda leading indicator of exchange crises (Kaminsky et al., 1998). Most empirical studies have been prepared on developed economies, even though more recently economists have shown considerable interest regarding other regions of the world.
In this paper, we verified compliance with the PPP in a sample of Latin American countries through two econometric tests, the first one proposed by Pesaran (2007) and the second by Hadri and Rao (2008). The first is to verify the stationarity for all possible pairs of real exchange rates that can be formed from the selected exchange rates, one of the advantages of implementing this test is that it does not require considering the real exchange rate of any country as a base or numerary, in this way allows to evaluate the stationarity among all the real exchange rates that may be formed from the selected countries. Whereas the second test, proposed by Hadri and Rao (2008), it is only applied to the region’s bilateral real exchange rates with respect to the United States Dollar, among the benefits of using the Hadri and Rao test ( 2008) are the fact that it takes into account the possible cross-section dependency between the units of the panel and that the series that comprise it present some kind of structural rupture, as is the case of the real exchange rate of the countries of the Americas Latina analyzed in this work. These countries have faced various real and nominal shocks in the past few decades, and therefore econometric tests should be applied that consider the possible presence of structural breaks in the period selected for study. However, the main advantage of applying the Hadri and Rao (2008) test is that it allows us to identify the type of PPP hypothesis that best fits each of the bilateral real exchange rates with respect to the United States. Broadly speaking, the Pesaran (2007) test results show evidence in favor of the PPP in all possible pairs of the real exchange rate of the Latin American countries analyzed, while the results of the Hadri and Rao tests (2008) suggest that there is evidence in favor of different hypotheses of the PPP in real bilateral exchange rates with respect to the United States Dollar. The rest of the article is structured as follows: section 2 provides a brief review of the empirical literature on the subject, section 3 describes the econometric methodology used in the work, section 4 shows the data and the econometric tests results, finally the conclusions are presented and possible future research lines are established on the topic addressed here.
2. Empirical literature review
Through non-linearity and diverse STAR model tests, Holmes (20029 confirmed that the series of real exchange rates of 13 Latin American countries have structural breaks.
Breitung and Candelon (2005) analyzed the PPP for a sample of five Asian countries (Thailand, Singapore, Malaysia, South Korea, and Hong Kong) and five Latin American countries (Mexico, Venezuela, Colombia, Argentina, and Brazil) by means of unit root tests with structural breaks that are determined exogenously and attributed to exchange crises. These authors found evidence of the PPP in the Asian countries that they attribute to their flexible exchange rate regime; by contrast, they reject the PPP hypothesis in the Latin American countries, arguing that governments pegged their exchange rates to the dollar for long periods.
Caporale and Gil-Alana (2010) studied the PPP for a group of 17 Latin American countries by means of fractional integration methods with structural breaks, justifying their use due to the occurrence of exchange crises and regime changes. Most results are inconsistent with the PPP, with the notable exception of Argentina, since here the authors found evidence of reversion to the mean in its real exchange rate.
Su, Tsangyao, and Chang (2011) investigate the validity of the PPP in a sample of 15 Latin American countries (Argentina, Bolivia, Brazil, Chile, Colombia, Costa Rica, Dominican Republic, Ecuador, Haiti, Honduras, Mexico, Paraguay, Peru, Uruguay, and Venezuela), with monthly data from December 1994 to February 2010. These authors used linear univariate unit-root test and a test of univariate stationarity with a Fourier function. Their results show that the PPP is not validated with the linear unit root test; on the contrary, the test using the Fourier function points to the fulfillment of the PPP in just four of the 15 countries (Brazil, Chile, Ecuador, and Uruguay).
Astorga (2012) examined the regression to the mean in the real effective exchange rates of six Latin American countries during the 20th century by means of unit root tests that are complemented by an error correction model including key fundamentals, such as terms of trade, trade opening, and relative productivities. Astorga’s use of unit root tests includes the structural breaks proposed by Zivot and Andrews (1992), Bai and Perron (1998), and Perron (2006), which allow him to incorporate different breaks in the level and the trend under the null hypothesis and an alternative. Astorga finds evidence that tends to support the fulfillment of the PPP in Argentina, Brazil, Chile, Colombia, Mexico, and Venezuela.
Rodríguez, Perrotini, and Santamaria (2016) test a version of the PPP that holds that a real exchange rate is stationary around a changing mean, known as a “Quasi-Qualified-PPP,” with data from a sample of 17 Latin American countries from 1960 to 2013, by means of a panel unit root tests with structural breaks. They also obtain unbiased estimates of the half-life of the convergence of the PPP, while controlling several potential sources of bias: i) aggregation; ii) estimation in small samples of dynamic-lag coefficients; and iii) temporary aggregation in the prices of commodities. Their results substantiate the validity of the Quasi-Qualified-PPP version, and the estimated half-life is around four years, with a 95 % confidence interval of between 2.7 and 6.8 years.
Fóffano and Lima (2016) empirically examine the validity of the PPP by means of linear and non-linear univariate unit-root tests on the real effective exchange rates of Argentina, Brazil, Chile, Colombia, Mexico, Peru, and Venezuela. Their results establish that the real exchange rate series of Argentina, Brazil, Chile, Colombia, and Peru have linear characteristics, while Mexico and Venezuela have non-linear characteristics. The authors apply linear unit root tests that show that the real effective exchange rate is stationary for Chile and Peru, while non-linear unit root tests reveal stationarity for Mexico’s real effective exchange rate. They found evidence to validate the PPP in just three of the seven countries they analyzed. Ayala, Blazsek, Cuñado and Gil (2016) proposed a Markov regime-switching unit root test to analyze the PPP for a sample of 14 Latin American countries.
Several studies have been conducted on other countries using unit root tests or panel stationarity tests with structural breakpoints, including that of Harris, Leybourne, and McCabe (2005), who test the joint stationarity hypothesis for a sample of bilateral exchange rates of 17 OECD countries vis-à-vis the dollar.
Their results reject the null hypothesis, leading them to dismiss the long-term validity of the PPP for these countries. Conversely, Holmes et al. (2012) carry out panel stationarity tests with structural breaks to test the PPP in OECD countries from 1972 to 2008. Their results led them to accept the stationarity in the multilateral real exchange rate. More recently, Bahmani, Jiang and Chang (2015) confirmed the validity of the PPP for 34 OECD countries between January 1994 and August 2013 with a panel unit-root test proposed by Bahmami et al. (2014), which allows for abrupt and smooth changes in the panel series. Their results indicate that the PPP occurs for half of the 34 OECD countries, for which reason they emphasize the need to adequately model various types of breakpoints that occur in series of these countries’ real effective exchange rates.
Chang and Han-Wen (2013) apply the apparently unrelated regression test in the proposed panel of Kapetanios et al. (SURKSS), proposed by Wu and Lee (2009) to investigate the long-term properties of the purchasing power parity principle (PPP) in nine countries in transition in the period from January 1995 to December 2008. Their results show that the PPP is not maintained for the nine countries studied. However, the SURKSS panel test suggests that the PPP is valid only for two of those nine countries. Among the implications of their study is that the PPP can be used to determine the equilibrium exchange rate only for Estonia and Hungary. Their study also emphasizes that there is weak evidence on the long-term PPP hypothesis in economies in transition.
Bahmani, Chang, Chen and Tzeng (2017) apply unit root tests by quantiles proposed by Koenker and Xiao (2004) and Galvao (2009) to review the PPP in seven countries in transition: Bulgaria, Cezech Republic, Hungary, Lithuania, Poland , Romania and Russia with monthly data for the period from January 1998 to March 2015, their results show that while traditional unit root tests do not reject the null hypothesis of the unit root, unit root tests by quantiles reject the null hypothesis of unit root in all countries. When finding generalized evidence in favor of compliance with the PPP, the authors consider solving the puzzle that this principle represents. Additionally, they find that the estimates of the half-life that are based on the autoregressive model by quantiles range from 1 to 2 years.
Soon et al. (2017) apply unit root tests of second generation panel to determine the stochastic properties of real exchange rates in a sample of 14 Asian countries. Based on three popular alternative definitions of currency crisis, they identify the different most important episodes of currency crisis in the region. Their results show overwhelming evidence in favor of the PPP after taking into account these heterogeneous observations considered by them as noisy and unstable. The unitary panel root test used by these authors, which controls cross-sectional dependence and is robust against structural ruptures, allows them to confirm that the crisis in all countries is well characterized by second-generation models of monetary crisis, that is, the causes of currency crises are not necessarily found in the economic fundamentals. According to Soon et al. (2017), the PPP emerges when breaks and cross-section dependence are taken into ac-count for these 14 countries.
3. Methodology
3.1 Analysis of convergence by focusing on pairs
The PPP hypothesis is derived from a condition of arbitrage, the law of one price, which states that any divergence from the price of a good in two countries, expressed in a common currency, will tend to be eliminated by trade or other market forces, thus leading to an adjustment that brings price equality (Pesaran, Smith, Yamagat, and Hvozdyk, 2009). For countries i=0,1,2,...,N, with United States as country zero, the logarithm of the real exchange rate,
With t=1,…,T, where
If
Our first test to verify the fulfillment of the PPP in the sample of Latin American countries is based on the pairs approach outlined by Pesaran (2007), initially developed to test convergence in output among a set of countries. Pesaran’s method (2007) considers all possible pairs of real exchange rates among the 17 countries and applies both unit-root and stationarity tests on each real exchange rate. One of the main advantages of this approach is that this allows us to test the PPP hypothesis for all possible pairs of real exchange rates and not just for a single currency, which in this case is considered a numeraire currency. Thus, if we consider N real exchange rates in the analysis, then the total possible pairs is equal to
A fraction of the
where
In this paper, the unit-root tests used to calculate
The ADF, ADF-GLS, and ADF-WS test were run on the following equation:
where the number of lags,
3.2 Test of Stationarity in Heterogeneous Panels with Structural Breaks
The next test we use here is Hadri and Rao’s (2008) panel stationarity test with structural breaks to analyze the stochastic properties of the real exchange rate in a sample of Latin American countries. This test extends Hadri’s (2000) original proposal of a procedure using the Lagrange multiplier to test the null hypothesis that all individuals in the panel,
Where
More recently, Hadri and Rao (2008) extend Hadri’s (2000) panel stationarity test, which allows for the possible incorporation of a structural break. Hadri and Rao (2008) proposed four additional models with different structural breaks as follows:
where
where
These six models allow us to test different versions of the purchasing power parity (PPP) (Holmes et al., 2012), and not just one version, such as in the work of Rodríguez et al. (2016), since assuming that the real exchange rates of the countries of the region have the same type of break can be very restrictive. Model (1) tests the traditional version of the PPP in which the real exchange rate is stationary around a constant mean, i.e., Purchasing Power Parity (PPP). Model (2) considers the possibility that the real exchange rate is stationary around a trend under the null hypothesis, i.e., Trend-PPP (T-PPP). Model (3) allows for the possibility that the real exchange rate can be stationary with a change in the mean, i.e., Quasi-/Qualified-PPP (Q-PPP). Model (4) tests trend stationarity with a change in the intercept. Model (5) is not theoretically classified, in spite of the possibility that a change will occur in the slope of the model. Model (6) has no name and has to do with trend stationarity with changes in the intercept and in the deterministic trend (Holmes et al., 2012; Ventosa and Gómez, 2013). By including a temporary trend, we can evaluate if the breakpoint in the PPP is due to changes in the productivity differentials, (Holmes et al., 2012). Thus, the different possibilities of structural change envisaged in models (3) to (6) allow us to test stationarity around a change in the mean (models 3 and 4), just in the trend of the series (model 5), or in both (model 6). These changes can be attributed to changes in the exchange rate regime, changes in the price of oil, changes in the government, or economic crises (Hegwood and Papell, 1998).
By means of a systematic approach, the model proposed by Hadri and Rao (2008) determines the appropriate model for each individual in the panel among the six specifications referred to previously. The approach involves finding, first, the unknown date of the breakpoint,
The statistics of the univariate KPSS test are given by:
where
whose longitude can be determined by modeling from the general to the specific with the Schwarz information criterion.
The stationarity test statistic in the Hadri and Rao (2008) panel is calculated by means of a simple mean of the individual or univariate KPSS test statistics in the following manner:
which we can standardize as follows, so that the limit follows a standard normal distribution:
Where
To keep initial values of
4. Data and empirical results
Data used in this study are the annual bilateral real exchange rates (vis-à-vis the dollar) for a sample of 17 Latin American countries, from 1960 to 2016. The real exchange rate for each country,
In all cases,
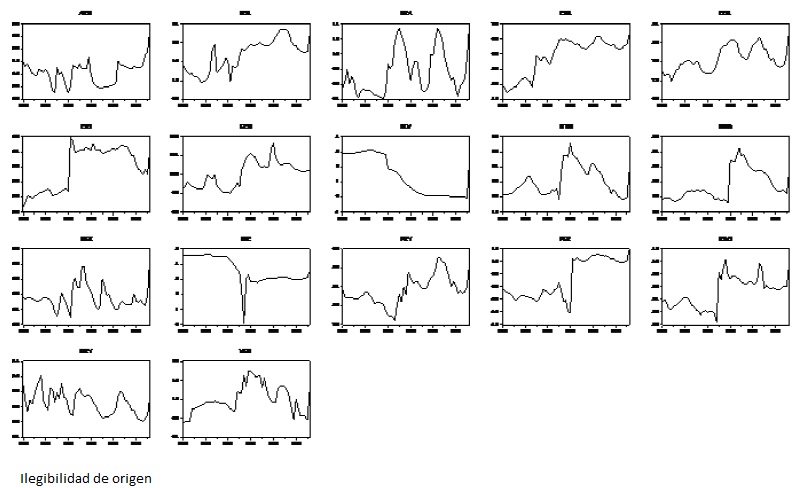
Source: Own elaboration.
Graph 1 Evolution of the natural logarithm of the bilateral real exchange rate for the sample of 17 Latin American countries: 1960-2016.
As Graph 1 show, the real exchange rates for most of the 17 countries display changes in volatility, passing through periods of low volatility to higher volatility, or vice-versa, and experiencing at least one structural break attribu-tabletochanges in exchange-rate policies, crises, external shocks, etc.
The results of the Pesaran (2007) unit-root test at 5 % and 10 % significance levels are displayed in Table 1. The fraction of rejections of the real exchange rates is significantly above 5 % and 10 % according to all unit-root tests.
Table 1 Fraction of real U.S. dollar rates,
| Case II: An Intercept Only | ||
|---|---|---|
| Sample period | 1960-2016 (T=557) | |
| Number of countries | N = 18 | |
| Number of pairs | 153 pairs | |
| Test (significance level) (%) | 5 | 10 |
| ADF (p) | ||
| p(AIC) | 0.16340 | 0.22876 |
| p(SC) | 0.15033 | 0.2222 |
| ADF-GLS(p) | ||
| p(AIC) | 0.28105 | 0.39869 |
| p(SC) | 0.31373 | 0.47712 |
| ADF-WS(p) | ||
| p(AIC) | 0.26144 | 0.31373 |
| p(SC) | 0.26797 | 0.35948 |
| Case III: An Intercept and a Linear Trend | ||
| Sample period | 1960-2016 (T=57) | |
| Number of countries | N=18 | |
| Number of pairs | 153 pairs | |
| Test (significance level) (%) | 5 | 10 |
| ADF(p) | ||
| p(AIC) | 0.22222 | 0.29412 |
| p(SC) | 0.19608 | 0.26144 |
| ADF-GLS(p) | ||
| p(AIC) | 0.3333 | 0.48366 |
| p(SC) | 0.31373 | 0.47059 |
| ADF-WS(p) | ||
| p(AIC) | 0.32026 | 0.42484 |
| p(SC) | 0.28105 | 0.43137 |
Source: Prepared by the authors.
The preceding table suggests a rejection of PPP non-fulfillment. With this result in mind, we now determine with the Hadri and Rao (2008) test what type of PPP is fulfilled with each real exchange rate for each country.
Table 2 displays results of applying the panel stationarity test in the presence of a structural break without serial correlation, as proposed by Hadri and Rao (2008), for the bilateral real exchange rate in Latin American countries with respect to the U.S. dollar.
Table 2 Results of the Hadri and Rao (2008) individual and uncorrelated panel stationarity tests: 1960-2016.
| Country | Test statistic | 95% | 99% | Model Selected | Date of break | Concept |
|---|---|---|---|---|---|---|
| Argentina | 0.050 | 0.293 | 0.451 | 3 | 2001 | Quasi-/Qualified-PPP |
| Bolivia | 0.027 | 0.064 | 0.083 | 6 | 1984 | Unnamed |
| Brazil | 0.015 | 0.129 | 0.190 | 4 | 1982 | Trend-Qualified PPP |
| Chile | 0.034 | 0.065 | 0.085 | 6 | 1983 | Unnamed |
| Colombia | 0.017 | 0.063 | 0.080 | 6 | 1985 | Unnamed |
| Costa Rica | 0.016 | 0.069 | 0.093 | 6 | 1980 | Unnamed |
| Dom. Republic | 0.028 | 0.136 | 0.200 | 4 | 1984 | Trend-Qualified PPP |
| Ecuador | 0.021 | 0.136 | 0.200 | 4 | 1985 | Trend-Qualified PPP |
| El Salvador | 0.089* | 0.087 | 0.121 | 6 | 1974 | Unnamed |
| Guatemala | 0.051 | 0.063 | 0.082 | 6 | 1986 | Unnamed |
| Honduras | 0.022 | 0.064 | 0.086 | 6 | 1989 | Unnamed |
| Mexico | 0.034 | 0.123 | 0.178 | 4 | 1981 | Trend-Qualified PPP |
| Nicaragua | 0.080 | 0.139 | 0.208 | 4 | 1987 | Trend-Qualified PPP |
| Paraguay | 0.021 | 0.190 | 0.267 | 3 | 1988 | Quasi-/Qualified-PPP |
| Peru | 0.036 | 0.188 | 0.261 | 3 | 1988 | Quasi-/Qualified-PPP |
| Uruguay | 0.023 | 0.128 | 0.185 | 4 | 1982 | Trend-Qualified PPP |
| Venezuela | 0.036 | 0.062 | 0.082 | 6 | 1986 | Unnamed |
| Panel | 0.035 | 0.888 | 1.171 |
Notes: *, ** indicate significance at the 5 % and 1 % level. Individually the null hypothesis is the stationarity of the series, while for the panel all series are stationary. Source: Prepared by the authors.
The results in Table 2 show that the real exchange rate of sampled countries in all cases has some type of break, given that models 1 and 2 were never selected. Interestingly, the model identified most frequently is model 6 that involves trend stationarity with changes both in the intercept and in the deterministic trend, and whose concept, or version, of the PPP has not been named. This result is similar to the one found by Holmes et al. (2012), who applied the same test to the real multilateral exchange rate of the OECD countries. In terms of the identified break dates, these are found in the 1974 to 2001 interval. Each one of the following years, 1982, 1984, 1985, 1986, and 1988, was identified for two countries; thus, the highest number of breaks occurred in the 1980s.
On an individual basis, El Salvador is the only country for which the null hypothesis of stationarity is rejected at the level of significance of 5 %, corresponding to the version of the PPP that has not been named; in the rest of the countries it is not possible to reject the null hypothesis of stationarity associated with each of the PPP hypotheses identified by the test. Likewise, considering the panel as a whole, it was not possible to reject the null hypothesis for stationarity, considering the heterogeneity shown by the bilateral real exchange rate for each country in the sample, considering both the date and the form of the breakpoints.
The test reveals that the bilateral real exchange rate for Argentina, Paraguay, and Peru was identified by model 3, stationarity around a mean with a change, which corresponds to the Quasi-/Qualified-PPP version. The model with the best fit for the bilateral real exchange rate for Brazil, Dominican Republic, Ecuador, Mexico, Nicaragua, and Uruguay was model 4, which assumes trend stationarity with a change in the intercept, corresponding to the Trend-Qualified PPP concept. The remaining countries, Bolivia, Chile, Colombia, Costa Rica, El Salvador, Guatemala, Honduras, and Venezuela, showed evidence of trend stationarity with a change in the intercept and in the deterministic trend, corresponding to model 6. The presence of a breakpoint in the trend of the real exchange rate of these countries can be interpreted as a change in productivity on the date of the break.
Table 3 displays the results of the Hadri and Rao (2008) test with serial correlation. As opposed to the results of the test without serial correlation in Table 2, in this case the individual KPSS tests with a structural break for Colombia and Nicaragua lead us to reject the null hypothesis of stationarity at the 5 % significance level, but not at 1 %. Yet, for the rest of the real exchange rates of the sampled countries, it is not possible to reject the null hypothesis of stationarity, independently of the criterion used in determining the lags in the test, which, in fact, is also heterogeneous among the panel units considered.
As with the test without serial correlation, the test shown in Table 3 for the panel as a whole does not allow us to reject the null hypothesis for stationarity. Thus we found evidence of weaker versions of the PPP in Latin America using the Hadri and Rao (2008) test applied to real exchange rates of a sample of countries from the region.
Table 3 Results of Hadri and Rao (2008) individual and panel stationarity tests with serial correlation.
| Test Statistic | Critical Values | Lag(s) according to BIC | ||
|---|---|---|---|---|
| 95% | 99% | |||
| Argentina | 0.035 | 0.065 | 0.086 | 1 |
| Bolivia | 0.048 | 0.112 | 0.160 | 1 |
| Brazil | 0.062 | 0.113 | 0.155 | 4 |
| Chile | 0.043 | 0.065 | 0.087 | 2 |
| Colombia | 0.075* | 0.064 | 0.083 | 4 |
| Costa Rica | 0.040 | 0.071 | 0.098 | 1 |
| Ecuador | 0.071 | 0.135 | 0.202 | 2 |
| Salvador | 0.038 | 0.141 | 0.204 | 2 |
| Guatemala | 0.032 | 0.063 | 0.081 | 1 |
| Honduras | 0.017 | 0.063 | 0.082 | 1 |
| Mexico | 0.074 | 0.0120 | 0.170 | 2 |
| Nicaragua | 0.066* | 0.064 | 0.084 | 1 |
| Paraguay | 0.142 | 0.186 | 0.261 | 4 |
| Peru | 0.048 | 0.189 | 0.270 | 2 |
| Dominican Republic | 0.026 | 0.132 | 0.191 | 1 |
| Uruguay | 0.062 | 0.196 | 0.277 | 3 |
| Venezuela | 0.025 | 0.063 | 0.083 | 1 |
| Panel | 0.053 | 0.418 | 0.583 | |
Notes: *, ** indicate significance at the 5 % and 1 % level. Individually the null hypothesis is the stationarity of the series, while for the panel all series are stationary. Source: Preparedbytheauthors.
5. Conclusions
In this paper we examine the principle of purchasing power parity (PPP) in a sample of real exchange rates of Latin American countries through two relatively new tests that of Pesaran (2007) and Hadri and Rao (2008). The first test checks fulfillment of the PPP with all pairs of the real exchange rates of the 17 countries considered herein. The second test helps determine what type of PPP hypothesis is foundin the various bilateral real-exchange-rate panel series, considered in the panel with a heterogeneous structural break in the units. The test allows for the possible presence of cross-section dependence among the units and serial correlation in the residuals. An advantage of this test is that it allows us to determine both heterogeneity of the date of the break and also the form that each break can take, since we can hardly assume that all the real exchange rates studied in the region have the same type of breakpoint or structural break. Another key advantage of this test is that it allows us to conclude if all the real exchange rates in the panel are stationary if the null hypothesis is not rejected jointly. The results of the Pesaran test (2007) suggest that the hypothesis of non-compliance with the PPP is rejected for all possible pairs of real exchange rates of the sample of 17 Latin American countries considered in the period - from 1960 to 2016. Since this test does not incorporate structural breaks in its specification, it can be considered as evidence of compliance with the PPP.
On the other hand, the results of the Hadri and Rao (2008) tests applied to the bilateral real exchange rates of these countries with respect to the United States Dollar, in addition to verifying the stationarity of the panel as a whole, allow us to identify what type of the PPP hypothesis is more adjusted to each real exchange rate of each country with respect to the United States Dollar because it allows the inclusion of a structural break. Other advantages of using this test is that it considers the possibility that the serial autocorrelation is present in the residuals of the panel and the possible dependence between the units. The results of Hadri and Rao’s (2008) test do not allow rejecting the null hypothesis of stationarity in the panel as a whole once different types of structural breaks have been considered in each of the bilateral real exchange rates with respect to the dollar from United States. One of the main implications of the results of this test is that in the particular case of the bilateral exchange rates of the Latin American countries with respect to the United States Dollar, the PPP is not met but there is evidence of compliance with different PPP versions. We should note that the most frequently identified model is 6, which corresponds to the case of trend stationarity with a change both in the intercept and in the determinist trend, still undefined in economic theory. Note also that, in this regard, a limitation of the Hadri and Rao (2008) testis that it considers only one structural break, even though, given the high volatility arising from the evolution of real exchange rates, it may be necessary to consider two or more breaks during our period of study.
In this way, the results of the Pesaran test (2007) show evidence in favor of compliance with the PPP in all possible real exchange rates that shape the sample of Latin American countries analyzed, while the results of the Hadri tests and Rao (2008) applied only to the bilateral real exchange rate of these countries with respect to the United States Dollar reveals evidence of compliance with weaker versions of the PPP in this case. In our opinion, these results are not contradictory because the Pesaran (2007) test considers all the possible real exchange rates of all the countries considered, while the Hadri and Rao test (2008) applies to a single panel in which the United States Dollar is taken as a numerary or base, so a possible future line of research that emerges from this work is to characterize the real exchange rates by taking various currencies as cash and thus be able to establish how congruent are the results of both tests.











 nueva página del texto (beta)
nueva página del texto (beta)


