1. Introduction
The existing income gap between different sectors of society has intensified among the last years all around the world, while the social status and political power have involved a divided humanity, thereby undermining social and economic development of nations. Indeed, according to Hardoon, D. (2017), just eight men own the same wealth as the poorest half of the world and, since 2015, the richest 1% has owned more wealth than the rest of the planet. This severe and increasing inequality is one of the major threat to social stability, that is why its study and understanding has become very relevant nowadays.
On the words of Ray (1998), the study of inequality is important for two main reasons: 1) from a philosophical point of view, an egalitarian society is desirable, especially if the initial conditions of the lives of individuals are crucial to their development and; 2) inequality has functional impacts that can weaken the growth of a country. Indeed, the inequality could reduce the process of economic growth for developing countries (Barro, 2000) and, hence, exacerbate the poverty. In addition, high levels of inequality can distort political decision-making. Evidence shows that sharp disparities in access to resources and opportunities can harm subjective wellbeing (UNDP, 2013).
Through the evolution of economic science, the study of economic development and poverty has become increasingly important, especially in developing countries. Classical and recent contributions (for example Sen, A. (1976, 1985); Anand and Sen (1997), Alkire (2002), and Stewart and Deneulin (2002) have come to the conclusion that these two issues are multidimensional problems, i.e., there should be considered factors such as education, health, access to services, nutrition, income, among others. However, it has become a convention that inequality is measured primarily using an income approach, this means that most of the indicators considered use income as the core of the measurement. On the other hand, when one is interested in measuring a specific aspect of inequality, the indicators used are exactly those of interest such as education or health. Due to the above, we consider that the measurement of inequality must assume all the parts and dimensions of human wellbeing.
The study of multidimensional inequality was pioneered by Fisher (1956), who developed the idea of a multidimensional distribution matrix and, later, by the seminal contributions of Kolm (1977), Atkinson and Bourguignon (1982) and, Walzer (1983). The most recent contributions correspond to Tsui (1995, 1999), Abul Naga and Geoffard (2006) and, Gajdos and Weymark (2006). However, there are no much empirical research. The reason why could be due to the difficult to implement those proposed indexes, mainly for policymakers.
Recently, Abul Naga (2010) uses the delta method to derive a large sample distribution of multidimensional inequality indices, and also presents a method for computing standard errors and obtains explicit formulas in the context of two families of indices. However, from our knowledge, his contribution and those of the previously cited papers, have been used empirically just once by Aaberge and Brondolini (2014).
It is unbelievable that, given the broad indices proposed, there is still not an official way to measure the inequality with a multidimensional approach. Hence, in this research we propose a straightforward method to measure multidimensional inequality. However, we do not formally asses the standard set of axioms that an inequality index should satisfy given the econometric treatment of data. In any case, we leave this task to further research.2
The natural antecedent of our index, by its multidimensional character, is the Human Development Index (HDI) proposed by the United Nations Development Program (UNDP) in 1990, which opened a new door to think about the welfare of people. However, after receiving strong criticism (for example: McGillivray, M., 1991, or Anand and Sen, 1992) the UNDP modified the methodology of the HDI in 2010 changing the minimum and maximum standards, as well as the formula.
In an attempt to consider a more accurate measure of human development, Hicks (1997) proposes an HDI that includes measurements of inequality, to do that he uses data from income, education, and fertility and mortality rates for different countries. According to his results, Hicks (1997) suggest that most Latin American countries, a region known to have the most severe income distribution problem, fall in rank when inequality is factored into development. Also Noorbakhsh (1998) proposed a modified HDI that takes into account the criticisms that have been made in the literature. He analyzes the discussion about the weight given to the HDI components, for which he uses the method of Principal Components Analysis (PCA). Noorbakhsh (1998) concludes that the equal weighting of the components of these indices is not a serious problem as indicated by some researchers.
Currently, the UNDP has five measures of human development: the HDI, the inequality-adjusted HDI, the Gender Development Index (GDI), the Gender Inequality Index (GII), and the Multidimensional Poverty Index (MPI), however there is still not a measure if inequality which considers the dimensions of human development.
The idea of using the PCA to construct an index has been widely adopted given that the components obtained have the desirable characteristic of being orthogonal (i.e., not correlated). Recently this method has been used in studies of development economics such as the one carried by Filmer and Prittchet (1999, 2001). In a similar stream and related with our research, McKenzie (2005) uses data on space and quality of housing to determine whether these can be used to measure inequality (i.e., as an alternative to traditional measures of income). Thus, McKenzie (2005) measures inequality with an asset index based on 30 indicators, which were obtained using the Household Income and Expenditure Survey of Mexico (ENIGH, by its acronym in Spanish). The main conclusion of the McKenzie’s research is that the relationship between the indicator of assets and consumption of non-durable goods is strong in terms of the levels of inequality.
Our research aims to develop a new methodology for the creation of an index which measures the inequality with a multidimensional approach. Our proposed method could be used with any data from household surveys that contains information of at least the following variables: income, education, health and some measure of access to services. We show how this method works using data from Mexico. Hence, we measure the degree of inequality using our Multidimensional Inequality Index (MII) among the Mexican states and we compare it with the results derived from the Gini index. We conclude that our index identifies greater inequality in those states where there are gaps in services and poor housing conditions. We also analyze areas; urban and rural, and gender inequality. We find that among the females there are less inequality than among males, with statistically significant differences. On the other hand, we find that rural areas are more unequal than urban ones.
2. The Model
The Principal Component Analysis (PCA) is a statistical technique used for data reduction. This technique helps to reduce the number of variables of any dataset by describing a number of uncorrelated linear combinations of the variables that contain most of the variance. The PCA was originated with the work of Pearson (1901) and Hotelling (1933). After that, the PCA has been used for different purposes; in Economics it is used to construct indices (Vyas and Kumaranayake (2006), and Roche (2008)) but also to forecasting purposes (for example Stock and Watson (2002), and Gálvez-Soriano (2018)).
The aim of the PCA is to find the vector of linear combinations of the variables with the greatest variance. The first principal component has the highest overall variance. The second major component has maximum variance among all linear combinations of the vector that are not correlated with the first principal component, etc. The last major component has the smallest variance among all linear combinations of vector variables.
For purposes of our research, let define
Given the PCA, we obtain
Although the selection of the eigenvector using the Kaiser criterion is standard and straightforward, it is important to include just the ones with enough variance with the purpose of have differences among the individuals of the household surveys.
Suppose that we consider just
The interpretation of our MII is analogous to the one of the Gini Index; namely, the values closest to 0 mean perfect equality, while the values closest to the unity represent perfect inequality.
3. Data
To perform the computation and measurement of the Multidimensional Inequality Index (MII), we use as source of information the ENIGH, for the year 2014, which is published by the National Institute of Statistics and Geography (INEGI). The ENIGH data provide a statistical overview of the performance of revenues and expenditures of Mexican households in terms of amount, origin and distribution. This survey is statistically representative at national level, and for the States of Puebla and Tabasco. Particularly we use the Socioeconomic Conditions Module (MCS), which is an annex to the ENIGH and which provides information on occupational and socio-demographic characteristics of household members, and the characteristics of the infrastructure of housing and household equipment, the latter was especially useful to include multidimensional characteristics to the MII. The MCS is statistically representative at national level and at State level, so do our results.
The multidimensional characteristics require, as Anand and Sen (1997) noted, to cover three main aspects of wellbeing: survival, education and income. Survival refers to the quality of life and is commonly measured with the expectancy of birth. Education could be measured as years of schooling, but also as illiteracy condition. Finally, the income component is measure as per-capita income but could also include measures of the provision of public services.
For the case of Mexico, the MII proposed is composed of 10 variables that characterize the socioeconomic status of household members, namely: institution that provides health service as the survival component, years of schooling as the education component, and total current income per-capita as the income component. Additionally, we consider overcrowding, fuel for cooking, drainage, access to potable water, construction material of walls, ceilings and floors of the house, as measures of the provision of public services in addition to the income component. The values of each variable were sorted in ascending order, giving the lowest value to the lower status and increasing with better conditions, except for the variable “overcrowding”.
The treatment of schooling was special, because in order to control for the agents’ age, we propose to consider the ratio of the exponential of years of schooling,
Where the years of schooling were calculated with the variables: approved level, degree approved and, in the case of Technical Career level, the school history variable. We only consider the population of 6 years and older. The lowest school year (1) corresponds to the first passing grade of primary, while the last school year (25) corresponds to the sixth year of doctoral studies. The value of 0 is assigned to those who have no years of study.
The reason to express the schooling in this way is the weight that is given to the years of schooling to adults, this means that it is normal for children and youth to be studying, so there are not a situation of inequality, while adults will be punished or rewarded for years of study according to their age.
Table 1 Descriptive Statistics
| Variable | Mean | Standard deviation |
Minimum Value |
Maximum Value |
|---|---|---|---|---|
| Agent characteristics | ||||
| Total Current Income Per Capita | 3,459.2 | 8,346.6 | 0.0 | 1,858,807.0 |
| Institution that Provides Health Service | 2.4 | 1.1 | 1.0 | 7.0 |
| Years of Study | 8.1 | 4.6 | 0.0 | 25.0 |
| Household characteristics | ||||
| Drain Destination | 4.5 | 1.0 | 1.0 | 5.0 |
| Water Origin | 6.4 | 1.5 | 1.0 | 7.0 |
| Walls Material | 7.8 | 0.8 | 1.0 | 8.0 |
| Roofs Material | 8.4 | 2.8 | 1.0 | 10.0 |
| Floors Material | 2.4 | 0.6 | 1.0 | 3.0 |
| Cooking Fuel | 3.5 | 1.2 | 1.0 | 5.0 |
| Crowding | 1.4 | 1.0 | 0.1 | 21.0 |
| Observations | 190,296 | 190,296 | 190,296 | 190,296 |
Source: Data from household's members interviewed in the ENIGH 2014.
Regarding the rest of the variables that make up the MII, we note that individuals of an average household of Mexico have a monthly income of $3,459.23 pesos with a standard deviation of $8,346.59. In the case of health, on average, the population is served by the Seguro Popular or by the Mexican Institute of Social Security (IMSS).4
On the other hand, regarding the characteristics of dwelling, on average, households are connected to a septic tank or public network, while the material of construction of the houses may be of brick, block, stone, quarry, cement or concrete walls and; cement or some other type of coating as wood or tile for floors. The fuel used for cooking in homes is mostly electricity and gas tank. The overcrowding indicator, on average, is 1.40 people. Finally, on average, members of Mexican families have 8.1 years of schooling equivalent to the second year of secondary school.
4. Empirics
Before applying the PCA we conducted a correlation analysis in order to assess the relevance of including the variables to be analyzed; Table 2 shows the correlation matrix of the 10 variables included in the MII. In general, there is a weak correlation between the variables, suggesting the relevance of using all in the PCA. The highest correlation is presented between the variables “Cooking Fuel” and “Drain Destination” which makes sense given that both are related to the development of a town.
Table 2 Correlation Analysis
| Variable | Income per Capita | Health Service | Drain Destination | Water Origin | Walls Material | Roofs Material | Floors Material | Cooking Fuel | Crowding | Years of Study |
| Income Per Capita | 1.00 | |||||||||
| Health Service | 0.16 | 1.00 | ||||||||
| Drain Destination | 0.09 | 0.15 | 1.00 | |||||||
| Water Origin | 0.09 | 0.15 | 0.39 | 1.00 | ||||||
| Walls Material | 0.05 | 0.09 | 0.25 | 0.20 | 1.00 | |||||
| Roofs Material | 0.10 | 0.17 | 0.34 | 0.32 | 0.38 | 1.00 | ||||
| Floors Material | 0.16 | 0.23 | 0.31 | 0.30 | 0.25 | 0.41 | 1.00 | |||
| Cooking Fuel | 0.13 | 0.21 | 0.47 | 0.38 | 0.25 | 0.40 | 0.39 | 1.00 | ||
| Crowding | -0.14 | -0.17 | -0.25 | -0.23 | -0.24 | -0.28 | -0.33 | -0.30 | 1.00 | |
| Years of Study | 0.04 | 0.03 | 0.01 | 0.01 | 0.01 | 0.01 | 0.02 | 0.01 | -0.02 | 1.00 |
Note: The correlation shown corresponds to the Spearman Correlation Coefficient.
The 10 selected variables,
Where barxj is the average of the
Table 3 Scoring coefficients (PCA)
| Variable | Component 1 | Component 2 | Component 3 | Unexplained |
| Income Per Capita | 0.15 | 0.66 | -0.25 | 0.39 |
| Health Service | 0.22 | 0.49 | -0.24 | 0.53 |
| Drain Destination | 0.38 | -0.19 | 0.06 | 0.52 |
| Water Origin | 0.35 | -0.15 | 0.03 | 0.60 |
| Walls Material | 0.30 | -0.25 | 0.14 | 0.64 |
| Roofs Material | 0.40 | -0.16 | 0.07 | 0.49 |
| Floors Material | 0.39 | 0.10 | -0.04 | 0.53 |
| Cooking Fuel | 0.41 | -0.07 | 0.00 | 0.48 |
| Crowding | -0.32 | -0.11 | 0.04 | 0.67 |
| Years of Study | 0.02 | 0.39 | 0.92 | 0.00 |
Note: Table 3 shows the scoring in each variable by component.
According to the scores on the variables we can see that the
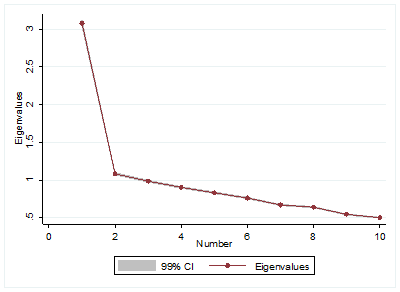
Source: Calculations based on the Kaiser test with a range of 99% confidence.
Graph 1. Selection of eigenvectors according to Kaiser Criterion.
To ensure the selection of the eigenvectors we plot the eigenvalues with a confidence interval of 99%. Graph 1 shows the eigenvalues after applying PCA, we can see that the first three components can be chosen, allowing us to reaffirm the previous selection.
We also apply the analysis of Kaiser-Meyer-Olkin (KMO) to compare the correlations and partial correlations between the 10 variables. If the partial correlations are relatively higher compared to the total ones, the extent of KMO is small implying that it is not possible to generate a low-dimensional representation with data. On average, the variables have a rating of 0.84 (Table 4) indicating that they are meritorious variables to be included in the analysis.
Table 4 Rating variables according KMO criterion
| Variable | KMO |
| Income Per Capita | 0.817 |
| Health Service | 0.860 |
| Drain Destination | 0.830 |
| Water Origin | 0.870 |
| Walls Material | 0.835 |
| Roofs Material | 0.837 |
| Floors Material | 0.859 |
| Cooking Fuel | 0.838 |
| Crowding | 0.884 |
| Years of Study | 0.730 |
| Total | 0.848 |
Because the interpretation of loadings makes more sense without rotating the eigenvectors than rotating them, we proceed to use it for the construction of the MII. Note that for some agents, the eigenvectors have corresponding negative elements, so we transform them in order to have positive numbers using its minimum values,
Using equation (1), we have that the MII for Mexico is obtained with the following formula:
We use this formula to calculate the MII nationally, by state, by areas: rural and urban, and by gender. In addition, to contrast the MII obtained, we calculate other indices of inequality: Coefficient of Variation, Gini index, Theil index, Atkinson index, among others.
4. Results
The application of the methodology that we propose suggests that Mexico has a MII equal to 0.85, i.e., it is a country with lots of multidimensional inequality. But how serious is this? Suppose there is a country with exactly the same characteristics as Mexico, but with a more equal income distribution. To do this we generated an income variable with a normal distribution, taking the average income of Mexico ($3,459.23 pesos) and assuming a lower standard deviation ($800). Given these assumptions, we get a MII of 0.50. This means that even with an improvement in income distribution in Mexico, our index suggests that there is a gap in living conditions and opportunities for Mexicans, however, the MII improves substantially. In contrast, if we taste the Gini index for this imaginary country, we get a Gini of 0.13 which suggest an egalitarian population. This clearly omits the inequality among the many human development indicators.
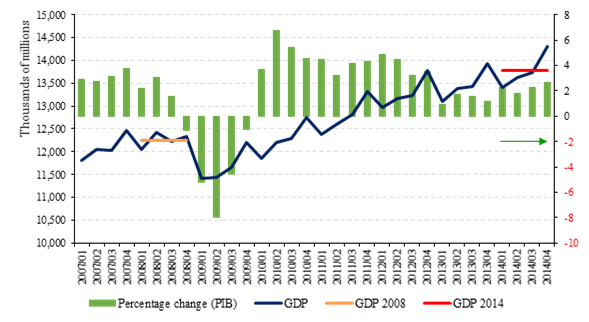
Source: Based on data from INEGI. The GDP is presented in constant pesos and its percentage change is calculated as the annual change over the same quarter last year.
Graph 2. Mexican GDP and its percentage change (2007-2014)
Furthermore, let consider the income distribution in Iceland, which implies approximately a Coefficient of Variation (CV) of 0.40 (the CV in Mexico was 2.40 in 2014). We use the Iceland data since it is the country with less inequality worldwide, according to the European Commission (2016), with a Gini index of 0.227. Again we take the other household characteristics equal to the Mexican ones. If Mexico could redistribute the wealth, as well as Iceland does, but preserving the same access to opportunities as in the present, we get a MII of 0.48. This means that our index still suggest the existence of inequality although the income is redistributed. That is why we propose that an income redistribution must be accompanied by an improvement in services that the government offers (both in quality and access), mainly the education system because of the loadings received in the PCA from this particular component.
Table 5 Conventional Inequality Measures between 2014 and 2008
| Inequality Measures | 2014 | 2008 | Difference (2014-2008) |
Change (%) |
2014* | Difference (2014*-2014) |
Change (%) |
|---|---|---|---|---|---|---|---|
| Multidimensional Inequality Index | 0.853 | 0.701 | 0.152 | 21.69 | |||
| Relative Mean Deviation | 0.367 | 0.361 | 0.005 | 1.48 | 0.396 | 0.029 | 7.97 |
| Coefficient of Variation | 2.403 | 1.624 | 0.779 | 47.99 | 6.853 | 4.450 | 185.22 |
| Gini Coefficient | 0.505 | 0.499 | 0.006 | 1.28 | 0.543 | 0.038 | 7.51 |
| Theil Entropy Measure | 0.551 | 0.501 | 0.050 | 10.02 | 0.755 | 0.204 | 36.97 |
| Atkinson Inequality Measure | 0.368 | 0.365 | 0.004 | 0.98 | 0.418 | 0.050 | 13.59 |
Note: The corresponding measures in column 2014* coincide to the ones with the income corrected by multidimensionality using the elements of the MII by agent.
On the other hand, as a reference point, we compere the MII in 2014 with the one in 2008, both for the Mexican data. The financial crisis of 2008 in the United States of America provoked a slowdown in Mexican economic activity since the four quarter of 2008. For this year the MII was 0.70, and six years later was 0.85. Hence, the multidimensional inequality in Mexico raised for this period, meaning worse conditions for the distribution of wealth. In contrast, the GDP increased by a mean rate of 2.1 percent (see Graph 2).
Table 6 MII by area and by gender
| Variable | MII | Difference | |
|---|---|---|---|
| Urban | Rura | ||
| Area | 0.8491 | 0.8656 | -0.0165*** |
| Population | 69,400,000 | 20,900,000 | |
| Variable | MII | Difference | |
| Male | Female | ||
| Gender | 0.8530 | 0.8527 | 0.0004*** |
| Population | 43,700,000 | 46,600,000 |
Note: We omitted the population from zero to five years old given that their no-schooling affected the index, despite the number of household members is considered in the variable "crowding".
***p<0.01,
**p<0.05,
*p<0.1
The conventional inequality measures also predict an increase of inequality between 2008 and 2014 but in different magnitudes. If we consider the percentage change in each index we could assess how intense was this increase. The results in Table 5 shows that agreed with our findings, other measures suggest an increase in inequality by 48 percent or by 10 percent (Coefficient of Variation and Theil Entropy Measure, respectively), while the MII estimates an increase in inequality by 22 percent. As an additional analysis we used the elements of the MII to control for inequality in opportunities when conventional measures are used (the way we do this is by using the elements of the MII, i.e., the observations by agent); in all cases we find that our index corrects the income variable for multidimensionality. These are good news for the users of this kind of measures to introduce an integral view of human development when inequality is analyzed.
Table 7 Gini coefficient vs MII by state
| Ranking | State | Gini | State | MII |
|---|---|---|---|---|
| 1 | Puebla | 0.578 | Chiapas | 0.867 |
| 2 | Chiapas | 0.513 | Guerrero | 0.867 |
| 3 | Coahuila | 0.510 | Oaxaca | 0.866 |
| 4 | Oaxaca | 0.508 | Veracruz | 0.860 |
| 5 | Distrito Federal | 0.507 | Tabasco | 0.860 |
| 6 | Yucatán | 0.507 | Campeche | 0.859 |
| 7 | Hidalgo | 0.506 | Puebla | 0.856 |
| 8 | Zacatecas | 0.506 | Michoacán | 0.856 |
| 9 | Quintana Roo | 0.500 | San Luis Potosí | 0.855 |
| 10 | Campeche | 0.498 | Yucatán | 0.855 |
| 11 | Aguascalientes | 0.490 | Hidalgo | 0.855 |
| 12 | Veracruz | 0.490 | Morelos | 0.855 |
| 13 | Guerrero | 0.489 | Durango | 0.853 |
| 14 | Querétaro | 0.488 | Zacatecas | 0.852 |
| 15 | Sinaloa | 0.487 | Tlaxcala | 0.852 |
| 16 | San Luis Potosí | 0.478 | Nayarit | 0.852 |
| 17 | Tamaulipas | 0.478 | Baja California | 0.851 |
| 18 | Sonora | 0.475 | Quintana Roo | 0.851 |
| 19 | Jalisco | 0.471 | México | 0.851 |
| 20 | Morelos | 0.468 | Guanajuato | 0.851 |
| 21 | Nayarit | 0.467 | Sinaloa | 0.851 |
| 22 | México | 0.464 | Baja California | 0.851 |
| 23 | Baja California Sur | 0.455 | Tamaulipas | 0.851 |
| 24 | Chihuahua | 0.455 | Chihuahua | 0.850 |
| 25 | Nuevo León | 0.455 | Querétaro | 0.850 |
| 26 | Tabasco | 0.454 | Colima | 0.850 |
| 27 | Guanajuato | 0.453 | Sonora | 0.849 |
| 28 | Colima | 0.452 | Coahuila | 0.847 |
| 29 | Michoacán | 0.450 | Jalisco | 0.847 |
| 30 | Durango | 0.448 | Aguascalientes | 0.846 |
| 31 | Baja California | 0.434 | Nuevo León | 0.845 |
| 32 | Tlaxcala | 0.414 | Distrito Federal | 0.845 |
We also tasted the MII to analyze the inequality between urban areas and rural ones, as well as by gender. Note that in all cases the MII is calculated considering the total population, thus, the differences corresponds to the inherent characteristics of the both aspects considered by our index. For example, we find that the rural areas in Mexico are more unequal than urban ones, maybe this is because in the former there are gaps in services and poor housing conditions, meanwhile in the later most of the populations have access to public services. We also find that among the males there are more inequality than among the females; given that the household characteristics does not change between male and female we conclude that the differences must be due to the income, health and education. In the area as well as in the gender analysis we obtained statistically significant differences (see Table 6).
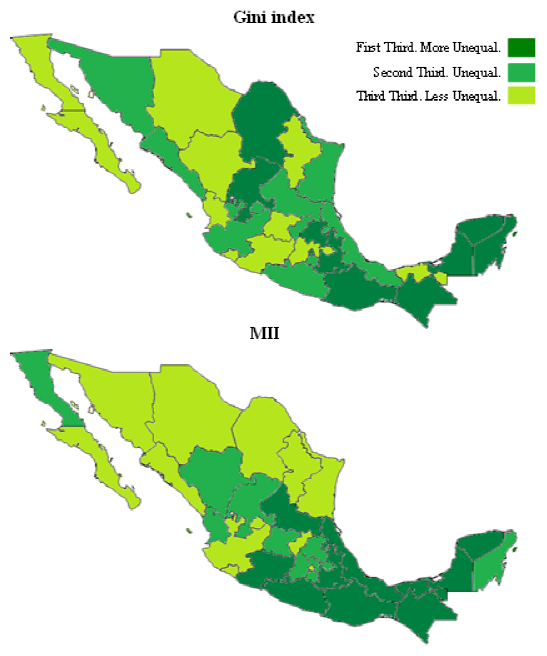
Finally, we compare the MII with the Gini index to assess the changes in the rankings when the inequality is measured among the states of the Mexican Republic (this kind of analysis could be done when comparing the rankings among countries). Although the Gini index considers that the most unequal state of Mexico is Puebla, the MII situate it in the seventh place.
The most radical change is in the Distrito Federal (DF) which passes from the fifth place to the last one, i.e., the MII consider that this state is the most egalitarian. This result must be related to the fact that most of people have access to basic services at the DF. That is why we conclude that our index identifies greater inequality in those states where there are gaps in services and poor housing conditions. Analogously the Gini index classifies the Tlaxcala state as the less unequal whilst the MII classifies it in the middle of the distribution (see Table 7 and Map 1).
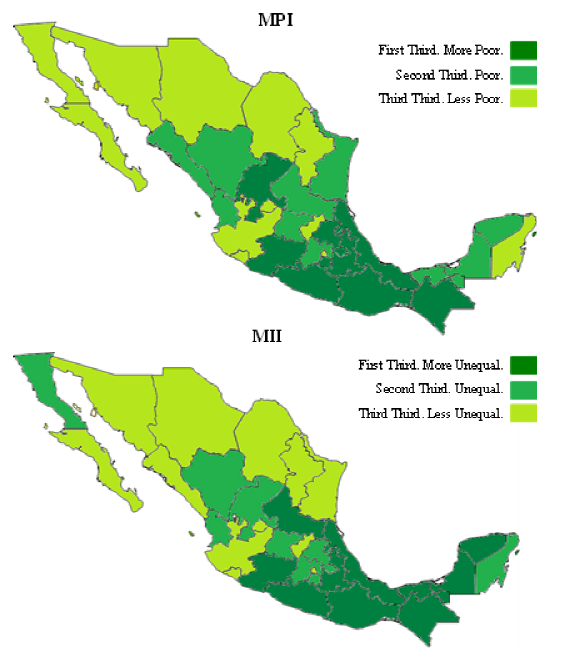
Given that most of the variables included in the MII are related to those used for CONEVAL in the Multidimensional Poverty Index (MPI) calculus, we conducted an analysis of both indices (see Annex).
After consider the ordering of Mexico states for both indices we conclude that, although there are similarities in the extremes of the distribution, the MII offers a more flexible view of services access. The reason is because the MPI classifies people according to binaries criterions, which yields a discrete distribution; by the other hand, the PCA deals the agents characteristics in the linear combination of the multidimensional variables, hence, the resulting MII has a quasi-continuous distribution. This characteristic provides a much rich information about the differences among agents.
6. Conclusions
In this research paper we propose a new methodology to analyze the inequality using a multidimensional perspective. This new methodology is based on a PCA to use the eigenvectors as the elements of a Multidimensional Inequality Index (MII). The eigenvectors are normalized and are included in the index as an arithmetic mean. The interpretation of the MII is analogous to the one of the Gini index.
In a simulation conducted we used an income distribution similar to the less unequal country in the world (Iceland), but unchanging the other characteristics for Mexico. We find that, if Mexico could redistribute the wealth as well as Iceland does, but preserving the same access to opportunities as in the present, the MII still suggest the existence of inequality. That is why we propose that an income redistribution must be accompanied by an improvement in services that the government offers, with an especial attention to education.
We also find that our results are consistent with those of conventional inequality measures when we analyze it between two periods of time; specifically we use the beginning of the financial crisis (2008) and the most recent period available (2014). Likewise, we propose to use the MII’s elements to correct the conventional measures to incorporate a multidimensional approach. In all cases the corrected inequality measures predicts a harsher inequality.
Finally, we compared the inequality among the states of Mexico using the Gini index and the MII, the later identifies greater inequality in those states where there are gaps in services and poor housing conditions. Furthermore, the inequality in Mexico is analyzed considering the gender and the region of the agents studied. In the first case, we find that among the females there are less inequality than among males, with statistically significant differences, while in the second case, we find that rural areas are more unequal than urban ones.











 nueva página del texto (beta)
nueva página del texto (beta)