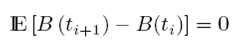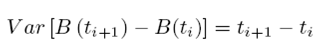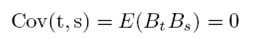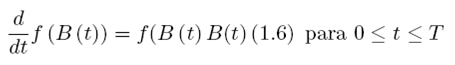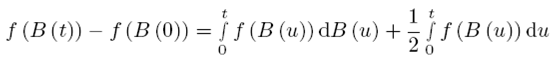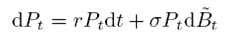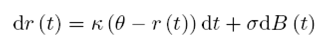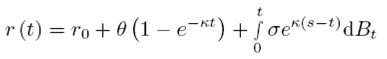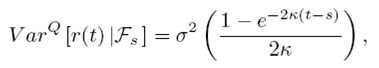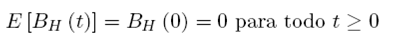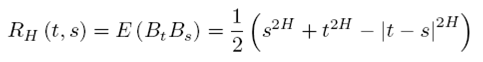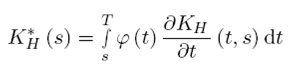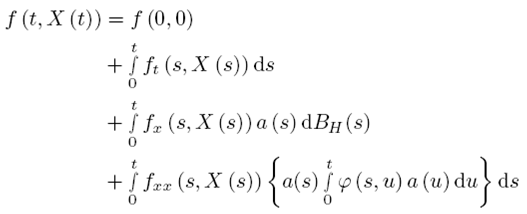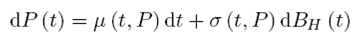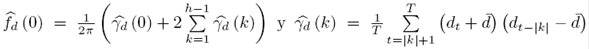1. Introducción
En el contexto financiero, especialmente en el mercado de renta fija, la tasa de interés cero cupón, objeto de estudio, es un referente internacional en cada uno de los mercados secundarios del precio de los títulos soberanos. En Colombia, adicionalmente, esta tasa es el referente de los precios del mercado con mayor volumen de negociación. En un día cualquiera el mercado donde la renta fija representa más del 80% del volumen negociado. Esta tasa conlleva un componente aleatorio que al proyectarlo a través de un proceso generador adecuado produce beneficios a los agentes del mercado de acuerdo a su posición.
Es por esto que cobra importancia modelar y pronosticar la curva de tasas de interés que establece el Banco Central con base en la metodología de Nelson y Siegel, lo que permite prever y asumir posiciones en ventanas de corto plazo y poder tomar decisiones oportunas ante cambios en la tasa estimada agregada. Para esto, este trabajo usa modelos de tasas de interés de corto plazo como soporte para la proyección. En particular, se usa el proceso Ornstein Uhlenbeck; sin embargo, dado el componente de persistencia de esta variable, se evidencia la necesidad de usar una alternativa fraccional, que en este caso es el proceso de Ornstein Uhlenbeck fraccional.
En esta propuesta entonces, primero se obtiene la estimación de cada una de las propuestas a partir de dos metodologías en donde la calibración de cada modelo permite obtener estimaciones de los parámetros los que a su vez ayudan a obtener pronósticos de la tasa de interés estudiada en ventas de tiempo de quince días, y segundo se comparan los resultados de los pronósticos a través de los procesos mencionados desde los componentes estadísticos y financiero, destacando la necesidad de usar modelos fraccionales dada la pérdida de precisión si se desconoce este patrón de las series temporales. Para esto, se realiza una evaluación de tal persistencia usando la constante de Hurst a través de dos metodologías desarrolladas en la literatura, periodograma modificado y rango re-escalado, descritos por Taqqu, Teverovsky, and Willinger, (2009). Resulta interesante identificar mayor precisión en los procesos de modelación fraccional que en el proceso clásico no fraccional, medida a través de métodos gráficos, una aplicación financiera de inversión y el test de comparación de pronósticos DM, Diebold y Mariano.
Es por esto que este documento describe la propuesta de los autores en cuatro apartados. La primera parte presenta la teoría que soporta el desarrollo de cada uno de los modelos, la segunda, describe la metodología para la estimación y evaluación de los modelos de proyección de las tasas de interés, la tercera muestra los resultados y la evaluación empírica, y finalmente, se exponen las principales conclusiones y recomendaciones frente a los principales resultados encontrados.
2. Movimientos Fraccionales Brownianos y Movimientos Brownianos
Un movimiento fraccional browniano es definido por Mandelbrot (2009) como la posibilidad de memoria de los datos de una serie de tiempo y su influencia en los eventos futuros, donde estos pueden tener una asociación positiva o negativa, dado el comportamiento de la serie que es evaluada por períodos de larga duración. Este tipo de patrón, conocido como persistencia, puede medirse a través del parámetro de Hurst Taqqu, Teverovsky, and Willinger, (2009). Esta medición, un valor en el intervalo [0,1], permite establecer el tipo de persistencia o aleatoriedad de la serie de tiempo evaluada.
Precisamente, esta constante es tenida en cuenta en la estimación de procesos generadores de precios o tasas de interés a través de los procesos fraccional brownianos. Sin embargo, frente a procesos brownianos, resulta más compleja debido a la ausencia de martingalas, lo que dificulta el cálculo de las integrales Itô, elemento esencial para aproximar los momentos del proceso estocástico generador.
Autores como Benth (2003) y Oksendal (2004) entre otros, han resuelto el problema de las martingalas, a partir del cálculo Maillavian y del producto Wick para hallar una solución a través de integrales fraccionales Itô, obteniendo una cuasi martingala; mientras que Nualart (2006) y Biagini (2011), ofrecen una solución discreta además de la continua, encontrando el mismo valor esperado en cero de BH(0) = E[BH(t)) = 0 para todo t ∈  y covarianza E(Bt Bs) =
y covarianza E(Bt Bs) = 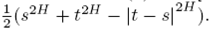
De acuerdo a lo anterior, si una serie es persistente, podría ser estimada a través de un proceso fraccional para obtener mejores resultados en comparación con un método que asume independencia de los datos para evaluar la serie.
Para entender mejor lo anterior, se presentan algunos elementos que soportan la estructuración de la propuesta.
2.1 Probabilidad y procesos estocásticos.
Para abordar la teoría de los procesos estocásticos que se encontrarán a lo largo de este trabajo, se analizan primero los espacios de probabilidad usados para medir los resultados obtenidos con ayuda de las series de tiempo y su relación con el espacio de números reales, aplicados a un movimiento browniano y un movimiento fraccional browniano.
Un conjunto ( Ω, A, P ) que tiene una familia de subconjuntos (A) ⊂ Ω donde los elementos de A son eventos que se miden en una función de probabilidad σ Algebra, se encuentran en un espacio borel B, un conjunto de variables aleatorias que contienen un espacio de probabilidad. Para obtener un resultado en un espacio de números reales  , es necesario usar la integral lebesgue ζ que ayuda a obtener la relación entre los conjuntos y conecta el espacio de probabilidad Ω a partir la probabilidad P en el espacio de los números reales
, es necesario usar la integral lebesgue ζ que ayuda a obtener la relación entre los conjuntos y conecta el espacio de probabilidad Ω a partir la probabilidad P en el espacio de los números reales 
Por lo tanto, una función continua se encuentra dentro de un espacio de probabilidad y tiene variables aleatorias X con una función f(x) perteneciente a un subconjunto A, con un área que se halla calculando una función de densidad en un espacio de probabilidad con ayuda de la integral lebesgue, que mide las variables aleatorias en el espacio de probabilidad Ω.
donde αi es número positivo real de Ai es el conjunto medible que contiene la función de valores αi. Estos elementos sirven para la medición bajo supuestos de independencia de datos y son utilizados para estimar el valor esperado en un movimiento browniano.
El cálculo del movimiento fraccional browniano, al tener el supuesto de persistencia y asumir memoria de largo plazo, dificulta el análisis de las variables que se generan en un espacio Ω; muchos de los supuestos y los espacios de probabilidad entre los que se mueven las variables aleatorias no son suficientes para obtener el cálculo necesario para llevar el resultado a un espacio de números reales  .
.
Los espacios de Hilbert y el Sobolev mantienen la isometría de los datos, para que las variables que presentan persistencia puedan ser medidas en un espacio de probabilidad Ω y arrojen resultados de los eventos en el espacio de los números reales Arendt and Urban, (2010).
El espacio de Hilbert está definido por un vector de números complejos o reales que tienen un producto escalar completo, donde cada sucesión de números converge. Un espacio de sucesiones L2 finitas tiene su convergencia por medio del producto de dos espacios vectoriales normados, cuyo objetivo es mantener la isometría entre dos variables, describiendo la relación que hay a causa de la función Øksendal B. (2007).
Un espacio Sobolev complementa el producto de dos variables, generado en un espacio de Hilbert dentro en tiempo continuo, manteniendo la distancia de los intervalos para obtener la medida de probabilidad dentro de un espacio de los números reales Øksendal B. (2004).
2.2 El Movimiento Browniano
El movimiento browniano con una familia, {B (t,.)} t≥0 originalmente fue diseñado para describir los movimientos de las moléculas a través de los fluidos, implementado más adelante en otras ramas de las ciencias como las matemáticas y la física Shreve, (2004).
Un movimiento browniano está constituido por un vector B(t,.) de variables aleatorias en un conjunto  , que es condicionado por un crecimiento de una serie de tiempo para 0 = t0 < t1 < … < tn donde la diferencia de los incrementos está dada por:
, que es condicionado por un crecimiento de una serie de tiempo para 0 = t0 < t1 < … < tn donde la diferencia de los incrementos está dada por:
Este incremento se observa en el conjunto (Ω, A, P) y se calcula a través de una distribución normal con un valor esperado y una varianza, como se describe a continuación:
Este proceso cumple las propiedades de una martingala, característica especial que ayuda a encontrar el valor de una variable aleatoria en un intervalo de tiempo definido, para un proceso browniano que se resuelve con ayuda de integrales Ito, Shreve (2004).
De esta forma, un movimiento browniano es una martingala, lo que quiere decir que para un intervalo |s , t| donde s ≠ t y s < t, se puede estimar cualquier valor intervalo que bajo las condiciones de los movimientos brownianos, es el valor esperado de una probabilidad en un tiempo s condicionada a una filtración Fs.
Lo anterior, implica que el valor esperado de un movimiento browniano B(t) con una probabilidad condicionada por una filtración Fs en un intervalo de tiempo entre s y t es B(s).
Con ayuda de las martingalas y la solución que ofrecen las integrales Itô, se puede estimar el valor esperado y la varianza de la distribución normal de un proceso browniano, fB(t) donde f es diferenciable. Esta solución se obtiene con ayuda de la serie de Taylor, que es la derivada con respecto a la variable y el tiempo, en el caso particular de las series financieras se obtiene una derivación de segundo orden con respecto a la variable aleatoria, que permite definir una ecuación parcial diferencial, dentro de un área a través de las integrales Shreve, (2004).
Por lo tanto (1.6) se puede definir con ayuda de las integrales Itô como:
Su desarrollo es producto de la primera derivada con respecto a la variable f´(B(t)), la primera derivada con respecto al tiempo y f´(B(0)) la segunda derivada con respecto a la variable que, complementada con la serie de Taylor es 1\2f''(B(t)).
Con ayuda de las serie de Taylor se resuelve la ecuación parcial diferencial de Black and Scholes, base de la teoría financiera y que sirve de raíz para el desarrollo de modelos de tasas de interés de corto plazo; esta ecuación desarrollada por Fischer Black and Myron Scholes (1971) determina a través de los paseos aleatorios las variaciones de los instrumentos financieros de renta variable, usando como base una variable aleatoria con una función de distribución normal estándar para generar los paseos aleatorios, y parámetros que miden la media y la desviación estándar de los instrumentos de renta variable.
Como la finalidad es analizar los procesos estocásticos para resolver el proceso Ornstein Uhlenbeck, se aplica el teorema de Girsanov para eliminar el principio de arbitraje y evaluar así el proceso Ornstein Uhlenbeck con el precio de riesgo del Mercado λ.
Al partir de una ecuación parcial diferencial del modelo Black and Scholes se obtiene:
Que bajo una transformación de tasas de interés dS t = rSt dt ayuda a despejar el movimiento browniano para encontrar una función sobre Ω que arroja una medida de riesgo neutral Q y que transforma el proceso browniano con ayuda del precio de riesgo del Mercado λ.
La ecuación 1.9 es la solución del teorema de Girsanov para el movimiento browniano, que despeja el principio de no arbitraje dentro del modelo y contiene el precio de riesgo del mercado. Con esta solución se define el modelo estocástico para tasa de interés de corto plazo que es:
2.3 Proceso Ornstein Uhlenbeck.
Definido el movimiento que generan los paseos aleatorios para estimar los rendimientos, se evalúa el proceso aplicado a tasas de interés de corto plazo conocido como Ornstein Uhlenbeck, uno de los primeros procesos utilizados para estimar rendimientos de instrumentos financieros de renta fija. En este proceso solo se analizará el cambio en los rendimientos de las tasas mas no en los precios de los bonos, aún así es importante establecer la relación que se mencionó en la ecuación (1.10), para obtener la estimación del precio de un bono con ayuda de los rendimientos en las tasas.
Es un proceso markoviano, que a través de una distribución normal trabaja con parámetros como el valor esperado y la varianza; todo resuelto a través de las integrales Itô y la martingala Brockwell, Davis and Yu, (2007).
Donde k es la tasa media de reversión a la tendencia y θ es el nivel medio de reversión o tendencia, junto con la volatilidad δ, que es la desviación estándar. Las medidas de reversión sirven para mantener la tasa entre un punto de oscilación y evitar así valores fuera de rango que llevan a la estimación a presentar errores Shreve (2004).
Entonces el Valor esperado es igual a:
Mientras que la Varianza es igual a:
El desarrollo del modelo tiene como objetivo determinar las variaciones diarias de la tasa de interés a partir de la ecuación (1.12), donde se le suma un valor inicial r0 para tener el resultado en r1 y así sucesivamente, hasta obtener cada uno de los valores durante el periodo en que se realizó la simulación.
2.4 El Movimiento Fraccional Browniano.
El movimiento fraccional browniano está definido por un movimiento gaussiano BH(t) = BH(t), ≥ 0 en un espacio de probabilidad (Ω, A, P). Como se puede ver, este movimiento está condicionado, a diferencia del modelo anterior, por un parámetro H como subíndice, que es el que define la persistencia o antipersistencia entre los datos. Este parámetro dentro del intervalo |0, 1| es evaluado en detalle, para datos con una dependencia positiva en un intervalo entre |1/2, 1| o que son independientes y por consiguiente, tienen un parámetro de Hurst H = 1/2 y, una varianza definida por la ecuación (1.3) Nualart, (2006).
Entonces el valor esperado para un movimiento fraccional browniano es definido:
En este caso la covarianza está definida por el valor esperado entre Bt y Bs .
La diferencia entre ambos es la forma del cálculo, pues el movimiento fraccional no se puede resolver a través de las ecuaciones Itô, por lo que es necesario buscar otros métodos de solución, como el producto Wick o las integrales Forward.
En la introducción se planteó que el objetivo era resolver el proceso fraccional a través de un proceso determinista, utilizando la solución que ofrecen Biagini, Campanino, and Fuschini, (2008) y Nualart (2006) para generar un operador que permita establecer una medida de probabilidad con ayuda de una función desde el espacio Sobolev  , generando una relación en el espacio Hilbert a través de un espacio lebesgue L2
que nos da la medida en el conjunto de los números reales.
, generando una relación en el espacio Hilbert a través de un espacio lebesgue L2
que nos da la medida en el conjunto de los números reales.
Este operador, definido como la isometría entre dos espacios métricos, es el puente entre los espacios que calcula el movimiento fraccional como un proceso discreto.
Así, el operador que ayuda a resolver el proceso fraccional es: K
H = (t, s)  con denominador para c H definido por la distribución beta, que bajo cálculos específicos se puede despejar como una distribución gamma y que ayuda a la función a converger hacia un valor esperado, mientras que la función
con denominador para c H definido por la distribución beta, que bajo cálculos específicos se puede despejar como una distribución gamma y que ayuda a la función a converger hacia un valor esperado, mientras que la función 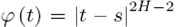 marca el intervalo entre el tiempo del cálculo Biagini, Campanino, and Fuschini, (2008).
marca el intervalo entre el tiempo del cálculo Biagini, Campanino, and Fuschini, (2008).
Donde 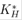 es un operador lineal para
es un operador lineal para 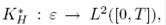 , para un ɛ definido como una función de densidad sobre un espacio Hilbert. Con este operador se obtiene un proceso discreto medido en un espacio lebesgue desde un espacio Sobolev que está definido como:
, para un ɛ definido como una función de densidad sobre un espacio Hilbert. Con este operador se obtiene un proceso discreto medido en un espacio lebesgue desde un espacio Sobolev que está definido como:
Siendo la derivada de la covarianza multiplicada por la función dada por el espacio Sobolev.
La complejidad del cálculo no permite que el proceso fraccional tenga una martingala, sólo es posible obtenerla a través del cálculo Malliavin. Este resultado lo obtuvo Benth (2003) y arroja una demostración conocida como Cuasi- Martingala, que resuelve el proceso fraccional browniano para obtener una ecuación diferencial parcial de un proceso discreto.
De esta forma, al solucionar la martingala con una filtración F Hs, se obtiene el mismo valor esperado de la variable aleatoria, por lo tanto  para un intervalo. 0 ≤ s ≤ t ≤ ∞ Este resultado no es una martingala por lo que Benth (2003) demostró que se puede obtener una convergencia hacia un valor esperado obteniendo una martingala
para un intervalo. 0 ≤ s ≤ t ≤ ∞ Este resultado no es una martingala por lo que Benth (2003) demostró que se puede obtener una convergencia hacia un valor esperado obteniendo una martingala 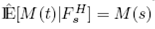 donde M(t) =
donde M(t) = 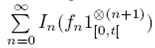 . Definiendo la Cuasi-martingala como:
. Definiendo la Cuasi-martingala como:
Donde gracias a la convergencia 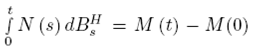 y reemplazándolo en (1.19) se obtiene M (t) que es una Cuasi- Martingala para un movimiento fraccional browniano.
y reemplazándolo en (1.19) se obtiene M (t) que es una Cuasi- Martingala para un movimiento fraccional browniano.
En el apartado del movimiento browniano se mencionó la integral Itô, que soluciona la ecuación diferencial parcial; por lo tanto, este apartado transforma el cálculo en una integral fraccional
En el tercer renglón de la ecuación (1.20), se puede ver que el movimiento fraccional browniano se resuelve con la Cuasi- Martingala para obtener el valor esperado y, el cuarto renglón muestra la función de covarianza en la segunda derivada con respecto a la variable aleatoria.
La transformación de Girsanov para el movimiento fraccional se produce de la misma manera que para el movimiento browniano, teniendo en cuenta que se trabaja para modelos de tasa de interés y que se empleará para estimar la tasa de interés con ayuda del proceso fraccional Ornstein Uhlenbeck, Maller (2009).
Por lo tanto, se tiene para un movimiento fraccional browniano el valor del precio de riesgo de mercado más el movimiento fraccional que es igual a:
Como en el anterior apartado, esta transformación sirve para su aplicación en un modelo de tasas de interés de corto plazo, que está basado en una distribución normal donde la diferencia del precio es:
Fuente: Generación propia de procesos fraccionarios brownianos en Matlab.
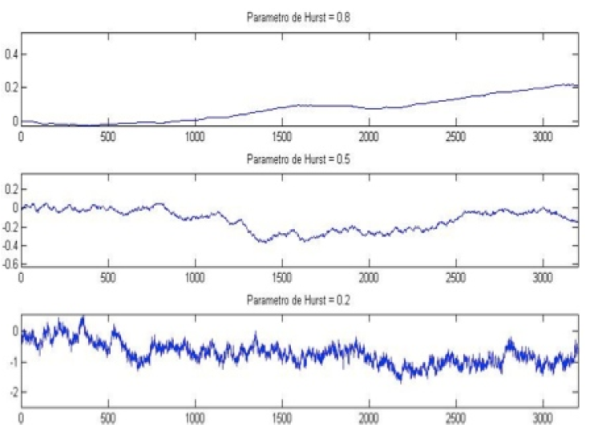
Cuadro 1 FBm simulados con diferentes parámetros de Hurst.
En la figura 1 se aprecia la independencia del movimiento browniano cuando el parámetro de Hurst tiene un valor de 0.5 frente a los procesos que se generan cuando existe persistencia (H > 0.5) y anti-persistencia entre los datos (H < 0.5)
2.5 Proceso Fraccional Ornstein Uhlenbeck.
El proceso fraccional se diferencia del anterior por el parámetro de persistencia y el método de cálculo de la covarianza, que tiene un efecto en la relación de los cambios en la tasa de interés. Partiendo de la solución que ofrece la ecuación (1.20), al mantener la persistencia de los datos, este modelo deja de ser un proceso markoviano Maller, Müller, and Szimayer, (2009), y por lo tanto se obtiene un proceso Ornstein Uhlenbeck, con la variación que se observa en la siguiente ecuación parcial diferencial:
Donde la forma fraccional Itô se resuelve con la ayuda de la Cuasi-Martingala nombrada en el apartado 1:
La forma diferencial, ayuda a que se puedan obtener los cambios en los rendimientos, que son los que se van a utilizar para analizar las diferencias entre ambos procesos.
3. Datos y Metodología
Para esta propuesta se estudian las series de las tasas cero cupón a uno, cinco y diez años, que se obtienen en la página web del Banco de la República de Colombia. Estas tasas se estiman con ayuda de la metodología Nelson y Siegel, tal como lo plantean los autores Arango, Melo, and Vasquez, (2001), obteniendo datos que sirven como referencia para la negociación de los Bonos Gubernamentales colombianos en el mercado de capitales colombiano.
En el proceso se obtienen los rendimientos continuos de las tasas, y luego se evalúa la existencia del patrón de persistencia. La estimación se hace con ayuda del código que ofrece Chen (2008). El código basa sus estimaciones en las metodologías de periodograma modificado y rango reescalado presentadas por Taqqu, Teverovsky y Willinger (2009), estudiadas también por Schlüchtermann y Grimm (2004).
Una vez que se tienen los resultados con respecto a la persistencia de la series, se selecciona la que presenta mayor patrón de persistencia medido a través de H.
Posteriormente, se genera el proceso de simulación de tasas. Para esto, se utiliza simulación de Montecarlo con diez mil escenarios para cada horizonte de tiempo en ventanas de pronóstico de quince días por ciento cinco días.
Para el cálculo de los parámetros del modelo que asume independencia, se utiliza el proceso de estimación de máxima verosimilitud que se encuentra detallado en García Franco (2003). En este trabajo se desarrolla la importancia del proceso de reversión de la media y la velocidad con que este tiende a la media.
Para resolver la ecuación parcial diferencial (1.11) se determina la distribución de la variable aleatoria obteniendo el valor esperado y la varianza bajo el supuesto de modelo gaussiano. Esta solución se puede ver en detalle en Franco (2003). Luego se obtienen las condiciones de primer orden para cada uno de los parámetros de la función de verosimilitud, a partir de los cuales se obtienen los estimadores via métodos numéricos.
Para estimar los parámetros en el modelo fraccional, Brouste and Iacus (2013) usaron una aproximación discreta, en este caso en especial se usa el paquete YUIMA del programa R que permite trabajar con ecuaciones estocásticas parciales diferenciales, y entre sus códigos, se puede estimar el modelo necesario para obtener los parámetros que se han presentado en este trabajo para el proceso fraccional Ornstein Uhlenbeck y que se resuelve por el método de mínimos cuadrados. Para esto, el paquete usa los estimadores alternativos numéricos propuestos por Hu and Nualart (2009) a través de simulación en la sección 4.
Para corroborar que el pronóstico con ayuda del proceso fraccional puede presentar mayor consistencia debido a la persistencia de la serie, se realizan tres tipos de evaluación o backtesting sobre los últimos 105 días de la serie. En el primer tipo, se realiza una evaluación gráfica, posteriormente, una evaluación financiera bajo el supuesto de cero costos de transaccionalidad sobre un valor hipotético de inversión, evaluando únicamente el pronóstico de signo, cambiando de estrategia o posición dependiendo del signo del pronóstico y por último se realiza la comparación estadística inferencial de las dos alternativas a través de estadísticas de error y el test de Diebold y Mariano, Diebold and Mariano (1995).
El RMSE (Root Mean Square Errors) evalúa la precisión de pronóstico promedio y con el Test de Diebold y Mariano se compara esta precisión para los dos modelos bajo una prueba de hipótesis. Esta prueba consiste en determinar a un nivel de significancia específico cuál de las dos metodologías tiene mejores resultados. Ambos utilizan la serie de errores como herramienta de cálculo. El objetivo de esta prueba es evidenciar estadísticamente si el modelo fraccional presenta mejores proyecciones bajo un pronóstico en rolling.
El estadístico del test bajo hipótesis nula 
Donde:
representa la función de auto-covarianza muestral de las series de diferencias.
4. Resultados
Se evaluó el patrón de persistencia en las tasas cero cupón de un año, cinco años y diez años, a partir del año 2003 hasta 2015 con periodicidad diaria. Se elige entonces la tasa cero cupón a cinco años, ya que fue la única serie que mostró evidencia significativa de persistencia con un parámetro de Hurst de 0,63. Tanto la tasa a un año como la tasa a diez años presentaron resultados de 0.52 y 0.57, respectivamente.
Estimando los parámetros en el proceso de Ornstein Uhlenbeck bajo el supuesto de independencia, se encontró que una media de los rendimientos de 0.0796, desviación estándar de 0.0796 y una reversión a la media de 5.4595.
Para el caso del proceso fraccional Ornstein Uhlenbeck, se estima una media de 0.06063052, una desviación de 0.04591231 y una reversión a la media de 0.05994112. Los valores iniciales para la estimación de parámetros se obtuvieron del proceso tradicional.

Fuente: Generación de estimaciones de tasas con Matlab a partir de datos del Banco de la República.
Cuadro 2 Estimación de las tasas con los dos modelos
En la figura 2, a izquierda, se pueden observar la media de las simulaciones, utilizados como pronostico, bajo el proceso tradicional, cuyo comportamiento muestra una caída de la tasa de interés, con un valor al final de 105 días de 5.93 %. Por su parte, al lado derecho, se muestra el comportamiento de las tasas de interés calculadas a través del modelo fraccional para el mismo intervalo, con un valor final de 6.3%.
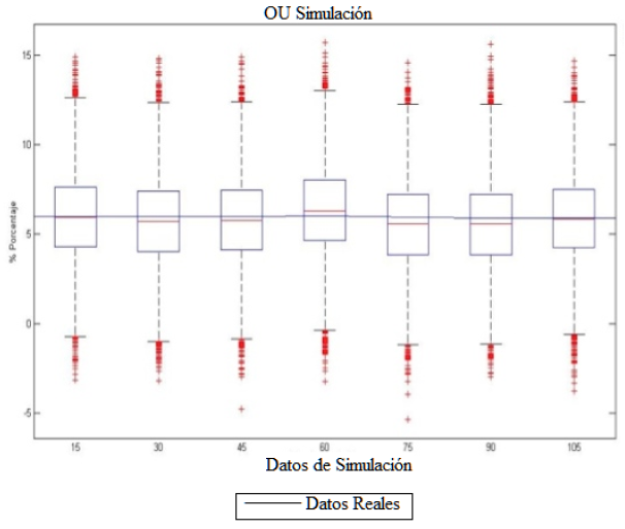
Otra comparación gráfica que permite ayudar a evaluar el pronóstico realizado, se realiza a través de un Box-plot, figura 3, de los escenarios de las simulaciones en intervalos de 15 días del modelo Ornstein Uhlenbeck. La línea media que atraviesa los cajas, representa el valor real de la serie, que para el backtestimg realizado, dado que esta se encuentra siempre dentro del rango intercuartilico, se considera visualmente, un pronóstico aceptable; no obstante con la posibilidad de valores extremos importantes.
Fuente: Simulaciones realizadas con Matlab a partir de datos del Banco de la República.
Figura 3 Resultados Proceso Ornstein Uhlenbeck.
Fuente: Simulaciones realizadas con Matlab a partir de datos del Banco de la República.
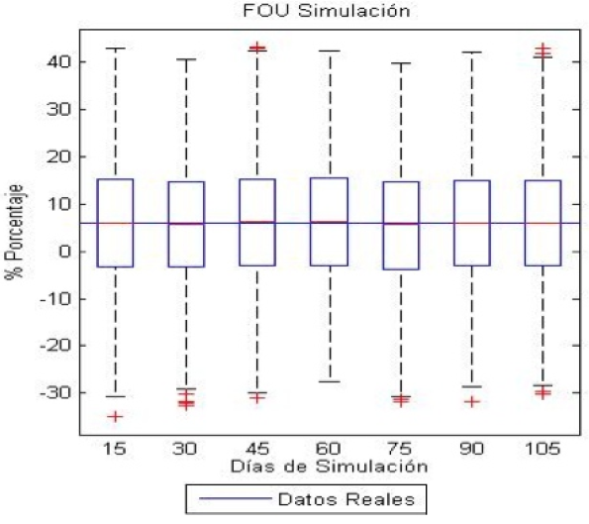
Figura 4 Resultados Proceso Fraccional Ornstein Uhlenbeck.
Al realizar la misma evaluación gráfica pero con el proceso fraccional Ornstein Uhlenbeck se evidencian leves mejorías visuales, se observa menos dispersión en el pronóstico y sus observaciones no se concentran en los extremos como si ocurre en el anterior proceso, aunque los valores extremos que se pueden llegar a presentar en el proceso fraccional, son mayores.
Las posibilidades de escenarios extremos visibles bajo las dos metodologías podrían sugerir posteriores desarrollos de evaluación de riesgo de mercado, de stress testing, sobre la variable en análisis.
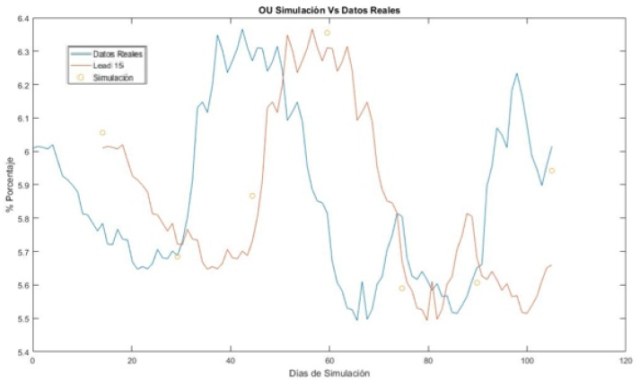
Para complementar el análisis gráfico, como ya se mencionó, se realiza un análisis financiero con el fin de determinar qué proceso tiene mayor exactitud al pronosticar la tendencia. La aplicación del primer modelo, con la simulación y pronóstico a quince días en comparación con los datos reales, se puede apreciar en la figura 5. La línea que empieza en una abscisa de cero, corresponde al comportamiento de la tasa de interés real durante el período observado, que determina el momento de la posición. La que inicia en 15 días, es el valor lead de 15 días real de la tasa spot al momento de evaluar la posición en comparación con los círculos que representan los pronósticos bajo el proceso de simulación. Se puede ver que los pronósticos a 15 días en los periodos de 15, 60 y 75 días fueron más imprecisos en el pronóstico de signo.
Fuente: Simulaciones realizadas con Matlab a partir de datos del Banco de la República.
Figura 5 Análisis de tendencia proceso Ornstein Uhkenbeck
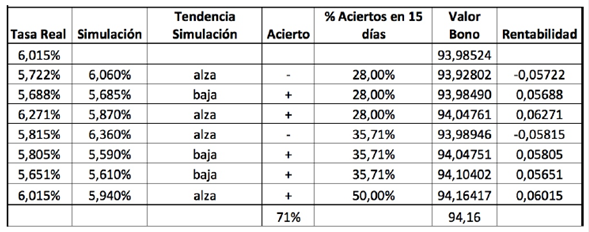
Para cuantificar en términos financieros el desempeño de pronóstico de signo, se estableció un precio del bono de 93.98 y se cambió la posición cada quince días según la tendencia que se pronostica de las tasas. Bajo este escenario se encuentra que para un rango de 105 días, la tasa de precisión de signo del modelo tradicional fue de 75%, lo que quiere decir, que conlleva a un precio final, que se obtiene al cerrar la posición de la estrategia, de 94.16. Bajo este escenario, la rentabilidad de la estrategia establece un 0.663% EA. Este valor que es bajo, se da a causa del poco movimiento que tuvieron las tasas en el período evaluado, ya que al principio del período la tasa se encontraba en 6.01% EA y al final del período la tasa se encontraba nuevamente en el mismo valor. Los resultados se pueden ver en la tabla 1. El valor agregado de la estrategia radica en obtener una rentabilidad mayor en el período en el que no se esperaban mayores movimientos de la tasa, realizando pronósticos de corto plazo, lo que permite mantener la rentabilidad de un portafolio en momentos en donde el mercado no muestra señales claras de un cambio en la tendencia.
Tabla 1 Resultados Análisis Financiero Proceso Ornstein Uhlenbeck
Fuente: Cálculos realizados con Matlab a partir de datos del Banco de la República.
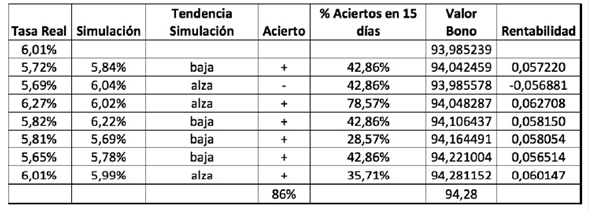
La misma estrategia se implementa, para el modelo fraccional como se observa en la figura 6. El valor del bono es 93.98 nuevamente al iniciar el período y el valor al cerrar la posición fue de 94.28, lo que significó una rentabilidad 1.099% EA para el mismo período. El modelo fraccional tuvo una efectividad en el pronóstico de signo de 85%, lo que asocia una mayor rentabilidad. La diferencia se puede ver en que el proceso fraccional fue más efectivo al predecir la tendencia y por lo tanto, las ganancias en cada posición acertada compensó las pérdidas en las posiciones en las que no se acertó la misma.

Fuente: Cálculos realizados con Matlab a partir de datos del Banco de la República.
Figura 6 Análisis de tendencia proceso Fraccional Ornstein Uhkenbeck
En comparación con la figura 5, la figura 6 muestra que las simulaciones se acercan mucho más a los resultados reales, generando mayor confianza en la estimación de las tasas de interés a través de este método que incorpora el patrón fraccional. Los resultados numéricos se pueden observar en la tabla 2, donde a diferencia de la estrategia usada con el otro modelo, ésta tuvo mejor desempeño en el pronóstico de tendencia.
Tabla 2 Resultados análisis financiero proceso fraccional Ornstein Uhlenbeck
Fuente: Cálculos propios en Matlab con datos del Banco de la República.
Se reitera que el pronóstico de la tendencia de cada uno de los modelos se realizó a través de la media de la generación de 10.000 escenarios de tasa bajo el proceso de simulación de Montecarlo. Con los resultados, se podría sugerir que a medida que la serie es más persistente, el porcentaje de acierto bajo simulación aumenta.
El RMSE comprobó parte de los resultados obtenidos anteriormente con respecto a la precisión promedio de pronóstico de cada uno de los modelos. La estadística para el modelo fraccional Ornstein Uhlenbeck fue de 0.0019, mientras que para el proceso Ornstein Uhlenbeck fue de 0.0028, lo que permite concluir que la estimación para el proceso fraccional presenta mejores cualidades de pronóstico que su alternativa no fraccional.
El test de Diebold y Mariano, mostrado en la tabla 3, exhibe la evaluación en Rolling de las dos alternativas. Se muestra d promedio para identificar el signo de la resta de errores, esperando valores positivos que indican una mejor precisión con el modelo fraccional. La columna F corresponde a los diferentes horizontes de evaluación y el estadístico de prueba se presenta en la última columna.
El test de Diebold y Mariano, mostrado en la tabla 3, exhibe la evaluación en Rolling de las dos alternativas. Se muestra d promedio para identificar el signo de la resta e errores, esperando valores positivos que indican una mejor precisión con el modelo fraccional. La columna F corresponde a los diferentes horizontes de evaluación y el estadístico de prueba se presenta en la última columna.
Tabla 3 Resultados test de Diebold y Mariano
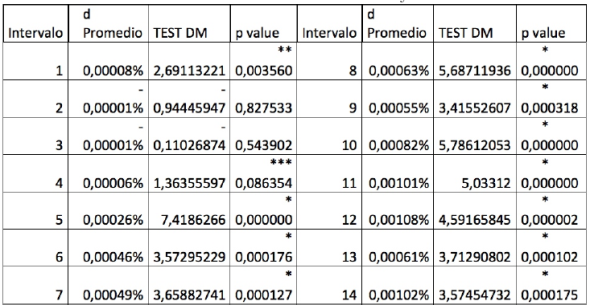
Criterios de significancia * 1%, ** 5% y ***10%. El test se muestra en valor absoluto.
Fuente: Cálculos propios en Matlab con datos del Banco de la República.
En este caso en particular casi todas las diferencias fueron positivas, con excepción del segundo y tercer horizonte de tiempo, aunque sin significancia estadística. Lo que claramente evidencia una mejor precisión con el proceso fraccional
5. Conclusiones y Recomendaciones.
La primera conclusión surge de la estimación de los parámetros del modelo en donde su valoración junto con la aplicación del parámetro de Hurst, puede generar períodos más volátiles como se puede ver en la figura 2. Aunque son procesos distintos debido a la implementación del parámetro de persistencia, los resultados nos dicen que la estimación de mínimos cuadrados realizada en el proceso fraccional, pudo influir en los resultados en comparación con la estimación por máxima verosimilitud realizada en el proceso que asume independencia.
Para lograr una buena estimación de las tasas, es importante que el número de simulaciones en cada uno de los pasos de ambos procesos sea significativo, puesto que el sesgo y el resultado al acertar la tendencia pueden variar de tal manera que la estrategia financiera no sea válida en términos del experimento realizado para comparar ambos modelos.
Complementando lo anterior, hacer un pronóstico mayor a 15 días con modelos de tasas de interés de corto plazo puede traer problemas en los resultados, ya que como se apreció en la figura 2, a pesar de que el resultado al final del período en el día 105 fue cercano a lo que sucedió realmente, dentro del período observado, existen resultados que se alejan considerablemente de los datos reales.
Los estadísticos RMSE y Diebold y Mariano, complementan el análisis gráfico y financiero y respaldan los resultados obtenidos por las simulaciones realizadas anteriormente, demostrando que efectivamente el pronóstico realizado a través del proceso fraccional, presenta resultados más confiables y es una buena alternativa de análisis, ya que la serie que se analizó dentro del proceso presento problemas de persistencia.











 nova página do texto(beta)
nova página do texto(beta)