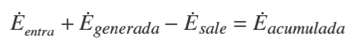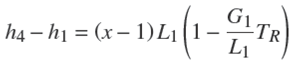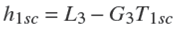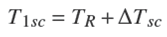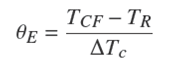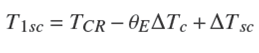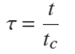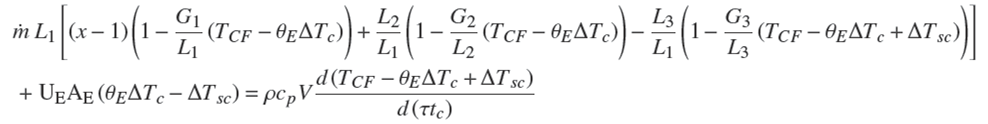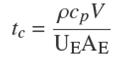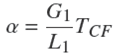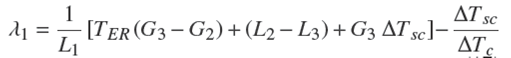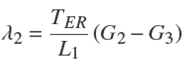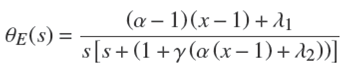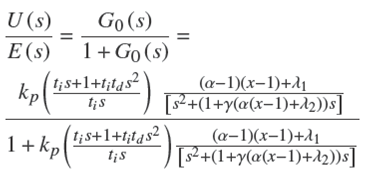1 Introducción
Los sistemas de refrigeración en la actualidad son esenciales para el confort del ser humano, ya sea para refrigerar productos perecederos, medicamentos, químicos, a nivel industrial, comercial y doméstico. Uno de los principales componentes de los sistemas de refrigeración es el evaporador que se encarga de retirar la carga térmica del espacio a refrigerar, aprovechando el cambio de fase del fluido refrigerante. Sin embargo, la dinámica de la operación del sistema provoca oscilaciones en la temperatura de trabajo del evaporador, lo que generará desgaste y esfuerzos mecánicos en el compresor (Navarro-Esbrí y col., 2010; Yamaguchi y col., 2009); además monitorea las condiciones de operación a las entradas y salidas de los equipos y componentes del sistema de refrigeración, encontrando que la temperatura en la zona de saturación del fluido puede oscilar hasta ± 6 °C, lo que genera una fluctuación en la presión de ±10bar, cuando se trabaja con CO2 como fluido refrigerante, que corresponde a las condiciones de los estados de saturación. Esta variación se atenúa, si el fluido de trabajo es el HFC-134a, ya que al considerar el mismo cambio de temperatura de acuerdo a las propiedades de saturación, la presión se vería afectada en una variación de 1.0 a 1.2 bar.
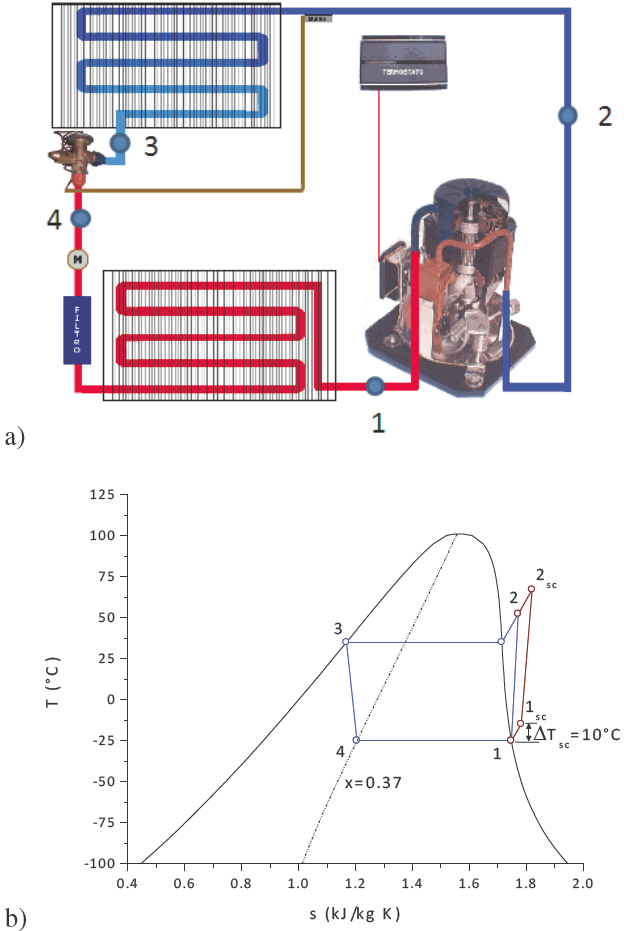
Así mismo, los sistemas de refrigeración mecánica funcionan con un control de lazo abierto tipo ON- OFF, donde la temperatura de la cámara fría fluctúa en un rango amplio en referencia a la temperatura de operación, por consiguiente, establecer la dinámica del sistema con base a la termodinámica del fluido puede mejorar el desempeño del sistema, así como sobrecalentar el fluido antes de entrar a la etapa de compresión, con el objetivo de disminuir las oscilaciones de la temperatura T y T1sc Figura 1.
Sen y col., (2001, 2004), Ollero de Castro y col., (2010), Seborg y col. (2011) presentan modelos matemáticos para establecer la dinámica de la temperatura en un intercambiador con fluidos incompresibles y sin que presenten un cambio de fase, además de aplicarle un control clásico, lo que permite controlar la señal de salida. Los modelos se obtienen a partir de balances de energía y del método de resistencia interna despreciable, para lo cual el número de Biot debe ser >>> 0.1, que generalmente para este tipo de sistemas se cumple, debido a que el fenómeno de transferencia de calor convectivo es dominante sobre el conductivo.
La operación del sistema de acuerdo con Dincer y col., (2010), depende de las propiedades y características termofísicas del fluido refrigerante; debido a esto, en este trabajo se desarrolla una metodología genérica que incluye las propiedades del fluido, así como el cambio de fase debido a la absorción del calor latente que proviene de la cámara de refrigeración. Un primer modelo es desarrollado por Salazar y col., (2013), donde muestra la dinámica del evaporador, sin embargo, sólo se considera el cambio de fase sin sobrecalentamiento de vapor, es decir, el estado final es vapor saturado seco.
2 Metodología
En la Figura 1 se muestra el ciclo de refrigeración por compresión de vapor utilizando como fluido refrigerante al HFC-134a. El ciclo está constituido por cuatro procesos, en primer orden se encuentra la absorción del flujo de calor en el evaporador, proceso 1-4, este proceso depende de las características inherentes del sistema, es decir, de las condiciones de entrada del fluido refrigerante al evaporador, estado 4 y de las condiciones de salida, estado 1 sc .
En el ciclo ideal, generalmente se analiza la salida del evaporador y entrada de la admisión al compresor como vapor saturado seco; sin embargo por cuestiones de estabilidad y seguridad en la operación del sistema de refrigeración se sobrecalienta el vapor para que no dañe al compresor. Por consiguiente, los principales parámetros que afectan la operación del sistema de refrigeración son la calidad del fluido refrigerante a la entrada del evaporador y la temperatura del fluido en la admisión del compresor. Aunado a estas características de operación, la temperatura en la cámara de refrigeración fluctúa con respecto a la carga térmica y la temperatura en su interior, lo que se ve reflejado en la temperatura de operación del evaporador. Por consiguiente, controlar la temperatura a la salida del evaporador es fundamental para un mejor desempeño del ciclo de refrigeración.
Para encontrar el modelo dinámico del evaporador se hace el balance de energía
En términos de las propiedades termodinámicas y de transferencia de calor, además de considerar que no se tienen fugas de refrigerante, se tiene la siguiente expresión
La diferencia de entalpías h4 - h1 , representa el cambio de fase del fluido por efecto del calor latente retirado de la cámara fría y h 1 − h1sc , es el incremento de energía por efecto del calor sensible en el sobrecalentamiento,
La metodología del modelo dinámico sin sobrecalentamiento del refrigerante se desarrolla en Salazar y col., (2013) y se considera como base para este análisis.
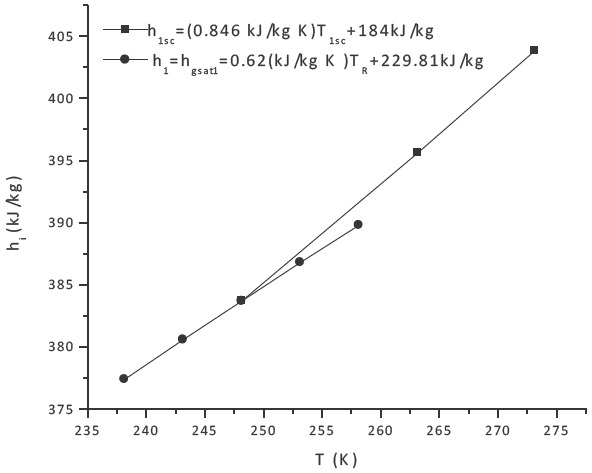
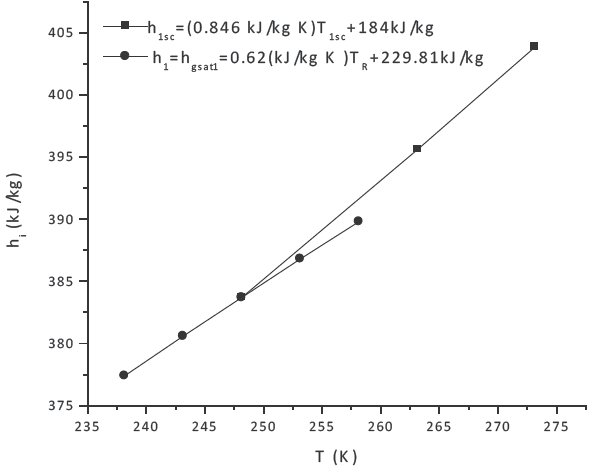
Con la finalidad de obtener un modelo dinámico en función de las temperaturas del evaporador, se utilizan correlaciones matemáticas para establecer la dependencia de la entalpía de cambio de fase, la entalpía del vapor saturado seco con la temperatura de cambio de fase, es decir, TR, y la entalpía de vapor sobrecalentado en función de T1sc , Figuras 2 y 3. En términos de coeficientes se obtienen correlaciones algebraicas de la forma hi = Lj −GjTk , por consiguiente se tiene,
A la salida del evaporador se obtiene vapor sobrecalentado, donde la temperatura se define como,
∆Tsc es el incremento de temperatura al sobrecalentar el vapor saturado seco.
Se definen variables adimensionales para obtener un modelo matemático adimensional; θ E es la temperatura adimensional en el evaporador y se define con base al cambio de fase del fluido refrigerante que se genera al absorber el flujo de calor proveniente de la cámara fría, por consiguiente está en función de la temperatura del espacio a refrigerar, TCF y TR , así como de un cambio de temperatura característico, ∆Tc
T1sc se define
También se define el tiempo adimensional τ,
Sustituyendo en la ecuación (1), se tiene que,
donde, el tiempo característico y el incremento de temperatura característico son:
Realizando procedimientos algebraicos se obtiene la ecuación dinámica del evaporador adimensional
donde
λ1 y λ2 son las constantes adimensionales que integran los parámetros de las entalpías de cambio de fase, de vapor saturado seco y sobrecalentado,
La ecuación (14) es una E.D.O de variables separables También, la ecuación (20) se puede escribir de la de primer orden lineal, y para obtener la solución en el dominio de la variable compleja "s" se le aplica la transformada de Laplace, por consiguiente la función de transferencia es,
Con base a las funciones de transferencia en el dominio de la variable compleja "s", se aplica el método de asignación de polos y el criterio de Routh- Hurwitz para encontrar las contantes Kp , Kd , Ki ; y probar la ley de control clásica proporcional integral derivativa, PID, (Kuo y col., 2008; Ogata y col., 2003, Rubio, 2012; Rubio, 2014).
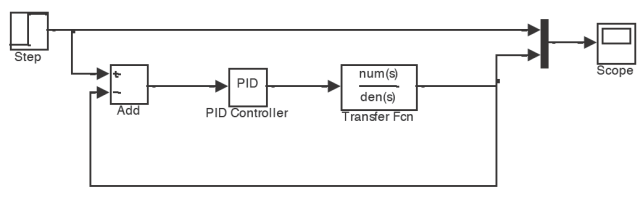
La ecuación (20) representa la dinámica de la entrada actuando sobre los parámetros de la misma para producir la respuesta E(s); es decir, es la representación matemática de la planta del sistema de la Figura 4,
También, la ecuación (20) se puede escribir de la siguiente forma
3 Resultados y discusión
En la Tabla 1 se presentan las condiciones de operación del evaporador y se considera una carga térmica de 2TR. En la Tabla 2 se presenta el valor numérico de las constantes adimensionales λ para las ∆Tsc = 0°C y 10°C.
Las constantes de control PID se presentan en la Tabla 3. Las Kp, Ki y Kd se obtienen para las condiciones de temperatura de cambio de fase de −15°C, x =0.37 y ∆Tsc = 0°C y 10°C.
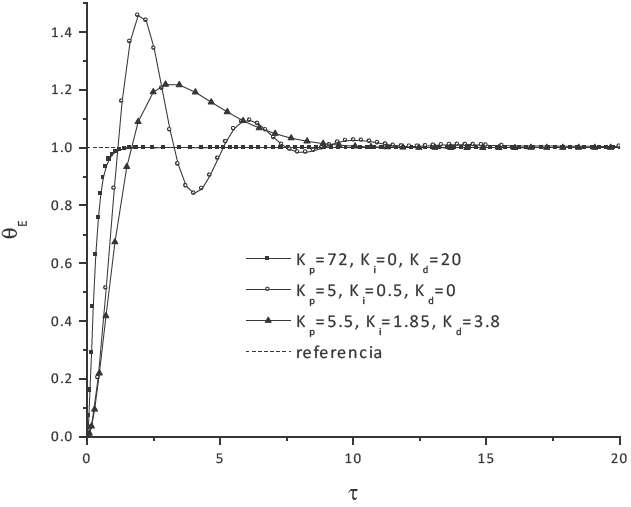
En la Figura 5 se muestra la respuesta de la señal del control PD, PI, PID para el evaporador con sobrecalentamiento de ∆T= 10°C, los valores se obtienen aplicando el método de asignación de polos. El control PD asienta la respuesta de salida en un τ menor a 5; sin embargo, el esfuerzo de control es muy grande comparado con el PID, aunque éste tiene un tiempo de asentamiento de τ = 10. El control PI no es una opción para este sistema, ya que no presenta un menor tiempo de asentamiento de la señal y los sobretiros son del 48%. El control PID es la mejor opción para este sistema, debido a que el esfuerzo es menor al PD y el tiempo de asentamiento es también aceptable.
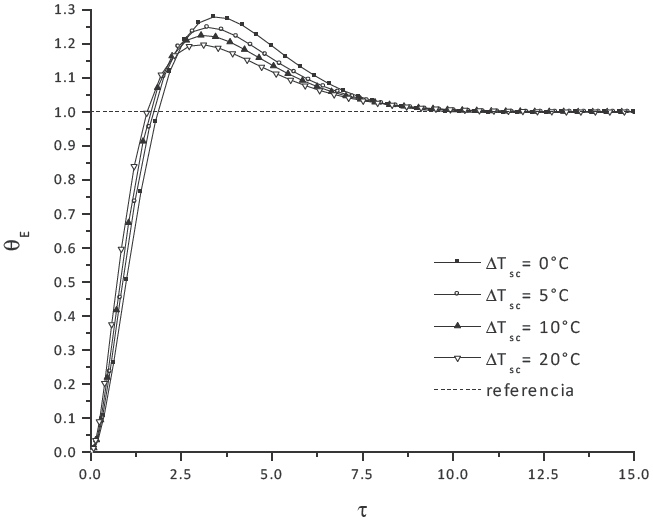
De acuerdo a las constantes de control PID, el esfuerzo de control disminuye conforme se sobrecalienta el vapor a la salida del evaporador; sin embargo, de acuerdo al comportamiento de la respuesta de salida mostrados en la Figura 6, se tiene que el sobrecalentamiento hasta ΔTsc= 10°C es el adecuado para el sistema, ya que al aumentar el valor de ∆T por encima de este valor, la estabilidad de la respuesta no semejora significativamente. Al comparar la respuesta del sistema, al control PID con las constantes obtenidas para ∆Tsc = 0°C, Figura 6 y de ∆Tsc=10°C, Figura 7, se muestra que como el esfuerzo de control que se requiere para controlar la salida del evaporador con vapor saturado seco es mayor a cuando se sobrecalienta, la variación del grado de sobrecalentamiento se atenúa cuando se considera este estado de salida.
En las Figuras 8 y 9 se muestra el comportamiento de la señal de salida aplicando el control PID. Los sobretiros de la señal se incrementan conforme aumenta la calidad del vapor, este fenómeno es representativo de un mal proceso de estrangulamiento, que precede a la entrada del fluido refrigerante al evaporador, disminuyendo así el efecto refrigerante, por consiguiente el sistema es más inestable. Sin embargo, los sobretiros de la señal disminuyen al aumentar el grado de sobrecalentamiento del vapor a la salida del evaporador, tal como se muestra en la Figura 7.
Al aplicar la ley de control PID a la dinámica del evaporador, se obtiene una metodología matemática que muestra el comportamiento a la salida del equipo, que es importante predecir y controlar para evitar daños al siguiente equipo, que es el compresor. Así mismo, esta metodología se puede utilizar para evaluar cualquier tipo de fluido refrigerante siempre que se investiguen sus propiedades termodinámicas del refrigerante o en otra aplicación con el vapor de agua, si se trata de una caldera o un generador de vapor.
Conclusiones
El incremento de la calidad del vapor hace más inestable la operación del evaporador, debido a que disminuye el efecto refrigerante del sistema de refrigeración, incrementando los sobre tiros hasta en un 15%, cuando la calidad varía en un intervalo de 0.37 a 0.7, lo que generará un mayor desgaste en las tuberías y uniones del evaporador. Sin embargo, la estabilidad del sistema se puede mejorar al sobrecalentar el vapor hasta 10°C, lo que implicaría una disminución de las elongaciones máximas de señal de respuesta hasta de 5%.
Los modelos dinámicos del evaporador se obtienen de forma genérica, ya que se puede evaluar para diferentes tipos de refrigerantes, siempre que se conozcan sus propiedades termofísicas. Para un trabajo futuro se plantea el desarrollo del modelo dinámico del evaporador considerando la variación del coeficiente global de transferencia de calor en función de la temperatura de trabajo del evaporador para diferentes tipos de refrigerantes, lo que implicaría establecer un control térmico no lineal.
Nomenclatura
A |
área, m2 |
c P |
calor específico a presión constante, kJ/kg K |
Ė |
flujo de energía, kW |
h |
entalpía por unidad de masa, kJ/kg |
K |
constante de control |
ṁ |
flujo másico, kg/s |
s |
entropía por unidad de masa, kJ/kg K |
T |
temperatura, °C, K |
t |
tiempo, s |
U |
coeficiente global de transferencia de calor, kW/m2 K |
V |
volumen, m3 |
x |
calidad del vapor |











 nueva página del texto (beta)
nueva página del texto (beta)