Simulación y control

 

Control múltiple entrada una salida (MISO) de un CSTR

 

Multiple input–single output (MISO) control of a CSTR

 

A. Velasco–Pérez^1*, J. Álvarez–Ramírez², y R. Solar–González³

 

¹ Facultad de Ciencias Químicas, Universidad Veracruzana. Prolongación de Oriente 6 No. 1009 Col. Rafael Alvarado. Orizaba, Veracruz 94340, México. *Autor para la correspondencia. E–mail: alvelasco@uv.mx Tel./Fax: (272) 72 4 01 20.

² Departamento de Ingeniería de Procesos e Hidráulica, Universidad Autónoma Metropolitana, Av. San Rafael Atlixco No. 186 Col. Vicentina 09340, México, D.F., México.

³ División de Estudios de Posgrado, Universidad del Istmo. Ciudad Universitaria, Ba. Sta. Cruz Tagolaba, Sto. Domingo Tehuantepec, Oaxaca 70760, México.

 

Recibido 5 de Enero 2011.
Aceptado 7 de Abril 2011.

 

Resumen

En este trabajo se aborda el control múltiple entrada–simple salida ( M ISO) de un modelo genérico simple de un CSTR. El diseño de control se basa en modelos simples entrada–salida y la inversión de filtros de adelanto–atraso. Se propone un procedimiento de síntesis de controladores basados en una factorizacion de plantas de múltiple entrada–una sa lida lo cual conduce a una estructura de control paralela. El controlador propuesto realiza el balance en el uso de las entradas de control por medio de un problema de optimizacion. Simulaciones numéricas muestran el desempeño y comparación del esquema de control contra su contraparte SISO.

Palabras clave: control MISO, CSTR, factorización, control paralelo.

 

Abstract

This paper addresses the multiple input – single output (MISO) control problem of a simple generic model of a CSTR. The control design is based on simple models and the inversion of dead–beat filters. It is proposed a synthesis procedure of controllers based on the factorization of MISO plants that leads to a parallel control structure. The proposed controller performs a balance in the use of the control inputs via an optimization problem. Numerical simulations show the performance and comparison of the control scheme against its counterparts SISO.

Keywords: MISO control, CSTR, MISO factorization, parallel control.

 

1 Introducción

Los reactores continuos de tanque agitado (CSTR) son las unidades de proceso de mayor importancia en un proceso químico industrial. En particular, el CSTR no isotérmico no adiabático es el reactor de mayor aplicación para muchas reacciones de interés industrial (Froment y Bischoff, 1990). Debido a su relevancia, el CSTR ha sido objeto de numerosos estudios sobre estabilidad (Aris y Amundson, 1958; Uppal y col., 1974; Pellegrini y Biardi, 1990; Paladino y Ratto, 2000; Melo y col., 2003; Perez y Albertos, 2004; Ma y col., 2010), estimación de estados (Jana, 2007; Fissore, 2008; Prakash y Senthil, 2008) y control de procesos (Alvarez–Ramirez, 1994; Viel y col., 1997; Alvarez–Ramirez y Puebla, 2001; Czeczot, 2006; Pan y col., 2007; Prakash y Srinivasan, 2009; Yazdi y Jahed–Motlagh, 2009; Favache y Dochain, 2010).

Desde un enfoque de control de procesos el control del CSTR se ha abordado con una gran variedad de técnicas de control lineal y no–lineal. Por ejemplo, control clásico y sus derivaciones (Alvarez–Ramirez y Puebla, 2001; Perez y Albertos, 2004; Jana, 2007; Prakash y Srinivasan, 2009), control adaptable (Czeczot, 2006; Pan y col., 2007), control robusto (Fissore, 2008;), control geométrico (Viel y col., 1997; Yazdi y Jahed–Motlagh, 2009), entre otros (Alvarez–Ramirez, 1994; Favache y Dochain, 2010; Prakash y Senthil, 2008). En la mayoría de los trabajos anteriores el control del CSTR se basa en enfoques de una entrada–una salida (SISO) donde la entrada manipulable es la temperatura o el flujo del medio de enfriamiento. Se debe hacer notar que la variable de mayor interés a controlar es la concentración de salida de algún componente de la mezcla reactante, lo cual en el caso no isotérmico se transfiere al control de la temperatura de operación del reactor (Ogunnaike y Ray, 1994).

Es bien conocido que en el CSTR la tasa de dilución del reactor se puede manipular para obtener un desempeño de control más satisfactorio. Esto conduce a un sistema que tiene grados de libertad adicionales para el diseño del control. Para el CSTR el uso de la tasa de dilución como variable manipulable adicional conduce a la posibilidad de manipular los siguientes pares de entradas en forma común: (i) tasa de dilución del reactor – tasa de dilución de flujo del de medio de enfriamiento – flujo de alimentación, (ii) tasa de dilución del reactor – temperatura del medio de enfriamiento, (iii) tasa de dilución del reactor –concentración de alimentación de reactantes.

Los sistemas de control con más entradas que salidas se conocen como sistemas no rectangulares y son muy comunes en procesos químicos y bioquímicos. A pesar de la relevancia de esta clase de sistemas en la literatura se han abordado escasamente, principalmente por modificaciones a esquemas de control multivariable de sistemas rectangulares (Reeves y Arkun, 1989; Chang y Yu, 1990). Una alternativa que se ha reportado en la literatura y que se ha aplicado gradualmente a procesos bioquímicos es a través de una estructura de control paralelo (Henson y col., 1995; McLain y col., 1996; Giovanini, 2007). El control paralelo tiene las características de proveer un buen desempeño a lazo cerrado bajo perturbaciones grandes y con saturaciones en la entrada de control (Monroy–Loperena y col., 2004; Alvarez–Ramirez y col., 2004).

En este trabajo se presenta el diseño de un esquema de control paralelo para un modelo genérico de un CSTR no isotérmico no adiabático. El modelo genérico del CSTR permite presentar las ideas del diseño de control en una forma simple, sin embargo, debido a que el esquema de control propuesto se basa en relaciones entrada–salida simple, las ideas que se presentan aquí se pueden extender en forma directa a modelos más complejos de CSTR o de otra clase de procesos donde se puede manipular más de una entrada de control y se desea controlar solo una variable. Los resultados numéricos muestran que el esquema de control paralelo resultante conduce a un mejor desempeño a lazo cerrado respecto a los esquemas de control SISO.

Con respecto a los resultados reportados en la literatura de control de CSTR dos contribuciones de este trabajo son las siguientes: (i) Se presenta un diseño sistemático simple para abordar el control de CSTR con más de una entrada de control y una variable a controlar que hace uso de la información mínima posible (modelos simples entrada–salida) del proceso, (ii) los resultados se pueden extender en forma directa a modelos de CSTR de mayor complejidad con base a modelos entrada–salida simples que se deriven a través del modelo no lineal del proceso o por medio de técnicas de identificación empírica (Ogunnaike y Ray, 1994; Erdogan y Gulal, 2009).

Este trabajo está organizado como sigue: En la Sección 2 se presenta la descripción de un CSTR y un modelo genérico simple. En la Sección 3 se presenta el diseño del esquema de control paralelo. En la Sección 4 se presentan simulaciones numéricas del esquema de control paralelo y su comparación con esquemas de control SISO.

 

2 Descripción y modelo genérico de un CSTR

En esta sección se presentan brevemente algunas características generales del CSTR, así como un modelo genérico que será usado como caso de estudio en este trabajo.

2.1 Descripción general de CSTR

En el CSTR los reactivos se introducen y los productos se extraen simultáneamente y en forma continua. Por lo general, se considera que un CSTR es homogéneo y por lo tanto se modela sin variaciones espaciales en la concentración, temperatura o velocidad de reacción en todo el recipiente (Froment y Bischoff, 1990). De hecho la consideración más importante en relación a la dinámica del CSTR es que ocurre un mezclado perfecto dentro del reactor. Esto significa que las propiedades de la mezcla reactante se consideran uniformes en cualquier parte dentro del recipiente de reacción y por lo tanto son idénticas a las propiedades de la corriente de salida. Otra consideración importante es que la corriente de entrada se mezcla instantáneamente con la mezcla presente en el reactor. En la práctica, si un elemento de material reactante que entra se distribuye uniformemente por todo el tanque en un tiempo mucho más corto que el tiempo de residencia promedio en el tanque, entonces el tanque se puede considerar bien mezclado. La Fig. 1 muestra un esquema general de un CSTR.

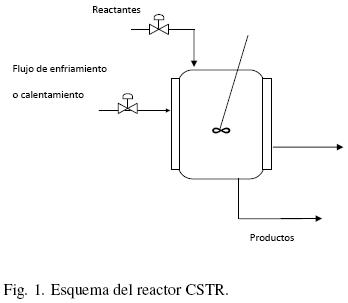
2.2 Modelo genérico simple de un CSTR

Existen interacciones complejas entre los fenómenos de transporte y las cinéticas de reacción que caracterizan los CSTR y determinan su desempeño (Froment y Bischoff, 1990). El modelado matemático de los mecanismos cinéticos y los fenómenos de transferencia de calor ha sido un área de investigación activa en ingeniería química en años recientes. Desafortunadamente en muchos casos la estructura de la cinética de reacción continua aun siendo incierta. En forma similar a otros artículos sobre CSTR, en este trabajo se hace uso de un modelo genérico donde se lleva a cabo la reacción química A 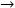B y se tiene una chaqueta de enfriamiento (Aris y Amundson, 1958; Uppal y col., 1974; Alvarez–Ramirez, 1994; Viel y col., 1997). Las variables del proceso son las concentraciones de reactantes y del producto x_A y x_B respectivamente, la temperatura del reactor T, y la temperatura de la chaqueta de enfriamiento T_j. Al formular los balances de masa y energía se obtienen las siguientes ecuaciones,

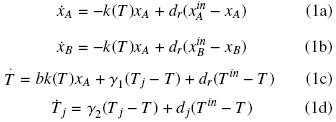
Donde la constante cinética se expresa de acuerdo a la ecuación de Arrenihus,

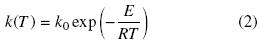
el superíndice in indica las condiciones de entrada, γ₁ y γ₂ indica los parámetros de transferencia de calor, b es la entalpía de reacción, y d_r y d_j son la rapidez de dilución de la mezcla reactante y del medio de enfriamiento respectivamente. El primer término a la derecha de la Ec. (1c) en el modelo (1) es la generación de calor por reacción, el segundo término se debe al enfriamiento/calentamiento de la mezcla reactante por la chaqueta de enfriamiento, y el tercer término es la pérdida de calor total debido al flujo de reactantes y la salida de productos. El calor que se remueve a través de la pared del reactor es proporcional al área de la pared y a la diferencia en temperatura entre la mezcla reactante y un medio de enfriamiento que circula a través de la chaqueta. En la práctica el proceso de extracción de calor se regula al manipular la velocidad del fluido de enfriamiento. En muchos casos la dinámica de la chaqueta es rápida en comparación con la dinámica del reactor, y, por lo tanto, la velocidad del fluido de enfriamiento se enlaza a la temperatura de la chaqueta (Ogunnaike y Ray, 1994).

Es bien conocido que la dependencia exponencial de la velocidad de reacción respecto a la temperatura del reactor es una de las no linealidades principales del CSTR. Como una consecuencia de la no linealidad de la cinética de reacción, el CSTR puede desplegar una gran variedad de comportamientos dinámicos, desde multiplicidad de estados estacionarios, oscilaciones sostenidas (Aris y Amundson, 1958; Uppal y col., 1974; Melo y col., 2003; Ma y col., 2010). Más aun, en la literatura se ha demostrado que el CSTR bajo esquemas de control retroalimentado puede conducir a inestabilidades del proceso a lazo cerrado (Pellegrini y Biardi, 1990; Alvarez–Ramirez, 1994; Paladino y Ratto, 2000; Perez y Albertos, 2004).

Muchos modelos reportados en la literatura de CSTR se pueden describir de acuerdo al modelo que se describe por las ecs. (1a) a (1d). Por otro lado, es bien conocido que para fines de control y optimización los modelos simples que retienen las características dominantes del proceso son más adecuados que modelos más complejos que pueden ser convenientes para fines de diseño. Más aun, el diseño de control que se presenta en este trabajo se basa en aproximaciones entrada–salida entre las entradas manipulables y la variable a controlar y por lo tanto la extensión de la técnica de control debe ser directa a modelos de CSTR más complejos que el modelo descrito por la Ec. (1a).

 

3 Diseño de un esquema de control paralelo

En esta sección se presenta el problema de control que se identifica en este trabajo y se presenta el desarrollo general del esquema de control propuesto.

3.1 Problema de control en CSTR

En CSTR el problema de control de interés principal es el control de concentración de algún componente de la mezcla reactante. Para el caso no isotérmico (adiabático y no adiabático), el problema de control se puede transferir comúnmente al control de la temperatura de la mezcla reactante debido a la correspondencia de la temperatura con la concentración.

Con la finalidad de controlar la temperatura o la concentración en un CSTR comúnmente en la práctica se usa la tasa de dilución de la chaqueta d_j como variable manipulada, sin embargo, la tasa de dilución del reactor d_r se puede manipular fácilmente y por lo tanto se usará como entrada de control adicional para mejorar el esfuerzo de control de la tasa de dilución de la chaqueta. Se debe notar que en algunas aplicaciones se puede considerar que la dinámica de la chaqueta de enfriamiento es muy rápida, y la esencia del problema de control se retiene si la temperatura de enfriamiento T_j, se considera como la variable manipulada principal, sin embargo, nuevamente, la tasa de dilución del reactor se puede usar como variable adicional de control (Ogunnaike y Ray, 1994). Así, el objetivo del control se puede establecer como el de regular la concentración del reactivo x_A(t) a un valor deseado x_A,d.

Si _A es la composición nominal del reactor, _r y _j son las tasas de dilución del reactor y de la chaqueta en condiciones nominales respectivamente, la salida regulada está dada por y(s) = x_A (s) – _A(s), y las entradas de control son u₁(s) = d_j(s) – _j y u₂(s) = d_r(s) – _r. Para completar el problema de control se supone lo siguiente:

A1 La variable a controlar esta disponible para fines de diseño de control.

A2 El modelo dinámico no lineal del CSTR tiene incertidumbres y está afectado por perturbaciones externas desconocidas.

A3 El diseño de control se basa en modelos aproximados entrada–salida simples.

Con relación a las consideraciones anteriores es importante notar lo siguiente:

• La consideración de medición de concentración en un CSTR es fuerte debido a la complejidad en muchos casos de contar con dispositivos para tal efecto, o en su caso debido al retraso en la medición que comúnmente inducen. Sin embrago, muchos modelos de CSTR son observables a través de mediciones de temperatura y se pude usar un estimado para contar con la disponibilidad de la concentración a controlar (Jana, 2007; Fissore, 2008; Prakash y Senthil, 2008).

• La consideración de incertidumbres de modelo en CSTR es realista. En procesos químicos en general existe un alto grado de incertidumbre debido a la presencia de parámetros cinéticos y de transferencia que se determinan en condiciones distintas a las que ocurren comúnmente en la práctica.

• El uso de modelos entrada–salida simple para fines de control es una consideración adecuada debido a las incertidumbre y complejidad de los modelos derivados por principios de conservación. Más aun, dicha consideración es valiosa para derivar esquemas de control que se basen en la información mínima disponible del proceso de tal forma que sea más fácil de llevar a cabo el diseño y la implementación del esquema de control resultante (Ogunnaike y Ray, 1994; Puebla y col., 2009).

3.2 Diseño de control múltiple entrada – una salida

Para el caso del CSTR que se presenta en la sección previa se tiene un sistema múltiple entrada – una salida (MISO por sus siglas en ingles). Específicamente un modelo rectangular dos entradas – una salida, de tal forma que se diseña un controlador que manipule simultáneamente la tasa de dilución de la chaqueta d_j y la tasa de dilución del reactor d_r. Con base a la representación en términos de las funciones de transferencia de las entradas u₁ y u₂, se tiene la función de transferencia,

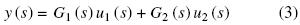
Donde por conveniencia de notación se ha definido y(s) = X_A(s) como la salida regulada, y u₁ (s) = Δd_j (s) y u₁ (s) = Δd_r (s) como las entradas manipuladas. El problema de diseño de control se puede establecer como

donde u (s) = (u₁ (s), u₂ (s)), Cs = (C₁ (s), C₂ (s)) y e_y (s) = y_sp (S) – y (S) es el error de regulación, tal que e_y(t) 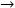0 asintóticamente. Nótese que el controlador retroalimentado resultante manipula en forma paralela ambas entradas del control u₁ (s) y u₂(s), para regular únicamente una salida y(s).

El diseño del control paralelo será diseñado con base en modelos lineales heurísticos de la respuesta al escalón del proceso alrededor del punto de operación nominal de acuerdo al proceso de curva de reacción (Ogunnaike y Ray, 1994). Los modelos lineales determinan la relación entrada–salida d_j 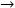X_A y d_r 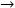X_A y en general se pueden aproximar a modelos estables de primer orden,

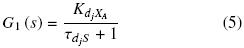
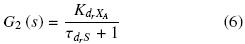
Esto es, las dinámicas entrada – salida d_j 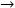X_A y d_r 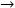X_A se aproximan como procesos estables de primer orden y representan la conexión dinámica entre las variables manipuladas d_j y d_r con la variable regulada X_A.

Para sistemas rectangulares de dos entradas –una salida, y motivados por el sistema de control responsable de la regulación de la presión sanguínea, Henson y col. (1995) propone una metodología sistemática para la síntesis de controladores paralelos para procesos biológicos. La idea principal es aprovechar las características específicas y objetivos operacionales de un proceso con dos diferentes tipos de variables manipuladas: (i) un proceso lento, y (ii) un proceso rápido. Con base a esta propuesta, el procedimiento para obtener un controlador múltiple entrada – una salida, consiste en cuatro pasos (Monroy–Loperena y col., 2004; Alvarez–Ramirez y col., 2004):

(i) Factorización de la función de transferencia de la planta.

(ii) Cálculo de un controlador maestro.

(iii) Uso de un problema de optimización de mínimos cuadrados para obtener un divisor de entrada y,

(iv) Inversión del filtro de adelanto–retraso para obtener las entradas de control finales a implementar.

3.2.1 Factorización

Para factorizar el proceso (3)–(6) se procede como sigue,

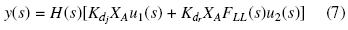
donde,

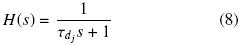
y F_LL(s) es un filtro de adelanto–atraso dado por,

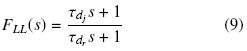
Nótese que F_LL(0) = 1.

3.2.2 ;Cálculo del control maestro

La segunda etapa consiste en el cálculo de un controlador maestro C_M(s) para la planta H(s). La idea es obtener un controlador simple para regular la salida y(s) de un problema de control estándar una entrada–salida (SISO por sus siglas en inglés). Para este fin, se introducirá una entrada de control intermedia definida como w(s),

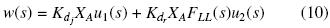
y se obtiene de la planta,

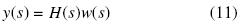
De esta forma, se obtiene una entrada de control w(s) de la planta (8).

La siguiente etapa será para distribuir el esfuerzo de control entre dos entradas de control físicas definidas como u₁(s) y u₂(s) , lo cual corresponde a un problema de inversión rectangular (con un grado de libertad), el cual, después de un proceso de regulación descrito en los pasos (iii) y (iv), lleva las expresiones para las entradas de control u₁(s) y u₂(s) como funciones de la entrada de control intermedia w(s), de acuerdo al esquema que se muestra en la Fig. 2.

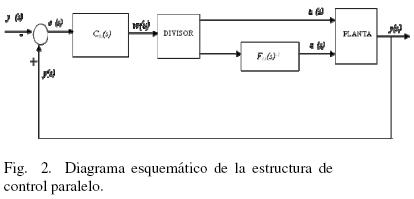
De esta forma en vez de definir ω como función de u₁ y u₂ , la Ec. (10) es una relación funcional entre señales u₁, u₂ y ω.

Se debe de notar que H(s) es estable y un proceso con ganancia unitaria en estado estacionario (es decir, H(0) = 1). Para este tipo de plantas pueden usarse controladores clásicos PI sintonizados con guías IMC (Morari y Zafiriou, 1989). De hecho, si

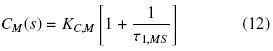
entonces,

Donde τ_C,M es una constante de tiempo de lazo cerrado asignada, la cuál como regla heurística puede tomarse del orden 0.5 a 0.75 veces τ_v.

Cálculo del divisor de la entrada de control

En la sección previa se ha presentado una forma de calcular la entrada del controlador maestro w(s) para asegurar la estabilidad en el sistema a lazo cerrado y la trayectoria asintótica de la salida deseada y_sp. Sin embargo, la entrada de control w(s) está compuesta por la contribución de dos entradas de control independientes K_djX_Au₁(s) y K_drX_AF_LL(s)u₂(s). Así, se requiere de un procedimiento para dividir tales contribuciones. En la literatura existen algunas estrategias para tal efecto que van desde reglas heurísticas a métodos más formales basados en problemas de control óptimo (ver por ejemplo Morari y Zafiriou, 1989).

En este trabajo, de manera similar a la propuesta de Mc Lain y col. (1989) para control paralelo no lineal, la regulación del problema del control rectangular se hace mediante la reducción del costo asociado con el control efectuado. Sea v₂(s) = F_LL(s)u₂(s). Abusando de la notación, se denota la entrada de control u₁(s) en el dominio del tiempo como u₂(s) (lo mismo para v₂(s) y w(s)), y se formula el siguiente problema de optimization de mínimos cuadrados,

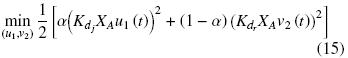
sujeto a la restricción,

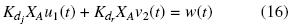
Donde 0 α 1 es una constante de peso en las entradas de control K_djX_Au₁(s) y K_drX_Av₂(s).

De esta forma, se puede ver que las Ees. (15) y (16) como resultantes de un problema de optimization tiempo–a–tiempo donde las entradas de control calculadas u₁(t) y v₂(t) minimizan el índice (15) para cada instante de tiempo t. Por supuesto, pueden utilizarse índices de desempeño más sofisticados, tales como una versión en tiempo infinito de (15).

3.2.4 Recuperación de U2 por inversión.

La última etapa consiste en recuperar la entrada actual u₂(s). Recordando que v₂(s) = F_LL(s)u₂(s), esta parte se puede resolver fácilmente si se observa que F_LL(s) es un filtro estable y de fase mínima, de tal forma que,

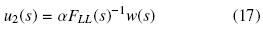
Esto es, la entrada de control actual se recupera, mediante la inversión del filtro adelanto–atraso F_LL(s). De esta forma, el controlador que manipula la tasa de dilución de la chaqueta, d_j es simplemente un compensador desintonizado con un factor 1 – α,

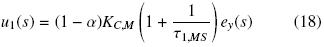
Donde e(s) es el error de regulación. Debe notarse que el papel del compensador u₂(s) adelanto–retraso (τ_dr s + 1)/(τ_dj s + 1) es una fase sincronizada del controlador con respecto a la fase del controlador u₁(s).

Con relación al diseño de control MISO los siguientes comentarios son pertinentes:

• Nótese que u₁ (S) = 0 (respectivamente u₂(S) = 0) cuando α = 1 (respectivamente α = 0). Esto es, cuando α = 1 la tasa de disolución de la chaqueta d_j toma su valor nominal _j y toda la dinámica y esfuerzo de control estacionario está en función al control de la tasa de dilución del reactor. A la inversa, cuando α = 0 el punto de referencia de la tasa de dilución del reactor se mantiene en su valor nominal _r y toda la dinámica y esfuerzo de control en estado estacionario se realiza por el controlador de la tasa de dilución de la chaqueta. Cuando 0 < α1, ambos controladores tienen una contribución no trivial a la regulación de la composición del reactante X_A. De esta forma, el esquema de control paralelo propuesto tiene una estructura de un controlador balanceado para 0 < α < 1 (Monroy–Loperena y col., 2004; Alvarez–Ramirez y col., 2004).

• Además del parámetro α, asociado al peso que se le asigna a las entradas de control, el esquema de control paralelo tiene dos parámetros de diseño τ_C,M y τ_I,M, los cuales se pueden proponer en función de la constante de tiempo más lenta de las respuestas entrada–salida del proceso y de la constante de tiempo τ_v.

• El controlador paralelo tiene una ventaja adicional con respecto a un esquema de control de una entrada, puede distribuir mejor el esfuerzo de control con saturaciones en las entradas de control. En el esquema de control paralelo la saturación de una de las señales de control puede compensarse con otra entrada de control, siendo capaz de regular la salida efectivamente.

 

4 Simulaciones numéricas

En esta sección se presentan simulaciones numéricas para el modelo genérico presentado en la Sección 2 usando el proceso de control MISO (d_j+ d_r 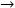X_A) presentado en la Sección 3. Se presenta además la comparación del desempeño del esquema MISO, respecto a los controladores SISO (d_j 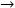X_A, y d_r 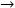X_A). Se debe notar que el diseño de control se basa en las funciones de transferencia simples entrada–salida y la implementacióín se efectúa en el modelo no–lineal del CSTR. Más aun, en las simulaciones numéricas se consideran perturbaciones típicas en esta clase de sistemas.

4.1 Parámetros de la simulación

Para la simulaciones se consideran los siguientes valores de los parámetros del reactor: k₀ = 1.3677x10⁸ min^–1, E/R= 7290.11 K, = 100 mol/m³, = 0 mol/m³, Tⁱⁿ = 300 K, b = –0.01196 K mol/m³, γ₁= 0.191 min^–1, γ₂ = 0.574 min^–1. Los valores nominales son _A = 8.3 mol/m³ y _j = 0.075 min^–1. Las entradas de control se saturan en los limites d_j = [0.025, 0.15] y d_r = [0.005, 0.015].

La Fig. 3 muestra el mapa en estacionario del reactor químico. La línea punteada indica una posible referencia de concentración, la cual puede alcanzarse con todas las intersecciones de la línea punteada en estado estacionario de la tasa de dilución de la chaqueta y el reactor.

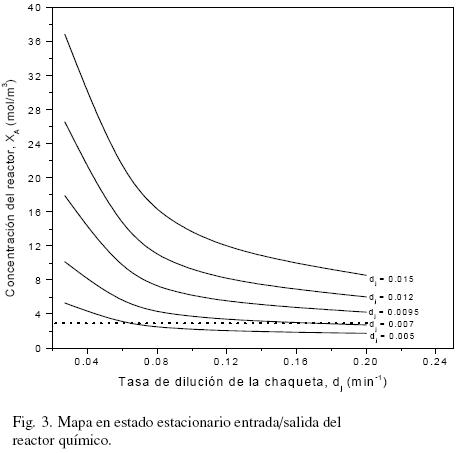
De la respuesta escalón, se determinan los parámetros k₁ = –76.5 mol/(m³min), k₂ = 1461 mol/(m³min), τ₁ = 48 min y τ₂ = 22 min. Utilizando ideas del sintonizado IMC, los parámetros del controlador son K_I = 0.0413 mol/(m³min) y λ = 20 min^–1. El parámetro α para los casos SISO se establece como 0 y 1 para los pares d_j 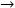X_A y d_r X_A, respectivamente. Para el control MISO se han seleccionado tres valores de α. La elección de los valores de α es para fines ilustrativos del desempeño de control para la regulación de la composición del reactante X_A, cuando se le asigna un peso mayor a la entrada de control d_j (α = 0.25), a la entrada de control d_r (α = 0.75), o un esfuerzo balanceado de las dos entradas de control (α = 0.5). En general, el valor de α se puede asignar a través del efecto de las entradas de control en forma individual y un compromiso entre el desempeño deseado del sistema a lazo cerrado. Una vez asignado el valor de α se obtiene la solución del problema de optimización (15) y (16) que determina los valores de las entradas de control.

4.2 Control SISO

Las figs. 4 y 5 muestran la respuesta del CSTR bajo la acción del controlador a un cambio de referencia en un tiempo de t = 2000 min y una perturbación en escalón de +25% en en t = 2600 min para los casos SISO con d_j(s) y d_r(s) como entradas de control respectivamente. Se puede observar que la respuesta del control SISO con el par d_r X_A es mejor (más rápida y suave) respecto al control SISO con el par d_j X_A. Esto se puede asociar a que la constante de tiempo de la tasa de dilución del reactor es aproximadamente 0.5 veces la constante de tiempo de la tasa de dilución de la chaqueta. Desde el punto de vista físico, esta diferencia se puede explicar mediante las dinámicas de la chaqueta presentes, las cuales actúan como un filtro pasa–bajas para la acción de control de la tasa de dilución de la chaqueta d_j(s).

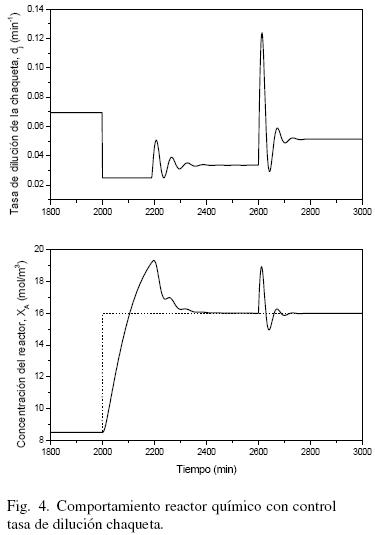
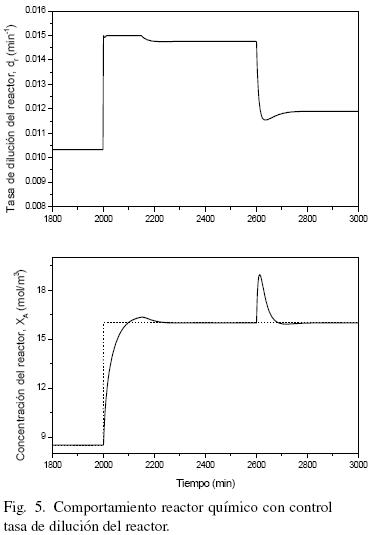
A pesar de que la respuesta cuando la tasa de dilución actúa sola puede ser aceptable, en la práctica los operadores son resistentes a grande variaciones en la tasa de dilución del reactor, lo cual puede tener un efecto significativo en la tasa de producción. Por otro lado, a pesar de que el uso de la tasa de dilución de la chaqueta en general es no cara desde un punto de vista de esfuerzo de control, la respuesta del CSTR controlado es lenta y algunas veces oscilatoria (ver Fig. 4). Con base a las observaciones anteriores se puede inferir que la arquitectura de control paralelo puede mejorar el desempeño de control del par d_j 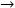X_A y además no hacer uso de entradas de control elevadas del par d_r X_A.

4.3 Control MISO

La Fig. 6 presenta la respuesta del CSTR controlado para los tres diferentes valores de α. Se puede observar que en comparación con la respuesta del sistema controlado cuando únicamente se utiliza la tasa de dilución de la chaqueta, la respuesta se mejora cuando α disminuye. Esto se debe a que el esfuerzo de control se comparte por las dos entradas de control y conduce a la disminución de variaciones severas en la tasa de dilución del reactor. Se puede observar además en la Fig. 6 que la contribución balanceada de las dos entradas de control permite disminuir la saturación de la dilución de la chaqueta de enfriamiento respecto al caso SISO y en general se disminuyen en forma importante los sobredisparos de la variable controlada, además de que se observa un mejor rechazo a perturbaciones.

4.4 Comparación SISO vs MISO

En la Fig. 7 se muestra el comportamiento del reactor químico cuando actúa únicamente el control de la tasa de dilución del reactor o bien cuando actúa únicamente el control de la tasa de dilución de la chaqueta, así como la respuesta del sistema bajo el esquema de control paralelo y en el cual se involucran a las entradas de control anteriores.

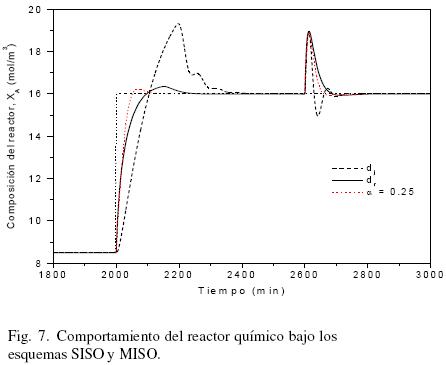
Observamos cómo bajo la estructura de control paralelo el sistema se recupera mucho más rápido a cambios de referencia y a perturbaciones en el sistema que bajo esquemas de control de un solo lazo.

 

Conclusiones

En este trabajo se ha abordado el problema de control múltiple entrada – una salida en un modelo genérico de un CSTR. Para el diseño de control se hace uso de modelos entrada–salida simples y, con base a una elección adecuada de la factorization entrada–salida del CSTR se deriva un esquema de control maestro que determina un problema de balance de las múltiples entradas de control. Una vez diseñado el control maestro se formula un problema de optimization simple para el balance óptimo de las entradas de control. Se presentaron además guías generales para la elección adecuada de los parámetros del controlador propuesto. Las simulaciones numéricas muestran que el desempeño del control MISO es mejor que el control SISO y que permite disminuir la saturación de la entrada de control, el sobredisparo de la variable controlada, y mejora el rechazo a perturbaciones. El mejor desepempeño del esquema de control propuesto respecto a sus contrapartes SISO se debe a la capacidad de manipular variables de entrada adicionales que disminuyen el esfuerzo de control de una sola variable y distribuyen además el efecto del cambio de las variables manipulables en la corrección más suave del sistema a controlar. A pesar de que el esquema de control MISO se aplica a un modelo genérico simple de un CSTR las ideas que se presentan aquí deben de encontrar aplicación en un modelos mas complejos de CSTR, así como para diferentes elecciones de las variables a manipular y a controlar. En efecto, a partir de modelos lineales simples entrada–salida que se deriven en forma teórica (linearization y derivación de la función de transferencia) o experimental (identificación empírica) los pasos que se presentan en la metodología de diseño se pueden extender en forma directa.

 

Referencias

Alvarez–Ramirez J. (1994). Stability of a class of uncertain continuous stirred chemical reactors with a nonlinear feedback. Chemical Engineering Science 49, 1743–1748.         [ Links ]

Alvarez–Ramirez, J y Puebla, H. (2001). On classical PI control of chemical reactors. Chemical Engineering Science 56, 2111–2121.         [ Links ]

Alvarez–Ramirez, J; Velasco, A; Fernandez–Anaya, G. (2004). A note on the stability of habituating process control. Journal of Process Control 14, 939–945.         [ Links ]

Aris R. y Amundson, N.R. (1958). An analysis of chemical reactor stability and control–I, II, III. Chemical Engineering Science 7, 121–155.         [ Links ]

Chang, J.W. y Yu, C.C. (1990). The relative gain for nonsquare multivariable systems. Chemical Engineering Science 45, 1309.         [ Links ]

Czeczot, J. (2006). Balance–based adaptive control methodology and its application to the non–isothermal CSTR. Chemical Engineering and Processing 45, 359–371.         [ Links ]

Erdogan, H. y Gulal, E. (2009). Identification of dynamic systems using multiple input–single output (MISO) models. Nonlinear Analysis: Real World Applications 10, 1183–1196.         [ Links ]

Favache, A. y Dochain, D. (2010). Power–shaping control of reaction systems: The CSTR case. Automatica 46, 1877–1883.         [ Links ]

Fissore, D. (2008). Robust control in presence of parametric uncertainties: Observer–based feedback controller design. Chemical Engineering Science 63, 1890–1900.         [ Links ]

Froment, G.F. y Bischoff, K.B. (1990). Chemical Reactor Analysis and Design. Wiley, New York.         [ Links ]

Giovanini, L. (2007). Cooperative–feedback control. ISA Transactions 46, 289–302.         [ Links ]

Henson, Ma., Ogunnaike, Ba. y Schwaber, Js. (1995). Habituating control strategies for process–control. AIChE Journal 41, 604–618.         [ Links ]

Jana, A.K. (2007). Nonlinear state estimation and generic model control of a continuous stirred tank reactor. International Journal of Chemical Reactor Engineering 5, A42.         [ Links ]

Ma, K.M., Valdes–Gonzalez, H. y Bogle, I.D.L. (2010) Process design in SISO systems with input multiplicity using bifurcation analysis and optimization. Journal of Process Control 20, 241–247.         [ Links ]

McLain, R.B., Kurtz, M.J., Henson, M.A. y Doyle, F.J. (1996). Habituating control for nonsquare nonlinear processes. Industrial & Engineering Chemistry Research 35, 4067–4077.         [ Links ]

Melo, P.A., Biscaia, E.C. y Pinto, J.C. (2003). The bifurcation behavior of continuous free–radical solution loop polymerization reactors. Chemical Engineering Science 58, 2805–2821.         [ Links ]

Monroy–Loperena, R., Solar, R. y Alvarez–Ramirez, J. (2004). Balanced control scheme for reactor/separator processes with material recycle. Industrial & Engineering Chemistry Research 43, 1853–1862.         [ Links ]

Morari, M. y Zafiriou, E. (1989). Robust Process Control. Prentice Hall, New York        [ Links ]

Ogunnaike, B.A. y Ray, W.H. (1994). Process Dynamics, Modeling and Control. Oxford University Press, New York.         [ Links ]

Paladino, O. y Ratto, M. (2000). Robust stability and sensitivity of real controlled CSTRs. Chemical Engineering Science 55, 321–330.         [ Links ]

Pan, T.H., Li, S.Y. y Cai, W.J. (2007). Lazy learning–based online identification and adaptive PID control: A case study for CSTR process. Industrial & Engineering Chemistry Research 46, 472–480.         [ Links ]

Pellegrini, I. y Biardi, G. (1990). Chaotic behavior of a controlled CSTR. Computers and Chemical Engineering 14, 1237–1247.         [ Links ]

Perez, M. y Albertos, M. (2004). Self–oscillating and chaotic behavior of a PI–controlled CSTR with control valve saturation. Journal of Process Control 14, 51–59.         [ Links ]

Prakash, J. y Senthil, R. (2008). Design of observer based nonlinear model predictive controller for a continuous stirred tank reactor. Journal of Process Control 18, 504–514.         [ Links ]

Prakash, J. y Srinivasan, K. (2009). Design of nonlinear PID controller and nonlinear model predictive controller for a continuous stirred tank reactor. ISA Transactions 48, 273–282.         [ Links ]

Puebla, H., Rodriguez, M.G., Martinez–Delgadillo, S.A., Mendoza, V. y Gomez–Callejas, S. (2009). A simple robust control approach for Cr (VI) regulation of wastewater at electrochemical mixed–flow reactors in series. Chemical Engineering Communications 196, 1278–1290.         [ Links ]

Reeves, D.E. y Arkun, Y. (1989). Interaction measures for nonsquare decentralized control structures. AIChE Journal 35, 603.         [ Links ]

Uppal, A., Ray, W.H. y Poore, A.B. (1974). On the dynamic behavior of continuous stirred tank reactors. Chemical Engineering Science 29, 967–985.         [ Links ]

Viel, F., Jadot, F. y Bastin, G. (1997). Global stabilization of exothermic chemical reactors under input constraints. Automatica 33, 1437–1448.         [ Links ]

Yazdi, M.B. y Jahed–Motlagh, M.R. (2009). Stabilization of a CSTR with two arbitrarily switching modes using modal state feedback linearization. Chemical Engineering Journal 155, 838–843.         [ Links ]