Introducción

Uno de los retos que tiene el sistema educativo mexicano en el siglo XXI es mejorar la calidad de la educación que ofrece, y con ello incrementar la cantidad de alumnos en los niveles más altos de las pruebas educativas internacionales y nacionales (^{Uribe, López-Córdova, Mancera y Barrios, 2012}; y ^{Castañeda, 2014}). Mejorar la calidad educativa es un procedimiento complejo que implica identificar variables que se asocien al rendimiento académico para establecer estrategias de intervención. Así lo declaran ^{Saucedo, Valle, Ulloa, Hubert y Potter (2015)}. Se necesita encontrar evidencia empírica sobre las variables macro demográficas que inciden en el proceso de enseñanza-aprendizaje en México, ya que es menos consistente y más escasa; de esta manera se podrían proponer cambios educativos para mejorar la calidad. Confirmando lo anterior, en el estudio realizado en el norte de México por ^{Vales García, Acosta Quiroz y Echeverría Castro (2015)} se menciona que existe la necesidad de relacionar el rendimiento académico con las variables sociodemográficas.

Marco Teórico

Pruebas para evaluar el rendimiento académico

A nivel internacional, los alumnos de sexto grado de primaria del estado de Nuevo León, han sido evaluados por el SERCE (Segundo Estudio Regional Comparativo y Explicativo) en 2006 (^{UNESCO-OREALC, 2008}) y el Tercer Estudio Regional Comparativo y Explicativo (TERCE) en 2013 (^{UNESCO-OREALC, 2013}). En ambas evaluaciones los resultados no fueron alentadores, según se muestra en la tabla 1. El porcentaje de niños de sexto grado de primaria en los niveles de logro III y IV en el Estado disminuyó en el TERCE (ver tabla 1).

Tabla 1 Porcentaje de alumnos por nivel en SERCE y TERCE. 

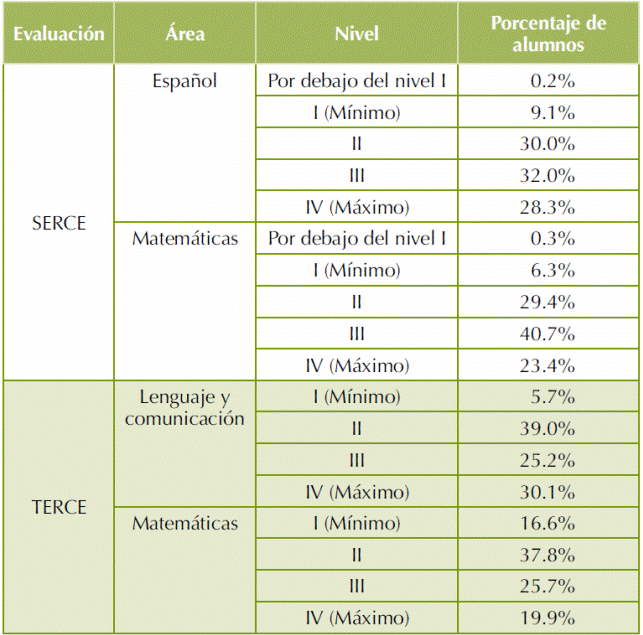
Fuente: elaboración propia con datos del INNE

La tabla 1 muestra que la mayor cantidad de escolares estaba en el nivel III en las áreas de español y matemáticas, mientras que en el TERCE, el porcentaje más alto de estudiantes se ubica en el nivel II, en las áreas de lenguaje y comunicación, y de matemáticas. Con respecto al rendimiento académico en evaluaciones nacionales, los alumnos del estado de Nuevo León, no han tenido buenos resultados. En 2013, prácticamente uno de cada dos alumnos de 3ro, 4to, 5to y 6to grados de Nuevo León tenía un nivel de logro bueno o excelente en español y matemáticas en los Exámenes Nacionales del Logro Académico en Centros Escolares (ENLACE). Además, en ese mismo año, el Estado tuvo un incremento de 19.4% y 27.8% de alumnos en español y matemáticas, respectivamente en los niveles de logro bueno o excelente en dichos grados con respecto al 2006, aunque dicho aumento fue inferior a la media nacional (^{SEP, 2013}).

Otra prueba en México que midió el rendimiento de los alumnos de sexto año de primaria en Nuevo León fueron los Exámenes de la Calidad y el Logro Educativos (EXCALE). Los EXCALE son evaluaciones que miden el logro del alumno en áreas y grados específicos y han sido aplicadas cada cuatro años desde el 2005 y hasta la fecha en el nivel de educación básica (^{INEE, 2016}). En los EXCALE, los logros fueron desalentadores. La tabla 2 muestra la distribución de los alumnos por área, nivel de logro y año. Como se puede observar, más de la mitad de los alumnos en cada área y año se concentran en el nivel de logro básico y por debajo del básico en las áreas de español y de matemáticas.

Tabla 2 Porcentaje de alumnos por área, nivel de logro y año en EXCALE. 

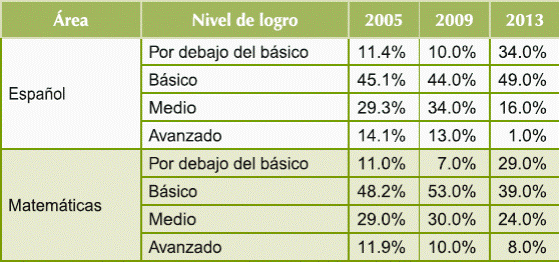
Fuente: Elaboración propia con datos del INEE

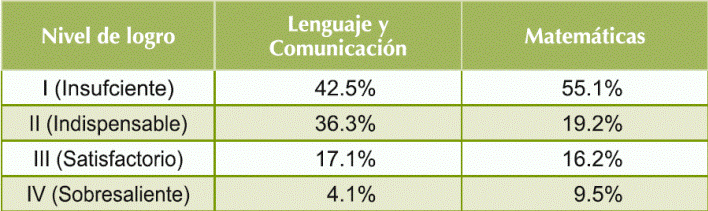
La evaluación nacional más reciente en los escolares del sistema educativo mexicano es la del Plan Nacional para la Evaluación de los aprendizajes (PLANEA), el cual fue diseñado por el INEE y la Secretaría de Educación Pública (SEP). En PLANEA, los resultados de los alumnos de sexto grado de Nuevo León siguen siendo pobres en las áreas de lenguaje y comunicación, y de matemáticas. La tabla 3 muestra la distribución de alumnos según el nivel de logro en cada área. Llama la atención que el 42.5% de los alumnos -en lenguaje y comunicación- y el 55.1% de los alumnos -en Matemáticas- egresan de ese nivel sin los aprendizajes suficientes para afrontar los retos que el sistema educativo mexicano les marca en el siguiente nivel de estudios. Uno de los efectos que tendrá este fenómeno es que el rendimiento académico de los escolares será insuficiente para lograr tener éxito.

Tabla 3 Porcentaje de alumnos por nivel de logro 

Fuente: elaboración propia con datos INEE

Identificar los factores que se relacionan al rendimiento académico de los alumnos, es el primer paso para marcar las estrategias a implementar como apoyo a los escolares y que logren tener éxito en su vida académica (^{García de Fanelli, 2014}). Hay ciertas variables sociodemográficas que serán incluidas en este estudio para verificar si están asociadas al rendimiento escolar en las áreas de matemáticas y lenguaje como son el tipo de educación -pública y privada-, el sexo, la edad, grado de marginación, considerando la disponibilidad de dicha información en la base de datos de ^{INEE (2016)}.

Metodología

La información que se analizó en el presente estudio, parte de los resultados de la primera aplicación de Planea Básica, cuya operación la llevó a cabo el INEE en conjunto con la Secretaría de Educación Pública (SEP). El INEE compartió en su página de Internet la base de datos que se obtiene de PLANEA, en donde se señala que tal información es del dominio público (^{INEE, 2015}). Se trabajó con la base de datos de PLANEA del año 2015 del estado de Nuevo León, México, debido a que el rigor metodológico que siguió el INEE en su aplicación cumple con los criterios para la selección de una muestra representativa. Es decir, que sea estadísticamente válida y con la cual se puedan hacer inferencias, el tipo de muestreo necesario y la correcta medición de los logros en lenguaje y comunicación y en matemáticas, además de la facilidad al acceso de la información porque fue publicada por el ^{INEE (2015)} en su página de Internet.

El tipo de estudio fue descriptivo y correlacional. La muestra fue representativa del total de alumnos del estado de Nuevo León, México ya que cumple con los criterios de aleatoriedad y tamaño de muestra para hacer inferencias. Se analizaron 4,007 estudiantes en el ciclo escolar 2014-2015, pertenecientes al sexto grado de educación primaria. Los criterios de inclusión en el análisis fueron que el alumno: 1) haya ingresado a primero de primaria con una edad de 6 años cumplidos al primero de diciembre, 2) tuviera una edad no mayor a 13 años cumplidos al momento de ser evaluado y 3) perteneciera al sistema educativo público o privado.

El INEE proporcionó, en la base de datos de PLANEA 2015, seis variables para realizar estudios a profundidad en las áreas de lenguaje y comunicación, y de matemáticas en cada una de las entidades federativas. En el caso del estado de Nuevo León, las variables que se proporcionaron y tomaron para llevar a cabo la presente investigación, fueron: 1) que el escolar haya ingresado a primero de primaria con una edad de 6 años cumplidos al primero de diciembre, 2) el tipo de escuela, pública o privada, 3) el grado de marginación o Índice de Marginación del Consejo Nacional de Población (CONAPO) donde se encuentra la escuela, 4) el número de preguntas contestadas correctamente en cada área, 5) la edad, y 6) el género del alumno.

Existen diferentes maneras de medir el rendimiento académico; la más común es por medio de las calificaciones en la escuela (^{Mazadiego y Vallejo, 2006}) o exámenes nacionales en áreas como matemáticas, lenguaje, entre otras. También se manejan como indicadores del rendimiento los promedios de asignaturas como Matemáticas, Español, etcétera (^{Castillo-Parra, Gómez y Ostrosky-Solís, 2009}). En otros casos, el rendimiento se mide por medio del número de aciertos en exámenes estandarizados (^{Florence, Asbridge y Veugelers, 2008}).

En el presente estudio, el rendimiento académico en LC (lectura y comprensión) y en MAT (matemáticas) se determinó por medio del número de preguntas contestadas correctamente o aciertos en cada área, el cual a su vez midió el logro de aprendizaje. En otras palabras, se contó con el nivel de logro (I: insuficiente, II: indispensable, III: satisfactorio y IV: sobresaliente) en las áreas de LC y de MAT de cada alumno, así como la respuesta (correcta o incorrecta) que cada escolar tuvo en las preguntas correspondientes al área evaluada.

Como parte de la medición del rendimiento académico, se verificó en cada área que mientras aumente el nivel de logro de un alumno, también se incremente el número de preguntas contestadas correctamente por medio de un análisis de varianza, en donde la variable dependiente fue el número de preguntas contestadas correctamente en LC y en MAT y el tratamiento fue el nivel de logro por área. Las variables consideradas en la investigación fueron:

En el estudio se describieron algunas de las características de los alumnos pertenecientes a la muestra. En seguida, se comparó el número de aciertos en LC y MAT entre las categorías de cada una de las variables, determinando primero si la distribución del número de aciertos de cada área, en cada una de las variables, era aproximadamente normal por medio de la prueba de Kolgomorov-Smirnov. Se aplicó la prueba U de Man-Whitney para contrastar el número de aciertos en LC y MAT para las variables tipo de escuela y sexo del alumno. Se utilizó también la prueba de Kruskal-Wallis para el grado de marginación de la localidad donde se encuentra la escuela y la edad del alumno. En todos los casos, se consideró un resultado estadísticamente significativo para un p-valor < 0.05.

^{Reyes, Escobar, Duarte y Ramírez (2007)} aplicaron un modelo de regresión logística binaria en donde tomaron el rendimiento estudiantil como variable dependiente (éxito o no éxito). Dicho modelo es útil cuando la variable dependiente es cualitativa dicotómica. Así pues, en el presente estudio, se generaron dos modelos de regresión logística binaria. En el primero de ellos, la variable dependiente fue el rendimiento académico en LC, en donde tal variable se codificó a cualitativa binaria, y cuyas categorías fueron: número de aciertos menor a la mediana (22 aciertos) y número de aciertos mayor o igual a la mediana (22 aciertos). Para el segundo modelo, la variable dependiente fue el rendimiento académico en MAT, también codificada a cualitativa binaria: número de aciertos menor a la mediana (21 aciertos) y número de aciertos mayor o igual a la mediana (21 aciertos). Para ambos modelos, las variables independientes que se utilizaron fueron: tipo de escuela, grado de marginación de la localidad donde se encuentra la escuela, sexo y edad del alumno. En cada modelo, la variable grado de marginación tuvo las siguientes categorías: 1) marginación muy baja o baja y 2) marginación media o muy alta o alta.

Por último, se hizo un análisis de correlación y regresión lineal simple; como variable dependiente se tomó el rendimiento académico en MAT (cuantitativa) y la variable independiente fue el rendimiento académico en LC (cuantitativa). Entre ellas, se calculó el coeficiente de correlación de Pearson, su respectivo p-valor y el coeficiente de determinación. También se generó el modelo de regresión lineal simple entre MAT y LC. Se consideró un resultado estadísticamente significativo para un p-valor < 0.05.

Resultados

La muestra estuvo conformada por un total de 4,007 estudiantes; 2,052 (51.2%) niños, 1,955 (48.8%) niñas. Las edades mínima y máxima fueron 11 y 13 años, respectivamente, con una edad media de 11.6 años y una desviación estándar de 0.6 años. El total de escolares que pertenecían a escuelas públicas fue de 3,499 (87.3%), 506 (12.6%) de privadas y 3 (0.1%) comunitarias, es un modelo de trabajo escolar que integra alumnos pertenecientes a diferentes conocimientos y edades de una comunidad. La cantidad de alumnos en escuelas con un grado de marginación medio, muy alto o alto fue de 1,394 (34.8%), mientras que 2,614 (65.2%) tuvieron un grado muy bajo o bajo. El 100% de las escuelas privadas se ubican en localidades con un grado de marginación muy bajo o bajo.

Como se comentó, el rendimiento académico se midió por medio del número de preguntas contestadas correctamente en cada área y este a su vez mide de forma indirecta el nivel de logro tanto en LC como en MAT. Es decir, mientras aumenta el nivel de logro, también se incrementa el número medio de respuestas contestadas correctamente en ambas áreas como se muestra en las figuras 1 y 2.

Fuente: elaboración propia

Figura 1 Nivel de logro y número medio de aciertos en LC. 

Fuente: elaboración propia

Figura 2 Nivel de logro y número medio de aciertos en MAT. 

Para verificar el supuesto de que al aumentar el nivel de logro, también se incrementa el número medio de respuestas contestadas correctamente en LC y MAT, se realizó un análisis de varianza (tabla 5) para determinar que efectivamente existe una diferencia significativa en el número de aciertos por nivel de logro y después se aplicó la prueba de Scheffe (tablas 6 y 7) para comprobar que el número de aciertos se distribuye en cuatro categorías, las cuales corresponden a los niveles de logro por área.

Tabla 5 Análisis de varianza. 

Fuente: elaboración propia

Tabla 6 Análisis post hoc para el número de aciertos en I.C.: Prueba de Scheffee 

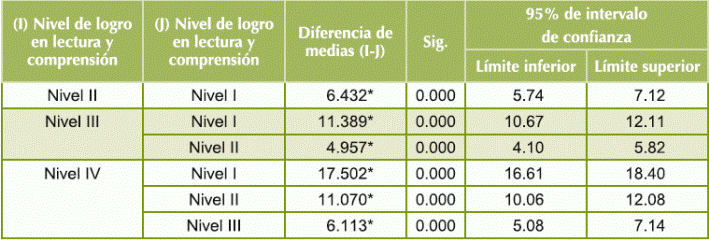
Fuente: elaboración propia

Tabla 7 Análisis post hoc para el número de aciertos en MAT: prueba de Scheeffee. 

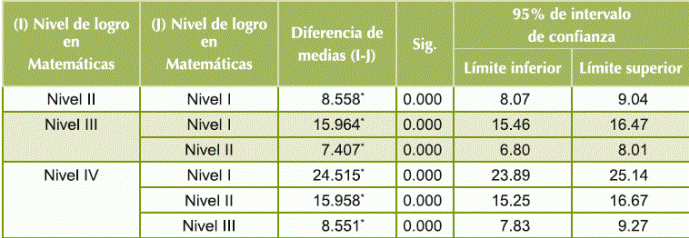
Fuente: elaboración propia

Los resultados muestran que al aumentar el nivel de logro en cada área, también se incrementa el número de aciertos. En otras palabras, estadísticamente es válido tomar el número de aciertos como indicador del nivel de logro. Por lo tanto, a partir de este momento, se utilizará rendimiento académico como sinónimo de nivel de logro.

Las tablas 8 y 9 muestran la comparación en la distribución del rendimiento académico en las áreas de LC y de MAT en cada una de las variables consideradas. Al aplicar las pruebas estadísticas correspondientes, se encontró que existe una diferencia significativa en la distribución del rendimiento académico en ambas áreas, en: el tipo de escuela, el grado de marginación de la localidad donde se encuentra la escuela, la edad del alumno y el sexo del alumno. En otras palabras, con referencia al tipo de escuela, los resultados muestran que es mayor el rango promedio del rendimiento académico obtenido por niños del sistema privado en ambas áreas. En el caso del grado de marginación, mientras este sea muy bajo o bajo, el rango promedio del rendimiento académico aumenta significativamente en cada área. En lo que se refiere al sexo, las mujeres obtienen un rango promedio superior al de los hombres en cada área. Por último, los resultados de la edad muestran que el rango promedio del rendimiento académico en LC y MAT es más alto a los 12 años.

Tabla 8 Comparacion en la distribución del rendimiento académico en L.C.  

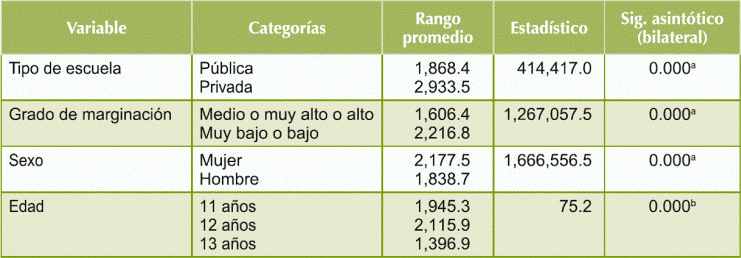
^a Prueba U de Man- Whitney

^b Prueba de Kruskal- Wallis

Fuente: elaboración propia con informacion de PLANEA 2015

Tabla 9 Comparación en la distribución del rendimiento académico en MAT. 

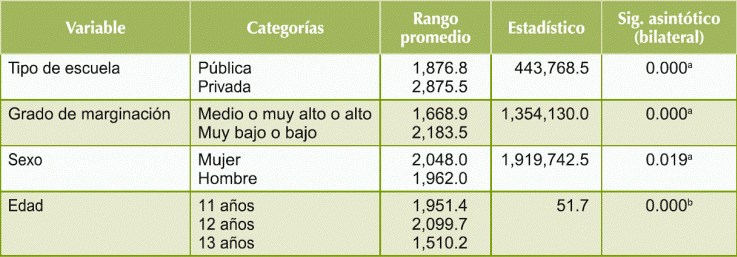
^a Prueba U de Man- Whitney

^b Prueba de Kruskal- Wallis

Fuente: elaboración propia von información de PLANEA 2015.

Los resultados de las tablas 8 y 9 indican que probablemente existe una relación entre las variables tipo de escuela, grado de marginación, sexo y edad con LC y MAT. Para determinar tal asociación, se generaron dos modelos de regresión logística binaria multivariada, uno para cada área. La tabla 10 muestra los resultados de ambos modelos.

Los modelos 1 para LC y 2 para MAT que se muestran en la tabla 10 tienen un nivel de predicción de 61.8% y 59.4%, respectivamente. Además, los resultados se pueden agrupar en dos factores: 1) riesgo es definido en este estudio como aquel que disminuye la probabilidad de obtener un rendimiento académico mayor o igual a la mediana en LC y en MAT y 2) favorecedor es entendido como un factor que aumenta la probabilidad de obtener un valor mayor o igual a la mediana en cada una de las dos áreas.

Tabla 10 Variables asociadas al LC Y MAT. 

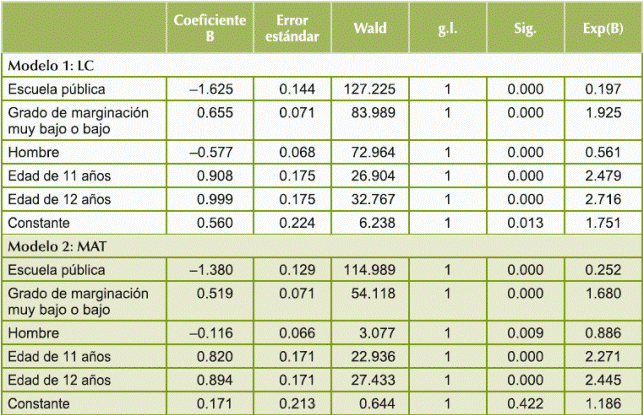
Nota: Para el modelo 1, -2log de la verosimilitud = 5,016.890; R cuadrado de Cox y Snell = 0.107; R cuadrado de Nagelkerke = 0.143. Para modelo 2, -2log de la verosimilitud = 5,182.021; R cuadrado de Cox y Snell = 0.072; R cuadrado de Nagelkerke = 0.096.

Fuente: Elaboración propia con información de PLANEA 2015

En otras palabras, los factores de riesgo para LC y MAT son el tipo de escuela y el sexo del alumno. Es decir, para LC un alumno de escuela pública tiene 0.19 veces más probabilidades de obtener al menos 22 aciertos que un alumno de escuela privada. Por otro lado, un estudiante de género masculino tiene 0.56 veces más probabilidades de tener un rendimiento académico no menor a 22 con respecto a una mujer. En el caso de MAT, un alumno de escuela pública tiene 0.25 veces más probabilidades de obtener 21 aciertos o más con respecto a uno de escuela privada, y un hombre tiene 0.88 veces más probabilidades de obtener al menos 21 aciertos con respecto a una mujer.

De forma análoga, se explican los factores favorecedores que son grado de marginación de la localidad donde se encuentra la escuela y la edad del alumno para ambas áreas. En el caso de LC, un estudiante que pertenezca a una escuela con un grado de marginación bajo o muy bajo tiene 1.92 veces más probabilidades de obtener al menos 22 aciertos; mientras que los niños de 11 y 12 años de edad tienen 2.47 y 2.71 veces, respectivamente, más probabilidades de obtener como mínimo 22 aciertos. Para MAT, los factores son algo similares; pertenecer a una escuela con un grado de marginación bajo o muy bajo, aumenta en 1.68 veces la probabilidad de obtener al menos 21 aciertos. Por último, un alumno de 11 años de edad tiene 2.27 veces más probabilidades de obtener un rendimiento académico superior o igual a 21, mientras que un niño de 12 años tiene 2.44 veces más probabilidades de obtener 21 o más aciertos. Finalmente, se determinó la asociación que existe entre las áreas de LC y de MAT. Se realizó un análisis de correlación lineal de Pearson y regresión lineal simple en el cual la variable dependiente fue el rendimiento académico en MAT y la variable independiente fue el rendimiento académico en LC.

En la figura 3, se puede observar una correlación lineal de Pearson, positiva y significativa de 0.725 (p-valor < 0.001) entre el rendimiento académico en ambas áreas. En otras palabras, cuando aumenta el rendimiento académico en LC, también se incrementa el rendimiento académico en MAT. El coeficiente de determinación es de 0.525. Es decir, el 52.5% de la variación en el rendimiento académico en MAT es explicado por el rendimiento académico en LC. El modelo de regresión lineal simple generado, fue: MAT = 4.013 + 0.809LC. El p-valor para la constante, el coeficiente correspondiente a la variable LC y el análisis de varianza del modelo fue de 0.000, en cada caso. En otras palabras, el modelo es significativo y de él se puede decir que por cada acierto que un alumno tenga en LC, se espera que el rendimiento académico en MAT aumente en 0.809. Además, el rendimiento académico esperado en MAT cuando no hay aciertos en LC es aproximadamente 4.013.

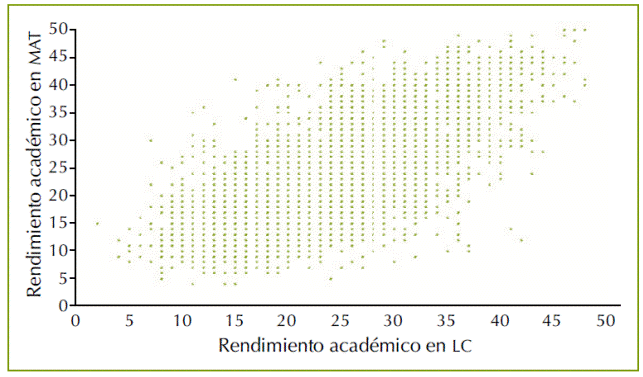
Correlación lineal de Pearson positiva y significativa (p-valor<0.001).

Fuente: Elaboración propia

Figura 3 Diagrama de dispersión entre el rendimiento académico en LC y MAT. 

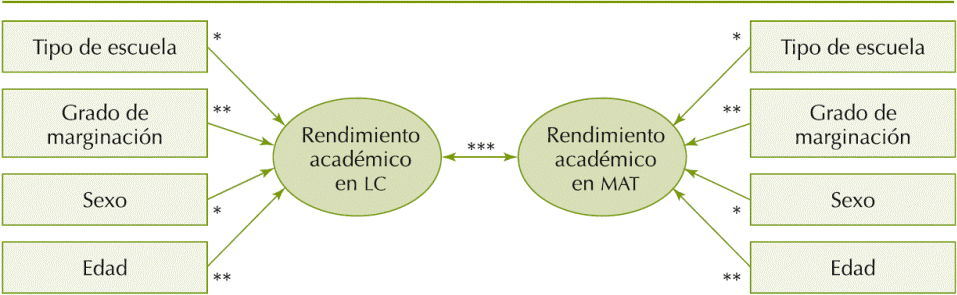
En síntesis, las asociaciones que se encontraron entre las variables que conforman los factores de riesgo y favorecedores, tipo de escuela, grado de marginación, sexo y edad con el rendimiento académico en LC, y con el rendimiento académico en MAT, y entre estas dos áreas, se pueden representar en la figura 4.

^*Factor riesgo

^** Factor de protección

^***Correlacion lineal positiva y significativa (p-valor<0.001)

Fuente: Elaboración propia

Figura 4 Asociación entre el rendimiento académico en LC y MAT y factores de riesgo y favorecedores. 

Discusión de resultados

Los análisis realizados a los resultados de PLANEA (2015) indican que existe una asociación entre el tipo de escuela, el grado de marginación de la localidad donde se encuentra la escuela, el sexo y la edad del alumno con el rendimiento académico en las áreas de lenguaje y comunicación y de matemáticas en escolares de sexto grado de educación primaria en el estado de Nuevo León, México. Se encontró un alto porcentaje (52.5%) de la variación en el rendimiento académico en matemáticas; esto es explicado por el rendimiento académico en lenguaje y comunicación. En otras palabras, existe una asociación positiva y significativa entre las dos áreas consideradas.

Dicho grupo de variables se pueden agrupar en los factores de: 1) riesgo y 2) favorecedores. En lo que respecta al factor de riesgo, pertenecer a una escuela pública disminuye significativamente las probabilidades de tener un mejor resultado en el rendimiento académico en lenguaje y comunicación, y en matemáticas, tal hallazgo coincide con ^{Urquijo (2009)} quienes determinaron que los escolares de escuelas privadas obtienen calificaciones superiores a los de escuelas públicas en lectura. Igualmente, con respecto al rendimiento académico en matemáticas, ^{Tuñón y Poy (2016)} reportan que la calificación media en Matemáticas es mayor en las escuelas privadas.

La segunda variable que conforma el factor de riesgo, es el género. Aquí se encontró que los hombres se ven menos favorecidos que las mujeres en las dos áreas analizadas. Este resultado concuerda con lo reportado por Backhoff et al., (2010), las mujeres alcanzan resultados superiores que los hombres en comprensión lectora. Por último, coinciden los resultados con ^{Rosário, Lourenço, Paiva, Rodrigues, Valle y Tuero-Herrero (2012)} al señalar que las calificaciones en Matemáticas son superiores en mujeres.

Las variables que integran el factor favorecedor para obtener niveles de logros altos, son el grado de marginación del lugar donde se ubica la escuela y la edad. Para el caso del grado de marginación, se encontró que las escuelas privadas se ubican en localidades con grado de marginación bajo o muy bajo. Estos resultados demuestran lo afirmado por ^{Villarreal, López, Bernal, Escobedo y Valadez (2009)} en cuanto a la necesidad de realizar reformas estructurales para mejorar la calidad de las escuelas en condición de marginación. Durante muchos años el sistema educativo mexicano ha dado prioridad a las áreas urbanas y a las necesidades de las clases medias, consolidando así un sistema de distribución desigual de la educación (^{Mier-Terán y Rabell, 2003}). ^{Segura (2017)} explica que el futuro de la desigualdad dependerá de la mejora en la calidad educativa de la futura fuerza laboral, mediante la cobertura en educación básica.

Para el caso de la variable edad, el hallazgo es similar con lo reportado por Backhoff et al. (2010) y ^{Carvallo-Pontón et al. (2007)} quienes comentan que los escolares con una edad correspondiente a su nivel de estudios obtienen mejores resultados y que por cada año de edad más en el nivel que le corresponde a un alumno, su rendimiento baja. Los resultados encontrados coinciden también con ^{Claessens, Duncan y Engel (2009)}, quienes encontraron que las habilidades de lectura y matemáticas con que ingresa un escolar a ese nivel son predictores de los resultados en cursos posteriores en esas áreas. La relación que se encontró en esta investigación sobre el rendimiento académico es consistente con lo encontrado por ^{Claessens, et al. (2009)}, quienes señalan que la mayoría de los alumnos que muestren un incremento en el rendimiento académico en lenguaje y comunicación, también lo harán en matemáticas.

Considerando los resultados de esta investigación, se propone un modelo ecológico educativo de intervención para reducir los factores de riesgos, basado en los postulados de ^{Bronfenbrenner y Gary (2000)} y ^{Larrauri (2009)}. Este modelo ecológico es integral y multifactorial, donde interactúan muchos agentes para circunscribir al sujeto como parte de acomodarse a diversos sistemas cambiantes. Este modelo ecológico atiende a varios sistemas, como son: el microsistema, el cual se refiere al entorno inmediato de cada individuo; el mesosistema, compuesto por dos entornos interrelacionados porque la persona vive y participa en ellos; el exosistema, o los entornos que influyen sobre la escuela; y el macrosistema, referido al sistema educativo a nivel nacional e internacional. Para mejorar la calidad educativa, se requiere trabajar desde diferentes sistemas de formación, retomando los lineamientos de algunos autores (^{Larrauri, 2009}; ^{Cvencek, Manu y Meltzoff, 2015}; ^{Carvallo-Pontón, 2016}) y los resultados obtenidos en esta investigación. Se sugiere elaborar una propuesta de intervención por ecosistemas educativos para colaborar con el mejoramiento de las habilidades lectoras y matemáticas de los escolares a nivel primaria, tal como se describe en la figura 5.

En la figura 5 se muestra cómo interactúan entre sí los diversos sistemas -microsistema, mesosistema, exosistema y macrosistema- en el ámbito educativo. Al tomar acciones para mejorar el rendimiento escolar y reducir los factores de riesgo, se hace la propuesta de intervención que se explica en la tabla 11.

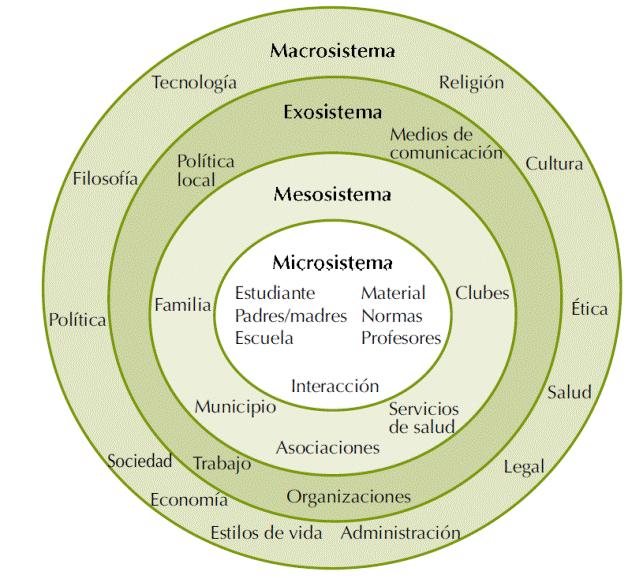
Fuente: elaboración propia basado en los postulados de ^{Bronfenbrenner y Gary (2000)} y ^{Larrauri (2009)}

Figura 5 Ecosistema educativo. 

Tabla 11 Propuesta de intervención desde la teoría del ecosistema educativo. 

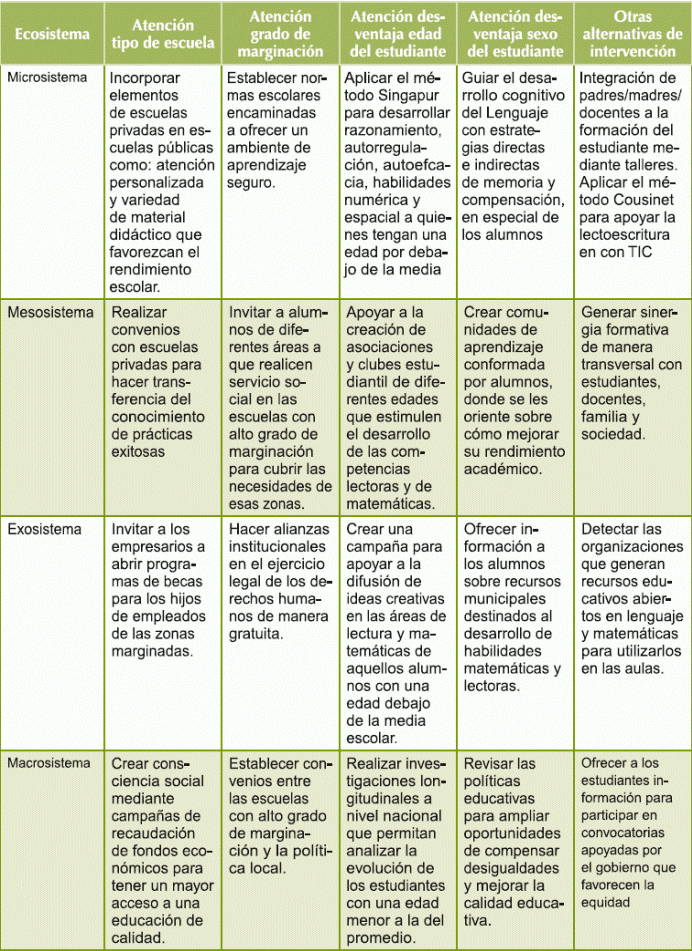
Fuente: elaboración propia

Tal como se señala en la tabla 11, las estrategias de intervención para cada una de los sistemas -microsistema, mesosistema, exosistema y macrosistema- están interconectadas entre ellas porque dependen entre sí. Requieren de la participación y la comunicación conjunta de los diversos actores para ofrecer una educación de calidad, equitativa y a la vez enfocada a mejorar el rendimiento académico en las áreas de la lectura y de matemáticas. Esta investigación pretende también contribuir al derecho que tiene cada niño de acceder a una educación de calidad, donde pueda alcanzar las metas de aprendizaje de manera equitativa, independientemente de su contexto socioeconómico. Tal como señalan ^{Murillo y Hernández-Castilla (2014)} la equidad es un derecho vinculado con la organización de cualquier sociedad que es amparada en valores democráticos y de progreso humano, basadas en la justicia y la igualdad.

Esta propuesta de modelo ecológico es congruente con lo que menciona ^{Moreno (2017)}, al considerar acciones más concretas que permitan mejorar la equidad educativa y así garantizar el derecho constitucional de los escolares a recibir una educación de calidad sin importar las condiciones de vida en las cuales hayan nacido. Adicional a esto, el modelo propuesto atiende el carácter multidimensional de la marginación que menciona ^{Edwards (2016)}, que afecta el acceso a una educación de calidad, y deben ser erradicada.

Conclusiones

A pesar de las limitaciones del estudio de no contar con más variables disponibles en la base de datos para llevar a cabo los análisis estadísticos correspondientes, se han presentado algunas propuestas de intervenciones a niveles microsistema, mesosistema, exosistema y macrosistema con la finalidad de mejorar la calidad educativa del sistema mexicano y reducir los factores de riesgos mencionados.

Las intervenciones sugeridas van desde trabajar el desarrollo de competencias cognitivas y metacognitivas en los discentes, involucramiento de docentes inspiradores, apoyo en la tecnología y medios de comunicación, sinergia entre los agentes formadores; hasta alianzas con la sociedad y el gobierno para la construcción de las políticas públicas encaminadas a favorecer a los ciudadanos, en este caso, para mejorar su educación. La propuesta de intervención desde la teoría ecosistema educativa, podría colaborar también con el desarrollo de la comunidad educativa. Tal como lo afirma ^{Gifre & Guitart (2013)}, la comunidad educativa podría influir en el bienestar y calidad de vida de la persona porque tiene una corresponsabilidad de formación (^{Cásares, 2009)}.

El ecosistema propuesto en la tabla 11, puede servir de referencia para los gestores educativos interesados en aumentar el rendimiento académico por parte de los alumnos de 6° año de educación primaria, ya que los resultados de la tabla 3 muestran que aproximadamente cuatro de cada diez alumnos tienen el nivel de logro insuficiente en lenguaje y comunicación, mientras que en matemáticas, cinco de cada diez alumnos se ubican en tal nivel.

Finalmente, el presente estudio ofrece evidencia científica que sugiere estrategias que podrían coadyuvar a una mejora en la calidad de la educación en el estado de Nuevo León, México.

Además, los resultados pueden servir de reflexión a profesores, administradores escolares y políticos para que contribuyan al establecimiento de medidas de apoyo académico y reducción del rezago en los alumnos del sistema educativo mexicano.