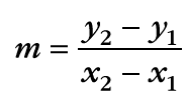Introducción
Desde hace más de una década se han desarrollado programas, aplicaciones y en general software educativo que apoya el aprendizaje de diferentes tópicos en el área de matemáticas. Al hacer una revisión de este tipo de software, se encontró que varios de ellos contribuyen al desarrollo de aspectos memorísticos y refuerzan el trabajo algebraico que se desarrolla en las aulas, pero pocos son los que pretenden mostrar al usuario una visión gráfica de la problemática a resolver. Es decir, se deja a un lado la visualización de las situaciones y con ello la construcción de los conceptos inmersos. (Gutiérrez, 2013). Estos programas son generalmente diseñados para ser utilizados en una computadora de escritorio, limitando el alcance y disponibilidad del software. Aunque existe la tendencia de incluir este software en las aulas para integrar sus capacidades a las herramientas del profesor, en México, se ha limitado su introducción debido a que se requieren aulas-laboratorio, con la infraestructura y mantenimiento asociado.
Por otro lado, se sabe que la población entre 6 y 34 años de edad un 73.6 % tienen acceso a Internet, 71.5% de los mexicanos cuentan con un celular y de estos uno de cada 3 (66.3%) tienen un smartphone (INEGI ENDUTIH, 2015). Este tipo de dispositivos, con capacidades de procesamiento, visualización y conexión a internet, constituyen la herramienta principal para el proceso de educación que se enmarcan en el m-learning.
Tomando en cuenta el hecho del uso cotidiano de los dispositivos móviles en los estudiantes, los distintos componentes que tienen incorporados; aunado a la importancia de crear aplicaciones que amplíen la cobertura, con herramientas que desarrollen capacidades en los estudiantes dentro y fuera de las aulas. Se propone una aplicación educativa para dispositivos móviles, con la cual el estudiante vizualice situaciones que le permitan analizar y llegar a conclusiones como parte de la construcción del concepto de la derivada, que es uno de los conceptos en donde muchos alumnos tienen tropiezos en su aprendizaje. Al respecto, Hitt (2013), señala que uno de los principales problemas de la enseñanza del Cálculo se centra en que se dejan de un lado las consideraciones visuales en la explicación del concepto de derivada. Este tema se contempla en las unidades de aprendizaje de Cálculo y Cálculo Aplicado, las cuales se ubican en los dos primeros semestres, como parte de la formación básica de la carrera de sistemas computacionales del IPN donde se hizo el trabajo experimental que se reporta en el presente artículo. (IPN, 2009).
El artículo se divide en 5 secciones, en la primera se presenta la problemática del estudio, en la segunda, se trabaja lo referente a conceptos y estudios relacionados a las dificultades en el aprendizaje del Cálculo y en particular de la derivada. En la tercera se plantean los objetivos de la investigación. En la cuarta sección se aborda lo referente a los instrumentos metodológicos empleados como son los cuestionarios inicial final, se sintetiza en un cuadro tanto la propuesta de enseñanza seguida por los estudiantes del grupo de estudio (GE), como las actividades que fueron empleadas con el grupo de control (GC). Los resultados y el análisis cualitativo de los cuestionarios son presentados en la quinta sección.
Marco teórico
Sobre el aspecto de la visualización, Tall (2013) comenta que:
... a pesar de que los proyectos de reforma han intentado una variedad de enfoques usando la tecnología, lo que ha ocurrido es, en buena medida, la retención de las ideas del cálculo tradicional, pero ahora sustentadas por gráficas dinámicas que ilustran el uso de la manipulación simbólica para calcular. (Tall, 2003, p. 129)
Por tanto, se requiere contar con actividades que presenten los elementos de la razón de cambio y derivada de forma que sean naturales al alumno, sin dejar de lado la parte simbólica y buscando un equilibrio entre estos aspectos, como señala Moreno (2013): “... un proceso intermedio, que respete la carga intuitiva de significado que acompaña la notación simbólica. En efecto el significado primigenio del Cálculo se articula alrededor de una serie de metáforas sobre el movimiento y la variación...”. (Moreno, 2013, p. 93). Este trabajo enfatiza el desarrollo de la visualización y el uso de la realidad aumentada como método de visualización en los dispositivos móviles, que permiten al alumno experimentar y de ahí obtener una interpretación de los símbolos que se utilizan en Cálculo.
Piaget y los esquemas cognitivos
Para Piaget “un concepto es un esquema de acción o de operación” (Piaget, 2003, p. 42), lo que implica que este tipo de “concepto” es una construcción cognitiva realizada por un estudiante con un propósito específico. Para Piaget los esquemas de acción son aquellas acciones que son producto de la “asimilación mental en donde se incorporan los objetos de la conducta que permitan observar de forma externa el pensamiento del aprendiz”. (Piaget, 2003, p. 18). Las acciones cognitivas que deben realizar los estudiantes para llegar a la reconstrucción de los conceptos matemáticos, son entre otras, el análisis, el razonamiento, la comunicación, el realizar operaciones. El llevar a cabo estas acciones es una de las principales dificultades que presentan los estudiantes. Por lo que en el presente artículo se trabajan estrategias que permiten al estudiante universitario desarrollar algunas de las acciones cognitivas mencionadas.
Aplicaciones en dispositivos móviles
En la actualidad los dispositivos móviles conjuntan recursos y herramientas que permiten al usuario no solo ejecutar llamadas telefónicas, sino gestionar tiempo, información, desplazamiento e interactuar continuamente con su entorno a través de sensores como la cámara fotográfica, transmisión de video, pantallas táctiles y sensores de movimiento. Todo ello los convierte en herramientas potentes y versátiles las cuales pueden ser empleadas para ayudar en el desarrollo de múltiples actividades educativas (Gómez, 2016).
Modelo Educativo del Instituto Politécnico Nacional México
El Modelo Educativo del Instituto Politécnico Nacional, (IPN), pretende que el estudiante logre un desarrollo integral. Para lo cual se requiere contar con un currículo flexible que permita diversificar los espacios de aprendizaje y la incorporación de estrategias en los salones de clase que fomenten el uso de las tecnologías disponibles (IPN, 2004).
Razón de cambio
El concepto de razón de cambio se expresa como el cociente entre dos variaciones. Matemáticamente se expresa como el cociente de dos diferencias o dos incrementos (Stewart, 2008). Es de gran interés poder medir y comprender estos cambios que se dan en el mundo físico mediante la construcción de modelos matemáticos y su resolución para poder extraer conclusiones sobre cómo se dan los cambios, cuándo y cómo afectan al modelo para a su vez permitir inferencias respecto al mundo físico que le permitan generar nuevo conocimiento.
Aprendizaje móvil
De acuerdo a Jhonson (2013), Danaher, Gururajan, y Hafeez-Baig (2009), el uso de dispositivos móviles en la educación constituye una opción que apoya a los procesos tanto de enseñanza como de aprendizaje. Para Josh (2011) y para Lugo (2012) el aprendizaje móvil constituye una buena forma para abordar contenidos educativos en diferentes sitios no solo en las instituciones creadas para ese fin, y que se pueden ajustar a las necesidades de tiempo de los estudiantes. Además Zurita y Nussbaum (2004), señalan que el aprendizaje móvil permite combinar el aprendizaje formal con el informal y promueve distintas estrategias que apoyan el trabajo educativo, ampliando el tipo de herramientas en el aprendizaje.
Realidad aumentada
Azuma, Behringer, Feiner, Julier y Macintyre (2001), señalan que la Realidad Aumentada permite representar una parte del mundo físico agregando elementos virtuales, lo que ayuda al estudiante a plantear situaciones que se presentan en diferentes áreas del conocimiento, sin la necesidad de realizar una manipulación en el mundo real que pudiera condicionar su factibilidad. Un ejemplo sería el visualizar las partes internas del cuerpo a partir de un maniquí que represente el cuerpo humano o ver cómo interactúan los sistemas circulatorios con la respiración simultáneamente, sin alterar a la persona (Hoffman,1997).
En el caso del concepto de razón de cambio, las aplicaciones en realidad aumentada (RA) permiten al estudiante visualizar situaciones de aplicación a través de hologramas, para ser analizadas mediante el uso de operaciones matemáticas correspondientes. (Thomburg y Mahoney, 2009). La RA está compuesta por una escena real, que se presenta por la cámara del celular con hologramas que aparecen y que se muestran en la pantalla de manera conjunta.
Objetivo
El propósito fundamental de nuestra investigación es mejorar el desempeño académico de estudiantes, en específico, en la solución de problemas relacionados a los conceptos de razón de cambio instantánea, tanto de tipo conceptual como algorítmico, mediante la capacidad de visualización de los estudiantes, empleando una aplicación instalada en sus dispositivos móviles.
Metodología
Se empleó una metodología cualitativa, lo que permitió documentar y analizar los procesos seguidos por los estudiantes en la construcción de los conceptos de razón de cambio y derivada de una función. (Sampieri, 2014). Moschkovich (2000) señala que los procesos empleados en la construcción de conceptos se dan a través de la práctica, lo que se tomó en cuenta al analizar cómo los alumnos empleaban la aplicación móvil para llevar a cabo la secuencia de enseñanza en comparación con los que no la utilizaron. Adicionalmente se emplearon aspectos cuantitativos para establecer la homogeniedad inicial de los dos grupos considerados: el de control y el de estudio, utilizando la prueba T-student con una p=0.05. Posteriormente se compararon las diferencias entre los resultados obtenidos de los cuestionarios, tanto inicial como final de ambos grupos, a través de la prueba T-student múltiple. Al obtener la diferencia entre los resultados de los cuestionarios de GC y GE se usa la prueba F para determinar si esta diferencia entre las dos muestras es estadísticamente significativa con una p < 0.05. Considerando que el cuestionario está dividido en dos tipos de preguntas, se hizo un análisis de tipo estadístico al respecto, utilizando nuevamente la prueba t-student múltiple, que considera la comparación de los posibles pares de información, estableciendo si hay una diferencia estadística para p <0.05, con el método Holm-Sidak.
Participantes
Se trabajó con dos grupos de 30 estudiantes cada uno, con una edad promedio de 17.5 años, seleccionados de forma aleatoria. Los alumnos estaban inscritos en la materia de Cálculo, la cual se imparte en el primer semestre del nivel superior en las carreras de ingeniería del Instituto Politécnico Nacional. Estos estudiantes tuvieron un primer acercamiento a la materia de Cálculo en el nivel bachillerato. Cada grupo tuvo un profesor titular asignado por la institución y el profesor investigador fue el que fungió como maestro durante el periodo de la aplicación de la secuencia de enseñanza.
Instrumentos metodológicos empleados
En ambos grupos se impartió el estilo de enseñanza acostumbrado, tipo de ejercicios o problemas que resolvían, así como registros de representación al que recurrían con mayor frecuencia al resolver problemas. Además de que se les aplicó una encuesta para saber las características de los dispositivos móviles usados por los estudiantes. Se aplicaron dos cuestionarios, uno previo a la implementación de la secuencia de enseñanza y el otro después de concluirla y fueron los mismos para ambos grupos. En la siguiente etapa la secuencia difiere en la presentación y resolución de problemas, en el GE el profesor-investigador abordó los temas de razón de cambio y derivada de una función, empleando la aplicación que estaba cargada en los dispositivos móviles de los estudiantes, mientras que en el grupo control (GC) se trabajaron los temas sin el empleo de ésta, sólo se dio la misma explicación empleando el pizarrón y plumones.
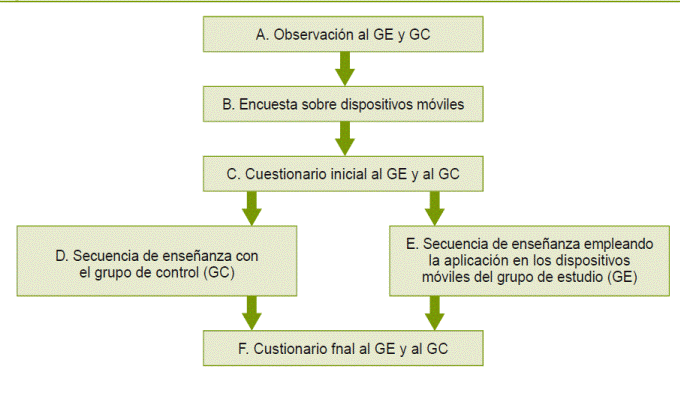
En la figura 1 se resume la secuencia de uso de los instrumentos metodológicos empleados en la investigación.
Descripción y resultados de los instrumentos metodológicos
Observación
La observación se llevó a cabo al inicio del segundo mes de clases del semestre, ambos grupos se encontraban trabajando temas de la unidad 2 del programa de estudios de Cálculo que lleva por título “Límites de funciones y continuidad”. El maestro titular del GC abordó el tema de continuidad de funciones y el del GE, trabajó el tema de límites. Se pidió autorización previa, tanto a los profesores titulares de los grupos como a los estudiantes, para que los temas de derivada y sus aplicaciones como la razón de cambio instantánea fueran trabajados por el profesor-investigador.
La observación fue realizada por dos investigadores en el campo de matemática educativa, y los grupos fueron atendidos por los maestros que tienen asignados para la unidad de aprendizaje de Cálculo en la unidad académica del IPN donde se realizó el estudio. Se usaron 3 fuentes de observación, lo que permitió emplear el método de triangulación para validar las observaciones. Una fuente la constituyó el protocolo de observación, la segunda fuente fueron los cuadernos de trabajo de los estudiantes y la tercera fue la plática que se tuvo con los maestros de los grupos. De tal forma que los aspectos que aparecen en las tres fuentes es lo que se consideró como válido para ser tomado en cuenta como característica que predomina en cada uno de los grupos. La observación permitió revisar los conocimientos previos de ambos grupos, así como la presencia de algunas dificultades en la resolución de problemas. Se diseñó un protocolo de observación que sirvió de guía para llevarla a cabo. Las preguntas que guiaron la observación se muestran en la tabla 1.
Los resultados obtenidos de las observaciones realizadas a los grupos fueron los siguientes. Se encontró en ambos grupos -el de control y el de estudio-, que los estudiantes tienen deficiencias al trabajar en dos registros de representación, el gráfico y el algebraico, ya que no lograron relacionarlos. En la mayoría de los casos tabularon algunos valores para encontrar la gráfica, pero no usaban los parámetros de las ecuaciones para construir las gráficas. De manera general se observó que los estudiantes están más familiarizados con la resolución de ejercicios más que con la de problemas, pues se les facilita aplicar alguna operación a la función dada, más que plantear una función para resolver una situación. En ambos grupos se observó que los maestros no hicieron referencia a temas que anteceden al expuesto, también, que los alumnos son poco participativos. En el GC un alumno formuló una pregunta sobre los tipos de discontinuidad que hay en una función. El maestro del grupo atendió su pregunta usando gráficas en su explicación. En el GE se observó que el profesor explicó la obtención de límites empleando alguna estrategia o regla para su obtención, pero no lo relacionó con el registro gráfico, volviéndose el trabajo mecánico que coincidió con los apuntes que se revisaron de los alumnos. Se observó en la clase, que en ambos grupos predominó una enseñanza tradicional con una actitud pasiva de los estudiantes.
Encuesta sobre dispositivos móviles
Las preguntas de la encuesta se enfocaron en los elementos con los que cuentan los dispositivos móviles de los estudiantes, con la finalidad de desarrollar aplicaciones que emplearan dichas características. Las preguntas se muestran en la tabla 2.
Las encuestas desarrolladas en la unidad académica del IPN indican que el 82% de los estudiantes tienen un teléfono inteligente, y que cuentan con varios sensores, además de pantalla multitáctil, cámara WiFi, GPS, entre otros. Estas características abren un abanico de opciones para la elaboración de aplicaciones que permitan al estudiante hacer uso de ellas en su proceso de aprendizaje. Los resultados obtenidos en la sección previa y ésta, permitió desarrollar la secuencia de enseñanza y hacer la herramienta contenida en la aplicación de los dispositivos móviles.
4.3.3 Cuestionario inicial
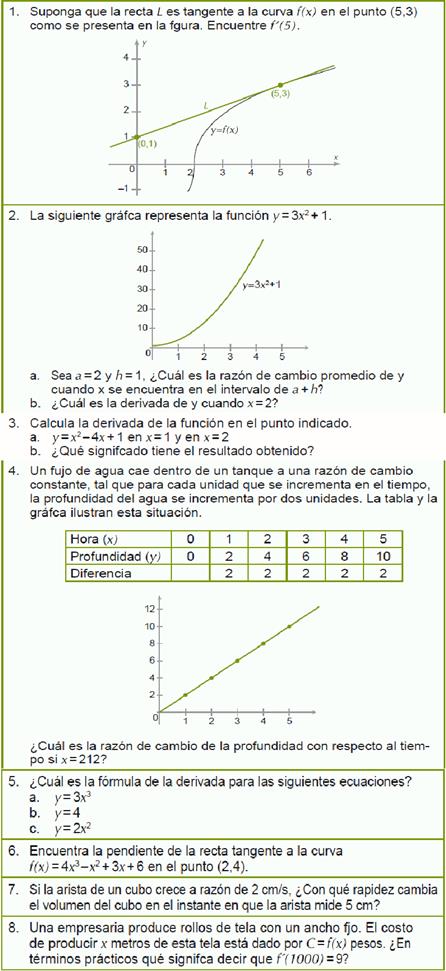
El cuestionario inicial se aplicó a ambos grupos (GE y GC), con la finalidad de revisar el estado inicial de ambos y detectar las deficiencias que tienen los alumnos en el tema de la derivada y una de sus aplicaciones en problemas de razón de cambio, para poder ubicar si esas deficiencias se deben a aspectos de carácter algorítmico o conceptual. El cuestionario inicial estuvo integrado por 8 situaciones problemáticas concernientes a la materia de Cálculo, en específico a los tópicos de la derivada y de razón de cambio; 3 de las 8 preguntas tenían incisos, en total el número de reactivos que debía responder el alumno fueron 12.
Estas preguntas se clasificaron en dos tipos: i) de tipo algorítmico y ii) de carácter conceptual. Las preguntas de tipo algorítmico, tienen que ver con que el estudiante siga un número de pasos para calcular un resultado. Las preguntas de carácter conceptual se refieren a las implicaciones que tienen los conceptos en las situaciones problemáticas presentadas, es decir el estudiante requiere haber comprendido el significado de la parte teórica para poder aplicarlo en la resolución de problemas.
El cuestionario inicial o de diagnóstico se calificó utilizando correcto o incorrecto y en el caso de no contestar la pregunta se tomó como incorrecto. En total fueron 12 reactivos, 5 evaluaron la parte algorítmica y 7 lo referente a la parte conceptual. Los resultados obtenidos se desglosan en la gráfica de barras correspondiente a la figura 2. Las preguntas del cuestionario diagnóstico se muestran en la tabla 3. En la gráfica de barras correspondiente a la figura 2 se observa el porcentaje de respuestas correctas por cada pregunta. Las preguntas no aparecen en el orden en que se presentaron a los alumnos, sino que se han dividido en conceptuales y algorítmicas para resaltar como en las preguntas algorítmicas los alumnos obtuvieron mejores resultados. Las mayores deficiencias se ubican en los conceptos de razón de cambio y derivada.
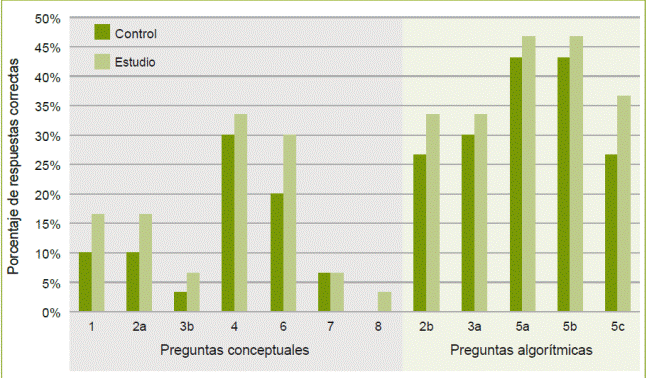
Figura 2 Porcentaje de respuestas correctas e incorrectas referentes a las preguntas conceptuales y las de tipo algorítmico en el cuestionario inicial.
En el cuestionario inicial el promedio general del grupo de estudio fue de 2.6 de 10 puntos, y el del grupo de control fue de 2.08. En las preguntas de carácter conceptual los promedios obtenidos fueron de 1.14 de 10 puntos para el GC y de 1.96 para el GE; mientras que en las preguntas de tipo algorítmico los promedios fueron de 3.40 para el GC y 3.93 para el GE. Mediante la prueba de t-student múltiple, se contrastaron los dos grupos al inicio del estudio. En relación con las preguntas de carácter conceptual, no se encontró una diferencia estadística significativa entre los dos grupos (p<0.05), pero para las preguntas de tipo algorítmico si existe una diferencia estadística con p=0.10, lo que se consideró como el resultado de la conformación de los grupos por parte del instituto.
En general ambos grupos mostraron deficiencias principalmente en los problemas asociados al concepto de derivada. Uno de los errores más frecuentes de los estudiantes fue la sustitución de valores de expresiones algebraicas dadas, pero se observó que no siempre es necesario hacer sustituciones sino operaciones con las funciones dadas, una práctica muy empleada por los alumnos. Otra situación que prevaleció en ambos grupos, es que los alumnos mostraron confusión al determinar los incrementos entre dos magnitudes, ya que restaron en lugar de hacer un cociente. Los problemas y ejercicios del cuestionario se enumeraron y en algunos de ellos se emplearon incisos marcados con las letras a, b y c, según fuera el caso.
Propuesta de enseñanza
Se trabajó el tema de razón de cambio y derivada durante cuatro sesiones, en donde el profesor-investigador, empleó una secuencia de enseñanza, la cual se estructuró con problemas y ejemplos iguales para los dos grupos, pero mientras que en el grupo de control (GC) se emplearon imágenes estáticas para resolver las situaciones planteadas, con ayuda del pizarrón y los pulmones, en el grupo de estudio (GE) fueron trabajadas empleando imágenes dinámicas, mediante el uso de la realidad aumentada dentro de la aplicación móvil, haciendo más interactivas las actividades.
La secuencia de enseñanza se construyó con base en los resultados obtenidos tanto de la observación como de la encuesta, con el propósito de apoyar al estudiante a que comprenda el concepto de la derivada desde el punto de vista geométrico y como límite. De la observación se encontró que la mayoría de los estudiantes están acostumbrados a trabajar en un contexto algebraico y no logran relacionar los diferentes registros de representación, lo que concuerda con lo señalado por Hitt (2003), por lo tanto, se usaron diferentes registros de representación (tabular, gráfico, analítico, icónico), para visualizar las situaciones planteadas en los problemas y establecer una relación entre ellos. A continuación, se describen las formas de trabajo con el GE y el GC.
1 a sesión
Esta sesión se inició comentando en qué consiste la razón de cambio y se dio un ejemplo en donde el estudiante llenaba una tabla tomando los datos de la gráfica presentada y respondía a preguntas, de tal forma que las respuestas a las preguntas condujeron al alumno a llegar a una expresión o fórmula que permite expresar a la razón de cambio promedio, así como su interpretación gráfica como la pendiente de una recta secante a una curva.
2 a sesión
En esta sesión se trabajó con otro ejemplo solicitando al estudiante encontrar la razón de cambio promedio. Se formularon otras preguntas permitiendo al estudiante llegar a la razón de cambio instantánea, expresada como el límite del cociente del incremento de la función entre el incremento de la variable, cuando este incremento tiende a cero.
También se revisó una gráfica y se concluyó que la razón de cambio instantánea representa a la derivada y su representación geométrica es la pendiente de la recta tangente a la curva en un punto. Se le pidió al estudiante resolver otro problema, empleando una tabla, una gráfica y finalmente usando la derivada de la función.
Recursos educativos digitales
Para el grupo de control se empleó el libro de texto, pizarrón, plumones, calculadora y la exposición del tema. Para el GE se usaron los recursos anteriores y un recurso digital interactivo que presenta los problemas de derivadas y de variación, auxiliándose con animaciones, representaciones, gráficas dinámicas responsivas, interacción con los sensores de posición del dispositivo móvil y realidad virtual.
Es importante señalar que la aplicación digital fue local instalándose en los dispositivos móviles de los alumnos y fue construida para este estudio por lo que se consideró como un prototipo. En la tabla 4, en la columna derecha se muestra una vista de la aplicación móvil usada por el GE y los recursos usados por el GC en la columna izquierda.
De las 4 sesiones trabajadas con el GC, faltó un alumno en la segunda sesión y en el GE faltaron dos alumnos, uno en la sesión 2 y uno en la sesión 3, pero tuvieron oportunidad de conocer y trabar de manera autónoma el material.
Cuestionario final
Después de trabajar con las secuencias de enseñanza, se realizó el cuestionario final, mostrado en la tabla 5, con la finalidad de percibir si existe algún comportamiento diferente entre los estudiantes del GC y los del GE.
Al igual que en el cuestionario inicial se hizo el análisis de cada una de las preguntas agrupadas de concepto y algorítmicas. En la gráfica de la figura 14 se observa una mejora significativa en el número de preguntas con respuesta correcta para el grupo de estudio (GE) respecto al grupo de control (GC). Esta mejora parece que reduce el desequilibrio entre las preguntas conceptuales y algorítmicas que en este caso tienen un promedio de 7.4 y 7.60 respectivamente por parte del GE.
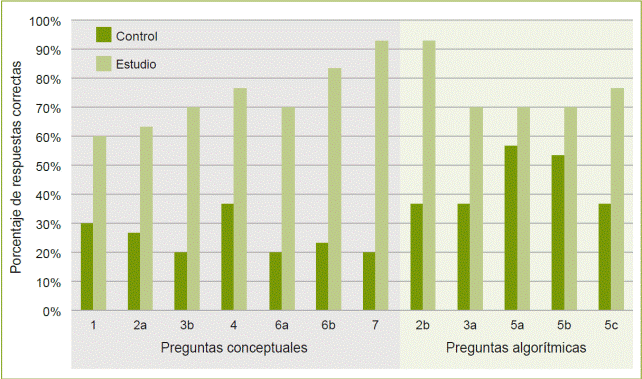
Figura 14 Porcentaje de respuestas correctas e incorrectas referentes a las preguntas conceptuales y las de tipo algorítmico en el cuestionario final.
Se puede considerar que hubo una mejoría considerable en el GE con respecto al GC ya que al comparar los promedios obtenidos en ambos grupos en el cuestionario final el del GE fue de 7.42 y el del GC fue de 3.3. En las preguntas de carácter conceptual los promedios obtenidos fueron de 2.5, para el GC y de 7.4 para el GE; mientras que en las preguntas de tipo algorítmico fueron de 4.4 para el GC y 7.6 para el GE. Tras un estudio empleando la t-student múltiple, se hizo una comparación entre los dos grupos. En relación a las preguntas de carácter conceptual y de tipo algorítmico, hubo una diferencia estadística significativa entre los dos grupos con p<0.05.
Análisis de los resultados
El análisis de las respuestas dadas por los estudiantes en los cuestionarios, tanto inicial como final, la observación del grupo y la encuesta sobre tipo y uso de móviles, sirvió para preparar o diseñar la secuencia de enseñanza.
Análisis de las respuestas dadas en el cuestionario inicial
Tanto en el grupo de control como en el de estudio se detectaron errores similares.
El problema 1, que solicita determinar la derivada de una función evaluada en f’(5), a partir de una gráfica; no fue resuelto o se hizo mal por la mayoría de los estudiantes. Manifestaron que no contaban con una expresión algebraica para derivarla y sustituir en ella el valor dado.
El problema 2a que a partir de una gráfica y la representación algebraica correspondiente, solicitaba obtener la razón de cambio promedio cuando la variable independiente sufría un incremento, fue resuelto de manera correcta por el 10% del grupo de control y el 16% del grupo de estudio. Fue muy bajo el porcentaje de alumnos que respondió de forma correcta al problema, debido a que sustituyeron las letras y no se percataron de los valores correspondientes.
El problema 2b, que presentó una expresión algebraica y solicitaba obtener su derivada, fue resuelto de forma correcta por más estudiantes (26% del grupo de control y 33% del de estudio), porque sustituyeron en la derivada de la función los valores proporcionados.
El problema 3a fue resuelto correctamente por el 30% del grupo de control y el 33% del grupo estudio. Aquí los estudiantes derivaron correctamente la función y sustituyeron el valor proporcionado en el problema. Los que se equivocaron fue porque derivaron de forma incorrecta o sustituyeron un valor diferente al que debía ser.
El problema 3b se solicitaba dar el significado de la obtención de la derivada de una función y su evaluación en el punto indicado. A los estudiantes les resultó difícil de resolver, sólo 1 de 30 alumnos del grupo de control y 3 de 30 del grupo de estudio lo tuvieron correcto. Los alumnos escribieron la derivada de la función señalando que no sabían su significado o que no lo recordaban, lo que conduce a señalar que la mayoría de los estudiantes no tiene construido el concepto de derivada.
En el reactivo 4 se proporcionaba la gráfica de una función y su representación tabular, y se solicitaba determinar la razón de cambio de la profundidad del agua con respecto al tiempo cuando la variable independiente (x) tenía un determinado valor. El 30% de alumnos del grupo de control y el 33% del grupo de estudio contestaron correctamente el problema, porque se apoyaron en la tabla para encontrar el resultado. El error consistió en que consideraron que debían encontrar el valor de la profundidad del agua, por lo cual sustituyeron el valor de x en la función y no leyeron el dato dado en la tabla. Esta situación refuerza lo dicho en el inciso e, referente a que muchos estudiantes no han logrado comprender que la razón de cambio instantánea se calcula mediante la derivada de la función, y tampoco han construido el concepto de razón de cambio instantánea.
En los reactivos 5a, 5b y 5c, se proporcionaban funciones mediante su expresión analítica y se solicitaba obtener su derivada. En el 5a y 5b tanto el grupo de control como el de estudio lo resolvieron de forma correcta, el 44% y 46% respectivamente. En el reactivo 5c las soluciones correctas fueron menores (26% y 36%), debido a que derivaron usando la regla para derivar un producto y no la de un cociente. Pero en general salieron mejor que en los restantes reactivos del cuestionario.
En el problema 6 se solicitaba encontrar la pendiente de la recta tangente en un punto dado de una función expresada en forma algebraica. Lo respondieron de forma correcta el 20% de los alumnos del grupo de control y el 30% de los del grupo de estudio, al derivar la función dada y evaluar la derivada en el punto indicado, pero en el 70% del GE y el 80% del GC, los alumnos, no lo lograron determinar la pendiente de la recta al no asociar que corresponde a la derivada de la función en el punto dado.
El problema 7 les fue muy difícil debido a que solo el 6% de ambos grupos lo resolvió de forma correcta. Los alumnos no han logrado comprender una relación de relaciones que es el tipo de problema que contenía el reactivo 7. Es decir, los estudiantes no lograron establecer una relación que es el cambio de volumen de un cubo cuando su arista cambia en el tiempo a razón de 2 cm/s.
El problema 8 fue considerado muy difícil porque sólo el 3% de los alumnos del grupo de estudio llegó a una respuesta correcta. El resto de los estudiantes no lo resolvió correctamente, ya que sustituyeron valores en la función y no en la derivada de la función.
Se puede observar que en general y en ambos grupos, el porcentaje de respuestas correctas corresponde a las preguntas de tipo algorítmico que a las de carácter conceptual, lo que indica que los alumnos se desenvuelven de mejor forma siguiendo pasos establecidos o que han memorizado a través de las reglas de derivación, y en contraste no han realizado mucho trabajo en la construcción del concepto de la derivada. Aunque en general ambos grupos mostraron grandes deficiencias en el tema de la derivada.
Análisis de los resultados del cuestionario final
El análisis realizado a las respuestas dadas en el cuestionario final, mostró con más claridad la mejoría que tuvieron los estudiantes y las deficiencias que seguían tendiendo. Más estudiantes del grupo de estudio (GE) que los alumnos del grupo de control (GC), lograron resolver de forma correcta las preguntas conceptuales como algorítmicas. En el caso de las conceptuales se muestran dos ejemplos:
-
En el caso de la pregunta 1, el 60% del grupo de estudio respondió correctamente, mientras que del grupo control solo fue el 30%. En este reactivo se solicitaba determinar la derivada de la función evaluada en 4 (f’(4)), apoyándose de una gráfica. Los alumnos del GC todavía requirieron conocer la expresión algebraica de la derivada de la función para sustituir el valor dado, en contraste con los alumnos del GE, quienes reconocieron que la derivada de la función es la pendiente de la recta tangente en el punto dado. De esta manera recordaron la fórmula de la pendiente de una recta, conocidos dos puntos, llegando así a la respuesta correcta:
La pregunta 2a fue resuelta correctamente por el 62% de los alumnos del grupo de estudio contra el 28% de los alumnos del grupo de control. Se observa que al igual que la pregunta 1, más alumnos del grupo de estudio relacionaron a la derivada de la función con la pendiente de la recta que pasa por el punto dado a la curva propuesta y sólo el 28% del grupo de control consideró esto.
Ocurrió algo similar en el resto de las preguntas que evalúan la parte conceptual, ya que un número mayor de estudiantes del grupo de estudio logró dar respuestas correctas, con respecto al grupo de control. Se observó que incluso en el problema en donde tenían que determinar la razón de cambio con respecto a otra variable; primero obtuvieron razones de cambio promedio de los valores de los incrementos, pero éstos fueron reduciéndose hasta obtener una aproximación a la razón de cambio instantánea adecuada, que corresponde a incrementos cada vez más pequeños. El proceso algorítmico de derivar la función y evaluarla les sirvió para obtener el resultado exacto.
En el caso de las preguntas algorítmicas tanto el grupo de control como el de estudio tuvieron una mejoría en relación a lo que obtuvieron en el cuestionario inicial, pero el grupo de estudio superó en mayor porcentaje al de control.
Análisis comparativo de las diferencias
Se obtuvieron mejores resultados en el cuestionario final comparado con el inicial, en ambos grupos (GE y GC). En el GC el promedio cambió de 2.08, que obtuvo en el cuestionario inicial, a 3.30 que obtuvo en el cuestionario final. En el caso del GE, el promedio de respuestas correctas cambió de 2.58, que obtuvo en el cuestionario diagnóstico a 7.47 que obtuvo en el cuestionario final. Al comparar los dos grupos con la prueba F, se observó que los incrementos son diferentes con una p<0.002. También se hizo el análisis de cada una de las preguntas agrupadas por las de concepto y las algorítmicas como se muestra en la figura 15.
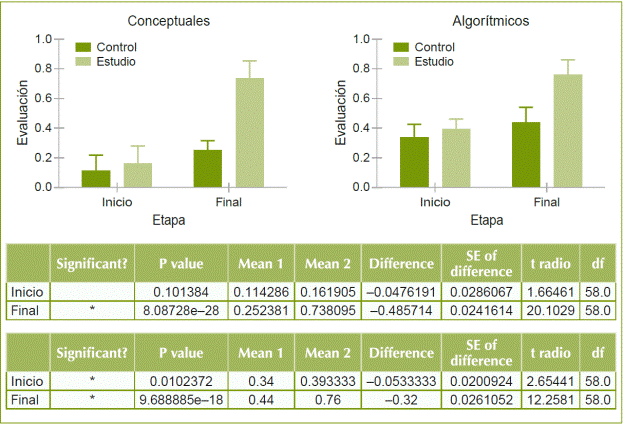
Figura 15 Gráficas y tablas que muestran la comparación entre los resultados inicial y final en las preguntas algorítmicas como las de concepto entre del GE y el GC.
Al comparar los dos grupos con prueba t-student múltiple, usando el método de Holm-Sidak que no asume ninguna distribución, sino una consideración previa de los datos, la significancia estadística se consideró con una p=0.05. La tabla superior corresponde a las preguntas asociadas al tipo conceptual. La tabla inferior corresponde a las preguntas asociadas a tipo algorítmico.
Como se puede observar en las tablas en la etapa inicial, los dos grupos comenzaron con un manejo parecido sobre la información de la derivada, pues no se encontró una diferencia significativa entre las evaluaciones de cada grupo, sin embargo, cuando se analiza la diferencia entre estos dos grupos después de haber desarrollado la secuencia de enseñanza, hubo una diferencia significativa entre los resultados de los dos grupos.
Para el caso de las preguntas algorítmicas, se analizó el desempeño de cada grupo de alumnos y se observó que, por causas ajenas al estudio, se presenta en el grupo de estudio un leve mejor desempeño en este tipo de preguntas, pero durante la secuencia de enseñanza el GC mejoró sus capacidades, aunque el GE lo superó en la evaluación final de manera muy significativa.
Conclusiones
La acción cognitiva que debe realizar el estudiante para hacer uso de los conceptos matemáticos en contextos distintos a lo aprendido, implica la reconstrucción de los mismos, y es una de las principales dificultades que enfrentan los estudiantes. En la investigación presentada en este artículo, se observó que el concepto de la derivada se reduce al esquema de operatividad por parte de los alumnos, sin asignar el significado geométrico o el de la razón de cambio instantánea mediante el proceso de obtención del límite. Con este antecedente, se diseñó y experimentó una aplicación y actividades didácticas, que permitieron observar la reconstrucción de sus esquemas cognitivos, apoyados en aspectos teóricos señalados por Piaget (2003, 2001).
Un factor importante, fue que durante las sesiones se promovió el intercambio libre de ideas entre los estudiantes, a través de reuniones en las que se argumentaban las estrategias de solución a los problemas y se implementaron las soluciones propuestas, lo que dio como resultado la modificación de sus acciones (Piaget, 2001).
Otra estrategia para modificar los esquemas cognitivos que exhibían los estudiantes, consistió en presentarles fenómenos cotidianos relacionados con los conceptos bajo estudio, empleando la interacción con el evento mediante realidad aumentada. También, la interacción del estudiante con el dispositivo móvil le permitió validar la aplicación de su esquema operativo de la derivada, al emplearlo como calculadora para hacer operaciones, como graficadora, cámara de video, para análisis, y mediante el uso de las aplicaciones de software disponibles.
Haciendo una comparación en costos entre una calculadora-graficadora y un celular, se puede decir que ambos precios son elevados, pero el estudiante en la actualidad encuentra más utilidad en su celular que en una calculadora. Entonces resulta fundamental desarrollar aplicaciones que pueda emplear en su celular para apoyar su aprendizaje.
Con las prestaciones actuales de los celulares se puede aprovechar este dispositivo como una herramienta tecnológica en la educación de manera más intensiva, ya que la mayoría de los estudiantes cuenta con un celular, por lo que este tipo de aplicaciones son factibles de integrar al sistema de educación, favoreciendo el aprendizaje por competencias promovido en el IPN.
Los resultados demostraron que el grupo de estudio obtuvo una mejora significativa en el desempeño final, en el caso del estudio de la derivada abordada desde el punto de vista de la razón de cambio instantánea. El hecho de haber resuelto los problemas de tipo conceptual no solo implica que el trabajo realizado con el uso de la aplicación y las actividades propuestas, permitió al estudiante modificar sus esquemas mentales relacionados al concepto de derivada y al de razón de cambio instantánea (Piaget, 2001), sino que también mejoró sus competencias relacionadas a la visualización de fenómenos, la reflexión y la resolución de problemas.
El estudio sobre el impacto del uso de la tecnología educativa en los procesos de aprendizaje bajo nuevos ambientes, es un reto vigente que requiere abordarse a través de investigaciones de campo, de esta forma se puede validar software educativo que existe en el mercado, así como construir nuevo software o sistemas computacionales, para ofrecer al docente de los diferentes niveles educativos, recursos digitales confiables para su uso en el aula y fuera de ella.











 nueva página del texto (beta)
nueva página del texto (beta)