Aleph

 

La enseñanza de las matemáticas y la tecnología

 

The teaching of Mathematics and Technology

 

Ramón Sebastián Salat Figols

 

Escuela Superior de Física y Matemáticas. Instituto Politécnico Nacional.

 

Recibido: 12/07/2013.
Aceptado: 21/08/2013.

 

Resumen

El objetivo de este trabajo es presentar argumentos en el sentido de que el uso de las herramientas de computación ha pasado a formar parte de la cultura del hombre como parte de un proceso histórico y cultural que marca una nueva etapa del desarrollo. Primero, se presentan los aspectos más importantes desde un punto de vista histórico; luego, se muestran algunos ejemplos de uso para ilustrar su potencial en la ciencia y en la educación. Finalmente, se plantean algunos elementos fundamentales con respecto a la relación entre la creación y el uso de herramientas computacionales y el pensamiento del hombre.

Palabras clave: Innovaciones tecnológicas, matemáticas, matemática educativa, tecnología educativa.

 

Abstract

The goal of this paper is to present arguments that the use of computational tools has become part of the culture of humanity, as part of a historical and cultural process that marks a new stage in its development. First, we present the most important aspects from a historical point of view; then we show some examples of use to illustrate its potential in science and education. Finally, we propose some fundamental elements with respect to the relation between creation and the use of computational tools and the thought of humanity.

Keywords: Technological innovations, mathematics, educational mathematics, educational technology.

 

Introducción

La tecnología ha influido en la enseñanza de las matemáticas de dos maneras diferentes. Una de ellas, debido a los cambios que el quehacer matemático ha tenido con la aparición de las computadoras, que pueden procesar rápidamente grandes cantidades de datos, lo cual ha influido en la definición de los programas de las asignaturas de matemáticas. Otra, debido a que las computadoras se han convertido en un recurso para potenciar el aprendizaje. En ambos aspectos, el efecto ha ido creciendo debido a los avances en la propia tecnología computacional y a un paulatino efecto de penetración de estos recursos en la sociedad en general.

El conocimiento de los dos aspectos es imprescindible para lograr una pertinente actualización de los programas de las asignaturas de matemáticas. Esto es, para evitar su obsolescencia con respecto a los cambios que a futuro se esperan.

Por otro lado, existen estudios que nos permiten entender mejor el modo en el que las herramientas computacionales modifican nuestros procesos cognitivos.

El propósito de este artículo es proporcionar elementos para establecer que las herramientas computacionales han pasado a formar parte de nuestra vida, desde un punto de vista cultural, y proporcionar una perspectiva de los aspectos señalados que permita al lector, por un lado, entender que el uso de la tecnología en la educación es un aspecto de gran importancia para la formación de los educandos y, por otro, proporcionar información actualizada que le permita adentrarse en los aspectos señalados.

 

Un breve repaso histórico

En 1834, el matemático Charles Babbage diseñó su máquina analítica. Ésta era capaz de realizar las cuatro operaciones aritméticas fundamentales: tenía una unidad de memoria; era programable, lo cual permitía el direccionamiento condicional y los ciclos; se introducían los datos con tarjetas perforadas; y era capaz de imprimir los resultados. Es decir, tenía las características de las computadoras de hoy (Bromley, 1982). Desafortunadamente, nunca pudo ser construida, pero, aun así, la idea de Charles Babbage dejó una importante huella en la historia de la computación. En 1945, el matemático John von Neumann diseñó una computadora electrónica llamada EDVAC, que fue construida y entró en operación en 1952 (Von Neumann, 1945). La EDVAC era capaz de resolver, por ejemplo, ecuaciones diferenciales parciales no lineales, y su diseño tenía una arquitectura que es la de la mayoría de las computadoras modernas. Quizá la diferencia más importante entre la EDVAC y las computadoras anteriores es que las anteriores podían realizar alguna tarea específica, y si se deseaba que realizaran otra había que cambiar las conexiones en los circuitos; mientras que la EDVAC podía cambiar de tarea si se introducía un programa en la misma memoria de la máquina. La EDVAC fue la materialización de la idea de Charles Babbage y de una genial invención de von Neumann. Una manera de conocer más acerca de la relación entre el desarrollo de la matemática y la computación, en sus orígenes, es estudiar la obra de von Neumann (Glim, Impagliazzo, Singer, 1988). Uno de los primeros trabajos importantes de simulación, usando la computadora, fue en la difusión de neutrones, para estudiar el fenómeno de la fisión nuclear; lo realizaron Stanislao Ulam y John von Neumann (Eckhardt, 1987).

Al principio, las computadoras se programaban en lenguaje de máquina; las instrucciones se introducían en la forma de números binarios; los programas eran listados de números en este formato. La programación era un trabajo sumamente tedioso y sujeto a muchas posibilidades de cometer errores. Se crearon los primeros lenguajes ensamblador, que traducían las instrucciones escritas con nombres cortos para las operaciones y números en hexadecimal al lenguaje de máquina. Después, se crearon lenguajes con los cuales era más sencillo escribir un algoritmo para resolver algún problema y el correspondiente compilador, el programa que traduce las instrucciones del lenguaje a lenguaje ensamblador. En 1956, nació el primer compilador Fortran, cuyo significado es Formula Translating System (Knuth, Trabb, 1976). Este compilador traducía un programa escrito en un lenguaje accesible para el público en general a un programa en lenguaje ensamblador, es decir, en el lenguaje utilizado por la máquina. Con los primeros compiladores Fortran, muchos científicos pudieron crear sus propios programas y utilizar la computadora en sus investigaciones. Pero, aun así, su uso era limitado, porque las computadoras solamente podían ser adquiridas y mantenidas por empresas e instituciones públicas. Una de las computadoras más económicas en la época era la PDP-8, y la Escuela Superior de Física y Matemáticas del Instituto Politécnico Nacional tenía una en 1968. Kemmeny y Kurtz (1968) crearon un nuevo lenguaje de programación, el BASIC, cuyas siglas en español son Código Simbólico de Instrucciones de Propósito General para Principiantes.

En la década de 1970 aparecieron las primeras computadoras personales, que permitieron que usuarios individuales tuvieran una.

En 1967, Bolt, Beranek, Newman y Papert desarrollaron el lenguaje Logo, marcando una etapa importante de influencia en la educación. El Logo se utiliza en la enseñanza para diseñar actividades para explorar conceptos matemáticos mediante la programación (Papert, 1995, 1996, 2000). En muchos planes y programas de estudio se incluyeron actividades con el lenguaje Logo (Sacristán, 2011).

Actualmente, existen las computadoras personales de muy bajo costo, comparativa y notablemente más poderosas que las de la década de 1970. También existen calculadoras programables que pueden graficar y tabletas para las cuales hay programas que las hacen muy útiles técnica y pedagógicamente.

Hoy existen sistemas operativos gratuitos para las computadoras personales -por ejemplo, algunas versiones de Linux-para los cuales hay una gran variedad de programas útiles para la educación y el trabajo profesional en las ciencias exactas. Por ejemplo, Maxima, Reduce y Xcas pueden efectuar cálculo simbólico y numérico; Scilab y Octave pueden realizar cálculo numérico; Geogebra sirve para explorar objetos geométricos; Lyx, para escribir trabajos científicos; el compilador gcc funciona para compilar programas en C y en Fortran; Python, Lua y Ruby, para escribir programas en lenguaje de scripts; gnuplot, puede realizar gráficos para las ciencias y la ingeniería.

Las calculadoras graficadoras y programables tienen diferentes recursos en un solo dispositivo, lo cual las hace muy útiles y fáciles de transportar. Usualmente, se pueden programar en BASIC, pueden graficar funciones en dos y tres dimensiones, y suelen tener un sistema de álgebra computacional. Además, podemos intercambiar información entre la calculadora y la computadora personal. Algunas tienen hoja de cálculo y un programa para explorar objetos geométricos.

Existen también las tabletas, delgadas y ligeras, que se transportan fácilmente y tienen recursos táctiles de interacción. Para ellas hay una gran variedad de programas para uso en las ciencias, la ingeniería y la educación, muchos de ellos gratuitos. Existen versiones de Xcas, Maxima, Octave, Python, Lua, y Reduce para tabletas. Además, algunos modelos recientes son comparativamente muy económicos.

 

Algunos ejemplos de uso de la computadora en matemáticas

Uno de los usos más difundidos de la computadora en el terreno de las matemáticas fue para demostrar el teorema del mapa de cuatro colores. El teorema existía como una conjetura desde 1852. A grandes rasgos, el teorema afirma que solamente se requieren cuatro colores para iluminar un mapa plano sin que dos regiones adyacentes compartan el mismo color. La computadora ayudó a reducir el número de casos particulares a considerar en la demostración (Appel, Haken, 1977).

Otro uso importante de la computadora en la ciencia es el de autómatas celulares para modelar el mundo físico (Wolfram, 2002).

Margolus y Toffoli (1987) utilizan la simulación en computadora de autómatas celulares para modelar la dinámica de los fluidos y estudiar fenómenos, como la reversibilidad, la difusión y el equilibrio.

Otro campo de estudio en el que la computadora ha sido un auxiliar importante es el del fenómeno de la percolación. A manera de metáfora, considere una cuadrícula en la que cada celda puede estar vacía u ocupada por un árbol y que en alguna de las celdas se inicia un incendio; interesan preguntas, tales como: ¿cuál es la probabilidad de que el incendio acabe con todo el bosque? Existe una cantidad particularmente importante de probabilidades, llamada probabilidad crítica de percolación, que hasta hoy solamente puede ser calculada aproximadamente por simulación en computadora. Para una introducción al tema puede consultar a Salat (2005).

Nagel y Schreckenberg (1992) introdujeron un autómata celular para modelar el tráfico de vehículos a escala microscópica. Para estudiar el tráfico de vehículos en una autopista de un solo carril se supone que está dividida en celdas de igual tamaño, cada una de las cuales puede estar vacía u ocupada por un vehículo. Los vehículos no pueden sobrepasar una velocidad máxima υ_max . Si la velocidad de un vehículo es υ, las reglas que definen al autómata son las siguientes: 1) si υ < υ_max , la velocidad se incrementa en 1; 2) si υ es menor que el número de celdas entre el vehículo y el siguiente más cercano, entonces υ se igual a dicho número de celdas; 3) si v υ > 0, υ disminuye en una unidad con probabilidad p; 4) el vehículo avanza υ celdas. Estas reglas se aplican de manera paralela a todos los vehículos. Por medio de la simulación puede estudiarse, por ejemplo, la formación y el comportamiento de los embotellamientos de tráfico. Una introducción al tema se halla en Salat (2006).

Otro recurso importante disponible es la hoja de cálculo. Con ella podemos ver, en una sola hoja, por ejemplo, la realización de un algoritmo. Las hojas de cálculo se usan frecuentemente en tareas de simulación en aspectos económicos y financieros.

A continuación se presentan algunos ejemplos sencillos de uso de la tecnología para la solución de problemas. El propósito de presentar estos ejemplos es mostrar cómo la tecnología nos ofrece nuevas perspectivas para analizar los problemas. El primer y el segundo problemas se refieren al uso de la computadora para realizar simulaciones que permitan estimar los parámetros π y . En el tercero se resuelve un problema de flotación, usando el cálculo simbólico; la ventaja de usar el cálculo simbólico es que se obtiene una expresión algebraica para la profundidad a la que se sumerge el cuerpo, lo cual permite manipulaciones simbólicas posteriores. El cuarto problema nos muestra cómo se puede usar el cálculo simbólico para convertir el método de iteraciones sucesivas de Picard en un recurso para aproximar las soluciones de ecuaciones diferenciales ordinarias de primer orden. En el quinto problema se muestra cómo el cálculo simbólico puede ayudarnos a trabajar con diferencias finitas y con aproximaciones por la fórmula de Taylor. Finalmente, se presenta el ejemplo del problema de las torres de Hanói, para ilustrar la fuerza del método recursivo en la programación.

 

1) Cálculo de π por simulación

Se lanzan aleatoriamente dardos a un cuadrado de lado 1 y se observa la proporción que cae en el interior del cuarto de círculo, que pasa por dos vértices opuestos del cuadrado y tiene por centro uno de los otros vértices (gráfica 1).

Esta proporción, cuando el número de dardos sea muy grande, será prácticamente igual a la razón del área del cuarto de círculo al área del cuadrado, esto es, igual a ^π/₄.

A continuación se presenta un programa en BASIC para la calculadora TI-Nspire™ CAS CX:

: Definecalcpi(n)=

:Prgm

:cuenta:=0

:For i,1,n

: x:=rand()

: y:=rand()

: d:=x^(2)+y^(2)

: If d<1 Then

: cuenta:=cuenta+1

: EndIf

:EndFor

:Disp 4*cuenta/n

:EndPrgm

Con un millón de dardos, se obtuvo 3.14051 como aproximación para π. Actualmente, dentro de la teoría de la simulación existen técnicas para mejorar el resultado, por ejemplo, las de reducción de la varianza.

 

2) Cálculo de por simulación

Si tomamos un número considerablemente grande de puntos uniformemente distribuidos en el intervalo (0,2) y nos fijamos en la proporción de los que son menores que , ésta será, aproximadamente, . Considerando que un número en el intervalo n (0,2) es menor que si, y solamente si, su cuadrado es menor que 2, la proporción de números del intervalo (0,2) que son menores que es igual a la proporción de números cuyo cuadrado es menor que 2. El siguiente programa en Python, se ejecutó en una tableta:

from random import random

n=10000000

cuenta=0

for i in range(n):

x=2. *random()

if x*x<2:

cuenta=cuenta+1

print 2. *float(cuenta)/float(n)

Considerando diez millones de puntos, se obtuvo 1.4141836.

 

3) Problema de flotación

Una boya esférica de radio 1 m y peso w se pone en la superficie del agua: ¿cuál es la profundidad y que se sumerge como una función de w?

Para que la boya esté en equilibrio, el peso de la misma debe ser igual al volumen del agua desalojada. El volumen del casquete esférico sumergido a una profundidad y es

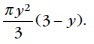
Luego, la ecuación de equilibrio es:

Donde ρ_a = 1000 ^kg/_m3 es la densidad del agua y g = 9.81 ^m/s² es el valor de la gravedad. Por comodidad, se toma

Así, la ecuación de equilibrio queda:

Si en la TI-Nspire™ cas cx ponemos la instrucción

nos da tres soluciones, de las cuales solamente una corresponde a la realidad física, a saber:

No todos los sistemas de álgebra computacional pueden resolver la ecuación (2) para y en forma simbólica. Se puede graficar la función para formarse una idea rápida de su comportamiento. La solución puede obtenerse mediante las fórmulas de Cardano, pero es bastante laborioso hacerlo de ese modo.

Los sistemas de álgebra computacional pueden llegar a ser muy útiles, como en el problema anterior, sin embargo, también requieren de una cuidadosa interpretación de los resultados. Por ejemplo, a la instrucción

el sistema responde x = 1, cuando en realidad la ecuación

no tiene solución. Si suponemos que existe un número real x que satisface la ecuación, entonces debe ser x ≠ 1, pasando x - 1 al miembro de la derecha en la ecuación y simplificando se obtiene (x - 1)² = 0, o sea, x = 1, lo cual contradice nuestra anterior afirmación de que x ≠ 1; por tanto, la ecuación no tiene solución.

 

4) Solución aproximada de una ecuación diferencial por el método de iteraciones sucesivas de Picard

Para demostrar el teorema de existencia y unicidad de la solución de una ecuación diferencial ordinaria de primer orden y' =f(x,y) sujeta a la condición y(0) = y₀, es usual emplear el operador:

Se demuestra que, bajo ciertas hipótesis, el operador tiene un punto fijo, y luego se demuestra que la función punto fijo es la solución de la ecuación diferencial. Este método puede emplearse también para aproximar la solución de una ecuación diferencial, usando un programa de cálculo simbólico. Por ejemplo, si queremos resolver la ecuación y'=xy² -y, sujeta a la condición y(0) = 1, podemos proceder del siguiente modo:

Define ƒ 1(s) = 1

Define g2(x) = 1 + (tg1(t)² - g1(t))

Define g3(x) = 1 + (tg2(t)² - g2(t))

...

Así se obtienen:

Realizar estos cálculos manualmente es un método impráctico; pero con un sistema de álgebra computacional este método proporciona un nuevo recurso para aproximar soluciones de ecuaciones diferenciales ordinarias.

 

5) Algunas posibilidades del cálculo simbólico.

Si en la TI-Nspire™ CAS CX, ponemos:

Define ƒ 1(x) = ƒ (x + h) - ƒ (x)

Define ƒ 2(x) = ƒ 1(x + h) -ƒ 1(x)

Define ƒ 3(x) = ƒ 2(x + h) -ƒ 2(x)

Si ponemos ƒ3(x) y apretamos ENTER, se obtiene la fórmula general para las terceras diferencias:

ƒ (x + 3h) - 3 ƒ (x + 2h) + 3 ƒ (x + h) -ƒ (x)

Si ponemos:

ƒ (x) := x²

y luego ƒ2(x) y apretamos ENTER, se obtiene: 2h². O sea, se obtiene la segunda diferencia para la función x². Incluso se puede trabajar con operadores, como el siguiente:

Si ponemos aprox (x²,2) y apretamos ENTER, se obtiene 2hx + h, que es la primera diferencia de la función, aproximada por la fórmula de Taylor a orden 2.

Es decir, los programas de cálculo simbólico facilitan la exploración del comportamiento de las funciones y de su aproximación.

 

6) El problema de las torres de Hanói

Se tienen tres postes y n aros, todos de diferente tamaño, insertados inicialmente en uno de los postes por orden de tamaño, de tal manera que el aro más grande está abajo y el más pequeño arriba. El problema consiste en mover los aros, uno por uno, de un poste inicial a otro final, usando el tercero como auxiliar. La condición es que en todo momento los aros estén ordenados por tamaño en todos los postes (con el mayor abajo y el menor arriba).

Numeremos los postes con 1, 2 y 3. Si tenemos un solo aro, claramente el problema tiene solución. Si suponemos que podemos pasar n aros del poste 1 al 3, utilizando el 2 como auxiliar, entonces también podemos pasar n+1 aros del poste 1 al 3, utilizando el 2 como auxiliar. Veamos cómo: pasamos los n aros más pequeños del poste 1 al 2, utilizando el 3 como auxiliar; luego, pasamos el aro mayor del poste 1 al 3; y finalmente, pasamos los n aros que están en el 2 al 3, utilizando el 1 como auxiliar. Así, por el principio de inducción matemática, el problema tiene solución para cualquier número de aros. Para saber cuáles movimientos tenemos que hacer podemos usar el siguiente programa en Python:

defhanoi(i,a,f,n_aros):

ifn_discos>0:

hanoi(i,f,a,n_aros-1)

print "de a ',a

hanoi(a,i,f,n_aros-1)

n_aros=4

hanoi(1,2,3,n_aros)

Cambiando el valor de la variable n_aros obtenemos las soluciones para el número de aros que deseemos, pero hay que considerar que el tiempo de ejecución del programa crece rápidamente con el número de aros. Para resolver el problema con n_aros, utilizando i como poste inicial, a como auxiliar y f como final, resolvemos el problema para n_aros - 1 número de aros; esto es, movemos los n_aros -1 del poste inicial al poste auxiliar (utilizando el que antes era final como auxiliar); luego, movemos el aro que queda en el poste inicial al final; por último, movemos los n_aros -1 que están en el poste auxiliar al final (utilizando como auxiliar el que antes era el poste inicial). Repetimos el proceso hasta que el número de aros sea 1. Es sorprendente que un programa tan sencillo pueda resolver un problema aparentemente bastante complejo. Este programa puede ejecutarse en muchas tabletas.

 

El pensamiento y sus herramientas

En esta sección se presentan algunos elementos fundamentales de la relación entre la creación y el uso de herramientas y el pensamiento del hombre; estos dos elementos están íntimamente ligados a lo largo de la historia de la humanidad.

Una característica importante de la mente del hombre es poder recordar a voluntad acontecimientos ocurridos anteriormente, independientemente del entorno o ambiente en el que se encuentre. El resto de los animales solo pueden recordar acontecimientos que de alguna manera estén relacionados con el entorno en el que se hallan (Donald, 1991). Esta diferencia tiene consecuencias importantes en el proceso cognitivo: la actividad mental de los animales es circunstancial; la del hombre, por el contrario, va más allá. Esta diferencia se refiere a la capacidad de la memoria interna. Donald (1991) señala que existen tres etapas importantes en el desarrollo de la mente del hombre. La primera, consiste en la aparición de las habilidades motrices de imitación, que le permiten comunicar acontecimientos a partir de secuencias de movimientos corporales. La segunda, es la aparición del habla. La tercera, es aquella en la que se externa la memoria, que en sus orígenes consistió en la aparición de la escritura (o incluso antes, si se consideran las pinturas rupestres). Donald (1991) también señala que en las dos primeras etapas el pensamiento del hombre dependía de su memoria biológica, que estaba limitada por lo que había visto u oído. La memoria externa admite cambios en la representación de la información; esto enriquece los procesos de pensamiento (Donald, 2001). La multiplicación de las formas de representación favorece la concepción de objetos, en abstracto, más allá de cualquiera de sus representaciones.

Los sistemas computacionales, al igual que los libros, crean grandes espacios de memoria externa que almacenan información, trascendiendo el tiempo y el espacio. Estos recursos cognitivos promueven el conocimiento social y acumulativo. Antes de que existieran dichos recursos, la información a la que un hombre podía acceder era aquella que podía transmitirse de una persona a otra. Con la aparición de la Web es posible acceder a un volumen mucho mayor de información que el que podía consultarse en las bibliotecas tradicionales. Al respecto, Donald (2001) señala los peligros para la evolución cultural por la aparición de la Web, en la cual existe una gran cantidad de flujo de información diversa sin un control que pueda dar rumbo a la educación. Ahora, la evolución del hombre depende más de los rápidos cambios tecnológicos que de los cambios biológicos.

Los recursos computaciones pueden pensarse como herramientas de mediación en los procesos cognitivos (Moreno, 2001), de manera similar al lenguaje y a la escritura como instrumentos intelectuales inventados por el hombre para realizar sus propósitos. Moreno (2001) también señala que la computadora, además de permitir la construcción de representaciones externas, permite efectuar transformaciones en ellas, es decir, estas representaciones son ejecutables, podemos actuar sobre ellas. Nuestros procesos cognitivos transcurren mediante nuestra interacción con los objetos matemáticos por medio de la computadora.

Con las computadoras amplificamos nuestras capacidades, podemos resolver problemas que por su complejidad de cálculo, por ejemplo, nos sería imposible resolver sin ellas. Pero, además, el uso de la computadora cambia la naturaleza de la actividad misma (Pea, 1985). Por ejemplo, en el problema de flotación presentado anteriormente, si no tuviéramos un sistema de álgebra computacional, tal vez hubiéramos resuelto la ecuación en forma numérica para diferentes valores de x. De la misma manera, con la calculadora simplemente podemos copiar la fórmula dada por el sistema de álgebra computacional y pegarla en la herramienta para graficar; si no tuviéramos la herramienta, quizá se nos ocurriría construir una tabla y la gráfica correspondiente, o bien utilizar herramientas de cálculo para estudiar su comportamiento.

Cuando volvemos cotidiano el uso de una herramienta, cuando se vuelve un recurso para un fin, cuando la usamos sin pensar en ella, la herramienta se convierte en un instrumento con un propósito ajeno a ella. Se vuelve transparente (o invisible); mientras esto no ocurra, la herramienta seguirá siendo ajena a nosotros, no la tendremos interiorizada como un recurso en nuestros procesos de pensamiento. Al respecto, cabe señalar que uno de los problemas del uso de la tecnología en los planes y programas de estudio de la mayoría de las instituciones educativas de hoy es, precisamente, que la tecnología aparece dentro de cursos específicos, cuyo tema de estudio es la misma tecnología. En realidad, su uso debería estar integrado en los programas de las diferentes materias; de no ser así, es difícil que se dé el paso de herramienta a instrumento.

Por otro lado, las herramientas computacionales tienen una característica muy importante: se reconstruyen sin cesar. Por ejemplo, en una computadora podemos agregar programas para diferentes propósitos, y la herramienta se desdobla en muchos posibles instrumentos. Puede decirse que ésta es la herencia de las grandes ideas de Charles Babbage y de John Von Neumann. Una misma computadora puede utilizarse, por ejemplo, para resolver problemas, como el de la flotación, presentado arriba, o puede usarse como un medio de comunicación entre los estudiantes y el profesor.

 

Conclusiones

Las computadoras actuales, en su mayoría, tienen una estructura a la que llamamos arquitectura de von Neumann, y surge por necesidades de la sociedad durante y después de la II Guerra Mundial. La idea fundamental de von Neumann -cuyo antecedente quizá pueda decirse que fue la máquina analítica de Charles Babbage- de modificar la capacidad de la computadora para realizar diferentes tareas, introduciéndole un programa, le dio una versatilidad de importantes consecuencias. En una sola computadora coexisten muchos instrumentos. La invención y la evolución de la computadora definen una nueva etapa de desarrollo, desde un punto de vista socio-cultural, para la especie humana. La disponibilidad de una memoria externa ampliada, en la que se pueden representar objetos matemáticos con los cuales se puede interactuar, cambia la naturaleza de los procesos cognitivos dentro del pensamiento matemático.

En la enseñanza de las matemáticas, si los programas de estudio de las asignaturas concentran el aprendizaje del uso de los recursos computacionales en unas pocas materias, en lugar de distribuirlos a lo largo de las diferentes asignaturas, entonces las herramientas difícilmente se convertirán en instrumentos, y, como consecuencia, no habrá una auténtica incorporación de las nuevas tecnologías en el proceso educativo. Y nuestros educandos, cognitivamente hablando, podrían quedarse en una generación anterior.

Incorporar la tecnología en los diferentes cursos implica repensar el contenido de los mismos y la metodología con la que se imparten. Es decir, no se trata de un mero ejercicio de agregar a los planes actuales algunos tópicos referentes a la tecnología. Por ejemplo, no es suficiente que el plan de estudios de una carrera de ciencias o de ingeniería tenga una materia dedicada a la programación: hay que repensar, además, los programas de otras asignaturas, para que utilicen esta herramienta como un recurso para mejorar el aprendizaje de otros temas.

Por otro lado, dada la rapidez con la que ocurren los cambios tecnológicos, es necesario fomentar que los alumnos aprendan por sí mismos, pues es imposible pretender que el conjunto de conocimientos que aprendan durante la carrera tenga vigencia durante toda su vida profesional.

Por tanto, queda mucho trabajo creativo por hacer en cuanto al uso de la tecnología en la enseñanza de las matemáticas, tanto en el campo de la investigación como en el de la creación de materiales y propuestas didácticas.

 

Referencias

Appel, K., y Haken, W. (1977). The solution of the Four-Color-Map Problem. Scientific American, 237, 108-121.         [ Links ]

Bromley, (1982). Charles Babbage's Analytical Engine, 1838. IEEE Annals of the History of Computing, 4(3), 196-217.         [ Links ]

Donald, M. (2001). Memory Palaces: The Revolutionary Function of Libraries. Queen's Quarterly 108(4), 559-572.         [ Links ]

Donald, M. (1991). Origins of the Modern Mind, Cambridge, MA.: Harvard University Press.         [ Links ]

Eckhardt, R. (1987). Stan Ulam, John von Neumann, and the Monte Carlo Method. Los Alamos Science, 15(Special Issue).         [ Links ]

Glimm, J., Impagliazzo, J., y Singer, I. (1988). The Legacy of John von Neumann. Proceedings of Symposia in Pure Mathematics, (50). Providence, Rhode Island: American Mathematical Society.         [ Links ]

Kemeny J. G., y Kurtz, T. M. (1968). Basic Programming. New York, NY: John Wiley & Sons, Inc.         [ Links ]

Knuth, D. E., y Trabb, L. (1976). The early development of programming Languajes. Stanford, CA: Computer Science Department, Stanford University.         [ Links ]

Moreno, L. (2001). Memorias del Seminario Nacional: Formación de docentes sobre el uso de nuevas tecnologías en el aula de matemáticas. Bogotá, Col.: Ministerio de Educación Nacional.         [ Links ]

Nagel, K., Schreckenberg, M. (1992). A cellular automaton model for freeway traffic. J. Phys. I France 2, 2221-2229.         [ Links ]

Papert, S. (2000). What's the big idea? Toward a Pedagogy of idea power. IBM Systems Journal, 39(3-4), 720-729.         [ Links ]

Papert, S. (1996). An exploration in the space of Mathematics Educations. International Journal of Computers for Mathematical Learning, 1(1), 95-123.         [ Links ]

Papert, S. (1995). La máquina de los niños. Replantearse la educación en la era de los ordenadores. Barcelona, Es.: Paidós.         [ Links ]

Pea, R. (1985). Beyond amplification: Using the computer to reorganize mental functioning. Educational Psychologist, 20(4), 167-182.         [ Links ]

Sacristán, A. I. (2011). Programación computacional para matemáticas de nivel secundaria. Notas para el maestro. CINVESTAV, Departamento de Matemática Educativa, Programa EMAT-Logo. Recuperado de: http://www.matedu.cinvestav.mx/~asacristan/Programa_emat-Logo.php        [ Links ]

Salat, R. S. (2006). Exploración del fenómeno de tráfico de vehículos con la calculadora. Números, (64).         [ Links ]

Salat, R. S. (2005). El fenómeno de la percolación. Miscelánea Matemática, 41, 23-30. Sociedad Matemática Mexicana.         [ Links ]

Toffoli, T., y Margolus, N. (1987). Cellular Automata Machines: A new environment for modeling. Cambridge, MA: MIT Press, Series in Scientific Computation.         [ Links ]

Von Neumann, J. (1945). First draft of a report on the EDVAC. IEEE Annals of the History of Computing 15(4), 28-75.         [ Links ]

Wolfram, S. (2002). A New Kind of Science. Winnipeg, Can.: Wolfram Media Inc.         [ Links ]

 

INFORMACIÓN SOBRE EL AUTOR:

Ramón Sebastián Salat Figols. Maestro y doctor en Ciencias, con Especialidad en Matemática Educativa en el CINVESTAV. Licenciado en Física y Matemáticas en la Escuela Superior de Física y Matemáticas. Actualmente, es profesor del Departamento de Matemáticas de la Escuela Superior de Física y Matemáticas. Participa en proyectos de investigación con registro en la Secretaría de Investigación y Posgrado del IPN. Tiene varios artículos publicados, entre ellos, en la revista Miscelánea Matemática de la Sociedad Matemática Mexicana. Fue director de la Escuela Superior de Física y Matemáticas de 1995 a 2002.