1. Introducción

Cuando se repasa la vida del matemático y astrónomo suizo Paulus Guldinus (1577-1643), judío y jesuita, se entiende que algunos fanáticos defensores del aristotelismo de Tomás de Aquino -pensamiento oficial del papado durante la Reforma- criticaron despiadadamente a los indivisibles matemáticos cavalerianos (^{Cavalieri, 1647, III}; ^{Andersen, 1985, p. 5}; ^{Koyré, 1978, p. 324 y ss.}; ^{Brunschvicg, 1912, p.165}). Para ellos, la metafísica escolástica debería seguir dictando los caminos de la “ciencia”. Se declararon contrarios a la tesis platónica del infinito actual y no advirtieron los hervores de rebelión que se cocinaban en los cazos matemáticos. Por otra parte, son muchos los testimonios escritos que prueban que los indivisibles matemáticos fueron acogidos por los pensadores que mejor entendieron el arrebatador Zeitgeist del siglo XVII. No sólo ^{Torricelli (1969)}, ^{Pascal (1658)} y ^{Roberval (1693)}, sino también ^{Leibniz (1956, p. 139)} y ^{Newton (1687, p. 35)} los comprendieron de buena o mala gana. Newton y Leibniz se alejaron de los indivisibles para acoger las fluxiones y las fluentes; o los infinitesimales, respectivamente. Luego los indivisibles fueron condenados al olvido. Desde el siglo XVIII la amnesia de los indivisibles ha reinado entre los matemáticos de profesión. Fueron acusados de ser oscuros y contrarios a las cosas del mundo. En este artículo se defiende el provecho de desempolvar a los olvidados indivisibles de Cavalieri, no solamente en favor de las matemáticas mismas, sino también para aprehender cómo éstas se encarnan en la historia material de los hombres. Se defenderá que los indivisibles no constituyen una teoría “oscura”. Todo lo contrario, conforman una teoría admirablemente erigida sobre las mejores tradiciones lógicas y matemáticas de Occidente. En la terminología de ^{Lakatos (1978)}, esta teoría es “empirista”, pues parte de unas proposiciones básicas con términos conocidos (empíricos), tal como se verá en la Sección 3 de más abajo.

La amnesia de los matemáticos ha sido internalizada por muchos historiadores de las matemáticas, quienes han decidido no entender los indivisibles por la simple razón de que no coinciden con su ideario del cálculo infinitesimal. Para ellos, los infinitesimales, las fluentes y las fluxiones constituyen el “glorioso origen” del cálculo infinitesimal. Este proceder ignora la censura -justificada- del obispo ^{Berkeley (1734)} a los Principia de ^{Newton (1687)}. Esto es solamente la punta de un iceberg que esconde bajo el agua los titánicos intentos posteriores por formalizar el cálculo infinitesimal como análisis matemático. Baste aquí con mencionar la reformulación euleriana y el largo padecer del análisis infinitesimal durante el siglo XIX (^{Hairer y Wanner, 1996}). En efecto, no tiene mucho sentido resaltar un momento particular dentro del turbulento devenir del análisis de lo infinito - continuo, pues a cada instante se puede percibir una cierta preservación de algo y una ruptura con lo anterior, como en toda creación cultural. Aquí se adopta una posición crítica frente a dicho estilo de historia de las matemáticas, que se concentra en explicar la disciplina contemporánea como el producto acabado y evidente de un movimiento lineal, continuo y en ascenso permanente -dicha historia quita todo lo que le incomoda en provecho de las “estructuras más firmes”-. Cabalmente, se ha de mirar a las matemáticas no sólo en ellas mismas, sino enmarcadas en sus circunstancias materiales de emergencia y ruptura permanentes. Además, se ha de leer con calma y mucho cuidado la Geometria de ^{Cavalieri (1653)}, pues allí es dónde yacen los elementos para una anamnesis del pensamiento de su autor.

En la Sección 2 se marca la diferencia entre los indivisibles como teoría y como método, distinción que resulta ser importante para revivir la memoria de estos objetos matemáticos. La Sección 3 presenta las definiciones del Libro II de la Geometria. Esto permite rescatar la rica elaboración especulativa contenida en la obra. Muchas intuiciones de Cavalieri perviven hasta hoy, aunque bajo formulaciones distintas. En la Sección 4 se examina el Teorema I del Libro II, en cuanto intento crucial para asignar magnitudes a las figuras geométricas, acierto de la conceptualización cavaleriana. Otro grupo de teoremas importantes del Libro II se trata en la Sección 5. Estos resultados se dan sin mayores explicaciones para exponer el entramado lógico que soporta el método de los indivisibles. Dicho método es el objeto de la Sección 6. No se dan muchos detalles, pues es la parte más conocida de la Geometria. En la Sección 7 se defiende la claridad de los indivisibles de Cavalieri, a pesar de la tradición que los etiqueta de incomprensibles. Finalmente, en la Sección 8, se esbozan algunas conclusiones.

2. Los indivisibles, teoría y método

La Geometria, desde su prefacio, es una teoría del espacio soportada por un andamiaje lógico similar al de los Elementos de Euclides. Los indivisibles son el sueño de Galileo para explicar la compositio continui (^{Raffo, 2016, p. 51 y ss.}). Dicho continuo es una creación cultural, que se venía gestando en los vientres mercantilistas de muchas pujantes ciudades europeas desde fines de la Edad Media. ^{Radford (2008)} ha documentado el cambio ocurrido en las concepciones de movimiento desde el siglo VIII hasta el Renacimiento. Tales estructuras culturales -épistèmes foucaultianas- abarcaban en sus comienzos lo finito-discreto. Hacia el fin de la Edad Media y comienzos del Renacimiento, por el contrario, ya se había aceptado en el inconsciente europeo que cada todo contenía infinitas partes y que las cosas cambiaban continuamente:

In the same way as time became minutely measurable, so too did space, through the invention of perspective […] This was the emergence of a new form of dynamic narrative in which the individual was displayed in concrete spatial and temporal settings. Through numbers, speed and time became systems. As such, they made possible the creation of unifying systems of knowledge representation. (^{Radford, 2008, p. 5}).

Por una impetuosa voluntad, los pensadores del siglo XVII matematizaron la nueva realidad del espacio, el tiempo y el movimiento. Ni Cavalieri ni Mengoli¹ alcanzaron a prever la resonancia que sus elucrubaciones iban a tener en Europa, ni mucho menos a sospechar las enemistades que ellas les iban a traer hasta el final de sus días (^{Tamayo, 2018}). Ciertamente, la lucha política por la verdad de una teoría hegemónica sobre lo infinito y lo continuo iba a ser brutal, casi sanguinaria (^{Hall, 2002}).

A pesar de su pretensión de teoría, desde el comienzo se habló de un «método» de los indivisibles. Quizás esto se deba al título de la obra: Geometria indivisibilibus continuorum nova quadam ratione promota. La intención de Cavalieri es clara: su objeto es la geometría, un estudio discursivo sobre las figuras en el plano y el espacio. Lo que puede desconcertar es que se estudie de una manera nueva, por medio de los indivisibles. Esto, quizás, significó que se trataba de un método, antes que una teoría. También ^{Pascal (1658, p.10) 2}, desde su dialéctica vertiginosa, lo entendió como una manera de hablar y no como la afirmación perentoria de una nueva realidad. Más recientemente, ^{Andersen (1985)} ha retomado esta tradición.

Es interesante examinar el uso de la palabra «método» en el siglo XVII, pues este siglo está lleno de métodos matemáticos y filosóficos. ^{Brunschvicg (1912)}, menciona, por ejemplo, la méthode des tangentes de Barrow (^{Brunschvicg, 1912, p. 174 y ss.}) y les méthodes pour les tangents (^{Brunschvicg, 1912, p. 177 y ss.}). Incluso dentro del propio cálculo infinitesimal, la méthode des infiniment petits (^{Brunschvicg, 1912, p. 248}, nota al pie) o méthode différentielle pour les tangentes (^{Brunschvicg, 1912, p. 190}, nota al pie) es equivalente y se opone a la méthode des fluxions de Newton (^{Brunschvicg, 1912, p. 192}) . Concretamente, una gran teoría se desdobla en varios métodos y algunos de ellos pueden ser equivalentes entre sí, aunque por vías distintas. Un simple método, por el contrario, señala solamente un camino de solución, a veces apenas una débil luz, una sugerencia. En el siglo de los indivisibles, los geómetras buscaban «buenos métodos» para dar razón de la infinidad matemática del «ser».

Aquí se alcanza un punto central de esta discusión. Como bien lo ha dicho Brunschvicg refiriéndose a Cavalieri:

Il y a une grande difficulté à suivre les détails techniques d’un ouvrage où l’auteur posait des problèmes nouveaux, et les étudiait à l’aide d’une méthode nouvelle, créant un langage sans y joindre d’ailleurs de symboles appropriés. (^{Brunschvicg, 1912, p. 192}).

La historia oficial de las matemáticas prefiere idolatrar las grandes teorías y menospreciar los simples métodos porque privilegia los enfoques hermenéuticos sobre los heurísticos. Los métodos tienen que ver con la invención y el descubrimiento, la imaginación y la originalidad. Proveen técnicas o procedimientos para resolver -quizás momentáneamente- los problemas inmediatos. Del lado de las teorías, por el contrario, reposa la perfección aparente de lo que no es humano ni cambiante, de lo ajeno a la historia,… de Dios. Los círculos hermenéuticos se acercan, poco a poco sin lograrlo, a la verdad absoluta, hyperuránion tópon…

Vale la pena recordar a los indivisibles -como teoría o método con sus aciertos y limitaciones- porque intentaron hablar de nuevas concepciones de espacio y tiempo, cuando lo finito - discreto perdió sentido en la mentalidad renacentista. Asimismo, con mayor profundidad para la historia de las matemáticas y su enseñanza, cobra más sentido indagar en las heurísticas y la inestabilidad de los descubrimientos, que en la estabilidad y en la falsa sensación de permanencia detrás de las grandes teorías.

3. Definiciones del Libro II

En relación con lo dicho, la mayoría de los análisis sobre la obra del milanés se consagran casi exclusivamente a describir la manera cómo los indivisibles sirven para calcular áreas y volúmenes (^{Andersen, 1985}; ^{Koyré, 1978}; ^{Brunschvicg, 1912}). Este proceder sepulta de tajo todo el prodigioso ejercicio de conceptualización de Cavalieri que, por cierto, soporta lógicamente tales cálculos. Incluso ^{Andersen (1985)}, que dedica una sección -muy breve- a bosquejar algunas nociones relativas a las figuras que se describen en el Libro I, se queda corta al enfocarse en detalles sobre las tangentes y la noción cavaleriana de magnitud.

Como aquí se quiere rememorar al autor, a continuación, se recorre de la mano del texto original el extraordinario trabajo de abstracción y generalización que Cavalieri puso antes de sus teoremas. Empero, antes conviene decir un par de palabras sobre la concepción y redacción de la Geometria. En particular, el primer libro de la obra no fue el primero que Cavalieri escribió: Il libro I è quel “libro delle propositione lematiche” che Cavalieri aveva “in confuso”, e che redasse in modo definitivo solo dopo aver scritto i quattro seguenti (cfr. Introduzione). (^{Lombardo-Radice, 1966, p. 59}).

Luego del descubrimiento de las omnes lineae, que describe con orgullo al comienzo (^{Cavalieri, 1653}, Praefatio), Cavalieri demostró muchos e importantes resultados, que acomodó de un solo golpe de inspiración en cuatro libros. Enseguida reflexiona sobre sus suposiciones y las ubica en el Libro I. Así, el primer libro es verdaderamente el quinto: un artificio de escritura para dar la impresión de un edificio construido desde los cimientos. Pero el estrés de la escritura no terminó allí:

Comme abbiamo ampiamente spiegato nell’Introduzione, il libro VII occupa unan posizione particolare nella Geometria di Cavalieri; esso venne composto alcuni anni che l’Autore aveva portato a termine i primi sei. La caratteristica di quest’ultimo libro va soprattutto cercata nel nuovo metodo ivi adottato, che in un primo tempo Cavalieri riteneva costituito “senza indivisibili”. Più tardi si accorgerà che, a rigore, neanche esso fa a meno di tale nozione, pur usandola in modo diverso; lo chiamerà quindi “secondo metodo degli indivisibili”. (^{Lombardo-Radice, 1966, p. 649}).

Esto se debió a las críticas sobre las bases metafísicas de los indivisibles. Ante la ortodoxia científica, Cavalieri recula de la posición defendida en lo que va escrito del libro e intenta recrear los indivisibles de manera que no riñan con los dogmas de su tiempo.

3.1. Regiones planas

El Libro II de la Geometria comienza con una definición rotunda:

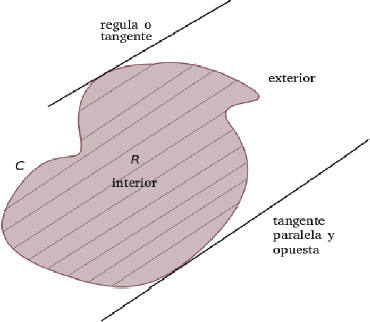
I. Si por tangentes opuestas a una figura plana cualquiera se levantan dos planos mutuamente paralelos -perpendiculares o inclinados respecto al plano de la figura dada, infinitamente prolongados de una y otra parte, de los cuales uno se mueve hacia el otro, concebido siempre paralelo al primero, hasta sobreponerse con el segundo- los segmentos individuales -que durante todo el movimiento se forman por las intersecciones del plano móvil y la figura dada, tomadas todas juntas- se llaman omnes lineae de dicha figura -referida a una regula (regla, referencia), […] (^{Cavalieri, 1653}; Liber secvndvs, Definitiones I.).

Como el tratamiento de los omnia plana para los sólidos es similar, aquí solamente se consideran figuras planas. Además, podemos prescindir de las representaciones tridimensionales y tratar intrínsecamente el caso plano. Así, la definición anterior se reinterpreta como: “si una de dos tangentes opuestas a una figura plana se mueve hacia la otra, manteniéndose en cada instante paralela a ella, los segmentos que se forman por intersección de la recta móvil con la figura se llaman todas las líneas de la figura, referidas a la dirección de las mentadas tangentes”. Con ello inaugura una geometría en la que el movimiento y lo continuo están entrelazados íntimamente. Lo infinito se torna acto bajo la forma de colección infinita. Dichas colecciones cobran significado preciso en los postulados y sus propiedades se desvelan en los teoremas.

No interesan las “equivocaciones” de Cavalieri a la luz de invenciones posteriores, sino defender que muchas cosas de la Geometria todavía perduran, bruñidas por las procelosas corrientes del tiempo. Por ello está permitido reescribir las definiciones en el lenguaje de la Geometría Diferencial de hoy. Aquí, los resultados valen, no para una aliqua figura plana, sino para una región conexa compacta R del plano euclidiano, encerrada por una curva regular de Jordan C. En términos profanos, R

• - es cerrada y acotada, en particular, está contenida en un círculo de radio finito;

• - dos puntos cualesquiera en R se pueden unir por un camino continuo que no se sale de ella;

• - la curva C es diferenciable con derivada no nula (en cada punto se puede trazar la recta tangente) y particiona el plano en dos partes (interior y exterior).

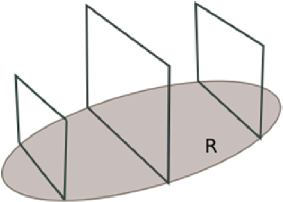
La Figura 1 sugiere esta noción de región plana. Los segmentos que se trazan con líneas más delgadas son algunos de los omnes lineae. Aunque Cavalieri no lo dice, estos segmentos son los “indivisibles” de R.

Figura 1 Región plana acotada R, encerrada por una curva de Jordan regular C. (elaboración propia) 

Este recurso del análisis de un texto -matemático-, por medio del cual se relacionan dos nociones de distintas épocas, surge normalmente cuando se abandonan los prejuicios críticos que quieren detectar “errores” en obras de tiempos pasados. En efecto, dicho recurso enfatiza los significados antes que los significantes, tal como algunos han creído detectar en los estudios de Michel Serres: Pour Serres, lire le texte, c’est travailler sur les choses mêmes, sur le monde dont part et parle le texte. Ainsi définie, la critique devient « une physique généralisée » (Feux 15) et l’interprétation reçoit pour tâche de saisir la matérialité de l’œuvre dans l’espace où elle se découpe. (^{Porée; 2000, p. 5}). Asimismo, realza la simbolización inherente al pensamiento, en la cual se pueden tender puentes entre instantes y lugares diferentes: Le feu réel dissémine les cendres, le feu métaphorique dissémine les signes. D’où chez Serres le triomphe du principe d’identité et/ou d’analogie, rendu par les termes d’isomorphisme, d’homologie, d’homorhésie. (^{Porée; 2000, p. 5}). Dichos “isomorfismos serresianos” se erigen como herramientas indispensables del análisis de los conceptos.

Tampoco se comete un anacronismo, porque no se están situando los conceptos o nociones en momentos o épocas que no les corresponden. Al revés: el enfoque tradicional de la historia de los conceptos matemáticos tiende al protocronismo.

3.4. “Sistema de Coordenadas”

Otro mérito de Cavalieri se plasma en un sistema para ubicar los puntos de una figura. Para ello introduce otra colección conformada por “todos los infinitos puntos” que cumplen cierta condición:

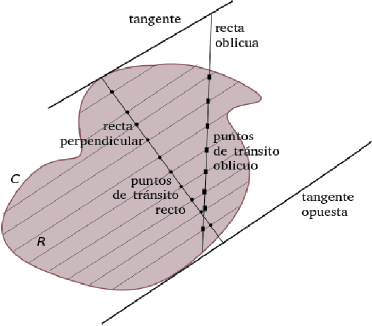
III. Si dos líneas rectas encuentran internamente planos tangentes opuestos -la una perpendicularmente, la otra oblicuamente-, los puntos de la intersección de la línea recta dada incidente perpendicularmente sobre los planos individuales -que tomados juntos se llaman “todos los planos” (prolongados para que puedan tocar la recta)-, o sea, los puntos que son intersección de ella y los planos móviles, generados en todo el movimiento, tomados juntos se llaman “todos los puntos de tránsito recto” […] (^{Cavalieri, 1653}; Liber secvndvs, Definitiones III.).

Cavalieri no usa “números reales” sino puntos. Su estilo euclidiano lo obligaba a considerar únicamente propiedades y variaciones geométricas. Esta restricción es voluntaria y evidencia su gran fuerza de voluntad, pues estaba al tanto de los logros del Álgebra renacentista, como lo deja ver en la Exercitatio quarta (^{Cavalieri; 1647, p. 283 y ss.}), donde acepta los métodos algebraicos de Beaugrand.

Volviendo a la Definición III, la relación con las coordenadas cartesianas es clara. La Figura 2 esboza estas nociones.

Figura 2 Recta perpendicular y oblicua con sus puntos de tránsito (elaboración propia) 

Hasta ahora todo parece normal para un lector contemporáneo. La sorpresa se presenta con la manera de ubicar los puntos en las rectas:

IV. Si tomamos los segmentos comprendidos entre uno de los extremos de la línea recta dada y los puntos individuales, que juntos se llaman “todos los puntos de tránsito recto u oblicuo de ella”; tales líneas, tomadas juntas, se llaman “todas las abscisas del segmento dado” […]

V. […], los segmentos rectos, situados sobre la línea dada de la definición antecedente, comprendidos entre los mismos puntos y el extremo restante, se llaman los “residuos de todas las abscisas” de la línea dada […]

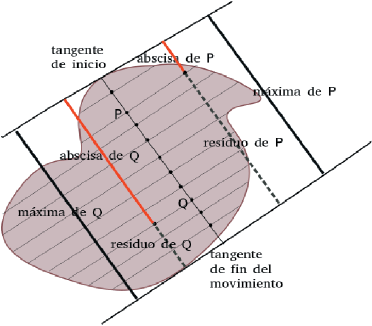
VI. Si por una cualquiera de aquellos segmentos, que se llaman todas las abscisas del segmento dado (segmento completo o total), se imagina tomada una vez el mismo segmento dado o uno igual a él, tales segmentos tomados juntos se llaman “las máximas de todas las abscisas” de la línea dada; o bien, se sobreentenderá siempre que sean las máximas de todas ellas, […] se dirá simplemente las “máximas de las abscisas”. (^{Cavalieri, 1653}; Liber secvndvs, Definitiones IV, V & VVI.).

Estas definiciones desconciertan, pero luego se revelan como evidentes y naturales. El punto se mueve de un extremo del segmento al otro y, en cada instante, se toman tres piezas de información: el segmento ya recorrido o abscisa, el segmento que falta recorrer o residuo y el segmento total que se alcanza al final del recorrido. La Figura 3 ilustra esta asignación para dos instantes dados.

Figura 3 Abscisas, residuos y máximas de los puntos de tránsito (recto) P y Q (elaboración propia) 

Abscissa, del verbo abscindo, quitar, denota la parte que se quita. Lo que queda es el residuus. Lo que se toma y lo que queda solamente cobran sentido cuando se explicita el todo o maxima. El uso de este superlativo es natural para la mente matemática contemporánea, puesto que evoca algunos hechos básicos de la Topología. El segmento considerado también es un compacto y se recorre según una función continua. Por lo tanto, dicha función es acotada y admite un valor mínimo y un valor máximo. Cf. ^{Hairer y Wanner (1996; p. 206}, Theorem 3.6). Claro está, hablar de valores extremos, solamente tendría sentido en el marco de “una relación de orden”.

La Definición VI va seguida de la observación sobre las correspondencias biunívocas de la subsección 3.2.

3.5. Parejas de elementos

En la Definición VII, “se asigna” un segmento cualquiera a una abscisa.

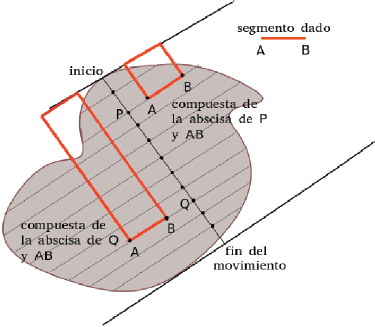
VII. Si a cada una de las abscisas de la línea recta dada se imagina juntado otro segmento igual a un segmento dado, las compuestas de todas las abscisas y los segmentos adjuntos, tomadas juntas, se llamarán “todas las abscisas de tal segmento adjunto dado” [...] (^{Cavalieri, 1653}; Liber Secvundvs, Definitiones VII.).

La naturaleza del segmento que se adjunta a cada abscisa no se explica. En este punto es inevitable no evocar las figuras bidimensionales de Nicolás de Oresme en De configurationibus qualitatum et motuum: un segmento representa la intensidad de una cualidad y el otro segmento representa la extensión de un cuerpo (^{Clagett, 1968}). De otro lado, los segmentos adjuntos son arbitrarios, de cualquier tamaño. Se podría pensar en tomar uno distinto para cada punto de tránsito y así, construir una figura (como una “aplicación”). Esto, empero, no está en Cavalieri. Lo único que se dice allí es que se asigna el mismo segmento, digamos AB, a cada punto punto de tránsito, como en la Figura 4. Esta figura no aparece en Cavalieri y solamente pretende explicar sus palabras. En favor de esta interpretación se tiene el testimonio de ^{Mengoli (1659)}, alumno de Cavalieri, quien usó representaciones similares. No es claro lo que Cavalieri entendía por adjunción de un segmento a otro.

Figura 4 Segmento adjunto AB compuesto con las abscisas de P y Q (elaboración propia) 

Con esto se concluye la descripción de las regiones del Libro II. Cavalieri no habla de “ordenadas”, ni siquiera utiliza esta palabra.

3.7. Semejanzas

Para ilustrar lo anterior, se analiza la definición A VIII del Libro II, referente a la construcción de ciertos sólidos. Es interesante ver cómo se las ingenia para levantar figuras semejantes sobre una región plana:

A. VIII. Dada una figura plana cualquiera y trazada -de algún modo- en ella un segmento recto con sus dos extremos sobre el contorno, si se concibe que dicho segmento recto describe una figura plana cualquiera, que no yace en el plano de la figura dada y si comprendemos así que el resto de tales segmentos, que hemos llamado “todas las líneas” de la figura dada, tomadas con referencia a una línea trazada, […] describen figuras planas semejantes, ubicadas propia y paralelamente a aquella descrita antes, de modo que todas los segmentos que se describen sean segmentos homólogos de la figura descrita, entonces todas las figuras descritas tomadas juntas se llamarán “todas las figuras planas semejantes de la tal figura dada” [...] (^{Cavalieri, 1653}; Liber Secvundvs, Definitiones A. VIII.).

La figura levantada, digamos un cuadrado, se copia por semejanza sobre todos los indivisibles de la original. La Figura 5 ilustra esta situación.

Figura 5 Cuadrados levantados sobre una figura base R (elaboración propia). 

Hoy se dice que los cuadrados cambian “suavemente” sobre la figura debido a las hipótesis impuestas sobre la región R. Esta construcción inspiró a otros pensadores de los indivisibles del siglo XVII. Por ejemplo, el concepto pascaliano de onglet, cuña, pestaña, (^{Pascal, 1658}; Traité des trilignes rectangles, & de leurs onglets) está estrechamente relacionado con esta noción de Cavalieri.

4. Teorema I, Libro II

Queda por precisar una noción práctica de omnes lineae, que sirva para determinar el “área de una región plana”. La primera tarea de Cavalieri consiste en demostrar que las omnes lineae son magnitudes o números, si se quiere.

El Teorema I del Libro II dice: “Todas las líneas en un tránsito recto de figuras planas cualesquiera [...] son magnitudes que guardan proporción entre sí” (^{Cavalieri; 1653, p. 108 y ss.}). Lo importante es que a cada región plana se le asigna una magnitud y dos magnitudes se pueden poner en proporción. A cada región R se le puede asignar un número real y Cavalieri no puede percatarse que los siglos van a esculpir estos asuntos como una teoría de la medida y la integración, cf.^{Jones (2001)}. No obstante, las ideas fundamentales están ya presentes en la Geometria y se asemejan mucho a la construcción de área que se hacía en algunos textos de Geometría Euclidiana a finales del siglo XIX y comienzos de XX:

136°. Def. I. - The area of a plane closed figure is the portion of the plane within the figure, this portion being considered with respecto to its extend only, and wihout respect to form.

A closed figure of any form may contain an area of any given extent, and closed figures of different forms may contain areas of the same extent, or equal areas. […]

137°. Areas are compared by superposition. (^{Dupuis; 1914, p. 91}).

En la popular Wentworth’s Plane Geometry, se usa cierta «unidad de superficie» y el área se mide con dichas «unidades» (^{Wentworth y Smith; 1910, p. 191}). Cavalieri solamente cuenta con omnes lineae y debe llenar el espacio plano con ellas. A continuación revisamos los pasos de su demostración, contenida en las páginas 108 a 111 de la Geometria.

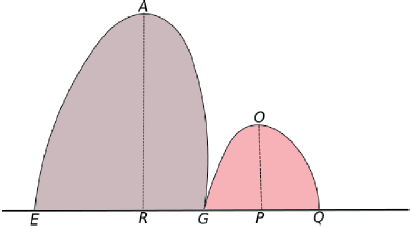
Se parte de dos figuras planas cualesquiera EAG y GOQ, levantadas sobre una regula común EGQ, sobre bases respectivas EG y GQ y alturas respectivas AR y OP. Las dos figuras se han dispuesto una junto a la otra, tocándose en el punto G. Esto supone algunos movimientos previos de las figuras. La Figura 6 bosqueja la situación.

Figura 6 Figuras de partida (elaboración propia) 

Luego se consideran los indivisibles de EAG y GOQ, paralelos a EGQ. Pueden suceder dos casos: AR y OP son iguales, o bien, distintos. Cuando son iguales, la correspondencia biunívoca de las alturas es evidente. Estos dos segmentos se pueden poner en proporción, de acuerdo con la Definición 4 del Libro V de los Elementos de Euclides: Rationem inter se habere magnitudines dicuntur, quae multiplicatae altera alteram superare possunt (^{Heiberg; 1884, p. 3}).

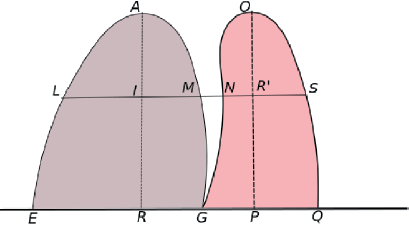
Después Cavalieri argumenta que lo propio vale globalmente y que una figura se puede «dilatar» hasta superar a la otra. ^{Andersen (1985)} ha reconocido que Cavalieri se apoya en rather loose considerations […] he did not perceive the problem of finding a maximum of those infinitely many n’s […] even if he had seen it, he would have had no way to establish the existence of that maximum. (^{Andersen; 1985, p. 318}). De alguna manera, Cavalieri llegó a una conclusión correcta para su posteridad: todas las líneas de una figura se vuelven mayores que todas las líneas de la otra figura aún cuando no sabía nada de funciones continuas que toman valores reales en un compacto. El factor es el máximo de las proporciones de LM en NS (Figura 7), o viceversa, tomadas sobre todos los puntos I y R’ en las alturas.

Figura 7 Figuras con igual altura (elaboración propia) 

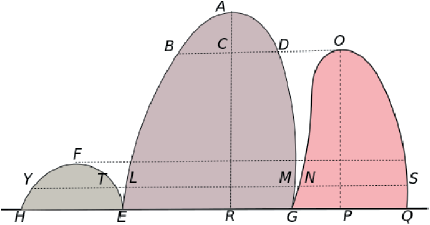
Cuando las alturas son distintas, como en la Figura 8, la parte de EAG con altura mayor a OP, o sea ABD, se corta y pone aparte sobre la regula con el nombre HFE. Cavalieri sabe que el proceso debe culminar en finitos pasos (compacidad junto con la propiedad arquimediana de los reales) . Considera el caso en que AR es igual a CR = OP más AC, con AC menor que OP. Las magnitudes proporcionales están garantizadas para EBDG y GOQ porque tienen la misma altura. Para lo que falta, el segmento NS (respectivamente YT ) y el segmento suma YT + LM > YT (respectivamente LM + NS > NS ) son magnitudes euclidianas. Lo propio para NS y YT. Esto vale hasta la paralela a la regula por F. El resto de los indivisibles son del tipo LM y NS, los cuales ya están resueltos. Enseguida se pasa de lo individual a lo global como antes. Es ingenioso que Cavalieri haya puesto a EAG entre FHE y GOQ, para evitar la ausencia de segmentos de FHE por encima de F.

Figura 8 Figuras con alturas distintas (elaboración propia) 

Los dibujos insinúan que Cavalieri ha ordenado los indivisibles. Por ejemplo, EG es mayor que BD en EAG y GQ es mayor o igual que NS en GOQ. Bajo tal suposición, las demostraciones se simplificarían grandemente. Quizás nunca se sabrá si Cavalieri tuvo la osadía de ordenar los indivisibles de las figuras, una audacia suprema que supone cierta intuición de las aplicaciones continuas.

5. Otros teoremas

Al ser magnitudes, los omnes lineae deberían verificar los teoremas sobre proporciones de Euclides. En especial, la Proposición 1 del Libro VI de los Elementos: Trianguli et parallelogramma sub eadem altitudine posita eandem inter se rationem habent ac bases. (^{Heiberg; 1884, p. 73}) . Para Euclides no hay una noción medianera entre figura y “área”. Para Cavalieri, de otro lado, los omnes lineae son una propiedad “numérica” de las figuras. Así, estas colecciones se deben considerar como una noción de área de la figura. Esto posibilita el sentido preciso del “Teorema II. Todas las líneas (segmentos) de figuras planas iguales son iguales, […] tomando una referencia cualquiera”. (^{Cavalieri; 1653, p.112}). Si dos figuras planas son iguales en el sentido euclidiano, entonces sus colecciones de segmentos (magnitudes) también son iguales. Este hecho es independiente de la elección particular de la regula. La demostración se ilustra en la Figura 9.

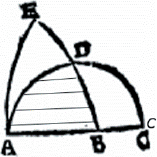
Los segmentos en ABD y la letra C son de elaboración propia

Figura 9 Dibujo de ^{Cavalieri (1653, p.112}) para el Teorema II. 

Claramente, ADC y AEB están formadas por puntos distintos. Pero son iguales en el sentido griego porque tienen igual área. La demostración se basa en la superposición de las figuras. Ellas se intersecan en la región ABD, donde se han trazado algunos indivisibles, que no aparecen en el original. Luego, se repite el proceso superponiendo las partes restantes AED y BDC. El proceso termina y la igualdad euclidiana de las figuras garantiza que las magnitudes son iguales.

Estos resultados completan el ciclo de implicaciones que abrió el postulado (subsección 3.8): si dos figuras son congruentes, entonces son iguales en el sentido euclidiano (tienen la misma área) . Por lo tanto, sus colecciones de indivisibles son iguales como magnitudes, lo cual provee una noción de congruencia para las omnes lineae. Sin embargo, esto último no aparece en Cavalieri. Bien lo ha detectado ^{Andersen (1985, p. 316)}:

In Geometria CAVALIERI took it for granted that his readers would understand what he meant by congruent collections of lines, but in Exercitationes (pp. 200-201) he added an explanation: When two congruent figures, F1 and F2, are placed so that they coincide, then each line in OF1(l) will coincide with exactly one line in OF2(l) (and vice versa), and the collections of lines are called congruent. (^{Andersen; 1985, p. 316}).

Con esta noción de congruencia, dos figuras planas son congruentes si y sólo si sus omnes lineae son congruentes.

El siguiente paso es considerar figuras cualesquiera: “Teorema III. Las figuras planas guardan entre sí la misma proporción que todas sus líneas referidas a una regula cualquiera [...]” (^{Cavalieri; 1653, p.113}). Si dos figuras guardan una proporción en el sentido euclidiano (sus áreas guardan tal proporción), entonces sus colecciones de indivisibles guardan la misma proporción. Para la prueba, ^{Cavalieri (1653, p. 113 y ss.)} usa copias repetidas de las figuras. Lo más interesante es que elabora dos demostraciones: una suponiendo que el continuo está formado por indivisibles y otra sin suponerlo. La demostración más fácil usa la hipótesis de los indivisibles como constituyentes del continuo. Para Cavalieri, solamente una de las dos teorías sería válida, pues sus axiomas son contradictorios. Como para Euclides, los axiomas son verdades absolutas sobre la naturaleza del ser y no, como para nosotros, simples juicios sintéticos a priori. No deja de ser interesante notar el ajedrez que conlleva el cambio de los axiomas de una teoría. Con este teorema la teoría arranca de verdad:

“Corolario. […], para encontrar la proporción que guardan entre sí dos figuras planas […] es suficiente determinar la proporción que […] guardan entre sí todas sus líneas […] con respecto a una regula cualquiera, hecho que pongo como máximo fundamento de mi nueva Geometría.” (^{Cavalieri; 1653, p.115}).

6. El método

La aplicabilidad de los teoremas reposa en las biyecciones de los segmentos:

Teorema IV. Si dos figuras planas se levantan con la misma altura y si, además, se trazan líneas rectas cualesquiera, paralelas entre ellas, con respecto a las cuales se toma la susodicha altura, se encontrará que las porciones de las líneas trazadas que cortan las figuras planas son magnitudes proporcionales, que siempre existen como homólogas o correspondientes en su propia figura. Además, las dichas figuras guardarán entre sí la proporción que haya entre uno cualquiera de los antecedentes con el consecuente que le corresponde en la otra figura. (^{Cavalieri; 1653, p. 115}).

Este teorema constituye el “principio de Cavalieri”. En algunos libros de texto contemporáneos este nombre se refiere a resultados similares sobre integrales, cf. e. g. ^{Marsden y Tromba (1988, p. 306)}.

La analogía con los Elementos es patente. La redacción es prácticamente idéntica. Ya se vio que Euclides pone dos triángulos o paralelogramos sub eadem altitudine. Cavalieri habla de dos “figuras cualesquiera” que se disponen in eadem altitudine. Para Euclides, las bases de los triángulos o paralelogramos deciden la proporción de las figuras. Para Cavalieri, el asunto es más difícil puesto que sus figuras no tienen una base reconocible. De todos modos, busca determinar la proporción de las figuras ayudándose con los indivisibles. Su intención es generalizar a Euclides.

^{Andersen (1985)} analiza el teorema con base en una “traducción libre” y simple: If two plane figures have equal altitudes, and if sections made by lines parallel to the bases and at equal distances from them are always in the same ratio, then the plane figures also are in this ratio. (^{Boyer; 1968, p. 362}). Se trata de un resumen de Boyer sobre una traducción de ^{Smith (1929, p. 605 y ss.)} para el primer teorema del Libro VII de la Geometria. Se percibe que se han perdido algunos aspectos importantes del original cavaleriano, sobre todo la enigmática frase homologis in eadem figura semper existentibus, que el grupo de edición de ^{Lombardo-Radice (1966)} ha traducido por esistendo sempre [linee] corrispondenti. Se habla, pues, de segmentos homólogos o correspondientes que existen siempre y tienen magnitudes proporcionales. ¿Qué son magnitudes homólogas? La respuesta está naturalmente en Euclides. La homología tiene que ver con cuatro magnitudes “continuamente” proporcionales: el antecedente de una es al otro antecedente como el consecuente de la primera es al otro consecuente. Tal es la Definición XI del Libro V de los Elementos: Respondentes magnitudines dicuntur praecedentes praecedentibus, sequentes sequentibus. (^{Heiberg; 1884, p. 5}).³ Tales magnitudes también se dicen homólogas, pues el adjetivo respondentes es traducción del griego ὁμόλογα (^{Heiberg; 1884, p. 4}). ¿Qué significa la existencia de estas magnitudes? Pues lo que quiere decir desde siempre en matemáticas, o en lógica: que es posible encontrar tales segmentos.

En la Figura 10 tomada de Cavalieri. Las figuras, de igual altura MC son CAM y CME. Si aceptamos la interpretación simplificada de Smith-Boyer-Andersen, todo fluye sin complicaciones. La figura CAM es a la figura CME, como BR es a RD, o como AM es a ME: así como uno de los antecedentes es a un consecuente, así todos los antecedentes son a todos los consecuentes (Proposición 12 del Libro V, Elementos). Cavalieri se da cuenta de que su interpretación de Euclides es bastante osada, pues se aplica a colecciones formadas por infinitos indivisibles.

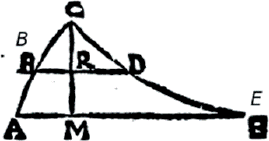
Las letras B y E son de elaboración propia

Figura 10 Dibujo de ^{Cavalieri (1653, p.112)} para el Teorema IV. 

Andersen no queda satisfecha con la Figura 10: In making the figure Cavalieri was not aware that the assumption (V.3) implies that the curves ABC and ECD have similar curvature at corresponding points. (1985, p. 316, Fig. V.1). La suposición (V.3) declara que BR: RD:: AM: ME.

La interpretación de Boyer-Andersen es adecuada para entender la demostración de Cavalieri y las proposiciones que siguen. Empero, el dibujo y la redacción suscitan otras ideas interesantes. Sobre todo, el asunto de la existencia de los segmentos homólogos. Ellos evocan el teorema del valor medio para integrales: si f es continua en [a, b], entonces existe un c en [a, b] tal que

Cf. ^{Hairer y Wanner (1996, p. 227)}. Cavalieri busca cuatro magnitudes homólogas. De allí proviene el reproche de Andersen sobre las curvaturas de la Figura 10. Hoy por hoy, la existencia de dos segmentos que guardan una proporción igual a la de las figuras está garantizada. Para la figura CMA , descrita por una función f, se tendría un c; para CME, descrita por g, un d. Entonces, CMA: CME:: f (c) : g(d). Los indivisibles BR y RD no estarían a la misma altura.

La invocación de este teorema no es exótica, pues su intuición había flotado en Europa durante siglos. Basta recordar la regla de Merton sobre la velocidad media y sus reelaboraciones en Oresme y Cusa (^{Boyer; 1959, pp.79-89}): (^{Edwards; 1979, p. 86 -90}); (^{Clagett; 1968, pp. 466- 467}). El valor medio contiene otro de los signos que esparcía el fuego metafórico del continuo en los días de Cavalieri.

El “principio de Cavalieri” sirve para estudiar muchas figuras geométricas. Baste aquí con recordar que “Si se traza una diagonal (diámetro) de un paralelogramo, entonces el paralelogramo es el doble de cualquiera de los triángulos formados por dicha diagonal.” (^{Cavalieri; 1653, p. 140}). La demostración consiste en establecer una biyección entre los segmentos de los dos triángulos determinados por la diagonal. Otra aplicación se puede leer en el Libro III, donde se estudia la teoría del círculo y la elipse. Esta vez la biyección entre los segmentos de un círculo y una elipse es evidente cuando se entiende que una elipse se obtiene dilatando el círculo en la dirección de un eje, mientras que en el eje perpendicular nada cambia.

7. Claridad y oscuridad de los indivisibles

Durante el siglo XVII los indivisibles fueron tachados de difíciles por los que no entendían las matemáticas (^{Tamayo, 2018, p. 49}). Pero los matemáticos sí recibieron el mensaje. Entre ellos se cuentan a: Angeli, Daviso, Mengoli, Torricelli, Fabry y Renaldinus (^{Andersen, 1985, p. 335}) . Incluso Guldino, el gran enemigo intelectual de Cavalieri, los entendió, así le pareciesen falsos. Ciertamente, Newton y Leibniz los comprendieron.

Pero algo sucedió en el siglo XVIII. De repente, nadie entendió a los indivisibles. La leyenda negra llegó hasta nuestros días. ^{Koyré (1978, p. 320 y ss.)}, ^{Andersen (1985)} y hasta el certero Boyer (1941, p, 85) aceptan la oscuridad de Cavalieri. Aquí se deja de lado esta costumbre: las secciones anteriores muestran un pensamiento matemático comprensible, aunque lleno de nociones que buscan todavía su significado. Lejos de lo que pudo haber sido y no fue, es hora de regresar al siglo XVII y redescubrir, al lado de sus contemporáneos del maestro, la claridad auténtica de los indivisibles.

Se debe asimismo abandonar el embeleco de que el latín de Cavalieri es enredado. Salvo por la primera oración gramatical de la Geometria , en la cual aparece una famosa metáfora sobre el oso y la miel (^{Tamayo, 2018, pp. 63-65}), el latín del maestro no ofrece mayor problema. Se le da la razón a sus traductores italianos: Il latino de fra Buonaventura ci è sembrato assai buono, migliore di quello di un Keplero o di un Guldino, senz’altro paragonabile a quello di Galilei […] (^{Lombardo-Radice, 1966, p. 45}, nota al pie).

8. A modo de conclusión

La epistemología internalista y tradicional de las matemáticas propone dos razones para explicar la dificultad de comunicar los indivisibles cavalerianos:

Tales razones pierden fuerza por las matemáticas mismas. La Teoría de Conjuntos provee ejemplos de continuos compuestos por “indivisibles” y los infinitesimales de Leibniz tampoco constituyen una teoría acabada. En verdad, se tuvo que esperar a la formalización de ^{Robinson (1966)} para que los infinitesimales obtuviesen su carta de ciudadanía matemática.

La visión material de las matemáticas aporta explicaciones más sencillas y evidentes: la dificultad de los indivisibles yace en los significantes y no en su significado. Los críticos de Cavalieri reconocen el mérito de su teoría porque da razón de lo infinito -continuo. Lo que no gusta es la manera de presentarla. Cavalieri se apegó a la tradición milenaria de la geometría griega en un tiempo en que los hombres hablaban un lenguaje matemático distinto. El desprecio consciente del Álgebra es la característica central de sus símbolos. Las muletillas euclidianas ya habían pasado de moda. La Geometría ya no era griega y antigua; sino moderna y cartesiana. ^{Lombardo-Radice (1966, p. 20)} lo ha dicho bien: la Geometria nuova di Cavalieri è scritta in latino, come lingua: e scritta al modo classico, greco, come costruzione.

La búsqueda de los símbolos aleja al historiador de la actitud que descalifica a Cavalieri como un “autor menor”. Tampoco puede considerarse como un estudiante de Cálculo, al cual se le muestran los errores. La historia oficial de las matemáticas debería revisar algunas suposiciones y métodos. En particular, debería aprender a diferenciar el rigor del formalismo.

En este artículo se ha mostrado que el método de los indivisibles cavalerianos contiene muchos resultados que son válidos para las matemáticas de hoy. Sin embargo, uno puede cavar un poco más adentro para caer en la cuenta de que el valor y la verdad de estos resultados no necesita de las matemáticas posteriores. El conjunto de definiciones, postulados, lemas, teoremas y escolios constituye un sistema, es decir, un conjunto de proposiciones cuidadosamente enlazadas entre sí que pretende explicar el continuo moderno-europeo, quizás por primera vez. Este sistema se sostiene por sí mismo y por la Geometría Euclidiana. Es bien conocido entre los historiadores de la matemática que los indivisibles fueron mal acogidos por las mayorías; pero apreciados y alabados por los grandes pensadores del siglo XVII: Torricelli, Mengoli, Pascal, Roberval, Wallis, entre otros, pero sobre todo por Leibniz y Newton. Éstos dos últimos creyeron y acogieron a los indivisibles, tal como lo han manifestado en varios lugares de sus monumentales obras. Lo que sucedió fue que más tarde en sus vidas los cambiaron por los infinitesimales o por las fluxiones para sintetizar en una sola teoría las cuadraturas (“integrales”) y la determinación de las tangentes (“derivadas”). Y aquí está nuestro punto: todos estos grandes matemáticos entendieron los indivisibles (antes de concebir sus nuevas teorías, así los hayan cambiado luego por otro concepto fundamental). Y he aquí nuestro humilde aporte al estudio de estas materias: el análisis histórico de una teoría pasada debe buscar fundamentalmente la reconstrucción del sistema original, mostrando las relaciones entre sus elementos y la forma como las conclusiones se desprenden de las premisas. El análisis de la validez de lo obtenido en las formalizadas matemáticas de hoy debe ser un producto posterior, que, en verdad, no es tan central como se podría creer a primera vista. De esta forma se vería que todas las investigaciones serias contienen su verdad, una verdad explicada a su propia manera. Si nos fijamos en dicha “propia manera” (notaciones y otros elementos de un lenguaje particular), comprenderemos por qué el sistema era claro y sencillo para su autor y para sus contemporáneos. En este sentido, se nos ha desvelado la claridad de Cavaleri. Con este método de trabajo se resolverían favorablemente algunas apreciaciones infortunadas que comenten algunos historiadores de las matemáticas, los cuales identifican la epistemología de las matemáticas con el estado actual de las matemáticas. Si podemos distinguir las diferencias entre estas dos disciplinas ya no se cometería más el error de hablar de “conceptos epistemológicamente correctos”, pues todos los conceptos de un autor, que han sido aceptados por toda una comunidad científica en cierto momento de la historia, son simplemente “correctos”. Aún más, son piezas clave para entender los cambios posteriores de las matemáticas. En particular, si nos fijamos bien, los indivisibles del siglo XVII han legado a la posteridad los problemas centrales del Análisis matemático contemporáneo: el continuo, la medida, la integración, entre otros. Algunos de estos conceptos no se han entendido todavía a cabalidad y los próximos siglos -muy seguramente- verán como ellos devienen en otros, más aceptables para los matemáticos del futuro.