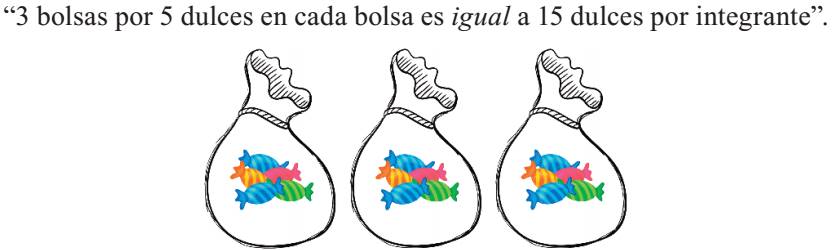1. Introducción
En el marco de la enseñanza de las matemáticas, a nivel mundial existe una discontinuidad entre la aritmética y el álgebra, lo cual implica una carencia en el entendimiento de las relaciones numéricas. El National Council of Teachers of Mathematics (NCTM, 2000), ha propuesto que la enseñanza del álgebra debería comenzar a partir de los primeros años de educación primaria. Esta propuesta es acompañada de múltiples estudios que han demostrado que la aritmética es inherente al álgebra en su composición estructural (Carraher y Schliemann, 2007).
A pesar de la naturaleza algebraica de las matemáticas, los alumnos de los niveles más básicos de educación no suelen tener oportunidades de hacer relaciones entre la aritmética y el álgebra antes de enfrentarse a una forma algebraica prefabricada (Herskovics y Kieran, 1980; Kieran y Chalou, 1993). Por ejemplo, el uso de símbolos para representar cantidades es un elemento crítico en la transición de la aritmética al álgebra, debido a que, en el aprendizaje del álgebra los alumnos se enfrentan con la necesidad de operar con representaciones simbólicas que no están vinculadas con un resultado numérico (Kieran, 1992).
La idea de enseñar el álgebra desde la primaria, no se refiere a que los alumnos aprendan lo mismo que los alumnos de secundaria o preparatoria, sino que tengan oportunidades, en una edad temprana crítica, para integrar entre sí a la aritmética y al álgebra (Carpenter et al., 2005; Molina, 2006). En otras palabras, se trata de que se adquieran dominios significativos de manera tal, que los alumnos puedan transferir el entendimiento (definido como el dominio de las relaciones conceptuales pertinentes a un tema o una tarea) de relaciones de cantidades a contextos novedosos, así como desarrollar habilidades y hábitos de pensamiento que les permitan resolver problemas matemáticos de un modo significativo.
¿Cómo crear vínculos significativos entre la aritmética y el álgebra? En la historia del aprendizaje en matemáticas comúnmente se prioriza el pensamiento operativo (procedimental) basado en la aplicación de algoritmos en la resolución de problemas. A pesar de que la aplicación de algoritmos es necesaria para resolver problemas matemáticos, resulta insuficiente para entender de manera significativa los aspectos más básicos de la aritmética y su relación con el álgebra. Stephens (2007) brinda un ejemplo de la aplicación del pensamiento operativo en la resolución de igualdades:
La respuesta “12” deriva de la relación entre la cantidad total de la izquierda de la igualdad (38) y la resta con el total de la derecha (26). En términos procedimentales, se compensa la cantidad que falta en el lado derecho de la igualdad de acuerdo con el total del lado izquierdo de la igualdad.
Existe otra manera de resolver el ejemplo anterior, de acuerdo con Stephens y Ribeiro (2012): la diferencia entre el primer número del lado izquierdo de la igualdad y el primero del lado derecho es +3. Por lo tanto, si se resta la misma cantidad, pero con el signo contrario (-3) podremos obtener el resultado correcto.
Esta estrategia basada en las relaciones numéricas en una igualdad implica, además de un dominio procedimental, un nivel de dominio conceptual. A este tipo de solución se le puede denominar la aplicación del pensamiento relacional.
La integración de los conceptos de pensamiento relacional, jerarquía de operaciones (order of operations en inglés) y representaciones simbólicas algebraicas, versó sobre una secuencia psicoeducativa (también llamada secuencia didáctica) basada en la manipulación de objetos concretos. En el marco conceptual se explica cómo se vinculan entre sí estos conceptos.
2. Marco conceptual
2.1. Pensamiento relacional
El pensamiento relacional es definido por Carpenter et al., (2005) como la acción de atender al conjunto de relaciones numéricas estructurales, que están inmersas en expresiones numéricas. Este concepto implica el uso y la aplicación de propiedades numéricas para transformar expresiones matemáticas, en vez de solamente calcular numéricamente y dar una solución. Por ejemplo, en la siguiente expresión: 38 + 47 = 47 + 38, ¿cómo se puede comprobar que la igualdad es verdadera? No es necesario calcular dicha igualdad, ya que aplicando la propiedad conmutativa se puede saber que han cambiado de lugar las cantidades de un lado de la ecuación. Este tipo de solución se enfoca en las relaciones de la expresión en lugar de en el cálculo aritmético, como principio estructural de las propiedades numéricas.
Un elemento clave para identificar estas relaciones es la concepción del signo igual. Carpenter et al., (2003) indican que el signo igual debe ser entendido como una relación que provee un balance en las cantidades de ambos lados de una igualdad. De este modo, cuando un estudiante concibe el signo igual como una manera de relacionar cantidades, es más probable que identifiquen una estructura subyacente a esas cantidades y poder implementar estrategias para resolver una expresión numérica (Knuth et al., 2006). El pensamiento relacional es importante en otras subáreas de las matemáticas, ya que muchas ideas matemáticas cruciales incluyen relaciones entre diferentes representaciones de números y operaciones entre ellos (Riadi et al., 2019).
Numerosos estudios han reportado que los estudiantes de primaria son capaces de utilizar el pensamiento relacional para resolver expresiones numéricas, a través de un entendimiento relacional del signo igual (Carpenter et al., 2003; Molina et al., 2006). El pensamiento relacional es una estrategia que puede promover competencias aritméticas y algebraicas, ya que la aritmética contempla no solo un dominio procedimental, sino el entendimiento de propiedades numéricas, siendo un auxiliar en el análisis de relaciones (dejando de lado la necesidad de usar operaciones numéricas), en la síntesis de expresiones, al pensar con base en las propiedades de las operaciones, así como en la manipulación de las expresiones numéricas, lo cual podría desarrollar en los alumnos un aprendizaje significativo de la aritmética, así como la posibilidad de adquirir nociones algebraicas a temprana edad (Molina, 2009). En el aprendizaje del álgebra elemental, su rol puede implicar integrar de un modo más eficiente las propiedades aritméticas (Carraher et al., 2007).
2.2. Álgebra temprana
El pensamiento algebraico puede ser definido como una aproximación tanto a situaciones como al desarrollo de modos de pensamiento, que enfatizan los aspectos generales y relacionales del álgebra, con herramientas no necesariamente simbólicas, que pueden ser usadas como soporte cognitivo, para introducir y nutrir el discurso tradicional del álgebra escolarizada, en edades tempranas, principalmente en la educación primaria (Kieran, 1996).
El desarrollo del pensamiento algebraico incluye un enfoque en varios rubros: las relaciones de cantidad; las operaciones y sus inversos; representar y resolver problemas; los números y las literales; así como en el significado del signo igual (Kieran, 2004).
Kaput (2008) propuso que el álgebra y el pensamiento algebraico, están compuestos por tres rubros:
El álgebra como estudio de estructuras y sistemas extraídos de cálculos y relaciones, incluidas las que surgen en la aritmética (álgebra como aritmética generalizada), y en el razonamiento cuantitativo.
El álgebra como estudio de funciones, relaciones y variación conjunta.
El álgebra como la aplicación de un grupo de lenguajes de modelado, tanto dentro como fuera de las matemáticas (p. 11).
La propuesta del autor establece las bases de comparación de diversos enfoques denominados álgebra temprana, que tienen el objetivo de integrar los rubros del álgebra y del pensamiento algebraico desde la primaria, en diversas edades y desde entornos tanto experimentales como escolarizados.
Blanton y Kaput (2005), indican que el álgebra temprana tiene como finalidad, la integración del pensamiento algebraico, basándose en la promoción de hábitos de pensamiento y representación, que puedan identificar el ámbito estructural de las matemáticas. De acuerdo con Carraher y Schliemann (2007), el “álgebra temprana” versa sobre el conocimiento algebraico, el pensamiento algebraico, y las representaciones y técnicas de estudiantes a edad temprana, relacionadas con la resolución de problemas que, generalmente, solo estudiantes más avanzados logran resolver utilizando la notación algebraica moderna. En el mismo sentido, Kieran et al., (2017) considera que el énfasis del álgebra temprana se encuentra en identificar y expresar estructuras numéricas.
Las estructuras numéricas se relacionan directamente con las propiedades matemáticas y se desarrollan gracias a la comparación entre problemas, expresiones o igualdades comunes entre sí. Warren y Cooper (2009), indican que la abstracción es facilitada por la comparación de diferentes representaciones y la identificación de puntos comunes que abarcan un modelo mental. En otras palabras, un alumno puede abstraer una estructura numérica, si tiene la oportunidad de relacionar expresiones o problemas matemáticos diferentes entre sí, en términos numéricos, que se transfieren de la misma representación general a diferentes representaciones, dentro de la misma estructura, para poder identificar puntos comunes que abarquen el núcleo del modelo. Por ejemplo, 5 + 2 = 10, es equivalente a 4 + 6 = 10 en términos estructurales, corresponden a la misma estructura: parte = todo (Davydov, 1962).
En este estudio, la intención es implementar el pensamiento relacional de un modo significativo, utilizando eventos concretos que hagan evidente esta relación estructural a partir de actividades fenoménicas o manipulativas. Freudenthal (1983) denomina a este tipo de actividades que implican el uso de objetos concretos relacionados con conceptos matemáticos didáctica fenomenológica. ¿Cuál sería la relación entre las propiedades numéricas, estructuradas numéricamente, con una didáctica de este tipo?
2.3. Jerarquía de operaciones
El entendimiento de ideas o conceptos matemáticos se puede acelerar a través de la representación de sus principios más básicos, en la interacción entre objetos y eventos concretos. La representación, entendida como un modo de interiorizar o entender un evento o fenómeno, ya sea concreto o abstracto, es la base del pensamiento algebraico y de la aplicación de las propiedades numéricas en la jerarquía de operaciones. El pensamiento relacional funge como unión entre estos conceptos, a partir de un modo de pensamiento que guía el entendimiento de relaciones de cantidades.
Así como la NCTM propone que la enseñanza del álgebra pueda comenzar desde la primaria, el Common Core State Standards for Mathematics (CCSSM, 2010) recomienda introducir las propiedades numéricas desde el tercer grado de primaria. Como parte importante de la implementación de las propiedades numéricas, Freudenthal (1974), asegura que la jerarquía de operaciones constituye una parte crucial del álgebra y distingue el lenguaje algebraico del lenguaje de la vida cotidiana. La jerarquía de operaciones implica la realización de expresiones o ecuaciones de un modo estructural, con base en las propiedades numéricas, en vez de únicamente a su posición lineal (de izquierda a derecha).
Gunnarsson et al., (2016), explican que las expresiones matemáticas implican varias convenciones. Una de esas convenciones describe el orden en el cual las operaciones se realizan. Este orden ha sido comúnmente reducido a través de mnemotecnias como PEMDAS (paréntesis, exponentes, multiplicación, división, suma y resta) por sus siglas en inglés. La necesidad de operar con expresiones o igualdades en orden se encuentra, en mayor cantidad, en el álgebra. Este orden no se basa en la típica secuencia de izquierda a derecha para resolver una expresión aritmética, por lo tanto, provoca que los alumnos de secundaria o bachillerato, así como algunos profesores, fallen al momento de interpretar una expresión matemática.
Asimismo, Dupree (2016) indica cuatro malinterpretaciones de la jerarquía de operaciones derivadas del uso de mnemotecnias: la multiplicación se realiza antes de la división, la suma se hace antes de la resta, las operaciones se resuelven de izquierda a derecha, y el paréntesis se resuelve primero. La comprensión del concepto del orden en la jerarquía de operaciones es, de acuerdo con Headlam (2013), un primer paso para adquirir una percepción de la lógica del álgebra, al operar con un problema aritmético. Por ejemplo, resolver la operación 4 + 2 × 5 puede resolverse de “izquierda a derecha” o de un modo estructural, a + bc. Entender la lógica detrás de esta operación, podría ser un paso hacia la comprensión del significado de una expresión algebraica como a + bc y obtener el resultado correcto, 14.
¿Cómo abordar una regla o convención como la jerarquía de operaciones de un modo significativo? Taff (2017) sugiere que se pueden analizar los componentes de una expresión matemática en sus términos y en sus factores. Los términos son los componentes de una expresión separado por un signo aditivo o negativo. El factor es cuando se multiplica una serie de números. En la figura 1 se observa una representación de este método denominado iTaff:

Figura 1 Modelo i Taff. Se pueden identificar los términos (term) y los factores (f) (Taff, 2017, p. 131)
Esta propuesta contempla una concepción de la jerarquía de operaciones, como una equivalencia estructural de factores de una expresión matemática, misma que también es visible en otras investigaciones. (Dupree, 2016; Liebenberg et al., 1999; Papadopoulos y Gunnarsson, 2020; Zorin y Carver, 2015).
En este estudio se propone el concepto de unidades operativas para el análisis de relaciones numéricas jerarquizadas bajo esquemas algebraicos. Tiene una base teórica en el planteamiento del Modelo iTaff. Las unidades operativas se definen como una cantidad que se deriva de la operación de otras dos cantidades. Por ejemplo, en la expresión

(Fuente propia)
Figura 2 Comparación entre la solución de una igualdad de modo intuitivo (de izquierda a derecha) y la solución con base en la propiedad conmutativa
La multiplicación de la expresión anterior se sitúa como el primer nivel jerárquico de la expresión, ya que sintetiza el producto de 3 por 6 (18). Este producto se suma con el 5 y de ese modo se llega al resultado de la igualdad, 23.
La habilidad de identificar una estructura en una forma generalizada es crucial al momento de enfrentar una actividad algebraica que implique transformaciones, ya que así estas transformaciones encuentran sentido. La relación entre la generalización y encontrar una estructura subyacente a una expresión o igualdad impulsa el desarrollo del pensamiento algebraico, brindando la posibilidad a los escolares de “mirar a través” de objetos matemáticos (Kieran, 2017).
Mirar a través de objetos matemáticos implica una descomposición y una recomposición en términos estructurales, con la única intención de hacer evidente una estructura numérica. Por ejemplo, una expresión como 5 + 5 + 5 = 15 es equivalente estructuralmente a 5 × 3 = 15. Por otra parte, 5 + 3 × 2 puede ser descompuesta en términos aditivos: 5 + 3 + 3, manteniendo la misma estructura conmutativa. Esta clase de equivalencias, además de buscar que los alumnos puedan generalizar una estructura, pueden hacer evidente la necesidad de operar con la jerarquía de operaciones, desde un punto de vista relacional, que puede ser llevado al campo del pensamiento algebraico, gracias a la jerarquía de operaciones.
La estructura constituye un contenido esencial para las matemáticas (Bourbaki, 1963), además, su entendimiento requiere un enfoque en las características más abstractas de los fenómenos de la vida cotidiana, que pueden ser expresados bajo un discurso lingüístico cotidiano propio de la semántica de los alumnos de primaria. Este estudio se basa en el entendimiento de las relaciones de cantidades que se encuentran en una expresión matemática, a partir de la identificación de una estructura subyacente a factores o unidades operativas, mismas que pueden ser significativas para los niños de primaria, en un entorno escolar en el que se desenvuelven.
En la figura 3, se puede observar la concepción que se plantea para analizar la jerarquía de operaciones, a partir de las unidades operativas constitutivas de una expresión numérica.

(Fuente propia)
Figura 3 Secuencia de la jerarquía de operaciones, donde los óvalos constituyen las unidades operativas.
Con base en el marco conceptual descrito, se pueden subrayar cuatro aspectos cruciales en el entendimiento de relaciones numéricas: 1) el pensamiento relacional; 2) la integración entre las relaciones aritméticas y algebraicas; 3) la estructura numérica inmersa en aplicación de las propiedades numéricas a partir de la jerarquía de operaciones; 4) las actividades fenoménicas como potenciadoras de un entendimiento significativo de las relaciones numéricas.
El pensamiento relacional puede promover que los alumnos de primaria vinculen los dominios tanto aritméticos como algebraicos de un modo estructural, a partir de la aplicación de la jerarquía de operaciones, utilizando objetos matemáticos concretos (actividades fenoménicas - manipulación de dulces). La integración de estos cuatro aspectos constituye el punto sustantivo del presente estudio y la aportación original al área de Matemática Educativa.
2.4.. Preguntas de investigación
1) ¿Cuál es el efecto del pensamiento relacional a través de actividades fenoménicas en la aplicación y el entendimiento de propiedades numéricas a través de la jerarquía de operaciones?
2) ¿Cómo se vincula una estructura numérica con la representación de la jerarquía de operaciones?
2.6. Objetivo
El objetivo general de este estudio fue promover el pensamiento relacional en el análisis de expresiones numéricas, utilizando la jerarquía de operaciones, en alumnos de tercer grado de primaria. Para realizar este objetivo, se analizaron las estrategias implementadas por los participantes, con base en representaciones gráficas y en el análisis de contenido de su discurso, en la resolución de problemas matemáticos en dos niveles de abstracción: concretos (actividades fenoménicas) y estructurales (expresiones numéricas aritméticas y de representación algebraica).
3. Método
3.1. Participantes y escenario
Para este estudio, se realizó un experimento de enseñanza multimétodo en un entorno escolarizado en una primaria pública de la Ciudad de México.
Los participantes fueron 30 estudiantes de tercer grado de primaria (8-9 años). Ninguno de ellos tenía experiencia en jerarquía de operaciones ni en representación simbólica-algebraica.
3.2. Planteamiento, recolección y análisis de datos
El experimento de enseñanza se implementó con la base metodológica de Miller y Mercer (1993) y Witzel et al., (2003), llamada concrete-representationalabstract (CRA), que está sustentada en la concepción didáctica fenomenológica de Freudenthal (1971). Esta estrategia brinda a los estudiantes experiencias cognitivas a partir de materiales concretos, orientados a la construcción de representaciones simbólicas para la formación de nociones matemáticas.
Para hacer la experiencia de una didáctica fenomenológica, se utilizaron dinámicas de operaciones concretas a partir de la distribución (suma, resta, multiplicación y división) de dulces. Se utilizaron dulces porque se consideró que podrían resultar apreciados por los participantes, por lo mismo podrían servir para motivarlos e inducir el entendimiento de relaciones de cantidad.
El diseño del experimento de enseñanza se muestra en la figura 4.
Los indicadores de la preevaluación se basan en dos pruebas psicométricas, WISC-IV (extraídos de la sección de aritmética y validada con población mexicana) y reactivos de la prueba PLANEA (Plan Nacional para la Evaluación de los Aprendizajes) estandarizado por el Instituto Nacional de Evaluación Educativa
(INEE). Además, se tomaron en cuenta los puntajes sistemáticos de la evaluación de la profesora, ya que consisten en evaluaciones longitudinales. Con los indicadores de la preevaluación se crearon los equipos de trabajo con 4 integrantes, distribuidos y balanceados en cuartiles por su promedio, de manera que en cada equipo había un integrante de cada cuartil (promedio muy alto, alto, medio y bajo), esto con base en la propuesta de aprendizaje cooperativo de Slavin (1995) y Johnson y Johnson (2014). En la tabla I se observan los puntajes promedio de los equipos formados, donde se puede apreciar que el promedio total de cada equipo es cercano, la mayor diferencia es de solo 6.38 puntos.
Tabla I Organización de los equipos de trabajo en la etapa de preevaluación.
| Equipo | Promedio pruebas estandarizadas | Promedio puntaje de matemáticas | Promedio total |
|---|---|---|---|
| %WISC-IV %Planea | % | % | |
| 1 | 74.85 | 60.50 | 67.07 |
| 2 | 61.03 | 69.85 | 65.44 |
| 3 | 64.68 | 56.70 | 60.69 |
| 4 | 62.14 | 65.73 | 63.33 |
| 5 | 66.73 | 62.33 | 64.53 |
| 6 | 59.64 | 66.56 | 61.94 |
| 7 | 62.72 | 69.21 | 65.97 |
En la secuencia psicoeducativa se realizaron 5 sesiones como se aprecia en la figura 4. Al finalizar cada sesión, se evaluó el desempeño de los alumnos con base en el porcentaje de las tareas realizadas con éxito.
La primera sesión consistió en la organización fenoménica de dulces en bolsas con base en igualdad por equivalencia. Los participantes en cada equipo tenían que organizar bolsas con la misma cantidad de dulces en ellas, de tal modo que todos los integrantes del equipo tuvieran la misma cantidad de bolsas y dulces. Por ejemplo, si en un equipo había 12 bolsas y 60 dulces, tenían que construir la lógica de la operación de dividir las bolsas para que cada integrante tuviera el mismo número (3 bolsas) y los dulces para que tuvieran el mismo número (5 dulces en cada bolsa). Ahora se les solicitó que encontraran cuántos dulces le tocó a cada uno de ellos. Para esto las bolsas representaban de manera concreta (fenoménica) un factor (3) y la cantidad de dulces dentro de cada bolsa otro factor (5), de tal modo que tenían que construir la lógica de la operación inversa al multiplicar el número de bolsas por el número de dulces en cada bolsa, para obtener el producto (15). En la figura 5 se observa una representación fenoménica de la actividad.
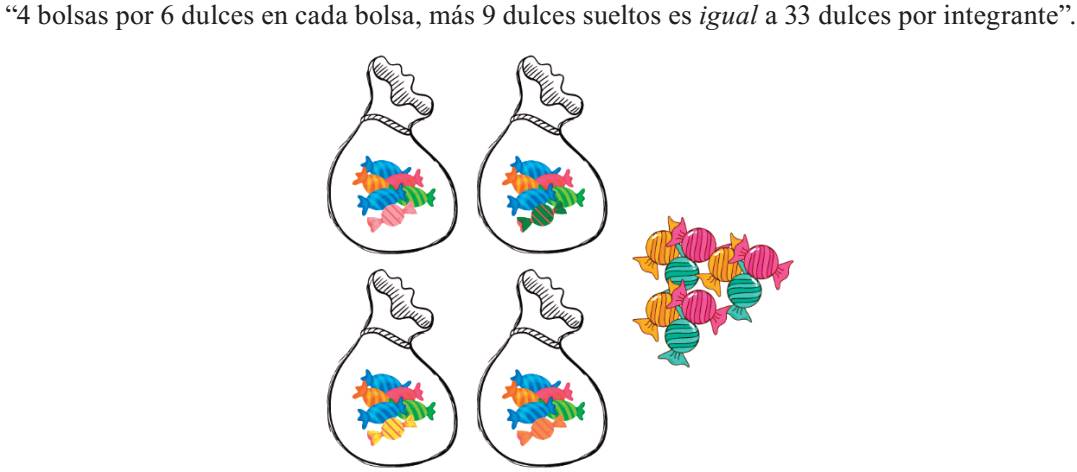
En la segunda sesión los alumnos tenían un número distinto de bolsas y dulces (por ejemplo, 16 bolsas y 96 dulces). Una vez que terminaban de dividir las bolsas y los dulces del mismo modo realizado en la anterior sesión, se les facilitaron otros 36 dulces por equipo, que tenían que construir la lógica de dividir, de tal modo que cada integrante tuviera la misma cantidad (9) pero sin introducirlos en bolsas, dulces “sueltos”. Los dulces sueltos representaban una cantidad aditiva, que requería la lógica de construir la suma del factor de la cantidad de bolsas, multiplicado por el factor de dulces en cada bolsa. En la figura 6 se observa la representación fenoménica de la actividad de esta sesión.
Dado que en la primera sesión los escolares repartieron el mismo número de dulces en las bolsas que tenían y en la segunda se agregaron dulces sueltos, ahora en la tercera sesión los estudiantes tenían que estructurar los arreglos fenoménicos, en el mayor número posible de modos lógicos de representar las estructuras numéricas que se les pudieran ocurrir. En la figura 7 se muestra las representaciones numéricas esperadas.

(Fuente propia)
Figura 7 Representaciones numéricas de igualdad por equivalencia, para cada conjunto de arreglos fenoménicos y la representación de unidades operativas
En la cuarta sesión, los alumnos recibieron bolsas con una cantidad fija de dulces, que no eran contables porque las bolsas no eran traslucidas (oscuras), llamadas “bolsas incógnitas” que operan como una cantidad desconocida. Posteriormente, se les proporcionó el número de dulces que tenían en total, de manera que debían construir la lógica de la operación de dividir ese número por el número de bolsas, para despejar la incógnita. Para evocar la operación inversa, ahora se les planteó cómo podrían saber el número total de dulces si este fuera la incógnita, pero conociendo ahora el número de dulces que hay en cada bolsa, de manera que tenían que construir la lógica de la operación de multiplicar el número de dulces en cada bolsa por el número de bolsas. Después se les dieron dulces sueltos, de manera que tenían que sumar esta cantidad para saber el total de dulces que había. Ahora, estas relaciones entre cantidades conocidas y desconocidas tenían que representarla en el mayor número de expresiones numéricas posibles. En la figura 8 se observa la recreación del arreglo fenoménico y de las expresiones numéricas esperadas.

(Fuente propia)
Figura 8 Representaciones numéricas posibles para cada conjunto de arreglos fenoménicos.
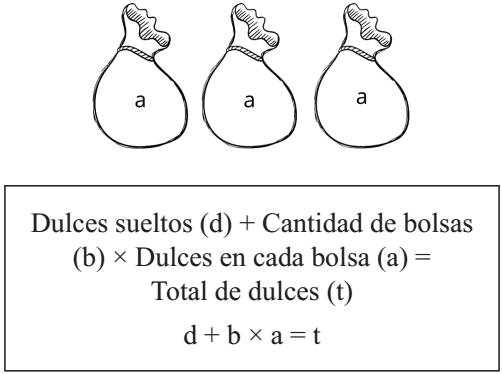
Finalmente, la quinta sesión tenía como objetivo concebir estructuralmente las propiedades de una función y variable a partir de distintos arreglos entre las bolsas y los dulces. Para esto, se repartieron dulces y bolsas a los distintos equipos en cantidades diferentes. Se les pidió que repartieran los dulces en función del número de bolsas, de manera que ahora el número de dulces en las bolsas, entre los equipos, es variable. Los alumnos tenían que representar del modo más general posible las cantidades que desconocían de dulces en cada bolsa. Únicamente tenían el dato de la cantidad de bolsas y de los dulces en total en cada equipo, por lo que el número en cada bolsa era variable. Para asignar una representación a las cantidades variables que desconocían, deberían elegir una alternativa de representación de las distintas variaciones de cantidades. Para evocar regularidad a los escolares se les invitó a referir la cantidad que era una incógnita variable con una letra, a partir de un consenso, ellos decidían la literal con que inicia su nombre. En la figura 9 se muestra la recreación del arreglo fenoménico y simbólico esperado.
(Fuente propia)
Figura 9 Representaciones numéricas simbólicas de la jerarquía de operaciones a partir de cantidades variables.
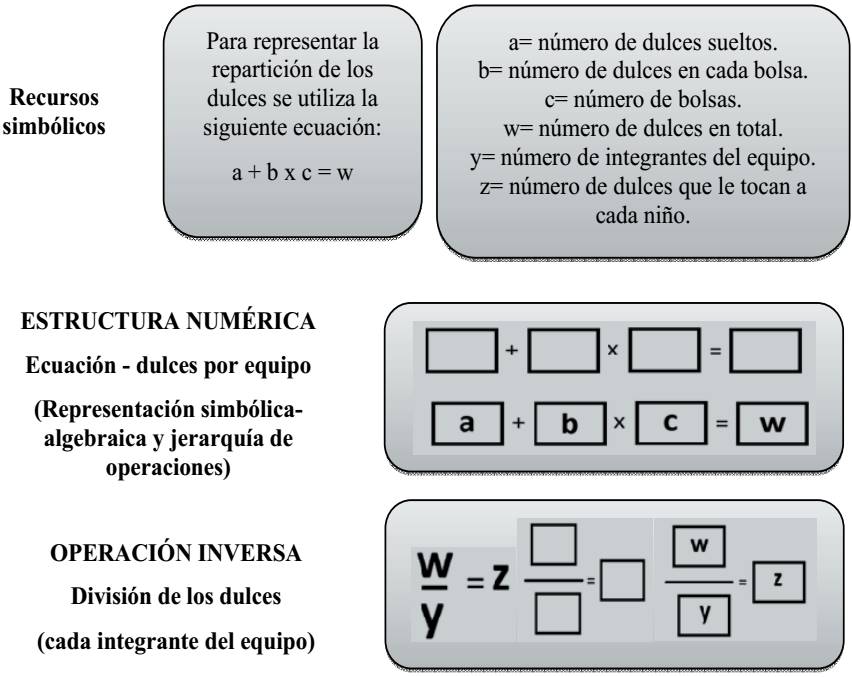
Una vez concluidas las sesiones de la secuencia psicoeducativa, los alumnos fueron evaluados en dos niveles: procedimental y conceptual. Para la evaluación procedimental se implementó una tarea de repartición de dulces a través de la representación de tres elementos: la jerarquía de operaciones, una estructuración numérica y la aplicación de un algoritmo de división. Cada integrante de los equipos tenía como objetivo repartir dulces de un modo equitativo en bolsas. Por ejemplo, se le pregunta al equipo, si cada uno tiene 5 bolsas y en cada bolsa hay 2 dulces, ¿cuántos dulces tiene cada uno? (5 × 2 = 10); si cada uno tiene 10 dulces y en su equipo son 4, ¿cuántos dulces en total tienen? (10 × 4 = 40); ahora, cada uno tiene 5 bolsas y son cuatro niños en el equipo ¿cuántas bolsas en total hay? (5 × 4 = 20). Posteriormente se le dan 8 dulces a cada niño. Sabiendo que hay 4 integrantes por equipo, se les pregunta ¿cuántos dulces se le repartió al equipo? (4 × 8 = 32). Finalmente, se le brinda a cada niño una estructura numérica a partir de cajas (figura 10) para poder organizar las relaciones numéricas, planteando que si “a” es igual a al número de dulces sueltos, “b” el número de dulces en cada bolsa, “c” el número de bolsas, “w” el total de dulces, “y” el número de integrantes del equipo y “z” el número de dulces que le tocan a cada niño, ¿cómo quedarían organizadas estas cantidades en la estructura numérica? También se proporciona una estructura numérica a partir de literales a + b × c (figura 10) y se pregunta cuál es el número de dulces en total. La estructura es para promover la concepción de la jerarquía de operaciones, de tal manera que, si los datos de las cantidades de la estructura eran correctos, podían operar con la división de los dulces para saber qué cantidad le tocaba a cada integrante del equipo.
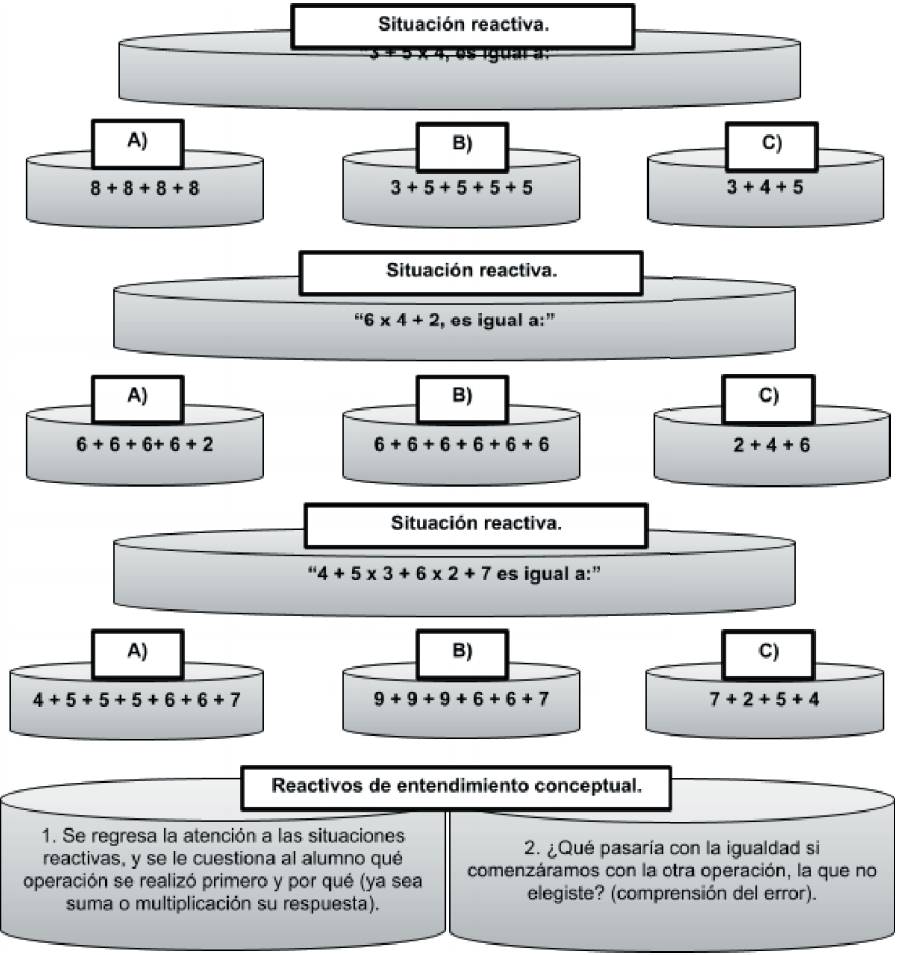
En la evaluación conceptual se realizó un análisis de contenido ad hoc (Kvale, 2008) a partir de una entrevista semiestructurada e individual de las estrategias utilizadas para resolver situaciones reactivas entre igualdades. La intención de estas situaciones reactivas consistía en aplicar la jerarquía de operaciones conceptualmente, al hacer las relaciones numéricas de una expresión multiplicativa con su equivalencia en cantidades aditivas (propiedad numérica conmutativa). Los ejemplos de las situaciones reactivas y las preguntas de la entrevista semiestructurada se encuentran en la figura 11 .
(Fuente propia)
Figura 11 Evaluación conceptual del entendimiento de los alumnos de la aplicación estructural de la jerarquía de operaciones con base en el pensamiento relacional. Son tres situaciones reactivas y dos preguntas de entendimiento
Tanto las tareas de la secuencia psicoeducativa, como de las evaluaciones procedimental y conceptual, fueron puntuadas con base en el porcentaje realizado con éxito de cada tarea (0%-100%). La aplicación de las tareas se realizó en el salón de clases.
4. Resultados
Los resultados se dividen en 4 secciones: 1) secuencia psicoeducativa, 2) nivel de logro en las evaluaciones procedimental y conceptual, 3) entendimiento con base en análisis de contenido del discurso y 4) evaluación de la validez de los indicadores.
4.1. Secuencia psicoeducativa
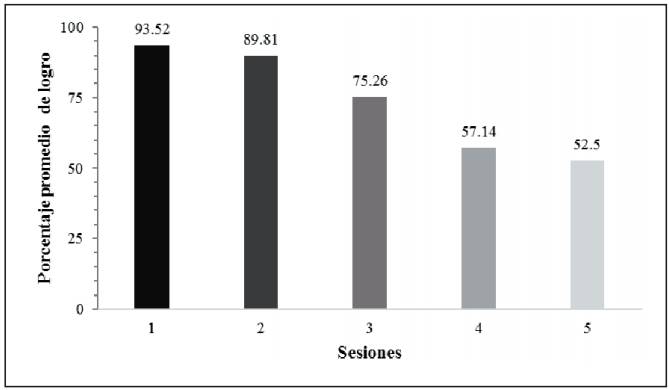
En la figura 12, se observa el porcentaje promedio de logro en las cinco sesiones de la secuencia psicoeducativa.
En la primera sesión, el puntaje promedio de los alumnos fue de 93.52%. En la segunda sesión el promedio del puntaje fue de 89.81%, mientras que en la tercera sesión la media del puntaje fue de 75.26%. En la cuarta sesión la media del puntaje fue de 57.14% y en la última sesión el promedio de la puntuación fue de 52.5%. Estos promedios permiten apreciar que en medida que las sesiones avanzaban, las tareas se volvían más complejas, por lo que el puntaje promedio disminuía.
4.2. Nivel de logro en las evaluaciones procedimental y conceptual
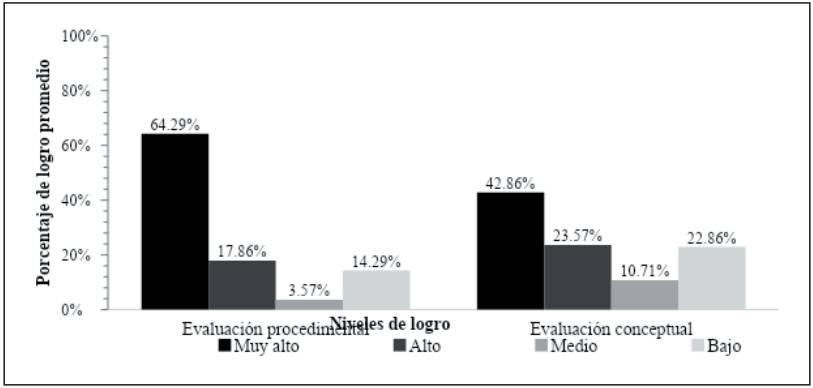
Para categorizar el desempeño de los estudiantes en las evaluaciones procedimental y conceptual, se utilizaron los puntajes totales de cada alumno en sus respuestas correctas a través de cuartiles: porcentaje de respuestas correctas, desempeño muy alto (100%-76%), alto (75%-51%), medio (50%-26%) y bajo (25%-0%). En la figura 13 se muestran los resultados categorizados en estos cuartiles.
En la evaluación procedimental, el 64.29% de los alumnos lograron un nivel de logro muy alto, un 17.86% un nivel de logro alto, solamente un 3.57% lograron un nivel medio y el restante 14.29% mostraron un nivel bajo. Por otra parte, en la evaluación conceptual, un 42.86% de los alumnos lograron un nivel de logro muy alto, un 28.57% un nivel alto, el 10.71% un nivel medio y un 17.86% un nivel de logro bajo. Cabe destacar que la evaluación conceptual se basa en una mayor cantidad de recursos de evaluación, principalmente aquellos basados en el análisis de los alumnos acerca de sus propias representaciones y toma de decisiones, por lo que es esperado que sea una evaluación más compleja y con un menor nivel de logro que la evaluación procedimental.
4.3. Entendimiento con base en análisis de contenido del discurso
Para evaluar el entendimiento de los alumnos, se emplearon dos situaciones reactivas (ver figura 11, parte inferior, número 1 y 2). Los siguientes fragmentos de la entrevista semiestructurada implementada corresponden a dos alumnos de los niveles de logro muy alto y alto.
Caso #1: nivel de logro muy alto
Investigador: en la primera expresión “3 + 5 × 4 es igual a:”, ¿por qué elegiste la opción “b”?
Estudiante: es lo mismo, aquí está el 3 y es igual que arriba, 4 por 5 es 5 veces 4 o 4 veces cinco, por eso son iguales.
Investigador: en la primera expresión “4 + 5 × 3 + 6 × 2 + 7 es igual a:”, ¿por qué elegiste la opción “a”?
Estudiante: porque aquí está el 4, aquí el signo y luego 3 veces el cinco, luego dos veces el 6 luego el signo y luego el 7.
Investigador: ¿Qué operación se hace primero y por qué?
Estudiante: Multiplicar, porque están unidos los números de aquí, cuando multiplicamos. Si sumamos primero, aquí sería 2 más 46 y no nos daría el resultado correcto.
Investigador: ¿Qué pasaría con la igualdad si comenzáramos con la operación contraria a la que acabas de indicar que comenzarías primero?
Estudiante: Sale mal el resultado porque está diferente la manera de la operación… ya lo pensé mejor, por ejemplo, una de estas multiplicaciones, 3 más 5 serían 8, pero se va a cambiar el 8 por el 5… eso hace que nos dé el resultado mal y el total esté más grande o pequeño.
Por eso primero multiplicamos aquí, no sumamos. La suma es trampa para hacerla más grande o chiquita y el resultado se obtiene con la multiplicación.
Investigador: ¿Cómo podrías representar la relación entre la multiplicación y la suma en una igualdad con cantidades que varían?
Estudiante: … a lo mejor usando los signos en las clases le hacíamos con los dulces que nos llevábamos, pero eran dulces y aquí pueden ser nada más los números.
Caso #2: nivel de logro alto
Investigador: en la primera expresión “3 + 5 × 4 es igual a:”, ¿por qué elegiste la opción “b”?
Estudiante: Porque si son 3 y lo multiplicamos 5 por 4, pues comenzamos por esa en vez de la suma. Es como si estuviera dividido el 5 y el 4.
Investigador: en la primera expresión “4 + 5 × 3 + 6 × 2 + 7 es igual a:”, ¿por qué elegiste la opción “a”?
Estudiante: Creo que es A, sí, es A, es la descomposición, aquí es cinco veces 3 y luego 6, a no, dos veces 6 y luego sumamos el 7.
Investigador: ¿Qué operación se hace primero y por qué?
Estudiante: Multiplicar. Porque si sumamos primero nos da una otro resultado, porque la multiplicación hay que hacerla para que nos dé el número, el resultado… si se suma primero el resultado se pierde, la multiplicación se haría, pero con otros números en el total.
Investigador: ¿Qué pasaría con la igualdad si comenzáramos con la operación contraria a la que acabas de indicar que comenzarías primero?
Estudiante: Nos daría un resultado mal si sumamos primero. Porque nos daría un resultado, por ejemplo, el 3 nos daría 8, por 4, 32, pero ese no es el resultado y no se descompondría.
Investigador: ¿Cómo podrías representar la relación entre la multiplicación y la suma en una igualdad con cantidades que varían?
Estudiante: … no sé, con números pues no puedo poner todos, pero a lo mejor con signos. En las clases con usted veíamos que hay como símbolos que usamos más que otros… yo lo haría así de dos maneras:
4.4. Evaluación de la validez de los indicadores
Se aplicó el Rho de Spearman a los datos obtenidos en todos los indicadores del experimento de enseñanza (ver figura 4).
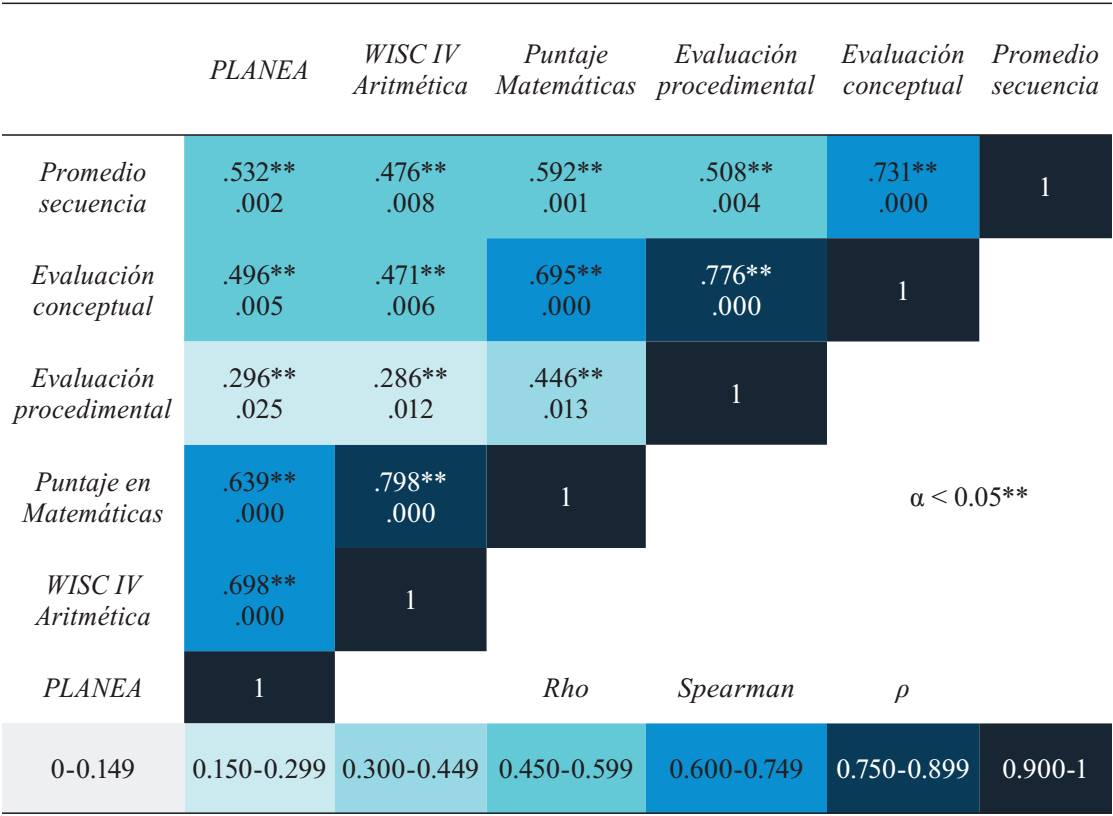
En la figura 16 se muestran las correlaciones (α < 0.05) en los indicadores que midieron el desempeño de los alumnos.
Las correlaciones más altas se ubican entre la calificación de los alumnos en matemáticas durante el año escolar con el puntaje de la prueba WISC IV (0.798 (p < 0.000)) y el desempeño de los escolares en la evaluación conceptual y procedimental (0.776 (p < 0.000)). La evaluación conceptual también tuvo una alta correlación entre el promedio de la secuencia (0.731 (p < 0.000)) y el puntaje de matemáticas (0.695 (p < 0.000)). La prueba PLANEA tuvo dos correlaciones altas entre el puntaje de la prueba WISC IV (0.698 (p < 0.000)) y el puntaje de matemáticas (0.639 (p < 0.000)). Por otra parte, el indicador de evaluación procedimental tuvo las correlaciones más bajas tanto con las dos pruebas estandarizadas de referencia como con el puntaje de los alumnos en matemáticas.
5. Discusión
El objetivo general de este estudio fue promover el pensamiento relacional en el análisis de expresiones numéricas, utilizando la jerarquía de operaciones, en alumnos de tercer grado de primaria. En vista de los resultados reportados, se puede afirmar que el objetivo se cumplió plenamente.
En primer lugar, es importante destacar que los resultados de las tareas de jerarquía de operaciones en población de alumnos de primaria son inéditos, en tanto no hay referentes en la literatura contemplando como variables de estudio el pensamiento relacional y las actividades fenoménicas. El referente en la literatura más cercano a los resultados del presente estudio, sin considerar el área de jerarquía de operaciones, se encuentra en la investigación de Venenciano et al. (2021), en la cual escolares de primer grado de primaria fueron capaces de desarrollar modos de pensamiento abstractos a partir de una aproximación relacional y estructural en la representación de las propiedades de objetos concretos, derivada de una adaptación del currículum de Davydov.
El 71.43% de los escolares, alcanzaron un nivel de logro de las tareas de evaluación conceptual muy alto o alto. De estos, el 42.86% lograron alcanzar un nivel muy alto de logro y un 28.57% lograron un logro en la evaluación conceptual alto. Esta evaluación tuvo un mayor nivel de relación con el constructo entendimiento, ya que se basó en un mayor nivel de recursos de evaluación: 1) un aspecto relacional, al evaluar el razonamiento de los alumnos en función de las equivalencias que observaban y cómo daban cuenta de ellas en su discurso; 2) el dominio conceptual de la jerarquía de operaciones, en su relación con estructuras de aritmética generalizada a partir del uso e interpretación de literales. Además, en varios casos las actividades fenoménicas promovieron una relación significativa con una representación abstracta de relaciones numéricas, como en el caso de las figuras 14 y 15.
El pensamiento relacional se ve reflejado en la argumentación de las soluciones de los alumnos, principalmente en la evaluación conceptual. En sus representaciones se muestra no solamente un modo simbólico de representar relaciones, sino un nivel de entendimiento conceptual con base en argumentos que sustentan sus decisiones.
Este estudio siguió una línea de investigación planteada por varios autores (Dupree, 2016; Glidden, 2008; Linchevski y Livneh, 1999: Papadopoulos y Gunnarsson, 2020; Taff, 2017), en cuanto a que la estructura de una expresión matemática requiere de un grado de significación para los alumnos, en la aplicación de las propiedades numéricas que contemplan la jerarquía de operaciones. El mayor aporte al campo de conocimiento de la jerarquía de operaciones consiste en generar la significación, en alumnos de primaria, de las propiedades numéricas a partir de actividades fenoménicas. En otras palabras, la integración del pensamiento relacional y las tareas fenoménicas a la estructuración numérica característica de la jerarquía de operaciones, lograron promover un entendimiento de tareas abstractas en alumnos de primaria.
El efecto de las actividades fenoménicas en la concepción relacional y estructural se puede notar en la evaluación conceptual, ya que a pesar de que las actividades de evaluación no se relacionaron directamente con la representación simbólica, en los dos casos presentados existió una relación entre las actividades fenoménicas de las sesiones de la secuencia psicoeducativa con su estructura numérica. Tal como en el presente estudio, este tipo de actividades han mostrado con anterioridad su eficacia en el entendimiento de conceptos matemáticos desde la perspectiva de la didáctica fenomenológica (Gravemeijer y Doorman, 1999; Larsen, 2013; Stephan y Akyuz, 2012).
Por otra parte, los resultados confirman que los alumnos de tercer grado de primaria pueden participar activamente en experiencias simbólico-algebraicas, que impliquen argumentar y representar la solución de un problema que contemplen el pensamiento algebraico, tal como lo afirman Blanton, Brizuela, Stephens, Knuth, Isler, Gardiner et al., (2017), quienes también indican que las intervenciones tempranas en álgebra con escolares de primaria, han demostrado mejorar el entendimiento algebraico de los alumnos, en los niveles de secundaria o bachillerato.
Si el desarrollo del pensamiento algebraico incluye un enfoque las relaciones de cantidad, las operaciones y sus inversos, así como representar y resolver problemas con números y literales a partir de un significado relacional del signo igual, tal como lo afirma Kieran (2004), todas las tareas del experimento de enseñanza se implementaron con una base conceptual derivada del pensamiento algebraico. Por lo tanto, los niveles de logro en los alumnos también se pueden vincular a la promoción del pensamiento algebraico. La representación de una estructura numérica se vincula con la jerarquía de operaciones a través del pensamiento algebraico, tal como lo afirma Freudenthal (1974). El uso del signo de interrogación, si bien no es parte de las convenciones acerca del empleo de literales en álgebra, representa un acercamiento para los escolares hacia la noción de incógnita o variable.
Asimismo, como parte de la validación de constructo convergente de los instrumentos utilizados en el experimento de enseñanza, las correlaciones entre los distintos indicadores muestran la consistencia y coherencia entre el desempeño de los alumnos con su grado de dominio matemático, en tareas de jerarquía de operaciones y estructuración numérica.
Las hipótesis del presente estudio, dados los resultados evaluados, se pueden confirmar: el pensamiento relacional se puede promover a partir de actividades fenoménicas; la introducción del pensamiento relacional en la aplicación de la jerarquía de operaciones puede promover habilidades de representación estructural de relaciones de cantidad.
5.4. Importancia del estudio: enseñanza y aprendizaje de las matemáticas
Se puede concluir que este estudio permite señalar la coherencia que hubo en los múltiples indicadores del desempeño de los escolares gracias a la evaluación de validez de los indicadores; mostrar que la estrategia educativa tiene factibilidad de ser implementada por un profesor de primaria en las condiciones escolares cotidianas; sustentar que en un escenario natural de la escolaridad pública de una primaria, es posible formar pensamiento relacional; evaluar el potencial de las experiencias fenoménicas para el entendimiento matemático y demostrar que los escolares a temprana edad, son capaces de entender jerarquía de operaciones a través del pensamiento algebraico y relacional, contemplando el potencial de la didáctica fenomenológica.











 nueva página del texto (beta)
nueva página del texto (beta)