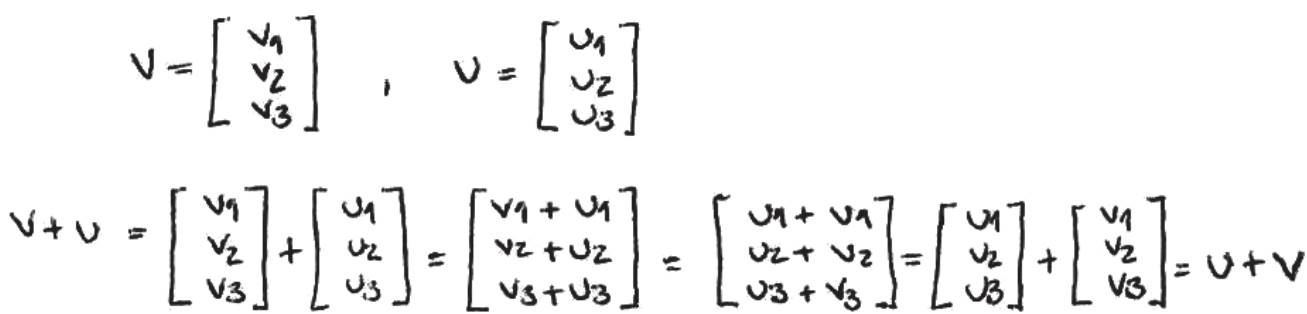1. Introdução
O cerne da Matemática como ciência em permanente construção são as demonstrações, envolvendo raciocínio para “convencer-se a si próprio, convencer um amigo, convencer um inimigo” (Mason, Burton, & Stacey, 1982, p. 106). Essenciais para compreender, estabelecer e comunicar o conhecimento matemático, no ensino as demonstrações permitem convencer os alunos “com base na razão, em vez da autoridade” (Lima, 1999, p. 5).
Apesar da sua relevância, uma tarefa cuja resolução passe por uma demonstração é, para muitos alunos, algo difícil “com letras”. Ainda que as mais recentes orientações curriculares portuguesas em Bivar et al. (2013, 2014) tenham vindo reforçar a importância da demonstração nos currículos do Ensino Básico e do Ensino Secundário, da nossa experiência, os seus reflexos ainda não são notórios no Ensino Superior.
No Ensino Superior português não há um documento condutor único, sendo os docentes das unidades curriculares da área científica de Matemática, na sua instituição, intervenientes na definição dos programas das mesmas. No que diz respeito à demonstração, em muitos casos, os docentes têm alguma liberdade, o que não significa que não estejam sujeitos a pressões, no sentido da menorização da demonstração, nos cursos que não formam futuros matemáticos.
Mesmo nos casos de unidades curriculares em que a demonstração é considerada, tal pode não conduzir à perceção dos processos associados ao raciocínio matemático dos alunos ou à criação de esquemas de demonstração por estes. Com efeito, fazer muitas demonstrações não significa que a demonstração seja trabalhada (Costa & Tadeu, 2006). É também difícil desenvolver a noção de demonstração quando o professor se limita a reproduzi-las.
Acresce o facto de ser escassa, pelo menos em Portugal, a investigação com alunos do Ensino Superior e, em particular, no âmbito da demonstração. Do nosso conhecimento, os estudos relativos a (esquemas de) demonstração reportam-se aos Ensinos Básico, como o de Rodrigues (2012), e Secundário, como o de Neto, Breda e Godino (2011). Também não abundam em Portugal os estudos cuja prática letiva passe pela aprendizagem pelos pares (Beites & Serôdio, 2015).
A aprendizagem pelos pares encontra fundamento na obra de Dewey, que enfatizou a importância da construção colaborativa do conhecimento. No registo pragmatista em que se move, Dewey concebe a importância das comunidades de aprendizagem enquanto possibilidades de acesso a várias perspetivas e à busca colaborativa de soluções. Por induzir a reorganização dos argumentos de alunos que tentam convencer os seus pares em discussões, escolhemos este método de ensino-aprendizagem.
O presente estudo tem por objetivo analisar os esquemas de demonstração nas produções de três alunos, em tarefas de demonstração para proposições de Álgebra Linear com valor lógico verdade. Procuramos compreender o raciocínio matemático dos alunos nessas produções, tentando aceder ao mesmo através das representações e suas transformações. Nos esquemas de demonstração não dedutivos, tentamos ainda compreender os significados associados que os alunos lhes atribuem.
Tendo em vista os objetivos descritos, procuramos responder às seguintes questões de investigação: Que esquemas de demonstração são elaborados pelos alunos para demonstrar proposições de Álgebra Linear com valor lógico verdade?; que representações e suas transformações são utilizadas pelos alunos nessas produções?; quais os significados atribuídos pelos alunos aos esquemas de demonstração não dedutivos?.
2. Enquadramento teórico
O lugar da demonstração no currículo matemático é um tópico central de discussão desde a década de 90 do século passado (Gabel & Dreyfus, 2017; Stylianides & Stylianides, 2017; Stylianides, Stylianides, & Weber, 2017). Efetivamente, o papel da demonstração no ensino da Matemática está longe de ser consensual, assim como não reúne unanimidade o critério do que torna uma demonstração aceitável ou não. Insistir na importância da demonstração, no âmbito do conhecimento matemático, implica entender a Matemática como ciência que privilegia, simultaneamente, a abordagem heurística e indutiva e a abordagem dedutiva, contestando a perceção, partilhada por vários educadores, que privilegia o desenvolvimento de competências investigativas e de resolução de problemas, considerando que estas permitem tornar a Matemática mais atraente e próxima da realidade dos alunos (Hanna, 2000; Stylianides & Stylianides, 2008).
2.1.Demonstração e suas Funções
Hanna (2000) pronuncia-se a favor da centralidade da demonstração no currículo matemático, realçando a importância de discutir quer a sua relevância, quer as suas limitações, com os alunos. De Villiers (2001) realça, a este propósito, que a necessidade de demonstração não é facilmente compreendida pelos alunos, devendo-se esta incompreensão menos a problemas de desenvolvimento cognitivo, mas sobretudo à sua motivação para a abordagem às mesmas, pelo que se torna imperativo tornar as demonstrações significativas para aqueles, explorando algumas das suas funções.
Mais do que o rigor, enfatizado pelo movimento da matemática moderna, nos anos 50/60 do século passado, Hanna (2000) realça a sua importância enquanto caminho para uma “efetiva compreensão matemática” (p. 7). Significa isto que a demonstração não serve, apenas, fins de justificação, mas, sobretudo, de um conhecimento mais aprofundado, pois, como referido pela autora, “a melhor demonstração não é apenas que aquilo é verdadeiro, mas também porque é que aquilo é verdadeiro” (p. 8). Deste modo, e em contexto de sala de aula, o grande desafio ao ensino da demonstração consiste na sua própria justificação, o que acaba por conceder prioridade à função de explicação da mesma.
É importante que os alunos compreendam que só através da demonstração é possível obter uma explicação cabal, isto é, verificar uma conjetura (De Villiers, 2001). Associada à confirmação, a demonstração é efetivamente a única forma de verificação de uma proposição. Embora mediante a exploração com casos particulares possamos alcançar um elevado grau de convicção acerca da validade de uma conjetura (De Villiers, 2001; Hanna, 2000), “a validade dos resultados matemáticos depende, em última instância, da demonstração” (Hanna, 2000, p. 12) e é mediante esta que o conhecimento matemático adquire o grau de certeza que o caracteriza, devendo esta ideia ser incorporada pelos alunos.
Reforçando esta linha de pensamento, há que referir que há muito do raciocínio dedutivo, base da demonstração, na própria exploração matemática e que, em última análise, apesar de atividades separadas, a exploração e a prova completam-se e reforçam-se no desenvolvimento do conhecimento e na aprendizagem da matemática. A complementaridade entre argumentos heurísticos e demonstrações corretas justifica uma outra função da demonstração, que pode ser utilizada em sala de aula, que é a função do desafio intelectual. Após um primeiro momento de exploração heurística, o professor pode e deve motivar os alunos no sentido de tentar elaborar uma demonstração ou, pelo menos, acompanhar o desenvolvimento de uma (Hanna, 2000). Despertar nos alunos a necessidade da demonstração, após uma exploração mais empírica, pode ser uma boa forma de os envolver neste processo (Stylianides & Stylianides, 2008) e um poderoso estímulo para aquisição de hábitos de pensamento, na medida em que o aluno é conduzido à demonstração a partir da experiência de um problema (Dewey, 1997).
Uma outra função especialmente significativa em sala de aula é a da demonstração como forma de comunicação, associada à sua dimensão social (Rodrigues, 2009). Efetivamente, a demonstração corresponde “a um argumento matemático, uma sequência de asserções relacionadas, a favor ou contra uma proposição” (Stylianides & Stylianides, 2008, p. 107), implicando, por conseguinte, uma aceitação consensual, por parte de uma determinada comunidade de aprendizagem e/ou científica, em torno do conjunto de fundamentos de partida (definições, lemas,...), consenso que se deve estender aos modos de argumentação (como se desenvolve) e formas de representação (como se expressa) utilizadas, bem como à demonstração como um todo. Deste modo, a demonstração em si mesma pode surgir como potenciadora e como momento real de concretização de uma aprendizagem pelos pares, cuja base, recordamos, consiste em convencer os pares com bons argumentos, o que nos remete para uma outra função da demonstração que é a do convencimento, traduzida no estabelecer a verdade de uma conjetura (De Villiers, 2001), neste caso através de um trabalho colaborativo.
Também Harel e Sowder (1998, 2007) usam o termo demonstração, não no sentido matemático estrito do mesmo, mas como aquilo que estabelece a verdade de uma proposição para um indivíduo ou comunidade. Esta definição evidencia a subjetividade da perspetiva dos autores, ao deixar claro que o que para um indivíduo ou comunidade pode ser considerado demonstração pode não o ser para outros e, até para os mesmos indivíduos, pode modificar-se ao longo do tempo. O mesmo acontece com o conceito de esquema de demonstração, o qual é detalhado na próxima secção. É sabido que os alunos constroem conhecimento novo apoiado no que já têm (Piaget, 1952), o que também no contexto da demonstração implica que o aluno irá refinar gradualmente o seu conhecimento e capacidade de demonstrar. Fica também claro que o ensino e a aprendizagem da demonstração se adequa a qualquer nível de escolaridade.
2.2.Esquemas de Demonstração
A perspetiva de Harel e Sowder (1998, 2007) apoia-se no conceito de esquema de demonstração, que é definido como o que constitui autoconvencimento e persuasão para um indivíduo ou comunidade. Dada uma afirmação, esta pode ser considerada uma conjetura ou um facto por um indivíduo, dependendo da sua certeza sobre a veracidade da mesma. Portanto, uma conjetura passa a facto para um determinado indivíduo logo que este a considere verdadeira. Ao processo usado pelo indivíduo (ou comunidade) para eliminar as dúvidas sobre a verdade da afirmação chamam processo de demonstração. Este admite dois subprocessos, um de autoconvencimento (relacionado com a eliminação das próprias dúvidas sobre a veracidade da afirmação) e outro de persuasão (usado por esse indivíduo ou comunidade para eliminar as dúvidas de outros sobre a verdade da afirmação), como referem Harel e Sowder (1998, 2007).
A observação das ações de alunos no seu processo de demonstração efetuadas por Harel e Sowder (1998) permitiram-lhes estabelecer as categorias dos esquemas de demonstração, as quais representam níveis cognitivos diferentes do desenvolvimento matemático dos alunos. As categorias que recordamos na Tabela I, cuja descrição foi adaptada de Kanellos, Nardi e Biza (2018), não são mutuamente exclusivas, pois o mesmo indivíduo pode manter mais do que um esquema de demonstração. A ideia de combinações de esquemas de demonstração surge no estudo de Kanellos, Nardi e Biza (2018), que refinou a perspetiva de Harel e Sowder (1998, 2007). No contexto do ensino não superior, os primeiros autores depararam-se com oito combinações dos esquemas de demonstração propostos por Harel e Sowder (1998, 2007).
Tabela I Classificação dos esquemas de demonstração (ED) segundo Harel e Sowder (1998, p. 245)
| Categorias | Subcategorias | Descrição |
|---|---|---|
| ED de convicção externa | As conjeturas são validadas por recurso a fatores externos, como: | |
| Autoritário | a autoridade de outro (pessoa ou material) | |
| Ritual | o ritual da argumentação apresentada | |
| Simbólico não referencial | a forma de escrita simbólica da argumentação | |
| ED empíricos | As conjeturas são validadas com recurso à experiência. | |
| Indutivo | A argumentação baseia-se num ou mais exemplos, em medições diretas, em concretizações de variáveis, etc. | |
| Percetual | A argumentação baseia-se em perceções (entendimento sensorial) | |
| ED dedutivos | As conjeturas são validadas para todos os casos (generalidade). A argumentação é organizada em etapas apropriadas para alcançar o objetivo final (pensamento operacional) e é baseada em regras lógicas (inferência lógica) | |
| Transformativo | A argumentação envolve as características de generalidade, pensamento operacional e inferência lógica (atrás referidas) | |
| Axiomático | Acrescenta à anterior o reconhecimento da fundamentação axiomática da teoria matemática correspondente |
Vários estudos mostram que os esquemas de demonstração empíricos são os mais utilizados pelos alunos dos diferentes níveis de ensino (Chazan & Lueke, 2009; Healy & Hoyles, 2000; Recio & Godino, 2001; Rodrigues, 2009), ficando convencidos que com um ou alguns exemplos demonstram a validade de certa afirmação e, em contrapartida, apresentam grandes dificuldades na compreensão da prova através de um contraexemplo. Recio e Godino (2001) concluíram que alunos universitários espanhóis evidenciaram limitações no uso espontâneo de esquemas de demonstração dedutivos para demonstrar proposições matemáticas elementares.
Lee (2016), por considerar que os estudos existentes não estudaram com profundidade a demonstração da falsidade de proposições e por entender que faltava perceber certas nuances cognitivas manifestadas pelos alunos nas demonstrações que apresentavam, desenvolveu um estudo que lhe permitiu estabelecer categorias mais finas para os esquemas de demonstração dos alunos. Esta categorização mais fina de Lee (2016) complementa a estabelecida por Harel e Sowder (1998, 2007).
No que respeita à construção de esquemas de demonstração dedutivos este autor classificou-os em sete níveis (de 0 a 6 por ordem crescente) que traduzem uma progressão através de quatro fases, a saber: tentativas que falham ao relacionar antecedente e consequente (nível 0); demonstrações baseadas em exemplos ou erros de raciocínio lógico (níveis 1 e 2); demonstrações baseadas em inferências dedutivas incompletas (níveis 3 e 4); demonstrações baseadas em inferências dedutivas coerentes (níveis 5 e 6).
Tabela II Classificação dos esquemas de demonstração dedutivos (EDD) (Lee, 2016, p. 33)
| Nível | Características | Descrição |
|---|---|---|
| 0 | Tentativas irrelevantes ou minimais em inferências | Não sabe como provar ou apela à convicção em fontes de conhecimento externas |
| Incapaz de relacionar o antecedente e o consequente com exemplos | ||
| 1 | Utilização novata de exemplos ou raciocínio lógico | Conclui que a implicação é verdadeira (ou falsa incorretamente) recorrendo a um ou mais exemplos, ou a um exemplo incorreto, ou a um contraexemplo |
| Falsifica a implicação “se P então Q” através de raciocínio lógico incorreto, isto é, “se não P então não Q” | ||
| Obtém uma propriedade matemática que não está relacionada com a implicação | ||
| 2 | Utilização estratégica de exemplos para raciocinar | Gera exemplos ao acaso ou por amostragem baseada em casos, ou casos extremos |
| Utiliza propriedades matemáticas inferidas a partir de exemplos gerados para obter conclusões | ||
| 3 | Utilização de inferências dedutivas com falhas graves na coerência lógica e na validade | Deduz propriedades matemáticas relevantes mas faltando uma ou duas inferências dedutivas para provar a implicação |
| Deduz que a implicação é verdadeira para alguns casos do antecedente mas omite outros casos | ||
| 4 | Utilização de inferências dedutivas com falhas menores na coerência lógica e na validade | Gera uma cadeia de inferências dedutivas para justificar conclusões, mas uma ou duas inferências podem ser interpretadas como indutivas, devido a insuficiente fundamentação, ou como erros de escrita |
| Apresenta desorganização na cadeia de inferências dedutivas | ||
| 5 | Construção de demonstrações dedutivas informais | Gera uma cadeia de inferências dedutivas para justificar a implicação utilizando justificações informais |
| 6 | Construção de demonstrações dedutivas utilizando representações formais | Gera uma cadeia de inferências dedutivas para justificar a implicação utilizando representações formais |
Quanto à construção de esquemas de demonstração por construção de contraexemplo, Lee (2016) estabeleceu seis níveis, de 0 a 5 por ordem crescente, também estes traduzidos em quatro fases de progressão similares às anteriores. Mais detalhes podem ser consultados na referência citada.
2.3. Representação e significação em processos de raciocínio matemático
Mata-Pereira e Ponte (2011, 2013) apresentam um quadro conceptual para o estudo do raciocínio matemático que envolve os processos de representação e significação (sense making), o qual está sintetizado no esquema da Fig. 1 e cujas componentes, e suas relações, passamos a detalhar.

Figura 1 Quadro conceptual para o estudo do raciocínio matemático (Mata-Pereira & Ponte, 2013, p. 20)
De acordo com Mata-Pereira e Ponte (2013), a definição de raciocínio matemático não é consensual entre os educadores matemáticos. No estudo agora apresentado adota-se a definição mais lata, considerando o raciocínio matemático como o processo de usar informação conhecida para obter informação nova, o qual pode ser de tipo dedutivo, indutivo e abdutivo (Mata-Pereira & Ponte, 2013). Raciocinar matematicamente envolve formular e enunciar questões, formular e testar conjeturas (incluindo generalizações) e produzir justificações. A formulação de conjeturas gerais a partir de casos particulares envolve, primordialmente, o raciocínio indutivo, mas também o raciocínio abdutivo pode ser, e é, usado para estabelecer hipóteses explicativas de factos observados. Por sua vez, o raciocínio dedutivo é usado na testagem das conjeturas e na construção das justificações. As justificações têm níveis de complexidade diferentes, a saber: (i) não justificar; (ii) apelar à autoridade externa; (iii) utilizar evidência empírica; (iv) utilizar um exemplo genérico; e (v) justificar dedutivamente (Lannin, 2005). Os estudos que levaram ao estabelecimento destes níveis basearam-se em estudos empíricos com alunos do Ensino Básico.
O facto de os conceitos matemáticos serem abstratos implica que, quer para pensar neles, quer para os comunicar, se tem de recorrer a representações. Seguimos a definição de representação matemática de Goldin (2008): configuração que pode substituir uma entidade de qualquer forma. As representações mais usadas são as palavras (linguagem verbal), os símbolos numéricos e algébricos (linguagem simbólica, também designada algébrica) e imagens, Tabelas, gráficos e esquemas (linguagem visual, também designada pictórica), as quais serão as consideradas neste estudo. Outros autores, como Mata-Pereira e Ponte (2011), 2013), discriminam mais os tipos de representações explicitando, entre outras, a linguagem geométrica e a linguagem estatística. Todas estas representações pertencem a sistemas de linguagem diferentes, com códigos e regras próprios.
De acordo com Duval (2006a, 2006b) há dois tipos de transformação de representações, estreitamente ligadas com o raciocínio matemático: tratamentos e conversões. Tratamentos são transformações de representações dentro do mesmo sistema de linguagem e conversões são transformações de uma representação, num dado sistema de linguagem, noutra representação equivalente, mas noutro sistema de linguagem. Segundo Duval (2006b) e Presmeg (2006) as conversões entre representações suportam e promovem a abstração matemática e o raciocínio matemático. No entanto, os mesmos autores e outros, como Callejo e Zapatera (2014), consideram que a conversão entre representações é a atividade cognitiva menos espontânea e a mais difícil.
Esta interligação de componentes só funciona se estiver embebida num processo de significação, no sentido de que o desenvolvimento da compreensão da situação, contexto ou conceito em estudo seja conseguido efetuando conexões com o conhecimento prévio do aluno (NCTM, 2009). Para tal é essencial conhecer o background do aluno, o nível de desenvolvimento e experiência matemática em que se encontra. As representações e transformações de representações são a forma visível do raciocínio matemático e, portanto, é através delas que o professor e o investigador em educação matemática pode aceder e analisar o raciocínio do aluno. Em geral, estas características variam de aluno para aluno numa mesma turma o que dificulta o papel do professor. Özkan, Tepedeldiren e Ünal (2011) defendem que uma forma de contornar esta dificuldade é recorrer a múltiplas representações na abordagem de um mesmo conceito.
3. Metodologia
3.1.Opções metodológicas
A abordagem seguida foi qualitativa e interpretativa, por um lado, por pretendermos estudar um fenómeno no seu ambiente natural e em toda a sua complexidade (Bogdan & Bilken, 2010) e, por outro lado, por considerarmos que os objetos e os acontecimentos não têm significado só por si. Como refere Yin (2009), os significados dos objetos e dos acontecimentos, geralmente não diretamente observáveis nem facilmente perceptíveis, são conferidos pelos indivíduos.
O design de investigação escolhido foi o estudo multicasos. O estudo de caso caracteriza-se pela compreensão aprofundada de um fenómeno contemporâneo, proporcionando os estudos multicasos a comparação entre casos diferentes (Baxter & Jack, 2008). Saliente-se ainda que “as evidências obtidas com casos múltiplos são frequentemente consideradas mais convincentes e, globalmente, o estudo é olhado como sendo mais robusto” (Herriot & Firestone, como citados em Yin, 2009, p. 53).
Selecionámos três alunos para garantir diversidade entre estes. A seleção dos alunos caso foi feita de entre os alunos de uma unidade curricular de Álgebra Linear, do 1.º ano de uma licenciatura do ensino superior, que tiveram a primeira autora como professora no ano letivo a que se refere o estudo e no ano letivo precedente. Os nomes empregues para referenciar os alunos caso, Alice, Maria e Pedro, são fictícios de modo a garantir questões de ordem ética.
Os três alunos estavam a repetir a unidade curricular por terem reprovado no ano letivo anterior com classificações finais entre 7 e 8 numa escala de 0 a 20 valores. No final da primeira aula do ano letivo do estudo, os três alunos referiram à professora que queriam esforçar-se. Também mencionaram, tal como outros alunos, ter gostado do método de ensino-aprendizagem, exemplificado nessa aula, diferente do ano letivo anterior (aulas tradicionais).
Da conversa informal, a professora ficou a saber que os três alunos tinham tido algum contacto com demonstrações no ensino secundário. Essencialmente, os três associavam essas experiências a algo feito pelo professor, embora em distintos conteúdos. A experiência e os conteúdos associados ao primeiro contacto com a demonstração, e o nível de desempenho em matemática, no ensino secundário foram os critérios de seleção diferenciadores considerados (ver Tabela III).
Tabela III Critérios diferenciadores dos alunos caso
| Alice | Maria | Pedro | |
|---|---|---|---|
| Nível de desempenho em matemática no ensino
secundário (de 0 a 20 valores) |
Médio classificações entre 12 e 14 |
Suficiente classificações entre 10 e 12 |
Bom classificações maioritariamente iguais ou superiores a 15 |
| Conteúdo(s) que associa ao contacto com a demonstração no ensino secundário | Geometria | Funções e Álgebra | Probabilidades Números Complexos |
| Experiência que associa ao contacto com a demonstração no ensino secundário | subdividir uma figura geométrica noutras figuras geométricas para mostrar algo geral | mostrar que a área de uma figura geométrica é dada por uma função definida por f(x) | demonstrar propriedades em tarefas de Probabilidades e de Números Complexos |
A recolha dos dados foi feita com recurso a: análise documental, observação participante e entrevista. No âmbito da primeira, analisaram-se produções da Alice, da Maria e do Pedro em tarefas propostas nas aulas, em testes escritos e em trabalhos de casa, estes últimos com resolução escrita à mão e digitalização da mesma recolhida via plataforma Moodle. Fruto da observação participante, foram tomadas notas de campo pela investigadora relativamente à prestação dos alunos caso.
Para além da conversa informal já referida, foi realizada uma entrevista semiestruturada no final do semestre a cada aluno caso, orientada por un guião, gravada em áudio e depois transcrita, em que as produções nas tarefas selecionadas para o presente trabalho foram objeto de discussão. Na entrevista procurou-se aceder aos processos de raciocínio dos alunos, tentando clarificar aspetos ambíguos e motivos inerentes aos esquemas de demonstração nas produções, sua representação e sua significação.
Em complemento à descrição dos factos, através de ciclos de observação, reflexão e interpretação, procedemos à interpretação dos factos com base no enquadramento teórico. Após a análise de cada aluno caso separadamente, com vista à elaboração de uma síntese e à enunciação de proposições interpretativas, levámos a cabo a confrontação dos três alunos caso para destacar elementos, por um lado, de homogeneidade e, por outro lado, de heterogeneidade.
Uma base para a análise dos dados é constituída pelas categorizações de esquemas de demonstração de Harel e Sowder (1998, 2007) e, de forma mais fina, de Lee (2016). Em particular, atendendo a que as tarefas cujas produções analisamos envolvem proposições que, pelo enunciado, têm assumidamente valor lógico verdade, seguimos as categorias para esquemas de demonstração dedutivos e as suas descrições.
Tendo em conta a noção de representação matemática de Goldin (2008) e o quadro conceptual de representação e significação de Mata-Pereira e Ponte (2013), analisamos as representações utilizadas e os significados atribuídos pelos alunos caso nos esquemas de demonstração das suas produções. Com os modos de representação de Duval (2006a, 2006b), procuramos ainda a presença de processos de tratamento e de conversão entre representações.
3.2.Características das aulas
Nas aulas foram usadas as linguagens natural, simbólica e visual, por a unidade curricular incluir Álgebra Linear e alguns tópicos de Geometria Analítica, mas, sobretudo, para proporcionar o contacto dos alunos com várias representações. Apesar de se pretenderem produções com esquemas de demonstração dedutivos, a ordem dos conteúdos de Álgebra Linear seguiu uma abordagem cálculo-abstração (Harel, 1987). Começar com matrizes e sistemas de equações lineares permite uma aprendizagem gradual no sistema de linguagem da Álgebra, preparando a compreensão de noções tradicionalmente difíceis para os alunos - espaços vetoriais e aplicações lineares.
As aulas foram norteadas pela aprendizagem pelos pares (Crouch & Mazur, 2001; Beites & Romano, 2014), método de ensino-aprendizagem que remete para a constituição de comunidades de aprendizagem, que são, desde há vários anos, encorajadas por educadores matemáticos construtivistas. Pretendemos assim dar importância ao conhecimento informal dos alunos e dos seus conceitos espontâneos, bem como ao trabalho de colaboração dos alunos com os seus pares em tarefas matemáticas, no sentido de encorajar o questionamento individual e em grupo, a comunicação de ideias matemáticas e a exploração conjunta (Kennedy, 2012).
Visámos também a apropriação das tarefas, o despoletamento do diálogo e a articulação dos esforços de compreensão (Bruce & Bloch, 2013), com o intuito da criação de situações de aprendizagem contrárias às propostas pela educação tradicional, marcadas pelo papel passivo e recetivo do aluno. Tentou-se, assim, uma demarcação de um ensino baseado na mera transmissão de conteúdos e centrado no professor (Branco, 2014). Com efeito, a criação de comunidades de aprendizagem amplifica o espaço de aprendizagem, transformando-o “num espaço no qual todas as pessoas podem ensinar e aprender” (Catela, 2011, p. 37).
Previamente a uma aula, os alunos leram sobre o tópico a abordar e resolveram um trabalho de casa associado, como o que consta na Fig. 2.
Apesar de existirem momentos expositivos pelo professor, em geral de curta duração, na aula houve momentos de votação individual com cartões coloridos, em que cada um começou com uma questão concetual despoletadora de discussão, como a da Fig. 3.
A percentagem de respostas corretas guiou a tomada de decisão da professora quanto ao passo seguinte, frequentemente discussão dos alunos com os seus pares (Beites & Romano, 2014; Beites & Serôdio, 2015; Crouch & Mazur, 2001).
3.3.Características das tarefas
Como “um único tipo de tarefa dificilmente atingirá todos os objectivos curriculares valorizados pelo professor” (Ponte, 2005), as tarefas propostas ao longo do semestre foram diversificadas. No que se segue, apresentamos as propostas que envolvem proposições de álgebra linear com valor lógico verdade e cujas produções dos alunos caso são analisadas no presente trabalho.
Na tarefa TCAV na Fig. 4, um trabalho de casa, pedia-se uma demonstração matricial da comutatividade da adição de vetores do espaço (pela terminologia das aulas, ℝ3). Uma resolução passa pela representação algébrica dos vetores com matrizes coluna, ou linha, e pela comutatividade da adição de matrizes demonstrada, no âmbito das propriedades da álgebra matricial, numa aula anterior. Alternativamente, pode-se invocar a comutatividade da adição de números reais nas entradas das matrizes soma resultantes.
A tarefa TSPI na Fig. 5, de um teste de avaliação, é inspirada num resultado clássico de classificação de sistemas de equações lineares com incógnitas reais. Uma demonstração compreende as seguintes partes: para cada λ Є ℝ, χλ é solução de DX=E; se λ1 ≠ λ2 então Xλ1 ≠ Xλ2; a classificação indeterminado por ℝ ter um número infinito de elementos. O mencionado resultado, na Fig. 6, e uma demonstração constavam das páginas para leitura no TPC3, preparatório para uma das aulas.
As dificuldades reportadas por muitos alunos no TPC3 e na exploração da demonstração na aula, com propriedades da álgebra matricial abordadas, levaram a professora a pedi-la de outra forma (Fig. 5) no teste. Concretamente, foi dada a expressão das soluções de DX = E em função de duas soluções distintas X0 e X1, a qual só aparecia na demonstração associada ao enunciado do resultado na Fig. 6. A necessidade de justificar que se λ1 ≠ λ2 então Xλ1 ≠ Xλ2, por redução ao absurdo ou por contrarecíproco, manteve-se sem pedido explícito.
Na tarefa TAPL na Fig. 7, um trabalho de casa, pedia-se uma demonstração para uma fórmula da área de um paralelogramo, definido por dois vetores (não paralelos) u e v de ℝ3, que envolve o produto vetorial desses vetores. Para além do conceito de produto vetorial de vetores do espaço, a resolução passa pela aplicação de uma razão trigonométrica conveniente. Concretamente, há que relacionar a altura do paralelogramo com um dos seus lados e com o ângulo formado pelos vetores u e v.
4. Apresentação de resultados
4.1.Alice
Na produção da Fig. 8 para a tarefa TCAV, a Alice começa por escrever o que é pedido em linguagem verbal. Pode observar-se, depois, a conversão para linguagem algébrica com a igualdade u + v = v + u, que salienta com recurso à linguagem visual e complementa com a explicitação “para quaisquer u e v”. Em nenhuma das linguagens a Alice menciona que os vetores são do espaço, mas, após o tratamento em notação matricial com matrizes coluna de tipo 3×1, nota-se que assim os considera.
Efetua a adição das matrizes que utilizou para representar e , obtendo as entradas da matriz soma de υ e ν. Na última igualdade na Fig. 8, para , a Alice substitui υ i + ν i por ν i + υ i mas não escreve, por palavras, que utiliza a comutatividade da adição de números reais. Deste modo, obtém as entradas da matriz soma de e sem escrever a expressão ν + υ. Apresenta assim dedução coerente num esquema de demonstração dedutivo, transformativo, com nível 5 pela informalidade.
A Alice indica, na entrevista, a propriedade comutativa da adição de matrizes com entradas reais para justificar a terceira igualdade após υ + ν. Diz “se nós tivermos a soma de uma matriz com outra e nós fizermos o inverso, acontece o mesmo”, onde inverso significa “Trocar a ordem das matrizes”. Refere que não fez o tratamento para ν + υ por escrever “logo o resultado”, mas não é um esquema de demonstração de convicção externa, autoritário, com nível 0, por não apelar a conhecimento externo.
Produz ainda o exemplo na Fig. 9, onde, como diz na entrevista, vê os vetores do plano como “vetores do espaço com zero na terceira coordenada que não é preciso escrever”, o que ilustra um tratamento. Mas não conclui daí o que pretendia, excluindo um esquema de demonstração empírico, indutivo. Também não há evidências de utilização novata de exemplos ou raciocínio lógico (nível 1) ou de utilização estratégica de exemplos para raciocinar (nível 2).
Não parece ter claro até onde deve chegar o esquema para demonstrar, mas na entrevista clarifica que “a demonstração seria só esta parte” (Fig. 8). A Alice refere ainda que o exemplo serve “para confirmar que aquilo que disse anteriormente estava bem”, pois “por letras torna-se mais complicado”. Assim, tem-se uma combinação de esquema de demonstração dedutivo, transformativo, com nível 5, com um exemplo, este para confirmar o que fez em linguagem simbólica no primeiro.
A Alice escreveu o que apresentamos na Fig. 10 em resposta à tarefa 3 do TPC 3 (Fig. 2), indicando, sem especificar, o que não fora claro no estudo pré-aula. Na entrevista recorda-se que teve dúvidas nessa demonstração, posteriormente solicitada na forma da tarefa TSPI do Teste 1 (Fig. 5).
Na aula em que a demonstração foi explorada, a Alice fez poucas intervenções ao longo da mesma mas reagiu à questão preparatória colocada pela professora. Perante como justificar, sem resolver, que 2 é solução da equação 3x=6, a Alice respondeu dizendo que havia que substituir x por 2 e ver que se obtém uma proposição verdadeira.
Na produção da Fig. 11 para a tarefa TSPI, a Alice começa por transcrever alguns dados do enunciado em linguagem algébrica, nomeadamente, DX = E e X
λ
= (1 - λ)X
0
+ Λx
1
. Escreve ainda
Na entrevista, perante a questão de como escrever simbolicamente que X 0 é solução de DX = E, a Alice realiza a conversão em linguagem verbal: “o DX 0 ... Ia ser o meu E. E o DX 1 ia ser também o meu E.”. Apesar da escrita precedente de X, a Alice parece saber testar se um elemento do conjunto em que está a trabalhar é solução de uma equação no mesmo.
Contudo, quanto a X
0
e a X
1
, refere: “pensei mal”, “tinha duas soluções distintas”, “eu associei que só poderiam ser mesmo essas”. Para além de soluções, atendendo à escrita
A referida igualdade matricial, acompanhada da consideração “isto se for um sistema linear homogéneo”, conversão da linguagem algébrica para a linguagem verbal, é clarificada na entrevista. A aluna diz estar a considerar DX = 0, onde 0 é a matriz nula de tipo adequado, e refere ter pensado num caso mais simples para tentar chegar às soluções, mas estas já estavam no enunciado (Fig. 5).
A entrevista ajuda a comprovar a combinação de esquemas de demonstração: simbólico, não referencial, com nível 0; de convicção externa, autoritário e ritual, com nível 0. O apelo a fontes de conhecimento externas pode ser apreciado por a demonstração ter sido explorada nas aulas: “neste contexto, sei que... iriam ser infinitas soluções”, num esquema com o significado de facto conhecido.
A manipulação simbólica, que a Alice não é capaz de esclarecer e atribuir significação na entrevista, leva a aluna a escrever depois que λ = 1 ˅ λ = 0. Segundo a Alice, atendendo à infinitude patente no enunciado e por ter feito “um exercício (...) que era dentro do mesmo género”, como um rito, conclui que o conjunto-solução é ℝ \ {0,1}. Assim, deixa subentendido que está a pensar em números reais.
Na entrevista, no seguimento da escrita DX 0 = E e DX 1 = E que representa simbolicamente que X 0 e X 1 são soluções de DX = E, a Alice refere que teria de multiplicar D por X λ e mostrar que dá E. Acaba por chegar a esta matriz recorrendo a propriedades da álgebra matricial, embora tenha pensado utilizar D-1 E que deduz a partir de DX = E.
A dedução precedente é feita apesar de D ser uma matriz retangular, voltando a utilizar os símbolos sem referência à sua função e ao significado associado. Confrontada com os tipos das matrizes, diz que só poderia usar D-1 se m = n. Mesmo que pudesse escrever D-1 E, a Alice não tem em conta que em DX λ já não tem onde substituir X por D-1 E.
Na produção da Fig. 12 para a tarefa TAPL, a Alice usa linguagem visual para representar um paralelogramo definido por dois vetores não paralelos. No esboço destaca, em linguagem algébrica, o ângulo por estes formado, as suas normas e a altura do paralelogramo. O tratamento do triângulo retângulo destacado, para obter um retângulo assinalado a sombreado e com uma seta, sugerindo uma translação do triângulo retângulo, é feito em linguagem visual.
Em linguagem algébrica, escreve a norma do produto vetorial dos vetores em função das suas normas e do seno do ângulo por eles formado. Substitui depois este por uma expressão obtida por conversão da linguagem visual para a linguagem algébrica. Após alguns tratamentos em linguagem algébrica, chega a uma expressão que converte para linguagem verbal: “Área do paralelogramo”.
Pelas deduções lógicas, através de inferências dedutivas coerentes, mas com informalidade, o esquema de demonstração na produção da Fig. 12 é, pelo exposto, dedutivo, transformativo, com nível 5.
4.2.Maria
Na produção para a tarefa TCAV da Fig. 13, um esquema de demonstração dedutivo, transformativo com nível 5, a Maria usa a linguagem algébrica para escrever o que parecem ser dois vetores arbitrários do espaço com notação matricial. Na entrevista alude ao enunciado da tarefa, onde consta que são vetores do espaço, para justificar a omissão do conjunto a que pertencem as matrizes coluna escritas. Ainda assim, a respeito da produção, salienta que a informação relativa às entradas “devia cá estar mas não está”, “Pertencem ao conjunto ℝ.”.
Apesar da igualdade central e dos tratamentos dos vetores em linguagem algébrica, a Maria não invoca a comutatividade da adição de números reais em linguagem verbal. Na entrevista refere a propriedade após exemplificar: “Adicionar, por exemplo, o 2 com o 3 (...) dá 5, há-de ser a mesma coisa que adicionar o 3 com o 2.”, pois “A ordem na soma não interessa”. A investigadora pergunta-lhe, então, se poderia ter resolvido a tarefa só com números específicos, mas ela é peremptória ao afirmar que não, por se tratar do “caso geral” a demonstrar.
A Maria não apresentou dúvidas na resposta à tarefa 3 do TPC 3 (Fig. 2), escrevendo o que apresentamos na Fig. 14. Nas aulas, ela respondeu às várias perguntas que a professora foi colocando como forma de construir os vários passos da demonstração, que mais tarde seria pedida na tarefa TSPI do Teste 1 (Fig. 5).
Na produção em linguagem algébrica para a tarefa TSPI na Fig. 15, a Maria escreve as conversões DX 0 = C e DX 1 = C da hipótese (X 0 e X 1 são soluções de DX = C). A entrevista permite-nos confirmar que ela aplica, sem ter escrito em linguagem verbal, a propriedade distributiva da multiplicação em relação à adição de matrizes no desenvolvimento de DX λ .
A Maria realça na entrevista que λ e 1- λ são números reais, o que permite escrever a terceira igualdade no desenvolvimento de DX λ . Refere-se à propriedade da álgebra matricial nos casos em que a aplicou através de uma representação informal em linguagem verbal. Por exemplo, diz “posso passar para o lado esquerdo” para a permuta de D e 1- λ.
Para fundamentar as últimas igualdades, menciona que “já tinha visto anteriormente que DX 0 era igual a C ” e “substituía e fazia o mesmo para o DX λ ”. Numa conversão da linguagem algébrica para a linguagem verbal, com a designação distributividade da multiplicação de matrizes em relação à adição de escalares, justifica o passo seguinte na entrevista.
Refere depois que “tinha que atribuir vários valores para λ, para ver... as soluções”, “Se fossem todas diferentes, pronto, infinitas soluções...”, “Ele era possível e indeterminado.”. Acrescenta: “Se eu obtivesse sempre a mesma solução, seria possível e determinado.”, o que, apesar da demonstração feita nas aulas, exclui um esquema de demonstração de convicção externa.
A investigadora vinca a questão de como saber se as soluções são distintas. Quanto a X 0 e X λ , a Maria refere que estava no enunciado. Questiona-a depois sobre se X 2 é distinta de X 0 e de X 1 e, perante a afirmação “É.”, como ver. A Maria diz “substituindo valores... Por exemplo, se o X 0 for 2 e o X 1 for 3”, não atribuindo, nesse momento, um signficado apropriado aos símbolos matemáticos, mas depois exclama “Eram matrizes coluna!”.
Após a digressão da Maria com casos particulares de matrizes coluna para ver que X 2 é diferente de X 0 e de X 1 , a investigadora pergunta se poderia escrever todas as soluções X λ e possibilidades para as matrizes a analisar. Ela diz que “Vão dar todos diferentes.”, atribuindo um significado de demonstração implicada por regularidade observada e regularidade esperada ao esquema, mas reconhece a impossibilidade da listagem pela infinitude de números reais.
A produção na Fig. 15 reúne assim, em simultâneo, características de esquema de demonstração dedutivo, transformativo, com nível 5, na parte que se refere a que, para cada λ, X λ é solução de DX = C, e de esquema de demonstração empírico, indutivo, com nível 1, na parte relativa ao número de soluções.
A investigadora, na entrevista, elabora uma redução ao absurdo para fundamentar que X 0 e X 2 são distintas: de X 0 = X 2 chega a X 0 = X 1 , uma contradição. É a própria Maria a referir que X 0 = X 1 “É falso”, pois “No enunciado já diz.”. A investigadora sugere então que a Maria considere dois números reais arbitrários e distintos, λ1 e λ2, para a estratégia geral.
Em diálogo com a investigadora, explicando os passos em linguagem verbal, a Maria deduz, em linguagem algébrica, X 0 = X 1 a partir de X λ0 = X λ2 . Depois de escrever X 0 = X 1 e “X Falso”, hesita perante (λ2 - λ1)X 0 =( λ2 - λ1)X 1 quando a investigadora lhe pergunta se λ2 - λ1 é distinto de zero para simplificar, mas recorda que λ1 e λ2 são diferentes.
A redução ao absurdo gera, no entanto, alguma confusão quando a Maria é interpelada para enunciar a conclusão do que fez e que, posteriormente, a investigadora tenta clarificar. Apresentamos o extrato transcrito da evidência da incompreensão do princípio da não contradição subjacente ao método de redução ao absurdo:
I: |
Tivemos [sic] a fazer uma data de passos e... chegámos à conclusão que isso implica que o é igual a X 1 . Isso é verdade? |
M: |
X 0 ser igual a X 0 ? É. |
I: |
O que é que nós sabemos do enunciado? |
M: |
Não, sabemos que eles são distintos. Então isto é falso! Pois não... |
I: |
... (risos) |
M: |
Isto é falso. |
I: |
Isto é falso. |
M: |
X 0 ... Exato. |
I: |
Então, o que é que isto significará? |
M: |
Significa que, para qualquer que seja [sic] o λ1 e o λ2... |
I: |
... |
M: |
X 0 e X 1 serão sempre distintos. |
Na produção da Fig. 16, a Maria começa por utilizar linguagem verbal para recordar a área de um paralelogramo em função da base e da altura deste, escrevendo a fórmula em linguagem algébrica. Apresenta, em linguagem visual, um esboço de um paralelogramo definido por dois vetores e não paralelos do espaço (aspeto que não refere formalmente). Neste destaca, em linguagem algébrica, os comprimentos dos vetores, o ângulo formado por estes, e a altura do paralelogramo.
Após uma introdução em linguagem verbal, escreve a norma do produto vetorial dos referidos vetores em linguagem algébrica. Relaciona depois, numa conversão da linguagem visual para a linguagem algébrica, a altura do paralelogramo com a norma de um dos vetores e a amplitude do ângulo por estes formado. A Maria realça ainda o motivo, recorrendo essencialmente a linguagem verbal, para utilizar a razão trigonométrica seno.
Salienta também, em linguagem algébrica, que a norma do vetor é igual à medida da base do paralelogramo. Realiza depois um tratamento em linguagem algébrica, transformando a primeira fórmula escrita noutra em que foi substituído por uma expressão anteriormente deduzida. No final do esquema de demonstração dedutivo, transformativo, com nível 5, na Fig. 16, a Maria conclui, em linguagem algébrica, o pretendido.
4.3.Pedro
O Pedro começa por escrever o que parecem ser dois vetores arbitrários do espaço com notação de triplos ordenados, o que ele confirma na entrevista em que também refere que υ1, υ2, υ3 e ν1, ν2, ν3 são números reais. Na produção da Fig. 17 nota-se o tratamento da notação inicial para a matricial, embora sem escrever o conjunto a que pertencem as coordenadas e as entradas. A referida transformação, dentro do sistema de linguagem algébrica, é assinalada em linguagem verbal através da expressão “Matricialmente”.
Considera, depois, dois vetores concretos do espaço em linguagem algébrica, com as mesmas transformação e notação utilizadas para os vetores arbitrários, evidenciando a falta de atribuição de um significado apropriado aos símbolos matemáticos. Vê neste caso particular, efetuando a adição com notação matricial, que a soma não depende da ordem das parcelas na adição dos vetores considerados. Assim, o Pedro apresenta um esquema de demonstração empírico, indutivo, com nível 1. Na entrevista diz que o fez por ser “mais fácil” e para a compreensão dele, e ainda por ser “mais palpável”.
Apesar de grande parte da produção da Fig. 17 corresponder a uma argumentação baseada num exemplo, o início da mesma e as respostas precedentes levam a investigadora a perguntar-lhe se o que fez é uma demonstração. Perante a pergunta, o Pedro refere que elaborou uma “demonstração específica, para um caso particular”. Na entrevista diz ainda que, para o “caso geral”, teria que passar pelas igualdades υi + νi= νi + υi. Menciona que a “adição de matrizes é comutativa”, o que vem da comutatividade da adição de “escalares”.
Na entrevista, o Pedro escreve um esquema de demonstração dedutivo, transformativo após a conversão das considerações em linguagem verbal para linguagem algébrica. Perante o motivo para não o ter apresentado antes, apoia-se na experiência empírica e na autoridade de outros, nomeadamente, em unidades curriculares distintas da do estudo em que adicionaram vetores: “já tinha percebido”; “tínhamos... em várias disciplinas feito”; “Para mim, somar a mais b ou b mais a iria de [sic] sempre dar o mesmo.”. Apesar de não percetível só com a produção, complementada com as explicações dadas na entrevista, o esquema de demonstração na Fig. 17 também é de convicção externa, autoritário, com nível 0.
Ainda relativamente ao motivo, o Pedro esclarece que “Fui à internet, vi isto”, mas não escreveu o esquema de demonstração dedutivo, pois diz que “não sabia se havia de demonstrar assim”. Acrescenta que “transcrever isto para o papel seria surreal, porque para mim não era, de facto, estar a demonstrar. Para mim demonstrar era tipo ter um caso particular, aí sim conseguia demonstrar.”. Refere ainda que “É sempre igual.” quando a investigadora lhe pergunta se a produção na Fig. 17 serve para outros vetores, atribuindo um significado de demonstração implicada por regularidade esperada ao esquema.
O Pedro escreveu o que apresentamos na Fig. 18 em resposta à questão 3 do TPC 3 (Fig. 2), embora sem especificar o que não tinha compreendido. Uma demonstração foi depois solicitada na forma da tarefa TSPI do Teste 1 (Fig. 5).
Na aula em que a demonstração foi explorada, o Pedro disse que não sabia como começar e perguntou como é que se pensou em X λ , o que representava - evidência das dificuldades com a notação. Referiu que havia que substituir X por Xλ em DX, que teria de dar C, e justificou os passos das inferências dedutivas com propriedades da álgebra matricial, mas que não conseguiria fazer sem a pista do Xλ.
Na produção para a tarefa TSPI na Fig. 19, o Pedro começa por transcrever um dado do enunciado em linguagem algébrica: DX = C. Com a mesma linguagem, após algumas considerações em linguagem verbal que incluem o significado de ter solução, escreve mais abaixo a expressão, para cada escalar real λ, de Xλ.
Usa linguagem verbal para o tratamento “apresenta duas soluções distintas é possível e indeterminado” de “é pelo menos possível”, configurando um esquema de demonstração de convicção externa, autoritário, com nível 0. A entrevista corrobora a hipótese, pois ele diz “A partir do momento que existe mais do que uma solução, temos um sistema indeterminado.”, não sentindo necessidade de demonstrar e atribuindo o significado de facto conhecido ao esquema.
Na entrevista dá exemplos de soluções atribuindo valores a λ, mas não consegue começar a demonstrar que, para cada λ, Xλ é solução de DX = C. Inicialmente, chega a escrever DXλ = C, que se quer provar, como parte da hipótese. Fruto do diálogo com a investigadora, acaba por elaborar os passos dessa parte da demonstração em linguagem algébrica.
O Pedro não sente necessidade de provar mais nada, pois se há um número infinito de números reais, então “existem infinitas soluções” dadas por Xλ. Na entrevista, salienta que isso depende do conjunto, o que é correto, mas fala das distintas soluções recorrendo a argumentos empíricos em que concretiza alguns valores de λ.
Por fim, explica a produção da Fig. 20 que não foi avaliada. O Pedro pensou na inversa de, D mas depois deu conta que “podemos não conseguir tirar uma inversa”. Explica que tal poderia suceder por a matriz ser retangular ou por ser quadrada, mas não invertível, pelo que riscou a estratégia de utilização de inversa para resolver um sistema de equações lineares possível.
Na produção da Fig. 21 para a tarefa TAPL, o Pedro elabora um esquema de demonstração empírico, indutivo, com nível 1. Com efeito, assinala com a expressão “c. q. d.”, em linguagem verbal, que conclui o pretendido a partir de dois vetores concretos do espaço, isto é, valida empiricamente. A escolha recai numa representação bidimensional, em linguagem visual e em linguagem algébrica, pela particularidade das cotas de ν e w serem iguais a zero. Na entrevista, atribui o significado de demonstração implicada por regularidade esperada ao esquema.
O Pedro faz uma conversão da linguagem visual para a linguagem algébrica e relaciona, essencialmente em linguagem algébrica, as áreas do paralelogramo definido por ν e w com a área de um triângulo, destacado por tratamento em linguagem visual. Realiza os cálculos com ν e w em linguagem algébrica, por dois processos: fórmula a deduzir na tarefa TAPL, parecendo incorrer em circularidade lógica; semi-produto da base pela altura. Nesta usa alguma linguagem verbal, com conversão para a linguagem algébrica, para destacar que está a calcular a área de um triângulo.
Nos tratamentos em linguagem algébrica aplicando a fórmula cuja dedução era o objetivo final da tarefa TAPL, salienta, em linguagem verbal, o motivo para multiplicar por
4.4.Comparação de resultados
A Alice, a Maria e o Pedro tiveram o segundo contacto com a demonstração no Ensino Superior, pelo menos, no semestre relativo à unidade curricular do estudo, em conteúdos de álgebra linear e de geometria analítica. Todos os alunos caso tiveram o primeiro contacto com a demonstração no ensino não superior, o que não implica que a demonstração tenha sido aí trabalhada. As diferentes experiências da Alice, da Maria e do Pedro são por estes associadas a distintos conteúdos do ensino secundário: geometria; funções e álgebra; probabilidades e números complexos, respetivamente. Na Tabela IV apresentamos um resumo dos resultados relativos aos alunos caso, com destaque para os tipos de esquemas de demonstração, representações e transformações de representações.
Tabela IV Resumo dos resultados obtidos, destacando os tipos de esquemas de demonstração (ED), representações (R) e transformações de representações (TR)
| Alice | Maria | Pedro | |||||||
|---|---|---|---|---|---|---|---|---|---|
| TCAV | TSPI | TAPL | TCAV | TSPI | TAPL | TCAV | TSPI | TAPL | |
| ED | combinação de ED dedutivo, transformativo, nível 5, com exemplo | combinação de ED simbólico, não referencial, com ED de convicção externa, autoritário e ritual, nível 0 | ED dedutivo, transformativo, nível 5 | ED dedutivo, transformativo, nível 5 | combinação de ED dedutivo, transformativo, nível 5, com ED empírico, indutivo, nível 1 | ED dedutivo, transformativo, nível 5 | combinação de ED empírico indutivo, nível 1, com ED de convicção externa, autoritário, nível 0 | ED de convicção externa, autoritário, nível 0 | ED empírico, indutivo, nível 1 |
| R | linguagem verbal linguagem visual linguagem algébrica |
linguagem algébrica linguagem verbal |
linguagem visual linguagem algébrica linguagem verbal |
linguagem algébrica | linguagem algébrica linguagem verbal |
linguagem verbal linguagem algébrica linguagem visual |
linguagem verbal linguagem algébrica |
linguagem algébrica linguagem verbal |
linguagem visual linguagem algébrica linguagem verbal |
| TR | conversão da linguagem verbal para a linguagem algébricatratamento em linguagem algébrica | tratamento em linguagem
algébrica conversão da linguagem algébrica para a linguagem verbal |
tratamento em linguagem
visual conversão da linguagem visual para a linguagem algébrica tratamento em linguagem algébrica conversão da linguagem algébrica para a linguagem verbal |
tratamento em linguagem algébrica | conversão da linguagem verbal para a
linguagem algébrica tratamento em linguagem algébrica |
conversão da linguagem visual para a
linguagem algébrica tratamento em linguagem algébrica |
conversão da linguagem verbal para a
linguagem algébrica tratamento em linguagem algébrica |
tratamento em linguagem verbal | tratamento em linguagem
visualcon versão da linguagem visual para a linguagem algébrica tratamento em linguagem algébrica conversão da linguagem algébrica para a linguagem verbal conversão da linguagem verbal para a linguagem algébrica |
Embora o nível de desempenho em matemática no ensino secundário da Maria seja o mais baixo dos alunos caso, ela consegue aproximar-se mais dos esquemas de demonstração dedutivos para as proposições com valor lógico verdade. Uma explicação pode residir no facto desse nível de desempenho não traduzir, necessariamente, o desempenho particular na elaboração de demonstrações. Também a experiência mais algébrica da Maria no primeiro contacto com a demonstração no ensino não superior, em conteúdos de funções e álgebra, pode constituir outra explicação. Ainda assim, pela falta de formalidade nas justificações, o nível máximo alcançado nos seus esquemas é 5.
Nas produções da Maria nota-se um menor número de transformações de representações entre linguagens. Este aspeto é particularmente visível para as tarefas TCAV, só com linguagem algébrica, e TSPI, em que a linguagem algébrica domina sobre a pequena presença da linguagem verbal. A explicação poderá ser a última do parágrafo anterior, por a Maria recorrer logo a representações em linguagem algébrica, realizando tratamentos sem precisar de conversões. Para a tarefa TSPI, a Alice e, sobretudo, a Maria realizam tratamentos em linguagem algébrica, mas o Pedro só efetua tratamento em linguagem verbal, num esquema de demonstração de convicção externa, autoritário, com nível 0.
Num esquema de demonstração dedutivo, transformativo, com nível 5, para a tarefa TAPL, a Alice faz uma conversão da linguagem algébrica para a linguagem verbal, só para assinalar que a expressão a que chegou é a pretendida. O Pedro, apesar de realizar mais conversões (da linguagem algébrica para a linguagem verbal e vice-versa), obtém um esquema de demonstração empírico, indutivo, com nível 1. Não só para a tarefa TAPL mas de um modo geral, a Maria aproxima-se mais dos esquemas de demonstração dedutivos com poucas conversões, mas estas podem ter ocorrido de forma não visível. Com efeito, a investigadora acede às representações nas produções, eventualmente com o complemento da entrevista, mas não às que podem ter ocorrido mentalmente, sem registo escrito.
O primeiro contacto da Alice com a demonstração no ensino não superior, em geometria e com experiência associada de subdivisão de figuras geométricas, pode também contribuir para explicar o seu esquema de demonstração dedutivo, transformativo, com nível 5, na produção para a tarefa TAPL. Apesar de todos os alunos caso usarem linguagem visual, o que era expectável pela tarefa, e conversão da linguagem visual para a linguagem algébrica, só a Alice realiza o tratamento da figura geométrica inicial que é transformada, por decomposição e reconstrução, num retângulo. Considera depois que os dois poliedros planos, paralelogramo e retângulo dele obtido, equidecomponíveis.
Nas produções da Alice e do Pedro acentua-se a presença da linguagem verbal, o que pode prender-se com a experiência não algébrica do primeiro contacto com a demonstração, e o número de conversões. Contudo, isso não se traduziu num maior número de esquemas de demonstração dedutivos, talvez pela simplicidade dessas conversões.Por exemplo, para a tarefa TCAV, a Alice executa uma conversão do enunciado da linguagem verbal para a linguagem algébrica, para saber onde tem de chegar. O mesmo faz o Pedro que, em contraste com os esquemas de demonstração dedutivos, transformativos, com nível 5, da Alice e da Maria (sem conversões), apresenta uma combinação de esquemas não dedutivos.
Um dos esquemas do Pedro para a tarefa TCAV é empírico, indutivo, com nível 1, num exemplo com o significado, por ele atribuído, de demonstração implicada por regularidade esperada. Esta tendência do Pedro volta a emergir na produção para a tarefa TAPL e na entrevista sobre a tarefa TSPI, mas é residual nas produções da Maria. Presencia-se, com o significado de demonstração implicada por regularidade observada e regularidade esperada, só quando apresenta exemplos para mostrar que há um número infinito de soluções na tarefa TSPI. Nesta situação, trata-se de uma combinação de esquemas de demonstração, um dedutivo, transformativo, nível 5, com um empírico, indutivo, nível 1.
Ainda nas produções para a tarefa TCAV, todos os alunos realizam, com nuances, tratamentos em linguagem algébrica. A Alice e a Maria trabalham com vetores arbitrários, enquanto o Pedro executa os tratamentos, maioritariamente, com vetores concretos do espaço. Nenhum aluno utiliza a estratégia mais curta com a sugestão do enunciado (representação matricial adequada) que, sem escrever entradas, passaria por invocar simplesmente a comutatividade da adição de matrizes, provada noutras aulas. Na entrevista, a Alice refere esta propriedade, mas não vislumbra o seu alcance para uma produção menos extensa no sentido mencionado.
Apesar do Pedro recorrer a vetores concretos do espaço, casos particulares, na produção para a tarefa TCAV, na entrevista escreve um esquema de demonstração dedutivo. Portanto, no sentido do conceito de demonstração em Matemática, ele parece saber fazer uma demonstração da comutatividade da adição de vetores do espaço e, em simultâneo, não achar relevante fazê-la. De facto, a respeito do esquema de demonstração dedutivo, transformativo, refere que não sabia se havia de demonstrar desta forma. Este aspeto remete para o conceito de demonstração para os alunos que, no caso do Pedro, acaba por variar consoante o contexto em que está.
Também na entrevista, os referidos casos particulares proporcionaram uma discussão da investigadora com a Maria, aparentemente facilitada pelo método de ensino-aprendizagem (aprendizagem pelos pares) das aulas associadas ao estudo. Como refere Maher (2010), “quando os alunos tentam convencer os outros de que as suas respostas estão corretas, eles podem reorganizar e reformular as suas representações de modo a tornar os argumentos convincentes.” (p. 4). A partir da discussão e do diálogo com a investigadora sobre a tarefa TSPI, a Maria elaborou ainda uma redução ao absurdo que, das evidências obtidas, não compreendeu na totalidade.
Salientamos que, para além da exploração completa da demonstração associada numa aula, a redução ao absurdo é um método de demonstração previsto no programa de matemática do ensino secundário. Contudo, tal não significa que tenha sido trabalhado no ensino secundário, incluído nos conteúdos de Lógica com presença transversal noutros conteúdos do programa em vigor para os alunos caso (Silva, Fonseca, Martins, Fonseca, & Lopes, 2001 / 2002) e inserido no domínio de conteúdo lógica e teoria de conjuntos do atual programa (Bivar et al., 2014). As discussões com os outros alunos caso não chegaram a esse ponto devido às dificuldades na parte inicial da TSPI.
A necessidade de exemplos é ainda sentida pela Alice na tarefa TCAV, de forma diferente. Apresenta uma combinação de esquema de demonstração dedutivo, transformativo, com nível 5, com um exemplo de significado confirmação. Partilhando o argumento “mais palpável” com o Pedro quando falam de exemplos na entrevista, a Alice não escolhe simplesmente dois vetores. A particularidade reside no tratamento dos vetores do espaço com terceira coordenada nula escolhidos, transformados em pares ordenados de números reais. A sustentação não invocada vem do isomorfismo entre os espaços vetoriais reais ℝ2 e {(x, y, 0): x, y Є ℝ}, munidos das usuais adição e multiplicação escalar.
A implementação da aprendizagem pelos pares visou a promoção das discussões entre alunos e ainda com a professora. Nas aulas, algumas foram despoletadas por questões conceptuais e outras resultaram das produções dos alunos caso nas tarefas TCAV, TPC3 associado à tarefa TSPI e TAPL. As funções da demonstração que se pretendiam implicadas eram, essencialmente, as de explicação, comunicação e convencimento. Mas os alunos caso nem sempre atribuíram esta última função a uma demonstração, o que é evidenciado com a produção da Alice para a tarefa TCAV - o anteriormente mencionado exemplo após um esquema de demonstração dedutivo, transformativo, com nível 5.
Observamos ainda o recurso a fatores externos nas produções para a tarefa TSPI da Alice e do Pedro (que não sente necessidade de demonstrar), com o significado, por eles atribuído, de facto conhecido. Este aspeto também surge na produção do Pedro para a tarefa TCAV, com características de convicção externa, autoritário, nível 0. Na produção da Alice presencia-se, simultaneamente, o ritual da argumentação pelo apelo a produções da aluna noutras tarefas. Neste sentido, numa combinação de esquemas de demonstração, emerge a escrita simbólica não referencial da argumentação, em que os símbolos não coincidem com o seu significado, sem conexão entre representação e significação.
Diversas dificuldades exibidas pelos alunos na elaboração dos seus esquemas de demonstração resultam, de facto, da não atribuição de um significado apropriado aos símbolos matemáticos. Este aspeto emerge, também, quando se pede uma demonstração de que se X 1 e X 2 são duas soluções distintas de um sistema de equações lineares, então qualquer combinação linear convexa destas é também uma solução. Concretamente, a Alice e a Maria, esta momentaneamente na entrevista, consideram X 1 e X 2 como números reais e não como n-uplos de números reais, o que indica que estes estudantes não compreenderam o conceito de solução de um sistema de equações.
A não atribuição de um significado apropriado aos símbolos matemáticos evidencia-se ainda na produção do Pedro para a tarefa TCAV, uma combinação de esquema de demonstração empírico, indutivo, nível 1, com um esquema de demonstração de convicção externa, autoritário, nível 0. Para além de considerar um exemplo uma demonstração, utiliza o mesmo símbolo para representar um
vetor arbitrário do espaço e um vetor concreto do espaço. A ausência de significado apropriado não se nota nas produções da Maria, registando-se apenas, na entrevista, a descrita ocorrência momentânea. Talvez este seja outro dos motivos para o maior sucesso da Maria nos esquemas de demonstração.
5. Discussão e conclusões
A demonstração no ensino-aprendizagem da matemática tem sido objeto de estudo de forma ténue em Portugal, mas com considerável expressividade internacional nos vários níveis de ensino (Hanna & de Villiers, 2012; Stylianides & Stylianides, 2017). Harel e Sowder (1998, 2007) apresentaram uma perspetiva compreensiva do ensino-aprendizagem da demonstração, complementada por Lee (2016), onde a noção de esquema de demonstração é central. Recentemente, Stylianides e Stylianides (2017) concluíram que a literatura existente até ao momento providencia enquadramentos teóricos de estudo e, ainda, o conhecimento sobre o lugar reduzido da demonstração no ensino e a sua (in)compreensão pelos alunos. Neste sentido, o ensino e a aprendizagem da demonstração, apesar de promoverem uma maior compreensão matemática (Balacheff, 2010; Hanna, 2000), são reportados como difíceis (Hanna & de Villiers, 2012).
O presente trabalho contribui para o campo da educação matemática, proporcionando elementos teóricos e metodológicos que podem apoiar investigadores e professores de matemática na compreensão das formas de pensamento dos estudantes e dos seus esquemas de demonstração de resultados matemáticos. Mais concretamente, analisámos os esquemas de três alunos caso em tarefas que visavam a demonstração de proposições de Álgebra Linear com valor lógico verdade. Os resultados evidenciam que as representações permitem o acesso parcial ao raciocínio, devido à existência de elementos associados não percetíveis nas produções. Em particular, só a entrevista a cada aluno caso permitiu classificar algumas das produções como elementos pertencentes a mais do que uma classe da categorização de Harel e Sowder (1998, 2007), ou seja, como combinações de esquemas de demonstração.
Trata-se de resultados novos, pois identificamos no ensino superior três das oito combinações identificadas por Kanellos, Nardi e Biza (2018) para o ensino não superior. Encontramos combinações dos níveis propostos por Lee (2016) e uma combinação nova: esquema de demonstração dedutivo, transformativo, nível 5, com um exemplo que serve para confirmar. Estes resultados são relevantes, uma vez que a ambiguidade das combinações tem, como referem Kanellos, Nardi e Biza (2018), interesse pedagógico, pois um professor alertado para a presença de mais do que um esquema de demonstração na mesma produção de um aluno pode intervir. Por outras palavras, pode traduzir um olhar construtivo do erro criando, como sugere Pinto (1998), uma estratégia didática após o erro ser observável para o professor.
A concretização do referido olhar poderá passar por: segunda oportunidade ao aluno, estratégia de retificação e melhoria, após as observações do professor e precedendo uma reclassificação das produções (Dias & Santos, 2016; Torre, 1993); aprendizagem pelos pares, considerando os erros na construção e na discussão de questões conceptuais (Beites & Serôdio, 2015); sessões de discussão de dúvidas norteadas pela análise de erros (Cury, 2007). Em particular, estas propostas poderão ajudar a combater as dificuldades, nomeadamente detetadas no presente trabalho, quando os alunos não atribuem um significado apropriado aos símbolos, em que os símbolos não coincidem com o seu significado. O sense making (Mata-Pereira & Ponte, 2013) é um aspeto relevante, pois a articulação entre significação e processos de raciocínio, estes sob a forma de representações, é fundamental para a compreensão da matemática (NCTM, como citado em Mata-Pereira & Ponte, 2013).
Nesta linha, num futuro trabalho de investigação, poderá ser importante recolher as argumentações dos alunos com os seus pares em sala de aula, em torno dos esquemas de demonstração por eles produzidos e em discussões de convencimento mútuo da sua validade. Efetivamente, a implementação de um ambiente pedagógico dialógico favorece uma melhoria da compreensão matemática, como ilustrado na presente investigação na entrevista facilitadora do diálogo entre a investigadora e a aluna Maria, por exemplo. Tendo em conta que a compreensão dos alunos, como evidenciado no estudo atual, é influenciada pela sua experiência anterior, pelas suas crenças e processos pessoais de verificação, seria interessante realizar um estudo com base na criação de uma espécie de “espaço filosófico” na sala de aula de Matemática (Kennedy, 2012), onde se discutissem conceitos (em particular, o de demonstração) no sentido de conseguir um entendimento alargado entre os estudantes.
Independentemente do nível de desempenho em matemática no ensino secundário, encontrámos representações e suas transformações (tratamentos e conversões) em todas as produções, mas com diferentes níveis cognitivos (Lee, 2016). Contrariamente ao expectável, o aluno caso com o melhor nível de desempenho em matemática no ensino secundário não foi o que produziu mais esquemas de demonstração dedutivos. Precisamente o aluno caso com o mais baixo nível de desempenho em matemática no ensino secundário é aquele que mais se aproxima dos esquemas de demonstração dedutivos que dariam resposta às tarefas propostas. Deste modo, constatou-sse, neste estudo, que a história académica prévia dos estudantes não é necessariamente um indicador do desempenho que um estudante pode vir a mostrar na construção de esquemas de demonstração. Trata-se de um contributo pedagógico relevante do presente estudo, pois constitui-se como um alerta ao professor.
Outro aspeto que sobressai, do aluno caso com o mais baixo nível de desempenho em matemática no ensino secundário, é que um menor número de transformações de representações numa produção de um aluno, nomeadamente as que correspondem a passar de um sistema de linguagem para outro - conversões, não significam necessariamente um nível mais baixo de abstração. De facto, pela entrevista realizada a cada aluno caso e a este em particular, parecem ter ocorrido processos mentais que levaram à escrita numa linguagem e a representações mais diretas para o objetivo pretendido, com eventuais processos mentais de conversão não visíveis nas produções. Esta contribuição do presente trabalho não contradiz os estudos que referem que as conversões, atividade cognitiva considerada menos espontânea e mais difícil, suportam e promovem o raciocínio e a abstração em Matemática (Duval, 2006b; Presmeg, 2006; Callejo & Zapatera, 2014), mas acrescenta que só os registos escritos podem não permitir averiguar da realização ou não de conversões.
As tarefas associadas ao estudo foram potencialmente promotoras da eliminação de descontinuidades entre os ensinos básico-secundário e superior. Segundo Costa e Catarino (2007), as mesmas surgem por não se fazerem conexões explícitas entre conceitos matematicamente interligados, um obstáculo para aprender álgebra linear devido à falta de ligação com o que os alunos já conhecem (Dorier, como citado em Costa & Catarino, 2007). Contudo, observámos que se o enunciado da tarefa é essencialmente um resultado conhecido do aluno, mesmo que não anteriormente demonstrado, a tarefa não parece ser a mais apropriada para mostrar a necessidade de uma demonstração, pelo menos não de modo isolado. Com efeito, tais tarefas não motivam a abordagem a uma demonstração, havendo que explorar algumas das suas funções para as tornar significativas (De Villiers, 2001), e, segundo o presente estudo, parecem facilitar a emergência de esquemas de demonstração de convicção externa. Trata-se de outro contributo pedagógico relevante do presente estudo, pois aponta para características a considerar numa tarefa de demonstração para que esta promova aprendizagens efetivas.
Elaborar uma demonstração em matemática envolve processos mentais complexos com raciocínio dedutivo (Lannin, 2005), que pode ser precedido por raciocínio indutivo mediante a formulação e o teste de conjeturas, com exemplos e contraexemplos (Beites, 2015). Apesar da sua importância, o raciocínio indutivo é negativamente apontado como emergente em esquemas de demonstração de álgebra, parecendo os tipos de tarefas facilitar o surgimento de certos tipos de esquemas de demonstração (Kanellos, Nardi, & Biza, 2018). No presente trabalho encontramos raciocínio indutivo em esquemas de demonstração empírico indutivos e, ainda, em combinações destes esquemas com outros, mas tal não era expectável nem deveria suceder. Com efeito, todas as tarefas associadas ao estudo são de demonstração para proposições de álgebra linear que, assumidamente pelo enunciado, têm valor lógico verdade.
Nos resultados encontrámos a utilização, por parte de alunos, de exemplos não constituíram um caminho para conjeturar, o que nos levou a outro aspeto relevante do presento estudo - a atenção dedicada aos significados, atribuídos pelos alunos, aos esquemas de demonstração não dedutivos. Um aluno caso apresentou uma combinação de um esquema de demonstração dedutivo, transformativo, com um exemplo, este com o significado, por ele atribuído, de confirmação. Os outros dois alunos caso também construíram exemplos, em esquemas de demonstração empírico indutivos e / ou combinações destes com outros esquemas, com o significado, por eles atribuído, de demonstração implicada por regularidade observada e / ou regularidade esperada. Deste modo, nos esquemas de demonstração não dedutivos das produções dos alunos caso, os exemplos serviram para complementar a insuficiência compreensiva da demonstração pelos alunos.
Esta insuficiência compreensiva mostra uma conceptualização da demonstração que não é consentânea com a noção de demonstração em matemática. De facto, há elementos que devem estar presentes numa demonstração (Stylianides & Stylianides, 2008): fundamentos (definições, lemas,...); argumentação (como se desenvolve; por exemplo, inferindo com modus ponens); representação (como se expressa; com linguagem algébrica, verbal ou visual); dimensão social (aceitação na comunidade matemática em que se cria). Para além de exemplos, que um aluno considera demonstração, detetámos outras situações em que o conceito imagem de demonstração dos alunos não coincide com o conceito definição (Tall & Vinner, 1981) de demonstração em matemática. Concretamente, dois alunos caso produziram esquemas de demonstração de convicção externa, autoritário, nivel 0. O significado, por eles atribuído, é o de facto conhecido, em que se chega a notar a ausência da necessidade de demonstrar.
Os resultados evidenciam também que a apresentação e a exploração completas de uma demonstração para uma proposição matemática, conjuntas com os alunos numa aula, pode não levar à compreensão de todos os elementos da demonstração por parte de cada aluno. Uma possibilidade de melhoria da compreensão de uma demonstração pelos alunos pode passar pela reorganização da apresentação da mesma pelo professor, e ainda pela reorganização da exploração, havendo que avaliar os efeitos sobre os alunos. A alteração da “flow of the proof” (Gabel & Dreyfus, 2017) pode consistir na ênfase de diferentes ideias, em particular cruciais (Weber & Hemmi, como citados em Gabel & Dreyfus, 2017), e detalhes que não sejam claros para os alunos, por vezes até omitidos pelo professor para não diminuir a qualidade pedagógica da demonstração (Lai & Weber, como citados em Gabel & Dreyfus, 2017).
Deste trabalho, cuja divulgação pode dar pistas para a prática letiva de outros professores, emergem desafios que se inserem no grande repto de como ensinar a demonstrar: contrariar a validação através da construção de exemplos; incorporar que a validade de um resultado depende da demonstração; mostrar que a construção de exemplos após um esquema de demonstração dedutivo é desnecessária; facilitar o sense-making; tornar clara e efetiva a apresentação e a exploração de uma demonstração. Deste modo, o futuro passa, como referem Stylianides e Stylianides (2017) após reflexão sobre o estado da arte na área da demonstração em Educação Matemática, por intervenções na sala de aula, apoiadas em investigação, de modo a gerar soluções para os desafios do ensino-aprendizagem da demonstração. De facto, “mathematics teachers at all levels, even experienced mathematicians, lack didactic knowledge regarding strategies for teaching proofs” (Gabel & Dreyfus, 2017, p. 187).











 nueva página del texto (beta)
nueva página del texto (beta)