1. Introducción
Dentro de la perspectiva de la resolución de problemas, el desarrollo de la prueba se presenta como una actividad clave en educación matemática (Hanna y de Villiers, 2008; Mariotti, 2006). Diversos estudios señalan que la construcción de la prueba no está exenta de obstáculos como, por ejemplo, la incapacidad de los estudiantes para desarrollar las estrategias de resolución apropiadas (Weber, 2001), la dificultad para dotar de sentido y coherencia a las proposiciones involucradas en el proceso de prueba (Zandieh, Roh y Knapp, 2014) o las dificultades para enlazar el proceso de argumentación con la construcción de la prueba formal (Alcock y Weber, 2010). En geometría, Duval (2016b) pone de manifiesto dificultades relacionadas con los procesos de visualización y razonamiento involucrados en la construcción de la prueba. Los procesos de visualización permiten establecer relaciones entre definiciones, propiedades o teoremas con subconfiguraciones identificadas en el proceso de argumentación conducente a la prueba. Esta acción puede desencadenarse o inhibirse en función de determinados factores como pueden ser la influencia de configuraciones prototípicas (Mesquita, 1998; Clemente, Torregrosa y Llinares, 2015; Saorín, Torregrosa y Quesada, 2017b), el conocimiento o no de las propiedades geométricas adecuadas (Reiss, Heinze, Renkl y Groß, 2008) o el modo en el que los estudiantes procesan la información (Pitta-Pantazi y Christou, 2009), poniendo de manifiesto la dificultad para conectar el proceso de argumentación con la construcción de la prueba (Duval, 2016b).
Douek (2010) señala la importancia de comprender las características organizativas que rigen el proceso de prueba para facilitar la transición argumentación - prueba. Heinze, Cheng, Ufer, Lin y Reiss (2008) indican que para desarrollar un proceso de prueba válido en geometría es necesario comprender la información dada, reconocer los elementos involucrados en la argumentación (premisas, argumentos, conclusión), construir la prueba en diferentes pasos y coordinar el proceso mediante la organización del discurso. En este sentido, Duval (2016b) pone de manifiesto la necesidad de organizar de forma adecuada los elementos del proceso de argumentación (premisas, teoremas, conclusiones) que permite construir y comunicar el proceso de prueba, en el que cada paso de razonamiento está conectado con el anterior mediante afirmaciones matemáticas que se superponen (conclusiones de un paso pueden utilizarse como premisas del siguiente). Por ello, el análisis del discurso escrito que comunica la prueba puede ayudarnos a entender el razonamiento desarrollado en el proceso de prueba y, por tanto, las dificultades antes comentadas.
Nuestra investigación se centra en el estudio de la forma en que los estudiantes desarrollan y organizan el discurso generado al comunicar el proceso de resolución de problemas geométricos de prueba en contexto de lápiz y papel. Para ello, consideramos los mecanismos de expansión discursiva de Duval (1999), entendidos como la forma en que se enlazan las afirmaciones matemáticas en el discurso generado, y el estatus o papel que desempeñan las afirmaciones matemáticas involucradas en cada paso de razonamiento. Así, nos planteamos las cuestiones de (1) cómo los estudiantes construyen un discurso escrito según una secuencia lógica de relaciones, en forma de afirmaciones matemáticas, establecidas a partir de los hechos geométricos identificados, y (2) cuál es el papel que desempeñan dichas afirmaciones matemáticas en el proceso de razonamiento desarrollado. La respuesta a dichas cuestiones puede aportar información sobre las características del razonamiento geométrico de los estudiantes que permiten o impiden concluir con éxito la prueba. Es aquí donde el modelo razonamiento configural (Torregrosa y Quesada, 2007), entendido como coordinación de procesos visualización, y su desarrollo pueden ayudarnos a comprender cómo los estudiantes asimilan las ideas que permiten generar un discurso coherente que refleje el razonamiento desarrollado.
2. Marco teórico
2.1. Coordinación de procesos de visualización: Razonamiento Configural
Para la resolución de problemas geométricos de probar es necesario relacionar conceptos o propiedades geométricas generales con configuraciones que representan hechos geométricos genéricos. Para ello, debe darse una interacción entre conocimientos y la configuración geométrica (o subconfiguraciones identificadas) que permita el establecimiento de afirmaciones matemáticas que generen un razonamiento lógico - deductivo que finalice con la solución al problema (tesis a demostrar). Duval (1998, 2016a) resalta la importancia de la visualización en esta interacción a partir de tres procesos cognitivos que denomina: aprehensión perceptiva, aprehensión discursiva y aprehensión operativa. La aprehensión perceptiva es la más intuitiva de los tres tipos de aprehensiones y permite la identificación simple de una configuración. La aprehensión discursiva es la acción cognitiva que permite la asociación de una configuración identificada con afirmaciones matemáticas (teoremas, definiciones, etc.), pudiendo realizarse desde la configuración hacia el discurso o viceversa, mediante un cambo de anclaje visual - discursivo o discursivo - visual. La aprehensión operativa se manifiesta al realizar modificaciones, físicas o mentales, sobre una configuración geométrica. Cuando se añaden o quitan elementos geométricos para obtener nuevas subconfiguraciones, tenemos una aprehensión operativa de cambio figural. Si las subconfiguraciones iniciales identificadas son manipuladas como las piezas de un puzzle, tenemos una aprehensión operativa de reconfiguración.
Torregrosa y Quesada (2007) y Torregrosa, Quesada y Penalva (2010) centraron su atención en la coordinación entre las aprehensiones operativas y discursivas involucradas en el proceso de resolución de problemas geométricos de probar. Este hecho, les permitió identificar características de las relaciones entre los elementos de una configuración geométrica, su asociación con diferentes afirmaciones matemáticas y el establecimiento de relaciones lógicas entre ellas que permiten el desarrollo de un razonamiento que conduce a resolver el problema. A dicho proceso lo denominaron “razonamiento configural”, con el objeto de subrayar las relaciones interactivas entre la configuración inicial (y sus posibles modificaciones) y las afirmaciones matemáticas pertinentes que conducen a un razonamiento lógico - deductivo al resolver problemas geométricos de prueba. El proceso de razonamiento configural presenta tres desenlaces: (a) “truncamiento”, cuando la coordinación entre las aprehensiones operativas y discursivas proporciona al resolutor la idea de cómo resolver el problema y permite generar un proceso deductivo que desemboca en el establecimiento de una solución al problema; (b) “conjetura sin demostración” cuando la coordinación entre aprehensiones permite establecer una solución, aunque basada en conjeturas no demostradas previamente; y (c) “bucle”, cuando el razonamiento conduce a una situación de bloqueo del proceso de resolución debido a que se establecen afirmaciones matemáticas que no son útiles para desarrollar un razonamiento lógico, de forma que los resolutores vuelven a la situación inicial una o varias veces ante la imposibilidad de avanzar hacia la solución.
El modelo razonamiento configural ha sido utilizado para analizar las respuestas de estudiantes a problemas geométricos de probar (Prior y Torregrosa, 2013; Llinares y Clemente, 2014; Clemente y Llinares, 2015; Clemente, Torregrosa y Llinares, 2015; Saorín, Torregrosa y Quesada, 2017a) y también, tras una ampliación del modelo propuesta por Torregrosa (2017), para analizar respuestas a problemas empíricos (aquellos que involucran el registro algebraico e introducen datos numéricos) geométricos (Saorín, Torregrosa y Quesada, 2017b). Dichas investigaciones ponen de manifiesto que el análisis mediante el modelo razonamiento configural puede permitirnos identificar y comprender distintos factores que pueden favorecer (o no) el desarrollo de un razonamiento lógico - deductivo que permita finalizar con éxito el proceso de resolución de problemas geométricos.
2.2. Razonamiento y discurso escrito
Entendemos razonamiento como cualquier acción que permite obtener nueva información a partir de información previa (conocida), ya sea la proporcionada por un enunciado (hipótesis iniciales) o la obtenida durante la resolución del problema. En este sentido, cuando los estudiantes resuelven por escrito problemas geométricos, el razonamiento desarrollado durante el proceso de resolución puede manifestarse a través del discurso escrito generado. De este modo, el texto escrito producido, y de forma más concreta, la forma que va adoptando a medida que se va resolviendo el problema, puede proporcionarnos información relevante acerca del razonamiento que conduce a concluirlo con éxito.
Clemente y Llinares (2015) identifican dos momentos durante el proceso de resolución de problemas de probar geométricos: (1) el proceso desarrollado hasta que el estudiante es capaz de encontrar la solución al problema mediante un razonamiento, y (2) la comunicación de la resolución mediante un discurso teórico (escrito) compuesto por afirmaciones matemáticas. Puesto que el discurso teórico refleja el razonamiento que conduce a la construcción de la prueba, las afirmaciones matemáticas que lo componen deben presentar una determinada organización, es decir, para construir una prueba es necesario organizar las afirmaciones matemáticas involucradas. En dicha organización discursiva hemos de considerar la función específica, que denominaremos estatus, que desempeñan las afirmaciones matemáticas dentro del discurso (Duval, 2016b) y si se da o no un cambio en dicha función para una misma afirmación matemática en diferentes niveles de la organización discursiva. Por tanto, el estatus de una afirmación matemática determina el lugar que ocupa dentro de la organización discursiva y por tanto la función que desarrolla.
Duval (2016b) considera que, en la construcción del discurso, además del estatus, hemos de considerar también los valores epistémicos, semánticos y lógicos de las afirmaciones matemáticas involucradas. Duval (1999) asocia el valor semántico de una afirmación con el contenido de la misma. Considera el valor epistémico como el grado de certeza o convicción asociado con una afirmación matemática, es decir, si el contenido de una afirmación es evidente, cierto, probable, etc. Dicho valor epistémico se relaciona con la base de conocimiento del resolutor, estando directamente conectado con la forma en que se comprende el contenido de una proposición. Por último, el valor lógico de una afirmación matemática es verdadero o falso, no dependiendo ni del contenido (valor semántico) ni de su comprensión (valor epistémico), ya que se obtiene mediante procesos lógico - deductivos.
2.2.1. Niveles de organización discursiva
En el presente trabajo consideraremos dos de los tres niveles de organización discursiva propuestos por Duval (1998): nivel global y nivel local. El nivel global estaría formado por el total del discurso teórico que conforma la prueba, en el que los “pasos” de razonamiento (niveles locales) que lo componen se relacionan entre sí por su conclusión (conclusiones locales). Consideramos como nivel local cada “paso” de razonamiento en que se divide el nivel global, que permite avanzar hacia la resolución del problema y en el que al menos tres afirmaciones matemáticas son organizadas en función de su estatus: hipótesis o conclusión previa; definición, teorema, propiedad o inferencia de información extraída del contexto de resolución; y conclusión local. Por tanto, cada “paso” de razonamiento se caracteriza por la organización de las afirmaciones matemáticas involucradas en función de sus estatus, pudiendo considerar como razonamiento el “paso” de premisa a conclusión a través de la aplicación de reglas (normas) del sistema lógico - deductivo dentro de cada nivel local de organización deductiva. Entendemos, por tanto, que un razonamiento deductivo conducente a probar un hecho geométrico involucra dos niveles diferenciados de organización discursiva: cómo se organizan las afirmaciones matemáticas dentro de cada “paso” deductivo y como se organización los diferentes “pasos” durante la resolución de problemas de probar.
2.2.2. Modos de expansión discursiva
Por otro lado, hemos de destacar la forma en que los estudiantes son capaces de desarrollar un proceso de argumentación que apoya la construcción de la prueba. Entendemos argumentación como el proceso utilizado para convencer, de forma razonada, a otros de la validez de las afirmaciones matemáticas establecidas que se tienen como verdaderas, y argumento como todo aquello (definiciones, teoremas, etc.) que permite validar o refutar una afirmación matemática dentro del proceso argumentativo (Duval, 1999). Por ello, podemos considerar el proceso discursivo como una forma de argumentación habitual. En particular, para el contexto en el que se desarrolla el presente trabajo, entendemos proceso discursivo como la construcción de un discurso argumentativo compuesto por afirmaciones matemáticas enlazadas entre sí de diferentes formas y que transmite el proceso de resolución del problema poniendo de relieve el razonamiento desarrollado que conduce al establecimiento de una solución. Duval (1999) denomina “modos de expansión” a las formas en que se van enlazando las afirmaciones a medida que se construye el discurso argumentativo (proceso discursivo). Considera dos modos de expansión discursiva: (1) acumulación y (2) sustitución. En la expansión por acumulación se genera un discurso a partir de información acumulada y expresada en forma de afirmaciones que no están, necesariamente, conectadas de forma lógica. Las relaciones establecidas por acumulación se relacionan entre sí sólo a nivel de contenido debido a que pertenecen al mismo contexto de resolución, pudiendo establecerse, por tanto, sin un orden lógico. Por ejemplo, tomando como referencia la Figura 1, afirmaciones matemáticas del tipo “los lados PM y PN son iguales” o “el segmento PQ es la altura del triángulo MPN ”, sólo representan información extraída de un mismo contexto de resolución que pueden establecerse en cualquier orden, siendo afirmaciones totalmente independientes entre sí, aunque relacionadas a nivel del contenido al que hacen referencia.
Por otro lado, el discurso generado por sustitución corresponde a una secuencia de afirmaciones matemáticas obtenidas, de forma progresiva y con un orden determinado y no modificable, a partir de inferencias lógicas, en el que las nuevas afirmaciones matemáticas obtenidas sustituyen a las anteriores en el razonamiento. Al ser cada afirmación consecuencia lógica de la anterior, su relación no depende de su contenido como en el caso de acumulación, sino de su estatus. Este hecho, conlleva que el discurso se organice y progrese en base a las diferencias de estatus de las afirmaciones implicadas, como por ejemplo al tomar como hipótesis de un paso de razonamiento la conclusión obtenida en otro paso deductivo anterior. Por ejemplo y utilizando la Figura 1 como referencia, si establecemos afirmaciones matemáticas del tipo “si los lados PM y PN son iguales, el triángulo es isósceles” o “si el triángulo es isósceles y el segmento PQ es bisectriz del ángulo P ˆ , corta al segmento MN en su punto medio”, observamos que cada una es consecuencia de la anterior a la que sustituye en el proceso de razonamiento, determinando que el discurso se construya como una secuencia lógica de afirmaciones establecidas siguiendo un determinado orden (y no otro).
De este modo, con base en el marco teórico expuesto y a partir de las cuestiones inicialmente planteadas, el objetivo del presente trabajo es identificar relaciones entre la forma en que los estudiantes construyen el discurso escrito (respuesta), el estatus de las afirmaciones matemáticas establecidas que lo componen y los desenlaces del razonamiento configural desarrollado que permite resolver con éxito problemas de probar en contexto geométrico.
3. Método
3.1. Participantes y contexto
En el estudio participaron 15 alumnos de 4º curso de Educación Secundaria Obligatoria (E.S.O.), con edades comprendidas entre 15 y 16 años. Puesto que los estudiantes de este nivel no estaban familiarizados con la resolución de problemas de probar geométricos, fueron agrupados en cinco grupos de tres alumnos con el objetivo de facilitarles, en la medida de lo posible, la resolución de los problemas propuestos. Además, se dedicó una sesión de 55 minutos al repaso de conceptos geométricos elementales que debían conocer de cursos anteriores en relación con las características, propiedades, clasificación y criterios de congruencia y semejanza de triángulos. Los grupos fueron identificados como G01, G02, G03, G04 y G05.
3.2. Instrumento
Los estudiantes debían resolver cuatro problemas en los que se presentaba una configuración geométrica asociada a un enunciado y se les solicitaba probar un hecho geométrico. El objetivo de los problemas era determinar cómo los estudiantes iban desarrollando procesos coordinados de aprehensiones discursivas y operativas, identificando subconfiguraciones que guiasen su razonamiento y les permitiese establecer una cadena o secuencia de argumentaciones que concluyese con la tesis a probar.
Los problemas fueron seleccionados considerando que los participantes tuviesen los conocimientos geométricos necesarios para resolverlos y la existencia de al menos una subconfiguración relevante que pudiera generar ideas para guiar el proceso de argumentación, teniendo en cuenta, además, que las posibles subconfiguraciones formasen parte de la configuración inicial, no siendo necesario la introducción de nuevos elementos (Figura 3).
Es necesario señalar que en P4 se da un solapamiento entre las subconfiguraciones relevantes a identificar, hecho que requiere acciones cognitivas más complejas para poder visualizarlas por separado. Por este motivo, se mostraron los diferentes elementos geométricos indicados en el enunciado en distintos colores, con el objetivo de “facilitar” su identificación. Entendemos, por tanto, que las configuraciones desempeñan un papel descriptivo, ya que, junto con el enunciado del problema, ayudan a contextualizar la situación geométrica planteada en cada caso y un papel heurístico al proporcionar diferentes estrategias de resolución en función de las subconfiguraciones identificadas.
3.3. Análisis
El análisis de las respuestas a los problemas se llevó a cabo en tres fases.
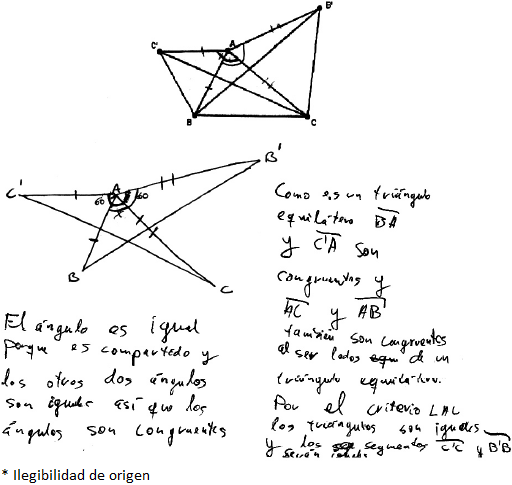
En la primera fase, realizamos la transcripción y segmentación de las respuestas escritas dadas por los estudiantes a los problemas propuestos en unidades de análisis, con el fin de identificar ciclos coordinados de aprehensiones operativas y discursivas desarrolladas durante el proceso de prueba. Consideramos como unidad de análisis cada una de las partes que componen el discurso escrito (incluidos dibujos, etiquetas o marcas en la configuración inicial, etc.) que ponen de manifiesto la identificación o utilización de propiedades, relaciones, definiciones, etc., por parte de los estudiantes durante la resolución del problema. La Figura 4 muestra la respuesta dada por G03 a P3 junto con las unidades de análisis consideradas. Dichas unidades han sido identificadas y numeradas sobre la propia respuesta de los estudiantes para facilitar su comprensión.
En la segunda fase, identificamos los desenlaces del razonamiento configural a partir de las unidades de análisis extraídas mediante el estudio de los ciclos coordinados de aprehensiones operativas y discursivas. Esta fase implica la identificación de los ciclos de reconocimiento de subconfiguraciones relevantes en el proceso de resolución y la posterior asociación de afirmaciones matemáticas que van formando el discurso escrito. En la Figura 5 se muestra, de forma esquemática, los diferentes ciclos de aprehensiones operativa / discursiva del razonamiento configural desarrollados por G03 al resolver P3. En este caso, consideramos que el razonamiento configural desemboca en conjetura sin demostración, ya que el razonamiento que permite a los estudiantes dar una solución al problema, se sustenta en dos conjeturas no demostradas con anterioridad. Es decir, deducen información nueva sobre la subconfiguración identificada (hecho geométrico a probar) a partir de afirmaciones matemáticas que no han sido demostradas previamente.
AOi: Aprehensión operativa “i”; ADi: Aprehensión discursiva “i”. Las dobles flechas representan coordinaciones entre aprehensiones
Figura 5 Razonamiento configural desarrollado por G03 al resolver P3 (Fase II)
En la tercera fase identificamos los modos de expansión del discurso puestos de manifiesto a partir de la organización del discurso escrito (respuesta) de los estudiantes. Además, consideramos el estatus otorgado a las diferentes afirmaciones matemáticas involucradas en el razonamiento que permite el establecimiento de la prueba, con el propósito de establecer relaciones entre el desarrollo del discurso, el cambio o no de estatus de las afirmaciones matemáticas implicadas (Duval, 2016b) y los desenlaces del razonamiento configural identificados.
En la Figura 6 se muestra, de forma esquemática, la organización del discurso, los modos de expansión del mismo y el estatus de las afirmaciones matemáticas involucradas en el desarrollo de la prueba para la respuesta de G03 a P3. En dicha figura podemos observar que el nivel global del discurso se compone de dos niveles locales o “pasos” de razonamiento, y que cada “paso” o nivel local está formado, a su vez, por tres afirmaciones matemáticas que se encuentran relacionadas directamente por su estatus: hipótesis (inicial) de cada “paso” de razonamiento; definición, teorema o propiedad a aplicar a la hipótesis inicial de cada “paso”; y una conclusión local establecida a partir de las dos anteriores afirmaciones.
4. Resultados
Los resultados los presentamos en función de los desenlaces del razonamiento configural identificados (Figura 7) indicando las características de los procesos discursivos desarrollados durante la resolución de los problemas asociados a dichos desenlaces. Por ello, dividiremos los resultados en tres apartados: “Truncamiento y organización discursiva”, “Conjetura sin demostración y organización discursiva” y “Bucle y organización discursiva”.
4.1. Truncamiento y organización discursiva
La Figura 8 muestra la respuesta dada a P4 por G02 cuyo razonamiento configural desemboca en truncamiento.
Sobre los lados
Figura 8 Respuesta de G02 a P4
En este caso, los estudiantes comienzan los ciclos de aprehensiones operativa /
discursiva (Figura 9) considerando la
subconfiguración formada por el triángulo ΔABC’ (AO0), a la que
asocian el concepto de triángulo equilátero (AD0). Ese hecho les
permite establecer la congruencia de los lados del triángulo indicado, en
particular, de los lados formados por los segmentos
Continúan identificando la subconfiguración formada por los triángulos ΔABB’ y
ΔACC’ (AO2) para centrar su atención en los ángulos con vértice en el
punto “A” que se forman en ambos triángulos por separado, es
decir, en los ángulos
Entendemos que el razonamiento configural desemboca en truncamiento cuando los ciclos de aprehensiones operativa / discursiva proporcionan la “idea” de cómo se resuelve el problema a los estudiantes, conduciéndoles a establecer una solución válida. En este sentido, los estudiantes son conscientes que, si demuestran la congruencia de los triángulos ΔABB’ y ΔACC’, de forma implícita queda demostrada la tesis del problema, finalizando por tanto el razonamiento configural una vez establecen la congruencia de los triángulos implicados en el razonamiento. Por ello, el razonamiento configural desemboca en truncamiento, ya que ha proporcionado la “idea” que permite a los estudiantes resolver el problema.
En relación a la organización del discurso (Figura 10), observamos que el nivel global se compone de cinco niveles o pasos locales.
Los estudiantes desarrollan los dos primeros pasos del razonamiento de forma análoga: consideran como hipótesis iniciales (hipótesis (1) e hipótesis (2)) los datos proporcionados por el enunciado: “los triángulos ΔABC’ y ΔAB’C son equiláteros”. Tras esto, los identifican en la configuración inicial para aplicarles la definición de triángulo equilátero (los lados y los ángulos de los triángulos equiláteros son congruentes) y concluyen cada paso (conclusión local (1) y conclusión local (2)) estableciendo la congruencia de dos de los lados de los triángulos identificados.
En el tercer paso consideran como hipótesis inicial (hipótesis (3)) la información desprendida de la subconfiguración relevante identificada con el objetivo de encontrar condiciones que permitan obtener el valor de los ángulos ∡CAC’ y ∡ BAB’ (pertenecientes a los triángulos ΔABB’ y ΔACC’). Para ello, vuelven a considerar el concepto de triángulo equilátero (dato proporcionado por el enunciado) y lo aplican a la subconfiguración para obtener que los ángulos ∡CAC’ y ∡BAB’ miden 60º más el espacio que comparten (que denominan “x”). Este hecho, les permite establecer la congruencia de los ángulos indicados (conclusión local (3)).
En el cuarto paso, las hipótesis iniciales consideradas son las congruencias de
los segmentos
En el quinto paso, la hipótesis inicial (hipótesis (5)) es la congruencia de los
triángulos ΔABB’ y ΔACC’ (conclusión local (4)). Al considerar que ambos
triángulos son congruentes, “infieren” que tienen todos sus lados y ángulos
correspondientes son también congruentes, hecho que les permite concluir que los
segmentos
La manera de proceder de los estudiantes respecto a los modos de expansión discursiva en este caso, muestra que los tres primeros “pasos” del razonamiento se desarrollan de forma similar. Al inicio del “paso 1” consideran los datos (hipótesis iniciales) proporcionados por el enunciado, por lo que comienzan identificando el triángulo ΔABC’ al que asocian el concepto de triángulo equilátero. Este hecho les permite “acumular” información (de forma implícita) referente al triángulo considerado, en particular, que tiene todos sus lados iguales. Una vez disponen de dicha información, la congruencia de dos de sus lados en particular, es consecuencia lógica del hecho geométrico considerado (triángulo ΔABC’ es equilátero). Por ello, entendemos que en el “paso 1” se dan los modos de “acumulación” (a partir de las hipótesis iniciales) y “sustitución” (que permite establecer la conclusión local).
De forma análoga, en el “paso 2”, identifican el triángulo ΔAB’C al que aplican el concepto de triángulo equilátero (al considerar los datos proporcionados por el enunciado) que les permite establecer (de forma implícita) la congruencia de sus lados, que les permite concluir el “paso” considerando la congruencia de dos de sus lados en particular. Por tanto, en el “paso 2” se dan la “acumulación” y la “sustitución”.
En el “paso 3” los estudiantes comienzan extrayendo información a partir de la subconfiguración relevante identificada (formada por los triángulos ΔABB’ y ΔACC’) con el fin de obtener el valor de los ángulos ∡CAC’ y ∡ BAB’. Una vez consiguen “acumular” la información suficiente para ello, la utilizan de forma lógica para establecer la congruencia de ambos ángulos y establecer la conclusión del “paso 3”, dándose, por tanto, los modos de “acumulación” y “sustitución”.
En el “paso 4”, los estudiantes no comienzan “acumulando” información extraída del enunciado o de alguna subconfiguración identificada, sino que “reutilizan” y “ordenan” la información generada en los pasos anteriores (conclusiones locales (1), (2) y (3)), cambiando su estatus (y por ello su valor lógico) al considerarlas como hipótesis del criterio de congruencia de triángulos a aplicar. Así, establecen la congruencia de los triángulos ΔABB’ y ΔACC’ tras aplicar el criterio L-A-L, por lo que la conclusión es consecuencia lógica de los hechos geométricos generados previamente en otros pasos del razonamiento y la aplicación de un criterio de congruencia de triángulos en particular. Por ello, en el “paso 4” se da únicamente el modo de sustitución.
El “paso 5” se desarrolla de forma similar al “paso 4”. Los estudiantes vuelven a establecer relaciones lógicas a partir de la conclusión local (4) (congruencia de los triángulos ΔABB’ y ΔACC’), cambiando su estatus al de hipótesis (5) para finalizar en una afirmación matemática con estatus de conclusión local (5), y, además, en este caso, de conclusión final. De esta manera, en los “pasos 4 y 5” se da únicamente el modo de sustitución, ya que el discurso sigue un orden lógico, en el que cada afirmación es consecuencia lógica de la anterior y que desemboca en la tesis solicitada.
4.2. Conjetura sin demostración y organización discursiva
Para ilustrar los resultados obtenidos para el desenlace conjetura sin demostración, reutilizaremos el ejemplo mostrado en el apartado de análisis (Figura 4).
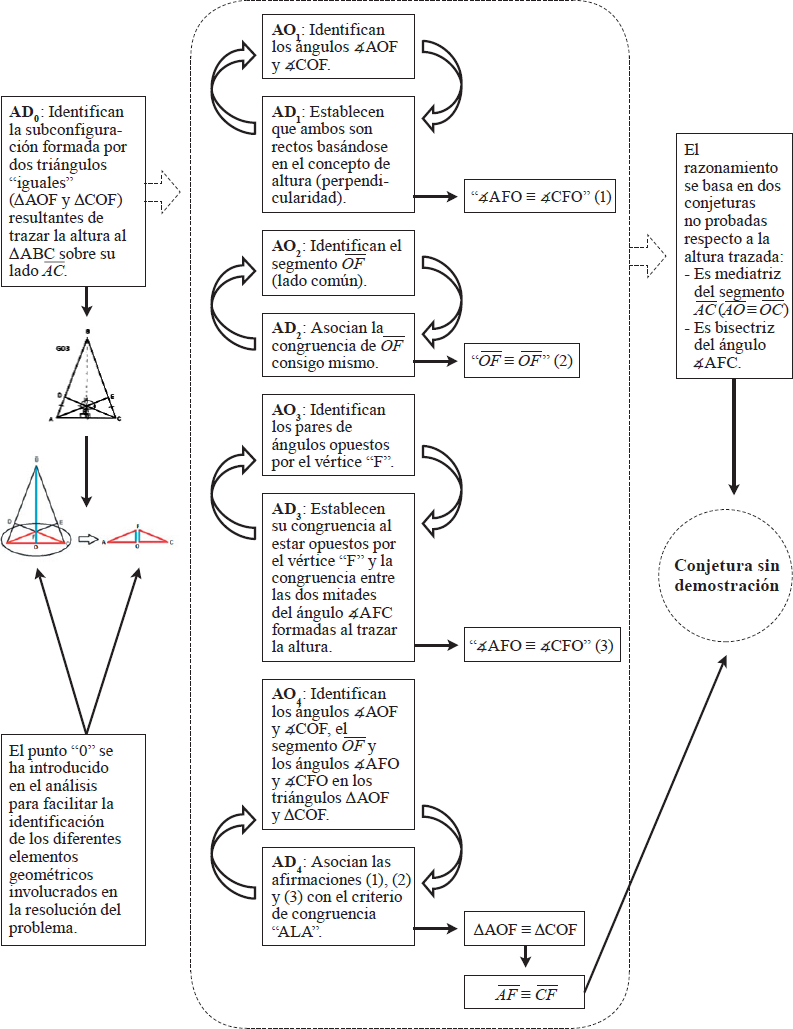
Los estudiantes comienzan el razonamiento configural (Figura 5) dibujando la altura del triángulo ∆ABC sobre el
segmento
Para el caso descrito, aunque los estudiantes son capaces de probar el hecho
geométrico que se les solicitaba en el problema, fundamentan el razonamiento
desarrollado en dos conjeturas no demostradas previamente: (1) suponen que la
altura es mediatriz del segmento
Respecto al discurso escrito (Figura 6), identificamos que el nivel global del proceso discursivo se compone de dos niveles locales (pasos). Los estudiantes no consideran en ningún momento los datos (hipótesis) proporcionados por el enunciado. Comienzan el primer paso extrayendo información de la subconfiguración relevante identificada con el fin de encontrar condiciones a verificar que les permita aplicar un criterio de congruencia de triángulos. Esta información extraída es utilizada en forma de tres afirmaciones matemáticas o condiciones que serán utilizadas para aplicar un criterio de congruencia de triángulo (definición / teorema / propiedad (1)). Dichas condiciones, debido al trazado inicial de la altura del triángulo ∆ABC en la configuración inicial, se hacen relativamente “evidentes” y fácilmente verificables considerando las dos conjeturas anteriormente descritas. Este hecho les permite aplicar el criterio de congruencia “A-L-A” (ángulo - lado - ángulo), que posibilita al grupo concluir (localmente), que los dos triángulos considerados al inicio del paso son congruentes.
En el segundo paso de razonamiento, la conclusión local (1) (congruencia de los
triángulos ΔAOF y ΔCOF) pasa a desempeñar el papel de hipótesis inicial (2), a
partir de la que “infieren” que en dos triángulos congruentes, todos sus lados y
ángulos correspondientes, son congruentes también, concluyendo que los segmentos
La manera de proceder de los estudiantes en este caso, pone de manifiesto que los alumnos “acumulan” información al inicio del “paso 1”, ya que extraen información (condiciones a verificar) a partir de la subconfiguración identificada, sin un orden lógico, únicamente con el objeto de poder aplicar un criterio de congruencia (aunque fundamentado en conjeturas no demostradas). Tras esto, los estudiantes ordenan la información obtenida y consideran aquella información que les permite aplicar el criterio de congruencia de triángulos identificado (condiciones verificadas), por lo que se da un cambio del estatus lógico de la información utilizada para aplicar dicho criterio de congruencia, dándose el modo de sustitución. Esto es así ya que establecen la congruencia de los triángulos identificados a partir de la aplicación del criterio A-L-A, es decir, la conclusión establecida es consecuencia lógica de los hechos geométricos (condiciones verificadas) generados previamente (aunque basados en conjeturas no demostradas previamente) y el criterio de congruencia aplicado, dándose un orden lógico y secuencial del discurso. Por ello, en el “paso 1” se dan los modos de acumulación y sustitución.
En el “paso 2”, únicamente se da el modo de sustitución, ya que sólo se establecen relaciones lógicas a partir de la información generada en el “paso 1” (congruencia de triángulos) para finalizar en una afirmación con status de conclusión local (2) (lados congruentes). De esta forma, la expansión del discurso por sustitución, se realiza con un orden lógico, donde cada afirmación involucrada es consecuencia de la anterior, concluyendo en la tesis solicitada.
4.3. Bucle y organización discursiva
En la Figura 11 mostramos la respuesta de G01 a P4 cuyo razonamiento configural desemboca en “bucle”.
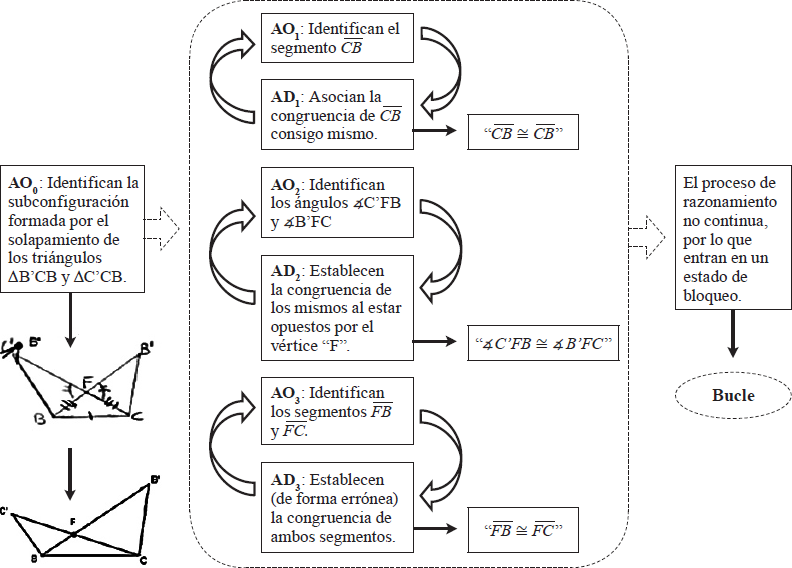
Los estudiantes inician el razonamiento configural identificando y dibujando la subconfiguración formada por los triángulos ΔB’CB y C’CB (AO0) (Figura 12). A partir de la subconfiguración detectada, realizan tres ciclos coordinados de aprehensiones operativa / discursiva con la finalidad de extraer información de la misma.
En el primer ciclo (Figura 12)
(AO1 / AD1), consideran el segmento
En el segundo ciclo (AO2/AD2), consideran los ángulos ∡C’FB y ∡B’FC opuestos por el vértice “F ”, asociándolos con la propiedad de que ángulos opuestos por el vértice son congruentes, estableciendo la congruencia de los ángulos considerados.
Respecto al tercer ciclo (AO3/AD3), consideran los
segmentos
Una vez establecen las tres afirmaciones matemáticas indicadas, no continúan con
la resolución del problema, entrando en una situación de bloqueo, por lo que el
razonamiento configural desemboca en “bucle”. Los estudiantes establecen una
afirmación matemática errónea (“
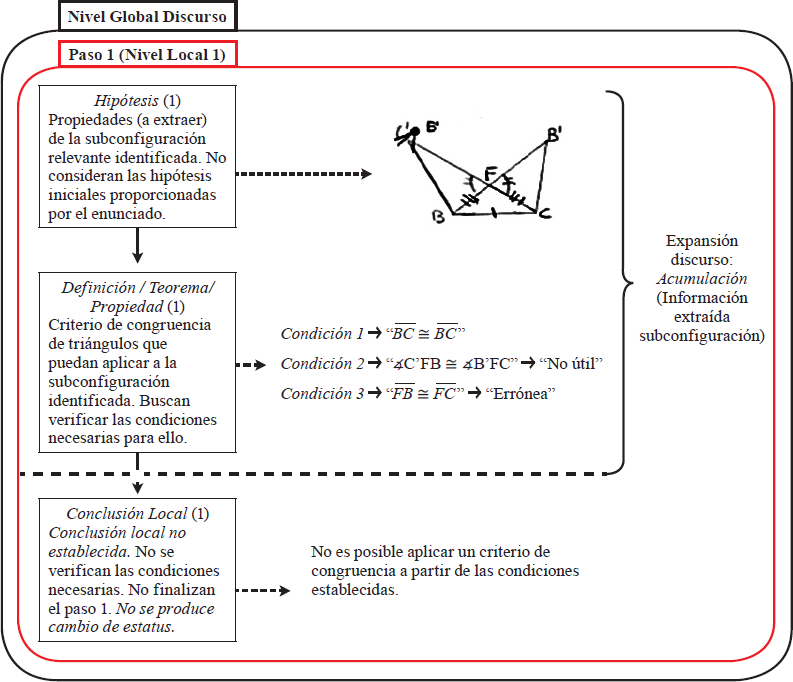
Por otro lado, el nivel global de la organización del discurso (Figura 13) se solapa con el nivel local, ya que encontramos un único “paso” en el discurso generado.
Esto se debe a que las afirmaciones matemáticas establecidas se sitúan dentro del mismo nivel local de organización del discurso. Como estas afirmaciones no verifican ningún criterio de congruencia que puedan aplicar a la subconfiguración identificada, los estudiantes no concluyen el “paso” iniciado, no generando más discurso escrito. Por tanto, no se produce un cambio en el estatus operativo de las afirmaciones involucradas, ya que no son capaces de finalizar el “paso” analizado con una afirmación matemática con estatus de “conclusión local” a partir de las afirmaciones con estatus de “hipótesis”.
Respecto al modo de expansión del discurso, encontramos que solo se da el modo de acumulación, ya que los estudiantes extraen información de la subconfiguración identificada sin importar la que sea, con el objeto de aplicar un criterio de congruencia. De hecho, de esa información “acumulada” en forma de condiciones a verificar, una de ellas es errónea y la otra no es útil, por lo que no pueden aplicarse a ningún criterio de congruencia.
5. Discusión y conclusiones
Nuestro objetivo es analizar el cambio de estatus de las diferentes afirmaciones matemáticas que componen el proceso discursivo en la resolución de problemas geométricos de probar. En particular, cómo se desarrolla y organiza el discurso escrito (respuesta) que permite comunicar la solución al problema con el fin de identificar relaciones con los desenlaces del razonamiento configural.
El razonamiento configural desemboca en truncamiento cuando los ciclos coordinados de aprehensiones operativas y discursivas permiten a los estudiantes “acceder” a la forma en que se resuelve el problema de forma lógico - deductiva. Los resultados ponen de manifiesto que una vez cesan estos ciclos, los estudiantes han establecido las afirmaciones matemáticas que permiten resolver el problema. En ese momento, los estudiantes dejan de considerar la/s configuración/es geométrica/s identificada/s para finalizar el problema estableciendo relaciones lógicas entre las afirmaciones matemáticas involucradas, desarrollando, por tanto, en la parte final del discurso escrito, un razonamiento independiente de cualquier subconfiguración geométrica identificada (Duval, 2016a), que permite a los estudiantes probar la tesis planteada. Por este motivo, consideramos que el papel de la configuración inicial va cambiando, desempeñando una función heurística (proporcionar estrategias de resolución en función de las subconfiguraciones identificadas) durante el razonamiento configural, para pasar a un papel sinóptico (mostrar elementos geométricos relacionados entre sí de forma conjunta) una vez cesan los ciclos entre aprehensiones.
A pesar de lo anterior, se nos plantea cierta ambigüedad para detectar con precisión el momento en el que se produce el truncamiento. En el caso mostrado en la Figura 9, los estudiantes una vez han establecido las tres afirmaciones que permiten resolver el problema, los ciclos del razonamiento configural cesan, puesto que las afirmaciones matemáticas establecidas son suficientes para probar el hecho geométrico solicitado en el problema. Sin embargo, el momento en el que los estudiantes son “conscientes” de cómo resolver el problema podría darse, por ejemplo, en el tercer ciclo del razonamiento configural, ya que el hecho de establecer las afirmaciones matemáticas (1) y (2) (Figura 9) a partir de las subconfiguraciones identificadas puede, de forma implícita o indirecta, hacer “visible” la forma de resolver el problema antes de establecer la afirmación matemática (3) (Figura 9) necesaria para aplicar el criterio de congruencia de triángulos. Por tanto, los ciclos coordinados de aprehensiones operativas y discursivas, pueden proporcionar a los estudiantes “la idea” que permite resolver el problema de forma lógico - deductiva, incluso antes de establecer todas las condiciones o relaciones necesarias que permitan finalizar el proceso de prueba. Este hecho hace menos evidente y claro el momento en el que se da el truncamiento en problemas geométricos de probar que en problemas geométricos empíricos (Saorín, Torregrosa y Quesada, 2017b).
Para los desenlaces conjetura sin demostración y bucle mostrados, observamos que los estudiantes no consideran las hipótesis iniciales proporcionadas por el enunciado. Este hecho parece estar relacionado con la subconfiguración relevante considerada en el proceso de resolución del problema. En el desenlace “bucle” (Figura 12) los estudiantes consideran la subconfiguración complementaria a la subconfiguración relevante necesaria para resolver el problema, que les lleva a establecer una afirmación matemática errónea “FB ≅ FC ” y otra sin utilidad “∡C’FB y ∡B’FC ”, que les conduce a una situación de bloqueo (bucle) del razonamiento configural al no poder aplicar ningún criterio de congruencia de triángulos. En este caso, la subconfiguración está formada por dos triángulos que presentan características más “familiares” para los estudiantes que los que componen la subconfiguración relevante que permiten solucionar el problema. En el desenlace conjetura sin demostración (Figura 5) los estudiantes trazan la altura al triángulo inicial, que les permite identificar los triángulos ΔAOF y ΔCOF y establecer dos conjeturas sobre las que basan su razonamiento. Aquí, es evidente que asocian el triángulo inicial con la representación “estándar” de triángulo isósceles, que les lleva a trazar su altura y establecer dos conjeturas válidas para este tipo de triángulos, aunque no hayan sido demostradas previamente. Por tanto, se hace patente la influencia de las configuraciones “familiares” o “prototípicas” (Clemente, Torregrosa y Llinares, 2015; Saorín, Torregrosa y Quesada, 2017b) en la identificación de subconfiguraciones relevantes, que puede conducir a un razonamiento no basado en las condiciones (datos) impuestas por el enunciado y, por tanto, desembocar en una solución no válida (o errónea) o en una situación de bloqueo. Este hecho pone de manifiesto que los estudiantes serán capaces de iniciar el razonamiento configural con mayor facilidad al identificar configuraciones relacionadas con los conocimientos geométricos previamente adquiridos (Gal, Linchevski, 2010).
5.1. La necesidad del cambio de estatus en el proceso de prueba
Los resultados sugieren que cuando se produce un cambio de status de las afirmaciones matemáticas que componen el razonamiento, el razonamiento configural desemboca en “truncamiento” o “conjetura sin demostración”. Este hecho permite a los estudiantes dar una solución al problema, independientemente de si ésta es válida, basada en conjeturas sin demostrar o errónea. Por contra, cuando el cambio de estatus de las afirmaciones matemáticas no se da, el razonamiento desarrollado entra en una situación de bloqueo (bucle), no permitiendo a los estudiantes emitir solución alguna al problema.
En el caso del truncamiento mostrado, tenemos que en los “pasos 1, 2 y 3” (Figura 10) del razonamiento, los estudiantes establecen tres afirmaciones matemáticas válidas con estatus de conclusión local. Tras esto, otorgan a las conclusiones locales (1), (2) y (3) el rol de hipótesis iniciales del “paso 4” (Figura 10) del razonamiento. Este cambio de estatus de conclusión local (1), (2) y (3) a hipótesis (4) iniciales, les permite iniciar un nuevo paso de razonamiento que finaliza con otra afirmación con estatus de conclusión local (4). Nuevamente, generan otro “paso” de razonamiento (“paso 5”) a partir de un nuevo cambio de estatus de la afirmación con estatus de conclusión local (4), que les permite establecer una nueva afirmación con estatus de conclusión local (5), que además es la solución (válida) al problema.
Para el caso de conjetura sin demostración (Figura 6), observamos que el “paso 1” de razonamiento comienza con la identificación de una subconfiguración geométrica que permite a los estudiantes inferir tres hechos geométricos (dos de ellos no demostrados previamente) que son utilizados como hipótesis iniciales (1). Esta información extraída es utilizada en forma de tres afirmaciones matemáticas o condiciones que serán utilizadas para aplicar un criterio de congruencia de triángulos que finaliza con una afirmación con estatus de conclusión local (1). Tras esto, otorgan a la conclusión local (1) el papel de hipótesis del “paso 2”, dotando a dicha afirmación de un estatus diferente a la inicial. Este cambio de conclusión local a hipótesis, les permite generar un nuevo paso de razonamiento que finaliza con otra afirmación con estatus de conclusión local (2), que además es la conclusión final (no válida) al problema.
Por ello, el lugar que ocupan las afirmaciones matemáticas en la organización discursiva, viene determinado por sus estatus (hipótesis, definición / teorema / propiedad y conclusión), es decir, por el papel particular que desempeñan en cada “paso” del razonamiento. Esto implica que, para construir una prueba, es necesario organizar las afirmaciones matemáticas dentro de cada paso deductivo según la secuencia indicada. Es decir, en cada “paso” de razonamiento se articulan las diferentes afirmaciones matemáticas implicadas atendiendo a su estatus, hecho que lleva a la “transformación” de las hipótesis iniciales de cada “paso” de razonamiento en conclusiones locales con valor lógico mediante un cambio de estatus, realizado a partir de la consideración de propiedades, definiciones, teoremas o inferencia de información (en el contexto del problema).
Por otro lado, el cambio de estatus de las afirmaciones involucradas en el proceso de prueba es una condición necesaria para que el razonamiento configural permita establecer una solución válida. Sin embargo, no es una condición suficiente, tal y como se refleja en el caso de la conjetura sin demostración (Figura 6), en el que las afirmaciones establecidas a partir de las subconfiguraciones identificadas permiten la construcción de un proceso deductivo que desemboca en una conclusión, aunque no válida, ya que se basa en afirmaciones no demostradas previamente. Por tanto, el cambio de estatus de las afirmaciones involucradas en el desarrollo de la prueba es una condición necesaria, pero no suficiente, para que el razonamiento configural desemboque en una solución válida, no basada en conjeturas sin demostrar. Se hace patente de nuevo, la influencia ejercida por la subconfiguración relevante identificada (Mesquita, 1998; Clemente y Llinares, 2015; Llinares y Clemente, 2014; Clemente, Torregrosa y Llinares, 2015; Clemente, Llinares y Torregrosa, 2017; Saorín, Torregrosa y Quesada, 2017b) en el proceso de prueba. Lo que sí está directamente relacionado con el cambio de estatus, es que permite el desarrollo de un proceso lógico - deductivo en el que los estudiantes son capaces de dotar de diferentes roles a los hechos geométricos involucrados en el proceso de prueba, aunque pueda estar fundamentado en afirmaciones anteriores erróneas o no válidas en el contexto del problema.
5.2. Construcción del discurso que comunica la prueba
Los resultados evidencian que las afirmaciones establecidas mediante el modo de “acumulación” son enunciadas con el objetivo de extraer información relacionada con el problema a resolver, ya sea a partir del enunciado (hipótesis iniciales) o inferida de la subconfiguración identificada. Estas afirmaciones no siguen un orden preestablecido, pudiendo ser establecidas en cualquier orden al estar relacionadas solo por su contenido, por lo que no influyen en el desenlace del razonamiento desarrollado a posteriori, presentando únicamente valores epistémicos y semánticos. Son afirmaciones matemáticas utilizadas como argumentos dentro del “contexto” de resolución de los problemas. De esta forma, podríamos asociar el desenlace bucle del razonamiento configural con el hecho de que se manifieste únicamente el modo de acumulación en un razonamiento, ya que las características descritas para las afirmaciones enunciadas mediante este modo discursivo, describen a la perfección las de las afirmaciones establecidas en la resolución de P4 por parte de G01 (Figura 13), cuyo razonamiento configural finaliza en bucle.
Por otro lado, el modo de “sustitución” muestra la utilización de afirmaciones matemáticas que forman parte de un proceso de razonamiento lógico - deductivo que conduce a los estudiantes a dar una solución al problema (correcta o no), manifestándose en los desenlaces truncamiento (Figuras 10) y conjetura sin demostración del razonamiento configural (Figura 6). En ambos casos, el proceso de construcción del discurso sucede de forma análoga, a pesar de que en el caso del desenlace conjetura sin demostración presentado, el razonamiento desarrollado se basa en conjeturas no demostradas previamente. Cada “paso” de razonamiento se inicia mediante una “fase de acumulación” de información que permite establecer afirmaciones con valores epistémicos y semánticos, para concluirlo con una “fase de sustitución”, en el que las afirmaciones adquieren, además, un valor lógico. En aquellos “pasos” en los que se dan ambos modos de expansión discursiva, los estudiantes siguen considerando la subconfiguración identificada, a pesar de que las conclusiones locales se obtienen mediante procesos lógico - deductivos. Una vez los estudiantes, poseen toda la información necesaria (en forma de conclusiones locales) para resolver el problema, inician “pasos” de razonamiento en los que se manifiesta únicamente el modo de sustitución. En estos “pasos”, las hipótesis iniciales no provienen de la “acumulación” de información inferida de la subconfiguración relevante identificada, sino que son afirmaciones matemáticas dotadas de un valor lógico en “pasos” anteriores, en las que se produce un cambio de estatus que permite continuar con el razonamiento conducente a obtener una solución al problema. Tal y como indica Duval (1999), se da un proceso de encadenamiento por reutilización de afirmaciones matemáticas, hecho que garantiza la continuidad entre dos pasos de un razonamiento lógico - deductivo. Por ello, consideramos que los valores semánticos y epistémicos de las afirmaciones matemáticas establecidas pueden vincularse al modo de acumulación, del mismo modo que el valor lógico puede vincularse al modo de sustitución, en consonancia con los resultados de Robotti (2012).
Por tanto, y como respuesta a las cuestiones planteadas al inicio del estudio, consideramos que para generar un razonamiento lógico - deductivo que finalice en una solución válida a problemas de prueba en contexto geométrico, es necesario que:
(1) Cesen los ciclos de aprehensiones operativas y discursivas (finalice el razonamiento configural) para dar paso a un razonamiento lógico-deductivo que permite finalizar el razonamiento desarrollado con la prueba requerida, generando un razonamiento independiente de cualquier proceso de visualización. Este hecho indica, además, que el papel de la configuración inicial cambia, ya que inicialmente desempeña un papel heurístico y cuando finaliza el razonamiento configural pasa a desempeñar un papel sinóptico.
(2) Se produzca un cambio en el estatus de las afirmaciones matemáticas involucradas en el razonamiento conducente a la prueba que permita, a una afirmación matemática, desempeñar diferentes roles en el proceso de razonamiento, independientemente de si es obtenida como resultado del proceso de coordinación entre aprehensiones (razonamiento configural) o bien, de forma lógico - deductiva a partir de otras afirmaciones anteriormente demostradas.
(3) El discurso escrito (entendido como proceso argumentativo) que permite comunicar la solución al problema, se desarrolle desde el modo de acumulación al modo de sustitución. En los primeros niveles locales encontramos ciclos de acumulación - sustitución que permiten establecer afirmaciones matemáticas a partir del contexto de resolución. Una vez se obtienen las afirmaciones necesarias para resolver el problema, los siguientes niveles locales se desarrollan por sustitución, ya que los estudiantes “reutilizan” dichas afirmaciones para concluir el problema mediante un proceso lógico - deductivo. Así, el nivel global de la organización discursiva, comienza con la acumulación de información (inicio del primer nivel local del discurso) que desencadena el proceso de razonamiento para finalizar con la comunicación de la solución (conclusión del último nivel local del discurso) mediante el modo de sustitución.
Sin embargo, éstas condiciones pueden no ser suficientes, ya que la influencia de la subconfiguración relevante identificada se hace patente en el proceso de razonamiento desarrollado. En este sentido, la argumentación desempeña un papel importante como enlace entre los diferentes ciclos de aprehensiones del razonamiento configural y el discurso escrito generado al resolver problemas geométricos de prueba, hecho que sería interesante desarrollar en trabajos posteriores.











 nova página do texto(beta)
nova página do texto(beta)