1. Introducción

Las analogías están presentes en discursos que pretenden enseñar algún concepto nuevo y así constituyen un recurso utilizado para comunicar ideas o experiencias nuevas (^{Curtis y Reigeluth, 1984}; ^{Godoy, 2002}) al relacionarlas con conocimientos existentes de modo que dicha relación sea significativa. El uso de la analogía es recurrente en nuestra forma de comunicación y no es ajeno al discurso de los profesores, quienes muchas veces producen y usan analogías de manera inconsciente durante sus clases (e.g., ^{Glynn, 1994}; ^{Glynn, Law, Gibson y Hawkins, 1994}; ^{Felipe, Gallareta y Merino, 2006}; ^{Ünver, 2009}).

En el caso de la enseñanza de las ciencias, ^{Dagher (1994)} señala que técnicas de abstracción como las analogías han contribuido al desarrollo del pensamiento científico y a la construcción del conocimiento, al otorgarle un lugar importante en el proceso de enseñanza-aprendizaje. En esta línea, se han conducido diversos estudios sobre la analogía como una herramienta para la enseñanza (e.g., ^{Duit, 1991}; ^{González, 2005}; ^{Oliva, 2008}), destacando sus potencialidades en el desarrollo del conocimiento y pensamiento creativo en los estudiantes debido a la posibilidad de describir nuevas ideas y replantear problemas (^{Polya, 1989}; ^{Pérez, 2007}). Otros estudios indagan en las características de las analogías, su composición y aspectos que se deben considerar cuando éstas se emplean en la enseñanza (e.g., ^{Godoy, 2002}; ^{Oliva, Aragón, Mateo y Bonat, 2001}; ^{Oliva, 2008}).

La revisión de la literatura revela la importancia de la analogía en la enseñanza de la matemática como método científico o como heurística para la resolución de problemas (^{Cruz, García, Rojas y Sigarreta, 2016}; ^{Novick y Holyoak, 1991}; ^{Polya, 1989}; ^{Walter y Baros, 2011}). Los estudios realizados se centran, principalmente, en el aprendizaje de los estudiantes (e.g., ^{Adams y Eliot, 2013}) o en su uso para la resolución de problemas (e.g., ^{Cruz et al., 2016}; ^{Polya, 1989}), y aunque se muestra como estrategia de enseñanza (e.g., ^{Cuya, Fortes y Nivera, 2017}; ^{Sarina y Namukasa, 2010}), no se profundiza en el conocimiento profesional del profesor de matemáticas.

En estas investigaciones se destaca la relevancia de que el profesor use analogías a la vez que promueva en sus estudiantes razonamientos por analogía (e.g., ^{Cuya et al., 2017}). Por ejemplo, reconocer analogía entre el rectángulo y el paralelepípedo rectangular o entre el área del rectángulo y el volumen del paralelepípedo rectangular como analogías dentro del cuerpo matemático, intra-matemáticas, o conocer la comparación entre el ajedrez y la resolución de ecuaciones (^{Adams y Eliot, 2017}) como analogía extra-matemática. Asimismo, como ^{Lakoff y Núñez (2000)} distinguen dos tipos de metáforas conceptuales en matemáticas, es posible hacer la misma distinción para las analogías: aquellas que tienen dominio de partida y llegada en la matemática (linking) y aquellas que tienen el dominio de llegada en la matemática y el de partida fuera de ella (grounding). El interés de este artículo reside en las analogías del segundo tipo, donde el dominio de partida es extra-matemático.

Dada la relevancia de la analogía en diversos ámbitos, ésta ha sido objeto de estudio desde diferentes perspectivas. Así, desde las ciencias cognitivas, comprender los procesos cognitivos implicados en el descubrimiento, la construcción y el uso de analogías es un objetivo importante de la investigación actual en esta área y genera muchas preguntas importantes (^{Bartha, 2016}), por ejemplo, acerca de cómo identifican los humanos las analogías. Desde el ámbito de la Didáctica de la Matemática, también se han planteado preguntas relevantes al respecto: ¿cómo influyen las analogías y las metáforas en la formación del concepto matemático?, ¿cómo el uso de las analogías se relaciona con el aprendizaje de los estudiantes? O la pregunta que rige esta investigación: ¿qué conocimientos pone en juego el profesor de matemáticas al usar una analogía? Si bien existen investigaciones que abordan el uso de analogías y metáforas en la enseñanza de la matemática (e.g., ^{Font y Acevedo, 2003}; ^{Sarina y Namukasa, 2010}) y otras que mencionan el conocimiento de la analogía en el estudio del conocimiento profesional del profesor de matemáticas (e.g., ^{Rowland, Huckstep y waites, 2005}; ^{Zakaryan et al., 2018}), hacen falta estudios que indaguen en el conocimiento del profesor de matemáticas sobre analogías en general.

El conocimiento sobre analogías y su uso es considerado parte del conocimiento del profesor desde la propuesta de ^{Shulman (1986)} en el conocimiento pedagógico del contenido (PCK), refiriéndose a la potencialidad que pueden tener éstas en la enseñanza de un tema. Por su parte, ^{Rowland et al., (2005)} dentro de Knowlegde Quartet, en la categoría trasformación que aborda aspectos del conocimiento del profesor en la acción, consideran las analogías en las formas en las cuales el conocimiento a enseñar es trasformado y desarrollado durante la planificación y la enseñanza, haciéndolo accesible a los alumnos. En la misma línea, ^{Carrillo et al. (2014)} incluyen el conocimiento sobre las analogías en el conocimiento de la enseñanza de las matemáticas en el PCK del modelo del Conocimiento Especializado del Profesor de Matemáticas (MTSK)¹ , de este modo, se considera que este conocimiento, junto con otros tipos de conocimiento del modelo, son propios de un profesor de matemáticas y son sólo útiles a él, de ahí el carácter especializado del mismo.

Por otra parte, investigar acerca del conocimiento del profesor sobre el concepto de función, su enseñanza y su aprendizaje es importante dado que es uno de los conceptos más relevantes en matemáticas y ha sido clave en el desarrollo de la matemática en general (^{Ponte, 1992}). Tanto el currículum escolar como los programas de formación de profesores de matemáticas incluyen ampliamente este concepto, particularmente en Chile, se destinan unidades completas a su estudio (Ministerio de Educación ^{[MINEDUC], 2016}). En cuanto a su presencia en el currículum escolar chileno, se sugiere ver la función como una máquina, además señala que la incorporación de representaciones, metáforas y analogías completa el proceso de aprendizaje de los estudiantes y favorece la compresión de los conceptos (^{MINEDUC, 2016}). Este acercamiento promueve la comprensión de la función de modo operacional (^{Sfard, 1991}), que consiste en describirla como un conjunto de procesos computacionales o calculatorios; la perspectiva estructural de la función como un conjunto de pares ordenados queda fuera del alcance del currículum.

Teniendo en consideración los antecedentes expuestos, en este artículo presentamos resultados de una investigación sobre el conocimiento especializado de dos profesores de secundaria al usar la analogía en la enseñanza del concepto de función con el fin de avanzar en la comprensión de su conocimiento al respecto y con el propósito de contribuir a la mejora de la formación inicial y continua de los profesores de matemáticas.

2. La analogía como recurso para la enseñanza

Un recurso utilizado en el proceso de enseñanza y aprendizaje de las ciencias es la comparación de objetos o estructuras nuevas con elementos conocidos por los estudiantes, tomando el conocimiento que poseen los estudiantes como base y referente para el nuevo conocimiento (e.g., ^{Oliva, 2008}).

Pero antes de considerarse como un recurso para la enseñanza, las analogías han sido ampliamente reconocidas por desempeñar un importante papel heurístico, como ayuda al descubrimiento, en una amplia variedad de entornos y con un éxito considerable, para generar conocimiento y formular posibles soluciones a los problemas (^{Bartha, 2016}). Según ^{Beuchot (2017)}, el concepto de analogía llega a estudiarse en filosofía debido al impulso que le asignan los pitagóricos en el área de las matemáticas. El autor señala que el estudio de este concepto cobra relevancia en la Modernidad donde decae y posteriormente vuelve a recuperarse por los pensadores románticos, entre otros+. Recientemente, su recuperación se basó en la necesidad filosófica de contar con un elemento que tuviera la “sensibilidad para lo que no es exacto, pero que tampoco requiera que sea ambiguo” (p. 6).

Se entiende por analogía la relación de comparación de estructuras que se establece entre dos dominios: uno familiar (llamado dominio fuente o análogo) y uno no familiar (llamado objetivo).

An analogy refers to comparisons of structures between domains. An analogy is a relation between parts of the structures of two conceptual domains and may be viewed as a comparison statement on the grounds that these structures bear some resemblance to one another (^{Treagust, Duit, Joslin y Lindauer, 1992, p. 413}).

De este modo, una analogía no pretende ser una comparación total y exhaustiva entre ambas estructuras, sino que destaca ciertos aspectos conocidos en el dominio fuente para que éstos se transfieran al dominio objetivo. Esto conlleva un proceso de selección de características del dominio fuente que se quieran resaltar en el dominio objetivo y, según ^{González (2005)}, siempre existirán diferencias estructurales entre los dominios fuente y objetivo. De acuerdo con ^{Bartha (2016)}, en la práctica especificamos una analogía simplemente al indicar las similitudes más significativas (y algunas veces las diferencias) y al manifestar las características de la analogía que ^{Beuchot (2017)} señala como univocidad y equivocidad, es decir, sin mostrar una comparación exacta que tampoco dé espacio a la ambigüedad.

Por otra parte, la teoría estructuralista más influyente, la teoría de mapeo de estructuras (^{Gentner, 1983}), evalúa las analogías sobre bases puramente estructurales. Desde esta perspectiva, las analogías son sobre relaciones, más que simples características, es decir, son las propiedades estructurales (las interrelaciones entre los hechos) las que determinan el contenido de una analogía. En este sentido, la analogía puede entenderse como una alineación estructural dada por un mapeo desde los elementos del dominio fuente a los elementos del dominio objetivo (^{Cuya et al., 2017}), tal que las relaciones entre los elementos del dominio fuente son preservadas por las imágenes de los elementos en el dominio objetivo. Este mapeo cobra relevancia cuando se pretende hacer familiar el dominio objetivo, pues se recurre al conocimiento previo que se posea sobre el dominio fuente, posibilitando la comprensión de las relaciones entre los elementos en el dominio objetivo a través de la comprensión de las relaciones conocidas entre los elementos del dominio fuente (^{Schlimm, 2008}).

En cuanto al razonamiento analógico, ^{Norton (2011)} argumenta que no existe un principio lógico universal para la inferencia analógica cuando se afirma que las cosas que comparten algunas propiedades también comparten otras. Según el autor, cada inferencia analógica está garantizada por alguna constelación local de hechos que deben determinarse e investigarse caso por caso. Siempre que no se trate de proporcionar una “lógica” universal de analogía, se identifican criterios generales para evaluar argumentos analógicos, algunos de los más importantes de los cuales son (^{Bartha, 2016}):

Si bien estos principios son demasiado vagos para proporcionar mucha información (e.g., ^{Bartha, 2016}), consideramos que éstos pueden ser útiles, sobre todo desde el punto de vista del conocimiento del profesor sobre la analogía.

En cuanto a la presentación de las analogías, ^{Curtis y Reigeluth (1984)} señalan dos formatos: el verbal, mediante el uso exclusivo de palabras, y el pictórico-verbal, que complementa las palabras con alguna imagen. Por otra parte, la relación entre los dominios fuente y objetivo puede ser estructural, referida al parecido físico o de construcción similar de los conceptos, o funcional, referida a la forma de funcionamiento de ambas estructuras. Un tercer tipo es la relación estructural-funcional resultante de la combinación de los dos anteriores.

En ciertos casos puede ser difícil distinguir entre metáfora y analogía. Siendo ambas recursos del lenguaje, la analogía permite establecer comparaciones entre distintas realidades y es un instrumento tanto para el desarrollo del pensamiento como para la explicación, mientras que la metáfora produce una interacción entre los dominios y busca que términos conocidos sirvan de referencia para términos nuevos (^{Pérez, 2007}). La metáfora se distingue al utilizar términos de los que se conocen sus características o evocan ciertas cualidades y permiten atribuirle a su vez dichas cualidades al término al que se hace referencia, funcionando “como si se tratara de un filtro que mediatiza la forma de ver el término que se trata de expresar” (^{Pérez, 2007, p. 206}). El significado literal de un término activa en el oyente una inconsistencia entre los términos utilizados, y el conjunto de significados de esos términos son interpretados de acuerdo con el dominio y el objeto involucrado. ^{Font y Acevedo (2003)} proponen como ejemplo de metáfora la función es una máquina para interpretar la función al usar un objeto real, evocando las características de la máquina para transferirlas a la función. En contraste, cuando se explicita la comparación, incluyendo generalmente la palabra “como”, se tiene una analogía (^{Oliva et al., 2001}; ^{Soto-Andrade, 2007}). Por ejemplo, al decir que la función es como una máquina lavadora, se compara el proceso o funcionamiento de la máquina lavadora con el proceso de mapeo que realiza la función. Tanto las analogías como las metáforas poseen el potencial para sugerir nuevas ideas y hacerlas inteligibles, y constituir una herramienta del profesor para potenciar lo inteligible y plausible de sus explicaciones (^{Dagher, 1994}).

Según ^{Pérez (2007)}, existe potencial en el uso de la analogía para la producción de conocimiento, dado que la analogía ayuda en la adquisición del conocimiento y actúa como guía del pensamiento creativo gracias a la capacidad de poder re-describir la realidad y replantear los problemas.

Del mismo modo, el uso de analogías en el proceso de enseñanzaaprendizaje puede ayudar a los estudiantes a aprender nuevos conceptos y a reflexionar sobre sus propios procesos científicos (^{Duit, 1991}). Sin embargo, el uso de una analogía puede conducir a la idea errónea del concepto comunicado y de la propia analogía como único modelo válido, lo que descartaría otros rasgos aún no destacados con dicha analogía, impidiendo, quizá, mejores explicaciones. Las ventajas o desventajas de una analogía se determinarán en cada caso de acuerdo con la utilidad que presenten para la resolución de problemas o para el proceso de enseñanza y aprendizaje (^{González, 2005}).

De ahí es preciso que el profesor sea consciente, al momento de usar una analogía, que ésta “presenta una imagen incompleta de la realidad y si confundimos esa imagen parcial con la totalidad, difícilmente podremos avanzar” (^{Pérez, 2007, p. 204}). Debido a que ninguna analogía hace coincidir perfectamente los dominios, ^{Glynn (1994)} sugiere que se presenten diversas analogías a los estudiantes para que ellos puedan tener diferentes perspectivas del concepto que se les está enseñando.

Por otra parte, las analogías no planificadas o sin la reflexión suficiente del profesor pueden originar efectos no deseados en el aprendizaje (^{Oliva, 2008}). Por tanto, el uso de una analogía para la enseñanza y el aprendizaje supone conocimiento tanto del objeto al que se hace referencia así como sobre su enseñanza, su aprendizaje y sobre las características que, según ^{Bartha (2016)}, permiten evaluar la solidez de la analogía.

3. El conocimiento especializado del profesor de matemáticas

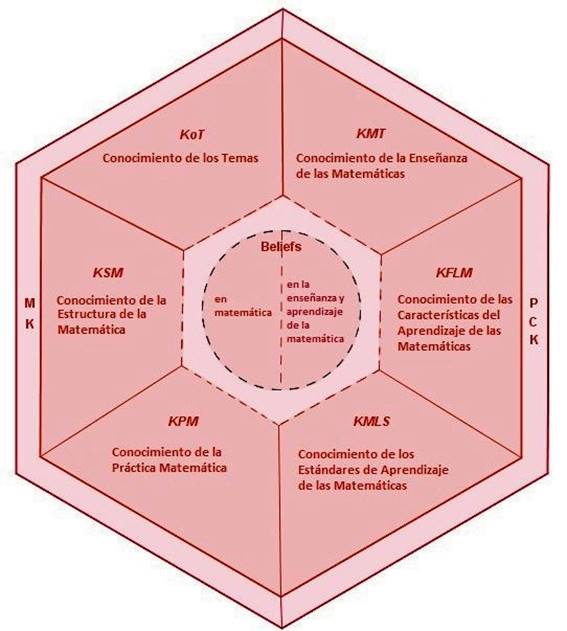
El MTSK es una conceptualización del conocimiento del profesor (^{Carrillo et al., 2018}) que pone énfasis en el carácter especializado de dicho conocimiento y abarca el conocimiento que le es útil y necesario sólo al profesor de matemáticas y que tiene relación con el proceso de enseñanza y aprendizaje de la matemática. El modelo MTSK recoge el espíritu del trabajo de ^{Shulman (1986)} y considera los dominios: Conocimiento Matemático (MK); Conocimiento Didáctico de Contenido (PCK), y además el dominio Creencias sobre la matemática y sobre su enseñanza y aprendizaje (figura 1).

Figura 1 Subdominios del MTSK (^{Carrillo et al., 2014}). 

El dominio MK comprende el conocimiento de la matemática como una disciplina científica y se compone de tres subdominios descritos a continuación:

Por su parte, el PCK está en estrecha relación con el conocimiento matemático de cara a su enseñanza y aprendizaje y se compone de los siguientes tres subdominios:

El MTSK considera que las creencias sobre la matemática y sobre su enseñanza y aprendizaje permean el conocimiento del profesor y ubican este dominio en el centro del modelo, sin embargo, este dominio no se considera en este estudio.

De acuerdo con ^{Carrillo et al. (2014)}, el carácter de especializado del conocimiento del profesor se encuentra en la integración y las relaciones entre conocimientos de todos los subdominios anteriores en distintas dimensiones, lo que deriva de su labor docente, siendo el resultado de esta interacción de distintas formas de conocer el contenido matemático y no del conocimiento del contenido en sí como una parte del dominio de conocimiento matemático necesario para la enseñanza (^{Carrillo et al., 2014}). Por su parte, ^{Scheiner, Montes, Godino, Carrillo y Pino-Fan (2017)} señalan que esta especialización da lugar a considerar la génesis y el desarrollo de las ideas matemáticas desde una perspectiva histórica y cognitiva, teniendo en cuenta las características del aprendiz. En este sentido, y de acuerdo con lo expuesto en la sección anterior, son las características de la analogía (como forma de pensamiento o razonamiento analógico en la resolución de problemas, forma de proceder en ciencias, particularmente en matemáticas, para establecer conjeturas y descubrimiento como estrategia de enseñanza que favorece la comprensión de ideas abstractas) las que permiten considerarla como parte del conocimiento especializado del profesor de matemáticas.

4. Metodología

Dado que nuestro objetivo es avanzar en la comprensión del conocimiento especializado del profesor de matemáticas en el uso de analogías en la enseñanza del concepto de función, considerando el conocimiento como una red compleja de elementos que tiene sentido en su realidad específica, adoptamos un paradigma interpretativo (^{Bassey, 1999}) y una metodología cualitativa que posibilitan comprender la práctica de los profesores y sus conocimientos manifiestos.

El diseño de la investigación corresponde a un estudio de casos de tipo instrumental (^{Stake, 2007}) donde los casos son dos profesores de matemáticas, Arturo y Jaime. En el momento del estudio, ambos se desempeñaban en los cursos de 8o básico (13-14 años) y 1o medio (14-15 años) de dos colegios privados en una localidad chilena. Los profesores fueron seleccionados por el compromiso que manifestaron con esta investigación y de acuerdo con las características de profesores expertos (^{Rojas, Carrillo y Flores, 2012}). Por ejemplo, poseen más de cinco años de experiencia, han enseñado el contenido al menos una vez y se han perfeccionado obteniendo el grado académico de magíster en la disciplina o en educación.

En nuestro estudio, para la recolección de datos, se observaron las sesiones de clases de ambos profesores destinadas a la enseñanza del concepto de función y se realizaron entrevistas a cada profesor. La fuente principal de datos han constituido las grabaciones en video de las nueve sesiones de clases por cada profesor. Dado el objetivo del estudio, se consideraron exclusivamente aquellas clases donde identificamos que los profesores ofrecieron una analogía para explicar algún aspecto de dicho concepto a sus estudiantes: las dos primeras clases, en el caso de Jaime, y la primera clase, en el caso de Arturo.

Las videograbaciones fueron transcritas y divididas en episodios, según el objetivo matemático del profesor. Las unidades de análisis consideradas son las comunicaciones escritas y orales del profesor con sus estudiantes, las que se trataron mediante el análisis de contenido, identificando, por una parte, la presencia de la analogía en el establecimiento de una comparación que determina dos dominios y las relaciones que vinculan sus elementos, y, por otra, las categorías y subdominios que propone el modelo MTSK. Con este fin, se consideró la diferencia entre indicio y evidencia de conocimiento (^{Flores-Medrano, 2015}), donde esta última corresponde a un elemento que permite afirmar la presencia de conocimiento profundo o superficial del profesor, mientras que el primero es una sospecha de existencia o inexistencia de conocimiento identificada por alguna acción del profesor. Los indicios requieren de información adicional para confirmarse como evidencia de conocimiento.

Después de un análisis preliminar de los datos, se elaboró una entrevista semi-estructurada para profundizar en los indicios de conocimiento especializado y aportar más evidencias sobre ciertos subdominios que enriquezcan el análisis. Estas entrevistas también fueron video-grabadas y transcritas para su análisis bajo los mismos criterios que las grabaciones de clases, lo que constituyó otra fuente de datos.

Los resultados del estudio muestran el conocimiento especializado de los profesores en el uso de analogía para la enseñanza del concepto de función a partir de las evidencias observadas directamente o confirmadas en la entrevista posterior.

5. Resultados

A continuación se describe el conocimiento especializado de Jaime y Arturo manifiesto en el uso de la analogía en la enseñanza del concepto de función.

5.1. El MTSK de Jaime en el uso de la analogía

Durante la primera clase, Jaime trabaja relaciones entre conjuntos representadas mediante diagramas sagitales que evidencian su conocimiento sobre representaciones para la función. El profesor propone ejemplos de funciones y relaciona los nombres de sus alumnos con su grupo musical preferido y sus nombres con sus apellidos. Con estos ejemplos, Jaime establece condiciones para definir el concepto de función como una relación que va desde un conjunto, en el que a cada elemento de ese conjunto se le asigna un único elemento del otro conjunto. La exposición de la definición de la función da cuenta del conocimiento de la misma de Jaime. Ésta se basa en la relación entre conjuntos, lo que asigna un significado a la función. En la definición proporcionada, se identifica el conocimiento de las propiedades de unicidad de imagen y exhaustividad que la definen. Lo anterior da cuenta del conocimiento sobre el concepto de función como Conocimiento del tema de Jaime.

En la segunda clase, destinada a resolver ejercicios, Jaime se apoya en la representación que incluye el texto del estudiante (figura 2) para mostrar una comparación entre la función y una máquina dispensadora de golosinas y con ello explicar un ejercicio propuesto en el mismo texto.

Figura 2 Ejercicios propuestos en el texto del estudiante 

Jaime: En la página 117 [del texto del estudiante] aparecen este tipo de ejercicios donde dice: “ingresa (una X), máquina y sale (egreso)”.

¿A qué se parece esto? A la máquina dispensadora de golosinas. Al colocar una moneda, la máquina acciona y sale un producto. Esto es similar a la Máquina 1: ingresa X “un valor”, la máquina trabaja con ese valor y sale otro valor que está en esta tabla. Aquí dicen los valores que ingresan o egresan de la máquina. Usted tiene que completar los cuadritos vacíos de acuerdo con el hecho de que salga o entre.

El uso de la palabra “parecido” es útil para comparar la máquina dispensadora con el concepto de función y el establecimiento de las siguientes relaciones entre los objetos de los dominios fuente y objetivo: a) la moneda se relaciona con el número X que ingresa; b) el proceso que realiza la máquina con la expresión algebraica o “fórmula” para la función, y c) el objeto resultante con el número en el conjunto de llegada dan cuenta de la presencia de una analogía para el concepto de función. El profesor presenta la analogía de manera verbal y se apoya en el diagrama del texto haciendo referencia a la función como una máquina (figura 2). Jaime recurre a la analogía para ayudar a sus estudiantes a comprender y realizar el cálculo de imagen y pre-imagen, estableciendo la analogía desde su carácter funcional al comparar la máquina de golosinas con el proceso que define la función.

En el siguiente extracto, el profesor explicita la comparación entre los dominios fuente (máquina dispensadora) y objetivo (concepto de función).

Jaime: ¿te acuerdas cuando decíamos que esto era parecido a esos dispensadores de golosinas, de bebidas que había en los hospitales, en el centro comercial? Yo tomaba una moneda, la ingresaba a la máquina, la máquina hacía su trabajo de acuerdo con lo que yo le pedía y después salía el producto que tú quisieras. Acá [en el texto del estudiante] está indicando algo parecido, similar. Yo voy a tomar un número X, va a ingresar a esta máquina, y esa máquina hace este trabajo (3x+1).

Jaime señala que lo obtenido es el resultado del funcionamiento de la máquina según lo que se le pide hacer, asociando una moneda a una golosina mediante una instrucción del usuario.

Para determinar la pre-imagen de un valor de egreso, Jaime recurre a la resolución de una ecuación de tipo f (x)=k. El uso de ecuaciones corresponde a conocimiento de una conexión auxiliar entre la función y la ecuación en su Conocimiento de la estructura de las matemáticas, pues la ecuación no es un concepto propio de las funciones, sino que Jaime la utiliza como una herramienta durante el estudio de las imágenes y pre-imágenes de una función. En el caso de la determinación de imágenes, Jaime hace la evaluación de la expresión algebraica, mostrando así conocimiento sobre procedimientos para determinar imágenes y preimágenes y el conocimiento de la representación algebraica para la función y la notación f (x)=y los que son parte del Conocimiento del tema.

Jaime muestra la función a través de la analogía como un proceso de entrada-salida, lo que evidencia el conocimiento sobre un significado de la función y revela su conocimiento de la analogía como estrategia de enseñanza, parte del Conocimiento de la enseñanza de las matemáticas.

Cuando, en la entrevista, se le pregunta a Jaime sobre la intencionalidad de esta analogía, señala que busca resaltar la condición de unicidad de imagen mediante la comparación entre la función y la máquina de golosinas.

Jaime: [La comparación] Es sólo para explicar. Lo había escuchado en otro lado; a cualquier máquina que uno le da un valor, uno le da una moneda, aplica la función y sale una sola golosina o una sola bebida. Yo quería relacionar el que yo tomaba un valor, le aplicaba la función y salía sólo un tipo. Ésa era la idea de fondo: yo tomaba uno, se le aplica la máquina y salía otro valor.

La relación que Jaime establece entre función y máquina dispensadora se basa en el uso de la máquina como una relación entre una moneda y un producto al entregar sólo un resultado, enfatizando el carácter univalente de la función. A pesar de que el proceso de calcular imágenes y preimágenes en una función es comparado en el texto con una máquina, Jaime presenta la analogía para resaltar la característica de unicidad en la asignación de imagen de la función. Esto da cuenta del conocimiento de una de las propiedades del concepto de función como parte del Conocimiento del tema.

Respecto al conocimiento sobre la potencialidad de esta analogía para la enseñanza de la función, se le pregunta al profesor sobre la ayuda a los estudiantes que ofrece la analogía, a lo que responde:

Jaime: No sé si les ayuda o no al concepto, porque son ejemplos que pienso pueden ser útiles para iniciar el proceso. Si me preguntas propiamente tal de esta máquina, claramente que no. No creo que ni siquiera se acuerden, pero en ese instante, para mí era un ejemplo que yo lo encontraba útil, por lo menos conocido, porque todos han comprado en algún dispensador, pero no creo que les haya servido para el resto de lo que uno ve de funciones.

En este extracto, Jaime identifica la potencialidad de la analogía sólo como ayuda en el estudio inicial de las funciones y reconoce su limitación respecto al tiempo en que ésta es útil, lo que da cuenta del conocimiento sobre las interacciones de los estudiantes con el contenido, parte del Conocimiento de las características del aprendizaje de la función.

5.2. El MTSK de Arturo en el uso de la analogía

Arturo inicia la primera clase explicando el concepto de correspondencia con un ejemplo que involucra a los estudiantes, sus sillas y mesas individuales. Inmediatamente después, propone la siguiente definición de función usando el concepto de correspondencia antes explicado:

Arturo: Entonces, ¿cómo vamos a definir una función? Como una correspondencia de elementos de dos conjuntos en la que a cada elemento de un conjunto de partida le corresponde un único elemento en el conjunto de llegada. Lo voy a escribir [en la pizarra]: “es una correspondencia entre elementos de dos conjuntos (no vacíos), A y B, tales que a cada elemento del conjunto de partida le corresponde un único elemento en el conjunto de llegada, B”.

En esta intervención se observa que Arturo conoce un significado para la función (correspondencia) y una definición para el concepto como parte del Conocimiento del tema. Al presentar la definición, Arturo elabora un diagrama sagital (imagen 1) en el que muestra una correspondencia entre los conjuntos A y B usando los elementos genéricos a, b, x e y. Esta representación tiene por objetivo identificar los componentes de la función incluidos en la definición: conjunto de partida, conjunto de llegada, codominio y sus respectivos elementos. Lo anterior da cuenta del conocimiento de las representaciones y notaciones de la función como parte del Conocimiento del tema.

Imagen 1 Diagrama sagital. 

En la definición que proporciona Arturo se incluyen las propiedades de unicidad de imagen y exhaustividad. Además, se condiciona que los conjuntos involucrados sean no vacíos, lo que evidencia conocimiento de las propiedades que hacen definible al concepto de función.

Una vez propuesto el diagrama sagital, Arturo hace una comparación entre la función y la máquina de lavar ropa, como se aprecia a continuación.

Arturo: Previo a darles más nombres, la función funciona igual que una especie de máquina. Un ejemplo podría ser la lavadora. La lavadora cumple una función, ¿cuál es la función?

Estudiante: ¡Lavar!

Arturo: ¿Qué es lo que usted hace? Toma una prenda sucia, la mete en la lavadora, y ¿cómo sale?

Estudiante: Limpia.

Arturo: La prenda sucia vendría a ser del conjunto de partida y la prenda limpia sería de llegada, eso es lo que hace una función. Acá [imagen 2] tendría la prenda sucia, hace la función, lo que le corresponda hacer, dependiendo de la máquina, y llega al otro lado, en este caso, como era la lavadora, llega limpia.

Imagen 2 Presentación pictórica-verbal de la analogía. 

En la intervención anterior, Arturo establece relaciones entre el proceso de lavar y el concepto de función siendo éstos los dominios fuente y objetivo, respectivamente, de una analogía. Además se vinculan los elementos de ambos dominios para explicitar la comparación. De esta forma, se puede afirmar que Arturo conoce una analogía para el concepto de función. Arturo presenta la analogía de manera pictórica-verbal y busca ofrecer una ayuda a sus estudiantes para comprender la definición del concepto. En la intervención anterior (imagen 2), Arturo explicita la relación entre los dominios fuente y objetivo: la ropa sucia es el conjunto de partida, la ropa limpia es el conjunto de llegada y el proceso de lavar es la operación que realiza la función, como un proceso de entrada-salida. Esta analogía compara la función con la máquina de lavar a nivel funcional (como dos procesos) y a nivel estructural, identificando explícitamente las relaciones entre los conjuntos y los procesos involucrados.

Cuando se le pregunta a Arturo sobre el motivo para presentar esta analogía, responde que intenta simplificar la idea matemática que está enseñando.

Arturo: Hago la explicación simple, luego hago una explicación más formal matemática, tratando de hacer una comparación. Siempre hago una traducción del lenguaje formal matemático a un lenguaje simple que ellos puedan comprender. En esta ocasión yo partí con un lenguaje simple y después lo llevé a un lenguaje matemático [...] La traducción del concepto, la traducción de la definición. Cuando tú tienes una definición matemática, de repente es muy dura para que alumnos de primero medio la puedan entender, entonces uno hace una explicación de eso, utilizando sinónimos, de tal forma que ellos puedan comprender lo que ahí está escrito, lo que quieres decir.

Esta explicación que indica Arturo es propuesta con el fin de hacer comprensible una idea a sus estudiantes. En este caso, la definición de función y la forma de orientar la ayuda ofrecida es a través de la analogía, lo que corresponde tanto a Conocimiento de la enseñanza de la función como a Conocimiento de las características del aprendizaje de ésta, lo que se evidencia cuando Arturo menciona las dificultades de los estudiantes al enfrentarse con definiciones formales y nuevos conceptos. El uso de la analogía da cuenta de su estrategia de enseñanza para el concepto, pues pretende aclarar la definición recién dada.

Como se observa en la imagen 2, Arturo aprovecha la analogía para destacar el carácter de proceso de la función y para introducir la notación asociada a las funciones combinando los elementos que la analogía provee con la notación formal. Estas relaciones son el puente para las notaciones y =f (x) y A --> B, presentando una combinación entre el lenguaje simbólico-matemático y la representación pictórica, todo esto como parte del conocimiento de los registros de representación y sobre cómo estas representaciones se articulan, como parte del Conocimiento del tema.

En la siguiente tabla I, presentamos el conocimiento especializado de Arturo y Jaime de acuerdo con los subdominios y las categorías del MTSK identificados en el uso de la analogía.

Tabla I Conocimiento especializado de Arturo y Jaime en el uso de la analogía 

Subdominio / categoría:	Arturo conoce	Jaime conoce
Conocimiento de los temas (KoT) / Definiciones	La univalencia La exhaustividad
	La función como correspondencia entre elementos La condición de conjuntos no vacíos La función como proceso (máquina lavadora)	La función como correspondencia entre elementos La condición de conjuntos no vacíos La función como proceso (máquina lavadora)
KoT / Registro de representación	El diagrama sagital El lenguaje algebraico La notación f(x)=y
KoT / Propiedades	El conjunto de partida El conjunto de llegada	El dominio y recorrido La pre-imagen, imagen
KoT / Procedimientos	El cálculo de imágenes y pre-imágenes
Conocimiento de la estructura de las matemáticas (KSM) / Conexiones auxiliares		El uso de la ecuación lineal f(x)=k para determinar la pre-imagen de k
Conocimiento de la enseñanza de las matemáticas (KMT) / Estrategia de enseñanza	El uso de diagrama sagital usando variables El planteamiento de la definición	El uso de diagrama sagital usando conjuntos no numéricos El planteamiento de la definición
	La presentación pictórica-verbal	La presentación verbal
	La función como una máquina lavadora	La función como máquina dispensadora
	Que ayuda a simplificar la definición y a comprender conceptos de dominio, codominio, imagen y pre-imagen	Que ayuda a comprender la unicidad de imagen y permite calcular imagen y pre-imagen
Conocimiento de las características del aprendizaje de las matemáticas (KFLM) / Fortalezas y dificultades asociadas al aprendizaje de la función	Las dificultades en la adquisición de nuevos conceptos (dominio, codominio)	La utilidad de la analogía sólo al inicio del estudio de la función Que los estudiantes suelen no recordar esta comparación

La primera columna de la tabla I contiene los subdominios y las categorías evidenciadas, mientras que la segunda y la tercera columna presentan los conocimientos evidenciados en el uso de la analogía por cada uno de los profesores. Las filas centradas representan conocimientos que ambos profesores han manifestado en ese subdominio/categoría.

6. Discusión

Como se puede ver en la tabla I, existen diferencias entre el conocimiento especializado identificado en ambos profesores. Esto puede deberse a que Arturo presenta la analogía después de definir la función para ayudar a la comprensión de esta definición, mientras que Jaime busca otorgar una ayuda para un procedimiento cuando plantea a sus estudiantes un ejercicio del texto. De acuerdo con ^{González (2005)}, el momento en que se presenta la analogía puede afectar el proceso de enseñanza-aprendizaje, al evidenciar conocimientos de diferentes subdominios.

La lectura de la tabla permite observar que los profesores presentan la función sólo desde el significado de proceso (^{Figueiredo, Contreras y Blanco, 2015}; ^{García y Serrano, 2000}; ^{Sfard, 1991}), visto como entrada y salida de objetos sin incluir, por ejemplo, el significado de la función como variación de magnitudes o como pares ordenados desde una perspectiva estructural (^{Sfard, 1991}), lo que puede limitar la concepción de la función por parte de los estudiantes (^{González, 2005}). Pese a esto, iniciar el estudio de la función desde la concepción del proceso favorece la comprensión del concepto en los estudiantes (^{Figueiredo et al., 2015}). Asimismo, el conocimiento de los profesores sobre la necesidad de que los estudiantes estén familiarizados con las máquinas presentadas para resaltar el significado de la función como proceso, guarda concordancia con lo que ^{Duit (1991)} señala como condición para que los estudiantes puedan razonar exitosamente por analogía, y, por otra parte, con las características que según ^{Bartha (2016)} fortalecen la analogía. Sin embargo, cabe recordar que la analogía presenta una imagen parcial (^{Pérez, 2007}) y requiere de comparaciones complementarias para la comprensión más profunda del concepto (^{Glynn, 1994}).

En ambos casos, la analogía es presentada a los estudiantes y no construida por ellos, contrario a la recomendación hecha por ^{Oliva (2008)}. Pese a ello, ambos profesores pretenden que sus estudiantes consigan establecer relaciones que les permitan comprender los nuevos conceptos, hecho que concuerda con la importancia que se le da a la analogía como recurso para la enseñanza (e.g., ^{Cuya et al., 2017}) y para resolver problemas asociados mediante el razonamiento analógico por parte de los estudiantes (^{Cruz et al., 2016}).

La pluralidad de características de la analogía posibilita observar, en su uso, la integración de conocimientos de diferente índole que ^{Carrillo et al. (2018)} y ^{Scheiner et al. (2017)} definen como conocimiento especializado del profesor de matemáticas. Así, se han visto distintos subdominios del conocimiento especializado del profesor en el uso de la analogía y se podrían considerar otros que no se observaron directamente. Por ejemplo, el conocimiento del profesor del hecho de que la máquina lavadora relacione objetos del mismo tipo (poleras con poleras) sin destacar una de las características relevantes de la función como es la naturaleza arbitraria de los conjuntos relacionados (^{Even, 1990}) o que la analogía de la función como una máquina presenta la función como un proceso pueden limitar la comprensión a sólo un significado de la función. Por ejemplo, concebir la función como una co-variación de magnitudes o conjunto de pares ordenados, perspectivas que son también parte del desarrollo histórico de las funciones (^{Ruiz-Higueras, 1994}).

Asimismo, el conocimiento del profesor acerca de las concepciones erróneas de los estudiantes cuando se limita la función a una máquina llevaría al profesor a reflexionar sobre cómo la analogía puede afectar el aprendizaje de los estudiantes como lo menciona ^{Oliva (2008)}. Por ejemplo, si la lavadora no entrega la ropa limpia o la máquina dispensadora no entrega la golosina solicitada, el estudiante puede pensar que no “hay una función” en esos casos, pues los objetos resultantes del proceso de lavar no pertenecen al conjunto de llegada (ropa limpia), o una moneda puede no tener imagen. Estas situaciones dan cuenta de la importancia de los distintos subdominios del conocimiento especializado del profesor en el uso de la analogía como estrategia de enseñanza.

7. Conclusiones

En este estudio nos hemos preguntado por los conocimientos que el profesor de matemáticas pone en juego al usar una analogía para la enseñanza de la función. De nuestros resultados podemos concluir que en dicho uso intervienen diferentes subdominios de conocimiento especializado del profesor de manera integrada.

Consideramos que, a pesar de que las analogías presentadas por los profesores son potentes al mostrar la función como un proceso, el conocimiento del profesor sobre el concepto de función, su enseñanza y su aprendizaje le permitirá idear otras analogías que ayuden a sus estudiantes a comprender el concepto desde otras perspectivas. Además, es importante que el profesor sea consciente de las características de la analogía que utiliza, su aplicabilidad, alcances y el contexto donde se presentará. Al respecto, podemos concluir que los distintos subdominios del conocimiento del profesor identificados en el uso de las analogías nos permiten profundizar en la comprensión de dicho conocimiento.

Dado que el concepto de función es un tema presente tanto en la matemática escolar como en la formación inicial de profesores, los resultados de esta investigación y de estudios sobre el conocimiento matemático y didáctico del profesor sobre la función, así como del uso de la analogía en su enseñanza, son potencialmente útiles para los formadores de profesores en el diseño de tareas en los cursos de formación inicial de profesores. Asimismo, estos resultados pueden utilizarse en la formación continua de profesores de matemática para diseñar nuevas propuestas de enseñanza considerando sus experiencias profesionales y las características de las analogías en la discusión de las ventajas, dificultades u obstáculos que se producen al utilizar la analogía como estrategia de enseñanza. La reflexión acerca de estos aspectos, en contextos reales, es una oportunidad para los profesores de (re)construir su conocimiento especializado (^{Zakaryan et al., 2018}).

Finalmente, este estudio aporta, a partir de datos empíricos, a la comprensión de este conocimiento y contribuye a la investigación en el área al profundizar en el conocimiento especializado sobre el uso de la analogía como estrategia de enseñanza y ofrece ejemplos de situaciones reales, provechosos en la formación de profesores.