1. Introducción
Esta investigación pretende relacionar la forma de resolver problemas matemáticos con ciertas estrategias de aprendizaje empleadas por el alumnado de Educación Secundaria Obligatoria. A continuación se introducen los conceptos más relevantes que se tratan en el presente estudio.
1.1. Los problemas aritmético - algebraicos
Las estrategias de resolución de problemas matemáticos con enunciado (o problemas verbales) son diversas y pueden estar condicionadas por varios factores asociados al tipo de problema, a la comprensión del texto o a la persona que resuelve, entre otros (p. ej., Bednarz & Janvier, 1996; Filloy, Rojano & Puig, 2008). Resulta evidente la importancia que tiene el aprendizaje de esta área de las matemáticas, como así reflejan los currículos de la mayoría de países en cualquier etapa educativa.
La familiaridad con la resolución de problemas permite la adquisición de multitud de competencias. En este sentido, se identifican tres grandes campos: la habilidad para entender el problema, la competencia para aplicar el procedimiento de resolución y la capacidad para construir esquemas mentales abstractos (Scheiter, Gerjets, & Schuh, 2010). Además, no solo representa un objetivo en el aprendizaje de las matemáticas, sino que es uno de los principales medios para hacerlo promoviendo hábitos de persistencia, curiosidad y confianza en situaciones desconocidas (NCTM, 2000).
En los primeros cursos de la Educación Primaria, una vez conocidas las operaciones aritméticas, se comienzan a enseñar problemas que se resuelven empleando precisamente esas operaciones (resolución aritmética). Tras adquirir competencia en dichas técnicas, se da paso a la resolución algebraica, usualmente al inicio de la Educación Secundaria (BOPV, 2007; BOPV, 2016).
El cambio de una forma de resolución a la otra ha sido estudiado debido a las dificultades que a menudo se detectan en el alumnado (Khng y Lee, 2009). Las diferencias profundas entre los tempranos hábitos aritméticos y el posterior aprendizaje del álgebra no suelen tener lugar de forma espontánea; esta es la razón por la que la intervención de la enseñanza puede ser clave en la transición de una técnica de resolución a la otra.
Hay diversidad de opiniones cuando se pretende definir el álgebra con la finalidad de resolver problemas y en lo que se refiere a la mencionada fase inicial. Carraher, Martinez y Schliemann (2008) considera que el álgebra es la aritmética generalizada de números y cantidades, además del cambio que supone calcular desde números y medidas particulares a pensar en relaciones entre grupos de números, es decir, en funciones. Para Radford (2014), la aritmética tiene un componente algebraico inherente y viceversa, el álgebra su componente aritmético. Otra característica asociada al álgebra y ampliamente observada es su carácter relacional (se relacionan números o cantidades) frente al operacional de la aritmética (se plantea la resolución mediante operaciones aritméticas) (Knuth et al., 2008).
Para adquirir el razonamiento algebraico temprano se debe aprender a generalizar, esto es, a identificar patrones y poder reconocer la norma; sin embargo, antes de emprender dicho aprendizaje, es necesario observar cómo el alumnado representa y razona por sus propios medios (Carraher et al., 2008). En este sentido, los currículos de una gran cantidad de países admiten que un conocimiento profundo de la aritmética requiere la comprensión tanto de generalizaciones de la matemática como de principios básicos del álgebra. Algunas investigaciones informan sobre métodos pre - algebraicos de razonamiento, informales, en los cuales la simbolización se entiende como una manera de facilitar la transición aritmética - álgebra en la resolución de problemas (Van Averom, 2003).
Jennings y Dunne (1996) se refieren a una reducción de la complejidad de los problemas y a una prolongación del uso de técnicas informales (aritméticas) con el fin de facilitar la tarea al alumnado. Stacey y MacGregor (1999) indican que el profesorado en vez de emplear problemas simples y resolverlos algebraicamente como método de preparación para problemas más complejos, lo que promueven es continuar resolviendo problemas usando la intuición, mediante métodos no algebraicos. Las mismas autoras añaden que, desde el punto de vista del alumnado, usar el álgebra para resolver un problema es una dificultad extra que no le resulta necesaria dado que la mayoría de los problemas propuestos en los libros de texto son fácilmente realizables desde la aritmética; en este contexto se encuadran los dos primeros problemas planteados al alumnado en el presente trabajo. Por este motivo proponen que, para apreciar el valor del álgebra, los problemas deben ser no fácilmente resolubles aritméticamente.
Las técnicas aritméticas mencionadas se introducen en Educación Primaria y tienen cierta continuidad (junto al procedimiento algebraico) en el primer ciclo de Educación Secundaria. Según Stacey y MacGregor (1999), la experiencia previa en aritmética conduce a “una compulsión para calcular” que dificulta el empleo de las estrategias algebraicas en el momento de buscar, seleccionar y nombrar la incógnita o incógnitas apropiadas, impidiendo incluso pensar en construir una ecuación. Esta misma tendencia hace que el alumnado quiera trabajar con valores conocidos y no con incógnitas.
Por lo expuesto hasta el momento, la investigación previa enfatiza la importancia de dar prioridad, incluso exclusividad, al empleo del álgebra en Educación Secundaria, tras la etapa necesaria de aprendizaje de técnicas heurísticas implementadas en Educación Primaria. Sin embargo, ciertos estudios indican que, aunque las técnicas heurísticas no garantizan efectividad en la resolución, permiten afrontar cada problema alentando el pensamiento crítico y creativo del estudiante, siempre y cuando no disponga de un algoritmo de resolución (Deulofeu, Figueiras & Pujol, 2011). Aunque la técnica algebraica de resolución de problemas no se considera un algoritmo (no facilita una rutina aplicable a cualquier problema) sí está compuesta por una serie de reglas que consisten básicamente en definir las incógnitas, construir una ecuación, resolverla y, por último, dar el valor correspondiente a las incógnitas que se pretenden hallar. Van Amerom (2003) también aboga por empezar resolviendo problemas mediante estrategias “informales” (aritméticas) como punto de partida previo a la resolución de ecuaciones e iniciarse con notaciones informales con el objetivo de suavizar la dificultad que entraña el aprendizaje de la simbolización algebraica.
1.2. Las estrategias de aprendizaje en matemáticas
Las estrategias de aprendizaje se han estudiado en las últimas décadas en relación a su importancia en el proceso de enseñanza - aprendizaje en multitud de áreas de conocimiento. Inicialmente, estas estrategias se asociaron con el procesamiento cognitivo de la información, lo que posibilitó la construcción de modelos que permitieran entender el funcionamiento de la cognición humana (Badia et al., 2012).
Las estrategias se pueden caracterizar como los pensamientos, comportamientos, creencias o emociones que ayudan a la adquisición, comprensión y transferencia de nuevos conocimientos y habilidades (Inglés, Martínez - González, & García - Fernández, 2013). El empleo de las mismas da pie a la puesta en marcha de un aprendizaje significativo, estratégico y autónomo, basado en el concepto de “aprender a aprender” y puesto en valor por la Unión Europea (European Commission, 2006).
Dependiendo del enfoque conceptual realizado para su examen, se han definido y categorizado un sinfín de estrategias de aprendizaje, medidas, en la mayoría de los casos, a través de cuestionarios. Por ejemplo, Gargallo (2012) propone una categorización en cuatro grupos de estrategias: (i) estrategias afectivas, disposicionales y de apoyo; (ii) estrategias metacognitivas, de regulación y control; (iii) estrategias de búsqueda, recogida y selección de información; y (iv) estrategias de procesamiento y uso de la información adquirida. Cada una de ellas presenta una serie de escalas más específicas. Diversos autores proponen tres grandes dimensiones como son las estrategias cognitivas, las metacognitivas y las contextuales (Liu, 2009, Pintrich, Smith, Garcia, & McKeachie, 1993).
La transcendencia educativa de las estrategias de aprendizaje se puede comprobar observando sus relaciones con importantes variables psicoinstruccionales como son la motivación escolar (Balam, 2015) o el autoconcepto (Núnez et al., 1998), entre otras.
Uno de los objetivos fundamentales de la investigación relativa a las estrategias de aprendizaje trata de focalizarse en el análisis de la variación del rendimiento académico en función del empleo de las mismas; este hecho se repite en cualquier área o ciclo educativo, también en matemáticas (Ahmed et al., 2013; Murayama et al., 2013).
En este sentido, los resultados sobre el Informe PISA 2003 (Programme for International Student Assessment) concluyen que la importancia de la estrategia de elaboración en matemáticas (por ejemplo, establecer conexiones con áreas relacionadas o buscar soluciones alternativas) se incrementa a medida que el nivel de rendimiento aumenta (Thiessen & Blasius, 2008). La investigación análoga sobre PISA 2000 (Chiu, Wing - Yin, & McBride - Chang, 2007) afirma que: (1) El empleo de la estrategia de repetición (o memorización de conceptos) está asociado negativamente con el rendimiento en matemáticas; (2) La estrategia de elaboración no tiene relación con el rendimiento; y (3) El empleo de estrategias metacognitivas correlaciona positivamente con el rendimiento en matemáticas.
Precisamente las estrategias metacognitivas adquieren especial relevancia en la investigación educativa en matemáticas y, más concretamente, en el desarrollo de habilidades para la resolución de problemas (Lai et al., 2001). Flavell (1979), precursor en el estudio de la estrategia, define la metacognición como el pensamiento sobre el pensamiento distinguiendo dos componentes: (i) el conocimiento de los procesos y productos cognitivos; y (ii) la capacidad para controlar, supervisar y evaluar dichos procesos. Estas estrategias se pueden catalogar como una alarma que informa sobre la propia cognición (Efklides, 2001).
La metacognición juega un papel muy importante en la resolución de problemas, así como en este estudio debido a las diferencias encontradas. Las habilidades metacognitivas ayudan a: 1) codificar estratégicamente la naturaleza del problema y a obtener una representación mental de sus elementos; 2) seleccionar las estrategias adecuadas para la consecución del objetivo; y 3) Identificar los obstáculos que impiden y dificultan el progreso (Davidson & Sternberg, 1998). Algunos estudios han revelado la importancia de la metacognición para hacer frente a la dificultad para resolver problemas matemáticos en el momento de emplear el conocimiento necesario de modo correcto o en el momento apropiado (McAfee & Leong, 1994). La complejidad para resolver problemas da pie a diferentes perfiles de resolución; de este modo, el alumnado no experto hace una lectura superficial del problema, eminentemente explorativa, y no supervisa el proceso (Pape, 2004). El experto, en cambio, se caracteriza por leer y analizar el problema para luego avanzar hacia la solución empleando diversas estrategias (meta) cognitivas como la planificación, la ejecución y la verificación (Baroody, Feil, & Johnson, 2007). En este sentido, el experto trabaja reconociendo los patrones de resolución y clasificando el tipo del problema antes de proceder a resolverlo. También relacionado con la metacognición, los resultados obtenidos por Elichiribehety y Otero (2004) muestran que, independientemente de la edad, un porcentaje elevado de los sujetos sometidos a estudio resuelven orientados por los procesos estratégicos de comprensión del enunciado, mientras que, cuando la transformación del enunciado verbal no puede realizarse en el marco algebraico, se emplea exitosamente el marco aritmético.
Con respecto a la cognición, Mayer (1986) une los términos pensamiento, cognición y resolución de problemas. Argumenta que el pensamiento es manipulación del conocimiento y es dirigido hacia la solución, en clara alusión a la manipulación de operaciones y a la búsqueda del resultado final, procedimientos ambos asociados a la resolución de problemas. Además, los problemas matemáticos verbales facilitan el análisis de los diferentes componentes cognitivos que operan en la inteligencia, tales como los componentes lingüístico - semánticos, los esquemáticos, los estratégicos y los operativos.
Según el currículo de la ESO (BOPV, 2007), la resolución de problemas aporta a la autonomía e iniciativa personal en el fomento de, al menos, tres competencias: la planificación, la gestión de los recursos y la evaluación. Aunque no se haga alusión explícita, todas estas aptitudes representan estrategias metacognitivas. El problema radica en la falta de concreción sobre la manera de resolver los problemas. Según el documento oficial, los problemas se resuelven o bien mediante el método analítico (algebraico) o usando modelos heurísticos (aritméticos), pero no establece una jerarquía que aconseje usar un método o el otro según el tema o el tipo de problema, y tampoco se sabe si son complementarios. En esta situación, se debe recordar que los métodos heurísticos o aritméticos son informales y por tanto no atienden a un patrón establecido, por lo que su aplicación no asegura el éxito en la resolución. En cambio, el dominio del método algebraico, sin ser estrictamente algorítmico, permite seguir unas pautas y dar con la solución a la totalidad de los problemas verbales planteados en Educación Secundaria.
Resultan evidentes, por tanto, los lazos existentes entre las matemáticas y la resolución de problemas y las estrategias de aprendizaje empleadas en el proceso de instrucción. Diversos estudios informan sobre la competencia matemática y la metacognición (Garofalo & Lester, 1985) y sobre el vínculo entre estas estrategias de control y el razonamiento matemático (Schoenfeld, 1985). No obstante, se encuentran escasísimas investigaciones que pretendan arrojar luz sobre las posibles relaciones entre la manera de resolver problemas y las estrategias de aprendizaje que se emplean. El estudio de dichos procedimientos de resolución y las estrategias de aprendizaje puestas en práctica constituyen el objeto del presente estudio.
2. Método
2.1. Participantes
En esta investigación participan 631 estudiantes de tres cursos de Educación Secundaria Obligatoria (ESO): 2º (32%), 3º (37%) y 4º (31%), de los cuales 336 (53.3%) son mujeres y 295 (46.7%) hombres. Por motivos de errores u omisiones en las respuestas a los cuestionarios la muestra final queda reducida a 565 sujetos. Las razones de la exclusión fueron no responder varios ítems o dar una respuesta múltiple a algunos de los mismos. La recogida de datos se ha realizado en 8 centros educativos que pertenecen a la Comunidad Autónoma Vasca, integrantes tanto de la red pública (5) como de la red privada concertada (3). Tras contactar con varios centros, finalmente se seleccionan aquellos que responden positivamente a la oferta de participación, por lo que se trata de una muestra de conveniencia.
En la Tabla 1 se muestra la distribución en función del curso académico y del sexo:
2.2. Instrumentos de medida
2.2.1. Problemas aritmético - algebraicos
Los tres problemas propuestos son introducidos por Stacey y MacGregor (1999) y van de menor a mayor complejidad en cuanto a su resolución con métodos no algebraicos. El segundo problema es análogo al primero, con la diferencia de que se piden tres resultados en lugar de dos (ver anexo 1).
Con el objetivo de medir las estrategias llevadas a cabo en cada problema propuesto, la codificación se ordena en cuatro categorías propuestas por Khng y Lee (2009): algebraica, si el planteamiento está definido por una o más incógnitas y se resuelve mediante una o más ecuaciones; aritmética, si tanto el planteamiento como la resolución se basa en una técnica aritmética, esto es, sin recurrir ni a incógnita ni a ecuación; mixta, categoría donde se ubican los problemas en los que se usa una letra en alguna parte de la resolución pero la técnica es predominantemente aritmética y, por tanto, se consideran procedimientos aritméticos; y sin estrategia / sin respuesta / planteamiento erróneo, donde se agrupan los métodos sin identificar o los problemas sin resolver.
A la hora de clasificar la resolución como aritmética se han dado como válidas la resolución aritmética y la mixta.
El instrumento de medida para las estrategias de resolución de problemas aritmético - algebraicos consta de tres problemas verbales a resolver. A cada individuo de la muestra se le agrupa en una categoría de las tres siguientes: grupo G3, G2 o G1 (Gasco, 2014). El grupo G3 (grupo de resolución de perfil algebraico), correspondiente a los sujetos que resuelven correctamente la totalidad de los problemas algebraicamente, o, en su defecto, resuelven dos algebraicamente y en el tercero hacen un planteamiento algebraico (planteando las incógnitas y la ecuación), aunque no den con la solución correcta por un error de cálculo y no procedimental; el grupo G2 (grupo de resolución de perfil mixto), compuesto por los individuos que utilizan estrategias tanto algebraicas como aritméticas, dependiendo del problema a resolver. Por tanto, se incluye en este grupo al alumnado que resuelve correctamente dos problemas algebraicamente y uno aritméticamente, o viceversa (dos aritméticamente y uno algebraicamente); y el grupo G1 (grupo de resolución de perfil no definido), al que pertenece el alumnado que no encaja ni en G3 ni en G2; es decir, no resuelve sistemáticamente ni de modo algebraico ni de modo aritmético, ni tampoco alternando ambas técnicas. Se incluyen en este conjunto a los sujetos que obtienen en algún problema (en uno, en dos o en los tres) la clasificación de sin estrategia / sin respuesta / planteamiento erróneo.
La pertinencia de tomar en cuenta el grupo G2 se debe a un estudio previo (Gasco & Villarroel, 2012) que indica que un gran número de sujetos usa la aritmética en problemas adecuados para ello y sin embargo emplea el álgebra para resolver otros de difícil desarrollo aritmético.
2.2.2. Estrategias de aprendizaje en matemáticas
El empleo de las estrategias de aprendizaje del alumnado se ha medido a través de un cuestionario basado en una versión para Enseñanza Secundaria del MSLQ (Motivated Strategies for Learning Questionnaire) (Pintrich et al., 1993) adaptado por Berger y Karabenick (2011) para ajustarse al estudio de las matemáticas. El cuestionario en castellano (Gasco-Txabarri, Ros, & Goñi, 2017) aquí propuesto se ajusta a una estructura heptafactorial formada por las mismas escalas del original pero dividiendo la escala de estrategias metacognitivas en dos: planificación y seguimiento - regulación. Además, los autores proponen la revisión / reformulación / eliminación de 8 de sus ítems; este estudio elimina los ítems indicados formando finalmente un total de 25. Esta versión reducida presenta índices mejores en el análisis factorial confirmatorio (χ2/gl: 2.95; NFI: .910; CFI: .939; RMSEA: .059) que la versión completa compuesta por 33 ítems. Los ítems se responden en base a una escala Likert de cinco puntos. A continuación, se concreta la configuración de la citada versión castellana:
- Estrategias cognitivas:
-. Repetición (3 ítems): Se miden las estrategias para aprender por repetición.
-. Organización (2 ítems): Se tienen en cuenta las maneras de gestionar los aprendizajes matemáticos.
-. Elaboración (2 ítems): Se mide por una parte cómo se relaciona el aprendizaje en matemáticas con otras materias y por otra la transformación de los conceptos matemáticos para una mejor comprensión personal.
- Estrategias metacognitivas:
- Planificación (5 ítems): Se recopila información sobre cómo se planifican los estudios.
-. Seguimiento (4 ítems): Contiene ítems relativos a la conciencia, conocimiento y control que tiene el alumnado sobre su propia cognición.
-. Regulación (3 ítems): Se refiere a la habilidad para controlar el esfuerzo y la atención frente a las distracciones o ante tareas difíciles.
- Estrategias contextuales y de gestión de recursos:
2.3. Procedimiento
En lo que respecta a la resolución de problemas, las dos únicas condiciones impuestas para la investigación son, por una parte, que la unidad didáctica referida a la resolución de problemas aritmético - algebraicos se haya impartido y finalizado con anterioridad a la fecha de la prueba y, por otra, que no se revele al alumnado la naturaleza concreta de la prueba matemática, más allá de que deberán hacer unos ejercicios de matemáticas.
Se solicita una cita con la dirección de cada centro elegido. Una vez obtenido el visto bueno, se explican las pruebas propuestas al profesorado de matemáticas de 2º, 3º y 4º de la ESO.
Se advierte de que la prueba es anónima y que los datos personales que se requieren son la fecha de nacimiento y el sexo, exclusivamente. Además, se informa de que los resultados obtenidos no influirán en la calificación escolar.
Dependiendo de cada individuo, la realización de la prueba dura entre 10 y 25 minutos, incluyendo la realización del cuestionario y de los problemas.
2.4. Análisis de datos
Se analizan las diferencias entre cursos implementando la prueba no paramétrica para k muestras independientes de Kruskal - Wallis. Para realizar los test post - hoc se ha empleado la prueba no paramétrica U de Mann-Withney. La razón de la elección de dichas pruebas no paramétricas es que los datos recogidos no cumplen los criterios ni de normalidad ni de homocedasticidad.
En las pruebas para el análisis de dos muestras independientes, concretamente en el test U de Mann-Withney, se ha calculado el tamaño del efecto (effect size), denotado por el parámetro r. La interpretación del coeficiente es la siguiente: r = .10, tamaño del efecto débil; r = .30, tamaño del efecto moderado; y a partir de r = .50 tamaño del efecto fuerte (r toma valores entre 0 y 1) (Field, 2009).
Todos los datos obtenidos tanto en los problemas como en el cuestionario se han analizado empleando el software estadístico IBM SPSS Statistics 21.
3. Resultados
A continuación, se presentan los resultados obtenidos. Se dividen en dos apartados: por una parte, la distribución del alumnado por curso y grupo de resolución y por otra las diferencias en el empleo de estrategias en función del grupo de resolución:
3.1. Distribución del alumnado por curso y grupo de resolución
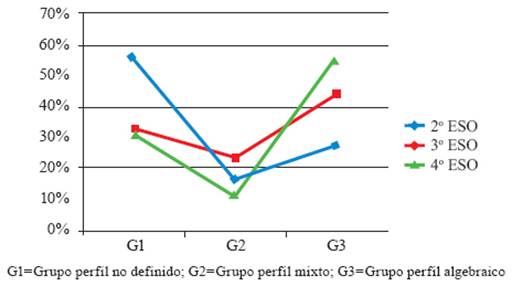
En la Tabla II se exponen las distribuciones de los grupos de resolución de problemas en función del curso académico:
Tabla II Distribución de los grupos de resolución en función del curso académico
| CURSO | |||||
| 2º ESO | 3º ESO | 4º ESO | Total | ||
| Grupo | G1 | 102 (57.9%) | 66 (33.2%) | 59 (31%) | 227 |
| G2 | 26 (14.8%) | 43 (21.6%) | 22 (11.6%) | 91 | |
| G3 | 48 (27.3%) | 90 (45.2%) | 109 (57.4%) | 247 | |
| Total | 176 | 199 | 190 | N = 565 | |
G1=Grupo perfil no definido; G2=Grupo perfil mixto; G3=Grupo perfil algebraico
La Chi cuadrado ha resultado de la siguiente manera: X2 (4, N = 565) = 45.7, p < .001. Por tanto, las diferencias observables son estadísticamente significativas. El tamaño del grupo G3 (grupo de perfil algebraico) aumenta en razón del curso académico pasado del 27.3% (2º de la ESO) al 57.4% (4º). La evolución del G1 (sin perfil definido) es de signo contrario: va disminuyendo en cantidad de estudiantes de curso en curso. El tamaño del grupo de perfil mixto (G2) aumenta de 2º a 3º (del 14.8% al 21.6%) para luego, en 4º, disminuir (11.6%). Es destacable la pequeña diferencia entre 3º y 4º en el grupo sin perfil de resolución definido (G1); la mayor variación entre 3º y 4º se aprecia entre el G2 y el G3, siendo el grupo algebraico (G3) el destacado en 4º (57.4% frente a 45.2%) y el grupo mixto (G2) en 3º (21.6% frente a 11.6%). En la Figura 1 se muestra la distribución porcentual descrita en la Tabla 2:
3.2. Diferencias en el empleo de estrategias en función del grupo de resolución
En la tabla III se exponen las variaciones inter - grupos de resolución en las puntuaciones obtenidas en las estrategias de aprendizaje:
Tabla III Diferencias en función del grupo de resolución
| Estrategia | Grupo | Media | Desv. típ. | Prueba de Kruskal - Wallis | |
| Repetición |
G1 G2 G3 |
2.88 2.97 3.06 |
0.98 0.98 0.890 |
No existen diferencias | .12 |
| Organización |
G1 G2 G3 |
1.71 2.93 3.18 |
.75 1.17 0.95 |
Existen diferencias | .00 |
| Elaboración |
G1 G2 G3 |
1.77 2.73 3.30 |
.60 1.20 1.00 |
Existen diferencias | .00 |
| Planificación |
G1 G2 G3 |
1.69 2.61 3.13 |
.54 0.81 0.78 |
Existen diferencias | .00 |
| Seguimiento - Regulación |
G1 G2 G3 |
2.01 3.67 3.96 |
.72 0.67 0.48 |
Existen diferencias | .00 |
| Recursos ayuda |
G1 G2 G3 |
2.80 3.81 3.86 |
.80 0.80 0.67 |
Existen diferencias | .00 |
| Entorno estudio |
G1 G2 G3 |
2.14 3.27 3.54 |
.70 0.47 0.75 |
Existen diferencias | .00 |
G1=Grupo perfil no definido; G2=Grupo perfil mixto; G3=Grupo perfil algebraico
Las diferencias son estadísticamente significativas en todas las estrategias (p < .001), exceptuando en la de repetición (nivel de significación: p > .05), estrategia cognitiva consistente en memorizar lo aprendido lo que significa que, aunque la mayoría de estrategias muestran variación, la repetición de los conocimientos parece tener otra tendencia diferente en lo que a cambios de curso se refiere.
A continuación, se han realizado los test post - hoc U de Mann-Withney con el fin de estudiar las diferencias dos a dos entre los grupos de resolución en el uso de estrategias en las que se han detectado diferencias. Los resultados entre los grupos G1 y G2 se exponen en la Tabla IV:
Tabla IV Diferencias post - hoc entre los grupos G1 y G2
| Test U de Mann-Whitney | ||||
| Estrategia | U | Z | p | r |
| Repetición | 4130.50 | - 08.71 | .00 | .49 |
| Elaboración | 5584 | - 06.71 | .00 | .38 |
| Planificación | 3621 | - 09.28 | .00 | .52 |
| Seguimiento -Regulación | 1407.50 | - 12.12 | .00 | .68 |
| Recursos ayuda | 3686.50 | - 09.20 | .00 | .52 |
| Entorno estudio | 3833.50 | - 09.00 | .00 | .50 |
G1=Grupo perfil no definido; G2=Grupo perfil mixto
Las diferencias estadísticamente significativas se producen en todas las estrategias evaluadas (p < .001); además, en todas ellas, el alumnado del grupo G2 obtiene puntuaciones superiores en comparación con el alumnado del grupo G1.
La estrategia de organización tiene en cuenta las maneras de gestionar los aprendizajes matemáticos. La estrategia cognitiva de elaboración mide cómo se relaciona el saber matemático con otras materias, además de la transformación que se realiza de los conceptos matemáticos para una mejor comprensión de los mismos. La planificación y el seguimiento - regulación, ambas estrategias metacognitivas, miden la preparación, el control y el conocimiento que tiene el alumnado sobre su propia cognición. La estrategia de recursos de ayuda se refiere a la búsqueda de ayuda en caso de dificultad y el entorno de estudio evalúa el ambiente elegido para estudiar.
En consecuencia, según estos resultados, el alumnado del G2 gestiona y relaciona mejor el aprendizaje matemático, tiene un mayor conocimiento, planificación y control de su cognición, pide más ayuda en caso de dificultad y gestiona mejor su espacio y tiempo de estudio.
En todos los tipos de estrategias el tamaño del efecto es entre moderado y fuerte por el hecho de que el parámetro r resulta mayor de .30 en todos los casos.
En la Tabla V se exponen las diferencias en el empleo de estrategias entre los grupos G1 y G3:
Tabla V Diferencias post-hoc entre los grupos G1 y G3
| Test U de Mann-Withney | ||||
| Estrategia | U | Z | p | r |
| Repetición | 6627.00 | - 14.23 | .00 | .65 |
| Elaboración | 6756.50 | - 14.21 | .00 | .65 |
| Planificación | 4043.00 | - 15.96 | .00 | .73 |
| Seguimiento - Regulación | 1686.50 | - 17.50 | .00 | .80 |
| Recursos ayuda | 8418.50 | - 13.01 | .00 | .60 |
| Entorno estudio | 5292.50 | - 15.14 | .00 | .69 |
G1=Grupo perfil no definido; G3= Grupo perfil algebraico
Las diferencias estadísticamente significativas se dan en todas las estrategias de aprendizaje medidas (p < .001). En cada una de ellas además el alumnado del grupo G3 obtiene puntuaciones superiores al alumnado agrupado en el G1.
En todas las diferencias el tamaño del efecto ha resultado ser fuerte (r > .50).
El análisis de diferencias en el uso de estrategias de aprendizaje entre los grupos G2 y G3 se presenta en la Tabla VI:
Tabla VI Diferencias post - hoc entre los grupos G2 y G3
| Test U de Mann-Withney | ||||
| Estrategia | U | Z | p | r |
| Repetición | 10570.00 | - 1.79 | .74 | - |
| Elaboración | 8721.00 | - 4.00 | .00 | .22 |
| Planificación | 7884.50 | - 5.00 | .00 | .27 |
| Seguimiento -Regulación | 9202.50 | - 3.42 | .00 | .19 |
| Recursos ayuda | 11384.50 | - 0.80 | .42 | - |
| Entorno estudio | 10247.50 | - 2.12 | .03 | .11 |
G2=Grupo perfil mixto; G3= Grupo perfil algebraico
Entre G2 y G3 las diferencias entre puntuaciones son estadísticamente significativas en las estrategias de la elaboración, la planificación, el seguimiento - regulación y entorno de estudio (p < .05); el tamaño del efecto es entre débil y moderado (.10 < r < .30). El alumnado del grupo algebraico G3 obtiene puntuaciones estadísticamente superiores en las cuatro estrategias mencionadas. En cambio, en la estrategia cognitiva de la organización y los recursos de ayuda no se han detectado diferencias (p > .05). Destaca, por tanto, la importancia de la diferencia en el empleo de estrategias metacognitivas a favor del alumnado que se incluye en el G3, además de la superioridad en la estrategia cognitiva de la elaboración.
4. Discusión
En lo respectivo a la distribución de los grupos de resolución por curso académico, los resultados obtenidos en el presente estudio indican que el empleo del álgebra es mayor en el curso 4º de la ESO que en 2º y también en 3º que en 2º; es decir, el grupo de resolución G3, que se corresponde con un perfil algebraico, es más numeroso tanto en 4º como en 3º en comparación con 2º. Por esta razón en 2º de la ESO predomina el grupo de resolución sin perfil definido (G1). Este grupo está caracterizado por no resolver sistemáticamente los problemas ni algebraicamente, ni aritméticamente, ni tampoco alternando los dos procedimientos de resolución. En este caso, el uso del álgebra crece a medida que el curso aumenta. Esta tendencia concuerda con lo descrito por Chen (1999) en el sentido de que el alumnado de cursos más avanzados es más eficiente debido a su capacidad para inducir un esquema general más sofisticado a partir de diversas operaciones de procedimiento; por tanto, más eficaces en la elección de la estrategia de resolución esencial entre los diversos problemas de origen. Dicho autor conecta estos datos con el hecho de que el conocimiento del alumnado más joven esté estrechamente relacionado con situaciones específicas y no con patrones.
La enseñanza - aprendizaje de las matemáticas representa uno de los bloques principales en la ESO. En este marco educativo, la resolución de problemas es una cuestión de gran importancia para el avance de las matemáticas y también para su comprensión y aprendizaje (BOPV, 2007). Tomando como referencia el currículo y con el fin de entender la evolución que puede haber de 2º de la ESO a 4º en la cuestión de la resolución de problemas aritmético - algebraicos, no se ofrece información significativa que especifique las diferencias entre los diferentes cursos. Acorde con los datos presentados, parece razonable suponer que a medida que el curso es superior se aprende a resolver problemas de mayor complejidad (como problemas con varias variables o ecuaciones de segundo grado), pero no se describen los cambios o exigencias relacionadas con los problemas de álgebra iniciales, de una sola incógnita, precisamente los problemas seleccionados para esta investigación. Parece lógico suponer que la práctica en la resolución de problemas mediante el procedimiento algebraico, unida a una mayor complejidad de los problemas, puede conllevar un empleo del álgebra más sistemático en problemas más “sencillos”. Los resultados obtenidos en este estudio corroboran esta hipótesis pero con matices; la puntualización puede deberse a la inclusión de métodos heurísticos en el currículo.
Los métodos heurísticos de resolución buscan la solución de un problema mediante técnicas no rigurosas como pueden ser el ensayo - error, reglas empíricas, diagramas, etc. En todos los cursos analizados, el currículo menciona estos métodos como parte de los contenidos a dominar en la parte concerniente a la resolución de problemas con el objetivo de reflexionar sobre el proceso de resolución de problemas (BOPV, 2007).
El estudio de esta dualidad a la hora de enfrentarse a un problema representa la aportación principal de la presente investigación y tiene como referente al grupo de resolución de perfil mixto (G2). Según Radford (2011) el pensamiento algebraico no es natural en el sentido de que no se tiene porqué desarrollar una vez que los estudiantes hayan madurado lo suficiente y lo califica como reflexión y acción cultural muy sofisticado.
Como se ha resaltado anteriormente, los resultados de esta investigación muestran la tendencia creciente a resolver los problemas algebraicamente al confrontar 2º de la ESO con los otros dos cursos superiores; no ocurre lo mismo en la transición de 3º a 4º. En este caso, mientras el grupo de perfil de resolución no definido se mantiene estable, la diferencia más significativa se produce en que el grupo de perfil mixto decrece en el paso a 4º en la misma medida que el grupo de perfil algebraico aumenta. La inclusión en esta investigación del grupo de resolución mixto constata el máximo que alcanza en 3º. Una explicación integral de este fenómeno debe analizar tanto el crecimiento del grupo en cuestión de 2º a 3º como el decrecimiento de 3º a 4º; la primera variación se puede interpretar como un aumento de la habilidad de resolución algebraica, acorde al cambio de curso, al mismo tiempo que se siguen utilizando técnicas informales debido todavía al peso de la experiencia previa en aritmética. Esto permite un mayor nivel de elección; la segunda fluctuación, esta vez descendente, parece deberse a una consciencia y control mayor sobre el poder de resolución algebraico logrado durante los dos cursos anteriores, relegando así los procedimientos aritméticos.
No obstante, y como se ha mencionado en el marco teórico, la dudosa eficacia de los modelos heurísticos generales planteados en la ESO no significa que una buena instrucción en dichos procedimientos no favorezca la competencia en resolución de problemas. De hecho, varias investigaciones han mostrado que un entrenamiento en el aula tanto en heurísticos como en estrategias de aprendizaje resulta efectivo en este sentido (Kramarski & Mevarech, 2003; Perels, Gürtler & Schmitz, 2005). Es necesario apuntar que los heurísticos ejercitados en dichos estudios son más elaborados y menos generales que los planteados en el currículo analizado.
A continuación, se discuten los resultados obtenidos en el empleo de estrategias de aprendizaje en matemáticas en función del grupo de resolución. Los resultados dibujan dos variaciones claramente diferenciadas entre los grupos de resolución con respecto a las estrategias de aprendizaje: por una parte, la concerniente a los grupos de resolución algebraico y mixto y, por otra, la correspondiente a los grupos algebraico y mixto en oposición al grupo de perfil no definido.
En primer lugar, se confirma que el conjunto de alumnado de perfil algebraico (G3) hace un uso mayor de las estrategias metacognitivas (planificación y seguimiento - regulación) que el grupo que alterna los procedimientos algebraicos y los aritméticos (G2 o grupo mixto), siendo ambas diferencias moderadamente relevantes. Esto se traduce en que los integrantes del grupo algebraico conocen y controlan los mecanismos de procesamiento de la información de una forma más eficaz que el alumnado perteneciente al grupo mixto. Además, también moderadamente, el alumnado que resuelve algebraicamente destaca también en la estrategia cognitiva de elaboración y en la de entorno de estudio y tiempo de estudio (débilmente) con respecto al conjunto que resuelve alternativamente. En el caso de la elaboración, el grupo de perfil algebraico evidencia mayor competencia relacionando y transformando los conocimientos matemáticos con el fin de lograr una mayor comprensión tanto de la propia materia como de otras.
La investigación previa, aunque ofrece una visión general de la relación entre la cognición - metacognición y la resolución de problemas matemáticos, no concreta la influencia que pueda tener el procedimiento para resolver dichos problemas, es decir, no discrimina entre un perfil de resolución algebraico y un perfil mixto. De hecho, no se han encontrado estudios que indaguen en la conexión entre la manera de resolver los problemas y la frecuencia en el uso de las estrategias de aprendizaje.
Volviendo a los datos obtenidos, los resultados logrados en la estrategia de elaboración y las dos de metacognición a favor del grupo de resolución algebraico frente al mixto resultan esclarecedores. A priori, se podría intuir que el alumnado que domina varias técnicas de resolución es más flexible y tendría más posibilidades de elección y de transformación del problema, propiedades asociadas a las estrategias referidas. Sin embargo, como se ha mencionado anteriormente, ciertos estudios parecen indicar que el empleo de heurísticos en la actual Educación Secundaria se limita a una instrucción escasa, rutinaria y parcial. En cambio, el método algebraico de resolución es efectivo y versátil, una vez superadas ciertas dificultades asociadas a su abstracción. En vista de los resultados, se podría inferir una interpretación alternativa de la flexibilidad en la resolución de problemas verbales aritmético - algebraicos. Dicha apreciación consiste en considerar el método algebraico como un procedimiento flexible tanto en la elección de las variables como en la ecuación; el álgebra ofrece la posibilidad de reformular ambos elementos indispensables para el planteamiento del problema y su resolución.
En segundo lugar, se observa que el grupo de perfil no definido (G1) obtiene medias inferiores que los grupos de perfil algebraico (G3) y de perfil mixto (G2) en organización, elaboración, organización, seguimiento - regulación, recursos de ayuda y entorno de estudio y tiempo de estudio, es decir, en todas exceptuando en la repetición. Es importante destacar que la relevancia de la diferencia es fuerte en todos los casos mencionados. Teniendo en cuenta la coincidencia de resultados en ambos grupos con respecto a G1, es razonable pensar que la diferencia se puede deber al rendimiento académico en matemáticas. A partir de la década de los 80, la metacognición se ha asociado a un mayor rendimiento en matemáticas (Areepattamannil & Caleon, 2013; Murayama et al., 2013). De la misma manera, la estrategia cognitiva de elaboración tiene más peso en el aprendizaje de las matemáticas en el alumnado con mayor rendimiento (Thiessen & Blasius, 2008). Este resultado coincide con la investigación de Czuchry & Dansereau (1998) aunque no con Chiu et al. (2007) que no encuentran relación probablemente porque no se distingue adecuadamente entre las estrategias de repetición y de elaboración, existiendo una alta correlación entre ambas. Incluso Areepattamannil y Caleon (2013) dan cuenta de un efecto negativo en el rendimiento de esta estrategia cognitiva achacándolo a que pueda estar eclipsada por el uso del control metacognitivo, es decir, una disminución de la elaboración puede ir acompañada de un aumento en el rendimiento debido al efecto positivo de las estrategias de control metacognitivas.
Por lo indicado previamente, la excepción se ha producido en la estrategia cognitiva de repetición en la que no se observan variaciones inter - grupos de resolución en la presente investigación. La ausencia de diferencias en dicha estrategia es perfectamente consistente con la explicación basada en el menor rendimiento del grupo sin perfil de resolución definido con respecto a los otros dos grupos. De hecho, el empleo de la estrategia de repetición está asociado negativamente con el rendimiento en matemáticas en el sentido de que memorizar es una estrategia ineficaz para el aprendizaje de nociones nuevas (Chiu et al., 2007). Según el NCTM (2000), el alumnado que memoriza procedimientos matemáticos no sabe ni cómo ni cuándo emplear lo que sabe y, por tanto, el aprendizaje no es efectivo. Asimismo, el Informe PISA (2009) advierte de que el empleo asiduo de la estrategia de repetición no se corresponde con mayor rendimiento en matemáticas. No conviene olvidar que la repetición se ha definido como estrategia de procesamiento superficial (Schiefele, 1991).
Sin embargo, Areepattamannil y Caleon (2013), a pesar de que aceptan que la memorización reduce el tiempo de procesamiento que puede ser asignado a las estrategias de aprendizaje profundo, no descartan la posibilidad de que el uso de esta estrategia pueda ser útil en el aprendizaje de conceptos introductorios en las matemáticas y en la construcción de conocimientos previos que puedan facilitar la aplicación de estrategias de aprendizaje profundo. Murayama et al. (2013) advierten de que las estrategias superficiales son adaptativas en algunas tareas (por ejemplo, de habilidad) o en las etapas iniciales de aprendizaje.
Por último, las estrategias de recursos de ayuda y ambiente y tiempo de estudio también adquieren importancia en el momento de superar las dificultades que entraña la resolución de problemas (Puteh & Ibrahim, 2010).
No se deben dejar de mencionar las limitaciones de este estudio; convendría ampliar la gama de problemas de cara a cerciorarse si ampliar o no la casuística de los grupos de resolución, así como aplicar el cuestionario a una muestra más extensa.
Como conclusión a las aportaciones expuestas, cabe destacar el aprendizaje estratégico del alumnado que resuelve los problemas algebraicamente frente al grupo que alterna aritmética y álgebra; esta diferencia está mediada por las estrategias de aprendizaje de alto nivel como son la elaboración y la metacognición. Por otro lado, asociado a un menor empleo de las estrategias, se infiere un menor rendimiento en el aprendizaje por parte del alumnado que no emplea adecuadamente ninguno de los dos procedimientos de resolución. Estos datos pueden ser un referente educativo en el sentido de que fomentar y reforzar el aprendizaje del álgebra en la resolución de problemas aritmético - algebraicos deriva en un aprendizaje más autónomo y de mayor control sobre el conocimiento. Dicha instrucción algebraica puede ser apoyada con técnicas aritméticas para introducir el problema o para comprobar ciertos resultados, pero no debería sustituir el método algebraico como procedimiento de resolución de primer orden.











 nova página do texto(beta)
nova página do texto(beta)