1. Introducción
Los resultados de investigación en matemática educativa, ya sean teóricos o prácticos, no son inmediatamente transferibles al aula. De hecho, al implementar un diseño innovador, fundamentado en la investigación, se debe considerar a la escuela como un escenario que impone ciertas condiciones en su funcionamiento y al profesor como la figura en quien se deposita la mayor responsabilidad de la actividad didáctica escolarizada (Montiel, 2010). En ese sentido, la investigación basada en el diseño se perfila como una vía de innovación, en tanto busca incrementar el impacto, la transferencia y la traducción de la investigación educativa en la mejora de la práctica, enfatizando la necesidad de construir teoría y principios de diseño que guíen, informen y mejoren, tanto la aplicación como la investigación en contextos educativos (Anderson & Shattuck, 2012).
En este artículo, presentamos una investigación basada en una propuesta teórica-didáctica que asume a la experiencia de aprendizaje como la participación de prácticas donde el conocimiento se pone en uso. La funcionalidad-trigonométrica (FT) es el planteamiento de Montiel y Buendía (2013) sobre la construcción social de la función trigonométrica, y que fundamentan en investigaciones enmarcadas en la teoría socioepistemológica.
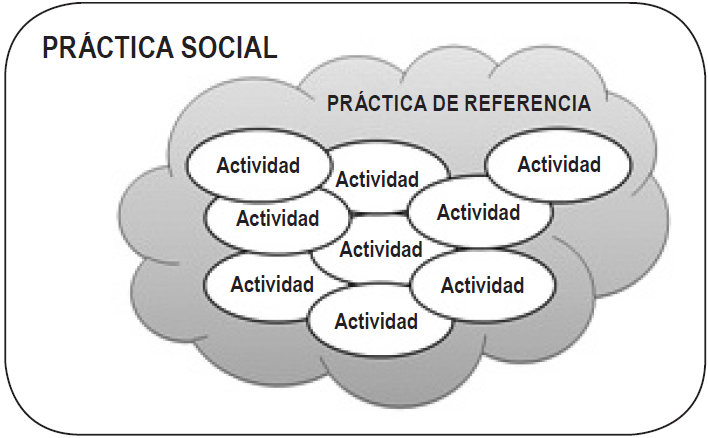
La situación-problema que diseñan las autoras en su planteamiento busca que el estudiante construya los significados que le son propios a esta función y que le den uso y sentido dentro y fuera de la matemática escolar. Esta propuesta se enmarca en el momento histórico de predicción que Montiel (2011) caracteriza haciendo uso de un modelo para la construcción social de conocimiento trigonométrico (Figura 1).
En este modelo, la autora identifica actividades como la medición, comparación, cálculo, aproximación, experimentación, graficación y modelación. Éstas están articuladas intencionalmente para cumplir el propósito específico de matematizar la física, en particular, para matematizar el movimiento oscilatorio, a lo que denomina como práctica de referencia. A su vez, reconoce que la práctica de referencia y sus actividades están normadas por la práctica social de la predicción, entendida como la necesidad de conocer un estado futuro con base en el presente y las variaciones de su pasado.
Se identifica una clara relación entre las actividades del modelo y las actividades didácticas incluidas en la situación-problema diseñada por Montiel y Buendía (2013), con excepción de la modelación. Dado que el modelo de Montiel se desarrolla a partir del estudio de la construcción social del conocimiento trigonométrico en escenarios históricos, la modelación se reconoce como una actividad científica y no se le presenta con una caracterización explícita y detallada. Sin embargo, al transitar a un escenario escolar, reconocemos que la modelación no constituye una actividad definida y controlada por el alumno, sino que se integra en todo el proceso de enseñanza-aprendizaje y, en ese sentido, toma un carácter didáctico, no necesariamente matemático.
La investigación se plantea entonces responder a la pregunta: ¿Qué caracteriza a la modelación cuando la actividad matemática se sitúa en un escenario escolar? Para dar respuesta, llevamos a cabo la puesta en escena formulada por las autoras recién mencionadas y, con base en la evidencia recolectada y su análisis, nos proponemos validar o robustecer la epistemología de prácticas configurada para explicar lo social de la función trigonométrica. Para atender ambos propósitos, fue necesario articular la propuesta teórica de las autoras con un constructo teórico sobre la modelación que nos permitiera analizar la actividad matemática de las estudiantes.
2. Fundamentación teórica
La FT es un planteamiento sobre la construcción social de la función trigonométrica desarrollado en el marco de la Teoría Socioepistemológica de la Matemática Educativa (Reyes-Gasperini y Cantoral, 2014; Cantoral, 2013; Cantoral & Farfán, 2004, 2003). Esta teoría se ocupa del estudio de fenómenos didácticos ligados al saber matemático y descansa en cuatro principios, tres de los cuales explican el porqué de los datos recolectados y su análisis a la luz de una epistemología de prácticas.
Por el principio de la “racionalidad contextualizada”, se reconoce que la racionalidad con la que se actúa depende del contexto en el que el individuo se encuentre en un momento y lugar determinado (Espinoza-Ramírez, 2009). Se asume la legitimidad de toda forma de saber, sea éste popular, técnico o culto, pues considera que, en su conjunto, constituyen la sabiduría humana (Cantoral, 2013). Por ello, se reconoce que la validez de dicho saber es relativa al individuo, como sujeto social, por lo que depende en gran medida del marco de referencia y del grupo social-cultural del cual su conocimiento emerge. Éste constituye el principio del “relativismo epistemológico” considerando entonces que el sujeto no sólo desarrolla conocimiento dentro de la escuela, sino que se encuentra en constante significación de los objetos sobre los que actúa, aun si lo hace de forma inconsciente. Esta dinámica de significación está en la base misma del desarrollo del pensamiento (Cantoral, 2013), por ello supone un principio de “resignificación progresiva”.
Consecuente con estos principios, se produce una descentración del objeto matemático (escolar). A partir de la evidencia recolectada y estudiada en las últimas décadas, se reconoce que el problema educativo no es el de la constitución de dicho objeto, sino el de su significación compartida mediante el uso culturalmente situado, dentro y fuera del aula, y a lo largo de todas las actividades de la vida diaria del aprendiz. En esta dirección, la FT constituye lo que en la teoría se denomina como epistemología de prácticas, es decir, una explicación sobre la construcción de los significados que le dan uso y sentido a la función trigonométrica, al seno de la actividad humana organizada en prácticas y normada por prácticas sociales, por lo que el principio normativo de la práctica social se manifiesta en la intencionalidad del diseño mismo; es lo que hace al aprendiz hacer lo que hace.
2.1. Funcionalidad-Trigonométrica
A nivel teórico, Buendía y Montiel (2011) comienzan esta propuesta analizando la actividad matemática retratada en la obra Introductio in analysin infinitorum (1748) de Euler. En sus trabajos, el conocimiento trigonométrico se introduce al cuerpo de la familia de funciones, sin embargo, en esta obra en particular, hace una presentación sistemática y ordenada de las herramientas, nociones y conceptos, incluida la relación funcional trascendente trigonométrica. En este estudio de corte histórico, las autoras identifican las propiedades periódica y acotada, y el uso de la unidad de medida como elementos de significación de la función trigonométrica, señalando que:
El uso de la unidad de medida (ángulos/radianes) es totalmente contextual y el reconocimiento de una propiedad, como la periódica, está más relacionado con el estudio y análisis del comportamiento del objeto matemático (la gráfica, por ejemplo) que con saber cómo aplicar la fórmula periódica en él. (p.76)
A partir de esto, las autoras analizan la evidencia de situaciones experimentales con estudiantes y profesores, y robustecen su propuesta con el estudio de las variaciones sucesivas en un comportamiento oscilatorio, en lo que denominarán como Funcionalidad-Trigonométrica (Montiel y Buendía, 2013). Las autoras establecen, particularmente para las funciones seno y coseno, que el estudiante construye la FT cuando:
Estudia lo trigonométrico desde un acercamiento variacional al movimiento oscilatorio, en donde se reconozca que el comportamiento trigonométrico se caracteriza y se distingue de otros comportamientos (algebraicos o trascendentes) por su variación y sus variaciones sucesivas, esto es, por cómo cambia y cómo cambian sus cambios.
Identifica una unidad mínima de análisis del comportamiento que le permite predecir al trabajar con objetos periódicos. La predicción se favorece por la distinción entre el “se repite” y el “cómo se repite”.
Reconoce lo acotado del comportamiento en el análisis de los datos en relación a las condiciones del experimento.
Hace uso de la unidad de medida adecuada a la experiencia física y la reconoce; en la relación tiempo-distancia y en la representación gráfica de los datos obtenidos del experimento.
Es posible identificar en estos elementos las propiedades de la función trigonométrica. Todas ellas son susceptibles de construirse sin interacción directa con los objetos matemáticos escolares, pero son la base para dotar de significado a la función como tal.
Con base en la clasificación de las propias autoras, la situación-problema puede considerarse un diseño experimental que, al igual que la propuesta de Grabovskij y Kotel’Nikov (1971), despojaría al estudio de lo trigonométrico, en el contexto físico, de las nociones geométricas que pueden llegar a causar dificultades en los estudiantes. Sin embargo, recientes investigaciones (Weber, 2005; Moore, 2014) han mostrado que la articulación coherente entre nociones geométricas y nociones de precálculo puede generar significados más robustos de la función trigonométrica en el estudiante. Éstas últimas, junto con los resultados de la presente, están siendo consideradas en la planeación de momentos de institucionalización de futuras experiencias de investigación basada en el diseño.
2.2. Modelación
Desde el enfoque teórico de la socioepistemología, se han realizado investigaciones dentro de las cuales la modelación juega un papel importante. Con los trabajos de Suárez y Cordero (2008), se inició una línea de trabajo sobre la “graficación-modelación”, donde muestran claramente el cambio de centración de los conceptos matemáticos a las prácticas, lo que implica considerar a las matemáticas como una herramienta para modelar. Por ejemplo, en esta investigación, Suárez y Cordero no declaran el estudio de los procesos de enseñanza-aprendizaje del concepto de función, sino que estudian las construcciones de los estudiantes cuando éstos modelan el movimiento en un ambiente tecnológico que favorece la toma de datos, la graficación y sus análisis. Para los autores, la modelación es “una construcción de conocimiento cuando un individuo enfrenta a una tarea matemática en la que pone en juego un saber”, perspectiva que, si bien encuadra con nuestras consideraciones teóricas de partida para la construcción de la FT, no nos permitía delimitar qué de la actividad se podría considerar modelación.
De una amplia revisión de diversas perspectivas sobre la modelación, tomamos el planteamiento de Confrey y Maloney (2007), aun cuando se posiciona en enfoques teóricos distintos, dado que comparte con la socioepistemología una postura respecto a la naturaleza del conocimiento matemático y a que su caracterización de la modelación permite delimitar cuándo se logra la modelación y qué es un modelo. Los autores parten de considerar a las matemáticas como una herramienta que permite a las personas darle sentido a su experiencia, adquirir juicios predictivos y ofrecer explicaciones, además de contribuir a su habilidad de identificar, dirigir y resolver problemas que se presentan en su entorno cultural y cotidiano.
Para Confrey y Maloney (2007) la modelación matemática es:
[…] el proceso de encontrarse con una situación indeterminada, problematizarla y hacer uso de la investigación, el razonamiento y estructuras matemáticas para transformar la situación. La modelación produce un resultado -el modelo- que es una descripción o una representación de la experiencia de la persona, que en sí misma ha cambiado a través del proceso de modelación.
La modelación no depende del mapeo a una definición particular de realidad en la teoría o para la evaluación. En su lugar precisa de la coordinación de resultados justificados con el método de investigación para proporcionar un medio que sirva para hacer frente a los problemas pendientes. Lo que se produce, representa y registra en la investigación de una situación indeterminada es un conjunto de representaciones que en sí mismas son artefactos clave en el proceso de modelación. Estos incluyen observaciones, respuestas, medidas, interacciones, indicadores y descripciones. Juntos pueden ser descritos como datos, sistemas de codificación, métodos de muestreo y colección de datos. Estos son típicamente mediados por varias tecnologías y son cercanos a los fenómenos observados, pero no son los fenómenos en sí mismos. Es a través de la coordinación de estos artefactos clave, junto con los medios para relacionarlos a través de la investigación, el razonamiento y la experimentación, que la situación indeterminada se convierte en una situación determinada, el todo unificado al que llamamos modelo (p. 60).
En el análisis que hacen de las experiencias didácticas, los autores no se refieren a un conocimiento matemático institucionalizado que se aplique y resuelva la situación, sino aquéllos de los que hace uso el estudiante, pero que le permiten lograr la modelación. De igual forma, no reconocen “un único” modelo válido, sino “el modelo del estudiante”, dándole igual valor a una fórmula que a un dibujo, siempre que estos sean la vía de transformación de la situación. Ambas consideraciones se corresponden con nuestros principios de racionalidad contextualizada y relativismo epistemológico, sin embargo, ampliamos la mirada de la modelación de la situación a la modelación para el desarrollo de un tipo particular de pensamiento matemático.
3. Consideraciones metodológicas
El estudio que aquí reportamos es un momento de un programa más amplio de investigación sobre la “Construcción Social de Conocimiento Trigonométrico”. Los resultados aportan a su avance, a la ampliación de las explicaciones a los fenómenos didácticos y al reconocimiento de piezas fundamentales para el rediseño pertinente del discurso matemático escolar. Es decir, no se concibe como una investigación con principio y fin, mucho menos presentamos resultados universales.
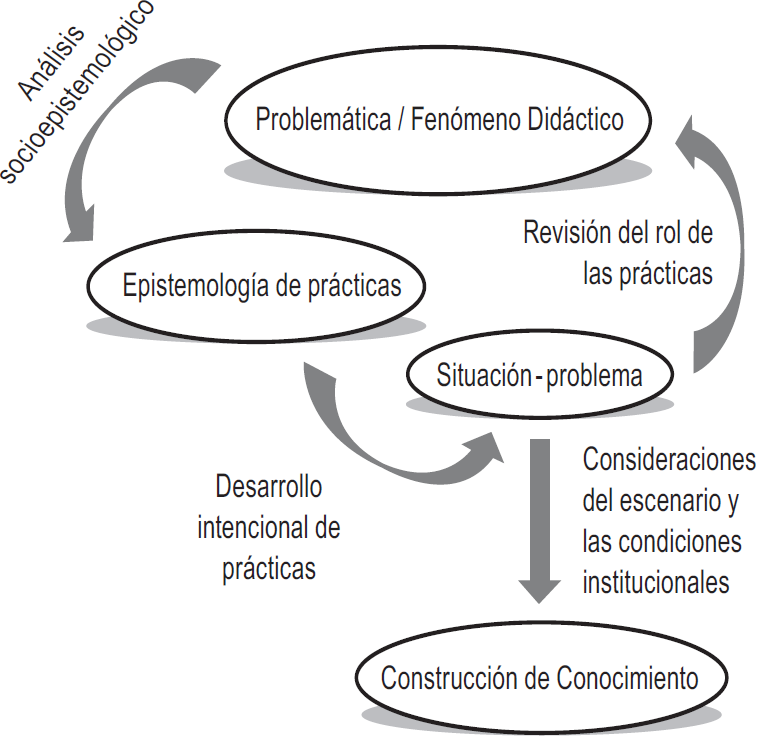
Este programa de investigación se conduce por una propuesta metodológica (Montiel y Buendía, 2012) que se ha ido configurando al seno de la socioepistemología (Figura 2). En particular, ubicamos el presente estudio en el momento que va de la situación-problema a la construcción de conocimiento, tomando en cuenta las condiciones del escenario en donde se realizó la puesta en escena. Las situaciones-problema pueden ser entendidas como un conjunto de condiciones de un fenómeno o preguntas que propician una problematización y serán el instrumento que permita el desarrollo de acciones en el sistema didáctico (Suárez, 2008).
Desde su planeación y diseño, una situación-problema debe dar cuenta de la resignificación del conocimiento matemático en juego, en tanto está fundamentada en una “epistemología de prácticas” producto de un “análisis socioepistemológico”. Para llevar a cabo una experiencia didáctica con ella, buscando la construcción del conocimiento mismo, tendrá que considerarse ampliamente al escenario y a las condiciones institucionales para lograr no sólo la innovación, sino un entendimiento amplio de cómo, cuándo y por qué la innovación funciona. Esta innovación, fundamentada teóricamente, nos ayuda a entender las relaciones entre la teoría educativa, los diseños instruccionales y la práctica. En ese sentido, el diseño de la situación-problema y el análisis de su implementación son fundamentales para validar y robustecer las epistemologías de prácticas propuestas, revisando el rol de las prácticas en el entendimiento y la explicación de la problemática inicial de investigación o los fenómenos didácticos identificados.
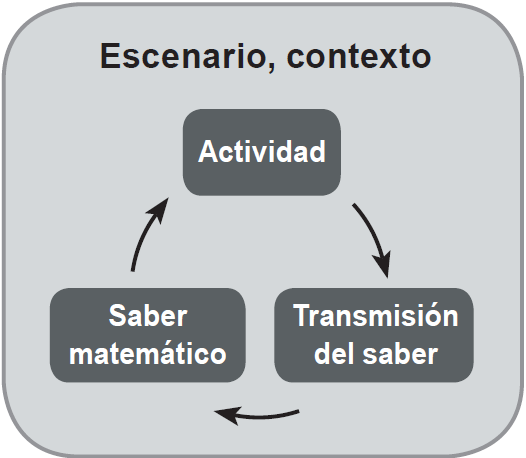
En nuestra investigación, el análisis de la experiencia didáctica hace uso de la unidad conformada por la interacción entre la actividad observable de los individuos, la intencionalidad explícita de transmitir un cierto conocimiento y el saber matemático en juego relativo al escenario (Figura 3), con el objetivo de identificar y explicar acciones y argumentaciones de los estudiantes relativas a la matemática en juego.
3.1. Población estudiantil
La investigación se llevó a cabo en el Instituto de Educación Media Superior del Distrito Federal (IEMS-DF), Plantel Iztapalapa 1, institución donde el docente se contrata de tiempo completo y desarrolla de manera obligatoria actividades de docencia, tutoría e investigación. La primera autora del presente artículo es profesora de esta institución y el estudio que aquí reportamos se llevó a cabo durante su curso de Matemáticas IV, correspondiente al cuarto semestre y en el que se abordan contenidos de precálculo.
El grupo completo estuvo conformado por quince estudiantes, en edades que variaban entre 16 y 22 años; fueron cuatro hombres y once mujeres. Todos ellos habían tomado tres cursos de matemáticas previamente, relacionados con aritmética, razones y proporciones, y geometría analítica; pudiendo estar en el curso sin haber aprobado uno, dos o los tres cursos. Cinco de estas estudiantes conformaron el grupo tutoral y fue con ellas que se realizó el estudio que aquí reportamos. Se trabajó con ellas durante las 15 sesiones correspondientes a la tutoría y durante seis sesiones regulares de clase donde ellas apoyaron al grupo completo para llevar a cabo la experiencia didáctica.
Para mantener la privacidad de las tutoradas, cambiaremos sus nombres, nos referiremos a ellas como Luz, Emi, Sara, Ana y Fer. Ellas asisten a la tutoría por decisión personal, no son elegidas del grupo completo, por eso se les reconoce como un tipo de organización estudiantil propia del sistema del IEMS-DF.
3.2. Adaptación y organización didáctica
Nuestro camino metodológico comienza con la adaptación de la situación-problema de Montiel y Buendía (2013), estimando las condiciones de nuestro escenario escolar. Se conservaron las mismas actividades y preguntas, pero se decidió incluir la experimentación con el péndulo y el manejo de tecnología (calculadora de capacidad gráfica, sensor de movimiento y programa de videos), y no dejar sólo los dibujos del experimento, para que las propias tutoradas obtuvieran los datos y las gráficas incluidas en cada actividad. Para incorporar la experiencia de resolución de la situación-problema al curso de Matemáticas IV, de manera que se integrara de forma natural, fue necesario hacer una planeación cuidadosa del contenido y las estrategias didácticas de todo el semestre. Esto se logró tomando el libro de Salinas, Alanís, Pulido, Santos, Escobedo y Garza (2007) como base de las actividades de clase. Este texto propone un acercamiento al precálculo con el estudio de fenómenos de cambio, se identifica y se analiza cómo se relacionan las cantidades en problemas particulares de cambio y variación.
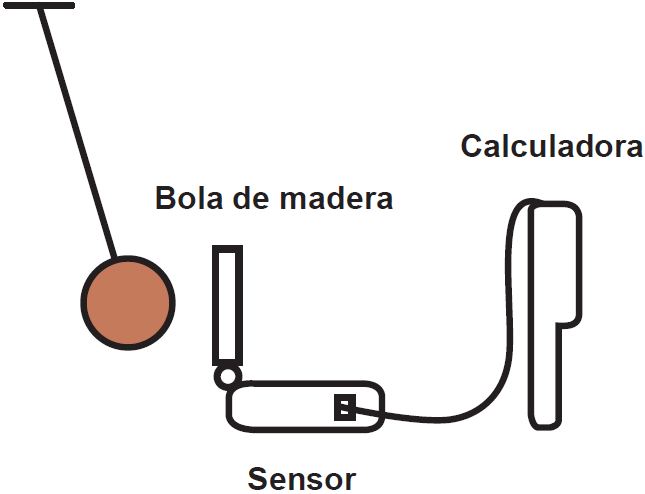
Se instaló el montaje del péndulo en un cubículo de profesor (Figura 4), de manera que fuera posible colocar un sensor de movimiento al lado del péndulo y que la distancia a la que se encontrara permitiera la toma de datos (las distancias entre el sensor y la bola), sin interferencias. El montaje quedó fijo en el cubículo con la finalidad de que no hubiera variaciones en las condiciones de la toma de datos durante las sesiones. Controlar esta variable de la experiencia fue fundamental para lograr la puesta en escena en los tiempos escolares que tenemos permitidos tanto para la tutoría como para la clase de matemáticas.
Se tomó en cuenta la sugerencia de Garrido (2010) de colocar el sensor a una distancia mayor de 50 cm., de la bola en reposo y que el ángulo al que se suelte el péndulo sea de 15°. La distancia a la que se colocó el sensor en nuestro montaje fue de aproximadamente 70 cm., respecto del péndulo en reposo.
3.3. Recolección y organización de datos
Se filmaron los momentos de experimentación y resolución de la situación-problema en las sesiones de tutoría y en el momento de apoyo al grupo completo. En total, se obtuvieron 14 horas de videograbación para analizar el papel de la modelación en la actividad de este pequeño grupo.
Se prepararon hojas de trabajo con la situación-problema que incluían la descripción de la experimentación con el péndulo de donde se tomaron los datos, las gráficas obtenidas (aunque hechas con otro programa de cómputo para tener una mejor resolución de la imagen) y espacio suficiente para los procedimientos, los dibujos, las respuestas y los argumentos verbales solicitados para dar respuesta a las preguntas de cada actividad. Debido a la dinámica escolar de trabajo con el grupo de tutoría, se espera que lo plasmado por las estudiantes en las hojas de trabajo sea muy similar porque trabajaron en equipo, sin embargo, se analizan como registros personales porque se asume que al plasmarlo en las hojas personales están de acuerdo en que ésa es la forma correcta de presentar lo trabajado como grupo.
Para transformar los registros en datos, se construyó una tabla que organizaba por actividad de la situación-problema lo siguiente:
3.4. Análisis de los datos
El pensamiento funcional trigonométrico es un tipo particular del pensamiento matemático, entendido éste como todas las formas posibles de construir ideas matemáticas, incluyendo procesos avanzados del pensamiento como la abstracción, justificación, visualización, estimación y razonamiento bajo hipótesis (Cantoral, Farfán, Cordero, Alanís, Rodríguez y Garza, 2005). En consecuencia, y como plantean Montiel y Buendía (2013), es necesario poner atención en las argumentaciones, los procedimientos y las explicaciones que el alumno configura, en forma escrita, icónica, corporal o verbal para responder a una tarea específica y que son vistos como los artefactos clave que señalan Confrey y Maloney (2007). Esto es visto como la actividad de las estudiantes que, en interacción con la situación -problema, su intencionalidad y la organización didáctica (polo de transmisión del saber), y la FT (polo del saber matemático a construir), constituye nuestra unidad de análisis dentro del escenario escolar del IEMS-DF y el contexto de estudio del cambio, y la variación del movimiento del péndulo.
Se distinguen dos momentos en el análisis de la experiencia didáctica. El primero consiste en la resolución de la situación-problema por parte de las tutoradas y, el segundo, de su participación como apoyo en la puesta en escena con el grupo completo. En cada momento, se organizan y analizan las producciones (qué hacen) escritas y verbales en relación con los cuatro elementos de la FT, tomando en consideración su intencionalidad (para qué lo hace) y las herramientas y estrategias que utiliza (cómo lo hace).
4. Matematización del movimiento del péndulo
En un escenario histórico, Montiel (2011) estudia e identifica en un quehacer científico la matematización de la física (específicamente la del movimiento oscilatorio) como la práctica de referencia que, normada por la predicción (práctica social), articula actividades (como la modelación) de las que emerge la función trigonométrica como herramienta matemática. Esta epistemología se basa en identificar históricamente el contexto donde se desarrolló una concepción matematizable del movimiento. De ahí que en la propuesta didáctica de Montiel y Buendía (2013) se proponga dicho contexto a través de la experimentación con el péndulo y el estudio de su movimiento, sus cambios y variaciones.
A la luz de nuestro estudio, asumimos a la matematización como la tarea de comprender e interactuar con la situación-problema. Esto implica partir de la interpretación y el lenguaje de las estudiantes, y hacer emerger, en cada actividad, significados a partir de un desarrollo de usos del conocimiento matemático en juego. En particular, se propone como la situación indeterminada o desconocida la matematización de un tipo particular de movimiento, a propósito de formar parte de un curso donde se estudiaron distintos tipos de movimiento y ello supone aprender un nuevo conocimiento con cada uno. Es importante señalar que, desde el diseño original, el estudio del movimiento del péndulo busca intencionalmente la resignificación de la función trigonométrica al seno de la matemática escolar, es decir, de aquéllo que da uso y sentido a la función. Claramente un estudio que pretenda el entendimiento del fenómeno físico al seno de la física escolar haría emerger herramientas matemáticas más complejas, de ahí la importancia de los enfoques transversales en la educación en el nivel medio superior, donde los tópicos científicos pueden abordarse de forma integral.
Considerando que “las transcripciones no son descripciones neutras, sino que se le integran supuestos teóricos sobre la naturaleza de las interacciones” (Ochs, 1979, citado en Barwell, 2009) y, como señala Barwell, “sirven para construir los estados mentales, tanto explícitos como implícitos, de los participantes de un estudio” (p. 259), realizaremos en esta sección la descripción de cómo enfrentan las tutoradas la situación indeterminada, vía la resolución de la situación-problema, como el análisis de datos que dé cuenta del desarrollo del pensamiento funcional-trigonométrico y del papel que juega un proceso de modelación. Éste podría servir también para el análisis retrospectivo del diseño y su adaptación para nuevas experiencias y escenarios educativos, pero no es el propósito del presente artículo.
4.1. Actividad 1
Dado que es la actividad inicial, se retoma la experiencia de las tutoradas con el péndulo y se establecen algunas condiciones iniciales. Inmediatamente después, se proporcionan los datos con que fue configurada la calculadora para la primera toma de datos (cada segundo, durante 15 segundos), una ilustración del sensor y el péndulo en reposo (Figura 5), y la gráfica 1 que muestra en un plano cartesiano los datos recolectados (Figura 6). A partir de estos dos apoyos visuales, se pregunta a las tutoradas: ¿A qué distancia se encontraba la bola al iniciar la toma de datos? ¿Encuentras en la gráfica todos los datos que describen lo que pasó?
Ambas preguntas tienen el objetivo de provocar una vinculación entre las condiciones del montaje del péndulo y la gráfica de datos, principalmente a través de la lectura de coordenadas en esta última. Para fortalecer este objetivo, se plantea la situación hipotética de una nueva configuración en la calculadora para hacer una segunda toma de datos, ahora cada medio segundo durante 15 segundos, y se le pide al estudiante ubicar en la misma gráfica los datos que se obtendrían.
Con excepción de una, en las preguntas de esta actividad no subyace la intencionalidad de desarrollar algún elemento de la FT, sin embargo, son fundamentales para dar respuesta a las siguientes. En esta primera actividad, se hacen las relaciones entre la gráfica y el experimento, se refina la lectura de las gráficas a nivel global y local, y se muestra el efecto, en la definición de la gráfica, de tomar datos en intervalos cada vez más pequeños. Además, el comportamiento constante de la primera gráfica será el punto de partida y contraste para caracterizar la naturaleza del movimiento que van a estudiar.
La intención de la pregunta “el ir y venir de la bola, ¿cómo se identifica en la gráfica?”, es introducir a las tutoradas en el estudio de los cambios y las variaciones del movimiento del péndulo, y a la identificación de sus particularidades. Cuando la profesora escucha las respuestas del tipo “va y viene” o “se aleja y se acerca”, interviene diciendo “describan cómo sé cuándo va y cómo sé cuándo viene; cuándo se aleja y cuándo se acerca… Eso, anótenlo, usen colores o lo que necesiten”. Con esta intervención, las tutoradas realizan lecturas locales en la gráfica buscando su relación con el experimento y, aunque discuten en conjunto para entender la intervención de la profesora y dar la respuesta apropiada, cada estudiante plantea en las hojas de trabajo su forma particular de responder.
Las respuestas de las tutoradas reflejan estar leyendo las gráficas como alturas en tiempos específicos (valor en el eje horizontal), explicando el ir del péndulo con un alejamiento respecto del sensor y con la altura que sube, en la gráfica, y el venir con un acercamiento y con la altura que baja en la gráfica. Aunque sólo la respuesta de Emi [1] alude a la forma ondulada de la gráfica, las otras respuestas reproducen gráficamente una parte del comportamiento ondulado (Figuras 7 y 8).
[1] Emi: En la gráfica se ve ondulado, cuando sube se aleja y cuando baja se acerca al sensor.
El contexto, el diseño de las actividades, el tipo de preguntas y, en general, la organización didáctica permitieron a las tutoradas el uso de lenguajes informales, cotidianos y escolares para dar respuesta o explicación a la situación. Particularmente, en la primera actividad, para el estudio del movimiento del péndulo y sus cambios, los artefactos clave consistieron en movimientos corporales descriptivo-explicativos, bosquejos gráficos, lecturas locales de la distancia como altura, lecturas globales del comportamiento ondulado y descripciones del acercamiento-alejamiento de la bola respecto del sensor en la gráfica. Considerando el tipo de experimentación, fue natural que se pusieran en funcionamiento las unidades de medida “segundo” y “metro”. A la luz de la FT, esto constituye el “uso situado de la unidad de medida” y se manifiesta en la lectura local sobre la gráfica como una distancia entre la pelota y el sensor en un momento del tiempo durante el movimiento. El uso de esta unidad de tiempo, obviamente, se mantiene durante toda la experiencia porque no hay cambio de situación física de estudio.
4.2. Actividad 2
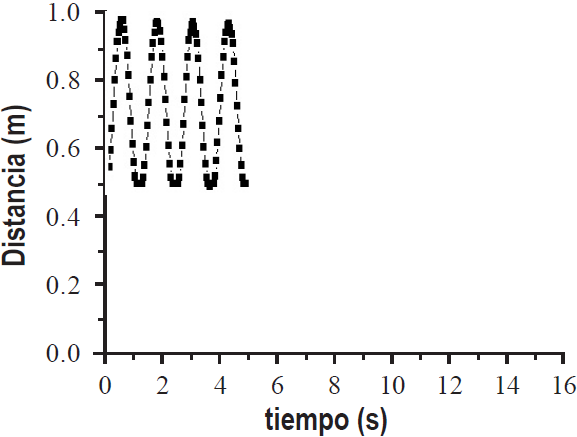
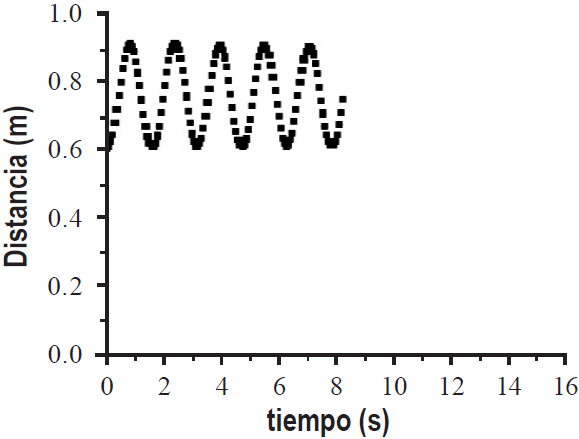
Se inicia la actividad proporcionando una nueva configuración para dos nuevas tomas de datos (cada 0.05 segundos, durante 16 segundos) y sus respectivas gráficas, una ilustración del sensor y el péndulo en movimiento (Figura 9) y las gráficas 3 y 4 que muestran en planos cartesianos los datos recolectados (Figura 10). A partir de estos datos, se les pregunta con respecto a la gráfica 3: En los primeros 5 segundos, ¿cuál es la distancia máxima que se alcanza entre el sensor y la bola? ¿Cuál es la distancia mínima?; en los últimos 5 segundos, ¿cuál es la distancia máxima que se alcanza entre el sensor y la bola? ¿Cuál es la distancia mínima?; ¿cómo explicarías la diferencia entre la distancia máxima (o mínima) de los primeros y la de los últimos segundos?
Estas preguntas tienen la intencionalidad de continuar el estudio de los cambios y las variaciones del movimiento del péndulo, ahora poniendo atención en las distancias máxima y mínima que se alcanzan entre el sensor y el péndulo para ir identificando gradualmente lo acotado del movimiento. Lo primero que reconocen las estudiantes es que las condiciones del experimento que dan lugar a la gráficas 3 y a la 4 son diferentes; todas hacen referencia a que en la toma de datos correspondiente a la gráfica 3 se tenía un popote que ocasionaba fricción y que el movimiento tiende a detenerse, como la respuesta de Emi [2].
[2] Emi escribe: En la gráfica 3, la toma de la distancia cuando se aleja es menor y posiblemente tenga popote porque se nota cómo disminuye su movimiento, aunque se tomaron en el mismo momento y con la misma distancia.
El análisis de los cambios en esta actividad se concreta pidiendo a las tutoradas que marquen con un color sobre la gráfica los puntos donde la distancia crece y, con otro color, los puntos donde disminuye. Con excepción de Sara (Figura 11), las tutoradas marcaron la gráfica indicando las zonas donde “crece” y “decrece” la distancia, términos que ya habían manejado en el curso regular para indicar intervalos en las gráficas.
La actividad se concluye con la pregunta: En las gráficas 3 y 4, ¿cómo determinas si la bola se aleja o se acerca del sensor? Esto con la intención de generar el análisis de los datos respecto de las condiciones del experimento, en particular, para relacionar el alejamiento/acercamiento con las zonas identificadas anteriormente.
En sus respuestas, las tutoradas muestran una asociación correcta entre el alejamiento/acercamiento en el experimento y el crecimiento/decrecimiento en la gráfica, aunque de manera implícita, por ejemplo:
[3] Ana escribe: Cuando crece se aleja, cuando decrece se acerca.
Sólo Sara alude explícitamente a las gráficas y dibuja, a un lado de su respuesta, una sección de la curva para ejemplificar el momento de alejamiento/ acercamiento (Figura 12). Sin embargo, aún en este caso, no se observa que lo identifique como un intervalo de crecimiento/decrecimiento.
En esta actividad se identifican, de nuevo, lecturas locales de la distancia como altura, lecturas globales del comportamiento ondulado y descripciones verbales, ahora en términos de aumento y disminución de la distancia; como los artefactos clave que producen las tutoradas para caracterizar los cambios en el movimiento del péndulo. A ellos, se incorpora la identificación de “zonas” en la gráfica donde hay crecimiento o decrecimiento, que si bien se colorean en trazo continuo no hay evidencia de la consideración del tiempo como intervalo.
Aunque ya se había identificado un significado gráfico al “va y viene” del movimiento, en esta actividad no se hace mención a la “repetición” de zonas de “crecimiento-decrecimiento”, o lo que en términos de la FT se caracteriza como identificar “qué se repite” y “cómo se repite” en el comportamiento en estudio.
Finalmente, lo acotado del movimiento se manifiesta con la localización de las distancias máxima y mínima en la gráfica, tomando los datos de sus medidas. De nuevo, se presenta la lectura de la distancia como altura, pero ahora como la altura vertical entre máximo y mínimo, por ejemplo cuando Sara [4] compara lo que sucede entre los primeros y los últimos segundos de la toma.
[4] Sara escribe: En la gráfica 3, la diferencia entre las distancias máxima y mínima de los primeros segundos a los últimos segundos es que en los últimos segundos ya es más evidente la disminución del movimiento y el rango entre la máxima y la mínima es cada vez más pequeño.
4.3. Actividad 3
Esta actividad inicia proporcionando una nueva configuración para la toma de datos (cada 0.05 segundos durante 15 segundos), sólo que esta vez, a diferencia de las anteriores, la bola cuelga de un cordón cuya longitud del techo al centro de la bola es de 60 cm., (Figura 13). Con esta configuración se obtiene la gráfica 5 (Figura 14), a partir de la cual se plantean las preguntas: (a) ¿Cómo se reflejan, en el comportamiento de las curvas, las distancias más lejanas del sensor? y (b) ¿cómo se reflejan, en el comportamiento de las curvas, las distancias más cortas del sensor?
En sus respuestas, Emi, Ana y Fer describen la curva como yendo hacia arriba cuando la bola se aleja y hacia abajo cuando se acerca. En cambio, Sara utiliza las nociones de punto máximo y concavidad hacia abajo cuando se aleja la bola del sensor y de una curva en donde el punto más cercano al sensor forma una concavidad hacia arriba.
Posteriormente, se les presentan en un mismo plano, las gráficas correspondientes a las dos tomas de datos, es decir, una con el péndulo colgando del cordón de 40 cm., y la otra con el cordón de 60 cm., (Figura 15) y se les pregunta: Al aumentar el tamaño del cordón, ¿percibes algún cambio en el valor de los datos o en la gráfica? ¿Cuál? Descríbelo detalladamente.
Para dar respuesta a esta pregunta, las tutoradas simulan el péndulo con lápices o con las manos para explicar, en el primer caso, que no importa la longitud del cordón, porque al posicionarlo a 20° siempre dará la misma distancia (Figura 16a) y, en el segundo caso, para explicar que lo largo afecta a lo rápido que se mueve el péndulo y, por lo tanto, a que se aleje más del sensor (Figura 16b).

Figura 16b Fer mostrando cómo al moverse más rápido, la distancia entre la bola y el sensor es mayor, y viceversa
Cuatro de las cinco tutoradas apoyan el último argumento y, finalmente, acuerdan que una es más grande que la otra debido a que el cordón es más grande.
[5] Sara escribe: Sí, ya había observado que la distancia con que se acerca y aleja la bola del sensor es mayor con el hilo a 60 y menor con el hilo de 40.
[6] Fer escribe: Que en una gráfica podemos decir que su cordón está a 40 y una 60, la de 40 cm es la gráfica más corta por lo mismo que su cordón es más corto.
De sus respuestas escritas, sus argumentaciones y movimientos se entiende que lo grande o lo corto se refiere a la diferencia en amplitud que se muestra entre las gráficas, es decir, que cambios en las condiciones del experimento generan cambios, en lo que ellas describen como tamaños de las gráficas.
En esta actividad, los aparatos clave previos se conservan y aparecen algunos como el uso de términos escolares, la simulación-corporización y un síntoma de “lectura continua” de la gráfica, cuando se dice que “va yendo” o cuando se identifica la concavidad. El elemento de la FT que más resalta es el uso de la condición acotada de la gráfica al identificar la longitud entre punto máximo y mínimo para explicar los cambios en las condiciones del experimento.
4.4. Actividad 4
Esta actividad inicia con una gráfica (Figura 17) que muestra las distancias entre el sensor y la bola, obtenidas a partir de una nueva configuración (cada 0.025 segundos, durante 5 segundos) . Se les pide considerar que la bola se comporta como el péndulo de un reloj, es decir, no se detiene, y usar la gráfica 7 para responder las siguientes preguntas: ¿Cuál sería la distancia a la que se encontraría el péndulo del sensor en el segundo 60? ¿Estará alejándose o acercándose al sensor? ¿Utilizaron alguna parte de la gráfica para poder realizar la predicción? Si la respuesta a la última pregunta es positiva, se les pide señalar qué parte.
Las estudiantes marcan el punto correspondiente al segundo 5 y lo utilizan para realizar la predicción (Figura 18). Surgen diferentes acercamientos, por ejemplo, los de Ana [7] y Sara [8].
[7] Ana escribe: Considerando que se comporta como el péndulo de un reloj, el movimiento es constante y en el segundo 60 estaría acercándose y alejándose al mismo tiempo.
[8] Sara escribe: En el segundo 5 se está acercando y al estar a 0.5 cm del sensor en ese instante, entonces en los múltiplos de 5 se está acercando, al ser el 60 múltiplo de 5, se está acercando al sensor a 0.5 cm de éste.
En una discusión de sus respuestas Emi y Sara reflexionan:
[9] Sara dice: Como se está diciendo, es un movimiento constante, no se va a detener, yo tomé el segundo 5, porque se está exactamente acercándose, pues eso es cada 5 y como el 60 es múltiplo de 5 entonces está acercándose.
[10] Luz dice: Nosotras pusimos que alejándose, fuimos viendo que sube y baja, sube y baja y como en el 10 sería sube entonces…
[11] Sara interrumpe y dice: Si usaron el 10, ya no utilizaron una parte de la gráfica.
Emi y Luz habían trabajado con la gráfica contando cuántas veces sube y cuántas veces baja, pero se pierden en estos cálculos y, después de escuchar los argumentos de Sara, cambian la respuesta y ocupan el segundo 5. Mientras tanto, Ana y Fer continúan con las actividades sin llegar aún a estas preguntas. Por la forma en que Sara analiza la gráfica, se identifica que está viendo sólo el instante, no lo que sucede antes y después y dado que éste coincide con la distancia más cercana al sensor, asume que se está acercando.
Las preguntas de esta actividad buscan intencionalmente hacer emerger aparatos clave que muestren el uso de lo periódico. En particular, surge una articulación de lo acotado y lo periódico cuando Ana [7] y Sara [9] argumentan que el movimiento es “constante”, que parece referirse a su regularidad y, por ello, pueden tomar lo que sucede los primeros 5 segundos (como la unidad mínima de análisis y repetición) para saber lo que va a pasar en el segundo 60.
Para concluir la actividad, se les pide encontrar la distancia entre la bola y el sensor en el segundo 28, para la toma de datos registrada en la gráfica 8 (Figura 19), y comparar el método de predicción utilizado para la gráfica 7 con el utilizado para la gráfica 8, indicando en qué difieren.
Con respecto a la gráfica 8, Sara afirma que el movimiento ya no es constante por lo que sólo podrá aproximar la distancia a la que se encontrará la bola. Para lograr esta aproximación, Emi utiliza una regla y la coloca verticalmente sobre la gráfica en el segundo 7 para medir y argumentar que la distancia va disminuyendo. Cuando la profesora les pregunta si la regla ayudaría a encontrar la distancia en el segundo 14, Luz y Emi marcan sobre la gráfica (Figura 20) dos líneas horizontales que pasan por los máximos y mínimos locales, y dos líneas verticales en los segundos 7 y 14. Refiriéndose a sus trazos, responden que en el segundo 14 se estaría alejando del sensor igual que en el segundo 7 y, en ambos, la bola estaría a aproximadamente a 0.9 m., del sensor. Al respecto, Sara argumenta que esto se debe al patrón de repetición.
[12] Sara escribe: 0.9 y se estaría alejando, ya que por la curva y su patrón de repetición, en el segundo 7 se aleja, entonces en su múltiplo 14 también.
[13] Sara dice: En la gráfica 8 ya no es constante, ahí ya va disminuyendo y tendríamos que sacar el patrón de cuánto disminuye.
Mientras Sara da su explicación, Emi verifica con la regla que realmente está disminuyendo.
[14] Sara dice: ¿Cómo podría saber la posición exacta?
[15] Profesora dice: ¿Cómo le hiciste en el anterior?
[16] Sara dice: Pues en el 7 sí puedo saber, se está alejando, entonces en el 14 también. En la segunda gráfica no es exacto porque nunca se repiten las mismas distancias, sólo se aproxima.
Las tutoradas identifican la unidad mínima de análisis en cada caso y, de acuerdo con la experiencia física, responden si se aleja o acerca la bola en el tiempo solicitado.
En las últimas respuestas, se pueden identificar nuevos artefactos clave como el “patrón de repetición” y las líneas guía que lo comprueban. Con ellos, las tutoradas reconocen que hay un cierto comportamiento “repetitivo”, pero distinguen “cómo se está repitiendo” (la disminución de las distancias entre máximo y mínimo).
Al localizar el segundo 7 como referencia (por ser divisor del segundo 28), las tutoradas determinan la “unidad gráfica” que se va a repetir y con base en la cual responder, evidenciando que el periodo mínimo, como tradicionalmente se identifica en la escuela para las funciones periódicas, no es el inmediatamente elegido para predecir un estado futuro. Su definición y uso dependerá de su funcionalidad.
4.5. Actividad 5
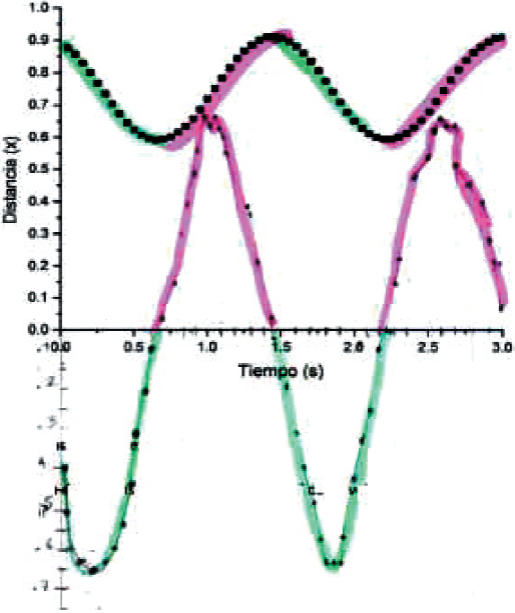
Debido a que los estudiantes, incluyendo a las tutoradas, ya habían cursado la asignatura de Física y abordado la velocidad en los temas previos a la experiencia didáctica, la introducción de las definiciones de velocidad promedio e instantánea, y de aceleración no supone un “tema nuevo” para ellas. En la hoja de trabajo, se les proporciona la fórmula para calcular las velocidades instantáneas en los tiempos dados en una tabla a completar, la cual incluye los datos (tiempo-distancia) obtenidos con el sensor durante 3 segundos, con un total de 60 tomas. Debido a que las tutoradas sólo tienen una calculadora, comienzan a dictar los datos a una de ellas y todas toman nota.
Los cálculos se dan en forma continua hasta obtener una velocidad instantánea “cero”. La profesora les cuestiona sobre lo que eso significa y todas responden que es el momento en que se detuvo la bola. Continúan con los cálculos hasta obtener un dato que les parece extraño, pues observan que los valores están disminuyendo y, de repente, obtienen un dato que aumenta. Lo realizan varias veces y no se convencen; debido a que reconocen el comportamiento de los datos, revisan los cálculos anteriores y encuentran un error en los cálculos. Prosiguen hasta confirmar que continua disminuyendo y terminan los cálculos convencidas de los datos que obtuvieron.
Tal como pide la actividad, las tutoradas ubican los puntos calculados (tiempo-velocidad instantánea) en la gráfica 9 y usan el marcatextos para señalar dónde las velocidades son positivas y dónde son negativas. Identifican que las zonas gráficas, marcadas anteriormente (crecimiento y decrecimiento de las distancias), coinciden con las marcadas ahora para velocidades positivas y negativas (Figura 21) y responden así a las preguntas planteadas:
En la secuencia: En términos de la gráfica de distancias y lo que representa en el experimento ¿cómo interpretarías las velocidades negativas?
[17] Sara escribe: Cuando se va acercando al sensor su velocidad es negativa.
[18] Luz escribe: Cuando se acerca es negativa y positiva cuando se aleja.
En la secuencia: ¿Visualizas alguna relación global o puntual, entre las gráficas de la velocidad y de la distancia? ¿Cuál o cuáles?
[19] Sara escribe: En las dos hay movimiento que aumenta y disminuye.
[20] Luz escribe: Sí, porque en las dos salen ondas.
En la secuencia: ¿Qué valores toma la velocidad en las “crestas” y los “valles” de la gráfica de distancias? En términos del experimento, ¿qué significarían estos puntos?
[21] Sara escribe: En estos puntos la velocidad es igual a 0.
[22] Luz escribe: Son iguales, están en cero.
En esta actividad, sobresale la intencionalidad de ahondar en el estudio del cambio y las variaciones del movimiento registrado. Graficar las velocidades en el mismo plano que la gráfica de las distancias y el uso de color constituyen un aparato clave para la emergencia del elemento de la FT referido a la naturaleza del comportamiento y sus variaciones. Naturalmente, este elemento está contextualizado en la “forma gráfica”, por ello, la respuesta de Sara alude a dos movimientos, aunque uno no lo es; la respuesta de Luz alude a “ondas”.
De nuevo, no hay alusión explícita a intervalos de tiempo, pero se reconoce un uso de ellos cuando identifican las zonas gráficas que relacionan “velocidad positiva con alejamiento” o “velocidad negativa con acercamiento”. La pregunta final de esta actividad pide el bosquejo de la gráfica de la velocidad dada una gráfica de distancias, de una toma de datos por 15 segundos. En las respuestas se observa que no hay un trazo ondulado, pero se identifica la relación entre máximos-mínimos de la gráfica de las distancias con los “ceros” de la gráfica de velocidad y los máximos- mínimos de la gráfica de la velocidad con el punto de inflexión de la gráfica de distancias.
4.6. Actividad 6
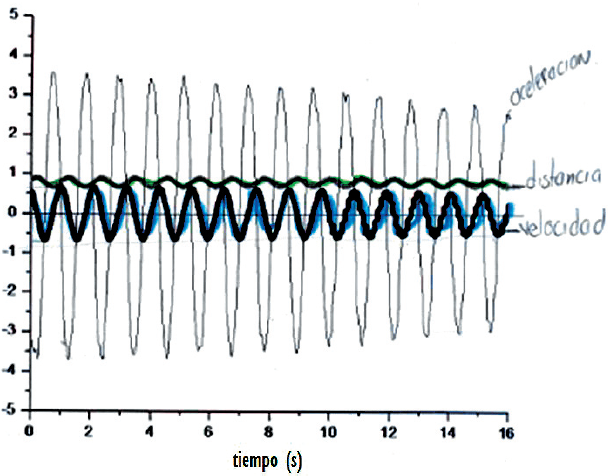
Ésta es la actividad final y en ella se presenta la definición de “aceleración media en intervalos de tiempo” para posteriormente presentar a las estudiantes cuatro gráficos donde se presentan simultáneamente las curvas que describen la distancia, la velocidad y la aceleración del movimiento registrado del péndulo. En cada caso, se les solicita identificar qué curva corresponde a la gráfica de la distancia y cuál a la gráfica de la aceleración.
En la sesión programada para la actividad, sólo asistieron tres de las cinco tutoradas, quienes la resolvieron guiadas sólo por las formas de las gráficas, sin hacer un análisis detallado de ellas. Sólo discutieron las tablas que llenaron con los valores máximos y mínimos de la distancia, la velocidad y la aceleración. En esta primera resolución, Sara, Emi y Luz eligen como gráfica de la distancia una con valores positivos y negativos, por lo que se planea, para la siguiente sesión, iniciar con el esquema del sensor y el péndulo para elegir la gráfica con base en el análisis de la situación.
Poniendo atención en las distancias entre el sensor y el péndulo cuando éste se alejó más y cuando se acercó más, se les pide relacionar éstas con la gráfica elegida. Después de analizar la situación, reconocen que no existen distancias negativas y, por lo tanto, la gráfica elegida no puede ser la que registra las distancias. Se les proporcionaron nuevas hojas para contestar y rápidamente ubican la gráfica correspondiente a la distancia y, a partir de ahí, asignan las otras a la velocidad y a la aceleración.
Sara dice que no logra ver la diferencia entre la aceleración y la velocidad. En reacción al comentario de Sara, la profesora plantea la pregunta: ¿Las dos son iguales?, a lo que todas responden que la gráfica de la velocidad es más chica. En seguida, la profesora pregunta sobre los signos: Si la bola se aleja, ¿la velocidad y la aceleración son positivas?
Es a partir de retomar la situación experimental que se analizan cuidadosamente las gráficas para elegir la que corresponde a cada una. Sara, Emi y Luz terminan la actividad y, al siguiente día, ayudan a Ana y a Fer a realizarla. En el llenado de tablas, hay ciertas variaciones porque son lecturas aproximadas a la gráfica, pero todas eligen apropiadamente las gráficas (Figuras 22 y 23).
De nuevo, el elemento de la FT se manifiesta contextualizado a la forma gráfica. Aunque no hubo explicación o argumento explícito a la forma de las tres gráficas, cuando Sara dice no reconocer “la diferencia” parece referirse a que ambas, gráficas de velocidad y de aceleración, son igualmente onduladas. Es su análisis respecto a las distancias, retomando la experimentación, identificaron cuál es cuál.
A lo largo de toda la experiencia, se mantuvo la lectura de las distancias como alturas, se identificaron las variables tiempo-distancia/velocidad/aceleración como las unidades de medida, según la actividad; se reconoce un uso implícito de los periodos de tiempo; la lectura de las gráficas se hace en lo global por su forma y comportamiento, y en lo local porque ello permite cuantificar las variables. Son las preguntas en cada actividad lo que permite que lo anterior se ponga en funcionamiento para identificar y usar el comportamiento periódico de la gráfica, distinguiendo no sólo la repetición, sino cómo es ésta; así como la naturaleza de este comportamiento en relación a sus variaciones.
5. Discusión y resultados
En nuestro escenario, las tutoradas están condicionadas a las normas escolares en general y de la clase de matemáticas en particular, por lo que modelar no es una actividad de su elección. A través de las actividades matemáticas diversas, intencionalmente propuestas para construir la FT, se busca que las estudiantes enfrenten, problematicen, comprendan y transformen la situación propuesta de “matematizar el movimiento del péndulo”. Así, para describir el proceso de modelación que viven las estudiantes, se describe y analiza, en la sección anterior, las formas en las que abordan cada actividad para dar respuesta a las preguntas.
Se agruparon las acciones de las tutoradas en acciones de socialización y actividades matemáticas, entendiendo éstas últimas como acciones intencionalmente provocadas por el diseño de la situación-problema. Las acciones de socialización se refieren a la interacción social de las tutoradas para la resolución de la situación-problema, considerando que, aun cuando entregaron sus hojas de trabajo en forma individual, interactúan como colectivo para entender los planteamientos de la situación-problema, las instrucciones y las preguntas de cada actividad, y para acordar ciertas respuestas del tipo “dar valores aproximados” o “dar argumentos y explicaciones amplias”.
Las actividades matemáticas como medir, calcular o aproximar, son solicitadas explícitamente por la situación-problema; sin embargo, identificamos otras de las que dependen las tutoradas para lograr la matematización. A éstas últimas las llamamos genéricamente como:
- Experimentación. La sesión de manejo de la calculadora de capacidad gráfica, el sensor de movimiento y el programa para crear los videos del péndulo no fue sólo de instrucción para el uso de la tecnología. Si bien se aprendió a utilizarlas, se hizo en el contexto de realizar mediciones, variar las condiciones del experimento, controlar variables como la distancia a la que es necesario colocar el sensor para no tener interferencias en la toma de datos, determinar el ángulo al que se suelta el péndulo para obtener las gráficas apropiadas a la secuencia, tomar datos y producir gráficas. Es decir, se hace un acercamiento a la situación indeterminada a través de las herramientas que van a permitir estudiarla.
- Recreación del experimento. Para dar respuesta a las preguntas en cada actividad, las tutoradas no sólo recordaban la experiencia del péndulo, sino que recreaban el movimiento con sus brazos o usando lápices, la regla o cualquier objeto que tuvieran a la mano al responder.
- Lectura de gráficas. Después de recrear el experimento, las tutoradas relacionaban el elemento de análisis (por ejemplo, la posición inicial de la bola o la distancia máxima o mínima que alcanzaba respecto del sensor) con su representación y localización en la gráfica. Según la pregunta, la lectura que realizan es local (un punto) o global (comportamiento).
En la argumentación o explicación a una respuesta, la recreación del experimento se considera una muestra de la significación de las gráficas, producto de la corporización que se lleva a cabo en la experimentación. En una concepción básica, esta corporización se entiende como la realización a través del experimento mental basado en la percepción y la reflexión sobre las propiedades de los objetos (Tall, 2006), y ahí ubicamos la base del desarrollo del conocimiento, en la acción del sujeto sobre el objeto, de donde se derivan los significados construidos.
Los datos en cada actividad evidencian el desarrollo del pensamiento funcional-trigonométrico en las tutoradas, no sólo al nivel de haberse manifestado cada uno de sus elementos, sino de haberse utilizado como argumentos para explicar la respuesta a cada una de las preguntas.
Para validar que las tutoradas lograron la modelación, fue necesario analizar su apropiación de la situación, momento que se provocó al llevarlas como equipo de apoyo para trabajar la situación-problema con el grupo completo. En esta etapa, cada tutorada orienta a pequeños grupos de estudiantes en la toma de datos, explicándoles cómo se colocan el péndulo y los sensores, cómo se maneja la calculadora para tomar y guardar los datos, y cómo se maneja la cámara para la captura en video del movimiento del péndulo. Las tutoradas muestran control sobre el manejo de las herramientas e identifican rápidamente si las tomas hechas por los estudiantes sirven o no para la secuencia de actividades que posteriormente realizarán. Por ejemplo, determinan si debe repetirse la toma de datos o explican cómo deben lanzar la bola para que se mueva en una trayectoria lo más alineada posible y que no salga de la visión del sensor.
Para apoyar a los estudiantes en la resolución de las actividades en las hojas de trabajo, las tutoradas retoman la experimentación con el péndulo y su relación con la gráfica, y reproducen la dinámica de la profesora de no darles las respuestas, sino hacer preguntas para que ellos mismos obtengan los resultados. Es decir, orientan al grupo de estudiantes a realizar la recreación del experimento y la lectura de gráficas para conseguir la apropiación de la situación que ellas mismas lograron.
Al igual que las tutoradas, los estudiantes del grupo recrean el experimento y realizan la lectura de las gráficas utilizando los recursos que tienen a la mano o sus manos y brazos, con el objetivo de relacionar el elemento de análisis del experimento con su representación en la gráfica. Aunque su análisis no fue objeto de estudio en la presente investigación, los registros en video y en las hojas de trabajo dan evidencia de la emergencia de los artefactos clave en los estudiantes del grupo completo, al manifestarse los elementos de la FT en los argumentos que construyen para explicar la respuesta a cada una de las preguntas. Por ejemplo, a la pregunta 6 “El ir y venir de la bola, ¿cómo se identifica en la gráfica?” y con la recomendación de la tutoradas por “describir y anotar cómo se sabe cuándo va y cuándo viene”, un estudiante responde reelaborando la gráfica y anotando sobre ella un punto de alejamiento y otro de acercamiento, y explicando verbalmente cuándo la bola está “más lejos” o “más cerca” del sensor (Figura 24).
Se identifica también que los estudiantes están leyendo las gráficas como alturas en tiempos específicos, por ejemplo, haciendo uso de líneas verticales (para ubicar el tiempo) y líneas horizontales (para ubicar la distancia) sobre la gráfica (Figura 25).
Analizar la actividad y la producción matemática del estudiante, reconociendo los procesos de construcción que le son propios, para reconocer su desarrollo del pensamiento matemático nos obliga a entender sus formas de explicar y argumentar. Es decir, ante un diseño didáctico no tradicional (al menos en el IEMS-DF) no podemos, ni debemos, esperar que el estudiante responda con conceptos matemáticos formales. Por ejemplo, la epistemología de prácticas de Montiel (2011) propone el manejo de una escala de tiempo infinitesimal (para lo local) - infinita (para lo global) en el estudio del movimiento oscilatorio, lo que se manifiesta explícita e intencionalmente en el diseño cuando se reducen los intervalos de tiempo en la toma de distancias entre la bola y el sensor, hasta donde lo permite la herramienta tecnológica. En la actividad y las producciones del estudiante, no se espera que éste hable de “intervalos”, ni de “infinitamente pequeños”; pero se le otorga ese significado a su expresión “… lo más curvita es por cada cuánto tomas los datos”.
Éstas son el tipo de evidencias recolectadas, organizadas y analizadas en la experiencia. Un momento de institucionalización escolar nos permitiría el paso de la construcción del estudiante al establecimiento del saber escolar que, para efectos de la investigación, no fue necesario por el objeto de estudio que se planteó de inicio. Aunado a ello, presupone establecer también procesos de institucionalización para el conocimiento físico en juego y ello puede resultar más complejo que abordar solamente la función trigonométrica. Sin embargo, una estrategia que hemos encontrado pertinente para transitar hacia una institucionalización, sólo de la matemática escolar en juego, es continuar con tareas como las que proponen Moore (2014) y Ozgün-Koca, Edwards y Meagher (2013). Éstas demandan del estudiante sólo mediciones y construcciones geométricas básicas, además, su fundamentación en el pensamiento cuantitativo y covariacional resulta significativa también para un futuro rediseño de la situación-problema, principalmente para ampliar el estudio de los cambios y las variaciones del movimiento del péndulo.
6. Conclusiones
Considerando que las tutoradas no hicieron alusión a la función trigonométrica, al movimiento oscilatorio o periódico, o a algún referente de la física para abordar la situación-problema, asumimos que representaba una situación indeterminada para ellas y, con base en ello, continuamos la puesta en escena según lo planeado en la adaptación del diseño.
El diseño no pretende el aprendizaje del movimiento oscilatorio como tal, ni de la función trigonométrica, sino la construcción de aquello que le da uso y sentido a ésta. Para ello, iniciamos estudiando el movimiento del péndulo. Son necesarias otras actividades, pero sobre todo un acercamiento distinto a su estudio para hablar, en sentido estricto, del movimiento oscilatorio y del estudio de sus variaciones sucesivas. Es posible que la experiencia aquí reportada sea sólo una fase de experimentación y acercamiento al fenómeno si nuestro enfoque hubiese sido desde la didáctica de las ciencias o de la física en particular. Sin embargo, a la luz de nuestro estudio, la implementación del diseño cumplió su objetivo como un ejercicio de matematización para rediseñar el discurso trigonométrico escolar y consideramos que el aprendizaje científico que podríamos identificar es solamente aquél relacionado con la observación, la medición, la recolección de datos, la identificación y el control de variables, la experimentación y el uso de varias representaciones matemáticas, actividades que Matthews, Gauld y Stinner (2005) consideran esenciales de la investigación científica.
Las estudiantes tutoradas logran modelar la situación planteada y, para ello, integran al conjunto de actividades que pide el diseño, la recreación del experimento y la lectura de gráficas. Los modelos construidos son principalmente las gráficas que, si bien realiza la calculadora, son manipuladas para identificar momentos concretos del experimento (lectura puntual) o analizar comportamientos (lectura global), con el propósito de argumentar sus respuestas. Con base en las evidencias y su análisis a la luz de nuestros referentes teóricos, identificamos a la modelación como una práctica de referencia pertinente en el contexto escolar del IEMS-DF.
Experiencias de innovación como ésta pueden ser la vía para rediseñar el discurso matemático escolar, desde el salón de clases, y para ir cambiando la actividad matemática de los estudiantes a una más participativa, es decir, pasar del “aprender matemáticas” al “hacer matemáticas”. En la medida en que pueda generarse este cambio, podríamos hablar de la modelación como la práctica social que norme la actividad matemática del estudiante. Ésa es nuestra expectativa.











 nova página do texto(beta)
nova página do texto(beta)