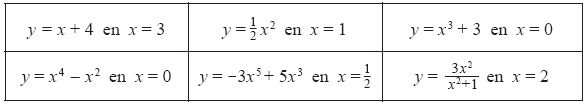1. Introducción
La investigación sobre el conocimiento y el desarrollo de las competencias profesionales del profesorado de matemáticas adquirió recientemente relevancia en el ámbito internacional (Silverman & Thompson, 2008; Even & Ball, 2009). La creación del espacio europeo de educación superior ha convertido la noción de competencia profesional en una noción clave en la formación universitaria y en particular en la formación inicial de futuros profesores. Un proyecto relevante relacionado con la creación de dicho espacio ha sido el proyecto Tuning (González & Wagenaar, 2003) −proyecto que se inició en Europa y después se extendió a América Latina− el cual clasifica las competencias de la enseñanza universitaria en genéricas (compartidas por cualquier enseñanza universitaria) y específicas (propias de cada ámbito disciplinario). En la formación universitaria las competencias son académicas, pero dado que la idea de fondo del modelo curricular por competencias es que aquello que se enseña en la universidad sea útil en la vida profesional, implica que las competencias académicas son el reflejo universitario de las competencias profesionales de la persona que ejerce la profesión para la cual los estudios universitarios preparan a los estudiantes (o bien están inspiradas en ellas). En lo que sigue, utilizaremos el término competencia para referirnos tanto a las competencias académicas de la formación inicial de los futuros profesores, como a las profesionales del profesor en servicio.
Para el caso de la formación inicial de los profesores de secundaria, la clasificación de las competencias en genéricas y específicas ha sido usada en las propuestas curriculares de diversos países y también en las propuestas de competencias profesionales realizadas por algunos investigadores. En Font y otros (2012) se propone una lista de competencias genéricas y específicas. Según estos autores, la competencia en análisis didáctico −entendida como: diseñar, aplicar y valorar secuencias de aprendizaje, mediante técnicas de análisis didáctico y criterios de calidad, para establecer ciclos de planificación, implementación, valoración y plantear propuestas de mejora− es una de las competencias específicas clave que deben desarrollar los futuros profesores de matemáticas de secundaria.
Según Weinert (2001), los enfoques por competencias pueden clasificarse en tres grandes grupos: a) Enfoque Cognitivo, b) Enfoque Motivacional y c) Enfoque Integral o de Acción Competente. La formulación de la competencia en análisis didáctico propuesta en Font y otros (2012) se realiza desde la perspectiva de la acción competente. Se entiende por competencias al conjunto de conocimientos y disposiciones que promueven un desempeño profesional eficaz, en contextos de formación docente referidos a los saberes matemáticos. Dicho en términos aristotélicos, las competencias aluden a una potencialidad que se actualiza en el desempeño de acciones eficaces (competentes).
La competencia en análisis didáctico de los futuros profesores de secundaria debe ser desarrollada y evaluada por los formadores de profesores, los cuales a su vez también deben tenerla desarrollada. En este artículo describimos la investigación que realizamos sobre el desarrollo de la competencia en análisis didáctico, en un proceso de formación dirigido a formadores de futuros profesores de matemáticas de secundaria, auspiciado por la administración educativa argentina. La pregunta que se quiere responder es la siguiente: ¿qué criterios se deben utilizar para diseñar una secuencia de tareas, en la formación de formadores de profesores, que permitan evaluar y desarrollar la competencia en análisis didáctico y qué cambios se deben realizar en su rediseño para mejorar su desarrollo?
Dado que las competencias se evalúan y se desarrollan a partir de la resolución de tareas, el diseño de tareas se convierte en la otra cara de la moneda del desarrollo y evaluación de competencias. En este artículo, para contestar a la pregunta anterior, se han diseñado e implementado tareas en la formación de formadores de profesores de Matemáticas, en las que estos han tenido que diseñar y rediseñar secuencias de tareas para sus alumnos, utilizando los criterios de idoneidad didáctica propuestos por el Enfoque Ontosemiótico de la Cognición e Instrucción matemática (EOS) (Godino, Batanero & Font, 2007). Dichos criterios sirven tanto para guiar la construcción de la secuencia de tareas como para valorar la idoneidad de su implementación, lo cual permite tener elementos para un rediseño de la secuencia de tareas que permita una futura implementación de más calidad.
2. Competencia en análisis didáctico y diseño de tareas
La formación de profesores de Matemáticas constituye un campo de investigación relevante. En particular, en la última década aumentó el interés por investigar el conocimiento y las competencias que necesitan los profesores de Matemáticas para conseguir una enseñanza eficaz (Burger & Starbird, 2005; Wilson, Cooney & Stinson, 2005; Hill et al., 2008). Diversos investigadores se han interesado por determinar las competencias que deben tener los profesores de secundaria de Matemáticas y han propuesto listas de competencias, clasificadas en genéricas y específicas, en las que se hallan, entre otras, competencias relacionadas con la reflexión sobre la práctica (Poblete y Díaz, 2003; Font, 2011; Font et al., 2012). Schoenfeld y Kilpatrick (2008) proponen otro modelo del desempeño experto en enseñanza de las Matemáticas que considera siete dimensiones, referidas a conocimientos y competencias profesionales del profesor de Matemáticas, siendo una de ellas la reflexión sobre la propia práctica (pensar cómo se desarrolló una situación en clase y qué se podría hacer para mejorarla).
Otros investigadores consideran que una de las competencias clave es la de "mirar con sentido", la cual permite al profesor de Matemáticas ver las situaciones de enseñanza y aprendizaje de las matemáticas de una manera profesional que lo diferencia de la manera de mirar de alguien que no es profesor de Matemáticas (Mason, 2002; Fernández, Llinares, & Valls, 2012). Dicha competencia también está relacionada con la reflexión sobre la práctica que deben desarrollar los profesores para realizar procesos de instrucción de calidad.
Font (2011), Font y otros (2012) y Giménez, Font y Vanegas (2013) consideran que una de las competencias clave, que deben desarrollar los futuros profesores de Matemáticas de secundaria, es la competencia en el análisis didáctico de procesos de instrucción, debido a su relevancia en la descripción, explicación, valoración y mejoramiento de los procesos instructivos. Asimismo, los autores plantean que los constructos teóricos del modelo de análisis didáctico propuesto por el Enfoque Ontosemiótico de la Cognición e Instrucción matemática (EOS) (Godino et al., 2007) pueden ser herramientas teóricas útiles para el desarrollo de esta competencia. En dicho enfoque se proponen cinco niveles para el análisis didáctico de procesos de instrucción (Font, Planas y Godino, 2010; Pochulu y Font, 2011; Contreras, García y Font, 2012), cada uno de ellos con sus respectivas herramientas: a) Análisis de las prácticas matemáticas realizadas en el proceso de instrucción; b) Análisis de objetos y procesos matemáticos activados en dichas prácticas; c) Análisis de las interacciones realizadas en el proceso de instrucción; d) Identificación del sistema de normas y metanormas que regulan el proceso de instrucción; e) Utilización de criterios de idoneidad didáctica para la valoración del proceso de instrucción con el fin de mejorarlo.
El desarrollo y evaluación de la competencia en análisis didáctico tal como la formulan Font y colaboradores (Font, 2011; Font et al., 2012; Giménez et al., 2013), implica analizar las prácticas profesionales de los profesores, o bien formadores de futuros profesores de secundaria en nuestro caso, para resolver las tareas profesionales propuestas, y el conocimiento matemático-didáctico activado en ellas, para encontrar indicadores que justifiquen la asignación de niveles de desarrollo a dicha competencia. En este esquema el diseño de tareas tiene un papel relevante.
Recientemente aumentó el interés en el área de la Educación Matemática sobre el diseño de tareas al considerarlo un aspecto clave para conseguir una enseñanza de calidad (por ejemplo, Mason & Johnston-Wilder, 2004; Tzur, Sullivan, & Zaslavsky, 2008; Zaslavsky & Sullivan, 2011). Este interés se manifestó, entre otros aspectos, en la creación del Topic Study Group, Research and development in task design and analysis, en The International Congress on Mathematics Education del 2008, y en la celebración del International Commision on Mathematical Instruction Study, específico sobre el tema en el año 2013, siendo uno de sus focos el diseño de tareas en la formación de profesores.
Las tareas son las situaciones que el profesor propone (problema, investigación, ejercicio, etc.), a los alumnos. Éstas son el punto de partida de la actividad del alumno, la cual, a su vez, produce como resultado su aprendizaje. La investigación sobre el diseño de tareas se interesó por diferentes aspectos. Por ejemplo, Swan (2007) estudió la naturaleza y tipología de tareas; Stein, Smith, Henningsen y Silver (2000), las características que debe cumplir una tarea para ser estimulante o retadora para el alumno; Charalambus (2010), el papel que tiene el profesor en la implementación de la tarea a fin de lograr un proceso cognitivo relevante en los alumnos; Giménez y otros (2013), el diseño de tareas en la formación de futuros profesores de Matemáticas de secundaria.
3. Objetivo y metodología de la investigación
Font (2011), y Giménez y otros (2013), proponen caracterizar la competencia en análisis didáctico de la siguiente manera: diseñar, aplicar y valorar secuencias de aprendizaje, mediante técnicas de análisis didáctico y criterios de calidad, para establecer ciclos de planificación, implementación, valoración y plantear propuestas de mejora. Estos autores, además, consideran: 1) que se pueden encontrar criterios e indicios del desarrollo de esta competencia (Font, 2011), y 2) que algunos de los constructos propuestos en el modelo de análisis didáctico que propone el EOS son útiles para el desarrollo de dicha competencia, sobre todo, el constructo criterios de idoneidad didáctica. En esta investigación asumimos esta caracterización de la competencia en análisis didáctico y tomamos como hipótesis de partida las dos consideraciones anteriores.
Nuestro objetivo es investigar cómo el proceso de construcción de una secuencia de tareas profesionales realizadas por los asistentes influye en el desarrollo de su competencia en análisis didáctico, en el contexto de diseño, implementación y rediseño de un curso de formación, dirigido a formadores de futuros profesores de Matemáticas de secundaria, organizado por la administración educativa de Argentina (que llamaremos ciclo formativo FFPMS). Dicho desarrollo se constata, entre otros indicadores, en cuanto los formadores de futuros profesores incorporan y usan adecuadamente herramientas teóricas (en particular, tipología de objetos matemáticos, tipología de procesos y criterios de idoneidad didáctica), para la descripción, explicación, valoración y mejora de procesos de enseñanza, dirigidos a la formación matemática de futuros profesores de secundaria (ciclo formativo que representaremos con las letras FPMS a partir de ahora). Para conseguirlo, utilizamos una metodología de investigación que tiene elementos de la investigación basada en el diseño (Cobb, Confrey, diSessa, Lehrer, & Schauble, 2003; Cobb & Gravemeijer, 2008). En particular, de acuerdo con esta metodología, (1) la experiencia se ha realizado en contextos naturales (de clase y/o cursos de formación), (2) buscando que el diseño, la implementación y la investigación fuesen interdependientes, y (3) se han considerado las siguientes fases: 1) Preparación del experimento; 2) Experimentación para apoyar el aprendizaje; 3) Análisis retrospectivos de los datos generados durante la realización del experimento (Cobb & Gravemeijer, 2008). Se trata de una metodología de investigación de diseño fundamentada en el empleo de herramientas del EOS. Por un lado, el diseño del ciclo formativo sirvió como un contexto para la investigación. Por el otro, los continuos análisis realizados junto a una mirada retrospectiva proporcionaron información para rediseñar y mejorar el ciclo formativo.
Los sujetos participantes fueron formadores de futuros profesores asistentes a un curso de formación continua, implementado durante periodos del año 2011 y de 2012, por el Instituto Nacional de Formación Docente (INFD) de Argentina.
El ciclo formativo FFPMS comprendió seis fases que se explican con detalles en el apartado 4.2: (a) Seminario virtual, cuyo propósito fue dar herramientas y acompañamiento para que en grupo los formadores diseñen y fundamenten una secuencia didáctica para el FPMS; (b) Encuentro presencial inicial, registrado en vídeo, donde los grupos asistentes presentaron los diseños de tareas del ciclo FPMS y su fundamentación, y al mismo tiempo, se realizaron rediseños y ajustes de las tareas en virtud de los análisis didácticos realizados con la colaboración de los otros grupos (e incluso, de los profesores del curso); (c) Implementación de la secuencia de tareas (ciclo FPMS), de la que se registraron dos clases consecutivas en vídeo (a elección de los propios grupos), por personal técnico del INFD, para ser utilizadas en análisis posteriores con todos los participantes de la capacitación (grupos de asistentes, profesores del curso y personal técnico especializado del INFD); (d) Selección de algunos episodios de las clases registradas en vídeo. Los profesores a cargo del curso, juntamente con personal técnico del INFD, seleccionaron los episodios con dos condiciones: i) que su duración fuese aproximadamente de cinco minutos, y ii) que a su criterio se pudieran observar, como mínimo, aspectos relevantes relacionados con las matemáticas implementadas, la gestión de la clase y el uso de recursos. (e) Análisis didáctico presencial de los episodios de clases. En este caso, los análisis fueron realizados por cada grupo de profesores que había implementado el ciclo formativo FPMS, a quienes se les sumó un representante de otro grupo que no pertenecía a la misma institución educativa La coordinación de este análisis estuvo a cargo de uno de los profesores responsables de la capacitación y de un técnico del INFD; y por último (f) Encuentro presencial final, registrado en vídeo, donde se analizaron seis episodios conjuntamente por todos los grupos. El criterio de selección se sustentó en la buena calidad didáctica, o bien, que se permitieran discutir puntos a mejorar. En esta sesión los participantes también realizaron sugerencias para tener en cuenta en futuras capacitaciones.
El diseño del FFPMS fue flexible y permitió realizar ajustes acordados en reuniones entre los profesores que estuvieron a cargo de la capacitación y técnicos del INFD, quienes iban evaluando la marcha de cada una de las fases.
La plataforma virtual, que sirvió de soporte para el seminario, permitió a cada equipo tener un espacio para interactuar entre ellos, con otros grupos y con los profesores. En particular, hubo foros de discusión sobre las tareas propuestas y chat de intercambios para aclarar dudas.
Los datos para la investigación que se presenta fueron obtenidos de: a) registros de la plataforma virtual −en particular, los borradores y el trabajo final del ciclo formativo FPMS de cada grupo−; b) registros audiovisuales de la implementación de las dos clases de la secuencia de tareas; y c) registros audiovisuales de las reflexiones y análisis que realizaron los asistentes durante los encuentros presenciales.
4. Criterios de diseño de tareas para el desarrollo de la competencia en análisis didáctico
Para atender a la pregunta sobre los criterios que deben ser considerados para el diseño de secuencias de tareas, el primer paso fue solicitar a los asistentes la confección de una secuencia de tareas pensada para ser implementada con sus alumnos (futuros profesores), de acuerdo con determinados criterios. El segundo paso, fue diseñar, implementar y rediseñar, también de acuerdo con ciertos criterios, un ciclo formativo para los formadores de futuros profesores, cuyo foco fuese la confección por parte de los asistentes de una secuencia de tareas pensada para sus alumnos. Los criterios para estas dos secuencias de tareas fueron tomados de ciclos formativos similares, ya experimentados con otros tipos de poblaciones (futuros profesores y profesores en servicio), que habían sido considerados como efectivos por los equipos de investigación que los habían implementado (ver apartado 4.1). De este modo, el ciclo formativo diseñado e implementado con formadores de profesores (FFPMS) surgió del rediseño de estas experiencias previas (ver apartado 4.2).
4.1. Criterios sobre diseño de tareas tomados a partir de las experiencias previas
Los criterios que presentamos aquí, y que se utilizaron tanto en el diseño del ciclo FFPMS como en la secuencia de tareas que diseñaron los asistentes al curso, surgen como resultado de distintas experiencias formativas destinadas a desarrollar la competencia en análisis didáctico en profesores tanto en formación como formados. Esas experiencias − en las que los autores, y miembros de sus equipos de investigación, estuvieron involucrados− tuvieron lugar en la Universidad de Barcelona (UB), Universidad Nacional de Villa María (UNVM) y Universidad Nacional de General Sarmiento (UNGS), la primera de España y las restantes de Argentina. En cada una de esas experiencias se pusieron de manifiesto aciertos y algunos inconvenientes que obstaculizaron, al menos parcialmente, el desarrollo de la competencia en análisis didáctico.
En Font (2011) y Giménez y otros (2013) pueden observarse detalles de las experiencias formativas que tuvieron lugar en la UB con futuros profesores (ciclos FPMS). De ellas se tomaron:
− Proponer tareas profesionales: tareas propuestas cuyo objetivo es realizar análisis didácticos con base en sus conocimientos, creencias, experiencias previas, o bien, utilizando herramientas teóricas que van emergiendo en el curso de formación en el que participan (Giménez et al., 2013).
− Atender al desarrollo de la competencia en análisis didáctico de procesos de instrucción − propuesta en Font (2011) y Font y otros (2012) − mediante sus indicadores de desempeño, agrupados en tres niveles de desarrollo de la competencia (N1, N2 y N3). Como consecuencia de la reflexión sobre la implementación de los tres ciclos formativos antecedentes a la presente investigación, se adaptaron los indicadores: se cambiaron en la última fila las casillas de la primera y segunda columna. Los indicadores se presentan en la tabla siguiente:
− Incentivar el uso de herramientas teóricas provenientes del EOS, en particular la noción de configuración epistémica y cognitiva de objetos primarios (Godino et al., 2007), por parte de los asistentes para caracterizar las matemáticas implicadas en la secuencia de tareas.
− El uso de los criterios de idoneidad didáctica propuestos por el EOS para el diseño y rediseño de tareas por parte de los asistentes al curso:
1. Idoneidad epistémica, para valorar si las Matemáticas que se enseñan son unas "buenas matemáticas". 2. Idoneidad cognitiva, para valorar, antes de iniciar el proceso de instrucción, si lo que se quiere enseñar está a una distancia razonable de lo que saben los alumnos y, después del proceso, si los aprendizajes logrados se acercan a los que se pretendían enseñar. 3. Idoneidad interaccional, para valorar si la interacción ha resuelto dudas y dificultades de los alumnos. 4. Idoneidad mediacional, para valorar la adecuación de recursos materiales y temporales utilizados en el proceso de instrucción. 5. Idoneidad emocional, para valorar la implicación (interés, motivación) de los alumnos en el proceso de instrucción. 6. Idoneidad ecológica, para valorar la adecuación del proceso de instrucción al proyecto educativo del centro, las directrices curriculares, las condiciones del entorno social y profesional, etc. (Font et al., 2010, p. 101)
Tal como argumentan Giménez y otros (2013), para valorar el proceso de instrucción realizado y hacer propuestas de mejora, los criterios de idoneidad didáctica propuestos por el EOS resultan útiles. Dichos criterios permiten realizar la valoración de las acciones realizadas en los procesos de instrucción. Los criterios de idoneidad son reglas de corrección útiles en dos momentos de los procesos de estudio matemáticos. A priori, los criterios de idoneidad son principios que orientan "cómo se deben hacer las cosas". A posteriori, los criterios sirven para valorar el proceso de estudio efectivamente implementado. Para ello, se necesitan indicadores de cada idoneidad. Siguen en la tabla 2, a título de ejemplo, solo dos indicadores de cada una.
La adopción de estos criterios conlleva el diseño de tareas para introducir a los asistentes al curso estas herramientas teóricas y otras tareas donde las tengan que utilizar.
Otra experiencia que tomó elementos de la anterior se puso en práctica en la UNVM, en este caso con estudiantes del Profesorado en Matemáticas. En ella se utilizaron los dos criterios comentados anteriormente (uso de la noción de configuración, epistémica y cognitiva, de objetos primarios y de los criterios de idoneidad didáctica con sus indicadores). Se observó que los estudiantes podían hacer un buen análisis de la calidad matemática del proceso de instrucción realizado por "otro profesor" utilizando los criterios de idoneidad didáctica (en particular el epistémico), pero no así cuando se trataba del suyo. Se considera que las explicaciones que justifican este hecho se fundan en que los alumnos presentan dificultades para describir y valorar la actividad matemática cuando ésta es rica en procesos y objetos matemáticos, entre otras razones porque, en algunos casos, ellos mismos no realizan de un modo sistemático este tipo de actividad matemática.
A raíz del trabajo de investigación desarrollado en las tres universidades (UB, UNGS y UNVM), se considera pertinente para la formación de profesores:
− Antes de realizar el diseño de tareas, se promueve la resolución (y su descripción) de problemas de modelización matemática con uso de software, y de problemas que permitan una diversidad de estrategias de resolución.
El hecho de que los futuros profesores hubieran realizado la actividad de resolución, y que en su narración aparecieran definiciones, procedimientos, diferentes estrategias, representaciones y argumentos permitió que pudiesen observar con más facilidad la activación de los componentes de una configuración de objetos primarios en la realización de una tarea matemática (nivel 1 de la tabla 1).
Este criterio permite que los asistentes realicen una actividad matemática rica, la narren y observen en la narración la aparición de los diferentes componentes de la configuración de objetos primarios y sus inter-relaciones.
− Proponer tareas de análisis de tareas de autoría ajena y libros de texto previo a tareas de diseño propio.
− Mantener el análisis didáctico utilizando las herramientas del EOS.
Cabe aclarar aquí que este último criterio se sostiene por dos motivos. Primero porque su utilización permitió un buen desempeño de los alumnos en los análisis de tareas de otros profesores y, segundo, el uso de la herramienta configuración epistémica/cognitiva resulta útil para analizar y evidenciar la trama de relaciones que caracteriza la comprensión matemática, según las nuevas orientaciones curriculares publicadas desde el Instituto Nacional de Formación Docente (INFD) de Argentina. El Proyecto de mejora para la formación inicial de profesores para el nivel secundario. Área: Matemática (INFD, 2010), introduce recomendaciones para que el futuro profesor alcance distintos grados de comprensión de la disciplina y cómo darse cuenta de ello. En particular, sobre los aspectos cognitivos referidos a la enseñanza de las Matemáticas, dice:
Comprender un objeto matemático significa haber transitado por diversas experiencias que le permitan al estudiante producir, organizar y reorganizar la red de relaciones que se deben establecer en la resolución de una situación problemática (intra y extra-matemática) que "obliga" al funcionamiento del objeto, los procedimientos o técnicas que se despliegan para resolverla, las definiciones, propiedades, argumentos que validan las acciones realizadas, todas ellas soportadas y reguladas por el lenguaje simbólico, propio de la Matemática, y la lengua natural. (INFD, 2010, p. 122)
Estos dos últimos criterios conllevan el diseño de tareas de análisis y descripción de la actividad matemática para ser contestadas por los asistentes al curso.
Por otra parte, se notó que, si bien introducían algún elemento de gestión de la clase, no habían "vivido" (aunque fuese hipotéticamente), la gestión que permitía implementar la secuencia de tareas diseñadas. Por esta razón, para aumentar el nivel de las idoneidades cognitiva, emocional, interaccional y mediacional, planteamos un segundo rediseño que facilitase la reflexión sobre la interacción necesaria para la implementación de su secuencia didáctica. Para ello, establecimos los siguientes criterios a modo de condiciones que debían tener en cuenta al diseñar, seleccionar o adaptar las tareas:
− Anticipar los errores y dificultades que tendrían los alumnos al enfrentarse a la tarea que se les presentaba.
− Describir cómo gestionarían la clase ante las dificultades o errores que anticipaban de sus alumnos. Esta descripción se materializaría como un diálogo hipotético entre profesor y alumno.
Estos dos criterios estaban pensados sobre todo para las tareas que debían de diseñar los asistentes para sus alumnos, y para tal fin se dieron pautas que se describen seguidamente.
En otra experiencia llevada a cabo en la UNGS con formación de profesores se advirtieron dificultades en los enunciados de las tareas siendo éstas muchas veces formuladas de un modo descriptivo, demasiado cerradas o sugiriendo cómo resolverlas. Las consignas deberían facilitar, entre otros aspectos, que las tareas promuevan procesos matemáticos relevantes y variados, como el de argumentación y el de modelización, que son indicadores de calidad matemática. Para ello se propusieron los siguientes criterios para la formulación de consignas de las tareas:
− Que la tarea no sea cerrada, es decir, que admita más de un camino posible de resolución. De esta manera, la misma puede generar diferentes tipos de actividad matemática en los alumnos y también, comparar las diferentes estrategias de resolución en una puesta en común, que permita establecer conexiones entre ellas (un indicador de riqueza matemática contemplado en el currículo).
− Que la tarea no brinde sugerencias de caminos posibles o resultados a aplicar.
− Que la tarea no se encuentre en extremo pautada. La razón es que si se pauta mucho con preguntas, no se promueven procesos relevantes como son la formulación de conjeturas o la validación. Es preferible que tenga pocas preguntas (las más generales) y que los alumnos hagan un proceso de análisis que les lleve a resolver cuestiones intermedias.
− Que la tarea requiera justificar las elecciones que se realizan los alumnos, así como también las que se rechazan. La razón es que se trata de promover un proceso matemático relevante como es el de argumentación.
−Si se propone una tarea en un contexto real, procurar que para resolverla este contexto sea significativo y relevante. Dicho de otra manera, evitar hacer preguntas en las que el contexto sea un "decorado" intrascendente. Esto evita que el alumno advierta que la intención del docente está en los objetos matemáticos sobre los cuales pregunta, en lugar de poner el foco en el interés del problema en su contexto.
− En la medida de lo posible evitar dar información que asegure existencia y/o unicidad de la solución de la tarea.
− Considerar incluir consignas que activen en los futuros profesores una reflexión sobre la propia actividad que realizaron para resolver la tarea. Se trata de conseguir una metarreflexión sobre su propia actividad con consignas variadas del tipo: comparar resoluciones diferentes, reflexionar sobre estrategias que no fueron útiles, establecer conexiones con otros conceptos matemáticos.
− Que el uso de nuevos recursos sea necesario para resolver la tarea. Por ejemplo, que permitan aplicar ciertas técnicas, o realizar ciertos gráficos o figuras que sin esta tecnología no serían posibles.
− Que lo solicitado con la tarea sea algo matemático y no referido al uso de software. Se pretende enseñar matemáticas y no sólo el uso de un programa particular, o comandos específicos.
Estos criterios estaban pensados sobre todo para las tareas que debían de diseñar los asistentes para sus alumnos.
Otras dificultades conocidas en estudiantes de profesorado, e incluso en docentes noveles, es saber cómo intervenir adecuadamente en la clase de Matemáticas al responder consultas, al atender a estudiantes que no saben cómo comenzar a resolver la tarea. Para considerar esta observación se adoptó como criterio que el diseño de un ciclo formativo contemple:
− Considerar momentos de anticipación de posibles errores, respuestas inesperadas o inacción ante cada tarea y prever intervenciones docentes apropiadas. Expresarlo a modo de diálogo, evitando descripciones vagas.
A su vez, se propusieron los siguientes criterios para realizar intervenciones docentes:
− Evitar dar más información que la estrictamente puesta en juego en la pregunta o respuesta del estudiante.
− Intervenir a partir de lo que el estudiante presenta, tratando de identificar lo que piensa y cómo lo hace. Evitar llevar al alumno al modo en el que el profesor tiene pensada la resolución. En cierta manera, se trata de generar un conflicto cognitivo en el alumno (en términos piagetianos) para que él mismo llegue por sí solo a la solución.
− Si no aparecen diversidad de resoluciones o errores, hacer una intervención pidiendo que los estudiantes den argumentos sobre la validez de las conjeturas o procedimientos seguidos por otros ante el mismo problema (por ejemplo, intervenciones del tipo "Los alumnos del otro curso dicen que es válido hacer...").
− Evitar decir directamente si la resolución es o no correcta. En cambio, pedir explicaciones para tratar de entender el modo de pensar que lo llevó al alumno hasta ahí.
− Considerar que no es necesario que en una única intervención el profesor resuelva la duda del alumno y posponer la resolución de la duda a intervenciones posteriores. Por ejemplo, ampliarle la duda, hacerle nuevas preguntas o recordarles estrategias utilizadas anteriormente.
− Evitar pedir sólo explicaciones cuando se advierte que la respuesta es incorrecta. Pedir explicaciones también cuando la respuesta es correcta puede develar un argumento inválido usado, es decir, que llegó a una solución correcta por un camino inapropiado.
El objetivo de estas sugerencias es reflexionar sobre el valor de prever intervenciones a raíz de los diseños de las tareas, lo cual ayudaría a planificar intervenciones que tuviesen mayor idoneidad cognitiva, afectiva e interaccional. Las sugerencias buscan, entre otros aspectos, aumentar la autoestima de los alumnos, evitar la exclusión de los alumnos con dificultades, facilitar procesos cognitivos y metacognitivos, que son indicadores de estas cuatro idoneidades.
Estos criterios estaban pensados sobre todo para las tareas que debían diseñar los asistentes para sus alumnos.
4.2. El ciclo formativo FFPMS
El ciclo formativo FFPMS se inició en mayo de 2011, y finalizó en marzo de 2012, y estaba dirigido a profesores de matemáticas encargados de formar a futuros profesores de matemáticas de los Institutos de Formación Docente (IFD) de Argentina. Surgió por iniciativa del INFD, y fue encargado a tres formadores que participaron en experiencias previas realizadas en diferentes centros de formación de profesores, valoradas positivamente por este Instituto por estar centradas en el diseño de tareas, el desarrollo de la competencia en análisis didáctico (experiencia explicada anteriormente) y por la incorporación de recursos TIC en la formación de profesores.
La primera fase consistió en un seminario virtual de diez semanas de duración titulado: "Secuencias didácticas para la formación matemática del profesor: un nuevo enfoque". Se solició la inscripción en grupos de tres personas, los cuales debían estar integrados por un docente de una asignatura del área de Matemáticas, otro de Didáctica de las Matemáticas o involucrado en las prácticas profesionales y un tercero, que debía tener conocimiento de las TIC. En total se inscribieron 33 grupos.
A cada equipo de profesores se le propuso (de acuerdo con el criterio de proponer realizar tareas profesionales), diseñar una secuencia de tareas para ser implementada en sus respectivos IFD (ciclo formativo FPMS). La secuencia de tareas se realizó sobre un tema matemático particular y debía estar alineada, necesariamente, con el enfoque didáctico que planteaba el documento curricular, el cual promueve que el futuro profesor atraviese por experiencias de formación desafiantes, pues serán determinantes posteriormente para su desempeño profesional en la escuela secundaria (INFD, 2010). Además, por una decisión de las autoridades del INFD, se tenía que incorporar el uso de software en el diseño.
De acuerdo con los criterios expuestos en el apartado 4.1., el equipo de formadores decidió proponer una lista mínima de aspectos a considerarse en la memoria presentada para finalizar el seminario virtual, con el fin de facilitar la reflexión colectiva. Además de la secuencia de tareas (punto 6), se demandaban los siguientes apartados:
Materia en la que se implementaría y año;
Contenidos involucrados;
Conocimientos anteriores que se requieren;
Objetivos / competencias. Se dejó que los profesores decidieran cómo preferían trabajar en cada IFD y de acuerdo a las exigencias que les imponía su institución;
Secuencia de contenidos. Podrían usar diferentes herramientas: mapa conceptual, red conceptual, esquema diseñado para ordenar los contenidos, etc.;
Tareas propuestas. Incluiría la formulación de las consignas o enunciados de las tareas, y el modo de trabajo previsto tanto en el aula como fuera de ella. Anticipación de errores / respuestas de estudiantes e intervenciones que haría el docente;
Propuesta de evaluación.
Fundamentación. La fundamentación del diseño de la secuencia didáctica, conlleva la consulta obligada del documento curricular y las herramientas de la Didáctica de las Matemáticas, abordadas en el seminario virtual.
Hay que resaltar que el apartado seis se formuló, sobre todo, a partir de los criterios expuestos para anticipar los errores y dificultades que tendrían los alumnos al enfrentarse a la tarea que se les presentaba y, también para describir cómo gestionarían la clase ante estas dificultades. A su vez, para el apartado 8 se tuvo en cuenta el criterio de fundamentar la calidad de su secuencia de tareas a partir del uso de los criterios de idoneidad.
El trabajo inicial de cada grupo fue proponer tipos de tareas relacionadas con el contenido central de la secuencia e identificar los roles del docente y de los alumnos, los objetivos que se conseguían con la resolución de las tareas planteadas y su vínculo con el documento curricular. Simultáneamente, los encargados del curso presentaron ejemplos de tareas que serían acordes con el documento curricular y otras que no, ya que el documento curricular era de reciente publicación y era dificultoso el hallazgo de este tipo de tareas en los textos de Matemáticas que utilizaban los asistentes.
La plataforma virtual asignó a cada grupo un espacio de foros y chat para interacción entre los miembros del grupo y, a su vez, interacción entre los grupos. Esto permitió a los formadores del curso acceder al registro de la interacción entre los grupos y encontrar evidencias de las dificultades que tenían para diseñar secuencias de tareas adaptadas a las exigencias curriculares. Si bien los asistentes reconocían los ejemplos presentados por los profesores del curso como acordes a las directrices curriculares (nivel 1 de la tabla 1), tenían dificultades para que sus propuestas de tareas también lo fuesen (nivel 2 de la tabla 1).
El octavo punto del modelo de memoria del trabajo final del seminario virtual contemplaba una fundamentación didáctica de la calidad de su propuesta, en la que tenían que utilizar, entre otros referentes, los criterios de idoneidad didáctica propuestos por el EOS. En algunos casos, el hecho de tener que hacer esta fundamentación dio como resultado nuevos rediseños, porque los mismos profesores llegaban a la conclusión de que algunos criterios de idoneidad didáctica no se cumplían. Los criterios que solían considerar menos idóneos eran el interaccional, mediacional y afectivo.
La segunda fase del ciclo formativo FFPMS consistió en un encuentro de tres días en la ciudad de Buenos Aires, en la que participaron todos los grupos, los 3 formadores y técnicos del INFD, con la finalidad de realizar los últimos ajustes al diseño de tareas de cada grupo. El propósito central apuntaba a que una vez que el grupo diera por finalizado el diseño de la secuencia de tareas, observasen que había elementos que permitían mejorar su calidad con un nuevo rediseño. Para ello, los formadores de profesores presentaron sus secuencias a sus colegas. Previo a esas exposiciones los profesores a cargo del ciclo formativo retomaron los criterios y propusieron al grupo completo que, ante cada presentación, se atendiera colectivamente a identificar si alguno de ellos no había sido atendido. En ese caso se pretendió promover una revisión y ajuste de cada secuencia, en caso de ser necesario en la que cada equipo colaborara con el análisis de propuestas ajenas, sabiendo que esto resulta más sencillo, tal como se expresa en los niveles de desarrollo de la competencia de análisis didáctico, mencionados en la tabla I. Después de este encuentro presencial, cada grupo tuvo un intervalo de tres semanas para rediseñar la propuesta que sería implementada.
En la tercera fase cada grupo implementó su secuencia de tareas (septiembre y octubre de 2011) filmando dos clases consecutivas (a elección de cada grupo) de 80 a 120 minutos cada una. La cuarta fase consistió en seleccionar de estas filmaciones dos episodios de no más de cinco minutos cada uno. Esta selección fue realizada por los profesores a cargo del curso, juntamente con el personal de apoyo del INFD, de manera que, a su criterio, se pudieran observar, como mínimo, aspectos relevantes relacionados con las matemáticas implementadas, la gestión de la clase y el uso de recursos. Asimismo dicha selección debía permitir advertir los criterios trabajados, sea porque estuvieron presentes o ausentes.
La quinta fase consistió en el análisis y reflexión de los episodios seleccionados y se realizó entre noviembre y diciembre de 2011. Para ello, se organizaron reuniones en diferentes puntos del país, lo cual permitió una reunión presencial entre los formadores y cada uno de los grupos. En estas reuniones presenciales, de aproximadamente dos horas, participaron los tres profesores del grupo que implementó la secuencia de tareas, uno de los formadores a cargo de la capacitación, un especialista en pedagogía del INFD y un miembro de otro grupo. El objetivo era hacer un análisis exhaustivo de los dos episodios seleccionados, de manera que se tuviesen elementos para rediseñar de nuevo la secuencia didáctica de cada grupo. Estas sesiones fueron registradas en vídeo y los elementos de rediseño quedaron para una futura implementación en el curso siguiente (no se tiene constancia de ella, ya que no eran exigencias del proceso de capacitación). Las intervenciones de los profesores a cargo del curso tuvieron como finalidad lograr que los asistentes al Ciclo reconocieran la adecuación o no de algunos de los criterios sobre los que se trabajó. Al finalizar las reuniones, los equipos reflexionaron sobre su evolución en la competencia de análisis didáctico.
La sexta y última fase consistió en un encuentro f inal presencial en marzo de 2012. El propósito fue que todos los grupos compartiesen reflexiones matemáticas, didácticas y sobre el uso de TIC, y fortalecer el conocimiento matemático y didáctico de los participantes en la capacitación, en general, y en particular sobre una selección de seis episodios filmados. El criterio para su selección fue que tuviesen una buena calidad didáctica, o bien que presentasen elementos para discutir y sobre los cuales pudieran incorporarse mejoras. También, en esta sesión final, registrada en vídeo, los participantes realizaron sugerencias que se podían tener en cuenta para la mejora de futuras capacitaciones del mismo estilo.
Un aspecto relevante del encuentro fue la demanda a los participantes de que aportaran evidencias de que la secuencia que ellos diseñaron e implementaron generaba comprensión matemática, tal como ésta se caracterizaba en el currículo (ver apartado 4.1). A pesar de que en un momento del curso se les hizo observar a los participantes que la herramienta configuración epistémica/cognitiva podría ser útil para analizar la comprensión de los alumnos, no siempre fue utilizada para dar evidencias de la comprensión conseguida por los alumnos que participaron de la implementación de su secuencia de tareas. En algunos casos, se limitaron a dar afirmaciones sin justificarlas con evidencias. En general, no les resultó sencillo dar una justificación razonable de que sus alumnos comprendieron lo que se les enseñó. Se considera, como posible explicación de este hecho, que el uso de una herramienta compleja como es la configuración epistémica/cognitiva de objetos primarios necesita de un tiempo de apropiación más largo y probablemente, de un proceso de instrucción específico y sostenido a lo largo de varias sesiones. Este aspecto se considera como uno de los que se debería mejorar al momento de un nuevo rediseño de un ciclo formativo.
Un aspecto que hay que resaltar es la tasa de abandono del curso (aproximadamente el 50%) y de los motivos aducidos para ello. Por una parte, hubo grupos que hubieran necesitado disponer de más tiempo para diseñar tareas de acuerdo con las orientaciones dadas en el curso. Por otra parte, para algunos grupos fue clave que el modelo de enseñanza de las Matemáticas que se promovía no era acorde al magistral, el arraigado para el nivel superior, y fue vista como compleja la transferencia y aplicabilidad para otros contenidos.
De los grupos que se mantuvieron en el curso, sus primeros diseños proponían secuencias de tareas alejadas de las orientaciones curriculares, hecho que no les era sencillo de advertir al no utilizar evidencias para sostener las propuestas. Esto marca una realidad factible que es la no advertencia de la distancia que puede llegar a existir entre los principios que se sustentan en el currículo escolar para la formación de profesores y los que efectivamente se traducen en las clases impartidas. Este es otro indicador de que en algunos casos, los profesores iniciaron el curso con un nivel muy bajo de competencia en análisis didáctico.
Por último, destacar que algunos profesores cometieron errores de tipo matemático en la implementación a raíz de respuestas no esperadas, en general debidas al uso de nuevas tecnologías. Algunos de ellos no fueron detectados en el proceso de triangulación con los otros miembros del grupo. Podría entenderse como otro indicador del bajo nivel de competencia en análisis didáctico con el que finalizaron algunos asistentes al curso, o relativizarse debido al hecho de la obligatoriedad del uso de TIC que desvió su atención al uso de los recursos y la gestión de la clase que les resultó diferente a lo usual. Se concluye, por tanto, que en un nuevo rediseño del ciclo se pondría más énfasis en un criterio que resultó efectivo en el ciclo implementado en la UNVM: antes de realizar el diseño de tareas, promover la resolución de problemas que permitan una diversidad de estrategias de resolución y en todos los casos con uso de TIC.
Una de las reflexiones que hizo el equipo de formadores sobre la implementación del ciclo FFPMS estuvo dirigida a encontrar evidencias del desarrollo de la competencia en análisis didáctico de los participantes, con relación al nivel que tenían cuando iniciaron el curso. A lo largo del ciclo, encontramos bastantes evidencias de dicho desarrollo. Una de las que nos pareció más significativa es que las secuencias que los asistentes diseñaron e implementaron, por una parte, eran acordes con las orientaciones que se les dio, en especial las curriculares y, por la otra, eran significativamente diferentes a las que implementaban previo al curso. Algunas evidencias de estas diferencias significativas se infieren de sus reflexiones finales de manera generalizada por los participantes. Por ejemplo:
Profesora 1: Tanto nuestros alumnos como nosotras estamos muy contentos con la implementación. Creo que ellos más que nosotras. El proceso nos depara tantas sorpresas; nuestros alumnos, tan pocos, trabajando a full, contentos con la propuesta, motivados, estoy muy feliz ya que mis clases son muchas veces dirigidas, y éstas me permitieron aprender que hay otra forma de enseñar, que os alumnos te enseñan un montón, ellos aprenden y nosotros con ellos. Por supuesto que observé muchas cosas de la secuencia que creo cambiaría o seguiría desarrollando más, ya lo charlaremos mejor con mis colegas, es una primera versión de la secuencia, es perfectible.
Profesora 2: Fue una linda experiencia. Me encantó ver cómo mis alumnos manejaban el software. Superaron mis conocimientos del software y eso me produce mucho placer. Estuvieron estupendos, trabajaron tranquilos y fueron totalmente espontáneos en las respuestas y las preguntas. Están súper motivados y siento que están descubriendo las ventajas de este modo de trabajo al momento de aprender matemática. Me encantó que comenzaran a derribar viejas estructuras, pensaron muchísimo, pero llegamos a las conclusiones esperadas. Reflexionan sobre el trabajo en forma permanente, reconocen que en ningún momento se les dio una clase sobre el uso del software, sino que están aprendiendo matemática usando las herramientas del mismo. En fin, estamos muy contentos.
Por tal motivo, se considera un indicador de un tercer nivel de desarrollo de la competencia en análisis didáctico, según la tabla I.
Se incluyen a continuación ejemplos de las primeras formulaciones de consignas de tareas realizadas por un equipo de profesores y la última versión implementada. Los cambios surgidos siguen los criterios mencionados y se sostuvieron con los equipos en cada devolución. Asimismo se incluye la anticipación de posibles intervenciones, al momento del diseño en la primera y última versión de la planificación de las tareas.
Una de las primeras formulaciones:
a) Representa gráficamente, con papel y lápiz las siguientes funciones y dibuja, si es posible, la recta tangente a la curva en un punto p de la misma. Fundamenta tu respuesta.
Realiza la actividad anterior utilizando como herramienta el software Geogebra, empleando el botón que te permite obtener la recta tangente y responde:
b) ¿Resulta igual la representación de la recta tangente, con papel y lápiz, que la representación utilizando la herramienta del Geogebra?
c) Reflexiona respecto de las actividades realizadas.
d) Establece semejanzas y diferencias en el trabajo efectuado.
En esta formulación se advierte la falta de utilización de varios de los criterios para elaborar consignas, encontrándose en extremo pautada, sin pedido de argumentación y el uso de TIC no resulta clave. La tarea sí incluye la ref lexión sobre las consignas propuestas.
Los profesores a cargo del ciclo formativo consideran que esta propuesta pone de manifiesto la dificultad de analizar las producciones propias a la luz de los criterios, lo que ubica al docente en un nivel inicial bajo de la competencia de análisis didáctico. Sin embargo, considerando que es un punto de partida esperado, se sostuvo la necesidad de que tomen su producción como ajena para analizarla, se los acompañó en esta tarea realizando intervenciones para que fuesen los propios autores quienes advirtiesen la distancia entre lo que los criterios expresan.
La última versión del grupo de profesores, tras las devoluciones del equipo coordinador es la siguiente, donde se observa un planteo abierto, se promueve la argumentación, se mantienen las consignas para reflexionar sobre lo realizado y se hace una anticipación de intervenciones para la puesta en común que atienden a los criterios mencionados.
Primer momento: trabajo individual.
a) Reflexiona sobre el concepto de recta tangente a una curva y registra por escrito las ideas, gráficos, frases, características o expresiones simbólicas, etc., que se te ocurran cuando piensas en este tema.
Segundo momento: intercambio en pequeños grupos con la consigna de acordar una respuesta para ser presentada al resto de la clase.
b) Comparte con tu subgrupo estas ideas, extrae conclusiones y registralas en el afiche entregado para compartir y debatir con la clase.
Tercer momento: intercambio con la clase
Finalizada esta actividad se compartirán los registros realizados en los afiches, para visualizar las diferentes respuestas de los subgrupos, de modo tal que quedará explícita la imagen conceptual de cada alumno, en sus apuntes, y del grupo en el afiche. Algunas expresiones o ideas que pueden aparecer son:
La recta tangente a la curva en un punto es la recta que "corta" a la curva en ese único punto.
La recta tangente a la curva en un punto es la recta que "toca" a la curva en ese único punto.
La recta tangente a la curva en un punto es la recta que "corta" a la curva en ese punto y deja a todos los demás puntos de la curva en un mismo semiplano.
Y, las representaciones gráficas que pueden aparecer son circunferencias o parábolas, etc.
Cuarto momento: trabajo individual nuevamente.
c) Representa gráficamente, con papel y lápiz, cinco funciones diferentes, y dibuja, si es posible, la recta tangente a la curva en un punto p de la misma. Fundamenta tu respuesta.
d) Realiza la actividad anterior utilizando como herramienta el software Geogebra y responde:
i) ¿Resulta igual la representación de la recta tangente, con papel y lápiz, que la representación utilizando la herramienta del Geogebra?
ii) Establece semejanzas y diferencias en el trabajo efectuado.
e) Reflexiona respecto de las actividades realizadas.
Respecto de la previsión de errores e intervenciones, el equipo señaló:
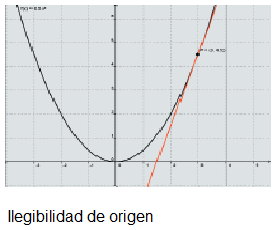
Suponemos que los estudiantes descartarán en un primer momento gráficas como éstas:
Esto se debe a que creemos que los estudiantes suponen que la recta tangente a la curva no puede tocar en más de un punto a la misma. Lo mismo ocurriría con el caso de las curvas que representan a las funciones trigonométricas.
Sí creemos que aparecerán gráficos como el siguiente:
Además, pensamos que aquí comienza un conflicto para los estudiantes, que los inicia en la idea de que el concepto de recta tangente no está claro para ellos.
Analiza lo que ocurre en un entorno del punto donde se busca la recta tangente, tratando de encontrar el significado geométrico de la misma. Realiza un documento que muestre el trabajo realizado por tu subgrupo, para ser entregado al finalizar el encuentro.
Quinto momento: trabajo en subgrupos e intercambio de las respuestas.
Reflexiona sobre el concepto de recta tangente, registrando por escrito las conclusiones obtenidas a partir del análisis de las actividades realizadas, para ser compartida al inicio del próximo encuentro.
Es probable que durante la discusión entre pares los estudiantes desestimen que la recta tangente corta o toca en un único punto a la curva y que advierta que la recta se confunde con la curva en un entorno del punto, lo cual los llevará a pensar que en las cercanías del punto la curva se comporta casi igual que la recta.
En este caso, el zoom en el Geogebra será un elemento que fortalecerá la conjetura de que la curva y la recta tangente comparten un segmento en común en los alrededores del punto. Este hecho, sumado a las anticipaciones sobre tangencia, al concepto en formación y a la búsqueda bibliográfica, permitirá avanzar hacia el ajuste de la noción, al tiempo que ayudaría a clarificar, en este caso, el alcance del software. Además, apelar a argumentaciones matemáticas será clave, en tanto es el objetivo del profesor en la clase de Matemáticas. Esto le otorga al nuevo diseño de la tarea una mayor idoneidad didáctica, de acuerdo a los indicadores propuestos por el EOS y atiende a los criterios generales mencionados, lo que permite tener evidencias de una mejora en la competencia de análisis didáctico.
5. Consideraciones finales
La revisión de la literatura muestra que inicialmente los criterios de idoneidad didáctica del EOS se diseñaron y fueron utilizados para valorar procesos de instrucción efectivamente implementados. Una de las novedades que se plantearon en los ciclos experimentados en Argentina fue utilizar los criterios de idoneidad directamente en el proceso de planificación de una secuencia de tareas. A partir de la experiencia, se considera que dichos criterios son elementos relevantes en un proceso de diseño instruccional, siempre y cuando se acompañen con indicaciones relacionadas con una hipotética implementación que los hagan operativos. Esto es, que haga reflexionar al profesor sobre los diferentes procedimientos de resolución que involucra la tarea, anticipación y tratamiento posible de los errores y dificultades que pudiesen tener los estudiantes, tipos de intervenciones a realizar durante la gestión de la clase, entre otros.
El ciclo FFPMS descrito muestra un caso de rediseño a partir de experiencias formativas previas. Resultó clave capitalizar experiencias anteriores estableciendo criterios que permitan ser reutilizados, trascendiendo los casos que les dieron origen. Fue necesario introducir, además de los criterios de idoneidad y sus indicadores, pautas concretas que diesen sugerencias de diseño y secuenciación de tareas. Específicamente, se tuvieron que introducir criterios para elaborar las consignas de las tareas y también sugerencias de intervención y gestión que hicieran pensar en una hipotética implementación de las tareas diseñadas. Esto, junto con la necesidad de fundamentar los diseños de tareas usando documentos curriculares y herramientas de la Didáctica de las Matemáticas, no sólo ayudó a lograr una mayor idoneidad didáctica de las secuencias, sino también, promovió el desarrollo de la competencia en análisis didáctico de los profesores.
La experiencia que se describió y analizó es un ejemplo relevante sobre cómo se pueden evaluar competencias profesionales en la formación de profesores. En los ciclos formativos FPMS y FFPMS se constató un desarrollo de la competencia en análisis didáctico de los participantes, lo cual se justifica en tanto se cumplieron algunos de los indicadores de esta competencia señalados en Font (2011). El desarrollo fue diverso debido, entre otras razones, a las características de los asistentes, la motivación y el tiempo. Sin embargo, en todos los casos, los participantes de los ciclos advirtieron su evolución logrando identificar obstáculos y facilitadores para desarrollar las tareas planteadas. Centralmente se identificaron dos cuestiones clave: la presencia de las nuevas tecnologías, como recurso obligatorio a ser incluido en las clases y el enfoque matemático que obligó a los participantes a articular los marcos geométrico, analítico, algebraico, numérico y verbal en sus propuestas. Por un lado, el uso requerido de las TIC puede haber tenido una influencia en la gestión de la clase y en el no reconocimiento de errores matemáticos que surgieron en las aulas. La anticipación de errores, aunque fuese una práctica usual en docentes, se ve modificada por las nuevas tecnologías de modo que muchos de ellos resultan novedosos e inesperados incluso en docentes con experticia. Los indicadores para valorar la idoneidad mediacional nos han permitido tener registro de estos casos. Asimismo en términos del enfoque que debieron plasmar con el contenido matemático abordado, las articulaciones entre los distintos marcos pueden haber facilitado en algunos casos argumentaciones que permitan sostener la validez o no de alguna cuestión; pero en otros casos la necesidad de moverse f lexiblemente entre una y otra perspectiva fue una actividad no usual, constituyendo otro rasgo inusual dentro de las prácticas usuales de enseñanza de las Matemáticas en el nivel superior. Estos hechos se pudieron identificar mediante los indicadores para valorar la idoneidad epistémica de las clases.
El trabajo de rediseño desarrollado, que partió de capitalizar experiencias anteriores, permitió construir criterios reutilizables que favorecen el desarrollo de la competencia en análisis didáctico. Consideramos central en la formación de profesores, tanto la inicial como la continua, el desarrollo de esta competencia debido a que es una herramienta clave para que el profesor logre aprendizajes significativos en sus estudiantes y tenga elementos para explicar qué es lo que ocurre, en caso de que advierta que su propuesta no resulta adecuada. Entendemos que los criterios aquí expuestos son un aporte para la formación docente y permiten mejorarla en este aspecto específico. Considerar el Enfoque Integral (Weinert, 2001), dentro de los enfoques de competencias nos permitió atender, desde la propuesta de criterios, al manejo específico de conocimientos, habilidades y reflexión para alcanzar un desempeño eficaz en una de las tareas específicas de la profesión docente que redunda en mejores aprendizajes matemáticos.











 nueva página del texto (beta)
nueva página del texto (beta)