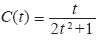Artículos

 

Desarrollo de un modelo epistemológico de referencia en torno a la modelización funcional

 

Development of a reference epistemological model around the functional modelling

 

Cecilio Fonseca Bon*, Josep Gascón Pérez**, Catarina Oliveira Lucas***

 

* Departamento Matemática Aplicada I, Universidad de Vigo, España. cfonseca@uvigo.es

** Departamento de Matemáticas, Facultad de Ciencias, Universitat Autónoma de Barcelona, España. gascon@mat.uab.cat

*** Estudiante de doctorado del Departamento Matemática Aplicada I, Universidad de Vigo, España. catarinalucas.mail@gmail.com

 

Recepción: Enero 26, 2012
Aceptación: Septiembre 19, 2013.

 

Resumen

En este trabajo se presenta el diseño matemático de una pequeña parte de un modelo epistemológico de referencia que, una vez completado, deberá sustentar la organización didáctica de un proceso de estudio que incluya: el desarrollo de la modelización funcional con parámetros, la razón de ser del cálculo diferencial elemental en la última etapa de secundaria y los primeros desarrollos del cálculo en varias variables en la universidad. Aquí nos concentramos en el momento en que ya se dispone de la derivada como herramienta de trabajo para mostrar el desarrollo progresivo y la completación relativa de las praxeologías matemáticas que se construyen a medida que se avanza en los diferentes niveles de la modelización funcional. Esta propuesta se hace en el ámbito de la Teoría Antropológica de lo Didáctico y constituye una pequeña contribución al objetivo didáctico de situar la modelización matemática como un instrumento que permite articular y dar sentido a la matemática escolar.

Palabras clave: Modelo epistemológico de referencia (MER), Tres niveles de modelización funcional, Teoría Antropológica de lo Didáctico (TAD).

 

Abstract

This paper presents the mathematical design of a small part of a reference epistemological model which, once concluded, should support the educational organization of a study process comprising: the development of the functional modelling with parameters, elementary differential calculus raison d'être in high school, and the first developments of calculus in several variables at university. Hereto we focus in the moment in which we already hold the derivative as a work tool to show the progressive development, and the relative completion of mathematical praxeologies that are built as progress gains ground in the different levels of functional modelling. This proposal is submitted from an Anthropological Theory of the Didactic scope and represents a small contribution to the didactic purpose of placing the mathematical modelling as an instrument that allows to articulate and give meaning to school mathematics.

Key words: Reference epistemological model (REM), Three levels of functional modelling, Anthropological Theory of the Didactic (ATD).

 

Resumo

Neste trabalho apresenta-se o desenho matemático de uma pequena parte de um modelo epistemológico de referência que, uma vez completado, deverá sustentar a organização didática de um processo de estudo que inclua: o desenvolvimento da modelação funcional com parâmetros, a razão de ser do cálculo diferencial elementar no ensino médio/secundário e os primeiros desenvolvimentos do cálculo em várias variáveis na Universidade. Aqui nos concentramos no momento em que já se dispõe da derivada como ferramenta de trabalho para mostrar o desenvolvimento progressivo e a completação relativa das praxeologias matemáticas que são construídas à medida que se avança nos diferentes níveis da modelação funcional. Esta proposta surge no âmbito da Teoria Antropológica do Didático e constitui uma pequena contribuição para o objetivo didático de situar a modelação matemática como um instrumento que permite articular e dar sentido à matemática escolar.

Palavras chave: Modelo epistemológico de referência (MER), Três níveis de modelação funcional, Teoria Antropológica do Didático (TAD).

 

Résumé

Dans ce travail on ébauche la représentation mathématique d'un modèle épistémologique de référence qui, une fois complété, devra appuyer l'organisation didactique d'un processus d'étude incluant le développement de la modélisation fonctionnelle avec paramètres, la raison d'être du calcul différentiel élémentaire au Lycée et les premiers développements du calcul à plusieurs variables dans les cours à l'Université. On va se centrer au moment où on dispose de la dérivée comme outil de travail pour montrer le développement progressif et la complétion relative des praxéologies mathématiques qui se construisent au fur et à mesure qu'on avance dans les différents niveaux de la modélisation fonctionnelle. Cette proposition s'inscrit dans le cadre de la théorie anthropologique du didactique et constitue une petite contribution à l'objectif didactique de situer la modélisation mathématique comme un instrument qui permet d'articuler et donner du sens aux mathématiques scolaires.

Mots clés: Modèle épistémologique de référence (MER), Les trois niveaux de la modélisation fonctionnelle, Théorie anthropologique du didactique (TAD).

 

1. ¿QUÉ PAPEL JUEGA UN MODELO EPISTEMOLÓGICO DE REFERENCIA EN LA FORMULACIÓN DE UN PROBLEMA DIDÁCTICO?

La formulación de un problema didáctico (en el sentido de problema de investigación en didáctica de las matemáticas) involucra siempre, de manera más o menos explícita, una interpretación del ámbito de la actividad matemática que está en juego. Así, cuando en el enunciado de un problema didáctico se habla de la enseñanza o el aprendizaje del concepto de derivada, de la geometría analítica o de los sistemas de numeración, se está sustentando inevitablemente una interpretación (un modelo, aunque sea muy impreciso) de la actividad matemática que acompaña a dicha noción o ámbito de la matemática escolar en la institución en cuestión.

En la Teoría Antropológica de lo Didáctico (en adelante, TAD) postulamos que la explicitación de dicho modelo es imprescindible para poder formular el problema didáctico como un auténtico problema científico. La citada explicitación constituye el núcleo de la respuesta que proponemos en cada caso a una dimensión básica del problema didáctico que denominamos "dimensión epistemológica del problema" (Gascón, 2011) y se materializa en un modelo epistemológico de referencia (o, abreviadamente, MER). La formulación de los otros aspectos o dimensiones del problema didáctico, así como las posibles respuestas a los mismos, se sustentan forzosamente en el MER del ámbito de la actividad matemática que está en juego.

En general, la estructura de los MER que construye la TAD es una red de praxeologías matemáticas cuya dinámica comporta ampliaciones y completaciones progresivas en el sentido que explicitaremos en lo que sigue (Ruiz-Munzón, Bosch & Gascón, 2011). En cuanto a la manera concreta de describir un MER, digamos aquí únicamente que suele hacerse mediante una red de cuestiones y respuestas donde éstas tienen estructura praxeológica.

Es importante subrayar que un MER debe considerarse como una hipótesis provisional a contrastar experimentalmente y, por lo tanto, susceptible de ser modificado y revisado constantemente. En otras palabras, un MER es una hipótesis científica que debemos poner a prueba de la contingencia.

Dado que la TAD interpreta la actividad matemática como una actividad humana institucionalizada, un MER (y la cuestión generatriz que viene a responder) se elabora en relación a una institución. Pero las instituciones no son compartimentos estancos y las cuestiones problemáticas se desarrollan a medida que se van estudiando, de manera que es posible concebir un MER que, potencialmente, pueda sustentar procesos de estudio situados parcialmente en dos o más instituciones (y en dos o más niveles educativos) como, por ejemplo, en secundaria¹ y en la universidad.

Por otra parte, es importante señalar que en los MER elaborados hasta la fecha en el ámbito de la TAD, la modelización matemática juega un papel esencial. En efecto, las praxeologías matemáticas que estructuran el MER suelen cumplir la siguiente condición: cada nueva praxeología no sólo amplía y completa relativamente a la praxeología anterior, sino que además puede considerarse como un modelo matemático de ésta (Bolea, 2003; Sierra, 2006; Barquero, Bosch & Gascón, 2011; Ruiz-Munzón et al., 2011). Esta relación estructural y dinámica entre las praxeologías que constituyen un MER es coherente con el postulado de la TAD según el cual toda actividad matemática puede interpretarse como una actividad de modelización (Chevallard, Bosch & Gascón, 1997).

Es por ello que para explicar con claridad el papel que juega un MER en la formulación de un problema didáctico en el ámbito de la TAD es preciso tomar en consideración cómo se conceptualiza la modelización matemática en esta teoría. Esto es lo que haremos brevemente en el siguiente apartado.

Para acabar, digamos que también es importante situar cada MER en relación a otros MER de los que de alguna manera depende y, en especial, de los MER más amplios que lo contienen. Y, por otra parte, distinguir (para unir, no para separar) el MER de los procesos didácticos que éste puede sustentar en una institución determinada².

En esta investigación nos situamos en el momento en que ya se dispone de la derivada como herramienta de trabajo y pretendemos mostrar la progresiva completación de las praxeologías matemáticas que se pueden construir a medida que se avanza en los diferentes niveles de la modelización funcional (en el sentido de Ruiz-Munzón et al., 2011). Es importante remarcar que el diseño matemático que presentamos aquí no es más que un componente de un MER más amplio que pretende recubrir: el inicio de la modelización funcional con parámetros, una posible razón de ser del cálculo diferencial elemental en el paso de secundaria a la universidad y los primeros desarrollos del cálculo diferencial en la universidad. El diseño completo de dicho MER y la experimentación –en el ámbito del primer curso de la enseñanza universitaria portuguesa- de una organización didáctica sustentada sobre una pequeña parte de este MER³ constituye el objetivo de una memoria de tesis doctoral en marcha.

 

2. EL PROBLEMA DIDÁCTICO DE LA MODELIZACIÓN MATEMÁTICA EN EL ÁMBITO DE LA TEORÍA ANTROPOLÓGICA DE LO DIDÁCTICO

El problema de situar adecuadamente el papel que juega (y el que podría jugar) la modelización en la enseñanza de las matemáticas constituye actualmente una de las cuestiones más acuciantes en todos los niveles educativos y, también, en el universo de investigación en Educación Matemática. Dicho problema podría plantearse en los términos siguientes:

"Una vez enseñados los contenidos matemáticos básicos, ¿cómo conseguir que las matemáticas se enseñen como una herramienta de modelización de situaciones, de tal forma que la enseñanza no se organice únicamente en función de los contenidos matemáticos sino de los problemas o proyectos que los estudiantes deben realizar?" (Barquero, 2009, p. 30).

Tal como indicaba Barquero en el trabajo citado, nos situamos así en una problemática de gran interés para la comunidad investigadora en Educación Matemática denominada "Modelización y aplicaciones". El estudio de dicha problemática y las acciones que se han llevado a cabo en las últimas décadas con el objetivo de integrar la modelización matemática en el ámbito de la matemática escolar han tenido un importante impacto tanto en la comunidad de investigadores como en las sucesivas reformas escolares en todos los niveles educativos. Sin embargo, los resultados obtenidos hasta el momento muestran que la integración de la modelización matemática en cualquiera de los niveles del sistema educativo choca con restricciones institucionales que van mucho más allá de la voluntad y la formación de los sujetos de las instituciones involucradas como, por ejemplo, las derivadas del aplicacionismo y del contrato didáctico vigente (Barquero, Bosch & Gascón, 2014). Se empieza así a tomar conciencia de lo que desde la TAD denominamos "dimensión ecológica" del problema de la modelización matemática (Gascón, 2011).

En este sentido, postulamos que para que la modelización pueda vivir con normalidad en nuestros sistemas de enseñanza, es necesario profundizar en el estudio de la citada dimensión ecológica del problema y utilizar los resultados de dicho estudio para diseñar dispositivos didácticos que permitan superar las dificultades que muestran actualmente las propias instituciones docentes (antes que los sujetos de las mismas) para acoger en su seno dicha actividad.

Como ya hemos dicho, la TAD considera que toda actividad matemática puede ser interpretada como una actividad de modelización (Chevallard, Bosch & Gascón, 1997), aunque su forma de interpretarla difiera en ciertos aspectos de las formas más habituales (Blum, 2002; Blum & Leiß, 2007). En concreto, proponemos tres modificaciones importantes en la forma de interpretar la noción de "modelización matemática":

(a) Se incluye la modelización intramatemática en la noción de "modelización". Consideramos la modelización matemática de sistemas matemáticos (esto es, la modelización intramatemática como, por ejemplo, la modelización algebraica de un sistema numérico o geométrico) como una parte esencial de la actividad de modelización que es inseparable de la modelización de sistemas extramatemáticos. Veremos, en efecto, que aunque el proceso de modelización parta de un sistema extramatemático (por ejemplo, de un sistema proveniente de las ciencias de la salud) como sistema a modelizar, el desarrollo progresivo de la actividad de modelización incluye rápidamente etapas en las que interviene la modelización intramatemática.

Esta ampliación de la noción clásica de modelización matemática es coherente con el desarrollo histórico de las matemáticas y permite considerar la modelización como un proceso de matematización progresiva de un sistema en el cual el primer modelo pasa a jugar el papel de sistema (matemático) y así sucesivamente, lo que conduce a trabajar con "modelos de modelos" del sistema inicial. Aparece así claramente el carácter recursivo de la actividad de modelización matemática.

(b) Se postula que los modelos que se construyen en la modelización matemática tienen estructura praxeológica y que la función de los modelos no tiene nada que ver con la de ser una imagen fidedigna del sistema modelizado. El análisis de la actividad de modelización nos conduce a considerar los sistemas y modelos como entidades con estructura necesariamente praxeológica. En efecto, el modelo epistemológico de la TAD no permite considerar la modelización de conceptos, ni de técnicas, ni de problemas aislados. Dada la naturaleza dinámica de las praxeologías y la profunda interrelación entre sus componentes, no podemos hablar de modelización de un componente de la praxeología independientemente del resto de sus elementos. Postulamos, en consecuencia, que toda modelización matemática presupone la modelización de una praxeología en su totalidad mediante otra praxeología matemática.

En cuanto a la naturaleza de los modelos y su relación con el sistema modelizado, no debemos caer en la ingenuidad de pensar que un modelo es una copia o reproducción fotográfica del sistema que modeliza, sino que es un añadido a dicho sistema, una construcción artificial. Se enfatiza así que la principal función del modelo no es la de parecerse al sistema que modeliza, sino la de aportar conocimientos sobre él y hacerlo de la forma más económica y eficaz posible. Para superar esta falsa interpretación podemos substituir, como propone Chevallard (1992), la metáfora del modelo como imagen del sistema por la del modelo como máquina cuyo funcionamiento permite producir conocimientos relativos al sistema modelizado.

Digamos, por último, que la problemática de la adecuación o ajuste del modelo al sistema comporta la tarea de comparación de diferentes modelos de un mismo sistema. Esta dialéctica de idas y venidas entre el sistema y sus posibles modelos origina un cuestionamiento progresivo de la adecuación del modelo al sistema y tiene por objetivo dar respuesta tanto a las cuestiones iniciales como a las que van apareciendo a lo largo del proceso de estudio.

(c) Se interpreta la modelización matemática como un instrumento capaz de articular y dar funcionalidad a la actividad matemática escolar. La TAD describe los procesos de modelización como procesos de reconstrucción y articulación de organizaciones matemáticas de complejidad creciente (Barquero, 2009) que necesariamente tienen que partir de cuestiones problemáticas que se plantea una comunidad de estudio y que constituyen la "razón de ser" de las citadas organizaciones matemáticas (en adelante, OM). La forma como se conceptualiza la complejidad creciente de las OM es la siguiente: las organizaciones (o praxeologías) matemáticas más elementales se llaman puntuales y están constituidas alrededor de lo que en determinada institución es considerado como un único tipo de tareas. Cuando una OM se obtiene por integración de cierto conjunto de OM puntuales, tales que todas ellas aceptan un mismo discurso tecnológico θ, diremos que tenemos una OM local caracterizada por dicha tecnología θ y la designamos mediante OM_θ. Análogamente se habla de OM regional cuando se obtiene por integración de OM locales y está caracterizada por una teoría Θ y hasta de OM global cuando incluye toda una disciplina.

La actividad de modelización matemática, tal como se conceptualiza en el ámbito de la TAD, puede considerarse como un instrumento que permite articular y dar sentido a la matemática escolar debido a su propia lógica interna de desarrollo. En efecto, la modelización matemática parte de una praxeología (que puede ser puntual) como respuesta provisional a una cuestión problemática. En esta praxeología surgen nuevas cuestiones problemáticas cuya respuesta requerirá considerarla como sistema a estudiar y construir para ello un modelo de la misma (carácter recursivo de la actividad de modelización) que será más amplio y complejo que el anterior y que puede englobar más de una praxeología puntual. Si este proceso continúa se puede extender a las praxeologías locales y articular así la actividad matemática escolar.

Una vez descritos los principales rasgos distintivos de la manera como la TAD conceptualiza la modelización matemática, podemos afirmar que el problema de la modelización matemática (y, en particular, el de la modelización funcional) y la correspondiente búsqueda de dispositivos que permitan la articulación y funcionalidad de los contenidos matemáticos escolares constituye un problema didáctico crucial. Como respuesta al mismo, en los procesos didácticos experimentados en el ámbito de la TAD, basados en la noción de recorrido de estudio e investigación introducida por Chevallard (2004, 2005, 2006), se ha puesto claramente de manifiesto que el estudio de "cuestiones vivas" cuya resolución suscita un proceso de modelización, junto con el recurso a las nuevas tecnologías (como, por ejemplo, las calculadoras simbólicas Wiris, GeoGebra o Mathematica) pueden facilitar el desarrollo de los distintos momentos didácticos en que se estructura el proceso de estudio, especialmente los momentos exploratorio, del trabajo de la técnica, tecnológico-teórico y de la evaluación (Chevallard, 1999; Chevallard et al., 1997) al tiempo que pueden ayudar a completar las praxeologías matemáticas en construcción.

Es importante subrayar que, obviamente, no son las TIC por sí solas las que facilitan mecánicamente el desarrollo del proceso de estudio. Como han puesto de manifiesto diversos autores (Artigue, 2002, 2011; Cantoral & Mirón, 2000), la transformación de un simple instrumento –por potente que sea– en un dispositivo didáctico eficaz constituye un problema de investigación didáctica no trivial y, en gran medida, abierto.

 

3. DISEÑO DE UN MODELO EPISTEMOLÓGICO DE REFERENCIA DE LA MODELIZACIÓN FUNCIONAL EN EL ÁMBITO DE LAS CIENCIAS DE LA SALUD

Presentamos a continuación el diseño matemático de una pequeña parte de un MER que puede ser descrito en términos de una arborescencia de cuestiones y respuestas (no predeterminadas de antemano) donde estas últimas constituyen praxeologías cada vez más amplias y relativamente más completas en el sentido descrito en Bosch, Fonseca y Gascón (2004). En este trabajo explicitamos únicamente algunos de los tipos de cuestiones que podrían generar las sucesivas praxeologías y sugerimos algunas de las técnicas útiles para estudiar dichas cuestiones, pero no podemos describir con detalle todos los componentes de las praxeologías porque esto requeriría explicitar las respuestas provisionales a las citadas cuestiones, el desarrollo de las técnicas que se utilizan (incluyendo las relaciones entre ellas), la correspondiente ampliación de los tipos de cuestiones que van apareciendo, los sucesivos discursos tecnológicos que permiten interpretar, justificar y construir dichas técnicas y hasta la teoría que articula y unifica dichos discursos (Chevallard, 1999).

Nos situamos en el momento en que la derivada, como herramienta de trabajo, ya forma parte del equipamiento praxeológico inicial de la comunidad de estudio para mostrar el desarrollo de las praxeologías matemáticas que se construyen a medida que se avanza en los diferentes niveles de la modelización funcional (Ruiz-Munzón et al., 2011).

Partiremos de una cuestión situada en el ámbito de las Ciencias de la Salud y, más concretamente, de una cuestión relativa a la concentración de un medicamento en el torrente sanguíneo. Mostraremos que el proceso de modelización funcional que da respuesta progresiva a esta cuestión (y a las que se derivan de ella) permite reestructurar, articular y dar sentido a los contenidos matemáticos relativos a la modelización funcional que aparecen en los últimos años de la enseñanza secundaria y en los inicios de la enseñanza universitaria.

En consecuencia, el problema subyacente que estamos abordando es el siguiente: ¿cómo conseguir que los conocimientos matemáticos que se estudian en el paso de la enseñanza secundaria a la universitaria en torno a la modelización funcional no se reduzcan a un conjunto desarticulado de conceptos y técnicas carentes de sentido, sino que aparezcan como herramientas para dar respuesta a cuestiones problemáticas que los estudiantes pueden asumir como propias?

Para empezar a responder a esta cuestión elaboraremos, como hemos dicho, una parte de un MER partiendo de una cuestión generatriz. De entre las múltiples cuestiones con sentido y con legitimidad funcional y social, y dada la importancia de recientes investigaciones de modelos matemáticos en el ámbito de las Ciencias de la Salud, podría estudiarse la siguiente cuestión generatriz (aunque, en última instancia, debe ser la comunidad de estudio la que acabe eligiendo la cuestión a estudiar):

Q₀: Con la finalidad de erradicar una epidemia se inyectó una determinada cantidad de medicamento a una población de individuos infectados. ¿Cómo podemos estudiar la variación de la concentración del medicamento en el torrente sanguíneo de estos pacientes?

Se trata de una cuestión con gran poder generador, intencionadamente muy abierta, que además de no proporcionar ningún dato numérico tampoco especifica cuáles son las variables que habría que tomar en consideración para describir el sistema.

 

3.1. Primer nivel de modelización funcional

En el trabajo de Ruiz-Munzón et al. (2011) se muestra claramente que la separación entre el lenguaje algebraico y el lenguaje funcional constituye uno de los principales indicadores del carácter prealgebraico de la matemática que vive en la enseñanza secundaria. Esta separación se pone claramente de manifiesto en el uso casi exclusivo de las fórmulas como meras escrituras abreviadas de reglas de cálculo y en la consiguiente incapacidad, al menos en la enseñanza secundaria, de interpretarlas como relaciones funcionales entre variables y utilizar así los modelos funcionales resultantes para estudiar propiedades de los objetos modelizados usando las técnicas matemáticas asociadas.

Siguiendo a la autora citada denominamos primer nivel de modelización funcional de un sistema el que se materializa en modelos que se expresan mediante funciones aisladas de una única variable y las correspondientes ecuaciones (e inecuaciones) asociadas. Este tipo de modelización incluye en cierta forma la modelización algebraica (en el sentido de Bolea (2003)) y viene a responder a cuestiones que hacen referencia a la variación de una magnitud del sistema en función de otra. Su puesta en marcha requiere, más allá de las técnicas puramente algebraicas, el uso de nuevas técnicas (que llamamos "funcionales" y "gráficas") que incluyen las relativas al estudio de la variación de magnitudes, crecimiento, decrecimiento, ritmo de variación, extremos, etc. Se trata, en definitiva, de técnicas que permiten el estudio elemental de las relaciones internas entre los elementos de una función y el análisis del comportamiento global de la misma.

Para ejemplificar el tipo de actividad matemática que tiene lugar en este primer nivel de modelización funcional formularemos algunas cuestiones derivadas de Q₀ que pueden abordarse en este nivel.

Como ya hemos indicado nos situamos en el momento en que una potencial comunidad de estudio dispone, como equipamiento praxeológico inicial, de las técnicas de derivación junto a la tecnología asociada, así como de las técnicas necesarias para llevar a cabo el estudio algebraico de funciones polinómicas, racionales y exponenciales elementales y de sus representaciones gráficas. Se supone que el citado equipamiento praxeológico inicial contiene las técnicas y las tecnologías necesarias para analizar las características fundamentales de dichos tipos de funciones, tales como el dominio y recorrido, el signo de la función, los ceros, la continuidad, las asíntotas, la paridad, la monotonía y los extremos.

Diremos únicamente que el desarrollo del citado proceso de estudio potencial debería desembocar –mediante el uso de técnicas didácticas⁴ que no analizaremos aquí (Chevallard, 1999)– en la elaboración por parte de la comunidad de estudio de cuestiones más específicas que Q₀ como, por ejemplo:

Q₁: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de un paciente si suponemos que t horas después de ingerido el medicamento, la concentración (medida en miligramos por litro) viene dada por la función

Algunas de las cuestiones derivadas de Q₁ que pueden responderse en este primer nivel de modelización funcional son las siguientes:

Q₁₁: ¿Se puede afirmar que la concentración del medicamento en el torrente sanguíneo aumenta con el tiempo?

Q₁₂: ¿Cómo varía dicha concentración a largo plazo?

Q₁₃: ¿A partir de qué momento se inicia la eliminación progresiva del medicamento del torrente sanguíneo? :

Q₁₄: ¿Cuánto tiempo después de la ingestión del medicamento se alcanza la máxima concentración en sangre? ¿De cuántos mg/l es dicha concentración máxima?

Q₁₅: ¿En qué momentos decrece más rápidamente la concentración?

Se podría intentar responder a estas cuestiones utilizando como primera técnica la representación gráfica de la función C(t) con lápiz y papel, esto es, calculando a mano el dominio de la función, el signo, la derivada, los intervalos de monotonía, los extremos relativos, etc., pero ésta es una técnica muy rudimentaria con un coste enorme. En el momento exploratorio de este primer tipo de tareas, la comunidad de estudio, en la búsqueda de una técnica más económica, podría utilizar un programa de geometría dinámica.

Así, para empezar a estudiar cualitativamente la variación de la concentración del medicamento en el torrente sanguíneo y responder aproximadamente a las cuestiones propuestas, la comunidad de estudio potencial podría empezar utilizando un instrumento informático como el GeoGebra que permite intuitivamente ver que la concentración crece, alcanza un valor máximo y después decrece. Dicho instrumento también permite comparar la gráfica con valores puntuales de la concentración (en la tabla adjunta) y pone de manifiesto cómo se relaciona la variación de dichos valores con la forma de la gráfica.

Figura 1

La necesidad de responder con exactitud (no sólo de manera aproximada) a las cuestionesQ_{13 y} Q₁₄obliga a utilizar técnicas más precisas como, por ejemplo, el programa de cálculo simbólico Mathematica. Pero incluso el uso de esta técnica requiere de una justificación e interpretación⁵ de los resultados aportados por la misma, lo que comporta necesidades tecnológicas que sumerge a la comunidad de estudio en el momento tecnológico-teórico.

Para responder a la cuestión Q₁₅ se pueden utilizar diversas técnicas. Así, por ejemplo, pueden construirse tablas numéricas de la función C(t) y de las funciones primera y segunda derivada. Aparece aquí la necesidad de interpretar los valores numéricos para descubrir cuál es el valor más negativo de la tasa de variación y en qué instantes ocurre. En otras palabras, se busca el valor mínimo de la función derivada. Para ello tenemos que estudiar la variación de la variación de la concentración, esto es, la segunda derivada de la función concentración. Tenemos así un ejemplo que muestra la razón de ser del estudio de la función derivada segunda toda vez que ninguna de las técnicas anteriormente utilizadas permitía contestar adecuadamente a este tipo de cuestiones. De este modo, el desarrollo del proceso didáctico generado por una cuestión problemática nos conduce al uso de una nueva técnica que aporta más información relevante sobre el sistema estudiado.

Una posible ampliación de la situación inicial puede surgir de la necesidad de comparar la evolución de la concentración del medicamento en dos organismos diferentes como, por ejemplo:

Q'₁: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de dos pacientes, Ana y Carlos, si suponemos que son administradas, por la primera vez, dosis terapéuticas iguales y que, durante las primeras 12 horas después de la toma simultánea del medicamento, las concentraciones, medidas en mg por litro de sangre, vienen dadas respectivamente por: A(t)=4t³e^-t y C(t)=2t³e^-0,7t ?

Algunas de las cuestiones derivadas de Q'₁ que requieren respuesta y pueden responderse en este primer nivel de modelización funcional son las siguientes:

Q'₁₁: ¿Cuánto tiempo después de la toma del medicamento, la concentración en sangre es la misma para ambos pacientes?

Q'₁₂: Cuando la concentración ultrapasa 7,5 mg/litro de sangre, el medicamento puede tener efectos secundarios indeseables. ¿Se produce esta situación para alguno de los dos pacientes? ¿Para cuál de ellos? ¿En cuántos mg/l sobrepasa los 7,5 mg/litro?

Q'₁₃: ¿Cuál es el valor máximo que alcanza la concentración del medicamento en cada uno de los organismos?

Esta ampliación del sistema inicial permite, por un lado, comparar dos modelos que se expresan mediante funciones aisladas de una única variable y, por otro, muestra la necesidad de trabajar en niveles superiores de modelización funcional puesto que este trabajo pone de manifiesto la importancia de interpretar en el sistema el significado de la variación de los parámetros del modelo.

En resumen, el paso de la modelización puramente algebraica al primer nivel de modelización funcional ha estado provocado por la emergencia de tipos de problemas cuya respuesta requiere el estudio de la variación de una magnitud del sistema en función de otra. Para estudiarlos se han requerido nuevas técnicas que llamamos "funcionales" y "gráficas", incluyendo las técnicas de derivación y las relativas al estudio local de una función (intervalos de monotonía, extremos relativos, etc.) y al comportamiento global de la misma. Correlativamente han surgido nuevas necesidades tecnológicas y teóricas para describir, interpretar y justificar las nuevas técnicas. En definitiva, podemos afirmar que se ha producido una clara ampliación y una completación relativa de la práctica matemática en el sentido que explicitan los indicadores del grado de completitud (Bosch, Fonseca & Gascón, 2004).

 

3.2. Segundo nivel de modelización funcional

En el citado trabajo de Ruiz-Munzón et al. (2011) se muestra que en la enseñanza secundaria los símbolos literales juegan casi únicamente el papel de incógnitas (en las ecuaciones) o el papel de variables (en el lenguaje funcional). En general el papel de los parámetros está prácticamente ausente, excepto en algunos casos muy particulares. En términos generales puede afirmarse que el juego sistemático entre las diferentes funciones de las "variables" está completamente ignorado.

Esta situación se prolonga a lo largo de toda la enseñanza secundaria y dificulta enormemente el paso del trabajo con las expresiones analíticas de funciones elementales al estudio de familias de funciones y al uso de estas familias como modelos de sistemas en los cuales aparecen relaciones entre magnitudes.

Siguiendo a esta autora, denominamos segundo nivel de modelización funcional de un sistema el que se materializa en modelos que se expresan precisamente mediante familias de funciones de una variable y las correspondientes ecuaciones (e inecuaciones) paramétricas asociadas.

En este segundo nivel de modelización se distingue todavía entre "parámetros" y "variables" de tal forma que sus papeles aún no se consideran intercambiables. Se trabaja, por lo tanto, con familias de funciones de una variable pero no se consideran funciones de varias variables.

Aunque es cierto que en el primer nivel de modelización funcional ya se podía iniciar el estudio elemental del efecto de la variación puntual (entre dos valores fijos) de alguno de los parámetros del modelo sobre las características del sistema (especialmente cuando se trataba de funciones muy elementales), veremos que el estudio sistemático de dichas variaciones requiere de técnicas para el estudio de familias de funciones reales de una variable que se apoyarán en la teoría de transformaciones elementales y dilataciones así como en las propiedades (forma de las gráficas, variabilidad, etc.) de los diferentes tipos de familias de funciones. Se requiere, en definitiva, una verdadera ampliación de la anterior praxeología con nuevas tareas, nuevas técnicas y un nuevo y más comprensivo discurso tecnológico-teórico.

Para ello se podría plantear el problema de ampliar el modelo funcional estudiado anteriormente de tal manera que el modelo generalizado pudiese ser aplicado, simultáneamente, a diferentes tipologías de pacientes. La concentración del medicamente en sangre, para cada tipo de pacientes, debería entonces caracterizarse por el valor de un parámetro α >0) que depende, a su vez, de determinadas características fisiológicas comunes a los pacientes de cada tipo. Entre los modelos que podrían aportar los estudiantes para generalizar el modelo que aparece en Q₁ podemos considerar el que proponemos en Q₂:

Q₂: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de un paciente si suponemos que t horas después de ingerido el medicamento, la concentración (medida en miligramos por litro) viene dada por la función C_u (t)=, con α >0?

Algunas de las cuestiones derivadas de Q₂ que requieren respuesta y pueden responderse en este segundo nivel de modelización funcional son las siguientes:

Q₂₁: ¿Se puede afirmar que la concentración del medicamento en el torrente sanguíneo aumenta con el tiempo para cualquier tipo de pacientes?

Q₂₂: ¿Cómo varía la concentración a largo plazo para los diferentes tipos de pacientes?

Q₂₃: ¿Cómo comparar la evolución de la concentración del medicamento para diferentes tipos de pacientes?

Q₂₄: ¿Hay algún momento en el que se alcanza una concentración máxima en sangre? ¿Cómo depende dicha concentración máxima del tipo de pacientes considerado?

Esta familia de funciones racionales incluye como caso particular la función explorada anteriormente en Q_x cuando se toma el coeficiente de t unitario, esto es, el parámetro α = \. Pero, en este segundo nivel de modelización funcional se pretende estudiar la variación de la concentración para diferentes valores de a como, por ejemplo: α = 0,5; α=5; α=10; α=28.3; etc., que, hipotéticamente, podría corresponder a diferentes tipos concretos de pacientes.

La respuesta a estas cuestiones requiere el uso de nuevas técnicas gráficas y de nuevas técnicas analíticas útiles para estudiar familias de funciones. Una de estas técnicas gráficas se sustenta en la representación, con GeoGebra, de la familia de funciones concentración del medicamento para los diversos valores del coeficiente de t. El análisis de las gráficas de esta familia apoya la conjetura de que cuanto mayor es el valor de α, más elevado será el valor máximo de la concentración del medicamento, como muestra la figura:

Figura 2

Sin embargo, se observa que el momento en que se inicia la eliminación del medicamento del organismo, o sea, el instante en que la concentración es máxima no depende del valor del parámetro α , pues es constante y aproximadamente igual a 0,71 horas después de la ingestión del medicamento.

Para determinar el valor de la concentración máxima en función de a pueden utilizarse técnicas gráficas o algebraicas con el GeoGebra:

Figura 3

El paso a este segundo nivel del proceso de modelización funcionalha permitido considerar el modelo estudiado en Q₁ como un caso particular de una familia de modelos o, mejor, ha permitido estudiar más profundamente un estado particular del sistema (definido por un valor particular a =1 de un parámetro) al considerar que dicho sistema viene mejor caracterizado por la correspondiente familia de funciones. El estudio de esta familia ha requerido nuevas técnicasgráficas apoyadas en la teoría de transformaciones geométricas elementales dilataciones así como nuevas técnicas analíticas de resolución de ecuaciones e inecuaciones con parámetros. En particular, se necesitan técnicas que relacionen la posición y la forma de la gráfica de una función concreta (dentro de una familia de funciones) con los valores de los parámetros que determinan dicha función dentro de la familia. Esta ampliación de la práctica matemática ha provocado, como no podría ser de otra manera, nuevas necesidades tecnológicoteóricas y, en definitiva, una clara ampliación y completación relativa de la anterior praxeología matemática en el sentido de Bosch et al. (2004).

 

3.3. Tercer nivel de modelización funcional

En la enseñanza secundaria, las fórmulas no se construyen nunca como resultado de un trabajo algebraico ni juegan propiamente el papel de verdaderos "modelos algebraicos" en los cuales las variables de cualquier tipo (parámetros o incógnitas) sean intercambiables.

Siguiendo de nuevo a Ruiz-Munzón et al. (2011), denominamos tercer nivel de modelización funcional de un sistema el que se materializa en modelos que se expresan mediante familias de funciones de dos o más variables y las correspondientes fórmulas asociadas.

En este tercer nivel de modelización el papel de los "parámetros" y de las "variables" es intercambiable y se estudia cómo repercute la variación conjunta de dos o más variables sobre la variación de una función. Esta tarea puede plantearse a partir de los modelos trabajados en el segundo nivel, pero la resolución completa de la misma requiere de técnicas que no están disponibles en el segundo nivel.

Partiendo del tipo de modelos exponenciales estudiados a raíz de la cuestión Q'₁ para comparar la evolución de la concentración en sangre de un mismo medicamento en dos pacientes y con el objetivo de profundizar en el estudio de la utilidad de este tipo de modelos, podría aparecer (en la comunidad de estudio la necesidad de responder a la siguiente cuestión general:

Q₃: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de un paciente si suponemos que, t horas después de ingerido el medicamento, la concentración (medida en miligramos por litro) viene dada por la función de incremento C(t)=αte ^{– kt} donde a y k son constantes positivas?

Empezaremos simplificando el problema de manera que pueda tratarse en el segundo nivel de modelización funcional. Para ello consideraremos en primer lugar la familia de funciones que dependen del parámetro a y donde k es un número real positivo fijo: C_α (t) =αte ^{– kt}. Se trata de estudiar la influencia que tiene sobre la función concentración la variación del parámetro a para una k fijada.

En concreto se puede plantear el siguiente problema simplificado:

Q₃₁: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de un paciente si suponemos que, t horas después de ingerido el medicamento, la concentración (medida en miligramos por litro) viene dada por la función C_α (t) = αte^-ktdonde k toma valores fijos como, por ejemplo, k=0,25; 0,75; 1; 5,4? ¿Cómo depende, en cada caso, el comportamiento de la función concentración C_α(t) del valor del parámetro α?

Para estudiar la variación de la concentración en función de a, se pueden representar las gráficas de la familia C_a(t) para los diferentes valores de k con el GeoGebra:

Figura 4

Se observa que, para cada valor de k fijado, cuanto mayor es el valor del parámetro α mayor es el valor máximo de la concentración.

También es posible la manipulación del valor de a usando el «selector» creado con el GeoGebra para observar la variación de la concentración del medicamento para cada valor de α.

A partir de estas gráficas se puede conjeturar que cuanto mayor es el valor del parámetro k menor es el valor máximo de la concentración. Esta conjetura la estudiaremos más adelante a partir de la cuestión Q₃₂.

Algunas de las cuestiones derivadas de Q_3l que requieren respuesta y pueden responderse en este nivel de modelización funcional son las siguientes:

Q₃₁₁: ¿Cómo determinar el intervalo de tiempo en el que la concentración del medicamento C_α(t) crece (o disminuye) en el torrente sanguíneo?

Q₃₁₂: Para las diferentes funciones de la familia C_α(t), ¿cómo varía la concentración a largo plazo?

Q₃₁₃: ¿En qué momento la concentración C_α(t) es máxima? ¿Cuál es el valor de dicha concentración máxima?

Q₃₁₄: ¿Cómo se interpretan, en términos de la variación de la concentración del medicamento, los intervalos de concavidad/convexidad de las gráficas de la familia de funciones C_α(t)? ¿Y los puntos de inflexión de dichas gráficas?

Estudiando la variación de la concentración en el caso en que k = 0,25 y haciendo variar el parámetro α, (usando el «selector» creado con el GeoGebra), se observa lo siguiente para el caso particular en que α =43,5:

Figura 5

Otra manera de simplificar el problema, análoga a la anterior y que también puede tratarse en el segundo nivel de modelización funcional consiste en fijar el parámetro α y considerar que el modelo viene dado por una familia de funciones de una variable que depende del parámetro k. Se trata de estudiar la influencia que tiene sobre la función concentración la variación del parámetro k para una a fijada. En concreto se puede plantear el siguiente problema simplificado:

Q32: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de un paciente si suponemos que, t horas después de ingerido el medicamento, la concentración (medida en miligramos por litro) viene dada por la función C_k (t) =αte ^-kt donde a toma valores fijos como, por ejemplo, α = 10; 12; 15; 21,5? ¿Cómo depende, en cada caso, el comportamiento de la función concentración C_k(t) del valor del parámetro k?

Para estudiar la variación de la concentración en función de k, se pueden representar, con el GeoGebra, las gráficas de la familia Ck(t) para los diferentes valores de α:

Figura 6

Se observa que, para cada valor de a fijado, cuanto mayor es el valor del parámetro k menor es el valor máximo de la concentración. También es posible la manipulación del valor de k usando el «selector» creado con el GeoGebra para observar la variación resultante de la concentración del medicamento.

Algunas de las cuestiones derivadas de que requieren respuesta y pueden responderse en este nivel de modelización funcional son las siguientes:

Q₃₂₁: ¿Cómo determinar el intervalo de tiempo en el que la concentración del medicamento C_k(t) crece (o disminuye) en el torrente sanguíneo?

Q₃₂₂: Para las diferentes funciones de la familia C_k(t), ¿cómo varía la concentración a largo plazo?

Q₃₂₃: ¿En qué momento la concentración C_k(t) es máxima? ¿Cuál es el valor de dicha concentración máxima?

Q₃₂₄: ¿Cómo se interpretan, en términos de la variación de la concentración del medicamento, los intervalos de concavidad/convexidad de las gráficas de la familia de funciones Ck(t)? ¿Y los puntos de inflexión de dichas gráficas?

Estudiando la variación de la concentración en el caso en que a = 21,5 y haciendo variar el parámetro k, (usando el «selector» creado con el GeoGebra), se observa lo siguiente para el caso particular en que k = 0,5:

Figura 7

Con esta modificación de las condiciones iniciales se puede verificar la influencia del parámetro k en la forma de la gráfica de la función concentración, cuando se fija el parámetro a y se hace variar el valor de k con el «selector» del GeoGebra. Observando los gráficos y las tablas de valores se comprueba que, al contrario de lo que ocurre con el parámetro a, cuanto mayor es el valor del parámetro k, menor es el valor máximo de la concentración puesto que se produce un achatamiento del gráfico de la función. Esta forma de utilizar las TIC es fundamental para visualizar el poder generador de la cuestión problemática inicial y para potenciar el momento exploratorio de un tipo de tareas y el correspondiente proceso de elaboración de una técnica, lo que constituye una dimensión básica de la actividad matemática (Chevallard, 1999).

Si volvemos a plantear la cuestión Q₃, que se sitúa en el tercer nivel de modelización funcional, es evidente que no se puede responder con las técnicas y los elementos tecnológico-teóricos que hemos utilizado hasta este momento.

Q₃: ¿Cómo estudiar la variación de la concentración de un medicamento en el torrente sanguíneo de un paciente si suponemos que, t horas después de ingerido el medicamento, la concentración (medida en miligramos por litro) viene dada por la función de incremento C(t) = αte ^{- kt} donde α y k son constantes positivas?

Podemos considerar que el modelo se ha materializado en una función de tres variables o bien en una familia de funciones de dos variables (ya sea dependiendo del parámetro a o bien del parámetro k). En concreto podremos expresarla:

C(α, k, t) = αte^{- kt}

C_k (α, t) = αte ^{- kt}

C_α (k, t) = αte ^{- kt}

Representando los parámetros a y k mediante las medidas respectivas de los segmentos [AC1] y [DF] es posible hacer variar ambas medidas y estudiar así algunos casos con valores fijos de los parámetros:

Figura 8

Pero si queremos estudiar cómo incide sobre la concentración el cambio simultáneo de los dos parámetros es necesario explorar nuevas técnicas relativas a la variación de una función con más de una variable. Surgen así nuevas necesidades tecnológico-teóricas que conducen al estudio y desarrollo de las derivadas parciales en la enseñanza universitaria. Otra forma de estudiar el comportamiento de la familia de funciones es la que podría llevarse a cabo mediante el recurso del programa de cálculo simbólico Mathematica sin olvidar que, también en este caso, se requerirían nuevos elementos tecnológico-teóricos para interpretar y justificar los resultados obtenidos.

C(α, k, t) = αte ^{– kt}

En resumen, hemos mostrado que una vez situados en el segundo nivel de modelización funcional (en el que la herramienta matemática fundamental son las familias de funciones de una variable real), surgen cuestiones relativas al sistema cuya respuesta requiere de manera natural trabajar (en el modelo) con funciones de varias variables reales (y hasta con familias de funciones de dos o más variables) lo que nos sitúa en el tercer nivel de modelización funcional. En este punto aparecen necesidades técnico-prácticas y tecnológico-teóricas (relacionadas con el cálculo diferencial de funciones de varias variables reales) que van mucho más allá de lo que es posible estudiar en la actual enseñanza secundaria (tanto en España como en Portugal) y que provocan, de nuevo, una clara ampliación y completación relativa de la anterior praxeología matemática en el sentido de Bosch et al. (2004).

 

4. CONSIDERACIONES FINALES SOBRE LA ECOLOGÍA DE LA MODELIZACIÓN FUNCIONAL EN LA ENSEÑANZA SECUNDARIA

Las cuestiones que forman parte de la dimensión ecológica del problema de la modelización funcional en la enseñanza secundaria giran en torno al por qué la relación institucional a la modelización funcional es como es y qué condiciones se requerirían para modificarla en una dirección determinada (Gascón, 2011). Para empezar a responder a estas cuestiones hemos analizado diversos materiales empíricos tanto en España (Fonseca, 2004) como en Portugal (Lucas, 2010).

Este análisis ha puesto claramente de manifiesto una sorprendente ausencia de la modelización funcional en la enseñanza secundaria y, en consecuencia, plantea muchas cuestiones en relación a las posibilidades efectivas de integrar en dicha institución una organización didáctica que viabilizara un proceso de estudio sustentado en el modelo epistemológico de referencia que hemos esbozado (nos referimos a los dos primeros niveles de modelización funcional).

Cuando nos preguntamos por las restricciones que dificultan la vida normal de la modelización funcional y por las condiciones⁶ que deberían instaurarse para que fuese posible su integración en los actuales sistemas de enseñanza, hemos de empezar por afirmar que, para la TAD, no es posible modificar las praxeologías matemáticas y didácticas que viven en una institución determinada como consecuencia exclusiva de la voluntad de los agentes de las instituciones en cuestión, sean éstos profesores, autores de cualquier tipo de materiales escolares o autoridades educativas. En particular, no podemos imponer de manera puramente voluntarista la vida normal de la modelización funcional en las instituciones escolares.

Este postulado está en la base del papel central que asignamos a la dimensión ecológica de los problemas didácticos, esto es, al estudio sistemático de las condiciones que hacen posible la génesis y difusión de las matemáticas y, en particular, a la indagación de las restricciones que inciden sobre dichos procesos. Como explica Chevallard (1991), el estudio sistemático de dichas restricciones es imprescindible para determinar el nivel institucional desde el cual se puedan crear las condiciones necesarias a la difusión del conocimiento matemático. Este punto de vista requiere situar el problema didáctico de la modelización funcional en el ámbito de la problemática de la transposición didáctica para poder tomar en consideración las restricciones que surgen en las diferentes etapas del proceso de transposición, desde las instituciones productoras del saber hasta las instituciones docentes. Son estas restricciones las que llamamos propiamente restricciones transpositivas (Chevallard, 1985, 1991).

En nuestro caso, la dimensión ecológica del problema de la modelización matemática hace referencia a las restricciones transpositivas que provocan transformaciones tanto en las praxeologías matemáticas que sustentan la actividad de modelización funcional como en la forma de organizarlas y de reconstruirlas en la escuela. Si no se toman en consideración las "fuerzas institucionales" que rigen el proceso de transposición didáctica, no será posible describir las condiciones que se requieren para que la modelización funcional pueda vivir en el sistema de enseñanza de las matemáticas ni, por tanto, diseñar de forma fundamentada los dispositivos didácticos necesarios.

Así, por ejemplo, la transposición puede facilitar la entrada en el sistema de enseñanza de ciertos objetos privilegiados en la institución sabia y dificultar la entrada de otros, en particular de los objetos considerados como extramatemáticos (o no matemáticos) que no tengan una existencia clara en el saber sabio y, también, de ciertos objetos matemáticos poco visibles en la institución sabia como, por ejemplo, determinadas técnicas matemáticas "artesanales". Estos efectos transpositivos condicionarán las posibles praxeologías escolares potencialmente sustentadoras de la modelización funcional.

Entre las deformaciones que las restricciones transpositivas pueden originar en la actividad de modelización matemática, destacaremos en primer lugar los rasgos de algoritmización que se manifiestan en la tendencia a cerrar las actividades de modelización, convirtiéndolas en "resolución de problemas aplicados" relativamente aislados que no suelen dar origen al estudio de un verdadero campo de problemas. Esta algoritmización puede provocar una pérdida de sentido de la modelización puesto que la presenta como una actividad que, lejos de tener como objetivo el estudio de un sistema, sólo sirve como "excusa" para la construcción de conceptos matemáticos sólo artificialmente "motivados". En segundo lugar, hemos de subrayar las restricciones que sobre la vida escolar de la modelización funcional han provocado las deformaciones transpositivas del papel que ha desempeñado, y sigue desempeñando, el cálculo diferencial en la construcción de modelos funcionales, en el trabajo dentro de los mismos y en la interpretación de dicho trabajo en términos del sistema.

Junto a estas restricciones, existen otras provenientes de los diferentes niveles de codeterminación didáctica (Chevallard, 2002) que inciden sobre la "vida" de la modelización matemática y, en particular, sobre la modelización funcional. Ello es debido a que la actividad de modelización constituye un prototipo de actividad sistemática, a largo plazo, que proporciona respuestas siempre provisionales y que requiere la asunción (por parte de la comunidad de estudio) de una comprensión permanentemente incompleta, lo cual choca con el contrato didáctico vigente en las instituciones escolares (Barquero et al., 2014).

Resulta, en definitiva, que la puesta en marcha de un proceso de estudio que permita la plena integración escolar de la actividad de modelización funcional sólo será posible si se cumple un conjunto de condiciones que no se dan de manera espontánea en los actuales sistemas de enseñanza. Investigaciones anteriores en el ámbito de la TAD (Ruiz-Munzón et al., 2011; Barquero et al., 2011) nos permiten postular que es posible favorecer la aparición y el desarrollo de dichas condiciones si estructuramos el proceso de estudio mediante un tipo de organizaciones didácticas que hemos denominado recorridos de estudio e investigación (REI) (Chevallard, 2004, 2005, 2006) con nuevos dispositivos y "gestos" didácticos, de estudio y ayuda al estudio, que hasta ahora permanecían recluidos en el ámbito privado de la investigación.

 

RECONOCIMIENTOS

Trabajo financiado por la beca SFRH/BD/77335/2011 de la FCT (Portugal) y por el proyecto: "La modelización matemática para la formación del profesorado de secundaria: del algebra al cálculo diferencial" (EDU201239312-C03-03).

 

REFERENCIAS BIBLIOGRÁFICAS

Artigue, M. (2002). L'integration de calculatrices symboliques à l'enseignement secondaire: les leçons de quelques ingénieries didactiques. In D. Guin & L. Trouche (Coord.), Calculatrices Symboliques. Transformer un outil en un instrument du travail informatique: un problème didactique (pp. 277-349). Grenoble, France: La Pensée Sauvage.         [ Links ]

Artigue, M. (2011). Tecnología y enseñanza de las matemáticas: desarrollo y aportes de la aproximación instrumental. Cuadernos de Investigación y Formación en Educación Matemática, 6(8), 13-33.         [ Links ]

Barquero, B. (2009). Ecología de la Modelización Matemática en la enseñanza universitaria de las Matemáticas (Tesis Doctoral no publicada). Universitat Autònoma de Barcelona, Barcelona, España. Obtenido de http://www.tdx.cat/handle/10803/3110        [ Links ]

Barquero, B.; Bosch, M., & Gascón, J. (2011). Los recorridos de estudio e investigación y la modelización matemática en la enseñanza universitaria de las ciencias experimentales. Enseñanza de las Ciencias, 29(3), 339-352.         [ Links ]

Barquero, B.; Bosch, M., & Gascón, J. (2014). Incidencia del "aplicacionismo" en la integración de la modelización matemática en la enseñanza universitaria de las ciencias experimentales. Enseñanza de las Ciencias, 32(1), 83-100.         [ Links ]

Blum, W. (2002). ICMI study 14: Applications and modeling in mathematics education – Discussion document. Educational Studies in Mathematics, 51(1-2), 149–171. doi: 10.1023 / A: 1022435827400        [ Links ]

Blum, W. & Leiß, D. (2007). How do students and teachers deal with modeling problems? In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modelling (ICTMA 12): Education, Engineering and Economics (pp. 222-231). Chichester, England: Horwood Publishing.         [ Links ]

Bolea, P. (2003). El proceso de algebrización de organizaciones matemáticas escolares (Tesis Doctoral no publicada). Universidad de Zaragoza, Zaragoza, España. Obtenido de http://www.atd-tad.org/documentos/bolea-p-2003-el-proceso-de-algebrizacion-deorganizaciones-matematicas-escolares/        [ Links ]

Bosch, M.; Fonseca, C., & Gascón, J. (2004). Incompletitud de las organizaciones matemáticas locales en las instituciones escolares. Recherches en Didactique des Mathématiques, 24(2-3), 205-250.         [ Links ]

Cantoral, R. & Mirón, H. (2000). Sobre el estatus de la noción de derivada: de la epistemología de Joseph Louis Lagrange al diseño de una situación didáctica. Revista Latinoamericana de Investigación en Matemática Educativa, 3(3), 265-292.         [ Links ]

Chevallard, Y. (1985). La transposition didactique: Du savoir savant au savoir enseigné. Grenoble, France: La Pensée Sauvage.         [ Links ]

Chevallard, Y. (1991). Didactique, anthropologie, mathématiques. La transposition didactique. La transposition didactique. Du savoir savant au savoir enseigné (2^de éd.). Grenoble, France: La Pensée Sauvage.         [ Links ]

Chevallard, Y. (1992). Concepts fondamentaux de la didactique: perspectives apportées par une approche anthropologique. Recherches en Didactique des Mathématiques, 12(1), 73-112.         [ Links ]

Chevallard, Y. (1999). L'analyse des pratiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques, 19(2), 221-266.         [ Links ]

Chevallard, Y. (2002). Organiser l'étude. 3. Écologie & régulation. In J.-L. Dorier, M. Artigue, R. Berthelot, & R. Floris. (Eds.), Actes de la 11^e École d'Été de didactique des mathématiques (pp. 41-56). Grenoble, France: La Pensée Sauvage. Obtenido de http://yves.chevallard.free.fr/spip/spip/article.php3?id_article=53        [ Links ]

Chevallard, Y. (2004). Vers une didactique de la codisciplinarité. Notes sur une nouvelle épistémologie scolaire. Journées de didactique comparée 2004, Lyon, France. Obtenido de http://yves.chevallard.free.fr/spip/spip/article.php3?id_article=45        [ Links ]

Chevallard, Y. (2005). La place des mathématiques vivantes dans l'éducation secondaire : transposition didactique et nouvelle épistémologie scolaire. In C. Ducourtioux, P. -L.Hennequin, (Éds.), La place des mathématiques vivantes dans l'enseignement secondaire (Vol. 168, pp. 239-263). Paris, France: APMEP. Obtenido de http://yves.chevallard.free.fr/spip/spip/article.php3?id_article=48        [ Links ]

Chevallard, Y. (2006). Steps towards a new epistemology in mathematics education. En M. Bosch (Ed.), Proceedings of the 4^th Conference of the European Society for Research in Mathematics Education (pp. 21-30). Barcelona, Spain: CERME 4. Obtenido de http://yves.chevallard.free.fr/spip/spip/article.php3?id_article=95        [ Links ]

Chevallard, Y., Bosch, M., & Gascón, J. (1997). Estudiar Matemáticas. El eslabón perdido entre la enseñanza y el aprendizaje. Barcelona, España: ICE/Horsori.         [ Links ]

Fonseca, C. (2004). Discontinuidades matemáticas y didácticas entre la Secundaria y la Universitaria (Tesis Doctoral, Universidad de Vigo). Obtenido de http://www.atd-tad.org/documentos/discontinuidades-matematicas-y-didacticas-entre-la-secundaria-y-la-universidad/        [ Links ]

Gascón, J. (1998). Evolución de la didáctica de las matemáticas como disciplina científica. Recherches en Didactique des Mathématiques, 18(1), 7-34.         [ Links ]

Gascón, J. (2002). El problema de la Educación Matemática y la doble ruptura de la Didáctica de las Matemáticas. Gaceta de la Real Sociedad Matemática Española, 5(3), 673-698.         [ Links ]

Gascón, J. (2003). From the Cognitive to the Epistemological Programme in the Didactics of Mathematics: Two Incommensurable Scientific Research Programmes? For the Learning of Mathematics, 23(2), 44-55.         [ Links ]

Gascón, J. (2011). Las tres dimensiones fundamentales de un problema didáctico. El caso del álgebra elemental. Revista Latinoamericana de Investigación en Matemática Educativa, 14(2), 203-231.         [ Links ]

Lucas, C. (2010). Organizaciones matemáticas locales relativamente completas (Memoria de investigación, Universidad de Vigo). Obtenido de http://www.atd-tad.org/documentos/organizaciones-matematicas-locales-relativamente-completas/        [ Links ]

Ruiz-Munzón, N.; Bosch, M. & Gascón, J. (2011). Un modelo epistemológico de referencia del algebra como instrumento de modelización. En M. Bosch et al. (Eds.), Un panorama de la TAD (Vol. 10, pp. 743-765). Barcelona, España: Centre de Recerca Matemàtica.         [ Links ]

Sierra, T. (2006). Lo matemático en el diseño y análisis de organizaciones didácticas: los sistemas de numeración y la medida de magnitudes (Tesis Doctoral no publicada). Universidad Complutense de Madrid, Madrid, España. Obtenido de http://biblioteca.ucm.es/tesis/edu/ucm-t29075.pdf        [ Links ]

 

Notas

¹ En España la secundaria consta de dos etapas: la enseñanza secundaria obligatoria o ESO (alumnos de 12 a 16 años) y la enseñanza secundaria postobligatoria o bachillerato (alumnos de 16 a 18 años). En el caso de Portugal, el tercer ciclo de la enseñanza básica está compuesto por tres años de escolaridad (alumnos de 12 a 15 años) y la enseñanza secundaria por otros tres (alumnos de 15 a 18 años). Desde 2009, en base a la Ley nº 85/2009, de 27 de agosto, la enseñanza secundaria portuguesa se tornó universal, gratuita y obligatoria.

² En el Programa Epistemológico de investigación en didáctica de las matemáticas en el que se sitúa la TAD (Gascón, 1998, 2002, 2003), "lo matemático" (el MER puede considerarse como una red de praxeologías matemáticas) y "lo didáctico" (los procesos didácticos sustentados en el MER) son como dos caras de una misma moneda y, en cierto sentido, inseparables.

³ En concreto la organización didáctica que pretendemos experimentar en el primer curso de la enseñanza universitaria portuguesa estará sustentada sobre los componentes del MER que ponen de manifiesto una posible razón de ser del cálculo diferencial elemental en el ámbito de la actividad de modelización funcional.

⁴ Entre dichas técnicas didácticas, y para que los estudiantes puedan tomar como propias las cuestiones en lugar de considerarlas como artificialmente impuestas, se puede proponer que busquen en los diferentes media (internet, textos de modelización, etc.) posibles modelos elementales que describan la evolución temporal de la concentración de un medicamento en sangre. De esta manera la comunidad de estudio puede decidir qué modelos se estudiarán efectivamente. En Q₁ proponemos simplemente uno de los posibles modelos a estudiar.

⁵ Un primer aspecto importante de dicha interpretación aparece desde el momento en que, utilizando un instrumento informático como, por ejemplo, GeoGebra, se obtienen las primeras gráficas de la función concentración del medicamento. Dado que la variable independiente es el tiempo, el dominio para el cual tiene sentido el modelo funcional construido se reduce únicamente al ámbito de los números reales no negativos, t ≥ 0. Y esto es así para todos los modelos funcionales que aparecerán en lo que sigue.

⁶ En la TAD se dice que una condición es una restricción para una persona o una institución si no puede ser modificada por dicha persona o institución, al menos en el corto plazo. Por lo tanto, todo son condiciones y la noción de restricción es relativa a las instituciones y a las diferentes posiciones institucionales. Así, por ejemplo, la forma de constituir los grupos-clase o la distribución del currículum en las diferentes asignaturas que se estudian en una institución docente son restricciones relativas a la posición de alumno (y a la posición de profesor) de dicha institución, pero puede ser una condición modificable desde otras posiciones institucionales como, por ejemplo, la de director del centro educativo o desde la posición de las autoridades educativas.