Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.17 no.2 Ciudad de México jul. 2014
https://doi.org/10.12802/relime.13.1722
Artículos
Acceso a la representación escrita de los números naturales: una secuencia didáctica para adultos de baja o nula escolaridad1
Access to a written representation of natural numbers: a didactic sequence for adults with little or no schooling
Santiago Palmas*, David Block**
* Centro de Investigación y de Estudios Avanzados, México. spalmas@cinvestav.mx
** Centro de Investigación y de Estudios Avanzados, México. dblock@cinvestav.mx
Recepción: Mayo 12, 2011
Aceptación: Septiembre 17, 2013.
Resumen
Este trabajo aborda la problemática de la enseñanza de matemáticas en la educación de adultos de baja o nula escolaridad. Tiene como objetivo contribuir al conocimiento de alternativas didácticas para la enseñanza, a adultos, de la representación escrita convencional de los números naturales con base en la recuperación de sus conocimientos matemáticos previos, adquiridos en su vida diaria y en su trabajo. Estos conocimientos por lo general no se expresan por escrito, sino oralmente. El estudio incluye una experiencia de ingeniería didáctica llevada a cabo con un adulto no alfabetizado del medio rural.
Palabras clave: Educación para adultos, Numeración, Registros semióticos, Didáctica de las matemáticas.
Abstract
This paper points out the difficulties in adults with little or no schooling when teaching mathematics. Our objective is to contribute to the spread of didactic alternatives for adults regarding the conventional written representation of natural numbers by recovering their former mathematical knowledge from their daily lives. This kind of knowledge is not often expressed in a written representation but in an oral one. The study includes a formal experience of didactic engineering with an adult with no schooling and from a rural area.
Key words: Adult education, Numbering, Semiotic data, Didactic of mathematics.
Resumo
Este trabalho aborda os problemas do ensino de matemática na educação de adultos com nível de escolarização inferior ou nulo. O objetivo é contribuir ao conhecimento das alternativas didáticas que existem para o ensino de adultos da representação escrita convencional dos números naturais, baseando-se na recuperação de seus conhecimentos prévios da matemática que foram adquiridos no seu dia a dia e no seu trabalho. Geralmente, esses conhecimentos não são expressados por escrito, mas sim oralmente. O estudo inclui uma experiência de engenharia didática que foi realizada com um adulto analfabeto da região rural.
Palavras chave: Educação para adultos, Numeração, Registros semióticos, Didática da matemática.
Résumé
Ce travail porte sur la problématique de l'enseignement des mathématiques dans l'éducation des adultes peu ou non scolarisés. Son but est de contribuer aux connaissances d'alternatives didactiques pour l'enseignement de la désignation écrite conventionnelle des nombres naturels sur la base de la récupération de leurs connaissances acquises préalables sur le sujet dans la vie quotidienne et dans leurs travaux. Ces connaissances préalables sont exprimées généralement à l'oral, non par écrit. L'étude inclut une expérience d'ingénierie didactique avec un adulte non alphabétisé du milieu rural.
Mots clés: Éducation des adultes, Numération, Registres sémiotiques, Didactique des mathématiques.
1. INTRODUCCIÓN
Hoy en día está bien documentado el hecho de que los adultos no escolarizados suelen desarrollar una habilidad significativa para el cálculo mental (Ávila, 2005; Delprato & Fuenlabrada, 2008; Ferreiro, Fuenlabrada, Nemirovsky, Block, & Dávila, 1983; Mariño, 1997). Sin embargo, probablemente aún no se sabe lo suficiente acerca de cómo aprovechar estos conocimientos en la enseñanza de la aritmética que se imparte a los adultos en los cursos de alfabetización. En las modalidades de enseñanza para este grupo de edad, tiende a prevalecer la opción por los procedimientos de cálculo convencionales, similares a las que se enseñan a los niños en la escuela, y no necesariamente por falta de alternativas —ver, por ejemplo, Mariño (1997)— sino porque se considera que dichos procedimientos tienen para los adultos el plus de la valoración social (Ávila, 2007; Delprato, 2006; Knijnik, 1997).
Sin dejar de reconocer la importancia de dicha valoración, pensamos que, sin embargo, la pertinencia de la enseñanza de los procedimientos de cálculo convencionales tiende a perder fuerza debido a la presencia casi universal de las calculadoras. Dicho instrumento ha tendido a cambiar las prioridades en la enseñanza de las operaciones aritméticas, incluso dentro de la misma escuela básica; se da mayor peso al conocimiento de los significados, a la comprensión de las técnicas y menos al dominio de destrezas de cálculo (Block, Moscoso, Ramírez & Solares, 2007)2. El grado de dominio que los adultos no alfabetizados suelen tener sobre la numeración y el cálculo no escrito, y en consecuencia sobre la noción de número, permite considerar que el reto, para ellos, se centra en el tránsito de la numeración oral a la escrita, el cual puede concebirse como una conversión entre dos registros semióticos (Duval, 1993) y, para la investigación didáctica, el reto es encontrar las formas más eficientes de realizarlo.
Algunos investigadores han señalado que los conocimientos previos de los adultos pueden llegar a erigirse en obstáculos para la adquisición de nuevos conocimientos matemáticos (Ávila, 2007; Delprato, 2006). Sin embargo, a lo que estos investigadores se refieren específicamente es a la adquisición de los algoritmos convencionales, los cuales guardan importantes diferencias con los procedimientos de cálculo que los adultos suelen utilizar. Ello abona, pensamos, a la necesidad de explorar vías alternativas a la de enseñar dichos algoritmos.
El trabajo que presentamos aquí forma parte de un estudio (Palmas, 2011) cuyo propósito se inscribe en la dirección arriba señalada: contribuir al desarrollo de alternativas didácticas en la enseñanza a adultos no alfabetizados que recuperen de manera significativa los conocimientos previamente construidos por ellos, bajo la hipótesis de que de esta manera se podrían lograr aprendizajes más significativos en periodos de tiempo más breves. Esta opción, como veremos, no excluye la recuperación de algunas de las situaciones didácticas utilizadas en la escuela básica. Hemos implementado dos sencillos dispositivos que buscan facilitar la conversión de numerales orales en numerales escritos y viceversa. Dado el dominio de la numeración oral que los adultos suelen tener, nos preguntamos en qué medida los dispositivos facilitan el acceso a la numeración escrita. Tener un primer acercamiento a la verificación de estas hipótesis mediante un estudio de caso fue el propósito del estudio que reportamos a continuación. Las preguntas de investigación que lo orientan son: ¿En qué medida las situaciones didácticas favorecieron los aprendizajes esperados? ¿Qué logros y qué dificultades se pusieron de manifiesto y qué dejan ver éstos acerca de las situaciones mismas? Y finalmente: ¿Qué puede decirse acerca de la hipótesis del papel de los conocimientos de matemáticas orales para acceder a la escritura de los números?
2. ACERCAMIENTO TEÓRICO Y METODOLOGÍA
Compartimos una visión de las matemáticas como producto social y cultural de la actividad humana. Asumimos que las personas generan en su actividad, al resolver determinado tipo de problemas de su vida diaria, matemáticas, así sea "con m minúscula" (Bishop, 1999), las cuales adoptan una enorme diversidad de manifestaciones3. Los conocimientos de cálculo oral que suelen desarrollar los adultos no alfabetizados constituyen un ejemplo palpable de ello. Asumimos que, no obstante lo anterior, la adquisición de ciertos conocimientos puede requerir de una enseñanza intencional. El presente trabajo se ubica en relación con dicha necesidad: su objeto de estudio es el funcionamiento de una secuencia de situaciones didácticas diseñada para adultos no alfabetizados, cuyo propósito es favorecer la adquisición de la numeración escrita. El estudio se realiza en el marco de la Teoría de las Situaciones Didácticas (TSD) (Brousseau, 2000, 2007), en la que se asume la hipótesis constructivista fundamental según la cual el aprendizaje de los conocimientos matemáticos pasa por su producción como herramientas de resolución de problemas. La teoría postula, asimismo, la posibilidad de caracterizar a los conocimientos mediante las situaciones específicas en las que éstos funcionan.
2.1. Metodología
Se utilizó la metodología llamada "ingeniería didáctica", la cual es específica para el estudio experimental de secuencias de situaciones didácticas (Artigue, 1995). La principal característica de esta metodología es la forma de llevar a cabo el análisis de los resultados: "se busca ponderar en qué medida los procedimientos de los alumnos observados a lo largo de la secuencia, se relacionan con las condiciones intencionalmente creadas a través de las situaciones, y si en dichos procedimientos es posible identificar elementos que den cuenta de ciertos aprendizajes" (Ramírez, 2006, pp. 31-32). La validación es "interna", en el sentido de que no se realiza mediante la comparación con un grupo control, sino por contrastación de los resultados obtenidos en la experiencia con el análisis previo de la secuencia didáctica.
La experiencia didáctica que aquí se reporta se llevó a cabo con un solo adulto, por lo que el presente estudio constituye un "estudio de caso", de corte cualitativo con experiencia de enseñanza (Cohen, Manion & Morrison, 2000). La investigación constó de varias fases que se describen a continuación.
1) Se realizó un estudio preliminar el cual constó de: (a) una revisión de la problemática didáctica de la representación de los números naturales; (b) una revisión de aportes de la investigación sobre conocimientos matemáticos de adultos no alfabetizados, así como de algunas propuestas para la enseñanza de los números naturales; y (c) un sondeo de los conocimientos sobre la numeración y el cálculo mental de algunos adultos.
2) La secuencia didáctica se diseñó a partir del estudio preliminar anterior. Tomando como referente teórico la TSD, se buscó que las principales situaciones propiciaran la puesta en juego del conocimiento por aprender: la escritura de los números, pero que a la vez éstas pudiesen ser abordadas sin disponer todavía de dicho conocimiento. Se procuró también que, cada vez que fuera posible, la situación misma devolviera al aprendiz retroalimentación sobre sus acciones para que él pudiera evaluarlas por sí mismo; es decir, se buscó que algunas de las principales situaciones tuvieran características de una situación "adidáctica" (Brousseau, 2007). No obstante, también se consideraron situaciones más típicamente escolares, o "didácticas", en las que el conductor planteaba directamente preguntas, o pedía la realización de determinadas acciones (por ejemplo, "escriba tal número"), y él mismo proporcionaba ayudas y evaluaba al final.
La secuencia constó de dos partes, una centrada en números chicos (1-20) y otra en números grandes (20-999), de manera que al abordar esta última el adulto tuviera cierta familiaridad con la representación de los primeros números. No hicimos el corte en el 9, como se solía hacer en las propuestas de los años setenta y anteriores, debido a que consideramos deseable que los numerales del 10 al 20 fueran vistos, en un primer momento, como símbolos arbitrarios, al igual que los menores que 10, posponiendo el análisis desde el punto de vista del sistema posicional (Lerner, Sadovsky & Wolman, 1994).
Simultáneamente al diseño de la secuencia, se realizó el "análisis previo" de la misma, en el que se justificaron las decisiones tomadas y se explicitaron los efectos esperados.
3) Se realizó un piloteo de la secuencia con uno de los adultos que participaron en el sondeo, el cual permitió identificar consignas poco claras, tareas difíciles de llevar a cabo, así como otros imprevistos.
4) Se aplicó la secuencia con otro de los adultos que participaron en el sondeo. Las dos partes de la secuencia se aplicaron en siete sesiones de entre 40 y 60 minutos a lo largo un periodo de tres meses (ver cuadro Tabla I). La responsabilidad de la conducción de las sesiones estuvo a cargo de uno de los investigadores participantes. Cada sesión fue videograbada, con el apoyo de un colaborador. Las sesiones se llevaron a cabo en la casa del adulto participante.
5) Se analizaron los resultados de la aplicación: para cada situación, se consideraron los propósitos didácticos de la misma y se contrastó lo sucedido con las previsiones hechas en el análisis previo. A la luz del desempeño observado en el adulto, se analizaron nuevamente, esta vez post facto, las características de la situación. Una primera versión de los resultados de este análisis fue discutida con dos especialistas, quienes no participaron en la experiencia. Los resultados obtenidos no pretenden, evidentemente, ser generalizados. Esperamos, en cambio, que aporten información valiosa, tanto del funcionamiento de las situaciones como de los procesos por los que atraviesan los adultos no escolarizados en el proceso de apropiación de la representación escrita de los números naturales.
2.2. El adulto aprendiz, su lugar de origen y algunos de sus conocimientos sobre número
Carmen, la mujer adulta con quien se llevó a cabo la experiencia didáctica, es oriunda de una pequeña comunidad (de entre 300 y 1000 habitantes) del municipio de Colón a 40 kilómetros de la ciudad de Querétaro. Carmen tenía sesenta años y no había asistido a la escuela. Le hicimos una pequeña entrevista para saber si tenía oportunidad de participar y si tenía interés en aprender a escribir números.
En el sondeo de conocimientos, Carmen no logró diferenciar entre dibujos, números y letras, pero sí reconoció el valor nominal de los billetes del sistema monetario nacional y pudo resolver mentalmente la mayoría de los problemas que le planteamos en el contexto comercial, que implicaban sumas y restas con números hasta de tres cifras. Para ello, utilizó procedimientos ya documentados (Ávila, 2005; Ferreiro et al., 1983) tales como la descomposición de las cantidades de dinero en centenas, decenas y unidades; el uso de la suma para calcular diferencias entre dos cantidades; el conteo de uno en uno, de diez en diez o de cien en cien, entre otras.
3. PRIMERA PARTE DE LA SECUENCIA DIDÁCTICA: NÚMEROS HASTA 20
3.1. Las situaciones
La secuencia se articula en torno al uso del dispositivo "Tira numérica" (Secretaría de Educación Pública, 1999a)4 el cual busca ofrecer a una persona que ya domina la serie oral de los primeros números, una manera de encontrar por sí misma la representación escrita correspondiente.

Consideremos que este dispositivo, originalmente diseñado para pequeños aprendices, podía tener un importante potencial para los adultos no alfabetizados en los procesos de aprendizaje de la representación simbólica de los primeros números, dado el dominio que suelen tener del conteo oral. Planteamos dos tipos de tarea que dan lugar al uso de numerales como medio para comunicar cantidades5: expresar cantidades de objetos o de dinero mediante numerales escritos (cuantificar, codificar) y, recíprocamente, concretizar cantidades expresadas con numerales (decodificar). Además, consideramos otras tareas centradas en las representaciones mismas: el tránsito entre las representaciones oral y escrita, la identificación de numerales en diferentes tipos de documentos impresos u otros portadores, la interpretación de su función (Ferreiro et al., 1983) y el análisis de características gráficas de los numerales, así como la ejercitación del trazo6.
3.2. La experiencia con Carmen
3.2.1. Tránsito entre representaciones con ayuda de la tira numérica
La introducción de la tira numérica se hizo con la siguiente consigna:
Maestro: Si quiere encontrar un número, comience a contar desde la izquierda, donde está el color rojo; cada cuadro lo cuenta y lo sigue con el dedo. Al último número que diga le corresponde el símbolo que señaló.
En seguida se planteó una primera actividad que implica el tránsito del registro escrito al oral:
El maestro escribió un numeral [4] en un papel y le preguntó a Carmen qué número era, usando la tira. Carmen fue contando de izquierda a derecha cada cuadro sobre la tira numérica haciendo una relación entre los números que decía y el cuadro que señalaba, pero no encontró el numeral [4],
Los rasgos gráficos que caracterizan a cada cifra son difíciles de notar para los adultos con baja escolaridad. Carmen dijo que el cuatro que se veía en la tira numérica y el cuatro escrito por el maestro no eran el mismo número porque uno estaba más pequeño y "no se juntaba arriba", refiriéndose a la parte en donde se intersectan las dos líneas, arriba del numeral. Cuando el numeral que se pedía a Carmen interpretar era uno de los de la tira, la tarea resultaba más sencilla, por ejemplo, en la misma sesión 1:
Se le señaló un número sobre la tira [5] y se le pidió decir qué número era. Carmen contó cada cuadro sobre la tira de izquierda a derecha mientras los enumeraba en voz alta. Al llegar al símbolo exclamó: -es el cinco.
Veamos ahora un ejemplo del tránsito del registro oral al escrito. Se trata de una actividad realizada en la sesión 2: se puso sobre la mesa un conjunto de tarjetas numeradas que tienen dibujada en la parte posterior una colección. Las tarjetas estaban colocadas sobre la mesa, alineadas en orden creciente y con el numeral visible7 (Figura 2). Bajo una de las tarjetas el maestro escondió un pedazo de hoja con un dibujo al que llamó el "tesoro". La actividad consistía en que el maestro decía debajo de qué número estaba el tesoro para que con esa "pista" Carmen lo encontrara.

Se escondió el tesoro debajo del número 6 y se dijo: "está debajo del número seis". Se introdujo la condición de que tenía que hacerlo en menos de tres intentos. Carmen contó en la tira numérica, tocando los numerales desde el 2 con la goma del lápiz, hasta llegar al 6. Buscó entonces el símbolo del seis entre las tarjetas numeradas, levantó primero el 9 (símbolo similar al 6), al ver que ahí no estaba el tesoro, levantó el contiguo (8) y dijo -no está en el ocho-. Volvió a ubicar al 6 en la tira y levantó el 11, el 7 y finalmente el 6.
Carmen usó de entrada la tira para encontrar el numeral propuesto. Al notar que el numeral parecido que ella encontró no era el indicado, parece haber optado por una búsqueda al azar, al menos durante un momento. Cabe observar que ya reconoció el nombre del numeral "8". En la tercera sesión manifestó un mayor dominio en el uso de la tira para interpretar un numeral: se le dio una tarjeta con el numeral 14 y se le preguntó qué número era. Carmen buscó en la tira, comparando los numerales de ésta, uno por uno, con el de la tarjeta; lo encontró, contó los numerales en la tira empezando por la izquierda, hasta el 14, y dijo: "éste es el catorce". Estos logros requirieron la familiarización de Carmen con las diferencias y similitudes entre grafías, así como una gradual apropiación de la tira numérica como herramienta. Otra dificultad que tuvo que superar fue la de comprender que en cada cuadro de la tira se representa un sólo numeral: al principio consideró a los numerales de dos cifras como dos numerales. Por ejemplo, interpretó el "10" como "diez y once"
3.2.2. Cuantificar e interpretar. La ayuda que aporta la colección
En las situaciones en las que los números orales y escritos fungen como expresiones del cardinal de colecciones, se agrega, a los dos registros en juego (el oral y el escrito), un tercer referente, el de la colección que es objeto de cuantificación. Ello brinda al adulto la posibilidad de utilizar el conteo de los objetos, o incluso la estimación visual de la cantidad, para verificar las correspondencias que establece entre las numeraciones oral y escrita. La presencia de las colecciones permite también que los números asuman su función esencial de expresar cantidades. Veamos una primera resolución de Carmen.
En la sesión 1, se le dieron a Carmen todas las tarjetas numeradas (veinte en total) revueltas, con los numerales visibles y se le pidió encontrar el trece. Primero, Carmen identificó el numeral trece en la tira: contando cada cuadro sobre ésta, del 1 al 13. Después, buscó entre las tarjetas, fijándose en los puntos detrás de cada tarjeta; fue desechando algunas hasta que encontró la tarjeta 13.
Así, Carmen prefirió buscar la colección contando los puntos, lo cual sabe hacer, en lugar de identificar el numeral, lo cual está aprendiendo y le cuesta trabajo. En las ocasiones sucesivas en que se planteó esta actividad, se restringió la posibilidad de voltear las tarjetas antes de escoger. Veamos un ejemplo tomado de la sesión 3, en el que Carmen logra interpretar el numeral con apoyo de la tira y en el que utiliza el conteo de la colección, esta vez, como medio de verificación.
Se le dio la tarjeta con el numeral 13, por el lado del numeral, sin indicarle qué número era, y se le pidió que entregara esa cantidad de frijoles con la restricción de no voltear la tarjeta (para no ver los puntos). Carmen identificó el numeral en la tira, en seguida contó el número de casilleros que hay desde el extremo izquierdo de la tira hasta ese numeral, así averiguó que el numeral en cuestión era el trece. Entonces tomó trece frijoles y se los dio al maestro. Volteamos entonces la tarjeta y pusimos un fríjol encima de cada punto: no sobraron ni faltaron frijoles.
De esta manera, el conteo de las colecciones dibujadas en las tarjetas numeradas le permitió verificar la decodificación del numeral.
3.2.3. El orden de los números y las relaciones "de vecindad" también ayudan
Consideramos que trabajar en torno al orden de los números en el registro escrito ayudaría a Carmen en su proceso de identificar y retener las relaciones entre la expresión oral de los números y las grafías. Presentaremos aquí un ejemplo con el juego del "Tesoro" que se explicó ya antes.
Al final de la sesión 2, jugando al "tesoro", se le pidió a Carmen esconder el tesoro y dar una pista para encontrarlo. Se le explicó que la pista no debía ser el número en el que estaba el "tesoro" sino cualquier otro número alrededor. Carmen lo escondió debajo del 8 y dijo: "(el tesoro) está después del cinco o del seis". Se levantó el siete y no había nada. Carmen corrigió y dijo: "luego, enseguida del siete".
La actividad exige decir el nombre de numerales expresados simbólicamente y tener en cuenta la relación de orden.
3.2.4. Distinguir y reproducir los trazos
La identificación y la reproducción de los trazos de grafías numéricas fueron difíciles para Carmen. Presentaremos primero algunos ejemplos de las dificultades para identificar los rasgos característicos de cada grafía. Anteriormente vimos el caso de un numeral "4", escrito por el maestro, que Carmen no reconoció como equivalente al de la tira numérica debido a una diferencia en la línea inclinada. En la misma sesión 1 Carmen pensó que los símbolos numéricos "5" y "3" correspondían al mismo número, lo cual explicó mostrando que la parte inferior de ambos era igual; en una sesión del trabajo con números grandes, ante la petición de leer el numeral "7", leyó "uno", probablemente debido a que las diferencias gráficas entre los dos numerales son pocas; al final de la última sesión hicimos una visita a una tienda cercana, observamos precios y números escritos en algunos productos de la tienda. Carmen intentó leer un "1" pero como la tipografía era con un ancho considerable y tenía una línea horizontal de base lo confundió con el "12".
Identificar qué es lo que en un numeral puede cambiar y qué es lo que no debe cambiar para que siga representando al mismo número es problemático para Carmen y probablemente para cualquier persona en proceso de aprender. Se intentó paliar esta dificultad con algunos ejercicios, por ejemplo, en cada renglón de una hoja se pusieron diferentes tipografías de un mismo número y se le pidió a Carmen hacer su propio numeral a un lado de la hoja y decir en qué se parecía y en qué no.
El trazo también implicó dificultades: en la primera sesión, cuando Carmen intentó por primera vez escribir un numeral (el 8), dejó ver el enorme trabajo que esto le implicaba por una falta de la destreza motora fina para escribir. Aunado a ello, ciertas características de las grafías le complicaron la tarea, por ejemplo, el que los numerales estuvieran anotados con caracteres gruesos (tipo "negrita") hizo que Carmen intentara copiar el numeral siguiendo el borde para después rellenarlo.
La tipografía de los números usados en un material para adultos requiere de un análisis más cuidadoso, pues como se ve, puede dar lugar a dificultades.
3.2.5. Indicadores del avance logrado
En el transcurso de las cuatro sesiones en las que se trabajó la primera parte de la secuencia, el progreso de Carmen en su capacidad de interpretar numerales o de cuantificar con numerales fue notorio. Mostraremos aquí algunas de las manifestaciones más claras de este progreso.
En la sesión 4 se pusieron todas las tarjetas numeradas, en orden creciente, de lado de los puntos; se le pidió que encontrara la tarjeta con diez puntos y que, con ayuda de la tira, escribiera en un papel el número de puntos. En seguida, se le indicó que, para verificar, comparara su número escrito con el del reverso de la tarjeta.
Carmen comenzó con un conteo de los puntos de algunas tarjetas (desechó algunas por simple estimación visual) tomando las tarjetas de izquierda a derecha. Se detuvo y nos preguntó si podía contar con los dedos; asentimos y continuó. Una vez que tuvo la tarjeta con 10 puntos, para escribir el 10, primero lo identificó en la tira y luego lo copió en una hoja. Comparó el numeral que ella escribió y el del reverso de la tarjeta y dijo: "sí es".
Otras manifestaciones del progreso logrado por Carmen fueron: solicitar la tira por iniciativa propia para hacer las tareas que se le pedían; reconocer algunos numerales sin la tira (el lyel8) y contar sobre la tira no a partir del uno, sino de un numeral que ya reconocía para localizar otro no conocido, por ejemplo, cuando se le pidió encontrar el tesoro debajo del [15], Carmen dijo que ya no se acordaba de qué número era y optó por numerar oralmente las tarjetas a partir del ocho hasta llegar all5 (ocho, nueve, diez...).
Nuestra expectativa fue que, conforme Carmen se familiarizara con los símbolos numéricos, fuera prescindiendo de la tira numérica. No obstante, en el tiempo breve que duró la experiencia, esto no ocurrió.
4. SEGUNDA PARTE DE LA SECUENCIA: NÚMEROS GRANDES (20-999)
4.1. Las situaciones
En la enseñanza, la introducción de la representación escrita de los números se ha hecho a través de una de dos vías: la que llamaremos analítica, que consiste en formar los numerales considerando el valor relativo de las cifras que los componen (una colección es sistemáticamente agrupada en decenas, centenas, etc. y el número se forma con cifras que indican, según su posición, cantidades de unidades, decenas, etc.) y la sintética, que, en cambio, consiste en identificar progresivamente regularidades en la serie numérica sin analizar, de entrada, los numerales en términos de lo que representa cada cifra: se observa que las cifras van cíclicamente de cero a 9, que después de un nueve vuelve el cero, pero aumenta una unidad la cifra del lado izquierdo, etc. En la enseñanza de la numeración a los niños ha prevalecido el acercamiento analítico, al menos desde las reformas de los años setenta del siglo pasado, aunque en los últimos 20 años se ha tendido a posponer un poco el momento de introducir dicha perspectiva, habida cuenta de la dificultad conceptual que representan para los niños las nociones de base y posición. (Block & Álvarez, 1999; Lerner et al., 1994).
En el ámbito de la educación de adultos la pregunta que se plantea entonces es ¿en cuál de las dos vías para la introducción al sistema decimal de numeración escrita, la analítica o la sintética, se maximiza el aprovechamiento del conocimiento que ellos ya tienen sobre la numeración oral y sobre el cálculo? En un estudio reciente (Broitman, 2012), se explora de manera incipiente8, pero con resultados muy prometedores, la perspectiva sintética. En el presente estudio optamos por estudiar la alternativa analítica pues si bien es la más usual en la enseñanza a los adultos (Delprato & Fuenlabrada, 2008), nos parece que se han explorado poco los recursos que ofrece para recuperar sus conocimientos previos. No obstante, estamos convencidos de que ambas vías presentan ventajas y también desventajas, por lo que es necesario seguir construyendo y estudiando alternativas que articulen los dos acercamientos.
Esta parte de la secuencia consiste en una serie de actividades en torno a un dispositivo que llamamos "El vale"9. Se trata de una tabla que tiene como encabezados un billete de $100, una moneda de $10 y una de $1. En el segundo renglón se anota la cantidad requerida de billetes o monedas de la denominación correspondiente, como se muestra en la Figura 3.
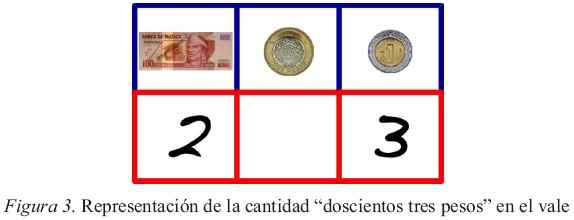
Este material, al igual que el de "La tira" que se usó con números hasta el 20, se concibió con la intención de permitir a un adulto acceder por sí mismo a la representación escrita de los números, en este caso hasta de tres cifras, a partir de sus conocimientos sobre la numeración oral, el cálculo mental (contar el dinero, descomponer una cantidad en billetes y monedas de distinta denominación y operar con dinero) y la escritura de los dígitos.
Se plantearon básicamente dos tipos de tareas: codificar (a partir de una cantidad de dinero o de un número oral, hay que expresar con cifras el número, al principio con apoyo de la tabla) y decodificar (dado un número escrito, se le debe nombrar o proporcionar la cantidad de dinero que indica). En estas situaciones se consideraron las siguientes variables didácticas10: tipo de tarea (codificar y decodificar); tabla con o sin encabezado; presencia o ausencia de la tabla, cantidades pequeñas (dos cifras) o grandes (tres cifras); cantidades con y sin ceros.
4.2. La experiencia con Carmen
La secuencia abarcó tres sesiones, de la cinco a la siete. El vale se presentó al comienzo de la quinta sesión, precedido de una actividad breve de reconocimiento de billetes y monedas. Carmen reconoció bien las monedas por su aspecto visual, por su tamaño, color, mas no por los numerales. La consigna para introducir el Vale fue la siguiente:
Maestro: Este material funciona para escribir número mayores que veinte, (...) funciona poniendo el número de monedas de $1, el número de monedas de $10 y el número de billetes de $100. (Se puso un ejemplo de escritura con dinero: se le dió un billete de $100, 2 monedas de $10 y 3 monedas de $1 ($123); ella contó el dinero y el maestro escribió la cantidad sobre el vale destacando que sólo se escribe el número de billetes y no el valor de los billetes).
La experiencia del piloteo nos permitió ver que las actividades de decodificación (dado un numeral escrito en el vale, determinar a qué cantidad corresponde) son más accesibles que las de codificación (dada una cantidad de dinero, expresar el numeral correspondiente); por lo cual, las primeras actividades que se trabajaron con Carmen fueron decodificaciones.
Al principio Carmen tuvo dificultades para utilizar el nuevo dispositivo. Su forma de proceder permitió identificar cuestiones que se dejaron implícitas en la explicación y que no eran obvias para ella. A continuación se destacarán algunas de las principales dificultades así como los logros.
4.2.1. El proceso de decodificación
No obstante los avances logrados en la primera parte de la secuencia, identificar y escribir los dígitos presentó todavía algunas dificultades para Carmen. Veamos un ejemplo de la quinta sesión. Se le presentó un vale con el numeral 528 y se le pidió que diera esa cantidad de dinero. Carmen tomó su tira numérica y comparó las cifras:
Carmen: ¿Serán como ochocientos?
Maestro: ¿Cuántos billetes de cien le tiene que dar al maestro?
Carmen: Cien pesos... (En seguida agrega) No (Busca en su tira, confunde el 3 con el 5 y dice a modo de explicación) Tiene la misma parte de abajo. (Finalmente identifica al cinco en la tira, cuenta cinco billetes y los aparta).
Maestro: ¿Cuántas monedas de $10 le pedimos? (Reconoce el "2" comparando el número del Vale con el de la tira, tuvo dificultad por las diferencias entre las grafías, contó las monedas y las juntó con los billetes. Al final reconoció muy fácil el 8, ella misma dijo que ése ya no se le olvida, y contó 8 monedas de $1).
El uso de la tira numérica en las situaciones con números grandes fue recurrente. La tira funcionó como apoyo para comparar grafías, para reconocer un dígito y como dispositivo de control. Fue un recurso que parecía dar seguridad a Carmen.
En el proceso de decodificar aparecieron otras dificultades menores que Carmen superó rápidamente, por ejemplo, pensar que la cifra de izquierda siempre representa los billetes de cien (cuando podrían ser los de 10) o bien que el billete de cien que aparece dibujado en el encabezado de la tabla es parte de la cantidad representada.
Veamos ahora cómo, en la sesión 5, Carmen decodifica el numeral 148 anotado en una tabla sin encabezado:
Maestro: ¿Cuál es?
Carmen: Este es el uno, éste es el ocho y el cuatro (al parecer los dice en el orden en que los reconoce). Serían cuatro monedas de diez y ocho de peso y luego uno de cien.
Maestro: ¿Y todo junto?
Carmen: (Carmen cuenta en silencio) Ciento treinta y ocho.
Maestro: (Le pregunta cuánto era por las monedas de diez, Carmen corrige).
Carmen utiliza su habilidad de cálculo mental para escribir un numeral. Aunque todavía recibe ayuda, el avance es visible.
4.2.2. El proceso de codificar
Como ya se comentó, estas actividades fueron más difíciles. Al principio se usaron billetes y monedas para apoyar la codificación. La dificultad más importante fue comprender que en la tabla se anota la cantidad de billetes o monedas, esto es, los valores absolutos y no el valor que representan (los valores relativos). En la sesión cinco se le dieron 212 pesos con dos billetes de $100 y una moneda de $10 y dos de $1, y se le pidió escribir ese número en el vale.
Carmen: ¿Los pongo dónde? (El maestro le explicó que sólo se escribe la cantidad de billetes).
Carmen: (anota [2] en la casilla debajo del $100).
Maestro: ¿Cuántas monedas de diez hay?
Carmen: Una.
Maestro: ¿Entonces qué ponemos aquí? (señalando el recuadro debajo de la moneda de $10).
Carmen: Tres.
Maestro: ¿Tres?,¿por qué?
Carmen: Diez. (El maestro explica que en la casilla sólo se escribe el número de monedas, no cuánto vale el billete)
Carmen: Doce... una (moneda).
Maestro: Entonces se escribe el uno.
Carmen: ¡Ah! yo pensaba que eran éstas con éstas (las dos de uno con la de diez).
Así, frente a una moneda de diez pesos y dos de un peso, y ante la falta de certeza de qué es lo que se registra, Carmen ve tres posibilidades:

Con las monedas de $1 no tuvo problema, anotó un "2" en el lugar adecuado. Al preguntarle ¿qué número está debajo del $10? (estaba el 1), ella respondió: "el diez" aunque en seguida rectificó y afirmó que era el uno. Al pedirle que dijera cuánto dinero había en total, contestó correctamente: doscientos doce.
En nuestro sistema de numeración, a cada cifra de un numeral le corresponden dos valores, el absoluto, por ejemplo, "dos", que remite a un número de agrupamientos (2 de 100) y el valor relativo, que remite al valor total representado (doscientos). El acercamiento analítico al sistema de numeración, al requerir analizar lo que representa cada cifra, exige que se tengan en cuenta estas dos valencias de los dígitos y esto constituye su principal dificultad. No obstante, como veremos, Carmen logró avances importantes.
Nos detendremos en una de las actividades de codificación, que implica también sumar y que pareció brindar una ayuda importante. Se trata del juego de "El cajero" (Secretaría de Educación Pública, 1994a, ficha 43), aplicado en la sexta sesión11. En este juego se usan tres dados de diferente color; cada uno corresponde a los billetes/monedas -de 100, 10 y 1- que se irán sumando. Se inició con un ejemplo, en el vale estaba anotado el número 64; se lanzó el dado correspondiente a los billetes de $100, salió "4" y se explicó a Carmen que había que sumar 4 billetes de $100 a los 64 pesos que ya estaban escritos en el vale.
Carmen: Cuatrocientos sesenta y cuatro (agrega que le falta un cuatro en el cuadro debajo de $100 en el Vale).
(Enseguida se arroja el dado de las monedas de $10 y sale el 1).
Maestro: Ahora tenemos que sumar uno de diez a 464.
Carmen: (suma mentalmente) Cuatrocientos setenta y cuatro.
Maestro: ¿Qué tenemos que cambiar para que en vez de 464 sea 474.
Carmen: El setenta (señala el 4 de los billetes de $100).
(Para ayudarla le pedimos que escribiera en una hoja en blanco, con el vale a la vista, el "cuatrocientos sesenta y cuatro" y el "cuatrocientos setenta y cuatro" y que los comparara; Carmen observó que el único que cambia es el seis).
La actividad continuó, había que sumar 4 de un peso a la cantidad anterior, 474:
Carmen: (suma mentalmente) Cuatrocientos setenta y ocho. Tenemos que cambiar el 4 por el 8 (lo escribe sin usar la tira).
(Regresamos al dado de $100y sale 1)
Maestro: ¿uno de $100 más 468?
Carmen: Calcula mentalmente) Quinientos sesenta y ocho, hay que cambiar el 4 por un 5.
Como puede verse, dados dos números expresados oralmente, con una diferencia de 100, Carmen logra saber que lo único que cambia es la cifra de las centenas; es decir, logra identificar el cambio en el registro de lo escrito, con lo cual muestra que puede empezar a traducir una transformación aditiva del sistema de numeración oral al registro escrito.
Notemos, sin embargo, que Carmen no opera, al menos no todavía, en el registro escrito, no suma de entrada "uno" a la cifra que indica la cantidad de billetes de cien, sino que suma mentalmente 468 más 100 y después observa que hay que cambiar el cuatro por el cinco. Esto confirma que durante un tiempo, para Carmen seguirá siendo mucho más cómodo realizar las trasformaciones en el registro de lo oral (y con cálculo mental), y después convertir al registro escrito, sin operar directamente en éste.
Mostraremos un ejemplo del desempeño logrado por Carmen. En la séptima sesión, cuando se introdujo la calculadora, se le explicó, con un ejemplo, que para introducir un número (185) se pone la cantidad de billetes/monedas de cada denominación en orden de mayor a menor (tomando como referencia el vale). Carmen apretó el 1, después el 8 y dijo: "sólo nos falta el cero". Le preguntamos qué número quería escribir a lo que respondió: "ciento ochenta y cinco" y agregó: "para 185 hay que apretar el 5". Apretó el 5. Le dijimos: "el número que aparece en la pantalla es el ciento ochenta y cinco".
En seguida le pedimos que "escribiera" el trescientos veinticuatro. Carmen optó primero por escribirlo en la tabla sin encabezado para luego apretar cada dígito en la calculadora. Podemos ver en esta decisión un indicio de una apropiación del vale como herramienta.
Finalmente se le pidió escribir el número veinticinco en una hoja en blanco y en la calculadora: ella lo escribió correctamente en una hoja, copiando sólo el 5 de la tira, diciendo: "dos de diez y cinco de a peso". Enseguida lo escribió en la calculadora, primero apretó el 2 y luego el 5. De esta manera, Carmen usa su conocimiento de la suma de veinte pesos más cinco pesos para, con ayuda de la descomposición propiciada por el vale, escribir "25".
5. CONCLUSIONES
Retomaremos aquí las preguntas centrales del estudio planteadas en la introducción y también haremos un comentario acerca del recurso al concepto de registro semiótico. Finalmente, destacaremos los aportes del estudio al conocimiento sobre los procesos de enseñanza y de aprendizaje de la numeración escrita por adultos no alfabetizados.
5.1. Sobre las situaciones didácticas
De no saber diferenciar números de letras y de dibujos a la posibilidad de escribir e interpretar, aún con dificultad, numerales de tres cifras, el avance de Carmen a lo largo de siete sesiones de menos de una hora fue notorio. En las primeras cuatro sesiones Carmen accedió a la escritura de los primeros 20 numerales utilizando su conocimiento previo del conteo de una manera que resultó tan simple como eficaz: identificaba el numeral que necesitaba contando sobre la tira. Estos resultados permiten conjeturar que la tira numérica podría constituir una herramienta útil en el proceso de aprender a escribir los números hasta 20, poniendo en juego de manera significativa el conocimiento del conteo de los adultos no alfabetizados. Cabe observar además que el conteo oral podría hacerse en cualquier lengua y con cualquier sistema. No obstante, esto deberá ser estudiado y verificado.
Con más dificultad, pero también con algunos resultados positivos, el dispositivo de El vale funcionó como herramienta provisional para codificar y decodificar los numerales más grandes con cierta autonomía, poniendo en juego conocimientos de cálculo mental. La dificultad más importante —comprender que una cantidad como doscientos se puede representar solamente con el dígito "2" ubicado en el casillero de los billetes de cien— es tributaria del acercamiento analítico a la numeración, el cual pone en juego la doble valencia de las cifras que componen los numerales (valor absoluto y valor relativo). Esta dificultad, aunada al hecho de que la mejor manera de acceder a la numeración y al cálculo escritos puede variar de un adulto a otro dependiendo de sus conocimientos previos (Delprato, 2006), justifica la necesidad de explorar más alternativas, en particular, como hemos dicho al principio de este texto, alternativas que articulen el acercamiento analítico que hemos explorado aquí, con un acercamiento sintético que priorice la identificación de regularidades del sistema de numeración escrito, sin detenerse a analizar sus características de base y posición, en una secuencia didáctica flexible, en el sentido de adaptable en función de las dificultades de cada persona.
Merece también un comentario el uso de algunas situaciones didácticas originalmente dirigidas a niños, como la del tesoro escondido, la del cajero, o de la comunicación de cantidades, o de algunos dispositivos como la tira numerada. En la experiencia con Carmen se confirma el hecho de que dichas situaciones permiten a los adultos, al igual que a los niños, utilizar sus conocimientos previos, en particular el conteo, pero de una manera distinta, pues el conocimiento que los adultos tienen de la numeración oral, y del cálculo, es mucho mayor que el de los niños que inician la primaria. Es decir, la situación o el dispositivo pueden ser los mismos, pero la relación que niños y adultos establecen con ellos es diferente. Es necesario precisar que, cuando se cuestiona "dar un trato de niño al adulto" en las propuestas de enseñanza, el problema no es necesariamente (aunque sí puede llegar a serlo) el uso de actividades que eventualmente también hacen los niños sino, más precisamente, el que las propuestas no tengan en cuenta los conocimientos previos del adulto, sus formas de relacionarse con una situación dada, los cuales pueden ser sensiblemente distintos a los de los niños.
5.2. Otros aspectos relacionados con la adquisición de la escritura de los numerales
Se evidenció que, en el proceso de establecer una asociación estable entre números orales y grafías, está implicada una acción que puede pasar desapercibida a quien ya domina un sistema de escritura: se deben aprender a distinguir las variaciones gráficas que corresponden al mismo número de aquéllas que no. Una secuencia didáctica debe considerar este aspecto, tanto en la elección de la tipografía más clara, como en la propuesta de actividades que ayuden a superar dificultades, por ejemplo, la clasificación de numerales que corresponden al mismo número, pero hechos con trazos de distinto tipo y también ejercicios de trazo.
Por otra parte, a lo largo de la secuencia fue posible conocer también algunas de las hipótesis sobre las reglas de escritura de los números que Carmen tenía o que elaboraba sobre la marcha: números diferentes se escriben con grafías diferentes; a dos trazos diferentes les corresponden numerales diferentes; a cada trazo gráfico le corresponde un número (por lo tanto en "10" hay dos números). Estas hipótesis que se fueron precisando y corrigiendo, como resultado de la utilización de la tira numérica12.
5.3. El papel de los conocimientos sobre la numeración oral, en la adquisición de la numeración escrita
Considerando el desempeño de Carmen con los dos dispositivos utilizados, "la tira numérica" y "el vale", puede decirse que el principio que subyace al funcionamiento de ambos, a saber, apoyarse en los conocimientos del adulto acerca de la numeración oral para facilitar su acceso a la numeración escrita, constituye una conjetura viable que merece ser estudiada con mayor amplitud. Esta conjetura, de verificarse, llevaría a matizar la conclusión a la que se llega en otras investigaciones acerca del papel de obstáculo que juegan los conocimientos del adulto con respecto a la adquisición de algunos conocimientos matemáticos convencionales (Ávila, 2007; Delprato, 2006).
5.4. Numeraciones oral y escrita como registros semióticos
Por último, cabe observar que la conceptualización del tránsito de la numeración oral a la escrita en términos de un trabajo de conversión de registros semióticos fue adecuada para destacar, en primer lugar, que el adulto se acerca a la numeración escrita desde otra numeración conocida por él, la oral. Carmen fue aprendiendo a identificar los números escritos que corresponden a los orales, pero, en un primer momento, operó únicamente en el registro oral. Por ejemplo, para saber qué número sigue del símbolo escrito "11", ella convirtió ese símbolo en su equivalente oral, "once", encontró en ese registro al sucesor, "doce" y después, buscó el equivalente escrito de ese numeral. Se esperaría que más adelante pueda operar directamente en el registro escrito.
5.5. Tres aportes del estudio
Para terminar, nos permitimos destacar tres aportes del estudio: en primer lugar, contribuye a sustentar la viabilidad de un mayor aprovechamiento de la numeración oral en un proceso de adquisición de la numeración escrita; además, identifica y fundamenta una dirección en la que puede ser conveniente continuar la exploración de alternativas didácticas, la cual se caracteriza por la integración de los acercamientos que hemos llamado analítico y sintético, con la inclusión de la calculadora. Por otra parte, el estudio contribuye a enriquecer el marco interpretativo del proceso de adquisición de la representación escrita de los números, al acompañarlo de un análisis didáctico de las alternativas de enseñanza de la numeración escrita y al concebirlo en términos de una conversión entre registros semióticos.
Finalmente, los resultados arrojan luz sobre un aspecto aparentemente nimio el cual, no obstante, resultó ser importante en el proceso de aprendizaje de la numeración escrita: las dificultades de identificación de los caracteres numéricos en función de sus características tipográficas de los numerales.
AGRADECIMIENTOS
Agradecemos a Margarita Ramírez Badillo y a Laura Reséndiz, así como a los árbitros, las minuciosas y reiteradas revisiones que hicieron de este texto y sus pertinentes observaciones. Para la elaboración de la tesis de la que se deriva el presente artículo, se contó con el apoyo de una beca de Consejo Nacional de Ciencia y Tecnología (CONACYT).
REFERENCIAS BIBLIOGRÁFICAS
Artigue, M. (1995). Ingeniería didáctica. En P. Gómez (Ed.), Ingeniería didáctica en educación matemática. Un esquema para la investigación y la innovación en la enseñanza y el aprendizaje de las matemáticas (pp. 33-59). D.F., México: Grupo Editorial Iberoamérica. [ Links ]
Ávila, A. (2005). El saber matemático de los adultos analfabetos. Origen y desarrollo de sus estrategias de cálculo. Revista Latinoamericana de Estudios Educativos, XXXV (3-4), 179-219. [ Links ]
Ávila, A. (2007). Del cálculo oral al cálculo escrito. Recherches en Didactique des Mathématiques, 27 (3), 313-348. [ Links ]
Bishop, Α. (1999). Enculturación matemática. La educación matemática desde una perspectiva cultural. Barcelona, España: Ediciones Paidós Ibérica. [ Links ]
Block, D. y Álvarez, Α. M. (1999). Los números en primer grado: cuatro generaciones de situaciones didácticas. Educación Matemática, 11 (1), 57-76. [ Links ]
Block, D., Moscoso, Α., Ramírez, M. & Solares, D. (2007). La apropiación de innovaciones para la enseñanza de las matemáticas por maestros de educación primaria. Revista Mexicanade Investigación Educativa, XII (33), 731-762. [ Links ]
Block, D. y Nemirovsky, M. (1988). Algunos procedimientos y representaciones matemáticas de adultos no alfabetizados. En F. Hitt, O. Figueras, L. Radford y E. Bonilla (Eds), Memorias de la Segunda Reunión Centroamericana y del Caribe sobre formación de profesores e investigación en Matemática Educativa (pp. 255-260). Guatemala, Guatemala: Reunión Centroamericana y del Caribe sobre formación de profesores e investigación en Matemática Educativa, [ Links ]
Broitman, C. (2012). Adultos que inician la escolaridad: sus conocimientos aritméticos y la relación que establecen con el saber y con las matemáticas (Tesis Doctoral no publicada). Universidad Nacional de La Plata, Buenos Aires, Argentina. [ Links ]
Brousseau, G. (2000). Educación y Didáctica de las Matemáticas. Educación Matemática, 12 (1), 5-37. [ Links ]
Brousseau, G. (2007). Iniciación al estudio de la teoría de las situaciones didácticas (D. Fregona, Trad.). Buenos Aires, Argentina: Libros del Zorzal. [ Links ]
Cantoral, R., Farfán, R. M., Lezama, J. y Martínez-Sierra, G. (2006). Socioepistemología y representación: Algunos ejemplos. Revista Latinoamericana de Investigación en Matemática Educativa. Número Especial, 9 (4), 83-102). [ Links ]
Cohen, L., Manion, L. y Morrison, Κ. (2000). Research Methods in Education. London, England: Routledge Falmer Education. [ Links ]
Chevallard, Y. (1998). Analyse des pratiques enseignantes et didactique des mathématiques: l'approche anthropologique. In Actes de l 'Université d' été de Didactique de la Rochelle 19-2, (pp. 88-101). Clermont-Ferrand, France: IREM de Clermont-Ferrand. [ Links ]
D'Ambrosio, U. (2001). Etnomatematica. Elo entre as tradições e a modernidade. Belo Horizonte, Brazil: Autêntica. [ Links ]
Delprato, F. (2006). Los adultos no alfabetizados y sus procesos de acceso a la simbolización matemática (Tesis de Maestría no publicada). Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, D.F., México. [ Links ]
Delprato, F. y Fuenlabrada, I. (2008). Así le hacemos nosotros: prácticas de numeración escrita en organizaciones productivas de mujeres con baja escolaridad. Cuadernos de Educación,6 (6), 337-349. [ Links ]
Duval, R. (1993). Semiosis y Noesis. En E. A. Sánchez y G. Zubieta (Eds. y Comp.), Didáctica de las Matemáticas. Escuela Francesa (pp. 118-144). D.F., México: Departamento de Matemática Educativa, Cinvestav. [ Links ]
Ferreiro, E., Fuenlabrada, I., Nemirovsky, M., Block, D. y Dávila, M. (1983). Los adultos no alfabetizados y sus conceptualizaciones del sistema de escritura. En Cuadernos de Investigación Educativa, No 10. D.F., México: Departamento de Investigaciones Educativas, Cinvestav. [ Links ]
Knijnik, G. (1997). Lo popular y lo legítimo en la educación matemática de jóvenes y adultos. En UNESCO-Santiago (Ed.), Conocimiento matemático en la educación de jóvenes adultos. Jornadas de reflexión y capacitación sobre la matemática en la educación (pp. 43-53). Santiago de Chile, Chile: UNESCO-Santiago. [ Links ]
Lerner, D., Sadovsky, P. y Wolman, S. (1994). El sistema de numeración: un problema didáctico. En C. Parra y I. Saiz (Comp.), Didáctica de las matemáticas. Aportes y reflexiones. Buenos Aires, Argentina: Paidós. [ Links ]
Mariño, G. (1997). Los saberes matemáticos previos de jóvenes y adultos: alcances y desafíos. En UNESCO-Santiago (Ed.), Conocimiento matemático en la educación de jóvenes y adultos. Jornadas de reflexión y capacitación sobre la matemática en la educación (pp.77-100). Santiago de Chile, Chile: UNESCO-Santiago. [ Links ]
Palmas, S. (2011). De la representación oral de los números a la escrita. Un estudio didáctico con dos adultos de baja o nula escolaridad (Tesis de Maestría no publicada). Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, D. F., México. [ Links ]
Palmas, S. y Block, D. (2011). Acceso a la representación escrita de los números. Una secuencia didáctica para adultos de baja o nula escolaridad. Primera parte, números hasta 20 y Segunda parte, Números mayores que 20. En Memoria Electrónica del XI Congreso Nacionalde Investigación Educativa. Ciudad de México, México: COMIE. [ Links ]
Ramírez, L. (2006). La enseñanza de los primeros números en preescolar. Exploración de una alternativa didáctica (Tesis de Maestría no publicada). Centro de Investigación y de Estudios Avanzados del Instituto Politécnico Nacional, D. F., México. [ Links ]
Secretaría de Educación Pública. (1994a). Fichero. Actividades didácticas. Matemáticas. Primer grado. D. F., México: SEP [ Links ]
Secretaría de Educación Pública. (1994b). Matemáticas Cuarto grado. Libro del alumno. D. F., México: SEP. [ Links ]
Secretaría de Educación Pública. (1999a). Matemáticas Primer grado. Libro del alumno. (3era. Rev. ed.). D. F., México: SEP. [ Links ]
Secretaría de Educación Pública. (1999b). Matemáticas Primer grado RECORTABLE (2da. Rev. ed.). D. F., México: SEP. [ Links ]
1 Los resultados que aquí se reportan, fueron presentados en el XI Congreso Nacional de Investigación Educativa, que se llevó a cabo en noviembre del 2012en la ciudad de México (Palmas & Block, 2011).
2 No solamente ha disminuido el espacio curricular para la práctica de los algoritmos, también han ido cambiando los algoritmos que son objeto de enseñanza: en los años 70 se enfatizó la comprensión de los algoritmos convencionales, en los años 90 se dio mayor peso al desarrollo de procedimientos no formales, y/o distintos a los convencionales, ver por ejemplo el caso de la multiplicación y de la división en los libros de texto (Secretaría de Educación Pública [SEP], 1994b).
3 Esta concepción es compartida en sus términos más generales por varias corrientes en el ámbito de la educación matemática, la Etnomatemática (D'Ambrosio, 2001), la Teoría Antropológica de los Didáctico (Chevallard, 1998), la Socioepistemología (Cantoral, Farfán, Lezama & Martínez-Sierra, 2006), por citar algunas.
4 Cuando se elaboró el estudio, los materiales oficiales para la escuela primaria eran los de la reforma de 1993. Cabe señalar que estos materiales son portadores de una gran riqueza de situaciones, elaboradas, muchas de ellas, dentro de la misma orientación didáctica que se asume en este estudio (Block et al, 2007).
5 Un análisis de las situaciones que ponen en juego al número de distintas maneras puede verse en Brousseau (2000).
6 En varios textos de G. Brousseau, (2000,2007) puede encontrarse una categorización de situaciones que ponen en juego números naturales.
7 Tarjetas "Número colección" en Secretaría de Educación Pública (1999b, recortable 27).
8 Se trata de un estudio sobre los conocimientos de adultos no escolarizados o semiescolarizados que no es de carácter didáctico, pero en las entrevistas ocurrieron intervenciones que revelaron un potencial didáctico importante.
9 Inicialmente habíamos llamado a este dispositivo "El cheque", pero el término resultó extraño para algunos adultos.
10 Las variables didácticas son los elementos de una situación que pueden ser modificados por el maestro y que afectan a la jerarquía de las estrategias de solución que pone en funcionamiento el alumno" (Brousseau, 2007).
11 Se trata de otra actividad originalmente diseñada para niños, que resulta muy útil en el trabajo con adultos, cuando se trata de comprender el carácter posicional de nuestro sistema de numeración. Ver por ejemplo Delprato (2006). El propósito de la actividad aquí fue seguir propiciando un análisis de la escritura de los numerales.
12 Los conocimientos que generan los adultos en su relación inicial con la escritura de los numerales están poco documentados, ver, por ejemplo, Block y Nemirovsky (1988).















