Artículos

 

Niveles de razonamiento geométrico en estudiantes de establecimientos municipalizados de la Región del Maule. Talca, Chile

 

Levels of geometric reasoning in students of statal schools of Maule Region. Talca, Chile

 

María Aravena Díaz*, Carlos Caamaño Espinoza**

 

* Universidad Católica del Maule, Chile. maravenadiaz@gmail.com.

** Universidad Católica del Maule, Chile. ccaamano@ucm.cl.

 

Recepción: Marzo 18, 2012;
Aceptación: Febrero 12, 2013.

 

Resumen

En esta investigación, que fue financiada por el Fondo Nacional de Desarrollo Científico y Tecnológico, FONDECYT 1090617, se analiza el nivel de razonamiento geométrico que presentan los alumnos de establecimientos municipalizados con altos índices de vulnerabilidad, de la Región del Maule, Chile. Para ello, se implementó un Diagnóstico considerando las temáticas de 6° Año Básico hasta 2° Año de Enseñanza Media, tomando como base el modelo de los Van-Hiele y los atributos distintivos en los procesos de razonamiento propuesto por Gutiérrez y Jaime (1998). La metodología fue de corte cuantitativa, donde se realizó un muestreo por conglomerados, con arranque probabilístico aleatorio de afijación proporcional. La muestra efectiva fue de 625 alumnos, representativos de la Región. A nivel de resultados, se coloca en evidencia que el alumnado se encuentra en el nivel más básico del razonamiento geométrico y con un grado de adquisición bajo respecto de los procesos de razonamiento.

Palabras Clave: Razonamiento geométrico, Niveles de razonamiento, Procesos de razonamiento, Educación Secundaria.

 

Abstract

In this research, financed by the National Fund for Scientific and Technological Development, FONDECYT 1090617, we analyze students' geometric reasoning from a municipal school, with high indices of vulnerability, in the region of Maule, Chile. Therefore, we made a diagnose test based on the Van-Hiele's model and Gutiérrez & Jaime's (1998) distinctive attributes in the reasoning process by considering the subjects students have from sixth grade, primary school, and from second grade, secondary education. The methodology was quantitative like where we took a sample by groups with a proportional allocation in a random sample. The effective sample was of 625 students which were representative of the area. Our main conclusion is that the students have a basic level of geometric reasoning and they have a low acquisition level in reasoning processes.

Key Words: Geometric reasoning, Levels of reasoning, Process of reasoning, Secondary Education.

 

Resumo

Nesta pesquisa, que foi financiada pelo Fundo Nacional de Desenvolvimento Científico e Tecnológico, FONDECYT 1090617, analisa-se o nível de raciocínio geométrico que apresentam os alunos de estabelecimentos municipalizados com altos índices de vulnerabilidade da Região do Maule, Chile. Para isso, implementou-se um diagnóstico considerando as temáticas do 6° Ano Básico até o 2° Ano do Ensino Médio, tomando como base o modelo dos Van-Hiele e os atributos distintivos nos processos de raciocínio proposto por Gutiérrez e Jaime (1998). A metodologia foi de corte quantitativa, na qual se realizou uma amostragem por conglomerados, com probabilidade aleatória de afixação proporcional. A mostra efetiva foi de 625 alunos representativos da Regiao. A conclusão principal é que este alunado se encontra no nível mais básico do raciocínio geométrico e apresenta um grau de aquisição abaixo dos processos de raciocínio.

Palavras Chave: Raciocínio geométrico, Níveis de raciocínio, Processos de raciocinio, Ensino Fundamental.

 

Résumé

Dans cette recherche, financée par le Fonds national pour le développement scientifique et technologique (FONDECYT, Chili), on analyse les différents niveaux du raisonnement géométrique des élèves d'écoles municipales de la région du Maule, dont le taux de vulnérabilité est très élevé. On a réalisé une étude comportant les thématiques vues dans la dernière année de l'éducation élémentaire jusqu'á la deuxième année de l'éducation secondaire (du 6eme au 4eme du collège dans le système éducatif francais). Pour faire analyse, on a pris l'approche de Van-Hiele et les niveaux de raisonnement de Gutierrez et Jaime (1998). On a réalisé un sondage stratifié proportionnel avec la méthode aléatoire avec un échantillon de 625 élèves représentant la population de la région. On conclue que les élèves de l'étude ont le niveau plus bas du raisonnement géométrique et présentent une basse acquisition des processus de raisonnement.

Mots Clés: Raisonnement géométrique, Niveaux de raisonnement, Rocessus de raisonnement, Collège (éducation secondaire).

 

1. Presentación general del problema

La investigación aborda un problema vigente relacionado con el aprendizaje de la geometría en los establecimientos públicos o municipalizados de la educación media chilena, donde asisten los alumnos más vulnerables y que presentan, en general, peores resultados en las pruebas de medición de la calidad de la educación (SIMCE) y pruebas de selección universitaria (PSU) en comparación con establecimientos privados y privados subvencionados. La preocupación por este segmento de alumnos es un tema central, tanto en las políticas públicas como en los informes de la OCDE (2009), donde se recomienda corregir las desigualdades para lograr la equidad y el acceso a la educación superior. En particular, la Región del Maule, donde se realizó la investigación, es una de las tres regiones con el menor ingreso per cápita (96.2 miles CLP), con 20% de pobreza y más de 30% de ruralidad. La educación pública es una de las más desfavorecidas en términos de calidad y equidad, puesto que la formación que se entrega, en general, no responde a las necesidades locales ni a los desafíos que la sociedad impone. Se agregan los bajos índices de logro en matemática, que no presenta diferencias significativas de los resultados del SIMCE entre los años 2006 y 2008.

Los alumnos presentan serias dificultades y obstáculos, tanto en la comprensión de los conceptos, como en los procesos geométricos y en el desarrollo de un pensamiento argumentativo y deductivo. Este hecho no les permite desarrollar procesos de pensamiento y razonamiento matemático (Aravena, Caamaño y Cabezas, 2007). La enseñanza de la geometría, salvo excepciones, no sólo en la región del Maule sino en Chile, ha hecho crisis dentro de la formación matemática, mostrando serias deficiencias, lo queda demostrado en los análisis de los resultados de las pruebas de medición tanto nacionales (SIMCE, 2003, 2006, 2010), como internacionales (PISA, 2000, 2006, 2009; TIMMS, 2003), donde se observa que las mayores dificultades de los estudiantes está en la comprensión de los problemas y en los procesos argumentativo - deductivos. Aunque cabe mencionar que los estudiantes que asisten a escuelas privadas de alto nivel socioeconómico tampoco escapan a esta situación (PISA, 2006, 2009).

El problema de la formación geométrica se arrastra desde la década de los setenta, especialmente en Latinoamérica, donde prácticamente se dejó de lado su enseñanza, en particular en la formación del profesorado y tal como lo plantea Cantoral (1995) ha sido difícil de revertir tanto a nivel conceptual como metodológico, ya que se privilegia un trabajo algebraico eminentemente algorítmico, sin aplicaciones y alejada de los contextos. Esto ha tenido como consecuencia que los alumnos pierdan capacidades que son consideradas clave en los procesos geométricos, tales como la visualización, las representaciones, la exploración, la modelización, la argumentación y la demostración (Aravena, Caamaño & Giménez, 2008; Aravena, Caamaño, González, Cabezas & Córdova, 2011).

A partir de la década de los noventa, con la implementación de la reforma educativa en Chile, se presta atención real al problema, pues se fortalece la enseñanza de la geometría en la formación inicial y se incorpora en la formación continua del profesorado. Es así como se han realizado acercamientos desde el Ministerio de Educación con relación a lo que debe enseñarse en los distintos niveles. Se han entregado propuestas metodológicas y orientaciones didácticas para diferentes temas, así como el diseño de textos para orientar el trabajo de aula, se han llevado a cabo acciones de perfeccionamiento para los docentes y desarrollado de programas remediales para mejorar las destrezas de los profesores, entre otros aspectos. Con todo, no se han podido superar las debilidades que hemos señalado (OCDE, 2004, OCDE & BIRD/ Banco Mundial, 2009).

Varios son los estudios que justifican las razones de dichas dificultades, entre las que se destaca la forma en que ésta es enseñada en la formación de profesores, con un enfoque formal, sobrecargada de estructuralismo, de abstracción y parcelación del conocimiento. Se coloca en evidencia que esta forma de enseñanza, que adquieren los profesores, tiende a ser reproducida en las aulas, generando en los alumnos escasa comprensión de los conceptos y procesos geométricos (Latorre, 2004; Aravena, et. al, 2011). Por otra parte, estudios en esta línea, presentan dos elementos que pudieran dar luz para entender estas dificultades. El primero es el poco tiempo que se le dedica al tema, impartido generalmente al final de los cursos, por lo que queda escaso tiempo para su enseñanza y aprendizaje (Corrales et al., 2001, citado en Blanco & Barrantes, 2003, p. 129); el segundo, es que los libros de texto incluyen las materias al final de los capítulos lo que contribuye a que no sean considerados por los docentes (Gómez, 2000).

Otro de los factores que ayudan a comprender esta problemática trata de la interacción que se da en las aulas. Un estudio realizado por Villalta, Martinic & Guzmán (2011) en establecimientos municipalizados vulnerables secundarios de dos comunas de la Región de Maule con los más altos resultados de aprendizaje en el SIMCE 2006 y 2008, en comparación con sus pares comunales vulnerables muestran que, en general, la mayor parte de los intercambios que se dan en la sala de clases entre profesor y alumno son de baja exigencia cognitiva. Los intercambios son del tipo pregunta - respuesta y de inducción de respuestas, donde el profesor ofrece pistas a los alumnos para que entreguen la respuesta esperada por éste, y en el caso de la interacción didáctica, el profesor es el protagonista del proceso.

Al mismo tiempo, los estudios son coincidentes en señalar que el aprendizaje de la geometría juega un papel fundamental en la resolución de problemas, puesto que si se considera como un modelo de representación y descripción de la realidad, se constituye en un importante elemento unificador (Fortuny & Giménez, 1998). Desde el punto de vista del aprendizaje, ayuda al estudiante a desarrollar diversos procesos de razonamiento, que en la mayoría de los casos tienen adecuados soportes gráficos y manipulativos. El documento "Perspectivas en la enseñanza de la geometría para el siglo XXI", elaborado por el ICME en los años noventa, deja claro la importancia de la geometría en el proceso de formación de los estudiantes, al ser considerada como "una herramienta para comprender, describir e interactuar con el espacio en que vivimos, es quizás la parte más intuitiva, concreta y unida a la realidad de las matemáticas" (ICMI, 1998, p.337, citado en Blanco y Barrantes, 2003, p.2).

El estudio abordó la problemática descrita en los párrafos anteriores, focalizándose en el análisis de los trabajos que han sido un referente en el ámbito de la geometría y en la resolución de problemas (Gutiérrez y Jaime, 1998; De Villiers, 1993). En particular, se analizaron los estudios centrados en los procesos cognitivos que se enfocan en la manera cómo se produce el aprendizaje de los conceptos geométricos, para explicar la evolución del pensamiento geométrico, colocando el énfasis en los procesos claves, tales como: visualización, reconocimiento, identificación, clasificación y representación. También se abordan los procesos de argumentación de los hechos geométricos: la generalización, aplicación y demostración; teniendo en consideración las interacciones que existen entre los procesos de visualización y razonamiento (Vinner & Hershkowitz, 1983; Hershkowitz, 1990; Vinner, 1991; Gutiérrez y Jaime, 1998; Duval, 1998; Fortuny y Giménez, 1998).

Entre los modelos que han sido ampliamente investigados y que muestran evidencia empírica respecto del razonamiento de los alumnos, encontramos el modelo de Van-Hiele, donde son varias las aportaciones en geometría plana y del espacio en las que se ha usado el modelo. Destacamos la utilización de éste para: (1) medir los niveles de razonamiento de los estudiantes de secundaria antes y después de un curso de geometría (Usiskin, 1982), resultados que han sido cuestionados debido a que se evaluaron los niveles con una prueba de selección múltiple; (2) describir los niveles de razonamiento mediante entrevistas orales, cuyos resultados indicaron que éstas son un descriptor muy exacto de los niveles de razonamientos que alcanzaban los estudiantes (Burger & Shaughnessy, 1986); (3) desarrollar y documentar un modelo de trabajo para evaluar el nivel de razonamiento de los estudiantes en los grados 6° a 9° (Fuys, Geddes, Lovett & Tischler, 1988); (4) analizar la evolución del razonamiento de los estudiantes del ciclo superior de básica y 2° medio, mediante un seguimiento (Gutiérrez, Jaime & Fortuny, 1991; Jaime, 1993); (5) caracterizar el nivel de razonamiento de los profesores en formación, donde se concluye que en geometría, la mayoría de los futuros profesores poseen una adquisición correspondiente a los niveles uno (reconocimiento) y dos (de análisis) (Gutiérrez & Jaime, 1993); y (6) caracterización del grado de adquisición de los estudiantes cuando son enfrentados a temas geométricos (Grenier,1988; Jaime & Gutiérrez, 1996; Gray, 1999; Owens, 1999; Guillén, 1996; Gutierrez, Pegg & Lawrie, 2004).

 

1.1. Problema de investigación

A partir de la situación descrita en la sección anterior, se detecta la necesidad de realizar un diagnóstico que permita, a nivel regional, identificar los niveles de razonamiento y grados de adquisición que han logrado los estudiantes durante su formación. Justificamos un estudio en esta línea, ya que pensamos que el análisis de los resultados de las pruebas nacionales (SIMCE) e internacionales (PISA), no permiten detectar el problema de fondo, lo que dificulta generar propuestas que nos lleven a obtener evidencia empírica sobre el tipo de razonamiento que utilizan los alumnos en geometría, las estrategias que utilizan y las dificultades y obstáculos que manifiestan, en particular, los que asisten a los establecimientos públicos con altos índices de vulnerabilidad, donde se observan las mayores deficiencias (OCDE, 2004; OCDE y BIRD, 2009). Conocer cómo razonan los alumnos y por qué lo hacen así, es un elemento clave para una intervención didáctica que ayude a superar y revertir la situación actual. (OCDE, 2004; OCDE & BIRD, 2009).

Los ámbitos que se articularon en esta investigación corresponden a los niveles de razonamiento del modelo de Van-Hiele y los atributos distintivos en los procesos de razonamiento para cada uno de los niveles, planteados por Gutiérrez y Jaime (1998). Dichos procesos, de reconocimiento y descripción, uso de definiciones, formulación de definiciones, clasificación y demostración, son los referentes para reconocer en qué nivel de razonamiento se encuentra el alumnado, ayudando además a la selección adecuada de los tipos de problemas para el diseño del diagnóstico.

De acuerdo con lo señalado, nos planteamos realizar un estudio con el siguiente problema: ¿Cuál es el nivel de razonamiento geométrico que han adquirido los estudiantes durante su formación desde la enseñanza básica hasta el segundo año de educación media en el contexto del modelo de los Van-Hiele? y ¿en qué grado han sido adquiridos de acuerdo con los atributos distintivos en los procesos de razonamiento?

 

1.2. Hipótesis general

El alumnado de segundo año de secundaria de establecimientos municipalizados de la Región del Maule presenta un nivel de razonamiento básico y un bajo grado de adquisición en los procesos de razonamiento geométrico.

 

1.2.1. Hipótesis particulares

H1: Los alumnos de educación media de alta vulnerabilidad presentan obstáculos y dificultades en el reconocimiento y utilización de propiedades matemáticas en la formulación, uso y clasificación de definiciones de los objetos geométricos.

H2: El alumnado de secundaria posee un bajo grado de adquisición en los procesos argumentativos, deductivos y de demostración.

 

1.3. Objetivos

(1) Diseñar un instrumento de diagnóstico basado en los niveles de razonamiento de Van-Hiele y en los atributos distintivos en los procesos de razonamiento. Implementar dicho diagnóstico en una muestra representativa de establecimientos municipalizados de segundo año medio de educación secundaria de la Región de Maule.

(2) Caracterizar y jerarquizar el nivel de razonamiento geométrico de los estudiantes de segundo año medio de educación secundaria de los liceos municipalizados de la Región del Maule.

(3) Analizar cuantitativamente el grado de adquisición en los procesos de razonamiento geométrico en cada uno de los niveles de Van-Hiele. Detectar aciertos, dificultades y obstáculos.

 

2. Marco teórico

En esta sección se describen, de manera global, las diferentes perspectivas teóricas que dan sustento a la investigación, en particular aquellas sobre cognición que apuntan a la identificación y construcción de los objetos geométricos y a los tipos de razonamiento que se manifiestan en el aprendizaje de la geometría.

 

2.1. Procesos cognitivos

En el estudio de los procesos cognitivos, consideramos los trabajos de Hershkowitz, Bruckheimer y Vinner (1987); Vinner y Hershkowitz (1983); Hershkowitz (1990); Vinner (1991), quienes señalan que en la identificación o construcción de ejemplos de un concepto se pueden distinguir al menos tres elementos: la imagen del concepto; la definición del concepto y un grupo de operaciones, mentales o físicas, como ciertas operaciones lógicas. Aclaran que la descripción es importante para la enseñanza de conceptos, porque se han delimitado los elementos que deben formarse en la mente para que ocurra la identificación y la construcción. Asimismo, los trabajos de Clements y Battista (1992) se constituyen en un aporte para este estudio, puesto que recopilan la investigación realizada sobre el conocimiento geométrico de los estudiantes desde tres perspectivas teóricas (la de Piaget, la de Van-Hiele y la ciencia cognitiva), donde dan especial atención a las representaciones de las ideas geométricas.

Resulta de interés para el estudio la caracterización de los procesos de visualización y razonamiento, en particular los trabajos de Presmeg (1986) que se han centrado en dar una clasificación sobre las distintas imágenes mentales a las que se les atribuye ciertas acciones cognitivas. En concreto, muestra una clasificación de imágenes mentales y un modelo visual y analítico en ejes ortogonales, separando la acción cognitiva de las distintas representaciones e imágenes mentales. De igual forma resulta relevante, en la resolución de problemas geométricos, el estudio de su coordinación como puerta de entrada hacia el razonamiento deductivo (Duval, 1998). Como consecuencia, la visualización no queda relegada a un simple papel ilustrativo de las afirmaciones geométricas, a la resolución de problemas e incluso a la prueba (Bishop, 1989; Zazkis, Dubinsky & Dautermann, 1996). En la línea de la demostración de los objetos geométricos, hemos tomado como referentes a De Villiers (1993); Harel y Sowder (1998); Ibañes y Ortega (2004) y Gutiérrez (2006). Estos últimos, recopilan las investigaciones sobre el aprendizaje de las demostraciones, los tipos de demostración, las diversas funciones que ejercen las demostraciones, los diferentes niveles de demostración, las concepciones de los estudiantes y los tipos de demostración que estos producen.

 

2.2. Modelo de razonamiento geométrico de los Van - Hiele

En la línea del modelo de los Van-Hiele, varios son los autores que, desde hace décadas, muestran la potencialidad del modelo para analizar el nivel de razonamiento en el trabajo geométrico. Entre los más relevantes se encuentran Jaime (1993), Jaime y Gutiérrez (1996) y Gutiérrez y Jaime (1998), quienes han presentado propuestas para analizar los elementos clave que debemos tener en cuenta en el diseño y aplicación de un diagnóstico, destacando el grado de adquisición de los niveles por parte de los estudiantes. Tales elementos se constituyen en el referente para este estudio, situándonos en una visión crítica de acuerdo con el contexto del país y de la región a las características de los alumnos y de los profesores. Nos basamos en los trabajos donde se han analizado los diferentes instrumentos que han sido utilizados para evaluar el grado de adquisición de los niveles, los contenidos, los tipos de problemas y las dificultades presentadas (Gray, 1999; Guillén, 1996; Jaime & Gutierréz, 1996; Lawrie, Pegg y Gutierrez, 2000, 2002; Owens, 1999; Gutierrez et al., 2004).

En este estudio, se ha tomado como base la propuesta de Gutiérrez y Jaime (1998), quienes presentan un análisis más fino en la descripción y adquisición del razonamiento de los estudiantes, al articular los niveles de razonamiento de los Van-Hiele con atributos distintivos en los procesos de razonamiento para cada uno de los niveles. Los procesos considerados son: reconocimiento y descripción de los objetos geométricos, observables en los niveles 1 y 2; uso de definiciones, desde el nivel 2 al 4; formulación de definiciones desde el nivel 1 al 4; clasificación de definiciones desde el nivel 1 al 3 y demostración observable en las producciones de los alumnos desde el nivel 2 al 4. Esta forma de análisis no es contradictoria ni excluyente con las propuestas de Vinner, Hershkowitz y Presmeg, respecto de la visualización, los procesos geométricos y la construcción del objeto. En Gutiérrez y Jaime (1998), se describe en detalle la matriz que se presenta en la tabla I, y que ha sido base en la construcción y análisis del diagnóstico.

 

2.2.1. Niveles y fases del modelo

De manera global se reconocen dos componentes esenciales en el modelo, la primera, se refiere a la descripción de los niveles de razonamiento, donde cada nivel está caracterizado por una forma distinta de comprensión y utilización de los conceptos geométricos, lo cual se refleja en una manera diferente de interpretarlos, definirlos, clasificarlos y hacer demostraciones. En la tabla II, se muestra un resumen de los niveles y las características principales para su utilización y en forma detallada se encuentra en los trabajos de Fuys, Geddes, Lovett y Tischler (1988), Jaime (1993) y en Jaime y Gutiérrez (1996).

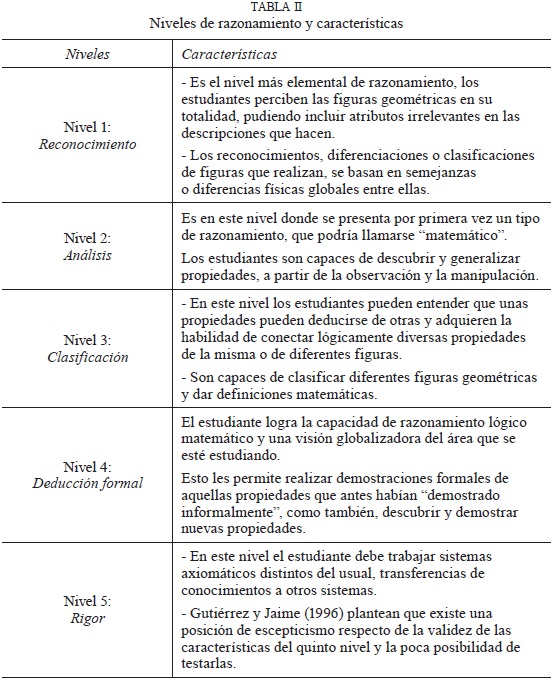
La segunda componente corresponde a las fases de aprendizaje, las que indican cómo organizar la enseñanza y cómo estructurar el trabajo de los estudiantes, para favorecer el avance de un nivel a otro. Éstas no están asociadas a un nivel determinado, sino que en cada nivel la enseñanza comienza con actividades de la primera fase y continúa con las fases siguientes. Esta idea sugiere que la transición de un nivel al siguiente no es un proceso natural; tiene lugar bajo la influencia de un programa de enseñanza- aprendizaje y requiere del aprendizaje de un nuevo lenguaje (Van-Hiele, 1957, citado en Jaime y Gutiérrez, 1996). En la Tabla III, se presentan las ideas centrales de las cinco fases del modelo base del estudio.

3. Metodología

La metodología utilizada en la investigación es de tipo cuantitativa descriptiva-interpretativa, que permitió caracterizar y jerarquizar el nivel de razonamiento geométrico que han adquirido los estudiantes en su formación geométrica.

Mostramos a continuación los métodos e instrumentos utilizados en el análisis al igual que la muestra de estudio.

 

3.1. Métodos e instrumentos de análisis

Para el análisis de las respuestas de los estudiantes en cada ítem, se consideraron los 4 niveles de Van- Hiele (Tabla II) y los atributos distintivos en los procesos de razonamiento (Tabla I). Para la construcción del instrumento de diagnóstico, que consta de diez ítems, se diseñó una matriz que articula los niveles que abarca cada ítem con los temas geométricos y los procesos evaluativos (Tabla IV). A partir del texto de geometría clásico de Omer Cano (1944) y los textos entregados por el Ministerio de Educación a los establecimientos públicos, ocho de los problemas fueron diseñados, modificados y estructurados por los investigadores, ya que los problemas presentados en estos textos no respondían al modelo propuesto ni a los procesos de razonamiento y dos de ellos tomados del test de Jaime (1993). La matriz que se presenta en la tabla IV y el test fueron validados mediante la triangulación de jueces expertos y para la fiabilidad del instrumento se utilizó el Alfa de Cronbach. Las temáticas abordadas fueron las que están en los planes de estudio desde sexto año de Educación General Básica hasta el segundo año de Educación Secundaria.

 

3.1.1. Criterios para la codificación

Para categorizar y jerarquizar el razonamiento geométrico y los grados de adquisición, se tomó como referencia la propuesta de Jaime (1993), donde relaciona el tipo de respuesta del alumno desde el punto de vista del conocimiento matemático (escala de 1 a 7), el peso en porcentaje de dicha respuesta (escala de 0 a 100) y la relación entre la precisión matemática y la consolidación de los niveles, lo que se muestra en la Tabla V.

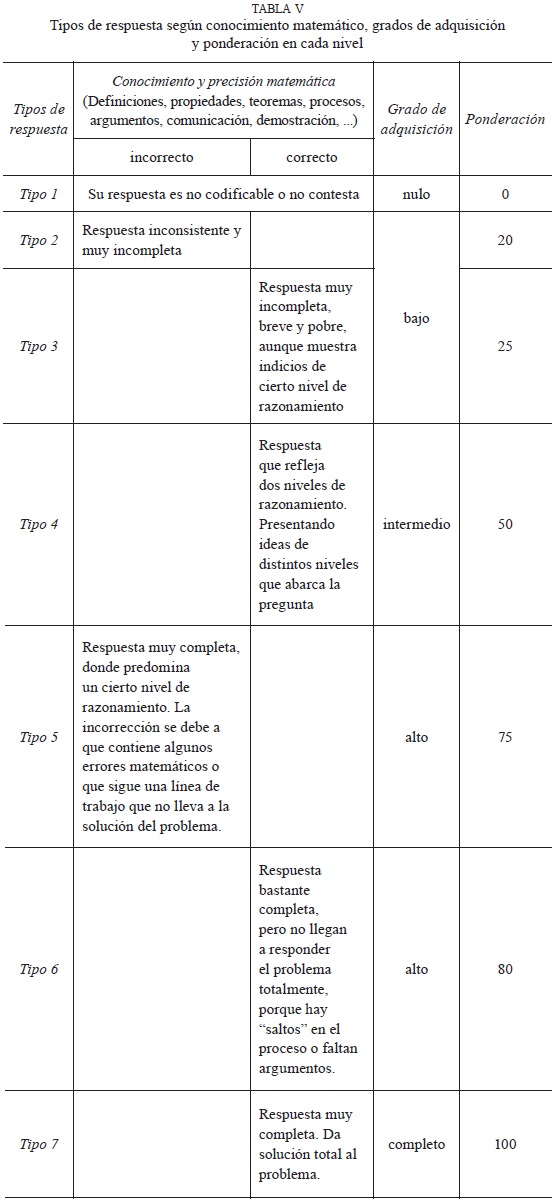
En la tabla VI, mostramos cómo se utilizaron los criterios para reconocer los grados de adquisición alcanzados por el alumnado. Para cada uno de los ítems, la matriz incorpora a los atributos, el nivel de razonamiento en que se ubica la respuesta, el tipo de respuesta considerando la justificación matemática, la idea de respuesta esperada y el grado de adquisición alcanzado. Presentamos sólo los grados de adquisición alto y completo, en cada uno de los ítems, que son base de ejemplificación en la presentación de los resultados y análisis. Para los otros grados se siguió la misma metodología considerando lo explicitado en la tabla V.

 

3.2. Población y muestra

La población corresponde a los alumnos de los segundos años medios de la educación secundaria de establecimientos municipalizados de la Región del Maule, pertenecientes al área científico humanista de procedencia urbana, de nivel socioeconómico medio, medio bajo y bajo, con un índice de vulnerabilidad promedio de 85%. Para la selección de la muestra, se utilizó la técnica de muestreo por conglomerado y para su diseño se realizó un mapeo de manera de analizar las comunas donde se concentran los establecimientos. Posteriormente, se hizo la selección con arranque aleatorio y afijación proporcional, quedando la muestra constituida de 18 cursos (de un total de 27 que cumplían con las características señaladas) que corresponden a 625 alumnos. El tamaño de la muestra se estimó considerando un nivel de confianza del 95% y un error de estimación del 5%. En la tabla VII, se puede observar la muestra efectiva.

 

4. Resultados y análisis.

Niveles de razonamiento y grados de adquisición

El siguiente capítulo presenta los resultados y análisis del diagnóstico que comprende un análisis de fiabilidad mediante el alfa de Cronbach, un estudio de los niveles de razonamiento alcanzados y la caracterización de la muestra de alumnos de la Región del Maule.

 

4.1. Análisis de fiabilidad

El análisis permitió determinar el grado en que los ítems se relacionan entre sí, obtener un índice global de la replicabilidad o de la consistencia interna de la escala en su conjunto e identificar elementos problemáticos que deberían ser excluidos de la escala. Considerando el análisis de fiabilidad, las escalas utilizadas serían fiables pues su coeficiente es superior a 0.70 tal como se observa en la tabla VIII.

 

4.2. Grados de Adquisición y Nivel de Razonamiento. Estudio del tipo de respuesta

En esta sección se presentan los resultados y análisis de los niveles de razonamiento y grados de adquisición alcanzados por los alumnos de acuerdo con sus respuestas en los diferentes ítems. De los diez ítems se han seleccionado para este reporte aquellos que son representativos respecto de los niveles que abarcaba cada uno de ellos, de acuerdo con lo explicitado en la tabla IV.

 

4.2.1. Niveles de respuestas que abarca el ítem: NI a N2

Para mostrar el nivel de razonamiento y los grados de adquisición alcanzados por el alumnado, se ha elegido como base el ítem 3 que se refiere a las propiedades de los cuadriláteros.

Ítem 3. En este ítem, que se muestra en la figura 1, los procesos distintivos corresponden a: reconocimiento, uso de definiciones y clasificación de definiciones.

(1) Niveles de razonamiento. Respecto del reconocimiento de las propiedades del rombo, sobre el 65% ubicó sus respuestas en el nivel 1, lo que demuestra que el alumnado no reconoce las propiedades matemáticas de esta figura geométrica y la clasificación que realiza de ella está referida a listar atributos físicos de la figura. En el nivel 2 de análisis, alrededor del 11% del alumnado reconoce propiedades matemáticas, utiliza algunas definiciones y las clasifica con atributos matemáticos. En la tabla IX, se observan los porcentajes en cada nivel.

(2) Grados de adquisición. En el caso del análisis conjunto entre el nivel de razonamiento y el grado de adquisición, se muestra en la tabla X que la mayoría del alumnado que ubica sus respuestas en un nivel 1 posee un grado de adquisición bajo (70%). Lo mismo ocurre para el nivel 2 de análisis (67%).

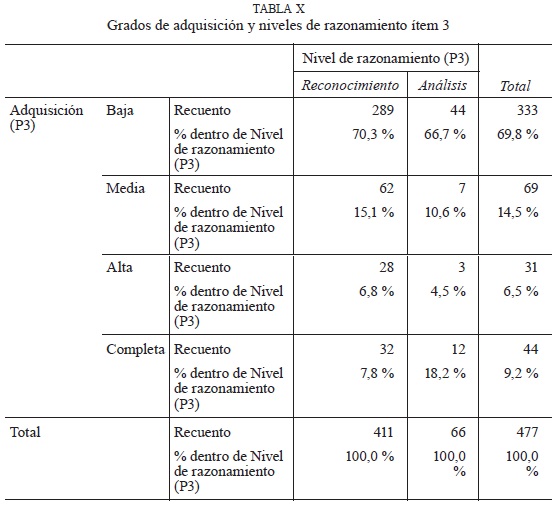
En la tabla anterior se observa que, de 411 alumnos que ubicaron sus respuestas en el nivel 1, alrededor del 70% posee un grado de adquisición bajo en los procesos de razonamiento. Hay un escaso porcentaje de alumnos que posee un grado de adquisición alto o completo, lo que llama la atención, ya que el nivel 1 es el más básico en los niveles de razonamiento y en ese nivel el grado de adquisición alto y completo significa haber reconocido atributos físicos o listar propiedades físicas de las figuras geométricas en forma correcta, como en este caso debían explicitar: "cuadrilátero de lados iguales, no todos los ángulos son iguales, tiene dos diagonales, lados opuestos paralelos".

Respecto de los que ubicaron su respuesta en el nivel 2, más del 66% se concentra en el grado de adquisición bajo, es decir, sus respuestas están matemáticamente erradas o sus respuestas son muy breves y pobres sin justificación o argumentación.

Lo anterior coloca en evidencia que éstos no reconocen las propiedades que posee un rombo, así como tampoco clasifica dentro de los cuadriláteros los atributos matemáticos que posee esta figura (tabla VI). La mayor parte del alumnado reconoce como propiedad tener cuatro lados y que los lados opuestos son paralelos. La mayor dificultad está en reconocer propiedades exclusivas del rombo, tales como que sus diagonales son perpendiculares o que son bisectrices.

Una de las dificultades para reconocer las propiedades exclusivas del rombo es la confusión que los alumnos presentan con respecto a esta figura, confundiéndola con el cuadrado en posición no estándar. En este aspecto coincidimos con Jaime, Chapa y Gutiérrez (1992) cuando plantea que para superar esta dificultad se debe recurrir a los ejemplos y contraejemplos que ayuden a incidir en la condición del cuadrado y del rombo, que de acuerdo a las teorías de Van Hiele y Vinner, un estudiante comienza a construir su imagen mental de un concepto de manera global a partir de ejemplos concretos.

En la figura 2, se puede observar la distribución del alumnado con sus respectivos grados de adquisición en cada uno de los niveles.

 

4.2.2. Niveles de respuestas que abarca el ítem: N2 a N3

Se ha considerado el ítem 4, por la importancia que presenta esta pregunta, ya que permite analizar cómo el alumno asocia las figuras geométricas con las propiedades matemáticas.

Los procesos de razonamiento corresponden a: reconocimiento y descripción de propiedades; utilización de definiciones y demostración empírica o informal.

Item 4. En este ítem, se pedía que el alumnado dibujara un polígono que cumpliera con las condiciones pedidas en los tres casos que abordaba, lo que se observa en la figura 3.

(1) Nivel de razonamiento. En la tabla XI, se observa que alrededor del 56% ubicó su respuesta en el nivel de análisis, siendo despreciable el porcentaje de alumnos que se ubican en el nivel 3. Respecto a demostrar informalmente, no hay ningún alumno que realice este proceso.

(2) Grados de adquisición. Sobre los grados de adquisición en el razonamiento geométrico, para cada uno de los niveles, se observa en la Tabla XII que la mayoría del alumnado que concentró su respuesta en el nivel 2 presenta un grado de adquisición bajo, sobrepasando el 85%.

Los alumnos que se ubican con un grado de adquisición bajo presentan dificultades en la identificación de los polígonos que cumplen con ciertas propiedades ya que sus respuestas están erradas desde el punto de vista matemático o dan respuestas muy breves y pobres, sin justificación. No reconocen las definiciones básicas de las figuras geométricas, tampoco logran una asociación entre los polígonos y las propiedades que estos poseen. Las justificaciones, respecto de las condiciones pedidas, son escasas o erradas.

En el caso de este ítem, para alcanzar un alto grado de adquisición o grado de adquisición completo en el nivel 2, se esperaba que los alumnos movilizaran los conocimientos matemáticos y representaciones de acuerdo con las condiciones del problema. Para el caso 1, no identifican que puede ser un rectángulo o un hexágono, que cumplía con dos propiedades de la lista y no cumplía con las otras dos (figura 3). Para el caso 2, no logran explicitar que era imposible encontrar un polígono que cumpliera con las condiciones pedidas y en el caso 3, también les es difícil identificar el cuadrado o rombo que cumple con las cuatro propiedades que se le presentaban en la lista (tabla VI). Se puede concluir que el grupo de alumnos posee escaso conocimiento de las propiedades geométricas de los polígonos, así como una falta de capacidad para argumentar, establecer condiciones y restricciones de acuerdo con problema.

En la figura 4, se observa la distribución del grupo respecto de los grados de adquisición en cada uno de los niveles.

 

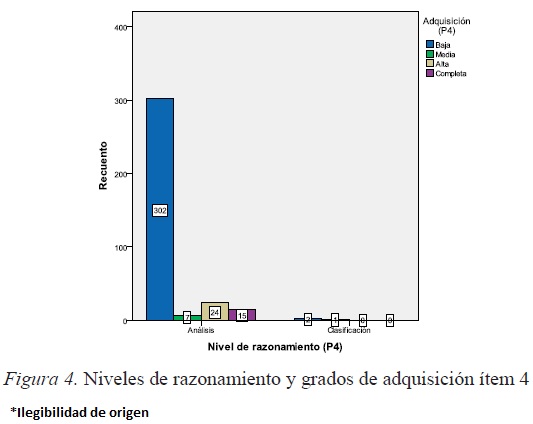
4.2.3. Niveles de respuestas que abarca cada ítem: N2 al N4

Para analizar las respuestas del alumnado se ha considerado los ítems 2 y 6. En ambos debían conjeturar y realizar la demostración. Las investigaciones reportan que este tipo de problemas presenta serias dificultades para el alumnado de este nivel, lo que se comprueba en esta muestra de alumnos. En esta línea, varios son los estudios que distinguen diferentes dimensiones y han buscado estrategias que les permita, a los alumnos, ir comprendiendo el proceso de demostración. (De Villiers, 1993; Harel & Sowder, 1998; Ibañes & Ortega, 2004). En este caso se aborda desde la concepción de Van-Hiele, donde se espera para el nivel 2 la verificación con ejemplos o demostración empírica; para el nivel 3, una demostración lógica informal con palabras y símbolos y para el nivel 4, demostración matemática formal.

Item 2. En el ítem que se presenta en la figura 5, el alumnado debía calcular el número de diagonales de diferentes polígonos, establecer la conjetura y demostrar para un polígono de n lados. Los procesos distintivos son: uso de definiciones y demostración.

(1) Niveles de razonamiento. Los resultados que se presentan en la Tabla XIII, muestran que de los 625 alumnos alrededor del 72% se concentra en el nivel 2, que era lo mínimo en que se podía contesar. Ningún alumno ubicó su respuesta en un nivel de razonamiento superior, que corresponde a clasificación y deducción formal.

(2) Grados de adquisición. En la Tabla XIV se observa que de un total de 454 alumnos cuyas respuestas se ubicaron en el nivel 2, alrededor del 90% se ubica en un grado de adquisición bajo, es decir, la mayoría de ellos no es capaz de usar la definición de diagonales de un polígono, con estructura simple, como tampoco dar una demostración empírica. Sus respuestas son matemáticamente incorrectas o muy incompletas. Los porcentajes para los otros grados de adquisición son despreciables.

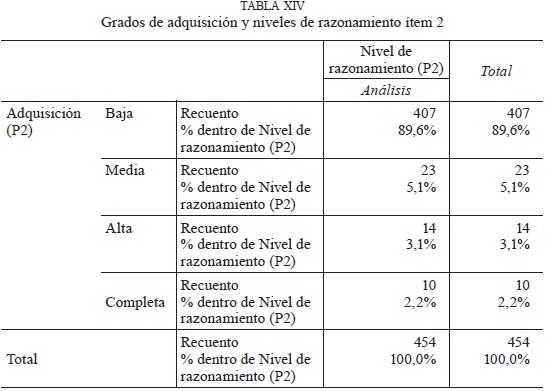
En la tabla anterior, se puede visualizar que la mayoría del alumnado que se ubica en un grado de adquisición bajo presenta dificultades para establecer algún método para encontrar el número de diagonales de los polígonos de tal forma de extraer alguna regularidad. Tal como se explicitó en la tabla VI, para alcanzar un alto grado de adquisición en el nivel 2, se requiere que el alumno realice un dibujo y trace las diagonales de diferentes polígonos, para establecer la conjetura para uno de n lados. Para el nivel 3, se espera que determine la conjetura y realice la demostración informal argumentando cómo llegó a la generalización y en el nivel 4, debe establecer hipótesis y tesis y demostrar formalmente, lo que le permitía ubicarse en un alto grado de adquisición en ambos casos, pero ningún alumno pudo ubicar su respuesta en esos niveles.

Los resultados obtenidos ponen de manifiesto que el alumnado no es capaz de plantear un enunciado general a partir de casos particulares que les lleve a un proceso de demostración, aunque ésta se desarrolle de manera lógica informal. Conjeturar y realizar demostraciones es muy importante en el aprendizaje de la geometría, por lo que coincidimos con las propuestas de Gutiérrez y Jaime (1998) quienes plantean que este tipo de actividad desarrolla el pensamiento lógico deductivo. Además De Villiers (1993) coloca de manifiesto que las demostraciones ocupan un lugar central en la actividad matemática, ya que constituye el método de validación de las afirmaciones.

En la figura 6, se observa la distribución del grupo respecto de los grados de adquisición alcanzados en el nivel 2.

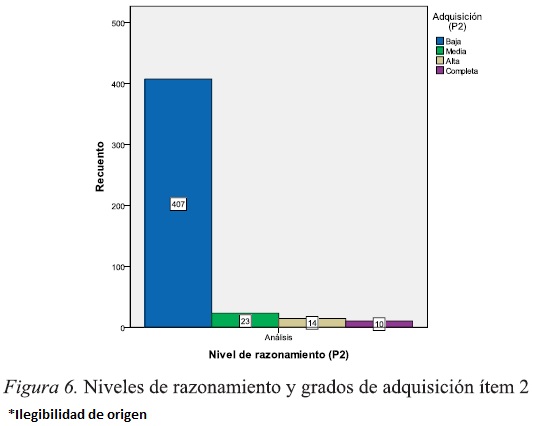
Ítem 6. En el ítem que se presenta en la figura 7 se pedía identificar el cuadrilátero que se formaba al unir los diámetros en la circunferencia y demostrar matemáticamente. Los atributos distintivos corresponden a: reconocimiento, uso de definiciones, clasificación de definiciones y demostración.

(1) Niveles de razonamiento. En la tabla XV se observa que de los 625 alumnos sólo el 67% ubicaron su respuesta en el nivel 2.

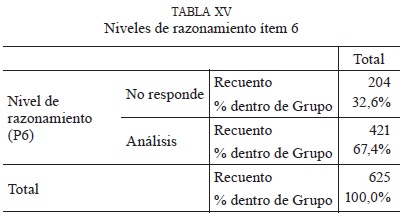
(2) Grados de adquisición. De los 421 alumnos que ubicaron sus respuestas en el nivel 2, alrededor de un 92% se concentra en un grado de adquisición bajo, es decir, sus respuestas son matemáticamente incorrectas o muy incompletas. En los otros grados de adquisición, los porcentajes son despreciables, como se observa en la tabla XVI.

La mayor dificultad del alumnado fue comprender las condiciones del problema que les permitía ubicar los diámetros para formar el cuadrilátero (figura 7), patrón que se detectó en la mayoría del alumnado. Asimismo, aquellos que lograron identificar el cuadrado o rectángulo, aseguraban que esa era la figura que se formaba, aceptando la veracidad de su afirmación "porque así se lo habían enseñado" y aquellos que trataban de realizar una demostración empírica, no lograron desarrollar algún proceso que les permita validar o probar sus afirmaciones, para ubicarse en un alto grado de adquisición. En este sentido, De Villiers (1991) manifiesta que los estudiantes aceptan la veracidad de una afirmación a partir de una fuente de convicción, muchas veces externa, y Gutiérrez (2006) recomienda que es necesario que los profesores planteen problemas y conjeturas que resulten ser parcialmente falsas, para que los alumnos empiecen a comprender la necesidad de las demostraciones. Otra dificultad, se refiere al escaso lenguaje que poseen para argumentar o explicar los procesos seguidos.

En la figura 8 se observa la distribución del alumnado en el nivel 2 con sus grados de adquisición.

A modo de resumen, en la figura 9 se muestran los grados de adquisición alcanzados en promedio por el alumnado en todos los ítems del test, donde se observa que se concentran con un grado de adquisición bajo en cada uno de los niveles de razonamiento.

 

5. Conclusiones e implicaciones didácticas

Con base en los resultados y análisis se ha caracterizado y jerarquizado al alumnado en el trabajo geométrico. De los ítems que abarcaban desde el nivel 1 al 2, la mayoría concentró su respuesta en el nivel 1 con un grado de adquisición bajo. Lo mismo ocurre para los ítems que abarcaban desde el nivel 2 al nivel 4. No hay ningún alumno que haya alcanzado un nivel 3 de razonamiento en un grado de adquisición alto y en cuanto al nivel 4, coincidimos con las investigaciones que dan cuenta que en este nivel los estudiantes no logran seguir una secuencia lógica aunque sea mediante un proceso discursivo natural.

 

5.1. Dificultades y obstáculos detectados en el diagnóstico

Respecto al reconocimiento y descripción de las figuras geométricas, se ha detectado una serie de dificultades y obstáculos que pone en evidencia que el alumnado, en un alto porcentaje, identifica atributos físicos de las figuras geométricas, pero desconoce las propiedades matemáticas de éstas de acuerdo con Gutiérrez y otros (2004).

Sobre el uso de definiciones y clasificación, los resultados son más desfavorables, ya que el alumnado no es capaz de reconocer que las figuras geométricas están dotadas de propiedades. Respecto de formular una definición, entregan una lista de atributos físicos de las figuras, tales como: lados, ángulos, tamaño y forma. Fortuny y Giménez (1998) plantean que la dificultad en la identificación de propiedades proviene de haber realizado un proceso memorístico más que comprensivo, validando así la hipótesis 1.

Uno de los mayores obstáculos es establecer generalizaciones y conjeturas. Este hecho les dificulta intentar alguna demostración, aunque sea de manera empírica o informal. El escaso porcentaje del alumnado que intentó realizar alguna demostración, mostró dificultades, incluso al verificar con ejemplos su veracidad y aquellos que lo intentaron mediante alguna explicación, presentaban inconsistencias en los procesos lógicos, lo que permite validar la hipótesis 2.

Se detecta, además, dificultades en los procesos de argumentación, elemento que era transversal en el diagnóstico, especialmente por el escaso dominio de un lenguaje geométrico.

Sobre los grados de adquisición se detecta el mismo patrón, el cual consiste en que el alumnado que concentra sus respuestas en el nivel 1 y 2 de razonamiento, se encuentra en un grado de adquisición bajo. Lo anterior es consistente con investigaciones que dan cuenta que un número significativo de alumnos de segundo año de secundaria siguen operando en el nivel 1 de razonamiento, lo que permite validar la hipótesis general.

Por último, aunque no es posible establecer generalizaciones a nivel nacional, podemos conjeturar que en diferentes regiones y condiciones similares, se obtienen los mismos resultados que en este estudio, por lo que sería de suma importancia implementar el diagnóstico para darle mayor validez.

 

5.2. Implicaciones didácticas

Con base en lo descrito en la sección anterior, reparamos que hay algunas sugerencias para generar un cambio en el proceso de enseñanza y aprendizaje de la geometría, que permita revertir los bajos niveles de razonamiento que presentan los alumnos vulnerables de la región: en primer lugar, resulta pertinente que en los procesos de aprendizaje se trabajen problemas del tipo que hemos planteado en este estudio, donde se considera la visualización, la intuición geométrica, la formulación de hipótesis, análisis de propiedades, de regularidades y formulación de conjeturas para avanzar hacia una comprensión y sentido de los procesos de demostración.

También resulta de interés cambiar los métodos tradicionales de enseñanza, especialmente en la formación inicial de profesores, fomentando la resolución de problemas con una, varias o ninguna solución, utilizar metodologías más eficientes como son, por ejemplo, los procesos de modelización. Se requiere también apoyar las diferentes formas de pensar del alumnado para que vayan organizando su estructura conceptual y busquen un método que les permita un aprendizaje comprensivo y relacional, esto se logra permitiendo mayores espacios de autonomía e independencia en el quehacer matemático. Los resultados descritos, han puesto en evidencia la necesidad de fomentar la comunicación matemática, para ir avanzando hacia la adquisición de un lenguaje matemático y a la argumentación de los hechos geométricos.

Finalmente, creemos que es necesario que las universidades establezcan una mayor vinculación con los establecimientos más vulnerables mediante una retroalimentación permanente, generando convenios para trabajar en seminarios de perfeccionamiento o propuestas de trabajo en conjunto para ir incorporando nuevos métodos y modelos de enseñanza y razonamiento en diferentes temas de matemática de tal manera que podamos avanzar hacia una mayor equidad e igualdad de oportunidades con los alumnos del sistema público.

 

Agradecimientos

La investigación es financiada por el Fondo Nacional de Desarrollo Científico y Tecnológico FONDECYT 1090617 (marzo de 2009 marzo de 2012) Comisión Nacional de Investigación Científica y Tecnológica Chile.

Agradecemos la colaboración del Dr. Ángel Gutiérrez R. de la Universidad de Valencia, España.

Realizó una estadía en Chile, en el marco del Proyecto a la Cooperación Internacional financiado por la Comisión Nacional de Investigación Científica y Tecnológica, CONICYT.

Nos apoyó en la discusión teórica del modelo, en la construcción de los instrumentos y métodos de análisis.

Y a los investigadores: Dra. Adela Jaime P, Universidad de Valencia, Dr. Joaquín Giménez R., Universidad de Barcelona, y Dr. Miguel Friz C., Universidad del Bío-Bío, Chile, por la revisión y validación de los instrumentos, al Ingeniero Estadístico y Master Marcelo Rodriguez G., por su apoyo técnico en la investigación.

 

Referencias bibliográficas

Aravena, M; Caamaño, C; Cabezas, C. (2007). Doblado de papel en el primer nivel de razonamiento del Modelo Didáctico de Van-Hiele y su proyección hacia la formalización del pensamiento geométrico. Revista Chilena de Educación Matemática 2(1), 76-88.         [ Links ]

Aravena, M.; Caamaño, C.; Giménez, J. (2008). Modelos matemáticos a través de proyectos. Revista Latinoamericana de Investigación en Matemática Educativa 11(1), 49-92.         [ Links ]

Aravena, M.; Caamaño, C.; González, J.; Cabezas, C.; Córdova, F. (2011). Resolución de problemas en contextos de aplicación. Propuesta Metodológica en la Formación Inicial de Profesores de Matemática. Talca: Tabor        [ Links ]

Bishop, A. J. (1989). Review of Research on Visualization in Mathematics Education. Focus on Learning Problems in Mathematics 11(1-2), 7-16.         [ Links ]

Burger, W. F.; Shaughnessy, J. M. (1986). Characterizing the Van Hiele levels of development in geometry. Journal for Research in Mathematics Educations 17 (1), 31-48.         [ Links ]

Blanco, L; Barrantes, M. (2003). Concepciones de los estudiantes para maestro en España sobre la geometría escolar y su enseñanza - aprendizaje. Revista Latinoamericana de Matemática Educativa 6(2), 107-132.         [ Links ]

Cano, O. (1944). Geometría. Monografía. España: La Salle.         [ Links ]

Cantoral, R. (1995). Acerca de las contribuciones actuales de una didáctica de antaño: el caso de la serie de Taylor. Mathesis 11(1), 55-101.         [ Links ]

Clements, D.H.; Battista, M.T. (1992). Geometry and Spatial Reasoning. In D. A. Grouws (Ed.) (1992), Handbook of Research on Mathematics Teaching and Learning (pp. 420-464). Nueva York: MacMillan Publishing.         [ Links ]

De Villiers M (1991). Pupils' needs for conviction and explanations within the context of geometry. Pythagoras 26, 18-27.         [ Links ]

De Villiers, M. (1993). El papel y la función de la demostración en matemáticas. Epsilon 26, 15-30.         [ Links ]

Duval, R. (1998). Geometry from a cognitive point of view. In C. Mammana & V.Villani (Eds.), Perspective on the Teaching of the Geometry for the 21 Century (pp. 37-51). Netherlands: Kluwer Academic Publishers.         [ Links ]

Fortuny, J.M.; Giménez, J. (1998). Geometría: La forma y las transformaciones geométricas. Barcelona. Autores.         [ Links ]

Fuys D., Geddes D, Lovett J.; Tischler, R. (1988). The Van Hiele model of thinking in geometry among adolescents. Journal for Research in Mathematics Education. Monograph 3.         [ Links ]

Gómez, B. (2000). Los libros de texto de Matemáticas. Números 43-44, 77-80.         [ Links ]

Guillén, G. (1996). Identification of Van Hiele Levels of Reasoning in Three-Dimensional Geometry. In L. Puig & A. Gutiérrez (Eds.), Proceedings of the 20^th International Conference of the Psychology for Mathematics Education (pp. 43-50). Valéncia: Universitat de Valéncia.         [ Links ]

Gutierrez, A.; Pegg, J.; Lawrie, C. (2004). Characterization of students' reasoning and proof abilities in 3-dimensional geometry. Proceedings of the 28^th International Conference of the Psychology for Mathematics Education (Vol. 2, pp. 511-518). Bergen: Bergen University College.         [ Links ]

Gutiérrez, A.; Jaime, A. (1998). On the assessment of the Van Hiele levels of reasoning. Focus on Learning Problems in Mathematics. Special Issue Elements of Geometry in the Learning of Mathematics 20(2-3), 27-46.         [ Links ]

Gutiérrez, A.; Jaime, A.; Fortuny, J. M. (1991). An alternative paradigm to evaluate the acquisition of the Van Hiele levels. Journal for Research in Mathematics Education 22(3), 237-251.         [ Links ]

Gutiérrez, A. (2006). La investigación sobre enseñanza y aprendizaje de la geometría. En Ricardo Luengo y Antonio Marín (Eds.) Geometría para el siglo XXI (pp.13-58) España: FESPM y SAEM Thales.         [ Links ]

Gray, E. (1999). Spatial strategies and visualization. In O. Zaslavsky (Ed.), Proceedings of the 23^rd International Conference of the Psychology for Mathematics Education (Vol.1, pp. 235-242) Haifa, Israel: University of Technion.         [ Links ]

Harel, G.: Sowder, L. (1998). Students' Proof Schemes: Results from exploratory studies. In E. Dubinski; A. Schoenfeld & J. Kaput (Eds.), Research on Collegiate Mathematics Education (Vol. 7, pp. 234-283). USA: American Mathematical Society.         [ Links ]

Hershkowitz, R.; Bruckheimer, M.; Vinner, S. (1987). Activities with Teachers Based on Cognitive Research. In M. Lindquist & A. Shulte (Eds.), Learning and Teaching Geometry, K-12. 1987 Yearbook (pp. 223-235). Reston-VA: The National Council of Teachers of Mathematics.         [ Links ]

Hershkowitz, R. (1990). Psychological Aspects of Learning Geometry. In P. Nesher & J. Kilpatrick (Eds.), Mathematics and cognition: A research synthesis by the International Group for the Psychology of Mathematics Education (pp. 70-95). Cambridge: Cambridge University Press.         [ Links ]

Ibañes M.; Ortega T. (2004). Origen, nudo y desenlace de una investigación sobre los Esquemas de Prueba. Aspectos Cognitivos. (Eds.), Líneas de Investigación en Educación Matemática (pp. 21-57). Badajoz: Sociedad Extremeña de Educación Matemática.         [ Links ]

Jaime, A. (1993): Aportaciones a la interpretación y aplicación del modelo de Van Hiele: La enseñanza de las isometrías del plano. La evaluación del nivel de razonamiento. (Tesis doctoral).Universidad de Valencia. Valencia. España Recuperado el 10 de marzo de 2008 de: http://www.uv.es/gutierre/archivos1/textospdf/Jai93.pdf        [ Links ]

Jaime, A.; Chapa, F.; Gutiérrez, A. (1992). Definiciones de triángulos y cuadriláteros: Errores e inconsistencias en libros de E.G.B. Revista Epsilon 23, 49-62.         [ Links ]

Jaime, A.; Gutiérrez, A. (1996). El Grupo de las Isometrías del Plano. Madrid: Síntesis.         [ Links ]

Latorre M. (2004). Aportes para el análisis de las racionalidades presentes en las prácticas pedagógicas. Estudios pedagógicos (Valdivia), (30), 75-91.         [ Links ]

Lawrie, C.; Pegg, J. & Gutierrez, A. ( 2000). Coding the nature of thinking displayed in responses on nets of solids, In. Nakahara & M Kayama (Eds) Proceedings of the 24^th International Conference of the Psychology for Mathematics Education ( Vol. 3, pp. 215- 222). Hiroshima: Hiroshima University.         [ Links ]

Lawrie, C.; Pegg, J. & Gutierrez, A. ( 2002). Unpacking students meaning of cross - sections: A frame for curriculum development, In Cockburn, A.D.; Nardi, E. (Eds.), Proceedings of the 26^th International Conference of the Psychology for Mathematics Education (Vol. 3, pp. 289- 296). Norwich UK: University of East Anglie.         [ Links ]

OCDE (2004). Informe Revisión de Políticas nacionales de educación. Chile Recuperado de http://www.scribd.com/doc/19341515/OCDE-Informe-Chile-2004        [ Links ]

OCDE y BIRD/Banco Mundial (2009). La Educación Superior en Chile. Revisión de Políticas Nacionales de Educación. Recuperado de: http://www.oecd-ilibrary.org/education/la-educacion-superior-en-chile_9789264054189-es        [ Links ]

Owens, K. (1999). The role of visualization in young students' learning, In O. Zaslavsky (Ed.), Proceedings of the 23^rd International Conference of the Psychology for Mathematics Education (Vol. 1, pp. 220-234). Haifa, Israel: University of Technion.         [ Links ]

PISA (2000). Competencias para la vida. Resultados de los estudiantes chilenos. PISA 2000. Recuperado el 15 de marzo de 2008 de http://www.simce.cl/fileadmin/Documentos_y_archivos_SIMCE/evaluaciones_inter/pisa_2000/informe_CHILE_PISA_2000.pdf)        [ Links ]

PISA (2006) The Programme for International Student Assessment. Recuperado el 15 de Marzo de 2008 de http://www.pisa.oecd.org/dataoecd/15/13/39725224.pdf        [ Links ]

PISA (2009). Resumen de Resultados. Unidad de Curriculum y Evaluación. Ministerio de Educación de Chile. Recuperado de: http://www.educacion2020.cl/sites/default/files/resumen_resultados_pisa_2009_chile.pdf        [ Links ]

Presmeg, N. C. (1986). Visualisation in high school mathematics. For the Learning of Mathematics 6(3), 42-46.         [ Links ]

Presmeg, N. (2006). Research on visualization in learning and teaching mathematics. In A. Gutiérrez & P. Boero (Eds.), Handbook of Research on the Psychology of Mathematics Education (pp. 210-213). UK: Sense Publishers.         [ Links ]

SIMCE (2003). Prueba SIMCE 2° Medio 2003.Análisis de Resultados. Recuperado el 20 de Septiembre de 2006 de http://www.biblioteca.mineduc.cl/documento/Informe_2_Medio_2003.pdf        [ Links ]

SIMCE (2006). Resultados Nacionales SIMCE. Recuperado el 10 de Junio de 2008 de http://www.simce.cl/fileadmin/Documentos_y_archivos_SIMCE/informe_resultados/Informe_nacional.pdf        [ Links ]

SIMCE (2010). Resultados Nacionales SIMCE. Recuperado el 15 de Noviembre de 2011, de http://www.agenciaeducacion.cl/wp-content/files_mf/informenacionalderesultadossimce2010247mb.pdf        [ Links ]

TIMSS (2003). Highlights From the Trends in International Mathematics and Science Study (TIMSS). Recuperado el 10 de Junio de 2008 de http://www.nces.ed.gov/pubs2005/2005005.pdf        [ Links ]

Usiskin, Z. (1982). Van Hiele levels and achievement in secondary school geometry. Recuperado de la base de datos: ERIC Document reproduction Service N° ED 220 288.         [ Links ]

Villalta M; Martinic S. & Guzmán M. (2011). Elementos de la interacción didáctica en la sala de clase que contribuyen al aprendizaje en contexto social vulnerable. Revista Mexicana de Investigación Educativa 16(51), 1137-1158.         [ Links ]

Vinner, S.; Hershkowitz, R. (1983). On concept formation in geometry. Zentralblatt für Didaktik der Mathematik 83(1), 20-25.         [ Links ]

Vinner, S. (1991). The Role of Definitions in the Teaching and Learning of Mathematics. In W. Zimmermann & S. Cunningham (Eds.), Advanced Mathematical Thinking. Mathematics. Education Library (pp. 65-79). Cambridge: Board.         [ Links ]

Zazkis, R.; Dubinsky, E. & Dautermann, J. (1996). Coordinating visual and analytic strategies: a student's understanding of the group D₄. Journal for Research in Mathematics Education 27(4), 435-457.         [ Links ]