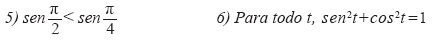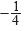Artículos

 

Generación interactiva del conocimiento para iniciarse en el manejo de implicaciones lógicas

 

Interactive construction of knowledge to start up applying the logical implications

 

Angélica Alvarado Monroy*, M^a Teresa González Astudillo**

 

* Universidad Juárez del Estado de Durango, México. aalvarado@usal.es.

** Universidad de Salamanca, España. maite@usal.es.

 

Resumen

La habilidad en el manejo de implicaciones lógicas es imprescindible para que los futuros matemáticos sean capaces de construir demostraciones. A pesar de su importancia, los estudiantes tienen grandes dificultades con esta tarea. En este artículo se presenta una investigación en la cual estudiantes universitarios realizaron tareas para la definición del concepto de proposición matemática (concretamente implicaciones lógicas), identificación de enunciados de este tipo, reconocimiento de sus componentes y de la función asociada al proceso de demostración. La construcción del concepto se generó en discusiones en pequeños grupos y en gran grupo guiadas por el profesor. Ambas fueron grabadas en su totalidad y analizadas con el modelo RBC-C (Schwarz, Dreyfus & Hershkowitz, 2009) para documentar cómo ocurre el proceso de construcción.

Palabras clave: Demostración, Interacción, Construcción social del conocimiento.

 

Abstract

The ability to apply the logical implications is essential for future mathematicians to develop demonstrations. Although its importance, students have a hard time putting this into practice. This article is about a research that shows college students performing some tasks, so they could come up with a definition of the mathematical preposition concept (especially the logical implication), the identification of these kinds of statement and its components, as well as its function associated with the demonstration process. The development of this concept was the result of small-group discussions, and then a final discussion with the whole group led by the teacher. Both were fully recorded and fully analysed with the RBC+C model (Schwarz, Dreyfus & Hershkowitz, 2009) in order to document this construction process.

Key words: Demonstration, Interaction, Construction of knowledge.

 

Resumo

A habilidade no tratamiento de implicações lógicas é imprescindível para que os futuros matemáticos sejam capazes de construir demonstrações. Apesar de sua importancia, os estudantes têm grandes dificuldades com esta tarefa. Neste artigo, apresenta-se uma pesquisa na qual estudantes universitários realizaram tarefas para a definição do conceito de proposição matemática (concretamente, implicações lógicas), identificação de enunciados deste tipo, reconhecimento de seus componentes e da funfao associada ao processo de demonstração. A construção do conceito foi gerada em discussões em pequenos grupos e em grandes grupos guiados pelo professor. Ambas foram gravadas totalmente e analisadas com o modelo RBC-C (Schwarz, Dreyfus & Hershkowitz, 2009) para documentar como o processo de construção ocorre.

Palavras chave: Demonstração, Interação, Construção social do conhecimento.

 

Résumé

Il est indispensable de bien maîtriser les implications logiques pour que les futurs mathématiciens soient capables de construire des démonstrations. Malgré son importance, les étudiants présentent des difficultés avec cette tâche. Dans cet article on présente une recherche dans laquelle des étudiants universitaires ont fait des exercices pour définir le concept de proposition mathématique (en particulier les implications logiques), identifier les énoncés de ce genre, reconnaitre ses composants et la fonction associée au procès de démonstration. La construction du concept fut générée au milieu des discussions dans des petits groupes et dans le groupe entier par le professeur. Les deux discussions ont été enregistrées complètement et analysées selon le modèle RBC-C (Schwarz, Dreyfus & Hershkowitz, 2009) à fin de documenter comment le procès de construction a lieu.

Mots clés: Démonstration, Interaction, Construction social des connaissances.

 

1. Introducción

Una de las principales actividades en Matemáticas es la de demostrar, es decir, a partir de un conjunto de afirmaciones iniciales se deducen, mediante reglas de razonamiento aceptadas por la comunidad de práctica, proposiciones o enunciados más complejos.

Sin embargo, en los últimos años, se ha desterrado del currículo escolar la práctica de la demostración: "La idea de demostración ha variado a lo largo del tiempo; depende del contexto y del entorno cultural. Desde el desarrollo de la matemática moderna que ponía un exagerado énfasis en la demostración formal, se ha producido un declive en su uso en la secundaria, esto tiene fuertes consecuencias en la transición a la universidad" (Gómez-Chacón, 2009).

Stylianides & Ball (2008) distinguen tres elementos involucrados en el manejo de las demostraciones: el primero es el relativo al conocimiento matemático necesario para realizar una demostración, el segundo se refiere al propio uso del lenguaje matemático y el tercero a la distinción entre las formas deducción empíricas y las deductivas. Sin embargo, dichos investigadores en sus investigaciones con profesores han mostrado que tienen un conocimiento débil acerca de la estructura lógico-lingüística de la demostración así como una inadecuada preparación para organizar actividades de demostración en el aula. Estos resultados también reflejan las ideas falsas que tienen los estudiantes, por ejemplo, consideran que los argumentos empíricos prueban y los deductivos no son suficientes para demostrar. Uno de los aspectos importantes en ese proceso de demostración es la precisión del lenguaje matemático, esto implica darse cuenta de cómo se presentan los argumentos matemáticos y cómo se definen los conceptos matemáticos (Vinner, 1991; Mariotti & Fischbein, 1997). Indiscutiblemente, estos elementos se relacionan con las formas de representar los argumentos y con el conjunto de enunciados aceptados (Stylianides & Ball, 2008). El desarrollo de la potencia matemática de un estudiante implica el aprendizaje de signos, símbolos y terminología inherente a la matemática. Esto se consigue fundamentalmente en situaciones donde se ofrece a los alumnos la oportunidad de leer, escribir y discutir ideas para las cuales el uso del lenguaje matemático resulte natural: "A medida que se comunican sus ideas aprenden a clarificar, refinar y consolidar su pensamiento" (Gómez-Chacón, 2009, p. 18).

Además, entre otras dificultades que los estudiantes enfrentan al tener que desarrollar una demostración, Moore (1994) señala la falta de habilidad para formular [e identificar] enunciados matemáticos, las imágenes inadecuadas que poseen de los conceptos, la ausencia de entrenamiento para generar y usar sus propios ejemplos y el poco entendimiento intuitivo de los conceptos involucrados en la demostración.

Una de las cuestiones que condicionan más la capacidad de los alumnos para demostrar es la identificada por Harel (2006), según la cual los alumnos se suelen centrar más en el significado de la proposición que en los aspectos relativos al estado. Como consecuencia, consideran muchas proposiciones matemáticas triviales al juzgarlas por su grado de verdad en lugar de su valor lógico. Además, en las implicaciones matemáticas, confunden el papel de la hipótesis y la conclusión (Dorier, Robert, Robinet & Rogalski, 2000; Ibañes & Ortega, 2003). Esto se confirmó en un estudio de caso (Alvarado & González, 2010) donde una alumna que se enfrenta con la demostración de implicaciones no admite el papel condicional de la hipótesis. En este mismo estudio se observó la falacia de afirmación del consecuente, es decir, para demostrar que p→q se utilizó como argumento que de la verdad de q se deduce p. Las justificaciones erróneas ofrecidas parten de verificar primero el consecuente y después el antecedente mediante la comprobación de casos particulares, e incluso, en algunas ocasiones, no se tuvo en cuenta el papel de la hipótesis.

El lenguaje cotidiano también representa un obstáculo para el aprendizaje de la demostración. Una implicación, en muchas ocasiones, admite diversas connotaciones de causalidad y temporalidad que hacen que su significado se aleje del sentido matemático. En otras ocasiones, el lenguaje ordinario le da un significado diferente a la implicación por la tendencia a sobreentender lo que no está dicho. En este sentido, Epp (2003) sugiere que la diferencia existente entre el lenguaje cotidiano y el matemático pueden conducir a cometer "el error de la recíproca" (de sip entonces q y q, deducen p), la dificultad para aceptar que p sólo si q es lógicamente equivalente a si p entonces q, la dificultad en la interpretación de proposiciones cuantificadas y a cometer errores al tratar de negar implicaciones. Además, cuando los alumnos trabajan en un ambiente matemático, las maneras informales de expresar las negaciones de los enunciados que contienen conectores (y/o) también pueden confundirlos.

Finalmente se percibe una ausencia de conocimiento de técnicas de demostración, de cómo elegir los hechos y los teoremas que se deben aplicar o de cuándo utilizar o no un conocimiento basado exclusivamente en la manipulación simbólica y el uso de procedimientos matemáticos (Weber, 2001). La lógica y la demostración se conciben de manera separada; para evitar esto, la enseñanza debería instruir acerca de la demostración como forma de validación y acerca de la utilidad del lenguaje como necesidad para desarrollarla y comunicarla. También se deben ofrecer a los estudiantes oportunidades, mediante el aprendizaje activo, para desarrollar actitudes matemáticas que favorezcan la adquisición de pensamiento por inculturación como la actitud inductiva y la de precisión y rigor (Gómez-Chacón 2009).

 

2. Marco Conceptual

Dado que los estudiantes deben construir conocimiento matemático abstracto, consideramos que la Abstracción en Contexto (AiC por sus siglas en inglés) propuesta por Schwarz, Dreyfus y Hershkowitz (2009) nos proporciona un marco conceptual y una metodología conveniente para el análisis del aprendizaje. En AiC la abstracción se define como "una actividad vertical¹ de reorganización de constructos matemáticos previos dentro de la matemática y con significados matemáticos para conducir hacia un constructo que es nuevo para el aprendiz" (Schwarz, Dreyfus & Hershkowitz, 2009, p. 24).

Un proceso de abstracción tiene tres etapas: la necesidad de un nuevo constructo, su emergencia y su consolidación. La abstracción no ocurre sin la necesidad de un nuevo contructo; esta necesidad puede derivarse de una motivación intrínseca para vencer contradicciones, sorpresas, o incertidumbre. La segunda etapa es central y es donde emerge el nuevo constructo, en ella se observan tres acciones epistémicas: R-acciones (Recognizing), donde el aprendiz reconoce que un constructo específico previo es relevante para la situación con la que están tratando; B-acciones (Building-with), el aprendiz actúa con los constructos reconocidos para alcanzar la comprensión de una situación o la solución de un problema y C-acciones (Constructing), usando las B-acciones para encajar e integrar constructos previos por matemátización vertical para producir un nuevo constructo. La C-acción se refiere a la primera vez que el aprendiz usa o menciona un constructo. En este proceso, las R-acciones están anidadas dentro de las B-acciones, y las B-acciones están anidadas dentro de las C-acciones. Las C-acciones pueden anidarse en las C-acciones de un mayor nivel. Por último, la tercera etapa, la consolidación, es un proceso a largo plazo que se genera cuando el constructo se menciona o se utiliza después de una C-acción. Esta etapa se caracteriza por evidencia personal, confianza, inmediatez, flexibilidad y cuidado cuando se trabaja con el constructo (Dreyfus & Tsamir, 2004) y también cuando el lenguaje es cada vez más preciso (Hershkowitz, Schwarz & Dreyfus, 2001), aunque para Kidron (2008) y para Gilboa, Dreyfus y Kidron (2011) el aumento en la precisión del lenguaje es característica de la etapa de construcción por sí misma y no únicamente de la de consolidación.

En AiC a las acciones epistémicas mencionadas se les conoce como modelo RBC (Recognizing, Building with, Constructing) y el modelo RBC-C con la segunda C correspondiente a la etapa de consolidación.

 

3. Metodología

La actividad presentada en este artículo es parte de una investigación más amplia sobre la introducción de la demostración a estudiantes universitarios. Previamente los estudiantes trabajaron en una actividad para construir definiciones de diferentes conceptos matemáticos con el propósito de desarrollar habilidades para "definir" y manipular definiciones.

Su diseño tiene como objetivo desarrollar habilidades que fortalezcan la estructura lógico-lingüística necesaria para el trabajo posterior con la demostración. Para lograrlo, la actividad se enfoca en la forma que tienen los enunciados matemáticos, en la importancia de encontrar su valor de verdad y en cómo desarrollar los argumentos que lo sustenten.

Los enunciados matemáticos que con mayor frecuencia enfrentan los estudiantes son las implicaciones. En un estudio exploratorio previo (Alvarado & González, 2009) encontramos que hay dificultades en la comprensión de este tipo de enunciados como saber reconocer el papel condicional de la hipótesis, problemas para distinguir entre hipótesis y conclusión, no estar familiarizados con otras formas de hipótesis diferentes a la habitual (si... entonces) y dificultades para argumentar el valor de verdad de una implicación.

Para solventar estas dificultades, se diseñó esta actividad en la que los alumnos debían identificar las características que debe tener una proposición matemática, que supieran cuál es el papel de la hipótesis y cuál el de la conclusión y que comprendieran cuándo se puede asignar un valor de verdad a un enunciado matemático. Consta de cuatro tareas que se enuncian a continuación:

1. Comenta con tus compañeros qué es una proposición matemática y escriban su definición.

2. ¿Cuáles de los siguientes enunciados son proposiciones matemáticas?

3) Los triángulos XYZ y RSTson semejantes 4) 3+n+n²

3. ¿Cuáles de las siguientes proposiciones matemáticas son verdaderas? Subrayen los enunciados matemáticos verdaderos y expliquen el porqué de su respuesta en los dos casos.

1) La raíz cúbica de cualquier entero es un número real.

2) x²+y ²> 1 (donde x e y son números reales)².

3) Si x>0, entonces log x>0 (donde x es un número real).

4) Para todo t, sec²t+tan²t = 1

4. En cada uno de los siguientes problemas, identifiquen hipótesis y conclusión.

1) Si el triángulo rectángulo XYZ con catetos de longitud x e y e hipotenusa de longitud z tiene área entonces el triángulo XYZ es isósceles.

2) n es un entero par ⇒ n² es un entero par.

3) Es posible resolver las dos ecuaciones lineales ax + by = e y cx + dy =f para x e y cuando a, b, c, d y f son números reales con ad-bc≠0.

4) La suma de los n primeros enteros positivos es .

5) r es un número irracional si r es real y satisface r ² = 2.

6) Si p y q son números reales positivos conentonces p≠q.

7) Cuando x es un número real, el valor mínimo de x (x -1) es al menos

En el estudio participaron ocho estudiantes del primer semestre de la Licenciatura en Matemáticas Aplicadas de la Universidad Juárez del Estado de Durango, México, con edad promedio de 18 años. Los estudiantes habían trabajado, en un semestre anterior, un esquema de organización de la matemática basada en presentación de definiciones, enunciados de proposiciones y teoremas, algunos acompañados de su demostración, así como ejercicios donde se aplicaban los conocimientos adquiridos. Sin embargo, no había evidencia en sus apuntes de explicaciones sobre lo qué es una proposición, cómo identificarla y menos cómo demostrarla.

Para desarrollar la sesión, los alumnos se organizaron en dos equipos (A y B) de cuatro estudiantes cada uno. La actividad se realizaba a partir de una hoja de trabajo que concentraba las cuatro tareas. El trabajo en pequeños grupos les dio oportunidades de leer, interpretar, discutir ideas y argumentar tratando de convencer a sus compañeros, registrando el acuerdo final por escrito. Esta actividad se realizó en poco más de una hora. Al terminar cada tarea se efectuó una puesta en común en gran grupo guiados por el profesor. En esta discusión, la validación de las ideas o producciones en pequeños grupos se apoya en el argumento matemático aportado por los estudiantes, más que en la autoridad del profesor. A partir de la discusión, el profesor realizó un cierre concentrando las ideas relevantes y, en ocasiones, introduciendo cuestiones nuevas relativas al proceso de demostración.

Las discusiones en equipos y la socialización fueron audio-grabadas y transcritas en su totalidad.

 

4. Resultados

A continuación se presentan los resultados de las cuatro tareas propuestas en la actividad en el grupo B, seguidas de la interacción en gran grupo guiada por el profesor a la luz del marco conceptual descrito.

4.1. Tarea 1. Definición de proposición matemática

En esta primera tarea el objetivo era reconocer una proposición matemática y sus componentes, destacando que lo característico es su valor de verdad. La consigna era comentar en pequeños grupos qué es una proposición matemática y una vez que estuvieran de acuerdo escribieran su definición.

El equipo B, para definir una proposición matemática, hace referencia a las "propiedades" que se incluyen en el enunciado, a la posibilidad de que sean "afirmativas o negativas" (en un sentido excluyente, entendiendo esa afirmación/ negación con la idea de que sean V o F) y a la existencia de una relación (=, í, >, <, etc.) en el enunciado. Esta definición fue negociada y construida a partir de ejemplos específicos. Inicialmente las acciones son de reconocimiento (R-acciones) de las características de esos enunciados por similitud con otros que ya han manejado.

[3] [Una proposición] Es una ecuación, ¿no? [4] Es una oración.

[5] De hecho una oración, porque una ecuación no es.

[6] Es una oración que puedes poner con F o V, por ejemplo, una pregunta.

[7] A ver, no, afirmación sí es.

[13] Donde afirman o niegan algo.

En este reconocimiento surgen ciertas palabras durante el diálogo como: ecuación [3], oración [4,5,6], pregunta [6], afirmación o negación [7,13,15,16,17,18], propiedad [18,19,20,21,26,30] que se van transformando en B-acciones cuando van afianzando el significado de esas nociones.

[15] Más bien ¿no?, no es una pregunta, más bien es una afirmación o una negación.

[16] (Mmh) entonces que le ponemos. Es el enunciado donde afirma, o

[17] Que puede ser afirmativo o negativo.

[18] Sí, pero ¿qué afirma y qué niega?, ¿una propiedad?

[19] ¿Por qué propiedad'

[20] Siempre para afirmar los enunciados va a tener "este es tal" o "no es así", o "debe ser así", sí ¿no?

[21] Puede ser un enunciado que tiene algunas propiedades o condiciones que pueden ser afirmativas y negativas. [22] ¿Y negativas?

[23] ¿Sí?

[24] Sí.

[25] ¿Qué?

[26] Más bien enuncia propiedades afirmativas o negativas, enuncia [28] Pero, es que, () más bien [proposición] matemática.

[30] Que es un enunciado, ponle es un enunciado cuyas propiedades son positivas o negativas, afirmativas o negativas.

La transformación de las R-acciones en B-acciones se produce cuando los alumnos van poniendo en práctica el significado de los términos que utilizan y los van aplicando en los diferentes ítems, por ejemplo, en [17] se indica de un enunciado "que puede ser afirmativo o negativo" y esto se utiliza en [18] para profundizar en esa idea, aunque esta edificación (B-acción) sucede entendiendo de manera peculiar las palabras "afirmación y negación". En [17] se están considerando como valor de verdad y en [18] en la forma de presentar el enunciado. Esto se va repitiendo en otros momentos del diálogo, unas veces en relación con el significado estricto de las palabras y la forma de presentar el enunciado [13], [16] [20] o [18] y en otros momentos en el sentido del valor de verdad del enunciado; es decir, como sinónimos de V y F [17, 21, 26 y 30].

Finalmente, se concluye la discusión con la siguiente conclusión: "enunciado cuyas propiedades son afirmativas o negativas". Aún no ocurre una C-acción, ya que no hay claridad en el uso y sentido de las palabras falso y verdadero, la construcción se realizará durante la interacción en gran grupo.

 

4.2. Tarea 2. Identificación de proposiciones matemáticas

Los estudiantes usan la definición de proposición negociada durante la tarea anterior, "Enunciado cuyas propiedades pueden ser afirmativas o negativas", para identificar, entre un listado, cuáles son proposiciones matemáticas.

Inicialmente se perciben las R-acciones cuando los estudiantes reconocen que el hecho de tener una "propiedad", por ejemplo, la igualdad a cero [35] permite decidir si el "enunciado" es F o V, aunque no se fijan en que los parámetros a, b y c de la ecuación ax² + bx + c = 0 no tienen valores numéricos y no se puede decidir el valor de verdad.

[33] Esta porque está afirmando que es igual a cero ¿verdad? [ax² +bx + c = 0].

[34] Bueno no necesariamente porque está afirmando, sino porque puede ser cierto, porque puede ser afirmativo o negativo.

[35] Bueno sí, pero nos está dando una propiedad pues, esto es igual a cero.

A continuación nos encontramos con las B-acciones; los estudiantes aplican la R-acción anterior para edificar el concepto y poder decidir de manera acertada, en otros enunciados, cuáles son proposiciones y cuáles no. Para ello utilizan como argumento [en los ítems 2 y 4] que no se puede decidir su valor de verdad ya que carecen de un signo de igualdad o de otra expresión o número para "comparar".

[39] Y puede ser que se cumpla o que no se cumpla, ya dependiendo de cómo sea, afirmativo o negativo. Pero por ejemplo esta no, en sí no me dice nada, nada más me dice -b... [Ejercicio 2,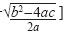

[40 ] Es una ecuación [expresión] y ya.

[46] También, "explique el porqué de sus respuestas" [leen]. Aquí, porque la ecuación [ax² + bx + c = 0] una propiedad de la ecuación es igual a cero, puede ser igual a cero nada más, sí. Y luego esta porque sólo nos da la ecuación [expresión] y ya [2].

[47] Ajá, en esta ecuación [expresión] no hay nada que afirmar o que negar [2].

[48] En esta [2] o en esta 3+n+n².

[51] Esta no hay algo que me permita decir que es falsa o es verdadera 3+n+n².

En relación con el lenguaje utilizado observamos que el sentido de las palabras afirmativo y negativo se usa para indicar V o F. Sin embargo, afirmar es asegurar o dar por cierto algo, y no necesariamente significa que sea V, al igual que negar no significa que sea una proposición F. Siguiendo la línea de la interacción, podemos apreciar en [34], [39] y [51] una mejora progresiva en la precisión del lenguaje utilizado por los estudiantes a lo largo del proceso de construcción del concepto. Al igual que en los trabajos de Kidron (2008) y de Gilboa, Dreyfus & Kidron (2011) observamos, que el hecho de que mejore paulatinamente la precisión en el lenguaje es una característica del proceso de construcción del concepto por si mismo y no sólo de una etapa de consolidación.

A continuación se produce un cambio en el contexto pasando éste a ser geométrico, realizándose una B-acción para decidir que "puede ser falso o verdadero".

[42] Ajá, y luego esta, porque nos está dando una propiedad [Los triángulos XYZ y RST son semejantes].

[43] Ahí está diciendo que son semejantes, pero puede ser falso o verdadero.

Para tomar una decisión adecuada en relación con este enunciado, se percibe una nueva R-acción correspondiente a reconocer que es necesario saber de qué triángulos se está hablando para tomar una decisión [44], esto produce un crecimiento en la comprensión del concepto.

[44] Sí, dependiendo de quienes sean [los triángulos] Esta pues me está diciendo...

Este es un componente importante para la emergencia del nuevo constructo, aunque todavía se perciba frágil ya que se reconoce que el enunciado en juego es una proposición matemática.

A continuación, en la siguiente proposición están de acuerdo en que es proposición matemática, utilizando una B-acción, que se da al tener en cuenta que la relación (<) les permite decidir si es falso o verdadero el enunciado.

[52] En esta sí ¿verdad?, pues es que, esta sí es cierto [sí es proposición matemática].

[53] Sí, esa sí es una proposición.

[54] La proposición de la ecuación, más bien, propiedad de la ecuación, es verdadera [sí es proposición matemática], así, ¿no?, no verdad.

[55] (Mm)... si quieres, no bueno.

Las R-acciones se están transformando en B-acciones por la puesta en práctica de las construcciones realizadas en los diferentes ítems. Además, esta construcción les permite reconocer que para que haya una proposición matemática se necesita la presencia de una relación [57]. No obstante, se producen algunas confusiones, por ejemplo, cuando consideran que la desigualdad que están manejando es una ecuación.

[57] [Al retornar y complementar la definición de proposición matemática] Que ahorita le podríamos poner, especificar, que en las que son verdaderas [son proposiciones] se maneja una relación entre dos pequeñas oraciones ¿no? Por ejemplo, aquí hay una oración

[58] Una ecuación y aquí hay otra ecuación

[59] Ajá. Hay una relación [<] entre dos que es la que puede, con la que se puede decidir [si es falso o verdadero]

[60] Entre dos elementos ¿no?

[61] Ajá, aquí, ¿sí?

Aplican esa B-acción en la siguiente proposición considerando que "es una propiedad" [63] que ya habían reconocido en [35].

[62] Ajá, y luego para todo [ángulo t, sen²t+cos²t = 1] [63] Ah esta es una propiedad

[64] Y ya ¿Esa y ya? Aquí hay una afirmación [proposición V]

Los alumnos han identificado tres aspectos en la definición de proposición que van a permitir la construcción de C-acciones: que hace referencia a una propiedad, puede ser afirmativa o negativa (en el sentido de V y F) y debe incluir una relación entre dos elementos. Al compartir las respuestas del trabajo en pequeños grupos, durante la socialización mediada por el profesor, éste selecciona la parte esencial produciéndose una C-acción, [71a] C₀.

[67] Profesor: ¿Qué entienden por proposición matemática?

[68] Alumno: Bueno, puede ser un enunciado que tiene algunas propiedades que pueden ser positivas, F o V

[69] Alumno: falsas o verdaderas.

[70] Alumno: Es un enunciado que se considera V o F, más sin embargo necesita de una demostración.

[71a] Profesor: Entonces, aquí lo primordial es que tiene que ser una afirmación o un enunciado y que nosotros tenemos que determinar si es F o V. Cuando no podemos determinar si es F o V no es una proposición matemática.

En este fragmento, para la emergencia de un nuevo constructo, es decir, cómo decidir cuándo se tiene una proposición matemática (segunda etapa en el proceso AiC) los estudiantes, inducidos por el profesor y por el trabajo previo [68-71], reconocen (R-acciones) para decidir si un enunciado es o no proposición matemática, concretamente que se pueda decidir su valor de verdad [73]. Ensayan B-acciones [75-76-77] y se produce una C-acción, C₁ en [78] cuando nos encontramos por primera vez que es utilizado el criterio de manera completa y adecuada sin que esto signifique que el constructo haya sido totalmente asumido puesto que aún es frágil y depende del ejemplo específico.

[71b] Profesor: Aquí tenemos un conjunto de proposiciones, todas son proposiciones, pero la idea es decir cuáles son proposiciones matemáticas. La 1) [ax² + bx + c = 0] Es o no es.

[72] Alumno: Sí es, según nosotros.

[73] Profesor: Ustedes pueden determinar si es F o V.

[75] Alumno: Sí //, dependiendo de los valores de a, b y,

[76] Alumno: ¿Tenemos valores?

[77] Alumno: No tenemos valores.

[78] Alumno: ¡Ah, entonces no es!

En la interacción vemos cómo la intervención autoritaria del profesor [81] frena el surgimiento de una nueva C-acción en un ejercicio diferente y, aunque la respuesta de un estudiante [82] es correcta, no hay un indicador de crecimiento en la comprensión y uso del constructo en nuevos contextos.

[81] Profesor: Esta 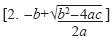podemos decir qué es proposición matemática.

La 2, es una afirmación, no es ni siquiera una igualdad y no tenemos valores. [82] Alumno: No es proposición matemática.

En el siguiente ítem se produce una C₂-acción derivada de C₁ al aplicarla a un contexto geométrico. Aquí se aprecia el carácter anidado del modelo RBC para comprender la abstracción matemática.

[83] Profesor: La que sigue [3] los triángulos... [XYZ y RST son semejantes] es proposición matemática ¿Cuándo sería proposición matemática?

[84] Alumno: Cuando supiéramos los triángulos.

[85] Alumno: No tenemos valores.

[86] Alumno: ¡Ah sí, no es proposición matemática!

Más adelante nos encontramos con tres C-acciones C₃ [88], C₄ [90-92] y C₅ [94-95] en las que, además, los estudiantes expresan cuál sería el valor de verdad de esas proposiciones. Este hecho muestra inmediatez, evidencia personal y confianza que son rasgos que pueden indicar consolidación del nuevo constructo (Dreyfus & Tsamir, 2004), lo que convierte al modelo en RBC-C con la última C de consolidación.

[87] Profesor: [intentan corregir su hoja de trabajo] No corrijan, no es necesario, dejen lo escrito. La que sigue [3 + n + n²] podemos determinar.

[88] Alumno: Tampoco.

[89] Profesor: La 5

[90] Alumno: Esa sí.

[91] Profesor: Podemos determinar si es F o V.

[92] Alumno: Sí, es falso.

[93a] Profesor: Entonces es necesario determinar si es F o V. No importa si es F, muchas veces se piensa que si fuera F entonces no es proposición matemática. Pero no, es proposición matemática si es F o si es V

[93b] Profesor: La 6 entonces dice [lee], para todo ángulo t, sen²t+cos²t = 1.

[94] Alumno: Sí es.

[95] Alumno: Es una proposición cierta.

[96] Alumno: De hecho esas cuando suceden se llaman identidades. Una cosa es ecuación y otra identidad. Por ejemplo la 1 es una ecuación, si supiéramos los valores de a, b, c, entonces para ciertos valores sería V, pero en una identidad como en 6 todos los valores que tome t cumplen y es identidad.

En C₅, respecto al cuantificador t, se ha entendido que se tiene una proposición que se cumple para cualquier valor que tome t. En [96] se aprecia que el profesor interviene, aprovechando la proposición que están tratando, para ampliar el conocimiento de los alumnos con la noción de identidad.

Para identificar una proposición matemática, primero se considera que en el enunciado se tenga alguna relación (=,>,<, semejanza) que permita decidir si es F o V. Después se consideran los valores sobre los parámetros u objetos que aparezcan en el enunciado para tener la posibilidad de decidir si es F o V. El lenguaje se ha ido depurando desde concebir una proposición simplemente como un enunciado afirmativo o negativo hasta llegar a que puede ser F o V.

 

4.3. Tarea 3. Justificación del valor de verdad de proposiciones matemáticas

La tarea propuesta a los equipos fue determinar y justificar, de una lista de cinco proposiciones, cuáles eran verdaderas y cuáles no. Por razones de extensión y de interés sólo se presenta la discusión correspondiente a la proposición 3) Si x > 0, entonces log₇x =>0 (donde x es un número real).

Al principio, los alumnos muestran desconcierto ante la tarea porque no recuerdan el concepto y notación del logaritmo y la abandonan. Después de realizar otros ejercicios, la retoman y se dan cuenta de que necesitan entender el significado del logaritmo (R-acción). Con ello se inician dos procesos de construcción que interactúan de manera paralela: construir el concepto de logaritmo como inversa de la exponencial, C₆ y decidir la verdad o falsedad de la proposición, C₇.

[184] [Pregunta sobre el logaritmo y al regresar al equipo inicia para explicar con un ejemplo] Logaritmo [log₇x] es a qué numero tendría que elevar el 7 para que me dé mayor que 0 [escribe]

[185] No, este número si es mayor que cero [log₇x]... esto me da x [7^p], donde x es un número real

Se constituye una R-acción [187] al utilizar un lenguaje algebraico apropiado. Sin embargo en [189] muestran algunos problemas en la traducción entre el papel de la x y de la a, puesto que están inmersos en un proceso de construcción del concepto de logaritmo.

[187] Esto dices tú, o sea log₇x es igual a a [log₇ x = a] dónde a es mayor a cero, es un número positivo [log ₇ x], creo que ya verdad, logaritmo, a ver, ¿7 a la qué?

[189] A la x, x es mayor que cero, entonces a es positivo donde [7^x=a para que valores a es positivo]

Proponen un contraejemplo [192] del que erróneamente piensan que es único. Sin embargo, esto supone una C-acción (C₆) del concepto de logaritmo dado que conciben de manera adecuada el lenguaje de los exponentes aunque, no entienden todavía el papel del contraejemplo, fundamental para decidir el valor de verdad de la proposición ([194,198,199]).

[192] Porque el único que no cumpliría sería el cero [valor de a, ya que log ₇1 = 0, es decir x = 1 > 0, pero log ₇ x = a =0, no positivo].

[194] Sería que log₇x fuera cero, pero lo que nos están especificando es que x es mayor que cero y que este también [a].

[198] Siete elevado a la qué me daría [x], donde x mayor que 0.

[199] Siete igual, nada más que llevaría el valor de x donde x es mayor a cero.

Como no manejan correctamente hipótesis y conclusión en un contraejemplo, y tienen problemas con el concepto de logaritmo, necesitan verbalizar varias veces lo que entienden por este concepto hasta lograr su construcción definitiva. La dificultad radica en que, por un lado, tienen una definición de logaritmo poco operativa a partir de exponentes, puesto que han de manejar dos variables (x y a) que son inversa una de la otra y a veces, sin ser conscientes, las intercambian. Por otro lado, al buscar un contraejemplo, han de probar que, para algún valor que verifique la hipótesis, no se verifica la conclusión; pero esto no lo tienen totalmente asumido ya que saben que para que una implicación sea verdad ambas premisas deben serlo.

Para poder resolver la tarea la retoman desde el principio realizando de forma paralela 1) una B-acción para edificar el significado de contraejemplo [200], 2) un proceso de consolidación del concepto recién construido, C₆, buscando afianzarlo con herramientas primarias de álgebra que les aclare el papel del exponente [198] con diferentes ejemplos y cambiando de notación [202] y 3) una B-acción edificando el papel que tiene la hipótesis en una implicación [200].

[200] Cierto ya que nos define que x es mayor que cero [la hipótesis] ¿no?

[201] Mayor que cero, ah sí, porque si lo elevamos a la uno a la dos a la tres.

[202] Ándale sí, o para p igual a cero [cambian la notación a log₇x = p, antes p era a]

Para poder concluir la tarea, necesitan trabajar conjuntamente con ambos conceptos: logaritmo y contraejemplo, por lo que retoman el planteamiento practicando con diversos ejemplos (B-acciones) que les ayuden en esa construcción.

[215] No, no es cierto, porque, a ver si x es mayor que cero por ejemplo 7 a la dos, bueno p = 2, bueno claro que no.

[217] No, mira qué número. Digamos que 49 [es x] y p vale dos.

Esto les conduce a activar de nuevo el contraejemplo inicial que demuestra que la proposición es falsa.

[219] Bueno, pero sería en el caso que x valga uno.

[221] Entonces a qué numero me da igual a uno, igual a 0, el uno cumple con que sea mayor que 0.

[223] Que x sea mayor que 0, pero no cumple con que este número [log₇ x = p] sea mayor que 0.

[224] Ajá, Ok, ya, sí. Por la propiedad.

Finalmente se concluye la discusión y en el registro escrito: "7 ^p= x, 7⁰ = 1, x = 0 pero log ₇1 = 0 y no cumple la proposición" se exhibe por primera vez una C-acción (C₇) de la comprensión del papel de los contraejemplos para probar que la proposición es falsa. Cabe destacar que esto indica la construcción grupal y no asegura la individual.

Durante la socialización [304] se reconoce la función del contraejemplo como relevante para la tarea (B-acción) y se muestra confianza en la comprensión del concepto recién construido de logaritmo [306]. Esta confianza es evidencia de una consolidación del concepto y la encontramos explícita en las diferentes formas de enunciar su contraejemplo [306]. Esta intervención invita, además, a validar la comprensión del logaritmo como "exponente".

[303] Profesor: Ahora, si tengo un número positivo x, pero supongo que es real, el log₇ x es positivo, ¿sí?

[304] Alumno: Es que hay un número con el que no se cumple.

[305] Alumno: Por ejemplo

[306] Alumno: Cuando x = 1 el exponente es cero, o sea 7⁰ = 1 y ya no cumple.

[307] Alumno: Si x vale 1, por ejemplo, entonces el logaritmo cuánto tendría que valer

[308] Alumno: Cero.

Un estudiante explicita la forma de la implicación [312] y el profesor aprovecha esa oportunidad para dar nombre a las proposiciones de este tipo [315] que se identifican con las implicaciones [316].

[312] Alumno: Es que aquí ya nos está diciendo, si pasa esto entonces... ¿cuándo es cero?, cuando el log₇1.

[315] Profesor: ¿Qué tipo de proposición es ésa?, de la forma si,.. , entonces.

[316] Alumno: Implica, es una implicación.

Se inicia [318] una exploración sobre cuándo es verdadero un enunciado de este tipo. Un estudiante sólo considera proposiciones en forma de ecuaciones o desigualdades que requieren conocer los valores condicionales [319]. El profesor no indica que su aportación es cierta para este tipo específico de proposiciones haciendo mención de los cuantificadores.

[318] Profesor: Sí, es una implicación. Y en una implicación cuándo podemos decir que un enunciado es verdadero

[319] Alumno: Si para todo se cumple.

[320] Profesor: No, esos son cuantificadores.

Al aplicar los constructos previos a la noción de implicación, los estudiantes establecen sus valores de verdad [321-323] deduciendo que la implicación es falsa porque la primera premisa es verdadera y la segunda falsa.

[321] Alumno: Si el primer enunciado es V y el segundo es V, todo es V

[322] Alumno: Si el primero es F y el segundo es F entonces es ( ) F

[323] Alumno: No, es V

[327] Profesor: Si el primero es V y el segundo es F

[328] Alumno: Es F

[332a] Profesor: Sí verdad. Entonces en este caso la implicación es F.

Encontrar estos valores de verdad de la implicación [321, 323, 327 y 328] constituye una nueva C-acción que llamaremos C₁₀, ya que por primera vez aparece enunciada como tal.

Realizar la tarea 3 resultó complejo para los estudiantes dado que al no manejar el concepto de logaritmo, tuvieron que construirlo. Esa construcción se realizó a partir del concepto de exponente aunque, en múltiples ocasiones, tuvieron que retomarlo por errores en la notación y confusión entre exponente y resultado. Entre los ejemplos buscados, únicamente tomaban en cuenta números naturales lo que les condujo a concluir, de manera errónea, que únicamente existía un contraejemplo (x = 1). También se percibe una lucha por comprender el papel del contraejemplo para probar que la proposición es falsa, lo que no resulta sencillo, pues para buscarlo, han de probar que, para algún valor que verifique la hipótesis, no se verifica la conclusión. Esto no lo tienen totalmente asumido ya que confunden el papel de ambas premisas y saben que para que una implicación sea verdad ambas deben serlo.

 

4.4. Tarea 4. Identificación de formas de implicaciones y sus componentes

En esta tarea se espera que los estudiantes identifiquen la forma "si,..., entonces" de la implicación, las variantes de esta forma y sus componentes. Primero se explora qué entienden por hipótesis y por conclusión en el contexto de las implicaciones. Posteriormente se les proporciona una lista de siete implicaciones con diferentes formas de presentación y se les pide que las identifiquen. Se les dan quince minutos para realizar la tarea en equipos y posteriormente se discute en grupo.

Lo primero que perciben es que la conclusión se deriva de la hipótesis [372] una vez que ésta se verifique [374]. Aquí ocurre una C-acción (C_n) dado que se hace explícito que la hipótesis es la parte de la implicación que se debe suponer cierta para obtener una conclusión.

[372] La conclusión depende de la hipótesis

[374] Ajá, pero al verificar la hipótesis, pero la hipótesis...

Sin embargo, en un intento por profundizar en los términos, piensan en la hipótesis como una propiedad justificándolo con un ejemplo [376-379], luego como un evento [382] y vinculándolo con el hecho de que de ella se extrae la conclusión, la consideran como evento independiente.

[383] que puede suceder o no.

[375] Es como una propiedad ¿no?

[376] La hipótesis vendría siendo una propiedad ¿no?

[378] Pero una propiedad ¿de qué?.

[379] Una propiedad así. Mira, por ejemplo este es un entero, sea x un entero... es una hipótesis, una propiedad, entonces.

[381] ¿Si le pongo que es una propiedad?

[382] O puede ser un evento ¿no?

[383] Un evento independiente.

Tras esta consideración y dado que si "ocurre" la hipótesis entonces "ocurre" la conclusión [385], consideran la relación que une a ambas [386 y 391].

[385] Porque si pasa esto, entonces pasa aquello. Entonces la conclusión es un...

[386] Otro evento que está en función del evento independiente...

[391] Una o más propiedades, bueno así, es un evento que está en función de la hipótesis, así.

Observamos, en esta interacción, que los estudiantes tienden a buscar similitudes usando términos no matemáticos para expresar conceptos de forma poco ajustada. Por ejemplo, en matemáticas, en una hipótesis se establecen o controlan las "propiedades o características" que se deben tener, mientras que en un evento no puedes determinar su ocurrencia.

En la hoja de trabajo se les solicitó que escribieran lo que entendían por hipótesis y conclusión en una implicación. En la socialización, al darse cuenta el profesor de las respuestas generadas en los equipos, cambia la intención de la tarea y pregunta "qué función tiene la hipótesis" [430] lo que induce una nueva aportación [432].

[430] Profesor: Primero, en el caso de la implicación, ¿qué función tiene la hipótesis?, ¿para qué me sirve?

[431] Alumno: Enunciado F o V, el cual consideramos para saber si alguna proposición, etc, es F o V

[432] Alumno: Para saber qué es lo que necesitamos [en la demostración], algo que debo tener en cuenta

[434] Alumno: Evento independiente que enuncia ciertas propiedades

Para afianzar esta idea, el profesor [435], a partir de un ejemplo, hace que los alumnos reflexionen sucediéndose una serie de B-acciones [436, 438 y 440] acerca de lo que sugiere la noción de hipótesis.

[435] Profesor: Regularmente en matemáticas cuando van a demostrar, esta parte [la hipótesis] para qué me sirve, qué me aporta en la demostración. Cuando ustedes escuchan la palabra "demuestra" por ejemplo [escribe], Demuestra que: si X es un espacio métrico entonces es compacto, esta proposición es falsa. Mmh. [busca otro ejemplo]. Bueno, por ejemplo, demuestre que si x es un número par entonces su cuadrado también es par [escribe]

[436] Alumno: Pues agarro un [número] par y de ahí empiezo

[437] Profesor: Pero entonces, ¿qué es?

[438] Alumno: Son las bases para probar

[439] Profesor: Son las bases, eso se supone que es como cuando yo quiero probar esto [señala la hipótesis "si x es un número par"] se considera que es

[440] Alumnos: Cierto, //verdadero

Un alumno [442 y 444], confunde los valores que se asignan a las premisas para establecer la tabla de verdad de una implicación con los valores que pueda tener un enunciado concreto lo cual induce al profesor a aclarar [445] este error.

[442] Alumno: Se supone, pero no se considera V, es que también cuando se considera la hipótesis F y se llega a que es V

[443] Profesor: ¿Cómo?

[444] Alumno: Si la hipótesis es F y llegas a que es V

[445] Profesor: Si se da en ambos [si supones la hipótesis F y V y la conclusión es V] quiere decir que a lo que llegas no depende de lo que supones, entonces es V

Recordando [447] nuevamente la proposición sobre el logaritmo se provoca una B-acción identificando el punto de partida (que x > 0 es cierto) dando lugar a la construcción del significado de hipótesis de acuerdo con su función en el proceso de demostración. Sin embargo, en este proceso "colectivo" de construcción, el efecto no es el mismo sobre todos los participantes e intervienen otros conceptos que aún no se diferencian. Así una alumna se da cuenta que, en el ejemplo citado, suponen cierta la hipótesis y llegan a que la proposición es F utilizando la palabra contradicción con el sentido de falsedad [450].

[447] Profesor: Pero en el proceso de demostrar cómo utilizan la implicación, regularmente dices si pasa esto [hipótesis] demuestra que esto [la conclusión] es V. Dan por hecho que la hipótesis o esta parte [señala en el pizarrón, si x es un número par] es V. Por ejemplo aquí en una proposición que tenían [busca en la parte previa] dónde fue (), aquí está, si x es mayor que cero entonces logaritmo base 7 de x es mayor que cero ¿verdad? Ustedes dijeron que era F, pero parten de qué hecho

[448] Alumno: De que x mayor que cero

[449] Profesor: Suponen que esto es verdadero [escribe y señala]

[450] Alumno: ¡Ah, y llegamos a una contradicción!

[451] Profesor: Y en ese proceso de demostrar analizan a partir de que x es mayor que cero

Un alumno [452] insiste en la idea de que la hipótesis puede ser F o V; las tablas de verdad que ya ha visto se imponen sobre la construcción que se ha hecho de la implicación. No es consciente del significado del proceso de demostración y por ello el profesor vuelve a recordar el papel de la hipótesis.

[452] Alumno: Pero entonces la hipótesis puede ser también F o V

[453] Profesor: En realidad la hipótesis vamos a partir del hecho de que es V y entonces llegamos a una conclusión que puede ser

[454] Alumno: Falsa o verdadera

[455] Profesor: Sí, y eso nos determina la verdad o falsedad de la proposición.

Se ha construido una C-acción [453-454], C₁₂, sobre el papel de la hipótesis en el proceso de demostración, pero sólo ha sido mencionada por el profesor.

 

4.5. Análisis

Las construcciones que surgen de las interacciones se van conformando como ramas que crecen a partir de otras, unas veces como extensión o derivadas de una combinación de construcciones. En la siguiente ilustración se muestran las C-acciones producidas a lo largo de esta actividad. A la derecha se describen las C-acciones, indicando cuándo ocurren, y si se producen en pequeño grupo (PG) o en gran grupo (GG).

Se puede apreciar cómo inicialmente se identifica una proposición matemática ligada a un objeto algebraico particular, ax²+bx+c = 0 (C₁). Esta construcción se retoma en otros contextos (C₂, C₃, C₄, C₅ y C₈) lo que forma parte de un proceso de consolidación, dado que el constructo deja de depender del contexto en el que se ha generado y, se va fortaleciendo de manera paulatina y no limitándose a la tarea encomendada de decidir si se trata de una proposición matemática, sino que tratan de buscar argumentos para sustentar el valor de verdad de una proposición (C₄, C₅). Al revisar el criterio para decidir si es o no proposición matemática C₁ se construye una nueva C-acción C₈.

Una vez que los alumnos adquieren confianza en el manejo del constructo y pueden utilizarlo en diferentes contextos, intentan ir más allá conectándolos para construir un nuevo constructo (C₇) sobre el papel de los contraejemplos. En el proceso se producen ciertas interrupciones cuando necesitan construir otro concepto (C₆) lo que produce una construcción paralela (C₆ y C₇). Este constructo se retoma en otra tarea donde surge C₁₀ en la que se menciona que una técnica para probar que una proposición es F es precisamente exhibir un contraejemplo; y esto se hace ya de manera consciente.

Algunas construcciones se dan como extensión de otras, por ejemplo, primero se construye el papel de la hipótesis en la implicación C₁₁ y después se extiende esta idea para señalar la forma de proceder cuando se quieren demostrar implicaciones C₁₂. La generación de un contraejemplo en una situación C₇ se generaliza para probar que una proposición es falsa C₁₀.

 

5. Conclusiones

En el desarrollo de esta actividad, la continuidad en las tareas, la organización de la sesión en equipos para la discusión, el registro escrito, la socialización de los acuerdos en gran grupo, así como la discusión guiada por el profesor para incentivar la construcción del conocimiento a partir de las construcciones logradas previamente, nos han permitido seguir y documentar la manera en que ocurre y se entrelaza la generación interactiva del conocimiento y el desarrollo de la actitud de precisión y rigor. El desarrollo de dicha actitud se muestra de diferentes formas que constituyen indicadores de la consolidación de los nuevos constructos en el modelo RBC-C. Tales formas pueden ser: evidencia personal, argumentar las ideas al compartirlas, mostrar confianza, inmediatez, manejo del constructo cambiando de contexto tanto en pequeño grupo como en gran grupo, buscando clarificar y refinar su pensamiento, lo que ha permitido que su lenguaje se muestre cada vez más preciso.

La discusión en pequeños grupos ha permitido confrontarlos con pares con el mismo nivel de conocimientos e identificar algunas debilidades en el lenguaje usando "afirmativas y negativas" como sinónimos de V y F; proposición como ecuación, oración, pregunta, afirmación o negación; no hacer distinción entre ecuación y expresión; contradicción como falsedad; dificultad con los conectores, entre otras. Estas debilidades se van diluyendo y se va refinando el lenguaje durante la interacción al compartir y argumentar sus ideas y al atender demandas de clarificación.

La construcción que van haciendo los alumnos del concepto de proposición no es lineal, más bien se produce por acumulación de saberes y de experiencias. Es cierto que en el inicio de la actividad predominan las R-acciones y no es sino al final de la segunda tarea cuando el profesor induce una primera C-acción. Esta construcción, a veces, necesita una vuelta atrás, como en el caso de la actividad del logaritmo para la que es necesario reconstruir un concepto, no ligado directamente con la noción de proposición pero sí necesario para realizar la tarea.

Los alumnos van construyendo el conocimiento de forma anidada, creando poco a poco su comprensión de cierto tópico matemático, completando aspectos de cada concepto así como diferentes inseguridades de carácter procedimental, de conocimiento o incluso de construcciones previas que se creían completamente consolidadas, lo que les permite adquirir un conocimiento más estable y, a partir de él, seguir avanzando.

Algunas construcciones son impuestas por el profesor, aunque otras surgieron en el seno del grupo al argumentar sobre sus ideas. Las dudas sirvieron en algunos casos para poder resolver algunos dilemas planteados en el desarrollo de las tareas, en otros, para avanzar y plantear nuevas cuestiones que dieron origen a conceptos relacionados con los inicialmente planificados pero no incluidos directamente en las tareas, como fue el caso de la noción de implicación.

Este estudio ha permitido comprobar que los alumnos universitarios necesitan realizar actividades de construcción de definiciones y proposiciones puesto que, aunque han demostrado por imitación, no son capaces de manejar sus rudimentos. En futuras investigaciones será necesario abarcar otros aspectos de la demostración como el uso de conectores lógicos, la necesidad de la demostración, su historia o los diferentes tipos de prueba.

 

Agradecimientos

Este trabajo se ha desarrollado en el marco del proyecto de investigación EDU 2011-29328 "La resolución de problemas y la tecnología en la formación y desarrollo profesional del profesor de matemáticas" del Plan Nacional de Investigación Científica, Desarrollo e Innovación Tecnológica 2008-2011 del Ministerio de Ciencia e Innovación de España. Agradecemos asimismo a los revisores su crítica constructiva y las sugerencias realizadas que han servido para mejorar significativamente el artículo."

 

Referencias Bibliográficas

Alvarado, A. & González, M. T. (2009). A study of university students' performance with proof. Proceedings CIAEM 61. Quaderni di ricerca in didattica (Scienze Mathematiche) of G.R.I.M. Supplemento n.2 al N.19, Palermo, pp. 348-352.         [ Links ]

Alvarado, A. y González, M. T. (2010). La implicación lógica en el proceso de demostración matemática: Estudio de un caso. Enseñanza de las Ciencias 28(1), 73-84.         [ Links ]

Dorier, J-L., Robert, A., Robinet, J. & Rogalski, M. (2000). The obstacle of formalism in linear algebra. En J-L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 85-124). Dordrecht: Kluwer Academic Publisher.         [ Links ]

Dreyfus, T. & Tsamir, P. (2004). Ben's consolidation ok knowledge structures about infinite sets. Journal of Mathematical Behavior 23(3), 271-300. DOI: 10.1016/j.jmathb.2004.06.002        [ Links ]

Epp, S. (2003). The role of logic in teaching proof. American Mathematical Monthly 110(10), 886-899.         [ Links ]

Gómez-Chacón, I. (2009). Actitudes Matemáticas: propuestas para la transición del bachillerato a la universidad. Educación Matemática 21(3), 5-32.         [ Links ]

Gilboa, N., Dreyfus, T. & Kidron, I. (2011). A construction of a mathematical definition: the case of parabola. Proceeding of the 35^th Conference of the International Group for the Psychology of Mathematics Education (Vol. XX, pp. 425-432). Ankara, Turquía: Middle East Technical University.         [ Links ]

Harel, G. (2006). Mathematics education research, its nature, and its purpose: a discussion of Lester's paper. Zentralblatt für Didaktik der Mathematik 38(1), 58-62.         [ Links ]

Hershkowitz, R., Schwarz, B. B. & Dreyfus, T. (2001). Abstraction in context: Epistemic actions. Journal for Research in Mathematics Education 32(2), 195-222.         [ Links ]

Ibañes, M. y Ortega, T. (2003). Reconocimiento de procesos matemáticos en alumnos de primer curso de bachillerato. Enseñanza de las Ciencias 21(1), 49-63.         [ Links ]

Kidron, I. (2008). Abstraction and consolidation of the limit procept by means of instrumented schemes: The complementary role of three different frameworks. Educational Studies in Mathematics 69(3), 197-216. DOI 10.1007/s10649-008-9132-6        [ Links ]

Mariotti, M. A. & Fischbein, E. (1997). Defining in classroom activities. Educational Studies in Mathematics 34(3), 219-248.         [ Links ]

Moore, R. C. (1994). Making the transition to formal proof. Educational Studies in Mathematics 27(3), 249-266.         [ Links ]

Schwarz, B.B., Dreyfus,T. & Hershkowitz, R. (2009). The nested epistemic actions model for abstraction in context. En B.B. Schwarz, T. Dreyfus & R. Hershkowitz (Eds.), Transformation of Knowledge through Classroom Interaction (pp. 11-42). London, UK: Routledge.         [ Links ]

Stylianides, A. & Ball, D. (2008). Understanding and describing mathematical knowledge for teaching: knowledge about proof for engaging students in the activity of proving. Journal Mathematics Teacher Education 11(4), 307-332. DOI 10.1007/s10857-008-9077-9        [ Links ]

Treffers, A. (1987). Three Dimensions. A Model of Goal and Theory Description in Mathematics Education: The Wiskobas Project. Dordrecht: Kluwer Academic Publishers.         [ Links ]

Vinner, S. (1991). The role of definitions in the teaching and learning of mathematics. En D. Tall (Ed.), Advanced mathematical thinking (Vol. 11, pp 65-81). Dordrecht, Holland: Kluwer.         [ Links ]

Weber, K. (2001). Student difficulty in constructing proof: The need for strategic knowledge. Educational Studies in Mathematics 48(1), 101-119.         [ Links ]

 

Notas

¹ Treffer (1978) considera que matematizar es organizar y estructurar la información que aparece en un problema, identificar los aspectos matemáticos relevantes, descubrir regularidades, relaciones y estructuras. Define la matematización vertical, como el tratamiento específicamente matemático de las situaciones, y la caracteriza a partir de procesos: representar una relación mediante una fórmula, utilizar, refinar, combinar, integrar y ajustar diferentes modelos, probar regularidades, generalizar y formular un concepto matemático nuevo.

² En este ejercicio faltó precisar que "x ey son cualesquiera números reales", caso en el que resulta falsa la proposición y el texto, como aparece, se puede interpretar que "para algunos números reales x e y", en cuyo caso sería una proposición verdadera.