Artículos

 

Cognições e tipo de comunicação do professor de matemática. Exemplificação de um modelo de análise num episódio dividido

 

Cognitions and types of communication of mathematics teachers. Illustration of an analytical model in a divided episode

 

C. Miguel Ribeiro*, José Carrillo**, Rute Monteiro**

 

* Centro de Investigação sobre o Espaço e as Organizações (CIEO), Universidade do Algarve, Portugal. cmribeiro@ualg.pt

** Universidade de Huelva, España. carrillo@ddcc.uhu.es

*** Centro de Investigação sobre o Espaço e as Organizações (CIEO), Universidade do Algarve, Portugal. rutemonteiro@ualg.pt

 

Recepción: Enero 20, 2011
Aceptado: Febrero 1, 2012

 

RESUMEN

En este artículo centramos nuestra atención en el aula y, de manera más concreta, en las acciones del profesor durante el proceso de enseñanza, ya que consideramos que dichas acciones se ven condicionadas o potenciadas por sus cogniciones (creencias, conocimiento matemático para la enseñanza y objetivos). Por tal motivo, exponemos y discutimos un modelo de análisis sobre la práctica del profesor, el cual se enfoca en sus acciones, cogniciones y tipo de comunicación matemática que promueve (como una exteriorización de las cogniciones), al igual que en sus relaciones. Con la intención de ejemplificar el proceso de modelización, recurrimos a una situación (episodio) en el que una profesora pretende presentar el contenido (concepto de milésima) durante dos momentos distintos. En primer lugar, abordamos lo que entendemos en relación con cada una de las componentes del modelo, y en segundo presentamos el proceso de modelización y las relaciones entre las componentes. Por último, debatimos sobre algunas implicaciones de este tipo de análisis para y en la formación de profesores.

PALABRAS CLAVE: Práctica docente, Cogniciones, Modelo de enseñanza, Relaciones entre cogniciones, Formación de profesores.

 

ABSTRACT

In this article we focus our attention on the classroom and, more specifically, on the actions of the teacher during the teaching process, since we consider that said actions are conditioned or strengthened by their cognitions (beliefs, mathematical knowledge for teaching and objectives). For this reason, we explain and discuss an analytic model in relation to the practice of the teacher, which focuses on their actions, cognitions and type of mathematical communication that promotes (as an exteriorization of cognitions), as well as in their relations. In order to illustrate the modeling process,we use a situation (episode) in which a teacher presents the concept (concept of millesimal) during two different moments. First of all, we tackle what we understand in relation to each of the components of the model and, secondly, we present the modeling process and the relationships between components. Finally, we discuss some of the implications of this type of analysis in the training of teachers.

KEY WORDS: Teaching practice Cognitions Teaching model Relationships between cognitions Teacher training.

 

RESUMO

Neste artigo, enfocamos a nossa atenção na aula e, de forma mais concreta, nas ações do professor durante o processo de ensino, já que consideramos que tais ações são condicionadas ou potencializadas por suas cognições (crenças, conhecimento matemático para o ensino e objetivos). Por este motivo, expomos e discutimos um modelo de análise sobre a prática do professor, o qual está enfocado nas ações, cognições e tipo de comunicação matemática que promove (como uma manifestação das cognições), assim como em suas relações. Com intenção de exemplificar o processo de modelagem, recorremos a uma situação (episódio) no qual uma professora simula apresentar o conteúdo (conceito de milésimo) durante dois momentos diferentes. Em primeiro lugar, abordamos o que entendemos com relação a cada um dos componentes do modelo, e, em segundo lugar, apresentamos o processo de modelagem e as relações entre os componentes. Por último, debatemos sobre algumas implicações deste tipo de análise para e na formação de professores.

PALAVRAS CHAVE: Docência, Cognições, Modelo de ensino, Relações entre cognições, Formação de professores.

 

RÉSUMÉ

Article centré sur la salle de cours, ce travail aborde plus concrètement le thème des professeurs et de leurs actes lorsqu'ils sont en train d'enseigner en partant du principe que lesdits actes semblent conditionnés ou favorisés par leur cognition (croyances, connaissance dans la matière qu'ils enseignent ici les mathématiques et objectifs à atteindre). Dans cette optique, un modèle analytique sur la pratique pédagogique du professeur est proposé et débattu, modèle focalisé sur leurs actes, leur cognition et le type de communication promu (en tant qu'extériorisation des cognitions) tout comme sur les rapports existant entre ces différentes composantes. Afin d'illustrer ce processus de modélisation, une situation (un épisode) a été retenue ou Ton observe une professeure essayer de présenter un contenu (le concept des millièmes) à deux moments distincts. A partir de cette situation, nous mentionnons, dans un premier temps, ce que nous comprenons dans la perspective de chacune des composantes du modèle. Puis, le processus de modélisation et les rapports entre ses composantes sont exposés. Enfin, quelques implications avec ce type d'analyse pour et au cours de la formation des professeurs sont discutées.

MOTS CLÉS: Pratique pédagogique, Cognitions, Modèle d 'enseignement, Rapports entre cognitions, Formation des professeurs.

 

1. INTRODUÇÃO

A forma como ocorre o processo de ensino depende, em larga medida, do papel desempenhado pelo professor, pois as decisões tomadas influenciam diretamente todo o processo. Centrarmos a nossa atenção na sua atuação, permite–nos obter um maior entendimento sobre o que na sua perspetiva se passa na sala de aula e sobre como as suas decisões e consequentes ações influenciam e são influenciadas pelas suas cognições. Como parte relevante destas relações, consideramos também o tipo de comunicação promovido, pois assumimos que elas se manifestam através deste e das ações levadas a cabo. Assim, quanto mais soubermos sobre estas dimensões, e suas relações, melhor podemos conhecer o seu processo de ensino (Schoenfeld 1998a; Ribeiro, Monteiro & Carrillo, 2009).

Para isso, iniciámos uma investigação ampla, distribuída por três fases distintas ao longo de um ano letivo, envolvendo duas professoras do Iº Ciclo¹ do ensino básico. Elaborámos um modelo a partir do de Schoenfeld (1998a, 1999) e de uma adaptação de Monteiro, Carrillo e Aguaded (2008) e Ribeiro, Carrillo e Monteiro (2008), que nos dáuma visão mais clara e ampla do processo de ensino. Algumas das alterações/adaptações prendem–se com a inclusão de algumas dimensões (e.g. tipos de comunicação matemática promovida (Brendefur & Frykholm, 2000; Carrillo, Climent, Gorgorió, Prat & Rojas, 2008)) e a especificação de alguns aspetos (subdomínios) do conhecimento de matemática do professor (Ball, Thames & Phelps, 2008), bem como a opção de assumir que os objetivos do professor desempenham um papel central aquando do início do processo de modelação. O modelo tem vindo a ser atualizado à medida que efetuamos a análise, por uma comparação constante entre as análises anteriores e os novos dados obtidos (Strauss & Corbin, 1997).

A inclusão do tipo de comunicação matemáticapromovidabaseia–seno facto de consideramos ser a forma como comunicamos um bom indicador de como encaramos cada situação que vivenciamos – assumindo as interações subjacentes a cada forma de comunicar, entre professor, alunos e conteúdo matemático, um papel importante de modo a permitir a compreensão / elaboração conjunta de conceitos (Reséndiz, 2006).

A elaboração de tal modelo encontra–se associada a um dos objetivos da investigação mais ampla relativo ao aceder a algumas dimensões do conhecimento profissional do professor na prática e o seu impacto nessa prática. Assim, a questão de pesquisa sobre a qual nos debruçamos aqui corresponde a saber:

Que cognições (crenças, conhecimentos (MKT) e objetivos) e tipos de comunicação matemática se encontram subjacentes às ações do professor numa aula de matemática no 1.° Ciclo e de que forma essas dimensões se relacionam?

De entre a panóplia de dimensões que se poderia incluir no conhecimento profissional dos professores, as cognições e tipos de comunicação matemática promovidos são aqui encarados como as dimensões que maior influência possuem no processo de ensino, pois assumimos que são as que irão moldar, não apenas a forma como o professor encara o seu papel na prática letiva, mas, fundamentalmente, como a efetiva. O foco na análise da prática do professor tem, também, por intuito entender o que é necessário saber / conhecer para tornar efetivamente produtiva a análise das dimensões envolvidas no processo de ensinar matemática, de cujos resultados se espera poder vir a proporcionar uma melhor e mais adequada formação de professores (nas suas distintas componentes).

A elaboração do modelo pretende permitir identificar, conjuntamente, as dimensões reveladas na prática e encontrar relações entre estas dimensões – possibilitando, desse modo observar como essas relações influenciam o processo de ensino. Neste texto focamo–nos essencialmente na exemplificação e discussão do processo de construção do modelo, ilustrando–o numa situação em que uma professora do 1.° Ciclo tem por objetivo apresentar o conteúdo (o conceito de milésima) em dois momentos distintos (sendo o segundo a continuação do anterior). Para além do processo de modelação, e sua discussão, abordamos ainda as relações emergentes entre as dimensões do conhecimento profissional consideradas. A partir das relações encontradas entre as dimensões em análise, e a sua pertinência relativamente ao que ocorre, como ocorre e porque ocorre no processo de ensino, discutimos também algumas implicações/potencialidades para o ensino e a formação.

 

2. AS COGNIÇÕES

Consideramos que as cognições crenças, conhecimentos, e objetivos que cada indivíduo possui. O facto de centrarmos a análise nas cognições prende–se com o aspeto de considerarmos que estas desempenham um papel fulcral no processo de ensino de cada professor – cada uma a seu nível – e que das relações entre elas se podem obter muitas informações sobre esse processo. As cognições do professor têm uma influência direta na sua prática pois moldam, e são moldadas, pela forma como este encara todo o processo bem como pela sua postura perante a sua própria ação e situação profissional. Dependendo do seu tipo de crenças relativamente ao processo de ensino, assim moldará e priorizará os seus objetivos, imediatos ou não, que são também delineados de acordo com os seus conhecimentos pois poderá potenciar umas situações em detrimento de outras.

Nesta secção apresentamos brevemente cada uma das dimensões cognitivas e o modo como as consideramos no presente artigo.

2.1. Crenças

Pela panóplia de definições de crenças que se podem encontrar (e.g. Pajares, 1992; Grootnboer, 2008) e devido à grande discussão que ocorreu a certa altura relativamente à distinção entre crenças e conceções, é importante, desde logo, clarificar que aqui assumimos crenças e conceções num mesmo sentido, não se diferenciando umas de outras, utilizando sempre a nomenclatura de crenças. Seguindo Garcia, Azcárate e Moreno (2006), mas sem efetuar a distinção assumida por estas autoras, encaramos as crenças dos professores como estando fundamentadas, por um lado, no empírico ou intuitivo, e por outro como produto do pensamento e entendimento sobre determinado conceito.

As crenças dos professores relativamente à matemática e a todo o processo de ensino e aprendizagem desempenham um importante papel nas suas próprias práticas letivas (Calderhead, 1996) pois são elas que condicionam o professor na seleção e priorização dos seus objetivos e ações (Aguirre & Speer, 1999), podendo condicionar ou potenciar determinado comportamento docente (Schoenfeld, 1998a, 1999).

Para a sua análise, utilizaremos o instrumento de Climent (2005), onde a autora considera as crenças como os posicionamentos que o investigador interpreta que o professor possui a partir da análise das suas opiniões. Climent apresenta um conjunto de indicadores de crenças de professores dos primeiros seis anos de escolaridade, relativamente a crenças sobre metodologia (prática letiva, atividades de sala de aula, fontes de informação, diferenciação individual, utilização de materiais manipulativos, objetivos do processo de ensino e programação), matemática escolar (orientação, conteúdo, como é considerada e finalidade), aprendizagem (como se realiza, de que forma se realiza, que processos se utilizam, qual é o papel / importância da argumentação dos alunos, interações professor/ alunos /matéria, tipos de agrupamento), o papel de alunos (participação na planificação, responsabilidade pela aprendizagem – chave de transferência E–A, o que faz, como o faz e para que o faz) e o papel do professor (o que faz /como o faz/metodologiaou atitude pedagógica/como atuae relativas à validação da informação).

2.2. Objetivos

Durante o processo de ensino os objetivos podem ser perspetivados a curto ou a médio/longo prazo. Considerando os objetivos como algo que se pretende atingir (Schoenfeld, 1998a), podem ser explícitos, ou não, podendo inclusivamente o indivíduo não estar completamente consciente do alcance das suas ações e do peso / importância das suas palavras/atuações. Tal como qualquer outra cognição, não podemos falar de objetivos isolados, mas sim num sistema de objetivos. Os seus diversos níveis (imediato, amédio e longo prazo) conjugam–se, de forma preferencialmente simbiótica, para permitir uma maior profundidade de alcance no núcleo de tal sistema, de modo a que o conjunto de ações executado com esse fim seja efetivamente proveitoso nesse sentido. Os objetivos que mais rica, e fidedigna informação nos podem fornecer são os que se tornam explícitos durante o processo de ensino, ou seja, os que se manifestam em ação.

Aguirre e Speer (1999) assumem que estes podem ser pré–existentes ou emergentes – durante a ação. Para nós, os objetivos emergentes encontram–se associados a improvisações de conteúdo (Ribeiro, Carrillo & Monteiro, 2009). Considerando o indivíduo como um ser completo, e seguindo a linha de Saxe (1991), defendemos que todos somos capazes de construir, adaptar, modelar e remodelar os nossos próprios objetivos (em particular qualquer professor, imerso no processo de ensino), de acordo com o nosso próprio percurso, experiências, vivências e conhecimentos.

Ao efetuar um estudo centrado nos objetivos, a informação poderá ser obtida de forma declarada ou não. Estes podem ser objetivos declarados imediatamente antes do início da aula ou no decurso de uma entrevista (correspondendo a parte do que Schoenfeld (1999) denomina de imagem da lição – onde podem estar incluídos aspetos que normalmente não foram explicitados na planificação mas que são importantes pois são estruturais para o decurso da aula). Estes podem ainda ser declarados durante o decurso da aula, referindo de forma explícita qual(ais) se pretende(m) que seja(m) a(s) aprendizagem(ns) dos alunos. Por outro lado podem ser também promovidos/perseguidos objetivos não declarados, os quais podem emergir na prática. Não existe, assim, obviamente, uma correspondência unívoca entre os objetivos que o professor pretende atingir e as acções que toma com esse fim.

2.3. Conhecimentos

O conhecimento profissional dos professores é distinto do de outros profissionais, mesmo utilizando diariamente a matemática, pois, é–lhes necessário conhecerem os conteúdos matemáticos a ensinar mas também distintas formas de os tornar compreensíveis para os seus alunos e de relacionar os que estão a ser abordados com os que podem vir a ser ou já o foram, explorando estas possíveis conexões. Para Shulman (1986), as três componentes fundamentais que sustentam a especificidade de cada matéria a ensinar são, respetivamente, o conhecimento: do conteúdo; didático do conteúdo e curricular. Ball e colegas (Hill, Rowan e Ball, 2005; Ball et al., 2008) refinam a conceptualização de Shulman (1986) e propõem uma outra divisão do conhecimento profissional docente relacionado com o conteúdo a ensinar (considerando também como fundamentais os três referidos anteriormente), introduzindo a noção de mathematical knowledge for teaching (MKT). Aglutinam o conhecimento curricular com o conhecimento didático do conteúdo, obtendo assim apenas duas grandes áreas que se encontram, por sua vez, cada uma delas subdivididas em três subdomínios. O conhecimento do conteúdo é, assim, constituído, pelo horizon content knowledge (HCK) (onde se incluem as conexões entre os conhecimentos ao largo da escolaridade), common content knowledge (CCK) (saber fazer) e specialized content knowledge (SCK) (saber para poderem ensinar a fazer), enquanto as três componentes do conhecimento didáctico do conteúdo (que contém o conhecimento curricular de Shulman) respeitam ao knowledge of content and teaching (KCT) (conhecer a matemática relacionada com a preparação das tarefas e os recursos), ao knowledge of content and students (KCS) (conhecer as dificuldades matemáticas dos alunos), e ao knowledge of content and curriculum (KCC) (conhecer os materiais curriculares e sua relação /correspondência com o currículo).

De entre os muitos marcos teóricos relativos ao conhecimento profissional dos professores, optámos pelo MKT (Ball et al., 2008) pois, como foi referido anteriormente, um dos nossos objetivos corresponde–se com aidentificação do conhecimento a que os professores recorrem (revelam), em cada momento concreto. Esta opção deveu–se à clareza da classificação que não apresenta demasiadas dimensões, não conduzindo a um excesso de detalhe que poderia ser, no âmbito do nosso estudo, menos significativo. Justifica–se também pela fácil compreensão, que impede que se verifiquem perdas de informação eventualmente relevante e ao facto de pretendermos também chamar a atenção para a necessidade de se discutir com maior "intensidade" e profundidade que matemática os professores necessitam saber para que possam, no decurso das suas funções, formar futuros adultos críticos, reflexivos e matematicamente competentes.

 

3. TIPOS DE COMUNICAÇÃO MATEMÁTICA PROMOVIDA

Neste contexto entendemos tipos de comunicação como os diferentes tipos de comunicação matemática apresentados por Brendefur e Frykholm (2000) – unidirecional, contributiva, reflexiva e instrutiva. Concebemos o ensino como um espaço de comunicação, onde o discurso (e ações) é o veículo que transporta a maioria das aprendizagens que ocorrem na sala de aula (Reséndiz, 2006), daí assumirmos que a forma como o professor comunica fornece inúmeras informações sobre si próprio, a forma como se encara e a todo o processo de ensino. Fornece indícios sobre a sua postura relativamente a cada assunto, bem como o à–vontade, ou não, com que se relaciona com este. Como Potari e Jaworski (2002), consideramos aqui a comunicação como base do estudo do processo de ensino e seus resultados, mas também de análise da forma como a influencia, e é influenciada, na e pela prática.

Existem diversas teorias de comunicação, dependendo da área em que nos movemos. Encarando a comunicação como transmissão de informação, é considerado um emissor e um recetor, circulando a comunicação entre estes, omitindo–se os elementos particulares considerados no processo. Considerando, por outro lado, a existência de uma interação entre os participantes, que negoceiam significados, assume–se a comunicação como um processo de interação social (e.g. Ferin 2002). Elegemos esta última mas cingindo–nos apenas ao professor, sem discutir o tipo de interações entre os alunos e a sua importância no processo de ensino. Centramo–nos, assim, especificamente no tipo de comunicação matemática oral do professor (promovida) e consideramos os quatro tipos de comunicação propostos por Brendefur e Frykholm (2000), os quais complementamos com alguns aspetos colhidos de Carrillo et al., (2008) – veja–se mais adiante a distinção que efetuamos referente à comunicação do tipo contributivo e reflexivo.

Estes distintos tipos de comunicação são concretizados utilizando diversas estratégias comunicativas, como, por exemplo, diálogo interativo, diálogo socrático, diálogo não planeado, monólogo, mini–apresentação (e.g. Schoenfeld 1999; Schoenfeld, Ministrell & Zee, 1999). Saliente–se o facto de considerarmos que, durante a aula, a comunicação não é necessariamente toda do mesmo tipo, podendo no decurso ocorrer distintos tipos. A identificação, em cada situação (episódio – veja–se definição mais adiante), efetua–se pelo modo predominante de comunicação matemática verificado, não contabilizado de forma numérica, mas sim pela importância que os episódios/acontecimentos representam no decurso da mesma.

A comunicação unidirecional associa–se ao tipo de ensino em que o professor é protagonista do processo, competindo ao aluno apenas reproduzir textualmente o que ouve. É o tipo de comunicação característico do ensino tradicional, em que o professor questiona, o aluno responde e o professor avalia a resposta dada – apenas como aceitável ou não. Nestas situações o professor recorre, por exemplo a uma mini–apresentação (amplificação de determinada noção ou aspeto de uma forma declarada) ou ao que denominamos de diálogo validativo (quando o professor apenas pretende validar os conhecimentos que circulam na aula) a que estão associadas pseudo–questões (Ainley, 1988). A comunicação contributiva reconhece já ao aluno uma participação no decurso da aula – embora singela: os alunos interagem entre si e com o professor, cuja interação é de natureza corretiva e não conteudística. São situações em que o professor recorre também ao diálogo validativo e socrático (diálogo que se estabelece entre professor e alunos, assumindo este a sua direção). Podem ocorrer também situações de diálogos interativos, cuja direção, embora aparentemente fornecida pelo aluno, está planeada pelo professor. A comunicação reflexiva caracteriza–se pelo facto de as interações entre alunos e professor detonarem as investigações a ocorrer. Incluímos neste tipo de comunicação a pretensão de modificar a compreensão matemática dos alunos (considerada por Brendefur e Frykholm (2000) na comunicação instrutiva), pois pensamos que este atributo caracteriza as atividades de investigação que lhes são facultadas (Carrillo et al., 2008). A comunicação instrutiva, para além do que ocorre na comunicação reflexiva, pretende ainda esclarecer o tipo de tarefa/conteúdo que se irá abordar seguidamente. Caracteriza–se também pela integração das ideias dos alunos – avanços e dificuldades – manifestadas ou intuídas, tanto pelo professor como pelos próprios alunos. Encontram–se também associados os diálogos interativos, para além dos não planeados, cuja direção é dada pelos alunos e em que o professor considera útil e necessário um esclarecimento, construção de conteúdo, ou negociação de significados.

Transversal a todas as formas de comunicação, encontramos o que denominamos diálogos de gestão, correspondentes aos que ocorrem com o intuito de facilitar o decurso da aula e / ou preparar as atividades, não possuindo necessariamente uma relação estrita com o conteúdo (embora relacionados com a área e tema específico), mas ocorrendo necessariamente para preparar a exploração desse conteúdo, e que podem ser englobados no conhecimento sobre o ensino e sobre o conteúdo.

Pela análise das dimensões do conhecimento profissional (e suas relações) auspicia–se um maior e mais profundo conhecimento do processo de ensino, desempenhando as ações da professora e o tipo de comunicação um papel de evidenciador dessas relações.

 

4. O PROCESSO DE MODELAÇÃO E O CONTEXTO ENVOLVENTE

Este texto integra uma investigação mais ampla, subordinada ao estudo do desenvolvimento profissional de duas professoras do I° Ciclo. Aí pretende–se investigar o papel e influência das dimensões do conhecimento profissional (que consideramos nucleares) do professor na prática, e a forma como estas se alteram ao longo do tempo – estando as professoras envolvidas num grupo de trabalho colaborativo. Nesse sentido, um primeiro passo é a elaboração de um modelo de ensino de cada uma delas. Aqui referir–nos–emos apenas à atuação de Maria, uma dessas professoras, apresentando e discutindo, em particular, o modelo de análise num episódio considerado atípico (observado em dois momentos distintos do decurso da aula).

Maria possui dezoito anos de experiência, sendo este o décimo ano de permanência na mesma escola (situada numa pequena vila do Algarve, Portugal), tendo sido, professora dos mesmos alunos desde o primeiro ano de escolaridade. Declara abertamente que possui uma má relação com a matemática, preferindo ensinar a Língua Materna. Recorre, fundamentalmente, ao manual e reconhece que não sabe muito mais dos conteúdos para além do que se encontra exposto nesses mesmos manuais. Porém, considera ser boa professora pois refere que os alunos gostam das tarefas que lheprepara e tenta que estas sejam apresentadas de modo a que eles se sintam motivados.

Para a análise da prática optámos pela elaboração de um modelo pois consideramos que este é um processo que permite ilustrar, de formamais percetível e simplificada, algo complexo. Na construção do desse modelo baseamo–nos nos trabalhos de Schoenfeld (1998a, 1998b, 1999) e de Ribeiro etal. (2008), bem como de Monteiro et al. (2008) para as Ciências da Natureza. Consideramos como elementos do modelo as dimensões nucleares do conhecimento profissional do professor: objetivos (explicitados nas entrevistas antecedentes (por via da imagem da lição) e / ou observados / inferidos no decurso da prática)²; as manifestações de crenças; os subdomínios do MKT e os tipos de comunicação matemática promovidos; os recursos e a(s) forma(s) de trabalho dos alunos. Focamos simultaneamente a atenção em cada uma destas dimensões de forma isolada, mas também na(s) forma(s) como se inter–relacionam e influem na prática.

Optámos por considerar a aula como um todo formado por partes disjuntas (episódios) e fenomenologicamente coerentes, os quais se encontram associados aos objetivos do professor e são delimitados por ações que correspondem aos eventos desencadeantes e de término. Para nomear os episódios, foi tido em conta, para além do objetivo da professora em cada situação concreta, os demais aspetos referidos anteriormente (conteúdo, comunicação matemática, forma de trabalho e recurso(s)). Cada episódio ocupa um determinado período de tempo e nele a professora interatua com os alunos exteriorizando as dimensões em análise. Durante estas interações identificam–se os indicadores (manifestações) de crenças³ e os subdomínios do MKT ativados – o que nos permite responder a um dos objetivos da nossa questão de pesquisa (que crenças e conhecimentos se encontram subjacentes às ações do professor numa aula de matemática no 1° Ciclo?).

Crenças e subdomínios do MKT foram identificados por exaustão (Strauss & Corbin, 1997), selecionando todos os episódios do mesmo tipo e efetuando a identificação que mais parecem evidenciar–se. Em cada cluster de episódios é efetuada uma análise transversal subordinada a estas dimensões, tornando assim o processo mais consistente, reduzindo, por triangulação, especificamente para as crenças, os indicadores atribuídos a cada episódio aos comuns a todos os do mesmo tipo identificados num mesmo cluster. Para os subdomínios do MKT o processo foi realizado no sentido inverso, considerando–se a reunião dos subdomínios correspondentes, sendo posteriormente efetuado o seu refinamento também por triangulação⁴. Uma vez que os conhecimentos são, muitos deles, transversais a vários episódios, e também, alguns, a todo o período de ensino, foi efetuada uma análise longitudinal e por enquadramento, considerando os episódios antecedentes e consequentes ao analisado.

Porém este processo de modelação não é linear pois, embora o professor possa ter uma ideia muito clara do que se passará, uma multiplicidade de situações pode levar a desviar o decurso da aula daquilo que foi imaginado (uma pequena mudança nas condições iniciais poderá induzir uma grande alteração no produto final). Por existirem objetivos prioritários, o professor poderá sentir necessidade de retomar o ponto em que estava antes do desvio (embora não deva ser demasiado rígido, alguma linha condutora deverá possuir de modo a ir ao encontro dos interesses, necessidades, percurso, ... dos alunos). As ações do professor devem ser, aqui, identificadas com a sua performance na sala de aula ao lidar com as situações de construção de conhecimento por parte dos alunos. Aquando da sua enunciação (cf., adiante, tabelas I e II) apenas nos focaremos na professora mas essas ações ocorrem, obviamente, em função dos alunos que tem pela frente e são, "por vezes", o reflexo das atividades destes.

Oprocessodemodelação–divisãodaaulaemepisódiosfenomenologicamente coerentes e identificação, nestes, das dimensões do conhecimento profissional –  inicia–se com a recolha de dados, áudio e vídeo, centrada na professora, e a respetiva transcrição, linha a linha, complementada pela visualização do vídeo – para captar as ações da professora. Esta recolha possibilita também uma futura reflexão sobre a sua própria atuação através da sua visualização (Star & Strickland, 2008).

Centrando–se a recolha de dados na professora, o investigador desempenhou um papel não participativo. Pretende obter–se um conhecimento mais profundo sobre uma realidade específica (o que a professora faz e porque o faz, naquelas aulas específicas), pelo que estamos perante um estudo de caso, utilizando uma metodologia de índole interpretativa (Stake, 2000).

A recolha de informação ocorreu durante um conjunto de aulas de introdução a novos tópicos (no caso vertente, o conceito de milésima) pois consideramos que são estas as situações em que, mais marcadamente, se obtêm mais ricas e profícuas informações sobre o processo de ensino e a forma como o professor o encara. Nesta análise, o tipo de comunicação desempenha um papel transversal pois influencia e é influenciado por todas as demais dimensões, existindo, inclusivamente, situações em que, para uma mesma ação, as manifestações de crenças que lhe estão associadas poderem diferir com o tipo de comunicação predominante nesse episódio.

 

5. UMA SITUAÇÃO EXEMPLIFICATIVA

Para ilustrar o processo de construção do modelo apresentamos um excerto de uma transcrição da primeira aula, de um conjunto de quatro dedicadas à introdução do conceito de milésima. Este episódio foi selecionado propositadamente parailustrar o processo de modelação e a análise efetuada pois consideramos que, dentro da complexidade do processo de ensino, este é relativamente simples, envolvendo um número bastante limitado de subdimensões de cada uma das componentes, o que permite uma apreensão mais profunda do modelo, do processo de modelação e da análise das (inter)relações entre as dimensões. A análise e discussão desta relativa simplicidade potencia também um equacionar de alguns dos possíveis motivos subjacentes à prática, servindo como rampa de lançamento para uma discussão mais ampla da matemática envolvida em cada situação específica e / ou a que lhe deveria(á) estar associada para uma efetiva aprendizagem (Ribeiro & Carrillo, 2011).

Por forma a contextualizar o episódio que se discute, e a modelação apresentada, referimos sumariamente episódios que antecederam este específico. Imediatamente após o início da aula, Maria, (recorrendo apenas ao diálogo) revê a que corresponde uma décima – expressando que se trata de uma das dezpartes em que se divide a unidade. Noutro episódio, revê a relação numérica entre décimas e centésimas, efetuando seguidamente (antes do episódio de apresentação que aqui de discute) uma revisão mais clarificadora do que corresponde efetivamente a uma décima, recorrendo a uma imagem por forma a promover uma visualização dessa correspondência – entre unidade e décima.

O episódio que aqui discutimos (e o processo de modelação do mesmo) encontra–se interrompido (no número de linhas) pois a professora, a certa altura, suspende o objetivo que persegue e executa três outros episódios, no caso, todos de revisão do conteúdo⁵ e em grande grupo. Dois destes episódios faziam parte da imagem dalição e são levados acabo associados aumacomunicação unidirecional, enquanto o último ocorre de forma contributiva. No que surge imediatamente a seguir (128–162)⁶ Maria revê a determinação da medida do lado de um retângulo (em quadrados), sabendo o outro, e o número total de quadrados que o compõem, tendo como recurso a projeção do acetato – Maria diz aos alunos: o retângulo está dividido em milpartes. Tem como evento desencadeante as duas últimas linhas da transcrição que se apresenta (128–129), também para evidenciar a continuidade. No episódio seguinte (163–243) Maria persegue o mesmo objetivo, mas agora com recurso ao desenho no quadro (o que revela também o nível de especificidade da divisão dos episódios). Embora fizessem parte da imagem da lição, a professora não tinha equacionado a sua realização deste modo intercalado. Antes de retomar a apresentação do conteúdo, revê, oralmente, de forma contributiva, a diferença entre quadrados e retângulos (244–268).

Após a sua suspensão, e execução dos três episódios de revisão intercalados referidos acima, Maria retoma o episódio, chamando a atenção para o acetato (que corresponde ao evento desencadeante da segunda ocorrência do episódio).

Dois dos passos para efetuar a modelação deste episódio estão já dados: identificar o objetivo específico a cada momento e determinar os eventos iniciais e finais correspondentes. Após a análise da transcrição e das conversas informais anteriores a posteriores à(s) aula(s) determinou–se que o objetivo de Maria é, aqui, o de apresentar o conceito de milésima, utilizando um acetato. Os eventos delimitadores correspondem à projeção do acetato e à solicitação da atenção dos alunos. Na primeira ocorrência não existe evento de término pois a professora suspende o objetivo a que se tinha proposto – daí que se verifique uma divisão do episódio em duas ocorrências – correspondendo o evento de término ao facto de a professora arrumar o projetor e dar assim por terminada a apresentação deste conteúdo com aquele recurso.

Neste episódio específico Maria executaum conjunto de cinco ações distintas que podem depender, ou não, do tipo de comunicação promovido. Na primeira ocorrência ocorrem duas ações independentes do tipo de comunicação. Por um lado, dialoga com o grupo, e diz o que vai apresentar de seguida (110–112) e, daí até ao final (113–127), dialoga com o grupo e projeta um acetato (com um retângulo dividido em mil partes iguais). Na segunda ocorrência as ações encontram–se associadas a uma comunicação unidirecional e à utilização do acetato como recurso. Estas podem ser resumidas como: recapitula a que corresponde cada quadrado pequeno do retângulo (do acetato) que se encontra dividido em mil quadrados (269–278); apresentao nome de cadaum dos mil quadrados em que a unidade está dividida (279–284) e, por fim, clarifica em quantas partes está dividida a unidade (285–292). (É de salientar aqui a importância da mudança propositada de linha na transcrição sempre que o objetivo específico associado àquele instante evolui, pois isso torna possível uma divisão fenomenologicamente coerente da prática em episódios e sub–episódios – ações).

 

6. APRESENTANDO A MODELAÇÃ

As observações podem ser sintetizadas de modo simplificado que, considerados todos os episódios, permite obter um modelo da prática. A modelação do episódio que se apresenta deverá ser entendida no contexto das aulas analisadas, tendo passado pelos processos de identificação de cada uma das componentes anteriormente descritas.

Na Tabela I encontramos a modelação correspondente à primeira ocorrência do episódio (Figura 1) – em termos de ações, e de evento desencadeante – acrescido das dimensões do conhecimento profissional consideradas. Na Tabela II (correspondente à segunda parte da transcrição apresentada – Figura 2), por questões de simplicidade, não se repetem os elementos do nosso modelo, apenas se refere o evento desencadeante e de término e se indicam as ações da professora correspondentes a esse período (linhas datranscrição).

 

 

Segundo a nossa conceção de episódio, o que aqui se analisa, embora dividido em duas situações distintas é apenas um, visto a professora visar o mesmo objetivo matemático e de o perseguir de forma idêntica. Por corresponder ao sexto episódio daprimeiraaulaé identificadopor [1.6], e as ações (sub–episódios), vão sendo numeradas àmedida que ocorrem ([1.6.1], ..., [1.6.5]).

É de salientar que a sequência de ações apresentada neste caso concreto pode não ocorrer em todos os episódios deste tipo, pois a professora pode considerar não ser necessária determinada ação ou, visto a aula ser uma sequência de acontecimentos fenomenologicamente coerentes, pode essa ação ter sido já realizada anteriormente no decurso de um outro episódio (e.g. escrever no quadro, projetar um acetato).

Dado o episódio dividir–se em duas ocorrências, o modelo reflete essa divisão pois, sendo todos os episódios disjuntos, o modelo vai evoluindo à medida que avançamos na transcrição. Assim, às duas ocorrências na transcrição estão associadas duas ocorrências no modelo. Por forma a simplificar a leitura, e por nesta segunda ocorrência as ações da professora se associarem ao tipo de comunicação matemática promovido, aquando da referência às ações da professora, do lado direito do modelo, onde se lê "P (...), recapitula o conteúdo", deve ler–se: "P dialoga com o grupo e, com recurso ao acetato, de forma unidirecional, recapitula o conteúdo".

Na modelação apresentamos as ações pela ordem de ocorrência neste episódio, para a tornar mais clara porém, não estando a mente humana mecanizada (ao contrário de um qualquer script que se implemente num programa computacional)⁸, noutra situação a professora poderá executa–las por outra ordem distinta (e.g. Ribeiro et al., 2008). Este facto é um dos aspetos que complexifica simultaneamente a prática letiva (pela multiplicidade de opções e de fatores que a influem) e, necessariamente, a obtenção de um mais amplo entendimento sobre esses fatores e a forma como a influenciam.

Assim, por uma modelação "direta" do processo letivo torna–se possível obter respostas para a primeira parte da nossa questão motivadora: que dimensões do conhecimento profissional do professor se encontram subjacentes às ações do professor numa aula de matemática no 1° Ciclo?. Essa identificação, apesar de nos fornecer algumas luzes e ideias que permitam contribuir para melhorar a formação de professores (dos mais distintos níveis) – que discutiremos na última secção deste texto –, não é ainda suficiente na tentativa de interpretar os motivos subjacentes ao que o professor faz e porque o faz durante a prática, sendo, assim, de suprema importância um maior entendimento relativo à(s) forma(s) como essas dimensões se (inter)relacionam e impactuam a prática.

6.1. Relações entre ações e crenças

As ações podem depender, ou não, do tipo de comunicação, pelo que podem agrupar–se nessas categorias, facilitando, assim, a associação dos indicadores de crenças (Climent, 2005), às respetivas ações. Recorde–se que estes indicadores foram identificados por análise exaustiva de um conjunto alargado de aulas e por comparações constantes para refinar as categorias selecionadas. A cada ação estão associados os indicadores correspondentes (mais evidentes e comuns no conjunto global das ações) e, entre parêntesis, indica–se a categoria a que correspondem.

Algumas ações encontram–se associadas a dois indicadores enquanto outras apenas a um. Esta disparidade não exalta a importância de umas/uns em detrimento de outras/outros; ocorre apenas para tornar mais explícitas as crenças que se encontram associadas a cada ação, permitindo refinar a análise do processo de ensino (Strauss & Corbin, 1997).

Abaixo evidenciam–se as relações entre as ações de Maria que ocorrem de forma dependente do tipo de comunicação matemática e as crenças que revela (omite–se aqui o conteúdo específico a que cada uma delas se encontra associada, mas esse pode ser consultado na Tabela II).

Estas manifestações de crenças, ao associarem–se a uma comunicação unidirecional, reforçam as relações de interdependência entre as distintas dimensões do conhecimento profissional do professor, evidenciando também alguns dos aspetos em que estes influem a prática (e as possíveis aprendizagens dos alunos, ou pelo menos as imagens com que estes ficam relativamente à matemática e ao processo de ensino). Manifestações de crenças e tipo de comunicação encontram–se, assim, pela conceptualização que assumimos, em plena sintonia, ativando–se mutuamente.

6.2. MKT identificado e ações associadas

As ações e tipo de comunicação promovido na aula permitem aceder ao MKT da professora a cada momento. Visto os subdomínios do MKT serem transversais a todo o episódio (e por vezes a todo o processo de ensino), não podemos afirmar que existe uma atribuição estreita entre cada uma das ações e os subdomínios identificados, porém, algumas delas – em particular as que são independentes do tipo de comunicação – associam–se ao knowledge of content and teaching (KCT), que correspondem, pelo menos numa observação direta, às ações da Tabela III. Neste episódio, que recorde–se foi selecionado também pela sua simplicidade, Maria revela dois subdomínios do MKT (CCK e KCT) que se encontram associados a determinadas ações da professora (períodos da aula). Esta associação não pode considerar–se estanque pois o MKT apresenta um carácter longitudinal (cuja ideia é transmitida pela coluna mais à direita da tabela seguinte) e por outro lado os subdomínios são (revelam–se) também locais/específicos (especificamente relacionados com determinada ação ou sequência de ações, e em cada situação específica).

 

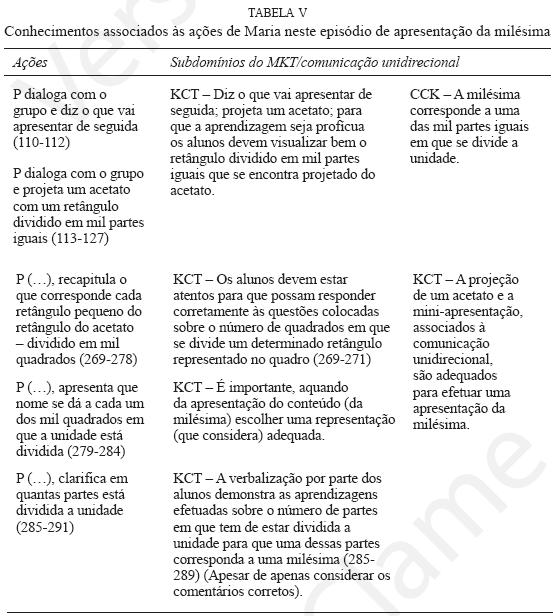
As duas primeiras ações (primeira ocorrência do episódio) são independentes do tipo de comunicação promovido e associam–se a um conhecimento das estratégias e sequenciação das tarefas (KCT). Transversalmente a todo o episódio Maria revela um CCK associado ao conhecimento da noção de milésima e um KCT que se manifesta na associação da projeção de um acetato e da mini–apresentação a uma comunicação unidirecional, assumindo–as como adequadas à apresentação da milésima.

Na segunda parte do episódio, ao recapitular, apresentar e clarificar o conteúdo concreto, para além do CCK e KCT transversais revela, fundamentalmente, associado a cada uma das ações específicas, um KCT – o que, pelo que se lhe encontra associado, evidencia também a importância que atribui à gestão da aula (necessidade de os alunos estarem atentos pois só assim podem responder corretamente às questões sobre o tópico matemático) e ao facto de as tarefas terem de ser atrativas e motivadoras para os alunos (escolha da representação mais adequada para apresentar o conteúdo).

A apresentação e discussão de um único episódio, e do seu processo de modelação, permite discutir também os subdomínios do MKT associados a esta situação específica (não efetuando aqui qualquer tipo de abstração) e, dessa forma, as relações entre as diferentes componentes em análise. Pelo processo de modelação, e análise das (inter)relações torna–se possível constatar o facto de ocorrerem ativações prioritárias de ações e/ou de crenças associadas mutuamente, ou seja, sem supremacia de umas relativamente a outras. As ações base deste cluster de episódios (de apresentação do conteúdo) correspondem às de rever, clarificar e apresentar o conteúdo (Ribeiro et al., 2008). Existem, portanto, ações nucleares (e as consequentes crenças associadas) às quais vão sendo aglomeradas outras que dão forma ao episódio concreto (e.g. projeta um acetato; diz o que vão apresentar de seguida) e que se encontram associadas especificamente ao KCT. MKT e objetivos são, portanto, concretizados através das ações, sendo estas também direcionadas pelas crenças. Existe, assim, uma dialética entre as dimensões consideradas (ações, crenças, MKT e tipo de comunicação matemática promovido) daí, também, que estes se considerem elementos indissociáveis (embora distintos) do mesmo conjunto.

 

7. BREVES COMENTÁRIOS E POTENCIALIDADES PARA A FORMAÇÃO DE PROFESSORES

Nesta secção sumariamos e discutimos os nossos resultados relativamente ao processo de modelação, às relações obtidas e algumas possíveis implicações para o /no ensino e formação de professores (inicial e contínua).

A análise daprática, e o processo de modelação apresentado, com as relações emergentes, tem por intuito possibilitar um aprofundamento na compreensão da prática, dos fatores que a influenciam (potenciam e/ou limitam – em termos das dimensões do conhecimento profissional do professor consideradas nucleares) e como/porque o fazem, procurando responder assim às nossas questões motivadoras. Esta aproximação tem sempre no horizonte (ainda que por vezes longínquo) possibilidades de aprender com essa mesma prática de forma a melhorá–la e à formação. O recurso ao modelo apresentado possibilita alcançar uma visão mais concreta desses fatores (na prática de Maria) e como o fazem, permitindo identificarpossíveis situações críticas na sua prática que urge colmatar (levando apotenciar as oportunidades de aprender facultadas aos alunos) e também equacionar a natureza das dimensões que deveriam estar presentes por forma a possibilitar aprendizagens efetivamente ricas e produtivas (Ribeiro & Carrillo, 2011). A opção pela elaboração de um modelo na busca de respostas às nossas questões motivadoras prende–se também com o facto de pretendermos deixar claro o não assumirmos a supremacia de alguma dimensão sobre as demais – dai também a nossa conceptualização do modelo formado por dimensões que, assumimos, se deverão conjugar simbioticamente num mesmo sistema.

No conjunto de aulas analisadas identificaram–se vários tipos de episódios de apresentação nos quais a professora suspende o objetivo em determinado instante para o retomar mais adiante. Para que isso ocorra duas situações se verificam: o percurso das atividades e / ou as questões dos alunos implicam a alteração da ordem da sequência inicialmente estipulada, ou emergiram novos objetivos que originaram improvisações. (Para mais informações sobre tipos de improvisações e sua ocorrência no decurso da aula consultar, por exemplo, Ribeiro et al. (2009) e Turner (2009).) Em qualquer destas situações o percurso da aula molda–se pelas intervenções/discussões dos alunos, pelo que, embora não se encontre (necessariamente) explícito ao analisar os episódios individualmente, Maria demonstra um Horizon Content Knowledge (HCK), relacionado especificamente com algum tipo/forma de conexões entre o tópico abordado naquele instante e os demais abordados nesse nível de escolaridade e em níveis distintos.

A análise da prática e das dimensões que a influem, e como o fazem, recorrendo ao modelo elucida, de forma explícita a impossibilidade em separar cada um das componentes do modelo, o que reforça também a ideia de que o conhecimento profissional do professor é algo por demais complexo formado por distintas dimensões, mas em que o todo é mais amplo que a soma destas. Concretamente, no que se refere ao MKT, ilustra também a dificuldade / impossibilidade em destrinçar os seus distintos subdomínios. Esta perceção – chamada de atenção – e tomada de consciência, por parte dos mais diversos intervenientes na ação e formação docentes poderá (pelo menos assim se espera) revelar alguma evidência da importância de explorar a matemática de forma integrada. Permitirá, também que os professores deixem de se focar essencialmente num conjunto de estratégias que consideram atrativas – (tarefas pedagogicamente excitantes), mas onde são perseguidos objetivos terminais e com uma prática que relega, efetivamente, os alunos e as suas aprendizagens para segundo plano (centrada no professor) e na obtenção de respostas imediatas a questões diretas (Tomás Ferreira, 2005) – tal como se verificou neste caso concreto com Maria –, e passem a focar–se em aspetos que lhe permitam preparar e implementar tarefas matematicamente ricas e desafiadoras (no sentido do MKT envolvido (e.g. Charalambous, 2008), associado a objetivos a longo prazo, o que as tornará, de forma expectável em matematicamente exigentes. Esta possibilidade de consciencialização trazida pelo recurso ao processo de modelação e (inter)relações constatadas poderá levar a uma reconfiguração da aproximação à prática por parte dos professores envolvidos⁹ (sempre com auxílio externo), deixando para outro plano a ênfase procedimental (Davis e Renert, 2009).

O processo de modelação potencia a emersão de ideias mais amplas e significativas relativamente aos professores em geral (quase como se de um estudo de caso instrumental se tratasse). Assim leva–nos a equacionar a natureza e tipo dos sistemas consistentes de cada uma das componentes em análise que cumprirá a cada professor possuir e que, em conjunto, formam um sólido e rico sistema de cognições (Ribeiro, 2010; Ribeiro et al., 2009). Apenas sendo detentores de um tal sistema geral –amplo e com uma capacidade mutacional e de enriquecimento constante–, envolvendo as distintas componentes, é possível permitirem aos seus alunos a capacidade de obterem uma compreensão relacional da matemática (Skemp, 1976), que deverá ser encarada e estendida à generalidade dos conteúdos, deixando de considerar a matemática como algo compartimentado e, simultaneamente, erradicando a ideia de uma visão instrumental baseada na memorização e na aplicação (muitas vezes sem compreensão) de procedimentos. É, portanto, importante e necessário que os professores desafiem os alunos constantemente, e esse desafio só será possível se os primeiros possuírem uma elevada auto–estima (Potari e Jaworski, 2002), consciente dos conhecimentos profissionais que detêm (nas suas mais diversas dimensões), conscientes das suas crenças (tanto quanto possível) e da implicação das suas ações na perseguição dos seus objetivos, podendo o modelo e processo de modelação aqui apresentado (com a consequente identificação das relações entre as suas dimensões) assumir um lugar de destaque na melhoria dessa prática e da formação.

 

AGRADECIMIENTOS

Este artigo foi parcialmente financiado pela Fundação para a Ciência e a Tecnologia (FCT) – Portugal.

Texto elaborado no âmbito do Projecto "Conocimiento matemático para la enseñanza respecto a la resolución de problemas y el razonamiento" (EDU2009–09789), Dirección General de Investigación y Gestión del Plan Nacional de I+D+i. Ministerio de Ciencia e Innovación (España).

 

REFERÊNCIAS

Aguirre, J., & Speer, N. (1999). Examining the relationship between beliefs and goals in teacher practice. Journal of Mathematical Behavior 18(3), 327–356.         [ Links ]

Ainley, J. (1988). Perceptions of teachers' questioning styles. In A. Borbás (Ed.), Proceedings of the 12^th Annual Meeting of the International group for the Psychology of Mathematics Education (pp. 92–99). Veszprém, Hungria: PME.         [ Links ]

Ball, D., Thames, M., & Phelps, G. (2008). Content knowledge for teaching: what makes it special? Journal of Teacher Education 59(5), 389–407. doi: 10.1177/0022487108324554         [ Links ]

Brendefur, J., & Frykholm, J. (2000). Promoting mathematical communication in the classroom: two preservice teachers' conceptions and practices. Journal ofMathematics Teacher Education 3(2), 125–153. doi: 10.1023/A: 1009947032694        [ Links ]

Calderhead, J. (1996). Teachers: Beliefs and Knowledge. In D. Berliner & R. Calfee (Eds.), Handbook of Educational Psychology (pp. 709–725). Nueva York: Macmillan.         [ Links ]

Carrillo, J., Climent, N., Gorgorió, N., Prat, M. y Rojas, F.(2008). Análisis de secuencias de aprendizaje matemático desde la perspectiva de la gestión de la participación. Enseñanza de las Ciencias 26(1), 67–76.         [ Links ]

Climent, N. (2005). El desarrollo profesional del maestro de Primaria respecto de la enseñanza de la matemática. Un estudio de caso. Tesis de doctorado. Recuperada de Michigan, Proquest Michigan University (www.proquest.co.uk).         [ Links ]

Charalambous, C. Y. (2008). Mathematical knowledge for teaching and the unfolding of tasks in mathematics lessons: Integrating two lines of research. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano & A. Sepulveda (Eds.), Proceedings of the 32^nd Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 281–288). Morelia, México: PME.Davis, B., & Renert, M. (2009). Mathematics–for–teaching as shared dynamic participation. For the learning of mathematics 29(3), 37–43.         [ Links ]

Ferin, I. (2002). Comunicação e culturas do quotidiano. Lisboa, Portugal: Quimera.         [ Links ]

Garcia, L., Azcárate, C. y Moreno, M. (2006). Creencias, concepciones y conocimiento profesional de profesores que enseñan cálculo diferencial a estudiantes de ciencias económicas. Revista Latinoamericana de Investigación en Matemática Educativa 9(1), 85–116.         [ Links ]

Grootenboer, P. (2008). Mathematical belief change in prospective primary teachers. Journal of Mathematics Teacher Education 11 (6), 479–497. doi: 10.1007/s10857–008–9084–x         [ Links ]

Hill, H. C., Rowan, B., & Ball, D. L. (2005). Effects of teachers' mathematics knowledge for teaching on student achievement. American Education Research Journal 42(2), 371–406. doi: 10.3102/00028312042002371         [ Links ]

Monteiro, R., Carrillo, J., & Aguaded, S. (2008). Emergent theorizations in Modelling the Teaching of Two ScienceTeachers. Research in Science Education 38(3), 301–319. doi: 10.1007/s11165– 007–9051–z         [ Links ]

Pajares, F. (1992). Teacher's beliefs and educational research: cleaning up a messy construct. Review of Educational Research 62 (3), 307–332.         [ Links ]

Potari, D. & Jaworski, B. (2002). Tackling complexity in mathematics teaching development: using the teaching triad as a tool for reflection and analysis. Journal for Research in Mathematics Education 5(4), 351–380. doi: 10.1023/A:1021214604230         [ Links ]

Reséndiz, E. (2006). La Variación y las explicaciones didácticas de los profesores en situación escolar. Revista Latinoamericana de Investigación en Matemática Educativa 9(3), 435–458.         [ Links ]

Ribeiro, C. (2010). A prática de uma professora e seus objectivos: percursos e (in)alterações. In H. Gomes, L. Menezes & I. Cabrita (Org.), Actas do XXI Seminário de Investigação em Educação Matemática 2010 (pp. 60–71). Lisboa, Portugal: APM        [ Links ]

Ribeiro, C. & Carrillo, J. (2011). Knowing mathematics as a teacher. In M. Pytlak, T. Rowland & E. Swoboda (Eds.), Proceedings of the Seventh Congress of European Society for Research in Mathematics Education, CERME 7 (pp. 2818–2826). Rzeszów: ERME. (ISBN: 978–83–7338– 683–9)         [ Links ]

Ribeiro, C., Carrillo, J. e Monteiro, R. (2008). Uma perspectiva cognitiva para a análise de uma aula de matemática do 1.° ciclo: um exemplo de apresentação de conteúdo tendo como recurso o desenho no quadro. En R. Luengo, B. Gómez, M. Camacho e L. J. Blanco (Eds.), Investigación en Educación Matemática XII (pp. 545–556). Badajoz, España: Sociedad Española de Investigación en Educación Matemática, SEIEM.         [ Links ]

Ribeiro, C., Carrillo, J. y Monteiro, R. (2009). De qué nos informan los objetivos del profesor sobre su práctica? Análisis y influencia en la práctica de una maestra. En M. J. González, M. T. González Astudillo y J. Murrillo (Eds.), Investigación en Educación Matemática XIII (pp. 415–424). Santander, España: Sociedad Española de Investigación en Educación Matemática, SEIEM.         [ Links ]

Ribeiro, C., Monteiro, R., & Carrillo, J. (2009). Professional knowledge in an improvisation episode: the importance of a cognitive model. In Durand–Guerrier, V., Soury–Lavergne, S. & Arzarello, F. (Eds), Proceedings of CERME6 (2030–2039). Lyon, France: ERME. Recuperado en Dicember de 2010 de
http://www.inrp.fr/editions/editions–electroniques/cerme6/working–group–10         [ Links ]

Saxe, G. (1991). Culture and cognitive development: Studies in mathematical understanding. Hillsdale, USA: Lawrence Erlbaum Associates.         [ Links ]

Schoenfeld,A. (1998a). On modeling teaching. Issues in Education 4(1), 149–162.         [ Links ]

Schoenfeld,A. (1998b). Toward a theory of teaching–in–context. Issues in Education, 4(1), 1–94.         [ Links ]

Schoenfeld, A. (1999). Models of the teaching process. Journal of Mathematical Behavior 18(3), 243–261.         [ Links ]

Schoenfeld, A., Ministrell, J., & Zee, E. v. (1999). The detailed analysis of an established teacher's non–traditional lesson. Journal ofMathematical Behavior 18(3), 281 –325. doi: 10.1016/S0732–3123(99)00035–8         [ Links ]

Shulman,L. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher 15 (2), 4–14.         [ Links ]

Skemp, R. (1976). Relational understanding and instrumental understanding. Mathematics teaching 77, 20–26.         [ Links ]

Stake, R. (2000). Qualitative case studies. In N. K. Denzin e Y. Lincoln (Ed.). Handbook of qualitative research. Qualitative case studies (435–454). Thousand Oaks: Sage.         [ Links ]

Star, J. & Strickland, S. K. (2008). Learning to observe: using video to improve preservice mathematics teachers' ability to notice. Journal of Mathematics Teacher Education 11(2),107–125.         [ Links ]

Strauss, A. & Corbin, J. (1997). Grounded theory in practice. Thousand Oaks, CA: Sage Publications.         [ Links ]

Stigler, J. & Hiebert, J. (1999). The teaching gap: Best ideas from the world's teachers for improving education in the classroom. New York, NY: The Free Press.         [ Links ]

Tomás Ferreira, R. A. (2005). Portuguese student teacher's evolving teaching modes: A modified teacher development experience. Unpublished Doctoral Dissertation, Illinois State University, IL, USA        [ Links ]

Turner, F. (2009). Developing the Ability to Respond to the Unexpected. In M. Joubert (Ed.), Proceedings of the British Society for Research into Learning Mathematics (Vol. 29(1), pp. 91–96). Cambridge (UK): British Society for Research into Learning Mathematics.         [ Links ]

 

NOTAS

¹ Primeiros quatro anos de escolaridade obrigatória em Portugal (alunos de 6 a 9 anos).

² Aqui indicamos os indicadores expressos na sua plenitude. Mais adiante, ao abordar as relações entre ações e crenças referiremos apenas as palavras–chave que se lhe podem encontrar associadas.

³ Foram efetuadas algumas menores adequações à especificidade do contexto a que foram aplicados – pois coincidimos com Stigler e Hiebert (1999), ao considerarmos que o processo de ensino é algo cultural, daí que seja também de sobeja importância incrementar o nosso entendimento sobre como essa culturalidade se estende/aplica às dimensões do conhecimento profissional do professor. Estes indicadores encontram–se, tal como o nome indica, associadas ao que o professor faz, exteriorizando determinado tipo de aproximação (e.g. a matemática escolar é exata e considerada acabada; não se utilizam materiais manipuláveis).

⁴ Esta triangulação e validação ocorreram também por via das discussões no âmbito do grupo de investigação, tanto a partir da confrontação das análises de vários elementos relativas a dados desta investigação como das discussões de outras situações de distintas sala de aula – tanto de Portugal como de Espanha.

⁵ As últimas três linhas desta primeira transcrição formam já parte de outro episódio intermédio.

⁶ Quando nos referirmos às linhas da transcrição consideramos sempre os valores apresentados incluídos nas referências que efetuamos.

⁷ Aqui indicamos os indicadores expressos na sua plenitude. Mais adiante, ao abordar as relações entre ações e crenças referiremos apenas as palavras–chave que se lhe podem encontrar associadas.

⁸ Entende–se script como um conjunto de instruções fornecidas a um programa que o computador executa sistematicamente, como um algoritmo, ao verificarem–se determinadas condições.

⁹ Aqui indicamos os indicadores expressos na sua plenitude. Mais adiante, ao abordar as relações entre ações e crenças referiremos apenas as palavras–chave que se lhe podem encontrar associadas.