Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.15 no.1 Ciudad de México mar. 2012
Artículos
Relaciones implicativas entre las estrategias empleadas en la resolución de situaciones lineales y no lineales
Implicative relations between strategies used in solving proportional and non–proportional problems
Ceneida Fernández*, Salvador Llinares**
* Universidad de Alicante, España. ceneida.fernandez@ua.es
** Universidad de Alicante, España. sllinares@ua.es
Recepción: Abril 23, 2010
Aceptación: Noviembre 15, 2011.
RESUMEN
Este estudio analiza las relaciones implicativas entre las estrategias usadas por 136 estudiantes de primer curso de educación secundaria en la resolución de problemas lineales y no lineales. En primer lugar, se describen las estrategias ocupadas por los alumnos y después, empleando el software CHIC, se identifican sus relaciones implicativas. Los resultados muestran que es importante que los estudiantes comprendan la idea de razón para que sean capaces de identificar las situaciones lineales; de igual manera, aportan información sobre los posibles precursores del desarrollo del razonamiento proporcional en los estudiantes de educación secundaria.
PALABRAS CLAVE: Razonamiento proporcional, Uso abusivo de la linealidad, Relaciones implicativas, Situaciones lineales, Situaciones no lineales.
ABSTRACT
This study analyzes the implicative relations between strategies used by 136 first year high school students in solving linear and non–linear problems. First of all, it describes the strategies used by students and then, using the CHIC software, it identifies implicative relations between them. The results demonstrate the importance of understanding the idea of reason in order to identify linear situations and information is provided in relation to possible precursors to the development of proportional reasoning.
KEY WORDS: Proportional reasoning, Abusive use of linearity, Implicative relations, Linear situations, Non–linear situations.
RESUMO
Este estudo analisa as relações envolvidas entre as estratégias usadas por 136 estudantes do primeiro ano do ensino médio na resolução de problemas lineares e não lineares. Em primeiro lugar, são descritas as estratégias utilizadas pelos estudantes, e depois, empregando o software CHIC, são identificadas as relações envolvidas entre elas. Os resultados mostram a importância da compreensão da ideia da razão para identificar as situações lineares, e é feita uma contribuição de informação sobre os possíveis precursores do desenvolvimento da lógica proporcional.
PALAVRAS CHAVE: Lógica proporcional, Uso abusivo da linearidade, Relações envolvidas, Situações lineares,Situações não–lineares.
RÉSUMÉ
L'analyse des relations implicatives entre les stratégies employées par 136 élèves en deuxième année de collège pour résoudre des problèmes linéaires et non–linéaires constitue le sujet de cette étude. Celle–ci commence, dans un premier temps, par une description desdites stratégies utilisées par les élèves. Puis, à l'aide du logiciel CHIC, elle se poursuit par une identification des relations implicatives qui existent entre ces stratégies. Les résultats obtenus démontrent l'importance de la compréhension de l'idée de raison lorsque l'on désire identifier des situations linéaires. Cette étude fournit également des informations sur les possibles précurseurs du développement du raisonnement proportionnel.
MOTS CLÉS: Raisonnement proportionnel, Utilisation abusive de la linéarité, Relations implicatives, Problèmes linéaires, Problèmes non–linéaires.
1. INTRODUCCIÓN
Durante años se ha demostrado que el razonamiento proporcional es extremadamente útil en la interpretación de fenómenos reales debido a que muchos aspectos de nuestra vida operan de acuerdo con esta estructura (Van Dooren, De Bock, Janssens & Verschaffel, 2008). De hecho, el razonamiento proporcional ha sido descrito como la consolidación del conocimiento aritmético en la escuela primaria y la cimentación de conceptos posteriores en la escuela secundaria (Karplus, Pulos & Stage, 1983; Lesh, Post & Behr, 1988). En este contexto, el concepto de razón como una función de un par ordenado de números o de valores de una magnitud (Freudenthal, 1983) y el concepto de proporción como una igualdad entre dos razones, son dos ideas fundamentales en el razonamiento proporcional. Se distinguen dos tipos de razones en base a la relación entre las cantidades. Por una parte, cuando se construye la relación multiplicativa entre dos elementos de la misma magnitud se denomina razón interna o escalar, y cuando se forman entre cantidades de magnitudes diferentes se denominan razones externas o funcionales. Por ejemplo, en el problema: "5 kilos de patatas cuestan 2 euros, ¿cuánto costarán 8 kilos de patatas?", la razón funcional vendría dada por la relación entre kilos y euros, mientras que la razón escalar serían las relaciones euros–euros o kilos–kilos. En las situaciones lineales, las razones internas son iguales [a/b = ƒ(a)/ƒ(b)] y las razones externas es una constante [ƒ(x)/x = k, para cualquier x]. A esta constante se le conoce con el nombre de constante de proporcionalidad. Vergnaud (1983) caracterizó este tipo de situaciones usando la idea de espacios de medida (en nuestro ejemplo, euros y kilos) y la idea de transformaciones internas y externas entre las variables–medida (Karplus et al., 1983; Modestou & Gagatsis, 2010). En esta investigación denominamos "problemas lineales" a las situaciones organizadas con la idea de razón y proporción.
Investigaciones recientes han mostrado que estudiantes de diferentes edades que resolvían situaciones lineales utilizando relaciones multiplicativas adecuadas también solían utilizar dichas relaciones en situaciones en las que no era adecuado su uso (De Bock, Van Dooren, Janssens & Verschaffel, 2002, 2007; De Bock, Verschaffel & Janssens, 1998; Ebersbach, Van Dooren, Goudriaan & Verschaffel, 2010; Fernández & Llinares, en prensa; Fernández, Llinares, Van Dooren, De Bock & Verschaffel, 2011; Modestou & Gagatsis, 2007; Van Dooren, De Bock, Evers & Verschaffel, 2009; Van Dooren, De Bock, Hessels, Janssens & Verschaffel, 2005). Este hecho ha puesto de manifiesto que el uso de estrategias correctas en la resolución de problemas lineales no conlleva necesariamente que los estudiantes puedan diferenciar los problemas lineales de los no lineales y puedan resolver adecuadamente las situaciones no lineales.
Por otra parte, las investigaciones han señalado que los estudiantes también suelen emplear estrategias erróneas en la resolución de los problemas lineales como calcular la diferencia entre las cantidades dadas y emplearla en el cálculo de la cantidad desconocida (estrategia aditiva) (Fernández & Llinares, 2011; Fernández, Llinares, Modestou & Gagatsis, 2010; Fernández, Llinares, Van Dooren, De Bock & Verschaffel, 2010; Hart, 1981; Misailidou & Williams, 2003; Tourniaire & Pulos, 1985). Por ejemplo en el siguiente problema lineal "En una fábrica de producción de tornillos dos máquinas fueron puestas en marcha al mismo tiempo, pero la maquina A es más lenta que la máquina B. Cuando la máquina A produce 600 tornillos, la máquina B produce 1200 tornillos. Cuando la máquina A haya producido 2400 tornillos, ¿cuántos tornillos habrá producido la máquina B?". La estrategia aditiva incorrecta seria: "como la diferencia entre los tornillos producidos por las dos máquinas es 1200–600 = 600, entonces la máquina B habrá producido 2400 + 600 = 3000 tornillos". En este sentido, decidir cuándo un problema está o no organizado por la idea de razón y proporción es esencial para el desarrollo del razonamiento proporcional y ha empezado a ser considerado una característica del desarrollo del razonamiento proporcional (Modestou & Gagatsis, 2009–a; Modestou & Gagatsis, 2010).
En particular, un ámbito de interés relevante para comprender mejor el desarrollo del razonamiento proporcional es identificar las características del comportamiento complementario en cuanto al uso no adecuado de relaciones multiplicativas en situaciones no lineales, y el uso no adecuado de relaciones no multiplicativas (por ejemplo, relaciones aditivas) en situaciones lineales. Es decir, la habilidad para resolver problemas lineales y la habilidad para diferenciarlos de los problemas no lineales. En este sentido, investigaciones previas han aportado análisis descriptivos de las estrategias usadas por los estudiantes en los diferentes tipos de problemas lineales (de valor perdido [donde tres datos son dados y se tiene que calcular el cuarto dato que es desconocido] como el problema lineal anterior, de comparación numérica [donde las razones son dadas y éstas deben ser comparadas] y de comparación cualitativa [una comparación es necesaria pero ésta no depende de valores numéricos específicos]) (Alatorre & Figueras, 2005; Christou & Philippou, 2002; Cramer & Post, 1993; Hart, 1984; Lamon, 1993; Misailidou & Williams, 2003; Tourniaire & Pulos, 1985) y han establecido niveles jerárquicos en el desarrollo de las ideas de razón y proporción (Misailidou & Williams, 2003; Tourniaire & Pulos, 1985). Sin embargo es necesario tener más información sobre las posibles relaciones entre los comportamientos de los estudiantes ante situaciones lineales y no lineales considerando diferentes componentes del razonamiento proporcional con el objetivo de intentar comprender mejor las características del desarrollo del razonamiento proporcional.
2. RAZONAMIENTO PROPORCIONAL
2.1. Componentes del razonamiento proporcional
Un aspecto relevante en el desarrollo del sentido numérico en los estudiantes de educación primaria y secundaria es la generación de relaciones significativas entre el pensamiento aditivo y multiplicativo (Lesh et al., 1988) y, en particular, la idea de que el modelo de la suma repetida para la multiplicación es incompleto y que es necesario un cambio cualitativo para complementar la relación entre el pensamiento aditivo y multiplicativo (Fernández & Llinares, 2011; Resnick & Singer, 1993; Van Dooren, De Bock & Verschaffel, 2010). Vinculado a este necesario cambio cualitativo está el desarrollo de la idea de covariación y de múltiples comparaciones que constituye el razonamiento proporcional (Lesh et al., 1988). Por tanto, el significado de la relación entre dos cantidades A y B parece ser una cuestión clave en la discriminación de las situaciones lineales de las no lineales. Por otra parte el desarrollo de la capacidad de discriminar estas situaciones parece que está inicialmente vinculado a un pequeño contexto de problemas y que gradualmente se amplía no siendo una cuestión de todo o nada (Gagatsis, Modestou, Elia, & Spanoudes, 2009; Lesh et al., 1989; Modestou & Gagatsis, 2009–b). Este desarrollo tiene que ver con la manera en la que los estudiantes dotan de sentido a las relaciones que se pueden establecer entre dos cantidades en una situación determinada. En este ámbito Modestou & Gagatsis (2009–a) han propuesto y testado un modelo de razonamiento proporcional (Figura 1) que asume que el razonamiento proporcional puede ser descrito mediante tres componentes que denominan razonamiento analógico, proporcionalidad y consciencia meta–analógica.

La componente "proporcionalidad" en este modelo representa la competencia en resolver problemas lineales incluyendo el reconocimiento de las relaciones de segundo orden que implica establecer una relación de equivalencia entre dos razones. Modestou y Gagatsis denominan a esta componente "routine proportionality" y se refiere a la habilidad de construir y algebraicamente resolver proporciones que implica la identificación de las relaciones de segundo orden (relación de equivalencia entre dos razones). Para apoyar la existencia de esta componente Modestou y Gagatsis indican siguiendo, a Piaget y Inhelder, que la existencia de una relación entre dos relaciones y el reconocimiento de esta similitud estructural es una característica esencial de la proporcionalidad. El modelo del razonamiento proporcional propuesto incluye también el reconocimiento y manejo de situaciones no lineales (que denominan consciencia meta–analógica), así como la competencia en resolver analogías numéricas y verbales (razonamiento analógico). Como consecuencia, un aspecto fundamental del razonamiento proporcional se vincula al éxito en analizar las relaciones entre cantidades en una situación dada para establecer si existe o no una relación proporcional. De manera consecuente, la tendencia de los estudiantes a usar el modelo lineal en problemas para los cuales no es adecuado está inevitablemente conectada a la ausencia del reconocimiento de una situación lineal y por tanto a deficiencias en el desarrollo del razonamiento proporcional. Modestou y Gagatsis (2009–a) incluyen esta competencia considerando la componente "consciencia meta–analógica" que se refiere al reconocimiento de situaciones que parecen lineales pero que no lo son y a la distinción de las situaciones que sí son lineales. Por ejemplo, la tarea de determinar si la situación "Un grupo de 5 músicos interpretan una pieza musical en 10 minutos. Otro grupo de 35 músicos interpretarán la misma pieza musical mañana. ¿Cuánto tiempo tardarán en interpretarla? ¿Por qué?" es o no lineal es un ítem que pertenece a este aspecto del razonamiento proporcional.
2.2. Estrategias correctas e incorrectas seguidas por los estudiantes en los problemas lineales
Considerando cómo los estudiantes usan las relaciones entre las cantidades, las investigaciones han identificado diferentes estrategias seguidas por los estudiantes cuando resuelven problemas lineales de valor perdido (Christou & Philippou, 2002; Cramer & Post, 1993; Lamon, 1993; Tourniaire & Pulos, 1985).
Estas estrategias son el enfoque escalar, si se centra en el uso de la razón interna; el enfoque funcional, si se centra en el uso de la razón externa; el uso de la razón unitaria; la estrategia constructiva que se caracteriza porque los estudiantes usan diferentes relaciones entre las cantidades para construir la razón y el algoritmo de productos cruzados (regla de tres) en el que el estudiante aplica un algoritmo en el que se colocan las 4 cantidades (3 conocidas y una desconocida) en forma de proporción (como igualdad de dos fracciones) y se aplica la aritmética de las fracciones para averiguar el dato desconocido (multiplicar en cruz y despejar la x).
El modelo de razonamiento proporcional propuesto por Modestou y Gagatsis, (2009–a) permite tener en cuenta cómo los estudiantes interpretan la relación entre las cantidades en cada situación lineal y no lineal a través de las características de las estrategias empleadas. Desde esta perspectiva, la manera en la que las estrategias correctas e incorrectas utilizadas por los estudiantes en las situaciones lineales y no lineales se relacionan puede aportar información sobre cómo los estudiantes aprenden a discriminar situaciones lineales de las que no lo son. Este hecho nos llevó a considerar un análisis de las estrategias usadas por los estudiantes que nos permitiera identificar las relaciones que se pueden establecer entre el uso de diferentes estrategias en las situaciones lineales y no lineales. Además, es necesario tener información más sistemática sobre qué aspectos de las situaciones lineales y no lineales determinan el uso de estrategias correctas e incorrectas por los estudiantes. Esta información es relevante para determinar precursores en el desarrollo del razonamiento proporcional.
En este sentido, el propósito de este estudio es aportar información sobre cómo los estudiantes de 12–13 años identifican las situaciones lineales y no lineales. Para ello, esta investigación se centra en analizar las relaciones implicativas entre las estrategias usadas por los estudiantes al inicio de la educación secundaria en problemas lineales y no lineales. Las preguntas de investigación son:
– ¿Qué relaciones implicativas existen entre las estrategias usadas por los estudiantes de educación secundaria (12–13 años) al resolver problemas lineales y problemas no lineales?
– ¿Qué aspectos influyen en el reconocimiento por parte de los estudiantes de ambas situaciones?
3. MÉTODO
3.1. Participantes y contexto
Los participantes en este estudio fueron 136 estudiantes del primer curso de educación secundaria (12–13 años) de cuatro centros diferentes con un número similar en cuanto al género. Los centros están situados en diferentes ciudades donde la mayoría de la población activa se dedica a los sectores de la industria y servicios.
En el primer año de educación secundaria el currículo relativo a la razón y proporción se centra en identificar situaciones lineales en contextos de descuentos y de cálculo de porcentajes y en reconocer situaciones no lineales. Además, los estudiantes se inician en el cálculo de cantidades desconocidas mediante el uso de tablas de series de números proporcionales y mediante el uso de relaciones multiplicativas, inicialmente, basadas en el doble, triple, mitad... entre cantidades de la misma magnitud y, posteriormente, en la identificación de la constante de proporcionalidad y en la introducción del algoritmo de la regla de tres.
3.2. Instrumentos y procedimiento
Se diseñó un cuestionario de siete problemas formado por cinco situaciones lineales y dos situaciones no lineales. Entre los problemas lineales había tres problemas de valor perdido, un problema de comparación numérica y un problema de comparación cualitativa. Los problemas no lineales correspondían a situaciones que reflejaban la función constante ƒ(x) = a, a ≠ 0 y la función ƒ(x) = x+b, b ≠ 0 que Van Dooren et al. (2005) denominaron "situación aditiva" ya que la estrategia correcta para su resolución se apoya en la identificación de relaciones aditivas entre las cantidades. La Tabla I muestra los problemas empleados en el cuestionario.

Los problemas fueron seleccionados teniendo en cuenta el modelo del razonamiento proporcional que subraya el papel relevante que desempeña el discriminar situaciones lineales de las que no lo son. Usamos problemas empleados en otras investigaciones porque habían sido buenos predictores tanto en el campo del desarrollo del razonamiento proporcional como en la identificación del uso abusivo de las relaciones lineales en situaciones no adecuadas.
Los estudiantes resolvieron los siete problemas en su clase habitual de matemáticas. El formato de presentación del cuestionario consistía en un cuaderno compuesto por ocho folios. Cada problema estaba en una página diferente. En un primer cuadro se les presentaba el enunciado del problema y en un segundo cuadro los estudiantes debían realizar los cálculos y justificarlos. Podían utilizar calculadoras, pero se indicó que escribieran las operaciones en el cuadro correspondiente. En la primera página se les pedía que pusieran sus datos y se les proporcionaba una serie de instrucciones.
3.3. Análisis
Los datos fueron analizados en dos fases. En la primera fase se siguió un proceso inductivo (Strauss & Corbin, 1994) y, para cada una de las tareas, se analizó el proceso de resolución seguido por cada estudiante con el propósito de identificar el tipo de estrategia correcta e incorrecta empleada en cada problema. Para ello, un grupo de tres investigadores analizó una muestra de respuestas a los diferentes problemas para generar descriptores de las estrategias que parecían estar utilizando los estudiantes en cada tipo de problema. Los descriptores generados para cada problema se fueron refinando al analizar nuevas respuestas. Este proceso se repitió para cada uno de los problemas y, finalmente, se consideraron las estrategias de todos los problemas en conjunto para ver si había solapamiento entre ellas. Las estrategias fueron agrupadas inicialmente como correctas (CS) e incorrectas (IS). Después asignamos una letra "a", "b",... a cada estrategia identificada y el número del problema donde se empleaba (Tabla II). Por ejemplo, el uso correcto del algoritmo de la regla de tres en el problema 5 era codificado mediante CSc5. Finalmente denominamos "otras" a las estrategias incorrectas no asignadas en algunas de las categorías anteriores y las respuestas en blanco. La descripción de las estrategias identificadas se realizará en el apartado de resultados. La segunda fase del análisis tenía como objetivo identificar las relaciones entre las estrategias usadas por los estudiantes en cada tipo de problema. Este objetivo respondía a la idea de intentar aportar información sobre la complementariedad entre dos componentes del modelo del razonamiento proporcional propuesto por Modestou y Gagatsis (2009–a), en particular, la componente "proporcionalidad" y la componente "consciencia meta–analógica". La información sobre cómo los estudiantes construyen las relaciones entre estas dos componentes del modelo de razonamiento proporcional procede, en este caso, de la identificación de las relaciones entre la resolución de problemas lineales, el reconocimiento de los problemas lineales y no lineales, y la resolución de situaciones no lineales. Para poder obtener este tipo de información necesitábamos realizar un análisis que permitiera identificar las relaciones entre las estrategias usadas por un estudiante en cada tipo de problema.

Para este fin realizamos un análisis estadístico implicativo de las estrategias mediante el software CHIC (Classification Hiérarchique Implicative et Cohésitive) (Gras, Suzuki, Guillet & Spagnolo, 2008). Para realizar este análisis, se codificó con un 1 el uso de una estrategia particular en un problema dado y con un 0 si el alumno no usaba esa estrategia en el problema. El análisis implicativo cruza siempre un conjunto de variables V y un conjunto de sujetos E. En nuestro caso, al ser variables binarias, se quiere dar sentido estadístico a expresiones tales como: "cuando se observa en un sujeto de E la variable α, en general se observa la variable b". Se trata por tanto de estudiar un modelo estadístico de una cuasi–implicación del tipo: "si a entonces b". En términos conjuntistas, si A y B representan las poblaciones respectivas, donde las variables α y b toman el valor 1 (si es verdadero) entonces equivale a medir la inclusión no estricta de A en B (Trigueros & Escandón, 2008). En este análisis, la implicación es admisible si el número de individuos de la muestra que la contradicen es muy pequeño en términos probabilísticos, en relación con el número de individuos esperado bajo la hipótesis de ausencia de relación.
En nuestro estudio la población son los estudiantes de secundaria y las variables son las estrategias empleadas en los diferentes problemas. Las relaciones implicativas entre las estrategias nos indican en qué medida el uso de una estrategia A en un problema Z está relacionado con el uso de una estrategia Β en un problema T con una determinada probabilidad. La medida de esta relación nos permite identificar cómo se está construyendo el desarrollo del razonamiento proporcional en relación a la componente "proporcionalidad " y a la "consciencia meta–analógica". En este caso, el análisis genera una gráfica jerárquica, en la que los distintos niveles identifican las implicaciones (e.g. "α" entonces "b") que se forman. Las estructuras generadas por el análisis implicativo no son transitivas pero permiten identificar qué dos elementos se unen a través de una implicación haciendo emerger una primera estructura conceptual entre los diferentes elementos de las componentes del modelo de razonamiento proporcional. Las implicaciones permiten dar cuenta de las estructuras conceptuales que los alumnos han construido al relacionar la estrategia usada por un alumno en un tipo de problema con la estrategia usada por el mismo alumno en otro problema y dando cuenta por tanto de la relación entre la "componente meta–analógica" y la habilidad de resolver los problemas lineales ("proporcionalidad") del modelo. En este sentido el análisis implicativo proporciona información acerca de las características de la estructura multiplicativa de los problemas lineales identificadas por los estudiantes y que determinan el uso particular de una estrategia determinada y la identificación de las relaciones entre las cantidades en las situaciones no lineales.
4. RESULTADOS
4.1. Estrategias correctas e incorrectas: Cómo los estudiantes tienen en cuenta las relaciones entre las cantidades en las situaciones lineales y no lineales
En este apartado describimos las estrategias usadas por los estudiantes en los diferentes problemas mostrando cómo los estudiantes tienen en cuenta las relaciones entre las cantidades (Tabla II; las celdas sombreadas indican que la estrategia no es aplicable). En los problemas lineales de valor perdido los estudiantes emplearon tres tipos de estrategias correctas: la identificación y uso de las razones (escalar o funcional), estrategia constructiva y el algoritmo de la regla de tres.
La estrategia "identificación y uso de las razones entre cantidades" (CSa) se basa en el reconocimiento por parte de los estudiantes de la igualdad de razones escalares o de la constante de proporcionalidad (la k en el modelo f(x) = kx) y su uso pertinente para realizar la acción que le pide el problema (calcular una cantidad desconocida o comparar). Esta estrategia es correcta en los problemas de valor perdido, en el problema de comparación numérica y en el problema de comparación cualitativa. Por ejemplo, empleando la razón funcional en el problema P1a los estudiantes buscan la razón unitaria "un kilo de patatas cuesta 0.4 €/kg (la constante de proporcionalidad). Puesto que se necesita saber el precio de 8 kg, 8x0.4 = 3.2€". Por otro lado, si emplean la razón escalar: "La relación entre los kilos de patatas que se tienen y los que se desean comprar es 8/5 (razón escalar), puesto que el precio de 5kg es 2€, por 8 kg se pagará (8/5)x2". En el caso del problema P6 de comparación numérica, el estudiante identifica las razones escalares o funcionales (las razones funcionales serían 100Km/90min y 120Km/ 105min) y realiza su comparación. En esta investigación estas dos estrategias (uso de la razón escalar o uso de la razón funcional) han sido colocadas en la misma categoría ya que, inicialmente, nuestro objetivo era identificar las relaciones implicativas entre las estrategias que se apoyaban en el reconocimiento de las relaciones correctas entre las cantidades.
La "estrategia constructiva" (CSb) adopta diferentes manifestaciones que se apoyan en la identificación y uso de las dos propiedades de las situaciones lineales, la constante de proporcionalidad (f(x)/x = k, para todo x) y la conservación de razones escalares. Estas dos propiedades se ponen de manifiesto en el uso del homomorfismo aditivo (f(a) + f(b) = f(a+b)).
Por ejemplo, el estudiante que calcula el precio de un kilo de patatas (reducción a la unidad, razón funcional, 2/5 = 0.4). A continuación usa este valor para obtener el precio de 3 kilos. Después, haciendo uso de la conservación de razones escalares, como el precio de 5 kilos de patatas es 2 euros (enunciado) y como ha obtenido que el precio de 3 kilos de patatas es 1'2 euros, entonces 8 kilos de patatas costará 3.2 euros, usando para ello el homomorfismo aditivo:
5 kg valen 2€
3 kg valen 1.2 €
entonces
5kg + 3kg valen 2€+1.2€
Finalmente, se identificó el uso del "algoritmo de la regla de tres" (CSc) que consiste en plantear una proporción y multiplicar en cruz y después dividir. En el problema P1a, esta estrategia vendría dada mediante el planteamiento de la igualdad 5/8 = 2/x, y la realización de las siguientes operaciones: "8x2 = 16 y después 16/5 = 3.2 €".
En relación al uso de las estrategias incorrectas empleadas en los problemas lineales de valor perdido y de comparación, éstas fueron agrupadas en 4 categorías: confusión de las relaciones entre las cantidades (ISa), estrategia constructiva errónea (ISb), identificación correcta de la razón pero uso incorrecto (ISc) y la estrategia aditiva (establer relaciones aditivas erróneas entre las cantidades en vez de relaciones multiplicativas (ISd)).
La estrategia incorrecta más empleada por los estudiantes fue el uso de estrategias aditivas (ISd). En el problema P5 (botes de pintura) la estrategia aditiva consistió en establecer la diferencia entre el número de botes usados por Marta y el número de botes usados por Sofía (6 –3 = 3). Por tanto, los botes de pintura roja que necesitará Sofía son 7+3 = 10 botes. De la misma manera, en los problemas lineales de comparación (problemas 3 y 6) esta estrategia consistía en usar relaciones aditivas entre las cantidades en vez de relaciones multiplicativas.
La estrategia "confusión de la relación entre magnitudes" (ISa) se caracteriza por la confusión del significado de la razón y/o el planteamiento de una regla de tres incorrecta (regla de tres cruzadas), que pone de manifiesto la dificultad de los estudiantes para identificar correctamente la relación entre las cantidades de las magnitudes. En la "estrategia constructiva errónea" (ISb) los estudiantes emplean el homomorfismo aditivo (f(a+b) = ƒ(a)+ƒ((b)) pero realizan una aproximación errónea. Algunas de las estrategias constructivas erróneas son combinaciones de estrategias aditivas y multiplicativas (Misailidou & Williams, 2003). Por ejemplo, apoyándose en la relación 5 Kg–2€ dada en el enunciado del problema P1, un alumno construyó otra segunda relación usando la idea de "doble" en las relaciones escalares lo que le permite decir que 10 Kg serán 4€. Sin embargo como el problema le pregunta por 8 kg (apartado P1a) parece que no es capaz de "alcanzar" 8kg mediante el procedimiento de doblar. Como consecuencia, realiza una aproximación cualitativa que se apoya en cierto reconocimiento de las relaciones aditivas escalares (2kg serán algo así como 0.5€, por lo tanto 8kg serán 3.5€). Por último, en la estrategia "identificación de la razón y uso incorrecto" los estudiantes identifican correctamente la razón tanto en las situaciones de comparación como en las de cálculo, pero no la usan adecuadamente o tienen dificultades en desarrollar una comparación de las razones obtenidas.
En relación a las dos situaciones no lineales P4 y P7 los estudiantes las reconocieron de manera desigual. La situación de los músicos (P4) fue reconocida por un 41% de los estudiantes y la situación de la carrera de atletismo (P7) por el 60%. Sin embargo, lo que es relevante en la situación de los músicos es la evidencia que proporciona respecto a la relación entre las componentes "proporcionalidad" y "consciencia meta–analógica" del modelo del razonamiento proporcional. En este problema del 59% de los estudiantes que no identificaron esta situación como no lineal, la mitad de ellos usaron relaciones multiplicativas, es decir usaron la linealidad en una situación no lineal (33% del total). En la situación de la carrera del atletismo, los datos son similares, el 40% de los estudiantes no consideraron la situación como no lineal, y de éstos un 42.5% aplicaron estrategias lineales para su resolución (es decir el 17% de la muestra). Estos datos apoyan la idea del uso abusivo de la linealidad en situaciones no adecuadas en los estudiantes de 12–13 años, indicando que estos estudiantes no reconocen los límites de la aplicación de la linealidad, dependiendo este reconocimiento del tipo de situación no lineal (ƒ(x) =a o ƒ(x) = x +10), y por tanto dan apoyo empírico a la consideración de la componente "consciencia meta–analógica" en el modelo del razonamiento proporcional.
4.2. Relaciones implicativas entre las estrategias
Para realizar el análisis implicativo de las estrategias consideramos como variables las estrategias correctas e incorrectas usadas por los estudiantes en cada uno de los problemas. El análisis implicativo, al 90% de significación, muestra tres estructuras implicativas (Figura 2) que agrupan a 15 de las variables estrategia–problema. Cada una de estas estructuras implicativas agrupa a un número diferente de variables mostrando tres ideas relevantes para entender el modelo del razonamiento proporcional: el uso del algoritmo de la regla de tres en los problemas lineales de valor perdido no conlleva el que los estudiantes puedan identificar las situaciones no lineales; la relevancia de la identificación de las razones (escalar o funcional) entre las cantidades en discriminar las situaciones lineales y no lineales y la relación existente entre el uso de relaciones aditivas entre las cantidades en vez de relaciones multiplicativas (la estrategia aditiva errónea) en problemas de valor perdido y la identificación de la situación no lineal de estructura aditiva (f(x) = x + 10).

La primera estructura implicativa en la Figura 2 relaciona nueve variables, tres de las cuales muestran estrategias incorrectas relativas al uso de procesos constructivos (ISb) y al uso de relaciones aditivas en vez de multiplicativas (estrategias aditivas, ISd) y seis son estrategias correctas que no incluyen el uso del algoritmo. En la configuración de esta estructura implicativa desempeña un papel relevante la identificación por parte de los estudiantes de las situaciones no lineales (situación de la banda de música, CSd4, y la carrera de atletismo, CSd7) ya que de alguna u otra manera agrupan al resto de las variables. Esta idea parece mostrar la existencia de diferentes precursores en la identificación de una situación no lineal de estructura constante (CSd4). Estos precursores son la identificación y uso de las razones entre las cantidades en los problemas lineales de valor perdido (CSa1b, CSa1a y CSa5), y en las situaciones de comparación numérica (CSa6). Estos distintos precursores indican que si el estudiante es capaz de identificar y usar las razones en los distintos problemas lineales de comparación o de cálculo también identificará la situación no lineal de tipo constante.
Además, las relaciones que emergen muestran la existencia de un precursor en la identificación de la situación aditiva de la carrera de atletismo (CSd7): El uso de estrategias constructivas y aditivas erróneas en las situaciones de razón y proporción en las que hay que calcular un dato (ISb1a, y ISd5). Esta implicación muestra que la capacidad de los estudiantes para trabajar con las propiedades de la estructura lineal (proporcional), ƒ(a+b) = ƒ(a)+ƒ(b) y ƒ(na) = nƒ(a) en situaciones lineales apoya su capacidad para reconocer la situación no lineal ƒ(x) = x +10, mostrando de esta manera el necesario desarrollo de la comprensión de dichas relaciones como paso previo al uso del algoritmo y por tanto el inicio de la relación entre la componente "consciencia meta–analógica" y la componente "proporcionalidad" en el desarrollo del razonamiento proporcional.
Finalmente existe una relación implicativa entre la identificación y resolución correcta de la situación no lineal de estructura aditiva (CSd7) y el uso de estrategias aditivas incorrectas en el problema lineal en el contexto de mezcla (ISd5). Esta relación es interesante ya que la estrategia aditiva es correcta en la situación no lineal de tipo ƒ(x) = x + 10, pero es una estrategia incorrecta en las situaciones lineales. Veamos las características de esta implicación con un ejemplo. El estudiante A18 empleó una estrategia aditiva en la situación no lineal P7 (carrera, ƒ(x) = x + 10) al indicar que "Víctor dará 40 vueltas porque se llevan 10 vueltas de ventaja". Esta estrategia es correcta en esta situación no lineal. Sin embargo, este mismo estudiante también empleó esta estrategia (ahora incorrecta) en la situación lineal en el contexto de mezcla (P5) "como la diferencia entre el número de botes de pintura amarilla y de pintura roja de Marta es 3 (6 –3 = 3), entonces Sofía necesitará 3 botes más de roja lo que hace un total de 10 botes". En esta resolución este estudiante aplica una relación aditiva entre las cantidades (botes de pintura azul y botes de pintura roja).
La segunda estructura implicativa muestra la relación entre el uso de una estrategia constructiva en una situación lineal de valor perdido (CSb1a) y la identificación de las razones y su comparación en un problema de comparación cualitativa (CSa3). Este resultado indica que los estudiantes antes de emplear estrategias constructivas para resolver problemas lineales de valor perdido, son capaces de emplear estrategias cualitativas y, portanto, resolver con éxito el problema de comparación cualitativa.
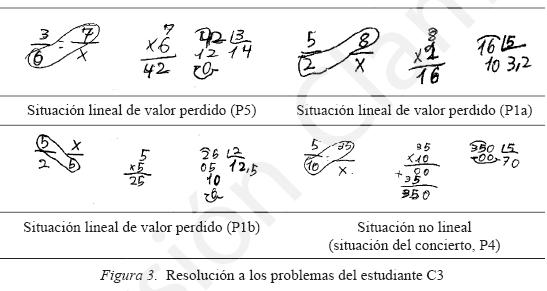
Para finalizar, la última estructura implicativa relaciona cuatro variables, tres de ellas relativas al uso del algoritmo de la regla de tres en situaciones lineales de valor perdido (CSc1a, CSc1b, CSc5) y la otra referente al uso incorrecto de relaciones de proporcionalidad (ISe4) en la situación de no linealidad constante. Las relaciones implicativas entre estas variables indican que algunos estudiantes que aplican el algoritmo correctamente en situaciones lineales también lo usan pero ahora de manera incorrecta en la situación no lineal P4 del concierto (f(x) = 10). Para ejemplificar estas relaciones veamos la resolución seguida por uno de los estudiantes en algunos de estos problemas. El estudiante C3 (Figura 3) emplea el algoritmo de la regla de tres para dar respuesta al problema lineal de valor perdido en un contexto de compra (P1a y P1b) y al problema lineal en un contexto de pintura (P5). Sin embargo, también usa una estrategia proporcional (en este caso emplea una regla de tres) en la situación no lineal de estructura constante (ƒ(x) = a, situación del concierto). Es decir, el uso del algoritmo de la regla de tres en los estudiantes de primero de educación secundaria no conlleva la necesaria capacidad de identificar la situación no lineal.
5. DISCUSIÓN
El presente estudio investiga cómo los estudiantes identifican y usan las relaciones entre las cantidades en las situaciones lineales y no lineales y proporciona información sobre qué aspectos de las estrategias usadas pueden ser considerados precursores del desarrollo del razonamiento proporcional. Esta información aporta evidencias que apoyan el modelo de razonamiento proporcional propuesto por Modestou y Gagatsis (2009–a) en el sentido de indicar cómo las componentes"proporcional" y "consciencia meta–analógica" empiezan a relacionarse. En este estudio hemos descrito las estrategias usadas por los estudiantes cuando resuelven problemas lineales de valor perdido, problemas de comparación y problemas no lineales (ƒ(x) = a, y ƒ(x) = x+b, b≠ 0) y nos hemos centrado en cómo los estudiantes identifican y usan las relaciones multiplicativas entre las cantidades al desarrollar sus estrategias. Los resultados obtenidos justifican la emergencia en el modelo del razonamiento proporcional de la habilidad en discriminar si una situación es proporcional o no como un aspecto constituyente de este razonamiento.
La categorización de las estrategias correctas e incorrectas usadas por los estudiantes en los problemas lineales y no lineales muestra la complementariedad entre las estrategias correctas que se apoyan en la identificación y uso de la razón en las situaciones lineales de valor perdido y las estrategias constructivas apoyadas en las propiedades de la linealidad. De esta manera, cuando el estudiante tiene dificultades en dotar de significado a la razón entre las cantidades genera estrategias constructivas. Por otra parte, cabe destacar el alto porcentaje de estudiantes que emplean estrategias aditivas apoyadas en la identificación y uso de relaciones aditivas incorrectas entre las cantidades para determinar el valor de la cantidad desconocida y los altos porcentajes de la categoría "Otras" indicando las dificultades que tienen los estudiantes en el primer curso de educación secundaria para identificar correctamente las relaciones entre las cantidades. Estos resultados van en la línea de lo obtenido en otras investigaciones centradas sobre este aspecto particular del razonamiento proporcional (Hart, 1984; Misailidou & Williams, 2003). Por otra parte, el uso abusivo de las relaciones de proporcionalidad en situaciones en las que no es adecuado es otra manifestación de esta dificultad (Eberbach et al., 2010; Fernández & Llinares, en prensa; Van Dooren et al., 2005, 2009) e indica el papel que desempeña la componente "consciencia meta–analógica" – ser capaces de reconocer problemas lineales y no lineales y de resolverlos – en el desarrollo del razonamiento proporcional.
De manera particular y en relación a la capacidad de los estudiantes en diferenciar las situaciones lineales y no lineales (como elementos de la componente "consciencia meta–analógica" del modelo de razonamiento proporcional), los resultados indican que esta capacidad depende de cuál es la estructura de la situación no lineal. En nuestra investigación los estudiantes de 12–13 años identificaron con mayor facilidad la situación de estructura aditiva (ƒ(x) = ax+b, b ≠ 0, a = 1; ƒ(x) = x + 10) que la de estructura constante (ƒ(x) = a, a≠0; ƒ(x) =10). Este resultado podría ser explicado por el hecho de que la frase "Pero Ana empezó a correr más tarde que Víctor" podría facilitar el reconocimiento de la situación no lineal de tipo aditivo. Sin embargo, cuando los estudiantes no reconocían la situación no lineal, la mitad de estos empleaban razones y proporciones para resolverla.
Finalmente, las relaciones implicativas entre las estrategias usadas por los estudiantes han agrupado los problemas según han sido resueltos por los estudiantes y nos han mostrado tres ideas que nos ayudan a comprender mejor el desarrollo del razonamiento proporcional al incorporar la consciencia meta–analógica como una componente relevante. Estas ideas son: (i) la importancia de la identificación y uso de la razón en el desarrollo de la capacidad de diferenciar las situaciones lineales de las no lineales, (ii) la identificación de precursores en el desarrollo del razonamiento proporcional, y (iii) que la resolución con éxito de una situación lineal a través del algoritmo de la regla de tres no es condición suficiente para suponer el desarrollo del razonamiento proporcional en los estudiantes.
Las relaciones implicativas entre las estrategias han puesto de manifiesto la importancia de la identificación de las situaciones no lineales, pero también el hecho de que las diferentes situaciones no lineales (constante, aditivo) son reconocidas de manera diferente. Así, por una parte se han agrupado las estrategias apoyadas en la identificación y uso de la razón como precursor de la situación constante, mientras que por otra, los precursores de la situación aditiva son la propia situación constante y las estrategias aditivas incorrectas aplicadas en las situaciones lineales. Además, las implicaciones identificadas indican que la comparación cualitativa es un precursor de las comparaciones cuantitativas en la constitución de la idea de razón y proporción como objetos mentales. Esta evidencia apoya las indicaciones desde el análisis fenomenológico (Freudenthal, 1983) y el desarrollo de la idea de razón y proporción en estudiantes de educación primaria (Fernández, 2009). Por otra parte, el uso de la regla de tres en los problemas lineales de valor perdido no implica necesariamente la capacidad para identificar las situaciones no lineales lo que proporciona apoyo empírico al modelo de razonamiento proporcional propuesto por Modestou y Gagatsis (2009–a). Así pues, parece que es importante la identificación de las razones en las situaciones lineales (comparación y valor perdido) para identificar la situación no lineal constante. Centrar la atención de los estudiantes en la idea de razón implica dotar de sentido a la covariación y a la idea de múltiples comparaciones (Lesh et al., 1898). Una manera de desarrollar esta aproximación es usar en la enseñanza tablas de cantidades proporcionales (Lamon, 2007) que permita a los estudiantes centrarse en dotar de sentido a la relación entre dos cantidades sobre la que se basa la idea de covariación (percibir algunas razones y compararlas) generando discusiones sobre diferentes soluciones. Solo a través del significado de la idea de covariación y de relación entre dos cantidades los estudiantes podrán estar en mejores condiciones de discriminar adecuadamente las situaciones lineales de las no lineales y por tanto empezar a desarrollar la componente de "consciencia meta–analógica". La importancia de las características que debe adoptar la enseñanza en este dominio matemático radica en que las evidencias de las investigaciones indican que la enseñanza puede desempeñar un papel activo en su desarrollo no siendo una cuestión sólo de madurez biológica.
Además, nuestros datos indican que la no identificación de la situación aditiva, se relaciona con la no identificación de la razón en las situaciones lineales. Este hecho se debe a que el estudiante, cuando no identifica la razón mayoritariamente va a buscar y usar las relaciones aditivas entre las cantidades. Luego la constitución de los significados de las ideas de razón y proporción se ha mostrado clave en la identificación de las razones, convirtiéndose de esta manera en un precursor en el desarrollo de la identificación de la relación de segundo orden constitutiva del razonamiento proporcional y por tanto clave en el desarrollo de la componente "proporcionalidad" en el desarrollo de razonamiento proporcional.
Las estructuras implicativas identificadas en el análisis realizado describen ciertas relaciones entre la comprensión conceptual de las situaciones lineales y no lineales por parte de los estudiantes y por tanto en el proceso de constitución de la idea de razón y proporción poniendo de manifiesto relaciones entre el desarrollo de las componentes "proporcionalidad" y "consciencia meta–analógica". La información reunida y las relaciones identificadas y descritas anteriormente pueden ser útiles para la organización del contenido en la enseñanza y la planificación de secuencias de actividades dirigidas a desarrollar estas dos componentes del razonamiento proporcional. Por ejemplo, es necesario una intervención más sistemática teniendo en cuenta la relación multiplicativa entre las cantidades, dando una especial atención al uso de las razones (Lamon, 2007) puesto que incrementa la capacidad de los estudiantes en reconocer las situaciones lineales y no lineales. Desde nuestros resultados, si los estudiantes tuviesen en cuenta la covarianza entre las cantidades y la invarianza de las razones, sería posible que ellos identificaran la relación multiplicativa en las situaciones proporcionales, aportando argumentos para su justificación.
Sin embargo, debemos reconocer que llegar a conseguir estos objetivos no es una tarea fácil (Miyakawa & Winslow, 2009; Modestou, Elia, Gagatsis & Spanoudis, 2008; Van Dooren, De Bock, Weyers & Verschaffel, 2004). Pero, la identificación de las relaciones implicativas entre las estrategias en las diferentes situaciones proporcionan información sobre cómo las secuencias de enseñanza podrían ser organizadas considerando que las estrategias constructivas, centradas en la identificación de la covarianza de las cantidades y la invariancia de las razones, pueden permitir a los estudiantes hacer explícitas las propiedades del modelo lineal y reconocer cuándo estas propiedades no existen o no son aplicables mediante el desarrollo de la consciencia meta–analógica.
REFERENCIAS BIBLIOGRÁFICAS
Alatorre, S. & Figueras, O. (2005). A developmental model for proportional reasoning in ratio comparison tasks. In Chick, H. L. & Vincent, J. L. (Eds.)., Proceedings of the 29th Conference of the International Group for the Psychology of Mathematics Education. (Vol. 2, pp. 25–32). Melbourne: PME. [ Links ]
Christou, C. & Philippou, G. (2002). Mapping and development of intuitive proportional thinking. Journal of Mathematical Behavior, 20 (3), 321–336. [ Links ]
Cramer, K. & Post, T. (1993). Connecting research to teaching proportional reasoning. Mathematicseacher, 86(5), 404–407. [ Links ]
De Bock, D., Van Dooren, W., Janssens, D. & Verschaffel, L. (2002). Improper use of linear reasoning: An in–deph study of the nature and the irresistibility of secondary school students' errors. Educational Studies in Mathematics, 50(3), 311–334. [ Links ]
De Bock, D., Van Dooren, W., Janssens, D.& Verschaffel (2007). The illusion of linearity. From analysis to improvement. New York: Springer. [ Links ]
De Bock, D., Verschaffel, L. & Janssens, D. (1998). The predominance of the linear model in secondary school students' solutions of word problems involving length and area of similar plane figures. Educational Studies in Mathematics, 35(1), 65–83. doi: 10.1023/A: 1003151011999 [ Links ]
Ebersbach, M., Van Dooren, W., Goudriaan, M. N. & Verschaffel, L. (2010). Discriminating non–linearity from linearity: Its cognitive foundations in five–year–olds. Mathematical Thinking and Learning, 12, 4–19. doi: 10.1080/10986060903465780 [ Links ]
Fernández, A. (2009). Razón y proporción. Un estudio en la escuela primaria. Universitat de València. Departament de Didàctica de la Matemática. [ Links ]
Fernández, C. y Llinares, S. (2011). De la estructura aditiva a la multiplicativa: efecto de dos variables en el desarrollo del razonamiento proporcional. Infancia Aprendizaje, 34(1), 67–80. [ Links ] Fernández, C. y Llinares, S. (en prensa). Características del desarrollo del razonamiento proporcional en la educación primaria y secundaria. Enseñanza de las Ciencias. [ Links ]
Fernández, C., Llinares, S.,Modestou, M. &Gagatsis,A. (2010). Proportional Reasoning: How task variables influence the development of students' strategies from Primary to secondary School. Acta Didactica Universitatis Comenianae Mathematics, 10, 1–18. [ Links ]
Fernández, C., Llinares, S., Van Dooren, W., De Bock, D. & Verschaffel, L. (2010). How do proportional and additive methods develop along primary and secondary school? In M. F. Pinto & T. F. Kawasaki (Eds.), Proceedings of the 34th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 353–360). Belo Horizonte, Brazil: PME. [ Links ]
Fernández, C., Llinares, S., Van Dooren, W., De Bock, D. & Verschaffel, L. (2011). Effect of number structure and nature of quantities on secondary school students' proportional reasoning. Studia psychologica, 53(1), 69–81. [ Links ]
Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht: Kluwer. [ Links ]
Gras, R., Suzuki, E., Guillet, F. y Spagnolo, F. (F.) (Eds.) (2008). Statistical Implicative analysis. Theory and Applications. London: Springer. [ Links ]
Gagatsis, A., Modestou, M. Elia, I. y Spanoudes, G. (2009). Structural modelling of development of shifts in grasping proportional relational relations underlying problem solving in area and volume. Acta Didactica Universitatis Comenianae, 9, 9–23. [ Links ]
Hart, K. (1981). Children s understanding of mathematics: 11–16. London: Murray. [ Links ]
Hart, K. (1984). Ratio: Children s strategies and errors. Windsor, UK: NFER Nelson. [ Links ]
Karplus, R., Pulos, S. & Stage, E. K. (1983). Early adolescents' proportional reasoning on 'rate' problems. Educational Studies in Mathematics 14(3), 219–233. [ Links ]
Lamon, S. (1993). Ratio and proportion: Children's cognitive and metacognitive processes. In Th. Carpenter, E. Fennema & Th. Romberg (Eds), Rational Numbers. An Integration of Research (pp. 131–156).Hillsdale, NJ: Lawrence Erlbaum Associates, Pub. [ Links ]
Lamon, S. (1999). Teaching fractions and ratios for understanding. Essential content knowledge and instructional strategies for teacher. Mahwah, NJ: Lawrence Erlbaum Associates, Pub. [ Links ]
Lamon, S. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. In F. K. Lester, Jr. (ed.), Second Handbook of Research on Mathematics Teaching and Learning (pp. 629–667). NC: Information Age Publishing. [ Links ]
Lesh, R., Post, T. & Behr, M. (1988). Proportional reasoning. In J. Hiebert & M. Behr (Eds.), Number Concepts an Operations in the Middle Grades (pp. 93–118). Reston, VA: Lawrence Erlebaum y National Council of Teachers of Mathematics. [ Links ]
Misailidou, C. & Williams, J. (2003). Diagnostic assessment of children's proportional reasoning. Journal of Mathematical Behavior 22(3), 335–368. [ Links ]
Miyakawa, T. & Winslow, C. (2009). Didactical designs for students' proportional reasoning: an "open approach" and a "fundamental situation". Educational Studies in Mathematics 72(2), 199–218. [ Links ]
Modestou, M., Elia, I., Gagatsis, A. y Spanoudis, G. (2008). Behind the scenes of pseudo–proportionality. International Journal of Mathematical Education in Science and Technology. 39(3), 313–324. [ Links ]
Modestou, M. & Gagatsis, A. (2007). Students' improper proportional reasoning: A result of the epistemological obstacle of "linearity". Educational Psychology, 27(1), 75–92. [ Links ]
Modestou, M. & Gagatsis, A. (2009–a). Proportional reasoning reformed. InA. Gagatsis, A. Kuzniak, E. Deliyianni y L. Vivier (eds.), First French–Cypriot Conference of Mathematics Education (pp. 19–33). Nicosia–Paris: University of Cyprus– University Paris Diderot 7. [ Links ]
Modestou, M. & Gagatsis, A. (2009–b). Proportional Reasoning: The strategies behind the percentages. Acta Academica Universitatis Comenianae Mathematics 9, 25–40. [ Links ]
Modestou, M. & Gagatsis, A. (2010). Cognitive and meta–cognitive aspects of proportional reasoning. Mathematical Teaching and Learning 12(1), 36–53. [ Links ]
Resnick, L. & Singer, J. (1993). Protoquantitative origins of ratio reasoning. In T. Carpenter, E. Fennema, y T. Romberg (eds.), Rational Numbers. An Integration of Research (pp. 107–130). Hillsdale, NJ: Lawrence Erlbaum Associates, Inc, Publishers. [ Links ]
Strauss, A. & Corbin, J. (1994). Grounded theory methodology: An overview. In N.K. Denzin y Y. Lincoln (Eds), Handbook of Qualitative Research (pp. 273–285). Thousand Oaks: Sage. [ Links ]
Tourniaire, F. & Pulos, S. (1985). Proportional reasoning. A review of literature. Educational Studies in Mathematics 16(2), 181–204. doi: 10.1007/BF02400937 [ Links ]
Trigueros, M. y Escandón, M.C. (2008). Los conceptos relevantes en el aprendizaje de la graficación. Un análisis a través de la estadística implicativa. Revista Mexicana de Investigación Educativa 13(36), 59–85. [ Links ]
Van Dooren, W., De Bock, D., Evers, M. & Verschaffel, L. (2009). Students' overuse of proportionality on missing–value problems: How numbers may change solutions. Journal for Research in Mathematics Education 40(2), 187–211. [ Links ]
Van Dooren, W., De Bock, D., Hessels, A., Janssens, D. & Verschaffel, L. (2005). Not everything is proportional: Effects of age and problem type on propensities of overgeneralization. Cognition and Instruction 23(1), 57–86. [ Links ]
Van Dooren, W., De Bock, D., Janssens, D. & Verschaffel, L. (2008). The linear imperative: An inventory and conceptual analysis of students' overuse of linearity. Journal for Research in Mathematics Education 39(3), 311–342. [ Links ]
Van Dooren, W., De Bock, D. & Verschaffel, L. (2010). From addition to multiplication... and back: The development of students' additive and multiplicative reasoning skills. Cognition and Instruction 28(3), 360–381. [ Links ]
Van Dooren, W., De Bock, D., Weyers, D. & Verschaffel, L. (2004). Challenging the predictive power of intuitive rules: A replication and extension study on the impact of 'more A – more B' and 'same A– same B'. Educational Studies inMathematics, 56, 179–207. [ Links ]
Vergnaud, G. (1983). Multiplicative structures. In R. Lesh & M. Landau (Eds.), Acquisition of Mathematics Concepts and Processes (pp. 128–175). London: Academic Press, Inc. [ Links ]














