Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.14 no.3 Ciudad de México nov. 2011
Artículos
O potencial das atividades centradas em produções de alunos na formação de professores de matemática
The potential of activities based on the production of students in mathematics teacher education
Ana Teresa de Oliveira,1 Gilda de la Rocque Palis2
1 Faculdade de Educação da Universidade Federal do Rio de Janeiro, Brasil. E–mail: anateresa@fe.ufrj.br
2 Departamento de Matemática e Departamento de Educação da Pontifícia Universidade Católica do Rio de Janeiro, Brasil. E–mail: gildalarocque@gmail.com
Recepción: Enero 20, 2011.
Aceptación: Septiembre 12, 2011.
RESUMEN
Este artículo presenta y discute el diseño e implementación de actividades centradas en el trabajo del estudiante como una estrategia de formación del profesorado para contribuir al desarrollo del conocimiento del contenido y el conocimiento pedagógico del contenido en los cursos de formación inicial y continua de profesores de matemáticas. Traemos diferentes contribuciones de investigaciones acerca del tema e ilustramos nuestra contribución en esta área mediante la descripción de la estructura básica de las tareas que hemos propuesto a los profesores de matemáticas del 6° al 9° grado en la escuela primaria y los docentes de secundaria y el análisis de una implementación específica. Realizamos una apreciación de lo que hemos aprendido sobre el potencial de las actividades apoyadas en el trabajo de los estudiantes en la formación del profesorado en matemáticas y sobre las formas de construirlas.
PALABRAS CLAVE: Formación de profesores de matemáticas, Educación matemática, Conocimiento del contenido y conocimiento pedagógico del contenido, Análisis de los trabajos del estudiante, Enseñanza del álgebra.
ABSTRACT
This article presents and discusses the design and implementation of activities focused on the work of the student as a strategy for teacher education in order to contribute to the development of content knowledge and pedagogical content knowledge in pre–service and in–service courses for mathematics teachers. We will provide different research contributions regarding the subject and we will illustrate our contribution to this area by describing the basic structure of tasks that we have proposed to grade 6 to 9 and high school mathematics teachers and the analysis of a specific task implementation. We will carry out an assessment of what we have learnt regarding the potential of activities based on the work of students in mathematics teacher education and regarding ways to construct them.
KEY WORDS: Mathematics teacher education, Mathematics education, Content Knowledge and pedagogical content knowledge, Analysis of student papers, Teaching of algebra.
RESUMO
Este artigo apresenta e discute o desenho e a implementação de atividades centradas em trabalhos de alunos como uma estratégia de formação docente visando contribuir para o desenvolvimento do conhecimento do conteúdo e do conhecimento pedagógico do conteúdo nos cursos de formação inicial e continuada de professores de Matemática. Trazemos diversos aportes de pesquisas sobre o assunto e exemplificamos a nossa contribuição nessa área com a descrição da estrutura básica de tarefas que temos proposto a professores de Matemática do 6° ao 9° ano do ensino fundamental e do ensino médio e a análise de uma implementação específica. Fazemos uma apreciação do que aprendemos sobre a potencialidade das atividades apoiadas em trabalhos de alunos na formação de docentes de Matemática e a respeito de maneiras de construí–las.
PALAVRAS CHAVE: Formação de professores de Matemática, Educação matemática, Conhecimento do conteúdo e conhecimento pedagógico do conteúdo, Análise dos trabalhos de alunos Ensino de Algebra.
RÉSUMÉ
Cet article aborde le thème de la conception et de l'utilisation des activités centrées sur le travail de l'élève dans un cadre précis : celui de la formation des professeurs de mathématiques pour développer leur connaissance de la matiére et leur connaissance pédagogique des contenus pendant les cours de formation initiale et continue. Cet article prend en compte divers travaux de recherche sur ce thème et reproduit, pour l'illustrer, le schéma de la structure basique des tâches que nous avons soumis aux professeurs de mathématiques de l'enseignement primaire et secondaire. Notre travail analyse également l'utilisation d'une tâche spécifique et se termine par une évaluation de ce que nous avons appris sur le potentiel des activités basées sur le travail des élèves dans le cadre de la formation des enseignants de mathématiques et sur les diverses formes qu'elles peuvent prendre.
MOTS CLÉS: Formation des professeurs de mathématiques, Éducation mathématique, Connaissance des contenus et connaissance pédagogique des contenus, Analyse des travaux de l'élève Enseignement de l'algèbre.
1. INTRODUÇÃO
Há muito se tem falado, no campo da educação, que um bom domínio dos conteúdos pelo professor não é, isoladamente, o que garante que o ensino, por ele proporcionado, seja eficiente. Outros conhecimentos, além do conhecimento dos conteúdos, são fundamentais ao professor para a atividade docente. Shulman (1986) foi um dos estudiosos do conhecimento do professor que colocou em discussão a composição desse conhecimento. Suas propostas de ideias e categorização do conhecimento passaram a apoiar, desde então, muitas pesquisas no âmbito da formação de professores. A busca por entender os saberes docentes, sua produção e suas diferentes naturezas tem sido uma questão recorrente. A valorização dos processos de construção de saberes pelos professores para fundamentar a sua prática tende a ser um fio condutor para o debate acerca da formação docente.
Outros pesquisadores merecem, também, destaque, pelas pesquisas voltadas para o entendimento do conhecimento dos professores e a natureza da atividade docente que realizam. Tardif, Lessard e Lahaye (1991), sinalizando para a pluralidade deste conhecimento, referem–se ao "saber docente" como um saber que envolve conhecimentos, competências, habilidades e atitudes. Em seu trabalho pioneiro, afirmam que "o saber docente é um saber plural, formado pelo amálgama, mais ou menos coerente, de saberes oriundos da formação profissional, dos saberes das disciplinas, dos currículos e da experiência" (Tardif et al, 1991, p. 218).
Na área de Educação Matemática, já se configura, como consenso entre pesquisadores, o fato de que o conhecimento do conteúdo matemático é um componente essencial do conhecimento do professor, mas que, além disso, são necessárias competências e habilidades para que o professor possa favorecer de maneira efetiva a aprendizagem matemática dos alunos.
A crença na afirmativa – quanto mais o professor de Matemática sabe sobre o conteúdo matemático, mais efetivo será o seu ensino foi abalada pelos estudos de Begle (1979) e Monk (1994), entre outros. A natureza do conhecimento matemático necessário para ensinar matemática escolar de forma eficiente é diferente da que é necessária para pesquisadores em matemática pura e para profissionais das diversas áreas que usam a matemática. Não se sabe ao certo como eles podem aprender matemática e usá–la eficientemente no ensino (Palis, 2003; Silver, 2006).
A questão abaixo, formulada por Ball (2000), resume, em parte, a intenção que nos move em apresentar e discutir as contribuições que as atividades centradas em produção de alunos podem dar à formação de professores de Matemática.
O que poderíamos fazer para trazer o estudo dos conteúdos mais próximo da prática, e preparar os professores para usar o conhecimento do assunto efetivamente no seu trabalho como professor? (Ball, 2000, p. 244, tradução nossa)
O trabalho aqui relatado pretende incentivar a reflexão, no sentido da compreensão do processo de aprendizagem matemática para ensinar e melhorar o entendimento sobre a natureza do saber docente relacionado à matemática escolar. Duas questões podem ser aqui apresentadas: Como desenhar e implementar atividades apoiadas em trabalhos de alunos na formação de professores de Matemática? Será que esta estratégia (análise do trabalho de alunos por professores) tem mesmo como melhorar o conhecimento matemático e pedagógico do conteúdo dos professores de Matemática?
2. REFERENCIAL TEÓRICO
Shulman (1986) situa–se entre os pesquisadores com bastante influência nos estudos sobre a concepção do saber docente (não especificamente relacionado à matemática). Sua descrição deste saber em três categorias constitui uma base para muitas reflexões nesta área.
Segundo Shulman, é possível distinguir o saber do conteúdo, o saber curricular (programas, materiais instrucionais, parâmetros, currículo horizontal e vertical) e o saber pedagógico do conteúdo, como constituintes do saber docente. Este último, o saber pedagógico do conteúdo, é um tipo especial de conhecimento que alia conteúdo e pedagogia, incluindo, dentre outros, quais representações são mais úteis para apresentar uma ideia matemática específica; as analogias, ilustrações, exemplos, explicações e demonstrações com maiores potenciais para tornar o conteúdo compreensível para os alunos; a compreensão do que faz a aprendizagem de certos tópicos ser difícil ou fácil; conhecimentos baseados em pesquisas a respeito das concepções mal formadas e conhecimentos prévios dos alunos relacionados aos tópicos lecionados mais frequentemente; estratégias para lidar / modificar concepções errôneas.
A literatura de pesquisa relacionada à formação de professores de Matemática, também influenciada pelos estudos de Shulman e de outros que se dedicam a entender o saber docente, tem enfatizado a ideia de que os professores precisam saber muito mais do que o conteúdo matemático específico para realizar uma boa prática; em particular, eles deveriam estar familiarizados com o que os alunos sabem e compreendem, para assim poder tomar decisões instrucionais apropriadas.
Ball e Cohen (1999) propõem que a essência da educação profissional para professores deveria se situar na prática de ensinar e ser constituída por estudossistemáticos de atividades centrais da prática letiva (selecionar/desenhar tarefas instrucionais, tomar em consideração o raciocínio dos alunos e acessar os seus conhecimentos) e deveria empregar materiais que representam o trabalho de ensinar (trabalho de alunos, material curricular, casos de instrução). Estes autores chamam a atenção para o fato de que os estudos centrados na prática não necessariamente precisam ocorrer em salas de aula, apesar de que a comoção do momento confere autenticidade à atividade realizada em tempo real.
Silver (2006), comentando sobre este ponto, diz que examinar a prática do ensino de perto pode incluir tarefas fundamentais que são desempenhadas fora dos limites da sala de aula, tais como: preparar aula, comentar por escrito o trabalho de um aluno e estudar casos de instrução. Acompanhar de perto como os alunos justificam ou quais significados dão às suas respostas, pode revelar informações que se perdem quando apresentam, unicamente, respostas.
As pesquisas, que a seguir trazemos neste texto, têm apontado o estudo e análise de trabalhos de alunos como atividades que podem levar professores a refletir sobre questões matemáticas e pedagógicas. A análise do raciocínio de alunos, como revelado em conjuntos de exercícios resolvidos por eles mesmos, pode propiciar aos docentes o desenvolvimento de uma base de conhecimentos sobre as concepções dos estudantes relacionadas aos conceitos e procedimentos subjacentes aos problemas tratados. Este desenvolvimento é fundamental para adquirir sensibilidade frente às dificuldades dos alunos, para poder dar sentido ao discurso dos estudantes e acessar o aprendizado dos mesmos. Este tipo de atividade, quando bem escolhida, por exemplo, envolvendo resoluções distintas, certas e erradas, é uma estratégia produtiva devido à riqueza de pontos de vista que podem surgir, tanto da parte dos alunos como dos professores.
Little, Gearhart, Curry e Kafka (2003) acompanharam grupos de análise de trabalhos de alunos de disciplinas variadas em alguns projetos de reforma curricular e formação docente. Little constatou que examinando o trabalho de alunos se ampliam as oportunidades de aprendizagem do professor. A pesquisa de Little não faz referência explícita a trabalhos com conteúdo matemático. No entanto, salienta que a falta de familiaridade dos professores com conceitos disciplinares básicos se manifestou com frequência, mas que sempre havia alguns professores com experiência relevante para atenuar esse constrangimento.
Pesquisas já bem consolidadas e que relatam os resultados dos programas de desenvolvimento profissional de professores nos primeiros anos da escola elementar, revelam, ainda, que a análise do pensamento dos alunos pode promover práticas instrucionais que levam a um melhor desempenho desses estudantes (Carpenter & Fennema, 1992). A pesquisa de Kazemi e Franke (2004),que se apóia na mesma matriz conceitual de Carpenter e Fennema, a denominada Cognitive Guided Instruction (na qual os professores de escola elementar analisam produções de seus próprios alunos), aponta como um dos principais resultados o fato de os professores passarem a prestar atenção detalhada no raciocínio dos alunos e se surpreenderem ao notar seus raciocínios inesperados.
Para séries mais avançadas, já estão surgindo evidências de que esta estratégia pode beneficiar o ensino e a aprendizagem de matemática. Pesquisas às quais tivemos acesso e que lidam especificamente com a análise de trabalhos de alunos de matemática na faixa escolar do 6° ao 9° ano do ensino fundamental, como as de Krebs (2005), Driscoll e Moyer (2001) e Seago e Goldsmith (2006), são comentadas a seguir. Todas elas apontam a análise de trabalhos de alunos como um catalisador para uma efetiva formação docente. Em nenhuma das três pesquisas foram utilizadas produções de alunos dos próprios professores sujeitos da pesquisa. Além disso, Krebs e Seago fizeram uso também de vídeos.
Em relação à escolha metodológica de propor aos professores que analisem os trabalhos dos seus próprios alunos em situação de grupo, Little et al. (2003) lembram que todo trabalho do aluno colocado para discussão é também um trabalho do professor, resultado de uma atividade proposta por ele e que mostra os frutos dos seus ensinamentos. Os professores participantes da pesquisa de Little viam o exame do trabalho do professor por meio do trabalho de seus alunos como um empreendimento bem delicado.
Krebs (2005) leva os professores a analisarem os trabalhos com conteúdo algébrico realizados por alunos do 8° ano. O modelo de atividade que implementa é mais abrangente, mais dispendioso em custo e produção do que o que apresentaremos neste artigo. Inicialmente, os professores sujeitos de sua pesquisa, analisam as produções escritas dos alunos, depois assistem aos vídeos que mostram os alunos resolvendo os problemas propostos e têm acesso também a entrevistas que foram realizadas com os estudantes após terem terminado a atividade. Os vídeos e entrevistas revelaram importantes dados adicionais sobre o pensamento dos alunos. Isto serviu de alerta para os professores em relação à complexidade de acessar a compreensão dos alunos. Professores usam, basicamente, respostas escritas pelos alunos para avaliar seu aprendizado e atribuir notas ao seu desempenho. No entanto, conclusões incompletas e mesmo incorretas podem ser inferidas, como ficou evidenciado pelo estudo de Krebs. Por outro lado, fazer vídeos e entrevistar alunos para todas as tarefas é impraticável.
A pesquisa de Krebs mostra professores reconhecendo o valor de usar evidências adicionais e apontando também a importância de ajudar seus alunos a estarem mais preparados para fornecer registros mais completos de seu raciocínio ao realizar certa tarefa. Em seu artigo, Krebs cita o trabalho de Crockett (2002) no qual, este autor concluiu que a análise dos trabalhos dos alunos foi a atividade mais eficiente para levar professores a reconsiderar o ensino de matemática. Crockett não se limitou a empregar produções escritas de alunos, também ouviu os estudantes enquanto trabalhavam e fez perguntas sobre suas resoluções.
A pesquisa de Seago e Goldsmith (2006) envolveu 74 professores do 5° ao 8° ano do ensino fundamental, empregou trabalhos de alunos sobre conteúdos algébricos e vídeos de salas de aula e investigou o efeito prático deste tipo de desenvolvimento profissional. Dentre os resultados apontados, os professores envolvidos na experiência aprenderam a analisar diferentes métodos para resolver um problema e a escolher representações matemáticas apropriadas.
Biza, Nardi e Zachariades (2007), com fins de desenvolver o conhecimento dos professores, envolvem–nos em cenários de sala de aula que, apesar de hipotéticos, mostram–se muito úteis para aprender a ensinar temas que são considerados fundamentais em matemática. Esses cenários incluem tarefas que trazem encaminhamentos e resoluções de ocorrência provável nas aulas de matemática. As tarefas podem ser utilizadas com professores em formação inicial ou continuada, e possibilitam ter acesso às concepções dos professores acerca de conteúdos matemáticos apontados como problemáticos pela literatura ou pela prática dos próprios autores.
As tarefas apresentadas aos professores estruturam–se da seguinte forma: eles devem refletir sobre os objetivos de um examinador que propõe um problema matemático X em um teste para seus alunos; examinar a resolução dada por um desses alunos (ficcional) ao mesmo problema X; e apresentar, por escrito, os comentários que faria para este aluno a respeito de sua resolução. Essa perspectiva de trabalho, segundo esses pesquisadores, favorece ou enfatiza a transformação do conhecimento teórico do professor numa prática teoricamente informada. Trata–se da construção a que Hill e Ball (2004) se referem como conhecimento matemático para o ensino, e Shulman (1986), como conhecimento pedagógico do conteúdo.
Driscoll e Moyer (2001) também trabalharam com produção de alunos do 6° ao 9° ano do ensino fundamental, envolvendo conteúdos algébricos. Dentre suas observações teóricas, salientaram que, para promover um desenvolvimento profissional efetivo, o conjunto de trabalhos de alunos a ser analisado deve abranger várias abordagens possíveis para a questão e também resoluções nas quais o pensamento do aluno não é nada claro.
Stylianou, Kenney, Silver e Alacaci (2000) argumentam que, se os alunos respondem a questões matemáticas sem fornecer explicações de como foram obtidas, ou não são questionados sobre suas estratégias de resolução, é difícil compreender e aprender como eles pensaram e como, num grupo de alunos, podemos encontrar respostas bastante diferentes para um mesmo problema. Esses autores procuram ilustrar as informações que a análise detalhada das explicações escritas que acompanham as respostas de alunos a tarefas matemáticas pode fornecer. Para isso, examinam as diferentes resoluções apresentadas por uma amostra de estudantes da 8ª série a uma questão matemática presente em uma avaliação de larga escala (NAEP1) realizada em seu país. A amostra foi divulgada pelo órgão avaliador.
A questão estudada está na figura um e a resposta correta é 420, de acordo com o critério de correção do NAEP.

Observou–se uma variação muito grande de respostas e encaminhamentos desde 20 pontos até milhões de pontos. Na figura dois apresentamos diferentes respostas presentes no artigo de Stylianou et al. (2000). O trabalho desses autores contém reproduções de diferentes estratégias usadas pelos alunos para chegar a esses resultados.

A análise cuidadosa das diversas resoluções por ele s realizada revela diferentes estratégias e cálculos levando a diferentes respostas (certas e erradas), e possibilita aprender mais acerca do pensamento matemático dos alunos. A variedade de respostas, certas ou erradas, e as explicações apresentadas pelos alunos para responder o problema em questão, discutidas por Stylianou et al. (2000), mostram dificuldades comuns dos alunos, quando enfrentam problemas de "busca de padrão".
Uma das respostas presente no conjunto analisado por Stylianou et al. (2000) é surpreendente, e nos leva a reflexões interessantes. O aluno considerou que da 1ª para a 2ª figura, o número de pontos triplica. E que da 2ª figura para a 3ª, o número de pontos dobra. Prosseguindo dessa forma, alternando entre dobrar e triplicar a cada passo, o aluno chega a 60 466 176 pontos na 20ª figura. Esse raciocínio desenvolvido por um aluno leva a uma resposta que pode ser inesperada, mas é possível, e interessante para a reflexão dos professores. Deixamos aqui uma pergunta para o leitor: Trata–se de uma resposta tão correta quanto 420?2
Finalmente poderíamos nos perguntar: Mas o que há de novo com esta tarefa de analisar trabalhos de alunos? Pensando bem, analisar trabalhos de alunos é uma tarefa frequente na prática docente. É verdade, mas em geral os professores a realizam sozinhos, com pouco tempo disponível e com a finalidade de atribuir uma nota. Nas reuniões de professores se examinam planos de aula, cronogramas, questões de avaliação, documentos curriculares, mas raramente analisam trabalhos realizados por alunos. O olhar atento ao trabalho de alunos, principalmente se realizado em grupo, tem características de formação que merecem ser exploradas dentro da ampla agenda da formação de professores.
Ao desenhar, implementar e analisar as atividades centradas em trabalhos feitos por alunos em nossa prática como professores de Matemática em cursos de formação inicial, continuada e de pós–graduação, temos como objetivo desenvolver os conhecimentos matemático e pedagógico do conteúdo matemático dos professores desta área.
A seguir exemplificamos nossa contribuição nesta área com a descrição da estrutura básica de tarefas que temos proposto a professores de Matemática do 6° ao 9° ano do ensino fundamental e do ensino médio e a discussão de uma implementação específica. Faremos uma apreciação do que aprendemos sobre a potencialidade de atividades apoiadas em trabalhos de alunos na formação de docentes de Matemática e a respeito de maneiras de construí–las.
3. ATIVIDADES APOIADAS EM PRODUÇÕES DE ALUNOS
Nesta seção, apresentamos a estrutura geral das atividades apoiadas em produções de alunos que foram por nós construídas e sua metodologia, seu público alvo, os objetivos das atividades, o conteúdo matemático subjacente às mesmas e os critérios norteadores da escolha dos trabalhos de alunos. Em Palis (2005) podem ser encontradas outras atividades desenhadas segundo este mesmo modelo.
3.1. Estrutura geral e metodologia de implementação das atividades. Dados coletados para análise
a. O trabalho começa com uma apresentação geral da atividade, seus objetivos e a descrição do trabalho escrito que será solicitado aos professores participantes.
b. Os professores resolvem um problema, individualmente, explicando seu raciocínio. Ao terminar, nos entregam o trabalho (o que nos possibilita uma breve leitura, a fim de obtermos uma idéia inicial do conhecimento matemático dos professores, e que pode ser importante na hora de decidir sobre realizar, ou não, interferências ao longo das discussões de grupo, e sobre como formar os grupos).
c. Os professores são solicitados a responder uma questão que lhes é proposta, individualmente, baseando–se em um conjunto de cópias de resoluções do mesmo problema que foi por eles resolvido (como dito em 1) e realizadas por alunos.
d. Os professores compartilham seus trabalhos.
e. Os professores, agora em grupos de três ou quatro, discutem suas respostas, conciliam seus raciocínios e chegam a uma resposta do grupo como um todo.
f. Os grupos apresentam o trabalho realizado. Segue–se uma discussão livre e nossos comentários finais.
g. Trabalho para casa: Responder, por escrito: – O que você acha que aprendeu ao longo desta atividade?
Os dados coletados para a nossa análise posterior abarcam todo o material entregue aos professores, as anotações por nós realizadas durante e após cada encontro, o trabalho realizado por escrito pelos professores ao longo dos encontros e a autoavaliação feita por eles ao término dos encontros.
3.2 Público–alvo
O trabalho com as diversas atividades foi feito com grupos de cerca de 24 professores licenciados em Matemática (professores de Matemática, do 6° ao 9° ano do ensino fundamental e do ensino médio). Na ocasião, estes professores estavam participando de um programa de formação continuada em ambiente de ensino universitário. Ensinavam em escolas diferentes e a participação no programa de formação era voluntária. Os participantes reuniram–se durante três a quatro horas para cada atividade do tipo aqui considerada, em diferentes ocasiões ao longo do programa no qual estavam inseridos.
3.3 Os objetivos das atividades
De maneira geral, o objetivo das atividades é promover o desenvolvimento do conhecimento matemático e pedagógico do conteúdo matemático em grupos de professores licenciados em Matemática. Para um professor, o desenvolvimento desses conhecimentos caminha em paralelo e ambos são privilegiados em nossas atividades. Se, por um lado, o conhecimento matemático do professor não basta para tornar seu ensino efetivo, indo ao encontro das ideias de Shulman (1986), o conhecimento matemático seguro pode ser essencial para desenvolver o conhecimento pedagógico do conteúdo no tocante a aspectos como, por exemplo, dar sentido ao raciocínio de alunos e saber quais representações e justificativas podem contribuir para o aprendizado matemático dos alunos.
Por outro lado (e não menos importante), entendemos que essas atividades têm grande potencial para desenvolver, nos professores, o respeito pela diversidade de formas de raciocínio que os alunos podem revelar. Alunos podem ser extremamente criativos e é importante que os professores se conscientizem a respeito de suas maneiras de pensar e as valorizem.
Além disso, pretendemos que os professores tenham a oportunidade de desenvolver uma base de conhecimentos sobre as concepções dos alunos a respeito de tópicos usualmente ensinados na faixa etária na qual trabalham.
3.4 O conteúdo matemático subjacente às atividades
Os problemas matemáticos que dão suporte às atividades são expressos em linguagem algébrica e oferecem oportunidades de trabalho com outras representações além da algébrica (por exemplo, gráfica, verbal, numérica, por esquema, etc.).
A escolha da Álgebra como ponto de partida leva em conta a sua posição como uma das áreas básicas da matemática da escola fundamental e média. É necessário criar oportunidades de aperfeiçoamento de docentes neste campo, preparando–os para enfrentar as dificuldades dos alunos, amplamente constatadas pelas pesquisas e debatidas nos fóruns em que se discutem os nós da aprendizagem de matemática. Uma visão geral desta problemática pode ser examinada em Stacey, Chick e Kendal (2004).
A escolha do problema matemático subjacente às atividades também leva em conta o potencial cognitivo das representações múltiplas no desenvolvimento de conceitos e processos matemáticos. Como já dizia Kaput (1987), o uso crescente de ferramentas tecnológicas digitais proporciona uma variedade de representações de ideias matemáticas com as quais alunos e professores podem trabalhar. Esse autor também aponta que professores e alunos iriam necessitar mais do que uma intuição desinformada para guiá–los; eles iriam necessitar de conhecimentos sistematizados, disponíveis e justificados para fazer escolhas, construções e interpretações no âmbito das representações múltiplas. Ponderamos que o trabalho com as possibilidades, limitações e eficácia de diferentes representações de um mesmo objeto matemático pode ser facilitado pelas novas tecnologias, mas não é realizável em circunstâncias didáticas tradicionais.
3.5 Os critérios norteadores da escolha dos trabalhos de alunos
As resoluções de problemas colocadas para análise pelos professores não eram de autoria de seus alunos. Concordando com Little et al. (2003), consideramos que, dessa forma, reduz–se o fator emocional no trabalho de análise, os pré–julgamentos e constrangimentos da parte dos professores.
Os trabalhos utilizados por nós foram selecionados entre várias resoluções de problemas, apresentadas por alunos em situações reais de sala de aula, ao fim do primeiro mês de uma disciplina regular de transição ensino médio/superior, na universidade. Não foram escolhidos problemas desafiadores, mas problemas que, de certa forma, podemos entender como de rotina, mas que não haviam sido resolvidos ou discutidos em sala de aula, antes de terem sido propostos aos alunos. Os problemas foram resolvidos pelos alunos individualmente, em sala e sem consulta a livros ou apontamentos. Tivemos o cuidado de selecionar um conjunto de resoluções de um mesmo problema, que incluísse diferentes encaminhamentos e representações, respostas certas, erradas e confusas. Estes critérios também estão presentes em outros trabalhos na área.
A seguir, trazemos, em detalhes, uma das atividades desenvolvidas, implementadas e analisadas por nós. Veremos que essa atividade, apesar de matematicamente simples, apresentou oportunidades muito importantes de aprendizagem docente. Fornecemos o enunciado da atividade e discorremos sobre a resolução do problema pelos professores, sobre a interação dos professores com as resoluções dos alunos, expomos alguns temas de discussão adicionais propostos ao grupo de professores e fazemos uma apreciação geral sobre o que aprendemos com essa atividade no âmbito da formação de docentes.
4. EXEMPLO DE UMA ATIVIDADE ESPECÍFICA
4.1. Enunciado
A atividade, cujo enunciado se vê abaixo, foi construída na linha das especificações anteriormente explicitadas. Há duas versões da atividade que são fornecidas juntamente com seu enunciado comum. Com relação ao conteúdo matemático, a tarefa tem como pano de fundo uma relação central e recorrente nos currículos de ensino médio. Trata–se da chamada Conexão Cartesiana, que pode ser expressa da seguinte forma: O ponto (a,b) pertence ao gráfico da equação f (x,y) = 0 se, e somente se, as suas coordenadas a satisfazem, isto é, f (a, b) = 0. Algumas pesquisas têm estudado a dificuldade dos alunos em situações nas quais esta conexão está subjacente (Knuth, 2000).

As resoluções de alunos que foram entregues aos professores para análise encontram–se nas figuras três a (4–5–6–7–8) nove.




4.2. Os professores e suas resoluções
Cerca de 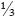 dos professores disse que não se lembrava da equação da circunferência, e não resolveu a questão. Não pensaram em determinar a equação da circunferência de centro e raio dados, a partir da expressão da distância entre dois pontos do plano. Esta postura é comum entre alunos: ou você já sabe "de cor" a equação da circunferência ou não sabe e acha que não tem recursos para deduzi–la. Os demais utilizaram a equação da circunferência para decidir se o ponto P pertence ou não à circunferência; mesmo assim, ¼ destes não decidiu corretamente a posição de P em relação à circunferência dada.
dos professores disse que não se lembrava da equação da circunferência, e não resolveu a questão. Não pensaram em determinar a equação da circunferência de centro e raio dados, a partir da expressão da distância entre dois pontos do plano. Esta postura é comum entre alunos: ou você já sabe "de cor" a equação da circunferência ou não sabe e acha que não tem recursos para deduzi–la. Os demais utilizaram a equação da circunferência para decidir se o ponto P pertence ou não à circunferência; mesmo assim, ¼ destes não decidiu corretamente a posição de P em relação à circunferência dada.
As dificuldades aritméticas surgidas no decorrer da resolução do problema pelos professores se concentraram na versão I, na qual alguns calculavam a expressão (23 – 3)2 + (25 + 5)2 após expandi–la e não após simplificá–la para 202 + 302. As dificuldades algébricas se apresentaram no uso da equação da circunferência na forma x2 + y2 – 2ax – 2by + a2 + c2 – r2 = 0 para decidir a posição relativa do ponto e da circunferência, pela perda de sentido da geometria subjacente. Apesar das equações (x–a)2 + (y–b)2 = r2 e x2 + y2 – 2ax – 2by + a2 + c2– r2 = 0 serem equivalentes, a primeira comunica mais facilmente a geometria subjacente do que a segunda.
4.3. Os professores e as resoluções dos alunos
Mais da metade dos professores participantes apresentou dificuldades com as questões matemáticas subjacentes aos raciocínios ou técnicas presentes nas resoluções dos alunos. A variedade de encaminhamentos nas respostas dos alunos que foram colocadas para análise, contrastou muito com a única forma de responder a questão corretamente e apresentada pelos professores. A surpresa para com essa variedade de caminhos foi referenciada por um dos professores. Ele afirmou: "no processo de avaliação pude aprender a dar mais valor às maneiras mais criativas de se resolver determinados exercícios ao invés daquelas que são imediatistas, também a comparar os diversos exercícios dos alunos para ter um critério mais justo"
As resoluções de alunos exibidas nas figuras três e quatro foram adequadamente analisadas pela maioria dos professores.
Na resolução da figura três, o aluno achou o quadrado da distância de C = (– 4,1) a P = (46,0) e comparou este número com o quadrado do raio dado R = 50. O uso adequado (subentendido) da implicação "Se a e b são números reais positivos e a2 > b2, então a > b", não foi mencionado por nenhum professor. Em nossa prática, constatamos que alunos e professores usam frequentemente a implicação "Se a e b são números reais e a2 > b2, então a > b", que não é verdadeira.
Na resolução da figura quatro, os professores não se incomodaram com o uso inadequado do sinal de igualdade 202 + 302 = 362 nem com o fato da justificativa à vista na resolução do aluno ter se interrompido na comparação dos quadrados 1300 > 1296.
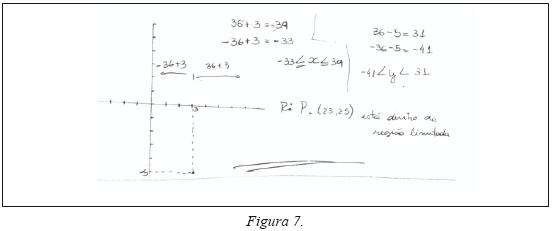
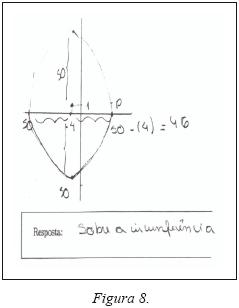
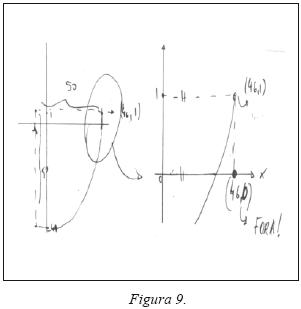
Com relação à resolução na figura cinco, alguns professores tiveram dificuldade em conciliar o desenho que "os convencia" (e ao aluno autor da resolução) que P estava na região limitada pela circunferência com o resultado algébrico, que apontava o contrário. Já a dificuldade do aluno com a resolução apresentada na figura oito e o argumento gráfico convincente da resolução na figura nove foram mais facilmente compreendidos pelos professores.
As resoluções apresentadas nas figuras seis e sete apresentaram mais dificuldades de interpretação para os professores.
Na figura sete, o aluno, de fato, verifica que o ponto P = (23, 25) está na região retangular dada pelo sistema de desigualdades: – 33 ≤ x ≤ 39, – 41 ≤ y ≤ 31 e não que pertence à região limitada pela circunferência. Esta segunda regiãoestá contida propriamente na primeira. Esta constatação foi bastante problemática para a maior parte dos professores.
Os professores tiveram muita dificuldade com a interpretação da resolução apresentada na figura seis. Nas suas cinco primeiras linhas, o aluno já havia obtido argumentos que poderiam levá–lo a concluir que o ponto P está fora da região limitada pela circunferência. No entanto, as manipulações que realiza "desfazem" a estrutura da equação da circunferência, e o que é obtido "parece" não fazer mais sentido para o aluno, que recomeça a resolução. O aluno volta à terceira equação obtida anteriormente, e a utiliza para achar os dois valores de y para os quais o ponto (23, y) pertence à circunferência dada. Encontra as seguintes aproximações desses valores: – 33,4 e 23,4. Com essas aproximações, o aluno fornece a resposta correta, pois 25 > 23,4.
No entanto, se, em vez do ponto P, o ponto dado fosse, por exemplo, Q = (23,24), o aluno também teria chegado à conclusão que o ponto Q pertence à região considerada, pois 24 > 23,4. Esta afirmativa, no entanto, é falsa; porque o ponto Q está no interior da mesma. Senão vejamos:
As expansões decimais (truncadas na quarta casa decimal) dos valores de y para os quais (23, y) pertence à circunferência dada são: 24,9332 e – 34,9332. Como – 34,9332 < 24 < 24,9332, o ponto Q = (23,24) está dentro da região.
4.4. Algumas discussões adicionais
Ao longo da apresentação das análises dos trabalhos dos alunos pelos professores, quando achávamos apropriado, colocávamos algumas questões matemáticas para reflexão e discussão entre os participantes. As questões emergiam das resoluções dos alunos e comentários dos professores; também se relacionavam com situações que a nossa prática aponta como problemáticas para muitos alunos. Intencionamos com isso favorecer a indagação sobre aspectos importantes do trabalho docente. Alguns elementos destacados por Shulman (1986) como necessários e fundamentais ao conhecimento pedagógico do conteúdo do professor mostraram–se fortemente presentes, como a escolha de uma melhor representação para uma ideia matemática específica, caminhos para tornar o conteúdo mais compreensível para os alunos, e estratégias para lidar / modificar concepções errôneas.
Por exemplo, acrescentamos à discussão da figura três o estudo da resolução de algumas desigualdades a uma variável dentre as quais as desigualdades x2 < 9 (frequentemente resolvida erroneamente para x < 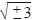 ) e x2 + 3 < 0(frequentemente resolvida erroneamente para x < ± 3). A dificuldade com a determinação da região retangular – 33 ≤ x ≤ 39, – 41 ≤ y ≤ 31, encontrada na resolução da figura sete, nos levou a propor discussões adicionais sobre conceituação e formas de representar as soluções de sistemas de desigualdades no plano, como, por exemplo, { y < x + 1, 2x – y – 3 < 0 }.
) e x2 + 3 < 0(frequentemente resolvida erroneamente para x < ± 3). A dificuldade com a determinação da região retangular – 33 ≤ x ≤ 39, – 41 ≤ y ≤ 31, encontrada na resolução da figura sete, nos levou a propor discussões adicionais sobre conceituação e formas de representar as soluções de sistemas de desigualdades no plano, como, por exemplo, { y < x + 1, 2x – y – 3 < 0 }.
Concepções errôneas relacionadas ao contexto gráfico estavam presentes nos trabalhos dos alunos e também no trabalho dos professores. Um dos professores participantes nos disse: "muitas vezes não nos damos conta de que certos erros de nossos alunos refletem algumas falhas que cometemos ao ensiná–los. Ou até mesmo, refletem erros nossos que carregamos ao longo da vida e dos quais 'um belo dia' notamos a existência".
Os professores mostraram estar pouco cientes das possibilidades e dos limites do quadro gráfico, deram pouca atenção às aproximações inerentes à leitura e marcação de pontos e colocaram extrema confiança em esboços gráficos. Com apoio das resoluções das figuras cinco, oito e nove foi possível provocar uma discussão frutífera sobre vários aspectos: a conceituação de plano cartesiano, as possibilidades e limitações da representação gráfica, a operação de "zoom", comum em ambientes providos de novas tecnologias, realizada na resolução da figura nove em contexto "papel e lápis".
Os valores da versão II do problema, presente nas duas resoluções nas figuras oito e nove, permitem uma melhor visualização gráfica do que possibilitam os valores da versão I na figura cinco. Este fato levou a uma constatação importante do ponto de vista pedagógico: mudanças nos valores atribuídos aos parâmetros do problema podem mudar as estratégias disponíveis para sua resolução. Dessa forma, valores numéricos presentes em exercícios podem ser considerados como parâmetros que fornecem uma margem de manobra para professores calibrarem tarefas para seus alunos.
O trabalho dos alunos com a abordagem da mesma questão, como encontrada em alguns livros didáticos por eles trazidos, levou a discussões produtivas. Os livros, em geral, destacam a apresentação das três situações possíveis de ponto em relação à circunferência. Em um dos livros trazidos para análise, as condições para decidir a posição relativa de um ponto P em relação a uma circunferência L, de centro C = (a, b) e raio r podem ser vistas na figura dez.

Posteriormente ao quadro referenciado na figura dez, apresenta–se o seguinte exemplo:

A discussão que se seguiu foi muito proveitosa; aospoucos os professores foram "descobrindo" as diversas facetas do exemolo. Initialmente, é possível ver que 0 resolução não se sustenta exatamente na apresentação geral que a precede. Além disso, a equação L é reescrita erroneamente e o uso do sinal de igual ao longo dos cálculos é totalmente inadequado. Contribuições variadas dos participantes levaram à constatação de que a equação L pode ser reescrita como (x–3)2 + (y–1)2 = 16, o que permite uma resolução algébrica dotada de sentido e também uma abordagem gráfica, devido aos valores numéricos envolvidos.
4.5. O que aprendemos com o estudo da implementação da atividade
O desenrolar dessa atividade permitiu aos participantes verbalizarem suas dificuldades conceituais, às vezes bastante sérias, em se tratando de professores de ensino médio.
É oportuno lembrar que a suposição de que o conhecimento do conteúdo matemático não é um problema para professores do ensino médio, em virtude destes terem cursado um número maior de disciplinas formais especializadas em matemática, pode ser falsa. Algumas pesquisas realizadas entre professores do ensino médio apontam dificuldades de professores deste segmento, relativas ao conhecimento matemático propriamente dito, mesmo sobre conceitos fundamentais do currículo escolar (Ball, 1990; Doerr, 2004).
O grupo de professores era bastante heterogêneo quanto ao domínio do conteúdo matemático abordado. Alguns professores mostravam um domínio excelente do conteúdo, um fator determinante para o bom funcionamento do grupo como um todo, pelas trocas e reflexões que as discussões possibilitaram. Estas constatações também são trazidas por Little et al. (2003).
Pelo fato de os alunos irem por caminhos completamente diferentes dos caminhos usuais dos professores (quando acertam e erram) e eles terem que discutir o que estes fizeram, essa atividade revelou possibilidades em termos de aprofundamento conceitual. Estratégias muito diferentes para resolver um mesmo problema não são encontradas nos livros didáticos com facilidade. Os livros tendem a enfatizar a representação algébrica, mas os alunos podem ir por outros caminhos, assim como mostramos nas resoluções que escolhemos para a realização da atividade.
Em todas as análises realizadas pelos professores foi preciso lidar com várias abordagens e representações distintas (algébrica, gráfica, verbal), sua escolha e adequação. Concepções errôneas relacionadas ao contexto gráfico estavam presentes nos trabalhos dos alunos e também no trabalho dos professores, tanto nas etapas de resolução como de análise. A pouca atenção às aproximações inerentes à leitura e marcação de pontos e a extrema confiança em esboços gráficos estiveram presentes em muitas ocasiões. Tanto professores como alunos envolvidos mostraram estar pouco cientes das possibilidades e limites da representação gráfica. Toda essa problemática criou espaço para discussões de questões importantes envolvendo o ensino e aprendizado de matemática, seja no âmbito do conhecimento do conteúdo como no âmbito do conhecimento pedagógico do conteúdo.
Alguns professores revelaram que, algumas vezes, não prestam muita atenção às respostas dos alunos ao corrigirem suas resoluções de exercícios. Alguns disseram, explicitamente, que não têm tempo para analisar os trabalhos de alunos com tanto cuidado. Em geral, as respostas dos alunos são comparadas a um prévio modelo de resolução. Esse aspecto nos remete à pesquisa de Kazemi e Franke (2004), na qual os professores do ensino elementar analisam produções de seus próprios alunos, que apontam o fato dos professores passarem a prestar atenção a detalhes do raciocínio dos alunos como um dos seus principais resultados. No nosso trabalho, um dos professores declarou que: "Ao avaliarmos nosso aluno devemos não somente buscar avaliar se ele acertou ou errou a questão, como também avaliar os caminhos encontrados por ele para obter a resposta final, mesmo que esta não seja a melhor ou a certa para determinado problema".
Desenvolver o interesse e respeito da parte dos professores pelos caminhos trilhados pelos alunos é um avanço no conhecimento pedagógico dos professores, possibilitado ao longo do desenvolvimento desta atividade. Como nos diz Shulman (1986), o conhecimento pedagógico do conteúdo inclui o conhecimento dos professores acerca das concepções, crenças e conhecimentos dos alunos sobre as disciplinas que estudam.
Ao longo do trabalho, os professores também salientaram: a complexidade do processo de identificação do raciocínio e do conhecimento do aluno somente pelo que ele escreve; a importância de "falar com o aluno para perguntar o que ele fez", como disse um professor; a necessidade de desenvolver critérios de correção cuidadosamente; e a inerente subjetividade do processo de "dar notas".
5. CONSIDERAÇÕES FINAIS
Retomando as duas questões por nós apresentadas na introdução deste artigo, temos a dizer, como formadoras de professores de Matemática e pesquisadoras, que as atividades centradas em produções de alunos têm revelado um grande potencial de desenvolvimento do conhecimento matemático e pedagógico desse conteúdo em oportunidades de formação docente.
Os estudos e pesquisas que aqui trouxemos mostram seus ganhos, reafirmados pelo que temos constatado em nosso trabalho, aqui exemplificado pelo estudo detalhado de uma atividade específica. Em diferentes seções deste texto, destacamos as diversas situações e questões que possibilitaram o desenvolvimento e o aperfeiçoamento do conhecimento matemático e do conhecimento pedagógico dos professores, ao longo da implementação da referida atividade.
Cabe ressaltar que o desenho da atividade por nós proposta não é o único, nem tampouco, a sua estrutura e forma de implementá–la. A escolha do material a ser analisado não segue, também, critérios semelhantes. Nos diversos estudos e pesquisas que se voltam para a temática tratada neste artigo, observamos estratégias e escolhas diferenciadas, que têm como ideia central a análise de produção de alunos por professores de Matemática.
As resoluções a serem analisadas podem ser simuladas, como defendem Biza et al. (2007), envolvendo os professores em cenários de aula que são hipotéticos, mas frutíferos para aprender a ensinar. Essas resoluções trazem situações muito prováveis de serem encontradas em produções matemáticas dos alunos.
Kazemi e Franke (2004) envolvem professores da escola elementar com a análise das produções de seus próprios alunos, para que estes desenvolvam um conhecimento profundo a respeito do pensamento matemático de seus alunos.
Krebs (2005) utiliza resoluções de questões que não foram feitas pelos alunos dos professores sujeitos de sua pesquisa. Esse autor sugere a complementação da análise da produção dos alunos disponibilizando vídeos mostrando os alunos trabalhando e o conteúdo de entrevistas realizadas com os alunos após a realização das tarefas.
A produção dos alunos a ser apresentada para a análise dos professores pode variar entre resoluções que levam não necessariamente a respostas erradas ou corretas, mas que evidenciem, também, caminhos inesperados, alternativos, pouco usuais, que não reproduzam procedimentos estereotipados e mecânicos. Essa diversidade de abordagens analisadas e discutidas é muito relevante para o aprendizado da docência.
As resoluções do problema que foram apresentadas e discutidas por Stylianou et al.(2000) são bastante sugestivas quanto ao uso que podemos fazer de questões presentes em testes de larga escala. Estes testes, além de envolverem um universo bastante diversificado de alunos, com diferentes trajetórias escolares, são significativos para a identificação de dificuldades comuns. O problema trazido por Stylianou et al. (2000) pode ser aproveitado para o desenho de uma atividade a ser implementada com professores, ou mesmo com alunos da educação básica.
Finalizamos destacando que consideramos importante assegurar espaço para esse tipo de atividade, na formação de professores de Matemática. Nossa experiência como formadoras e pesquisadoras revela que a análise do trabalho de alunos pode ser, e frequentemente é, uma atividade de resolução de problemas matemáticos e didáticos para os professores que a realizam.
REFERÊNCIAS
Ball, D.L. & Cohen, D.K. (1999). Developing practice, developing practitioners: Toward a practice based theory of professional education. In G. Stykes & L. Darling–Hammond (Eds.), Teaching as the learning profession: Handbook ofpolicy and practice (pp. 3–32). San Francisco: Jossey Bass. [ Links ]
Ball, D.L. (1990). Prospective elementary and secondary teachers' understanding of division. Journal for Research in Mathematics Education 21 (2), 132–144. [ Links ]
Ball, D. L. (2000). Bridging Practices: Intertwining content and pedagogy in teaching and learning to teach. Journal of teacher education 51 (3), 241–247. [ Links ]
Begle, E. (1979). Critical Variables in Mathematics education: Findings from a survey of empirical literature. Washington, D.C. : The Mathematical Association of America and the National Council of Teachers of Mathematics. [ Links ]
Biza, I; Nardi, E. & Zachariades, T. (2007). Using Tasks to Explore Teacher Knowledge in Situation–Specific Contexts. Journal of Mathematics Teacher Education10 (4–6), 301–309. doi: 10.1007/s10857–007–9043–y [ Links ]
Carpenter, T.P. & Fennema, E. (1992). Cognitively guided instruction: Building on the knowledge of students and teachers. International Journal of Educational Research 17, 457–470. [ Links ]
Crockett, M.D. (2002). Inquiry as professional development: creating dilemmas through teachers'work. Teaching and Teacher Education 18 (5), 609–624. [ Links ]
Driscoll, M. & Moyer, J. (2001). Using students' work as a lens on algebraic thinking. Mathematics Teaching in the Middle School 6 (5), 282–287. [ Links ]
Doerr, H.M. (2004). Teachers' knowledge and the teaching of algebra. In K. Stacey, H. Chick, & M. Kendal (Eds.), The Future of the Teaching and Learning of Algebra.The 12th ICMI Study (pp. 267–290). Melbourne, Australia: The University of Melbourne. [ Links ]
Hill, H.C. & Ball, D.L. (2004). Learning mathematics for teaching: Results from California's mathematics professional development institutes. Journal for Research in Mathematics Education, 35(5),330–351. [ Links ]
Kazemi, E. & Franke, M.L. (2004). Teacher learning in mathematics: Using student work to promote collective inquiry. Journal of Mathematics Teacher Education 7 (3), 203–235. [ Links ]
Kaput, J.J. (1987). Representation Systems and mathematics. In C. Janvier (Ed.) Problems of representation in the teaching and learning of mathematics (pp. 19–26). Hillsdale, NJ: Lawrence Erlbaum. [ Links ]
Knuth, E.J. (2000). Student Understanding of the Cartesian Connection: An Exploratory Study. Journal for Research in Mathematics Education 31 (4), 500–508. [ Links ]
Krebs, A.S. (2005). Analyzing Student Work as a Professional Development Activity. School Science and Mathematics 105 (8), 402–411. [ Links ]
Little, J.W., Gearhart, M., Curry, M. & Kafka, J. (2003). Looking at Student Work for Teacher Learning, Teacher Community, and School Reform. Phi Delta Kappan 85 (3), 184–192. [ Links ]
Monk, D.H. (1994). Subject area preparation of secondary mathematics and science teachers and student achievement. Economics of Education Review 13 (2), 125–145. [ Links ]
Palis, G.L.R. (2003). Atividades para aprender Matemática para ensinar. Anais do III Seminário Internacional de Pesquisa em Educação Matemática, Santos, SP. [ Links ]
Palis, G. L. R. (2005). Continuing education: Activities based on student work – how we did it and what we have learned from it. Paper apresentado na 15th ICMI Study Conference: The Professional Education and Development of Teachers of Mathematics, Águas de Lindóia, Brazil. Disponível em http://stwww.weizmann.ac.il/G–math/ICMI/Palis_Gilda_ICMI15_prop.doc. [ Links ]
Seago, N. & Goldsmith, L. (2006). Learning Mathematics for Teaching. In J. Novotná, H. Moraová, M. Krátká & N. Stehlíková (Eds.), Proceedings 30th Conference of the International Group for the Psychology of Mathematics Education, (Vol. 5, pp. 73–80). Prague, Czech Republic: Charles University in Prague, Faculty of Education. [ Links ]
Shulman, L.S.(1986). Those Who Understand: Knowledge Growth in Teaching. Educational Researcher 15(2), 4–14. [ Links ]
Silver, E.A. (2006). Formação de Professores de Matemática: desafios e direções. Trad de O. Figueiredo. Boletim de Educação Matemática 19 (26), 125–152. [ Links ]
Stacey, K., Chick, H. & Kendal, M. (2004). The Future of the Teaching and Learning of Algebra, The 12th ICMI Study (Vol. 8). Dordrecht, Holland: Kluwer [ Links ]
Stylianou, D. A., Kenney, P. A, Silver, E. A. & Alacaci, C. (2000). Gaining Insight into student's thinking through Assessement tasks. Mathematics teaching in the Middle School, 6 (2), 136-144. [ Links ]
Tardif, M, Lessard, C & Lahaye, L.(1991). Os professores face ao saber: esboço de uma problemática do saber docente. Teoria e Educação 4, 215–233. [ Links ]
1 National Assessesment of Educational Progress, USA.
2 No site "The On–Line Encyclopedia of Integer Sequences", cujo endereço é http://www.research.att.com/~njas/sequences/index.html, é possível encontrar um número considerável de sequências bem definidas de números inteiros que contem a tripla 2,6,12. Entre com a tripla 2,6,12 e aperte search. A sequência obtida por sucessivas multiplicações por 2 e por 3, iniciando em 1, é a seqüência A026549.
3 Foi solicitado aos professores que trouxessem um livro didático de Matemática para o 3° ano do ensino médio para a realização da etapa quatro.














