Articulos

 

Learning mathematics with adult learners: drawing from parents' perspective¹

 

Javier Díez–Palomar*, José María Menéndez** y Marta Civil***

 

* Universidad Autónoma de Barcelona, Javier.Diez@uab.cat

** Radford University, jmenendez2@radford.edu

*** The University of Arizona, civil@math.arizona.edu

 

Recepción: Enero 8, 2010
Aceptación: Noviembre 4, 2010.

 

RESUMEN

En este artículo exploramos, a través de una serie de talleres con familiares, aspectos relacionados con la relación entre las matemáticas de la vida cotidiana y las matemáticas que se explican en la escuela, en el ámbito de la educación de personas adultas. Las personas participantes fueron animadas a reflexionar desde su perspectiva de la enseñanza y aprendizaje de las matemáticas a través de diferentes actividades en los talleres. Todas las sesiones fueron gravadas en video. Nuestro análisis de múltiples episodios revela tres aspectos: contextualización, transferencia del conocimiento matemático y creación de sentido. Utilizamos tres viñetas para ilustrar estos tres aspectos. Las implicaciones de nuestro estudio para la educación de personas adultas se centran en las matemáticas como prácticas situadas producidas como consecuencia de la interacción entre las personas adultas que están aprendiendo en espacios igualitarios.

PALABRAS CLAVE: Participación de familiares, matemáticas, personas adultas.

 

ABSTRACT

This article explores issues related to the relationship between everyday mathematics and academic mathematics within adult education, through a series of workshops with parents. Participants were encouraged to reflect on their perspective on learning and teaching mathematics through different activities in the workshops. All sessions were videotaped. Our analy sis of multiple episodes revealed three topics: contextualization, transferring the mathematical knowledge, and sense making. We use three vignettes to illustrate these topics. Our study implications for adult education focus on mathematics as a situated practice produced as a consequence of interaction among learners in egalitarian spaces.

KEY WORDS: Parents' involvement, mathematics, adult learners.

 

RESUMO

No presente artigo discutimos aspectos da relação da matemática do dia a dia com a matemática ensinada na escola, por intermédio de uma série de seminários destinados a famílias de crianças em idade escolar, oferecidos no âmbito de educação para adultos. Durante os seminários, os participantes foram encorajados a reflectir sobre as suas perspectivas de ensino e de aprendizagem da matemática. Todas as reuniões foram gravadas em vídeo. A nossa análise de diversos episódios revela três aspectos: contextualiçao, transferência de conhecimento matemático e criação de significado, que ilustramos em três vinhetas As implicações do nosso estudo para a educação de adultos estão centrados na matemática como um conjunto de prácticas localizadas, produzidas como resultado da interacção entre os adultos em espaços de aprendizagem igualitários.

PALAVRAS CHAVE: Participação das famílias, matemática, educação de adultos.

 

RÉSUMÉ

Dans cet article, nous explorons, dans le contexte de l'éducation des personnes adultes et au travers d'une série d'ateliers où les participants sont des parents d'élèves, certains aspects de la relation entre les mathématiques de la vie quotidienne et les mathématiques qui s'apprennent à l'école. Les participants ont été encouragés à développer leur point de vue sur l'enseignement et l'apprentissage des mathématiques, alors qu'ils prenaient part aux différentes activités poursuivies dans nos ateliers. Toutes les sessions ont été filmées. Notre analyse, basée sur plusieurs enregistrements, révèle trois aspects importants: la contextualisation, le transfert de la connaissance des mathématiques, et le développement de la compréhension. Nous présentons trois vignettes qui illustrent ces aspects. Les implications de notre étude en ce qui concerne l'éducation des personnes adultes sont centrées sur les mathématiques en tant que pratique contextualisée, résultant de l'interaction entre adultes qui apprennent dans des espaces égalitaires.

MOTS CLÉS: Participation des familles, mathématiques, personnes adultes.

 

1. INTRODUCTION

In September 2007, at the Final Conference of EMMA (European Network for Motivational Mathematics for Adults) in Florence several questions related to approaches to adult mathematics education arose, including, Is pedagogy transmission–based or participative–constructed? What is the role of egalitarian dialogue²? How can we include all participants' voices inside the classroom practices? What kinds of barriers do teachers face when teaching mathematics to adults? Among all these topics, the role played by the notion of transfer arose as a common issue embedded in all of them. The dilemma of transfer has long been studied as one of the most crucial problems of learning both, in adult and children mathematics education.

In this article we address questions about the pedagogical approaches in the teaching of mathematics to adult learners. In particular, we focus on parents as adult learners. We draw on data from a study with parents and we build on prior work related to pedagogy and content when working with parents (Civil, 2001, 2002). We aim to contribute to the debate about how everyday mathematics relates to academic mathematics within adult education. We want to elucidate the ways in which adult learners bring their own experiences to the academic arena to learn mathematics. Can we use these ways to design mathematical activities for adult learners? The next section presents the theoretical framework for our study. Then, we present the methodology used to collect and analyze the data. After that, we discuss several examples to illustrate elements of teaching and learning mathematics based on our work with parents. We conclude with some implications to consider when working with adult learners.

 

2. RESEARCH ON ADULTS LEARNING MATHEMATICS

How to teach mathematics to adult people has been a topic of discussion for a long period of time. Kaye (2006) summarizes the most important contributions to this field, from the lens of the Adults Learning Mathematics (ALM) community highlighting the importance of out–of–school settings where adults are able to develop strategies to use mathematics as a tool to solve problems: such a buying and selling, cooking, etc. (see also Curry, Schmitt, & Waldron, 1996). Wedege (1998) claimed that learning foradults includes learning in everyday life situations. Carraher, Nunes and Schliemann developed over the years a research program on the characteristics of what they called everyday mathematics (Carraher, 1991; Nunes, Schliemann, & Carraher, 1993; Schliemann, 1995; Schliemann, Carraher, & Ceci, 1997). These researchers focused on the mathematical practices of poor street vendor children in Brazil. While these children did not perform well on pencil and paper, school–type mathematics tasks, they were quite successful in solving problems related to their out–of–school settings. This body of research shows that children —and adults— with limited formal schooling could solve arithmetical operations, apply properties of integers and the decimal system, use proportional reasoning (Carraher, Carraher, & Schliemann, 1982, 1985), employ notions related to measurement (Carraher, 1986), geometry (Schliemann, 1985) and probability (Schliemann & Acioly, 1989). These results were consistent with other researchers (Abreu & Carraher, 1989; Gerdes, 1986; Harris, 1987).

The notion of context became a key element to understand how adult learners make sense of formal mathematics. Carraher and Schliemann (2002a) claim that "much of the work in developing flexible mathematical knowledge depends on our ability to recontextualize problems" (p. 264). According to them, we need to draw upon experiences that children have acquired in everyday settings. Researchers working with adult learners also reach to this conclusion. The Framework for adult numeracy standards (Curry, Schmitt, & Waldron, 1996) calls attention to the crucial role of context when designing academic activities for adult learners.

However everyday mathematics has been a controversial topic throughout the literature on mathematics curricula (Moschkovich & Brenner, 2002). Some researchers affirm that mathematics does not require formal instruction, while others highlightthe importance of schooling. Should everyday practices be included in the mathematics classroom? Several researchers have looked into this question, illustrating the affordances of doing so as well as the tensions (e.g., see the different articles in Moschkovich & Brenner, 2002; Civil, 2007). Nevertheless, important theoretical and empirical discussions still remain on what we mean by everyday mathematics and academic mathematics and how we can connect both forms of mathematics.

Several studies stress the potential of daily life contexts as situations in which adults use mathematics as tools to solve problems (Hoyles, Noss, & Pozzi, 2001; Knijnik, 2003; Lave, 1988). Plaza, González, Montero, and Rubio (2004) suggest that adult learners build on their memories and experiences to make sense of mathematics problems; hence they prefer activities in context. FitzSimons and Godden (2000) underscore the importance of the sociocultural contexts in adult education.

Drawing on constructivism some researchers assert that we need to incorporate adults' perspective in the teaching and learning practices (Gordon, 1993). By constructivism we mean the theoretical approach to learning as a result of a construction process in which the individual draws on his/her prior cognitive structures (or schemes), in order to build new ones adding new knowledge grounded on his/insights from the real world. According to Noddings (1990) constructivism holds that all knowledge is constructed and that the instruments of construction include cognitive structures that are either innate (Chomsky, 1968) or are themselves products of developmental construction (Piaget, 1953, 1970). However, FitzSimons and Godden (2000) claim that some interpretations of constructivism ignore sociocultural and political contexts, which are also important in understanding how adults learn mathematics. Vygotsky (1978) asserted that learning is a socio–cultural process in which interactions with other people play a crucial role to build the new cognitive categories. The works of Flecha (2000), Freire (1970), and Mezirow (1997) also illustrate that such interaction becomes a way for adults to share their knowledge and improve their learning. According to Aubert, Flecha, Garcia, Flecha and Racionero (2008), interaction refers to any kind of communication between two or more individuals. This communication may be grounded in dialogue, discussion, reading, and conversation, using oral and textual tools as resources to conduct it. Adults —as well as children— learn by talking with other peers, sharing their thoughts, troubles and ideas to solve the mathematical activities. Learning emerges as an individual output from this social process, which is the interaction among adult learners, teachers, facilitators and other agents involved within the learning practice. Research suggests that the difficulties that many adult learners face in learning could be explained by the gap between formal mathematics and what some researchers call everyday mathematics or daily life mathematics (Díez–Palomar, 2004; FitzSimons & Wedege, 2007).

Based on a sociocultural point of view, Evans (2000) proposes the thesis of the transfer of knowledge to explain how the gap between formal mathematics and everyday mathematics is produced. He argues that adult learners make sense of mathematics through their previous experiences. This is a process of transfer from the real life to the school concepts. Carraher and Schliemann (2002a) note that this notion of transfer is one of the key problems in studying learning. Individuals need to be familiar with new situations to recognize that they can apply prior learned knowledge to solve the problems embedded in the se new situations (Carraher & Schliemann; Guberman & Greenfield, 1991).

Expanding on the work of Evans (2000), Díez–Palomar proposes the notion of dialogic spaces, where adults use their own voices to bring their experiences grounded on everyday situations, to learn mathematics (Díez–Palomar & Molina, 2009; Díez–Palomar & Prat, 2009; Díez–Palomar, 2009). Building on Evans' thesis, Díez–Palomar proposes to focus on the idea of sharing knowledge between adult learners and teachers, rather than transferring knowledge from teachers to adult learners (as students). Adult learners, teachers, facilitators or any other educative agent participating in the learning practice become involved in a dialogue in which every individual may provide his/her own arguments to explain a given problem or activity. These dialogic spaces are egalitarian in the sense that every single person has de same opportunities to bring his/her arguments to explain the subject of study.

 

3. METHOD

This article is grounded in data from a study carried out with parents in the Southwest of the U.S. from 2005 to 2007. Through parents' voices we explore different ways to teach and to learn mathematics with adult learners. We build extensively on prior research with parents and mathematics (Civil, 2001, 2002, 2004; Civil & Andrade, 2003). We draw on situated learning episodes using a sociocultural perspective (Civil, 2002; González, Andrade, Civil, & Moll, 2001) and a dialogical perspective (Flecha, 2000). We also take into account a cognitive–affective perspective, which characterizes much of the ALM research tradition.

Data come from mathematics workshops for parents and from interviews with them that focus on their perceptions of teaching and learning mathematics. Participants in these workshops were parents of Mexican origin. All of them were native Spanish speakers and only one or two of the participants in each group identified themselves as having some knowledge of English. Their educational levels ranged from second grade to college degrees, with a median of sixth grade, corresponding to that of an 11 or 12 years old student in a typical U.S. school. We conducted a number of series of workshops in two different schools (one elementary school and one middle school).

We invited parents to participate in these workshops through members of the community and the school administration. In the middle school, Marisol, one of the mothers who had participated in a similar project, was responsible for the recruitment. During the time of our study, she was working at the middle school and was well connected with the community. At the elementary school the recruitment developed from a group of mothers who were already coming to the school in the mornings for other activities and the assistance of a curriculum specialist.

Participants were encouraged to reflect on their perspective on learning and teaching mathematics through different activities. The mathematics content of these workshops focused on the curriculum used at each school. Additional topics in the workshop presentations included areas of personal interest as identified by the parents.

The timeframe for these workshops at the middle school spans from September 2006 to May 2007, and the interviews took place during April–November 2007. At the elementary school the workshops took place from January 2005 to April 2006 and the interviews took place during March and April 2006. The attendance varied between six and seven parents at each session at the elementary school and it ranged from three to six the first half of the year in the middle school and from 12 to 14 the second half. Although there are many approaches to curriculum and learning design, such as backwards design³ (Wiggins & McTighe, 1999), the workshops were modeled after a project developed by Civil and colleagues (Civil, Bratton, & Quintos, 2005, Civil & Quintos, 2009). The content of the workshops was packaged in modules of seven sessions. Each session ran for 1.5 hours and began with a brief introduction to the mathematical concept to be studied. Participants were introduced to some problems to be worked out individually and in small groups and concluded with a group discussion of the solution to the problems. The first set of sessions at the middle school took place early in the morning after the parents had taken their children to school. The remaining set of sessions were held in the evenings in response to a set of requests from the participants who argued that it was more likely that their husbands would be able to participate if the workshops were held after work hours. In the middle school the second author facilitated the workshops. All the sessions at the elementary school took place in the morning and were facilitated by the first author and one to two graduate students (depending on the semester). All the facilitators were native speakers of Spanish and all the sessions at both schools took place in Spanish.

In orderto collectthe data, all sessions were audio and video recorded using video cameras. Researchers took notes after every session. We also used interview and focus group protocols to collect data from adult learners (parents). All interviews and selected clips from the video taped data were transcribed by undergraduates and checked by the researchers. Data was transcribed in the original language (Spanish), and then translated into English. We used grounded theory (Glaser & Strauss, 1967) as our methodological approach. For the qualitative analysis of the data, we used a software package (TAMS Analyzer⁴). This resulted in several categories that were progressively refined.

In this article, we focus on only one of the large categories, namely the one related to learning mathematics as adults. We then selected excerpts from the transcripts and discussed them within the research team in order to agree on our interpretation. A discourse analysis framework was used as methodological approach to the qualitative work at this stage (Denzin & Lincoln, 2005; Gee, 1999). Drawing on this methodological approach, we looked at language as human communication, but also as cultural practice (Gee, 1999) since we need to understand individuals' voices within their particular cultural and social context. The excerpts we present in the following section were chosen as examples to illustrate our findings.

 

4. RESULTS AND DISCUSSION

We have organized our discussion along three topics that emerged from our data analysis: contextualization, transferring the mathematical knowledge, and sense making. Through these topics we explore how adult learners use mathematics in different situations (problems, activities, investigations), and how they become key dimensions to understand adults' learning process. Each topic is illustrated with one vignette.

4.1. Vignette 1: Learning mathematics in (with) context

The mathematics topic in this vignette involves reading a graph and using it to represent and to explain a particular phenomenon in our world. The facilitator, José María, used an example based on how one of his friends uses his car during the week. He showed a graph representing how much gasoline the car has from Monday to Sunday, day by day. Then everybody in the class discussed the story underlying the graph. Parents came up with some interpretations on how that person uses his car to go to work every day, and then uses his car to go away on the weekend, when he gets gasoline, and so forth. After that exchange, José María asked parents to form small groups to work on a story related to some aspect from their daily life experiences and to use a line graph to represent that activity and to explain it to the whole class. After about thirty minutes, one of the mothers (Luisa) came to the front of the classroom to present her group's work (see Figure I).

Luisa explained how that line represented the physical energy that somebody spends in a week. On the horizontal axis the group wrote the days of the week, from Monday to Sunday. Then, on the vertical axis they represented the energy level, from less to more. Luisa narrates her group's explanation in the next quote:

Luisa: That's the level of energy we have daily. So, there are times when we wake up with a lot of energy, there are times when we wake up with less energy (pointing at the levels on the graph, on Monday and Tuesday with a pen). There are times when we go up, we are going up (pointing on the high point on Wednesday) and down (going down with the pen on Wednesday). On Thursday we wake up so–so, with less energy (pointing at Thursday), on Friday with less (she points going down on Friday with the pen), on Saturday energy is going down (points with the pen) and Sunday we are exhausted (turns to look at the class). Yes, and on Monday we start all over again, that is how I understand it.⁵

(Math for parents workshop, Sept. 2006)

The connection to her daily life seemed quite natural to Luisa, and the connection between a line graph and the progression of a phenomenon over time was readily grasped. Luisa's explanation captures the notions of increasing and decreasing in an intuitive way, based on the direction she gave to each line segment in her graph. Thus, this can be used as a context to introduce notions such as axes, function, coordinates, direction, and decreasing and increasing functions. This is an example of what Lave and Wenger (1991) have called situated learning. In their research Lave and Wenger learned about adults' personal histories, drawing on adults' experiences with grocery shopping and dieting. They found that adults used arithmetic procedures and concepts like integers, decimals, fractions, ratios, arithmetic operations, and so forth, when they went shopping although the adults did not recognize their use of these concepts. These practices arise spontaneously, as prompted by the need to solve a practical problem, in the shopping context. Everyday activities —such as shopping— provide the perfect frame to make sense of formal mathematics. According to Plaza et al. (2004), adults use daily life situations to make sense of the formal mathematics taught in a class. Plaza and his colleagues re–address aprior finding in adult mathematics education: adults use mathematics as a tool to solve problems in everyday life situations (Knijnik, 2003; Lave, 1988) and in working situations (Abreu & Carraher, 1989; Hoyles, Noss, & Pozzi, 2001; Schliemann, 1985). Lave and Wenger (1991) concluded that learning occurs in situated environments. Adults use their daily life experiences to understand formal mathematics, putting them in context (thus context becomes part of the cognitive process of learning). Our data seem to be consistent with this analysis. Luisa turned to her everyday knowledge to interpret the graph.

Plaza et al. (2004) suggest that adults attending basic education courses tend to prefer concrete mathematics rather than an abstract one, and they choose ways to represent mathematics closer to their everyday experiences rather than algorithms or proofs. These authors define concrete as contextualized and abstract as non–contextualized situations. Here we use the adjective abstract to refer any kind of mathematical symbolism or formal procedure, such as algorithms, numerals, operation symbols, etc. By concrete mathematics we understand any kind of situation that involves mathematics in its description, but without symbolisms or formal procedures, such as algorithms or mathematical expressions such equations, for instance. A concrete situation may be a context to promote the understanding of an abstract idea, such as the one described in our example of the daily energy. A graph, which is a formal symbol connected to a mathematical idea in an abstract way, is contextualized by adult learners in a number of different ways. Adults use their own experiences to make sense of the line drawn on paper, hence each group of learners comes up with a series of concrete examples to explain the meaning of that graph.

4.2. Vignette 2: Transferring the mathematical knowledge

This session focused on the study of the slope, in particular we wanted to develop the intuitive concept of the slope as the degree of steepness of a straight line and to help make sense of the formula by the time it gets introduced. The participants had been working with graphs —as in Vignette 1— and the facilitator (José María) introduced the idea of slope through a practical example. In the previous session, he had asked parents to measure different sets of stairs (the height or rise and the width or run of each step) in the neighborhood, for example sidewalks with steps, the stairs in their houses or apartment complexes, at the park, benches is the stadium, etc., and to bring those measurements to the next working session.

Parents came back with several measurements written in their notebooks. José María then asked the parents which one was the hardest stair to climb, and which one was the easiest one. Rigoberto shared with the group his notes. He had written down in a piece of paper the length of the vertical line of the step (rise) and the length of the horizontal line of the step (run) for a number of stairs that he found in his neighborhood. Several parents were familiar with the specific stairs Rigoberto described. Then participants in the group discussed which one was the easiest or the hardest stair to climb, since they knew some of them (because they lived in the same neighborhood as Rigoberto did). With this information José María was almost ready to explain what slope means and how to calculate it. However, rather than writing on the board the formula,

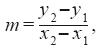
for the straight line passing through the points P(x₁, y₁) and Q(x₂, y₂), he said: "You have to divide the length of the vertical line (rise) over the length of the horizontal one (run)". Rigoberto presented the results of dividing the rise over the run of his data. This result provides crucial information for the discussion. With the results, participants went back to their arguments about which one was the hardest stair, and which one was the easiest. Then, they were in the situation to make sense to Rigoberto's numbers by linking their everyday knowledge of their neighborhood stairs –the steepness of the sets of stairs described by Rigoberto, and the information coming out of Rigoberto's calculations, the numerical values associated to the corresponding steepness. However, at this point it was not clear that there was an understanding of the slope as the ratio (direct variation) of the rise to the run. After a discussion about how to translate rise and run into Spanish came up, Marisol came back to the mathematical idea with these words:

In this excerpt we can see several interesting aspects. Marisol was trying to understand the concept of slope making connections with her experience grounded in her knowledge of the real world (see line 3). She assumes that slope depends on height, thus the more height, the more slope we can notice. We can hypothesize that Marisol was making a connection between her experience and the new mathematical concept that José María was introducing in that session. This is a common practice for adult learners. They have a repertoire of previous knowledge grounded on their life experiences (Knowles, 1968). At that point (line 4) José María asked Marisol whether the slope depends on the vertical part only or on the horizontal part. Somebody answered that both mattered (the combination). Then Esperanza elaborated more on this idea. She said that we have to take into account both, vertical and horizontal, in order to determine the height of the slope (see lines 6 and 10). José María asked again how we could calculate the measure for the slope. He used the word measure rather height, which was the word used by Esperanza to talk about the slope. This word, altura (height), is a more common and intuitive word than measure. In this context, height is not used in the same way as they would use it to refer to the height of a building, for example, but more as in comparison with the horizontal displacement. For this reason, we see her use of that specific word as transference from the real–world–based knowledge to the formal one. This suggests that Esperanza has an understanding of what slope means in her everyday experience and she was using that knowledge to make sense of the formal meaning of slope (as well as Marisol did).

4.3. Vignette 3: Making sense of mathematics through previous experience

Adults' everyday experiences are rich in terms of mathematics. Although we may not necessarily use formal mathematics to approach everyday problems, our informal methods often involve some sort of mathematical reasoning. This next vignette comes from a session at the elementary school where we were working on problem solving strategies. We presented this problem to the group of mothers (the problem was given in Spanish):

Problem: Johnbuys awatchfor $60, and after that, he soldittoPaulfor$80. One week later, John buys this watch from Paul for $100, and after that he sold it to Kevin for $120. How much has John earned?⁷

Ruth, Elena and Tamara were solving the problem together and engaged in a lively discussion about how much John had earned. Ruth seemed to have understood the problem before the others, becoming the more capable peer envisioned by Vygostky (1978) who described learning as a process carried out both in context and collectively. Vygostky suggested that learners could go further (in their own process of learning) if they collaborate with other more capable peers. The zone of proximal development (ZPD) is the potential that everybody is able to develop with the help of another person more capable. Thus, in this problem Ruth was the more capable peer, and took the lead in explaining why John earned $40 dollars after buying/selling the watch several times. Tamara and Elena tried to understand Ruth's explanation. In particular, Tamara seemed to have a hard time keeping track of the different transactions. The facilitator (Javi) asked Tamara if she understood and. Tamara answered: "no." The following dialogue ensued, in which now Elena also takes an active role (it had been mostly Ruth up to then):

We can observe that there is a pattern of participation: It seems like Elena and Ruth feed off each other. Elena was arguing with Ruth about how much John has earned after selling and buying and selling again the watch. Tamara was still listening and trying to follow the dialogue. We argue that both dialogue (Flecha, 2000) and participation are components of the learning process. When learners are engaged in the interaction, they also participate in the process of learning. In a dialogic practice (Flecha, 2000), individuals share their own approaches to solve the mathematical problem. Even if not all learners are able to provide the right answer, all of them have the opportunity to participate in the dialogue, in the creation of meaning adding their own arguments, examples and counterexamples, looking forthe solution. Inthis sense, all learners may participate until they solve the problem. However, it could be the case that somebody does not (fully)understandallthe arguments andmathematicalideasaroundtheproblem, and so, we cannot say that participation always leads to effective learning. It could also be the case that some learners do not participate in an active way —making statements, providing examples, arguing, etc.—, but they can be using their internal voices to interiorize all the arguments that other peers are putting on the floor. This raises questions about the role played by the internal talk (Vygotsky, 1978): Are silent learners also engaged in the participation (and consequently in the process of learning) or are they not? Is silent participation another type of active participation or not? In this excerpt we provided an example of dialogue. The fictitious situation (John buying and selling a watch) became a role–playing situation where the characters were Tamara, Ruth, and Elena. Our data show that Tamara was first a silent observant, but then she takes an active role in the whole interaction, as we will see in the excerpt below. The discussion of this problem continues because Tamara is still saying that she does not understand it. Ruth asks Tamara to read and says that she will work it out on the white board. Tamara starts reading it by personalizing it. She puts herself in the problem, and her peers play along:

They put themselves in the situation as a way to interiorize the process of argumentation and create meaning as a consequence of that. Ruth uses everyday (informal) language as a tool to transfer the mathematical meaning, the formal one, to Tamara, but in her own words. One example of this is in the use of the word red (lines 11 and 21). Ruth was making connections between the real world and formal mathematics. Ruth was talking about negative numbers, which correspond to the idea of red numbers, debt, in the real world. The use of the term red number to represent a negative number, as used in accounting, has permeated into everyday life, and here we see it being used in a formal mathematical context. This connection to the real world is common in adult education (as discussed in Vignettes 1 and 2). Adult learners usually go to their daily life experiences to find meaningful examples to connect with formal mathematics ideas. Drawing on prior research (Díez–Palomar, 2004; Díez–Palomar, Giménez Rodríguez, & Garcia Wehrle, 2006) it is plausible to affirm that this strategy is quite common when adult learners try to understand a mathematical concept or process. As we see in these excerpts, the language is quite informal: red (rojo), bad (malo), good (bueno); as in "but you have twenty bad, you have one hundred good left" (pero tienes veinte malos, te quedan cien buenos) (lines 21 and 23). Dialogue between peers became a crucial aspect in the whole process. Without dialogue (that is, without that space for dialogue which was the classroom), Ruth and Elena would have not been able to build on Tamara's ZPD.

 

5. IMPLICATIONS FOR ADULT EDUCATION

What have we learned about adults learning mathematics from our work with parents? There are several items that seem to have an influence on this process. Here we present three ideas drawing from our analysis.

Statement 1: Learning is situated —embedded— in a particular context. Consequently, in working with adults learning basic mathematics, we should try to find ways to connect formal mathematics with situations framed on adults^' everyday experiences.

Our findings provide some evidence of the importance of context in the learning process. Adults use their everyday experiences to understand mathematical ideas. Vignettes 1 and 2 are evidence of this claim. This conclusion is consistent with prior research (Knowles, 1968; Lave & Wenger, 1991). Drawing on this literature we already know that context is a subject of matter both for children (Moschkovich & Brenner, 2002; Nunes, Schliemann, Carraher, 1993) and for adult learners (Curry, Schmitt, & Waldron, 1996; Díez–Palomar, 2004; Díez–Palomar, 2009; Knijnik, 2003; Lave, 1988; Schliemann & Acioly, 1989). However, the concept of context is somehow controversial. What does it mean "to be a contextualized activity"? According to Carraher and Schliemann (2002b), we need to specify whom we are working with. As we discussed in vignette 2, adult learners who are attending basic mathematics courses prefer activities much more connected to their everyday experiences, rather than symbolic expressions and procedures. Plaza et al. (2004) suggest that we need to design courses drawing on everyday mathematically meaningful situations, and build on these situations to move adult learners from concrete to abstract mathematics. Our analysis introduces a new element to this discussion: Adults may choose to put themselves into the problem, as in role–playing, to get a better understanding of the situation. Vignette 3 was an example of this.

Statement 2: Learning is produced through interactions among learners. Hence in working with adults we should emphasize and promote interactions among the participants.

Researchers have underscored the importance of interactions in the process of learning (Flecha, 2000; Freire, 1970; Vygotsky, 1978). Individual learning is a result of a process of interiorization where individuals internalize new concepts and ideas through interactions with peers. Vygostky proposed the ZPD to explain how this process works. According to him, learners may be able to reach up to a level of understanding, which they already have (in potential), but they need the help of a more capable peer to be able to reach that level of understanding. This is true for both, children and adults. Flecha suggests that inter–subjective⁹ interaction is a crucial factor for learning. Flecha asserts that adults engaged in learning situations may use dialogue to interact with each other. In this inter–subjective interaction (among individuals), adults have the opportunity to share their own arguments (drawing on their experiences and prior knowledge) to solve the problem. In doing so, they may share examples and counterexamples with their peers, to help all of them to reach and understand the correct answer. Sometimes the way that adults (and children) explain to their peers a specific concept is clearer than the teacher's explanation, because the peer may use examples more familiar to the other peers than the ones used by the teacher¹⁰. However, interactive episodes may be more complex than the ones described up to this point. What happens when there is no (explicit) dialogue among learners? Is passive participation also a kind of interaction? To be engaged in a dialogue as silent listener, without saying anything, but following all the arguments, is (or not) a type of interaction? Is this a (needed) step of any inter–subjective situation? In the example provided in vignette 3, Tamara was first a silent observant, and afterwards, when see was able (or maybe she felt confident) to share her thinking, she participates in the dialogue. This notion of passive participation may be an arena for further studies.

Statement 3: Learning is not unidirectional from teacher to students. Learning is a social practice where everybody participates. For this reason, in working with adult learners we should strive to build spaces where adults can feel comfortable and safe to participate and to share their own knowledge.

Egalitarian dialogue (Flecha, 2000) among participants may lead to learning. Dialogue is a way to share different approaches to the knowledge. As we saw in the vignettes discussed here, learners interact with each other when they are doing mathematics. The concept of egalitarian dialogue does not mean that every single actor in the classroom has the same knowledge. What it means is that everybody —teachers/facilitators, students (parents)— should have the same possibilities to share their own knowledge, drawing on arguments and not on power relations. It is this notion of power that differentiates this approach from other approaches in adult education that while they may promote discussion and dialogue in mathematics they are not necessarily grounded on Freire's (1970) work, which is at the basis of Flecha's work with adults. Even though some progress has been reached in mathematics classrooms regarding student participation, group work and mathematical discourse in the classroom, we claim that these environments may still not address power issues. Furthermore, at least in our local context, the approaches to adult education are often teacher centered, aimed at passing a test such as the GED (General Education Diploma). The vignettes given in this article provide evidence of participants interacting and sharing their ideas. We do not claim, however, that these are examples of egalitarian dialogues, as power issues and affective issues do play a role. But this is exactly why we bring it up for discussion, to show how even when adults are discussing mathematics, there may be power issues present. For example, in vignette 2, we see Marisol dominating the dialogue; she could be seen as being in a position of power, not only because she works at the school but also because she was the one responsible for the recruitment of these parents to these workshops.

According to Díez–Palomar (2009) and Díez–Palomar and Prat (2009) a place where participants feel comfortable to share different approaches to learning and to solving a mathematical problem may lead to deeper learning. Vignette 3 is an example of that finding: Tamara was unable to understand how John gets $40 after selling the watch several times. However, Tamara was confronted with a problem here that has to do with the initial $60 that John has, which is how that $60 is understood, where it came from, and how the rest of the money is contextualized in light of that original $60. Tamara's lack of understanding of "how John gets $40 after selling the watch several times" may be based on a different understanding of how to interpret that original $60, and Tamara may not realize that there is not a common understanding of that original $60. But Tamara persisted in her wanting to understand. She felt comfortable enough to say that she did not understand and seemed to be genuinely interested in trying to make sense of the problem. Then Ruth took the lead and tried to explain to Tamara how John was able to earn $40 dollars. Between Tamara and Ruth they used role–playing (supported by comments by Elena). This vignette illustrates ateam effort at trying to reach a shared understanding of the problem.

 

6. FURTHER RESEARCH

Reflecting on our study and its related literature, we may conclude that context, interaction, concrete mathematics, egalitarian dialogue, dialogic spaces and prior experience are topics that play a crucial role in how adults learn mathematics. However, our research raises a number of questions for further research. Here we only outline questions related to the first two topics in this list, context and interaction. One question around the concept of context is, What is in context or contextualized and what is it not from a mathematics teaching and learning point of view? How does using contexts to present a mathematical idea impact adult learners' understanding? And a related question is, What type of problems do we need to work with adult learners? This leads yet to another question: How to design curriculum and learning experiences for adult learners. Are well–known approaches to curriculum design, such as backwards design (Wiggins & McTighe, 1999) suitable to working with adult learners?

Around the concept of interaction, our analysis suggests that internal voice may play a crucial role in learners' understanding (and engagement in dialogue with other peers within the classroom). This opens up a line for further research moving beyond the idea of active participation as way to animate learning. Is there a silent period in which (adult) learners needs to step on before getting into the dialogue with their peers to share their thoughts around a particular activity ? How can we analyze this silent period? What are the elements that (adult) learners put together throughout this period of time?

These are just some examples of possible questions to further extend this work that may enrich and clarify our understanding of how adult learners learn and what are the best pedagogical approaches to the teaching of mathematics to adult learners.

 

ACKNOWLEDGMENTS

The work presented here is part of the research agenda of CEMELA (Center for the Mathematics Education of Latinos/as), which is funded by the National Science Foundation –ESI 0424983. We also thank the Fulbright Commission for the support given to the first author, through the Fulbright Visitor Program. The views expressed here are those of the authors and do not necessarily reflect the views of the funding agencies.

 

REFERENCES

Abreu, G. de, & Carraher, D.W. (1989). The mathematics of Brazilian sugar cane farmers. In C. Keitel, P. Damerow, A. Bishop, & P. Gerdes (Eds.), Mathematics education and society (pp–68–70). Paris, France: Science and Technology Eduation–UNESCO.         [ Links ]

Aubert, A.; Flecha, A.; Garcia, C.; Flecha, R. y Racionero, S. (2008). Aprendizaje dialógico en la sociedad de la información. Barcelona, España: Editorial Hipatia.         [ Links ]

Carraher, D.W. (1991). Mathematics in and out of school: A selective review of studies from Brazil. In M. Harris (Ed.), Schools, mathematics and work (pp. 169–201). London, UK: Falmer Press.         [ Links ]

Carraher, D.W. & Scliemann, A. D. (2002a). The transfer dilemma. The Journal of the Learning Sciences 11 (1), 1–24.         [ Links ]

Carraher, D. W. & Schliemann, A. D. (2002b). Is everyday mathematics truly relevant to mathematics education? Journal for Research in Mathematics Education. Monograph 11, 238–283.         [ Links ]

Carraher, T. N. (1986). From drawings to buildings: working with mathematical scales. International Journal of Behavioural Development 9, 527–544.         [ Links ]

Carraher, T. N.; Carraher, D. W. & Schliemann, A. D. (1982). Na vida, dez; na escola, zero: os contextos culturais da educaçao matemática [In life, 10, in school, zero: the cultural contexts of learning mathematics]. Cadernos de Pesquisa 42, 79–86.         [ Links ]

Carraher, T. N.; Carraher, D. W. & Schliemann, A. D. (1985). Mathematics in the streets and in schools. British Journal of Developmental Psychology 3, 21 29.         [ Links ]

Chomsky, N. (1968). Language and mind. New York, USA: Harcourt Brace Jovanovich.         [ Links ]

Civil, M. (2001). Mathematics for parents: issues of pedagogy and content. In L. Johansen & T. Wedege (Eds.), Proceedings of the Eighth International Conference of Adults Learning Mathematics. A Research Conference (pp. 60–67). Roskilde, Denmark: Centre for Research in Learning Mathematics.         [ Links ]

Civil, M. (2002). Adult learners in mathematics: a look at issues of class and culture. In J. Evans, P. Healy, D. Kaye, V. Seabright & A. Tomlin (Eds.), Policies and practices of adults learning mathematics: Opportunities and risks. Proceedings of the 9^th International Conference of Adults Learning Mathematics. A Research Forum (pp. 13–23). Stevenage, UK: Avanti Books.         [ Links ]

Civil, M. (2007). Building on community knowledge: an avenue to equity in mathematics education. In N. Nasir & P. Cobb (Eds.), Improving access to mathematics: diversity and equity in the classroom (pp. 105–117). New York, USA: Teachers College Press.         [ Links ]

Civil, M. & Andrade, R. (2003). Collaborative practice with parents: the role of the researcher as mediator. In A. Peter–Koop, V. Santos–Wagner, C. Breen & A. Begg (Eds.), Collaboration in teacher education: Examples from the context of mathematics education (pp. 153–168). Boston, MA: Kluwer.         [ Links ]

Civil, M. & Quintos, B. (2009). Latina mothers' perceptions about the teaching and learning of mathematics: Implications for parental participation. In B. Greer, S. Mukhopadhyay, S. Nelson– Barber & A. Powell (Eds.), Culturally responsive mathematics education (pp. 321–343). New York, NY: Routledge.         [ Links ]

Civil, M., Bratton, J. & Quintos, B. (2005). Parents and mathematics education in a Latino community: Redefining parental participation. Multicultural Education 13(2), 60–64.         [ Links ]

Curry, D., Schmitt, M. J. & Waldron, S. (1996). A framework for adult numeracy standards: the mathematical skills and abilities aduls need to be equipped for the future. The Adult Numeracy Practitioners Network System Reform Planning Project. Funded by the National Institute for Literacy.         [ Links ]

Denzin, N. K., & Lincoln, Y. S. (2005). The SAGE Handbook of Qualitative Research. Thousand Oaks, USA: Sage Publications.         [ Links ]

Díez–Palomar, J. (2004). La enseñanza de las matemáticas en la educación de personas adultas. Un modelo dialógico. Unpublished doctoral dissertation, University of Barcelona, Spain.         [ Links ]

Díez–Palomar, J. (2009). La enseñanza de las matemáticas a personas adultas desde un enfoque didáctico basado en el aprendizaje dialógico. Enseñanza de las Ciencias 27 (3), 369–380.         [ Links ]

Díez–Palomar, J. & Molina, S. (2009). Contribuciones de la educación matemática de las familias a la formación del profesorado [Contributions of families' mathematics education to teaching education]. In M. J. González, M. T. González & J. Murillo (Eds.), Investigación en Educación Matemática XIII(pp. 211 225). Santander, Spain: SEIEM.         [ Links ]

Díez–Palomar, J. & Prat, M. (2009). Discussing a case study of family training in terms of communities of practice and adult education. In V. Durand–Guerrier, S. Soury–Lavergne et F. Arzarello (Eds.), Proceedings of the Six Conference of European Research in Mathematics Education, CERME 6 (pp. 1462–1472). Lyon, France: INRP.         [ Links ]

Díez–Palomar, J., Giménez Rodríguez, J. & Garcia Wehrle, P. (2006). Cognitive trajectories in response to proportional situationsin adult education. Adults Learning Mathematics: An International Journal 1 (2), 16–27.         [ Links ]

Evans, J. (2000). The transfer of mathematics learning from school to work not straightforward but not impossible either! In A. Bessot & J. Ridgway (Eds.) Education for mathematics in the workplace (pp. 5–15). Dordrecht, The Netherlands: KluwerAcademic Publishers.         [ Links ]

FitzSimons, G. E. & Wedege, T. (2007). Developing numeracy in the workplace. Nordic Studies in Mathematics Education 12 (1), 49–66.         [ Links ]

FitzSimons, G. & Godden, G. L. (2000). Review of research on adults learning mathematics. In D. Coben, J. O'Donoghue & G. FitzSimons (Eds.), Perspectives on Adults Learning Mathematics (pp. 13–46). Dordrecht, The Netherlands: KluwertAcademic Publishers.         [ Links ]

Flecha, R. (2000). Sharing words. Theory and practice of dialogic learning. Lanham, M. D: Rowman & Littlefield.         [ Links ]

Freire, P. (1970). Pedagogía del oprimido [Pedagogy of the oppressed]. Montevideo, Uruguay: Tierra Nueva.         [ Links ]

Galbraith, T. (1990). Bridging mathematics: some recurring themes. In P. L. Jones (Ed.),Bridging mathematics: an international perspective (pp. 141–143). Melbourne, Australia: Swinburne Institute of Technology.         [ Links ]

Gee, J. P. (1999). An introduction to discourse analysis: Theory and method. New York, USA: Routledge.         [ Links ]

Gerdes, P. (1986). How to recognize hidden geometrical thinking: a contribution to the development of anthropological mathematics. For the Learning of Mathematics 8, 35–39.         [ Links ]

Glaser, B. G. & Strauss, A. L. (1967). The discovery ofgrounded theory: strategies for qualitative research. New York, USA: Aldine de Gruyter.         [ Links ]

González, N., Andrade, R., Civil, M. & Moll, L. (2001). Bridging funds of distributed knowledge: creating zones of practices in mathematics. Journal of Students Placed at Risk 6 (1–2), 115–132.         [ Links ]

Gordon, S. (1993). Mature students learning statistics: The activity perspective. Mathematics Education Research Journal 5 (1), 34–49.         [ Links ]

Guberman, S. R. & Greenfield, P. M. (1991). Learning and transfer in everyday cognition. Cognitive Development 6, 233–260.         [ Links ]

Harris, M. (1987). An example of traditional women's work as a mathematics resource. For the Learning of Mathematics 7 (3), 26–28.         [ Links ]

Hoyles, C., Noss, R. & Pozzi, S. (2001). Proportional reasoning in nursing practice. Journal for Research in Mathematics Education 32, 4–27.         [ Links ]

Kaye, D. (2006). Theoretical framework for adults learning mathematics. In M. Horne & B. Marr (Eds.), Connecting voices in adult mathematics and numeracy: practitioners, researchers and learners. Proceedings of the Adults Learning Mathematics (ALM), 12th Annual International Conference jointly with the Australian Council for Adult Literacy (ACAL) and in cooperation with the Australasian Bridging Mathematics Network (BMN) (pp. 237–242). Melbourne, Australia: AML–ACAL.         [ Links ]

Knijnik, G. (2003). La invasión del extranjero: de la peseta al euro y los retos para la educación matemática. UNO. Revista de Didáctica de las Matemáticas 32, 23–37.         [ Links ]

Knowles, M. (1968). Andragogy, not pedagogy. Adult Leadership 16 (10), 350–352.         [ Links ]

Lave, J. (1988). Cognition in practice. Cambridge UK: Cambridge University Press.         [ Links ]

Lave, J. & Wenger, E. (1991). Situated learning: legitimate peripheral participation. Cambridge, UK: Cambridge University Press.         [ Links ]

Mezirow, J. (1997). Tranformative learning: theory to practice. New Directions for Adult & Continuing Education 74, 5–8.         [ Links ]

Moll, L.; Amanti, C.; Neff, D. & González, N. (1992). Funds of knowledge for teaching: using a qualitative approach to connect homes and classrooms. Theory into Practice 31, 132–141.         [ Links ]

Moschkovich, J. N. & Brenner, M. E. (2002). Journal for Research in Mathematics Education. Monograph 11, pp. V–X.         [ Links ]

Noddings, N. (1990). Constructivism in mathematics education. Journal for Research in Mathematics Education. Monograph 4, 7–18.         [ Links ]

Nunes, T.; Schliemann, A. D. & Carraher, D. W. (1993). Mathematics in the streets and in schools. Cambridge, UK: Cambridge University Press.         [ Links ]

Piaget, J. (1953). Logic and psychology. Manchester, England: Manchester University Press.         [ Links ]

Piaget, J. (1970). Genetic epistemology. New York, USA: Columbia University Press.         [ Links ]

Plaza, P.; González, M–J.; Montero, B. & Rubio, C. (2004). Matemáticas críticas y transformadoras en la educación de personas adultas [Critical and transforming mathematics in adult education]. Málaga, Spain: Ediciones Aljibe.         [ Links ]

Schliemann, A. D. (1985). Mathematics among carpenters and carpenters apprentices: implications for school teaching. In P. Damerow, M. Dunckley, B. Nebres and B. Werry (Eds.), Mathematics for all (pp. 92–95). Paris, France: UNESCO.         [ Links ]

Schliemann, A. D. (1995). Some concerns about bringing everyday mathematics to mathematics education. In L. Meira and D. Carraher (Eds.), Proceedings of the 19^th International Conference for the Psychology of Mathematics Education (Vol. 1, pp. 45–60). Recife, Brazil.         [ Links ]

Schliemann, A. D., & Acioly, N. M. (1989). Mathematical knowledge developed at work: the contribution of practice versus the contribution of schooling. Cognition and Instruction 6 (3), 185–221.         [ Links ]

Schliemann, A. D., Carraher, D.W., & Ceci, S.J. (1997). Everyday cognition. In J. W. Berry, P. R. Dasen and T.S. Sarawathi (Eds.), Handbook of cross cultural psychology (Vol. 2, pp. 181–220). Boston: Allin & Bacon.         [ Links ]

Vygotsky, L. S. (1978). Mind in society: the development of higher psychological processes. Cambridge, MA: Harvard University Press.         [ Links ]

Wedege, T. (1998, July). ALM as a community of practice and research. ALM Conference, Utrecht, Netherlands.         [ Links ]

Wiggins, G., & McTighe, J. (1999). Understanding by design. Alexandria, VA: Association for Supervision and Curriculum Development.         [ Links ]

 

NOTAS

¹ Parts of this article were presented at ICME 2008, in Mexico. The proceedings from the conferences were compiled in the book Coben, D., & O'Donoghue, J. (Eds.) (2010) Adult Mathematics Education. Papers from Topic Study Group 8, ICME 11. International Congress on Mathematical Education. NCE–MSTL – ALM.

² Flecha (2000) defines egalitarian dialogue in the context of a classroom as the inclusion of all voices (the teachers' and the adult learners'). All participants may contribute to the learning process, since all have different experiences and prior knowledge regarding the concept under discussion. Egalitarian dialogue means that all participants have the same opportunities to share their points of view. The validity of a contribution is its truthfulness, not the power position of the person who presents the contribution.

³ Wiggins and McTighe use backwards design to refer to an approach that centers on identifying the desired results and working backwards to reach those results. They propose a step process: 1) standard: desired results; 2) evidence of learning, and 3) curriculum and instruction. Civil and her colleagues, instead of doing this procedure, they first develop the activities having in mind the curriculum used by teachers at the school involved in the learning process, and then they use these activities with parents within the workshops, in order to teach them the kind of mathematics that their children are doing in the school.

⁴ TAMS Analyzer is software developed by Matthew Weinstein for qualitative analysis. It is useful to codify and select quotes along the data set. Then, you can sort them and ask the software for reports to identify the main topics existing throughout the data.

⁵ All transcripts have been translated from Spanish to English.

⁶ Cantinflidad, or rather cantinflada refers to a style of speech used by the Mexican actor and comedian Mario Moreno Cantinflas (1911–1993) characterized by the use of many words in a convoluted way and vacuous in content.

⁷ This problem is inspired on a similar one written by Martin Gardner (1988), Matemática para divertirse (original book published in 1986 by Dover Publications Inc, New York, Entertaining Mathematical Puzzles). The problem is called "The second–hand motorcycle." It says: "Bill sell his motorcycle to Tom for $100. After using it for a few days, Tom realized that he was broke, so he re–sells it to Bill again for $80. Next day, Bill sells it to Herman for $90. How much does Bill earned?" (Gardner, 1988, p. 21).

⁸ To have some amount of money "in red" is an informal way to mean that a person has debts, in Spanish.

⁹ Intersubjective refers to a relation between two or more individuals, while intrasubjective refers to the kind of dialogue that somebody has with him/herself (this is synonymous of internal voice).

¹⁰ Aubert et al. (2008) explain the case of two children engaged in a discussion about how to draw the infinity symbol. One of the children was not able to draw that symbol in his notebook. He was trying to do it several times, without success. Then, his peer told him: "it is easy, just write the number eight, but in a sleeping position".