Artículos

 

Construcción del concepto de dependencia lineal en un contexto de geometría dinámica: un estudio de casos

 

Construction of the Concept of Linear Dependence in a Context of Dynamic Geometry: A Case Study

 

Carmen Aranda¹ y M. Luz Callejo²

 

¹ IES Pere Mª Orts i Bosch, Alicante, España; maranda231b@cv.gva.es

² Departamento de Innovación y Formación Didáctica, Universidad de Alicante, España; luz.callejo@ua.es

 

Recepción: Agosto 4, 2009.
Aceptación: Junio 7, 2010.

 

RESUMEN

Este artículo presenta un experimento de enseñanza en el dominio del álgebra lineal en un contexto de geometría dinámica. Se describe una trayectoria hipotética de aprendizaje para construir el concepto de dependencia lineal en términos del mecanismo de reflexión sobre la relación actividad–efecto. Los resultados muestran que el uso simultáneo del lenguaje analítico y geométrico, así como la interacción dinámica con estos sistemas de representación en un contexto tecnológico, pueden favorecer las generalizaciones necesarias para desarrollar los procesos de abstracción reflexiva que inciden en la elaboración del concepto de dependencia lineal.

PALABRAS CLAVE: Dependencia lineal, geometría dinámica, experimento de enseñanza, proceso de generalización.

 

ABSTRACT

This article presents a teaching experiment in the domain of linear algebra in a context of dynamic geometry. It describes a hypothetical learning trajectory in order to construct the concept of linear dependence in terms of the mechanism of reflection on the effect–activity relationship. The results demonstrate that the simultaneous use of analytical and geometrical language, as well as the dynamic interaction with representation systems in a technological context, can encourage the generalizations required in order to develop reflexive abstraction processes that have a bearing on the creation of the concept of linear dependence.

KEY WORDS: Linear dependence, dynamic geometry, teaching experiment, generalization process.

 

RESUMO

Este artigo apresenta uma experiência de ensino no domínio do álgebra linear num contexto de geometria dinâmica. Descreve–se uma 'trajetória hipotética de aprendizagem' para la construção do conceito de dependência linear em termos do mecanismo de 'reflexão sobre a relação atividade–efeito'. Os resultados mostram que o uso simultâneo da linguagem analítico e geométrico e a interacção dinâmica com estes sistemas de representação num contexto tecnológico, pode favorecer as generalizaciones necessárias para desenvolver os processos de abstracção reflexiva que implicam a construção do conceito de dependência lineal.

PALAVRAS CHAVE: Dependência lineal, geometria dinâmica, experiência de ensino, processo de generalização.

 

RÉSUMÉ

S'inscrivant dans un contexte de géométrie dynamique, cet article est la présentation d'une expérience d'enseignement dans le domaine de l'algébre linéaire. On y décrit une trajectoire hypothétique d'apprentissage afin de construire le concept de dépendance linéaire par rapport au mécanisme de réflexion portant sur la relation activité–effet. Les résultats obtenus montrent que l'utilisation simultanée du langage analytique et de la géométrie, ainsi que celle de l'interaction dynamique avec ces systèmes de représentation dans un contexte technologique, peuvent favoriser les généralisations nécessaires pour développer les processus d'abstraction réfléchissante qui ont une incidence sur l'élaboration du concept de dépendance linéaire.

MOTS CLÉS: Dépendance linéaire, géométrie dynamique, expérience pédagogique, processus de généralisation.

 

1. INTRODUCCIÓN

El álgebra lineal es una rama de la matemática que forma parte de los programas de bachillerato científico en los cursos previos a la universidad. Su enseñanza–aprendizaje exige la articulación de tres tipos de lenguajes, el geométrico de 2 y 3 dimensiones, el aritmético de Rⁿ y el algebraico (Hillel, 1997), que corresponden a tres modos de pensamiento: el de la geometría sintética, el aritmético–analítico y el analítico–estructural, respectivamente (Sierpinska, Defence, Khatcherian & Saldanha, 1997).

El modo de pensamiento de la geometría sintética utiliza el lenguaje de figuras geométricas, planos y líneas, intersecciones, así como sus representaciones gráficas convencionales.

En el modo aritmético–analítico, los objetos geométricos se representan como conjuntos de n–uplas de números en Rⁿ que satisfacen ciertas condiciones; por ejemplo, sistemas de ecuaciones o desigualdades. Asimismo, contempla las componentes numéricas de los objetos geométricos, como los puntos o vectores, y requiere que un sistema lineal de ecuaciones se escriba usando todos sus coeficientes:

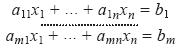
El pensamiento analítico–estructural va más allá de este tipo de análisis, ya que sintetiza los elementos algebraicos de las representaciones analíticas dentro de conjuntos estructurales. Por ejemplo, el sistema de ecuaciones anterior se puede escribir de forma matricial o vectorial:

donde: A₁ ,...A_n y B son vectores m–dimensionales.

Para Sierpinska "[...] el hecho más interesante es que el álgebra lineal puede ser vista como el resultado de la superación de dos obstáculos o dos posiciones dogmáticas: una que rechaza la entrada de los números en la geometría, y la otra, llamada de la 'intuición geométrica', que se ubica en el dominio puro de la aritmética" (2000, p. 232).

Los tres tipos de lenguaje mencionados coexisten. A veces se puede pasar de uno a otro; sin embargo, no son equivalentes: "Saber cuando un lenguaje se usa metafóricamente, cómo se relacionan los distintos lenguajes y modos de pensamiento y cuándo uno es más apropiado que otro es la dificultad principal de los estudiantes" (Dreyfus, Hillel & Sierpinska, 1998, p. 210).

Ahora bien, la dificultad de relacionar los distintos lenguajes ha sido puesta de relieve por Soto (2003), en referencia a la conversión entre representaciones gráficas y algebraicas de conceptos del álgebra lineal en R² y en R³. Por otra parte, Torregrosa & Quesada (2007) han puesto de manifiesto la necesaria coordinación de los procesos cognitivos en geometría, como la visualización y los procesos de razonamiento, que implican el uso de los tres tipos de lenguaje.

Otro problema es el obstáculo del formalismo o tendencia de los estudiantes a comportarse como si las representaciones simbólicas formales de los objetos del álgebra lineal (números, vectores, ecuaciones o coordenadas) fueran los objetos en sí mismos, por lo cual manipulan las representaciones mecánicamente sin comprender su significado y sin percibir las relaciones entre ellas (Dorier, Robert, Robinet & Rogalski, 1997; Sierpinska, 2000).

Uno de los primeros conceptos de estudio en el álgebra lineal es el de la dependencia lineal, que resulta importante para construir otras nociones como independencia lineal, sistema generador, base, espacio vectorial o transformación lineal. En relación con este concepto, las investigaciones han señalado que con frecuencia los estudiantes lo ven sólo en términos algorítmicos; es decir, usan los procedimientos algorítmicos sin comprender su significado y no saben relacionar sus diferentes representaciones (Andreoli, 2005; Oropeza & Lezama, 2007).

Para abordar las dificultades citadas se sugiere el uso de las tecnologías como instrumentos de mediación semiótica que permitan introducir relaciones y conceptos matemáticos (Maschietto, 2008), ya que tienen potencialidad para presentar simultáneamente varias representaciones de un mismo concepto y favorecen la interacción y el dinamismo (Heid & Blume, 2008; Lagrange & Artigue, 2009). Por tal motivo, se han elaborado propuestas en torno a diferentes conceptos del álgebra lineal que articulan distintos lenguajes mediante el uso de software de geometría dinámica y tratan de combinar aspectos analíticos e intuitivos a través de una aproximación geométrica (Dreyfus, Hillel & Sierpinska, 1998; Hoyos, 2006; Uicab & Oktac, 2006).

En este sentido, Duval (2006) indica que construir el significado de los objetos matemáticos implica, por una parte, la capacidad de transformación de las representaciones, que admite dos formas, la conversión y el tratamiento, según que el sistema semiótico cambie o se mantenga; por otra, la coordinación interna entre representaciones, ya que la mera yuxtaposición simultánea de varias representaciones de un mismo objeto es insuficiente, pues se limita a un reconocimiento mediante asociaciones que son particulares en cada caso.

Diversas investigaciones refieren los aspectos que caracterizan a la integración de herramientas computacionales en la enseñanza de las matemáticas para apoyar la construcción de significados (Castillo, 2008; Haspekian, 2005). Ferrara, Pratt y Robutti (2006) señalan que el trabajo en pequeños grupos, así como la discusión y el uso simultáneo de representaciones dinámicas e interactivas, pueden facilitar que los estudiantes construyan los significados matemáticos, aunque poco se conoce sobre el modo en que se da este proceso. Tal situación plantea cuestiones de investigación relativas a cómo los estudiantes generan el significado de los conceptos del álgebra lineal en contextos computacionales que favorecen el manejo de diferentes sistemas de representación.

Este artículo aporta información sobre cómo los alumnos de bachillerato (17 a 18 años) elaboran caracterizaciones equivalentes del concepto de dependencia lineal de vectores en R² y en R³ usando el lenguaje analítico y geométrico, mediante la descripción de un experimento de enseñanza en un entorno tecnológico con el applet Descartes (http://recursostic.educacion.es/descartes/web/).

La función de este applet consiste en proporcionar una herramienta que permite representar y manipular vectores en R² y R³, usando de forma coordinada el lenguaje geométrico (puntos, vectores, sistemas de referencia, colinealidad, paralelismo y coplanariedad de vectores), que concierne al modo de pensamiento de la geometría sintética, y el lenguaje analítico (representación de vectores como combinación lineal a partir de un sistema generador o por sus componentes respecto a un sistema de referencia), que atañe al modo de pensamiento analítico–aritmético (Dreyfus, Hillel & Sierpinska, 1998).

En concreto, queremos conocer en qué medida los alumnos aprovechan o no el potencial de utilizar simultáneamente las representaciones analítica y geométrica vinculadas al concepto de dependencia lineal; por tal motivo, analizamos sus trayectorias de aprendizaje mediante las acciones de generalización y las generalizaciones de la reflexión de la taxonomía de Ellis (2007). Para el diseño y planificación de la instrucción se describe una trayectoria hipotética de aprendizaje (Simon & Tzur, 2004), cuyo modelo es el mecanismo de reflexión sobre la relación actividad–efecto (Simon, Tzur, Heinz & Kinzel, 2004), que explica el desarrollo de los conceptos matemáticos.

El objetivo de esta investigación consiste en analizar si un experimento de enseñanza diseñado ad hoc (Gravemeijer, 2004) con escenas del applet Descartes ayuda a que los estudiantes de bachillerato (17 a 18 años) construyan o consoliden las caracterizaciones equivalentes al concepto de dependencia lineal en R² y en R³ mediante el lenguaje analítico y geométrico.

 

2. MARCO TEÓRICO

El marco teórico de esta investigación complementa la caracterización del mecanismo cognitivo, que se centra en la relación actividad–efecto (Simon et al., 2004), con una taxonomía sobre los procesos de generalización (Ellis, 2007).

2.1. Mecanismo de reflexión sobre la relación actividad–efecto y trayectorias hipotéticas de aprendizaje

El mecanismo de reflexión sobre la relación actividad–efecto fue elaborado por Simon et al. (2004) a partir de la idea de abstracción reflexiva de Piaget (1977), quien caracterizó tres tipos de abstracción: la empírica, la pseudoempírica y la reflexiva. La abstracción reflexiva se apoya en las dos primeras, debido a que surge cuando se abstraen propiedades comunes de varios objetos y se realizan acciones sobre ellos mediante la interiorización y coordinación de las acciones, así como la creación de nuevos objetos (Dubinsky, 1991).

Dicho mecanismo trata de describir la construcción de un nuevo concepto, pues intenta operativizar la "transposición a un plano superior" y la "reconstrucción" a las que hace referencia Piaget para explicar el proceso de abstracción. Por ello, ofrece "lentes teóricas" con el fin de analizar los conocimientos disponibles de los estudiantes y cómo los utilizan para construir nuevos conceptos (Tzur, Hagevik & Watson, 2004). Tzur y Simon (2004) han identificado dos fases en la elaboración de un nuevo concepto: la de participación es el proceso donde el alumno abstrae una regularidad en la relación entre la actividad realizada y el efecto producido, mientras que la de anticipación se refiere al uso de la regularidad abstraída en situaciones distintas a las que se llevó a cabo la abstracción.

En un estudio sobre el proceso de abstracción matemática que se llevó a cabo con una muestra amplia de estudiantes de secundaria, Roig (2008) identificó tres momentos en la fase de participación: proyección, reflexión y anticipación local. En el de proyección los alumnos construyen un conjunto de registros o unidades de experiencia, en el de reflexión abstraen la regularidad a partir de la información procedente del conjunto de registros, y en la de anticipación local aplican la regularidad identificada (la concepción matemática que organiza la situación) a nuevos casos particulares.

Roig considera, en términos del mecanismo de reflexión sobre la relación actividad–efecto, que "las acciones propias de la fase de proyección están anidadas en la coordinación de información que caracteriza la reflexión" (2008, p. 228), pues se produce en forma paralela a la generación de casos particulares.

Por otra parte, desde la caracterización del proceso de abstracción que proporciona el mecanismo cognitivo de la reflexión sobre la relación actividad–efecto, Simon y Tzur (2004) han elaborado la idea trayectoria hipotética de aprendizaje. Para generarla, es necesario conocer los conceptos previos de los estudiantes y tener presente los objetivos de aprendizaje, las tareas matemáticas que se usan para fomentar el aprendizaje y las hipótesis sobre el proceso de aprendizaje en el contexto de un conjunto particular de tareas. Estos dos últimos puntos son interdependientes y no necesariamente llevan un orden, ya que las tareas se seleccionan a partir de las hipótesis sobre el proceso de aprendizaje, mientras que las hipótesis están basadas en las tareas a realizar.

Aquí, señalan Simon y Tzur, entra en juego la manera en que se caracteriza el mecanismo de reflexión sobre la relación actividad–efecto porque se plantea la necesidad de seleccionar aquellas tareas que, desde las actividades disponibles para los alumnos, sean la base del aprendizaje pretendido. "El mecanismo ofrece un marco para pensar sobre cómo las tareas pueden fomentar el proceso de aprendizaje" (Simon & Tzur, 2004, p. 101). En el caso que nos ocupa, donde complementamos la abstracción reflexiva con los procesos de reflexión para dar cuenta sobre el aprendizaje de la idea de dependencia lineal en R² y en R³, necesitamos caracterizar los procesos de generalización para describir la trayectoria hipotética que permitirá seleccionar las tareas.

2.2. Taxonomía de la generalización

Para analizar la actividad cognitiva de los estudiantes en la realización de tareas usamos la taxonomía de la generalización, elaborada por Ellis (2007), adoptando el punto de vista de lo que el estudiante considera como general en un proceso de abstracción creativa compatible con la perspectiva piagetiana. Ellis distingue dos grandes categorías:

– Las acciones de generalización (AG) que describen la actividad mental de los estudiantes, la cual se infiere a partir de sus acciones sobre los objetos y/o su discurso. Las acciones son de tres tipos: relacionar, buscar y extender.

– Las generalizaciones de reflexión (GR), que se refieren a la habilidad de un estudiante para identificar o usar una generalización que él mismo ha creado. Unas veces se manifiestan al hacer explícita una propiedad común, un modelo o una relación de semejanza entre situaciones. En otras, su resultado no se expresa ni verbalmente ni por escrito; por ejemplo, cuando se aplica la idea de una situación anterior a un nuevo problema. Las generalizaciones son de tres tipos: afirmación, definición y transferencia.

La diferencia entre estas dos categorías radica en que, mientras las acciones son inferidas, las generalizaciones se evidencian a partir de declaraciones o acciones observables. Por otra parte, cuando los estudiantes hacen una afirmación acerca de una generalización, a veces es posible reconstruir el razonamiento previo hasta llegar a las acciones que dieron origen a su aseveración.

Hay una estrecha relación entre ambas categorías, ya que en algunas ocasiones las generalizaciones de reflexión son expresiones verbales o aplicaciones de las acciones de reflexión; en otras representan un paso más, cuando formalizan una acción en un principio o regla algebraica, e incluso hay veces en que los resultados de las acciones de generalización van más allá de la situación que las provocó o no están vinculados con una acción de generalización identificable. Según Ellis, la diferenciación entre los dos tipos de categorías permite identificar qué acciones se conectan con más frecuencia a tipos particulares de afirmaciones generales.

Roig (2008) asocia los diferentes momentos de la fase de participación en el proceso de reflexión con la taxonomía de Ellis, al caracterizar el momento donde los estudiantes tratan de identificar la regularidad en el conjunto de registros que constituyen las relaciones entre la actividad realizada y el efecto producido. Para ello, incluye en la fase de proyección las acciones de relacionar y buscar, y en la de anticipación local la acción de extender, junto con la afirmación y la definición.

Las generalizaciones a que han llegado los estudiantes tras el proceso de reflexión (afirmación o definición) pueden ser expresadas o usadas en el contexto que las ha provocado, con lo que se sitúan en el momento de anticipación local. Dicho aspecto lo referimos en esta investigación como proceso de construcción, o trascender el contexto (transferencia), y lo ubicamos en la fase de anticipación, a la que denominamos proceso de consolidación.

 

3. DISEÑO DEL EXPERIMENTO DE ENSEÑANZA

El objetivo de aprendizaje del experimento de enseñanza (Gravemeijer, 2004) es que los estudiantes construyan o consoliden el concepto de dependencia lineal, identificando sus caracterizaciones equivalentes en lenguaje analítico y geométrico.

Como ya se ha explicado, se utilizó el entorno de geometría dinámica que ofrece el proyecto Descartes (Núñez, 2005), en el que los alumnos disponían simultáneamente de la representación geométrica y la analítica de vectores en R² y R³, y podían modificarlas manipulando controles gráficos (extremos de vectores o giro de ejes) o numéricos (al cambiar o introducir valores). Este formato, que recibe el nombre de escena, permite experimentar y obtener respuestas inmediatas; asimismo, ofrece al mismo tiempo la representación geométrica y la expresión analítica.

Una de las escenas seleccionadas representa vectores en R³ en un sistema de referencia ortogonal con origen en un punto fijo O (Figura 4). Se pueden girar los semiejes al arrastrar el ratón para mostrar diferentes proyecciones en R² de la representación de los vectores en R³, con la restricción siguiente: el semieje Z, representado por un segmento que inicialmente aparece en posición vertical, se puede girar alrededor de O en un plano que en R³ es perpendicular a la pantalla plana del ordenador. Por tanto, su representación en este plano es siempre un segmento vertical de longitud variable o el punto O. De igual manera, como sucede en toda proyección, se pierde la información sobre las propiedades de los objetos en el espacio 3D.

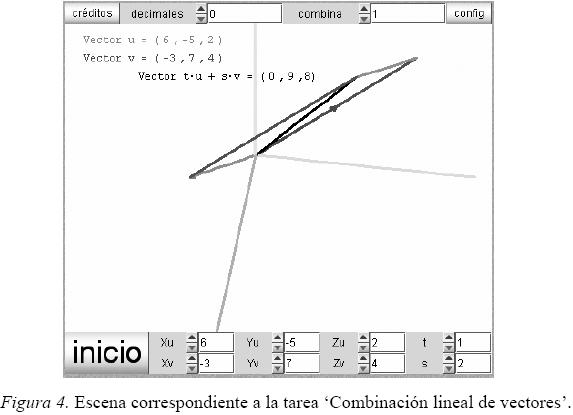
Las investigaciones dan a conocer la dificultad para identificar a las subfiguras deformadas por las proyecciones. Ante este panorama, los alumnos tienen que aprender a identificar planos para trabajar la geometría tridimensional (Jahn & Flores, 2008). En la escena seleccionada, la combinación lineal de dos vectores se visualiza mediante un paralelogramo y una diagonal que se deforman al girar los semiejes hasta que llegan a convertirse en un segmento.

Los participantes en el experimento habían estudiado previamente la dependencia lineal en R² y en R³, utilizando lápiz y papel. Partimos de la hipótesis de que el carácter estático de dicho entorno no facilita la coordinación interna entre representaciones y, por tanto, la construcción del concepto, ya que las manipulaciones sobre los escalares o los vectores de la representación analítica no se ven reflejadas en el cambio de la representación geométrica y viceversa. Sin embargo, creemos que las tareas diseñadas en el experimento facilitan la relación entre ambos tipos de representación (Kieran & Drijvers, 2006).

Nuestra hipótesis sobre la construcción o consolidación del concepto de dependencia lineal en R² y en R³ cuando se utiliza un entorno tecnológico dinámico e interactivo, en el que los estudiantes disponen simultáneamente de la representación analítica y gráfica de vectores que pueden manipular directamente y constatar sus efectos, se describe a continuación.

El experimento de enseñanza se desarrolló en dos sesiones. La primera contempló el trabajo de la dependencia lineal en R² con 2 vectores (Tarea 1) y 3 vectores (Tarea 2); la segunda abordó la dependencia lineal de 3 vectores en R³ (Tarea 3).

3.1. Trayectoria hipotética de aprendizaje del concepto de dependencia lineal

La Figura 1 muestra el proceso hipotético de construcción o consolidación del concepto de dependencia lineal mediante el experimento de enseñanza. Los óvalos representan el proceso de resolución de una tarea. Los rectángulos indican las "lentes teóricas" adoptadas para analizar el proceso: los de color negro, la taxonomía de Ellis (2007); los de blanco, las fases y subfases del proceso de abstracción. La flecha gruesa representa la reflexión anidada en la proyección (Tzur & Simon, 2004; Roig, 2008).

Nuestra hipótesis es que los estudiantes, después de tratar de comprender las indicaciones y cuestiones de las tareas y familiarizarse con las escenas del applet, realizarán acciones experimentando con los vectores particulares que de manera simultánea están representados en forma geométrica y analítica (tabla I).

Las acciones les ayudarán a relacionar el efecto que surge al modificar la representación geométrica de un vector sobre la expresión analítica y viceversa, ya que cambia inmediatamente las coordenadas de los vectores y viceversa. Además, la modificación de los escalares se traduce en la alteración del vector que es la combinación lineal de otros. Los alumnos pueden buscar otros ejemplos para comprobar o rechazar hipótesis; por ejemplo que dos vectores linealmente dependientes son colineales o paralelos, o que tres vectores en el plano son siempre linealmente dependientes.

Se espera que dichas acciones vayan dirigidas a inferir propiedades de tipo analítico (dos vectores en R² son linealmente dependientes si existe un número que multiplicado por uno de ellos da el otro; tres vectores en el plano siempre son linealmente dependientes porque uno de ellos se puede expresar como combinación lineal de los otros dos; tres vectores en R³ pueden ser o no linealmente dependientes) y geométrico (dos vectores son linealmente dependientes en R² si y sólo si son colineales o paralelos; tres vectores son linealmente dependientes en R³ si y sólo si son coplanarios), al igual que a relacionar las propiedades antes citadas por el uso simultáneo y coordinado de los lenguajes geométrico y analítico (si un vector se puede expresar como combinación lineal de otro son colineales o paralelos; si un vector se puede expresar como combinación lineal de otros dos que no son paralelos son coplanarios).

Tras el proceso de reflexión sobre las acciones con vectores particulares en diferentes posiciones, se puede llegar a extender tales situaciones a todos los vectores de R² y R³ y afirmar propiedades (por ejemplo, dos vectores en R² pueden ser o no linealmente dependientes; tres o más vectores en R² son siempre linealmente dependientes; lo mismo se da en cuatro vectores o más en R³) y a definir caracterizaciones equivalentes de la dependencia lineal en términos geométricos y analíticos (un conjunto de vectores es linealmente dependiente si y sólo si uno de ellos se puede expresar como combinación lineal de los otros; en particular, dos vectores en R² son linealmente dependientes si y sólo si son colineales o paralelos; tres vectores en R³ son linealmente dependientes si y sólo si son coplanarios).

Estas generalizaciones pueden ser expresadas o usadas en las escenas en que se apoyan las acciones, de ahí que se sitúen en la subfase de anticipación local (construcción del concepto) o bien trasciendan el contexto, al ubicarse en la fase de anticipación (consolidación). Aquí, los estudiantes podrían extender algunas afirmaciones o definiciones sin apoyarse en acciones de relacionar y buscar; por ejemplo, extender la afirmación "tres vectores en R² son siempre linealmente dependientes" a "tres vectores en R³ son linealmente dependientes si y sólo si son coplanarios", donde considerarían a los vectores coplanarios en R³ como vectores en R². También podrían extender algunas definiciones, como la de dependencia lineal, en términos geométricos: "dos vectores en R² son linealmente dependientes si y sólo si son colineales o paralelos" a "tres vectores en R² son linealmente dependientes si y sólo si son coplanarios".

A continuación, mostramos cada una de las tareas y lo que se espera de ellas en términos de la taxonomía de la generalización de Ellis (2007).

3.2. Primera sesión: Dependencia lineal en R²

Tarea 1. Dos vectores

Esta tarea¹ tiene como objetivo que los alumnos puedan generar un conjunto de registros sobre la relación entre una acción (modificar los parámetros relativos a dos vectores) y el efecto producido (el vínculo entre el paralelismo o no de dos vectores, y los valores de los parámetros).

La escena en la que se apoya es dirigida y proporciona la definición de vectores linealmente dependientes. Se pueden mover los vectores y variar los escalares (Figura 2) para que los alumnos experimenten, a través del cambio de los parámetros, cómo se representa la dependencia de manera gráfica.

La escena presenta dos situaciones al mismo tiempo. Una donde los dos vectores son linealmente dependientes (vectores paralelos), y otra en que no lo son (vectores no paralelos). A las preguntas se responde eligiendo una opción de un menú: si la respuesta es correcta aparece una ventana de confirmación; si no lo es, aparecen mensajes de error que orientan para encontrar la solución correcta. Tras responder a las preguntas de la escena se pide a los estudiantes que describan los significados que desde la experimentación guiada han podido generar sobre la frase "si alguno de ellos es combinación lineal de los demás", y contesten por escrito las siguientes interrogantes:

Tarea 2. Tres vectores

El objetivo de esta tarea² es que los estudiantes asocien una combinación lineal expresada analíticamente con su representación gráfica.

La escena en que se basa (Figura 3) tiene una trama con tres vectores, , y 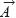, que se pueden modificar al pinchar (hacer click) en sus extremos (controles gráficos); el cambio se refleja en la expresión analítica y en la trama. La escena ofrece posibilidades de manipulación gráfica de los vectores y ayuda a deducir que tres vectores no nulos en R² son siempre linealmente dependientes; por tanto, uno de ellos es la combinación lineal de los otros dos.

La tarea pretende generar un conjunto diferente de registros sobre la relación entre la actividad de modificar los parámetros y los efectos que produce en la representación gráfica de los vectores. Para ello, propusimos a los alumnos las siguientes indicaciones y cuestiones:

El potencial de las dos tareas se puede expresar en términos de los tipos de generalizaciones (Ellis, 2007) que se espera que lleven a cabo los estudiantes (tabla II).

3.3 Segunda sesión: Dependencia lineal en R³

Tarea 3. Combinación lineal de vectores

El objetivo de esta tarea³ es que los alumnos hagan inferencias, al afirmar que dos vectores LI en R³ generan vectores coplanarios y no tienen las componentes proporcionales (dos a dos). Y, por tanto, que tres vectores LD son coplanarios porque se puede expresar uno de ellos como CL de los otros.

La escena en que se apoya la tarea tiene dos vectores dibujados, en rojo y en azul, con origen O en un sistema de referencia ortogonal con semirrectas de diferentes colores (Figura 4)⁴. Se pueden cambiar las coordenadas de sus extremos, así como dos parámetros, t y s. El botón 'combina' permite ver el vector resultante de la combinación lineal t + s .

Se propuso a los estudiantes la siguiente guía de trabajo:

Las dos primeras cuestiones buscan que los alumnos se familiaricen con los elementos de la escena, como la introducción a las representaciones geométricas planas de objetos en R³, mientras que la tercera va dirigida a que los estudiantes expresen en lenguaje geométrico y analítico la dependencia lineal de tres vectores que son coplanarios, y por tanto uno de ellos se puede expresar como una combinación lineal de los otros.

La tabla III contiene los tipos de generalizaciones (Ellis, 2007) de esta tarea en R³.

 

4. MÉTODO

4.1. Participantes

Seis estudiantes de 2^o de bachillerato (17 a 18 años de edad) participaron en este experimento de enseñanza de manera voluntaria, animados por su profesor de Matemáticas. Se formaron tres parejas, pero por problemas técnicos no se pudo recoger los datos de una de ellas. Las dos parejas objeto de este trabajo son:

1) Enric y Santi, de rendimiento medio–alto.

2) Toni y Rosa, de rendimiento medio.

El nivel de rendimiento corresponde a la calificación académica que obtuvieron en el curso anterior de Matemáticas.

Los datos recogidos para esta investigación se tomaron de los archivos con las capturas de las pantallas de las tareas hechas con el programa CamStudio (http://camstudio.es/), de los diálogos entre los estudiantes mientras efectuaban las tareas y de las producciones escritas en las hojas de tareas.

Los alumnos trabajaron por parejas durante dos sesiones de 50 minutos en el aula de Informática.

4.2. Recogida y análisis de datos

Se recopilaron los datos de las acciones que efectuaron los alumnos en la pantalla del ordenador, las declaraciones orales registradas en archivos digitales (Codes, Sierra & Raboso, 2007) y sus hojas de respuesta.

Para el análisis de los datos se siguió el siguiente proceso. En primer lugar, se hizo la trascripción de la comunicación oral de las sesiones, que fueron ilustradas con las capturas de las pantallas y se indicaron las acciones realizadas con la escena del applet. Se consideró como unidad de análisis a cada una de las acciones o declaraciones —orales o escritas— de los estudiantes.

En segundo lugar, se asoció a cada unidad de análisis el tipo de acción de generalización y el producto de la generalización, según la taxonomía de Ellis (2007). Para ello, se concretó y adaptó la taxonomía a las tareas propuestas (tablas I y II), cuyas categorías fueron revisadas una vez que los investigadores se familiarizaron con las acciones e intervenciones de los estudiantes. A continuación, dos investigadores codificaron por separado las declaraciones y acciones y discutieron las discrepancias, lo cual permitió identificar el proceso de construcción del concepto de dependencia lineal mediante la acción de extender, apoyada en las acciones de relacionar y buscar, así como en los resultados de tales acciones, expresados con afirmaciones y definiciones. De igual manera, permitió caracterizar la consolidación, ya sea a través de la acción de extender (cuando no está apoyada en las acciones de relacionar y buscar) y de los resultados de esta acción, expresados como afirmaciones y definiciones.

En tercer lugar, se hizo la descripción de las trayectorias de aprendizaje, a través de las acciones de generalización y las generalizaciones de reflexión como indicadores del aprendizaje de los estudiantes, que exponemos en la sección de resultados.

 

5. RESULTADOS

5.1. Trayectoria de aprendizaje de Enric y Santi Dependencia lineal en R²

Aunque esta pareja había trabajado previamente el concepto de dependencia lineal utilizando lápiz y papel, las tareas propuestas en el experimento no las consideraron como meros ejercicios de aplicación. Prueba de ello son sus acciones al tratar de responder la tarea inicial (Dos vectores), ya que cuando los vectores eran paralelos y de sentido contrario Santi no sabía relacionar el efecto de cambiar el signo del escalar sobre el sentido del vector. Cuando apareció una ventana de error que indicaba que se moviera un vector sobre otro, Santi y Enric decidieron cambiar el signo del escalar. A partir de este momento respondieron correctamente y con seguridad las preguntas de este apartado.

Cuando los vectores no eran paralelos, Enric comenzó a dudar en el momento de responder a las cuestiones:

[15] Enric [Lee]: ¿Existe algún número que multiplicado por el vector 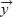nos dé el ?
[16] Santi: No.
[17] Enric: ¿Sí?

Sin embargo, al examinar las situaciones donde la magnitud y el signo de los escalares tomaban valores particulares, extendieron las observaciones particulares al caso general y definieron el concepto de DL en R², vinculando la expresión analítica (combinación lineal o producto de un vector por un escalar) con la representación geométrica (igual dirección, pero no necesariamente igual sentido):

[33] Enric: Dos vectores son linealmente dependientes cuando...
[34] Santi, Enric: ...uno se puede poner como combinación lineal del otro.
[38] Enric: Geométricamente si tienen la misma dirección. Son linealmente dependientes. Tengan el sentido que tengan tendrán siempre la misma dirección.

En la tarea 'Tres vectores' Santi y Enric hicieron las acciones sugeridas. Afirmaron que al modificar el sentido, pero no la dirección del vector 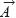, "cambia el signo de la combinación lineal de y "; sin embargo, centraron su interés en la modificación de los vectores y que generan la trama. Inicialmente distinguieron la trama de la escena como "una base de R²" y al modificar y exploraron el caso límite, donde las direcciones de y coincidían y desaparecía la trama cuadriculada, reconociendo que eran LD y no formaban base:

[102] Enric[Lee]: ¿Qué significa la trama inicial dibujada?
[103] Enric: Representa una base de R²...
[104] Enric [Lee]: ¿Qué pasa tanto con los vectores iniciales como al modificar los vectores?
[105] Santi: Que cambia la trama.
[106] Enric: Sí, bueno, ¿qué pasa? Que siempre representan la combinación lineal del vector 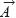, por ejemplo.
[107] Santi: Pongamos eso, pongamos excepto... que siempre representará la combinación lineal excepto.
[108] Enric: Aquí el pequeño muestra la proporción.
[109] Santi: Multiplicarlos...
[110] Enric: Excepto cuando sean linealmente dependientes.

En su diálogo no hacen ningún tipo de consideraciones de tipo geométrico que relacionen los vectores , y 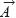de la escena.

Dependencia lineal en R³

En la tarea 'Combinación lineal', Santi y Enric siguieron al pie de la letra las indicaciones correspondientes al primer apartado de la tarea. Dieron valores a las componentes de los vectores y luego identificaron las semirrectas como "los ejes de coordenadas", pero Santi le confesó a Enric: "no sé lo que estoy haciendo".

Ambos respondieron la pregunta "¿cuántas formas conoces de expresar que tres vectores son linealmente dependientes?", sin efectuar acciones sobre la escena. Se plantearon si eso significaba "decirlo" o "expresarlo matemáticamente", lo cual les llevó a definir de tres formas, escribiendo:

Que uno de ellos se puede expresar como combinación lineal de los otros

son escalares

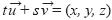donde t y s son escalares

La segunda fue una expresión ajena a las tareas, que probablemente recordaron de la clase, mientras que la tercera aparecía en la tarea.

Ahora bien, la manipulación del applet no les llevó a afirmar que "tres vectores LD en R³ son coplanarios", una idea a la que también podrían haber llegado por extensión de la afirmación "dos vectores LD en R² son colineales o paralelos", o "tres vectores en un plano son LD".

En resumen, cabe destacar que Enric y Santi:

1) En R² relacionaron la dependencia lineal con la representación gráfica y analítica de dos vectores; la acción de extender a partir de casos particulares al caso general propició que definieran de forma geométrica y analítica cuando dos vectores cualesquiera en R² son linealmente dependientes. Sin embargo, sólo caracterizaron analíticamente la dependencia lineal de 3 vectores.

2) En R³ sólo definieron la dependencia lineal en lenguaje analítico.

5.2. Trayectoria de aprendizaje de Toni y Rosa

Dependencia lineal en R².

El trabajo realizado por Toni y Rosa antes del experimento de enseñanza sobre el concepto de dependencia lineal utilizando lápiz y papel tampoco fue suficiente para construir tal noción, ya que en la primera tarea, 'Dos vectores', Toni expresó dudas, mientras que Rosa se sintió más segura. Por otra parte, la pareja necesitaba familiarizarse con las posibles opciones de respuestas para descartar y elegir.

Para responder la pregunta de si "dados dos vectores paralelos existe algún número que multiplicado por uno de ellos dé el otro", esta pareja hizo coincidir los orígenes de los vectores y desplegó el menú de respuestas con objeto de descartar y elegir. De este modo, llegó a afirmar que los vectores paralelos y son LD, como indica el siguiente diálogo:

[14] Toni: A ver si se puede mover, ahí, al punto (origen).
[Rosa sitúa el origen del vector sobre el origen de , el extremo de queda fuera de la escena]
[15] Rosa: No, pero sí. Vamos a ver las soluciones posibles. Pero sí, sí que se puede.
[16] Toni: Seguro que se puede. Se cruza.
[Leen] En caso afirmativo ¿cuál es? [Despliegan el menú con las opciones].
[17] Rosa: Como es más pequeño... [se refiere a que es más pequeño que ]
[18] Toni: No, no, espera, pero tiene que ser un número que multiplicado por nos dé entonces sería 2.
[19] Rosa: Que dé...
[20] Toni: No, 1.5 [escribe 1.5 en la escena].
[21] Rosa:Ah claro, lo decíamos al revés.
[22] Toni: Multiplicar el . Entonces, sería –1.5, = –1.5 por . Ah, claro porque como está al revés...
...
[31] Rosa–Toni: Por lo tanto, son dependientes.
[Relacionan la posición de los vectores (paralelismo, dirección y sentido) y los valores de los parámetros (magnitud y signo)].

En el apartado con vectores no paralelos, inicialmente Toni no sabía si un vector se podía poner como CL de otro no paralelo; Rosa tenía claro que no:

[38] Toni: Sí o no, puede ser, ¿no?
[39] Rosa: Yo creo que no porque tienen que tener la misma dirección.

La pareja seleccionó dos respuestas contradictorias: "no hay un número que multiplicado por el vector 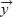dé " y " es combinación lineal de 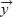". La escena les indicaba que "deben repasar la operación de números por vectores" y les remitía de nuevo a una con dos vectores paralelos, donde podían multiplicar un vector por un escalar. Tras dar los valores 2.5 y –0.5 a los escalares, relacionaron la magnitud y el signo del escalar con el módulo, la dirección y el sentido del vector. Toni dijo "está claro", refiriéndose a que se mantenía la dirección y cambiaba el módulo en función de la magnitud del escalar y el sentido para escalares negativos. De ahí, extendieron las observaciones de los casos particulares analizados al caso general para llegar a definir cuando dos vectores son LD:

[121] Toni: Uno es combinación lineal del otro.
[122] Rosa: [Tienen] la misma dirección.

En la tarea 'Tres vectores', Toni y Rosa hicieron diversas observaciones sobre el efecto del cambio de representación geométrica de los vectores de la escena en la modificación de los escalares de la combinación lineal.

Tal como se les pidió, modificaron el vector 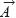, inicialmente + tirando del extremo sin cambiar la dirección:

[149] Rosa: Al modificar A cambia el número [refiriéndose a que los dos escalares son iguales].
[150] Toni: Claro, entonces sería… cambia el número que multiplica los dos vectores [ y ].
[151] Rosa: α [refiriéndose a los escalares].
[152] Toni: … [que multiplica] la suma de los dos vectores.
[153] Toni: Pero una cosita, cambia de la misma forma o si los giras cambia éste y éste... [refiriéndose a cada uno de los escalares].
[154] Rosa: No, si 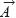tiene la misma dirección cambian de la misma forma, ¿no?
[155] Toni: Éste y éste, ¿no? Y entonces los dos serían α, ¿no?
[156] Rosa: Yo creo que sí.
[157] Toni: Mira… cámbialo por allí a ver si cambia uno u otro.
[158] Rosa: Aquí no ves que son los dos iguales, aquí, pero si… [señalan los vectores y en la escena].
[159] Toni: Si lo mueves cambian, claro, cambian los dos [mueven el punto A, situado en el extremo del vector A ].
[160] Rosa: Pero si tienen la misma dirección, no.
[161] Toni: No cambian, entonces es α los dos.

Tras estas exploraciones donde relacionaron la modificación del módulo del vector 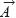sin cambiar la dirección con los escalares de la combinación lineal, Rosa y Toni sólo llegaron a afirmar que los dos escalares "cambian de la misma forma", "los dos serían α". Esta afirmación parece mostrar que su foco de atención estuvo más centrado en la expresión analítica que relacionaba los tres vectores que en su significado geométrico, a pesar de que habían manipulado la representación geométrica y planteado la relación entre la modificación del vector 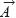(con la misma dirección o girándolo) y de los escalares de la CL.

Luego se les pidió que modificaran el vector , o ambos, y buscaran obtener el vector 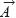inicial con otra combinación lineal. Manipularon los vectores y de nuevo centraron su atención en los escalares:

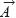[180] Toni: Si cambias o para que no cambie hay que cambiar los escalares.

Pero no llegaron a afirmar que tres vectores con distinta dirección en R² siempre son LD, pues se apoyaron en la trama de la escena, que dibujaba un paralelogramo de lados las direcciones de la trama y tenía como diagonal el vector 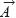. Cuando se les pidió que modificaran el vector 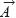cambiando la dirección con el objetivo de que lo relacionaran con y , afirmaron:

[206] Rosa: En este caso serían dos números [refiriéndose a los escalares].
[207] Toni: Que un número cambiaría del otro vector.
[210] Toni: Sería a + β

En este caso tampoco llegaron a relacionar la expresión de la CL con su significado geométrico; es decir, con la idea de que las CL de dos vectores LI generan todos los vectores de R².

Cuando se les preguntó qué significaba la trama inicial dibujada fueron afinando la descripción:

[229] Toni: Se trata de un sistema de referencia en el espacio 3D.
[232] Rosa: No, en el plano.
[235] Rosa: Es el sistema de referencia para ir modificando los vectores
[238] Rosa: y son un sistema de referencia porque son linealmente independientes.

Dependencia lineal en R³.

En la tarea 'Combinación lineal', cuando se les pidió que representaran los vectores de la base canónica dando valores a las coordenadas de y , Toni se preguntó:

[646]: Claro pero esos [señalando los vectores y que tenían distinta dirección] ¿son linealmente dependientes o qué?

Esta pregunta pone de manifiesto que Toni seguía sin poder diferenciar entre la idea de obtener una CL de los dos vectores y que aquellos sean LD.

Por otra parte, la pareja respondió a las cuestiones planteadas al calcular analíticamente los escalares de la combinación lineal , situándose siempre en el registro analítico, aunque identificaron de manera correcta los elementos geométricos de la escena (ejes y vectores). Se centraron en el tratamiento dentro del registro analítico sin convertir al geométrico y sin llegar a afirmar que en R³ tres vectores LD son coplanarios.

Además, si bien dieron valores a los escalares para obtener vectores, no afirmaron con claridad "qué significa que tres vectores en el espacio son LD".

En resumen, cabe destacar que Toni y Rosa:

1) En R², y tras las dudas iniciales, esta pareja fue capaz de relacionar los escalares de la combinación lineal y la posición de los vectores. En estas tareas, sólo en una ocasión, para dos vectores, extendió los casos particulares al general, llegando a afirmar que dos vectores que tienen la misma dirección son linealmente dependientes; luego dieron la definición en términos analíticos. Pero cuando se trató de tres vectores estuvo más centrada en la expresión analítica que relacionaba los vectores LD en vez de su significado geométrico, y definió la dependencia lineal sin llegar a asociar el registro analítico con su significado geométrico.

2) En R³, la pareja focalizó su atención en el tratamiento analítico, de modo que las afirmaciones y definiciones no muestran la conversión entre la representación analítica y geométrica del concepto.

 

6. CONCLUSIONES Y DISCUSIÓN

En este trabajo hemos expuesto un experimento de enseñanza utilizando un applet donde aparecen simultáneamente representaciones analíticas y geométricas, de carácter dinámico e interactivo, vinculadas con el concepto de dependencia lineal de vectores. Con ello queríamos fomentar las acciones cognitivas necesarias para coordinar los dos sistemas semióticos, relacionando ambos tipos de representaciones con el fin de construir el concepto de dependencia lineal. En este apartado nos centraremos en dos puntos: primero, el grado de construcción del concepto por parte de los estudiantes; segundo, la potencialidad de los contextos tecnológicos que integran diferentes tipos de representación en el aprendizaje de los conceptos del álgebra lineal.

1. El experimento de enseñanza se diseñó con tres tareas relativas a distintas situaciones vinculadas al concepto de dependencia lineal en R² y en R³. Con base en la taxonomía de Ellis (2007) hemos entendido que la construcción del concepto de dependencia lineal se manifiesta cuando en el proceso de resolución hay evidencias de la acción de extender, apoyada en las de relacionar y buscar, lo cual da como resultado afirmaciones y definiciones que muestran la coordinación interna (Duval, 2006) entre la representación analítica y geométrica de tal noción. La consolidación surge cuando la acción de extender, las afirmaciones y definiciones no se apoyan en otras acciones.

Las trayectorias de aprendizaje de las dos parejas estudiadas han sido diferentes, pero en la coordinación de los dos sistemas semióticos, el analítico y geométrico, muestran características comunes:

a) Hay evidencias de que en ambas parejas hubo un proceso de construcción del concepto de dependencia lineal de dos vectores en R², ya que al definirlo vincularon las representaciones analítica y geométrica, apoyándose en las acciones de relacionar y extender. Esto dio como resultado algunas afirmaciones y definiciones en las que se muestra la coordinación interna entre las representaciones analíticas y geométricas. Asimismo, las parejas supieron discriminar las características visuales de las relaciones entre los vectores que eran matemáticamente relevantes (paralelismo) y establecer el nexo entre el registro analítico y el geométrico.

b) Los estudiantes definieron la dependencia lineal de tres vectores en R² o R³ sólo en lenguaje analítico (combinación lineal), pero no en lenguaje geométrico (coplanariedad). A través de sus acciones focalizaron su atención en el tratamiento analítico, a pesar de que las escenas presentaban la yuxtaposición de dos representaciones de un mismo objeto en dos registros diferentes.

Esto último indica que la construcción de un concepto es un proceso progresivo de extensión a nuevas situaciones y de coordinación entre distintos sistemas semióticos. También confirma los resultados de otras investigaciones sobre la dificultad de relacionar distintas representaciones de conceptos del álgebra lineal (Dreyfus, Hillel & Sierpinska, 1998; Soto, 2003), en concreto el de dependencia lineal (Andreoli, 2005; Oropeza & Lezama, 2007).

Además, se corrobora la afirmación de Duval, referente a que "la yuxtaposición de dos representaciones de un mismo objeto en dos registros diferentes no puede resolver el problema cognitivo del reconocimiento del mismo objeto representado, porque las diferencias de contenido de las representaciones varían independientemente de los objetos representados" lo explica por la necesidad de la doble discriminación para convertir una u otra de estas dos representaciones. Por una parte, señala que es preciso "ser capaz de ver diferencias entre dos representaciones que parecen globalmente semejantes"; por otra, "ser capaz de distinguir en las representaciones de un registro las características del significante que son matemáticamente pertinentes, para relacionarlas con una representación en otro registro, y las características significativas en un registro que no lo son para la conversión en el otro registro" (2006, p. 160).

En nuestro caso, se trataría de reconocer dos objetos diferentes, la dependencia y la no dependencia lineal de vectores tanto en R² como en R³, en dos representaciones cuyos contenidos parecen semejantes (varios vectores en R² o en R³ en distinta posición relativa) porque corresponden al mismo registro, el geométrico. La primera discriminación en el registro visual es la posición relativa de dos vectores en R² o de tres vectores en R³; la segunda, el reconocimiento de las propiedades matemáticas relevantes (por ejemplo, si hay o no paralelismo entre dos vectores en R², si son o no coplanarios tres vectores en R³), ya que permite asociar el registro geométrico y el analítico.

Sin embargo, como precisa Duval, "cambiar la representación de objetos o relaciones matemáticas de un sistema semiótico a otro es siempre un salto cognitivo" (2006, p. 150) porque supone pasar del carácter cualitativo y global de la representación geométrica al carácter lineal, operativo y simbólico de la representación analítica, o viceversa. Nos preguntamos cómo facilitar, más allá de nuestro experimento de enseñanza, las condiciones para que se dé la construcción de este concepto y de otros mediante la coordinación interna de las representaciones.

2. Los participantes en el experimento habían trabajado previamente la dependencia lineal en R² y en R³ con lápiz y papel, pero no sabíamos en qué medida habían construido el concepto. La manera en que se enfrentaron a la primera tarea de nuestro experimento de enseñanza parece indicar que las nuevas tareas no fueron para ellos meros ejercicios de aplicación de los conocimientos previos.

El experimento de enseñanza constató que la actividad de los alumnos en contextos tecnológicos diseñados ad hoc, donde se integran diferentes tipos de representaciones interrelacionadas, ayuda a avanzar en la construcción del concepto de dependencia lineal, ya que por la interacción y el dinamismo las acciones de relacionar, buscar y extender facilitaron a los estudiantes la coordinación interna (Duval, 2006) entre las representaciones analíticas y geométricas de este concepto, en el caso de dos vectores en el plano. Sin embargo, algunas investigaciones que reúnen el uso de lápiz y papel y los entornos tecnológicos señalan que "el valor epistémico de técnicas de lápiz y papel parece jugar un papel no sólo complementario, sino esencial" (Kieran & Drijvers, 2006, p. 258). Por ello, consideramos que el rediseño del experimento de enseñanza, donde se combinen e integren ambos tipos de técnicas, enriquece su valor epistémico.

Ahora bien, el diseño de la escena de la primera tarea (Dos vectores) fue muy adecuado para el propósito de la investigación, debido a que ofreció dos situaciones contrapuestas (dos vectores LD y dos que no lo son) y arrojó los resultados esperados. No obstante, la aproximación geométrica de las otras escenas no mostró con tanta claridad la caracterización geométrica de tres vectores LD en R² o en R³ (coplanariedad), de ahí que los estudiantes centraran su atención en el tratamiento analítico. Por otra parte, la representación en R² de situaciones en R³ presentó dificultades para los alumnos (Jahn & Flores, 2008); si bien los programas de geometría dinámica pueden facilitar su representación, es preciso que los estudiantes aprendan a familiarizarse y manipulen adecuadamente estas representaciones.

Las investigaciones realizadas con applets de características semejantes a las de Descartes indican que "se ha hecho un considerable esfuerzo por explotar el potencial de la tecnología para ofrecer múltiples representaciones relacionadas. Algunos resultados sugieren que la relación de representaciones en la pantalla puede facilitar que se construyan las conexiones mentales. Sin embargo, poco se comprende de este proceso (...). Necesitamos saber más sobre las formas en que los alumnos hacen estas conexiones" (Ferrara et al., 2006, p. 255).

En este sentido, nuestra investigación confirma que el uso simultáneo de representaciones geométricas dinámicas e interactivas puede ayudar a avanzar en la construcción del concepto de dependencia lineal (Oropeza & Lezama, 2007; Steward & Thomas, 2007), pero la tecnología no es la determinante del proceso de aprendizaje, sino la actividad cognitiva de los estudiantes, como la doble discriminación (Duval, 2006), en la medida en que toman conciencia y reflexionan sobre la actividad matemática que llevan a cabo (Heid & Blume, 2008).

 

AGRADECIMIENTOS

Este estudio ha sido financiado por la Universidad de Alicante, España, en el marco del proyecto Construcción y uso de estructuras matemáticas específicas, número GRE08–P03. Los autores agradecen a los revisores sus sugerencias.

 

REFERENCIAS BIBLIOGRÁFICAS

Andreoli, D. I. (2005). Construcción de los conceptos de dependencia e independencia lineal de vectores en alumnos de primer año de la Universidad (tercera fase). Comunicaciones Científicas y Tecnológicas, Universidad Nacional del Nordeste (UNNE). Corrientes. Recuperado de http://www.unne.edu.ar/Web/cyt/com2005/9–Educacion/D–004.pdf        [ Links ]

Castillo, S. (2008). Propuesta pedagógica basada en el constructivismo para el uso óptimo de las TIC en la enseñanza y el aprendizaje de la matemática. Revista Latinoamericana de Investigación en Matemática Educativa, 11 (2), 171–194.         [ Links ]

Codes, M., Sierra, M. & Raboso, M. (2007). Innovación en la recogida de datos para una investigación de carácter cualitativo. Un ejemplo con alumnos universitarios en un entorno computacional. En M. Camacho, P. Flores & P. Bolea (Eds.), Actas de Investigación en Educación Matemática XI (pp. 261–271). Tenerife, España: Sociedad Española de Investigación en Educación Matemática.         [ Links ]

Dorier, J. L., Robert, A., Robinet, J. & Rogalski, M. (1997). The Obstacle of Formalisme in Linear Algebra. In. J. L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 85–124). Dordrecht: Kluwer Academic Publishers.         [ Links ]

Dreyfus, T., Hillel, J. & Sierpinska, A. (1998). Evaluation of a Teaching Design in Linear Algebra: The Case of Linear Transformations. Paper presented at the first Conference of the European Society for Research in Mathematics Education (CERME–1). Recuperado de http://www.fmd.uniosnabrueck.de/ebook/erme/cerme-1proceedings/papers/g2-dreyfus-et-al.pdf        [ Links ]

Duval, R. (2006). Un tema crucial en la educación matemática: la habilidad para cambiar el registro de representación. La Gaceta de la Real Sociedad Matemática Española 9 (1), 143–168.         [ Links ]

Dubinsky, E. (1991). Reflective Abstraction in Advanced Mathematical Thinking. In D. Tall (Ed.), Advanced Mathematical Thinking (pp. 95–123). Dordrecht: Kluwer Academic Publishers.         [ Links ]

Ellis, A. B. (2007). A Taxonomy for Categorizing Generalizations: Generalizing Actions and Reflection Generalizations. The Journal of the Learning Sciences, 16 (2), 221–262.         [ Links ]

Ferrara, F., Pratt, D. & Robutti, O. (2006). The Role and Uses of Technologies for the Teaching of Algebra and Calculus. In A. Gutierrez & P. Boero (Eds.), Handbook of Research on the Psychology of Mathematics Education. Past, Present and Future (pp. 237–273). Rotterdam–Taipei: Sense Publishers.         [ Links ]

Gravemeijer, K. (2004). Local Instruction Theories as Means of Support for Teachers in Reform Mathematics Education. Mathematical Thinking and Learning, 6 (2), 105–128.         [ Links ]

Haspekian, M. (2005). An "Instrumental Approach" To Study the Integration of a Computer Tool Into Mathematics Teaching: The Case of Spreadsheets. International Journal of Computers for Mathematical Learning, 10 (2), 109–141.         [ Links ]

Heid, M. K. & Blume, G. W. (2008). Algebra and Function Development. In M. K. Heid & G. W. Blume (Eds), Research on Technology and the Teaching and Learning of Mathematics. Research Syntheses 1 (pp. 55–108). Charlotte, North Carolina: National Council of Teachers of Mathematics–IAP.         [ Links ]

Hillel, J. (1997). Des niveaux de description et du problème de la représentation en algèbre linéaire. In J. L. Dorier (Ed.), L'enseignementde l'algébre linéaire en question (pp. 231–247). Grenoble: La Pensée Sauvage.         [ Links ]

Hoyos, V. (2006). Funciones complementarias de los artefactos en el aprendizaje de las transformaciones geométricas en la escuela secundaria. Enseñanza de las Ciencias, 24 (1), 31–42.         [ Links ]

Jahn, A. P. & Flores, J. V. (2008). Exploring Three–dimensional Objects Through Dynamic Representations Using Cabri 3D: An Experience with Brazilian School Students. In 11th International Congress of Mathematical Education. Recuperado de http://tsg.icme11.org/tsg/show/23#inner–documents        [ Links ]

Kieran, C. & Drijvers, P. (2006). The Co–emergence of Machine Techniques, Paper–and–Pencil Techniques and Theoretical Reflection: A Study of CAS Use in Secondary School Algebra. International Journal of Computers for Mathematical Learning, 11 (2), 205–263.         [ Links ]

Lagrange, J. B. & Artigue, M. (2009). Student's Activities About Functions at Upper Secondary Level: A Grid for Designing a Digital Environment and Analyzing Uses. In M. Tzekaki, M. Kaldrimidou & H. Sakonidis (Eds.), Proceedings of the 33^rd Conference of the International Group for the Psychology of Mathematics Education (Vol. 3, pp. 465–472). Greece: PME.         [ Links ]

Maschietto, M. (2008). Graphic Calculators and Micro–Straightness: Analysis of a Didactic Engineering. International Journal of Computers for Mathematical Learning, 13(3), 207–230. doi: 10.1007/s10758–008–9141–7         [ Links ]

Núñez, A. (2005). El proyecto Descartes en el aula. Nuevas metodologías y contenidos. En I. M. Gómez Chacón (Ed.), Usos matemáticos de internet (pp. 123–147). Madrid: MEC.         [ Links ]

Oropeza, C. & Lezama, J. (2007). Dependencia e independencia lineal: una propuesta de actividades para el aula. REIEC 2 (1). Recuperado de http://www.exa.unicen.edu.ar/reiec/files/anio2/num1/REIEC_anio2_num1_art2.pdf         [ Links ]

Piaget, J. (1977). Studies in Reflecting Abstraction. Sussex: Psychology Press.         [ Links ]

Roig, A. I. (2008). Análisis de las fases del proceso de abstracción matemática en estudiantes de secundaria (Tesis inédita de doctorado). Universidad de Alicante, Alicante, España.         [ Links ]

Sierpinska, A. (2000). On Some Aspects of Student's Thinking in Linear Algebra. In. J. L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 209–246). Dordrecht: Kluwer Academic Publishers.         [ Links ]

Sierpinska, A., Defence, A., Khatcherian, T. & Saldanha, L. (1997). À propos de trois modes de raisonnement en algèbre linéaire. In J. L. Dorier (Ed.), L'enseignement de l'algébre linéaire en question (pp. 249–268). Grenoble: La Pensée Sauvage.         [ Links ]

Simon, M. A. & Tzur, R. (2004). Explicating the Role of Mathematical Tasks in Conceptual Learning: An Elaboration of the Hypothetical Learning Trajectory. Mathematical Thinking and Learning, 6 (2), 91–104. doi: 10.1207/s15327833mtl0602_2         [ Links ]

Simon, M. A., Tzur, R., Heinz, K. & Kinzel, M. (2004). Explicating a Mechanism for Conceptual Learning: Elaborating the Construct of Reflective Abstraction. Journal for Research in Mathematics Education, 35 (5), 305–329.         [ Links ]

Soto, J. L. (2003). Un estudio sobre las dificultades para la conversion gráfico–algebraica relacionadas con los conceptos básicos de la teoría de espacios vectoriales en R² y R³ (Tesis inédita de doctorado). Cinvestav–IPN, México, D.F., México.         [ Links ]

Steward, S. & Thomas, M. O. J. (2007). Embodied, Symbolic and Formal Aspects of Basic Linear Algebra Concepts. In J. H. Woo, H.C. Lew, K. S. Park & D. Y. Seo (Eds.), Proceedings of the 31st Conference of the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 201–208). Seoul: PME.         [ Links ]

Torregrosa, G. & Quesada, H. (2007). Coordinación de procesos cognitivos en geometría. Revista Latinoamericana de Investigación en Matemática Educativa, 10 (2), 275–300.         [ Links ]

Tzur, R., Hagevik, A. & Watson, M. E. (2004). Fostering mathematical meaning via scientific inquiry: a case study. In M. J. Heines & A. B. Fuglestad (Eds.), Proceedings of the 28^th Conference for the International Group for the Psychology of Mathematics Education (Vol. 4, pp. 345–352.). Bergen: PME.         [ Links ]

Tzur, R. & Simon, M. A. (2004). Distinguishing Two Stages of Mathematics Conceptual Learning. International Journal of Science and Mathematics Education, 2, 287–304. doi: 10.1007/s10763–004–7479–4        [ Links ]

Uicab, R. & Oktaç, A. (2006). Transformaciones lineales en un ambiente de geometría dinámica. Revista Latinoamericana de Investigación en Matemática Educativa, 9 (3), 459–490.         [ Links ]

 

NOTAS

¹ http://descartes.cnice.mec.es/materiales_didacticos/Vectores3D_d3/vectores3D_07.htm. Autora: Ángela Núñez Castaín.

² http://descartes.cnice.mec.es/materiales_didacticos/vectores/CombiVectores.htm. Autor: José Ireno Fernández Rubio.

³ http://descartes.cnice.mec.es/materiales_didacticos/Vectores_espacio_d3/Vectores_esp_3.htm. Autor: Matías Pérez García.

⁴ Ver colores en la página web de la escena, cuya dirección de la página en la nota 3.