Artículos

 

Análisis epistemológico de la secuencia numérica

 

Epistemological analysis of numerical sequence

 

Catalina María Fernández Escalona*

 

* Departamento de Didáctica de las Matemáticas, de las Ciencias Sociales y de las Ciencias Experimentales, Universidad de Málaga, España; cfernandez@uma.es

 

Recepción: Mayo 13, 2009
Aceptación: Diciembre 18, 2009.

 

RESUMEN

La secuencia numérica requiere de un soporte conceptual ordinal para su construcción, que es posible definir a través de las relaciones dadas en un sistema de progresiones. Tener en cuenta el soporte conceptual ordinal nos lleva a integrar la secuencia numérica en un sistema conceptual e interpretativo coherente que pasa por las concepciones y creencias sobre la secuencia numérica, lo cual remite inmediatamente a consideraciones de tipo epistemológico y didáctico.

Los planteamientos epistemológicos se circunscriben al problema de la naturaleza, origen y modo de existencia del número natural y de la aritmética elemental, de manera que la construcción de la secuencia numérica va a depender, en este punto, de las conclusiones que se establezcan en torno al problema mencionado.

PALABRAS CLAVE: Epistemología de la secuencia numérica, número ordinal, número natural, Educación Matemática.

 

ABSTRACT

The construction of a numerical sequence requires an ordinal model of conceptual support that can be defined by the given relationships in a system of progressions. Taking into account the ordinal model of conceptual support leads us to a coherent conceptual/interpretative system which takes into consideration conceptions and beliefs regarding numerical sequencing that immediately takes us back to epistemological and didactic considerations.

Epistemological approaches are confined to looking at the nature, origin and mode of existence of the natural number and elementary arithmetic, so that construction of the numerical sequence relies, at this point, on the conclusions that are drawn in regard to the said problem.

KEY WORDS: Epistemology of numerical sequence, ordinal number, natural number, Mathematics Education.

 

RESUMO

A sequência numérica requer um suporte conceptual ordinal para a sua construção, que é possível definir através das relações dadas num sistema de progressões. Ter em conta o suporte conceptual ordinal leva–nos a integrar a sequência numérica num sistema conceptual e interpretativo coerente que passa pelas concepções e crenças sobre a sequência numérica, o que remete imediatamente para considerações de tipo epistemológico e didáctico.

As exposições epistemológicos circunscrevem–se ao problema da natureza, origem e forma de existência do número natural e da aritmética elementar, de maneira a que a construção da sequência numérica vá depender, neste ponto, das conclusões que se estabelecem em torno do problema mencionado.

PALAVRAS CHAVE: Epistemologia da sequência numérica, número ordinal, número natural, Educação Matemática.

 

RÉSUMÉ

Un support conceptuel ordinal est nécessaire à la construction de la séquence numérique. Il est possible de dèfinir ce support grâce aux relations données dans un système de progressions. Le fait de prendre en compte le support conceptuel ordinal nous amène à intégrer la séquence numérique dans un système conceptuel et interprétatif cohérent basé sur les conceptions et les croyances relatives a la séquence numérique. Et ce phénomène nous renvoie immédiatement à des observations d'ordre épistémologique et didactique.

Etant donné que l'approche épistémologique est circonscrite au problème de la nature, de l'origine et du mode d'existence du numéro naturel et de l'arithmétique élémentaire, la construction numérique va dépendre, à ce niveau–ci, des conclusions auxquelles on parviendra en abordant le problème qui est le nôtre.

MOTS CLÉS: Épistémologie de la séquence numérique, numéro ordinal, numéro naturel, Éducation mathématique.

 

1. EL PROBLEMA DE INVESTIGACIÓN

Existen corrientes epistemológicas que consideran a las relaciones lógicas ordinales del número natural como el origen de toda la construcción matemática y el concepto primario generador de la secuencia numérica. Por consiguiente, sustentan todo el edificio matemático (Fernández, 2001). En este sentido, la construcción de número natural que vamos a considerar en este trabajo es aquella que define explícitamente la secuencia numérica a partir de las relaciones lógicas ordinales, vistas como conceptos primarios que generan series. Dichas relaciones son:

– Las asimétricas biunívocas, que definirían "el inmediato posterior al lado de".

– Las asimétricas transitivas, que darían lugar a "la clase de todos los siguientes".

Las definiciones que intervienen en esta construcción de la secuencia numérica son consistentes, ya que los dos tipos de relaciones son equivalentes.

Concebimos a la secuencia numérica como un tipo de serie que puede generarse a partir de relaciones lógicas ordinales (en el sentido que acabamos de precisarlas). Sus definiciones están dadas a partir de la construcción que Bertrand Russell (1903/1982) hace de las relaciones de orden, quien a su vez se basa en las relaciones asimétricas biunívocas especificadas por Bolzano (1851), que conlleva como concepto primario lo que él mismo denomina como "inmediato posterior al lado de e inmediato anterior al lado de " (Fernández, 2003).

Dicho método de construcción se da frente a otros, como el de Vivanti (Russell, 1982), que se caracteriza por definir fácilmente los siguientes a un término y los anteriores, los cuales son vistos como conceptos primarios para que, a partir de ellos, se puedan precisar el siguiente inmediato y el anterior inmediato (Fernández, 2003).

Con todo ello, nuestro problema de investigación es plantear una construcción lógica de la secuencia numérica en un contexto ordinal, interesándonos por el sistema de relaciones lógicas existente entre sus términos, y omitimos el significado cardinal de cada uno de ellos. En esta línea de construcción definimos la secuencia numérica en estos términos: "La secuencia numérica es una progresión dada por la relación generatriz de Bolzano, es decir, es una progresión¹ en el sentido de Bertrand Russell" (Fernández, 2001, p. 22). Será esta concepción la que consideraremos a lo largo del presente trabajo.

Frente a esta definición existen otras construcciones matemáticas del número natural. En Fernández y Ortiz (2008) hallamos que, para Mill (1917), los números son resultado de inferencias inductivas y de generalizaciones empíricas. El hecho de identificar la cantidad tres, con independencia de la disposición espacial o constelación, es una verdad adquirida inductivamente sobre la que se funda la ciencia de los números (p. 108).

Por su parte, Frege (1884/1972) recurre a un planteamiento lógico para afirmar que las aserciones sobre números y sobre las cosas son distintas por su carácter y su sentido, lo cual implica que quien confunda el sentido de unas y otras es que no comprende lo que es la aritmética, sino que desconoce y falsea su verdadera significación. La aportación principal de Frege es el concepto de "número cardinal", cuya más sencilla ejemplificación son los elementos de la serie 0, 1, 2, 3,..., y considera al número cardinal como la propiedad de una clase.

Cantor (1955) realiza una construcción a partir de la idea intuitiva de conjunto que va de lo general a lo particular, por lo cual se trata de un proceso deductivo y no inductivo, como ha afirmado Mill. Cantor hace uso de los números cardinales sin definirlos, ya que sólo establece una relación de equivalencia entre conjuntos mediante biyecciones para determinar cuándo dos conjuntos tienen el mismo número cardinal. Asimismo, señala cuándo el cardinal de un conjunto es menor que el de otro con llevar a cabo una aplicación inyectiva del primero en el segundo. De este modo, elabora una aritmética cardinal y otra ordinal, integradas en lo que se denominó aritmética de conjuntos (p. 108).

Según Cassirer (1979), los matemáticos tienen discrepancias al elegir entre la teoría cardinal y la teoría ordinal. La cardinal parece imponerse de un modo más claro que la ordinal a todas las consideraciones en torno a los orígenes psicológicos del número. La clase se presenta así como lo anterior al número y forma la constante lógica de la que debe derivarse todo el contenido del concepto de número.

Ambas teorías entrañan la necesidad de una continuidad y una transición. La ordinal tenía que demostrar de qué modo podía hacer frente al punto de vista de la pluralidad y de la cantidad, en sentido estricto; la cardinal debía poner de manifiesto un principio donde pudieran enhebrarse mediante un orden fijo las cantidades definidas, de manera independiente. En las dos propuestas han colaborado destacados matemáticos: en los planteamientos ordinales podemos destacar a Hemhlotz, Kronecker, Dedekind y Peano; en los cardinales, a Cantor, Frege y Russell (Fernández y Ortiz, 2008).

En esta diversidad de paradigmas, el marco teórico que consideramos es el que ofrece la figura 1, pues explica el contexto matemático donde enmarcamos la secuencia numérica en función de las relaciones ordinales.

Para delimitar el conocimiento lógico de la secuencia numérica dentro del marco general del número natural, en su aspecto ordinal, efectuamos una revisión epistemológica del número natural bajo la perspectiva de tres corrientes: el convencionalismo, el logicismo y la epistemología genética. Una vez hecho el análisis epistemológico de la secuencia numérica veremos cómo se ha tratado en Educación Matemática, atendiendo a periodos históricos relevantes del siglo XX: el aritmetista, el conjuntista y el postconjuntista.

 

2. EPISTEMOLOGÍA DEL NÚMERO NATURAL

En el último cuarto del siglo XIX grandes matemáticos como Dedekind, Weierstrass, Heine, Cantor y otros definieron los números reales a partir de los racionales, que eran entendidos como parejas de números enteros. Basta recordar que los números enteros pueden concebirse a su vez como parejas de números naturales, para concluir que son una pieza fundamental en todo el edificio matemático.

Como los números naturales tienen gran importancia en la construcción de toda la matemática, incluso en la actualidad se intenta conocer más sobre su origen, al plantearse las siguientes preguntas: ¿en matemáticas hay algo anterior a estos números? ¿cómo surgen?, ¿cómo se definen?, ¿cómo se presentan?, ¿cómo se usan? Una cosa está clara para todos los matemáticos: Los números naturales se presentan en secuencia.

Por tanto, para la construcción de toda la matemática y, en concreto su aritmetización, es muy importante precisar el conjunto de los números naturales, más concretamente la secuencia numérica, ya que estamos de acuerdo con J–B. Grize (1979) cuando afirma:

En la matemática, todo aquello que puede enunciarse en el lenguaje de los sistemas formales reposa en la noción de número natural, por medio de las funciones recursivas [...]. Un primer hecho resulta importante. Tan pronto intentamos, ya sea pensar, con mayor modestia incluso, utilizar en forma totalmente práctica un número n, lo hacemos siempre como miembro de la serie de los números naturales. De lo cual se desprende un primer enfoque del problema, que consistiría simplemente en describir esa serie y los razonamientos que sostiene, pero del modo más preciso posible (Grize, 1979, p. 109).

Dicha cuestión la abordaremos en el sentido planteado por Grize, y buscaremos en las principales corrientes epistemológicas el entendimiento de la secuencia numérica como una componente del número natural, siguiendo el esquema de la figura 2.

De este modo, dentro del marco general de la epistemología del número natural estudiaremos las corrientes del convencionalismo, el logicismo y la epistemología genética, con la intención de realizar un análisis epistemológico sobre la secuencia numérica como componente del número en su aspecto ordinal.

 

2.1. Convencionalismo

En filosofía, el convencionalismo es una concepción que señala que las leyes y teorías científicas son convenciones que dependen de una libre elección entre varios modos alternativamente posibles de describir el mundo natural. La aparición de un convencionalismo sistemático en el dominio cognoscitivo se verifica sólo a finales del siglo XIX, tras el descubrimiento de la posibilidad de geometrías no euclidianas cuando desaparece el carácter evidente de los axiomas geométricos. En el ámbito de la matemática se considera a Poincaré como un gran teórico del convencionalismo (Ortiz, 1997).

El convencionalismo trae consecuencias importantes para el aprendizaje de la matemática y, en concreto, para la enseñanza del número. Según Helmholtz (1887/1945):

Podemos considerar los números como una serie de signos arbitrarios elegidos, pero a los cuales les aplicamos un modo determinado de sucesión a título de sucesión regular o, conforme a la expresión habitual, de sucesión natural. El orden de los signos numéricos es tan convencional como el orden de las letras en las diversas lenguas; orden que, una vez adoptado y empleado de una manera constante, toma igualmente una apariencia normal y regular [...]. Se evita la noción de número cardinal y la idea de unidad. La serie ordinal basta para constituir el número (Brunschvicg, 1929, p. 398).

Para los convencionalistas, la adición entra en el marco de la enumeración puramente ordinal. Por ejemplo, a+b designa el término de la serie sobre el que se cae si se cuenta 1 para a+1, 2 para a+2, etc., hasta que se hayan contado b términos. Brunschvicg (1929) dice que Helmholtz fundamenta la teoría de las operaciones aritméticas sin recurrir a la intuición (intuicionismo) ni tampoco tiene en cuenta las teorías lógicas de las construcciones numéricas, pues no hace alusión a la idea de colección de unidades homogéneas.

De este modo, si suponemos que estamos en presencia de un grupo de términos distintos podemos hacer corresponder un signo de nuestra serie ordinal a cada uno de dichos términos. Siempre que no haya laguna ni repetición obtendremos el mismo número, sea cual sea el orden que se asigne a los términos del grupo. La acción de contar es la base de todos los cálculos (Ortiz, 1997).

Las tesis convencionalistas tienen éxito debido al reduccionismo en la tesis de Mill. En este sentido, el origen del número no es sólo la cantidad, sino también la repetición o la combinación. Por citar algunos ejemplos:

– La repetición es temporal, pero secuencial. Podemos hablar de momentos distintos, de cantidades de tiempo y de frecuencias, de tal manera que, aunque sean idénticas, podemos diferenciar en el tiempo las oscilaciones de un péndulo y contarlas; la repetición nos lleva a contar. Las unidades son totalmente idénticas y sólo se distinguen en su distribución temporal. Aquí podemos decir que la repetición y la acción de contar están en íntima relación.

– En lo que se refiere a la combinación, no hay duda que las posibles combinaciones de unos dígitos representan un número.

Helmholtz alude a un parentesco genético directo entre el número y el tiempo, idea que comparten otros grandes pensadores como Kant o Brouwer. Así, en su pequeño tratado Contar y medir, mostraba que el punto de partida del número se sitúa en la sucesión temporal de nuestros estados de conciencia. "Contar es un procedimiento que descansa en nuestra facultad de recordar el orden de sucesión de nuestros estados de conciencia" (Piaget, 1979, p. 76). Basta entonces numerar, mediante un procedimiento verbal convencional, los términos de esta serie para obtener una sucesión de números de orden que permitan definir la suma ordinal por su simple sucesión y la igualdad de los dos números ordinales.

 

2.2. Logicismo

Los modelos lógicos, que explican la construcción del número natural, tienen consecuencias relevantes para nuestro trabajo porque, a través de ellos, podemos situar la secuencia numérica en el marco conceptual de las relaciones ordinales, así como hacer un estudio intrínsecamente ordinal del número natural partiendo del ordinal, sin considerar al cardinal.

Esta corriente epistemológica ofrece un cuadro explicativo de la secuencia numérica que aparece en la siguiente página (Figura 3).

Tanto Dedekind como Peano no están interesados en definir la naturaleza de los términos numéricos, lo cual no sucede con B. Russell. Aquí la discusión central reside en establecer y determinar qué es la secuencia numérica, si bien resulta claro para todo el mundo que son unos términos puestos en relación. Russell, Peano y Dedekind la identifican con las progresiones que generan las relaciones biunívocas; lo único en que difieren es la naturaleza de los términos que se ponen en relación. Para Peano y Dedekind esta no es una cuestión intrínsecamente importante, pero sí lo es para Bertrand Russell, quien insiste en definir los términos que componen una progresión, en particular la de los números naturales mediante los números cardinales.

Dedekind empieza su construcción de los números naturales con la definición de los números ordinales:

Si en la contemplación de un sistema singularmente infinito N, ordenado por una representación, no tenemos en cuenta, por completo, la naturaleza peculiar de sus elementos, reteniendo solamente la posibilidad de distinguirlos, y considerando solamente las relaciones en que se hallan colocados por la representación ordenatriz, entonces esos elementos se llaman números naturales o números ordinales, o simplemente número (Russell, 1982, p. 290)

La definición que establece Dedekind sobre sistema singularmente infinito, contenida en su libro Was sind und was sollen die Zahlen? (2ª edición, 1893, § 71, 1887/1988), es la siguiente:

Es una clase que puede representarse en sí misma por medio de una relación biunívoca, y que además es tal que llega a ser la cadena, respecto a esa relación biunívoca, de un término singular de la clase no contenido en la imagen de la misma (Rusell, 1982, p.290).

Llamando R a la relación biunívoca y N a la clase, existen cuatro puntos en esta definición:

– La imagen de N está contenida en N; es decir, todo término con el que N guarde relación R está en N.

– N es la cadena de uno de sus términos.

– Este término es tal que ningún N tiene la relación R con él.

– La relación Res biunívoca. El sistema abstracto definido simplemente por la posesión de esas propiedades son los números ordinales.

La refutación de Bertrand Russell a esa construcción (que considera, por otro lado, lógicamente correcta) se basa en el hecho de la no–definición explícita de los términos que componen el sistema:

Los ordinales de Dedekind no son elementos. Si no deben ser nada en absoluto deben ser intrínsecamente algo; deben diferir de otras entidades como los puntos de los instantes o los colores de los sonidos (...). Una definición formulada de ese modo indica siempre alguna clase de entidades que tiene una naturaleza genuina propia, y que no depende lógicamente del modo en que han sido definidas (...). Debe recordarse que con la teoría lógica de los cardinales se pueden demostrar tanto los axiomas de Peano como los de Dedekind (Russell, 1982, p. 290).

La teoría de Peano puede ser vista como una axiomatización de la noción de progresión que planteó Russell. Los conceptos indefinidos de Peano son cero, entero finito y sucesor de; por el último entendió siguiente inmediato (Russell, 1982). Su primera teoría apareció en la edición de 1896 de Formulaire de Mathématiques, y fueron probados dos hechos importantes:

1. Hay interpretaciones de los tres conceptos indefinidos que hacen verdaderos todos los cinco axiomas. La primera ley de la aritmética y los teoremas que le siguen también son ciertos (el sistema de Peano fundamenta la aritmética).

2. Peano y uno de sus colaboradores, Padoa, demostraron que los cinco axiomas en cuestión son absolutamente necesarios para elaborar o hacer posible la aritmética. Cada axioma puede ser revisado independientemente de los otros cuatro. Peano y Padoa lo comprobaron por muestreo, al seleccionar grupos de cuatro axiomas entre los cinco propuestos.

Peano reconoce que cualquier colección de términos que cumpla los siguientes requisitos: 1) tiene un primer elemento; 2) no tiene último término; 3) no repite término alguno, y 4) es tal que cualquier término puede ser alcanzado desde el primero en un número finito de pasos, haría verdaderos todos los axiomas. Un sistema que integre una colección de términos y cumpla estas propiedades es lo que llamaremos progresión.

El resultado general de la teoría de Peano es el mismo que el de Dedekind, el primer matemático moderno que propuso una teoría completa sobre las relaciones numéricas en Was sind und was sollen die zahlen (1887). Dedekind identificó los números naturales con los números ordinales, a los que definió como una abstracción de términos a partir de lo que todas las progresiones tienen en común: "Estos elementos se llaman números naturales o números ordinales, o simplemente números" (Dedekind 1988, p. 36).

Históricamente existen objeciones contra la caracterización precedente de los números naturales. La más popular fue planteada por Russell, al señalar que cualquier progresión puede ser tomada como la base de la matemática pura. Nosotros podemos dar el nombre "0" a su primer término, el nombre "número" a todo el conjunto de términos y el nombre "sucesor" al próximo en la progresión. Cada progresión diferente dará una interpretación distinta de toda matemática pura tradicional. En el sistema de Peano no hay nada que distinga a las interpretaciones diferentes de sus ideas primitivas.

La teoría de las progresiones de Bertrand Russell se encuentra estrechamente ligada con la aritmética de Peano. Tratar la secuencia numérica como una progresión supone que todos los términos están entrelazados por relaciones asimétricas transitivas obtenidas a partir de relaciones asimétricas biunívocas y todo estaría dado en términos de "posición relativa", sin entrar a formar parte del sistema la noción de cantidad o cardinalidad de los números. Así, todo lo relacionado con la aritmética finita se puede deducir de tales progresiones:

Suma²

a + 0 = a

a + s_i (n) = s_i (a + n)

Multiplicación

a × 0 = 0

a × s_i (n) = (a × n) + a

A partir de estas definiciones se continúa con la sustracción, división, términos positivos y negativos y fracciones racionales; fácilmente queda demostrado que entre dos fracciones racionales cualesquiera existen siempre una tercera. Así, resulta fácil continuar con los irracionales y con los números reales. Esta es la razón por la que algunos matemáticos como Helmholtz, Dedekind y Kronecker plantearon que los números ordinales son previos a los cardinales, pues se entiende que el número ordinal asociado con cualquier término en una progresión da por perdido el número cardinal de una colección, incluidos los términos dados. Este es el hecho más importante de la teoría de Dedekind, y sugiere que, por lo que pueda ser el número natural, constituye ante todo una progresión.

Sin embargo, Russell afirma que puede demostrarse toda la aritmética tanto de los cardinales como de los ordinales sin mencionar al otro, ya que las proposiciones son simbólicamente idénticas, pero difieren en su significado. Asimismo, dice que no hay ninguna prioridad entre uno y otro porque ambos pueden definirse independientemente, mas una vez definidos uno implica al otro.

Bertrand Russell defiende la idea de que todas las propiedades ordinales o las de las series de números finitos sólo se emplean en la matemática común, y a través de un procedimiento de abstracción se llega a deducir toda la aritmética. Los números forman una progresión, pero no son los que se usan en la vida diaria; el hecho de que sean cardinales los hace verdaderamente importantes.

 

2.3. Epistemología genética

La perspectiva genética del conocimiento es una visión evolutiva sobre los estados de conocimientos, más que de los conocimientos en sí mismos. Desde un punto de vista ontogenético, los conocimientos evolucionan en los sujetos al pasar por diferentes estados que manifiestan competencias operatorias cada vez más completas (Ortiz, 1997).

El sujeto transita de unos estados de conocimiento más primitivos a otros más evolucionados, debido a una progresión hacia una completitud de estructuras: pasa de no poder establecer relaciones con cierta complejidad lógica o matemática a poder establecerlas. La evolución genética individual podemos caracterizarla, desde un punto de vista lógico–matemático, como un pasaje de un no poder establecer una relación a poder establecerla.

Las posturas empiristas, aprioristas o convencionalistas sobre la naturaleza del número no satisfacen a Piaget, quien señala:

Desde las acciones iniciales, las relaciones entre el sujeto y los objetos es un testimonio de un fenómeno mucho más complicado de lo que dejan suponer las interpretaciones empiristas, aprioristas o convencionalistas [...]. La acción de enumerar no puede estar determinada únicamente por los objetos, puesto que ella los estructura en función de un esquema operatorio, que es asimilación de las cosas al doble acto de reuniry ordenar, y puesto que asimilar significa agregar a los objetos caracteres nuevos que no estaban incluidos anteriormente a la acción del sujeto, así la reunión elemental 1+1=2 añade a cada uno de los objetos contados como unidades 1, 1, la nueva propiedad de constituir un todo 2 (Piaget, 1983, p. 128).

Para Piaget, en la evolución de la aritmética son importantes las aportaciones de las acciones intencionadas que realiza el sujeto sobre los objetos. Dichas acciones presentan la doble vertiente de la adaptación cognitiva: asimilación y acomodación. También es primordial captar en sus raíces las conexiones de las construcciones matemáticas nacientes con las estructuras operatorias del sujeto (Piaget, 1983).

La epistemología genética considera, por una parte, que las ideas lógicas sirven como un eficaz punto de partida para elaborar los números; por otra, que la matemática es un sistema de construcciones que apoya sus puntos de partida en las coordinaciones de las acciones y las operaciones del sujeto, las cuales avanzan mediante una sucesión de abstracciones reflexivas de niveles cada vez más elevados (Piaget, 1987).

Piaget apunta que el número es producto de la coordinación de las dos estructuras lógicas: clasificación y seriación. Del mismo modo que ignoramos las diferencias entre los objetos al clasificar un conjunto de ellos, también lo hacemos cuando asignamos al conjunto su número cardinal. Por ejemplo, si vamos a cardinar las muñecas que hay sobre una mesa las consideramos todas iguales, aunque entre ellas haya diferencias de color o tamaño; esto también se realizaría para construir la clase de las muñecas. Así, el número en su aspecto cardinal encierra de manera una componente de clase (Piaget y Szeminska, 1982).

La seriación consiste en contar los objetos del conjunto para calcular su número cardinal. Si bien en el proceso de recuento los objetos son tratados como si fuesen iguales, obviando las características que los diferencian unos de otros, no ocurría si no se tuviera en cuenta un aspecto que hace que los objetos sean tratados como diferentes. En el proceso de determinar el valor cardinal por medio de la enumeración debemos ordenar los objetos: contar primero uno, luego el siguiente y así sucesivamente. Resulta obvio que el orden de la enumeración no tiene importancia, pero sí está claro que debe haber algún orden al momento que se realiza el recuento. Es preciso contarlos en alguna forma de sucesión y tener en cuenta cuáles fueron enumerados en un momento determinado con el fin de no contar más de una vez un mismo objeto.

Este proceso de ordinación³ no es una componente de clase, sino se vincula con la estructura lógica de seriación. Si distribuimos los objetos en el orden en que fueron enumerados estaremos frente a una verdadera serie, ya que los objetos constituyen un encadenamiento aditivo de relaciones asimétricas exactamente análogo a cualquier otra serie. En el caso que nos ocupa, las diferencias entre los objetos que determinan la serie es de posición ordinal (primer objeto contado, segundo objeto contado); determinar cuáles son las diferencias permite llevar a cabo el proceso de recuento, aplicándolo a una colección de objetos tratados desde dos puntos de vista. En un principio todos los objetos son equivalentes o iguales, y por eso una unidad se añade a la otra (igual que una clase se reúne con otra); en un segundo lugar, todos los objetos son vistos como diferentes, lo que nos permite ponerlos en secuencia o serie al aplicarles la enumeración.

De esta concepción del número obtenemos la interrelación entre el aspecto cardinal y ordinal, según la teoría piagetiana de construcción del número natural:

Los números finitos son necesariamente cardinales y ordinales al mismo tiempo, y ello resulta de la naturaleza misma del número, que es ser un sistema de clases y relaciones asimétricas fusionadas en un mismo todo operatorio. Los cardinales resultan así de una abstracción de la relación y esa abstracción no modifica la naturaleza de sus operaciones, puesto que todos los órdenes posibles que pueden atribuirse a n términos se resuelven en la misma suma cardinal n. Por su parte, los ordinales resultan de una abstracción de la clase, abstracción que es también legítima, y por esta misma razón el n–ésimo término finito corresponderá siempre a un conjunto cardinal n. Pero esta doble abstracción de ninguna manera impide que el número entero finito siga siendo uno, ni que implique la indisociable solidaridad de las totalidades y del orden (Piagety Szeminska, 1982, p. 187).

Hay una correlación entre el desarrollo del aspecto cardinal y el ordinal, de tal forma que si un niño se encuentra en la primera etapa, según la génesis del cardinal, también está en la primera etapa de la correspondiente al ordinal y viceversa. Lo mismo sucede con las etapas sucesivas.

A la primera etapa de la seriación, que es pre–ordinal, puesto que el niño no comprende espontáneamente el orden progresivo de los elementos, corresponde (tanto por el promedio de edad en que se efectúa como desde el punto de vista estructural) la primera etapa de la cardinación, o sea, aquella en que no hay ninguna conservación de las cantidades, y en que el niño, cuando debe reproducir una hilera o una figura, no establece una correspondencia término a término sino que se limita a construir otra hilera de la misma longitud u otra de conjunto semejante globalmente a la primera (Piaget y Szeminska, 1982, p. 176).

La convergencia entre el aspecto cardinal y el ordinal del número natural se establece atendiendo, fundamentalmente, a dos cuestiones:

i) La serie numérica (aspecto ordinal) se aplica a una colección de elementos para obtener el número cardinal. A su vez, esa colección de elementos puede estar constituida por una serie, en cuyo caso se establecería una correspondencia serial entre la secuencia numérica y la serie de la que se quiere conocer el número de elementos que posee.

ii) La segunda cuestión que liga el cardinal con el ordinal se basa en que cualquier serie está constituida por un encadenamiento de unidades de esta forma: 1, (1+1), (1+1+1)... Esto implica que avanzar una posición (aspecto ordinal) supone aumentar en uno la cantidad (aspecto cardinal), y recíprocamente, al aumentar en uno la cantidad se avanza una posición.

En los estudios de Piaget se pone a prueba la capacidad del niño para distinguir la posición ordinal en una serie, los valores cardinales que son determinantes de esta posición y determinados por ella, así como la relación entre los valores y la posición.

Cabe aclarar que Piaget y Szeminska (1941/1982) restan todo interés al conteo memorístico y al uso de la secuencia numérica en el niño preescolar porque el concepto de número piagetiano es abstracto (surge del funcionamiento de la abstracción reflexionante) y muy distinto, portante, del concepto práctico o empírico que suele adquirirse precozmente por la abstracción simple. En consecuencia, el conteo conceptual u operatorio es una habilidad que el niño alcanza después de haber consolidado lógicamente la correspondencia biunívoca, la conservación y el número.

Si en nuestro trabajo queremos estudiar el desarrollo de la secuencia numérica en el niño bajo la perspectiva de las teorías lógicas, entonces la trataremos como una serie que tiene la estructura de seriación; aplicaremos el estructuralismo de Piaget a la secuencia numérica como serie (Fernández, 2001). Debido a que el estudio de la estructura lógica de seriación es un análisis genético, el tratamiento de la secuencia numérica como una serie en el sentido piagetiano implica ahondar en las capacidades necesarias que el niño debe manifestar para llegar a establecer las relaciones intrínsecas de un elemento de la secuencia (posición relativa) con todos los demás. Se trataría de estudiar el paso de la seriación a la sistematización de la secuencia mediante las capacidades seriales que el niño necesita aplicar para llegar a dicha sistematización. La expresión sistematización de la secuencia se traduce en la terminología piagetiana como alcanzar el éxito operatorio de la serie, que consiste en construir las relaciones ordinales entre los términos de la secuencia numérica (Fernández, 2001, p. 89).

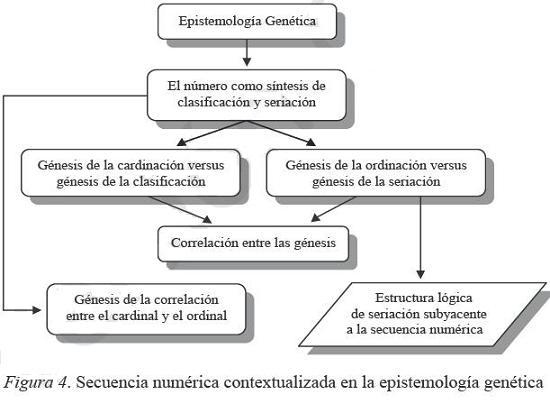
De manera esquemática, todas las explicaciones sobre la construcción del número natural según la epistemología genética, y cómo quedaría enmarcado el estudio de la secuencia numérica en esta corriente, quedan recogidos en el cuadro de la figura 4:

 

3. SECUENCIA NUMÉRICA EN EDUCACIÓN MATEMÁTICA

Los distintos planteamientos sobre los orígenes y naturaleza del número natural implican consideraciones didácticas en las que, algunas ocasiones, prevalece el número ordinal sobre el cardinal, mientras que en otras pasa lo contrario.

Con base en los estudios hechos por Ortiz (1997), la transmisión de la aritmética en España durante el siglo XX contempla tres periodos:

Un primer periodo aritmetista con fundamentación inductivista, pero con un planteamiento didáctico convencionalista; un segundo periodo conjuntista con origen estructuralista, que es deductivista, y un tercer periodo post–conjuntista con intenciones constructivistas. En el período aritmetista se considera la naturaleza inductiva del número natural, primando el aspecto ordinal, y en el periodo conjuntista la naturaleza lógica del número natural prima las clases y el aspecto cardinal. No hemos profundizado en el periodo post–conjuntista, ya que al ser muy reciente aún se encuentra en fase de implantación (Ortiz, 1997, p. 299).

Con respecto a la secuencia numérica (acción de contar) y los periodos encontrados, Ortiz señala:

La acción de contar es resaltada en los periodos estudiados como fundamental en la construcción escolar del número natural, siendo aún más patente en el periodo aritmetista (Ortiz, 1997, p. 299).

Entendiendo el aritmetismo como aquella corriente que considera que el origen del número natural es inductivo, predominando el aspecto ordinal ante el aspecto cardinal (Ortiz, 1997, p. 298).

Con base en el aritmetismo, en Educación Matemática podemos encontrar a autores que fundamentan la didáctica de la aritmética en la secuencia numérica (Abellanas, 1960). Dentro de una tendencia post–conjuntista identificamos la línea de Razonamiento Inductivo Numérico (Ortiz, 1997), que considera a la secuencia numérica como la serie numérica básica por excelencia; en este sentido, la didáctica de la misma se presentaría de acuerdo con el esquema inclusivo (Figura 5).

Por otra parte, en el periodo conjuntista, que coincide con el movimiento de las matemáticas modernas, hallamos dos concepciones distintas para la enseñanza del número natural. Una de ellas es la de Freudenthal (1973 y 1983), quien aboga por la secuencia numérica como base de la didáctica, y la otra es de Dienes (1970), que se basa en el aspecto cardinal.

La figura 6 sintetiza las tendencias en Educación Matemática sobre la didáctica del número natural, basada en la secuencia numérica.

La didáctica del número natural en el periodo aritmetista ya ha sido tratada en este mismo apartado. Podemos añadir lo que se indicó en el punto relativo a la corriente epistemológica del convencionalismo, cuando especificamos que la acción de contar es la base de todos los cálculos, al partir de una serie de signos arbitrariamente elegidos, pero ordenados (Helmholtz, 1945).

El periodo post–conjuntista, donde nos encontramos en la actualidad, marca el predominio del aspecto ordinal del número natural en un contexto epistemológico y escolar totalmente aritmetista. Debemos resaltar en Educación Matemática las investigaciones hechas en la Universidad de Málaga sobre Razonamiento Inductivo Numérico (Ortiz, 1997) y Relaciones Lógicas Ordinales entre los términos de la secuencia numérica (Fernández, 2001). Para el inductivismo numérico, el origen ontogenético debe estar en la construcción individual de la secuencia numérica en su perspectiva ordinal; para el marco de las relaciones lógicas ordinales, la didáctica del número natural tiene que basarse fundamentalmente en el aspecto ordinal, y generar toda la secuencia a partir de dichas relaciones.

Es importante destacar cómo en el periodo conjuntista se ha abordado el número natural en Educación Matemática desde dos frentes distintos: uno el aspecto ordinal y otro el aspecto cardinal. Dentro del ámbito escolar se ha desarrollado fundamentalmente el aspecto cardinal, pero en este punto son relevantes las declaraciones de Freudenthal (1983) cuando manifiesta que esto precisamente llevó al fracaso de las matemáticas modernas en el periodo señalado; él aboga por el número para contar como base para toda la Didáctica de la Matemática. Por otra parte, Dienes (1970) es un claro defensor del aspecto cardinal para la enseñanza–aprendizaje del número natural.

Para Freudenthal, la secuencia numérica es el pilar fundamental de las matemáticas. Portanto, entre las distintas concepciones del número que atienden a su fenomenología prevalece con gran relevancia el número para contar, al que se considera como el devanado en el tiempo de la secuencia de números naturales. "El número para contar es matemáticamente llamado el número ordinal; es formalizado mediante la inducción completa y los axiomas de Peano" (Freudenthal, 1983).

Freudenthal prefiere al número para contar en Educación Matemática en vez del número para cardinar por los siguientes motivos: 1) contar llega pronto a convertirse en una necesidad teórica para el niño, quien llega a utilizar el conteo más allá de lo que sus propias necesidades prácticas le exigen; 2) contar es la base de la aritmética más elemental; 3) el contar es una actividad no sólo para obtener el número cardinal de un conjunto, sino también una actividad rítmica en el tiempo; 4) el concepto y así sucesivamente es operatorio en toda la instrucción aritmética, así como en todas las reglas que se aprenden; 5) el número para cardinar es matemáticamente insuficiente; 6) el aspecto cardinal de los números naturales es irrelevante en comparación con el aspecto del conteo; 7) el aspecto cardinal es insuficiente para la didáctica de los números naturales.

No hay ninguna duda de que la importancia del aspecto cardinal en la psicología se ha debido a Piaget, aunque Freudenthal (1983) lo critica con base en los siguientes puntos:

– Piaget estudió el concepto de número bajo el aspecto cardinal. Creía que el concepto de número natural se puede derivar totalmente de las potencias; matemáticamente puede ser esto cierto, pero creyó que también lo era psicológicamente. No obstante, aquí interviene la cuestión, ya planteada, de que el aspecto cardinal del número natural es matemáticamente insuficiente.

– Cuando trata el número ordinal bajo este enfoque no tiene nada que ver con el número ordinal ni con el número para contar. Es tal su indiferencia hacia el conteo que no menciona si los niños entrevistados saben contar y hasta dónde pueden llegar.

En consecuencia, las didácticas basadas en la teoría de Piaget, según Freudenthal, no consideran el número para contar, con lo que dejan de lado a los juegos de conteo en el afán de calcular sistemáticamente el número de objetos de las colecciones, que no varía ante las transformaciones espaciales, debido a la exagerada importancia que se otorga al aspecto cardinal. De este modo, un primordial eslabón entre la aritmética mental y la escrita, como el hecho de interpretar las sumas al contar hacia adelante y las restas al contar hacia atrás, es simplemente olvidado.

Otra visión diferente es la de Dienes, quien aboga por una didáctica basada en el aspecto cardinal. Su teoría de Dienes parte de la siguiente concepción de número: "El número es una propiedad de los conjuntos" (1970, p. 32). Por tanto, siguiendo a Bertrand Russell, cuando Dienes ocupa el término número en realidad está haciendo mención a número cardinal; su didáctica está basada en la cardinalidad o aspecto cardinal del número natural, cuya base es el concepto de equipotencia de Cantor.

La didáctica de Dienes se sustenta en la equipotencia entre conjuntos, es decir, en el aspecto cardinal del número. Plantea que la secuencia numérica debe ser aprendida desde la perspectiva cardinal, de ahí que se deba hacer caso omiso al conocimiento que los niños pudieran tener sobre su recitado. Indica que hay que comparar dos términos consecutivos a través de la cantidad de elementos que representa cada uno para comprobar que difieren en un único elemento (noción igualmente cardinal). Portanto, el siguiente de un término en la secuencia representa aumentar en uno la cantidad precedente.

En el periodo post–conjuntista es preciso tomar en cuenta las teorías de Procesamiento de la Información, donde el análisis de la secuencia numérica pasa a ser considerada como una componente del conteo. La teoría cardinal parece se sobrepone de manera más clara que la ordinal en todos los razonamientos en torno a los orígenes psicológicos del número.

Las investigaciones realizadas en psicología han demostrado que los niños manejan la secuencia numérica desde muy temprano (Fuson, 1988; Gelman y Gallistel, 1978; Sarnecka y Gelman, 2004), pero es posible que sólo sepan que la secuencia de conteo se compone de números y que éstos han de repetirse siempre en el mismo orden (Baroody, 1988), sin que por ello se infiera una cierta comprensión conceptual como, por ejemplo, que el orden de emisión de los términos de la secuencia se mantiene constante a lo largo de sucesivas aplicaciones de la misma, o que cada elemento de la lista es único (Fuson, 1988).

Un gran número de investigaciones (Fuson, 1988; Fuson y Hall, 1983; Gelman y Gallistel, 1978; Saxe, 1979; Song y Ginsburg, 1988; Wagner y Walters, 1982) se dirigen a estudiar la adquisición y conceptualización de la secuencia numérica por parte del niño pequeño. Otros trabajos han demostrado que la habilidad de contar no tiene una meta en sí misma, sino se trata de un comportamiento instrumental, esto es, de una estrategia extraordinariamente potente en el desarrollo matemático del niño. En tal sentido, se ha investigado la capacidad de los niños para resolver problemas donde el conteo se usa como procedimiento (Cowan, 1996; Fuson y Hall, 1983; Sophian, 1995).

En esta línea de trabajo hemos de destacar los estudios que observan cómo el niño utiliza la secuencia numérica para determinar el cardinal de una colección o conjunto: Gelman y Gallistel (1978) establecen el principio de cardinalidad; Klarhr y Wallace (1973) analizan al conteo como "operador cuantificador", mientras que Schaeffer, Eggleston y Scott (1974) determinan cuatro estadios diferenciados hasta que el niño logra el uso funcional del conteo para calcular el cardinal de un conjunto con menos de 10 elementos.

Las investigaciones en las teorías procesuales tratan profundamente el aspecto cardinal del número natural y no atienden al aspecto ordinal. La mayoría de los trabajos con relación al carácter funcional del conteo en su "ordinalidad" llevan como soporte mental la "cardinalidad", ya que estudian comparaciones ordinales cuantitativas. Cada número de la secuencia representa a priori el cardinal de un conjunto para que después se realice la comparación entre los términos. Dicha comparación se da entre magnitudes, no en cuanto a su posición en la secuencia numérica (Fernández, 2001).

 

4. POSICIONAMIENTO DE LA AUTORA

Como se ha indicado anteriormente, los modelos lógicos —que explican la construcción del número natural— tienen consecuencias muy importantes para nuestro trabajo, ya que a través de ellos podemos situar la secuencia numérica en el marco conceptual de las relaciones ordinales, así como realizar un estudio intrínsecamente ordinal del número natural que parte del ordinal, sin considerar el cardinal.

Con base en estos modelos he definido a la secuencia numérica del siguiente modo: "Es una progresión dada por la relación generatriz de Bolzano, es decir, una progresión en el sentido de Bertrand Russell" (Fernández 2001, p. 22). La definición se emplea para alcanzar la solución del problema planteado: llegar a una construcción lógica de la secuencia numérica en un contexto ordinal dado por un sistema de relaciones lógicas existente entre sus términos, que omita el significado cardinal de cada uno de ellos.

Esta caracterización de la secuencia se elige frente a las que puedan extraerse de otras posturas aquí presentadas, ya que nos permite concretar las relaciones lógicas ordinales, mediante las relaciones asimétrica y biunívocas de Bolzano, y las asimétricas transitivas de Vivanti: siguiente inmediato, siguiente, entre, entre inmediato, primer elemento, primer y último elemento (Fernández, 2001, p. 24).

Por otra parte, el origen del conteo en el niño está supeditado a relaciones lógicas–ordinales que se desarrollan en el proceso de construcción mental del número natural, y están implícitas en todas las construcciones matemáticas de la aritmética. Ahora bien, muchas de esas relaciones se han considerado en las investigaciones en psicología infantil sin la trascendencia que precisan, ya que el aspecto cardinal del número natural se ha entendido como soporte del aspecto ordinal. El conteo se ha utilizado para obtener el cardinal de colecciones numerables, no para lograr el término de una serie o el lugar que ocupa un término en relación con otro; su empleo ha sido tratado básicamente desde un punto de vista acumulativo (Fernández y Ortiz, 2008).

 

5. CONCLUSIONES/ SÍNTESIS

Si recapacitamos en la relación entre la interpretación y la construcción del conocimiento ordinal de la secuencia numérica en el niño (Geary, 2006; Geary, Hoard, Byrd–Craven y Desoto, 2004), los modelos ordinales del número natural y los casos notables de las relaciones que generan series, se llega a la conclusión de que dicho conocimiento no se aplica en el vacío. Es decir, subyace en la sucesión de términos numéricos un entramado de relaciones lógicas ordinales que hacen posible la construcción del número natural en su aspecto ordinal.

Como se ha puesto de manifiesto en el análisis logicista de la secuencia numérica, a ella se llega mediante las relaciones ordinales que surgen en un sistema de progresiones. Por tanto, la secuencia numérica, independientemente de la naturaleza de sus términos, tienen un soporte conceptual ordinal para construirla.

Varios planteamientos epistemológicos coexisten sobre el número natural que condicionan el significado de construcción de la secuencia. Estos son:

– La postura convencionalista, basada en los aspectos ordinales para construir el número natural. El soporte inicial es la acción de contar y la verbalización de la secuencia numérica. Para este enfoque, que parte de la estructura superficial sin considerar a la estructura profunda, los numerales y los signos numéricos son convenciones o normas que actúan mediante unos criterios.

– La secuencia numérica en el seno de la corriente logicista se desarrolla dentro del sistema de progresiones que, según Bertand Rusell (1982), coincide con el sistema de Peano y con el de Dedekind. Las relaciones ordinales y el número ordinal bastan para desarrollar la secuencia y el número natural. Existen modelos para construir la secuencia numérica que no precisan de la definición previa de los términos numéricos y, por tanto, son independientes del número cardinal.

– Para la epistemología genética, el número natural es una síntesis de dos estructuras operatorias: clasificación y seriación. Como consecuencia, el número es cardinal y ordinal, de ahí que se construyan ambos aspectos de modo simultáneo; por ello hay la correlación entre ambas génesis. La estructura operatoria de seriación deriva en la ordinación⁴ y, entonces, el tratamiento de la secuencia numérica es el de una serie.

Las diferentes posiciones epistemológicas ante el número natural condicionan la transmisión escolar de la aritmética, pero en todos los casos la secuencia numérica resulta importante para su aprendizaje. Aquí nos encontramos con prioridades opuestas:

– Prioridad del número ordinal. Con base en la fenomenología de Freudenthal, el número para contar es el pilar en el que se sustenta toda la matemática y también su didáctica, mientras que el número para cardinar resulta matemática y didácticamente insuficiente (Freudenthal, 1973, p. 171).

– Prioridad del número cardinal. Se intenta una construcción lógica de la aritmética a partir de las nociones previas a la de número; por ejemplo, la de conjuntos. La secuencia numérica se obtiene como una sucesión de números cardinales, mientras que el tratamiento didáctico de siguiente de un número aumenta en uno la cantidad. Dienes defiende este modelo.

Las principales conclusiones de nuestro estudio se pueden resumir en los siguientes puntos:

I. Secuencia numérica y relaciones lógicas ordinales en el origen del número natural.

C1 Que los números naturales están dados en secuencia es el único punto incuestionable en todas las teorías explicativas del origen del número. La interpretación de su papel elaborador depende de la concepción epistemológica del número natural.

C2 Para el convencionalismo, el principio del número radica en la secuencia numérica y en la acción de contar; la serie ordinal es suficiente para construir el número.

C3 Para los logicistas existen conceptos primarios que determinan la secuencia numérica y, por tanto, el número. Estos tienen como referencia a las relaciones seriales⁵, como las asimétrica–biunívocas de Bolzano o las asimétricas–transitivas de Vivanti–Gilman.

C4 Desde la epistemología genética, el problema tocante a la construcción de la secuencia numérica sólo puede ser resuelto en función de su desarrollo.

II. Secuencia numérica y enseñanza del número en la escuela.

C5 Las distintas interpretaciones epistemológicas sobre la secuencia numérica se han reflej ado en la enseñanza del número en la escuela. Así. los planteamientos conjuntistas introducen los conceptos de cardinal y de correspondencia, con lo cual se producen intentos por reducir la aritmética a la lógica y el número natural a las clases, mientras que los planteamientos aritmetistas abogan por el número ordinal (Ashcraft, 1982; Brannon, 2002).

C6 En cuanto al número cardinal, se intenta una construcción lógica de la aritmética a partir de la noción de conjuntos. La secuencia numérica se obtiene como una sucesión de números cardinales, y el tratamiento didáctico de siguiente de un número aumenta en uno la cantidad.

C7 Con respecto al número ordinal, se intenta que la secuencia numérica⁶ sea matemática y didácticamente suficiente.

Con todo ello podemos indicar que se cumple lo siguiente:

– Existen corrientes epistemológicas que consideran a las relaciones lógicas ordinales del número natural como el origen de toda la construcción matemática (Dedekind, 1988; Peano, 1979; Russell, 1982).

– Hay líneas en Didáctica de la Matemática que privilegian el aspecto ordinal del número natural frente a su aspecto cardinal.

En definitiva, podemos considerar algunos objetivos clave para la didáctica del número natural con escolares de 3 a 6 años:

– Conseguir la integración de las habilidades y rutinas presentes en la acción de contar en estrategias que manifiesten algún tipo de relación lógica ordinal entre los términos numéricos.

– Estudiar el tipo de relaciones que los niños utilizan para secuenciar los números.

– Analizar la correlación real entre el recitado correcto de la secuencia numérica y la construcción de las relaciones lógicas ordinales en el niño.

– Establecer las operaciones aritméticas con base en un recuento progresivo que se base en las relaciones ordinales presentes en la secuencia numérica.

Por último, para abordar la operacionalización didáctica de las definiciones de secuencia numérica y relaciones lógicas ordinales, nos remitimos a la investigación que presentan Fernández y Ortiz (2008).

Siempre es posible encontrar un contexto ordinal adecuado para explorar la secuencia numérica y las relaciones ordinales en niños de temprana edad. Hemos de buscar situaciones que nos permitan observar un empleo ordinal de la acción de contar por parte de los niños para poder demostrar que, paralelamente a una construcción cardinal, hay una ordinal del número natural. Se trata de hacer un uso ordinal de la secuencia.

Ahora bien, si proponemos al niño tareas donde tenga que determinar la posición ordinal de un elemento en un conjunto contable a través de la secuencia numérica, sólo evaluaremos las competencias ordinales del sistema mediante su uso. Dichas tareas son relevantes para nuestro estudio frente a otras en las que el recitado de la secuencia numérica puede ser memorístico, ya que si ponemos al niño simplemente a contar objetos nos resultará difícil evaluar si establece o no relaciones lógicas entre sus términos. O bien, si proponemos las habituales tareas de comparación de magnitudes evaluaremos el isomorfismo entre la cardinalidad y la ordinalidad (a es mayor que b si y sólo si a es posterior a b, y a es menor que b si y sólo si a es anterior a b), pero nos alejaríamos de nuestro objetivo, que consiste en comparar de dos términos cualesquiera de la secuencia a través de su posición ordinal.

Este tipo de tareas sobre el uso funcional ordinal de la secuencia numérica supone la aplicación práctica, mediante la acción de contar las propiedades internas del sistema: los términos de la secuencia numérica y operaciones lógicas ordinales entre ellos. En Fernández y Ortiz (2008) se analiza la evolución de las relaciones lógicas–ordinales en un grupo reducido de niños seleccionados al azar, donde se proporcionan las siguientes orientaciones a los maestros, teniendo en cuenta para cada edad las competencias o habilidades a conseguir en función de las relaciones lógicas ordinales:

Clase de 3 años: Los niños de 3 años en general no tienen en cuenta el dato, por ello la competencia o habilidad lógica ordinal sería localizar posiciones ordinales. Una actuación concreta en el aula, atendiendo a la competencia dada, sería: "Se presentan filas de objetos. El niño tiene que averiguar el primero, el quinto, etc. Recíprocamente, se dan unas posiciones ordinales y el niño tiene que distinguir a qué objeto de la fila corresponden ".

Clase de 4 años: Estos niños tienen en cuenta el dato, por lo que pueden desarrollar la competencia de "localizar posiciones lógicas ordinales ".

Clase de 5 años: La característica fundamental en esta clase es que ya no dependemos de objetos tangibles. No se presentan filas de objetos, sino se manejan con la secuencia numérica, ya que los niños han conseguido el éxito operatorio en las relaciones lógicas ordinales que hay entre los términos de la secuencia numérica, lo cual permite realizar estas actuaciones en el aula:

– Localizar el siguiente y el anterior de cualquier número entre 1 y 10.

– Contar a partir de un término.

– Contar a partir de un término hasta llegar a otro.

– Contar a partir de un término a n–términos.

En definitiva, nuestra investigación cambia las competencias básicas en el aspecto de conteo. Así, la habilidad "recitado memorístico de la secuencia numérica" se cambia por las competencias en función de las relaciones lógica–ordinales que se dan entre los términos numéricos: "si en a ocurre tal cosa, ¿qué ocurre en bV Algunas de estas competencias serían:

– Determinar todos los posteriores de a hasta llegar a b (primer y último elemento).

– Determinar todos y cada uno de los términos de la secuencia del tramo a, b (entre).

– Tener un elemento generatriz de la serie sobre el cual razonar inductivamente (primer elemento).

– Determinar los "siguientes" mediante el "siguiente inmediato", y recíprocamente.

– Determinar el "siguiente inmediato" conociendo los siguientes.

El dominio de la secuencia numérica es significativo desde el punto de vista que concierne a los modelos ordinales de la lógica formal del número natural: las competencias ordinales que manifiestan los niños están en relación con los axiomas de los modelos ordinales del número natural.

De acuerdo con los resultados descritos, hemos dado un pequeño paso aclaratorio en la dirección que plantea Geary D. C. (2006, p. 804) para conocer cómo los niños aprenden matemáticas en la escuela (Fernández y Ortiz, 2008, p. 129).

 

REFERENCIAS BIBLIOGRÁFICAS

Abellanas, P. (1960). Introducción a la matemática. Madrid: Saeta.        [ Links ]

Ashcraft, M. H. (1982). The Development of Mental Arithmetic: a Chronometric Approach. Developmental Review 2, 213–136.        [ Links ]

Baroody, A. J. (1988). El pensamiento matemático de los niños. Madrid: Aprendizaje Visor.         [ Links ]

Bolzano, B. (1851). Paradoxien des Unendlichen. Lepizig: C.H. Reclam.         [ Links ]

Brannon, E. M. (2002). The Development of Ordinal Numerical Knowledge in Infancy. Cognition. International Journal of Cognitive Science 83 (2), 223–240.        [ Links ]

Brunschvicg, L. (1929). Las etapas de la filosofía matemática. Buenos Aires: Lautaro.         [ Links ]

Cantor, G. (1955). Contributions to the Founding of the Theory of Transfinite Numbers. New York: Dover.        [ Links ]

Cassirer, E. (1979). El problema del conocimiento. México: Fondo de Cultura Económica.         [ Links ]

Cowan, R. (1996). Even More Precisely Assessing Children's Understanding of the Order–Irrelevance Principle. Journal of Experimental Child Psychology 62 (1), 84–101.         [ Links ]

Dedekind, R. (1988). Was sind und was sollen die Zahlen? Veweg: Braunschwieg (versión original: 1887).        [ Links ]

Dienes, Z. P. (1970). La construcción de las matemáticas. Barcelona: Vicens Vives.         [ Links ]

Fernández, C. (2001). Relaciones lógicas–ordinales entre los términos de la secuencia numérica en niños de 3 a 6 años. Tesis de doctorado no publicada, Universidad de Málaga.         [ Links ]

Fernández, C. (2003). Pensamiento numérico y su didáctica (3–6 años). Málaga: Dykinson, S. L.         [ Links ]

Fernández, C. y Ortiz, A. (2008). La evolución del pensamiento ordinal en los escolares de 3 a 6 años. Infancia y Aprendizaje 31 (1), 107–130.        [ Links ]

Frege, G. (1972). Fundamentos de la artimética. Madrid: Laia (versión original: 1884).         [ Links ]

Freudenthal, H. (1983). Didactical Phonomenology of Mathematical Structures. Dordrecht: D. Reidel Publishing Company.         [ Links ]

Freudenthal, H. (1973). Mathematicsas as an Educational Task. Dordrecht: D. Reidel Publishing Company.        [ Links ]

Fuson, K. (1988). Children's Counting and Concepts of Number. New York: Spring er–Verlag.         [ Links ]

Fuson, K. & Hall, J. (1983). The Acquisition of Early Number Word Meanings: A Conceptual Analysis and Review. In H. Ginsburg (Comp.), The Development of Mathematical Thinking (pp. 49–107). New York: Academic Press.         [ Links ]

Geary, D. C. (2006). Development of Mathematical Understanding. In W. Damon & R. Lerner et al. Handbook of Child Psychology. Cognition, Perception and Language (Vol. 2, pp. 777–810): New York: Wiley.         [ Links ]

Geary, D. C., Hoard, M. K., Byrd–Craven, J. & Desoto, M. C. (2004). Strategy Choices in Simple and Complex Addition: Contributions of Working Memory and Counting Knowledge for Children with Mathematical Disability. Journal of Experimental Child Psychology 88 (2), 121–151.        [ Links ]

Gelman, R. & Gallistel, C. R. (1978). The Child's Understanding of Number. Cambridge: Harvard University Press.         [ Links ]

Grize, J. B. (1979). Observaciones sobre la epistemología matemática de los números naturales. En J. Piaget, et al., Tratado de lógicay conocimiento científico (Vol. II, Epistemología de la lógica, pp. 109–120). Buenos Aires: Paidós.         [ Links ]

Helmholtz, F. (1945). Las etapas de la filosofía matemática. Buenos Aires: Lautaro (versión original: 1887).        [ Links ]

Klhar, D. & Wallace, J. G. (1973). The Role of Quantification Operators in the Development of Conservation. Cognitive Psychology 4, 301–327.        [ Links ]

Mill, J. S. (1917). Sistema de lógica inductiva y deductiva. Madrid: Daniel Jorro Editor.         [ Links ]

Ortiz, A. (1997). Razonamiento Inductivo Numérico. Un estudio en educación primaria. Tesis de doctorado no publicada, Universidad de Granada.        [ Links ]

Peano, G. (1896). Formulaire de mathématiques. Turín: Bocca Fréres, Ch. Clausen.         [ Links ]

Peano, G. (1979). Los principios de la arimética. Oviedo: Clásicos El Basilisco.         [ Links ]

Piaget. J. (1987). La epistemología genética. Madrid: Debate.         [ Links ]

Piaget. J. (1983). Introducción a la epistemología genética (Tomo I, El pensamiento matemático). Buenos Aires: Paidós.         [ Links ]

Piaget, J. (1979). Tratado de lógica y conocimiento científico. Epistemología de la matemática. Buenos Aires: Guadalupe.         [ Links ]

Piaget, J. y Szeminska, A. (1982). Génesis del número en el niño. Buenos Aires: Guadalupe (versión original: 1941).         [ Links ]

Russell, B. (1982). Los principios de la matemática. Madrid: Espasa–Calpe (versión original: 1903).         [ Links ]

Sarnecka, B. W. & Gelman, S. A (2004). Six does not Just Mean a lot: Preschoolers see Number Words as Specific. Cognition 92, 329–352.         [ Links ]

Saxe, G. (1979). Developmental Relations Between Notational Counting and Number Conservation. Child Development 50, 180–187.         [ Links ]

Schaeffer, B., Eggleston, V. H. & Scott, J. L. (1974). Number Development in Young Children. Cognitive Psychology 6, 357–379.         [ Links ]

Song, M. J. & Ginsburg, H. P. (1988). The Effect of the Korean Number System on Young Chidren's Counting: a Natural Experiment in Numerical Bilingulism. Internatinal Journal of Psychology 23,319–332.         [ Links ]

Sophian, C. (1995). Representation and Reasoning in Early Numerical Development: Counting, Conservation and Comparisons Between Sets. Child Development 66 (2), 559–577.         [ Links ]

Wagner, S. & Walters, J. A. (1982). A Longitudinal Analysis of Early Number Concepts: From Numbers to Number. In G. Forman (Comp.). Action and Thought (pp. 137–161). New York: Academic Press.        [ Links ]

 

Notas

¹ Una progresión de Bertrand Russell es una serie discreta que tiene términos consecutivos, comienzo pero no fin, y que además es conexa.

² Por s_i(n) se entiende el siguiente inmediato de n que sería n + 1

³ El término ordinación pertenece a la terminología piagetiana: ordinación versus cardinación.

⁴ Terminología usada por Piaget para referirse al aspecto ordinal.

⁵ Relaciones que generan series o progresiones.

⁶ Se identifica, según la fenomenología de Freudenthal, con el número para contar.