Artículos

 

Hacia un nuevo paradigma en la enseñanza del Cálculo dentro de una institución educativa

 

Towards a new paradigm in teaching calculus at an educational institution

 

Patricia Salinas* y Juan Antonio Alanís**

 

* Departamento de Matemáticas. Instituto Tecnológico y de Estudios Superiores de Monterrey, Campus Monterrey, México; npsalinas@itesm.mx

** Departamento de Matemáticas. Instituto Tecnológico y de Estudios Superiores de Monterrey, Campus Monterrey, México; juan.antonio.alanis@itesm.mx

 

Recepción: Diciembre 4,2008
Aceptación: Agosto 31, 2009

 

RESUMEN

Estudios de reconocidos investigadores sobre la problemática de la enseñanza y aprendizaje del Cálculo nos permiten reconocer un paradigma tradicional de enseñanza, el cual ha sido practicado en la institución educativa a la que pertenecemos. La revisión de diversos artículos en torno a alternativas de enseñanza nos sugiere tendencias en la manera como se proponen cambios; algunos sólo afectan a la forma de enseñar, otros reparan en el contenido a enseñar. Observamos que recurrir a la historia de la génesis del conocimiento ha permitido identificar en el contenido matemático del currículo una variable que influye en la apropiación de las nociones y procedimientos del Cálculo. En cierto momento, el qué enseñarse integra al cómo enseñar y cobra un sentido didáctico la presencia de la actividad matemática en el aula. En el marco del acercamiento socioepistemológico ubicamos el surgimiento de una propuesta para la enseñanza del Cálculo, cuya implantación en la institución educativa en cuestión asume a la investigación como sustento.

PALABRAS CLAVE: Cálculo, enseñanza del Cálculo, Socioepistemología.

 

ABSTRACT

Studies by renowned investigators on the problematic of teaching and learning calculus enable us to recognize the traditional teaching paradigm that has been practiced in the educative institution to which we belong. The revision of diverse articles on teaching alternatives suggests tendencies in the way changes are proposed; some only affect the teaching method, others consider the content to be taught. We observe that resorting to the history of the genesis of knowledge has permitted the identification of a variable in the mathematical content of the curriculum which influences the acquisition of the notions and procedures of calculus. At some point, the what to teach becomes part of how to teach and from there mathematics activity takes on a didactic sense in the classroom. In the framework of the socio–epistemological approach we find the emergence of a proposal for the teaching of calculus, which implementation in the educative institution in question is based on research.

KEYWORDS: Calculus, teaching of Calculus, Socioepistemology.

 

RESUMO

Estudos de investigadores reconhecidos sobre a problemática do ensino e aprendizagem de Cálculo permitem–nos reconhecer um paradigma tradicional de ensino, que tem sido praticado na instituição educativa a que pertencemos. A revisão de vários artigos sobre alternativas de ensino sugere tendências na forma como são propostas mudanças, algumas das quais só afetam a forma de ensinar, outras dão atenção ao conteúdo de ensino. Constatamos que o recurso à historia da gênese do conhecimento tem permitido identificar no conteúdo matemático do currículo uma variável que afeta a apropriação das noções e procedimentos de cálculo. Num certo momento, o que ensinar se integra no como ensinar, o que leva a presença da atividade matemática em sala de aula a assumir um sentido didáctico. No quadro da abordagem socioepistemológica situamos o surgimento de uma proposta para o ensino de Cálculo, cuja implantação na nossa instituição de ensino assume a pesquisa como base.

PALAVRAS CHAVE: Cálculo, ensino do Cálculo, Socioepistemologia.

 

RÉSUMÉ

Les travaux de chercheurs reconnus dans leur domaine ayant pour thème la problématique de l'enseignement et de l'apprentissage du calcul nous permettent de mettre à jour un paradigme traditionnel dans l'enseignement, celui qui a été utilisé au sein de l'institution éducative dont nous faisons partie. L'étude de plusieurs articles consacrés à l'enseignement alternatif semble nous montrer des tendances en ce qui concerne les formes adoptées pour proposer des changements. Ces derniers ne modifient parfois que la forme de l'enseignement alors que d'autres articles abordent le contenu de l'enseignement. Et nous observons que le fait d'avoir recours à l'histoire de la genèse de la connaissance nous permet d'identifier dans les contenus mathématiques du programme une variable qui influe sur l'intégration des notions et des processus entrant dans le domaine du calcul. A un certain moment, le quoi enseigner est incorporé au comment enseigner. C'est à partir de là que l'existence de l'activité mathématique en classe acquiert un sens didactique. Dans le cadre d'une approche socio–épistémologique, nous situons done à un moment précis l'apparition d'une proposition pour enseigner le calcul dont l'application dans l'institution educative en question est fondee sur la recherche.

MOTS CLÉS: Calcul, enseignement du Calcul, Socioépistémologie.

 

1. INTRODUCCIÓN

La investigación educativa relacionada con la matemática ha adquirido su dimensión propia, ya que genera conocimiento al responder a preguntas que se formulan con el propósito de entender lo que ocurre cuando el contenido matemático se instala en el sistema escolar para convertirse en objeto de enseñanza y aprendizaje. Al principio resultó simple pensar que con el conocimiento de la matemática y ciertas habilidades pedagógicas bastaban para ejercer la práctica docente. Actualmente se reconoce que la problemática adquiere tintes muy particulares que conciernen a aspectos cognitivos (cómo se aprende), didácticos (cómo se enseña) y epistemológicos (cómo se concibe el saber a enseñar y aprender). Esto se sitúa en el entorno social que enmarca la interacción entre el contenido matemático, los estudiantes y el profesor (dónde se enseña–aprende).

La acción de intervenir eficazmente en el sistema didáctico para mejorar el aprendizaje de las matemáticas excede al simple proceder de buena voluntad. Más bien, exige el compromiso de profundizar en el conocimiento de la problemática y hacer de la práctica docente cotidiana un espacio de reflexión sobre el saber adquirido. Este trabajo intenta ofrecer elementos que inciten al lector a dicha meditación, al ubicar el surgimiento de una propuesta para la enseñanza del Cálculo que, apoyada en la investigación, se ha estado abriendo camino en una institución educativa que promueve la innovación.

Consideramos que, a través de la literatura tocante a la investigación y prácticas educativas que han estado gestándose, podemos transmitir a la comunidad de investigadores el debate que tal propuesta ha experimentado entre las posiciones que cuestionan el cómo enseñar y las que inquieren qué debe enseñarse en Cálculo. Nuestra posición sostiene que es determinante propugnar por interrogantes tanto sobre el contenido del Cálculo como sobre la forma en que el contenido se estructura y enseña.

Una revisión a diferentes estudios que sistematizan resultados a escala mundial sobre el proceso de enseñanza–aprendizaje nos permitió reconocer que, en la institución educativa de la que formamos parte desde 1990, ha sido practicado lo que puede llamarse un modelo tradicional de enseñanza del Cálculo. Caracterizaremos este paradigma de enseñanza normalizado en las aulas, cuyos alcances de aprendizaje están fuertemente cuestionados, como lo muestran investigaciones hechas en diferentes instituciones donde se puede identificar dicho enfoque.

Tras analizar diferentes propuestas de cambio, nos percatamos que puede hacerse una clasificación si diferenciamos cuándo —de manera declarada o no— se está buscando transformar el cómo se enseña el contenido tradicional del Cálculo (el modo) y cuándo las acciones están afectando el contenido, el qué enseñar. Sin pretender ser exhaustivos, reseñaremos algunos reportes con el fin de organizar la discusión sobre la búsqueda de alternativas que conlleven a mejorar la enseñanza del Cálculo, distinguiendo el grado en que se afecta la forma de enseñar y/o el contenido a enseñar.

De este modo, identificaremos reportes que cuestionan el qué enseñar por su contacto con la génesis del conocimiento matemático, lo cual, a nuestro juicio, permite a los investigadores ampliar su visión del objeto de enseñanza; tal perspectiva rescata el papel de la matemática como actividad humana que se relaciona con la necesidad de dar solución a problemas reales. Conocer la historia de cómo surgen las nociones invita a que ese significado se integre a experiencias donde la actividad matemática es parte fundamental del aprendizaje.

Asimismo, desde este enfoque resaltaremos investigaciones de corte histórico–epistemológico que amplían las posibilidades de intervenir en el proceso de enseñanza del Cálculo, como respuesta al carácter social de la construcción del conocimiento. El énfasis en las prácticas sociales que dan sentido al surgimiento de las nociones y procedimientos del Cálculo sugiere un cambio de modelo de enseñanza, en el que se correspondan mutuamente tanto el contenido como la forma en que se pretende que sea aprendido.

Este panorama nos permitirá ubicar en la matemática educativa a una propuesta para la enseñanza del Cálculo en nuestra institución educativa, cuyo diseño surgió en 1996 como consecuencia de las tesis doctorales de Alanís (1996) y Pulido (1997). La propuesta se ha estado nutriendo del nuevo conocimiento generado en el área y su consolidación es una meta a la que responde la investigación doctoral de Salinas, que actualmente está en curso.

De acuerdo con Artigue, hay diversas razones que obligan en la actualidad a repensar la manera en que el Cálculo (Análisis) es enseñado; la situación actual se caracteriza por un "sentimiento general de crisis que parece trascender diferencias culturales" (2003, p. 214). La investigación, aclara, ofrece mucho en qué reflexionar, pero también tiene limitaciones por su vinculación con la complejidad del proceso educativo.

La investigación puede informar reflexiones y elecciones, no puede guiar de una manera mecánica, ni puede pedírsele hacerse cargo, de una manera científica, de cuestiones que principalmente dependen de valores ideológicos y políticos. Más aún, sus resultados, contrario a teoremas matemáticos, son dependientes del tiempo y el espacio, e incluso si coherentes, no están establecidos dentro de un paradigma unificado y no guían a elecciones didácticas idénticas (Artigue, 2003, p. 221).

Con este escrito referimos tendencias que se han dado al alterar el modelo de enseñanza del Cálculo. Lo haremos a través de la identificación y organización de propuestas cuyas acciones afectan el cómo enseñar y/o el qué enseñar, así como de ubicar, en el tiempo y el espacio, a la propuesta surgida en nuestra institución educativa, que pretende ser una alternativa viable para constituirse en un nuevo paradigma en dicha institución. Si bien nuestra propuesta posee bondades y limitaciones que hemos valorado sistemáticamente a la luz de su ejercicio, su consolidación es materia del estudio que realizamos bajo la auténtica convicción de que la investigación educativa debe ser una actividad rectora de la práctica docente, que comprometa la toma de decisiones y sustente la innovación.

 

2. RECONOCIMIENTO DE UN PARADIGMA TRADICIONAL Y SUS CONSECUENCIAS

Existe un gran número de investigaciones que abordan la problemática de la enseñanza y aprendizaje del Cálculo; Robert y Speer (2001) ofrecen una amplia revisión de los diferentes estudios a nivel mundial. A nuestra forma de ver. este desarrollo se justifica ante el esclarecimiento de un paradigma tradicional de enseñanza que deja mucho que desear en cuanto al aprendizaje: elevados índices de reprobación, aprendizaje sin comprensión y actitud negativa hacia el aprendizaje de las matemáticas son hechos que han sido reportados en los últimos treinta años con respecto a los cursos de Cálculo en el nivel medio superior y superior de educación. En lo que sigue, intentaremos apoyar la evidencia de este paradigma que identificamos durante nuestra actividad académica en una institución de prestigio ubicada al norte de México.

Artigue (1995) hizo pública a la comunidad una realidad que para 1995 era difícil justificar. La problemática de enseñanza del Cálculo era evidente: existe gran dificultad en lograr que los estudiantes muestren una comprensión satisfactoria de sus conceptos y métodos y la enseñanza tradicional se protege en el aprendizaje de prácticas algorítmicas y algebraicas que son a la vez el centro de la evaluación. Para 2001, la situación no parecía haber cambiado: "la mayoría de los estudiantes piensan que la manera más segura para tratar satisfactoriamente con este dominio es no tratar de comprender, sino sólo funcionar mecánicamente" (Artigue, 2001, p. 213). En 2003, el Cálculo sigue siendo una preocupación de los investigadores; Artigue (2003) comenta que la situación actual se caracteriza por un sentimiento general de crisis que, aunque no sea percibido de la misma manera, sí parece trascender las diferencias culturales. Las dificultades en el aprendizaje no han cambiado de manera sustancial.

El movimiento de reforma del Cálculo, que en Estados Unidos inició en 1986, es una reacción contra una práctica generalizada como la que Artigue menciona. Dicho movimiento ha tenido el apoyo de diferentes fuentes, entre ellas "de científicos que estaban frustrados por la inhabilidad de los estudiantes para usar el Cálculo inteligentemente en aplicaciones reales y por administradores que estaban molestos por el alto fracaso o las tasas de deserción de los cursos de Cálculo" (Steen, 2003, p. 197). Su avance ha logrado que se pongan a discusión varias cuestiones, entre ellas la búsqueda de un adecuado balance entre dos dimensiones relativamente independientes: contenido y contexto. Algunos acercamientos son fuertes en una de esas dimensiones y otros en ninguna porque se siguen focalizando en mecánicas a expensas del contenido y el contexto. Tal vez ningún acercamiento enfatiza ambas dimensiones, ya que se requiere mucho más tiempo y esfuerzo del que los estudiantes tienen destinado para ello (Steen, 2003).

En México, Cantoral, Cordero, Farfán e Imaz (1990) advierten cuál es la premisa más importante de la que debe partirse en el estudio sobre el fenómeno de la enseñanza del Cálculo: la estructura general del discurso matemático teórico constituye la base menos propicia para comunicar las ideas del Cálculo. Señalan que no debe olvidarse que su enseñanza es para futuros usuarios del mismo y no para expertos en su discurso teórico, pero aclaran que no están a favor de técnicas como aligerar conocimientos o emplear rutinas. En un trabajo posterior, Cantoral y Mirón señalan una dislexia escolar en Cálculo, su enseñanza logra que los estudiantes deriven, integren y calculen límites elementales, pero no son capaces de dar un sentido más amplio a esas nociones que les haga reconocer, por ejemplo, cuándo un problema requiere de calcular una derivada (Cantoral y Mirón, 2000).

El estudio teórico de Gascón (2001) revela la correspondencia entre modelos docentes y modelos epistemológicos generales que han existido en la historia de las matemáticas. Nos resulta conveniente situar en esta perspectiva a lo que queremos dar a entender como el paradigma tradicional en la enseñanza del Cálculo, identificándolo como consecuencia del ejercicio normalizado de ciertos modelos docentes. Gascón (2001) propone que se considere a tres teorías epistemológicas generales o patrones de organización matemática: euclídeas, cuasi empíricas y constructivistas. En relación con ellas identifica diferentes tipos de práctica docente y explica cómo les subyacen estos diferentes modelos epistemológicos. Gascón comenta que el modelo epistemológico de las matemáticas de una institución escolar incide en el modelo docente, que atañe a la manera como se gestiona y organiza el proceso de enseñanza de las matemáticas en la institución.

El modelo epistemológico del euclideanismo trata sobre la organización de la matemática para que se resuelva el problema de fundamentación, esto es, dar a la matemática una justificación lógica y base firme como teoría científica. La incidencia del euclideanismo se percibe en dos modelos docentes clásicos, el teoricismo y el tecnicismo, donde se identifica a la matemática como producto de la fundamentación de la matemática. El teoricismo plantea que enseñar matemáticas es mostrar teorías cristalizadas, y asume implícitamente que la forma en que la teoría se presenta corresponde a cómo se aprende; en este sentido, el proceso de enseñanza se considera trivial porque basta con mostrar lo ya producido. Sin embargo, como Gascón precisa, todos los datos empíricos disponibles contradicen esta conclusión, ya que hay enormes dificultades para que un estudiante utilice adecuadamente un teorema, aplique una técnica o compruebe si un objeto cumple una definición. Por su parte, de acuerdo con el tecnicismo, el proceso de enseñar matemáticas se identifica con el enseñar técnicas algorítmicas, con lo cual queda trivializada la actividad de resolución de problemas. El tecnicismo, asevera Gascón, "tiende a olvidar los 'auténticos' problemas, esos cuya dificultad principal consiste en escoger las técnicas adecuadas para construir una 'estrategia de resolución' " (2001, p. 136).

Por su parte, el estudio teórico de Artigue (2001) que trata del fruto de la investigación educativa hecha durante más de 20 años, pone hincapié en los reportes negativos de los primeros resultados con respecto al Cálculo o Análisis elemental. "Los resultados obtenidos proporcionan evidencias estadísticas de las limitaciones tanto de las prácticas educativas tradicionales como de las prácticas educativas que favorecen los enfoques formales y teóricos que reflejan el estilo Bourbaki" (p. 208). Indica que, como reacción espontánea de los sistemas educativos a tales dificultades, se produce una especie de círculo vicioso conveniente para garantizar una eficiencia aceptable en los cursos de Cálculo: el profesor aumenta la diferencia entre lo que enseña y lo que evalúa, mientras que el estudiante, guiado por el contenido de la evaluación, se forma una creencia sobre la matemática que no le ayuda a enfrentarse al pensamiento matemático avanzado.

Es precisamente este señalamiento de Artigue el que nos conlleva a interpretar que el modelo docente tecnicista se viene a constituir en la institución educativa como una reacción al ejercicio del modelo docente teoricista. El modelo tecnicista brinda una alternativa viable a la institución, una vez que el docente comprueba "en aula propia" que el modelo teoricista fracasa en lograr el aprendizaje de aquello que ofrece como enseñanza. Pensamos que de este modo en algún momento llega a ser normal identificar en las aulas que la enseñanza del Cálculo se focaliza en técnicas algorítmicas que se alternan con la presencia de definiciones y resultados formales que los justifiquen.

Al ingresar en 1990 como profesores a nuestra institución educativa, pudimos observar que estaba normalizada esta práctica docente a la que denominamos paradigma tradicional en la enseñanza del Cálculo, cuyas características reparan en el contenido que es objeto de enseñanza y en la estrategia de enseñanza que se utiliza.

El contenido matemático se presenta estructurado de manera formal y rigurosa. Por formal entendemos una ausencia de significados reales asociados con las nociones y procedimientos de esta rama de la matemática. Por riguroso entendemos una secuencia de definiciones, teoremas y demostraciones lógicamente validadas, todo organizado de tal forma que las nociones y procedimientos anteriores dan sentido a los subsecuentes. Esta presentación formal y rigurosa (resultado de la fundamentación) culmina con aplicaciones del contenido matemático que dejan la impresión de que son consecuencia natural del dominio de la teoría. El índice de libros de texto tradicionales muestra ese tipo de estructura en el contenido: números reales, funciones, límites, continuidad, derivada, aplicaciones de la derivada, integral y aplicaciones de la integral.

Es entendible que esta presentación tradicional del contenido se vincule con una estrategia de enseñanza tradicional del profesor que se limita a exhibir (enseñar) la estructura, ya que presupone que así se dará el aprendizaje. Por tanto, para enseñar la derivada habrá que enseñar antes límites (porque la derivada es un límite) y para enseñar límites habrá que enseñar antes funciones (porque los límites son de funciones) y para enseñar funciones habrá que enseñar antes los números reales (porque son funciones de variable real). Al llegar al capítulo de aplicaciones, el estudiante tal vez pueda repetir la definición de derivada y habrá calculado suficientes derivadas por definición, pero sobre todo estará habituado a derivar funciones con el uso de las reglas de derivación y sorteará las dificultades algebraicas que dicho método demanda. Bajo esa misma forma de trabajar, incorporará a sus conocimientos las aplicaciones de la derivada como procedimientos repetitivos del tipo para obtener el máximo se deriva y se iguala a 0.

Es de esperar que el estudiante adopte un papel pasivo durante el proceso de transmisión del contenido y que su aprendizaje se evidencie mediante el dominio de esa estructura de conceptos y procedimientos rigurosamente organizados, aunque en mayor medida a través de su habilidad para resolver ejercicios rutinarios de corte algorítmico que han sido diseñados para facilitar al profesor la emisión de una evaluación. Con ello, se alivia un tanto la baja eficiencia de los cursos.

 

3. BÚSQUEDA DE ALTERNATIVAS QUE AFECTAN EL CÓMO ENSEÑAR

A la fecha, diversos reportes de investigación en revistas especializadas continúan dando evidencia de la necesidad de repensar la enseñanza del Cálculo, con el fin de vencer la limitada comprensión de sus nociones y procedimientos. La investigación ha pasado de referir dificultades a proponer alternativas basadas en nuevas estrategias didácticas; el uso de nuevas herramientas tecnológicas para reforzar o descubrir ideas matemáticas; el desarrollo y empleo de distintos marcos teóricos; la realización de investigaciones cualitativas en pequeñas poblaciones, e incluso ha formulado secuencias didácticas que afectan los currículos y son llevadas a cabo en grupos escolares completos. La selección de artículos que hicimos para elaborar este trabajo, sin pretender ejemplificar de manera exhaustiva, busca ofrecer una muestra organizada de las tendencias actuales, en la que se perciba cómo el análisis va tomando un giro de cuestionar el cómo enseñar a cuestionar el qué enseñar, aunque en cierta medida y con cierta reserva.

De este modo, incluimos el trabajo que reporta Zhang (2003) sobre un curso tradicional de Cálculo: en sesiones de 150 a 350 estudiantes, los profesores imparten exposiciones formales para transmitir el conocimiento y los estudiantes observan, escuchan, toman notas y reciben información pasivamente. En dos semestres cubren contenidos tradicionales: funciones, sucesiones, límites, continuidad, derivadas y diferenciales, integrales, ecuaciones diferenciales y series. El profesor funge como líder en la transmisión de esta información y el estudiante es un receptor pasivo de la información que posee el profesor.

Zhang expresa que pocos estudiantes logran aprender estas ideas la primera vez que las encuentran y perciben al Cálculo como abstracto, aburrido y difícil de aprender. Afirma que la investigación muestra que las estrategias de enseñanza centradas en el profesor tienen desventajas porque no permiten un ambiente de aprendizaje activo. El interés del estudiante disminuye y, en la mayoría de los casos, se apropia de un aprendizaje superficial, enfocado en la memoria y la reproducción. Zhang, quien tuvo una reciente experiencia en la Universidad de Sydney, Australia, busca regresar a China para mejorar la calidad en la enseñanza del Cálculo mediante estrategias de enseñanza centradas en el estudiante.

Notamos en el trabajo anterior un ejemplo en el que la preocupación por la problemática del aprendizaje no incluye aspectos sobre el contenido tradicional del Cálculo. Zhang sólo cuestiona el modo en que este contenido debe acercarse al estudiante; a final de cuentas, dice, "los objetivos principales del curso son dar a los estudiantes los conceptos y teoría del Cálculo, hacerlos entender las ideas matemáticas y desarrollar sus habilidades para pensar lógica, profunda y creativamente" (2003, p. 100).

Desde nuestro punto de vista, la introducción de la tecnología computacional en la enseñanza pudo ser vista al principio como un medio para resolver la problemática: los libros de texto tradicionales se acompañaban con mejores imágenes, mientras que en el aula se ocupaban calculadoras que graneaban para mostrar el mismo contenido; un diferente cómo para mostrar un mismo qué. La evolución de los recursos tecnológicos, de acuerdo con Moreno–Armella, Hegedus y Kaput, ofrece una nueva perspectiva teórica para investigar el potencial didáctico de los ambientes tecnológicos dinámicos continuos, que pertenecen a la última etapa en tal desarrollo. Entre las etapas anteriores se ubican las graneadoras, que son medios de computación estática que responden computacionalmente a una acción humana y las hojas de Cálculo, que representan una etapa de medios dinámicos discretos donde "la co–acción entre usuario y ambiente puede existir" (2008, p. 103).

El ejemplo sobre el uso de tecnología que seleccionamos maneja un recurso computacional dinámico discreto. La investigación de Gordon y Gordon se enfoca en aprovechar la idea del ajuste de funciones con datos a favor de que el estudiante descubra el teorema fundamental del Cálculo. Su motivación radica en que la manera como se presenta el teorema en cursos tradicionales, donde se introduce a la función área como integral definida, los estudiantes la encuentran "sacada de la manga del profesor" (2007, p. 598). Gordon y Gordon no comentan sobre la experiencia con estudiantes de su acercamiento al teorema con el uso de la hoja de cálculo, pero manifiestan la convicción de que la problemática sobre el aprendizaje del teorema puede aliviarse mediante la aplicación del recurso computacional para obtener valores numéricos, a los que después se ajusta una función matemática. Al final, expresan su preocupación por desembocar en la presentación tradicional del contenido: "por supuesto, una vez que la 'fórmula' ha sido descubierta o conjeturada, uno puede voltear a los argumentos algebraicos de límite para probar los resultados formalmente" (p. 604). Queda la impresión de que el modo de introducir el teorema no es tradicional, pero ha de pagarse el precio de arribar a la presentación formal del resultado, como si con ello se estuviese validando el acercamiento didáctico.

Con Gordon y Gordon (2007) ilustramos un caso en el que el manejo de recursos tecnológicos ofrece una alternativa innovadora para presentar cierto contenido matemático. El cómo y en cierto sentido el qué enseñar se modifican; sin embargo, la validez del resultado matemático sigue justificándose por su presentación formal y rigurosa.

Asimismo, seleccionamos el artículo de Thompson y Silverman (2007) para ilustrar la aplicación de resultados de investigación de índole cognitiva. Thompson y Silverman consideran algunas dificultades documentadas sobre la concepción de función como proceso; su estudio va dirigido a determinar las dificultades que tiene el estudiante para comprender una idea importante del Cálculo: la acumulación. Argumentan que los estudiantes encuentran difícil "pensar en algo que se está acumulando cuando no pueden conceptualizar los 'bits' que se están acumulando" (p. 117). A su vez, la expresión matemática de la función de acumulación 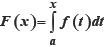posee tantas partes que varían (como x, t, f(t), F(x)) que resulta natural la dificultad para entender y emplear dicha notación.

Thompson y Silverman cuestionan el débil aprendizaje de la integral expresada en la función de acumulación cuando el sentido de F(x) es representar el área acotada entre una gráfica de una función f(x) y el eje x, una imagen que debe preexistir en la mente del estudiante. En la expresión aparecen simultáneamente los problemas con la comprensión sobre el proceso de acumulación del área y con el proceso de determinación para los diferentes valores de la función de acumulación. Thompson y Silverman indican que la mayor fuente de problemas con la comprensión matemática de la acumulación se da porque es raro que dicha idea se enseñe en los cursos o, si se enseña, es raro que se tenga intención de que se aprenda.

La idea de Thompson y Silverman consiste en elaborar una alternativa para la enseñanza del Cálculo tomando en cuenta aspectos cognitivos que permitan la apropiación de un discurso coherente en los estudiantes donde participen significados de las nociones de derivada (razón de cambio) e integral (acumulación) y se dominen conexiones entre razones de cambio de cantidades, acumulación de cantidades, funciones como modelos, límites, antiderivadas, convergencia uniforme y puntual, al igual que funciones de dos o más variables. "Aunque se necesita más trabajo para desarrollar la instrucción que logre esto, creemos que enfocarse en funciones de acumulación, como se ha discutido en este capítulo, será algo central" (Thompson y Silverman, 2007, p. 129).

Debido a que no es común referirse a la integral como función de acumulación, pensamos que el cómo intentan presentarla Thompson y Silverman altera el qué enseñar, y le otorga un significado diferente al tradicional del área. Sin embargo, a lo largo del trabajo se nota la preocupación por hacer que los estudiantes lleguen a conceptualizar la función de acumulación y, con ello, comprendan finalmente el sentido de la definición formal de la integral como el límite de sumas de Riemann.

Para ilustrar una última alternativa, que contempla la importancia de a quién se dirige la enseñanza, elegimos el reporte de Bingolbali, Monaghan y Roper (2007), quienes están interesados en esclarecer el aprendizaje del Cálculo que evidencian estudiantes de ingeniería, a diferencia del aprendizaje que concierne a los alumnos de una carrera de matemáticas. Se obtuvo información de estudiantes de primer semestre de matemáticas y de ingeniería mecánica en una Universidad de Turquía para comparar las concepciones de los grupos en cuanto a la noción de derivada. Los grupos tenían sus respectivos módulos de Cálculo y el método que emplearon incluyó la aplicación de cuestionarios, la observación de exposición en clase, el desempeño en aula de los estudiantes, las notas de clase y la realización de entrevistas.

Algunos resultados del estudio señalan diferentes concepciones y preferencias en los grupos. En particular, los alumnos de ingeniería manifestaron su interés por ver a la matemática como una herramienta y por desear que el conocimiento matemático fuera relevante en las aplicaciones de ingeniería. Esto se contrapone a la idea de concebir a la matemática como disciplina mental.

Nosotros sostenemos que los resultados del estudio envían un fuerte mensaje a los participantes involucrados en la educación matemática de los ingenieros: en que sus puntos de vista y expectativas deberían ser tomadas en consideración, en la decisión de qué matemáticas les sean enseñadas (Bingolbali, Monaghan y Roper, 2007, p. 774).

Este trabajo nos marca la pauta para cuestionar la pertinencia del orden clásico que presenta un contenido tradicional del Cálculo, en relación con el estudiante que lo verá como objeto de aprendizaje. En otras palabras, es legítimo considerar el carácter instrumental que tienen los cursos de Cálculo en el currículo universitario cuando se investiga la problemática de su aprendizaje. Pensamos que el papel que desempeña el Cálculo en el currículo debe ser el de medio o herramienta que le permita al estudiante entender la realidad de otras áreas del conocimiento; es en tal contexto donde deberíamos estudiar las dificultades del aprendizaje.

Con esta reseña hemos querido mostrar algunas opciones que plantean la necesidad de experimentar diferentes acercamientos al Cálculo. Cambiar el cómo enseñar es la primera alternativa que se presenta. El uso de aprendizaje activo, tecnología, ideas importantes (ajuste, acumulación) y utilidad instrumental del conocimiento matemático son, sin duda, acciones válidas que buscan un aprendizaje viable en el aula.

Hacemos la precisión de que estos trabajos no corresponden a los modelos docentes clásicos. Gascón (2001) plantea que un modelo epistemológico cuasi empírico se distingue del euclideanismo porque concibe en forma distinta el desarrollo de una teoría matemática, ya que acentúa periodos en que la teoría es informal, periodos que preceden a la formalización. En ellos tiene sentido descubrir soluciones a problemas interesantes, establecer y probar conjeturas, contrastar, refutar, buscar contraejemplos; todas estas actividades son reivindicadas en su papel de generadoras de conocimiento. La influencia del modelo cuasi empírico en el modelo docente consiste en recuperar la actividad matemática exploratoria en el proceso.

A nuestro juicio, dichos estudios introducen la actividad en el aula, ya que intentan involucrar al estudiante en el proceso de aprendizaje, como interactuando con una teoría informal. Sin embargo, queda la impresión de que su uso se limita a predisponer al estudiante para arribar al contenido matemático en su versión formal, con lo cual se quiere garantizar que el objeto de aprendizaje es matemáticas y no otra cosa. Desde nuestra perspectiva, es necesario hacer consciente nuestro modelo epistemológico porque nuestra visión de la matemática afecta al cómo uno la hace presente en el aula.

 

4. LA HISTORIA INFLUYE PARA PROBLEMATIZAR EL QUÉ ENSEÑAR

Al parecer, una visión más amplia de lo que es la matemática comienza a perfilarse en el aula. No sólo consiste en un sistema conceptual lógicamente estructurado o en un lenguaje simbólico con sintaxis propia, sino en una actividad humana de resolución de problemas, como lo muestra su historia. Tzanakis y Arcavi (2000) establecen argumentos a favor de integrar a la historia en la enseñanza; uno de ellos alude a las bases didácticas de los profesores, quienes a través del estudio de la historia toman conciencia sobre los procesos creativos involucrados, lo cual les permite enriquecer su conocimiento matemático y apreciar mejor su naturaleza.

Jankvist (2009a, 2009b) reconoce que la literatura ofrece una gran cantidad de argumentos a favor del uso de la historia en la enseñanza de las matemáticas, y que la discusión se enfoca hacia la necesidad de desarrollar investigaciones empíricas que valoren la eficacia de su uso. Concibe a la historia como una herramienta que puede ser utilizada como un medio que ayuda al aprendizaje de conceptos o teorías, no sólo en términos de motivación, sino también de cognición. Sostiene además, que es posible que el propósito principal del uso de la historia tenga que ver más bien con el interés de aprender la historia en sí misma, como ocurre en el nivel secundario superior danés, donde los estudiantes deben conocer sobre la evolución de las matemáticas y su interacción con la evolución científica. Janviskt (2009b) afirma además, que "Entonces, cuando se habla de la eficacia de usar la historia en la educación matemática, me parece razonable distinguir entre la eficacia de la historia como una herramienta y la eficacia de la historia como una meta" (p. 69).

En un estudio teórico Jankvist (2009a) propone una forma de organizar y estructurar la discusión de las razones para usar y de las maneras de usar la historia en educación matemática mediante la categorización de dos razones diferentes para el uso, articuladas con tres diferentes modos de uso. Para los fines del presente escrito, retomaremos el uso de la historia como una herramienta para apoyar el aprendizaje de los estudiantes. Dentro de esta categoría se maneja el argumento típico de servir como factor motivacional pues capta el interés del estudiante o muestra una "cara humana" en la matemática. Pero también se argumenta que la historia puede usarse a modo de herramienta cognitiva o bien como un argumento evolutivo al servicio del aprendizaje. Dentro de la categorización de los modos de uso distinguimos los acercamientos basados en la historia porque nos permiten expresar nuestro interés por perspectivas que, sin discutir abiertamente el desarrollo histórico, pueden influir en el establecimiento del orden y la manera en que sean tratados ciertos temas en el aula. En este apartado comentaremos dos acercamientos basados en la historia que la manejan como una herramienta para inspirar un argumento evolutivo, relacionado con la génesis del Cálculo.

Farmaki y Paschos (2007) declaran la utilidad de integrar a la historia de la génesis del conocimiento matemático para dirigir a los estudiantes del conocimiento básico al complejo, de la misma manera que la humanidad ha progresado en la historia de la matemática. Su trabajo es una variación de "lo que puede ser llamado esencialmente como el acercamiento genético a la enseñanza y aprendizaje" (Tzanakis y Arcavi, 2000, p. 208), donde se enfatizan razones por las cuales los conceptos, métodos y teorías dan respuesta a problemas matemáticos específicos. Estos autores identifican en la historia un momento genético para el concepto de función, su representación gráfica y la integral; se refieren al método para estudiar el movimiento que fue utilizado en el siglo XIV por matemáticos de la Escuela de Merton, Oxford y Oresme en París.

El propósito del diseño que efectúan Farmaki y Paschos es reconstruir las ideas relevantes que involucra el momento genético, pero en una versión apropiada para el aula, de ahí que ocupen elementos modernos como ejes cartesianos, notaciones y procedimientos algebraicos. Hacen una secuencia de actividades con problemas en el contexto del movimiento uniforme, con el fin de motivar a los estudiantes hacia el desarrollo simultáneo del pensamiento algebraico, geométrico y analítico a través de su solución. Estos problemas se plantean con base en la representación gráfica de la velocidad respecto al tiempo, donde juega un papel central el planteamiento que formula Oresme de concebir a la distancia recorrida en un tiempo dado mediante el área de la figura en esa representación, el área de un rectángulo. Nombran holística a dicha representación gráfica porque las tres variables (velocidad, tiempo y distancia) están representadas en ella, aunque de manera diferente.

En un estudio exploratorio, que constó de siete sesiones, Farmaki y Paschos aplicaron sus actividades a 58 estudiantes para investigar sobre las habilidades para comprender los conceptos y procesos tratados. En su reporte describen las sesiones guiadas por el profesor y los problemas de movimiento uniforme diseñados, así como refieren extractos de entrevistas individuales a dos estudiantes. Las últimas dos sesiones se destinaron a resolver los problemas mediante la reconfiguración de la figura –tratada en sesiones anteriores– cuya solución se reduce a encontrar el lado de un rectángulo del que se conoce el otro lado y su área. Entre los resultados, incluyen una representación esquemática de las operaciones cognitivas de los estudiantes en los registros gráfico y algebraico, al resolver las ecuaciones de primer grado que surgen del problema. En dicho esquema se ocupa el marco de Duval (2002) para describir procesos dentro de un mismo registro de representación, o bien entre ellos (conversiones). Asimismo, reportan observaciones sobre la información analizada; entre ellas, señalan que 12 de los 58 estudiantes lograron emplear las transformaciones y reconfiguraciones de las figuras.

Farmaki y Paschos consideran su acercamiento didáctico como un aporte para la integración de la historia de las matemáticas en la enseñanza, y afirman que una planeación apropiada podría abarcar más allá de los problemas relativos al movimiento uniforme. Agregan que las ideas del pasado deberían ser usadas con fines educativos "para inspirar un cambio en las actividades de enseñanza con metas específicas que lleven a la esencia del conocimiento matemático" (2007, p. 104).

Jankvist (2009a) comenta que desde tiempo atrás prominentes matemáticos habían manifestado su convicción en que la historia es una guía para la enseñanza y aprendizaje. Entre ellos destaca Freudenthal, un reconocido matemático holandés que desde 1971 había manifestado su preocupación por la problemática educativa, al cuestionar la anti–didáctica inversión hecha en la enseñanza: que el resultado del trabajo de los matemáticos se tomaba como punto de partida para la educación en matemáticas. Gravemeijer y Doorman (1999) pertenecen al grupo de investigadores conocido como Realistic Mathematics Education (RME), cuyo origen se apoya en el trabajo de Freudenthal. Ellos se basan en la idea de hacer que el estudiante redescubra o reinvente el conocimiento matemático usando su propio talento y experiencia con el ambiente que le rodea.

La RME centra su objetivo en el diseño instruccional de elaborar una ruta donde la matemática sea contemplada como actividad y no como sistema acabado. A través de problemas en contexto (experiencialmente reales al estudiante), Gravemeijer y Doorman proponen iniciar con la actividad de matematizar (organizar desde una perspectiva matemática), en la que proponen llevar a cabo una reinvención guiada de las matemáticas para "tender un puente" entre el conocimiento informal y la matemática formal. El término modelo emergente refiere un diseño heurístico poderoso; ellos seleccionan problemas que ofrezcan a los estudiantes la oportunidad de que desarrollen un modelo emergente específico de la situación. Para identificar esos problemas, el diseñador toma en cuenta su propio conocimiento y experiencia de aprendizaje, se inspira en la historia de la matemática y además observa soluciones informales que los estudiantes ponen en juego cuando están resolviendo problemas aplicados en los que no conocen una solución estándar.

Al revisar la historia del Cálculo, Gravemeijer y Doorman (1999) proponen que su desarrollo comience con la elección de la gráfica de la velocidad respecto al tiempo como el modelo para los problemas de velocidad y distancia. Observan que Oresme fue el primero en dibujar gráficas para visualizar el problema del movimiento; por tal motivo, esperan que el trabajo con gráficas discretas de la velocidad se constituya en el estudiante como un modelo de aproximaciones discretas al fenómeno del movimiento rectilíneo con aceleración constante. Mientras interactúan con esta idea, esperan ver que surja en los estudiantes la acción de modelar la velocidad instantánea con una barra vertical, de tal modo que la gráfica de la velocidad, ya continua, sea la base para el estudio más formal del Cálculo. El papel del profesor resulta determinante para tratar de mantener lo más cercana posible la brecha entre lo que los estudiantes hacen y lo que se ha mostrado que deban hacer. Cabe aclarar que, si no llegan a inventar el modelo emergente, el profesor necesita tener gran cuidado de aproximar las invenciones de los estudiantes lo más cerca posible de lo que se persigue.

Bajo estas consideraciones Gravemeijer y Doorman elaboran una secuencia para Cálculo para estudiantes de preparatoria. En su trabajo no reportan la experiencia con estudiantes; sin embargo, puntualizan que aún y cuando la idea de usar rectángulos pueda ser manejada por los estudiantes, esto no significa que no queden problemas por resolver. Un problema central es la coordinación de la altura y el ancho de las barras cuando se ocupan para visualizar una aproximación discreta del movimiento. El siguiente problema consiste en la comprensión sobre la relación entre el área de la gráfica y la distancia total recorrida en un periodo largo de tiempo, lo cual demanda que el estudiante maneje acertadamente las relaciones entre movimiento, representación y aproximación, que forman parte de un proceso de reinvención que dista en mucho de ser un aprendizaje simple.

La propuesta de Gravemeijer y Doorman contempla crear un ambiente de aprendizaje en el que los estudiantes "puedan asirse" con las ideas básicas y promover la reinvención de la teoría, ya que afirman que la matemática formal surge de la actividad matemática del estudiante. "Este es también un objetivo de RME, donde el diseño instructional se enfoca o apunta a la creación de oportunidades óptimas para la emergencia del conocimiento matemático formal" (1999, p. 116). Dicho grupo proclama un ideal:

Si los estudiantes tienen la experiencia del proceso de reinventar las matemáticas como una ampliación del sentido común, entonces no van a experimentar dicotomía entre la experiencia de la vida diaria y las matemáticas. Ambas serán parte de una misma realidad (Gravemeijery Doorman, 1999, p. 127).

Los trabajos que hemos referido señalan la utilidad de la historia como una fuente para producir secuencias didácticas en las que la actividad matemática —previamente identificada— sea protagonista del diseño. Formulan una alternativa distinta al introducir el estudio del movimiento con el fin de ofrecer al estudiante un significado asociado a la representación gráfica de la velocidad y esperando con ello que apoyen su pensamiento al involucrarse posteriormente en el estudio del Cálculo. Es importante observar que estos reportes dejan percibir las dificultades que surgen en el aprendizaje del estudiante cuando se promueve la interacción de una nueva forma (cómo) y con contenidos que no coinciden con el tradicional (qué).

Gascón (2001) sostiene que la información empírica sobre el aprendizaje muestra que el proceso de estudio de las matemáticas es no trivial, no mecánico e incontrolable por el profesor. Toma como evidencia los datos tocantes al fracaso en el desempeño de los estudiantes ante problemas matemáticos no estandarizados y la excesiva algoritmización del conocimiento. Gascón identifica la incidencia del modelo epistemológico cuasi empírico de la matemática en dos modelos docentes, el modernista y el procedimentalista, en los cuales cobra importancia el desarrollo del conocimiento matemático en la enseñanza y la actividad de resolución de problemas se constituye como el diseño central del proceso didáctico.

El modernismo tiende a identificar la actividad matemática con una exploración libre y creativa de problemas no triviales, mientras que el procedimentalismo "sitúa como principal objetivo del proceso didáctico el dominio de sistemas estructurados de técnicas heurísticas" (Gascón, 2001, p. 142). La resolución de problemas es empleada como estrategia didáctica en ambos modelos, pero su aplicación tiene distinto enfoque: los problemas están aislados en el modernismo y en el procedimentalismo cobra importancia trabajar con clases de problemas, atendiendo al dominio de sistemas estructurados de procedimientos matemáticos no algorítmicos con el uso de estrategias complejas.

La perspectiva de Gascón (2001) hace reflexionar sobre el uso de la historia de la matemática en la enseñanza. Sin duda, es útil estudiar la génesis del conocimiento matemático como fuente de inspiración para diseñar experiencias que contemplen problemas no triviales relacionados con tópicos particulares; por ejemplo, el movimiento uniforme o el uniformemente acelerado. Sin embargo, nuestra posición contempla la historia en sí como un objeto de investigación al cual recurrir para desentrañar los mecanismos de desarrollo de un área completa, como el Cálculo, y que sean ocupados para diseñar secuencias donde resulte coherente el desarrollo de las nociones y procedimientos matemáticos. Dicha información puede dar luz sobre la organización del discurso matemático del Cálculo favorable para evidenciar su utilidad en la solución de una problemática global que le ha dado sentido y razón de ser. Esta debe ser una forma más redituable de mirar a la historia de la matemática y apreciar sus ventajas didácticas, seguramente en concordancia con un modelo docente acorde con el procedimentalismo.

 

5. ACERCAMIENTO SOCIOEPISTEMÓLOGICO: DE CONCEPTOS A PRÁCTICAS SOCIALES

Cantoral y Farfán (2003) argumentan a favor de una visión de la historia de la matemática fructífera para estudiar la problemática tocante al proceso de enseñanza del Cálculo, resaltando los orígenes empíricos de su desarrollo. Esta visión se ha conformado a medida que la Matemática Educativa forma un campo de investigación autónomo. El acercamiento socioepistemológico es el nombre con el que los investigadores mexicanos denominan a su aproximación a la investigación educativa, que propusieron explícitamente en 1997. Debido a su carácter sistémico y situado, se procura un acercamiento que "permita la incorporación de las cuatro componentes fundamentales en la construcción del conocimiento: su naturaleza epistemológica, su dimensión sociocultural, los planos de lo cognitivo y los métodos de transmisión vía la enseñanza" (p. 265).

Robert y Speer apuntan que esta perspectiva ha sido ocupada por el Centro de Investigación y de Estudios Avanzados (Cinvestav) "a efecto de estudiar el aprendizaje y la enseñanza de la variación, desde la preparatoria hasta estudios avanzados en ingeniería" (2001, p. 285). Los investigadores pertenecen al Área de Educación Superior del Departamento de Matemática Educativa, a la que definen como una disciplina del conocimiento que se ocupa de estudiar los fenómenos que ocurren cuando los saberes matemáticos se introducen al sistema de enseñanza. Cantoral y Farfán refieren la evolución de la problemática que aborda esta disciplina, que culmina en el establecimiento de una línea de investigación llamada pensamiento y lenguaje variacional, que se ocupa de los fenómenos relacionados con la enseñanza–aprendizaje del Cálculo y el Análisis Matemático. Cantoral y Farfán señalan que el desarrollo de la problemática de la Matemática Educativa se describe a través de cuatro momentos diferentes: "didáctica sin estudiantes, didáctica sin escuela, didáctica sin escenarios y didáctica en escenarios socioculturales" (2003, p. 257).

En la etapa didáctica sin estudiantes se ubica cierta "sensualidad didáctica" para abordar la problemática: los matemáticos proponen maneras de presentar el contenido matemático con la idea de que la mejoría en el aprendizaje del estudiante sea consecuencia inmediata de una mejor presentación de los contenidos. La didáctica sin escuela incluye un cierto acercamiento cognitivo a la problemática, donde las dificultades en el aprendizaje de los estudiantes son descritas y explicadas con base en marcos teóricos construidos para ello. Cabe aclarar que esta etapa toma en cuenta la mente del estudiante, pero no la sitúa en un aula escolar. La etapa didáctica en la escuela pero sin escenarios socioculturales considera abiertamente la conveniencia de ir a la génesis del conocimiento matemático para indagar las condiciones en que tuvo lugar. Las consideraciones de tipo epistemológico intentan esclarecer las dificultades intrínsecas del conocimiento matemático para ser adquirido, y que pueden estar presentes en el aprendizaje de los estudiantes. Por último, la etapa didáctica en escenarios socioculturales plantea las particularidades de la problemática de la enseñanza en la educación superior, donde la matemática escolar posee ese carácter instrumental de estar al servicio de otras disciplinas científicas y prácticas de referencia (Cantoral y Farfán, 2003).

Al situarnos en la última etapa podemos diferenciar a la perspectiva socioepistemológica de las que describimos en el apartado anterior. No basta con estudiar el referente epistemológico de las condiciones que posibilitan o dificultan la construcción del conocimiento e intentar reproducir la historia en el aula, sino que es menester otorgar un papel protagónico a la componente social. Cantoral dice que el conocimiento matemático tiene un origen y función social porque se asocia a prácticas humanas socialmente establecidas. La filiación entre la naturaleza del conocimiento y la actividad humana, mediante la cual y en razón de la cual se produce el conocimiento, es la tesis de la orientación socioepistemológica que subyace en la línea de investigación del pensamiento y el lenguaje variacional. Hacer un diseño para el aula escolar exige tener un mayor conocimiento del fenómeno de enseñanza aprendizaje, precisa Cantoral, ya que "este es un acto social, cultural, política y económicamente establecido y justificado por instituciones educativas" (2004, p. 5).

Diversas investigaciones se enmarcan en este acercamiento, cuyo énfasis reside en el interés de modelar el papel de la práctica social en la producción del conocimiento, a fin de diseñar situaciones didácticas que den sentido y significado al saber matemático escolar. Los estudios aportan conocimiento sobre las "caracterizaciones del ejercicio de las prácticas que anteceden a la producción o construcción de conceptos y al desarrollo del saber" (Cantoral, Farfán, Lezama, y Martínez–Sierra, 2006, p. 85). Cabe mencionar lo que el enfoque socioepistemológico interpreta con su noción de práctica: "no es lo que hace en sí el individuo o el grupo, sino aquello que les hace hacer lo que hacen" (Covián, citado por Cantoral et al. 2006, p. 85).

La investigación de corte socioepistemológico identifica como prácticas el medir, predecir, modelar y convenir. Se enfoca a delimitar el papel que juega el escenario histórico, cultural e institucional en la actividad humana. Las prácticas han sido ejemplificadas con el afán de valorar su papel en la formación del conocimiento matemático y su representación en la situación escolar. El problema que motiva a la investigación puede ser la dificultad de los estudiantes para aprender algún concepto (por ejemplo, la comprensión de la integral definida con base en la típica explicación escolar área bajo la curva); sin embargo, estudiarlo desde la perspectiva socioepistemológica persigue el fin de contribuir a una visión alternativa que contemple las prácticas sociales relacionadas (Cabanas y Cantoral, 2006).

Bajo esta perspectiva queda identificada la necesidad de reconstruir el conocimiento matemático con propósitos didácticos amplios, donde se incluya el hecho fundamental que caracteriza al sistema de educación superior: "Más aún, y tal vez incluso más importante: la matemática escolar está al servicio de otros dominios científicos y otras prácticas de referencia, de donde adquiere sentido y significación" (Cantoral y Farfán, 2003, p. 265). En esta forma, la metáfora para la reconstrucción del conocimiento matemático debe "cambiar de la adquisición del objeto a la participación en prácticas intencionadas asociadas con el objeto específico" (Buendía y Cordero, 2005, p. 300).

Buendía y Cordero (2005) dan un ejemplo ilustrativo de las implicaciones en que esta forma socioepistemológica estudia y entiende el fenómeno educativo, particularizado al aprendizaje de la periodicidad de las funciones. En su trabajo observan que los estudiantes tienen una ausencia de significado asociado a la definición formal de la propiedad de periodicidad, además de que asocian de manera indiscriminada cualquier clase de repetición con la gráfica periódica. Reportan la construcción de una situación de enseñanza sobre el aspecto periódico de las funciones, en la que la práctica social de la predicción se transforme en un argumento para redefinir lo que es periódico. Se muestra que, como consecuencia del ejercicio de la práctica de predecir, la función y la gráfica periódica adquieren un significado para el estudiante que es funcional en el contexto donde lo periódico adquiere importancia, aunque sea ajeno al establecimiento de una definición matemática formal.

El acercamiento socioepistemológico llega a problematizar el saber matemático que es objeto de enseñanza; cuestiona el qué enseñar y lo declara como una variable a considerar en la investigación. A nuestro juicio, su cuestionamiento necesariamente está vinculado con la forma de acercar el conocimiento al estudiante (el cómo enseñar). Mediante el diseño de una situación que es puesta en escena dentro del aula escolar, se busca esclarecer el ejercicio de aquellas prácticas que en el estudiante se constituyen en argumentos y le permiten dotar de significado funcional a los contenidos matemáticos. La intención del diseño de escenarios didácticos se dirige a propiciar el accionar de prácticas en esa realidad social que se construye en el aula, acentuando la importancia de la interacción entre estudiantes, el profesor y el conocimiento.

 

6. CONSTRUYENDO UN NUEVO DISCURSO ESCOLAR DEL CÁLCULO

Entre las primeras investigaciones que aportaron eventualmente a consolidar el acercamiento socioepistemológico está la de Alanís (1996). Como una implicación de la investigación doctoral realizada por Ricardo Cantoral, su director de tesis, Alanís fija como meta para un curso auricular la apropiación de la idea paradigmática que condujo a Newton a inventar el Cálculo. Alanis se apoya en las premisas que estableció Cantoral para estudiar el fenómeno de enseñanza–aprendizaje del Cálculo, y afirma que "el fin último de la investigación de este grupo es la construcción de discursos didácticos del Cálculo cuyo paradigma no sea el discurso teórico" (p. 20). A diferencia de otros procesos de innovación, precisa, "nuestro punto de partida no es cómo hacerle para que los estudiantes ganen dicho discurso; nuestro punto de partida es, justamente, cambiarlo o rediseñarlo" (Alanís, 2000, p. 236). Para este fin puntualiza la importancia de una lectura adecuada de la historia de la matemática, que permita localizar las ideas fundamentales en el desarrollo del Cálculo.

Como producto de su investigación, Alanís (1996) lleva a cabo el diseño de una serie de secuencias didácticas que permiten esclarecer cambios en los contenidos a enseñar en un curso de Cálculo, así como en los roles de profesor y estudiantes, a fin de que puedan apropiarse de las ideas fundamentales del Cálculo. Por medio del análisis epistemológico que realiza como parte de su investigación, fundamenta el establecimiento de la meta de un curso de Cálculo en su versión newtoniana; después de que un análisis didáctico le constata que la enseñanza tradicional no se traza una meta similar, profundiza su análisis epistemológico hasta culminar en el diseño de las secuencias.

De igual manera, propone a la Cinemática como el contexto inicial adecuado para abordar el problema de "predecir cuál va a ser la posición de una partícula que se mueve en línea recta". Argumenta que, al dar una respuesta cada vez más elaborada a dicho problema de predicción, el estudiante tiene la oportunidad de apropiarse de la idea paradigmática de Newton. La cuestión ¿cuál va a ser o cuál fue el valor de una magnitud que está cambiando? queda constituida como hilo conductor en el cual puede desarrollarse un curso que permita referir los conceptos y procedimientos del Cálculo, aunque no en el orden ni con el significado y peso con el que aparecen en un discurso tradicional.

Alanís propone abordar tal cuestión, en primer lugar, para el caso del movimiento rectilíneo con velocidad constante; en segundo, para el caso donde la velocidad no sea constante, pero sí lo sea la aceleración; en tercero, para el caso en que la aceleración no sea constante, pero sí lo sea la razón con la que ésta cambia. De este modo se induce la respuesta al caso general del movimiento rectilíneo donde una de las sucesivas razones de cambio es constante. En dicha secuencia resulta clave el papel del movimiento uniforme, ya que para estudiar el movimiento variado habrá que considerarle como la situación límite de movimientos constantes por intervalos (Alanís, 2000).

La investigación de Alanís (1996) sienta las bases para elaborar una innovación en la enseñanza del Cálculo, en la que las nociones y los procedimientos emergen en calidad de herramientas para abordar problemas reconocibles en diferentes áreas de interés, con lo que se atiende al carácter instrumental del Cálculo en las diferentes carreras universitarias, no de Licenciatura en Matemáticas.

Ahora bien, la construcción de un discurso escolar que retomó la investigación de Alanís (1996) en estructura, e integró tanto la investigación de Pulido (1997) como el conocimiento generado por estudios de corte cognitivo, fue desarrollada en una primera fase durante cuatro años, concretándose en dos libros de texto en el 2002 y el 2003, titulados Elementos del Cálculo. Reconstrucción conceptual para el aprendizaje y la enseñanza y Matemáticas preuniversitarias. Significado de nociones y procedimientos, respectivamente. En la institución de educación superior donde surgió dicha propuesta se ha introducido esta forma de enseñar Cálculo en los cursos regulares, habiendo contemplado la capacitación a los profesores. Los libros fueron ocupados durante dos años para apoyar la innovación del primer curso de Cálculo en el nivel superior. Después se juzgó conveniente trasladarlos al último año de preparatoria y al curso introductorio del nivel superior, al que se inscriben estudiantes que provienen de preparatorias ajenas a la institución.

Para el 2005, el libro Elementos del Cálculo era utilizado oficialmente en el tercer año de preparatoria, y Matemáticas preuniversitarias en el curso introductorio del nivel superior. Los cursos del nivel superior fueron objeto de una innovación que buscó consolidar, profundizar y ampliar el conocimiento que la propuesta ofrecía, mediante el diseño de nuevas secuencias didácticas, acordes con el uso del Cálculo en las materias de ingeniería. El desarrollo de manuales de apoyo impresos en la institución y de bases de datos en la plataforma tecnológica para la distribución de cursos auriculares apoyan la implantación de la propuesta en los cursos regulares de Matemáticas I, II y III de Ingeniería.

El escenario social que surge en la institución educativa donde se lleva a cabo la innovación tiene características que hacen pensar en las ventajas para este cambio en el paradigma de la enseñanza del Cálculo. Aspectos relativos al modelo educativo, tipo de estudiantes e infraestructura tecnológica son variables que deben apreciarse por su influencia para la implantación. Por otro lado, la estructuración del contenido, atendiendo a la práctica de predicción, ha permitido que una mayor proporción de estudiantes tenga acceso al conocimiento matemático y le encuentre sentido y utilidad. Trabajos como el de Buendía y Cordero (2005), descrito en el apartado anterior, confirman las ventajas que ofrece el nuevo discurso estructurado alrededor de la práctica de predecir. En las evaluaciones que estudiantes emiten al profesor y al curso (cuestiones que son una política de la institución), observamos que la oportunidad de entender el contenido matemático con el tratamiento de una problemática ajena a la formalización de la teoría se está convirtiendo en un factor motivacional que cambia favorablemente la actitud de los estudiantes hacia el aprendizaje del Cálculo.

Actualmente están en proceso de elaboración los currículos y el texto para los tres cursos del nivel profesional, así como la revisión de la primera versión de la propuesta, que se aplicó en los libros de texto citados. Se continúa tomando en cuenta el análisis de los avances en investigación educativa, sobre todo la enmarcada bajo el acercamiento socioepistemológico, al igual que la información sobre la influencia de la propuesta en el nivel universitario y preuniversitario, obtenida a través de los estudios de Pulido (2007) y Salinas y Sánchez (2009). Aún es prioridad atender el carácter instrumental que tienen los cursos del sector curricular de matemáticas dentro del programa de carreras profesionales en la institución educativa, donde se requiere indagar qué uso se da a la matemática en los cursos representativos de especialidad.

El nuevo discurso busca integrar, didácticamente hablando, un acercamiento newtoniano con uno leibniziano a la génesis del Cálculo, bajo la convicción de ofrecer así mayores oportunidades al estudiante para que se apropie de las ideas que subyacen en la construcción de sus nociones y procedimientos, destacando su carácter de herramientas para resolver problemas reales que atañen al estudio del cambio. Su característica distintiva de integrar la práctica de la predicción como promotora del surgimiento y evolución del Cálculo le permite constituirse en una propuesta global para el aprendizaje, cuyo interés no está puesto en conceptos ni en temas aislados, sino en la totalidad del discurso, donde cada parte es explicable por el todo y a su vez el todo se explica por sus partes.

Al introducir el acercamiento newtoniano juega un papel fundamental la selección de una secuencia de problemas que introducen paulatinamente al estudiante al proceso de aproximar el valor de una magnitud bajo estudio a través de cierto procedimiento numérico. El método de Euler, nombre con el que se identificará tal procedimiento en el discurso escolar, permite la incorporación simultánea de las nociones razón de cambio y cambio acumulado, y propicia que las nociones de derivada e integral se vean implicadas desde el inicio de un primer curso de Cálculo. El efecto de esta incorporación simultánea y temprana de dichas nociones se ha convertido en un objeto de investigación con el propósito de robustecer la propuesta; a ello está dirigida la investigación en curso de Salinas, dirigida por Alanís.

En el tiempo que hemos dedicado a construir la propuesta nos hemos sentido obligados a establecer formalmente las nociones y procedimientos del Cálculo. Pero, ¿hasta qué punto es esto necesario cuando el estudiante ha ganado un significado para ellos y, con él, la credibilidad de su utilidad para solucionar la problemática de predicción que ha acompañado al discurso? ¿No será ésta más bien una inquietud de quienes hemos aprendido matemáticas bajo una visión de sistema conceptual lógicamente estructurado? ¿Qué tan conveniente sería que quienes tienen deseos y capacidad para trabajar la matemática en su presentación formal y rigurosa transiten antes por su calidad de herramienta para resolver problemáticas reales y vivan la necesidad de fundamentar el conocimiento práctico adquirido?

Tales inquietudes nos siguen acompañando y comienzan a ventilarse en la comunidad de investigadores. Eso entendemos cuando Artigue comenta que la transición hacia niveles elevados de conceptualización —objetos definidos formalmente— requiere de reconstrucciones de una naturaleza diferente. "Los conceptos formalizados, como el concepto formalizado de límite, no pueden ser construidos en continuidad con recursos intuitivos asociados a la experiencia social y física" (2003, p. 219).

 

7. UNA REFLEXIÓN FINAL

En este artículo presentamos una clasificación que no pretende ser exhaustiva, pero permite evidenciar una tendencia en los cambios tocantes a la enseñanza del Cálculo para mejorar su aprendizaje. Observamos las acciones inmediatas que responden a una afectación del cómo enseñar y buscan allanar el camino hacia el trato formal y riguroso de las nociones en juego. Luego, notamos que el estudio de la historia de la matemática influye en el diseño de experiencias didácticas que retoman caminos ocurridos en la generación del conocimiento y plantean nuevas expectativas, incluso de dificultades. Además, identificamos en el acercamiento socioepistemológico una manera peculiar de estudiar la historia que llega a problematizar el qué enseñar, y promueve una didáctica en escenarios socioculturales donde las prácticas favorecen la necesidad de conceptos; una afectación del cómo enseñar se induce en reciprocidad.

Por otro lado, a través de revisar estudios que organizan los alcances de la investigación, situamos el ejercicio de un paradigma tradicional de la enseñanza del Cálculo en la institución educativa donde somos profesores. La institución, atenta a la innovación, ha propiciado el surgimiento de una nueva propuesta para la enseñanza del Cálculo —actualmente en proceso de consolidación— que se enmarca en el acercamiento socioepistemológico, y toma a la práctica de predicción como hilo conductor en el desarrollo de las nociones y procedimientos del Cálculo.

En 1995, Artigue expresó: "el mundo de la investigación, por un lado, y el de la innovación, por el otro, están lejos de establecer vínculos estrechos" (1995, p. 98). Con nuestra propuesta queremos mostrar un esfuerzo por relacionar dichos mundos. El esfuerzo se circunscribe a una institución educativa donde se tiene la responsabilidad de construir una propuesta global para la enseñanza del Cálculo, cuya difusión sea apoyada con la publicación de libros de texto. Dicha responsabilidad ha exigido estar al tanto de los nuevos resultados en la investigación mundial, incluso si se hace sobre el aprendizaje de conceptos en una presentación tradicional. Asimismo, ha sido necesario día con día experimentar la enseñanza ante 40 estudiantes de cada curso, lo cual nos ha exigido una preparación como profesores e investigadores para estar alerta sobre cómo está habitando la propuesta.

Asumir que la investigación educativa permee a la práctica docente es una acción que compromete la toma de decisiones para dar cabida a la innovación. Los riesgos que esto implica se han corrido, ya que los aspectos relativos a la capacitación de profesores y los aprendizajes previos de los estudiantes han sido manejados en lo posible. Sin embargo, cuando se posee la actitud de compromiso con el ejercicio de la crítica y la autocrítica —actitud característica del profesor investigador— cada pregunta resuelta es el final de un proceso y, a la vez, el inicio de uno nuevo.

 

AGRADECIMIENTOS

Los autores agradecen al Instituto Tecnológico y de Estudios Superiores de Monterrey (ITESM) el apoyo recibido para realizar este trabajo en la Cátedra de Investigación en Matemática Educativa del campus Monterrey.

 

REFERENCIAS BIBLIOGRÁFICAS

Alanís, J. A. (1996). La predicción: un hilo conductor para el rediseño del discurso escolar del Cálculo. Tesis de doctorado, Cinvestav, México        [ Links ]

Alanís, J. A. (2000). La predicción: un hilo conductor para el desarrollo de un curso de Cálculo. En R. Cantoral (Ed.), El futuro del Cálculo Infinitesimal. ICME 8 (pp. 233–245). México: Grupo Editorial Iberoamérica.        [ Links ]

Artigue, M. (1995). La enseñanza de los principios del Cálculo: problemas epistemológicos, cognitivos y didácticos. En M. Artigue, R. Douady, L. Moreno y P. Gómez (Eds.), Ingeniería didáctica en educación matemática (pp. 97–140). México: Grupo Editorial Iberoamérica.        [ Links ]

Artigue, M. (2001). What can we learn from educational research at the university level? In D. Holton (Ed.), The teaching and learning of mathematics at university level: an ICMI study (pp. 207–220). Holland: Kluwer Academic.        [ Links ]

Artigue, M. (2003). Reaction. Learning and teaching analysis: What can we learn from the past in order to think about the future? In D. Coray, F. Furinghetti, H. Gispert, B. R. Hodgson & G. Schubring (Eds.), One hundred years of l'enseignement mathématique: moments of mathematics education in the twentieth century. Monograph No. 39 (pp. 211–223). Genova, Italia: L'Enseignement Mathématique.        [ Links ]

Bingolbali, E., Monaghan, J. & Roper, T. (2007). Engineering students' conceptions of the derivative and some implications for their mathematical education. International Journal of Mathematical Education in Science and Technology 38 (6), 763–777.        [ Links ]

Buendía, G. & Cordero, F. (2005). Prediction and the periodical aspects as generators of knowledge in a social practice framework. A socioepistemological study. Educational Studies in Mathematics 58 (3), 299–333.        [ Links ]

Cabanas, G. y Cantoral, R. (2006). La integral definida: un enfoque socioepistemológico. En C. Dolores, G. Martínez y R. Farfán, et al. (Eds.), Matemática educativa: algunos aspectos de la socioepistemología y la visualización en el aula (pp. 3–25). México: Días de Santos.        [ Links ]

Cantoral,R. (2004). Desarrollo del pensamiento y lenguaje variacional, una mirada socioepistemo lógica. Acta Latinoamericana de Matemática Educativa 17(1), 1–9. México: Comité Latinoamericano de Matemática Educativa A. C.        [ Links ]

Cantoral, R., Cordero, F., Farfán, R. e Imaz, C. (1990). Cálculo–Análisis. Una revisión de la investigación educativa reciente en México. En R. Cantoral, F. Cordero, R. Farfán y C. Imaz (Eds.), Memorias del Segundo Simposio Internacional sobre Investigación en Educación Matemática (pp. 55–69). México: Universidad Autónoma del Estado de México.        [ Links ]

Cantoral, R. y Farfán, R. (2003). Mathematics education: A vision of its evolution. Educational Studies in Mathematics 53 (3), 255–270.        [ Links ]

Cantoral, R., Farfán R. M., Lezama, J. y Martínez–Sierra, G. (2006). Socioepistemología y representación: algunos ejemplos. Revista Latinoamericana de Investigación en Matemática Educativa. Número Especial, 83–102.        [ Links ]

Cantoral, R. y Mirón, H. (2000). Sobre el estatus de la noción de derivada: de la epistemología de Joseph Louis Lagrange al diseño de una situación didáctica. Revista Latinoamericana de Investigación en Matemática Educativa 3 (3), 265–292.        [ Links ]

Duval, R. (2002). Representation, vision and visualization: Cognitive functions in mathematical thinking. Basic issues for learning. In F. Hitt (Ed.), Representations and mathematics visualization (pp. 311–336). México: PMENA–Cinvestav–IPN.        [ Links ]

Farmaki, V. & Paschos, T. (2007). Employing genetic 'moments' in the history of mathematics in classroom activities. Educational Studies in Mathematics 66, 83–106.        [ Links ]

Gascón, J. (2001). Incidencia del modelo epistemológico de las matemáticas sobre las prácticas docentes. Revista Latinoamericana de Investigación en Matemática Educativa 6 (1), 129–159.        [ Links ]

Gordon, S. P. & Gordon, F. S. (2007). Discovering the fundamental theorem of calculus. Mathematics Teacher 100 (9), 597–604.        [ Links ]

Gravemeijer, K. & Doorman, M. (1999). Context problems in realistic mathematics education: A calculus course as an example. Educational Studies in Mathematics 39, 111–129.        [ Links ]

Jankvist, U. T. (2009a). A categorization of the "whys" and "hows" of using history in mathematics education. Educational Studies in Mathematics 71, 235–261.        [ Links ]

Jankvist, U. T. (2009b). On empirical research in the field of using history in mathematics education. Revista Latinoamericana de Investigación en Matemática Educativa 12 (1), 67–101.        [ Links ]

Moreno–Armella, L., Hegedus S. & Kaput, J. (2008). From static to dynamic mathematics: historical and representational perspectives. Educational Studies in Mathematics 68, 99– 111.        [ Links ]

Pulido, R. (1997). Un estudio teórico de la articulación del saber matemático en el discurso escolar: la transposición didáctica del diferencial en la fisica y la matemática escolar. Tesis de doctorado, Cinvestav, México.        [ Links ]

Pulido, R. (2007). De la regla de tres a la ecuación de continuidad (o la innovación en la enseñanza y aprendizaje del Cálculo). En R. Cantoral, O. Covián, R. Farfán, J. Lezama y A. Romo (Eds.), Investigaciones sobre enseñanza y aprendizaje de las matemáticas: Un reporte latinoamericano (pp.113–132). México: Clame.        [ Links ]

Robert, A. & Speer, N. (2001). Research on the teaching and learning of Calculus/Elementary analysis. In D. Holton (Ed.), The teaching and learning of mathematics at university level: An ICMI study (pp. 283–299). Holland: Kluwer Academic.        [ Links ]

Salinas, P., Alanis, J. A., Pulido, R., Santos, F., Escobedo, J. C. y Garza, J. L. (2002). Elementos del Cálculo: Reconstrucción conceptual para el aprendizaje y la enseñanza. México: Trillas.        [ Links ]

Salinas, P., Alanís, J. A., Pulido, R., Santos, F., Escobedo, J. C. y Garza, J. L. (2003). Matemáticas preuniversitarias. Significado de nociones y procedimientos. México: Trillas.        [ Links ]

Salinas, P. y Sánchez, T. (2009). Valoración del ejercicio de una nueva manera de enseñar Cálculo. En C. Narváez y N. Yépiz (Eds.), Memorias del III Congreso de Investigación, Innovación y Gestión Educativas. México: Instituto Tecnológico y de Estudios Superiores de Monterrey.        [ Links ]

Steen, L. A. (2003). Analysis 2000: challenges and opportunities. In D. Coray, F. Furinghetti, H. Gispert, B. R. Hodgson & G. Schubring (Eds.), One hundred years of I'enseignement mathématique: moments of mathematics education in the twentieth century. Monograph No. 39 (pp. 191–210). Genova, Italia: L'Enseignement Mathématique.        [ Links ]

Thompson, P. W. & Silverman, J. (2007). The concept of accumulation in calculus. In M. Carlson & Rasmussen(Eds.), Making the connection: Research and teaching in undergraduate mathematics (pp.117–131). Washington D.C.: Mathematical Association of America.        [ Links ]

Tzanakis, C. & Arcavi, A. (2000). Integrating history of mathematics in the classroom: An analytic survey. In J. Fauvel y J. van Maanen (Eds.), History in mathematics education: An ICMI study (pp. 201–240). Dordrecht, The Netherlands: Kluwer. Kluwer.        [ Links ]

Zhang, B. (2003). Using student–centered teaching strategies in calculus. In M. Peat (Ed.), The China papers: Tertiary science and mathematics teaching for the 21^st century 2, 100–103.        [ Links ]