Serviços Personalizados
Journal
Artigo
Indicadores
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista latinoamericana de investigación en matemática educativa
versão On-line ISSN 2007-6819versão impressa ISSN 1665-2436
Relime vol.12 no.3 Ciudad de México Nov. 2009
Artículos
Análisis de una praxeología matemática universitaria en torno al límite de funciones y la producción de los estudiantes en el momento de la evaluación
Analysis of a college mathematics praxeology with respect to the limit of functions and students' productions at the moment of assessment
Ana Rosa Corica* y María Rita Otero**
* Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET); Universidad Nacional del Centro de la Provincia de Buenos Aires, Argentina; acorica@exa.unicen.edu.ar
** Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET); Universidad Nacional del Centro de la Provincia de Buenos Aires, Argentina; rotero@exa.unicen.edu.ar
Recepción: Febrero 27,2009.
Aceptación: Octubre 21,2009.
RESUMEN
Este artículo presenta los resultados parciales de una investigación cuyo propósito es describir y comprender las organizaciones matemáticas en torno al límite de funciones que se estudian en una institución universitaria, así como la producción de los estudiantes en el momento de la evaluación. Se adopta como sustento teórico a la Teoría Antropológica de lo Didáctico.
Dicho estudio se realizó en un curso de Cálculo, al que asistían 283 estudiantes, y correspondía al primer año del ciclo básico que llevaban todas las carreras de Ciencias Básicas y Aplicadas en una Facultad de Ciencias Exactas. Las conclusiones parciales indicarían que en esta universidad se estudian organizaciones matemáticas puntuales y rígidas que sólo conducen a la revisión de algoritmos algebraicos.
PALABRAS CLAVE: Cálculo, organización matemática, Teoría Antropológica de lo Didáctico, nivel universitario.
ABSTRACT
This article presents the partial results of an investigation which aim is to describe and understand mathematical organizations concerning the limit of functions that are studied in a university institution and the students' production at the time of an evaluation. The work is upheld by the Anthropological Theory of Didactics.
This study was carried out in a calculus course attended by 283 students and which corresponded to the first year of the basic cycle common to all Basic and Applied Sciences degree courses in an Exact Sciences faculty. The partial conclusions would indicate that in this university precise and rigid mathematical organizations are studied that only lead to the revision of algebraic algorithms.
KEY WORDS: Calculus, mathematical organizations, Anthropological Theory of Didactics, university level.
RESUMO
Este artigo apresenta resultados parciais de urna investigação cujo objetivo é descrever é compreender as organizações matemáticas em torno do limite de funções que são estudadas numa universidade, assim como a produção de alunos no momento da avaliação. Tem como suporte a Teoría Antropológica da Didática.
Este estado foi realizado num curso de Cálculo, frequentado por 283 alunos, e correspondía ao primeiro ano do ciclo básico de todos os cursos de Ciências Básicas e Aplicadas de urna Faculdade de Ciências Exactas. As conclusoes parciais indicam que nesta universidade são estudadas organizações matemáticas pontuais e rígidas que levam somente a urna revisão de algoritmos algébricos.
PALAVRAS CHAVE: Cálculo, organização matemática, Teoría Antropológica da Didáctica, ensino superior.
RÉSUMÉ
Nous présentons les résultats partiels d'une recherche pour décrire et comprendre les Organisations Mathématiques autour de la Limite de fonctions qui sont étudiées dans une institution universitaire et la production des étudiants au moment de l'évaluation. Nous avons adopté le cadre théorique la Théorie Anthropologique du Didactique.
L'étude a été réalisée dans un cours de Calcul, composé par 283 étudiants, qui correspond à la première année du cycle basique de toutes les carrières relatifs à la formation dans les Sciences Basiques et Appliquées dans une Faculté de Sciences Exactes. Les conclusions partielles indiqueraient que dans l'Université s'étudient des Organisations Mathématiques ponctaelles et rigides qu'ils conduisent seulement à la revision d'algorithmes algébriques.
MOTS CLÉS: Calcul, organisation mathématique, Théorie Anthropologique du Didactique, niveau universitaire.
1. INTRODUCCIÓN
Los problemas en educación matemática son diversos y de diferente naturaleza; sin embargo, autores como Artigue (1998) y Contreras (2001) comparten la idea de que la enseñanza del Cálculo en el nivel universitario es uno de los puntos más problemáticos. En la educación superior, el Cálculo ocupa un lugar central, ya que "sus vínculos tanto con las matemáticas elementales como con la matemática avanzada, así como su papel en la matemática y en las ciencias, lo hacen un conjunto de conocimientos con valor teórico y empírico indispensable en la educación superior" (Farfán, 1997, p.l).
En la investigación que atañe a la didáctica de las matemáticas es conocido que las prácticas actuales del Cálculo se basan en la transmisión de conocimientos, donde se enfatiza el desarrollo de habilidades algebraicas y se desatiende la búsqueda de comprensión sobre las nociones (Artigue, 1998; Contreras, 2001; Zúñiga, 2007). Para iniciar un estudio relativo a los tratamientos didácticos de las nociones de Cálculo, consideramos fundamental iniciar con la noción de límite, ya que ocupa una posición central en este campo. En primer lugar, como objeto matemático que se gesta en diferentes contextos: geométricos, aritméticos, métrico, topológico y asociado a otros objetos matemáticos, de ahí que se convierta en el eje central sobre el que se estructura el cálculo diferencial e integral y otras nociones de las diferentes ramas de la matemática. Y en segundo lugar, por su carácter instrumental porque es una herramienta para abordar los problemas que nacen en el interior de la matemática y en las ciencias aplicadas (Bezuidenhout, 2001; Cornu, 1991; Dorier, 1995).
Las investigaciones que se han desarrollado en el ámbito de la enseñanza–aprendizaje de las nociones de Cálculo han experimentado durante los últimos años una evolución significativa en sus enfoques y propósitos. Transitaron por los estudios que caracterizaron las dificultades y obstáculos en el aprendizaje de nociones de Cálculo, acompañados por aspectos de naturaleza epistemológica, cognitiva y didáctica (Aparicio y Cantoral, 2006; Artigue, 1995; Azcarate y Delgado, 1996; Bezuidenhout, 2001; Cornu, 1991; Crespo, 2004; Godino, Contreras y Font, 2006; Sierra, González y López, 2000; Tall, 1991; Tall y Vinner, 1981). También se ha documentado que ciertos problemas derivan del tipo de tratamiento escolar que se confiere a las nociones de función, límite, continuidad, diferenciación e integración (Azcarate y Deulofeu, 2000; Aparicio y Cantoral, 2003; Hitt, 1994; Tall y Vinner 1981). Otros trabajos se han preocupado por analizar las razones que subyacen a tales dificultades y por proporcionar soluciones efectivas, a través de propuestas didácticas que se sustentan en diversos marcos teóricos (Blázquez y Ortega, 2002; Espinoza y Azcarate, 2000; Mamona–Downs, 2001; Tall, 1986; Tall, Blokland, & Kok, 1990).
En los últimos años de estudio sobre la didáctica de la matemática en el ámbito universitario, los investigadores han trasladado el foco de interés del alumno al profesor, o al menos empezaron a verlos como componentes del sistema didáctico que compartían el mismo protagonismo. Esto ha mostrado la complejidad que implica el estudio de la matemática en la universidad, no sólo por las características del profesor y de los estudiantes, sino también por los cursos de matemática universitaria y los rasgos de la universidad como institución, que condiciona, limita y determina los límites de actuación (Moreno, 2003).
Nuestra investigación ahonda en las características de la enseñanza de la matemática en la Universidad; de manera especial, se centra en el análisis didáctico sobre la actividad matemática del profesor universitario en torno al estudio del límite funcional, a partir de la Teoría Antropológica de lo Didáctico (Chevallard, 1999). Dicho referencial teórico ha resultado ser una poderosa herramienta para describir las prácticas docentes en un ámbito muy poco explorado, como es el universitario.
A continuación, presentamos los resultados parciales de un estudio hecho en un curso de Cálculo, correspondiente al primer año de una Facultad de Ciencias Exactas, que buscó dar respuesta a las siguientes cuestiones:
1. ¿Qué características tiene la Organización Matemática efectivamente enseñada (OMEE) en el curso de Cálculo?
2. ¿Qué aspectos de la OMEE se consolidan en el momento de la evaluación?
Los datos que reportó este trabajo sirvieron para una tesis de doctorado, que se encuentra en elaboración, acerca de los procesos de enseñanza del límite y continuidad funcional en el nivel universitario. En primera instancia, se hace una breve introducción al marco teórico; luego se describe la metodología empleada y las características de la Organización Matemática que se acaba por reconstruir en el curso. Finalmente, se extraen algunas conclusiones relativas a la gestión de Organizaciones Matemáticas en la universidad.
2. MARCO TEÓRICO
El principio fundamental de la Teoría Antropológica de lo Didáctico (TAD) radica en que toda actividad humana regularmente hecha puede describirse con un modelo único, denominado praxeología (Chevallard, 1999). La noción de praxeología u organización matemática constituye la herramienta fundamental para modelizar cualquier actividad matemática, y consta de dos niveles:
– El nivel de la praxis o del saber hacer, que engloba un cierto tipo de tareas y cuestiones que se estudian, así como las técnicas para resolverlos.
– El nivel del logos o del saber, en el que se sitúan los discursos que describen, explican y justifican las técnicas que se utilizan, los cuales reciben el nombre de tecnología. Dentro del saber se postula un segundo nivel de descripción–explicación–justificación (esto es, el nivel tecnología de la tecnología) que se denomina teoría.
Para Chevallard, Bosch y Gascón (1997), el sistema de tareas de los docentes muestra dos grandes componentes asociados:
– Las tareas de concepción y organización de mecanismos de estudio1, así como la gestión de sus medios ambientes (Organizaciones Matemáticas).
– Las tareas de ayuda al estudio, particularmente la dirección de estudio y enseñanza, cuyo cumplimiento es debido a la puesta en ejecución de técnicas didácticas determinadas (Organizaciones Didácticas).
2.1. La Organización Matemática
Una Organización Matemática (OM) se constituye alrededor de uno o varios tipos de tareas matemáticas que conducen a la creación de técnicas matemáticas, las cuales se justifican por tecnologías matemáticas desarrolladas en el marco de una teoría matemática.
Los términos tipo de tarea, técnica, tecnología y teoría son doblemente relativos. En primer lugar, son relativos a la institución de referencia: lo que es considerado como un tipo de tarea — o bien una técnica, tecnología o teoría— en una institución no tiene que serlo en otra. Las técnicas existen en la medida en que pueden responder a algún tipo de tarea planteada en la institución considerada. En segundo lugar, las nociones tipo de tarea, técnica, tecnología y teoría son relativas a la función que cumplen en una actividad matemática determinada. Así, un mismo objeto matemático (por ejemplo, el teorema de Bolzano) puede ser considerado como una técnica para realizar un tipo de tareas (por ejemplo, para demostrar que toda función polinómica de tercer grado tiene por lo menos un cero real) o servir como elemento tecnológico común a un conjunto de tipos de tareas y técnicas (por ejemplo, las técnicas de cálculo aproximado de ceros de funciones polinómicas).
Los cuatro elementos citados son imprescindibles para construir cualquier praxeología; sin embargo, Chevallard (1999) también propone la noción género de tareas, con la que se refiere a un contenido que se encuentra especificado. La noción tipo de tarea supone un objeto relativamente preciso. Por ejemplo, calcular el valor límite de una función en un punto es un tipo de tarea, pero calcular es lo que se denomina un género de tareas (se caracteriza por solicitar un determinativo).
Un género de tareas no existe más que bajo la forma de diferentes tipos de tareas. Durante toda la escolaridad, por ejemplo, el género calcular se enriquece de nuevos tipos de tareas: tal vez en un principio los estudiantes comiencen por simples cálculos aritméticos, luego aprendan a realizar cálculos con vectores y más tarde a calcular una integral, etc. También ocurrirá lo mismo con los géneros demostrar, construir, etc.
A su vez, Chevallard (1999) introdujo la distinción de diferentes tipos de OM, según el grado de complejidad de sus componentes:
– Organizaciones Puntuales (OMP): Están generadas por lo que se considera en la institución como un único tipo de tarea y está definida a partir del bloque práctico–técnico.
– Organizaciones Locales (OML): Es el resultado de integrar diversas praxeologías puntuales. Cada praxeología local se caracteriza por una tecnología que sirve para justificar, explicar, relacionar entre sí y producir las técnicas de todas las praxeologías puntuales que la integran.
– Organizaciones Regionales (OMR): Se obtienen mediante la coordinación, articulación y posterior integración de diversas praxeologías locales a una teoría matemática en común.
– Organizaciones Globales (OMG): Surgen al agregar varias praxeologías regionales a partir de la integración de diferentes teorías.
2.2. Las Organizaciones Didácticas
Las Organizaciones Didácticas (OD) son el resultado de un trabajo complejo y continuado que se lleva a cabo durante largo tiempo en las instituciones, cuya dinámica de funcionamiento incluye a ciertas relaciones invariables que es posible modelizar. Aquí se presentan los dos aspectos inseparables del trabajo matemático: el proceso de construcción matemática, que atañe al estudio, y el resultado mismo de esta construcción, la OM. En efecto, no hay OM sin un proceso de estudio que la engendre, pero tampoco hay proceso de estudio sin una OM en construcción (Bosch, Espinozay Gascón, 2003).
La consideración de los diversos procesos que conciernen a la construcción matemática permite identificar sus aspectos invariantes, es decir, las dimensiones o momentos que estructuran cualquier proceso de elaboración matemática, independientemente de sus características culturales, sociales, individuales o de otra índole. Así, el proceso de estudio se sitúa en un espacio determinado por seis momentos didácticos:
1. El momento del primer encuentro con un determinado tipo de tareas.
2. El momento exploratorio del tipo de tareas.
3. El momento de construcción de un entorno tecnológico–teórico, que explica y justifica las técnicas puestas en funcionamiento y permite la elaboración de nuevas técnicas.
4. El momento de trabajo de la técnica, que provoca la evolución de las técnicas existentes y la construcción de nuevas.
5. El momento de la institucionalización, que delimita y precisa aquellos elementos constituyentes de la organización matemática construida.
6. El momento de la evaluación de la praxeología construida.
Cada momento puede ser vivido con distintas intensidades en diversos tiempos, tantas veces como se necesite a lo largo del proceso de estudio e, incluso, es habitual que algunos aparezcan de manera simultánea.
2.3. Unidad mínima de análisis didáctico
La unidad mínima de análisis es un constructo teórico fundamental cuya estructura y dinámica son descritas mediante los términos primitivos de la teoría, por lo cual debe remitir a un conjunto de indicadores empíricos. Por tanto, la unidad de análisis ocupa un lugar central y privilegiado en la relación entre la teoría y los datos empíricos, ya que conforma uno de los rasgos esenciales para caracterizar la disciplina en cuestión. Ahora bien, para describir e interpretar los hechos didácticos hay que referirlos a una secuencia del proceso didáctico que incluya, por lo menos, al proceso de reconstrucción escolar de una OML. Es decir, esta OM se define como unidad mínima de análisis didáctico (Bosch y Gascón, 2005).
Con el fin de precisar lo anterior, tomemos en cuenta el siguiente esquema de la transposición didáctica (Chevallard, 1985):

En el Esquema 1, I1 es la institución productora del saber matemático, I2 la noosfera, I3 la institución escolar e I4 la comunidad de estudio, protagonista del proceso didáctico. El saber aprendido se compone de aquellos elementos praxeológicos que al final del proceso didáctico integrarán el medio matemático del grupo, y podrán ser utilizados por la comunidad de estudio, de manera relativamente no problemática, para que hagan nuevos tipos de tareas y el estudio de nuevas cuestiones. La TAD postula que no es posible explicar las características del saber aprendido (ni ninguno de los fenómenos didácticos que emergen en I4) sin tomar en consideración todas las etapas de la transposición.
Además, como la unidad de análisis de los procesos didácticos tiene que contener una organización didáctica escolar que permita construir como mínimo una OML, puede reconstruirse artificialmente en la institución escolar, al ser el resultado final de un proceso de ampliaciones y complementaciones progresivas. La OMP transita por una serie de praxeologias intermedias, que generan de manera sucesiva un determinado desarrollo evolutivo de las cuestiones problemáticas y los tipos de tareas asociados, los cuales serán las razones de ser de la OML en I3. Por tanto, la OD asociada a dicha OML contiene en cierta forma a la OML y a todas las OM que la preceden en el proceso de construcción.
Sobre la OD inciden las restricciones que provienen de las diferentes etapas de la transposición didáctica, que se manifiestan tanto en la OM efectivamente enseñada como en la OM a enseñar y en la OM aprendida:
a) La OM a enseñar constituye un modelo praxeológico de las matemáticas que se proponen en el diseño curricular. La matemática a enseñar no se presenta al profesor como una OM estructurada y provista de una razón de ser, sino como un conjunto de materiales praxeológicos —tareas, técnicas y elementos tecnológicos— bastante desarticulados.
b) Pero estas restricciones que provienen de la OM a enseñar no pueden ser adecuadamente interpretadas si no se dispone de un punto de vista epistemológico, que proporciona la OM de referencia, cuya descripción necesita hacerse a partir de determinadas OM sabias que legitiman de forma epistemológica el proceso de enseñanza. La OM de referencia es la que ocupa el investigador para realizar su análisis y no coincide necesariamente con la OM sabia de la cual proviene, aunque se formula en términos próximos a ésta y a la OM a enseñar.
c) Finalmente, la OD dependerá de las restricciones transpositivas que proceden de las características de la OM aprendida a la que conducirá el proceso didáctico, y de la manera cómo la institución escolar interprete los objetivos de este proceso.
Asumimos como exigencia metodológica que el análisis de los problemas didácticos debe considerar a todas las etapas de la transposición didáctica. Esto implica la necesidad de utilizar los datos empíricos que emergen de todas y cada una de las instituciones citadas.
De acuerdo con la metodología que se desprende del marco teórico, en la globalidad de nuestra investigación se definió a una Organización Matemática de Referencia y se reconstruyó la Organización Matemática a enseñar y efectivamente enseñada. De esta última, resaltamos que sólo por fines prácticos del análisis hicimos una descripción en la que consideramos, por un lado, los componentes matemáticos que se acaban por estudiar; por otro, los componentes didácticos que conducen a tal estudio. Aclaramos que no se puede emprender el estudio de una OM sin una OD que la engendre, ni se puede poner en juego ninguna OD sin una OM que estudiar. Focalizamos nuestra atención en la descripción de la OM que se acaba por estudiar.
3. METODOLOGÍA
Se propone un estudio de corte descriptivo e interpretativo sobre un curso de Cálculo, denominado Análisis Matemático I (AMI), que se imparte en una Facultad de Ciencias Exactas de una universidad argentina. El curso, que se compone de 283 estudiantes —cuyas edades oscilan entre los 18 y 20 años— corresponde al primer año de las carreras de Ingeniería en Sistemas, las licenciaturas en Matemática, en Física o en Tecnología Ambiental, así como los profesorados en Matemática, en Física o en Informática. Por ello, es uno de los pilares básicos para la formación.
3.1. Descripción de la organización institucional de AMI
El curso de Análisis Matemático I dura cuatro meses, y se compone de clases teóricas (CT) y prácticas (CP), que se imparten dos veces por semana. Cada CT comprende 90 minutos, mientras que cada CP 120 minutos. Asimismo, se ofrece semanalmente una clase de consulta, que dura 120 minutos, donde los estudiantes tienen la oportunidad de hacer consultas en forma personalizada.
El curso está a cargo de un profesor (P1), quien se ocupa exclusivamente de organizar y dirigir las CT, un coordinador (P2), quien organiza las CP y dirige en ciertas ocasiones las CT, y de profesores que dirigen las CP. Las CT se ofrecen a todos los estudiantes en un aula tipo anfiteatro, mientras que las CP son desarrolladas en cuatro aulas. Estas clases las imparten el profesor responsable, cuya principal actividad es dirigir la sesión para las tareas propuestas, decidir las técnicas a emplear y las instancias de clase en que se abordan, y dos profesores ayudantes, que cumplen el rol de asistir a las consultas de los alumnos en forma personalizada. Ahora bien, la actividad en las CT se ciñe a que el profesor muestre la resolución de las tareas, con muy baja participación de los estudiantes. En las CP el profesor también presenta la resolución de las tareas, pero hay mayores oportunidades de diálogo con los alumnos; además, se destina aproximadamente una hora de cada CP para que los estudiantes resuelvan tareas y consulten sus dudas personales.
Durante los cuatro meses que comprende el curso se propone estudiar nueve unidades temáticas, cuyo desarrollo incluye material teórico y práctico:
1. Estructura del conjunto de los números reales
2. Funciones
3. Sucesiones de números reales
4. Límite y continuidad de funciones
5. Derivadas
6. La integral definida
7. Cálculo de primitivas
8. Series numéricas
9. Series de funciones, series de potencias y serie de Taylor
El diseño del material teórico, que está a cargo del P1; consta de teoremas, definiciones y proposiciones fundamentales para el proceso de estudio sobre las OM. Por su parte, el material para las CP, que diseña el P2, básicamente se estructura del siguiente modo: una introducción, en la que se enuncian los principales teoremas, definiciones y proposiciones para realizar los tipos de tarea, y la presentación de algunos ejercicios resueltos.
La acreditación del curso propone la aplicación de exámenes individuales y escritos. Se ofrecen dos formas para la evaluación, y los estudiantes tienen que optar por una:
Modalidad promoción: Consiste en tres exámenes individuales y escritos; en cada uno se evalúa una unidad temática o módulo, y hay dos instancias para poder volver a presentarlos en caso de no aprobarlos (a estos tipos de evaluación se les denomina de compensación). Los exámenes se integran con tareas de características similares a las estudiadas tanto en las CP como en las CT, y se aprueban con 4 puntos de 10. Esta opción de evaluación permite promocionar el curso2, al obtener 7 o más en cada uno de los exámenes o en los primeros exámenes de compensación.
Modalidad tradicional: Consta de un examen parcial, individual y escrito, que evalúa tareas de características similares a las desarrolladas en las CP, y también contempla dos exámenes de compensación. Los exámenes se aprueban con 4 puntos como mínimo sobre 10 puntos, ya sea en el examen parcial o en los dos de compensación. La aprobación implica sólo la cursada de los módulos y requiere que los estudiantes presenten a posteriori (en un término de tres años) un examen, escrito e individual, que incluye tareas similares a las estudiadas en las CP y CT para concluir la aprobación del curso.
Los exámenes de promoción se aplican aproximadamente cada 4 ó 5 semanas, mientras que los de tradicional ocurren al finalizar todo el desarrollo del curso.
3.2. Recolección de datos
Durante el año 2005, en el curso de Cálculo se realizaron tres meses de observación no participante y se recabaron las versiones en audio de las clases teóricas y prácticas, las explicaciones que hicieron los profesores en el pizarrón, los apuntes de clase de los alumnos y los exámenes de los estudiantes.
El proceso de estudio sobre el límite funcional sucedió en dos CT y dos CP. Los registros de audio de las CT se llevaron a cabo en las aulas tipo anfiteatro, con un sistema que llevaba el profesor. También se registró toda la escritura que hizo el profesor en el pizarrón, lo cual dio mayor claridad en el momento de reconstruir la OM.
En las CP, el sistema de audio fue llevado por un profesor ayudante, con el cual se recabó la actividad del profesor responsable y también algunas consultas de los estudiantes al profesor ayudante. Tal procedimiento en las CP se llevó a cabo en dos de los cuatro cursos que se desarrollaban por cada encuentro semanal. Se trabajó con aquellos cursos donde los profesores ayudantes llevaban el sistema de audio; sin embargo, el seguimiento de determinadas CP fue imposible porque los profesores, en ocasiones, no se ocupaban de los mismos cursos, de ahí que no se mantuviera la continuidad en el proceso de estudio. Además, para un mismo curso de CP nada garantizaba que fueran los mismos alumnos porque la asistencia no era obligatoria, y podían concurrir a cualquiera de las cuatro CP del mismo tipo que se impartían cada semana, optando por aquella que mejor se ajustara a sus conveniencias.
3.3. Instrumento de análisis
El análisis sobre las clases del curso requirió que fueron transcritos los audios de la totalidad de aquellas relativas al estudio del límite funcional. Luego, a los registros de cada clase se les segmentó en episodios para distinguirlos cuando el discurso giraba en torno a una determinada tarea. Con el objeto de organizar y estudiar los datos obtenidos en cada clase, se elaboraron dos tablas; la Tabla I nos permitió efectuar un análisis profundo acerca del proceso de estudio, como lo vivieron sus protagonistas.

La Tabla I colocó los géneros de tareas junto a las tareas que los integraban; dichos aspectos fueron tratados en el aula por sugerencia del profesor. Asimismo, recogió el conjunto de acciones que se llevaron a cabo en el aula para resolver una cierta tarea (técnicas) y los elementos tecnológicos que aparecieron en la clase de manera explícita (bloque tecnológico).
La Tabla II constó de un material que nos permitió hacer un análisis global sobre el proceso de estudio. En la tabla se distinguió el momento predominante del estudio en cada episodio, así como los momentos secundarios (aquí se ofrece información para que el observador se sitúe en el proceso de estudio y lea su desarrollo de manera compacta). Además, registró los gestos del profesor y los alumnos durante el proceso de estudio, focalizando la atención en el tipo de preguntas que formulaba el profesor y el tipo de respuesta que se obtenía de los estudiantes. Por cuestiones de espacio, y por no formar parte del análisis que muestra este trabajo, no detallamos completamente dicha tabla.

3.4. Metodología para el análisis de los exámenes
Para este estudio se consideraron los exámenes que constaban de tareas vinculadas exclusivamente al límite funcional: el primer parcial por módulo, el primer examen de compensación por módulo y el primer examen de compensación por parcial. Esto condujo a la recolección de 337 exámenes, en los que se analizaron las producciones de los estudiantes; a cada tarea se le asignó un puntaje de acuerdo con los objetivos de nuestra investigación.
4. ANÁLISIS DE RESULTADOS
4.1. Análisis de las clases de AMI
La Organización Matemática efectivamente enseñada (OMEE) apareció como resultado del proceso de estudio, al ser el producto de las prácticas que el profesor desarrolló con sus alumnos en el aula. Para organizar nuestra presentación, se adoptó la siguiente notación:
Gx: Género de tareas.
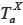 : Tipo de tarea que conforma al género de tarea Gx.
: Tipo de tarea que conforma al género de tarea Gx.
 : Tarea correspondiente a
: Tarea correspondiente a 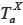 .
.
Aquí hacemos la distinción entre tarea y tipo de tarea en el siguiente sentido: la identificación de la tarea nos permitió definir las OMP que se acababan de estudiar, mientras que los tipos de tarea reúnen a ciertas tareas que difieren entre sí por pequeñas variaciones en las técnicas que se emplean para hacerlas, pero tienen características en común que las reúnen bajo el mismo tipo de tareas.
En el curso de Cálculo, las funciones que se estudian son de una variable real; por tanto, cada vez que hablemos de funciones nos referiremos a este tipo. En la siguiente presentación, para indicar que la variable tiende a un cierto valor real empleamos la notación x x0, y para señalar que la variable tiende a infinito escribimos x
x0, y para señalar que la variable tiende a infinito escribimos x ∞.
∞.
A continuación, mostramos los resultados que generó el análisis de los datos contemplados en la Tabla I, que fue diseñada para cada una de las clases bajo estudio. En las clases se estudian tareas que corresponden a cuatro géneros:
G1: Definir: Engloba aquellos tipos de tareas que tienen como objetivo reconstruir ciertas definiciones matemáticas; la actividad docente se centra en tal reconstrucción, y no sólo en recitar las definiciones.
G2: Demostrar: Engloba aquellos tipos de tareas que requieren de la formulación de una secuencia de enunciados organizados, según determinadas reglas.
G3: Calcular: Hace referencia a tareas que implican llevar a cabo ciertos procedimientos basados en reglas que son tomadas como verdaderas para obtener un resultado; y predecir algunos acontecimientos dentro de la matemática u otras disciplinas.
G4: Representar gráficamente: Engloba a tareas que implican la realización de esquemas y representaciones gráficas.
A continuación, detallamos los tipos de tareas que emergen de cada clase estudiada.
G1 : Definir
 : Definir el límite de funciones de variable real.
: Definir el límite de funciones de variable real.
: Definir el límite de funciones en un punto.
: Definir el límite por derecha de una función cuando x
x0.
: Definir el límite por izquierda de una función cuando x
x0
: Definir límites infinitos.
G2: Demostrar
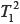 : Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones.
: Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones.
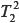 : Demostrar propiedades que relacionan el límite de operaciones entre funciones con el valor del límite de éstas cuando x
: Demostrar propiedades que relacionan el límite de operaciones entre funciones con el valor del límite de éstas cuando x x0.
x0.
: Demostrar la existencia del límite de funciones logarítmicas compuestas con diferentes familias de funciones cuando x
x0.
: Demostrar la existencia del límite de funciones exponenciales compuestas con diferentes familias de funciones cuando x
x0.
: Demostrar la existencia del límite de funciones que resultan de efectuar operaciones entre funciones cuando x
x0.
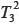 : Demostrar la existencia del límite de funciones cuando x
: Demostrar la existencia del límite de funciones cuando x x0.
x0.
: Demostrar la existencia del límite de funciones trigonométricas.
: Demostrar la existencia del límite de funciones definidas a trozos.
: Demostrar la existencia del límite de funciones que son producto del cociente entre diversas familias de funciones.
G3 : Calcular
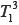 : Calcular el límite de funciones cuando x
: Calcular el límite de funciones cuando x x0.
x0.
: Calcular el límite de funciones definidas a trozos.
: Calcular el límite por derecha de funciones definidas a trozos.
: Calcular el límite por izquierda de funciones definidas a trozos.
: Calcular el límite de funciones trigonométricas.
: Calcular el límite de funciones polinómicas.
: Calcular el límite de funciones que son producto del cociente entre diversas familias de funciones.
: Calcular el límite de funciones que se componen con expresiones irracionales.
: Calcular el límite de funciones exponenciales compuestas con diversas familias de funciones.
: Calcular el límite de funciones logarítmicas compuestas con diversas familias de funciones.
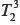 : Calcular el límite de funciones cuando x
: Calcular el límite de funciones cuando x x∞.
x∞.
: Calcular el límite de funciones que son producto del cociente entre diversas familias de funciones.
: Calcular el límite de expresiones compuestas con la expresión
.
: Calcular el límite de funciones que se componen con expresiones irracionales.
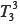 : Hallar un intervalo del dominio de funciones tal que el límite sea l cuando x tiende a un valor real finito.
: Hallar un intervalo del dominio de funciones tal que el límite sea l cuando x tiende a un valor real finito.
: Hallar un intervalo del dominio de funciones definidas a trozos tal que exista el límite conjeturado.
: Hallar un intervalo del dominio de funciones racionales tal que exista el límite conjeturado.
: Hallar un intervalo del dominio de funciones módulo tal que exista el límite conjeturado.
: Hallar un intervalo del dominio de funciones polinómicas tal que exista el límite conjeturado.
G4 : Representar gráficamente
 : Trazar la gráfica de funciones.
: Trazar la gráfica de funciones.
: Trazar la gráfica de funciones de una variable real.
Las tareas que se realizan en el curso hacen patente la relevancia que tiene el estudio de aquellas relativas al cálculo de límite frente a las restantes, ya que 16 tareas conciernen al género calcular, 7 al género demostrar, 4 al género definir y una al género representar gráficamente.
La clasificación de las tareas fue un trabajo complejo porque en el curso se estudia una diversidad de expresiones, lo cual dificultó la intención de agruparlas en aquellas funciones más conocidas por los estudiantes (racional, exponencial, logarítmica, irracional, trigonométrica y polinómica). Es decir, se presenta la más diversa combinación de ellas. Por ello, AMI no propicia el estudio de tareas que permitan trabajar las características de familias de funciones y luego se realicen síntesis sobre su comportamiento.
En el Esquema 2 sintetizamos los principales elementos que constituyen la OMEE relativa al límite funcional. Aquí, cada tipo de tarea define una OMP (a cada OMP la identificamos como OMPx, donde x toma valores numéricos).
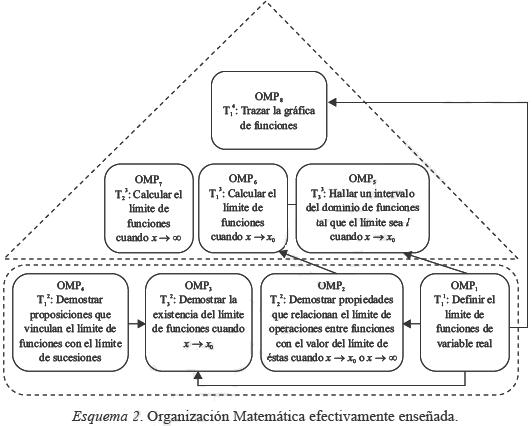
Establecemos que la OMEE reconstruida sobre el límite funcional durante el curso es una OML que se centra en la problemática de determinar la existencia del límite de funciones de variable real. Dicha OML se compone de 8 OMP: las organizaciones OMP1, OMP2, OMP3 y OMP4 se estudian de manera exclusiva en las CT, donde se consolida el bloque tecnológico que justifica algunas técnicas necesarias para realizar los tipos de tarea que integran las restantes OMP. A lo largo del proceso de estudio notamos que surgen una serie de definiciones, teoremas y proposiciones que forman los cimientos de la OMEE; sin embargo, resultan insuficientes, pues en ocasiones se emplean técnicas para resolver algunas tareas que carecen de entorno tecnológico. Es decir, se las presenta como autojustificadas.
El tipo de tarea constitutivo de la OMP1 se identifica con el género de tareas G1 : Definir. La OMP1 se conforma por el tipo de tarea  : Definir el límite de funciones de variable real, que a su vez incluye a cuatro tareas. El tipo de tarea que conforma a la OMP1 hace referencia a interpretar enunciados con el propósito de reconstruir las definiciones fundamentales sobre las que se estructura la OMEE.
: Definir el límite de funciones de variable real, que a su vez incluye a cuatro tareas. El tipo de tarea que conforma a la OMP1 hace referencia a interpretar enunciados con el propósito de reconstruir las definiciones fundamentales sobre las que se estructura la OMEE.
Las OMP2, OMP3 y OMP4 se identifican con el género G2: Demostrar. La OMP4 se integra por el tipo de tarea 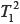 : Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones. Al hacer este tipo de tarea se consolida la tecnología que justifica parte de las técnicas empleadas para llevar a cabo las tareas constitutivas de la OMP3.
: Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones. Al hacer este tipo de tarea se consolida la tecnología que justifica parte de las técnicas empleadas para llevar a cabo las tareas constitutivas de la OMP3.
El tipo de tarea que constituye la OMP2 es el 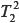 : Demostrar propiedades que relacionan el límite de operaciones entre funciones con el valor del límite de éstas cuando x
: Demostrar propiedades que relacionan el límite de operaciones entre funciones con el valor del límite de éstas cuando x x0, mientras que el tipo de tarea que integra la OMP3 es el
x0, mientras que el tipo de tarea que integra la OMP3 es el 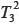 : Demostrar la existencia del límite de funciones cuando x
: Demostrar la existencia del límite de funciones cuando x x0. Destacamos que la tecnología que se consolida en el
x0. Destacamos que la tecnología que se consolida en el 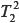 justifica algunas técnicas empleadas para realizar el tipo de tarea que constituye la OMP6.
justifica algunas técnicas empleadas para realizar el tipo de tarea que constituye la OMP6.
El G1 y el G2 no engloban organizaciones aisladas, pues la OMP que engloba el G1 es la base sobre la que se fundamentan las tareas que integran al G2, pero a su vez las tareas que componen al G2 son las que dan sentido a las del G1.
Las OMP5, OMP6 y OMP7 quedan representadas por el género de tareas G3: Calcular. El tipo de tarea que constituye la OMP5 es el 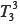 : Hallar un intervalo del dominio de funciones tal que el límite sea I cuando x
: Hallar un intervalo del dominio de funciones tal que el límite sea I cuando x x0, y comprende cuatro tareas. El tipo de tarea que representa a la OMP6 es el
x0, y comprende cuatro tareas. El tipo de tarea que representa a la OMP6 es el 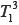 : Calcular el límite de funciones cuando x
: Calcular el límite de funciones cuando x x0, y abarca nueve tareas. El tipo de tarea que define a la OMP7 es el
x0, y abarca nueve tareas. El tipo de tarea que define a la OMP7 es el 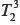 : Calcular el límite de funciones cuando x
: Calcular el límite de funciones cuando x ∞, y tiene tres tareas.
∞, y tiene tres tareas.
Las tareas relativas al G3: Calcular poseen diferente estatus, ya que los tipos de tareas que componen a la OMP6 y la OMP7 aluden a calcular el límite de diferentes funciones con el uso de propiedades del límite funcional, mientras que la tarea constitutiva de la OMP5, de acuerdo con el estudio sobre el material teórico–práctico editado por los profesores del curso, nace bajo la razón de ser: Demostrar la existencia del límite de diferentes familias de funciones de variable real, por lo cual se debería ubicar en el G2: Demostrar. En particular, la OMP5 no debería existir porque el tipo de tarea que la define debería ser el representante de la OMP3, pero como la técnica empleada por los profesores para hacer el tipo de tarea que define a la OMP5 se reduce a determinar un intervalo en el que la función tomaría un valor dado, sin completar tal demostración, consideramos que es funcional a tareas constitutivas del género Calcular.
El bloque tecnológico de la OMP5 se consolida al hacer el tipo de tarea que define la OMP1 mientras que para el tipo de tarea que implica la OMP6 el entorno tecnológico se afirma de manera parcial en la OMP2. Hay algunas propiedades que juegan un rol fundamental para poder realizar el tipo de tarea que conforma la OMP6, pero sólo aparecen enunciadas en el material teórico propuesto por los profesores del curso, sin ser demostradas, lo cual conduce a que se asuman como herramientas incuestionables y utilizables.
Por otro lado, la OMP7 carece de entorno tecnológico porque la OM que se acaba por reconstruir no consolida el ámbito que justifique las técnicas para realizar el tipo de tarea que la constituye3. Este resultado parecería responder a la restricción temporal que enfrentan los profesores del curso, ya que el programa analítico propone el estudio de nueve unidades en un lapso de tiempo muy breve (cuatro meses), y sólo el 10% de las CT y las CP se destinan al estudio del límite funcional. Por ende, ante la necesidad de sacrificar nociones, se rescinde el entorno tecnológico de la OMP7. También consideramos que la reducción del estudio al trabajo aislado de las técnicas atañe a otra restricción: la de las posibilidades de los alumnos y la necesidad del sistema de mostrar algún resultado positivo, ya que algunos alumnos tienen que aprobar el curso.
Finalmente, la OMP8 queda representada por el género de tarea G4 : Representar gráficamente. El tipo de tarea que compone a esta OM es el  : Trazar la gráfica de funciones, mientras que el entorno tecnológico que justifica las técnicas empleadas para realizar este tipo de tarea se consolida en la OMP1.
: Trazar la gráfica de funciones, mientras que el entorno tecnológico que justifica las técnicas empleadas para realizar este tipo de tarea se consolida en la OMP1.
Resaltamos que todas las OMP que se estudian tienen el propósito de mostrar cómo se resuelven las tareas propuestas. No se proponen tareas que lleven al cuestionamiento del entorno tecnológico, que consiste en un aspecto importante sobre la exigencia de justificar las actividades correspondientes. Lo que interesa en AMI es dar respuestas a tareas del tipo cómo; es decir, las respuestas se limitan a una simple información que conducen a elaborar una OML compuesta por OMPs que se vinculan débilmente. Esto es la consecuencia de usar técnicas que sólo viven en la superficie del saber, es decir, que requieren del empleo de vastos elementos tecnológicos y se formulan como únicas e incuestionables. La actividad se concentra en realizar operaciones algebraicas con límites y se desliza hacia posturas algorítmicas más fáciles de gestionar y evaluar, lo cual alimenta un enfoque algebraico y reduccionista del Cálculo.
Las tareas constitutivas del G1 y G2 son abordadas exclusivamente en las CT por los profesores que piensan en el funcionamiento de AMI. Y las tareas que se acaban por estudiar en las CT consolidan parte del entorno tecnológico que justifica las técnicas para realizar las tareas de las CP. Esto es, las tareas que se estudian en las CT garantizan la supervivencia de las que abarcan las CP.
En las CP, el estudio se centra en tareas relativas al género Calcular, y una tarea corresponde al género Representar gráficamente, que se vincula sólo con la OMP1. Mientras que el estudio del tipo de tarea que concierne a la OMP8 pierde relevancia frente a los demás, pues sólo aborda un único ejemplar de tarea en las CP y no propone ninguno de ellos en el momento de evaluación.
La manera en que se gestionan las CT responde a lo que Chevallard ha caracterizado con la analogía del saber monumental. Así, los estudiantes son puestos frente a un saber ya hecho, como si se tratara de un museo que visitan y recorren de manera prefijada, donde los objetos son mostrados y no hay posibilidad de reconstrucción. Sólo los tipos de tareas que componen el G3 y el G4 quedan a cargo de los profesores de las CP, y los estudiantes parecen estar autorizados a involucrase en el hacer de los tipos de tareas, pues la garantía reside en que durante las CT se les mostró lo necesario para poder llevarlo a cabo.
4.2. Estudio de los momentos de evaluación de AMI
El momento de la evaluación se comprende en un sentido amplio porque no hay una correspondencia estricta con lo que se define en la TAD. La permanencia en el campo indica que para los profesores la evaluación se reduce al examen. Ciertamente, esto dista mucho de la definición que propone la TAD sobre el momento de la evaluación, pero el examen es el único elemento relativamente asimilable de la OD a la noción del marco teórico adoptado. En el curso hay una única situación de evaluación: la de examen individual y escrito.
A continuación, se presentan los resultados que arrojó el estudio de las producciones de los alumnos en los exámenes. Nuestro análisis se restringe a las instancias que involucran las tareas relativas al estudio del límite funcional, como se detalla a continuación:
– Primer examen parcial por módulo: El examen abarca cuatro temas, integrados por tres tareas que se relacionan con el estudio del límite funcional. Analizamos 223 exámenes, distribuidos de la siguiente manera: tema 1, 58 exámenes; tema 2, 55; tema 3, 55, y tema 4, 55.
– Primer examen de compensación por módulo: Compuesto por dos tareas vinculadas con el estudio del límite funcional. Estudiamos 67 exámenes.
– Primer examen compensación de parcial: Incluye sólo una tarea que concierne al estudio del límite funcional. Centramos nuestra atención en 47 exámenes.
Las tareas que contemplan los exámenes que se estudian pertenecen a los géneros Demostrar y Calcular. Quedan excluidas las relativas al género Representar gráficamente.
Los tipos de tareas del primer examen parcial por módulo son:
: Calcular el límite de funciones cuando x
x0 o
: Calcular el límite de funciones cuando x
∞
: Hallar un intervalo del dominio de funciones tal que el límite sea I cuando x tiende a un valor real finito
: Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones
Los tipos de tareas que presenta el primer examen de compensación por módulo son similares a los del primer examen parcial por módulo, a excepción de la tarea relativa al género Demostrar, ya que en el primer examen de compensación por módulo no se incluye ninguna tarea referente a tal género.
Por su parte, en el primer examen de compensación por parcial sólo hay una tarea que atañe al estudio del límite funcional, la cual forma parte del 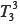 . En esta instancia, los alumnos ya no tienen oportunidad de promocionar el curso, por lo cual se evalúan las tareas que conciernen a las estudiadas en las CP y las pertenecientes a todos los bloques temáticos.
. En esta instancia, los alumnos ya no tienen oportunidad de promocionar el curso, por lo cual se evalúan las tareas que conciernen a las estudiadas en las CP y las pertenecientes a todos los bloques temáticos.
Los ejemplares de tareas en cada examen se detallan a continuación:
A continuación, detallamos los principales resultados que se obtuvieron a partir del análisis a las producciones de los estudiantes en los momentos de evaluación, contemplando a 337 exámenes. Para el estudio de dichas producciones adoptamos un criterio de puntuación congruente con los objetivos de la investigación y las características de las tareas.
El análisis hecho a las producciones de los alumnos, relativas al tipo de tarea 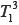 : Calcular el límite de funciones cuando x
: Calcular el límite de funciones cuando x x0 y
x0 y 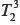 : Calcular el límite de funciones cuando x
: Calcular el límite de funciones cuando x ∞, indica que en el primer examen parcial por módulo el tema 3 presentó dificultades, ya que un gran porcentaje de estudiantes ni siquiera intentaron resolver la tarea o usaron técnicas inadecuadas (87%), mientras que sólo el 4% resolvió correctamente la tarea. Esto contrasta con los resultados obtenidos para el tema 1, pues reúne el mayor porcentaje de alumnos que resolvieron bien la tarea (40%). La gran diferencia de resultados entre los temas 1 y 3 podría atribuirse al tipo de expresión involucrada en el tema 3 y a la relevancia que se da a la tarea involucrada en el tema 1 por parte de los profesores en las CP. Así, la tarea del tema 1 ocupa un lugar especial en el material práctico porque se ubica como una tarea diferenciada de las demás y se proponen siete casos prototípicos para estudiar. Además, nuestro estudio sobre las CP muestra la importancia que los profesores le otorgan: el estudio se realiza en una CP destinada sólo a este tipo de tarea y a aquellas que agrupa el
∞, indica que en el primer examen parcial por módulo el tema 3 presentó dificultades, ya que un gran porcentaje de estudiantes ni siquiera intentaron resolver la tarea o usaron técnicas inadecuadas (87%), mientras que sólo el 4% resolvió correctamente la tarea. Esto contrasta con los resultados obtenidos para el tema 1, pues reúne el mayor porcentaje de alumnos que resolvieron bien la tarea (40%). La gran diferencia de resultados entre los temas 1 y 3 podría atribuirse al tipo de expresión involucrada en el tema 3 y a la relevancia que se da a la tarea involucrada en el tema 1 por parte de los profesores en las CP. Así, la tarea del tema 1 ocupa un lugar especial en el material práctico porque se ubica como una tarea diferenciada de las demás y se proponen siete casos prototípicos para estudiar. Además, nuestro estudio sobre las CP muestra la importancia que los profesores le otorgan: el estudio se realiza en una CP destinada sólo a este tipo de tarea y a aquellas que agrupa el 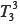 .
.
El análisis sobre las producciones de los estudiantes, relativos al tipo de tarea 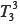 : Hallar un intervalo del dominio de funciones tal que el límite sea I cuando x tiende a un valor real finito, señala que en el primer examen parcial por módulo un bajo porcentaje de estudiantes (8%) no intentó realizar la tarea. La menor proporción de alumnos que resolvieron bien la tarea corresponde al tema 2(15%). Atribuimos la diferencia a que en el tema 2 se requiere suponer un valor de δ < 1 para acotar y establecer la relación entre δ y ε; nuestras observaciones muestran que para los estudiantes las acotaciones siempre deben realizarse suponiendo que δ=1. Para confirmar lo anterior, de todos los estudiantes que realizaron los "temas" restantes, donde se puede demostrar que δ = 1, sólo dos alumnos supusieron valores de δ≠1 para el tema 3. Inferimos que los estudiantes no comprenden el significado de δ y se centran en la resolución algebraica más que en demostrar la existencia del límite.
: Hallar un intervalo del dominio de funciones tal que el límite sea I cuando x tiende a un valor real finito, señala que en el primer examen parcial por módulo un bajo porcentaje de estudiantes (8%) no intentó realizar la tarea. La menor proporción de alumnos que resolvieron bien la tarea corresponde al tema 2(15%). Atribuimos la diferencia a que en el tema 2 se requiere suponer un valor de δ < 1 para acotar y establecer la relación entre δ y ε; nuestras observaciones muestran que para los estudiantes las acotaciones siempre deben realizarse suponiendo que δ=1. Para confirmar lo anterior, de todos los estudiantes que realizaron los "temas" restantes, donde se puede demostrar que δ = 1, sólo dos alumnos supusieron valores de δ≠1 para el tema 3. Inferimos que los estudiantes no comprenden el significado de δ y se centran en la resolución algebraica más que en demostrar la existencia del límite.
Por otro lado, es elevado el porcentaje de alumnos que no consiguen resolver bien las tareas, aunque lo intentan: el primer examen parcial de módulo registró el 31% y el primer examen de compensación por parcial el 32%. Sus errores se refieren tanto a la manipulación algebraica de las expresiones como a la confusión del estudio del límite de funciones con el límite de sucesiones.
Finalmente, el análisis a las producciones de los estudiantes relativas al 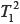 : Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones muestra que un alto porcentaje de estudiantes no consiguió abordar la tarea o lo hizo de manera incorrecta (90% de 223 estudiantes). Sólo el 3% efectuó correctamente la demostración, y el 7% intentó demostrar y lo hizo correctamente en uno de los sentidos, con lo que supuso haber demostrado la proposición. Los resultados indican que muy pocos alumnos comprenden las tareas que proponen las CT.
: Demostrar proposiciones que vinculan el límite de funciones con el límite de sucesiones muestra que un alto porcentaje de estudiantes no consiguió abordar la tarea o lo hizo de manera incorrecta (90% de 223 estudiantes). Sólo el 3% efectuó correctamente la demostración, y el 7% intentó demostrar y lo hizo correctamente en uno de los sentidos, con lo que supuso haber demostrado la proposición. Los resultados indican que muy pocos alumnos comprenden las tareas que proponen las CT.
Si se plantean bajo los parámetros de nuestra investigación, estos intentos de enseñar a demostrar en la universidad resultan ilusorios. La forma en que los profesores universitarios pretenden enseñar a demostrar se reduce a mostrar cómo se usan las técnicas, que aparecen autojustificadas, carentes de razón de ser y únicamente viven para ser reproducidas. Sólo se propone un único tipo de tarea, el 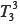 , oculto bajo el género Demostrar, que se reduce al de Calcular, y parece haber sido concebido como un medio para tranquilizar la conciencia de los profesores universitarios, respondiendo a las exigencias de la noósfera: en el nivel universitario se enseña a demostrar a los estudiantes.
, oculto bajo el género Demostrar, que se reduce al de Calcular, y parece haber sido concebido como un medio para tranquilizar la conciencia de los profesores universitarios, respondiendo a las exigencias de la noósfera: en el nivel universitario se enseña a demostrar a los estudiantes.
Llevar a cabo una tarea que involucre actividades de argumentación, prueba o demostración implica un trabajo a largo plazo, el cual debe centrarse en plantear problemas donde los estudiantes puedan desarrollar una actitud reflexiva y dispuesta a formular conjeturas y discutir su validez (Ferreira, Rechimont y Parodi, 2008).
5. REFLEXIONES FINALES
La TAD ha permitido caracterizar las OM, identificando géneros de tareas, tipos de tareas, técnicas y tecnologías. La OM que se estudia en esta institución fue descrita mediante el análisis de los elementos constitutivos que propone la teoría y de su articulación. También centramos nuestra investigación en las tareas que se consolidan en el momento de evaluación, al igual que las producciones de los estudiantes frente a dichas tareas. De este modo, se ha reconstruido la OMEE con el análisis de las CT y las CP en torno al límite funcional.
– En las CT se trata de fortalecer el entorno tecnológico de la OM, aunque se hace una selección muy restringida de los teoremas y las proposiciones a demostrar, mientras que los restantes aparecen como autojustificados. La actividad en las CP se reduce a efectuar tareas relativas al género Calcular. Sólo hay una en que se trata de introducir a los estudiantes a la tarea de demostrar, pero la juzgamos insuficiente. Esta singularidad sería una acción que intentan los profesores universitarios para cumplir con la exigencia que nace en la noósfera: las demostraciones funcionan como paranociones para los estudiantes de nivel medio, pero deberían funcionar como nociones para los estudiantes de nivel universitario.
– Los resultados confirman que el teoricismo dominante en la enseñanza universitaria de la matemática, caracterizado por la concepción de que el saber matemático es un conocimiento acabado y sólo se toma el fruto final de esta actividad (Gascón, 2001), provoca una desconexión creciente entre el bloque práctico–técnico y el bloque tecnológico–teórico de las OM estudiadas. La relación entre ambos bloques es muy asimétrica: mientras el tecnológico–teórico dicta los contenidos del práctico–técnico, éste tiene una incidencia nula en la constitución, desarrollo y estructura del tecnológico–teórico.
– Lo que se propone como evaluación en el curso bajo estudio corresponde a la idea del examen, ya que asumimos que la evaluación es parte del proceso de reconstrucción que atañe al conocimiento matemático. No es un dispositivo diferenciado que sirve únicamente para comprobar resultados, sino una dimensión inseparable de los procesos de enseñar y aprender. La idea de examen remite a la concepción de que con tal instrumento es posible medir los aprendizajes, por lo que se instaura como un acto final del proceso de estudio, lo cual se infiere de los dispositivos de evaluación propuestos. El análisis de los exámenes indica una continuidad entre lo que efectivamente se reconstruye en el aula y lo que se solicita en la evaluación. Esto es así porque la evaluación se constituye en un momento adicional de institucionalización en el sistema didáctico y precisa algunos aspectos de la OM, debido a que las tareas propuestas en las evaluaciones informan sobre qué aspectos de una noción se destacan y cuáles no. En este caso particular, se enfatiza el género de tareas Calcular, que coincide con el aspecto más trabajado en las clases de AMI y particularmente en las CP.
REFERENCIAS BIBLIOGRÁFICAS
Aparicio, E. y Cantoral, R. (2003). Sobre la noción de continuidad puntual: Un estudio de las formas discursivas utilizadas por estudiantes universitarios en contextos de geometría dinámica. Epsilon. Revista de la Sociedad Andaluza de Educación Matemática Thales 56, 169–198. [ Links ]
Aparicio, E. y Cantoral, R. (2006). Aspectos discursivos y gestuales asociados a la noción de continuidad puntual. Revista Latinoamericana de Investigación en Matemática Educativa 9(1), 1–29. [ Links ]
Artigue, M. (1995). Ingeniería didáctica. En P. Gómez (Ed.), Ingeniería didáctica en educación matemática (pp. 97–140). México: Grupo Editorial Iberoamérica. [ Links ]
Artigue, M. (1998). Enseñanza y aprendizaje del análisis elemental: ¿qué se puede aprender de las investigaciones didácticas y los cambios curriculares? Revista Latinoamericana de Investigación en Matemática Educativa 1 (1), 41–56. [ Links ]
Azcárate, C. & Delgado, C. (1996). Study of the evolution of graduate student's concept images while learning the notions of limit and continuity. Actas del PME 20 (2), 289–296. [ Links ]
Azcárate, C. y Deulofeu, J. (2000). Investigaciones acerca de la enseñanza y aprendizaje del análisis en España. En R. Cantoral (Ed.), El futuro del cálculo infinitesimal (pp. 355–361). México: Grupo Editorial Iberoamérica. [ Links ]
Bezuidenhout, J. (2001). Limits and continuity: some conceptions of first–year students. International Journal of Mathematical Education in Science and Technology 32 (4), 487–500. [ Links ]
Blázquez, S. y Ortega, T. (2002). Nueva definición de límite funcional. UNO. Revista de Didáctica de las Matemáticas 30, 67–82. [ Links ]
Bosch, M. y Gascón, J. (2005). La praxeología local como unidad de análisis de los procesos didácticos. En C. De Castro y M. Gómez (Eds), Análisis del currículo actual de matemáticas y posibles alternativas (pp. 135–160). Madrid: Edebé. [ Links ]
Bosch, M., Espinoza, L. y Gascón, J. (2003). El profesor como director de procesos de estudios. Análisis de organizaciones didácticas espontáneas. Recherches en Didactique desMathématiques 23(1), 79–135. [ Links ]
Chevallard, Y. (1985). La transposition didactique. Du savoir savant au savoir enseigné. Grenoble: La Pensée Sauvage. [ Links ]
Chevallard, Y. (1999). L'analyse des pratiques enseignantes en théorie anthropologique du didactique. Recherches en Didactique des Mathématiques 19 (2), 221–266. [ Links ]
Chevallard, Y., Bosch, M. y Gascón, J. (1997). Estudiar matemática. El eslabón perdido entre la enseñanza y el aprendizaje. Barcelona: ICE/Horsori. [ Links ]
Contreras, A. (2001). El límite en el bachillerato y primer año de universidad. Perspectivas desde los enfoques epistemológicos y semióticos. Obtenido en julio 1, 2008, del sitio web de la Universidad de Granada, Grupo Didáctica de la Matemática como Disciplina Científica de la SEIEM http://www.ugr.es/~jgodino/siidm/huesca/limitebachillerato.pdf [ Links ]
Cornu,B. (1991). Limits. In D. Tall (Ed.), Advanced Mathematical Thinking (pp. 153–166). Dordrecht: Kluwer Academic Publishers. [ Links ]
Crespo, C. (2004). El concepto de continuidad y sus obstáculos epistemológicos. En L. Díaz (Ed.), Acta Latinoamericana de Matemática Educativa (volumen XVII, pp. 39–44). México: Comité Latinoamericano de Matemática Educativa AC. [ Links ]
Dorier, J. (1995). Meta level in the teaching of unifying and generalizing concepts in mathematics. Educational Studies in Mathematics 29 (2), 175–197. [ Links ]
Espinoza, L. y Azcárate, C. (2000). Organizaciones matemáticas y didácticas en torno al objeto "limite de una función": una propuesta metodológica para el análisis. Enseñanza de las Ciencias 18 (3), 355–368. [ Links ]
Farfán, R. (1997). Ingeniería didáctica: Un estudio de la variación y el cambio. México: Grupo Editorial Iberoamérica. [ Links ]
Ferreira, N., Rechimont, E. y Parodi, C. (2008). Diferentes marcos en la resolución de problemas por demostrar. En P. Lestón (Ed.), Acta Latinoamericana de Matemática Educativa (volumen XXI, pp. 50–59). México: Comité Latinoamericano de Matemática Educativa, AC . [ Links ]
Gascón, J. (2001). Incidencia del modelo epistemológico de las matemáticas sobre las prácticas docentes. Revista Latinoamericana de Investigación en Matemática Educativa 4 (2), 129–159. [ Links ]
Godino, J., Contreras, A. y Font, V. (2006). Análisis de procesos de instrucción basado en el enfoque ontológico–semiótico de la cognición matemática. Recherches en Didactique des Mathématiques 26(1), 39–88. [ Links ]
Hitt, F. (1994). Teacher's difficulties with the construction of continuous and discontinuous functions. Focus on Learning Problems in Mathematic 16 (4), 10–20. [ Links ]
Mamona–Downs, J. (2001). Letting the intuitive bear on formal: a didactical approach for the understanding of the limit of a sequence. Educational Studies in Mathematics 48 (2–3), 259–288. [ Links ]
Moreno, M. (2003). Análisis del conocimiento de los profesores universitarios de matemáticas sobre la enseñanza de las ecuaciones diferenciales y sus aplicaciones. En E. Castro (Ed.), Investigación en Educación Matemática. Séptimo Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 257–268). Granada: Universidad de Granada. [ Links ]
Sierra, M., González, M. y López, C. (2000). Concepciones de los alumnos de bachillerato y curso de orientación universitaria sobre límite funcional y continuidad. Revista Latinoamericana de Investigación en Matemática Educativa 5(1), 71–85. [ Links ]
Tall, D. (1986). The complementary roles of short programs and prepared software for mathematics learning. Bulletin of the IMA 23, 128–133. [ Links ]
Tall, D. (1991). The psychology of advanced mathematical thinking. In D. Tall (Ed.), Advanced Mathematical Thinking (pp. 3–21). Dordrecht: Kluwer Academic Publishers. [ Links ]
Tall, D. & Vinner S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics 12 (2), 151–169. [ Links ]
Tall, D., Blokland, P. & Kok, D. (1990). A graphic approach to the calculus (for IBM compatible computers). USA: Sunburst, Pleasantville, NY. [ Links ]
Zuñiga, L. (2007). El cálculo en carreras de ingeniería: un estudio cognitivo. Revista Latinoamericana de Investigación en Matemática Educativa 10 (1) 145–175. [ Links ]
1 Se hablará de estudio para referirse a todo aquello que se hace en una determinada institución para llevar a cabo las tareas que se plantean.
2 Cuando se indica que un estudiante promociona significa que aprueba el curso, mientras que si obtiene una calificación entre 4 y 6 puntos en cada examen parcial aprueba la cursada, pero deberá acreditar un examen individual y escrito, en el término de tres años, que engloba tareas con características similares a las estudiadas en las CP y las CT.
3 En particular, se omite el estudio del siguiente teorema: Sea r cualquier entero positivo, entonces:















