Artículos

 

Consideraciones metodológicas para la interpretación de procesos de interacción en el aula de matemáticas

 

Methodological considerations for interpretation of interactions in the mathematics classroom

 

Nuria Planas* y Nuria Iranzo**

 

* Universitat Autónoma de Barcelona, España; nuria.planas@uab.cat

** Universitat Autónoma de Barcelona, España; nuria.iranzo@uab.cat

 

Recepción: Diciembre 18, 2008
Aceptación: Mayo 18, 2009

 

RESUMEN

En este artículo se presenta parte de un modelo de análisis para la descripción e interpretación de procesos de interacción en el aula de matemáticas. Se argumenta la importancia de introducir casos reales de aula que contribuyan a deconstruir e interpretar la clase de matemáticas, desde la doble perspectiva de los contenidos matemáticos y de la interacción social. Para ello, se plantea el uso operativo y la integración de nociones asociadas a distintas tradiciones teóricas, principalmente las de práctica matemática, norma sociomatemática y conflicto entre significados. Una vez descrito el modelo de análisis, se aplica en la transcripción de un episodio de clase ocurrido en un aula de secundaria, correspondiente a una escuela de Barcelona, España. Finalmente, se exponen reflexiones acerca del interés y la potencialidad del modelo para generar conocimiento científico sobre la interacción en situaciones de enseñanza y aprendizaje de matemáticas.

PALABRAS CLAVE: Procesos de interacción, datos de aula, prácticas matemáticas, normas sociomatemáticas, conflictos entre significados.

 

ABSTRACT

In this article, a part of model to analyze the description and interpretation of interactions inside the mathematics classroom is presented. The importance of real classroom cases that contribute to the deconstruction and interpretation of the mathematics classroom is argued from the double prospective of the mathematical content and the social interactions. To do so, the operational use and the integration of notions associated with different theoretical traditions, especially the ones related to mathematical practices, sociomathematical norms, and conflict of meanings are presented. Once the analytical model is described, its use is applied to a transcribed episode of a lesson in a secondary classroom of Barcelona, Spain. Finally, reflections about the interest and potential of the model to generate scientific knowledge about the interaction in teaching and learning mathematics situations are discussed.

KEY WORDS: Process of interaction, classroom data, mathematical practices, sociomathematical norms, conflicts between meanings.

 

RESUMO

Neste artigo apresentamos parte de um modelo de análise para a descrição e interpretação de processos de interacção na aula de Matemática. Defendemos a importância de introduzir casos reais de sala de aula que contribuam para desconstruir e interpretar a aula de Matemática, desde a dupla perspectiva dos conteúdos matemáticos e da interacção social. Para isso, privilegiamos o uso operativo e a integrado de noções associadas a tradições teóricas distintas, principalmente as de prática matemática, norma sociomatemática e confuto de significados. Urna vez descrito o modelo de análise, este é aplicado a transcrição de um episodio de sala de aula ocorrido mima aula do Ensino Secundario, de urna escola de Barcelona, em Espanha. Finalmente, reflectimos sobre o interesse e as potencialidades do modelo para gerar conhecimento científico sobre a interacção em situações de ensino e aprendizagem de Matemática.

PALAVRAS CHAVE: Processos de interacção, dados de aula, práticas matemáticas, normas sociomatemáticas, conflitos entre significados.

 

RÉSUMÉ

On présente dans cet article une partie d'un modele d'analyse pour la description et interpretation de processus d'interaction en classe de mathématiques. On argumente l'importance d'introduire des experiences réalisées en classe qui contribuent á déconstruire et interpreter la classe de mathématiques avec la double perspective des contenus mathématiques et de 1'interaction sociale. Dans ce but, on met en question l'intégration et l'usage opératif de notions associées á différentes traditions théoriques: la pratique mathématique, les normes socio–mathématiques et les conflits entre les divers sens. Aprés avoir décrit le modele d'analyse développée, celui–ci est appliqué á une experience réalisée avec des eleves de l'école secondaire de Barcelone (Espagne). Finalement, on présente des reflexions sur l'intérét et la puissance du modele pour le développement de connaissance scientifique sur l'interaction dans des situations d'enseignement et apprentissage des mathématiques.

MOTS CLÉS: Processus d'interaction, données de classe, pratiques en mathématiques, normes socio–mathématiques, conflits entre sens.

 

1. INTRODUCCIÓN

En este artículo damos a conocer parte de un modelo de análisis para la descripción e interpretación de procesos de interacción en el aula de matemáticas, desde la doble perspectiva de los contenidos matemáticos y de la interacción social. De acuerdo con los principios de una epistemología de la práctica (Fortuny y Rodríguez, 2003; Penalva, Escudero y Barba, 2006), partimos de la transcripción de casos reales de aula que sirvan como un ejemplo de cuestiones relevantes para generar conocimiento científico en el área de educación matemática.

Respecto al análisis de los contenidos matemáticos, aplicamos el modelo de identificación de prácticas matemáticas, que describen Font y Planas (2008) con base en la noción de práctica matemática tal como ha sido caracterizada por Godino y Batanero 1994). Para el análisis de la interacción social en el aula, recurrimos al modelo de identificación de normas y conflictos, que refieren Planas y Edo (2008) basándose en los conceptos de norma sociomatemática y conflicto entre significados, los cuales han reinterpretado Planas (2005), así como Hoffmann, Lenhard y Seeger (2005).

La integración de las nociones de práctica matemática, norma sociomatemática y conflicto entre significados en un mismo modelo de análisis, y desde perspectivas conceptuales complementarias, tiene que mejorar la descripción y comprensión de lo que ocurre en el aula, para más tarde estar en condiciones de valorar la idoneidad de aspectos sobre lo ocurrido. En este sentido, sugerimos consultar Planas, Fortuny e Iranzo (2009), o bien Ramos y Font (2008) para tomar en cuenta la dificultad de operativizar la noción de idoneidad didáctica, sin haber desarrollado una descripción previa suficiente en torno a los sucesos del aula.

Nuestro modelo actual se centra en tareas de descripción y explicación. La primera parte del texto introduce los términos de práctica matemática, norma sociomatemática y conflicto entre significados–, y los sitúa en el marco de tres enfoquesteóricos consolidados dentro de laeducaciónmatemática: el ontosemiótico, el sociocultural y el lingüístico. La segunda parte del artículo explica nuestro modelo para analizar los aspectos de la interacción en situaciones de enseñanza y aprendizaje de las matemáticas, aplicándolo al caso de la transcripción de un episodio en un aula de matemáticas que pertenece a una escuela secundaria de Barcelona, España. La última sección contiene reflexiones sobre la potencialidad del modelo de análisis y, más en general, sobre la necesidad de avanzar hacia la integración de perspectivas conceptuales complementarias para generar conocimiento científico en nuestra área.

 

2. MARCO TEÓRICO

En el segundo volumen del International Handbook of Mathematics Teacher Education, que lleva como título "Tools and processes in mathematics education", Tirosh y Wood (2008) compilan trabajos que se basan en una gran variedad de perspectivas teóricas. Dentro de la introducción mencionan la importancia de realizar esfuerzos que tiendan a integrar elementos de perspectivas teóricas distintas. Con respecto a los procesos de enseñanza y aprendizaje de las matemáticas en el aula, D'Amore y Godino (2007), en un estudio teórico sobre los puntos de vista ontológico, semiótico y antropológico, también destacan la necesidad de integrar marcos de referencia ante la creciente proliferación de aproximaciones teóricas.

Nuestro trabajo considera tres perspectivas teóricas complementarias y, dentro de cada una, resalta enfoques tradicionales a los que de algún modo hemos contribuido en trabajos anteriores. En primer lugar tomamos la perspectiva ontosemiótica (Godino, Batanero y Font, 2007), que se ha consolidado en la última década, como muestra el trabajo documental de Lunares (2008). En segundo lugar, tomamos la perspectiva sociocultural, que se enmarca en trabajos sobre interacción social y participación en el aula de matemáticas desarrollados durante los últimos años (Civil y Planas, 2004; Planas y Edo, 2008). Por último, nos referimos a la perspectiva lingüística, centrada en la corriente vigotskiana reinterpretada desde la teoría de la actividad (Engestróm y Miettinen, 1999; Inagaki, Hatano y Morita, 1998).

De un modo más general, nuestro trabajo se sitúa en el grupo de estudios sobre las prácticas de enseñanza y aprendizaje de las matemáticas. Algunos destacan la problematización de las situaciones de enseñanza y la gestión que el profesor hace tanto del contenido matemático como la interacción con los alumnos. En esta línea ubicamos a las investigaciones de Callejo, Valls y Lunares (2007), Lunares (2002, 2007); así como la de Iranzo y Fortuny (2008), donde se integran supuestos de tipo sociocultural en la interpretación conjunta de las prácticas matemáticas y didácticas del aula y la práctica del profesor.

 

2.1. Perspectiva ontosemiótica y prácticas matemáticas

La noción de práctica matemática es clave en el desarrollo del enfoque ontosemiótico en educación matemática; Godino, Batanero y Font (2007) hacen una síntesis de sus fundamentos teóricos. En la perspectiva ontosemiótica la enseñanza y el aprendizaje de las matemáticas se entienden como una actividad que está constituida por prácticas, mientras que el conocimiento matemático se interpreta en función de las instituciones culturales y los contextos sociales donde el aprendiz y el formador están implicados y desarrollan sus modos de hacer. Godino y Batanero (1994) conciben como práctica matemática a cualquier acción o manifestación que lleva a cabo un sujeto para resolver problemas matemáticos, comunicar la solución a otros sujetos, así como para validar y generalizar la solución a otros contextos y problemas. En suma, son prácticas que se configuran mediante la articulación de objetos y procesos de tipos distintos que tienen en común la pertenencia al discurso de las matemáticas.

De modo más general, la práctica matemática puede relacionarse con la noción de norma, ya que atiende a las prácticas institucionales y las desviadas. En el caso de la matemática escolar, los discursos históricos dominantes han llevado a valorar ciertas prácticas como normativas, por ser representativas de lo que está permitido hacer y decir en la actividad matemática (Civil y Planas, 2008). No obstante, todo sujeto construye y lleva a cabo prácticas en el aula que no siempre corresponden a las expectativas de adecuación al discurso de las matemáticas. D'Amore, Godino y Font (2007) hablan de prácticas desviadas respecto a la institución que se tome como referencia.

Se supone que cualquier proceso de instrucción debe contribuir a avanzar desde las prácticas personales a las institucionales, que serán distintas según la institución. No obstante, a menudo las divergencias entre las prácticas personales y las institucionales se manifiestan en forma de conflictos sobre lo que uno espera o "lo que se espera de uno"; algunos pueden interpretarse como evidencias del desajuste entre las prácticas realizadas y/o esperadas por los aprendices y las prácticas ejemplificadas y/o esperadas por la institución.

En este sentido, un modelo de análisis didáctico que integre las nociones de prácticas, normas y conflictos tiene que prestar atención a qué prácticas se interrumpen cuando aparecen conflictos entre significados y cuáles se promueven; qué conflictos pueden atribuirse a la experiencia de distancias entre prácticas personales e institucionales; de qué modo las normas del aula contribuyen a regular las prácticas desviadas; hasta qué punto algunas de ellas no son regulables, y qué normas se desprenden del uso de ciertas prácticas, entre otros aspectos.

Más allá de las relaciones que puedan establecerse entre prácticas, normas y conflictos, la importancia que se da al énfasis en el análisis de las prácticas en lugar del énfasis en la identificación de los conocimientos, (aspecto que todavía resaltan muchos modelos de análisis didáctico), supone un fuerte posicionamiento teórico. Este planteamiento señala aquello que "pasa" a los participantes del aula –ya sea porque ellos han hecho que pase o porque se han visto más o menos involucrados en una cierta secuencia de sucesos–, destacando el valor y la experiencia de lo que les "pasa" en su proceso de construcción de identidades matemáticas.

Por tanto, estamos ante un enfoque que no trata de descubrir qué se piensa, sino de describir qué se hace (identificación de prácticas), qué valor se da a lo que se hace (identificación de normas) y qué experiencias personales y colectivas se generan sobre lo que se hace (identificación de conflictos). Planas y Civil (2009) argumentan porqué es importante situar la identificación de normas y conflictos con respecto a las prácticas que suceden en el marco de la experiencia del sujeto como aprendiz en el aula.

 

2.2. Perspectiva sociocultural y normas sociomatemáticas

En el ámbito de las teorías socioculturales en educación matemática es frecuente el uso de las nociones de norma social, norma de la práctica matemática y norma sociomatemática (Yackel y Cobb, 1996), con el fin de explicar los procesos sociales mediante los cuales alumnos y profesores construyen el orden del aula de matemáticas. Dentro del contexto que implica al aula, la noción de norma se refiere a las obligaciones que rigen las interacciones entre profesor y alumnos (Voigt, 1995) y, en general, a las convenciones establecidas de manera histórica sobre cómo comunicarse y reaccionar ante las intervenciones de otros.

Se supone, por ejemplo, que los alumnos tienen que aportar argumentos que completen sus afirmaciones en torno a la resolución de una tarea. Como señalan D'Amore, Font y Godino (2007), este planteamiento es normativo porque las intervenciones de los estudiantes se valoran con base en el grado de argumentación y, sobre todo, en la coherencia interna de sus explicaciones. No obstante, las normas de adecuación que se piden a los alumnos no siempre coinciden con las normas que rigen las actuaciones del profesor. Puede ocurrir, por ejemplo, que se soliciten argumentaciones donde se concluya acerca de una hipótesis, pero que el profesor no actúe como modelo de tal práctica. A pesar de ello, puede hablarse sobre la existencia de un conjunto de normas del aula, más allá de las normas de actuación del profesor y las de los alumnos, así como de las diferencias entre unas y otras.

En el caso del aula de matemáticas, hay normas vinculadas a la actividad matemática que son propias de la puesta en práctica de objetos y procesos matemáticos. Voigt (1995) menciona las obligaciones relativas a cómo valorar la solución a un problema, cómo decidir sobre la corrección de una explicación matemática, cómo concluir acerca de la completitud de una demostración o cómo reconocer la adecuación de un algoritmo de cálculo. Dichos ejemplos de normas sociomatemáticas se emplean para evaluar la práctica matemática de alumnos y profesor.

Planas (2005) describe las normas sociomatemáticas en modo amplio para representar aspectos de las matemáticas que son susceptibles de ser enseñados y aprendidos en la institución escolar y en el aula donde se estén usando. La descripción de las normas sociomatemáticas que se acaban imponiendo refiere la actividad matemática que es posible desarrollar y la que se obstaculiza. Las prácticas que no se ajusten a ciertas normas pueden continuar manifestándose públicamente, mas quien las sostenga corre el riesgo de situarse en la "periferia" del discurso del aula. De acuerdo con estas consideraciones, la descripción de normas sirve para entender mejor hasta qué punto los alumnos que abordan conjuntamente la resolución de una tarea matemática tienen una representación propia de dicha tarea y de lo que implica su resolución, y hasta qué punto estas representaciones son distintas a las del profesor.

Planas y Edo (2008) señalan que las normas esperadas en un aula pueden identificarse al detectar rupturas en los patrones de interacción social, que a menudo indican disfunciones entre las normas esperadas y las normas hechas efectivas. Asimismo, examinan las normas mediante el estudio de cambios en los discursos públicos del aula. La identificación de normas y cambios en su uso viene facilitada por la de los procesos sociales de conflicto entre dos o más participantes. El proceso de conflicto consiste en una forma de relación donde las personas discrepan en el uso de ciertas normas; dicho conflicto puede mantenerse, reducirse o superarse tras la participación activa de las distintas partes. Los datos del trabajo de Planas y Edo muestran los procesos de conflicto con un profesor cuyas intervenciones ayudan a modificar el uso de normas. Aunque estos procesos de conflicto no determinan en forma unívoca el uso de normas que acaban prevaleciendo, sí facilitan la presencia de unas antes que otras. En Planas y Civil (2009) se precisa la idea de proceso social de conflicto a favor de conflicto entre significados, a fin de destacar el papel del discurso antes que el de los sujetos en la responsabilización del conflicto.

 

2.3. Perspectiva lingüística y conflictos entre significados

El conjunto de acciones que configuran una práctica representan sólo una posibilidad o modo de hacer entre un universo de posibilidades. Un momento del desarrollo de una tarea matemática contiene más de una práctica posible, de ahí que no siempre sea fácil comprender qué significados matemáticos y sociales se atribuyen a cada práctica. El conflicto semiótico, en sentido amplio, nace de la disparidad de interpretaciones que los distintos participantes atribuyen a las necesidades de regulación sobre un mismo momento de la tarea matemática y, por tanto, su origen reside en la diversidad de normas esperadas (Font y Planas, 2008; Planas y Setati, 2009). De modo más concreto, esta clase de conflicto puede identificarse en situaciones donde hay disparidad de interpretaciones en torno a una misma expresión usada en el aula (Godino, Batanero y Font, 2007).

Ambas aproximaciones a la noción de conflicto semiótico permiten analizar la interacción social, desde el punto de vista de las distancias entre los significados de referencia. De ahí que el conflicto semiótico, ligado a las diferencias en las expectativas de regulación sobre la tarea matemática y a la diversidad de representaciones de las normas, sea relevante en el estudio de la gestión de la interacción social. Hoffmann, Lenhard y Seeger (2005), al igual que Mercer y Littleton (2007), mencionan la noción de conflicto entre significados en un sentido parecido al del conflicto semiótico, al situarlo en un entorno donde se confrontan actividades. Como Engestróm y Miettinen (1999), dichos autores interpretan la noción de actividad en el sentido de la acción dirigida por una tarea y una intencionalidad.

A pesar de que la caracterización de conflicto entre significados tiene un fuerte componente sociocultural, lo ubicamos dentro de la perspectiva lingüística, que enfoca a la disparidad de normas como signos de representación a través de los cuales los sujetos piensan y actúan en un contexto de prácticas. Alsina y Planas (2008) mencionan varios conflictos entre significados que identificaron en aulas de matemáticas. Se documentan, por ejemplo, situaciones de conflicto en torno a la interpretación del concepto comunicar (matemáticas), que puede entenderse como transmitir, participar en, poner en relación o compartir, entre otros significados. Si se ocupa el término comunicar, las normas que regulan la actividad matemática en el aula serán distintas, en función de los significados que se adopten y los modos de hacer que emplearán los alumnos al responder a esta diversidad.

En Planas (2007) se explican casos en los que el profesor usa la expresión comunicar para favorecer la discusión y el intercambio de ideas matemáticas; sin embargo, varios alumnos se limitan a explicar sus ideas sin relacionarlas con otras ya expresadas. Para comprender mejor cómo se produce un conflicto acerca de qué significa comunicar (matemáticas), conviene detectar las prácticas matemáticas del aula que le preceden y las normas sociomatemáticas que emplea el profesor, además de los entornos de enseñanza y aprendizaje de las matemáticas donde los alumnos y el profesor han participado con anterioridad. En este sentido, la descripción del conflicto es local, mientras que la explicación de su origen requiere de una mirada longitudinal más amplia.

Para describir los conflictos que surgen de la diferencia de interpretaciones entre sujetos, resulta útil considerar la dialéctica entre prácticas institucionales y personales, que en algunos casos pueden ser prácticas desviadas. Es de esperar que algunos significados personales dados por los alumnos a la actividad matemática –o eventualmente por el profesor– sean significados no reconocidos, desde la perspectiva de los discursos propios de la institución escolar. De acuerdo con tal supuesto, la identificación de conflictos entre significados puede llevar a la precisión de las distancias entre prácticas, así como de situaciones de confrontación en el uso de normas. Esta triple identificación puede hacerse en el entorno de una transcripción de clase; no obstante, una explicación detallada sobre los orígenes y las implicaciones de las relaciones entre conflictos, prácticas y normas hace necesario un mayor conocimiento del contexto de la transcripción.

 

3. DESCRIPCIÓN DEL MODELO DE ANÁLISIS

En el estudio actual, nuestra interpretación de los procesos de interacción debe entenderse con base en su particularización y operativización por medio de las fases de análisis. Con el propósito de mejorar la comprensión en torno a los fenómenos del aula de matemáticas, proponemos un modelo de análisis sobre ciertos aspectos de transcripciones de aula, el cual se basa en la aplicación de cuatro fases que corresponden a los cuatro dominios de conocimiento que queremos resaltar:

Nivel 1. Identificación de prácticas matemáticas

Nivel 2. Identificación de normas sociomatemáticas

Nivel 3. Identificación de conflictos entre significados

Nivel 4. Exploración de relaciones entre prácticas, normas y conflictos

Los tres primeros niveles de análisis son descriptivos, ya que pretenden responder a cuestiones sobre qué matemáticas se usan en el aula, cómo se usan y qué dificultades aparecen con su uso, en razón de que una práctica se asocia a normas distintas o se hace referencia a ella con varias expresiones lingüísticas, entre otros aspectos. El primer nivel de análisis viene dado por la acción de identificar prácticas matemáticas, distinguiéndolas de intervenciones instructivas más generales que conciernen a la gestión de la actividad en el aula. La aplicación de este nivel requiere ser capaz de reconocer no sólo la articulación de contenidos matemáticos en los discursos de los alumnos y el profesor, sino también concebir al conocimiento matemático como una secuencia de prácticas efectivas que informan sobre los procesos de aprendizaje.

Tras haber elaborado un listado de prácticas, se plantean los dos niveles siguientes. El segundo nivel describe las normas reguladoras de las prácticas matemáticas que han sido identificadas; para concluir sobre la naturaleza normativa de una práctica, es necesario poder inferir su regularidad. El carácter temporalmente local de nuestro modelo –pensado para ser aplicado en episodios breves de aula–se limita a observar la intencionalidad normativa de ciertas prácticas. Algunas normas que señalamos no son, portante, normas desde un punto de vista colectivo, debido a que sólo parecen tener reconocimiento en el marco de referencia de los alumnos que las sostienen; sin embargo, reflejan expectativas de actuación y para los alumnos son obligaciones que sus compañeros y el profesor debieran tener en cuenta.

Como preparación al tercer nivel, prestamos atención a la existencia de más de una norma en la interpretación de una práctica. El estudio de un conjunto de transcripciones que atañen a varias sesiones en una aula, o eventualmente el análisis de la transcripción completa de una sesión de clase, informaría sobre la evolución de la diversidad de normas para interpretar una práctica y permitiría concluir acerca de la preeminencia de unas normas sobre otras, señalando qué intencionalidades normativas se mantienen. La aplicación de nuestro modelo en periodos cortos de una sesión de clase responde al propósito de enfatizar la existencia de la diversidad de normas, no tanto la evolución efectiva de cada norma. El trabajo en este nivel supone la existencia de un conocimiento 'metamatemático' suficiente para poder reconocer, por una parte, las condiciones que se piden a ciertas prácticas para ser consideradas matemáticas; por otra, la variabilidad de expectativas dentro del discurso de las matemáticas en torno al desarrollo y la evaluación de dichas prácticas.

El tercer nivel describe los conflictos entre significados que atañen a la interpretación de prácticas y normas. Atiende a los conflictos desde una doble perspectiva, centrada en la diversidad tanto de las representaciones de objetos matemáticos como de las normas sociomatemáticas coexistentes para regular una práctica; este último tipo gira en torno a la diversidad de significados ante la interpretación del desarrollo matemáticamente adecuado de una práctica de aula. La aplicación de este nivel supone el trabajo de un conocimiento 'semiótico' sobre las representaciones de objetos matemáticos y las dificultades que se relacionan con la coexistencia de normas distintas al poner en práctica las representaciones.

Asimismo, el tercer nivel requiere ser capaz de identificar las situaciones de confrontación entre las representaciones de los objetos, así como estar atento al caso de las normas sociomatemáticas en el que se pide qué tipo de objeto, con su diversidad de representaciones, influye en el desarrollo de las prácticas. El conocimiento 'semiótico'tiene que ver con el conocimiento matemático: saber bien el concepto de derivada de una función implica saber bien, entre otros aspectos, las formas de representación y regulación de dicho concepto. No obstante, para construir conocimiento semiótico no basta con un buen conocimiento matemático; conviene haber desarrollado un conocimiento metamatemático sobre las condiciones en que existen el discurso de las matemáticas y el discurso escolar. Para el concepto de derivada de una función, estos discursos pueden fijar ciertas normas (el cálculo de derivadas es una estrategia matemática que rectifica funciones) y dejar otras sin establecer; por ejemplo:¿la representación gráfica de la tangente de una función en un punto basta para probar la derivada de esa función en tal punto?

Finalmente, el cuarto nivel de análisis, que tiene carácter exploratorio, pretende relacionar los tres niveles anteriores. La secuencia creciente de estudio, que va de la identificación de las prácticas a la identificación de los conflictos, así como la caracterización de los niveles 1, 2 y 3, garantiza que se establezcan relaciones emergentes entre prácticas, normas y conflictos. Este último nivel plantea una búsqueda más sistemática de relaciones con base en la ubicación de prácticas, normas y conflictos en las trayectorias individuales de los participantes respecto a su interacción con el profesor.

La aplicación del cuarto nivel supone el trabajo de un conocimiento didáctico–matemático situado. Aquí, los conflictos se interpretan como obstáculos (ante la comprensión de procesos matemáticos, de normas sobre el uso de estos procesos o de normas de adecuación a las formas de instrucción, entre otros) en una situación de enseñanza y aprendizaje, donde las prácticas y las normas son evaluadas por los contenidos que derivan del discurso del profesor y de la interacción con él. A pesar de que es una fase de análisis predictiva, resulta esencial para elaborar conocimiento didáctico–matemático, ya que conduce a un análisis integrado de datos en función de su influencia en los procesos de enseñanza y aprendizaje de las matemáticas, fijándose en la gestión que el profesor hace de la interacción.

Nuestro modelo de análisis no hace referencia a la idoneidad o la pertinencia de las formas de interacción y enseñanza en el aula, ni tampoco aporta recomendaciones sobre cómo mejorarlas. Argumentamos, sin embargo, la importancia de desarrollar investigación educativa sobre dominios de conocimiento de tipo evaluativo, más allá de los estrictamente descriptivos y explicativos. Dejamos para más adelante la incorporación del conocimiento de tipo evaluativo, que habrá de sumarse a la profundización de los conocimientos que se han denominado matemáticos, metamatemáticos, semióticos y didáctico–matemáticos. Por el momento, damos prioridad a recoger la información sobre qué se va a valorar. De igual manera, nuestro modelo actual sólo recoge algunos aspectos relevantes para construir conocimiento sobre cuestiones de interacción en el aula de matemáticas. Para decidir acerca de la idoneidad de ciertos procesos de interacción se tendrá que ampliar su descripción, incluyendo, por ejemplo, datos concernientes a las tareas matemáticas.

 

4. APLICACIÓN DEL MODELO DE ANÁLISIS

Para ejemplificar el modelo de análisis, partimos de una transcripción de aula que se obtuvo a raíz de un registro en audio. Los participantes formaban un grupo de 25 alumnos (con edades de 14 y 15 años) que pertenecían a una escuela pública de secundaria cercana a Barcelona. La sesión de clase se insertaba en el primer trimestre del curso 2007–2008, y la condujo una profesora con quien habíamos colaborado en estudios anteriores. Cabe mencionar que no se dio ninguna consigna de actuación a la profesora, de modo que la selección y gestión de la tarea formaron parte de una planificación prevista sin nuestra intervención.

Nuestro conocimiento de la profesora, junto con las visitas anteriores que hicimos a sus clases, nos llevó a pensar en la conveniencia de recoger datos en una de sus aulas por la elevada participación de la mayoría de alumnos y la frecuente interacción entre ellos. Si bien nuestro modelo podía ser aplicado en cualquier entorno de aula, era razonable pensar que las dinámicas activas facilitarían en mayor medida la obtención de datos sobre las prácticas y las normas. Una situación didáctica de tipo magistral pondría de relieve las prácticas y normas del profesor y, a su vez, dificultaría la identificación de prácticas y normas de los alumnos.

Al aplicar nuestro modelo, en primer lugar ubicamos la transcripción en la situación didáctica planteada en el aula, de acuerdo con los participantes que intervenían directamente en los procesos de interacción. Luego, trabajamos el modelo de acuerdo con las fases de identificación de las prácticas, normas y conflictos, así como de la exploración de relaciones emergentes entre las formas de aparición de estos tres tipos de objetos.

 

4.1. Contexto y situación didáctica en el aula

Al momento de recopilar los datos en el aula, la profesora y los alumnos llevan cuatro semanas de trabajar juntos, pero de todas las sesiones anteriores sólo dos las han dedicado a resolver tareas contextualizadas. En la planificación de la materia, la profesora (quien participó en un curso de formación permanente) ha programado sesiones entorno a la resolución de problemas de contexto real, que deben contribuir a mejorar la motivación y el interés de los alumnos. En ellas no está previsto que se trabajen conocimientos matemáticos nuevos, ni se busca la continuidad de clases anteriores y posteriores donde se introducen temas auriculares específicos. Durante el mes de octubre, por ejemplo, se enseña el tema de polinomios sin pretender establecer vínculos con las sesiones de resolución de problemas. A los alumnos se les explica que a lo largo del curso se irán planteando clases en las que se pondrá a prueba su capacidad de aplicar contenidos matemáticos variados en situaciones de la vida real.

La sesión de clase seleccionada plantea una tarea abierta con un enunciado de contexto real, donde los alumnos tienen que identificar las medidas de referencia que permitan comparar los envases con los cuales se comercializa una conocida marca de galletas. El enunciado, que se da por escrito, dice:

Hemos ido a comprar y nos hemos encontrado con cuatro formatos diferentes de envases para una misma marca de galletas [se menciona la marca]. ¿Con qué envase os quedaríais y porqué?

Se pide a los alumnos que formen equipos de 3 ó 4 integrantes. Se dejan los cuatro envases cerrados encima de una mesa, con el precio y el peso neto marcado en una etiqueta. Dos envases, uno grande y otro pequeño, contienen galletas pequeñas, y otros dos, uno grande y otro pequeño, incluyen galletas grandes. También se dejan dos balanzas sobre las que no se da ninguna instrucción. Al principio, todos los grupos hacen uso de las balanzas para pesar los envases, o bien para pesar las galletas tras abrir los envases. Algunos grupos buscan cuál es la galleta más cara. Otros toman el envase, su peso neto y la cantidad de galletas como unidades de referencia. Tras el tiempo de trabajo en equipo, se pide una redacción sobre el procedimiento seguido en cada grupo. Los últimos veinte minutos se destinan a la discusión conjunta de las estrategias de resolución. El episodio que transcribimos ocurre entre el inicio de la puesta en común y la síntesis de ideas:

[1] P: ¿Ya tenéis claro con qué envase os quedaríais?

[2] Al: Nos quedaríamos con la caja grande, porque con menos de un euro de diferencia con la segunda caja más grande tiene mucha más comida.

[3] P: ¿Cuál es la segunda caja más grande?

[4] Al: Una de las cajas grandes, la alargada, la de ciento veintiocho gramos.

[5] P: Vale.

[6] A2: Nosotros hemos sido más exactos. Hemos comparado directamente las galletas grandes y luego hemos hecho lo mismo con las galletas pequeñas. La galleta más cara es la del paquete pequeño de cuatro galletas y la más barata es la de la caja grande, donde vienen treinta y seis galletas.

[7] P: ¿Cuatro y treinta y seis? ¿Por qué dices que es más barato o más caro?

[8] A2: Porque hemos calculado el precio de una galleta. Calculamos elprecio dividiéndolo entre el número de galletas que hay, y nos ha dado el precio de una galleta.

[9] P: Pero las galletas son eso, galletas, y tienen medidas diferentes.

[10] A2: Sí. Hemos hecho lo mismo dos veces porque al principio hemos creído que si quieres comprar la galleta grande no vas a comprar la pequeña, por muy bien que te salga de precio.

[11] P: Vale.

[12] A3: A nosotros no nos ha preocupado ser exactos. Primero hemos pensado porqué se hacen dos formatos diferentes de galletas. Hemos puesto que si una persona va a comprar sola, no comprará un paquete grande de sesenta y ocho galletas para ella sola, por muy barato que sea.

[13] A4: En realidad lo importante no es quién compra las galletas ni quién las fabrica. Al dividir hemos mirado el peso, pero también se podría mirar la cantidad de galletas. El paquete pequeño con cuatro galletas vale cero sesenta y cinco por cuatro galletas. Si lo piensas así, no miras el peso de los envases.

[14] P: ¿Queréis saber que es la galleta más cara?

[15] A4: Sí.

[16] P: Lo que decís es que es la galleta más cara para vosotros, pero para el fabricante...

[17] A2: La más económica.

[18] P: Está bien pensado, pero continúo sin saber con qué envase os quedaríais. Estáis mencionando muchas cosas a la vez. Demasiadas ideas.

[19] A2: Nosotros hemos mirado muy bien las galletas. Hemos visto que la grande pesa quince gramos y tiene ocho coma veinticinco centímetros de diámetro. Y el diámetro de la galleta de diez gramos es cinco coma cinco centímetros. Hemos visto que no son la mitad ni el doble.

[20] P: ¿Por qué habéis buscado relaciones entre los dos tipos de galletas?

[21] A2: Por curiosidad.

[22] P: Bien, gracias. Vamos a consultar a otro grupo.

[23] A5: Nosotros hemos contestado que el segundo envase, porque tiene el doble de galletas y vale dos coma quince euros. Hemos imaginado qué pasaría si todos los envases llevaran las mismas galletas. El primero, si llevara las mismas galletas, valdría dos coma treinta y ocho euros, y por eso es mejor el primer envase.

[24] P: ¿De qué envase habláis?

[25] A5: Del que vale dos coma quince euros.

[26] A2: Nosotros nos hemos preguntado cuál es la galleta más cara. La más cara es la del segundo envase y la más barata la del último envase.

[27] P: ¿La más cara es la de la caja pequeña de galletas grandes?

[28] A2: Sí.

[29] P: ¿Y cómo sabéis que es la más cara?

[30] A2: Porque lo hemos mirado con los precios.

[31] A6: Pero es la más cara si sólo miramos los envases con galletas grandes. La caja pequeña de galletas grandes es más cara que la caja grande de galletas grandes. Luego tomamos las más baratas de cada tipo.

[32] P: Así, ¿es la más cara o no?

[33] A2: Si lo miramos con los euros es la más cara, pero si lo miramos, por ejemplo, con los gramos, no lo sería.

[34] P: Eso es muy interesante. Este paquete tiene muchas galletas grandes y si lo pensamos en gramos...

[35] A2: Bueno, al final también hemos buscado cuánto vale cada gramo de galleta, porque A6 decía que era mejor comparar todas las galletas y no mirar por separado las grandes y las pequeñas, para decidir sin separar los envases.

[36] A6: Hemos pesado una galleta y hemos visto cuánto dinero costaba cada gramo. [37] P: Muy bien.

[38] A7: Hay que decir que depende. ¿Por qué hacen diferentes envases para el mismo tamaño de galleta? Porque si haces una fiesta y vienen dieciocho amigos no compras cinco paquetes de cuatro galletas, sino que compras directamente el de dieciocho. Por eso se fabrican más formas.

[39] P: ¿Y entonces?

[40] A5: De los cuatro formatos, ¿cuál es el más económico para el fabricante? Esto es lo que nos preguntan y lo que tenemos que calcular. Ese nos va peor a nosotros. Hemos dicho que el paquete pequeño de cuarenta gramos porque en comparación con el grande, que tiene dos bandejas dentro, sale más rentable y además cuidamos el medio ambiente.

[41] P: Muy bien.

[42] Al: Ahora sí que no entiendo qué pedía el problema. Yo he hecho una tabla para colocar los cuatro envases con sus precios y con el peso de cada envase. Tenemos que escoger un envase, no una galleta. ¿Por qué estáis midiendo el diámetro de las galletas?

[43] A3: Para complicar las cosas. La cuestión es buscar números.

[44] A6: Estamos resolviendo el problema y sabemos mucho.

[45] A2: Nos ha dado las balanzas para mirar bien las galletas. [46] Al: O para pesar los envases si queríamos.

[47] A2: Pero el peso de los envases ya está escrito en el envoltorio y esto ya vale. Lo que hay que pesar son las galletas, para eso son las balanzas.

[48] Al: Si hubieras pesado los envases te habrías dado cuenta de que el peso marcado no está bien. Nosotros hemos tenido que arreglar lo que primero habíamos escrito en la tabla.

[49] A7: Pero eso pasa porque el peso marcado es sin el envase. [50] A2: Hay que ser exacto, hay que pesar las galletas.

[51] Al: Pero no sabemos si todas las galletas pesan igual. No habéis sido nada exactos porque habéis mirado una galleta y ya está, para luego mirarla como no tocaba.

[52] A2: Hemos tomado el peso de una galleta porque no podíamos estar todo el día pesándolas todas. Lo importante es haberse fijado en la galleta más barata y en la más cara.

[53] P: ¿Estos datos? Me cuesta seguir porque las matemáticas están un poco disfrazadas.

[54] Al: Porque las galletas sean redondas no hay que buscar el diámetro, además no son una circunferencia perfecta. Lo han hecho y luego no lo han usado para nada.

[55] A2: No lo hemos usado, pero así sabemos más cosas sobre las galletas. Nos ha dado galletas redondas, no cuadradas. Tienes que usar todo lo que sabes.

[56] A3: Si compras muchas galletas baratas redondas que no te vas a comer, eso es muy caro.

[57] P: Por lo que veo, este problema ha dado mucho de sí. Yo ahora haría un poco de resumen en la pizarra de lo más importante que se ha dicho.

En este episodio intervienen hasta siete alumnos de cuatro grupos: A1 y A4; A2 y A6; A3 y A7, así como A5. Los portavoces son A1, A2, A3 y A5. A pesar de que la profesora ha pedido que en la puesta en común sólo participen los portavoces, A4, A6 y A7 toman la palabra. En la puesta en común no se llegan a completar resultados, aunque cuatro de los seis grupos han escrito ventajas e inconvenientes de los envases y han escogido un único envase, que no es el mismo para todos los grupos. La interacción gira en torno a preguntas sobre aspectos puntuales de la resolución. Después del turno 57, se inicia un episodio de comparación en la pizarra de resultados numéricos escritos por cada grupo. La profesora divide las dos pizarras en tres partes y pide a los seis portavoces que anoten sus resultados.

 

4.2. Identificación de prácticas matemáticas

La tabla I muestra las principales prácticas matemáticas públicamente realizadas o sugeridas a lo largo del episodio anterior. La noción de práctica matemática adoptada (Godino y Batanero, 1994) hace que señalemos las acciones de la profesora y de los alumnos en las que se hace referencia a objetos y/o procesos matemáticos, pudiendo haber grados muy distintos de profiindización. En algunos casos simplemente se mencionan a los objetos matemáticos, de modo que la práctica consiste en reconocer dichos objetos en el contexto de una tarea de aula. La finalidad de este tipo de prácticas es más discursiva que actuativa y, en general, tiene que ver con la repetición textual de prácticas anteriores o con la demanda de ciertas confirmaciones. En otros casos, las prácticas relacionan objetos y procesos matemáticos, por lo cual tienen un carácter más exploratorio. Responden a finalidades de indagación, síntesis y justificación de contenidos matemáticos.

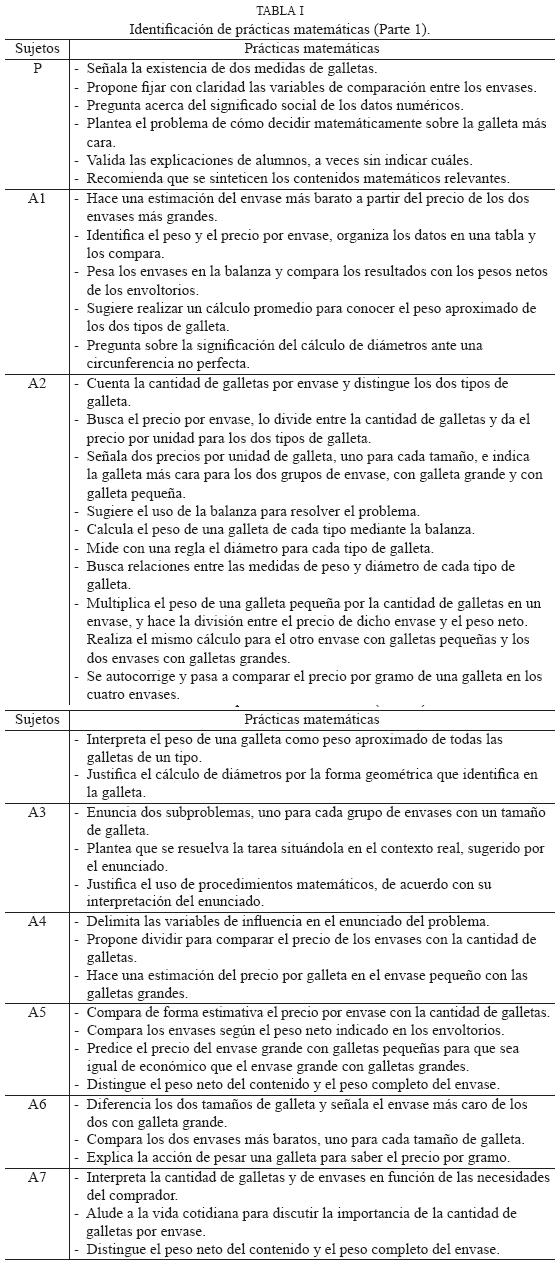
Ahora bien, la comunicación de la resolución de la tarea requiere clarificar las variables consideradas (precio por envase, precio por galleta, cantidad de galletas, necesidades del comprador), y luego explicar los procedimientos de comparación entre los envases, de acuerdo con las variables escogidas. La mayoría de las intervenciones de los alumnos se centran en uno de estos aspectos y a veces se refieren a ambos. A2 lleva a cabo el mayor número de prácticas matemáticas de ambos tipos. Se observa que los alumnos de un mismo grupo no necesariamente introducen prácticas que aluden auna misma estrategia de resolución. Es interesante notar que Al y A4 destacan estrategias distintas en la puesta en común, a pesar de que se pidió a los grupos que defendieran una posición común.

En general, hay tres estrategias de resolución distintas: a) buscar el precio por unidad de galleta en cada envase; b) buscar el precio por gramo de galleta en cada envase; c) decidir el envase más adecuado en función de las necesidades del comprador. La profesora realiza prácticas matemáticas como respuesta a las intervenciones de los alumnos, y solicita aclaraciones sobre las estrategias que, en su opinión, se explican de manera confusa. Los estudiantes refieren estrategias de comparación, pero no siempre clarifican qué envases y variables se comparan; incluso hay intervenciones breves de los alumnos en las que no detallan las variables, a pesar de que se supone que ya han sido explicadas en las discusiones de los grupos. Todo esto hace que la profesora adopte un papel de explicitación sobre la información no dada. De la observación al resto de la sesión, sabemos que el proceso de institucionalización de prácticas se da a partir del turno 57, cuando la profesora propone el uso de la pizarra para concluir.

 

4.3. Identificación de normas sociomatemáticas

La tabla II contiene algunas de las principales normas sociomatemáticas públicamente usadas o sugeridas en los procesos de interacción del episodio transcrito. Por cuestiones de espacio, en la tabla III seleccionamos una única norma para cada participante y aportamos algunas de las prácticas matemáticas y otras de tipo más general a partir de las cuales se infieren. Tenemos información sobre las prácticas más generales por la descripción del contexto de la tarea y de la situación didáctica. Detallamos los resultados sobre las normas supuestamente implicadas en la aparición de los dos conflictos entre significados que referimos en el apartado 4.4.

Respecto a la enunciación de las normas, partimos de la forma en que se mencionan las prácticas matemáticas y destacamos la función reguladora de algunos contenidos mediante los cuales se expresan dichas prácticas. Por ejemplo, una de las prácticas de A7 es: Alude a la vida cotidiana para discutir la importancia de la cantidad de galletas por envase. Esta práctica, junto con otras, hace razonable inferir la siguiente norma: La resolución de una tarea matemática puede centrarse en el contexto real.

En otras normas, el paralelismo con las prácticas no resulta obvio. Por ejemplo, para la norma la curiosidad es un criterio válido para justificar el desarrollo de las prácticas matemáticas hallamos varios referentes, entre ellos pregunta sobre la significación del cálculo de diámetros ante una circunferencia no perfecta o justifica el cálculo de diámetros por la forma geométrica identificada en la galleta. La norma anterior se infiere al comprobar que algunos alumnos miden el diámetro de los dos tamaños de galleta y buscan relaciones entre ambos, sin que estas prácticas sean requeridas para solucionar el problema. Cuando se les pregunta sobre el desarrollo de tales prácticas (ver turnos 20 y 21), explican que actúan por curiosidad y continúan realizando cálculos tras haber planteado prácticas que serían suficientes para la resolución.

Por otra parte, asignamos las normas a sujetos concretos, en tanto que su enunciación se infiere de prácticas hechas por ellos y no responden necesariamente a las expectativas de otros sujetos sobre lo que debe ocurrir en el aula. Las normas explicitadas o sugeridas por la profesora tampoco admiten una interpretación en términos de lo que espera que ocurra en el aula, pues pueden estar vinculadas a prácticas que se contradicen.

El paso de la tabla II a la tabla III resulta especialmente complejo desde un punto de vista metodológico. Nuestro modelo concibe al proceso de inferencia de normas en una forma principalmente interpretativa. Se parte de la lectura de transcripciones con textos que han sido dichos en el aula para llegar a enunciar otros textos que no han sido mencionados, pero pueden ser observados con base en el conocimiento de la situación didáctica y de la interacción. Para ello resulta fundamental la triangulación de perspectivas, a fin de que pueda justificarse que más de un investigador ha logrado ver las mismas normas a partir de los mismos datos.

En el caso de este artículo, cada una de las autoras por separado hizo una lista de prácticas y normas; luego las pusieron en común para ver las coincidencias y diferencias. Se hizo una reunión para consensuar la lista final de prácticas; sin embargo, ante las abundantes diferencias entre las dos listas iniciales de normas se recurrió a un tercer investigador del equipo, a quien se le dieron todos los datos de aula y se le pidió que hiciera una tercera lista de normas. Con las tres listas de normas elaboradas se efectuó otra reunión para consensuar una única lista, en la que sólo se incluyeron las normas sobre las que hubo acuerdo y se decidió cómo debían ser literalmente formuladas.

 

4.4. Identificación de conflictos entre significados

En el episodio que se analiza hallamos dos conflictos principales. Para inferirlos se actuó del mismo modo que en la identificación de prácticas y normas; asimismo, se recurrió de nuevo al tercer investigador del equipo. Hubo un acuerdo en que el primer conflicto tenía que ver con el dilema sobre el uso del contexto real al que aludía el enunciado en la resolución de una tarea matemática. El conflicto comienza a manifestarse en los turnos 12 y 13, cuando A3 y A4 cuestionan los criterios usados para seleccionar las prácticas que contribuirían a resolver una tarea de matemáticas, contextualizada en una situación de la vida cotidiana. Ambos proponen enfoques distintos:

[12] A3: A nosotros no nos ha preocupado ser exactos. Primero hemos pensado porqué se hacen dos formatos diferentes de galletas. Hemos puesto que si una persona va a comprar sola, no comprará un paquete grande de sesenta y ocho galletas para ella sola, por muy barato que sea.

[13] A4: En realidad, lo importante no es quién compra las galletas ni quién las fabrica. Al dividir hemos mirado el peso, pero también se podría mirar la cantidad de galletas. El paquete pequeño con cuatro galletas vale cero sesenta y cinco por cuatro galletas. Si lo piensas así, no miras el peso de los envases.

Casi todos los alumnos mencionan la importancia del contexto real y sitúan el procedimiento para seleccionar un envase según sus contenidos (cantidad y tamaño de las galletas, forma o peso). Hay, en general, un uso conjunto y complementario tanto del contexto real, que dan los envases, como del contexto académico, que atañe a las matemáticas que se pretenden trabajar. No obstante, en ocasiones identificamos un uso excluyente de uno de los contextos con respecto al otro; por ello, la confrontación entre el contexto real y el académico escolar lleva a plantear prácticas distintas en función del contexto priorizado. Esto sucede en turnos concretos como los siguientes, donde un alumno plantea el uso de cálculos, mientras otro propone una solución abierta de tipo cualitativo:

[38] A7: Hay que decir que depende. ¿Por qué hacen diferentes envases para el mismo tamaño de galleta? Porque si haces una fiesta y vienen dieciocho amigos no compras cinco paquetes de cuatro galletas, sino compras directamente el de dieciocho. Por eso se fabrican más formas.

[40] A5: De los cuatro formatos, ¿cuál es el más económico para el fabricante? Esto es lo que nos preguntan y lo que tenemos que calcular. Ese nos va peor a nosotros. Hemos dicho que el paquete pequeño de cuarenta gramos porque en comparación con el grande, que tiene dos bandejas dentro, sale más rentable y además cuidamos el medio ambiente.

O bien en los siguientes turnos, donde un alumno plantea consideraciones geométricas asociadas a su percepción del contexto académico del enunciado, y otro propone relativizar las soluciones en función de consideraciones que aluden a su percepción del contexto real:

[55] A2: No lo hemos usado, pero así sabemos más cosas sobre las galletas. Nos ha dado galletas redondas, no cuadradas.

[56] A3: Si compras muchas galletas baratas redondas que no te vas a comer, eso es muy caro.

Notamos que algunos estudiantes sustituyen la situación inicial de comparación y selección de envases por una de compra, donde el interés del comprador se considera crucial. Por una parte, observamos que las prácticas matemáticas de Al, A2, A4, A5 y A6 coinciden con procedimientos habituales en el entorno escolar. Por otra, las prácticas matemáticas de A3 y A7 reducen la resolución del problema a tomar una decisión sobre el envase más adecuado en función del interés del comprador. El primer grupo no atiende a las condiciones de subjetividad incluidas en el enunciado, mientras que el segundo no considera los problemas de generalización que puedan derivarse al hacer una interpretación excesivamente local de la tarea.

Aquí estamos ante un ejemplo de conflicto de tipo genérico, ya que la literatura de investigación en educación matemática ha documentado abundantemente la confrontación entre las normas de uso del contexto real y las del contexto académico en los procesos de resolución de problemas contextualizados (para discusiones complementarias sobre este tipo de conflicto, ver Jurdak, 2006, y Palm, 2008). En nuestro ejemplo, la confrontación de significados viene dada por el conflicto entre prácticas matemáticas asociadas a cada contexto, y no tanto entre normas de actuación que orienten de modo general y explícito sobre cómo enfrentarse a enunciados contextualizados. Se plantea la resolución de la tarea situándola en el contexto real que sugiere el enunciado, mas no se dice que cualquier tarea de este tipo deba ser pensada dando prioridad al contexto real. Este matiz es importante, ya que hay una gran diferencia entre sugerir que ' la resolución de una tarea matemática contextualizada puede situarse en el contexto real' y decir que 'debe'.

En el mismo episodio hay un segundo conflicto, que se relaciona con el dilema sobre el establecimiento y uso de relaciones matemáticas innecesarias para la resolución de una tarea. Dicho conflicto empieza a manifestarse en el turno 42, cuando Al cuestiona los procedimientos seguidos por otros alumnos:

[42] A1: Ahora sí que no entiendo qué pedía el problema. Yo he hecho una tabla para colocar los cuatro envases, con sus precios y con el peso de cada envase. Tenemos que escoger un envase, no una galleta. ¿Por qué estáis midiendo el diámetro de las galletas?

A1 y A2 mantienen un diálogo acerca de los conocimientos matemáticos necesarios en resolución de la tarea, pero van más allá y acaban refiriéndose a cuestiones sobre la conveniencia de ajustarse al uso de las matemáticas estrictamente necesarias para resolver una tarea cualquiera. En este caso, el conflicto de nuevo se plantea en términos de la confrontación entre normas: La búsqueda de relaciones matemáticas tiene sentido si la resolución de la tarea lo requiere. Para complicar las cosas. La cuestión es buscar números contra la búsqueda de relaciones matemáticas no siempre tiene que contribuir a la resolución de la tarea. Estamos resolviendo el problema y sabemos mucho".

El conflicto se manifiesta en distintas partes del episodio. Vemos, por ejemplo, los turnos donde Al entiende que el grupo de A2 ha medido el diámetro de los dos tipos de galleta porque ha asociado tal práctica escolar a la presencia de una forma circular, sin pensar su adecuación en el caso de la tarea sobre los envases:

[54] A1: Porque las galletas sean redondas no hay que buscar el diámetro, además no son una circunferencia perfecta. Lo han hecho y luego no lo han usado para nada.

[55] A2: No lo hemos usado, pero así sabemos más cosas sobre las galletas. Nos ha dado galletas redondas, no cuadradas. Tienes que usar todo lo que sabes.

En dos turnos anteriores, A6 ha expresado una idea similar a la necesidad de usar todo lo que se sabe en la resolución de un problema, al asociar estamos resolviendo un problema con sabemos mucho:

[43] A3: Para complicar las cosas. La cuestión es buscar números.

[44] A6: Estamos resolviendo el problema y sabemos mucho.

Algunos estudiantes sustituyen la situación primera de comparación y selección de envases por una situación de uso de las matemáticas que, de algún modo, consideran asociadas al enunciado de la tarea. Al y A6 no sólo reprochan a sus compañeros el uso de prácticas matemáticas innecesarias, sino que además valoran su calidad. Al refuerza sus argumentos sobre la necesidad de ajustar las prácticas implementadas con apreciaciones sobre la precipitación que atribuye a algunos de sus compañeros por no centrarse en unas pocas prácticas, y haber dedicado tiempo a obtener y comprobar datos que no deberían incluirse en la resolución:

[51] A1: Pero no sabemos si todas las galletas pesan igual. No habéis sido nada exactos porque habéis mirado una galleta y ya está, para luego mirarla como no tocaba.

Ninguno de los conflictos anteriores va acompañado de un proceso de institucionalización de prácticas que haya conducido la profesora; de manera general, los conflictos surgen de interacciones entre los alumnos. Por ello, los estudiantes que debaten la confrontación de significados refieren su experiencia de conflicto sin interpelar a la profesora. La valoración de algunas prácticas de los alumnos y de algunas normas sugeridas por ellos se deja para el momento de síntesis de las ideas principales en la pizarra, cuando la profesora toma la palabra sin aludir a las situaciones de conflicto. En el próximo apartado indicaremos la importancia de analizar el papel de la profesora en la aparición y la gestión de conflictos.

 

4.5. Exploración de relaciones entre prácticas, normas y conflictos

En este apartado relacionamos de manera más sistemática las prácticas, normas y conflictos desde la perspectiva de la interacción social; además, prestamos atención a la secuencia de interacciones con la profesora en torno a la experiencia de conflictos. Buscamos puntos críticos de la interacción entre los alumnos y la profesora en los cuales puede haber disparidad de interpretaciones que requieran procesos de negociación y cambios. Entendemos que se trata de puntos críticos cuando las intervenciones mantienen las distancias entre significados y dificultan la adopción de posiciones complementarias.

Ahora bien, en el caso del episodio que se analiza, nos centramos en los dos conflictos detectados. Llamamos Conflicto 1 al que atañe a la confrontación entre el contexto real y el contexto académico, y Conflicto 2 al que se refiere a la confrontación entre el uso de relaciones matemáticas más o menos ajustadas a las demandas de resolución de una tarea.

La tabla IV indica hasta qué punto el conflicto entre el contexto real y el académico, además de estar condicionado por las percepciones de los alumnos sobre la tarea, tiene que ver con las intervenciones de la profesora durante la resolución. La profesora explora las prácticas de los alumnos, pero no se posiciona de manera clara en la formulación de prácticas ni en la validación de las alternativas que proponen los grupos. Realiza prácticas de demanda de clarificación de las prácticas de los alumnos, y sólo en algunos momentos refrasea intervenciones con el propósito de que se completen argumentos.

En general, la manera como la profesora organiza el trabajo, en que da una gran autonomía a los alumnos para intervenir en la puesta en común, sin especificar los contenidos que se aceptarán como válidos al final de la sesión, genera dudas que no se resuelven. Con sus intervenciones la profesora llega incluso a sugerir normas distintas cuando, por un lado, señala la importancia del contexto real, al decir que las galletas "son" galletas y, por otro, destaca la relevancia del contexto académico, al afirmar que le cuesta seguir los razonamientos porque las matemáticas están "disfrazadas". En los turnos intermedios recurre a comentarios evaluativos, sin concretar qué argumentos evalúa ni indicar qué contenidos matemáticos considera más relevantes. Resulta significativo el momento posterior a los turnos 13 y 14, donde se han confrontado los enfoques del contexto real y del escolar; la profesora interviene sin tomar partido y, de algún modo, envía el mensaje de que ambos enfoques son válidos.

La tabla V refiere que la aparición del Conflicto 2 también tiene que ver con las intervenciones de la profesora durante la resolución de la tarea. La situación didáctica generada al responsabilizar a los alumnos de que otorguen sentido al discurso matemático de sus compañeros hace que surjan dudas acerca de qué prácticas son adecuadas. La profesora pregunta sobre el modo en que se exploran las prácticas, sin señalar que algunas no son útiles en la resolución de la tarea.

De nuevo, la profesora sugiere normas distintas cuando, por un lado, acepta el desarrollo de prácticas innecesarias para que se satisfaga la curiosidad de algunos alumnos; por otro, señala la conveniencia de ordenar y seleccionar la gran cantidad de prácticas mencionadas para continuar los procesos de resolución de los grupos. Aunque hay una intervención directa de la profesora en el tumo 53, donde refiere las dificultades para entender los procesos de resolución atribuibles a la diversidad de las prácticas planteadas, en tumos anteriores se ha alentado la aparición de esta diversidad mediante la validación de las formas de discusión entre los alumnos. El tumo 57 puede entenderse como el inicio de la delimitación de las prácticas adecuadas.

 

5. REFLEXIONES SOBRE LA POTENCIALIDAD DEL MODELO

Finalizamos nuestro artículo con reflexiones entorno al modelo de análisis, poniendo hincapié en sus limitaciones y potencialidad. Desde el enfoque de las limitaciones, conviene resaltar que cualquier modelo de análisis sobre la interacción en el aula es necesariamente un modelo que prioriza algunos puntos que conforman la complej idad asociada a los fenómenos de comunicación, participación e interacción social. Entender la complejidad y la multidimensionalidad de la interacción en las situaciones de enseñanza y aprendizaje de las matemáticas no puede hacerse con la aplicación de un único modelo. Por ello, es necesario adoptar una visión 'ecológica' de la construcción de saberes más amplia, donde se consideren los conocimientos diversos que surgen al aplicar varios modelos centrados en aspectos complementarios del aula.

En tal sentido, nuestro modelo de análisis para interpretar los procesos de interacción en el aula de matemáticas pretende contribuir a generar conocimiento sobre algunas de las características discursivas y normativas del contexto de aprendizaje. Quedan muchos otros aspectos por analizar, que son propios de la interacción social y también atañen a las características del contexto de aprendizaje; para algunos de ellos ya existen modelos de análisis suficientemente validados. Es el caso del estudio sobre los procesos de negociación de significados; aquí Scott, Mortimer y Aguiar (2006) han desarrollado métodos para analizar las situaciones de interacción en clases de ciencias, que en Gallart y Planas (en prensa) se aplican en clases de matemáticas. También son conocidos los métodos de Rochera, Colomina, Onrubia y Coll (2000) para estudiar la creación de actividad conjunta y de ayuda educativa en situaciones de interacción, que Edo (2004) centra en clases de matemáticas.

Hechas estas observaciones sobre la necesidad de contar con más de un modelo de análisis para estudiar la complejidad de la interacción en el aula, pasamos a argumentar el interés y potencialidad de nuestro modelo. En primer lugar, propone una metodología de aproximación a la realidad del aula a partir del uso operativo de nociones teóricas cuya relevancia se ha probado por separado en el desarrollo de diversos estudios empíricos anteriores. La vinculación de las nociones de normas y conflictos con la noción central de práctica matemática permite identificar e interpretar los contenidos públicos de la interacción, desde un marco teórico propio para el aula de matemáticas.

Por otra parte, la fundamentación de cada noción en un paradigma distinto garantiza en gran medida una visión holística de la interacción. La noción de práctica matemática, tomada del enfoque ontosemiótico, ubica a la interacción principalmente en una institución; la noción de norma sociomatemática, que concierne al enfoque sociocultural, la sitúa en una cultura y un discurso, mientras que la noción de conflicto entre significados, propia del enfoque lingüístico, la coloca en un nivel más individual de la comprensión sobre la institución y el discurso; asimismo, la vincula con el grado de apropiación del lenguaje de la disciplina.

Desde la perspectiva sobre la singularidad de cada aula y sesión de clase, la metodología aplicada permite situar el conocimiento de la interacción en relación con los contextos sociales e institucionales, que dan las prácticas y las normas, y los contextos personales, que surgen por la multiplicidad de interpretaciones acerca de los conflictos entre significados. El análisis de la interacción como un triple sistema de significados sociales, institucionales y personales, ubicados en un entorno determinado de aula, ha sido facilitado por la opción de integrar tres enfoques teóricos; la triple mirada a las dimensiones social, institucional y personal propicia el análisis de la interacción en función de la diversidad de relaciones que se establecen con los significados asignados a las prácticas matemáticas. Hay interacciones, por ejemplo, que dan lugar a significados muy distintos para una misma práctica; algunos de ellos son más cercanos al significado institucional y sugieren situaciones extremas de comunicación.

En este sentido, la identificación de conflictos puede entenderse como un tipo de información relevante acerca de las condiciones de la comunicación en el aula. Aún así, para tener un mejor conocimiento sobre las condiciones de la comunicación, sería necesario un análisis longitudinal que mostrara cómo se gestionan los conflictos entre significados, a medida que los participantes comparten más tiempo en el aula y aprenden a intercambiar referentes y prácticas.

 

AGRADECIMIENTOS

El desarrollo de este estudio se ha realizado en el marco de dos proyectos: ARIE 2007–00028 y MQD 2008–00154, ambos financiados por la Direcció General de Recerca de la Generalitat de Catalunya.

 

REFERENCIAS BIBLIOGRÁFICAS

Alsina, À. y Planas, N. (2008). Matemática inclusiva: propuestas para una educación matemática accesible. Madrid, España: Narcea.        [ Links ]

Callejo, M. L., Valls, J. y Limares, S. (2007). Interacción y análisis de la enseñanza: aspectos clave en la construcción del conocimiento profesional. Investigación en la Escuela 61, 5–22.        [ Links ]

Civil, M. & Planas, N. (2004). Participation in the mathematics classroom: does every student have a voice? For the Learning of Mathematics 24 (1), 7–13.        [ Links ]

Civil, M. & Planas, N. (2008). Voices on non–immigrant students in the multiethnic mathematics classroom. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano & A. Sepulveda (Eds.), Proceedings of the Joint Conference PME32–PMENA XXX (Vol. 4, pp. 121–127). México: Cinvestav.        [ Links ]

D'Amore, B., Font, V y Godino, J. D. (2007). La dimensión metadidáctica en los procesos de enseñanza y aprendizaje de la matemática. Paradigma 28 (2), 49–77.        [ Links ]

D'Amore, B. y Godino, J. D. (2007). El enfoque ontosemiótico como un desarrollo de la teoría antropológica en didáctica de la matemática. Revista Latinoamericana de Investigación en Matemática Educativa 10 (2), 191–218.        [ Links ]

Edo, M. (2004). Joc, interacció i construcció de coneixements matemátics. Tesis de doctorado, Universitat Autónoma de Barcelona, España.        [ Links ]

Engeström, Y. & Miettinen, R. (1999). Activity theory and individual and social transformation. In Y. Engestróm, R. Miettinen & R. L. Punamáki (Eds.), Perspectives on activity theory (pp. 19–38). Cambridge, USA: Cambridge University Press.        [ Links ]

Font, V. & Planas, N. (2008). Mathematical practices, semiotic conflicts and socio–mathematical norms. In O. Figueras, J. L. Cortina, S. Alatorre, T. Rojano & A. Sepulveda (Eds.), Proceedings of the Joint Conference PME32–PMENA XXX (Vol. 3, pp. 17–23). México: Cinvestav.        [ Links ]

Fortuny, J. M. y Rodríguez, R. (2003). El aprendizaje de las matemáticas como participación en una práctica de una comunidad virtual. En E. Castro (Ed.), Actas del VII Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 299–310). Granada, España: Universidad de Granada.        [ Links ]

Gallart, M. y Planas, N. (en prensa). Conversaciones matemáticas en el aula de matemáticas trilingüe. En C. Escobar y otros (Eds.), Actas del III Encuentro sobre Semi–inmersión en Cataluña. Bellaterra, España: Universidad Autónoma de Barcelona.        [ Links ]

Godino, J. D. y Batanero, C. (1994). Significado institucional y personal de los objetos matemáticos. Recherches en Didactique des Mathématiques 14 (3), 325–355.        [ Links ]

Godino, J. D., Batanero, C. & Font, V. (2007). The onto–semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education 39 (1–2), 127–135.        [ Links ]

Hoffmann, M. H. G., Lenhard, J. & Seeger, F. (2005). Activity and sign: grounding mathematics education. New York, USA: Springer.        [ Links ]

Inagaki, K., Hatano, G. & Morita, E. (1998). Construction of mathematical knowledge through whole–class discussion. Learning and Instruction 8, 503–526.        [ Links ]

Iranzo, N. y Fortuny, J. M. (2008). La influencia del SGD en las estrategias de resolución de problemas de geometría. En R. Luengo, B. Gómez, M. Camacho y L. J. Blanco (Eds.), Actas del XII Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 321–332). Badajoz, España: SEIEM.        [ Links ]

Jurdak, M. (2006). Real world, situated and school contexts. Educational Studies in Mathematics 63 (3), 283–301.        [ Links ]

Llinares, S. (2002). La práctica de enseñar y aprender a enseñar matemáticas: la generación y uso de instrumentos de la práctica. Revista de Enseñanza Universitaria 19, 115–124.        [ Links ]

Llinares, S. (2007). Análisis de la práctica de enseñar matemáticas e interacción: elementos clave en el proceso de llegar a ser maestro en el ámbito de la Didáctica de la Matemática. En M. I. Berenguer y otros (Eds.), Actas de las XIII Jornadas para el Aprendizaje y la Enseñanza de las Matemáticas (CD–ROM). Badajoz, España: Federación Española de Profesores de Matemáticas.        [ Links ]

Llinares, S. (2008). Agendas de investigación en educación matemática en España: una aproximación desde "ISI–web of knowledge" y ERIH. En R. Luengo, B. Gómez, M. Camacho y L. J. Blanco (Eds.), Actas del XII Simposio de la Sociedad Española de Investigación en Educación Matemática (pp. 25–54). Badajoz, España: SEIEM.        [ Links ]

Mercer, N. & Littleton, K. (2007). Dialogue and the development of children's thinking: a sociocultural approach. London, UK: Routledge.        [ Links ]

Palm, T. (2008). Impact of authenticity on sense making in word problem solving. Educational Studies in Mathematics 67(1), 37–58.        [ Links ]

Penalva, M. C., Escudero, I. y Barba, D. (2006). Conocimiento, entornos de aprendizaje y tutorización para la formación del profesorado de matemáticas. Granada, España: Proyecto Sur.        [ Links ]

Planas, N. (2005). El papel del discurso en la construcción del discurso de la práctica matemática. Cultura y Educación 17 (1), 19–34.        [ Links ]

Planas, N. (2007). The discursive construction of learning in a multiethnic school: perspectives from non–immigrant students. Intercultural Education. European Journal of lntercultural Studies 18 (1), 1–14.        [ Links ]

Planas, N. y Edo, M. (2008). Interacción entre discursos en una situación de práctica matemática escolar. Cultura y Educación 20 (4), 441–457.        [ Links ]

Planas, N. & Civil, M. (2009). Working with mathematics teachers and immigrant students: an empowerment perspective. Journal of Mathematics Teacher Education, DOI: 10.1007/sl0857–009–9116–l.        [ Links ]

Planas, N., Fortuny, J. M. e Iranzo, N. (2009). Análisis de casos por un equipo de investigación–acción: ejemplos para la formación del profesorado de matemáticas. UNO. Revista de Didáctica de la Matemática 51, 1–10.        [ Links ]

Planas, N. & Setati, M. (2009). Bilingual students using their languages in the learning of mathematics. Mathematics Education Research Journal, 21 (2), 105–127.        [ Links ]

Ramos, A. B. y Font, V. (2008). Criterios de idoneidad y valoración de cambios en el proceso de instrucción matemática. Revista Latinoamericana de Investigación en Matemática Educativa 11 (2), 233–265.        [ Links ]

Rochera, M. J., Colomina, R., Onrubia, J. y Coll, C. (2000). Actividad conjunta y habla: una aproximación al estudio de los mecanismos de influencia educativa. En P Fernández y M. A. Melero (Eds.), La interacción social en contextos educativos (pp. 193–326). Madrid: Siglo XXI.        [ Links ]

Scott, P., Mortimer, E. & Aguiar, O. (2006). The tension between authoritative and dialogic discourse: a fundamental characteristic of meaning making interactions in high school science lessons. Science Education 90, 605–631.        [ Links ]

Tirosh, D. & Wood, T. (2008). Tools and processes in mathematics teacher education: an introduction. In D. Tirosh & T. Wood (Eds.), The International Handbook of Mathematics Teacher Education (pp. 1–14). Rotterdam, Holland: Sense Publishers.        [ Links ]

Voigt, J. (1995). Thematic patterns of interaction and sociomathematical norms. In P. Cobb & H. Bauersfeld (Eds.), The emergence of mathematical meaning: interaction in classroom cultures (pp. 163–199). Hillsdale, NJ: Lawrence Erlbaum.        [ Links ]

Yackel, E. & Cobb, P. (1996). Sociomathematical norms, argumentation and autonomy in mathematics. Journal for Research in Mathematics Education 27, 458–477.        [ Links ]