Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.12 no.2 Ciudad de México jul. 2009
Artículos
Conflictos semióticos de estudiantes mexicanos en un problema de comparación de datos ordinales
Semiotic conflicts of mexican students for a problem of comparison of ordinal data
Silvia Mayen*, Carmen Batanero** y Carmen Díaz***
* Instituto Politécnico Nacional, México; smayen@correo.ugr.es
** Universidad de Granada, España; batanero@ugr.es
*** Universidad de Huelva, España; carmen.diaz@dpsi.uhu.es
Recepción:Agosto 20, 2008
Aceptación: Junio 2, 2009
RESUMEN
En este trabajo analizamos las respuestas a un problema de comparación de datos ordinales en 643 estudiantes mexicanos de Educación Secundaria y Bachillerato. Utilizando las ideas del Enfoque Onto–Semiótico propuesto por Godino y sus colaboradores, realizamos un análisis de las respuestas abiertas, clasificándolas según la medida de tendencia central utilizada y los conflictos semióticos detectados. Mediante el test Chi–cuadrado estudiamos la relación entre el tipo de respuesta y el grupo de estudiantes. Observamos mejores resultados entre los alumnos de Secundaria, quienes utilizan en mayor medida la mediana y la moda, aunque también dejan con mayor frecuencia respuestas en blanco.
PALABRAS CLAVE: Comprensión, conflictos semióticos, comparación de distribuciones, datos ordinales, media, mediana.
ABSTRACT
This study analyzes the responses of 643 Middle and High School students from Mexico to an open ended problem about the comparison of ordinal data. Following the onto–semiotic approach developed by Godino and colleagues, the responses were categorized by the choice of measure of central tendency and the observed semiotic conflicts. A Chi–square test was used to investigate the relationship between the type of response and the level of the students. We observed better results for the secondary students, the majority of whom used the median and the mode, although a greater percentage of them gave no response.
KEYWORDS: Understanding, semiotic conflict, comparison of distributions, ordinal data, mean, median.
RESUMO
Neste trabalho analisamos as respostas dadas por 643 alunos mexicanos, do terceiro ciclo do Ensino Básico e do Ensino Secundario, a um problema de comparação de dados ordinais. Utilizando as ideias do enfoque Onto–Semiótico proposto por Godino e seus colaboradores, realizamos urna análise das respostas abertas, classificando–as segundo a medida de tendência central usada pelos alunos na resolução e os conflitos semióticos detectados. O teste de Qui–quadrado foi usado para analisar a relação entre o tipo de resposta e o grupo de estudantes. Observamos melhores resultados com os alunos do Ensino Básico, que utilizam mais vezes a mediana e a moda, contado também deixam com maior frequência respostas em branco.
PALAVRAS CHAVE: Compreensão, conflitos semióticos, comparação de distribuições, dados ordinais, media, mediana.
RÉSUMÉ
Les réponses apportées au problème que pose la comparaison de données ordinales portant sur 643 collégiens et lycéens mexicains constituent le sujet de cette présente étude. Faisant nótre l'approche ontologique et sémiotique proposée par Godino et son equipe de travail, nous procédons a une analyse des réponses ouvertes et a leur classification tout en prenant en compte la mesure de la tendance céntrale utilisée et les problémes sémiotiques qui ont été detectes. Utilisant le test du chi carré, nous abordons les relations qui existent entre le type de réponse donnée et le groupe d'étudiants observes. Nous remarquons de meilleurs résultats chez les collégiens qui utilisent plus réguliérement la médiane et le mode bien qu'ils répondent moins fréquemment aux questions.
MOTS CLÉS: Comprehension, problèmes sémiotiques, comparaison de distributions, donnés ordinales, moyenne, médiane.
1. INTRODUCCIÓN
Las medidas de tendencia central (media, mediana y moda) han suscitado gran interés en investigadores como Pollatsek, Lima y Well (1981), Barr (1980), Cai (1995), Gattuso y Mary (1996), Watson y Moritz (1999, 2000) o Cobo (2003), quienes analizan los errores y dificultades para su aprendizaje en alumnos de diversas edades. Dichos trabajos se han centrado principalmente en la media aritmética, y las tareas que proponen aluden a datos numéricos medidos en escala de intervalo, en el que determinadas diferencias numéricas corresponden a las mismas diferencias en la magnitud subyacente.
Sin embargo, el análisis exploratorio de datos (perspectiva que se recomienda actualmente en el currículo de matemáticas para educación secundaria) da un gran peso a los estadísticos de orden, que consideran la posición relativa de los valores de la variable en el conjunto de datos. Uno de estos estadísticos es la mediana, que Nortes (1993, página 69) define de la siguiente manera: si suponemos ordenados de menor a mayor todos los valores de una variable estadística, se llama mediana al valor de la variable tal que existen tantos datos con valores de la variable superiores o iguales como inferiores o iguales a él.
También el análisis exploratorio de datos introduce algunas representaciones gráficas que se basan en los estadísticos de orden (como el gráfico de la caja), los cuales, si bien son apropiados para los datos medidos en escala de intervalo, cobran mayor relevancia ante los datos ordinales, que se pueden clasificar y ordenar, mas no se puede realizar operaciones aritméticas con ellos. Los datos ordinales aparecen en muchas situaciones cotidianas, como el nivel de estudios de una persona o el grado de acuerdo en un cuestionario de opinión. Por tanto, sería importante que la enseñanza de la estadística en secundaria tuviese en cuenta este tipo de datos, si queremos formar ciudadanos competentes para interpretar la información estadística que concierne a la vida profesional y cotidiana. Ello requeriría tener un conocimiento sobre las posibles dificultades que presentan los estudiantes en el conocimiento y uso de datos ordinales.
El propósito de esta investigación es analizar los conflictos que tienen los estudiantes cuando se les pide que comparen dos conjuntos de datos ordinales en una situación comprensible para ellos. Asimismo, tratamos de averiguar si los alumnos perciben que la mediana es la medida de tendencia central que se debe calcular en un conjunto de datos ordinales cuando esté definida (pues la media no lo está), y que ofrece más información que la moda cuando sea posible calcularla. También deseamos evaluar si los estudiantes calculan correctamente las medidas de tendencia central en este tipo de datos. Con todo ello seguimos las investigaciones previas, ofrecemos información sobre la comprensión de los estudiantes mexicanos para tales conceptos y comparamos los resultados con los que obtuvo Cobo (2003) en su trabajo con jóvenes españoles.
A continuación describiremos brevemente el marco teórico y las investigaciones previas, así como expondremos las conclusiones de nuestro estudio.
2. MARCO TEÓRICO Y ANTECEDENTES
2.1. Marco teórico
Este trabajo se sitúa en el enfoque ontosemiótico que proponen Godino y sus colaboradores (Godino, 1999 y 2002; Godino, Font y Wilhelmi, 2006; Godino, Batanero y Font, 2007; D'Amore y Godino, 2007), donde el significado de los objetos matemáticos (por ejemplo, la mediana) se considera altamente complejo y está compuesto por diversos elementos de significado, los cuales tendremos en cuenta:
– Situaciones–problema (aplicaciones extramatemáticas o ejercicios). Por ejemplo, la comparación de datos medidos en la escala ordinal o de razón, cuando se presentan valores atípicos, serían problemas de los que surge la idea de mediana.
– Lenguajes (términos, expresiones, notaciones, gráficos) en sus diversos registros (escrito, oral, gestual). Serían, por ejemplo, las palabras "mediana", "percentil del 50%", así como los símbolos y gráficos asociados.
– Conceptos–definición (que se introducen mediante definiciones o descripciones). Por ejemplo, la definición de mediana como valor central o que divide una distribución ordenada de datos en dos partes iguales.
– Proposiciones o propiedades (enunciados sobre conceptos). Por ejemplo, que la mediana no es una operación interna, no tiene elemento neutro ni cumple la propiedad asociativa; su valor no se ve afectado por los valores atípicos.
– Procedimientos (algoritmos, operaciones, técnicas de cálculo), como los diferentes algoritmos de cálculo para datos aislados, que se agrupan en tablas o a partir de gráficos.
– Argumentos (enunciados usados para validar o explicar proposiciones y procedimientos).
El enfoque ontosemiótico distingue el significado institucional y el personal de un mismo objeto matemático (en este caso, la mediana). El significado institucional incluye las prácticas matemáticas que se intenta transmitir al estudiante en una institución de enseñanza, mientras que el significado personal estaría formado por las prácticas matemáticas que adquiere el estudiante, algunas de las cuales podrían no coincidir con las pretendidas en la institución. Para el caso de la mediana, dichos elementos son analizados con detalle por Cobo y Batanero (2000), quienes muestran su complejidad, aunque la abordan desde el punto de vista de la estadística descriptiva.
Godino (2002) señala que en las prácticas matemáticas intervienen objetos ostensivos (símbolos o gráficos) y no ostensivos (evocados al hacer matemáticas), los cuales son representados en forma textual, oral, gráfica o simbólica. Por ejemplo, en el trabajo matemático los símbolos (significantes) remiten a entidades conceptuales (significados). Un punto crucial de la enseñanza es lograr que los alumnos dominen la semántica de tales símbolos, además de su sintaxis.
La investigación en didáctica de las matemáticas ha mostrado la importancia que tienen las representaciones en la enseñanza y el aprendizaje; sin embargo, una cuestión que todavía no ha sido suficientemente analizada es la variedad de objetos que desempeñan el papel de representación y de objetos representados (Godino, Batanero y Font, 2007). El interés de Godino, Batanero y Font es ahondar en este aspecto, tomando de Eco (1995)1 la noción de función semiótica como una "correspondencia entre conjuntos" que pone enjuego tres componentes:
– Un plano de expresión (objeto inicial, considerado frecuentemente como el signo).
– Un plano de contenido (objeto final, que se concibe como el significado del signo; esto es, lo representado, lo que se quiere decir, a lo que se refiere un interlocutor).
– Un criterio o regla de correspondencia (alude a un código interpretativo que asocia los planos de la expresión y del contenido).
El enfoque ontosemiótico resalta la diversidad de objetos que se ponen en juego durante la actividad matemática, ya que cualquier tipo de elementos de significado que hemos descrito puede aparecer como parte de la función semiótica, tanto en el plano de la expresión como en el del contenido. La idea de función semiótica destaca el carácter esencialmente relacional de la actividad matemática y sirve para explicar algunas dificultades y errores de los alumnos, como se observa en los trabajos de Godino (2002); Godino, Batanero y Font (2007), y D'Amore y Godino (2007), quienes llaman conflicto semiótico a las interpretaciones de expresiones matemáticas hechas por los estudiantes que no concuerdan con las pretendidas por el profesor o el investigador. Dichos conflictos semióticos causan equivocaciones en los alumnos no por su falta de conocimientos, sino por no haber relacionado adecuadamente los dos términos de una función semiótica.
Nuestra investigación se orienta a determinar los conflictos semióticos que tienen los estudiantes de secundaria y bachillerato en relación con la mediana, dentro de una situación en la que se comparan datos ordinales. La identificación de los conflictos semióticos permite establecer condiciones de control sobre los procesos de estudio en que tales objetos se ponen en funcionamiento (Godino, Font y Wilhelmi, 2006). Para detectarlos, se lleva a cabo un análisis semiótico de las respuestas de los estudiantes, centrando la atención en las funciones semióticas que instauran entre los diversos elementos de significado como parte de las prácticas matemáticas que efectúan al resolver el problema. Seguiremos el método de las investigaciones previas que se basan en el enfoque ontosemiótico para analizar los libros de texto (Cobo, 2003; Contreras y Ordóñez, 2006; Godino, Font y Wilhelmi, 2006), las respuestas de los estudiantes (Cobo, 2003) o los procesos de instrucción (Ramos y Font, 2008).
2.2. Investigaciones sobre la comprensión de la mediana
Las investigaciones previas afirman que la definición de mediana no es clara para los estudiantes. Barr (1980) hizo un estudio con alumnos de 17 a 21 años, y concluyó que interpretaban la mediana como el centro de "algo", pero no comprendían a qué se refería.
Algunos estudiantes que son capaces de calcular la mediana cuando los datos se dan en forma de lista tienen dificultad para determinarla a partir de una tabla de frecuencias. Incluso los alumnos universitarios consideran difícil de aceptar que se puedan emplear dos algoritmos diferentes para el cálculo de la mediana, dependiendo del tipo de datos (agrupados o no agrupados), y que puedan obtenerse valores distintos en el cálculo con datos agrupados al variar la amplitud de los intervalos de clase. Tampoco comprenden cómo se pasa de la definición de la mediana a su cálculo (Schuyten, 1991).
Por su parte, Estepa (2004) sugiere que los alumnos se encuentran con obstáculos para calcular la mediana si parten de las representaciones gráficas de las frecuencias acumuladas, ya que no están acostumbrados a las funciones discontinuas con saltos. Si tienen que interpolar para hallar el valor de la mediana incurren en errores por sus fallas de razonamiento proporcional. Además, los estudiantes no tienen el suficiente dominio para manejar las desigualdades que aparecen asociadas a la definición de mediana y su cálculo.
Otros errores que distinguió Carvalho (1998, 2001) al analizar el cálculo de lamedianaen alumnos de 13 a 14 años fueron: a) no ordenarlos datos al calcularla mediana, entendiendo que la mediana es el centro de la lista de datos no ordenada: b) calcular el dato central de las frecuencias absolutas ordenadas de forma creciente; es decir, confundir la frecuencia con el valor de la variable; c) calcular la moda en lugar de la mediana.
2.3. Comparación de las distribuciones de datos
Una característica esencial del análisis estadístico es que trata de describir las propiedades de los conjuntos de datos y no de cada dato aislado. Konold, Pollatsek, Well y Gagnon (1997) han observado cómo los estudiantes razonan al comparar dos distribuciones de datos e indican que el uso de las medidas de tendencia central como estrategia para compararlos no es intuitivo. Los alumnos se centran en las frecuencias absolutas y no en las relativas, incluso cuando las muestras sean de tamaño muy diferente; además, estudian las diferencias entre las distribuciones al comparar las frecuencias de los valores de la variable que coinciden en ambos grupos. Konold, Pollatsek, Well y Gagnon plantean que la dificultad surge cuando los estudiantes no han dado el paso de pensar en los valores de la variable como una propiedad de los individuos aislados a comparar las propiedades de los conjuntos de datos.
También Batanero, Estepa y Godino (1997) informan sobre las siguientes estrategias incorrectas en alumnos de licenciaturas en Educación cuando comparan dos distribuciones: a) usar sólo valores aislados en las dos distribuciones para comparar; b) esperar un aumento/disminución similar en todos los casos para muestras relacionadas. Watson y Moritz (1999, 2000) clasifican dichas estrategias de acuerdo con un modelo jerárquico, e indican que en un primer nivel los estudiantes son capaces de comparar conjuntos de igual tamaño, al calcular el total o realizar comparaciones visuales de las distribuciones a partir de una gráfica. En un segundo nivel, comparan los conjuntos de datos de diferente tamaño mediante un razonamiento proporcional. Las estrategias incluyen la comparación de la suma de valores que presenta la variable en cada grupo, efectuar comparaciones visuales y comparar las medidas de tendencia central de los dos grupos.
Mientras que los estudios anteriores se han centrado en datos medidos en escala de intervalo, Cobo (2003) utiliza un ítem que contiene datos ordinales como parte de su cuestionario sobre la comprensión de las medidas de tendencia central. Su interés no se fija específicamente en la mediana ni en los conflictos semióticos que le atañen, sino en la descripción del significado personal de los estudiantes sobre las medidas de tendencia central. En nuestro trabajo nos centraremos únicamente en este ítem, profundizando el análisis semiótico de las respuestas de los estudiantes. También analizaremos las diferencias entre tres grupos de estudiantes, incluyendo a alumnos de bachillerato, un nivel escolar que no tomó en cuenta Cobo.
3. MÉTODO
3.1. Muestra
La muestra estuvo compuesta por 643 alumnos mexicanos, cuyas edades comprendían de 14 a 19 años, que pertenecían a dos niveles: 481 de bachillerato que estaban matriculados en seis centros de estudios científicos y tecnológicos del Instituto Politécnico Nacional, y 162 de secundaria que asistían a dos instituciones.
Los alumnos de secundaria (nivel básico en México), cuyas edades eran de 14 y 15 años de edad, cursaban el tercer año. Habían estudiado por primera vez las medidas de tendencia central en el mismo curso en que pasamos el cuestionario. Se dedicó aproximadamente un mes para estudiar el tema y su enseñanza se hizo alrededor de dos meses antes de aplicar el cuestionario.
Respecto a la otra parte de la muestra, la integraron estudiantes de sexto semestre de bachillerato (tercer año), con edades de entre 16 y 19 años, aunque la mayoría tenían 17 y 18. En el mismo curso en que se les aplicó el cuestionario habían estudiado estadística, incluyendo el tema de medidas de tendencia central (media, mediana, moda). Aquí tomamos dos diferentes grupos de estudiantes: un primer grupo, de 356 alumnos, contestó el cuestionario aproximadamente un mes después de estudiar el tema; el segundo grupo, de 125 alumnos, lo hizo al finalizar el curso, unos seis meses después. De manera general, los alumnos de cada nivel escolar eran de clase social media y llevaban el mismo programa de estudios.
3.2. Problema propuesto y método
El problema que se analiza está tomado originalmente de Godino (1999) y posteriormente fue usado por Cobo (2003). Debido a que los datos corresponden a una variable ordinal que no admite el cálculo de la media, la tendencia central de los datos sólo puede resumirse por la mediana y la moda. Asimismo, se requiere de conocimiento sobre la media, como el hecho de que no es una medida adecuada para datos ordinales. Este ítem registró el mayor número de respuestas incorrectas en un estudio comparativo previo (Mayen, Cobo, Batanero y Balderas, 2007), tanto en alumnos mexicanos como españoles, lo cual sugiere que su dificultad no es específica de un solo contexto educativo. La figura 1 reproduce el problema propuesto, que se estudiará a continuación.

Para resolver este problema, en el que los datos son ordinales y hay un número impar de datos, la solución óptima es comparar las medianas de los dos grupos en vez de las modas, ya que la mediana atiende al orden de los datos, no sólo a su frecuencia. Para calcularla en cada grupo, el alumno tendría que ordenar previamente los valores, y luego buscar el valor de la variable correspondiente al dato que ocupa la posición central en cada uno de los grupos, como se indica a continuación:
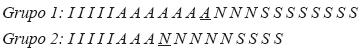
Como el primer grupo tiene 23 elementos, el dato que ocupa la posición central está en el lugar número 12; entonces, el valor de la mediana corresponde al aprobado (A). En el segundo grupo, de 17 elementos, el valor de la mediana es notable (N) porque el dato central está en la posición 9. Portante, el segundo grupo es superior al primero.
La solución, aparentemente sencilla, entraña una gran complejidad semiótica, como se observa en el análisis de la solución (tabla I). Para facilitar la lectura, hemos dividido la solución del problema en unidades de análisis. En la columna izquierda representamos los pasos en la solución, y en la derecha las funciones semióticas que establece el alumno en cada paso.

El análisis muestra que la actividad requiere no sólo la comprensión de muchos conceptos y propiedades previos, sino también de la aplicación y comprensión de los procedimientos y representaciones, utilizando una argumentación de tipo análisis–síntesis. Los procesos matemáticos que describe Godino (2002) aparecen en diversos momentos:
a) Procesos de particularización (por ejemplo, al concretar la idea general de mediana a la mediana particular del conjunto de datos).
b) Representación y significación (al simbolizar los datos o interpretar el problema).
c) Materialización–abstracción (al pasar de un objeto matemático a una situación real donde se aplica; por ejemplo, cuando se visualiza el peso de un niño concreto).
Si el conjunto de datos que ofrece el problema tuviese un número par de valores, habría dos valores que ocuparían el lugar central. En este caso, donde hay dos valores centrales diferentes, habría una indeterminación porque los dos valores centrales cumplirían la definición de mediana. Cuando los datos están medidos en escala de razón, el convenio para calcular la mediana en un caso de indeterminación es tomar el valor medio de los dos centrales. Notamos en estos procedimientos el carácter convencional de algunas reglas matemáticas que explican, según Godino, Font y Wilhelmi (2006), algunos conflictos semióticos de los estudiantes.
Es razonable que, debido a tal complejidad, algunos estudiantes tengan conflictos en los diferentes pasos del proceso y no lleguen a la solución esperada. Por este motivo, se han considerado también correctas las respuestas donde el alumno resuelve el problema al comparar adecuadamente las modas, que están definidas en un conjunto de datos ordinales. En caso que el alumno transforme los datos a numéricos, calcule y compare acertadamente las medias, hemos considerado su respuesta como parcialmente correcta.
El análisis que describiremos a continuación se centra en los razonamientos de los estudiantes al resolver el problema, e identifica los objetos estadísticos que usan correcta e incorrectamente. Nuestra intención es comprobar si las dificultades halladas en las investigaciones previas se presentan en los alumnos mexicanos, con qué frecuencia y si varían según el nivel escolar. Queremos también explicar dichas problemáticas en términos de conflictos semióticos.
4. RESULTADOS
Una vez que tuvimos las respuestas de los estudiantes, se inició un proceso cíclico de categorization en el que se compararon las contestaciones similares. Se realizó un análisis semiótico de las respuestas típicas en cada categoría para inferir los objetos y procesos matemáticos que el estudiante emplea en su resolución. De igual manera, a través de un proceso inductivo de revisión y comparación se clasificaron las respuestas, considerando en primer lugar la medida de tendencia central que se usa (media, mediana, moda o ninguno), y en segundo las respuestas que corresponden a una misma de ellas, atiendo a la existencia de conflictos semióticos semejantes. Así se obtuvo una lista de las categorías de respuestas que se describen a continuación, y se analiza un ejemplo de cada una. También se muestra la tabla de análisis semiótico del primer ejemplo (categoría C1) para ilustrar el método seguido en dicho análisis.
C1. Respuestas basadas en la media aritmética
En estas respuestas, el alumno identifica correctamente que el problema se soluciona a través de una medida de tendencia central; asimismo, realiza algún tipo de transformación en el conjunto de datos para convertirlos en cuantitativos. La respuesta hubiera sido correcta si el estudiante, una vez cambiados los datos a numéricos, hubiera hallado su mediana. No obstante, consideramos parcialmente correcto el caso de que se calcule la media y la comparación sea adecuada, ya que el alumno no discrimina bien los diferentes tipos de variable estadística y no es consciente de que la media no tiene sentido en los datos ordinales. El carácter ordinal viene dado por el tipo de dato y no por el código que se usa para representarlo.
Hemos distinguido en este grupo las siguientes respuestas:
C1.1. Transforma los datos ordinales y calcula correctamente la media. En el análisis de la respuesta, que se transcribe a continuación y es descrita con detalle en la tabla 2, el alumno asigna valores numéricos a las categorías. Luego, calcula correctamente el valor de la media aritmética en cada grupo y sustituye los datos de cada grupo por su media para compararlos. Es decir, identifica los datos de manera correcta al enfocar a la distribución como un todo, pero toma la media y no la mediana para resolver el problema. Por ello, la solución no coincide con la esperada.


C1.2. Conflicto en el algoritmo de la media (divide por un número incorrecto). Al igual que en el caso anterior, el alumno asigna valores a las categorías, resuelve el problema con la comparación de las medias y designa como mejor al grupo con mayor media. Sin embargo, se añade al conflicto descrito en la categoría C1.1 otro conflicto en el algoritmo, pues el estudiante confunde el divisor por el cual hay que dividir. En el ejemplo que reproducimos a continuación, asigna los valores 6, 8, 9 y 10 a insuficiente, aprobado, notable y sobresaliente, respectivamente; es decir, lleva a cabo una correspondencia numérica que no conserva la escala de medida. Calcula la frecuencia de casos para cada categoría en cada grupo por medio de las ideas de variable y frecuencia, que relaciona con el contexto del problema; luego, halla la media aritmética en cada grupo. Así, el alumno tiene errores de cálculo, divide el segundo grupo entre el número de elementos que conforman la muestra del primer grupo, y no identifica cuál es el mejor promedio para los datos presentados.

C1.3. Confunde los conceptos medida de tendencia central y valor de la variable. Al igual que en los casos anteriores, el alumno identifica el campo de problemas y también la medida de tendencia central como representante de un conjunto de datos. Pero cuando da un valor numérico a los códigos refleja un conflicto sobre el tipo de variable. En el ejemplo que aparece en la figura 4, el alumno señala como medida de tendencia central más adecuada el "Aprobado", que en realidad es un valor de la variable. Por tanto, hay un conflicto semiótico que consiste en confundir el valor de la variable y la medida de tendencia central.

C1.4. Calcula la media de frecuencias relativas. A los conflictos anteriores se añade otro, que concierne a que el estudiante usa el valor de la frecuencia relativa
y no el de la variable al calcular la media, por lo que confunde estos conceptos. En el ejemplo que contiene la figura 5, el alumno calcula la media de las frecuencias relativas, no la media de la variable. Los valores que se obtienen en los dos grupos son prácticamente iguales porque la suma de las frecuencias relativas ha de ser igual a la unidad; por ello, llega a un valor cercano a 1/4 al dividir entre el número de categorías. Dicha estrategia es equivalente a asignar una frecuencia idéntica de "1" a todas las categorías, por lo cual llega a una solución incorrecta. Este conflicto no fue identificado por Cobo (2003) ni lo hemos encontrado en las investigaciones previas.

C1.5. Halla el número esperado de alumnos por categoría si no hubiese diferencias en los grupos. En el ejemplo de la figura 6, a diferencia de los casos anteriores, el alumno no asigna códigos numéricos a los valores de la variable. Al resolver el problema, primero compara las frecuencias para cada valor de la variable en los dos grupos con el fin de ver si uno supera claramente al otro, mas no detecta una ventaja clara. Luego, halla una frecuencia media para cada categoría de la variable al dividir entre dos el número total de alumnos por categoría en ambos grupos. Es decir, define un grupo medio, el cual ofrecería el número esperado de alumnos por categoría si se dividiera el número de insuficientes, aprobados, notables y sobresalientes en dos partes iguales. Hay un conflicto para definir la media, que es interpretado como distribución media. No hemos encontrado este tipo de respuesta en las investigaciones previas.

C1.6. Una estrategia parecida a la anterior consiste en hallar la media del número de alumnos por categoría en cada grupo, al dividir el total de alumnos entre el número de categorías. Es decir, el estudiante halla el número esperado de alumnos por categoría en una distribución uniforme dentro de cada uno de los grupos. La conclusión que obtiene esincorrectaporque lafrecuenciaesperadasiempre damayor en el primer grupo porque es mayor el tamaño de la muestra, independientemente de los valores de la variable. Hay también conflicto semiótico porque confunde los conceptos de valor de la variable y frecuencia. Se observa también que el estudiante confunde las nociones de frecuencia absoluta y porcentaje, un conflicto que tampoco ha sido descrito en otras investigaciones.

C1.7 El estudiante indica que habría que calcular la media en cada grupo, pero no la calcula. En el ejemplo que presentamos en la figura 8, el alumno identifica que se trata de un problema relacionado con las medidas de tendencia central; de ahí que considere a la media como la más adecuada. No explica cómo llegó a la conclusión de que el grupo 1 es mejor, pero es razonable si se calcula la media.

C2. Respuestas basadas en la mediana
Son todas aquellas respuestas donde el estudiante identifica correctamente que se trata de un problema cuya solución se obtiene a través de la mediana, que calcula o tratar de calcular sin transformar los datos. Además de haber identificado a la comparación de datos ordinales como un problema que se soluciona por la mediana, el alumno discrimina los datos ordinales de los datos medidos en escala de razón. Dentro de esta categoría hemos diferenciado las siguientes respuestas:
C2.1. Cálculo correcto de las medianas. Se trataría de la solución correcta al ítem que aparece en la tabla I, cuyo análisis fue hecho anteriormente, donde el estudiante muestra también un buen conocimiento procedimental sobre el cálculo de mediana y su correcta aplicación a los datos ordinales.
C2.2. Comienza el cálculo de las medianas en los grupos, pero no finaliza el problema. Un estudiante inicia bien la primera parte del problema, al ordenar los conjuntos de datos. Sin embargo, en la segunda parte da como mejor medida de tendencia central un valor de la variable.

C2.3. Proporciona una respuesta correcta sin mostrar los cálculos. El alumno muestra conocimientos sobre la definición de la mediana y la propiedad de ser un estadístico que tiene en cuenta el orden de los datos. Sin embargo, no podemos obtener información sobre su capacidad de cálculo. En algunos casos, como el de la figura 10, da una justificación confusa al considerar "mejor" al grupo 1, por lo cual deducimos que el cálculo de la mediana ha sido incorrecto.

C3. Respuestas basadas en la moda. El alumno utiliza las modas para hacer la comparación y calcula las modas en forma correcta. Aunque no llega a la solución óptima, es una estrategia correcta, porque la moda está definida para variables ordinales; asimismo, considera a todos los datos en la comparación. Este tipo de respuesta también se encuentra en los trabajos de Carvalho (1998, 2001) y Cobo (2003). En el ejemplo que aparece en la figura 11, el alumno afirma que el primer conjunto es mejor porque incluye más valores de sobresalientes (moda del conjunto). Por tanto, emplea correctamente la definición y el algoritmo de la moda, pero tiene un conflicto en la segunda parte del problema, cuando confunde el valor de la variable (S) con la moda.

C4. No reconoce la comparación de dos conjuntos de datos como un campo de problemas relacionado con las medidas de tendencia central. El estudiante no usa las medidas de tendencia central para resolver el problema, de ahí que refleje una deficiente adquisición de la idea de distribución. El mismo comportamiento lo identifican Batanero, Estepa y Godino (1997) en su trabajo sobre la asociación estadística, al igual que Cobo (2003). Konold, Pollatsek, Well y Gagnon (1997) opinan que estos alumnos no habrían dado el paso de pensar en los valores de la variable como una propiedad de los individuos aislados a comparar las propiedades de los conjuntos de datos (medidas de tendencia central). Hemos encontrado las siguientes variantes dentro de este grupo.
C4.1. Calcula porcentajes o frecuencias relativas de cada categoría. En la figura 12, el alumno hace un recuento de las frecuencias absolutas que tienen los diferentes valores de la variable en cada categoría y grupo (halla las distribuciones de frecuencias). A continuación, calcula la distribución de frecuencias relativas de la variable en cada uno de los grupos, pero tiene un conflicto debido a que no relaciona el problema con las medidas de tendencia central. En lugar de esto, compara algún valor aislado y aparentemente toma como mejor al grupo 1 porque tiene mayor frecuencia relativa en la categoría de Sobresaliente. Estepa (2004) denomina concepción local de la asociación a la conducta que consiste en comparar sólo valores aislados, en un problema de asociación entre dos variables. Los estudiantes que siguen esta estrategia pueden llegar a la respuesta correcta, dependiendo de qué valor comparen.

C4.2. Una variante del ejemplo anterior la hallamos cuando el alumno calcula porcentajes en cada categoría y agrupa algunas de ellas. El ejemplo de la figura 13 indica que el alumno efectúa un recuento de las frecuencias absolutas que tienen los diferentes valores de la variable y calcula la distribución de porcentajes de la variable en cada uno de los grupos; utiliza la idea y el cálculo de porcentaje. Para obtener la conclusión correcta, compara el total de Notables y el de Sobresalientes; es decir, usa sólo una parte de los datos para hacer la comparación y manifiesta una concepción local de la asociación.

C4.3. Con una estrategia similar a la anterior, algunos estudiantes comparan sólo frecuencias absolutas para resolver el problema y sólo emplean una parte de los datos. Además de la concepción local de la asociación (Estepa, 2004), estos alumnos estarían en el primer nivel de comprensión del concepto de distribución, según Watson y Moritz (1999, 2000), pues no utilizan las frecuencias relativas para comparar los datos; por tanto, su estrategia sería válida sólo para conjuntos de datos de igual número de elementos. En el ejemplo de la figura 14 se observa que el alumno establece primero una correspondencia entre símbolos y valores de la variable y halla la frecuencia absoluta en cada categoría. Luego, compara el número total de aprobados y elimina los insuficientes en cada grupo, con lo que incurre un conflicto porque sólo se fija en parte de los datos (los aprobados). Otro conflicto es comparar las frecuencias absolutas, ya que la comparación no tiene en cuenta el tamaño de la muestra.

C4.4. Dar como respuesta un valor de la variable (por ejemplo, "notable") sin hacer referencia a medidas de tendencia central ni calcularlas. Estos alumnos muestran el mismo conflicto que el caso Cl .3 (confundir una medida de tendencia central con el valor de la variable), pero no intentan calcular la media, la mediana o la moda. No parecen reconocer que la solución del problema involucra una medida de tendencia central ni muestran conocimientos de los algoritmos de cálculo.
C5. Consiste en que el estudiante da una respuesta en la que sólo indica, por ej emplo, que el primer grupo es mejor, pero no lo justifica con cálculos o razonamientos.
La tabla III presenta la distribución de frecuencias de las categorías descritas. Hay una gran variedad de respuestas y la mayoría se relacionan con la media. Vemos que el uso de la mediana en datos ordinales no es intuitivo para los estudiantes, lo cual coincide con los resultados del trabajo de Cobo (2003). En los estudiantes que participaron, lo más frecuente (17%) es dar un valor cualquiera de la variable sin utilizar medidas de tendencia central, mostrando un conflicto en la comprensión de tales conceptos. Aunque Cobo (2003) indica que un 15% de sus estudiantes no usa las medidas de tendencia central para resolver el problema, no informa en concreto sobre la confusión entre medida de tendencia central y valor de la variable. La segunda respuesta más frecuente consiste en utilizar la media correctamente (15.1%); sin embargo, Cobo (2003) no informa sobre el número de estudiantes que usa la media en este ítem.

Otro grupo de alumnos supone que hay que usar la media, pero la calculan con algunos conflictos o no saben calcularla. Si se suman todos los casos representan un 18%, lo cual muestra que tampoco es sencillo obtener la media en datos ordinales porque parte de los alumnos no llega a establecer una correspondencia numérica adecuada que permita el cálculo.
Un 12% usa la moda y la calcula correctamente; aunque esta no es la mejor solución, no la podemos considerar incorrecta porque la media puede calcularse para datos ordinales. En la investigación de Cobo (2003), el 7.6% de los estudiantes de 4° de secundaria (16 años) resuelve el problema calculando correctamente la moda.
El resto de los alumnos no asocia el problema con las medidas de tendencia central; utiliza sólo una parte de datos o comete otros errores. Un 5.3% de los alumnos resuelve el problema con el cálculo correcto de la mediana, mientras que en Cobo (2003) el 4.2% de los alumnos de 4° de ESO (15–16 años) emplean la mediana correctamente. Hacemos notar también el alto porcentaje de respuestas en blanco que dejan estos alumnos.
La tabla IV resume los datos con la agrupación de las respuestas que hacen referencia a una medida de tendencia central específica. Los resultados indican que, a pesar de tratarse de variables ordinales, la tercera parte de estudiantes (33.7%) trata de utilizar la media para dar una respuesta; en porcentajes menores emplean la mediana (12%) y la moda (12%). Por otra parte, un 27.1% de los alumnos da una respuesta que no se vincula con las medidas de tendencia central, un problema que también se presentó en la investigación de Estepa (2004). Sobre tal dificultad, Konold, Pollatsek, Well y Gagnon (1997) sugieren que los estudiantes no han llegado a comprender la idea de distribución como propiedad de un conjunto de datos.

La tabla V compara el uso de medidas de tendencia central que emplean los tres grupos de estudiantes. Notamos que hay mejores resultados en los alumnos de secundaria, a pesar de que son menores en edad, ya que usan más la mediana y la moda, aunque también dejan más respuestas en blanco. El primer grupo de alumnos de bachillerato es el que más usa la media, mientras que el segundo grupo emplea la moda o da respuestas sin relación con las medidas de tendencia central. La impresión es que el énfasis en la enseñanza de la media a nivel bachillerato podría dificultar el trabajo con datos ordinales.
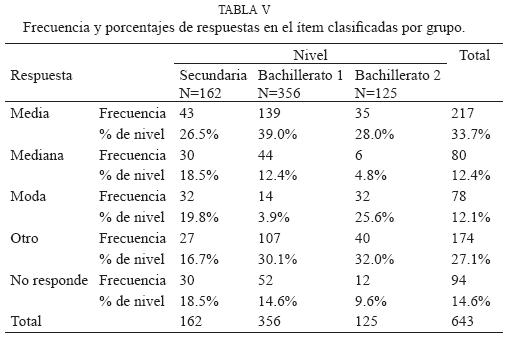
Por medio del test Chi–cuadrado estudiamos la relación entre el tipo de respuesta y el grupo de alumnos. Se obtuvo un valor Chi cuadrado = 76.144 con 8 grados de libertad y una significación menor a 0.001, cumpliéndose las condiciones de aplicación, por lo que podemos considerar las diferencias como estadísticamente significativas. Esto indica que la distribución de respuestas, según el tipo de medida de tendencia central, varía en función del nivel educativo en que se administra el cuestionario.
5. CONCLUSIONES
Nuestro estudio indica que la comparación de datos ordinales, incluso en un contexto familiar para el alumno como es el de las calificaciones, no es intuitiva. Incluso es menos intuitivo para los jóvenes de bachillerato que para los de secundaria, por lo que la enseñanza no parece ayudar a fomentar dicha intuición en nuestros estudiantes. Debido a la importancia de los datos ordinales en la vida diaria y el análisis exploratorio de datos, sería necesario utilizar problemas similares al que mostramos en este trabajo en la enseñanza secundaria y bachillerato, si queremos preparar a los alumnos para que interpreten críticamente la información estadística que se presenta con datos ordinales en diferentes contextos.
Por otro lado, nuestro análisis confirma la existencia de los siguientes conflictos semióticos en los alumnos, que son descritos por Cobo (2003) respecto a la comparación de los datos ordinales y la comprensión de las medidas de tendencia central:
a) No reconocer la comparación de dos conjuntos de datos como un campo de problemas que se resuelve por las medidas de tendencia central.
b) Suponer definida la media en un conjunto de datos ordinales.
c) No discriminar datos ordinales y numéricos.
Hemos identificado además, nuevos conflictos que podemos clasificar en relación a los tipos de objetos matemáticos considerados en el enfoque onto–semiótico en la forma siguiente:
– Conflictos relacionados con los campos de problemas: No usar las medidas de tendencia central en la comparación de dos conjuntos de datos. En su lugar, algunos estudiantes resuelven el problema comparando datos aislados; de este modo, presentan la concepción local de asociación que describió Estepa (2004).
– Conflictos relacionados con definiciones de distintos objetos matemáticos: Confundir las medidas de tendencia central con el valor de la variable; la media con las frecuencias absolutas; las frecuencias absolutas con los porcentajes, y el valor de la variable con la frecuencia. Estos conflictos son preocupantes en los estudiantes de bachillerato, ya que dificultarán su comprensión de otros conceptos estadísticos que deberán estudiar en la universidad, los cuales están basados en las ideas de variable, valor, frecuencia absoluta y relativa y medida de tendencia central.
– Conflictos relacionados con las propiedades de las medidas de tendencia central o con conceptos relacionados con ellas: Suponer definida la media en un conjunto de datos ordinales, o confundir la variable ordinal con la variable medida en escala de razón o intervalo.
– Conflictos al aplicar un procedimiento: Calcular la media de las frecuencias; establecer una correspondencia que no conserva la escala de medida; establecer correspondencias diferentes en grupos que se quiere comparar, o aplicar una correspondencia que transforma un conjunto variable en otro constante.
Esta larga lista indica puntos a mejorar en la enseñanza, que abarcan no sólo la necesidad de que los estudiantes trabajen con datos ordinales, sino también aspectos conceptuales y procedimentales que atañen a la media, la mediana y las ideas aún más elementales de variable estadística y distribución. La semejanza de algunos resultados con los que obtuvo Cobo (2003) con alumnos españoles de menor edad sugiere que los conflictos descritos no son específicos de ninguno de los dos sistemas educativos, sino son compartidos por estudiantes mexicanos y españoles, y se mantienen con la edad.
Ahora bien, el diseño de la enseñanza en ambos países debe tenerlos en cuenta, pues la comprensión de los diversos elementos del significado es independiente y su significado tiene que construirse de manera progresiva. No podemos esperar que si se enseña a los alumnos a calcular la media, la mediana y la moda en variables medidas en escala de razón puedan deducir y comprender por sí mismos sus diversas propiedades o adquieran la competencia suficiente para usar correctamente la medida de tendencia central más adecuada en datos ordinales. Esperamos que el análisis mostrado en este trabajo sea útil a los profesores e incida en la mejora de la enseñanza del tema.
REFERENCIAS BIBLIOGRÁFICAS
Barr, G. V. (1980). Some student's ideas on the median and the mode. Teaching Statistics 2, 38–41. [ Links ]
Batanero, C, Estepa, A. y Godino, J.D. (1997). Evolution of student's understanding of statistical association in a computer–based teaching environment. In J. B. Garfield y G. Burrill (Eds.), Research on the Role of Technology in Teaching and Learning Statistics. 1996 IASE Round Table Conference (pp. 183–198). University of Minnesota, USA: The International Association of Statical Education. [ Links ]
Cai, J. (1995). Beyond the computational algorithm. Student's understanding of the arithmetic average concept. En L. Meira (Ed.), Proceedings of the 19th PME Conference (Vol.3, pp. 144–151). Recife, Brazil: Universidade Federal de Pernambuco. [ Links ]
Carvalho, C. (1998). Tarefas estadísticas e estrategias de resposta. Comunicación presentada en el VI Encuentro en Educación Matemática de la Sociedad Portuguesa de Ciencias de la Educación. Portugal, Castelo de Vide. [ Links ]
Carvalho, C. (2001). Interacao entre pares. Contributos para a promocao do desenvolvimiento lógico e do desempenho estatistico no 7° ano de escolaridade. Tesis de doctorado, Universidad de Lisboa. [ Links ]
Cobo, B. y Batanero, C. (2000). La mediana en la educación secundaria obligatoria: ¿un concepto sencillo? UNO 23, 85–96. [ Links ]
Cobo, B. (2003). Significado de las medidas de posición central para los estudiantes de secundaria. Tesis de doctorado: Universidad de Granada. [ Links ]
Contreras, A. y Ordóñez, L. (2006). Complejidad ontosemiótica de un texto sobre la introducción a la integral definida. Revista Latinoamericana de Investigación en Matemática Educativa 9 (1). 65–84. [ Links ]
D'Amore, B. y Godino, J. (2007). El enfoque ontosemiótico como un desarrollo de la teoría antropológica en la didáctica de la matemática. Revista Latinoamericana de Investigación en Matemática Educativa 10 (2), 191–218. [ Links ]
Eco, U. (1995). Tratado de semiótica general. Barcelona, España: Lumen. [ Links ]
Estepa, A. (2004). Investigación en educación estadística. La asociación estadística. En R. Luengo (Ed.), Líneas de investigación en Educación Matemática (pp. 227–255). Badajoz, España: Servicio de Publicaciones de la Federación Española de Sociedades de Profesores de Matemáticas–Universidad de Extremadura. [ Links ]
Gattuso, L. y Mary, C. (1996). Development of concepts of the arithmetic average from high school to University. Proceedings of the 20th Conference of the International Group for the Psychology of Mathematics Education (Vol. I, pp. 401–408). Valencia, España: Universidad de Valencia. [ Links ]
Godino, J. D. (1999) Análisis epistémico, semiótico y didáctico de procesos de instrucción matemática. Trabajo presentado en el grupo de trabajo "La didáctica de la matemática como disciplina científica" en el III Simposio de la Sociedad Española de Investigación en Educación Matemática (SEIEM). Valladolid, España. [ Links ]
Godino, J. D. (2002). Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactiques des Mathematiques 22 (2–3), 237–284. [ Links ]
Godino, J. D., Batanero, C. y Font, V (2007). The onto–semiotic approach to research in mathematics education. ZDM. The InternationalJournal on Mathematics Education 39 (1–2), 127–135. [ Links ]
Godino, J. D., Font, V y Wilhelmi, M. (2006). Análisis ontosemiótico de una lección sobre la suma y la resta. Revista Latinoamericana de Investigación en Matemática Educativa. Número Especial, 131–155. [ Links ]
Konold, C, Pollatsek, A., Well, A. y Gagnon, A. (1997). Students analyzing data: research of critical barriers. In J. B. Garfield & G. Burrill (Eds.), Research on the role of technology in teaching and learning statistics. Voorburg, The Netherlands: International Statistical Institute. [ Links ]
Mayen, S., Cobo, B., Batanero, C. y Balderas, P. (2007). Comprensión de las medidas de posición central en estudiantes mexicanos de bachillerato. UNION 9, 187–201. [ Links ]
Nortes, A. (1993). Estadística teórica y aplicada. Burgos, España: Santiago Rodríguez. [ Links ]
Pollatsek, A., Lima, S. y Well, A. D. (1981). Concept or computation: student's understanding of the mean. Educational Studies in Mathematics 12, 191–204. [ Links ]
Ramos, A. B. y Font, V (2008). Criterios de idoneidad y valoración de cambios en el proceso de instrucción matemática. Revista Latinoamericana de Investigación en Matemática Educativa 11 (2), 233–265. [ Links ]
Schuyten, G. (1991). Statistical thinking in psychology and education. In Vere–Jones (Eds.), Proceedings of the Third International Conference on Teaching Statistics (pp. 486–490). Voorburg, The Netherlands: International Statistical Institute. [ Links ]
Watson, J. M. y Moritz, J. B. (1999). The developments of concepts of average. Focus on Learning Problems in Mathematics 21 (4), 15–39. [ Links ]
Watson, J. M. y Moritz, J. B. (2000). The longitudinal development of understanding of average. Mathematical Thinking and Learning 2 (1–2), 11–50. [ Links ]
1 Un signo está constituido siempre por uno (o más) elementos de un plano de la expresión colocados convencionalmente en correlación con uno (o más) elementos de un plano del contenido (...). Una función semiótica se realiza cuando dos funtivos (expresión y contenido) entran en correlación mutua" (Eco, 1995, 83–84).














