Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista latinoamericana de investigación en matemática educativa
versão On-line ISSN 2007-6819versão impressa ISSN 1665-2436
Relime vol.12 no.1 Ciudad de México Mar. 2009
Artículos
ALGUNAS CARACTERÍSTICAS DE LAS ARGUMENTACIONES Y LA MATEMÁTICA EN ESCENARIOS SIN INFLUENCIA ARISTOTÉLICA
SOME CHARACTERISTICS OF THE ARGUMENTATIONS AND THE MATHEMATICS IN SCENARIOS WITHOUT ARISTOTELIAN INFLUENCE
Cecilia Crespo Crespo*, Rosa María Farfán** y Javier Lezama***
* Instituto Superior del Profesorado "Dr. Joaquín V. González". Buenos Aires, Argentina; crccrespo@gmail.com
** Departamento de Matemática Educativa, Centro de Investigación y Estudios Avanzados, Cinvestav, México; rfarfan@cinvestav.mx
*** Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada, Cicata del IPN, México; jlezamaipn@gmail.com
Recepción: Febrero 18, 2008
Aceptación: Junio 23, 2008
RESUMEN
Este trabajo muestra, en primer lugar, una caracterización de escenarios culturales que no tuvieron influencia aristotélica, de ahí que las argumentaciones utilizadas difirieran de las que se originaron en Grecia. En dichas culturas se abordaron y trabajaron algunos conceptos matemáticos cuya aceptación y tratamiento tardaron varios siglos en el pensamiento occidental, lo cual pone de manifiesto el carácter de construcción cultural de las formas de argumentación, así como la posibilidad de elaborar conceptos matemáticos sobre la base de otras vertientes de pensamiento.
Asimismo, el estudio refiere la presencia, en el aula de matemática, de algunas formas de argumentación no correctas para la lógica aristotélica.
PALABRAS CLAVE: Socioepistemología, argumentaciones, construcción sociocultural.
ABSTRACT
This work shows, first, a characterization of cultural scenarios that did not have Aristotelian influence; hence its argumentations used are different than the ones originated in Greece. In such cultures some mathematical concepts were used in a way that took several centuries to be accepted in western thinking. This shows how culture affects forms of argumentation and posits the possibility of the development of mathematical concepts based on other thinking sources.
Furthermore, this study describes some argumentation forms, present in the mathematical classroom, which are incorrect according to Aristotelian logic.
KEY WORDS: Socioepistemologogy, argumentations, sociocultural construction
RESUMO
Este artigo mostra, em primeiro lugar, uma caracterização dos cenários culturais que não tiveram influência aristotélica, daí que as argumentações utilizadas difiram das que foram originadas na Grécia. Nessas culturas foram abordados e trabalhados alguns conceitos matemáticos cuja aceitação e tratamento tardaram vários séculos no pensamento ocidental, o que salienta o carácter de construção cultural das formas de argumentação, assim como a possibilidade de elaborar conceitos matemáticos com base noutras vertentes do pensamento.
Além disso, o estudo refere também a presença, na aula de Matemática, de algumas formas de argumentação incorrectas na lógica aristotélica.
PALAVRAS CHAVE: Scocioepistemologia, argumentação, construção sociocultural.
RÉSUMÉ
Dans un premier temps, ce travail est une description de contextes spatio–temporels qui n'ont pas été influencés par la pensée aristotélicienne. Les techniques argumentatives utilisées dans ces lieux diffèrent donc complètement de celles venant de Grèce. Dans ces cultures non–aristotéliciennes, quelques concepts mathématiques ont ainsi été abordés et travaillés. Mais plusieurs siècles ont été nécessaires pour qu'on les accepte et qu'on les utilise dans la culture occidentale. Ceci démontre que les techniques argumentatives et l'élaboration d'éventuels concepts mathématiques basés sur d'autres courants de pensée relèvent de la construction culturelle.
Dans un deuxième temps, ce travail aborde le thème des techniques argumentatives considérées, pendant des cours de mathématique, comme incorrectes par rapport à la logique aristotélicienne.
MOTS CLÉS: Socioépistémologie, techniques argumentatives, construction socioculturelle.
1. INTRODUCCIÓN
Este trabajo forma parte de una investigación que emplea la perspectiva de la socioepistemología. Su objetivo radica en comprender el carácter sociocultural de las argumentaciones matemáticas (Crespo Crespo, 2005, 2006, 2007a, 2007b, 2007c; Crespo Crespo y Farfán, 2005, 2006), intentando mostrarlas como el resultado de acciones de una comunidad en un escenario sociocultural. Desde esta perspectiva teórica, se sostiene que tanto el discurso matemático escolar como la práctica educativa de aula, no deben considerarse como zonas exentas de cultura, dado que la construcción de un conocimiento matemático está unido a aspectos que rebasan la mera organización teórica del contenido (Aparicio y Cantoral, 2006).
Nuestra cultura occidental, de sustento aristotélico, ha construido formas de argumentación basadas en esta lógica, e incluso durante siglos se han considerado como características del ser humano. Sin embargo, en el aula ocurren algunas situaciones que evidencian el carácter de construcción social de la argumentación matemática, las cuales hay que atender en el discurso matemático escolar.
Desde que Aristóteles sistematizara las argumentaciones lógicas mediante las leyes de la lógica clásica, estas normas han sido identificadas no sólo como las que forman los preceptos del pensamiento humano, sino también como las que rigen el desarrollo de la ciencia. Han sido consideradas durante siglos como indiscutibles y, en cierta manera, han marcado el avance y los rumbos del pensamiento científico de Occidente.
Ahora bien, si realmente dichos preceptos fueran innatos y propios de la razón humana, deberían haber estado presentes en todas las culturas y épocas, así como ser enunciados y aceptados en los distintos escenarios socioculturales. No obstante, como es posible apreciar en las descripciones que mostraremos a continuación, en algunos escenarios socioculturales hubo manifestaciones de lógicas que no aceptaban como leyes a los principios aristotélicos. El principio de no contradicción y el del tercero excluido no aparecieron espontáneamente en todos los escenarios que no tuvieron influencia aristotélica; no fueron la base de sus formas de pensamiento. En algunas oportunidades fueron otros los principios fundamentales de la lógica del pensamiento en ciertas culturas, donde obviamente no afloraron argumentaciones como la reducción al absurdo, pues se sustentan fuertemente en esos principios aristotélicos.
2. ACERCA DE ALGUNAS CULTURAS SIN INFLUENCIA ARISTOTÉLICA
En nuestra sociedad resulta sumamente difícil pensar en la posibilidad de que la ciencia progrese sin un firme sustento en los principios lógicos identificados por los griegos siglos atrás, ya que con base en ellos se han hecho nuestras formas de pensamiento científico. Sin embargo, algunas civilizaciones no tuvieron las mismas bases y fueron capaces de elaborar conceptos matemáticos de manera distinta a los de la ciencia occidental. A continuación se presentan algunos ejemplos que ponen en evidencia tal hecho. Nos centraremos básicamente en culturas donde aparecieron conceptos cuya construcción en occidente fue costosa, como el cero y el infinito.
2.1. Egipto: la matemática del cálculo y de las necesidades materiales
2.1.1. El pensamiento lógico en el Antiguo Egipto
El nacimiento de la filosofía se sitúa en Grecia; sin embargo, es posible identificar características prefilosóficas en el pensamiento del Antiguo Egipto, sobre todo en ciertas concepciones del universo y de la divinidad. Estas disquisiciones fueron hechas por los sacerdotes y hierogramáticos, quienes eran los depositarios y transmisores del conocimiento en esa cultura. El pensamiento religioso egipcio, de índole físico y metafísico, fundamentó técnicas rituales e instrucciones laicas que perduraron a través de textos rituales y escritos de educación o propaganda, donde se aseguraba la buena marcha del Cosmos. La intención de dicha filosofía era garantizar el buen funcionamiento de las cosechas y la sociedad, sin proponerse explícitamente alentar la reflexión personal.
Los conocimientos matemáticos, tanto aritméticos como geométricos, se transmitieron en manuales de cálculo práctico. En los textos de la época de los faraones, es posible encontrar "balbuceos que prefiguran, en mayor o menor medida, los primeros pasos de la filosofía griega" (Parain, 2002, p.11). La ciencia tenía facetas sagradas y profanas: los sacerdotes se desempeñaban en un principio como escribas, médicos, embalsamadores, arquitectos e ingenieros; luego fue apareciendo la especialización. Las escuelas sacerdotales impartían una educación de carácter práctico y profesional, ya que los conocimientos científicos tenían carácter eminentemente práctico, mientras que sus métodos educativos se basaban en memorizaciones y azotes (Abbagnano y Visalberghi, 2005).
En el Imperio Antiguo (2800–2300 a.C.) surgió la necesidad de coordinar las tradiciones que habían aparecido previamente, debido a que los mitos narraban los mismos fenómenos bajo imágenes distintas, donde los dioses toman identidades distintas y contradictorias. Desde una postura aristotélica esto hubiera desembocado en incoherencias y contradicciones, tomando como base a los principios de identidad y no contradicción. Hay quienes han dado la interpretación de que se trataba de diferentes aproximaciones, con la intención de salvar la incoherencia que surge bajo la visión occidental, teñida por la lógica clásica; sin embargo, aún esta diversidad de aproximaciones parece contradictoria. Las leyes de la lógica en Egipto fueron distintas: se dio sin problemas un polimorfismo de divinidades que no condujo a inconsistencias y contradicciones, además de que permitió la construcción de explicaciones teóricas acordes con la concepción de ciencia de este escenario, tanto en sus facetas sagradas como profanas.
2.1.2. El tratamiento de algunos conceptos matemáticos que surgieron en el escenario de Egipto
De la antigua cultura de Egipto no han sobrevivido rastros de demostraciones rigurosas de resultados matemáticos, ni tampoco de argumentaciones lógicas que justifiquen los procedimientos presentados en las técnicas de cálculo. Se supone, por lo general, que se arribaba a los resultados matemáticos no por demostración, sino por vías empíricas y tentativas, como el caso de la existencia de ternas pitagóricas y su aplicación al trazado de perpendiculares. Algunos especialistas de la historia de la matemática afirman, sin embargo, que "no se puede sostener que se trata en ambos casos de reglas empíricas a las que se llega mediante un penoso esfuerzo de ensayo y error para problemas específicos, sin ninguna conciencia de una aplicación general" (Joseph, 1991, p.181).
El desarrollo matemático en este pueblo pone en evidencia la relación entre las necesidades materiales de una sociedad y la naturaleza de la matemática que desarrollaron. No estaban interesados en generalizar ni en abstraer u organizar sistemáticamente los conocimientos que poseían; sólo mostraron interés por resolver problemas prácticos, como se manifiesta en papiros que han sido traducidos, donde es posible identificar algunas características comunes en relación con el tratamiento de los conceptos matemáticos. Por una parte, comenzaban con la presentación de una fórmula, sobre la que ofrecían posteriormente tres o cuatro ejemplos de su uso; por otra, no explicitaban la concepción de la matemática como una ciencia, ni de métodos para validar el conocimiento matemático.
Para esta cultura, la geometría se restringía a aritmética aplicada. Si bien suele plantearse que los griegos se basaron en fórmulas de origen egipcio para determinar áreas y volúmenes, no se tienen indicios de la manera en que los egipcios llegaron a sus reglas y fórmulas. La consistencia de éstas era verificada a través de ejemplos numéricos y puesta de manifiesto en expresiones como "la producción de lo mismo", "el correcto procedimiento de este tipo de problemas", "manera de trabajarlo", "estos son los procedimientos correctos y propios", "esta es la manera en la que usted lo hace". Algunos autores se inclinan a sostener que el aporte egipcio a las argumentaciones puede ser considerado implícito (Gillings, 1972), y que esta cultura tuvo una visión distinta a la de los griegos sobre lo que es el pensamiento y la razón.
El fundamento del método aplicado por los egipcios era que funcionaba. No consideraron necesario argumentarlo como una verdad universal que mostrara el proceso del pensamiento lógico. En otras palabras:
Un argumento o demostración no simbólicos pueden ser rigurosos cuando se dan para un valor particular de la variable; las condiciones de dicho rigor son que el valor particular de la variable debe ser típico, y que una ulterior generalización de cualquier otro valor debe ser inmediata (Gillings, 1972, p.233).
Los egipcios explicaron y definieron su procedimiento en una secuencia ordenada de pasos; como conclusión, agregaron una forma para verificar que se daba una solución correcta al problema. Esta era su visión de la ciencia, por lo que construyeron la matemática con las características que se acaban de describir.
El mismo sistema de numeración egipcio puede interpretarse como la traducción de su método de contar, alineando, acumulando y asociando elementos. Por su parte, el sistema que ocupaban para expresar fracciones era una supervivencia de los mitos de Osiris; su simbolismo tenía un importante lugar en ritos mágicos y funerarios (Ifrah, 1997).
2.1.2.1. El cero
A menudo se ha dicho que el concepto de cero no puede encontrarse en el Antiguo Egipto; sin embargo, algunos historiadores de la matemática creen ver un antecesor de dicha noción en el símbolo  . Éste era utilizado para expresar las ideas de belleza, completitud y perfección; su gráfico consistía en la abstracción de una tráquea humana, corazón y pulmones. Los sonidos consonantes de su nombre eran nfr, pero los sonidos vocales son aún desconocidos por los egiptólogos.
. Éste era utilizado para expresar las ideas de belleza, completitud y perfección; su gráfico consistía en la abstracción de una tráquea humana, corazón y pulmones. Los sonidos consonantes de su nombre eran nfr, pero los sonidos vocales son aún desconocidos por los egiptólogos.
Por otra parte, en los planos para la construcción de los templos, palacios y grandes edificios aparecen líneas niveladoras horizontales para guiar la construcción. En estas construcciones, hechas con grandes bloques de piedra maciza, era necesario que tuvieran profundos cimientos para su estabilidad y garantía de durabilidad. Para construir los diferentes niveles que quedarían bajo tierra, los egipcios utilizaban líneas niveladoras como referencia, nombradas a partir del nfr. En 1931 todavía eran visibles en la Gran Pirámide de Gizeh los signos de  , seguidos por uno o dos cubos que señalaban los niveles sobre o bajo la superficie; el
, seguidos por uno o dos cubos que señalaban los niveles sobre o bajo la superficie; el  representaba el nivel cero.
representaba el nivel cero.
De igual manera, es posible encontrar este símbolo en los registros contables mensuales de la dinastía 13 del Reino Medio (1770 a.C.), donde aparecen cuentas de doble entrada, separadas en columnas, para distinguir cada tipo de género. Al final del mes la cuenta debía estar equilibrada para cada artículo. Tras los ingresos habidos se indicaban los desembolsos realizados y se cerraba la cuenta mensual con un saldo igual a cero, lo cual puede notarse en los símbolos nfr que estaban al final de varias columnas. Esta era la forma en que simbolizaban el equilibrio.
Recientes descubrimientos arqueológicos han revelado la existencia de contactos regulares entre Egipto y Mesopotamia hacia el 3300 a.C. y el 3100 a.C. (Ifrah, 1997), los cuales pueden pensarse como una base de intercambios culturales en los que pudo haberse transmitido el concepto del cero.
2.2. India: un escenario en el que fue posible la contradicción
2.2.1. El pensamiento lógico de la India Antigua
Los Vedas son la fuente de información más antigua sobre el pensamiento de la India. Aunque no es posible determinar con exactitud el tiempo en que fueron escritos –sólo que son anteriores a Buddha, quien murió alrededor del 480 a.C–, se les data entre el 3000 y el 1200 a.C. No se trata de una única obra, sino de libros escritos en sánscrito que corresponden a varios períodos literarios, donde se compila parte de la poesía religiosa y popular que hubo durante el período védico.
En dicho período se personificaron las diversas fuerzas de la naturaleza, como el fuego (agni), el viento (vãyu) y el sol (surya), que rodeaban e influían en el hombre y en el orden cósmico, y se manifiestan a través de deidades que son adoradas. Sin embargo, estos dioses en etapas posteriores fueron reconocidos como una energía común: "lo que no es sino uno, los sabios lo llaman con nombres diferentes" (Hiriyanna, 1960, p.16), dando una concepción monoteísta. De manera análoga, sostenían que los hombres eran diferentes entre sí, pero que el hombre no constituía la materia, sino compartía una causa única primordial, que se manifestaba como el universo en toda su diversidad.
El objeto de la filosofía védica no fue satisfacer la curiosidad teorética, sino adaptar la conducta a las propias convicciones intelectuales, con lo que la religión y la filosofía se entremezclaron de manera inseparable. Bajo esta concepción, la verdad no se conocía en su totalidad: los demás podían enseñar las verdades que habían alcanzado y los métodos que emplearon; sin embargo, a menos de que se repitiera satisfactoriamente su proceso y se redescubrieran aquellas verdades, no se podría lograr la convicción. Había hechos que estaban más allá de la razón, los cuales no se podían demostrar de manera absoluta; la filosofía debía indicar la probabilidad de su verdad (manana), con lo que se profundizaba e intensificaba la convicción a través de la meditación.
A partir de esta corriente del pensamiento hindú se generaron el naturalismo y otras dos escuelas del pensamiento, consideradas no védicas: el jainismo y el budismo. La primera se limitó a la India; la segunda se difundió fuera, llegando a países como China y Japón.
Hacia el siglo III o IV a.C., la gran cantidad de material filosófico heterogéneo era recopilado por los sütras, cuya función fue consolidar la doctrina de una escuela en particular y criticar las que disentían de ella.
Los sütras, quienes se centraban en la naturaleza y función del conocimiento, proponían una investigación del pramã o conocimiento válido. La lógica naturalista concebida en esta época en la India generó "una ciencia tanto de prueba como de descubrimiento" (Hiriyanna, 1960, p.52) que no se llevó a cabo por medio del razonamiento, sino por los sentidos. La percepción no sólo podía revelar la existencia y naturaleza de las cosas no conocidas sino también podía ser un medio de comprobarlas, al someterlas a la prueba de los sentidos o de la observación directa. La mayor parte de los lógicos indios aceptaban tres pramãnas o medios inmediatos para el conocimiento válido: la percepción, la inferencia y el testimonio verbal. Aunque algunos sólo aceptaban este último si se encontraba en los dos anteriores.
Al hablar de la inferencia naturalista no debe pensarse en las formas silogísticas, sino en la búsqueda como fuente de conocimiento en relación con la percepción de signos y su posible significado, no con respecto a la argumentación lógica. La lógica nyaya valoraba la especulación racional como base de una doctrina coherente del conocimiento. Si bien su sustento fue empírico, generó una teoría de razonamiento racional apoyada en la causalidad. A manera de ejemplo, por inferencia en este sentido se diría que hay fuego al observar humo; el humo es tomado como signo de la existencia del fuego.
La causalidad es creadora, por lo cual se le denomina a esta visión lógica la teoría del efecto no preexistente (Hiriyanna, 1960, p. 112). La legitimidad de la inferencia se restringe sólo a los casos en que la existencia de la causa se infiere de la presencia de algo que se puede demostrar, que es su efecto. Así, la existencia del humo está relacionada con la del fuego, ya que el fuego es la causa necesaria del humo. La inferencia alude a dos posibilidades: resolver la duda en la propia mente o en la de otro. En la segunda opción cobra importancia el lenguaje, de ahí que sea posible encontrar la siguiente forma de razonamiento:
– En la colina hay fuego (proposición, tesis)
– Porque en ella hay humo (razón)
– Donde hay humo hay fuego; por ejemplo, en la cocina (proposición general seguida de ejemplificación)
– En la colina hay humo, que va siempre acompañado de fuego (generalización)
– Por consiguiente, en la colina hay fuego (conclusión)
Debemos observar que la proposición universal se apoya en la ejemplificación obtenida de la observación y la generaliza. Este tipo de razonamiento no es totalmente deductivo; también contiene una componente inductiva.
Para la escuela nyaya, los medios del conocimiento eran el testimonio, la analogía, la percepción y la inferencia. Veía al testimonio como lo digno de fe, transmitido en forma oral o escrita. La analogía permitía definir un objeto sobre la base de semejanzas con otros. La percepción consistía en la relación entre los objetos captables por medio de los sentidos y la imagen que teníamos del objeto. En la inferencia, su esquema de razonamiento se basaba en cinco enunciados, aunque la escuela nyaya precisó que los enemigos de la deducción eran la ambigüedad, la no conclusión y los argumentos absurdos. Sobre el absurdo, recurrir a él significaba que no se tenía lógica y que se debía ser dialécticamente vencido por quien operara con lógica y argumentos racionales (D'Amore, 2005a).
Asimismo, identificó los casos en que los razonamientos llevaban a sofismas, entre los cuales mencionó al absurdo intrínseco, generado por la aparición de términos que decían lo contrario de lo que debieran afirmar, y al absurdo explícito, que se originaba por la contraposición de dos términos del silogismo que se excluían recíprocamente.
El jainismo es una de las formas más antiguas de religión no védica de la India. Uno de sus rasgos distintivos se encuentra en su creencia de la existencia independiente y eterna del espíritu y la materia, de lo animado y lo inanimado. El conocimiento o la conciencia es la esencia del espíritu, mientras que el conocimiento empírico consiste en una de sus manifestaciones, bajo las limitaciones de la naturaleza inanimada; las percepciones verdaderas se llevan a cabo por medio de la intuición. Para los jainas, las verdades tienen su origen en la visión intuitiva de un santo (yogin), en tanto que el conocimiento se da en dos manifestaciones: lo inmediato y lo mediato. El inmediato es obtenido por percepciones exteriores (sentidos) e interiores (sensaciones); el mediato, por la inferencia y el testimonio verbal.
Una de las escuelas principales de lógica que aparecieron en la India en la antigüedad fue la de los filósofos y lógicos jainas; estos últimos se preocuparon por la relación entre racionalidad y consistencia del pensamiento. En la India clásica tuvo gran importancia la actividad filosófica; entre las temáticas que debatían estaban la eternidad, la universalidad y la esencia del todo en las partes. Las argumentaciones a favor o en contra de cada posición eran defendidas por los filósofos de la época.
El pensamiento de los jainas tuvo ciertas características que difirieron radicalmente del pensamiento griego. La aceptación del pluralismo fue una de ellas; otra, la del escepticismo. Dichos rasgos podrían parecer contrarios, ya que el escepticismo rechaza todas las proposiciones, mientras que el pluralismo las acepta todas; sin embargo, Ganeri (2002) dice que tienen en común que niegan que sea posible resolver un problema privilegiando una única posición; o sea, adoptando una posición dogmática. Para el escéptico, el problema reside en el principio del tercero excluido; para el pluralista, en el principio de no contradicción.
La lógica de los jainas tenía un carácter conciliador, con lo que respetaba la posibilidad del pluralismo; al formular que la realidad no excluía los rasgos contradictorios, aceptaba la posibilidad de la indeterminación. En las afirmaciones de los jainas convivían el "siempre es", el "nunca es" y el pensamiento de una realidad inescrutable que no admitía la expresión de ninguno de los otros dos modos (Hiriyanna, 1960, p.84). Cada concepción aludía a un aspecto singular de la realidad, mas ninguna era absoluta y correcta. La verdad se lograba al juntar las verdades parciales.
En este esquema de razonamiento surgían valores de verdad que iban más allá de los aceptados por la lógica bivalente. Los posibles valores de verdad que aceptaron y utilizaron los jainas fueron:
– Quizá una cosa es
– Quizá no es
– Quizá es y no es
– Quizá es inexpresable
– Quizá una cosa es y es inexpresable
– Quizá una cosa no es y es inexpresable
– Quizá una cosa es, no es y es inexpresable
Esta concepción de la verdad, de carácter relativista, se le denomina como la doctrina del quizá (Hiriyanna, 1960). Sin embargo, para dicha visión del mundo el fin de la vida es dar al alma un estado en el que se alcance la omnisciencia, del cual se obtengan todas las perfecciones por medio del conocimiento, la paz y el poder infinitos, a través de la concentración mental.
En la lógica jaina, durante el siglo I a.C., o incluso antes se proponía un silogismo, que puede ejemplificarse de la siguiente manera:
1. En esta colina hay fuego (proposición, tesis).
2. En cuanto que algo perceptible (condiciones de la proposición).
3. Porque hay humo (razón).
4. Hay humo sólo donde hay fuego (condiciones de la razón).
5. Cabe que haya humo sin haber fuego, como con la niebla (contraproposición, anti–tesis).
6. La niebla es diferente, el humo se eleva, la niebla cae (oposición a la contra–proposición).
7. El humo en una cocina de leña se produce por el fuego (ej emplificación).
8. Si la madera está seca no se produce humo (crítica del ejemplo).
9. Si se produce humo es porque hay fuego (respuesta a la crítica).
10.En esta colina hay fuego (conclusión).
Tal esquema de razonamiento es totalmente distinto de los silogismos aristotélicos. En él se puede observar cómo coexisten en ciertos momentos posturas contradictorias, aunque al final concluye en la obtención de la tesis como conclusión.
La tercera etapa del pensamiento filosófico de la India Antigua corresponde al budismo. El budismo inició como religión y posteriormente se vio obligado a convertirse en una filosofía para defender su posición frente a las escuelas del pensamiento hindú y jaina. El budismo primitivo, que se enraizó con el brahmanismo, mostró a la doctrina de Buddha como una reacción frente a las ceremonias rituales demasiado complejas, así como una defensa de la moralidad y del acercamiento de la religión a todos, permitiendo que el discípulo pensara por sí mismo para que pudiera de esa manera llegar a la verdad. Su objetivo era el hombre como aspirante a la perfección, más que el hombre que la había logrado. El budismo tenía en su principio una visión pesimista de la vida, al considerarla como un mal cuyo origen era la ignorancia y el desconocimiento de la verdadera naturaleza del hombre; dicho mal se podía superar por medio del desarrollo del yo superior a través del conocimiento y la práctica de la meditación (yoga). La doctrina budista no sólo se difundió más allá de los límites de la India, sino también derivó en numerosas sectas.
Filosóficamente, el budismo concibió a todas las cosas como inestables y cambiantes; veía a la estabilidad como ilusoria o una ficción de la mente. Para el jainismo, las distintas visiones del cambio colaboran en el conocimiento de un objeto, mientras que para el budismo los sentidos sólo dan sensaciones momentáneas; cada objeto es una serie de particularidades, aunque está desprovisto de ellas. Esta es la visión del budismo himayána.
Por su parte, el budismo yogãcãras afirma que el conocimiento no se refiere a los objetos exteriores, de ahí que reduzca la realidad al pensamiento: la mente asume formas que revive de impresiones anteriores. De esta forma, niega los objetos exteriores e incluso las otras personas. En la teoría del budismo mãdhyamika hasta se llega a negar el propio yo; postula un nihilismo en el que la realidad última es el vacío (sünya) o la vacuidad en sí. Esta posición tan extremista, que no es aceptada por todos los budistas y se opone totalmente opuesta a la de los jainas, afirma que la realidad ni "es" ni "no es"; tampoco "tanto es como no es", ni "deja de ser ni de no ser".
Excluye todos los predicados concebibles, incluso el de inexistencia, y por lo tanto hay que considerar que la realidad última está más allá de toda concepción y no que sea la nada absoluta. En efecto, tal interpretación está lógicamente implícita en la doctrina, puesto que la negación de todo, sin un fundamento positivo es inconcebible. Según esta interpretación, en última instancia la doctrina deja de ser relativista, pues acepta un absoluto aunque lo considere completamente inefable (Hiriyanna, 1960, p.105)
Para los budistas, el vacío y la nada no son sinónimos. La naturaleza del vacío (shunya) es el akasha, el éter, el último y más sutil concepto de las filosofías hindú y budista, que es la esencia de lo no creado y eterno. Cabe destacar que los budistas llegaron a diferenciar entre veinticinco especies de vacuidad: el vacío de la no existencia, del no ser, de lo no formado, de lo no nacido, de lo no producido, de lo no creado, de lo no presente, de la no sustancia, del no pensamiento, de la inmaterialidad, de la insustancialidad, del no valor, de lo ausente, de lo insignificante, del con poco valor, del sin valor, de lo nulo, de lo despreciable, de la nada (Ifrah, 1997, p.1 158).
Una característica que debe considerarse en cualquiera de los enfoques lógicos de la India es que la materia de su lógica es el pensamiento, no la forma lingüística en que se lo puede expresar. La India, cuna del cero con todas sus funciones, también se caracterizó por tener ideas filosóficas totalmente distintas a las griegas, en particular sobre el principio del tercero excluido.
Historiadores de la cultura hindú comentan:
En todas las cuestiones los filósofos budistas llegan a responder desde luego por la afirmación, después por la negación, después de una manera que no es la negación ni la afirmación. A una pregunta como, por ejemplo, '¿Buda existe después de muerto?', responde: 'Buda existe después de muerto, Buda no existe después de muerto, Buda no es más existente que no existiendo después de la muerte' (Le Bon, 1901, p.358).
2.2.2. El tratamiento de algunos conceptos matemáticos que surgieron en el escenario de la India
2.2.2.1. El cero
En los Vedas hay referencias a conceptos matemáticos (de Mora y Jarocka, 2003), entre ellas el uso de palabras–cifra propia de esta etapa del sánscrito:
0. Infinito=amanta; cero=bindú; vacío=sunya
1. Tierra=urvara, ksiti, go, dhara, o bien luna=abja, indu, candra
2. Parejas o gemelos=asvin, dasra, yama, etc., o bien ojos=caksus, netra, nayana
3. Fuego=agni
4. Punto cardinal=dis, o bien las cuatro edades del mundo=yuga
5. Flecha=bana, sara
6. Sabores=rasa, o bien sistemas filosóficos=darsana
7. Sabios= Rsi, o bien corceles del sol=asva
8. Versos octosilábicos=anustubh
9. Números=anka, o bien planetas=grata
Asimismo, se identifican cosas siempre que estén en grupos de cierto número de elementos; por ejemplo, que realicen definiciones de los números por abstracción, siguiendo un procedimiento similar al que hizo Russell para los números naturales. No existe en el primer periodo ninguna palabra que aluda a la resta (de Mora y Jarocka, 2003), aunque sí a "contar hacia delante" y "contar hacia atrás". El Rg Veda menciona a la multiplicación, ya que escribe el número veintiuno como "tres veces siete", y la única referencia a la división aparece en el concepto de "tantas partes iguales".
Con relación a la nada, en el Rg Veda encontramos:
En la edad primera de los dioses,
el Ser nació del No–Ser.
Inmediatamente nacieron los orígenes
y después la fuerza que se mueve hacia arriba.
(Rg Veda X.72.3, citado por de Mora y Jarocka, 2003, p. 32)
En otro verso de este libro, se lee:
Entonces no había Ser ni tampoco no–Ser,
ni espacio ni más allá cielo.
¿Qué había en la envoltura? ¿Dónde estaba? ¿Quién lo cuidaba?
¿Era algo el agua profunda que no tenía fondo?
Ni la muerte ni la no muerte existían.
Nada en la nada distinguía la noche del día.
Sin aire, el Uno respiraba originando su propio movimiento.
Nada más existía.
(Rg Veda X. 129.1; citado por de Mora y Jarocka, 2003, p. 32)
Resulta notorio el vínculo que se presenta en este texto entre la nada y el Ser, así como la posibilidad de transformarse una en el otro, lo cual es radicalmente distinto a la postura griega y la concepción occidental de nada; además, contrasta con lo que enuncia Parménides en relación con la posibilidad de pasar del no Ser al Ser:
Que el ser es, implica que no ha nacido, pero si hubiese nacido significa que previamente no existía el ser, y, en ese caso, tendría que haber nacido de la nada, pero, aparte de que sólo puede hablarse de lo que es y no de la nada, ¿qué necesidad le haría pasar de no ser a ser? (Citado por Eggers Lan, 1995, p.33)
En el contexto del pensamiento de la India, la nada y el cero surgieron desde una visión filosófica más que matemática: como ausencia de algo, no como resultado de una operación; más como el cardinal del conjunto vacío, cuya propiedad estriba en no tener elementos. Después se transformó en una cifra, en un número que significaba un lugar vacío en un número. Ahora bien, los Vedas no contienen de manera explícita ninguna referencia al cero como cifra, ninguna palabra para representarlo. Sunya encarna la nada, el vacío, el lugar vacío, el sitio desocupado (de Mora y Jarocka, 2003).
Uno de los legados matemáticos de las culturas de la India a Occidente es el cero, que cumplía tres funciones dentro de la matemática (Lizcano, 1993). La primera lo identificaba como un número, con la misma jerarquía que cualquier otro. La segunda lo distinguía como detrás de la unidad en un número, permitiendo multiplicarlo por la base; por ejemplo, el cero de 10 en un sistema de numeración de base 10. La tercera permitía su empleo en un número para identificar la ausencia de cierto orden de unidades, como el cero de 205. La civilización occidental debe a los hindúes el invento del cero, con sus tres funciones: el lugar vacío en una columna de un número posicional, la nada como número y como elemento para operar.
Sunya es el nombre de la marca del vacío en lengua sánscrita: su primera representación fue un pequeño círculo. Este nombre adoptó el budismo para designar al vacío o la vacuidad en su doctrina de la nada. El cero cobró su valor como número significante de la nada; así pasó a cumplir las tres funciones con que lo conocemos nosotros. La traducción correspondiente hecha por los árabes fue sifr, y luego fue traducido al latín como zephirum, que derivó en zephiro: cero. La llegada de esta última cifra, el sifr, dio origen a la palabra cifra para designar a toda la colección.
Guedj (1998) señala que la creación del cero para ocupar el lugar vacío en un número expresado en notación posicional permite "significar una ausencia por medio de una presencia". De esta forma, el cero representa la existencia de la ausencia, al dar el paso del "no hay" al "hay cero".
La aparición por escrito más antigua del símbolo que asociamos con el cero, una pequeña circunferencia, data en la India del año 876 a.C., por lo cual se piensa que era conocido con anterioridad. Los grafismos usados para el cero indio fueron, y aún siguen utilizándose, un pequeño círculo o un punto. En de Mora y Jarocka (2003, p.36) se ofrece la siguiente reflexión:
Si el cero es la nada absoluta es, en cierto sentido el infinito. Y si se responde que la nada es ausencia total, es decir el no–ser, cabe recordar que el infinito también es el no–ser para la dimensión humana. Además de que si el infinito, pese a todo, es finito, el no ser también contiene en sí mismo al ser.
Esto nos permite pasar a otro concepto matemático cuyo abordaje se dio en India de manera totalmente distinta a lo que pasó en Occidente.
2.2.2.2. El infinito
Los jainas eran pensadores dedicados a la reflexión y al estudio de problemas de diversas áreas: místicas, metafísicas, religiosas y científicas. Se familiarizaron con las especulaciones numéricas puestas en juego por medio de grandes números, calificando a los compuestos por ochenta o incluso por cien cifras como pequeños. Para ellos, la totalidad de los seres humanos de la creación eran 296; definían distancias como la recorrida por un dios en seis meses si cubría una distancia de 100,000 yojanna (aproximadamente 10 kilómetros) en cada parpadeo de sus ojos, o bien el tiempo que tardaría en vaciarse una vasija cúbica de un yojanna de lado, llena con lana de corderos recién nacidos, si se quitaba una hebra de lana cada cien años. Al intentar situar los límites cada vez más lejos, aparecieron conceptos como lo "imposible de contar", lo "innumerable", "el número imposible de concebir" y finalmente el infinito. Para esta doctrina, el universo es indestructible porque es infinito tanto en tiempo como en espacio (Ifrah, 1997).
Los jainas clasificaron los números en numerables, innumerables e infinitos. Los numerables podían ser mínimos, intermedios y máximos; los innumerables, casi innumerables, verdaderamente innumerables e innumerablemente innumerables, y los infinitos, casi infinitos, verdaderamente infinitos e infinitamente infinitos (de Mora y Jarocka, 2003).
A su vez, reconocían cinco tipos de infinitos (Ifrah, 1997):
– Infinito en un sentido
– Infinito en dos sentidos
– Infinito en volumen
– Infinito en todas partes
– Perpetuamente infinito
Los jainas fueron los primeros pensadores que al tratar el infinito desecharon la idea de que todos los infinitos eran iguales, con base en una concepción distinta a la que se encuentra en la matemática actual. La idea de igualdad de todo lo infinito fue aceptada en Occidente hasta muchos siglos después, con los trabajos de George Cantor, a fines del siglo XIX. Sin embargo, desde la óptica de Cantor, lo que los jainas reconocieron como distintos tipos de infinito era en realidad un mismo tipo de infinito. Para los jainas, las cantidades infinitas se correspondían con los cardinales numerables, con el  de Cantor.
de Cantor.
La preocupación filosófica de los jainas en relación con el infinito radicó en analizar si el número de almas podría agotarse. Sus especulaciones aritméticas no sólo permitieron que en este escenario fuera posible descubrir de manera natural el cero en su función posicional, sino también toda la connotación abstracta que llevaba consigo este concepto. Mil años antes que en Occidente, los indios reconocían al cero y al infinito como conceptos inversos. Para ellos, dividir por cero equivalía a infinito. Definieron al infinito como la cantidad que no sufría modificación alguna si se le sumaban o restaban números finitos.
La palabra sánscrita cuyo significado es infinito es ananta, que significa textualmente: "sin fin". Había sido empleada anteriormente para designar diez millones y también, curiosamente, para denominar al cero; esta es una clara muestra de la relación entre dos conceptos tan distintos. En la mitología hindú designa a una gigantesca serpiente que simboliza la eternidad y la inmensidad del espacio. Ananta, el Señor de los Infiernos, es representado como una serpiente enroscada sobre sí misma en una especie de 8 acostado o en la repetición de este símbolo, sobre la que muchas veces descansa Vishnú. En 628, el matemático y astrónomo indio Brahmagupta habló del infinito matemático, al que llamó khachheda y definió como la "cantidad cuyo denominador es cero".
El cero y el infinito continuaron siendo manejados en la matemática de la India durante el medioevo. Hasta ese momento, consideraban que X/0 = X. Fue Baskara II quien "probó que el resultado era infinito. Demostró matemáticamente lo que la teología hindú sabía desde por lo menos mil años antes. Que el infinito, dividido, sigue siendo infinito, lo que se expresa con esta ecuación: ∞/X = ∞" (de Moray Jarocka, 2003, p.75).
Cabe destacar que, desde la matemática, infinito e indefinido representaban conceptos distintos, ya que indefinido significa vago, impreciso. El "error" cometido por los indios se basa claramente en la confusión de estos conceptos. Sin embargo, no puede decirse que desluzcan los descubrimientos que debemos a este pueblo. Como las concepciones indias de cero y de infinito no son operatorias, no les fue necesario hacer una diferenciación entre ambos términos, con lo que pudieron ocuparlos de manera indistinta.
2.3. China: el imperio de la tradición
2.3.1. El pensamiento lógico en la Antigua China
Los primitivos pobladores de China adoraban las fuerzas de la naturaleza y les rendían culto. Tenían asimismo muy arraigado el culto a los antepasados para mantener comuniones entre el pasado y el presente. Su religiosidad estuvo dominada desde un principio en la valorización del orden humano y el natural, una misión que el Cielo había confiado al Soberano y se reflejaba en sus libros de rituales. El Cielo era considerado como la realización de un principio de orden superior a las voluntades de los hombres y con potencia justiciera, guardiana de juramentos y de la providencia. Si bien la mitología china no tenía relaciones directas con su filosofía, algunas de sus creencias desempeñaron un papel fundamental en la organización del pensamiento, como las ideas de totalidad, orden y responsabilidad (Parain, 2002).
La historia de la civilización china se desarrolló de manera continua a lo largo de cuatro mil quinientos años. El escenario de China se caracterizó desde tiempos remotos por un ideal de inmovilidad institucional, con la preocupación reinante de conservar el orden familiar, político y social.
Toda ambición de originalidad era combatida e imperaba el tradicionalismo más cerrado, como lo demuestra el hecho mismo de que en China haya sobrevivido hasta nuestros días un sistema ideográfico de escritura muy complicado, mientras que egipcios y babilonios superaron la fase ideográfica pura en el segundo milenio antes de Cristo (Abbagnano y Visalberghi, 2005, pp.25–26).
A los símbolos se les concedía un papel central en la construcción del universo mental. La imagen no era un simple simulacro del objeto, sino involucraba toda la realidad del objeto, conteniendo toda su fuerza y energía, manifestada en el lenguaje y la magia. El número, como símbolo, cumplía un papel especial en combinaciones armónicas, correspondencias, secuencias y jerarquías que contribuían al orden universal. El ying y el yang eran los principios mayores que regían los intercambios del devenir; eran inseparables, complementarios, simbolizaban las apariencias sensibles y las fuerzas que se oponían y compensaban en el cosmos. Todo estaba formado y regulado por la combinación del ying y el yang, dos modalidades primarias de un principio único. La ley que presidía las mutaciones se llamaba Tao, un término con innumerables significaciones.
Las dos tendencias filosóficas principales de la China Antigua fueron la de los letrados, de índole positiva y práctica, y el taoísmo, que abarcaba metafísica y mística. Sus representantes fueron Confucio y Lao–Tsé, respectivamente.
Aunque Confucio (552–479 a.C.) no escribió ninguna obra, renovó mediante sus interpretaciones y comentarios el sentido de los textos viejos. Partió del principio moral y humanista que debía regir la familia y la sociedad, el respeto a los mayores y la posición social; creía en la predestinación, al afirmar que "el hombre superior debía tener como única preocupación la de conocer la voluntad celeste" (Parain, 2002, p.244), así como enseñaba a sus discípulos a discernir entre el bien y el mal mediante ejemplos prácticos, con lo que desarrollaba en ellos el razonamiento y la personalidad y los preparaba para seguir la vía (Tao) que el Cielo les ha marcado. La filosofía confucionista no concedía valor al conocimiento teórico, lo cual se constata al analizar su matemática, que no tuvo un desarrollo abstracto ni deductivo, pero ofrecía una rica tradición de observación empírica.
El papel del Tao se volvió central en la filosofía de Lao–Tsé, a quien se le considera como contemporáneo a Confucio. Las ideas de Lao–Tsé estaban dirigidas a iniciados y les aportaban temas de meditación dispuestos sin orden lógico, por lo que algunos las han interpretado como magia y naturalismo (Parain, 2002). En aquella época, en China había técnicas de meditación semiespeculativas emparentadas con las de los yoguis de la India y los chamanes siberianos, que se basaban en el principio de que la respiración favorecía la concentración y contemplación estática. En este intento por fundamentar la concepción de la sabiduría en el pensamiento racional se generó un misticismo contemplativo de tendencias mágicas.
Los seguidores del confucionismo trataron de discernir lo verdadero de lo falso por métodos más seguros, apoyando sus razonamientos en los procesos de comparar y concluir. No temieron al uso de paradojas, y las contradicciones no fueron un problema en su manera de pensar el cosmos:
El pensamiento chino se ve impelido a no evadirse de lo concreto y a no contrastar las contradicciones: los aspectos contrarios sólo se oponen en apariencia, la unidad es lo único real y los reconcilia. (Parain, 2002, p.296)
Una vez más aparecen el ying y el yang para explicar la armonía del universo. La lógica del pensamiento chino tuvo características deductivas completamente distintas de la aristotélica, como lo muestra el siguiente ejemplo:
Un ladrón es un hombre, pero es esencial que sea un ladrón. Se puede odiar a un ladrón sin dejar de amar a los hombres. Matar a un ladrón no es lo mismo que matar a un hombre.
El interés de los chinos por la lógica formal, según la concepción occidental, tardó muchos siglos en despertar, ya que la adoptaron hacia fines del siglo XIX y principios del XX. Hasta entonces, su ciencia y toda su sociedad se desarrollaron sobre la base de la contemplación; las contradicciones, como ya se dijo, fueron consideradas sólo aparentes.
2.3.2. El tratamiento de algunos conceptos matemáticos que surgieron en el escenario de China
La matemática china tuvo una creciente aplicación en diversas disciplinas a través de los calendarios, topografía, cronología, arquitectura, meteorología, comercio o pago de impuestos. Tuvo una marcada preferencia por lo concreto.
2.3.2.1. El cero
En China coexistían cuatro sistemas numéricos. Los números standard o modernos (utilizados desde el siglo III a.C.), los oficiales (versión decorativa de los standard), los comerciales (diseñados para escribir rápidamente, datan del siglo XVI) y los números con palitos (utilizados en la matemática y demás ciencias).
Para representar números en el sistema standard, los chinos ocuparon un sistema decimal con trece símbolos fundamentales: uno para cada uno de los dígitos no nulos, así como el 10, el 100 y el 1000. Estos símbolos aún son empleados en la actualidad. Se trata de un sistema híbrido basado en reglas multiplicativas.
Por ejemplo1: para representar 821, se expresa como indica la figura 1.
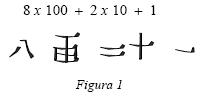
En la notación tradicional, los símbolos se ordenaban de arriba hacia abajo, en forma vertical (actualmente se escriben horizontalmente), por lo que 821 en notación tradicional sería como se muestra en la figura 2.

Este sistema de numeración no necesitaba del cero; sin embargo, a partir de la dinastía Ming se incorporó un ideograma para identificar ese hueco, el ling, que significa gota de rocío; todavía se usa para significar que falta una potencia de 10 en un número. De esta manera, si se quiere escribir 801 queda como la situación que ilustra la figura 3.

Este, como hemos dicho, no fue el único sistema de numeración que se usó en China. Allí, como también en Japón y en Corea, los matemáticos conocieron bajo el nombre chino suan zi y el japonés sangi —que significa cálculo por medio de fichas–, un sistema decimal en el que los números estaban dados por el lugar que ocupaban las cifras. Se trataba de un sistema de características similares al nuestro en el que se representaban los números con palitos, pero con algunas diferencias notables; la fundamental era que había 9 cifras (Figura 4).

Si se representaba 23, como 
 se corría el riesgo de confundir dónde empezaba el 3 y terminaba el 2 en caso de que no se separaran lo suficiente ambas cifras. Por ello, comenzaron a intercalarse cifras en distinta posición (vertical y horizontal) para las cifras contiguas de un número. Entonces, 23 quedaba como
se corría el riesgo de confundir dónde empezaba el 3 y terminaba el 2 en caso de que no se separaran lo suficiente ambas cifras. Por ello, comenzaron a intercalarse cifras en distinta posición (vertical y horizontal) para las cifras contiguas de un número. Entonces, 23 quedaba como 
 .
.
Pero aún faltaba solucionar el problema de la ausencia de una potencia de 10, ya que durante mucho tiempo se dejó un hueco entre la cifra anterior y la siguiente. Así, 203 fue escrito como 
 .
.
Las operaciones con números así representados se hacían en un tablero en el que la ausencia de una potencia de diez en un número correspondía a un hueco vacío en el tablero, al cual se le denominaba wu, y actuaba como un cero. Hacia el siglo XII se comenzó a llenar el hueco con un punto y posteriormente con una pequeña circunferencia. A través de esta representación, algunos historiadores ven influencias de la matemática hindú, aunque unos sostienen la hipótesis de la influencia china en India, y otros que ambas invenciones fueron autónomas.
2.3.2.2. El infinito
El infinito surgió en la China como aplicación a ciertas ideas de su cosmogonía, puestas de manifiesto en la creencia de la existencia de infinitos mundos, posiblemente con gran influencia del budismo. En su visión, el cielo está vacío, inmensamente alto y alejado, sin límites, que se extiende hasta el infinito (Lloyd, 1993).
Basado en la idea de convergencia del perímetro de polígonos inscriptos en una circunferencia, Liu Hui se refirió a la noción de convergencia y de mejores aproximaciones que nunca alcanzan el valor exacto, aceptando la idea de iteraciones que se continuaban indefinidamente. A partir de la característica de pragmatismo propia de la matemática china, el infinito fue utilizado cuando el resultado al que conducía era útil; no recurrieron a la aplicación de demostraciones axiomáticas deductivas, como los griegos. Sin embargo, también hallaron paradojas similares a las de Zenón, mas la reacción fue distinta de la que se dio en Grecia: Hui Shi, en lugar de dedicarse a realizar refutaciones, simplemente se lamentó del gasto infructuoso de talento (Lloyd, 1993).
La aparición del infinito en la China posee ciertas características que se asemejan a la de este concepto en la escuela. Mientras los niños construyen su idea de infinito fuera de escenarios escolares, no se constituye en un concepto conflictivo (Lestón, 2008). Pero al enfrentarse al infinito matemático surgen las paradojas y conflictos.
2.4. América precolombina
Siglos antes de la llegada de Cristóbal Colón a América, existían en el continente americano áreas pobladas por gran variedad de pueblos; muchos de ellos habían alcanzado un alto grado de desarrollo cultural. Hemos recibido de ellos un legado artístico admirable, pero gran cantidad de sus conocimientos culturales han sido destruidos por el choque de culturas que se generó.
2.4.1. El pensamiento lógico en América precolombina
Los mayas fueron una de las culturas más antiguas del área mesoamericana. La cultura maya se desarrolló en tres periodos: el Preclásico, entre el 3000 a.C. y el 300 d.C.; el Clásico, entre el 300 y el 900 d.C., y el Posclásico, entre el 900 y 1546 d.C.
La sociedad maya estaba integrada por clases sociales: nobles, sacerdotes, pueblo y esclavos, mientras que la base de su economía era la agricultura. Los principales dioses se vinculaban con la agricultura y el tiempo; los mayas concebían al hombre como dependiente de los dioses que dominaban al mundo. El creador del mundo era Hunab y se pensaba que su hijo ltzamná, señor de los cielos, de la noche y del día, había otorgado a los mayas la escritura, los códices y quizá el calendario. Por ello, se le invocaba en las ceremonias propiciatorias del nuevo año para evitar desastres. Los mayas poseían tres calendarios: el solar, el venusino y el litúrgico, lo cual muestra la importancia que los mayas dieron al tiempo no sólo como ordenador de los acontecimientos, sino como fenómeno sobrenatural que regía la creación.
Las creaciones culturales de los mayas se basaban en una concepción religiosa del cosmos, la cual planteaba que el universo había nacido de las energías sagradas que se manifestaban de manera múltiple y por diversos seres naturales que provocaban el acontecimiento, según el ciclo temporal. Con esta idea del cosmos, el pueblo maya hizo de la religión el centro de su existencia; asimismo, construyeron conocimientos orientados a la construcción, el conteo, la observación de la bóveda celeste, la pintura y la escultura, pero también desarrollaban actividades cotidianas como la siembra y la confección de artesanías. Salazar de León (2005, p. 84), dice sobre la manera de pensar que tenían los mayas:
Algo que sí es característico de la cultura maya y que en Occidente se ha ido perdiendo, es la importancia de las explicaciones dadas por los ancianos y las personas mayores, ya que estas explicaciones son consideradas con un fuerte contenido de espiritualidad y sabiduría.
Por otra parte, la mitad sur del México actual fue habitada por diversos pueblos. Los aztecas fueron uno de estos pueblos que, mediante alianzas militares con otros grupos, logró una rápida expansión y dominó el área central y sur del actual México entre los siglos XIV y XVI.
En el mundo de los aztecas, la educación iniciaba en la casa. Los padres transmitían a sus hijos valores para la vida y la convivencia, basados en el respeto, el amor y el recto criterio. La instrucción era continuada por los sacerdotes, quienes tenían a su cargo las tres escuelas existentes, el Calmécac, el Telpochcalli y el Cuicacalli, destinadas a la formación de sacerdotes, guerreros y artistas, respectivamente, mediante las enseñanzas propias de cada actividad.
El fin de la educación en estas tres escuelas era para ser guerrero o sacerdote, es decir, trascender la personalidad de la persona. En estas escuelas, los maestros del conocimiento lograron formalizar y sistematizar diversos conocimientos, entre los que destacan los de tipo matemático, transmitidos de manera oral de generación en generación, a través del idioma náhuatl. (Espinoza Ocotlán, 2006, p.16)
Con respecto a la construcción del conocimiento, una de sus características principales era la contemplación de los hechos y los fenómenos que se sucedían en la naturaleza y en las actividades humanas. La visualización y algoritmia, en este caso, se desarrollaron a través de la experiencia, la observación de la periodicidad y la reproducibilidad de las actividades o fenómenos (Espinoza Ocotlán, 2006). Puede inferirse, por tanto, que la manera de validar resultados matemáticos en estas culturas fue por medio de la contemplación y concordancia con los fenómenos naturales y humanos.
2.4.2. El tratamiento de algunos conceptos matemáticos que surgieron en el escenario americano
2 .4.2.1. El cero
Las culturas mesoamericanas, como los mayas y los aztecas, presentaron un rasgo en común en la construcción de conocimientos matemáticos con la cultura india: el desarrollo de la noción, el símbolo, el concepto y uso del cero. Sin embargo, las bases sobre las que se hizo este concepto son distintas a la consideración de la nada en la India. Era un cero tangible y concreto, propio de las culturas que realizaban una atenta observación de la naturaleza y sus manifestaciones concretas.
Los conocimientos aritméticos de los mayas se conocen a través de códices relacionados con la astronomía y la adivinación. Debido a influencias de otros pueblos americanos, los mayas utilizaron un sistema de numeración mixto que tenía peculiaridades singulares y notables en América: era posicional y se caracterizaba por la presencia y utilización del cero.
En su sistema de numeración más sencillo, heredado de los zapotecas y los olmecas (Ifrah, 1997), los símbolos básicos eran un punto que representaba al 1  y una barra que simbolizaba al 5
y una barra que simbolizaba al 5  . Dichos símbolos hacían alusión a un guijarro y a un cayado, respectivamente. Con ellos, los mayas simbolizaban los números de 1 a 19 mediante adición, a través de la colocación de tantas barras y puntos como fuese necesario. Por ejemplo:
. Dichos símbolos hacían alusión a un guijarro y a un cayado, respectivamente. Con ellos, los mayas simbolizaban los números de 1 a 19 mediante adición, a través de la colocación de tantas barras y puntos como fuese necesario. Por ejemplo:
17 se escribe como: 
Asimismo, los diecinueve símbolos generados formaban parte de un sistema posicional en el cual se colocaban las cifras una abajo de la otra; cada posición adquiría valores veinte veces mayores que la inferior, salvo para la tercera posición, que en lugar de corresponder a 202, multiplicaba al número por 360. Esta anomalía, que impedía hablar del sistema maya como vigesimal, dificultó enormemente su operatoria, pero se encontraba directamente relacionada con las unidades de medición de tiempo.
La incorporación de un tercer símbolo, que se representaba con el caparazón de una caracola marina  permitía indicar las unidades faltantes. Ponemos como ejemplo (Figura 5):
permitía indicar las unidades faltantes. Ponemos como ejemplo (Figura 5):

Se considera que este es uno de los sistemas más económicos en cuanto a la cantidad de símbolos. Además, permite registrar cantidades que alcanzan millones de unidades, debido a las facilidades que ofrece el sistema posicional de numeración. La función del cero en un número consiste en identificar la ausencia de cierto orden de unidades, mas no posee su valor cardinal. Hay otra notación numérica maya en la que las veinte cifras se representaban a través de dibujos de cabezas; esta era utilizada en los calendarios religiosos.
Podemos reconocer una fuerte similitud entre su cosmovisión y la noción del cero. En el caso de las culturas mesoamericanas, la ausencia de dicotomías del tipo bueno–malo favoreció considerablemente la constitución de la noción del cero. (Cantoral, 2001, p. 64).
2.5. Reflexiones sobre algunas de las características del pensamiento no aristotélico
Hay que admitir que la lógica aristotélica no se presentó en los escenarios orientales y americanos. El principio de contradicción y el del tercero excluido no tienen validez en los entornos que describimos. Incluso las antinomias no asustan a las filosofías no aristotélicas, pues admiten que los extremos se complementan y permiten la aparición, evolución y desarrollo de ciertos conceptos matemáticos cuya aparición en Occidente tardó siglos y fue terriblemente cuestionada.
La creencia de que existe una verdad objetiva en el mundo de los fenómenos también está poco extendida en los escenarios no aristotélicos, donde la verdad muchas veces es un concepto relativo que difiere según los planos de la conciencia. Salazar de León (2005, p.34), afirma:
La ciencia occidental se encuentra también, y con derecho propio, en este mundo que se quiere sin fronteras y que forma una totalidad de manifestaciones; totalidad que unifica en un conjunto las diversas características de las variadas culturas, tanto en los aspectos filosóficos como en los científicos y en el conjunto de los modos del saber. No hay ninguna razón para pensar que la ciencia occidental sea la depositaria de un saber absoluto, ni para que no podamos suponer que las aportaciones de otros modos de entendimiento de la realidad no pudieran ser significativas para el encuentro con el conocimiento de la realidad y, por ende, de la verdad.
En la China Antigua, las ideas filosóficas se basaron en la coexistencia y equilibrio entre el ying y el yang. Todo ser era una combinación de lo femenino y lo masculino, de la energía pasiva y de la acción; nada era totalmente ying o totalmente yang. Esto dio un sustento simbólico sobre el que fue posible construir diferentes modos de oposiciones numéricas; de igual manera, abrió la posibilidad de que surgieran objetos matemáticos como el cero y la aparición del infinito a partir de la cosmogonía.
La simetría, en cuanto al equilibrio que preside el paradigma chino, fue radicalmente distinta de la filosofía de la Grecia clásica. Para los griegos no era posible pasar del ser al no ser, ni tampoco cambiar el género o la naturaleza de un objeto. No existía ningún elemento identificable que estuviera en el límite del ser y el no ser; por ello, en Grecia no apareció el cero con estas características.
La visión griega del mundo y el uso de la lógica para develar su funcionamiento en cierta manera impidieron la génesis de ciertos conceptos matemáticos, como el cero y el infinito. En su exigencia de consistencia lógica y bivalencia, dichos conceptos no pudieron ser construidos de manera natural, como se nota en otras culturas que no recibieron la influencia aristotélica. Los griegos, señala Rarrow, "carecían del hilo místico que podía entretejer el concepto de cero en un sistema práctico de explicación" (2001, p.60). Sólo Parménides consideró al no ser como algo de lo cual era posible filosofar, aunque alejado de fines prácticos.
Sin embargo, como se acaba de mostrar, las antiguas culturas de Oriente y Mesoamérica elaboraron conceptos matemáticos e incluso desarrollaron algunas construcciones que en Occidente sólo pudieron ser abordadas y trabajadas científicamente hasta muchos siglos después. En este trabajo nos centramos únicamente en dos de esos conceptos, el cero y el infinito, cuya construcción en Occidente se vio pospuesta por los conflictos que generaba su abordaje al convivir con las ideas intuitivas y con los principios aristotélicos.
El hecho de encontrar formas de argumentación no aristotélicas en culturas que no tuvieron tal influencia, y de que hayan sido capaces de construir argumentaciones que les permitieron razonar sobre los conceptos matemáticos que elaboraban, ofrece evidencia acerca de que el ser humano no posee los principios aristotélicos como una de las características innatas de su pensamiento. Dichos preceptos son construcciones surgidas en el entorno sociocultural de Grecia que fueron aceptadas en Occidente durante siglos.
3. LOS ESTUDIANTES Y LAS FORMAS DE RAZONAR NO ARISTOTÉLICAS
A continuación, se reportan dos experiencias donde queda de manifiesto que las formas de argumentación surgidas en el aula no siempre tienen como base a la lógica aristotélica, a pesar de que es enseñada como sustento de las ciencias en el aula (Crespo Crespo, 2007a).
3.1. Una experiencia sobre la aparición de argumentaciones nyayas en el aula
Bruno D'Amore (2005a) introduce a partir de las características de la lógica nyaya –que, como ya mencionamos, surgió en la India en oposición al budismo–una experiencia en la que identifica, en ejemplos extraídos de las clases de matemática a alumnos entre 14 a 15 años, ciertos comportamientos argumentativos que se acercan a estructuras argumentativas nyayas. Dichas argumentaciones se presentaron de manera espontánea, sin que hubieran sido producidas por el investigador. D'Amore afirma:
Yo no creo, incluso después de esta investigación, que estos estudiantes piensen en estricto acuerdo con la lógica nyaya. El recurrir a esta lógica en el análisis del razonamiento matemático de los estudiante, evidencia, sin embargo, el hecho que el análisis didáctico presupone, de una forma u otra, un marco de referencia y que existen diferentes lógicas posibles para dar explicación del comportamiento deductivo de los estudiantes. (D'Amore, 2005a, p. 84)
Desde nuestra óptica, los resultados de la investigación anterior estarían denotando que la forma de razonar aristotélica, que usualmente presuponemos como natural en el aula de matemática, no tiene tal carácter. La lógica no es innata; se trata de una construcción sociocultural que a veces los alumnos la sienten con un carácter artificial. Si durante siglos se ha aceptado que la aristotélica es la forma de razonar del ser humano, se debe a que hemos nacido en una sociedad que tiene sumamente arraigada tal cultura.
En la investigación que muestra D'Amore pueden identificarse claramente las etapas del pensamiento lógico védico en el planteo e intentos de demostración de propiedades matemáticas por parte de los estudiantes.
La primera de las experiencias que se refieren en este trabajo consiste en una recreación de la investigación de D'Amore, aunque fue cambiado el escenario y la propiedad matemática que daba origen a la experimentación. Sobre la base de la publicación citada se planteó a una maestra, participante en un curso de capacitación de geometría, el siguiente enunciado:
Si un cuadrilátero tiene sus diagonales perpendiculares y se cortan mutuamente en su punto medio, entonces es un rombo.
Tras la lectura del enunciado, los pasos que siguió y las reflexiones que realizó la maestra fueron los siguientes:
1. AB = BC = CD = DA (dibuja un rombo y le da los nombres correspondientes a los vértices).
2. Yo sé que BD es perpendicular a AC; se cortan en O, y AO = OC y BO = OD
3. Pero si las diagonales son perpendiculares y se cortan en partes iguales, entonces los lados son iguales, o sea es un rombo (mientras habla va marcando en la figura que realizó).
4. Las diagonales son perpendiculares y se cortan en partes iguales.
5. Los cuatro lados son iguales; es un rombo.
La propiedad no está demostrada, pero la actuación de la maestra frente al problema planteado es similar a la que reporta D'Amore, en la que se identifican las etapas de la argumentación nyaya. Cada uno de los pasos propuestos se puede corresponder con las fases de las argumentaciones nyayas:
1. Afirmación: P(A). La afirmación aún no probada es afirmada inicialmente.
2. Razón: F(A). Se afirma la causa que se atribuye para que P(A) ocurra.
3. Tesis:
[F(x)
P(x)] . Se enuncia la proposición general y ejemplifica la tesis en un caso particular: F(B)
P(B), en este caso marcando en la figura de análisis realizada.
4. Aplicación: F(A). Se afirma, la hipótesis del caso general se vuelve al caso en examen. Una fuerza ejerce una acción sobre la figura analizada.
5. Afirmación: P(A). Se reafirma el consecuente que se quería probar.
Al llegar a este punto, la propiedad es asumida como verdadera. Indudablemente, si se analiza la corrección del razonamiento, se dirá que no fue correcto; sin embargo, la maestra afirmó que lo había probado, aunque no de manera formal. Era consciente de que no se le aceptaría matemáticamente su razonamiento, mas ella lo consideró como una prueba de la propiedad. Por tanto, había generado una estrategia de argumentación no aristotélica, pero que satisfacía a su autora en lugar de la que tenía carácter deductivo. Dio evidencia de que la lógica deductiva era artificial para ella; sin embargo, no resulta posible afirmar que la lógica nyaya sea más intuitiva. Consideramos que será necesario seguir indagando acerca de las formas de argumentación que no son construidas en la escuela y que penetran en las aulas de matemática (Crespo Crespo, 2007c), a fin de buscar respuestas sobre la manera en que surgen y provocan convencimiento.
3.2. Una experiencia sobre la resistencia a la utilización de argumentaciones aristotélicas
La siguiente experiencia que se expone fue realizada con una estudiante del Profesorado de Informática durante la asignatura Matemática 2, cuyos temas abarcaban la presentación de los conceptos fundamentales de la lógica clásica (proposicional y de predicados), su mecanización mediante las álgebras de Boole y algunos rudimentos de las lógicas no clásicas (las polivalentes y la difusa). Los estudiantes, al momento de la experimentación que reportamos, habían adquirido los conocimientos de la lógica clásica, pero no habían tratado ningún concepto de lógicas no clásicas. Por ello, no es posible considerar que la alumna seleccionada para nuestro estudio tuviera nociones de lógicas no clásicas.
Esta actividad fue planteada a los alumnos en una evaluación escrita. Un ejercicio de esta índole había sido resuelto en clase en diversas oportunidades, donde se discutió su resolución y fundamento:
Dado el siguiente razonamiento, se pide:
a. Formalizarlo en lógica de predicados de primer orden. Indicar los dominios de cada función proposicional.
b. Formalizarlo como proposiciones categóricas.
c. Determinar su validez.
d. Si es válido, demostrarlo por el método deductivo. Si no lo es, modifique una premisa para que lo sea:
Algunos físicos son matemáticos. Ningún químico es matemático. Por lo tanto, algún físico no es químico.
La solución esperada para la actividad era la siguiente:
a. P(x) = x es físico
Q(x) = x es matemático
R(x) = x es químico
DomP = DomQ = DomR = {personas}
b. A = clase de los físicos
B = clase de los matemáticos
C = clase de los químicos
c. A partir de la formalización hecha en proposiciones categóricas, se representa cada una de las premisas en diagramas de Venn, con la convención de que una cruz marcada en un sector significa la existencia de algún elemento en dicho apartado de los conjuntos, mientras que un sector rayado indica que se encuentra vacío. Los diagramas de Venn así obtenidos serían como los que ilustra la figura 6.
Con la representación de las premisas, y observando el sector que corresponde a la conclusión A\C, se nota la existencia de algún elemento en el mismo, de lo cual se infiere que el razonamiento es válido.
d. A partir de la determinación de que se trata de un razonamiento válido, se procede a aplicar el método deductivo:
Una de las estudiantes presentó la siguiente resolución: los puntos a y b fueron realizados según lo esperado. Al llegar al punto c, en lugar de aplicar el método de los diagramas de Venn, planteó una variante de la prueba de invalidez que se ocupa en la lógica proposicional. En dicho método, a partir de la verdad de las premisas se supone la falsedad de la conclusión y se intenta asignar valores de verdad a las proposiciones simples. Si se logra, surge como conclusión que el razonamiento es no válido; si hay una contradicción, se concluye que es válido. Este procedimiento no es aplicable a la lógica de predicados, ya que por la presencia de cuantificadores puede tratarse de dominios infinitos; además, no puede en general especializarse a todas las proposiciones con seguridad en el mismo elemento.
La estudiante eliminó los cuantificadores. Supuso la verdad de las premisas, pero también de la conclusión, al presentar lo siguiente:
Y por lo tanto el razonamiento es válido.
Esta manera de pensar desde la lógica aristotélica es incorrecta. No es posible inferir la validez del razonamiento de la secuencia que hizo la alumna. Ella, a continuación, resolvió de manera correcta el ítem d de la actividad.
Las preguntas que surgían al observar lo que había realizado la alumna para resolver la problemática eran:
1. ¿Por qué no aplicó el método de los diagramas de Venn?
2. ¿Qué la llevó a intentar una estrategia parecida a la prueba de invalidez, pero hizo de manera incorrecta las suposiciones originales?
3. ¿Por qué eliminó los cuantificadores?
4. ¿Conocía realmente lo que estaba haciendo, o era producto de una construcción incompleta del conocimiento?
Con el propósito de buscar respuesta a algunas de estas interrogantes, se entrevistó a la alumna. Las preguntas que se le hicieron llevaban como fin clarificar cuáles eran los fundamentos sobre los que había presentado su resolución. El extracto de la entrevista se transcribe a continuación:
E: ¿Por qué eliminaste los cuantificadores?
A: Los cuantificadores los eliminé por la regla de especialización.
E: ¿En qué elemento especializaste?
A: En cualquiera, en x.
E: Pero hay un cuantificador existencial.
A: Sí, pero yo quería un elemento cualquiera para poder demostrar que es válido. Esas reglas las usé en la parte d.
En relación con las causas por las que no había utilizado el método de los diagramas de Venn, que había sido visto en clase, dijo:
E: ¿Por qué no utilizaste los diagramas de Venn?
A: No me gusta demostrar con dibujos. Los matemáticos siempre dicen que los dibujos no son seguros, que es mejor escribirlo en matemática.
E: ¿Escribirlo en matemática? ¿Qué es eso?
A: Como lo hacen ustedes, que lo dicen con palabras y lo escriben con símbolos.
E: ¿De manera más formal, quieres decir? ¿Usando formalismo?
A: Sí. En clase utilizamos el método de los diagramas de Venn para este tipo de problemas, pero a mí no me gusta. Me parece más seguro este. Además, funciona bien porque es válido; pude hacer el punto d y de esa manera me di cuenta de que estoy pensando bien.
La docente tenía evidencia, obtenida en clases anteriores, de que la alumna conocía el método de prueba que se le había solicitado, ya que en la clase anterior a la actividad los estudiantes lo habían aplicado para resolver problemas, y ella los había realizado correctamente. En este caso, lo que presentaba parecía inspirado en la prueba de invalidez, por lo cual se le preguntó:
E: El método que utilizaste, ¿es similar a la prueba de invalidez?
A: Sí, pero no es igual. Eso de suponer que no es válido para ver que es válido no me convence. Si quiero ver que es válido, veo si es válido. Si quiero ver si es inválido, veo si es inválido. ¿Por qué voy a mezclar?
E: Pero, ¿hay otra posibilidad aparte de que sea válido o inválido?
A: No creo, o al menos no definimos nada más. Pero yo pienso para adelante. Me propongo lo que quiero ver y avanzo. Si no llego me propongo lo otro y avanzo. Eso de suponer que no para ver que luego es sí, me parece rebuscado.
De esta entrevista se puede inferir que la alumna conoce las reglas de inferencia y los métodos de determinación de validez de razonamientos; sin embargo, su uso no es el esperado. La no utilización de diagramas de Venn para la determinación de la validez del razonamiento es fundamentada por la estudiante en la no aplicación de recursos gráficos. Se observa en ella una clara inclinación a aplicar recursos analíticos en lugar de los gráficos. Esta es una posición que en los últimos tiempos ha cobrado importancia en la escuela: el predominio de los recursos algebraicos y analíticos en detrimento de los gráficos. Tal situación ha provocado que en el aula no se esté aprovechando lo suficiente la visualización para favorecer la construcción de conceptos, lo cual se refleja cuando los docentes hacen uso de la estrategia de visualización, pero los alumnos no entienden su importancia y consideran que no es válida.
En este caso, donde hay un rechazo de la alumna hacia las argumentaciones gráficas, se observa cómo se ha construido la no aceptación de este tipo de argumentaciones a partir de experiencias previas en el aula. No se ha asumido la importancia de las figuras de análisis y la diferencia de su utilización en relación con el razonamiento sobre casos particulares. Sin embargo, los libros de texto muestran el empleo de este tipo de métodos, que son enseñados en diversas asignaturas. Cabe entonces la pregunta: ¿qué valor dan los estudiantes a este tipo de argumentaciones?
Por otra parte, en la explicación realizada por la alumna se nota la presencia de formas de argumentación inductivas, a través de razonamientos abductivos. También se observa un rechazo a las argumentaciones indirectas, mediante el uso de la reducción al absurdo. Al igual que en experimentaciones que dimos a conocer anteriormente (Crespo Crespo, 2005, Crespo Crespo y Farfán, 2005, 2006), se evidencia en los estudiantes de carreras informáticas el rechazo a los métodos de argumentación indirectos y muestran una clara inclinación a las argumentaciones directas.
Si se analizan las respuestas de la alumna en la entrevista y la resolución que hizo, podemos detectar ciertos rasgos de pensamiento no aristotélico:
– No aceptación del método de los diagramas de Venn, por considerarlo un método gráfico y, por ende, poco fiable.
– No aceptación del principio del tercero excluido, con lo que deja abierta la posibilidad de que exista otro tipo de razonamiento, aparte de los válidos e inválidos.
– No aceptación de la prueba de invalidez, basándose en la poca fiabilidad de los métodos de demostración indirectos.
– Confusión entre formalismo y rigor. Como aclara D'Amore (2005b), refiriéndose a la interpretación de contrato didáctico, en la escuela el alumno piensa que debe hacerlo con rigor, de acuerdo a lo que supone espera el maestro. En segundo lugar, el alumno estima que en matemática debe hacer cálculos; por tanto, lo que se les pedía no era matemática.
– Presentación de una forma de razonamiento no aristotélica, con gran similitud del pensamiento nyaya, tal como se reporta en D'Amore (2005a). La estudiante partió de la tesis, al suponer que el razonamiento era válido. Para ello debía exponer la razón: si las premisas son verdaderas, la conclusión también. En ese punto recurrió a ejemplificar la proposición general: aquí eliminó los cuantificadores y realizó la asignación de los valores de verdad de las proposiciones simples. Finalmente, hizo la generalización correspondiente.
– Resulta notable, y también interesante, que de la entrevista se infiere que aquellas respuestas que podrían haber sido consideradas incorrectas en una evaluación no provenían del hecho de que la alumna no tuviera los conocimientos necesarios, sino de que la construcción que había realizado en las formas de razonamiento válidas diferían de las que fueron enseñadas en clase, desde la visión aristotélica. Ella conocía la manera de argumentar deductivamente para dar la respuesta esperada; sin embargo, justificó su no utilización basándose en que su falta de convencimiento se debía al empleo de recursos gráficos, por medio de una figura de análisis. No reconoció que la deducción que llevó a cabo en el último ítem hubiera sido por sí misma una respuesta válida. Pero su manera de argumentar, que sí es incorrecta desde el punto de vista deductivo, la consideró convincente y arguyó que la deducción mencionada corroboraba su corrección.
4. ALGUNAS CONSIDERACIONES FINALES
En este artículo se ha presentado evidencia de que los principios de la lógica clásica, asumidos como las leyes del pensamiento humano durante siglos, son en realidad construcciones socioculturales. Por una parte, vemos que no sólo no se encuentran presentes en todos los escenarios socioculturales, sino que en culturas en las que no afloraron fue posible construir ciertos conceptos matemáticos con características distintas a los de la matemática de base griega. Podría decirse que la presencia de los principios lógicos aristotélicos en un escenario sociocultural no sólo no favoreció el surgimiento de ciertos conceptos matemáticos como el cero o el infinito, sino que más bien inhibieron la construcción de estos objetos matemáticos, ocasionando que debieran transcurrir varios siglos para su aparición.
En este trabajo se muestran ejemplos sobre formas de argumentar presentes en el aula de matemática que no tienen características aristotélicas. Ambas argumentaciones difieren, por tanto, de lo que se esperaría para ser consideradas válidas.
El primero de los casos se trata de una estructura de argumentación que recuerda las que se utilizaban en la India durante el período védico. Si bien no es posible pensar que esta forma de razonamiento sea conocida por quien la utilizó, nos pone frente a formas de argumentación que no tienen influencia aristotélica, pero generan convicción. El otro ejemplo se presenta a través de las respuestas y explicaciones de una estudiante, quien inicialmente da respuestas a una situación problemática escolar presentada dentro de un escenario académico, en la que si bien no resuelve aplicando argumentaciones lógicas aristotélicas, muestra en la entrevista posterior conocimiento de las mismas, aunque en algunos casos no las acepta y considera mejores las que utilizó.
Se refuerza mediante estos ejemplos la hipótesis de que las formas de argumentación en su carácter de construcciones socioculturales no son innatas, sino que se han construido y son la base de las prácticas sociales de demostración que caracterizan a la comunidad matemática. Nuestra forma de argumentar en la matemática se ha construido en una cultura de base fuertemente aristotélica, lo cual hace que se asuma a esta lógica como innata. Sin embargo, a pesar de que hemos analizado en este trabajo sólo dos ejemplos de posición frente a ciertas argumentaciones presentes en el aula de matemática, no son casos aislados, ya que presentan opiniones que muchas veces hemos detectado en nuestras clases y consideramos que deben ser analizadas cuidadosamente.
Las dificultades que se ponen de manifiesto al realizar demostraciones matemáticas en el aula se deben, en muchas ocasiones, a que no se detecta la existencia y características de otros tipos de argumentaciones en los estudiantes, ya que se asume como natural al razonamiento aristotélico. Sin embargo, las maneras de argumentar en matemática no se han mantenido estáticas a través de la historia y en los distintos escenarios socioculturales porque se trata de construcciones socioculturales. En nuestra opinión, la comprensión de ese carácter de construcción social para las argumentaciones y las demostraciones como prácticas sociales podrá ayudar a tener una mayor percepción sobre las formas de argumentación en el aula.
Para lograr que los alumnos comprendan la necesidad de argumentar matemáticamente, e incluso de demostrar propiedades matemáticas, resulta indispensable que construyan la significatividad de la argumentación. Esto deberá ser comprendido a partir de que los docentes asuman que las demostraciones matemáticas son prácticas sociales; así es posible que los alumnos entiendan la importancia de la argumentación para justificar y dar validez a las propiedades matemáticas. En esta significatividad se estará reconociendo el status de las argumentaciones como construcciones socioculturales. Estas argumentaciones, no todas son verbales y en algunas oportunidades se manifiestan a través de gestos (Aparicio y Cantoral, 2006) u otros recursos visuales. Su análisis debe ser tenido en cuenta para comprender el valor que los estudiantes dan a las formas de validación en el aula de matemática.
La escuela tiene como uno de sus desafíos actuales identificar y comprender la presencia de formas de argumentación que los alumnos construyen fuera de ella y que penetran en las aulas. Tal fenómeno se pone de manifiesto en el aula de matemática, y consideramos que es relevante investigar sobre la manera en que estas formas de argumentación puedan ser analizadas, a fin de comprobar si es posible aprovecharlas para favorecer la construcción de conceptos.
REFERENCIAS BIBLIOGRÁFICAS
Abbagnano, N. y Visalberghi, A. (2005). Historia de la pedagogía. México: Fondo de Cultura Económica. [ Links ]
Aparicio, E. y Cantoral, R. (2006). Aspectos discursivos y gestuales asociados a la noción de continuidad puntual. Revista Latinoamericana de Investigación en Matemática Educativa 9(1), 7 – 30. [ Links ]
Barrow, J. (2001). El libro de la nada. Barcelona: Crítica. [ Links ]
Cantoral, R. (2001). Sobre la articulación del discurso matemático escolar y sus efectos didácticos. En G. Beitía (Ed.), Acta Latinoamericana de Matemática Educativa 14. (pp.64–75). México: Iberoamericana. [ Links ]
Crespo Crespo, C. (2005). El papel de las argumentaciones matemáticas en el discurso escolar. La estrategia de deducción por reducción al absurdo. Tesis de Maestría no publicada, CICATA, México. [ Links ]
Crespo Crespo, C. (2006). La identificación de argumentaciones por reducción al absurdo en escenarios académicos de la matemática desde la óptica de los estudiantes. Trabajo presentado en el VI Congreso Virtual de Enseñanza de las Matemáticas, Guadalajara, México. [ Links ]
Crespo Crespo, C. (2007a). Los estudiantes ante formas de argumentar aristotélicas y no aristotélicas. Un estudio de casos. Revista Electrónica de Investigación en Ciencias (Reiec) 2(1), 84–100. [ Links ]
Crespo Crespo, C. (2007b). El reconocimiento de argumentaciones por reducción al absurdo en escenarios académicos y no académicos. En C. Crespo Crespo (Ed.), Acta Latinoamericana de Matemática Educativa 20 (pp. 542–547). México: Clame. [ Links ]
Crespo Crespo, C. (2007c). Las argumentaciones matemáticas desde la visión de la socioepistemología. Tesis de Doctorado no publicada, CICATA, México. [ Links ]
Crespo Crespo, C. y Farfán, R. M. (2005). Una visión de las argumentaciones por reducción al absurdo como construcción sociocultural. Revista Latinoamericana de Investigación en Matemática Educativa 8 (3), 287–317. [ Links ]
Crespo Crespo, C. y Farfán, R. (2006). Las argumentaciones por reducción al absurdo como construcción sociocultural. En G. Martínez (Ed.), Acta Latinoamericana de Matemática Educativa 19 (pp. 766–781). México: Clame. [ Links ]
D'Amore, B. (2005a). La argumentación matemática de jóvenes alumnos y la lógica hindú (nyaya). En UNO. Revista de Didáctica de las Matemáticas 38, 83–99. [ Links ]
D'Amore, B. (2005b). Bases filosóficas, pedagógicas, epistemológicas y conceptuales de la Didáctica de la Matemática. Barcelona: Reverté. [ Links ]
de Mora, J. M. y Jarocka, M. L. (2003). Apuntes para una historia de las matemáticas y astronomía en la India Antigua. México: Universidad Nacional Autónoma de México. [ Links ]
Eggers Lan, C. (1995). El nacimiento de la matemática griega. Buenos Aires: EUDEBA. [ Links ]
Espinoza Ocotlán, P. (2006). La matemática náhuatl: estudio del sistema de numeración náhuatl. Tesis de Maestría no publicada, CICATA, México. [ Links ]
Ganeri, J. (2002). Jaina logic and the philosophical basis of pluralism. History and Philosophy of Logic 23 (4), 267–281. [ Links ]
Gillings, R. (1972). Mathematics in the time of the pharaons. New York: Dover Publications. [ Links ]
Guedj, D. (1998). El imperio de las cifras y los números. Barcelona: Grupo Zeta. [ Links ]
Hiriyanna, M. (1960). Introducción a la filosofía de la India. Buenos Aires: Sudamericana. [ Links ]
Ifrah, G. (1997). Historia de las cifras. Madrid: Espasa–Calpe. [ Links ]
Joseph, G. (1991). La cresta del pavo real: Las matemáticas y sus raíces no europeas. Madrid: Pirámide. [ Links ]
Le Bon, G. (1901). Las civilizaciones de la India (Vols. 1 y 2). Barcelona: Montaner y Simón Editores. [ Links ]
Lestón, P. (2008). Ideas previas a la construcción del infinito de escenarios no escolares. Tesis de Maestría no publicada, CICATA, México. [ Links ]
Lizcano, E. (1993). Imaginario colectivo y creación matemática. Barcelona: Gedisa. [ Links ]
Lloyd, G. (1996). Finite and Infinite in Greece and China. Chinese Science 13, 11–34. [ Links ]
Parain, B. (Ed.). (2002). El pensamiento prefilosófico y oriental. México: Siglo XXI Editores. [ Links ]
Salazar de León, E. (2005). Análisis comparativo de los conceptos de matemática maya y kaxlan. El caso de las comunidades de Santa Isabel y La Unión, municipio de Chisec, departamento de Alta Verapaz. Tesis de Licenciatura no publicada, Universidad San Carlos de Guatemala, Guatemala. [ Links ]
1 En los números que hemos escrito utilizamos a título ilustrativo estilizaciones de las cifras chinas que aparecen en Ifrah (1997).



















