Artículo

 

Interpretando la comprensión matemática en escenarios básicos de valoración. Un estudio sobre las interferencias en el uso de los significados de la fracción

 

Interpreting mathematical understanding in basic contexts of assessment. A study on the interferences in the use of the meanings of the fraction

 

Jesús Gallardo*, José Luis González** y Wenceslao Quispe***

 

* Universidad de Málaga. Málaga, España, E–mail: gallardoromero@telefonica.net

** Universidad de Málaga. Málaga, España, E–mail: gmari@uma.es

*** Universidad Nacional del Altiplano. Puno, Perú, E–mail: collasuyow@yahoo.com

 

RESUMEN

Este trabajo examina algunos aspectos del problema de la interpretación de la comprensión en matemáticas. A partir de la configuración específica de uno de los escenarios básicos donde se manifiesta este problema, se desarrolla una propuesta para la interpretación del aprendizaje comprensivo. Propuesta que se sustenta en un modelo operativo para la valoración de la comprensión del conocimiento matemático. Su potencialidad práctica se pone de manifiesto en su aplicación, mediante un estudio realizado con profesores en formación, en el contexto de las fracciones. Las evidencias obtenidas en el uso de algunos significados de la fracción, sustentan una caracterización de la comprensión elaborada con base en las distintas prioridades de elección y disponibilidad de empleo de este objeto matemático, en su espacio fenomenológico y epistemológico.

PALABRAS CLAVE: Interpretación, valoración, comprensión en matemáticas, análisis fenomenológico y epistemológico, significados de la fracción.

 

ABSTRACT

This work examines some aspects of the problem of interpretation of mathematical understanding. Starting with the specific configuration of one of the basic context where this problem arises, a proposal for the interpretation of learning for understanding is developed. The proposed model is based on an operational model of the value placed on the understanding of mathematical content. Its practical potential is revealed through its application, with pre–service teachers, in the context of fractions. The evidence obtained using some fraction meanings, support a characterization of the understanding based on different priorities and availability in the use of this mathematical object, within its phenomenological and epistemological field.

KEY WORDS: Interpretation, assessment, mathematical understanding, phenomenological and epistemological analysis, meanings of fractions.

 

RESUMO

Este artigo analisa alguns aspectos do problema da interpretação da compreensão em Matemática. A partir da configuração específica de um dos cenários básicos onde se manifesta este problema, desenvolve–se uma proposta para a interpretação da aprendizagem compreensiva. A proposta é sustentada por um modelo operativo para a valorização da compreensão do conhecimento matemático. A sua potencialidade é evidente na sua aplicação, no âmbito de um estudo realizado com professores em formação, no contexto das fracções. As evidências obtidas no uso de alguns significados de fracção sustentam uma caracterização da compreensão elaborada com base nas diferentes prioridades de selecção e disponibilidade para a utilização deste objecto matemático, num espaço fenomenológico e epistemológico.

PALAVRAS CHAVE: Interpretação, valorização, compreensão em Matemática, análise fenomenológica e epistemológica, significados de fracção.

 

RÉSUMÉ

Ce travail examine le problème de l'interprétation de la compréhension des mathématiques. À partir de la configuration spécifique d'un contexte fondamental où se manifeste ce problème, nous développons une proposition orientée vers l'interprétation de l'apprentissage compréhensif. C'est une proposition qui s'appuie sur un modèle opérationnel pour l'évaluation de la compréhension du savoir mathématique. Le potentiel pratique de cette proposition apparaît dans son application à l'étude des fractions, réalisée avec des professeurs en formation. Les preuves obtenues dans l'usage de certaines significations de la fraction démontrent une caractérisation de la compréhension fondée sur différentes priorités de choix et la disponibilité d'emploi de la fraction dans son contexte phénoménologique et épistémologique.

MOTS CLÉS: Interprétation, évaluation, compréhension des mathématiques, analyse phénoménologique et épistémologique, signification de la fraction.

 

1. INTRODUCCIÓN

La enseñanza y el aprendizaje con comprensión suelen admitirse como objetivos deseables y prioritarios en Matemática Educativa, lo que ha motivado un aumento en iniciativas que se ocupan esencialmente del desarrollo de la comprensión en el aula de matemáticas (Hiebert, Carpenter, Fennema, Fuson, Wearne, Murray, Olivier & Human, 1997; Carpenter, Fennema, Fuson, Hiebert, Human, Murray, Olivier, & Wearne, 1999; NCTM, 2000). Con frecuencia, estas iniciativas se ven afectadas por dificultades y limitaciones importantes cuando la comprensión en toda su extensión no es tomada en cuenta (Sierpinska, 2000).

El estudio de la comprensión encuentra en la valoración un condicionante metodológico, que por su reconocida naturaleza interpretativa, sitúa la cuestión de la interpretación en la base de la investigación sobre comprensión en matemáticas (Gallardo y González, 2007a). Nuestra postura es, que este argumento justifica la conveniencia de incrementar los esfuerzos destinados a profundizar en las particularidades de la interpretación en los principales escenarios de valoración¹. Estos escenarios están presentes en el aula de matemáticas como estrategia para la obtención de información sobre los distintos aspectos relacionados con el fenómeno de la comprensión.

En los últimos años hemos venido trabajando una aproximación multifacética, dirigida al estudio de la valoración de la comprensión en matemáticas. Nuestras investigaciones dan cuenta de su operatividad en la interpretación del desempeño matemático de los alumnos (Gallardo, 2004; Gallardo & González, 2006a, 2006b, 2007b). Esta aproximación proporciona además, un procedimiento metodológico (basado en un análisis fenomenológico y epistemológico), para la identificación y organización de situaciones matemáticas que se usan en el diagnóstico y valoración de la comprensión.

En este artículo se presenta una síntesis de la configuración actual de dicha aproximación. Se introduce a través de la caracterización de uno de los escenarios básicos de valoración, el de la producción individual en una prueba escrita. Los referentes teórico–metodológicos que constituyen nuestra propuesta, se toman como base en una exploración que llevamos a cabo con profesores en formación, a quienes se les pidió resolver problemas elementales, donde intervienen diversos significados del concepto de fracción. Se caracteriza e interpreta el fenómeno de interferencia entre significados, en términos de comprensión. Este fenómeno se produce cuando los participantes utilizan a la fracción en situaciones distintas, desde su ámbito de aplicación.

 

2. EL PROBLEMA DE INVESTIGACIÓN

El desarrollo de procesos educativos orientados a la comprensión, plantea retos significativos a las investigaciones en Matemática Educativa. Sobresalen aquellos que atañen al problema de la interpretación de las respuestas y los comportamientos observables en los alumnos, objeto de estudio en este trabajo.

Se sustenta en las preguntas siguientes:

– ¿Qué exigencias impone la Matemática Educativa a la interpretación para cumplir con sus expectativas de desarrollo de la comprensión del conocimiento matemático?;

– ¿En qué términos habría de darse la interpretación en matemáticas?;

– ¿Cuál es el enfoque interpretativo que resulta más ventajoso para cumplir con el propósito del desarrollo comprensivo de las matemáticas?

El problema de investigación se enmarca en el área problemática delimitada por las bases conceptuales del grupo de investigación Pensamiento Numérico y Algebraico (Castro, Rico y Romero, 1997) de la Sociedad Española de Investigación en Educación Matemática (SEIEM), por la línea de investigación relacionada con el diagnóstico y la evaluación de la comprensión del conocimiento matemático (González y Ortiz, 2000), que se desarrolla en la Universidad de Málaga (España), y por las vías de aplicación del modelo de valoración en matemáticas propuesto en la tesis doctoral de Gallardo (2004).

El objetivo que nos planteamos fue: configurar una opción metodológica efectiva basada en este modelo concreto para afrontar con operatividad la interpretación de la comprensión matemática en diferentes escenarios básicos de valoración. Su consecución implicó:

– Analizar los componentes de los escenarios básicos de valoración presentes en el aula de matemáticas.

– Caracterizar su complejidad relacional con base en el modelo considerado, y considerar para cada escenario una propuesta metodológica asociada, a partir de la cual se interprete la comprensión matemática que acontece en él.

– Mostrar en cada escenario la operatividad y viabilidad práctica de la propuesta interpretativa, mediante su aplicación en conocimientos matemáticos particulares que revelen aspectos significativos de su comprensión.

En el artículo se exponen los avances alcanzados en la investigación. Son resultado de considerar uno de los escenarios básicos de valoración de menor complejidad relacional: el constituido por el profesor, quien se interesa por obtener información sobre la comprensión del estudiante inmerso en una actividad matemática escrita individual. El conocimiento matemático en cuestión es el número racional positivo, en su representación fraccional. Entendemos que el empleo de los distintos significados de la fracción propicia la manifestación de fenómenos de comprensión observables e interpretables (Quispe, 2008).

 

3. MARCO TEÓRICO

3.1. Antecedentes

Los antecedentes se organizaron en dos bloques, uno relativo a la comprensión en matemáticas, su valoración e interpretación, y el otro, a la comprensión de los significados de la fracción.

 

3.1.1. Enfoques en la investigación sobre comprensión en matemáticas

Desde una perspectiva general y con fines integradores, identificamos dos orientaciones básicas sobre comprensión del conocimiento matemático en las investigaciones en nuestra disciplina:

a) Las investigaciones que toman como punto de partida a una aproximación 'atomizada' del problema y que dirigen su atención a indagar sobre algunas de las distintas dimensiones identificadas en la comprensión, entre las que se distinguen:

Origen y fuentes. Estas dimensiones son interés de investigaciones que se enfocan hacia las situaciones y circunstancias responsables de la aparición de la comprensión, y a los acontecimientos concretos previos generadores de tales situaciones. Por ejemplo: Con base en las ideas constructivistas piagetianas sobre la génesis del conocimiento, ampliamente extendidas, la comprensión surge en un espacio de experiencias, desequilibrios cognitivos, respuestas adaptadas y búsqueda de estabilidad asociada (English & Halford, 1995).

Naturaleza y funcionamiento. Factores que son del interés en estudios que se ocupan del qué es y cómo se produce la comprensión. Suelen abordarse al amparo de propuestas teóricas interpretativas de la relación reconocida entre los estados mentales del sujeto y su comportamiento externo observable. Esta orientación la encontramos en el empleo de tipologías generales de comprensión (Hiebert & Lefevre, 1986) o de referencias metafóricas (Davis, 1992) así como en el enfoque representacional que vincula la comprensión a las representaciones y conexiones internas del conocimiento matemático (Hiebert & Carpenter, 1992; Goldin, 2002).

Evolución. Dimensión en la que se apoyan investigaciones relacionadas con la faceta dinámica de la comprensión y con el principio de que ésta se va desarrollando en el individuo a lo largo del tiempo. La comprensión es un fenómeno que emerge, se desarrolla y evoluciona (Carpenter & Lehrer, 1999).

La teoría dinámica de Pirie–Kieren para el crecimiento de la comprensión matemática (Pirie & Kieren, 1994; Kieren, Pirie & Calvert, 1999) aparece entre las propuestas más consolidadas y con mayor influencia en el estudio de esta dimensión. Los modelos jerárquicos de categorías o niveles, como es el modelo de proceso de dos ejes desarrollado por Koyama (2000), constituyen otra de las estrategias extendidas en la investigación sobre la evolución.

Factores. Esta dimensión incluye aspectos condicionantes de la comprensión, tales como: la especificidad del objeto de comprensión, las capacidades cognitivas generales del sujeto, la valoración personal que este realiza sobre el propio objeto o las características del medio (Sierpinska, 1994; Godino, 2000).

Efectos. Está asociada con los resultados o productos de la comprensión siguientes: los comportamientos adaptados, la aplicación de conocimientos, la resolución de problemas o la descripción de acciones (todos ellos efectos externos observables), y también efectos internos como las nuevas estructuras cognitivas y semánticas resultantes de un cambio en la comprensión (Duffin & Simpon, 2000).

b) Las investigaciones que consideran una aproximación 'integral' al fenómeno de la comprensión del conocimiento matemático a través de sus relaciones, reconocidas con otras configuraciones cognitivas con las que comparte protagonismo, como: el significado, el aprendizaje, el pensamiento matemático o las competencias. Esta visión se aprecia en trabajos clásicos como los de Byers y Erlwanger (1985), donde la comprensión se vincula con el aprendizaje y la memoria; en Godino y Batanero (1994), donde la relación se establece con el significado de los objetos matemáticos; Bender (1996), que trata la imagen y la comprensión como modos de pensamiento distintos aunque estrechamente relacionados; o, más recientemente, en Warner, Alcock, Coppolo & Davis (2003), quienes estudian la contribución del pensamiento matemático flexible en el crecimiento de la comprensión.

Adicionalmente, interesa subrayar que en los estudios sobre comprensión del conocimiento matemático está presente el problema de la naturaleza interpretativa de la valoración, como un condicionante metodológico de primer orden². Por lo general, las aproximaciones en Matemática Educativa suelen reconocer y compartir las siguientes premisas:

– La elevada complejidad de la valoración.
– La existencia de limitaciones inherentes a su propia naturaleza.
– La influencia de la especificidad del conocimiento matemático.
– La adecuación de las manifestaciones observables como vía para obtener información sobre la comprensión de los alumnos.

Entre las principales contribuciones realizadas en este sentido destacan:

a) Las que plantean valorar la comprensión en función de la representación y las conexiones internas del conocimiento matemático (Hiebert & Carpenter, 1992),

b)  Las que hacen hincapié en la superación de obstáculos epistemológicos (Sierpinska, 1994), y por último, c) Las que se enfocan en las relaciones con significados institucionales preestablecidos (Godino & Batanero, 1994). Del mismo modo, resaltan los métodos y técnicas centrados en la elaboración de perfiles de comprensión (Pirie & Kieren, 1994) y las estrategias y procedimientos de valoración multifacética basados en el análisis del conocimiento matemático, tal es el caso de los análisis semántico y estructural propuestos en Niemi (1996), el análisis de los significados praxeológicos de los objetos matemáticos derivado del enfoque ontosemiótico de la cognición e instrucción matemática (Godino, 2002) o la aproximación que fundamenta este trabajo.

 

3.1.2. Aportes sobre los significados de la fracción y su comprensión

El conocimiento de que la fracción manifiesta distintos significados se reporta desde investigaciones sistemáticas (Kieren, 1976, 1988, 1993; Behr, Harel, Post & Lesh, 1992; Gairín, 1998; Escolano & Gairín, 2005), en las que distinguen los siguientes:

Parte–todo. Significado que se manifiesta al concebir a la fracción a/b como la relación existente entre dos cantidades específicas: un "todo" o unidad b (continua o discreta), representando un número total de partes iguales, y una "parte" a, destacando un número particular de esas partes iguales tomadas del total.

Cociente. Significado que enfatiza la fracción a/b como la operación de dividir un número natural entre otro no nulo. En este caso, la fracción es el resultado de una situación de reparto donde se busca conocer el tamaño de cada una de las partes resultantes al distribuir a unidades en b partes iguales.

Medida. Significado que tiene su origen en medir cantidades de magnitudes que, siendo conmensurables, no se corresponden con un múltiplo entero de la unidad de medida. La fracción a/b emerge entonces de la necesidad natural de dividir la unidad de medida en b subunidades iguales y de tomar a de ellas hasta completar la cantidad exacta deseada.

Razón. Este significado muestra a la fracción como índice comparativo entre dos cantidades o conjuntos de unidades. La fracción a/b como razón evidencia la comparación bidireccional entre los valores a y b, siendo esencial el orden en el que se citan las magnitudes comparadas: si la relación de A respecto de B es a/b, entonces B es a/b respecto de A.

Operador. Significado que hace actuar a la fracción como transformador o función de cambio de un determinado estado inicial. Así, la fracción a/b empleada como operador es el número que modifica un valor particular n multiplicándolo por a y dividiéndolo por b. Los porcentajes, por ejemplo, son un caso particular de fracción como operador.

Estos significados forman parte de la propia naturaleza compleja del número racional positivo y se contemplan como organizadores de los contextos y situaciones donde tiene sentido el empleo de la fracción (Freudenthal, 1983; Puig, 1997). Las características epistemológicas y fenomenológicas de estos significados se reflejan también a nivel cognitivo, al mostrarse como condicionantes de la comprensión que los estudiantes poseen de la fracción. Respecto del aprendizaje y la comprensión de las fracciones se conocen particularidades como las señaladas en Post, Cramer, Behr, Lesh & Harel (1993), Lamon (2001), Gairín & Sancho (2002), Valdemoros (2004), Dos Santos (2005), y en Clarke & Sukenik (2006):

– La comprensión de la fracción exige la identificación y el dominio de sus distintos significados.

– La comprensión de los significados de la fracción genera dificultades intrínsecas de distinta índole si bien algunos de ellos (por ejemplo, parte–todo) suelen mostrarse más asequibles que otros (p.ej., medida).

– El predominio en el aprendizaje de unos determinados significados llega a interferir u obstaculizar el uso y la comprensión del resto de significados.

– La comprensión de la fracción se ve perjudicada por aquellas propuestas curriculares que priorizan el aprendizaje de ciertos significados (p.ej., parte–todo, cociente) en detrimento de otros (p. ej., medida, razón, operador).

– La valoración y el desarrollo de la comprensión de la fracción demanda que las tareas matemáticas en el aula abarquen la mayor diversidad posible de situaciones y fenómenos diferentes en los que se requiera o tenga sentido el uso de todos los significados de la fracción.

Este trabajo está dirigido a interpretar y fundamentar desde nuestro modelo, algunas de las particularidades sobre el aprendizaje y comprensión de fracción ya reportadas , especialmente las que se refieren a las prioridades e interferencias que surgen en el uso de sus significados.

A continuación, se describen los principios teórico–metodológicos que configuran la propuesta, así como de algunas evidencias empíricas con profesores en formación que reflejan su operatividad en el estudio de la comprensión de la fracción y sus significados.

 

3.2. Referentes de un modelo operativo para la interpretación de la comprensión en matemáticas

Esta sección se estructura en tres apartados: El escenario básico de valoración, el modelo de investigación y el concepto de interferencia en la selección y uso del conocimiento matemático.

 

3.2.1. El escenario básico de valoración

Se concibe como el espacio en el que un profesor indaga qué es lo que ha comprendido un alumno de un conocimiento matemático específico, a través de sus realizaciones personales. En este escenario básico diferenciamos los siguientes elementos y relaciones (Figura 1).

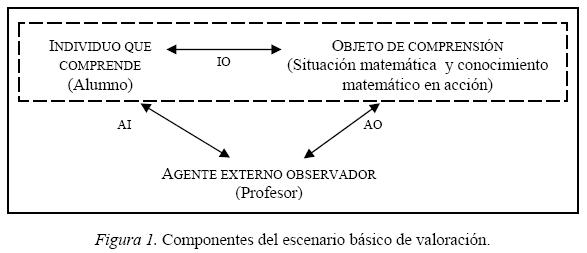
Elementos

(a) El conocimiento matemático como objeto de comprensión, puesto en acción a través de una situación problemática.

(b) El estudiante que comprende y que intenta resolver la situación haciendo uso de su comprensión, contemplado como un intérprete en el escenario de valoración.

(c) El profesor, como agente observador e intérprete que trata de profundizar en la comprensión matemática del alumno a través de lo acontecido en la situación.

Relaciones

(d)  Entre el agente observador y el conocimiento matemático (AO) se genera el vínculo relativo al dominio fenómeno–epistemológico del primero sobre el segundo. Alrededor de esta relación, suelen surgir cuestiones ligadas con la naturaleza de situaciones matemáticas pertinentes para su empleo en el diagnóstico y valoración de la comprensión.

(e) El estudiante y el conocimiento matemático puesto en acción (IO) conforman el primero de los dos espacios para la interpretación. Durante la resolución el alumno se ve inmerso en un proceso interpretativo abierto, originado al momento que intenta reconciliar la experiencia matemática que está viviendo, con las formas de describirla y con las expectativas sobre ella previamente generadas (Brown, 2001). La relación IO sugiere, entre otras, cuestiones relativas a los registros escritos que habrían de dar cuenta de esta actividad interpretativa del estudiante.

(f) El agente intérprete de la comprensión del alumno (AI) necesita disponer de bases teóricas y metodológicas para transformar, mediante interpretaciones fundadas, las acciones registradas en información útil. Una visión particular de la comprensión en matemáticas o una propuesta derivada sobre cómo afrontar la valoración de la misma forman parte de esta fundamentación. El vínculo AI plantea, sobre todo, cuestiones concernientes a las particularidades de los posibles enfoques propuestos.

Descrito el escenario de valoración, nuestra aproximación propone para sus componentes los siguientes referentes interpretativos:

A. El conocimiento matemático como objeto de comprensión

Se concibe al conocimiento matemático como una entidad concreta, con dos estructuras básicas: la estructura epistemológica y la fenomenológica. Ambas estructuras se consideran específicas y exclusivas, constituidas con fines valorativos y al margen del sujeto. La primera surge de las relaciones con otros conocimientos matemáticos, y la segunda de las situaciones que dan sentido al propio conocimiento.

I. Estructura epistemológica. Los conocimientos matemáticos son entidades representables, con significado y relacionadas entre sí. Consideramos que cada conocimiento matemático posee una estructura constituida por las siguientes componentes:

– Representaciones externas o registros semióticos.
– Conocimientos constituyentes.
– Relaciones con otros conocimientos.
– Significados.

Los modos de uso del conocimiento matemático dependen de estos componentes, en consecuencia, fue este el primero de los referentes interpretativos que adoptamos.

II. Estructura fenomenológica. El conocimiento matemático puesto en acción que considera las relaciones existentes con aquellas situaciones problemáticas en las que tiene sentido su uso. El criterio fenomenológico por el que un conocimiento matemático interviene en una situación de forma necesaria (situación de aplicación exclusiva), en una o varias formas de uso determinadas, o como alternativa entre otros conocimientos (situación de aplicación no–exclusiva), constituye el segundo de los referentes interpretativos de nuestra propuesta de valoración.

Ambas estructuras permiten imaginar en clave topológica, una red tridimensional de nodos, cada uno de ellos representan un conocimiento matemático o una situación problemática asociada, conectados entre sí mediante vínculos epistemológicos (conocimiento–conocimiento) y fenomenológicos (conocimiento–situación).

B. El sujeto que comprende (primer intérprete)

Desde la perspectiva del alumno, entendemos que la matemática se muestra esencialmente como un conjunto de medios para la gestión óptima, sistemática y fundada de las situaciones que involucran un determinado tratamiento de la información. La resolución de estas situaciones requiere, entre otros aspectos:

– La identificación de los conocimientos matemáticos susceptibles de poderse emplear como medio para la resolución de la tarea;

– La decisión sobre cuál conocimiento matemático emplear, y de qué modo, entre las posibilidades identificadas previamente.

En nuestra propuesta se introduce a la noción de conjunto personal de situaciones asociada a un conocimiento matemático, como el conjunto de todas las situaciones que son identificadas por el individuo como susceptibles de ser resueltas mediante dicho conocimiento matemático. Se trata de una fenomenología subjetiva y que constituye el principal referente interpretativo de nuestra aproximación con relación al alumno que comprende. La compresión queda determinada por las características del conjunto personal de situaciones.

C. El agente externo observador (segundo intérprete)

El agente responsable de la valoración necesita planteamientos teóricos y estrategias metodológicas operativas, que contribuyan en la obtención de información objetiva, con la que garantizan descripciones e interpretaciones cercanas a la realidad cognitiva de los estudiantes. La interpretación, que se basa en las características del conocimiento matemático y en la interacción visible del alumno sobre él, también requiere de los referentes que se desarrollan en los apartados siguientes.

3.2.2. El modelo de investigación

Para complementar las bases expuestas, fundamentaremos a la interpretación y a la valoración de la comprensión del conocimiento matemático en los supuestos y principios que a continuación se describen:

(i) Una idea operativa de la comprensión en matemáticas y su valoración

Un punto de partida es que la comprensión de un conocimiento matemático está ligada a las experiencias matemáticas que se producen a través de las situaciones en las que interviene dicho conocimiento. En este sentido, los estudiantes manifiestan una cierta comprensión con relación a un conocimiento matemático concreto cuando, ante situaciones de desequilibrio cognitivo, que deciden voluntariamente abordar, elaboran y emiten a su satisfacción respuestas adaptadas, donde hacen un uso significativo (esto es, libre, consciente e intencional) de este conocimiento. En definitiva, el uso intencional del conocimiento matemático en situaciones pertenecientes a su ámbito fenómeno–epistemológico da cuenta de la comprensión, de lo que un individuo utiliza y cómo lo utiliza, en los términos ya señalados, proporciona información específica sobre lo que comprende y cómo lo comprende.

La valoración de la comprensión del conocimiento matemático, se sustenta en el modo en que se aplica en las situaciones propias de su esfera fenómeno–epistemológica.

(ii) Un procedimiento para la determinación de situaciones adecuadas para la valoración

La visión adoptada sobre la comprensión y su valoración requiere del agente intérprete procedimientos, útil en la identificación y selección de tareas que generen experiencias matemáticas favorables, para observar y valorar la comprensión. Esta opción demanda de una parte, analizar la naturaleza del conocimiento matemático y su estructura epistemológica, y de otra, tomar en cuenta su relación con los fenómenos y situaciones que lo hacen significativo para establecer la correspondiente estructura fenomenológica. Con este propósito, se propone un procedimiento metodológico, constituido por las fases siguientes:

Primera fase. Una vez aceptada la imposibilidad de conocer la totalidad de situaciones donde tiene sentido el uso de un conocimiento matemático particular, se busca concretar el conjunto más amplio posible o una muestra extensa y representativa del campo de problemas que le den sentido. Esta fase consiste precisamente en la identificación y delimitación de tal conjunto, al que denominamos conjunto genérico de situaciones³. Para ello se lleva a cabo, siempre que sea necesario, la consulta y revisión de fuentes documentales, en el que se atienda a la epistemología y fenomenología del conocimiento matemático, como las siguientes:

– Antecedentes de investigación sobre enseñanza y aprendizaje matemático;
– Muestra representativa de libros de texto de matemáticas;
– Textos dirigidos a la formación didáctica del profesorado de matemáticas;
– Obras complementarias (manuales de matemáticas, textos de divulgación, etc.).

Los resultados primarios obtenidos incluyen: (a) una batería inicial de tareas o conjunto genérico provisional de situaciones; (b) una primera caracterización de la estructura fenómeno–epistemológica del conocimiento. Los resultados dependen de la naturaleza del conocimiento matemático y de la información disponible sobre él.

Segunda fase. Estructuración fenómeno–epistemológica del conjunto genérico de situaciones, mediante la ordenación y categorización de las tareas. Esta fase puede incluir una consulta a expertos sobre la idoneidad de los resultados y las posibilidades de modificación del campo genérico de situaciones y de las propias categorías establecidas. La estructura obtenida en esta fase es la referencia empleada para la selección de un conjunto reducido de situaciones representativas de cada categoría para el diagnóstico y la valoración de la comprensión.

En caso de no disponer de antecedentes empíricos suficientes para garantizar la relevancia y potencialidad de las estructuras, categorías y situaciones, se aborda una tercera fase de experiencia empírica exploratoria, destinada a:

– Depurar la categorización y representación de situaciones observando el desempeño de los estudiantes frente a ellas.

– Identificar y establecer de forma provisional, comportamientos y respuestas tipo asociados a las distintas categorías situacionales.

Un ejemplo de aplicación de este procedimiento se expone en Gallardo y González (2006a), que se usa para el caso del algoritmo estándar escrito para la multiplicación de números naturales, presente en los programas curriculares españoles de Educación Primaria (6–12 años).

3.2.3. Interferencias en la selección y uso del conocimiento matemático

De acuerdo con el modelo, para sustentar la valoración de la comprensión en el uso del conocimiento matemático, se necesita profundizar en la naturaleza de dicho uso, tomando como base la caracterización de las circunstancias, particularidades o eventos más significativos que acontecen en las distintas oportunidades de su empleo. Como señalamos previamente, se identifica como acción idónea de comprensión, a la aplicación del conocimiento matemático en su forma precisa, en toda situación de su esfera fenómeno–epistemológica. No obstante, esta condición ideal suele diferir en numerosas ocasiones del desempeño real de los estudiantes cuando se enfrentan a situaciones de distinto tipo, que desde nuestra aproximación, dan lugar a una variedad de sucesos interpretables en términos de comprensión.

Un ejemplo de ello lo encontramos en el fenómeno de interferencia que acontece en la elección, previa a la utilización del conocimiento matemático a la que se ve sometido el resolutor. Situaciones matemáticas que hemos catalogado de aplicación no–exclusiva⁴. En estos casos, entendemos que se generan en los alumnos decisiones donde los posibles conocimientos a emplear se vinculan, se confrontan y se anteponen unos a otros aunque no siempre de forma acertada. Finalmente, las posibles interferencias de unos conocimientos sobre otros durante el proceso de reflexión selectiva, terminan condicionando su uso posterior en la resolución de la tarea dada.

Este fenómeno de interferencia, así caracterizado, se vislumbró en Gallardo (2004), con alumnos que no reconocían el algoritmo estándar escrito para la multiplicación de números naturales, como medio de resolución de situaciones pertenecientes a su ámbito fenómeno–epistemológico. También se identificó en estudiantes que aún reconociendo la idoneidad del uso del algoritmo, preferían utilizar otros conocimientos⁵.

Las manifestaciones externas motivadas por el fenómeno de interferencia, posibilitan extraer información relativa a la estructura del conjunto personal de situaciones que el individuo asigna al conocimiento matemático. En primer lugar, el observar dónde emplea el conocimiento matemático el alumno y el establecer el correspondiente vínculo situación–conocimiento, permite concretar la extensión de su conjunto personal de situaciones. En segundo lugar, el análisis complementario de las interferencias en la selección y uso del conocimiento matemático en sus distintas variantes, abre además, una vía de acceso operativa al estudio de la naturaleza de los vínculos fenómeno–epistemológicos. Desde nuestro enfoque estas dos facetas específicas del conjunto personal de situaciones, se muestran como indicadores esenciales de la comprensión, y son el origen y la referencia para la interpretación en el escenario básico de valoración examinado.

 

4. ESTUDIO EMPÍRICO

Se llevó a cabo un estudio empírico de carácter exploratorio, en el que se muestra la potencialidad práctica de la propuesta interpretativa en el escenario de valoración elegido. En particular nos interesó evidenciar y caracterizar al fenómeno de interferencia en la elección y uso del objeto matemático fracción y sus significados. Al mismo tiempo, se buscó evidenciar aspectos relevantes de la comprensión de este conocimiento matemático, mediante la descripción de dicho fenómeno.

 

4.1. Metodología

4.1.1. Participantes

En el estudio participaron 60 profesores en formación, quienes cursaban los últimos tres años de la carrera profesional de Educación Secundaria, especialidad de Matemáticas y Computación, de la Facultad de Ciencias de la Educación de la Universidad Nacional del Altiplano de Puno, Perú. Los criterios para la selección de la muestra fueron: la naturaleza de la investigación y las facilidades que se ofrecieron por la institución para la realización de este trabajo.

4.1.2. Tareas

Los resultados de investigaciones previas sobre el aprendizaje de la fracción y la naturaleza de sus significados, contribuyeron para que la aplicación en la determinación y selección de situaciones, se facilitara y se redujera considerablemente.

Las tareas que se usaron en este trabajo son resultado de la estructura fenómeno–epistemológica de la fracción, y que corresponden a situaciones donde resulta legítimo el uso de este conocimiento sobre algunos sus significados. Resumiendo:

Epistemológicamente se optó por trabajar con la parte de la estructura de la fracción concerniente a sus cinco significados. La comprensión se interpreta con base en las particularidades que de su empleo hacen los estudiantes.

En lo que se refiere a la fenomenología, resultó operativo que las tareas o situaciones propuestas a los estudiantes, estuviesen en la categoría de aplicación no–exclusiva. Esto es, porque interesó que las tareas, propias de cada uno de los cinco significados de la fracción, dejaron abierta la posibilidad de que se emplearan significados distintos. Los usos de la fracción resultado de estas situaciones, son los que generan los episodios de comprensión que se pretenden interpretar desde nuestra aproximación.

Las tareas que resolvieron los estudiantes (tabla I), son ejemplos representativos de situaciones de aplicación no–exclusiva, características de los significados de fracción: parte–todo, en sus contextos continuo y discreto, cociente, medida, razón y operador, respectivamente. Ese tipo de situaciones hacen posible observar el referente teórico de la interferencia entre conocimientos matemáticos y su comprensión, en función de la disponibilidad de ser empleados.

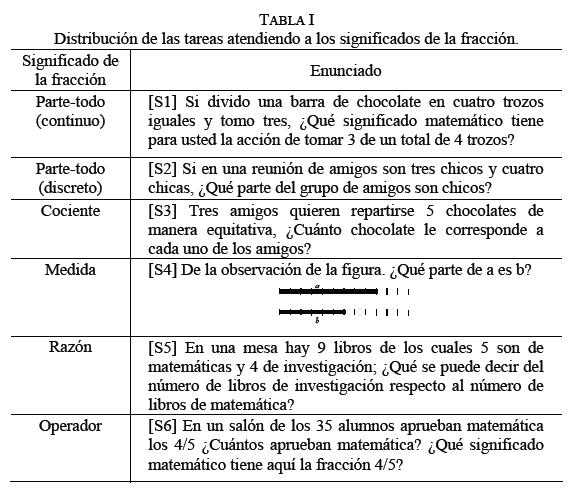
Las tareas se presentaron a los participantes a través de un cuestionario⁶. Se resolvieron de forma individual, durante una clase ordinaria, en un tiempo máximo de 45 minutos.

4.1.3. Análisis de respuestas

El fenómeno de interferencia se observó e interpretó, a partir de las respuestas escritas que presentaron los participantes en cada tarea. Las respuestas fueron clasificadas como sigue:

A. Empleo propio de la fracción. En esta categoría se incluyen las respuestas que manifiestan el vínculo fenómeno–epistemológico entre la situación y el uso de la fracción en su significado oportuno. En ella diferenciamos entre respuesta correcta e incorrecta, pertinente para la interpretación de la comprensión de acuerdo con la propuesta.

B. Interferencia en el uso de la fracción. En las respuestas se presenta el fenómeno de interferencia en el uso de los significados de la fracción, cuando se emplea uno o varios significados, determinados en detrimento del considerado propio (Interferencia Interna o Endógena). Incluye además, aquellas respuestas en las que, por emplearse otros conocimientos o simplemente por no aportar información suficiente, no se aprecian las evidencias necesarias para identificar el vínculo fenómeno–epistemológico existente entre la situación propuesta y la fracción, como opción para su resolución en alguno de sus significados (Interferencia Externa o Exógena). Todo ello con independencia de la adecuación de la solución presentada.

C. Respuesta dudosa. Se conciben como dudosas, las respuestas que no pueden ser incluidas en las dos categorías anteriores⁷. Este tipo de respuestas, requiere de justificaciones complementarias por el resolutor, pero que por el carácter exploratorio del estudio no se ha solicitado para su análisis.

 

4.2. Análisis e interpretación de resultados: Ámbitos en la comprensión de los significados de la fracción

Los resultados profundizan en los aspectos relativos a la comprensión de la fracción, que se manifiestan en su elección y empleo: la extensión de los conjuntos personales de situaciones de los participantes, a través del análisis de interferencias externas, y la naturaleza del vínculo 'situación–fracción', mediante el estudio de interferencias internas. En los apartados siguientes se describen los casos que consideramos relevantes. Se identifican en cada una de las facetas y se interpretan en términos de la comprensión, siguiendo nuestro modelo.

4.2.1. Interferencia externa: Extensión de los conjuntos personales de situaciones asociados a la fracción

En la tabla II se presenta la frecuencia con que aparecieron las respuestas de los estudiantes a las tareas, atendiendo a la categoría que usamos en su clasificación. Los resultados numéricos muestran que hubo un empleo mayoritario de la fracción sobre otros conocimientos. El establecimiento general del vínculo 'situación–fracción' y el uso preferencial dado a la fracción en situaciones no–exclusivas se interpretan precisamente como acciones favorables que respaldan una valoración preliminar positiva de la comprensión de los participantes en lo referente a la extensión de sus conjuntos personales de situaciones.

La puntuación de la categoría de respuesta interferencia externa, da cuenta de cómo algunos profesores en formación, no logran establecer el vínculo 'situación–fracción' y, por tanto, a reconocer la situación como perteneciente al conjunto genérico de situaciones asociado a la fracción.

Se puede considerar entonces que sus conjuntos personales de situaciones se muestran reducidos en esta parcela fenomenológica, respecto a los de aquellos estudiantes que sí superaron la interferencia externa en la prueba. Esto a su vez, se interpreta como una limitación en la comprensión de la fracción. Un ejemplo de este hecho se presentó en un estudiante de quinto curso, quien no dio muestras suficientes de elección y empleo de la fracción en dos de las seis situaciones planteadas, S3 y S5. Este hecho revela una comprensión reducida en los significados cociente y operador (véase figura 2). En el primer caso, se aprecia que la resolución viene dada mediante la aplicación de otro conocimiento matemático, el algoritmo estándar escrito para la división de números naturales, de uso extendido en el ámbito hispanoamericano. En el segundo, resulta evidente la ausencia de uso de algún significado de la fracción.

Se aprecia que la respuesta del estudiante en S3 alude directamente a la relación entre comprensión y competencia matemática de nuestro modelo. Sin embargo, no evidencia su comprensión de la fracción. Esto se deduce porque no manifiesta que haya identificado la tarea como perteneciente a su esfera fenómeno–epistemológica. Es posible encontrar indicios con respecto al algoritmo señalado previamente. El registro escrito muestra a un estudiante competente⁸ ante la situación propuesta, al momento que decide emplear un procedimiento adecuado a su conveniencia y ajustado a los requerimientos del problema. Desde nuestro modelo se desprende una distinción entre comprensión y competencia matemática, que se fundamenta no tanto en diferencias de carácter funcional, sino más bien en la interpretación referida con este ejemplo.

4.2.2. Interferencia interna: Naturaleza fenómeno–epistemológicos de la fracción de los vínculos

El modelo establece el vínculo 'situación–fracción', que garantiza la superación del fenómeno de interferencia externa. La condición siguiente para la comprensión, establece el empleo de aquel significado de la fracción que le es propio a cada situación. El estudio empírico exhibe que esta condición no siempre se cumple y surge entre los participantes el fenómeno de interferencia interna. Los resultados presentados en la tabla II muestran la presencia de este fenómeno en el desempeño de los estudiantes, en 78 respuestas. Con el fin de ahondar en este tipo de respuestas, en la tabla III se describen con más detalle los diferentes casos de interferencia entre significados de la fracción, junto con las frecuencias absolutas registradas en la prueba. Se identificaron ocho casos diferentes de interferencia interna, producidos entre los significados:

(a) Parte–todo sobre el resto de significados.
(b) Cociente sobre operador.
(c) Razón sobre parte–todo, medida y operador.

En el trabajo de los alumnos se distinguen adicionalmente tres variantes básicas de interferencia interna, en la relación entre posibles iniciativas de uso planteadas en la elección de la fracción:

Variante 1. Integración de los significados interferente(s) e interferido a través de su empleo conjunto y colaborativo en la resolución.

Variante 2. Consideración independiente de distintos significados para su uso en la tarea.

Variante 3. Preferencia no siempre acertada en el uso de unos significados sobre otros. Este caso se concibe como el escenario genuino de conocimientos enfrentados en su elección y reemplazados en su empleo.

En el ejemplo A (véase figura 3) se muestra un caso de interferencia interna de los significados cociente y parte–todo sobre operador. Se recoge de la producción de un alumno de quinto curso, que en su respuesta a la primera pregunta recurre al par de significados operador y cociente en forma colaborativa (variante 1). En su respuesta a la segunda pregunta, recurre al significado parte–todo con independencia de los dos anteriores (variante 2). En el ejemplo B de la misma figura, un estudiante de tercer curso también evidencia una interferencia interna del significado razón sobre operador, solo que en esta ocasión, el primero reemplaza al segundo (variante 3). Variantes como éstas en las acciones de los alumnos revelan matices complementarios en la comprensión de los significados de la fracción, que permanecen ocultos en el análisis tanto de las interferencias externas como de la adecuación en el uso del significado propio en cada situación.

Consideramos que tanto las interferencias internas como las identificadas, constituyen indicadores de primer orden de las particularidades de los posibles vínculos que los participantes establecen (a nivel interno) entre los significados de la fracción ante su utilización. Estas interferencias facilitan la caracterización de la estructura fenómeno–epistemológica de los distintos conjuntos personales de situaciones vinculados a los significados de la fracción. La amplitud y complejidad de la red de interferencias internas entre significados que se manifiestan en cada caso, emergen como criterios fundamentales para valorar la comprensión de los estudiantes y establecer diferencias entre ellos como las expuestas en los ejemplos.

4.2.3. Adecuación del uso del significado propio

Si se parte del supuesto que se ha superado todo tipo de interferencia, la manifestación de la comprensión de la fracción aún exige que su empleo en su significado propio, sea correcto en cada situación dada. El número de respuestas correspondiente a la categoría de empleo propio correcto refleja que esta faceta de comprensión se ha presentado de forma desigual en las distintas situaciones propuestas en la prueba (véase tabla II). Actuaciones como la recogida en la figura 4 ilustran el caso del estudiante que, aun haciendo uso del significado de fracción correspondiente a la tarea, expresa limitaciones de comprensión relativas a la propia naturaleza del significado. En este ejemplo, el empleo propio del significado parte–todo viene acompañado de una confusión acerca del papel que desempeñan y la posición que ocupan la parte y el todo en la representación numérica de la fracción. Se trata en definitiva, del tercer aspecto diferente, exteriorizado en la comprensión de los significados de la fracción.

 

5. CONSIDERACIONES FINALES

En este trabajo se exponen las ideas centrales de un modelo en desarrollo para la interpretación de las acciones de los alumnos en uno de los escenarios básicos de valoración de la comprensión, extendidos en el aula de matemáticas, la resolución escrita individual de situaciones matemáticas. Aun cuando el problema de la interpretación de la comprensión en matemáticas es complejo, nos aproximamos a su estudio desde una perspectiva constituida por un planteamiento teórico operativo y una estrategia metodológica sustentada en el análisis fenómeno–epistemológico. El planteamiento teórico ofrece la posibilidad de sortear algunas fronteras internas de la comprensión. La estrategia metodológica, favorece la obtención de información, la cual garantiza la descripción e interpretación (cercanas a la realidad) de las distintas situaciones cognitivas existentes en los estudiantes.

La evidencia empírica recogida y ejemplificada alrededor de la comprensión de los significados de la fracción, refleja aspectos de la potencialidad descriptiva y prescriptiva del modelo de interpretación sugerido.

Para la práctica docente, el estudio proporciona un método operativo para la organización de situaciones matemáticas así como una referencia objetiva con la que es posible afrontar la interpretación en términos de comprensión de las acciones de los estudiantes. A través de la experiencia sobre los significados de la fracción se dan muestras del uso que podría darse a estas situaciones en el aula de cara a la valoración y al desarrollo de la comprensión del conocimiento matemático en los alumnos. Se revela en consecuencia, el apoyo que a través del modelo puede ofrecerse al profesorado en la toma de decisiones sobre contenidos o formas de enseñanza.

Nuestro interés es continuar trabajando desde nuestra disciplina, hacia el desarrollo de aproximaciones a la comprensión del conocimiento matemático, que incluyan además de aspectos como los presentados, propuestas curriculares sistemáticas que contemplen con un mayor acierto la complejidad global de la comprensión de los conocimientos matemáticos y su inclusión efectiva en los diseños y desarrollos curriculares ordinarios. En este sentido, pensamos que los principios establecidos en esta investigación, para la interpretación de la comprensión en escenarios de valoración se sitúan en un contexto de interés para los estudios recientes sobre enseñanza y aprendizaje de las matemáticas.

 

AGRADECIMIENTOS

Agradecemos las sugerencias que hicieran a este trabajo los miembros del grupo de investigación Pensamiento Numérico y Algebraico de la SEIEM, así como a los revisores anónimos de Relime.

 

REFERENCIAS BIBLIOGRÁFICAS

Ainley, J. & Lowe, A. (1999). Can written questions differentiate between degrees of understanding? Mathematics Teacher 168, 32–35.         [ Links ]

Behr, M., Harel, G., Post, T. & Lesh, R. (1992). Rational number, ratio and proportion. En D. A. Grouws (Ed.) Handbook of Research on Mathematics Teaching and Learning (pp. 233–296). New York: MacMillan Publishing Company.         [ Links ]

Bender, P. (1996). Basic imagery and understandings for mathematical concepts. En C. Alsina, J. M. Álvarez, B. Hodgson, C. Laborde & A. Pérez. 8° Congreso Internacional de Educación Matemática (ICME). Selección de Conferencias (pp. 57–74). Sevilla, España: SAEM Thales.         [ Links ]

Brown, T. (2001). Mathematics Education and Language. Interpreting Hermeneutics and Post–Structuralism. Dordrecht: Kluwer Academic Publishers.         [ Links ]

Byers, V. & Erlwanger, S. (1985). Memory in mathematical understanding. Educational Studies in Mathematics 16, 259–281.         [ Links ]

Carpenter, T. & Lehrer, R. (1999). Teaching and learning mathematics with understanding. En E. Fennema & T.A. Romberg (Eds.) Mathematics classrooms that promote understanding (pp. 19-32). Mahwah, N.J.: Lawrence Erlbaum Associates.         [ Links ]

Carpenter, T., Fennema, E., Fuson, K., Hiebert, J., Human, P., Murray, H., Olivier, A. & Wearne, D. (1999). Learning basic number concepts and skills as problem solving. En E. Fennema & T.A. Romberg (Eds.) Mathematics classrooms that promote understanding (pp. 45–61). Mahwah, N.J.: Lawrence Erlbaum Associates.         [ Links ]

Castro, E., Rico, L. y Romero, I. (1997). Sistemas de representación y aprendizaje de estructuras numéricas. Enseñanza de las Ciencias 15 (3), 361–371.         [ Links ]

Clarke, D. M. & Sukenik, M. (2006). Assessing fraction understanding using task–based interviews. En J. Novotná, H. Moraová, M. Krátká & N. Stehlíková (Eds.). Proceedings 30th Conference of the International Group for the Psychology of Mathematics Education, Vol. 2 (pp. 337–344). Praga: PME.         [ Links ]

Davis, R. B. (1992). Understanding "Understanding". Journal of Mathematical Behavior 11, 225–241.         [ Links ]

Dos Santos, A. (2005). O conceito de fração em seus diferentes significados: Um estudo diagnóstico junto a professores que atuam no encino fundamental. Tesis de Maestría. Sao Paulo, Brasil: Pontificia Universidad Católica de Sao Paulo.         [ Links ]

Duffin, J. M. & Simpson, A. P. (2000). A search for understanding. Journal of Mathematical Behavior 18 (4), 415–427.         [ Links ]

English, L.D. & Halford, G.S. (1995). Mathematics Education: Models and processes. Mahwah, N.J.: Lawrence Erlbaum Associates.         [ Links ]

Escolano, R. y Gairín, J. M. (2005). Modelos de medida para la enseñanza de números racionales en educación primaria. UNIÓN Revista Latinoamericana de Educación Matemática 1, 17–35.         [ Links ]

Freudenthal, H. (1983). Didactical phenomenology of mathematical structures. Dordrecht: Reidel Publishing Company.         [ Links ]

Gairín, J. M. (1998). Sistemas de representación de números racionales positivos. Un estudio con maestros en formación. Tesis de doctorado no publicada, Universidad de Zaragoza, España.         [ Links ]

Gairín, J. M. y Sancho, J. (2002). Números y algoritmos. Madrid: Síntesis.         [ Links ]

Gallardo, J. (2004). Diagnóstico y evaluación de la comprensión del conocimiento matemático. El caso del algoritmo estándar escrito para la multiplicación de números naturales. Tesis de doctorado no publicada, Universidad de Málaga, España.         [ Links ]

Gallardo, J. & González, J. L. (2006a). Assessing understanding in mathematics: steps towards an operative model. For the Learning of Mathematics 26 (2), 10–15.         [ Links ]

Gallardo, J. y González, J. L. (2006b). Una aproximación operativa al diagnóstico y la evaluación de la comprensión del conocimiento matemático. PNA, 1, 1, 21–31.         [ Links ]

Gallardo, J. y González, J. L. (2007a). Fronteras en la investigación sobre comprensión en Educación Matemática. Números, 66.         [ Links ]

Gallardo, J. y González, J. L. (2007b). Diagnóstico y evaluación de la comprensión del conocimiento matemático: el caso del algoritmo estándar para la multiplicación de números naturales. En E. Castro y J. L. Lupiañez (Eds.) Investigaciones en Educación Matemática: Pensamiento numérico (pp. 157–184). Granada: Editorial Universidad de Granada.         [ Links ]

Godino, J. D. (2000). Significado y comprensión de los conceptos matemáticos. Uno 25, 77–87.         [ Links ]

Godino, J. D. (2002). Un enfoque semiótico y ontológico de la cognición matemática. Recherches en Didactique des Mathématiques 22 (2/3), 237–284.         [ Links ]

Godino, J. D. y Batanero, C. (1994). Significado personal e institucional de los objetos matemáticos. Recherches en Didactique des Mathématiques 14 (3), 325–355.         [ Links ]

Goldin, G. (2002). Representation in mathematical learning and problem solving. En L. D. English (Ed.) Handbook of international research in Mathematics Education (pp. 197–218). Mahwah, N. J.: Lawrence Erlbaum Associates.         [ Links ]

González, J. L. y Ortiz. A. (2000). La investigación en Educación Matemática en la Universidad de Málaga: Estructura y fundamentos. En L. C. Contreras, J. Carrillo, N. Climent y M. Sierra (Eds.) Actas del IV Simposio de la Sociedad Española de Investigación en Educación Matemática SEIEM (pp. 131–146). Huelva: Universidad de Huelva.         [ Links ]

Hiebert, J. & Carpenter, T. P. (1992). Learning and teaching with understanding. En D. A. Grouws (Ed.) Handbook of research on mathematics teaching and learning (pp. 65–97). New York: MacMillan Publishing Company.         [ Links ]

Hiebert, J. & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis. En J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 1–27). Hillsdale, N. J.: Lawrence Erlbaum Associates.         [ Links ]

Hiebert, J., Carpenter, T. P., Fennema, E., Fuson, K.C., Wearne, D., Murray, H., Olivier, A. & Human, P. (1997). Making sense: Teaching and learning mathematics with understanding, Portsmouth, N. H.: Heinemann.         [ Links ]

Kieren, T. E. (1976). On the mathematical, cognitive and instructional foundations of rational numbers. In R. Lesh (Ed.), Number and measurement: Papers from a research workshop (pp. 101–144). Columbus, OH: ERIC/SMEAC.         [ Links ]

Kieren, T. (1988). Personal Knowledge of rational numbers: Its intuitive and formal development. En J. Hiebert & M. J. Behr (Eds.) Number concepts and operations in the middle grades (pp. 162–181). Reston, VA: National Council of Teachers of Mathematics.         [ Links ]

Kieren, T. (1993). Rational and fractional numbers: From quotient fields to recursive understanding. En T. P. Carpenter, E. Fennema & T. A. Romberg (Eds.) Rational numbers: An integration of research (pp. 49–84). New Jersey: Lawrence Erlbaum Associates.         [ Links ]

Kieren, T., Pirie, S. & Calvert, L. G. (1999). Growing minds, growing mathematical understanding: mathematical understanding, abstraction and interaction. En L. Burton (Ed.) Learning mathematics: From hierarchies to networks (pp. 209–231). London: Routledge.         [ Links ]

Koyama, M. (2000). A research on the validity and efectiveness of "two–axes process model" of understanding mathematics at elementary school level. En T. Nakahara & M. Koyama (Eds.) Proceedings of the 24th Conference of the International Group for the Psychology of Mathematics Education, Vol. 3 (pp. 159–166). Hiroshima, Japan: PME.         [ Links ]

Lamon, S. J. (2001). Presenting and representing: from fractions to rational numbers. En A.A. Couco y F. R. Curcio (Eds.) The roles of representation on school mathematics (pp. 146–165). Reston, Virginia: National Council of Teachers of Mathematics.         [ Links ]

NCTM (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.         [ Links ]

Niemi, D. (1996). Assessing conceptual understanding in mathematics: Representations, problem solutions, justifications, and explications. The Journal of Educational Research 89 (6), 351–363.         [ Links ]

Pirie, S. & Kieren, T. (1994). Growth in mathematical understanding: how can we characterise it and how can we represent it? Educational Studies in Mathematics 26, 165–190.        [ Links ]

Post, T., Cramer, K., Behr, M., Lesh, R. & Harel, G. (1993). Curriculum implications of research on the learning, teaching and assessing of rational number concepts. En T. P. Carpenter, E. Fennema & T. A. Romberg (Eds.), Rational numbers: An integration of research (pp. 327–361). Hillsdale, NJ: Lawrence Erlbaum Associates.         [ Links ]

Puig, L. (1997). Análisis Fenomenológico. En L. Rico (Coord.) La Educación Matemática en la Enseñanza Secundaria (pp. 61–94). Barcelona: Horsori.         [ Links ]

Quispe, W. (2008). Interferencias en la comprensión de los significados del número racional. Tesis de maestría no publicada, Universidad Nacional de San Antonio Abad del Cusco–CUES, Perú.         [ Links ]

Sierpinska, A. (1994). Understanding in mathematics. London: The Falmer Press.         [ Links ]

Sierpinska, A. (2000). Mathematics classrooms that promote understanding (Book Review). ZDM 2, 45–50.         [ Links ]

Valdemoros, M. (2004). Lenguaje, fracciones y reparto. Revista Latinoamericana de Investigación en Matemática Educativa 7 (3), 235–256.         [ Links ]

Vergnaud, G. (1997). The nature of mathematical concepts. En T. Nunes & P. E. Bryant (Eds.) Learning and teaching mathematics (pp. 5–28). London: Psycology Press, Ltd.         [ Links ]

Warner, L. B., Alcock, L. J., Coppolo, J. & Davis, G. E. (2003). How does flexible mathematical thinking contribute to the growth of understanding? En N. A. Paterman, B. J. Dougherty & J. Zilliox (Eds.) Proceedings of the 27th Conference of the International Group for the Psychology of Mathematics Education, Vol. 4 (pp. 371–378). Honolulu, USA: PME.        [ Links ]

 

NOTAS

¹ Los diferentes escenarios básicos se originan cuando se intenta obtener información sobre la comprensión en fases distintas del proceso de enseñanza y aprendizaje (resolución individual de una tarea, discusión generada en un grupo reducido o las intervenciones durante una explicación de clase). Si bien todos los escenarios comparten elementos comunes, cada uno es específico y diferente a los demás, por lo que se recomienda profundizar en las particularidades de la interpretación de la comprensión en cada uno de ellos.

² En realidad, la actividad interpretativa habitual que se ejerce al tratar con los problemas de enseñanza y aprendizaje de las matemáticas nos sugiere incluso posicionar la interpretación en el núcleo de la discusión sobre los problemas fundamentales de la Matemática Educativa.

³ La noción de conjunto genérico de situaciones adoptada difiere de la de campo conceptual de Vergnaud (1997), por cuanto se aplica a conocimientos matemáticos específicos y se enuncia en términos de posibilidad y no de requerimiento de uso. Por otra parte, la relación de los conjuntos situacionales, personal y genérico se aproxima a la sugerida por Freudenthal (1983) entre objeto mental y concepto o, en términos de Puig (1997), entre campo semántico personal y campo semántico del concepto. Igualmente, el análisis semántico de Niemi (1996) puede identificarse con el análisis epistemológico, mientras que su análisis estructural difiere del análisis fenomenológico de nuestro modelo. Finalmente, a diferencia de la propuesta de Godino y Batanero (1994), la reflexión fenómeno–epistemológica que proponemos no va dirigida a analizar la génesis institucional y personal del conocimiento matemático, sino a determinar conjuntos de situaciones para el diagnóstico y valoración de la comprensión.

⁴ Aquellas que admiten varias posibilidades de resolución mediante el empleo de distintos conocimientos matemáticos, entre los que se encuentra como opción el conocimiento dado en alguno de sus posibles modos de empleo.

⁵ La elección del conocimiento matemático para la resolución de una situación no–exclusiva junto con el posible fenómeno de interferencia a que da lugar constituyen lo se denominó en esta investigación escenario de conocimientos en competencia.

⁶ La interpretación comprensiva implica una exigencia comunicativa entre el estudiante y el agente intérprete de su comprensión. Se articula principalmente, en el escenario de valoración examinado, a través de registros escritos, diálogos directos o una combinación de ambos. Esto trae consigo claras consecuencias metodológicas en lo referente a los instrumentos de recogida de datos a emplear. En este trabajo se optó por el desempeño individual frente a un cuestionario escrito y por el análisis posterior de la información recopilada mediante este método.

⁷ La consideración de esta última categoría de respuestas está justificada y resulta pertinente por las limitaciones propias que presentan las producciones y registros escritos de los escolares cuando se utilizan como fuente para la interpretación de la comprensión matemática (Ainley & Lowe, 1999; Brown, 2001; Gallardo y González, 2007a).

⁸ Tomamos como referencia genérica la idea de competencia matemática como capacidad del individuo para resolver situaciones prácticas cotidianas, utilizando para este fin conceptos y procedimientos matemáticos. El énfasis se sitúa en el proceso y en la actividad, aunque también en los conocimientos. Entre otros aspectos, la competencia matemática entraña, en distintos grados, la capacidad y la voluntad de utilizar modos matemáticos de pensamiento y representación.