Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.11 no.3 Ciudad de México ene. 2008
Artículo
Un estudio socioepistemológico de lo logarítmico: la construcción de una red de modelos
A socioepistemological study of logarithms: the construction of a network of models
Marcela Ferrari* y Rosa María Farfán**
* Unidad Académica Matemáticas, Universidad Autónoma de Guerrero, México, E–mail: marcela_fe@yahoo.com.mx
** Departamento de Matemática Educativa, Centro de Investigación y Estudios Avanzados, Cinvestav, México, E–mail: rfarfan@cinvestav.mx
RESUMEN
Desde una visión socioepistemológica, el entramado de prácticas sociales y representaciones sociales que las mismas generan, establecen un diálogo diferente al discurso escolar imperante. En este reporte, reflexionaremos sobre los argumentos que los alumnos de licenciatura en matemáticas utilizaron, ante la construcción geométrica de las funciones cuadrática y logarítmica utilizando el ambiente de geometría dinámica, para reconocer y describir las funciones mencionadas. Este trabajo se ha desarrollado utilizando la ingeniería didáctica como metodología de investigación por tanto incluimos algunas reflexiones desde el discurso matemático escolar, desde la epistemología de la función logaritmo y un breve estado de arte de estas nociones.
PALABRAS CLAVE: Socioepistemología, curva logarítmica, covariación, geometría dinámica.
ABSTRACT
From a socioepistomological view, the intertwined social practices and self–generated social representations, establish a dialog different from the prevailing school discourse. In this report, we reflect about mathematics majors' argumentations about the geometric construction of the quadratic and logarithm functions using a geometric dynamic system. This work has been developed using the engineering didactic as a research method hence we include some reflections from the mathematical school discourse, from the epistemology of the logarithm function, and a brief state of the art about these notions.
KEY WORDS: Socioepistemology, logarithmic curve, covariation, dynamic geometry.
RESUMO
Do ponto de vista socioepistemológico, a rede de práticas sociais e de representações que as mesmas geram, estabelecem um diálogo distinto do discurso escolar vigente. Neste artigo, reflectiremos sobre os argumentos que os alunos da licenciatura em matemática utilizaram, perante a construção geométrica das funções quadrática e logarítmica utilizando o ambiente de geometria dinâmica, para reconhecer e descrever as funções mencionadas. Este trabalho desenvolveu–se utilizando a engenharia didáctica como metodologia de investigação, portanto incluímos algumas reflexões a partir do discurso matemático escolar, da epistemologia da função logaritmo e um breve estado da arte destas noções.
PALAVRAS CHAVE: Socioepistemologia, curva logarítmica, covariação, geometria dinâmica.
RÉSUMÉ
En adoptant un point de vue socioépistémologique, il est possible de parler d'une trame constituée par les pratiques sociales _et les représentations sociales que ces dernières génèrent_ qui serait à la base d'un dialogue différent du discours éducatif dominant. Dans cet article, notre réflexion portera sur les arguments développés par les étudiants en licence de mathématiques lorsqu'ils abordent la construction géométrique des fonctions quadratiques et logarithmiques et qu'ils se servent de la géométrie dynamique pour les reconnaître et les définir. Ce travail a pour base théorique l'ingénierie didactique en tant que méthode d'investigation, raison pour laquelle nous y incluons certaines réflexions faites à partir d'un discours mathématique éducatif et d'autres à partir de l'épistémologie de la fonction logarithme ainsi qu'un bref état de l'art qui porte sur ces notions.
MOTS–CLÉS: Socioépistémologie, courbe logarithmique, covariation, géométrie dynamique.
1. INTRODUCCIÓN
Se percibe hoy en nuestra disciplina, la Matemática Educativa, un gran desarrollo de investigaciones en torno a la construcción de conocimiento matemático desde una perspectiva social. Algunos, como los socioconstructivistas (Carlson, Oehrtman, & Thompson, 2007; Dubinsky, 2000; Dubinsky & Macdonald, 2003), que la miran desde estructuras mentales, donde la cohesión y la colaboración se entremezclan para dar lugar a la abstracción reflexiva y al fortalecimiento de estructuras. Otros, como los socioculturales (Falcade, Laborde, & Mariotti 2007; Bartolini Bussi, 1998), que dirigen la mirada a los contextos sociohistóricos y temporales donde las herramientas median entre el sujeto y el objeto, imbuidos en prácticas sociales. O aquellos, como los inter accionistas (Krummheuer, 2007; Cobb & Machain, 2003), que se enfocan en la generación de discursos desde la interacción y negociación de significados, donde la relación profesor–estudiante es el foco principal de análisis. O, por último los socioepistemólogos (Cantoral y Farfán, 2004; Cantoral, Farfán, Lezama y Martínez–Sierra, 2006; Cordero, 2005), que reconocen la necesidad de desarrollar investigaciones sistémicas en torno a la construcción social del conocimiento matemático.
Este trabajo surge al seno del grupo de socioepistemólogos preocupados desde hace unos años, por desarrollar un acercamiento teórico que contemple los cuatro polos que conciernen a esta problemática bajo el supuesto que no se puede comprender ni analizar los fenómenos didácticos sin estudiar a fondo el discurso matemático escolar y por tanto cuestionar los mecanismos de su transmisión; sin rever el devenir en objeto a ser enseñando ni la forma en que vive en la escuela, lo que conlleva a cuestionar los contenidos y significados que se proponen en las curricula; sin recabar y analizar las concepciones de los alumnos y docentes respecto a un contenido específico y por tanto sin tomar una postura respecto a qué significa aprender o apropiarse de una noción; por último, sin tener presente que la matemática es una actividad humana, cultural e históricamente determinada.
Bajo esa perspectiva, nos interesa discutir el papel que juegan los argumentos geométricos como detonadores de una red de modelos donde la covariación sea el eje principal en la exploración de algunas funciones estudiadas en Cálculo respecto a la construcción social del conocimiento, tomando cierta distancia de las prácticas escolares que hoy por hoy observamos en los salones de clases.
En general, hablar de función implica entrar en un vasto campo de reportes e ideas, de explicaciones y preguntas, que parece inagotable. Al realizar un estado de arte sobre el tema, uno observa que persiste el distanciamiento entre aquellos investigadores que buscan un único mecanismo de apropiación de la noción de función (Dubinsky & MacDonald, 2003; Carlson, Jacobs, Coe, Larsen & Hsu, 2002, etc.) y, aquellos como Ferrari (2007), Martínez–Sierra (2006) y Montiel (2006), entre otros, que reconocemos la importancia de dar cuenta de las características específicas de las funciones.
Estas dos perspectivas se entrelazan en aquellos reportes que se apoyan en el uso de tecnología, particularmente en aquellos donde se recurre al ambiente de la geometría dinámica. La mayoría de los investigadores confluyen en que las herramientas de Cabri y los signos relacionados permiten un discurso sobre ellos y sobre su comportamiento que da una contribución fundamental a la construcción de la red de significados interconectados que conciernen a la noción de función (Falcade, Mariotti & Laborde, 2004), considerándose además, que en la investigación se toma al uso del software de geometría dinámica (SGD) como instrumento para hacer matemática en senso lato y no sólo geometría (Paola, 2006).
Valdez (2003), por ejemplo, para acercar a los estudiantes a la función cuadrática, propone una actividad en dos etapas. La primera donde el papel del alumno es observar el trazo de una parábola que se genera con el movimiento de un punto por la directriz y vinculado con otro (el foco) mediante una circunferencia; y la segunda, donde se le propone construir la parábola, es decir, reconstruir lo que ha observado mediante cierta guía. Propone entonces que "el alumno visualice la propiedad que define a una parábola [...] para que la transición a la parte algebraica le sea más fácil". Considerando además que "el alumno, auxiliado de sus instrumentos computacionales, construya una versión del conocimiento". Intenta recuperar aquí, la esencia de una cónica donde la distancia entre punto–foco y punto–directriz se mantiene constante utilizando "traza" y "animación" como herramientas.
Por su parte, Dahan (2004) propone utilizar "expresión", "aplicar una expresión" y "lugar geométrico" ya que desde su perspectiva, permiten trabajar simultáneamente los registros simbólico, numérico y gráfico. En este acercamiento interesa poner en juego la variación de las ordenadas de manera global apoyándose en la expresión algebraica de la curva, entre otras las funciones cuadráticas, intentando observar el efecto que produce variar los parámetros con el simple cambio de los valores colocados en la expresión algebraica que gobierna la construcción de la curva.
Para Mariotti, Laborde y Falcalde (2003) en cambio, en ambientes de geometría dinámica la idea de variación puede ser vinculada con el movimiento, de modo que sea posible experimentar la variación en forma de movimiento, ya que los puntos pueden ser arrastrados por la pantalla y representar las variables básicas; incorporando y representando la idea de variación y de dependencia funcional. Consideran además, que de la combinación de observación y acción surge la idea de covariación, que es experimentada por la coordinación entre ojos y manos.
Furinghetti y Paola (2003) por otro lado, intentan escudriñar el razonamiento de los estudiantes observando la transición desde la percepción (observación de figuras en el ambiente SGD) a la teoría, coincidiendo con Santos–Trigo y Espinoza–Pérez (2002) en que la exploración con este tipo de software amplifica el potencial de conjeturas producidas, al mismo tiempo que estimula probar la validación de la producción de las mismas.
Así, un ejemplo de la primera visión sobre función ya mencionada, lo constituye Falcade, et al. (2004) enfocándose en la contribución de la herramienta "traza" en la emergencia de la idea de función como una correspondencia punto por punto en una discusión áulica evidenciando, además, cómo el logro de esta definición matemática es difícil para los estudiantes y cómo el profesor puede utilizar tales potencialidades de la herramienta para lograr este objetivo. Confieren al profesor la tarea de organizar una secuencia de tareas involucrando herramientas para activar y apoyar el proceso de internalización en sus estudiantes. Por otro lado, tiene que orquestar las discusiones para dirigir este proceso hacia la construcción, necesariamente intersubjetiva, de un cierto significado matemático específico que puede ser, a veces, bastante diferente del significado personal de los estudiantes. Por esta razón, en algunos casos, tiene que inducir ciertos cambios conceptuales para ayudar al estudiante a lograr completamente estos procesos.
Por otro lado, varios investigadores se han interesado en el estudio de la covariación como una herramienta para la comprensión tanto de la noción de función (Confrey & Smith, 1995; Confrey y Dennis, 2000; Carlson et al., 2002) como de otros conceptos del Cálculo, tales como: la derivada (Zandieh, 2000), el teorema fundamental del Cálculo (Thompson, 1994) o el concepto de límite (Contrill, Dubinsky, Nichols, Schwingendorf, Thomas & Vidakovic, 1996; Carlson, Larsen & Jacobs, 2001).
Uno de los primeros trabajos reportados en este rumbo es el realizado por Thompson (1994), sobre límite y problemas de acumulación. Del análisis de los resultados recabados se concluye que parece que los estudiantes de cálculo de primer semestre fueron capaces de aplicar efectivamente sus habilidades de razonamiento covariacional en una variedad de contextos. Las imágenes que emergen en estos contextos sugieren que el razonamiento covariacional podría ser, utilizando el término de Tall, una "raíz cognitiva" para comprender y completar tareas específicas para límites y acumulación.
El "razonamiento covariacional" mencionado se define en Carlson, Jacob y Larsen (2001), como las actividades cognitivas involucradas en la coordinación de dos cantidades que varían mientras se atiende a las formas en que cada una de ellas cambia con respecto a la otra. Estos investigadores coinciden con la visión de Saldanha y Thompson (1998) de que las imágenes de covariación son evolutivas y se usa el término "desarrollo" en el sentido de Piaget (1970), para significar que las imágenes de covariación pueden ser definidas por niveles los cuales emergen en una sucesión ordenada.
En opinión de Saldhana y Thompson (1998), la noción de covariación tiene que ver con la imagen mental de dos cantidades calculadas simultáneamente. Describen la comprensión de la covariación como "mantener en la mente, de manera simultánea, una imagen sostenida de dos cantidades" (p. 298). En esta teoría, las imágenes de covariación son vistas como un desarrollo que involucra la coordinación de dos cantidades, es decir, la coordinación continua de ambas cantidades para la misma duración de tiempo
En este sentido, seguimos las ideas de Confrey y Smith (1994, 1995) ya que explican la noción de covariación como aquella que vincula el movimiento entre valores sucesivos de una variable coordinándolo con un movimiento entre los correspondientes valores sucesivos de la otra variable. Consideran también que, en la aproximación covariacional, una función es comprendida como la yuxtaposición de dos secuencias, cada una de las cuales es generada independientemente a través de modelar datos.
Así, en este trabajo nos referiremos a la covariación como la relación entre las variaciones simultáneas de dos cantidades. Nos interesa aquí que se perciba el tipo de crecimiento que sufre cada uno de los elementos que intervienen y aceptar la íntima relación que se establece entre ambos. Tomamos como eje de discusión la función logaritmo, función trascendente cuya naturaleza es muy peculiar y para profundizar su percepción la contrastamos con las funciones polinomiales, en particular, con la función cuadrática.
Nos incorporamos así, a la segunda visión mencionada con otros, como Cantoral y Montiel (2001) o Ferrari y Martínez–Sierra (2003), que miran a la visualización como un mecanismo para la construcción social del conocimiento y por tanto, de formación de significados matemáticos, donde reconocer la naturaleza de cada función es necesario para enriquecer el universo gráfico de los estudiantes, lenguaje que puede discutirse desde las operaciones gráficas.
Desde nuestra visión socioepistemológica, cobran vida varios elementos que han caído en desuso ante cambios de paradigmas; tal es el caso de la irrupción, en el siglo XVIII, del lenguaje algebraico–analítico como soporte del rigor del lenguaje matemático apoyado principalmente por Euler y Cauchy, dejando en segundo plano los modelos geométricos y numéricos. Esta desvinculación de argumentos, que podrían enriquecer el acercamiento a la noción de función, se evidencia también en el discurso matemático escolar actual donde, en la mayoría de los textos de Cálculo, la presentación de elementos gráficos es netamente ostensiva.
2. BRISAS SOBRE EL DISCURSO MATEMÁTICO ESCOLAR ACTUAL
Al analizar la forma de encarar la construcción gráfica dentro del contexto general de libros escolares, fundamentalmente de Álgebra y Cálculo para Bachillerato y Licenciatura, es interesante observar cómo se reafirman las presentaciones ostensivas de ciertas funciones. Se percibe en ellos, una evolución hacia el uso de elementos del lenguaje visual, tanto icónico como gráfico cartesiano. Irrumpen efectivamente una exuberancia de imágenes y colores que los distinguen de los clásicos textos en blanco y negro del siglo pasado.
En general, se reflexiona sobre las gráficas de las funciones en los primeros capítulos ya que, con mayor o menor profusión de acuerdo al autor, se constituyen en un elemento complementario de cada noción presentada, aunque, en realidad, sin ser un argumento de discusión de las mismas, sino, en la mayoría de los casos, como "interpretaciones geométricas" de los conceptos.
En la mayoría de este tipo de textos, se inicia la discusión de cómo graficar funciones mediante el trazado de puntos. La secuencia que establecen para tal fin es:
Paso 1: Obtener las coordenadas de unos cuantos puntos que satisfagan la ecuación.
Paso 2: Construir la gráfica de esos puntos en el plano. Paso 3: Unir los puntos mediante una curva suave.
(Purcell y Varberg, 1993, p. 33)
En las últimas ediciones esta estrategia es extendida con argumentos más globales como "traslación vertical y horizontal" mediante y = f (x) + K o y = f (x + K), además de "reflexión – expansión – contracción" con y = –f (x) o y = cf (x), aunque son poco retomados en el discurso posterior de los textos, quedando confinados en su primer o segundo capítulo.
En general, en cada iniciación al lenguaje gráfico escolar, nos apoyamos en los tres pasos mencionados, que genera total dependencia de la expresión analítica de la función. Efectivamente, conociéndola, podemos construir una tabla de valores, graficar los pares ordenados y luego trazar la curva. Esta dependencia también es fomentada por algunas herramientas tecnológicas como las calculadores graficadoras, o el software Derive, aunque nos permiten explorar exhaustivamente los movimientos mencionados arriba. En los cursos de Cálculo, incorporamos en general, visiones más globales mediante el uso de la primera derivada para establecer si la función crece o decrece, la segunda derivada para prever la concavidad de la misma y a veces, involucramos el estudio de las asíntotas verticales u horizontales.
Sin embargo, cuando les solicitamos a un grupo de estudiantes durante el desarrollo de un curso de Didáctica de las Matemáticas (octavo semestre de Licenciatura) que: grafiquen una función y expliquen cómo la realizaron, sin más detalles con el fin de establecer qué entendían por ese pedido, encontramos que la mayoría se quedaron unos instantes desconcertados, exigiendo datos para realizar esta tarea. Luego de unos minutos, la mayoría optó por graficar una parábola, apareciendo en sus hojas, una expresión algebraica, una tabla, varios puntos graficados y unidos con un trazo continuo.
Iniciamos entonces una discusión grupal preguntándoles: ¿Qué se requiere para graficar funciones?, y nos encontramos con una única respuesta: fórmula –tabla – gráfico, sin eso no podemos graficar, idea que confirma uno de los equipos reproduciendo en el pizarrón su producción. La profesora esboza, al lado del trazo anterior de los estudiantes, una curva representando una función cuadrática similar a la de ellos, la llama f(x) y les solicita: esbocen ahora la gráfica de f(x) + 1. Aparece un nuevo desconcierto, ¿Cuál es la fórmula maestra? o ¿Nos puede dar la tabla de la función? reconfirmando que no han construido una visión global de un modelo gráfico de funciones, y por tanto, tampoco cierta libertad de esbozar una gráfica para discutir alguna idea sin interesar el rigor sobre cómo se grafica, que generalmente transmitimos escolarmente, donde nos preocupamos más porque desarrollen el modelo algebraico y quizás sin detenernos en sus propias necesidades, urgidos por cumplir con el programa de estudios que se nos ha asignado en nuestra institución.
En este sentido, Harel y Lim (2004) reportan un estudio sobre el conocimiento base que los profesores manejan en sus clases, definiéndolo como la interrelación de tres componentes críticos: conocimiento del contenido matemático, conocimiento de la epistemología del estudiante, y conocimiento pedagógico (Shulman, 1986, 1987; Cohen & Ball, 1999, 2000; Harel, 1998, todos citados en Harel & Lim, 2004). Allí, comentan que el profesor observado se enfoca en su propio modo de entender el concepto de función ignorando el de sus estudiantes, donde su estilo de intercambio no genera una discusión libre, sino más bien un intento por entregar su propio conocimiento. Además, parece considerar a las matemáticas escolares como un conjunto fijo de conceptos y procedimientos que pueden ser organizados sistemáticamente en tópicos y subtópicos que deben ser entregados y recordados por los estudiantes. Por tanto, la pregunta de por qué los estudiantes podrían estar interesados en el concepto de función no es parte de las consideraciones epistemológicas o pedagógicas de este profesor ya que considera que sólo la definición del concepto (en el sentido de Tall y Vinner, 1981) es suficiente para que los estudiantes venzan sus dificultades con las funciones.
El análisis que Harel y Lim (2004) presentan en su artículo, nos hace reflexionar sobre cómo la mayoría de los profesores olvidamos que enseñar matemáticas no sólo se trata de transmitir un concepto matemático a nuestra "mejor manera", sino observar la epistemología de nuestros estudiantes y del concepto en sí, de las prácticas escolares establecidas y hasta a veces cristalizadas, que generan un discurso matemático escolar distante de la esencia propia de una práctica discursiva enriquecedora, donde alumnos y profesores desafíen al conocimiento mismo y viceversa.
Esta distancia entre lo que creemos decir en clase y lo que interpretan nuestros estudiantes se observa también en algunas producciones de muchachos de ingreso a la licenciatura cuando se les solicita graficar una función, en este
caso  . Observamos en ellos (ver Figura 1a), el riguroso seguimiento de los pasos enseñados: tabla –puntos – unión... pero con resultados distintos. Ambos muchachos trazan la tabla, pero uno percibe el problema de x = –1 por lo que explora y determina el dominio de la función lo que lo lleva a considerar una asíntota vertical, en tanto que el otro, al tener dificultades para calcular las ordenadas de –1 y –3, evidencia su anclaje a la "unión de los puntos" para trazar la gráfica solicitada.
. Observamos en ellos (ver Figura 1a), el riguroso seguimiento de los pasos enseñados: tabla –puntos – unión... pero con resultados distintos. Ambos muchachos trazan la tabla, pero uno percibe el problema de x = –1 por lo que explora y determina el dominio de la función lo que lo lleva a considerar una asíntota vertical, en tanto que el otro, al tener dificultades para calcular las ordenadas de –1 y –3, evidencia su anclaje a la "unión de los puntos" para trazar la gráfica solicitada.

Este mismo recurso, realizar trazos continuos, aparece en otros reportes de alumnos que exploran con calculadoras graficadoras o Derive, al reproducir con papel y lápiz las imágenes que observan en las pantallas (ver Figura 1b) sobre todo cuando las funciones implican asíntotas verticales en su gráfica, tal es el caso de la función tangente y su valor absoluto.
Nos preguntamos entonces, ¿De qué se apropiaron realmente al repetir estas instrucciones? ¿Cómo generar en los estudiantes una actitud crítica a sus producciones? Pregunta que se intensifica cuando analizamos algunos reportes de muchachos que asisten a un curso de Ecuaciones diferenciales (segundo semestre de Ingeniería) ante la tarea de explorar con Derive los movimientos de ciertas funciones, particularmente la traslación y = f(x) + K y argumentar sus respuestas. La conclusión a la que la mayoría confluye es: sumarle una constante a la función hace que suba o baje; o la función corta al eje y más arriba cuando K es positiva y más abajo cuando K es negativa. Pero no falta la extensión de este argumento al tratar con la función logarítmica, dando evidencia de la no construcción de argumentos que soporten la naturaleza de la misma (Ver Figura 2) al expresar: como se puede ver en la gráfica la función logaritmo tiene un comportamiento similar a la exponencial en cuanto a la forma, también al agregar una constante a la función afecta su desplazamiento sobre el eje y.

Por otro lado, se les solicita que exploren la multiplicación de una función por una constante, es decir y = cf(x), y entreguen un informe explicando sus hallazgos. En las conclusiones parciales, que leemos en sus reportes, algunos estudiantes mencionan "incrementar–decrementar"; otros "estirar o escoger" pero otros sólo perciben el efecto de reflejar sobre el eje x diciendo que "siguen un comportamiento positivo o negativo". En el caso de la función logaritmo, reconocen que utilizar una constante positiva mayor que 1 eleva la curva, en tanto que al ser negativo, la invierte. Sin embargo, al reproducir las gráficas en el papel milimetrado, centran su construcción alrededor del origen, y no del punto (1, 0) (Ver Figura 3a), explicando sus conclusiones diciendo: al multiplicar nuestro lnx por 9, nos muestra como incremento 9 unidades en la gráfica, la cual extiende hacia la derecha de manera positiva, sobre el eje y; como en el caso anterior multiplicamos, ahora nuestro lnx con –9 encontramos una gráfica que tiene un decremento de 9 unidades, extendiéndose sobre el cuarto cuadrante.

Otros cambian la expresión de "incrementar unidades" por "estirar de manera proporcional" ideas tan distantes una de otra, ya que una evoca la suma en tanto que la otra, la multiplicación. Por ejemplo, establecen que: "Al multiplicar una función por un valor real, provoca que ésta, se estire o se encoja según el número por el que se multiplicó de manera proporcional, y si ésta es multiplicada por un número negativo, se obtiene una reflexión respecto al eje de las x, a su gráfica positiva " conclusión asociada a la gráfica b (ver Figura 3b), reforzando nuestra hipótesis sobre la importancia de reconocer la naturaleza de cada función para desarrollar un pensamiento funcional más robusto.
Por su parte, Sánchez (2007) considera que: uno podría fácilmente concluir que, el uso de software en un escenario de instrucción a distancia, influye de manera positiva en el desempeño de las personas involucradas en la resolución de actividades matemáticas, sin embargo, como se puede apreciar en la figura, la influencia que ejercen estas herramientas en las técnicas de resolución, pueden traer como consecuencia concepciones erróneas acerca del objeto matemático analizado. En esta situación, a pesar de que se utiliza la técnica del análisis de casos particulares, el profesor obtiene una conclusión equivocada sobre el efecto que produce el parámetro sobre la gráfica de la función cuadrática (ver Figura 4).

Concluye así, que la incorporación de este tipo de dispositivos facilita la emergencia de nuevas técnicas, pero que no siempre influyen positivamente al construir conceptos matemáticos asociados, evidenciando la relación existente e indisoluble entre las técnicas y los procesos de conceptualización de las matemáticas (Lagrange, 2005, citado en Sánchez, 2007).
Por otro lado, Carlson et al. (2007), consideran que los estudiantes con una visión de acción (Dubinsky & Harel, 1992) a menudo piensan en el gráfico de una función como sólo una curva (o un objeto fijo) en el plano; ellos no ven el gráfico como la definición de un mapeo general de un conjunto de valores de entrada a un conjunto de valores de salida. Así, la ubicación de puntos o la prueba de recta vertical para evaluar funciones sobre un gráfico son sólo conceptos sobre la geometría del gráfico, no sobre un mapeo más general que lo convierte en función. Además, sin una visión generalizada de entradas y salidas, los estudiantes no pueden pensar en una función como un proceso que puede ser invertido para obtener, por ejemplo, la función inversa, siendo limitado sólo comprender tareas como intercambiar x y y resolviéndolo para y o reflejar el gráfico de función a través de la línea y = x. Un estudio reciente con más de 2000 estudiantes de precálculo al final del semestre (Carlson, Oehrtman, & Engelke en prensa) mostró que sólo el 17 % de estos estudiantes determinó correctamente la función inversa para un valor específico, dándoles una tabla de valores de ciertas funciones.
En general, los textos de Cálculo discuten la función inversa desde la simetría geométrica de las funciones respecto a la recta y = x, siendo extendida en la mayoría de los alumnos a otros tipos de simetrías (ver Figura 5a). Ejemplo de ello es el rescate de uno de los argumentos más utilizados escolarmente en un reporte de tres estudiantes, de segundo semestre de Ingeniería Industrial, donde la función exponencial y la función logaritmo aparecen como inversas desde una gráfica simétrica, en tanto que en la segunda exponencial elegida asocian otra exponencial como su inversa (ax  a–x).
a–x).

Aparece la misma idea en el caso de la hipérbola equilátera  al elegir a x como su inversa (x –1
al elegir a x como su inversa (x –1 x) donde establecen que: en este caso la función hiperbólica se transforma mediante la acción de la inversa en la recta que pasa sobre el origen (ver Figura 5b); confundiendo en ambos casos la función inversa con su recíproco.
x) donde establecen que: en este caso la función hiperbólica se transforma mediante la acción de la inversa en la recta que pasa sobre el origen (ver Figura 5b); confundiendo en ambos casos la función inversa con su recíproco.
Estas confusiones tienen su lógica quizás en los distintos sentidos que adoptan las palabras "inversa" y "recíproca" dentro y fuera de las matemáticas.
Efectivamente, la palabra "inversa" aparece en el discurso matemático escolar en distintos momentos como: la "función inversa" que nos remite a aquellas funciones que intercambian su dominio e imagen gracias a que son funciones biyectivas; o como "proporción inversa" que nos informa que mientras un valor crece el otro decrece. Esta confusión se refuerza en otros cursos, tal como en los de Química donde se presenta a los estudiantes la noción de concentración de una disolución como aquello que es directamente proporcional a la cantidad de soluto e inversamente proporcional al volumen de la disolución. Raviolo, Siracusa, Gennari, y Corso (2004), consideran que esta doble dependencia es una de las responsables de las dificultades que tienen los estudiantes al resolver problemas de disoluciones, mencionando además que, en los resultados del estudio de Stavy (1981, citado en Raviolo, et al., 2004, p. 380), los alumnos menores de 14 años, mostraron que la principal dificultad para comprender el concepto de concentración estaba conectada con la dificultad de comprender la función inversa, presentando a ésta como: un incremento en la cantidad de solvente decrece la concentración, dándole así un giro a la definición matemática de la función inversa asociándola al recíproco.
Si exploramos un poco el uso de "recíproco" encontramos que, en lógica, designa a otro teorema cuya hipótesis es la tesis de un primer teorema y cuya tesis es la hipótesis del primero, ¿Intercambio que nos lleva a la inversa? Además, no es necesario ir muy lejos para encontrar este frecuente uso de estas palabras como sinónimos. Por ejemplo, en una de las enciclopedias libres de Internet hallamos la siguiente definición: Sea f una función real biyectiva, cuyo dominio (conjunto de definición) es I y cuyo conjunto imagen es J = f(I). Por ser biyectiva, f admite una función recíproca o inversa, denotada f –1 (Wikipedia: la enciclopedia libre, 20071).
Efectivamente, en matemáticas se escribe A–1(x) como abreviatura de la función inversa de A(x), pero el signo A–1 también significa 1/A, es decir, el recíproco de una función, ya que el (–1) nos anuncia un exponente negativo. Así, ¿La palabra recíproco nos lleva también a "invertir" con el mismo sentido de inverso? Podríamos seguir enumerando ejemplos del entremezcle escolar de estos términos, algunas veces utilizados como sinónimos y otras, como la que nos interesa para los logaritmos, con un sentido distinto, que los alejan. No es extraño entonces, hallar en los estudiantes esta no distinción entre ambas ideas, y observar que no se han apropiado de la noción de función, y particularmente, de lo inverso.
Bayazit y Gray (2004), luego de analizar cómo dos profesores turcos introducen el concepto de función inversa y qué relación se percibe respecto a que los estudiantes no logran construir esta noción como objeto (Dubinsky, 1991), concluyen que el aprendizaje significativo de los estudiantes mejoraría aprovechando una variedad de sistemas representativos apropiados, examinando el concepto con tareas conceptualmente enfocadas y cognoscitivamente provocativas, uniendo la función inversa al concepto de "uno a uno y sobre" de la función así como el concepto de función en sí mismo, y asegurando la participación activa de los estudiantes dentro del proceso de construcción de conocimiento.
Tall (2007) por su parte, reporta que Bayazit (2006) percibe que uno de los profesores turcos, interpreta las dificultades de los estudiantes con la función inversa como un indicador de su inhabilidad de moverse hacia adelante y hacia atrás entre los elementos de dominio y co–dominio sin perder de vista la condición "uno a uno y sobre". Parecería que su deseo del éxito anuló sus concepciones más profundas de proporcionar una práctica de enseñanza orientada por la acción en la cual las dificultades de sus estudiantes e ideas falsas quedan al margen, reforzándose reglas y procedimientos que conducirían al éxito en los tipos de problema que aparecen en exámenes.
Así, para Tall (2007), existen dos cuestiones importantes: el hecho de tomar en cuenta las ideas que han encontrado los estudiantes en su aprendizaje cotidiano, y ayudarlos a enfocar aquellas ideas esenciales como base de un pensamiento más sutil. Le interesa entonces, hablar de "la compresión de conocimiento" (Thurston, 1990) refiriéndose al cambio de un proceso que ocurre en el tiempo (como la adición) a un concepto que puede ser pensado como una entidad mental; donde a este empleo dual de un símbolo como proceso y concepto le llama procepto (Gray & Tall, 1994). Así, el estudio de procedimientos eficientes para hacer matemáticas es una parte importante del aprendizaje, pero a largo plazo, es esencial comprimir el conocimiento en los conceptos imaginables que trabajarán de modo más sofisticado. Esto sugiere que los profesores tengan que actuar como mentores para racionalizar el empleo de ideas que los estudiantes han encontrado antes y animarlos para comprimir el conocimiento en ideas poderosas unidas de manera coherente.
Efectivamente, no es posible hablar de la matemática escolar, sin reflexionar sobre el papel que el profesor, indiscutible iniciador del diálogo respecto a la noción en turno marcada por el programa que la institución le proporciona al inicio del semestre, juega en este micromundo generado por los alumnos, en espera de la instrucción que socialmente se ha determinado para insertarse en el mundo laboral, en encajar en un mundo que a veces nos rechaza por no cumplir con los cánones clásicos respecto a lo que significa tener éxito escolarmente. Entran en juego allí, las representaciones sociales que construimos y nos construyen como profesores, como alumnos, como institución. Justamente, analizar la problemática que la apropiación que la función logaritmo genera en las aulas, nos permite discutir varios aspectos. Aquellos que consideran que se requiere que el alumno construya al menos, una visión de proceso de la función fomentando la formación de una visión de objeto (Dubinsky, Weller, Clark, Loch, McDonald, & Merkovsky, 2000), o aquellos que piensan que desarrollar un razonamiento covariacional les permitirá construir una visión más integral de las funciones (Carlson, et al. 2007) donde proponer actividades cognitivamente provocativas sean el medio para logarlo.
Otros (Falcade et al., 2007) en cambio, proponen recuperar la idea de movimiento como generador de los primeros pasos hacia la formalización del concepto de función que hoy conocemos, donde el SGD sea una herramienta importante para disminuir la distancia entre las concepciones de los estudiantes y el concepto de función.
La mayoría acepta la necesidad de proponer actividades que involucren distintos registros, soportados o no por la tecnología, pero recayendo en la imperiosa idea de que los estudiantes reconozcan la dependencia entre variaciones, ya sea desde la posibilidad de adoptar una visión de "entrada–salida" (Carlson, et al., 2007) o de arrastrar un punto para observar la traza que deja en la pantalla como evidencia de la covariación puesta en juego (Falcade et al., 2007). Acercamientos que reflexionan globalmente sobre la noción de función, en búsqueda de lograr que los alumnos desarrollen un pensamiento funcional aplicable a distintos modelos. Sin embargo, el análisis que presentamos en esta sección sobre los argumentos que utilizan los estudiantes cuando les solicitamos que exploren gráficamente ciertas funciones, involucrando distintas operaciones (suma de una constante, expansión, compresión, inversión, recíproco, entre otras), evidencia una problemática importante, ¿Qué sucede con la función logaritmo? ¿Por qué los criterios aplicados a las polinomiales parecen no ser útiles para las trascendentes? ¿Por qué nuestros alumnos no perciben esto? ¿Por qué ni siquiera se lo cuestionan?
En los ejemplos presentados sobre las construcciones con que los alumnos expresan su imaginario gráfico, escolarmente guiado, observamos que genera un ambiente de discusión rico y amplio ya que las primeras percepciones o transmisión de sus entendimientos nos permiten abordar con mayor profundidad lo que el lenguaje algebraico y numérico nos proporciona. El arraigo de reproducir literalmente sentencias escolares o la ausencia de una visión crítica nos evidencian un pensamiento funcional alejado de la posibilidad de reconocer funciones desde sus particularidades, mismas que anuncian su naturaleza. De cierta manera, nos advierte sobre la necesidad de extender argumentos que siendo útiles para algunas funciones se convierten en obstáculos para otras, permitiéndonos así rever nuestra interpretación inicial y por tanto, profundizar nuestro conocimiento de la función estudiada.
3. BRISAS EPISTEMOLÓGICAS SOBRE CIERTAS CURVAS
Al pensar en todos los elementos que han tenido que entre mezclarse desde la antigüedad, elementos que hallamos en reportes epistemológicos o en originales, observamos que confluir en lo que hoy llamamos curva, y más particularmente función, está muy ligado a la modelación del movimiento tanto en el lenguaje de los físicos como de los matemáticos. Para ambos no es extraño basar sus explicaciones en la covariación de progresiones, ya sean aritméticas o geométricas; elementos que tomaremos como eje de nuestra discusión hacia lo logarítmico.

En esta sección, intentaremos seguir la pista de varios científicos interesados en la descripción del movimiento de los cuerpos, preocupación percibida ya en Aristóteles (384–322 a.C.) considerado como uno de los más influyentes filósofos griegos, que advirtió una tendencia a desviar la filosofía hacia la formalización matemática. Sin ser exhaustivos, comentaremos algunos aportes de Oresme, Bradwardine, Galileo, Newton y Huyens para dar evidencia de la importancia que ha jugado el lenguaje matemático en sus producciones. Paralelamente a esta línea se desarrollan elementos geométricos que configuran las curvas en un estadio inicial estático, contemporáneo del pensamiento aristotélico pero que se despegaría hacia el reconocimiento de las variaciones y por ende de covariaciones con la emergencia de la geometría analítica, mencionaremos aquí a Stiffer, Descartes, Napier, Agnesi y Euler como baluartes del desarrollo del lenguaje matemático.
Este entretejido sutil que surge entre científicos preocupados por utilizar el lenguaje matemático para describir fenómenos de la naturaleza y aquellos que se sienten desafiados por crear herramientas matemáticas que permitan realizar tal tarea cae a veces en una visión reduccionista en aquellos que intentan marcar un límite entre el pensamiento físico y el matemático. En nuestro acercamiento socioepistemológico, no buscamos determinar estas limitantes sobre el descubrimiento de un objeto sino justamente dilucidar aquellas prácticas sociales que modelan estas visiones generando representaciones sociales y herramientas dando cabida a la construcción del conocimiento.
Hablamos entonces de prácticas sociales como generadoras de herramientas y representaciones sociales, que nos permitan generar conocimiento y construirnos modificándolas y modificándonos. Hablamos de práctica de referencia, como reflejo de usos y contextos, de ámbitos en donde se desarrollan y nos desarrollamos. Y, por último, hablamos de prácticas discursivas, como generadores de argumentos y significados. La posibilidad de entremezclarlos, donde unas prácticas contienen a otras, se autocontienen, y son contenidas, donde no nos interesa conocer donde inician o donde terminan, sino que sólo nos interesa reflejarlas en nuestros diseños en búsqueda de que lo logarítmico surja de y con ellas. Se requiere entonces, que los logaritmos sean usados, formulados y teorizados para construirse y existir.
Para Piaget y García (1996) lo que interesa en un estudio epistemológico es la detección de los mecanismos que entran en juego cada vez que se produce el pasaje de una etapa a otra en la evolución de los conceptos y de las teorías. De iniciar este rastreo de ideas, iniciaríamos con la física de Aristóteles ya que desempeña un papel de primordial importancia durante la AntigFedad clásica y todo el medioevo; cambiando visiones al incentivar a sus discípulos no sólo a cultivar la observación, sino que también a coleccionar materiales para apoyar el método inductivo que desarrollaban en sus investigaciones.
Aristóteles rompe así, con el universo ideal platónico y admite conocer el mundo sobre la base de la experiencia y de la razón. Inicia entonces, la búsqueda por entender el medio en el que vivimos y los fenómenos que en él se desarrollan. Su metodología se reduce a cierto número de observaciones inmediatas, percibiendo sólo dos movimientos naturales simples: el circular que "es el movimiento que gira alrededor del centro (del universo)"; y el movimiento en línea recta que es "el que se dirige hacia arriba o hacia abajo"... El movimiento circular es perfecto, mientras que la línea recta no lo es (ibidem).
Surge así, una manera de hablar científicamente de una necesidad humana, la de predecir, práctica social que encuentra desde el inicio de la humanidad diferentes maneras de desarrollarse en ámbitos específicos tales como el movimiento (Cantoral, 2001), lo periódico (Buendía y Cordero, 2005) o lo sinusoidal (Montiel, 2006) generando distintas herramientas vinculadas con las prácticas de referencia estudiadas. Sin embargo, como el eje de nuestro estudio es lo logarítmico, hemos centrado nuestra mirada a dos actividades, las de facilitar cálculo y modelar, que por sí mismas las caracterizamos como prácticas sociales por generar representaciones sociales (Jodelet, 1986) particulares así como herramientas generales, modificándose a su vez.
Incursionamos así en ciertos argumentos donde se pueden distinguir tres tipos de transformaciones asociados a la construcción de lo logarítmico: procesos de sociogénesis, que tienen que ver con la construcción y transformación de objetos específicos en ciertas comunidades específicas, de ontogénesis, relacionados con el desarrollo de los individuos en relación con las prácticas y de microgénesis, relacionados con la evocación de las prácticas en la interacción social (Duveen y Lloyd, 1990). Coincidimos además, con Moscovici (1984 citado en Castorina, 2003) quien comparte la base epistemológica de Piaget y otros constructivistas ya que considera al sujeto y al objeto de conocimiento como correlativos y co–constitutivos pero rechaza la idea de que esos términos designen entidades independientes. El corolario ontológico de esta postura es que las representaciones sociales forman parte de las realidades representadas y que en esta construcción se confiere el contenido de lo que se construye la misma significación que al proceso de construcción.
Consideramos así que estas prácticas se entremezclan y distancian en el derrotero de los logaritmos, pues una, en búsqueda de artefactos para facilitar la multiplicación y por tanto apoyar al desarrollo de la astronomía o la economía, encausa la discusión hacia la relación entre dos progresiones una geométrica y la otra aritmética, que nos lleva a multiplicar sumando. En tanto que la otra, dirige los esfuerzos hacia modelar fenómenos de la naturaleza tales como la caída de cuerpos, cuadrar curvas u otras cuestiones dentro de las matemáticas pero bajo la misma relación, la covariación de las progresiones mencionadas.
A manera de síntesis de los principales argumentos que han estado presentes en la construcción de lo logarítmico generando una red de significados, rescatamos sucintamente aquellos que consideramos confluyen en el diseño de nuestra exploración con estudiantes. Tomamos tres etapas: 1) los primeros esbozos del estudio del movimiento, donde se enlazan las reflexiones variacionales aristotélicas con las exploraciones numéricas de Arquímedes, enriqueciéndose más adelante con las representaciones de Oresme y Bradwardine así como la discusión que proponen respecto al estudio del movimiento de cuerpos en el espacio mediante el uso de progresiones; 2) exploraciones logarítmicas en dos ámbitos, el físico (los aportes de Newton y Huygens al estudiar la caída de cuerpos en un fluido) y el matemático (mediante el estudio de la obra de Napier, Briggs, Debeaun y Leibnitz) que recogen las ideas anteriores y donde lo numérico y lo geométrico encuentran un marco algebraico que los fortalece; y, 3) irrupción en variaciones infinitesimales que abre la posibilidad de resignificar la naturaleza de los logaritmos (donde nos apoyamos en los trabajos de Agnesi, Saint Vincent y Euler principalmente).
4. ORIENTACIONES PARA EL DISEÑO
Luego de reflexionar sobre los argumentos que apoyaron el desarrollo y consolidación de la idea de logaritmos como función, varios de ellos fuera del lenguaje matemático que hoy utilizamos y otros, directamente involucrados a la génesis del mismo que llevaran a la gestación de función en sí, buscamos evidenciar que lo numérico, lo gráfico y lo algebraico como red de modelos entremezclados con las prácticas de referencia y sociales nos crean un ámbito de argumentación y por ende de construcción de un discurso alrededor de lo logarítmico.

Los argumentos gráficos que estamos explorando surgen de las ideas de Agnesi (1748), utilizar la semejanza de triángulos para evidenciar la naturaleza de ciertas funciones. Sin embargo, no es éste el único argumento que nos interesa utilizar. Efectivamente, el uso de la semejanza de triángulos se fundamenta en la coordinación de dos patrones de crecimiento, regidos por progresiones aritméticas y geométricas. Si tomamos como argumento la covariación entre dos progresiones aritméticas, donde el carácter variacional está regido por la diferencia, estamos hablando de las funciones polinomiales, las lineales en primera instancia y al extender el argumento a la diferencia de ordenadas (primera, segunda, etc.) estamos hablando de funciones cuadráticas, cúbicas, etc. Si en cambio lo hacemos entre una progresión aritmética y otra geométrica, donde el carácter variacional está regido por la razón, nos abocamos a explorar funciones trascendentes, particularmente la exponencial y logarítmica ya que las trigonométricas no siguen este patrón.
En el caso de este estudio, nos abocamos a discutir con los muchachos de licenciatura dos funciones particulares, las que llamaremos curva cuadrática y curva logarítmica, involucrando a la geometría dinámica como herramienta técnica. Cada manera de construir se basa en el trazo de triángulos semejantes, su diferencia radica en el movimiento que se le imprime al punto de inicio de la construcción, así como en la partición de los ejes involucrados que depende del tipo de progresión que se convoque (Ver Anexo).
¿Qué nos interesa entonces? Percibir mediante la construcción mecánica de las curvas su naturaleza, es decir, reconocer las progresiones que se involucran en cada una al identificar patrones generados por distintos tipos de triángulos que surgen al trazar semirrectas con cierta inclinación y entrelazarlas con verticales u horizontales dependiendo de la curva. Pero fundamentalmente, la covariación entre ambos.
Iniciamos entonces las actividades diseñadas con la construcción geométrica de las curvas manipulándolas desde la elección de las coordenadas de los tres vértices del triángulo inicial, dirigiendo el desarrollo de ideas mediante preguntas como: ¿Cómo construirías más puntos? ¿Cuáles son los patrones de crecimiento de abscisas y ordenadas? ¿Cómo determinarías cualquier punto de la curva?, entre otras, solicitando que expliquen cada una de sus respuestas con más de un argumento. Así, partimos de la idea de que es necesaria la construcción de una red de modelos, donde lo geométrico, lo numérico y lo algebraico, generen la plataforma que les permita, a los estudiantes y profesores, hablar de lo logarítmico.
Luego del análisis preliminar, que hemos bosquejado en los puntos anteriores, decidimos involucrar al SGD como disparador de la construcción de la red de modelos que deseamos que los estudiantes aborden. A diferencia de otros diseños realizados para acercar a los alumnos a la noción de función (Valdez, 2003; Dahan, 2004 o Falcade et al., 2007) recurriendo al movimiento que propicia Cabri mediante la herramienta "traza", nos refugiamos en él para la construcción de dos curvas a partir del trazo de un triángulo inicial que las determina. Trazando rectas y respetando la partición de los ejes propuesta, los estudiantes van introduciéndose en un mundo de puntos y variaciones, de crecimientos y semejanzas, de curvas y covariaciones, que los llevan a salirse del ambiente geométrico para discutir sus primeras ideas.
Proponerles iniciar las exploraciones con la curva cuadrática se debe a que escolarmente han tenido un acercamiento a ella desde los últimos cursos de secundaria (13–15 años), y ha sido retomada en bachillerato y licenciatura. No es raro entonces, observar que la reconocen desde los primeros puntos que trazan en Cabri, ya que el crecimiento de las ordenadas gracias a la gestión de crecimientos de las abscisas, permiten visualizar la curva. Aquí les funcionarán varios argumentos, se sentirán más confiados, elemento que se debilitará al incursionar en la segunda actividad matemática, la curva logarítmica. El traspaso de argumentos que han sido aliados de sus explicaciones para la función cuadrática será frecuente hacia la segunda actividad, ya que percibirán a la nueva curva como una parábola acostada. Esperamos que al explorarla, noten las diferencias y reconozcan en ella a la función logaritmo sorprendiéndose de la covariación que el diseño pone en juego, esa relación entre una progresión geométrica (en el dominio) y una aritmética (en la imagen). Deseamos que a su vez, se desprendan del ambiente que el SGD propone ya que en él se pueden determinar las coordenadas de los puntos construidos así como la expresión analítica de las cónicas sin necesidad de introducirlas. Justamente esa limitación, no poder trazar funciones sin contar con la expresión analítica de las mismas que herramientas como "traza", "lugar" o "aplicar una expresión" requieren, obligará a los estudiantes a buscar otros argumentos para hacerlo, robusteciendo así la red de modelos que irán construyendo.
Para la exploración, escogimos estudiantes de séptimo y octavo semestre de Licenciatura en Matemáticas, área Matemática Educativa, por haber sido sometidos a la instrucción escolar de estas funciones y que habían demostrado cierta fragilidad en la apropiación de las mismas. Nos interesa observar el tránsito entre modelos, analizando los argumentos que esbozan al responder las preguntas propuestas en el diseño. Encontramos una interesante creatividad entremezclada con una fragilidad argumentativa que nos dan pautas para el análisis de la red de modelos que generan al explorar las curvas que les presentamos.
Para reportar las producciones de estos muchachos decidimos presentarlos bajo el título "Caso" siendo los dos primeros las producciones de los estudiantes de octavo semestre que luego de realizar su reporte en clase fueron invitados a discutir sus respuestas en una entrevista que fuera videograbada. Además, gracias a su participación rediseñamos algunas de las preguntas propuestas y que generaran nuevas exploraciones.
Los siguientes casos, corresponden a las actividades realizadas en clase con nueve alumnos de séptimo semestre y que fueran discutidas con todo el grupo y registradas utilizando la observación participante, notas de campo, y los informes escritos de las exploraciones que habían realizado durante la semana asignada para ello y que, cada equipo de trabajo, entregara al final de la experiencia presentándolos a sus compañeros utilizando power point.
5. PRODUCCIONES DE LOS ALUMNOS
5. 1. Caso 1: Exploración de la función cuadrática
Una estudiante de octavo semestre, es entrevistada un par de días después de haber resuelto en clase la primera actividad de aprendizaje con varias debilidades en su argumentación. Durante la sesión, demuestra cierta destreza para construir la curva y sin gran dificultad traza varios puntos de la curva dentro del triángulo inicial OAB (Ver Figura 6a). El argumento que utiliza para explicar su construcción fue la proporcionalidad. Abstrajo que la construcción que se proponía se basaba en puntos medios (así determinó los cuatro puntos solicitados en OA y los cuatro sobre AB siguiendo el diseño) y vuelve a hacerlo para determinar los puntos que llama Q, R, S, y T.

Más adelante se le pregunta si podría extender la curva, es decir, determinar algunos puntos fuera del triángulo OAB y, luego de reflexionar unos minutos, contesta: "Si, se puede. Es que los puntos van creciendo exponencialmente y eso continuaría infinitamente. Se trata de una parábola ¿No?" Acompaña esta afirmación recorriendo con el dedo los puntos determinados e indica cómo seguiría la curva.
Sin embargo, no logra determinar las coordenadas de estos puntos utilizando argumentos geométricos, sólo los determina utilizando la herramienta "coord. o ecuación". Traslada estas coordenadas a la tabla que propone la actividad siguiente y rellena las columnas de las diferencias sin encontrar ningún patrón de crecimiento debido al redondeo que propone Cabri. Escribe allí: "los puntos encontrados en la parábola crecen exponencialmente en forma irregular". Se le pregunta inmediatamente por qué cree que el crecimiento es exponencial, ¿A qué te refieres con eso? A lo que contesta: "crece rápido", "proporcionalmente" sin realmente argumentar su comentario anterior.
No reflexiona sobre la precisión de los valores determinados con Cabri y no le llama la atención esa "irregularidad" de la columna de AAy donde debería haber encontrado una constante. Se le cuestiona entonces, sobre cómo determinar si esos puntos pertenecen o no a la curva que se está construyendo y, traza entonces la curva utilizando la herramienta "cónica" que une los puntos con lo que queda satisfecha de su respuesta y responde que cualquier punto puede ser determinado trazando verticales hasta que corte a la curva.
Aprovechando esta idea de que "se puede extender", se le solicita que construya al menos un punto fuera del triángulo OAB pero sin trazar la curva. Luego de varios intentos y minutos de reflexión, decide que se deben trazar puntos medios, repetir la construcción anterior. Marca el punto (12, 0) para repetir la estrategia utilizada en OA. Pero antes de concretarlo, prefiere trazar una circunferencia con centro en A y radio EA, con lo cual determina la primera abscisa fuera del triángulo OAB sobre el que trabajará (Ver Figura 6b) para mantener el patrón inicial de crecimiento de las abscisas que se solicita en la actividad. Inmediatamente después traza una vertical por ese punto y comienza a evidenciar problemas para continuar con la construcción. Observa que no tiene elementos para trazar puntos medios e intenta determinar "otro B para arriba" es decir, determinar otros puntos a la misma distancia que los que había construido. Sin embargo, tampoco lo concreta y decide trazar una semirrecta desde O, pasando por B estableciendo que el punto de intersección entre esta semirrecta y la vertical trazada era el punto buscado. No logra entonces visualizar que puede utilizar el mismo argumento que había usado para determinar la abscisa, pero ahora sobre una vertical.
Se le solicita que argumente su respuesta, y rápidamente observa que ese punto no puede pertenecer a la curva que se está construyendo, que "debería estar más arriba". La entrevistadora le solicita que le explique lo que hizo para determinar la vertical, y ante su reflexión abstrae que puede repetirlo utilizando el punto B, destrabándose así la construcción de este punto. Termina la sesión con una discusión sobre la tabla de coordenadas y las diferencias (primera y segunda) cuyos resultados le sorprenden al determinarlas con mayor precisión: "no sabía que las segundas diferencias son una constante", "primera vez que lo veo". Estas expresiones dieron pauta de la pobreza de argumentos y del uso de modelos así como de la dificultad que evidencia para integrarlos, elementos presentes en algunos de los muchachos debido a lo que han construido en su formación escolar.
En la interacción con esta alumna, se percibe la timidez de equivocarse en sus respuestas perdiendo así la posibilidad de discutir abiertamente sobre la naturaleza de esta función agravada un poco por su resistencia a pasar de un modelo a otro ya que le desconcierta no conocer la expresión analítica. Analizando sus comentarios (escritos como orales) y sus gestos, observamos la complejidad de construir una visión global de la función cuadrática al no lograr abstraerse de la información que Cabri le ofrece. Tímidamente argumenta sobre cómo extender la construcción geométrica pero no tiende lazos hacia otros modelos, es decir, opta por no apoyarse, por ejemplo, en el modelo numérico, o quizás en éste para determinar el modelo algebraico dándonos la pauta de su desinterés por armar su propia red de modelos proveniente de no sensibilizarse de ciertas ideas covariacionales.
5.2. Caso 2: Exploración de la función logarítmica
Luego de analizar el informe entregado por dos estudiantes de octavo semestre donde se observa que construyen geométricamente algunos puntos de la curva; rellenan la tabla de valores de una manera muy particular utilizando "coord. o ecuación" y trazan una curva mediante "cónica" (Ver Figura 7), se les invita a reflexionar sobre las coordenadas de los puntos de la curva que han trazado, evidenciando en los siguientes diálogos escogidos el papel que juega el ambiente SDG en los argumentos de estos alumnos.

Entrevistador: A ver... explíquenme cómo determinaron estos puntos (indicando la pantalla)
Estudiante 1: Ahí, viéndolo... 2–1 de este lado (marcando en la pantalla los puntos de la rejilla)
Estudiante 2: ¿El A?, no el A es 2–0....
Estudiante 1: 2–1
Estudiante 2: El M 2–1, y el N 4–2
Estudiante 1: 8–4 (marcando con el cursor cada punto que mencionan)
Estudiante 2: 8–3 ¿No?
Estudiante 1: 8... mmmm.... a pues si... sería 4–16
Estudiante 2: Si, sería 16–4
Entrevistador: Mmm entonces las determinaron por observación ¿No?
Estudiante 1: Si, si la vista no nos engaña.. jajá...
Entrevistador: Bueno, pero convénzanme que son ésas las coordenadas...
Estudiante 2: Pues con las coordenadas, la herramienta del Cabri... Cabri nos las dice.
Estudiante 1: Y con los puntos de la rejilla, coinciden con ellos. . .
Vemos que aceptan acríticamente las coordenadas que determina este ambiente geométrico, actitud que se encuentra en la mayoría de los estudiantes participantes de esta investigación. Por otro lado, al solicitarles que construyan más puntos de la curva preguntándoles si se podría hacerlo, comentan:
Estudiantes: Si...
Entrevistador: ¿Cómo?
Estudiante 2: Y... siguiendo el.... mmmm... siguiendo el mismo... eh... procedimiento que llevábamos...
Entrevistador: ... Aja... ¿Y cómo sería?
Estudiante 2: ... Mmmm...
Entrevistador: Con las rectas horizontales y las semirrectas... y encontraríamos puntos en sus intersecciones...
Estudiante 2: Bueno, se puede encontrar una formulita...
Estudiante 1: Se ve que x sería el cuadrado de 2; 2 – 4 – 8 – 16
Estudiante 2: Y 1 2 3... y van siguiendo la secuencia.
Entrevistador: Si miramos la tabla que hicieron... ¿Cómo se movería esta tabla? ¿Cómo varían las abscisas y cómo las ordenadas?
Estudiante 2: ... mmmm
Estudiante 1: Una va con el orden de los números naturales... (Indica con el dedo las ys)
Entrevistador: En las y.. ¿Y en las xs?
Estudiante 1: En la x?... 2 al cuadrado...
Entrevistador: ¿2 al cuadrado?...
Estudiante 2: Del 2 si... para el primero...
Estudiante 1: No... espera...
Estudiante 2: 2x2 es 4
Estudiante 1: No sería cuadrado... mmmm... sería 2 por n
Entrevistador: Y el n... ¿Quién es?... ¿Qué sería n?
Se les da una hoja y se les invita a discutir la siguiente afirmación: "la tabla sólo puede tomar valores a la derecha del cero, es decir, x > 1. El patrón de crecimiento es múltiplo de cada punto, (2x) para las abscisas y para las ordenadas va aumentando 1 a partir del cero, pues las rectas horizontales que intersectan a la parábola toman valores enteros consecutivos en el eje 'y'" argumento con el cual intentaban describir la función en su informe inicial.
Luego de varios minutos de exploración donde los muchachos discuten numéricamente la tabla recurriendo varias veces a la gráfica esbozada en la pantalla, surge el siguiente diálogo:
Estudiante 2: 2x2 ... mmm... en x no?
Estudiante 1: Es el doble de uno... el doble de otro...
Entrevistador: ¿Por qué empezaron en el 1–0?
Estudiante 1: ¿En los negativos?
Entrevistador: ¿Por qué no escribieron nada aquí? (señalando la tabla del informe entregado) leamos lo que escribieron...
Estudiante 2: Porque se salen de la curva que estamos construyendo, pues a menos que 1... al parecer no están en la curva... (Afirma esto mirando la curva trazada, ver Figura 8)

Entrevistador: ¿Podemos sólo extender la curva hacia la derecha?
Estudiante 1: Si...
Entrevistador: ¿Qué pasaría con el punto B? ¿Pertenece a la curva?
Estudiante 1: ... (0, B) no pertenece a la curva porque la parábola tiene vértice (A,0) y no toca el eje "y"
Respuesta que argumentan desde la curva que habían trazado utilizando la herramienta "cónica" de Cabri que une, con una hipérbola, los cinco puntos que geométricamente habían construido. Al solicitarles que construyan geométricamente más puntos de la curva entre A y B, visualizan que la curva trazada se aleja de los puntos de la curva construida percibiendo que se trata de una función logarítmica (Ver Figura 8) que, luego de arduos trabajos numéricos logran descifrar que se trataba de la función y = log2 x.
En este caso se observó cierta apatía en la resolución, priorizaron aquí a las respuestas inmediatas que Cabri proponía de acuerdo a las herramientas gestionadas y sin cuestionarse más allá. Fue necesario confrontarlos con sus propias respuestas para lograr cierto desequilibrio y duda en lo que hacían, lo cual resultó muy fructífero para ellos pues sorprenderse de que se trataba de una función logarítmica, muy diferente a la cónica que proponía Cabri para ajustar una curva a los puntos construidos geométricamente, generó sonrisas y cierta satisfacción por discutirle a una herramienta técnica. Presentan un intermitente acercamiento a ideas covariacionales, apoyándose fundamentalmente en dos modelos, el numérico y el algebraico para describir la curva en tanto que el modelo geométrico se convirtió en el modo de comprobar lo que establecían.
5.3. Caso 3: Las producciones de Luís
Una pareja de estudiantes (Luís y Nadia) constituyen un interesante equipo de trabajo ya que mientras uno decide explorar la primera actividad numéricamente, el otro se queda observando la construcción geométrica, generando diferentes maneras de discutir la construcción de la curva propuesta. A diferencia de los otros equipos de trabajo, ellos no advierten inmediatamente que se trata de una función cuadrática. En su discusión se escucha que:
Luís: Es una cónica
Nadia: No, me parece que es una exponencial, algo así como dos a la x
Luís: No, no lo creo
Nadia, pese a haber completado la tabla de coordenadas, observando que se halla una constante en la segunda diferencia de las ordenadas, y ser capaz de extender la tabla numéricamente, no percibe que son argumentos que nos hablan de una cuadrática. Le solicita a su compañero que trace los segmentos que unan los puntos construidos para ver si pueden descubrir la curva que se está construyendo. Luís lo hace, y como no pueden deducir la curva, deciden seguir construyendo más puntos para acortar los segmentos y "observar mejor" la curva que se está formando.
Entre ambos siguen construyendo más puntos, se detienen al encontrar la clásica partición escolar de x de una unidad. Determinan, mediante la herramienta "Coordenadas y ecuación", las coordenadas de todos los puntos construidos. Reconstruyen la tabla y las diferencias de las ordenadas y perciben que la segunda diferencia no es constante, como había ocurrido con la primera partición. Pese a que el entrevistador les sugiere que verifiquen las coordenadas que Cabri les proporciona, no hacen caso y siguen explorando la curva de dos maneras diferentes: Luís, geométricamente para construir más puntos fuera del triángulo inicial OPQ; en tanto que Nadia sigue explorando numéricamente en búsqueda de regularidades que la lleven a encontrar "el patrón geométrico", refiriéndose a la expresión de una exponencial. Al no hallar ninguna regularidad, abandona la búsqueda y vuelve a discutir con Luís respecto a los interesantes hallazgos de su compañero.
Luís logra visualizar que, para construir el siguiente punto, de acuerdo a su nueva partición de unidades, debe incrementar una unidad por encima de Q y repetir la construcción, una vertical por x = 9 y una semirrecta por este nuevo punto. Se apoya para ello de la "rejilla" (Ver Figura 9). Ambos se convencen de que está correctamente construido pues se cumple con el patrón numérico que habían encontrado, aquel que explican de la siguiente forma:
Luís: Si vamos por los impares (refiriéndose a las abscisas) todos terminan en 13 (refiriéndose a los decimales en juego) y si vamos por los pares, se alternan enteros y los que terminan en medios.
En tanto que Nadia abstrae la relación entre el número de "saltos" que realizan con las abscisas, y el número de "saltos" en las ordenadas y le comentan a su compañero:
Nadia: Mira, si acá nos movimos dos veces (señala las abscisas en el triángulo que nosotros resaltamos) acá también son dos (señalando el número de semirrectas involucradas). Si, mira (abren otra de sus parábolas construidas) si acá nos movemos 4 veces, acá también debemos que contar con cuatro semirrectas... y esto pasa en todas las curvas que hemos trazado.
Estas ideas ya habían sido percibidas por Luís al construir más puntos de la curva, ya que era el responsable de manejar el mouse, aunque no lo comparte con su compañera. Estos comentarios, lo llevan a dejar esta ventana y abrir otra para construir una curva desde el primer triángulo determinado. Elije el triángulo con vértices (0,0), (0, 2) y (2, 2) (Ver Figura 10, donde lo hemos sombreado para resaltarlo). Luís se concentra en determinar puntos equidistantes en la recta vertical que traza por (0, 2) y (2, 2). A partir de esta partición vertical, traza las semirrectas desde (0,0) y halla otros puntos de esta curva mediante las verticales trazadas de acuerdo a la distancia inicial de las abscisas, mostrándonos que vincula los dos crecimientos simultáneamente, ya que no duda sobre qué rectas debe involucrar.
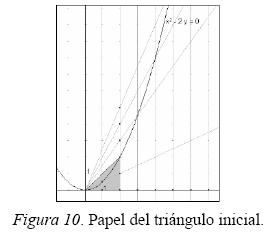
Repite estas ideas con otros triángulos iniciales y se convencen de que se trata de funciones cuadráticas, quedándoles como tarea explicar sus descubrimientos ya que ante la pregunta:
Entrevistador: ¿Pueden explicarme estos hallazgos?
Nadia: Déjenos pensarle, lo incluiremos en el informe.
Luís: Toda curva así construida es una parábola del tipo y = kx2 argumento que extrae del uso de la herramienta "cónica" y "coordenada o ecuación" de cabri aplicándolas a varias de sus producciones.
Se observa en este caso la tímida aparición de ideas covariacionales presentes en su intento por integrar una red de modelos aunque evidenciando su preferencia por uno de los modelos, el geométrico en el caso de Luís y el numérico en Nadia. El menos visitado fue, en este caso, el algebraico declarando que nunca habían explorado este tipo de acercamiento a funciones.
En el reporte de la segunda actividad Luís trabaja solo ya que Nadia se integra en otro equipo de trabajo (ver Caso 5). Luego de construir los puntos de la curva en estudio siguiendo los pasos de la actividad, se le solicita que construya más puntos y que describa la función involucrada. En este sentido, declara "que se trata de una parábola acostada, por tanto debe ser simétrica respecto al eje x". Como la herramienta "cónica" no traza lo que desea ver, naturalmente desecha ese comando y se enfrasca en reproducir la construcción pero hacia abajo (Ver Figura 11). Lo logra y declara que el punto B no puede pertenecer a la curva pues se trata de una parábola. Se le solicita que construya la tabla de coordenadas correspondiente a los puntos que ha determinado y sustente con ella su afirmación. En su informe explica:
"Como ya contamos con el patrón de crecimiento de nuestra curva, pues ahora determinamos su ecuación, la cual descubrimos que es: x = 2y. Pero esta expresión cabri no la reconoce, así que tuvimos que buscar una manera diferente de expresar esta función de forma que podamos observar gráficamente la curva, llegamos a la expresión siguiente: log(x)/log(2).
Después lo que hicimos fue crear la expresión y aplicarla en los ejes coordenados, lo cual pudimos constatar que los puntos trazados coinciden con puntos sobre la curva, la cual es la que estábamos buscando."
Al realizar esta tarea percibe que la covariación en juego es muy diferente al caso anterior que involucraba una función cuadrática, y que por lo tanto no puede tratarse de una cónica. Desecha su afirmación y se aboca a determinar la expresión analítica demorando bastante en abstraerla y en aceptar que no es una función simétrica respecto a uno de los ejes. Luego de extender numéricamente la tabla sin observarse en él dificultades para hacerlo hacia la izquierda, problema que se presentara en la discusión anterior con los dos estudiantes, Luís regresa hacia el ambiente Cabri y construye geométricamente más puntos para comprobar sus exploraciones, confirmándolas luego al trazar, mediante "aplicar una expresión", la curva logarítmica involucrada.
Se observa en este estudiante una mayor libertad para pasar de uno a otro modelo propuesto en la actividad, alterando repetidamente el orden implícitamente esbozado en la actividad (geométrico, numérico, algebraico) lo cual se esperaba con el fin de observar que cada estudiante construye su propia red de modelos.
5.4. Caso 4: Las producciones de Berta
Al resolver la primera actividad y construir la curva, Berta se interesa por analizar la relación que existe entre los triángulos que determinan los puntos construidos. Para ello, construye los triángulos, los colorea para distinguirlos y observa que para construir un nuevo punto de la curva necesita un triángulo más grande cuyo cateto vertical debería estar en x = 10, para respetar el patrón de las abscisas. Se centra luego en las ordenadas y declara que: "para el punto L, la diferencia es 0.5; para M dos "saltos" de 1, para N tres saltos de 1.5, y para Q cuatro saltos de 2 unidades" (Ver Figura 12a).

Predice entonces que el siguiente punto deberá realizar un salto de 2.5 y repetirlo 5 veces, por lo que determina numéricamente la construcción del punto que llama R. Construye este punto utilizando la herramienta "número" y "transferencia de medidas".
Finalmente traza, mediante la herramienta "cónica" la curva y comprueba visualmente que su construcción es correcta ya que la curva pasa por ese punto.
A la siguiente sesión, nos presenta un interesante argumento para sustentar geométricamente que el punto R pertenece a la construcción. Lo hace mediante el trazo de circunferencias, descubriendo que las semirrectas puestas en juego en la determinación de los puntos de la curva mantienen la misma distancia, por tanto, "se puede utilizar las últimas dos semirrectas para determinar la siguiente y no se necesita contar los saltos anteriores" (Ver Figura 12b). Entre sus conclusiones, escribe en su informe:
"Como observamos esta curva se comporta muy bonita y al tener varios puntos de la curva nos surgió la inquietud de saber con que curva estábamos tratando... Por el comportamiento que seguí supusimos que se trataba de una parábola, pero lo constatamos usando un comando de cabri llamado "cónica", puesto que si resultaba cierta nuestra hipótesis en base a los elementos que teníamos resultaría determinar la ecuación de dicha curva...."
Para determinar la expresión algebraica, consulta un libro de geometría analítica y trabaja con foco y directriz, por tanto con la expresión general:
"Y así sucedió, la curva con la que estábamos tratando era la parábola, después calculamos su ecuación, se facilita por que tiene su vértice en el origen, tiene como eje un eje coordenado (el eje y en nuestro caso) y además contábamos con varios puntos de la misma."
El uso de la herramienta "cónica" la lleva a refugiarse en la geometría analítica, elemento que no habíamos previsto ya que supusimos que el trabajo numérico los llevaría a pensar en variaciones y funciones cuadráticas trasladándolos a determinar la expresión analítica mediante la resolución de un sistema de ecuaciones para determinar los parámetros de la misma.
Sin embargo, Berta nos da ejemplo de la necesidad de convencerse de lo que Cabri propone, explorando en primera instancia la parte numérica de la construcción para determinar un punto fuera del triángulo inicial para continuar con una exploración geométrica sustentada por la construcción de círculos pasando luego a la búsqueda de la expresión analítica. Genera así, su propia red de modelos, un rico ámbito para argumentar y robustecer su acercamiento a las funciones cuadráticas.
Vemos entonces que esta alumna desarrolla varios argumentos para describir la función cuadrática al explorarla geométrica, numérica y algebraicamente. Al incursionar en la segunda actividad, intenta repetir aquellos argumentos que le fueron útiles en la actividad anterior, como por ejemplo el caso de las circunferencias ya que su primera impresión, al igual que la de todos los alumnos, fue que se trataba de una parábola acostada (Ver Figura 13a). Rápido percibe que no se comporta como una parábola, los círculos le permiten determinar el próximo punto de la curva directamente, muy diferente a la construcción anterior.

Numéricamente abstrae la covariación existente, reconoce que debe ser una logaritmo, pero declara no recordar cómo determinar eso, o cómo calcularlo por lo que recurre a Internet para informarse sobre ellos. Su nueva construcción, le permite contestar sin problemas que "el punto B no pertenece a la curva, ya que el eje y es su asíntota" (Ver Figura 13b). En este caso, no intenta unir los puntos con la herramienta "cónica" como la mayoría de sus compañeros realizan, ya que desde la determinación de las coordenadas percibe que se trata de otro tipo de función.
Finalmente, opta utilizar las herramientas "expresión" y "aplicar una expresión" que para utilizarlas se requiere la expresión algebraica de la curva que se desea trazar. Para ello, logra determinar que x = 2y y que al aplicar función inversa se trata de la función y = log2x. Se preocupa un poco al observar que Cabri sólo acepta, como las calculadoras, el logaritmo decimal y el natural, y regresa a Internet a leer sobre logaritmos. Su búsqueda tiene una intención muy clara, hallar una manera de cambiar base y logra reescribir su expresión algebraica como  .
.
Observamos, en estos dos últimos casos (Luís y Berta), que en la exploración de la función cuadrática ambos muchachos mostraron una interesante soltura en la construcción de su propia red de modelos, pero que ante este nuevo desafío se sintieron maniatados. Sólo lograron construir su red de modelos luego de leer sobre los logaritmos, y por haber sufrido el revés de que los argumentos que les fueron muy útiles en la actividad anterior no les daban gran apoyo lo que los obligó a buscar otras posibilidades, y por tanto, aceptar la diferente naturaleza de esta función.
La exploración numérica que involucra una progresión geométrica (en las abscisas) y una aritmética (en las ordenadas) les dio la pista para percibir la covariación subyacente en ellas que gobierna a la curva y que la aleja de las funciones polinomiales dándole su propio espacio en la estructura matemática.
5.5. Caso 5: Una red de modelos
Un equipo de trabajo conformado por dos muchachas y un muchacho (Nadia, Nélida y Juan) generan una producción interesante alrededor de la función logaritmo. Los tres habían trabajado en la primera actividad en equipos de dos, pero ante la ausencia de sus compañeros, se reúnen en la clase para explorar la segunda actividad.
Recordemos que Nadia había compartido el trabajo anterior con Luís, por tanto trae la frescura de la interacción con su compañero que reportáramos en el caso 2. Nélida, en cambio, había trabajado con otra muchacha priorizando el ámbito geométrico en la exploración de las funciones cuadráticas, no habiendo jugado un papel importante los otros modelos propuestos, el numérico y el algebraico. En su informe, aparece un interesante argumento sobre una proporcionalidad especial que se da en la curva que se está construyendo. Observan que el triángulo OPQ es proporcional al triángulo OAX y que además, la hipotenusa del primero es el punto medio de la altura del triángulo OAB (Ver Figura 14). Perciben que esto se cumple en todos los triángulos que se construyen dentro del triángulo inicial y que puede ser extendido hacia fuera para construir más puntos de la curva. Efectivamente, trazan por OB una semirrecta para determinar S en la vertical que pase por un punto (que llaman R) tal que A sea punto medio de OR. Si esto se cumple, abstraen que S debe ser el punto medio del cateto vertical del triángulo buscado para determinar el punto de la curva. Repiten su argumento para varios puntos y luego trazan la curva mediante "cónica", confirmando sus sospechas, se trata de una cuadrática.

Juan por su parte, había formado equipo con José, con el cual habían estudiado con mucho cuidado las longitudes de los segmentos que unen los puntos construidos siguiendo las instrucciones de la actividad y las áreas que aparecían en los triángulos respectivos. Observan varias regularidades, pero no logran descifrar el papel que juega en la función cuadrática que habían determinado, abandonando la búsqueda y reportando los datos que Cabri les proporcionaba sin mayor exploración.
Vemos entonces, que los tres conforman un nuevo equipo de trabajo, en el cual logran potenciar su creatividad ya que cada uno aporta una visión distinta sobre cómo explorar y discutir la curva que se les propone en la segunda actividad. Rápido perciben que se trata de una logarítmica pero no pueden dilucidar cómo determinarla para lo cual se apoyan en una página de Internet sobre esta noción. Así, entre la construcción geométrica, su tabla de valores y una exploración numérica de la misma, determinan la expresión analítica (Ver Figura 15).

Este grupo, logra explicar la construcción de puntos geométricamente, trazando horizontales y semirrectas; numéricamente repitiendo el patrón de multiplicar por 2 al anterior para las abscisas y sumar 1 para las ordenadas; pero también declara en su informe que: "Para encontrar otros puntos escribimos la expresión antes encontrada y seleccionamos la opción aplicar expresión, y de esta forma encontramos otros puntos."
Este equipo, sigue explorando y decide reportar sobre la construcción de curvas logarítmicas en otras bases hallando argumentos interesantes como los que expresan en su informe: "Realizamos la construcción de logaritmo en base tres siguiendo la construcción dada en clase, en donde tomamos un triángulo de base ½ y altura uno". (Ver Figura 16a).

Vemos que algunos de los grupos de trabajo aceptan el desafío de explorar y sobrepasan las expectativas que inicialmente habíamos previsto en nuestro análisis a priori, tal como lo demuestra este trío de muchachos al avocarse a analizar el papel que juega el triángulo inicial de la construcción geométrica concluyendo que les permite manipular la base de sus logaritmos. Esto no les basta, y también reportan sobre lo que pasaría si la construcción se extiende hacia la izquierda, invadiendo los x < 0 .
En esta exploración, se apoyan con Derive pues habían descubierto que reconoce las expresiones algebraicas escritas libremente, tales como x = 2y ya que "distingue" la variable dependiente (y) y la independiente (x) en tanto que Cabri sólo acepta expresiones del tipo 2x para trazar su gráfica, argumento que aparece en su informe final (Ver Figura 16b).
Esto los lleva a reportar su red de modelos que crean para describir la curva que han construido y que sintetizamos en un esquema (ver Figura 17).
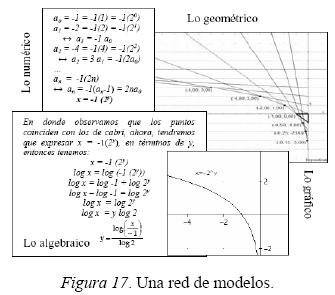
Es interesante observar cómo manipulan las propiedades de los logaritmos donde "log–1" aparece varias veces sin pudor, sin ningún rigor, para llegar al resultado que deseaban obtener para trazar la curva en Derive y luego comprobar la integración de sus ideas.
A varios de sus compañeros, se les preguntó qué pensaban de esta resolución y encontramos que algunos expresan: "No es una respuesta correcta, ya que la propiedad que usa loga(xy) = loga x + loga y, sólo se cumple cuando x y y son positivos y ellos en su ejemplo toman x = –l y x = 2y y esto no se puede hacer". Además agrega: "creo que Cabri toma a los paréntesis como valor absoluto, es decir,  "
"
Otro compañero en cambio, establece que: "Al revisar el análisis que la compañera realizó de esta actividad, no observé algún error ya que en su desarrollo muestra la figura a la cual hace mención, y su respectiva ecuación la cual es correcta ya que al graficarla con el programa Cabri utilizando la expresión que ella muestra  resulta la misma gráfica. La cual indica que la exploración que ella realizó mediante la tabla y los procedimientos que muestra son correctos. No sólo porque el resultado es correcto, sino que también verifiqué los pasos que realizó y las propiedades que utilizó de los logaritmos para concluir con la expresión".
resulta la misma gráfica. La cual indica que la exploración que ella realizó mediante la tabla y los procedimientos que muestra son correctos. No sólo porque el resultado es correcto, sino que también verifiqué los pasos que realizó y las propiedades que utilizó de los logaritmos para concluir con la expresión".
"Bueno, respecto a la forma de la gráfica se observa que todos los valores que toma x están entre (–∞,0), los cuales son negativos... [Trabaja con la expresión]... y al final lo que estamos obtenido es el cociente de logaritmos positivos lo cual está bien definido y por tanto el programa Cabri no tiene dificultad para trazar esta expresión ya que toma sólo valores de x para los cuales la expresión tiene sentido."
Vemos entonces que algunos de los estudiantes exigen mayor rigor en la manipulación de las expresiones, en tanto que otros aceptan como transparente el dominio de la función que está en juego. La mayoría, le otorga a una herramienta técnica la capacidad de decidir, "...Cabri toma a los paréntesis como valor absoluto"... o "Cabri no tiene dificultad para trazar esta expresión ya que toma sólo valores de x para los cuales la expresión tiene sentido"... esa frase: "Cabri dice" se encuentra con más frecuencia de la que se desearía escuchar, evidenciando el debilitado espíritu crítico que los muchachos desarrollan en la aulas.
Por otro lado, un argumento que es interesante discutir con los alumnos es el que surgió en este reporte, al explorar el efecto que hace manipular el triángulo inicial de construcción. Nadia, lo realiza en la primera actividad, arrastrando el triángulo de inicio para trazar funciones cuadráticas y determina que el efecto es "trasladar la curva a través del eje x". Sin embargo, en su exploración se observa que sólo mueve el triángulo (como se evidencia en la Figura 18) anclando los puntos origen de las semirrectas que se deben trazar en el eje y por tanto no traslada la construcción.

Concluye entonces que: "Observamos que nos da 2(2y) y 3(2y) respectivamente, cuando el triángulo se desplaza una coordenada, pero notemos que, en valor que nos da el dos y el tres que multiplica a 2y, no los da el lado de triángulo que está más lejos del origen. Entonces tenemos que cuando se desplaza n–1 coordenadas, nos da x = n(2xy)".
Sin embargo, no puede aclararles a sus compañeros qué está ocurriendo en realidad. Sólo menciona que "recorrer el triángulo, hace que la curva se recorra" dándonos a entender que considera que se traslada por el eje x al igual que en la actividad anterior de las cuadráticas, por tanto no se percata que el efecto en realidad es una traslación vertical.
Como vemos, proponer a los alumnos explorar ciertas funciones en este ambiente que la geometría dinámica produce, se ve potenciado por la creatividad de los muchachos. Nos sorprenden con sus búsquedas, con sus conclusiones que nos permiten observar cómo van construyendo lentamente su capacidad de criticar sus propias opiniones, haciéndose cargo de sus decisiones.
Se observa además cómo comienzan a percibir la covariación en estas curvas y la no extensión de los argumentos que funcionaron en la curva anterior. Además, comienzan a construir sus propias redes de modelos, donde se percibe que cada uno de los entrevistados se desenvuelve con mayor soltura en el modelo que prefieren, algunos el algebraico; otros el numérico, y no falta el que intenta resolver todo en el geométrico, pero ninguno deja de involucrar los tres modelos en algún momento de su resolución.
6. A MODO DE CONCLUSIÓN
En este artículo, hemos reportado una investigación que desarrollamos en torno a la apropiación de la noción de función, particularmente la función logaritmo, tal que en nuestra perspectiva teórica se convierte en la búsqueda de lo logarítmico, como una construcción de una red de modelos, imbuida de prácticas y de representaciones sociales.
Este estudio, sustentado por la socioepistemología, nos permitió percibir las prácticas sociales que guiaron el desarrollo de los logaritmos, la de facilitar cálculos y la de modelar, ambas cobijadas por la predicción. El entremezcle de estas dos prácticas, así como las prácticas de referencia involucradas en su construcción, sin poder realmente dilucidar si la covariación logarítmica ha comandado este desarrollo o ha sido el resultado de muchos esfuerzos por crear una herramienta matemática tan poderosa, elementos que han inquietado nuestras exploraciones justamente bajo la idea de que tanto la interacción sujeto–práctica bajo una luz especial, temporal y situada, como el proceso y evolución de herramientas, son elementos inseparables, co–constitutivos de lo logarítmico.
Las reflexiones realizadas desde este estudio socioepistemológico, nos permitió generar dos actividades matemáticas entrelazadas, convocando a la SGD como generador de una ambiente rico y dinámico que facilitara a los estudiantes el movimiento entre modelos y por ende la construcción de su red.
Analizando la intermitencia de argumentos provenientes de percepciones covariacionales que implica una compleja abstracción y otros, evidenciando cierto alejamiento de esta última, nos permite observar que en general, los estudiantes que participaron en el estudio tienden a "creer" sin discutir: "Cabri lo dice", traspasando la responsabilidad epistemológica de las respuestas a una herramienta técnica lo cual evidencia la necesidad de fomentar una visión crítica y a la argumentación colectiva e individual.
Además, el diseño logra hacerlos reflexionar sobre la naturaleza de las dos funciones convocadas a esta experiencia, la función cuadrática y la logarítmica, que se evidencia al solicitarles argumentar sus respuestas. Perciben y viven la no extensión de argumentos entre funciones, es decir, aquellos que fueron valiosos en la función cuadrática no funcionan en la función logarítmica... lo que refuerza la hipótesis que es necesario reconocer la naturaleza de cada función tomándola desde la covariación.
Analizando comentarios (escritos como orales) y gestos de los estudiantes al involucrarse en las actividades de aprendizaje diseñadas, observamos un destello en la complejidad de construir una visión global de ciertas funciones.
Requerirles abstraerse de la información que Cabri les ofrece, y argumentar sobre cómo determinar más puntos y describir la curva en juego, les exige por ejemplo extender la construcción geométrica o apoyarse en el modelo numérico, o quizás en éste para determinar el modelo algebraico dándonos la pauta que la riqueza argumentativa y por ende de sensibilizarse sobre ciertas ideas covariacionales depende fuertemente de la construcción de su propia red de modelos.
Iniciar la discusión, respecto a funciones particulares, con una construcción geométrica, resquebraja las concepciones escolares sobre graficarlas y conlleva a explorarlas de manera más integral. Consideramos entonces que la geometría dinámica nos proporciona un ambiente de discusión que genera argumentos particulares sobre covariación cuando se propicia la construcción de una red de modelos.
REFERENCIAS BIBLIOGRÁFICAS
Agnesi, M. (1748). Instituzioni analitiche ad uso della gioventú italiana. Libro Secondo del Calcolo Differenziale (2 tomos). Milano, Italia: Nella Regia Ducal Corte. [ Links ]
Bartolini Bussi, M. G. (1998). Verbal interaction in the Mathematics Classroom: A Vygotskian Analysis. En: H. Steimbring, M.G. Bartolini Bussi y A. Sierpinska (Eds.) Languages and Communication in the Mathematics Classroom (pp. 65–84). Reston, Virginia, USA: National Council of Teachers of Mathematics. [ Links ]
Bayazit, I. (2006). The Relationship between teaching and learning the Function Concept. PhD Thesis, University of Warwick. [ Links ]
Bayazit, I. & Gray, E. (2004). Understanding inverse functions: the relationship between teaching practice and student learning. En: M. Hoines y A. Fuglestad (Eds.), Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, 2004 Vol 2 (pp 103–110). Bergen University College. Consultado en diciembre de 2007. Disponible en: http://www.emis.de/proceedings/PME28/RR/RR199_Bayazit.pdf [ Links ]
Bradwardine, T. (1328). De proportionibus velocitatum in motibus. Disponible en http://www.fondoantiguo.us.es-obras. Consultado en abril de 2003. [ Links ]
Briggs, H. (1620). Arithmetica logarithmica. (Traducido y comentado por I. Bruce (2004). University of Adelaide, Australia). Disponible en: http://www–history.mcs.st–andrews.ac.uk/Miscellaneous/Briggs/index.html. Consultado en enero de 2004. [ Links ]
Buendía, G. & Cordero, F. (2005). Prediction and the periodical aspect as generators of knowledge in a social practice framework: A socioepistemological study. Educational Studies in Mathematics 58, 299–333. [ Links ]
Cantoral, R., Farfán, R. M., Hitt, F. y Rigo, M. (1983). Historia de los conceptos de logaritmo y exponencial. México: Cinvestav–IPN, Sección de Matemática Educativa. [ Links ]
Cantoral, R. (1990). Categorías relativas a la apropiación de una base de significados propia del pensamiento físico para conceptos y procesos matemáticos de la teoría elemental de las funciones analíticas: Simbiosis y predación entre las nociones de "el Praediciere" y "lo Analítico". Tesis de Doctorado. Departamento de Matemática Educativa. Centro de Investigación y Estudios Avanzados– Instituto Politécnico Nacional. México. [ Links ]
Cantoral, R. (2001). Matemática Educativa: Un estudio de la formación social de la analiticidad. México: Grupo Editorial Iberoamérica. [ Links ]
Cantoral, R. y Montiel, G. (2001). Funciones: Visualización y pensamiento matemático. México: Edición especial CASIO, Prentice Hall. [ Links ]
Cantoral, R. & Farfán, R. M. (2004). La sensibilité á la contradiction: logarithmes de nombres négatifs et origine de la variable complexe. Recherches en Didactique des Mathématiques 24(2–3), 137–168. [ Links ]
Cantoral, R., Farfán, R. M., Lezama, J. y Martínez–Sierra, G. (2006). Socioepistemología y representación: Algunos ejemplos. Revista Latinoamericana de Investigación en Matemática Educativa. Número Especial, (pp. 83–102). México. [ Links ]
Carlson, M., Larsen, S. & Jacobs, S. (2001). An investigation of covariational reasoning and its role in learning the concepts of limit and accumulation. En: R. Speiser, C. Maher y C. Walter (Eds.), Proceedings of the 23rd Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education 1 (pp. 145–153), Snowbird, UT: PME–NA. [ Links ]
Carlson, M., Jacobs, S., Coe, E., Larsen, S. & Hsu, E. (2002). Applying covariational reasoning while modelling dynamic events: A framework and study. Journal for Research in Mathematics Education 23(5), 352–378. [ Links ]
Carlson, M. P., Oehrtman, M., & Thompson, P. W. (2007). Foundational reasoning abilities that promote coherence in students' understanding of functions. En M. P. Carlson & C. Rasmussen (Eds.), Making the connection: Research and teaching in undergraduate mathematics (pp. 150–171). Washington, DC: Mathematical Association of America. Consultado en diciembre de 2007. Disponible en: http://cresmet.asu.edu/media/pdf/pubs/carlson/Oehrtman–Carlson–Thompson_final.pdf [ Links ]
Carlson, M., Oehrtman, M., & Engelke, N. (en prensa). The development of an instrument to assess precalculus students' conceptual understandings: The Precalculus Concept Assessment Instrument. [ Links ]
Castorina, J. A. (Comp.) (2003). Representaciones sociales. Problemas teóricos y conocimientos infantiles. España: Gedisa. [ Links ]
Cobb, P. & Machain, K. (2003). Learning about covariation. Cognition and instruction 21(1), 1–78. Disponible en: http://www.fi.uu.nl/publicaties/literatuur/5024.pdf Consultada en agosto de 2005. [ Links ]
Cohen, D. K. & Ball, D. L. (1999). Instruction, capacity, and improvement (CPRE Research Report No. RR–043). Philadelphia, PA: University of Pennsylvania, Consortium for Policy Research in Education. [ Links ]
Cohen, D. K. & Ball, D. L. (2000). Instructional innovation: Reconsidering the story. Paper presented at the Annual Meeting of the American Educational Research Association, New Orleans. [ Links ]
Confrey, J. & Smith, E. (1994). Exponential functions, rates of change, and the multiplicative unit. Educational Studies in Mathematics 26, 135–164. [ Links ]
Confrey, J. & Smith, E. (1995). Splitting, covariation, and their role in the development of exponential functions. Journal for Research in Mathematics Education 26(1), 66–86. [ Links ]
Confrey, J. y Dennis, D. (2000). La creación de los exponentes continuos: un estudio sobre los métodos y la epistemología de John Wallis. Revista Latinoamericana de Investigación en Matemática Educativa 3(1), 5–31. [ Links ]
Contrill, J., Dubinsky, E., Nichols, D., Schwingendorf, K., Thomas, K. & Vidakovic, D. (1996). Understanding the limit concept: Beginning whit a coordinated process schema. Journal of Mathematical Behavior 15, 167–192. [ Links ]
Cordero, F. (2005). El rol de algunas categorías del conocimiento matemático en educación superior. Una socioepistemología de la integral. Revista Latinoamericana de Investigación en Matemática Educativa 8(3), 265–286. [ Links ]
Costé, A. (1997). L'œuvre scientifique de Nicole Oresme. Le Bulletin de la Société historique de Lisieux, Fascicule 37, Janvier 1997. Disponible en: http://www.math.unicaen.fr/lmno/Oresme/Oresme.html. Consultada en junio de 2004. [ Links ]
Dahan, J.–J. (2004). How to construct curves of functions o fine variable, of parametric, polar and random functions. Surfaces in several perspectives. Disponible en: http://www.univ–irem.fr/commissions/ci3m/CDci3m/toulouse/ConfNewOrleans.htm. Revisado: 22 de enero de 2007. [ Links ]
Descartes, R. (1647). La geometría de René Descartes. Español–Francés. [Traduc. R. García –Cenlex–IPN]. Colección Clásicos de la Ciencia México: Limusa, Serie Matemáticas. [ Links ]
Dubinsky, E. (1991). Reflective Abstraction in Advanced Mathematical Thinking. En D. Tall (Ed.), Advanced Mathematical Thinking (pp. 95–123), Netherlands: Kluver Academic Publisher. [ Links ]
Dubinsky, E., & Harel, G. (1992). The nature of the process conception of function. En G. Harel & E. Dubinsky (Eds.), The concept of function: Aspects of epistemology and pedagogy. MAA Notes, 25, 85–106. [ Links ]
Dubinsky, E. (2000). De la investigación en matemática teórica a la investigación en matemática educativa: un viaje personal. Revista Latinoamericana de Investigación en Matemática Educativa 3(1), 47–70. [ Links ]
Dubinsky, E. & MacDonald, M. A. (2003). APOS: A Constructivist Theory of Learning in Undergraduate Mathematics Education Research. En: D. Holton et al. (Ed.), The Teaching and Learning of Mathematics at University Level: An ICMI Study, (pp.275–282). USA: Kluwer Academic Publishers. [ Links ]
Dubinsky, E., Weller, K., Clark, J., Loch, S., McDonald, M. & Merkovsky, R. (2000). An examination of Student Performance Data in Recent RUMEC Studies. Disponible en http://www.math.kent.edu/~edd/publications.html. Consultada en marzo de 2006. [ Links ]
Duveen, G. y Lloyd, B. (1990). Las representaciones sociales como una perspectiva de la psicología social. (Capítulo 2). En J. A. Castorina, (Comp.) (2003). Representaciones sociales. Problemas teóricos y conocimientos infantiles. España: Gedisa. [ Links ]
Euler, L. (1835). Introduction a ¡'analyse infinité simale. París, Francia: L'Ecole Polytechnique. (Trabajo original publicado en 1748). [ Links ]
Falcade, R. Mariotti, M. A. & Laborde, C. (2004). Towards a definition of function. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education. Vol 2 (pp. 367–374). [ Links ]
Falcade, R., Laborde, C. & Mariotti, M. A. (2007). Approaching functions: Cabri tools as instruments of semiotic mediation. Educational Studies in Mathematics 66, 317–333. [ Links ]
Farfán R. M. (1997). Ingeniería didáctica: Un estudio de la variación y el cambio. México: Grupo Editorial Iberoamérica. [ Links ]
Ferrari, M. y Martínez–Sierra, G. (2003). Construcción de funciones con calculadoras graficadoras. En Acta Latinoamericana de Matemática Educativa. Vol. 16. Tomo II (pp. 710–716). México: Grupo Editorial Iberoamérica. ISBN 956–8298–03–7. [ Links ]
Ferrari, M. (2007). Construcción social del conocimiento matemático: La función logaritmo. Memoria Predoctoral. Departamento de Matemática Educativa. Cinvestav–IPN, México. [ Links ]
Furinghetti F. & Paola D. (2003). To produce conjectures and to prove them within a dynamic geometry environment: A case study. Proceedings of the 27th Conference of the International Group for the Psychology of Mathematics Education, Vol 3 (pp. 237–244), Honolulu, USA. Disponible en: http://www.didmatcofin03.unimo.it/pubblicazioni/RR_furinghetti.pdf. Consultada en octubre de 2007. [ Links ]
Gray, E. & Tall, D. O. (1994). Duality, Ambiguity and Flexibility: A Proceptual View of Simple Arithmetic, Journal for Research in Mathematics Education, 26 (2), 115–141. [ Links ]
Hairer, E. & Wanner, G. (1998). Analysis by Its History. New York, USA: New York, USA: Undergraduate Texts in Mathematics, Springer–Verlag. [ Links ]
Harel, G. (1998). Two dual assertions: the first on learning and the second on teaching (or vice versa). The American Mathematical Monthly, 105, 497–507. [ Links ]
Harel, G. & Lim, K. L. (2004) Mathematics teachers' knowledge base: preliminary results. En: M. Hoines y A. Fuglestad (Eds.), Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education, 2004 Vol 3 (pp 25–32). Bergen University College. Consultado en diciembre de 2007. Disponible en:http://www.emis.de/proceedings/PME28/RR/RR268_Harel.pdf [ Links ]
Huygens, C. (1690). Discours de la cause de la pesanteurgens, C.. Reeditado por IREM de Dijon (abril–1981). [ Links ]
Jodelet, D. (1986). La representación social: fenómenos, conceptos y teoría. En S. Moscovici (Comp.) Psicología Social II. Pensamiento y vida social. Psicología social y problemas sociales. (pp. 469–494). España: Paidós. [ Links ]
Krummheuer, G. (2007). Argumentation and participation in the primary mathematics classroom. Two episodes and related theoretical abductions. Journal of Mathematical Behavior 26, 60–82. [ Links ]
Lagrange, J.B. (2005). Using symbolic calculators range, Jto study mathematics. En D. Guin, K. Ruthven y L. Trouche (Eds.), The Didactical Challenge of Symbolic Calculators: Turning a Computational Device into a Mathematical Instrument (pp. 113–135). E.U.A.: Springer. [ Links ]
Mariotti, M. A., Laborde, C. & Falcade, R. (2003). Function and graph in DGS environment. Proceedings of the 27th Conference of the International Group for the Psychology of Mathematics Education, Vol 3 (pp. 237–244), Honolulu, USA. Disponible en: http://www.didmatcofin03.unimo.it/pubblicazioni/RR_mariotti.pdf. Consultada en octubre de 2007. [ Links ]
Martínez–Sierra, G. (2006) Los procesos de convención matemática constituyentes en la construcción social de la matemática de la variación y el cambio: el caso de las funciones elementales. En: G. Martínez–Sierra (Ed.) Acta Latinoamericana de Matemática Educativa 19(1), (pp.745–751). México: CLAME, versión digitalizada. Disponible en http://clame.org.mx/. Consultada en julio de 2006 [ Links ]
Montiel, G. (2006). Construcción social de la función trigonométrica. En: G. Martínez–Sierra (Ed.) Acta Latinoamericana de Matemática Educativa 19(1), (pp. 818–823). México: CLAME, versión digitalizada. Disponible en http://clame.org.mx/. Consultada en julio de 2006. [ Links ]
Moscovici, S. (1984). The phenomenon of social representations. En: R. M. Farr y S. Moscovici (comps.) Social representations (pp 3–69). Cambridge, Cambridge University Press. [ Links ]
Napier, J. (1614). A description of the admirable table of logarithms. London: Nicholas Okes (1616). Editie vertaald uit het Latijn door Edward Wright. Disponible en: http://www.ru.nl/w–en–s/gmfw/bronnen/napier1.html. Consultada en abril de 2003. [ Links ]
Newton, I. (1993). Principios matemáticos. (A. Escohotado & M. Saenz, Trad.). Barcelona, España: Altaya. (Trabajo original publicado en 1686). [ Links ]
O'Connor, J. J. & Robertson, E. F. (2003). Mathematics in various cultures. Disponible en: http://www–groups.dcs.st–and.ac.uk/~history/Indexes/HistoryTopics.html. Consultada en junio de 2004. [ Links ]
Oresme, N. (1968). Nicole Oresme and the medieval geometry of qualities and motions/ (Traducido y comentado por Marshall Clagett). Madison: The University of Wisconsin Press. [ Links ]
Paola, D. (2006). Nuove tecnologie e studio delle grandezze che variano. L'insegnamento della Matematica e delle scienze integrate. Consultada en julio de 2007. Disponible en http://www.didmatcofin03.unimo.it/pubblicazioni/domingo.pdf [ Links ]
Piaget, J. (1970). Genetic Epistemology. New York: Columbia University Press. [ Links ]
Piaget, J. & García, R. (1996). Psicogénesis e historia de la ciencia. México: Siglo XXI. [ Links ]
Purcell, E. y Varberg, D. (1993). Cálculo con geometría analítica. México: Prentice–Hall Hispanoamericana. [ Links ]
Raviolo, A., Siracusa, P., Gennari, F., y Corso, H. (2004). Utilización de un modelo analógico para facilitar la comprensión del proceso de preparación de disoluciones. Primeros resultados. Enseñanza de las Ciencias 22(3), 379–388. Consultado en diciembre de 2007. Disponible en: http://ddd.uab.es/pub/edlc/02124521v22n3p379.pdf [ Links ]
Saldhana, L. & Thompson, P. W. (1998). Re–thinking covariation from a quantitative perspective: Simultaneous continuous variation. En S. B. Berensen, K. R. Dawkins, M. Blanton, W. N. Coulombe, J. Kolb, K. Norwood, y L. Stiff (Eds.), Proceeding of the 20th Annual Meeting. North American Chapter of the International Group for the Psychology of Mathematics Education. Vol 1., (pp. 298–303). Columbus, OH: ERIC Cleainghouse for Science, Mathematics and Environmental Education. [ Links ]
Sánchez, M. (2007). Profesores de matemáticas y sus concepciones: El caso de los parámetros de la parábola. En C. Crespo (Ed.). Acta Latinoamericana de Matemática Educativa. Vol. 20 (pp. 341–346). México: CLAME. [ Links ]
Santos–Trigo, M. & Espinosa–Pérez, H. (2002). Searching and exploring properties of geometric configurations using dynamic software, International Journal of Mathematical Education in Science and Technology 33, 37–50. [ Links ]
Shulman, S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15, 4–14. [ Links ]
Shulman, S. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1–22. [ Links ]
Sierpinska, A. (1992). On understanding the notion of function. En: E. Dubinsky y G. Harel (Eds.), The concept of function. Aspects of epistemology and pedagogy (pp. 25–58). EE.UU.: Mathematical Association of America. Volumen 25. [ Links ]
Stavy, R. (1981). Teaching inverse functions via the concentrations of salt water solution. Archives de Psychology, 49, pp. 267–287. [ Links ]
Tall, D. & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151–169. [ Links ]
Tall, D. (2007). Encouraging mathematical thinking that has both power and simplicity. En: Collaborative Studies on Innovations for Teaching and Learning Mathematics in Different Cultures (II) – Lesson Study focusing on Mathematical Thinking. APEC–TSUKUBA International Conference 2007. Consultado en diciembre de 2007. Disponible en: http://www.criced.tsukuba.ac.jp/math/apec/apec2007/paper_pdf/DavidTall.pdf [ Links ]
Thompson, P. W. (1994). Imagines of rate and operational understanding of the fundamental theorem of calculus. Educational Studies in Mathematics 26, 229–274. [ Links ]
Thurston, W. P. (1990). Mathematical Education, Notices of the American Mathematical society, 37 (7), 844–850. [ Links ]
Valdez, E. (2003). Las aplicaciones del CABRI–GÉOMÈTRE II en la enseñanza de la función cuadrática: una estrategia constructivista del aprendizaje. Mosaicos Matemáticos 11, 135–142. [ Links ]
Zandieh, M. (2000). A theorical framework for analyzing student understanding of the concept of derivative. En: E. Dubinsky, A. Schoenfeld y J. Kaput (Eds.), Research in collegiate mathematics education. IV (Vol 8, pp. 103–127). Providence, RI: American Mathematical Society. [ Links ]


NOTA
1 Disponible en: http://es.wikipedia.org/wiki/Funci%C3 %B 3 n_rec%C3 %ADproca, consultada en diciembre de 2007.
















