Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.11 no.2 Ciudad de México jun. 2008
Artículos
O ESTUDO DE RELAÇÕES FUNCIONAIS E O DESENVOLVIMENTO DO CONCEITO DE VARIÁVEL EM ALUNOS DO 8.° ANO
THE STUDY OF FUNCTIONAL RELATIONSHIPS AND THE DEVELOPMENT OF THE CONCEPT OF VARIABLE IN 8TH GRADE STUDENTS
Ana Matos*, João Pedro da Ponte**
* Escola Secundária da Lourinhã. Lourinhã, Portugal; anamatos2006@gmail.com
** Departamento de Educação e Centro de Investigação em Educação. Faculdade de Ciências da Universidade de Lisboa, Lisboa, Portugal; jpponte@fc.ul.pt
Recepción: Octubre 08, 2007
Aceptación: Mayo 08, 2008
RESUMEN
Este trabajo aborda la relación entre la resolución de tareas de investigación y exploración que involucran relaciones funcionales y el desarrollo del pensamiento algebraico en alumnos de 8o. grado, poniendo especial atención a la forma como interpretan y utilizan el lenguaje algebraico. La metodología, de índole cualitativa e interpretativa, se aplicó a dos estudios de caso que fueron seleccionados al enseñar una unidad de 16 clases, la cual abarcó temas como secuencias de números, funciones y ecuaciones de primer grado. En cuanto a la recopilación de datos, incluyó dos entrevistas (una hecha antes y otra después de la unidad de enseñanza), la observación participante de clase por la maestra, que consignó en un diario, y los registros escritos de los alumnos. Los resultados de la investigación muestran que el énfasis en el estudio de relaciones funcionales, con base en tareas de exploración e investigación, favorece el desarrollo del significado para el lenguaje algebraico y la construcción de una visión más amplia sobre el uso de símbolos.
PALABRAS CLAVE: Álgebra, pensamiento algebraico, relaciones funcionales, variables, tareas de investigación.
ABSTRACT
This study analyses the relationship between solving exploratory and investigation tasks involving functional relationships and the development of algebraic thinking in grade 8 students, giving special attention to the way they interpret and use the algebraic language. The methodology, qualitative and interpretative, is based in two case studies of students involved in a teaching unit of 16 classes which included the study of numerical sequences, functions and first degree equations. The data collection involved two interviews (one carried before and the other after the teaching unit), the participant observation of the classes by the teacher, registered in her diary, and gathering of students' written records. The results show that the emphasis in the study of functional relationships based on exploratory and investigation tasks promotes the development of meaning for the algebraic language and the construction of a wider vision regarding the use of symbols.
KEY WORDS: Algebra, algebraic thinking, functional relationship, variables, investigation tasks
RESUMO
Este estudo aborda a relação entre a resolução de tarefas de investigação e exploração, envolvendo relações funcionais, e o desenvolvimento do pensamento algébrico em alunos do 8.° ano, dando especial atenção ao modo como estes interpretam e utilizam a linguagem algébrica. A metodologia, de índole qualitativa e interpretativa, é baseada em dois estudos de caso de alunos que viveram uma unidade de ensino de 16 aulas, que incluiu os temas sequências de números, funções e equações do 1 ° grau. A recolha de dados envolveu duas entrevistas (uma realizada antes e outra depois da unidade de ensino), a observação participante de aulas pela professora, registada no seu diário de bordo, e os registos escritos pelos alunos. Os resultados da investigação sugerem que a ênfase no estudo de relações funcionais, com base em tarefas de exploração e investigação, promove o desenvolvimento de significado para a linguagem algébrica e a construção de uma visão mais ampla sobre o uso de símbolos.
PALAVRAS CHAVE: Álgebra, pensamento algébrico, relações funcionais, variáveis, tarefas de investigação.
RÉSUMÉ
Ce travail aborde la relation entre la résolution de tâches de recherche et d'exploration impliquant des relations fonctionnelles, ainsi que le développement de la pensée algébrique chez les élèves de huitième degré. De même, celui–ci porte une attention particulière à la façon d'interpréter et d'utiliser le langage algébrique. La méthodologie, est qualitative et interprétative, est appliquée à deux études de cas sélectionnées à partir de l'enseignement d'une unité. Cette unité portait sur les suites numériques, les fonctions et les équations du premier degré et comprenait 16 séances de classe. En ce qui concerne le recueil de données, deux entretiens ont été réalisés (un avant l'unité d'enseignement et l'autre après l'unité), l'observation participante de classe pour l'enseignant, qui l'a consigné dans un journal, et les productions écrites des élèves. Les résultats de la recherche montrent que l'accent sur l'étude de relations fonctionnelles, basée sur des tâches d'exploration et de recherche, favorise le développement du signifie pour le langage algébrique et la construction d'une vision plus large sur l'usage de symboles.
MOTS CLÉS: Algèbre, pensée algébrique, relations fonctionnelles, variables, tâches de recherche.
1. INTRODUÇÃO
A representação de relações funcionais, a resolução de problemas e equações dos 1.° e 2° graus, o estudo de equações literais e a generalização e demonstração de propriedades válidas em certos conjuntos numéricos são exemplos de situações onde a linguagem algébrica assume um papel essencial. Em Portugal, estas situações são trabalhadas no 8.° ano de escolaridade (frequentado por alunos com 13 anos no caso de não terem tido retenções anteriormente) sendo os símbolos usados com diferentes finalidades e em várias situações. Os alunos deste ano de escolaridade já viveram experiências que lhes proporcionaram contacto com esta linguagem, nomeadamente o estudo de equações do 1.° grau no 7.° ano. No entanto, a utilização de símbolos algébricos e a construção do conceito de variável trazem–lhes usualmente dificuldades significativas e merecem, por isso, a nossa atenção. Tendo em conta as potencialidades das tarefas com carácter exploratório e investigativo na aprendizagem da Matemática, procuramos estudar o possível contributo de uma unidade de ensino que enfatiza a resolução deste tipo de tarefa no desenvolvimento do pensamento algébrico dos alunos do 8.° ano. Para isso, analisamos neste artigo o modo como os alunos interpretam a linguagem algébrica e a utilizam na resolução de problemas, antes e depois da unidade de ensino.
2. DESAFIOS NO ENSINO–APRENDIZAGEM DA ÁLGEBRA
A tradicional (sobre)valorização do simbolismo na Álgebra escolar tem dado lugar, principalmente desde a década de oitenta do século passado, a um modo mais abrangente de encarar este domínio e a uma maior valorização do pensamento algébrico. Kaput (1999) considera que o pensamento algébrico surge quando, através de processos de conjectura e argumentação, se estabelecem generalizações sobre dados e relações matemáticas, expressas através de linguagens cada vez mais formais. Este processo de generalização pode ocorrer com base em situações aritméticas, geométricas, de modelação matemática e em quaisquer outras situações matemáticas leccionadas desde os primeiros anos de escolaridade. Deste modo, este autor identifica cinco facetas do pensamento algébrico, intrinsecamente relacionadas entre si: (i) a generalização e formalização de padrões e restrições; (ii) a manipulação de formalismos, guiada sintacticamente; (iii) o estudo de estruturas abstractas; (iv) o estudo de funções, relações e de variação conjunta; e (v) a utilização de múltiplas linguagens na modelação matemática e no controlo de fenómenos. Para o NCTM (2000), tornar o pensamento algébrico acessível a todos os alunos é um desafio que se coloca à educação matemática.
Apesar de a Álgebra não se cingir à vertente simbólica, é um facto que uma das suas grandes potencialidades advém da utilização de símbolos, muitos deles literais. Estes símbolos permitem expressar ideias matemáticas de forma rigorosa e condensada (Sfard & Linchevski, 1994). Além disso, possibilitam um distanciamento em relação aos elementos semânticos que representam, ganhando independência e tornando–se poderosas ferramentas para a resolução de problemas (Rojano, 1996).
Diversas investigações alertam–nos para o facto de os símbolos poderem ser utilizados para representar aspectos matemáticos bastante diversificados e poderem, também, ser interpretados de modos distintos, consoante a situação. Entre 1974 e 1979, a equipa do projecto Concepts in Secondary Mathematics and Science (CSMS), identificou seis tipos diferentes de resposta dadas por alunos, entre os 11 e os 6 anos, quando confrontados com o uso de símbolos literais (Küchemann, 1981):
(i) Letra avaliada. Substituição imediata da letra por um valor numérico, sem qualquer operação sobre ela, enquanto incógnita;
(ii) Letra não considerada. Reconhecimento da presença da letra, mas sem a necessidade da respectiva atribuição de significado;
(iii) Letra como objecto. Observação das letras como abreviaturas para objectos ou como os próprios objectos em si;
(iv) Letra como incógnita. Visão das letras como números específicos, mas desconhecidos, sobre os quais é possível operar directamente;
(v) Letra como número generalizado. Reconhecimento de que a letra representa vários números ou, pelo menos, do facto de poder ser substituída por mais do que um valor;
(vi) Letra como variável. Reconhecimento de que a letra representa um conjunto de valores cuja alteração provoca uma alteração sistemática nos valores de cada uma das expressões em que está inserida.
Na investigação desenvolvida pelo projecto CSMS, embora a interpretação da letra dependa da natureza e da complexidade da questão em causa, as respostas mais frequentes dos alunos incluem–se nas categorias "letra como objecto" e "letra não considerada". Estas categorias e a que foi designada por "letra avaliada" incluem estratégias de resolução onde se evita o uso da letra de modo mais elaborado. Ainda assim, um número considerável de alunos consegue um bom desempenho nas questões que exigem o uso da "letra como incógnita". As interpretações em que demonstram mais dificuldades situam–se nas categorias "letra como número generalizado" e "letra como variável" (Kieran, 1992; Küchemann, 1981).
Ao reflectir sobre a utilização da linguagem algébrica, Usiskin (1988) destaca, também, a possibilidade de uma letra ser usada com diferentes finalidades, nomeadamente, como: (i) instrumento que permite a expressão de uma generalização; (ii) representante de um valor particular desconhecido (incógnita) ou de uma constante; e (iii) argumento ou parâmetro de uma função. Ursini e Trigueros (2001) defendem que as distintas interpretações da linguagem algébrica geram dificuldades adicionais a muitos alunos. Após a análise das estratégias usadas na resolução de problemas que envolvem símbolos, estas autoras propõem três categorias principais sobre a sua utilização, que designam por "modelo 3UV": incógnita, número generalizado e variável numa relação funcional.
English e Warren (1989) observam que, tradicionalmente, nos currículos de Matemática, é dada maior relevância à interpretação das letras como incógnitas. Pelo seu lado, Schoenfeld e Arcavi (1988) criticam o facto de, por vezes, os programas de Matemática encararem a utilização de variáveis como algo que, após alguma prática, a grande maioria dos alunos acaba por compreender. Os autores argumentam que, no cenário escolar, a construção do conceito de variável é um processo complexo, considerando–o mesmo como um tópico central no ensino–aprendizagem da Matemática e na construção de conceitos matemáticos mais avançados.
Diversos estudos têm identificado as dificuldades sentidas pelos alunos quando utilizam a linguagem algébrica. Booth (1984) categoriza–as em três áreas principais: (i) a interpretação das letras; (ii) a formalização dos métodos usados; e (iii) a compreensão de notações e convenções. Diversos autores (Booth, 1988; Kieran, 1992; MacGregor & Stacey, 1997) apontam aspectos mais específicos, frequentes no desempenho dos alunos, como a interpretação do sinal "=", como um indicador de um procedimento a realizar e a não aceitação da expressão algébrica como uma entidade com existência própria, que não carece de fechamento (lack of closure). Com efeito, a utilização multifacetada da simbologia constitui uma fonte de potencialidades em Álgebra mas, simultaneamente, uma fonte de conflitos e dificuldades para muitos alunos.
Arcavi (1994, 2006) defende que o ensino da Álgebra deve visar o desenvolvimento do sentido do símbolo. Para o autor, este objectivo inclui a promoção da capacidade de manipular e interpretar expressões algébricas e da consciência de que os símbolos podem desempenhar papéis distintos consoante os contextos, intuindo a existência dessas diferenças. O autor apresenta exemplos ilustrativos do sentido do símbolo, observados em situações de sala de aula, em alunos que realizam tarefas de cariz algébrico, e sustenta que eles estão ao alcance de todos, mesmo daqueles que usualmente sentem maiores dificuldades na disciplina de Matemática. A construção plena e multifacetada do conceito de variável e a promoção do sentido do símbolo são assim dois desafios que se colocam no ensino–aprendizagem da Álgebra.
3. UNIDADE DE ENSINO
No documento Principles and Standards for School Mathematics, o NCTM (2000) defende que os alunos devem compreender os diversos significados e usos da linguagem algébrica, através da representação de quantidades, nomeadamente na resolução de problemas. O estudo de funções inclui a necessidade de compreender o modo como duas variáveis se relacionam, isto é, de conseguir explicitar uma relação funcional a partir de um certo conjunto de dados. Este processo baseia–se, essencialmente, na exploração de padrões e regularidades, actividade que, segundo diversos autores (e.g., Driscoll, 1999; NCTM, 1989, 2000), contribui para o desenvolvimento do pensamento algébrico e que, por esse motivo, deve ser promovida desde os primeiros anos de escolaridade.
A presente unidade de ensino1, concretizada no 8.° ano, contempla o estudo de diversos temas do programa de Matemática português: Sequências de números, Funções e Equações do 1." grau (ME–DGEBS, 1991). O seu objectivo principal é a promoção do desenvolvimento do pensamento algébrico, com base na exploração de relações funcionais. Mais concretamente, esta unidade tem, como objectivos específicos, o desenvolvimento das capacidades de:
– Identificar e descrever padrões e regularidades, em situações em que exista variação, e formular generalizações;
– Representar e analisar relações funcionais através de tabelas e gráficos ou usando linguagem algébrica;
– Atribuir significado às expressões algébricas e utilizar eficientemente a linguagem algébrica, quando utilizada em diferentes contextos e com diferentes finalidades: como instrumento de generalização, como argumento de uma função e como incógnita na resolução de problemas e equações.
A unidade de ensino envolve um total de 16 blocos de 90 minutos, com a distribuição que se apresenta na tabela I, e é sustentada por oito tarefas de carácter exploratório e investigativo (Ponte, 2004) que pretendem abrir caminho à construção de novos conceitos, em cada um dos subtemas abordados. O tema Sequências de Números inclui a resolução de três tarefas. Nas duas primeiras os alunos exploram padrões em sequências associadas a representações pictóricas e em sequências numéricas, com diversos graus de dificuldade. Todas elas proporcionam oportunidades para a generalização desses padrões, que, num primeiro momento, pode ser descrita em linguagem corrente, mas progressivamente vai sendo expressa com recurso a linguagem simbólica, de um modo cada vez mais formal. A terceira tarefa tem como objectivo propiciar o contacto dos alunos com a representação gráfica destas sequências, a procura de regularidades e a estimação de valores. Este tema coloca em jogo a utilização da letra como número generalizado e da letra como incógnita (na resolução de equações simples).

O tema Funções é introduzido por duas novas tarefas que envolvem relações entre variáveis, mas agora no caso geral em que a variável independente é contínua. Na primeira destas tarefas a relação entre as variáveis é de proporcionalidade directa, o que não se verifica na tarefa seguinte. Em ambas as tarefas são trabalhadas as diferentes formas de representação das relações funcionais, a passagem de informação de uma representação para outra e são analisadas as potencialidades de cada uma delas. Uma terceira tarefa, relativa a este tema, diz respeito à interpretação de gráficos distância–tempo e à construção de uma possível situação que eles possam modelar. Embora se recorra ao uso da letra como número generalizado e como incógnita, a ênfase, nesta fase, encontra–se na utilização da letra como variável e na noção de dependência.
Por fim, as duas últimas tarefas aprofundam o estudo de Equações do 1° grau, já iniciado no 7.° ano e revisitado a propósito dos temas anteriores, alargando–o à resolução de problemas e equações com denominadores. As equações literais surgem pela primeira vez a partir da actividade investigativa desenvolvida pelos alunos, resultando da generalização de relações existentes entre mais do que duas variáveis. Após este momento inicial, sustentado pelo contexto da situação explorada pelos alunos, surge a resolução destas equações em ordem a uma das variáveis. Nesta fase da unidade de ensino predominam a utilização da letra como incógnita e como número generalizado.
Nas tarefas de carácter exploratório e investigativo os alunos são desafiados a trabalhar uma situação, formulando–a como problema matemático, explorando e relacionando os dados, estabelecendo e testando conjecturas, e validando e argumentando relações (Ponte, 2007). A ênfase nestas tarefas tem sido defendida por diversas razões: (i) serem indispensáveis para fornecer uma visão integral da Matemática; (ii) estimularem uma participação do aluno que favorece a aprendizagem significativa; (iii) fornecerem pontos de entrada múltiplos para alunos com diferentes níveis de desempenho; e (iv) estimularem um modo holístico de pensamento, relacionando muitos tópicos, promovendo o raciocínio significativo (Oliveira, Segurado, Ponte & Cunha, 1999).
Processos importantes do raciocínio matemático como a identificação de padrões e regularidades, a representação, a generalização e a particularização podem ser de grande utilidade na exploração de relações funcionais. A actividade investigativa favorece também a exploração e colocação de questões por parte dos alunos, a formulação de conjecturas, o seu teste e reformulação e, por fim, a sua justificação e avaliação. A resolução deste tipo de tarefa permite que o aluno aprenda enquanto mobiliza os seus próprios recursos cognitivos e afectivos, ao perseguir um dado objectivo (Ponte, Brocardo, & Oliveira, 2003).
A apresentação deste tipo de tarefa no início de cada subtema, complementada por algumas instruções, procura tirar o maior partido da intuição dos alunos, que se envolvem autonomamente na sua exploração, a princípio, naturalmente, de modo informal. As tarefas foram concebidas e seleccionadas tendo em atenção a inclusão de situações inspiradas na realidade e, também, de situações inerentes à própria Matemática. A unidade de ensino inclui, ainda, a realização de exercícios de aplicação e problemas, maioritariamente retirados do manual escolar usado pelos alunos, visando a consolidação de conhecimentos.
O modo de trabalho utilizado nestas aulas tem em conta os objectivos a atingir em cada momento, incluindo trabalho individual, em pares e em pequenos grupos. No final da realização de cada tarefa ou grupo de tarefas decorre sempre uma discussão aprofundada envolvendo toda a turma onde os alunos partilham oralmente as suas estratégias de resolução com os colegas. A troca de ideias e o confronto de estratégias distintas levam a que estes momentos sejam espaços privilegiados para a colocação de dúvidas por parte dos alunos e para a discussão e sistematização dos conceitos em jogo. Durante a realização das tarefas os alunos fazem registos escritos do seu trabalho, o que os ajuda a organizar o seu raciocínio e constitui um apoio para a participação na discussão. Na resolução de duas delas, em particular, os registos escritos dos alunos são analisados pela professora que coloca novas questões a cada grupo. Estas questões estimulam os alunos, nas aulas seguintes, a ir um pouco mais além nas suas explorações. A avaliação na unidade de ensino inclui modalidades diversificadas, baseando–se num teste individual, duas fichas de trabalho resolvidas em pares, dois relatórios escritos das tarefas de investigação (já mencionados) e a observação efectuada pela professora, ao longo das aulas.
4. METODOLOGIA
Esta investigação usa uma metodologia qualitativa, de cunho descritivo e interpretativo (Denzin & Lincoln, 1994; Bogdan & Biklen, 1994). A unidade de ensino acima descrita foi realizada numa turma do 8.° ano de uma escola da área suburbana de Lisboa, leccionada pela primeira autora deste artigo, que assumiu, simultaneamente, o papel de professora e investigadora. Trata–se, assim, de uma investigação sobre a sua própria prática profissional (Ponte, 2002). Da turma faziam parte 27 alunos cujas idades oscilavam entre os 13 e os 16 anos. Reflectindo a imigração que se observa actualmente em Portugal, 10 destes alunos eram de nacionalidade estrangeira, provindo de países de língua oficial portuguesa – Angola, Cabo Verde, S. Tomé e Príncipe, Guiné e Brasil –ou de países do leste europeu, como a Roménia. A turma contava com diversos alunos com pelo menos uma retenção no seu percurso escolar e caracterizava–se por ter um aproveitamento global fraco na generalidade das disciplinas. Existia, no entanto, uma boa relação entre os alunos e os respectivos professores. A turma foi seleccionada por ter um horário que possibilitava a concretização dos procedimentos definidos para a recolha de dados. Os dados foram organizados em dois estudos de caso (Ponte, 2006; Yin, 1984), referentes a alunos desta turma, escolhidos de acordo com os seguintes critérios: (i) terem aproveitamento escolar diferenciado, um acima e outro abaixo da média; (ii) posicionarem–se, de modo distinto, em relação à disciplina de Matemática, um evidenciando interesse por ela e outro não.
Os dois alunos seleccionados para a realização dos estudos de caso são Sofia e André, que preenchiam estes critérios. Analisando os respectivos percursos escolares, é notória a distinção entre eles. Sofia tinha 13 anos e frequentava o 8.° ano pela primeira vez. Embora em algumas disciplinas manifestasse insegurança, era a aluna da turma que, globalmente, obtinha melhores classificações. No seu desempenho em Matemática revelava dificuldades relativamente a conceitos leccionados em anos anteriores e estava pouco à vontade na definição das suas próprias estratégias de resolução. Pelo contrário, André tinha 16 anos e, embora também frequentasse o 8.° ano pela primeira vez, contava já com três retenções. No final do 1.° período, teve classificação 2 em sete disciplinas2. Apesar disso, ocasionalmente, envolvia–se nas tarefas propostas na aula de Matemática. Dado o fraco aproveitamento global da turma, o desempenho de Sofia fazia–a sobressair relativamente aos restantes alunos, que a consideravam como "a melhor da turma", atribuindo a André o estatuto de "aluno mais problemático".
A postura de ambos os alunos em relação à escola e ao seu percurso escolar era, também, contrastante. Sofia era uma aluna bastante motivada para os estudos, enquanto André afirmava só andar na escola por obrigação. Relativamente à Matemática, Sofia afirmava gostar da disciplina, tal como das restantes, por ser "interessante". André, por seu lado, afirmava não gostar, porque "a matéria era complicada" e por não se interessar pelas aulas. Cada um destes alunos constituía um caso único na turma. Ambos acederam prontamente a participar neste estudo e revelaram disponibilidade para a realização das entrevistas. Sofia, no entanto, mostrou maior timidez do que André ao longo do processo de recolha de dados.
Os dados nos quais se baseia este artigo provêm sobretudo de duas entrevistas, realizadas em momentos distintos: a primeira antes da realização da unidade de ensino e a segunda depois de concluídas todas as actividades inerentes a esta unidade. As entrevistas, semi–estruturadas e individuais, tiveram por base um guião construído previamente e foram gravadas em vídeo, transcritas e analisadas. De cada um dos respectivos guiões fazia parte uma tarefa a resolver pelos alunos durante a entrevista. A tarefa resolvida na primeira entrevista continha um conjunto de questões sobre uma sequência associada a uma representação pictórica, uma questão sobre a interpretação da linguagem algébrica e um problema que envolve a linguagem algébrica. Esta entrevista teve como principal objectivo conhecer, numa fase inicial, as estratégias e os processos utilizados pelos alunos na exploração de situações que envolvem relações funcionais simples, baseados nos seus próprios recursos intuitivos. Além disso, visava compreender o modo como os alunos interpretam o papel da linguagem algébrica. A tarefa da segunda entrevista, mais longa do que a primeira, continha novamente um conjunto de questões sobre uma sequência associada a uma representação pictórica, uma questão relativa à interpretação da linguagem algébrica e um problema que envolve a linguagem algébrica. Além disso continha um grupo de questões sobre funções e duas questões que apelavam à resolução de uma equação com denominadores e de uma equação literal em ordem a uma das variáveis. Com a segunda entrevista pretendíamos identificar eventuais alterações induzidas pela vivência das experiências vividas durante a unidade de ensino no que se refere às estratégias e aos processos que utilizam e ao modo como interpretam e utilizam a linguagem algébrica em diferentes situações.
Neste artigo analisamos em pormenor os resultados relativos à questão 1 (Figura 1), que se refere ao modo como os alunos interpretam a linguagem algébrica. Esta questão, inspirada nas considerações de Usiskin (1988) sobre os diferentes usos da letra e na investigação de Küchemann (1981), envolve a apresentação aos alunos de um conjunto de expressões com as quais eles já tinham contactado anteriormente em tarefas contextualizadas resolvidas na aula:

Relativamente a estas expressões os alunos deviam explicar o papel que cada uma das letras poderia desempenhar, em cada caso. A questão foi incluída com a mesma formulação em ambas as entrevistas, para que se pudessem analisar e comparar as considerações efectuadas pelos alunos, antes e depois da unidade de ensino. Para esta questão foram seleccionadas expressões nas quais cada letra pudesse ser vista como representante de um conjunto de valores ou um elemento de uma propriedade, válida para um determinado conjunto de números, bem como expressões onde a letra desempenhasse o papel de incógnita, com o qual os alunos tinham trabalhado no ano lectivo anterior.
Assim: (i) a expressão A = c x l 3 foi escolhida por se tratar de uma fórmula simples de uma área, com a qual todos os alunos também já tiveram contacto, estando presentes diversas letras que podem ser interpretadas como variáveis, relacionadas de um modo específico; (ii) as expressões n+3, 2x n2 exemplificam a utilização da letra como número generalizado, assim como a(b + c) = ab+ac , que pode dizer respeito à propriedade distributiva da multiplicação em relação à adição, quando abc, e c são números reais. Por fim, (iii) a + 1 = 24 e 2x + 3=4x–1 são equações, onde a e x assumem o papel de incógnitas. A primeira é uma equação de tipo aritmético uma vez que a letra está presente apenas num dos seus membros. Por seu lado, a segunda equação, um pouco mais complexa, é de tipo algébrico, uma vez que a letra encontra–se em ambos os membros (Filloy & Rojano, 1989).
Neste artigo analisamos também o desempenho dos alunos em duas situações problemáticas envolvendo expressões algébricas. Na questão 2, proposta na primeira entrevista (Figura 2), as expressões podem tomar diversos valores, dependendo de um valor x desconhecido. O problema não tem uma resposta única, sendo, sobretudo um cenário propício para a experimentação e a colocação de hipóteses:

A questão 3, colocada na segunda entrevista (Figura 3), envolve uma corrida de 2000 metros na qual participam Miguel, que percorre 4 metros por segundo, e Rita, que percorre 3 metros por segundo mas tem um avanço inicial de 200 metros. Nesta situação são consideradas duas funções que relacionam o tempo com as distâncias percorridas por cada um dos participantes. A situação é acompanhada por um gráfico que ilustra o que sucedeu, sem muito pormenor, e pelas expressões algébricas das duas funções.

Nos dois problemas seleccionados tivemos em conta que: (i) a comparação das expressões algébricas sugere, na questão da primeira entrevista, a existência de uma desigualdade entre o número de calendários de cada uma das gémeas, ao passo que na segunda entrevista se procura uma igualdade entre os valores gerados por ambas as expressões; (ii) a situação proposta na segunda entrevista é acompanhada por uma outra representação – um gráfico – que fornece um auxílio adicional à sua interpretação. No entanto, apesar destas diferenças na formulação das questões, ambas permitem analisar o modo como os alunos trabalham com expressões algébricas do tipo ax e ax + b, em que a e b são números reais (a é não nulo).
Foram ainda efectuados registos de diálogos e outras ocorrências da aula pela professora no seu diário de bordo e recolhidos os registos escritos pelos alunos durante as aulas. A análise dos dados assumiu um carácter descritivo e interpretativo, sendo feita de forma indutiva e exploratória, ouvindo a voz dos participantes (Bogdan & Biklen, 1994). Para ambos os alunos, a análise do modo como interpretam a linguagem algébrica e da forma como a utilizam em situações diversas tem em conta as categorias que evidenciaram: (i) letra como incógnita; (ii) letra como número generalizado; e (iii) letra como variável. No que diz respeito ao modo como os alunos resolvem problemas envolvendo a linguagem algébrica são analisadas as suas dificuldades e as estratégias de resolução.
5. O CASO DE SOFIA
5.1. Desempenho antes da unidade de ensino
5.1.1. Interpretação da linguagem algébrica
Na primeira entrevista, quando se depara com as expressões algébricas da questão 1, Sofia reflecte sobre o papel das diversas letras e refere–se imediatamente ao que considera ser necessário fazer: "Temos que descobrir o valor delas". Deste modo, apresenta uma concepção muito pragmática sobre os símbolos, relacionada com o que pensa ser esperado da sua actividade enquanto aluna.
Letra como incógnita. Sofia não revela dificuldades em identificar o papel da letra quando esta é usada como incógnita, nomeadamente em duas equações. Tal como refere inicialmente, a sua preocupação é descobrir o seu valor. Esta tarefa torna–se simples no caso da equação a +1 = 24, uma vez que, de forma intuitiva, facilmente encontra o valor de a: "Esta aqui, tem que ser 23, porque 23 mais 1 dá 24". Nesta equação de tipo aritmético, utiliza o facto numérico 23 + 1 = 24 para apontar 23 como solução. A aluna interpreta o símbolo a como uma entidade que pode tomar um valor específico e revela ser capaz de, substituindo esse símbolo por 23, obter uma proposição verdadeira.
As suas dificuldades surgem no caso da equação da alínea f), 2x + 3 = 4x–l, de tipo algébrico, cuja solução não é tão visível por conter termos com incógnita em ambos os membros. Tal como se verifica no excerto que se segue, o discurso de Sofia evidencia o seu contacto anterior com a resolução de equações do 1.° grau:
Professora: E na f). Qual seria o objectivo, na f)?
Sofia: Eh... Ver se estas duas contas são iguais. O resultado...
Professora: Quais contas?
Sofia: 2x + 3 e 4x–1.
Professora: E como é que fazemos essas "contas"?
Sofia: Eh... Já não me lembro. [pausa prolongada]
Professora: Mas tu... Mesmo sem te lembrares, se tu pensasses sobre isso... O que é que tu achas que teria lógica fazer?
Sofia: Pôr de um lado... Pôr, de um lado, os números com letras e, do outro, só os números... [silêncio prolongado]
Professora: Estás a falar de quê, de resolver a equação, é isso?
Sofia: Sim... [timidamente]
A aluna revela a noção de que os dois membros da equação devem ser expressões equivalentes. No entanto, designa 2x + 3 e 4x–l por "contas" e afirma não se lembrar do modo de continuar o procedimento de resolução. Com a utilização do termo "conta", não é claro se se refere à ideia de adicionar indevidamente os termos, em cada um dos membros, ou à eventual substituição de x por um valor que seja solução da equação. No entanto, apesar da insistência da entrevistadora para esclarecer o seu pensamento, a aluna não vai mais além. Pelo contrário, opta por mencionar, de forma abreviada, os procedimentos que utilizou, no ano anterior, para a resolução de equações do 1.° grau, sugerindo a necessidade de isolar os termos com incógnita. Neste ponto, revela novamente insegurança e desconforto por não se recordar do modo como proceder, com pormenor, e acaba por não desenvolver mais a sua resposta.
Letra como número generalizado. Na primeira entrevista, o discurso de Sofia não contém qualquer evidência do reconhecimento da letra como possível representante genérico de um certo conjunto de números. Na sua análise, ignora, por completo, a expressão n + 3 e refere explicitamente não conseguir atribuir significado a a (b + c) = ab + ac. No que diz respeito à expressão 2x, acaba por identificá–la com o dobro de x mas esta identificação surge apenas após alguma confusão com o produto de x por x. A aluna manifesta, novamente, o seu desconforto por não se recordar do que aprendeu a este propósito no ano lectivo anterior:
Sofia: Esta aqui (2x) é... Acho que é... x vezes x ou...
Professora: x vezes x ...
Sofia: Ou 2 vezes x ... Ou...
Professora: É tudo a mesma coisa?
Sofia: Não, 2 vezes x ! Ou, não sei, eu não me lembro.
No que diz respeito a n2, refere que significa "n vezes n". Não é claro, do seu discurso, se associa a letra à possibilidade de representação de um ou mais números. Nesta fase a aluna manifesta, mais uma vez, a sua insegurança quanto à correcção das suas respostas.
Letra como variável. O significado que a aluna atribui à expressão A = c x l está relacionado com a identificação que faz com o conceito de área, que já domina. Relativamente a esta expressão a aluna volta a tentar descobrir "o valor" de uma letra, tal como o tinha feito relativamente às restantes equações. Deste modo, descreve o seu procedimento habitual, quando tem de calcular a área de um rectângulo, dadas as suas dimensões, que lhe permite descobrir o valor de A. De forma implícita, evidencia compreender que existe dependência entre as variáveis, ao sugerir que aquele valor depende dos valores do comprimento e da largura, interpretados como valores conhecidos: "Aqui da... Da área do... Do rectângulo. Nós temos que saber a medida do comprimento e a da largura, para sabermos a área".
No final da primeira entrevista a aluna refere que a questão 1 foi aquela em que sentiu mais dificuldades, justificando a sua resposta do seguinte modo:
Sofia: Não sei, é porque tem assim mais... Incógnitas... E...
Professora: Tem mais incógnitas? Onde é que tu estás a ver uma incógnita?
Sofia: Não sei... É tipo estas letras que... Fazem um bocado confusão.
Professora: Fazem um bocado de confusão, porquê?
Sofia: Não sei, não tem lá valor nenhum em concreto...
5.1.2. Uso da linguagem algébrica na resolução de problemas
Na situação proposta na questão 2 da primeira entrevista, Sofia tem de seleccionar a gémea com maior número de calendários. Tendo em conta os diferentes valores possíveis de x, é necessário que pondere sobre a expressão que, quando avaliada, permitirá obter um valor maior: 2x, que diz respeito a Joana, ou x + 4, que corresponde a Filipa.
Sem efectuar qualquer tipo de exploração da situação, a aluna aponta Joana como a gémea com mais calendários, baseando a sua argumentação no que as duas expressões algébricas lhe parecem transmitir. A sua resposta revela a noção intuitiva que tem de que o dobro de um número será sempre maior do que a soma desse número com quatro unidades:
Sofia: Talvez seja esta [aponta para Joana].
Professora: E porquê, és capaz de explicar porque é que te inclinas mais para essa resposta? [pausa] Olhas para lá e parece–te... ?
Sofia: Não, mas... Não sei... Eu tenho uma vaga ideia que isto é 2 vezes x, ou x vezes x. E... Era o dobro. Então esta (Filipa) tem só metade do que ela tem e mais quatro. Então tem menos do que ela...
Esta ideia revela a influência de experiências prévias em Aritmética no raciocínio de Sofia, no que diz respeito ao modo como encara as duas operações – adição e multiplicação –. Embora a sua resposta não seja válida para todos os valores possíveis de x, não mostra, em qualquer momento, a intenção de realizar um processo de experimentação que lhe permita confirmar ou refutar a sua conjectura. Mais uma vez não parece aceitar que a resposta a este problema possa depender do valor de x, isto é, que a sua variação possa provocar alteração nos valores de cada uma das expressões algébricas em que está inserida: 2x e x + 4 . A aluna evidencia, deste modo, que não interpreta a letra como variável.
5.2. Desempenho depois da unidade de ensino
5.2.1. Interpretação da linguagem algébrica
Letra como incógnita. Na segunda entrevista, Sofia continua a sentir–se bastante confortável sempre que a letra pode ser interpretada como incógnita. Apesar de ter resolvido equações por métodos formais na sala de aula, no período que decorreu entre as duas entrevistas, continua a utilizar um método intuitivo quando a situação assim o permite. Deste modo, tal como fez na primeira entrevista, identifica de imediato o valor 23 como solução da equação de tipo aritmético a +1 = 24, por ser o único valor que somado com uma unidade permite obter 24.
Na equação de tipo algébrico da alínea f), 2x + x + 4x x1, a aluna permanece calada durante algum tempo. Quando é questionada sobre o seu silêncio, explica que está a tentar resolver a equação. Numa primeira fase, escreve o seguinte:

A sua intenção seria resolver a equação pelo processo que envolve a transposição de termos de um membro para o outro. No entanto, a resolução rápida que efectua leva–a a cometer um erro, logo na primeira equivalência, passando o termo 3 para o 2° membro, sem a respectiva alteração de sinal. Quando acaba de escrever, continua a olhar fixamente para o que fez, em silêncio, procurando identificar eventuais incorrecções na sua resolução. Antes de corresponder ao pedido da professora para que explique o seu processo de resolução, Sofia opta por resolver a equação novamente. Mais tarde explica que o fez por se ter apercebido de que tinha cometido um erro ao passar um termo parao 2°membro daequação.
Professora: Não me queres explicar o que fizeste? Porque é que estás tão pensativa a olhar para aí?
Sofia: (traça uma cruz sobre o que fez) Enganei–me ali num sinal (recomeça a escrever).
Professora: E agora o que é que estás a fazer?
Sofia: Pois, fiz tudo de novo, por causa que aqui, enganei–me num sinal.
Professora: Hum, hum.
Sofia: Não troquei o +3 pelo –3. E agora já troquei.
Sofia evidencia a capacidade de analisar criticamente o seu trabalho, tentando encontrar eventuais erros. Quando isso acontece mostra que é capaz de os corrigir, obtendo, desta feita, a solução correcta. No entanto, para ficar plenamente convicta da correcção do resultado, verifica se o valor que encontrou é efectivamente solução da equação:
Professora: E agora sabes se está certo?
Sofia: Fazendo as contas, substituindo o x pelo 2...
Está certa.
Professora: Então, estávamos a falar do papel que a letra assume nessa expressão... O que é o x, nesse caso?
Sofia: Pois, é o 2.
Professora: Pois... É o 2. E tens mais alguma hipótese?
Questionada sobre a unicidade da solução, Sofia resolve testar, por meio de outra verificação, se x = –2 poderia ser também solução. Esta atitude pode ter sido influenciada pela sua experiência naresolução de equações do 2° grau, que em alguns casos têm como soluções dois números simétricos. A aluna toma a iniciativa de fazer esta verificação como precaução, procurando garantir que não se esquece de uma solução. Rapidamente verifica que –2 não é solução, dando a sua resposta anterior por concluída.
Letra como número generalizado. Na segunda entrevista, Sofia, manifesta progressos visíveis na interpretação da letra como possível representante de vários números. Relativamente às expressões n + 3 e a(b + c) = ab +ac, às quais não se tinha referido na primeira entrevista, responde o seguinte:
Professora: E na b)?
Sofia: Então, na b) é n, que pode ser qualquer número, mais três.
Professora: O que é que essas letras têm... Qual é o papel dessas letras, aí? Porque é que alguém escreve a, parêntesis, b mais c, fecha parêntesis, é igual a ab mais ac?
Sofia: Então, é para multiplicar o a pelo b e o a pelo c.
Professora: Só quando é um a, um b e um c que estão em questão, é isso?
Sofia: Não, pode ser qualquer número ou letra.
Observa–se que, neste momento, distingue claramente o significado de expressões como 2x e n2, manifestando mais uma vez a possibilidade de a letra tomar mais do que um valor:
Sofia: 2x é dois vezes qualquer número.
Professora: (...) Então e na g) (n2)?
Sofia: Então, é n vezes n.
Professora: n vezes n?
Sofia: Sim.
Professora: E isso quer dizer o quê?
Sofia: Então é um número, que pode ser qualquer, multiplicado por si mesmo.
Professora: Hum, hum. Então é o mesmo do que na d) (2x)?
Sofia: Não (convicta).
Professora: Não, porquê?
Sofia: Porque, na d), (2x) é duas vezes esse número e na g) (n2) é esse número vezes esse número.
Letra como variável. É na interpretação da letra como variável que Sofia revela maiores dificuldades em explicar o seu raciocínio. Dada a sua familiaridade com a fórmula dada, continua a associá–la, naturalmente, ao conceito de área. No entanto, exprime de uma forma bastante mais clara do que na primeira entrevista a relação de dependência entre as variáveis:
Sofia: O significado? Então, o A, da área, é igual ao comprimento vezes a largura.
Professora: Hum, hum. Sim. Mas qual é o papel que elas (as letras) desempenham? Servem para quê? São todas... Alguma delas é incógnita? Alguma delas é variável, como é que é?
Sofia: Sim, são variáveis, porque a área depende do comprimento e da largura.
5.2.2. Uso da linguagem algébrica na resolução de problemas
Na questão 3 pretende–se determinar em que instante se cruzam Rita e Miguel, isto é, o valor x para o qual as distâncias percorridas por ambos são iguais. Sofia não hesita, formulando uma equação que envolve as expressões algébricas respeitantes a cada uma das funções:
Sofia: Pois. Então, vou, ver qual é que é... Pronto, quando é que eles se vão encontrar. Tentar... (escreve)
Professora: Hum, hum. E essa expressão que escreveste?
Sofia: (pausa, enquanto a aluna analisa o gráfico)
Professora: Diz lá, o que é que estás a ver?
Sofia: Eu estava aqui a ver se eles se encontravam aos 200 segundos.
Como se pode observar, Sofia formula a equação e resolve–a correctamente, embora sem utilizar os sinais de equivalência. Depois de a resolver, verifica graficamente a sua solução, evidenciando ser capaz de trabalhar com diferentes representações das relações funcionais e de procurar certificar–se se o seu raciocínio tem sentido no contexto da questão.
Confiante de que ambos os amigos se cruzam ao fim de 200 segundos, utiliza novamente as expressões algébricas, mas agora para determinar a distância percorrida:
Sofia: (escreve)
Professora: E então?
Sofia: Eles vão–se encontrar aos 800 metros.
Por fim, Sofia explica que transformou a resolução deste problema na procura de um valor específico que produzisse um mesmo valor em ambas as expressões:
Sofia: Nesta... Pronto... Nesta equação...
Professora: Pois, nessa equação...
Sofia: (Nesta equação) Que eu fiz, tinha que dar um número exacto.
Professora: Pois. E porque é que tu escolheste essa equação 4x = 3x + 200?
Sofia: Porque a distância que ele tinha percorrido tinha que ser igual à que ela percorreu.
Na primeira entrevista, como vimos, Sofia tinha grande dificuldade em resolver equações. Nesta tarefa a aluna formula uma equação e utiliza a letra x no seu papel de incógnita, resolvendo–a correctamente e determinando o valor que corresponde a uma distância comum. Nota–se que recorre à equação como um instrumento que lhe permite resolver o problema de forma eficaz. Por fim, interpreta o valor obtido no contexto da situação e avalia correctamente o valor de ambas as expressões para x = 200, determinando a distância percorrida por Rita e Miguel no instante em que se cruzam. Observa–se, assim, que consegue utilizar adequadamente a linguagem algébrica, tirando partido das expressões de que dispõe.
6. O CASO DE ANDRÉ
6.1. Desempenho antes da unidade de ensino
6.1.1. Interpretação da linguagem algébrica
Após a leitura da questão 1 da primeira entrevista, André reage negativamente ao facto de todas as expressões incluírem símbolos literais, dizendo: "Isto das letras é mais confuso para mim". Refere, no entanto, relativamente a 2x e 2x+ 3 = 4x –1 que está "mais habituado a vê–las". Em seguida, procura desistir da interpretação das restantes, afirmando rapidamente: "As outras, não sei". Os comentários que faz a partir desse momento surgem apenas após nova insistência da professora.
Letra como incógnita. Quando analisa o papel desempenhado pelas letras, André utiliza espontaneamente o termo "incógnita". No que diz respeito à expressão da alínea c), a +1 = 24=, começa por dizer não lhe atribuir qualquer significado mas, em seguida, acrescenta: "a não ser que o a significasse um número que uma pessoa desconhece. Por exemplo, esse a, se fosse o 23, era mais 1... Pronto, 24". O facto de interpretar a letra como incógnita, leva–o a procurar descobrir o seu valor. Tal como fez Sofia, resolve intuitivamente a equação a +1 = 24 observando que 23 +1 = += . O aluno parece também compreender o que é uma equação e reconhecer se um valor é uma das suas soluções, quando obtém uma proposição verdadeira, após a substituição. Em seguida, perante uma equação mais complexa, de tipo algébrico, revela maiores dificuldades e sugere: "Na f) também é para fazer a conta". A continuação do diálogo permite compreender que, quando utiliza o termo "conta", se refere à adição indevida de termos que não são semelhantes. Por este motivo, enquanto observa a equação 2x + 3 + 4x –1, exprime a sua surpresa pelo facto de no 2° membro existir o termo 4x, quando esperava que a soma de 2x com 3 desse origem a 5x:
André: Aqui, como é que é isto? 4x.? Se tem 2x+ 3, vai dar igual. ..
Professora: Não pode dar ali 4x?
André: Não, é a maneira... Não percebo como vai dar.
Professora: O que é que tu esperavas que desse? Explica lá.
André: Não, porque... Não sei... Também o 3 o que é que podia estar aqui a fazer, se está aqui o 4x? Mas se isto é a somar e depois vai dar igual a 4x menos 1...(...) Se eu somasse ficaria 5x, não é, stora?
É notório que André observa o binómio 2x + 3 como uma expressão que não está terminada e que lhe sugere a possibilidade de simplificação. Deste modo, não interpreta o sinal "=" como um sinal que exprime uma relação de equivalência e considera o sinal "+" como um indicador da necessidade de proceder a uma adição, cujo resultado surge à direita do "=". Esta sua interpretação da expressão algébrica do 1.° membro e dos sinais "+" e "=" impede–o de conseguir resolver a equação de forma correcta.
Letra como número generalizado. Esta interpretação da letra é menos frequente no desempenho do aluno, no momento da primeira entrevista, uma vez que se refere preferencialmente à letra como incógnita:
André: Não sei... Aqui.. Por exemplo, onde está a dizer... 2x ... Tem uma letra... É uma incógnita.
Professora: É uma incógnita? O que é que quer dizer isso? Uma incognita...
André: Acho que.. É uma coisa que assim... Não se sabe, pronto... Tem um 2, não sabemos o que é que vem a seguir então, fica o x.
Neste excerto, é visível que André interpreta a letra x como uma entidade que representa apenas um número particular desconhecido. A entrevista prossegue do seguinte modo:
Professora: E não sabemos, colocamos lá um x. Para quê?
André: Para fazer a conta. Professora: Que conta?
André: Aqui na d) (2x) não tem, mas na f) (2x + 3 = 4x – 1), por exemplo. Na d) não tem nenhuma conta, tem um 2 a seguir ao x.
Observa–se que o aluno não identifica a operação de multiplicação existente entre a parte numérica e a parte literal do monómio 2x , evidenciando aqui uma nova dificuldade na interpretação da linguagem algébrica. Na sua primeira referência ao significado de 2x coloca a hipótese deste ser um número formado por dois algarismos, sendo 2 o das dezenas e x o das unidades. No diálogo que se segue, o aluno reage ao cenário eventual de que x tivesse o valor 4, confirmando este raciocínio, embora sem revelar grande confiança na sua validade:
Professora: E se tu soubesses o x? Vamos imaginar que era um 4 (...).
André: Podia ficar 24. Não sei, stora.
Professora: Ficava 24?
André: Não pode, acho eu, tirar assim o x para meter um 4. Já tinha que fazer a conta.
Professora: Qual conta?
André: Não sei, uma conta. Ou dizer.. É igual... x é igual a 4.
André não aceita esta particularização do valor de x, sugerindo que para obter esse valor seria necessário fazer "uma conta" que não identifica com clareza, ou obter, por algum processo, a equação x = 4.
Quando está perante expressões algébricas em que a letra pode representar mais do que um número, sente–se bastante inseguro. O seu comentário sobre a expressão n2 indica que a reconhece como uma potência e identifica o seu expoente, mas revela alguma preocupação por não conhecer a base: "Há aqui um expoente, não é? Mas eu não tenho um número que seja a base." A igualdade a(b + c) = ab + ac a única em que o aluno considera o papel da letra enquanto número generalizado, referindo que a, b e c podem estar no lugar de quaisquer números:
Professora: E na e) (a(b + c) = ab + ac)? O que é que tu achas da e)?
André: Na e) eu acho que também é fácil porque está a substituir os números. Professora: Está a substituir os números? (...)
André: É como se substituísse os números. Professora: Quais números?
André: Não, uns números quaisquer.
Em seguida, André afirma reconhecer alguma validade nesta expressão. No entanto, não consegue explicar o que o leva a ter esta sensação e é notório que volta a não identificar a operação de multiplicação subjacente, não relacionando a expressão com a propriedade distributiva de que esta operação goza, em relação à adição:
André: Tem aqui o a, não é?
Professora: Sim.
André: E depois tem o parêntesis, b mais c, é como se fossem os números.
Professora: Sim.
André: E depois tem o igual, que está aqui a explicar, que é igual a ab + ac (...). Não, mas é pela maneira como está a conta, como está isto feito, parece que tem lógica.
É curioso observar que ao longo desta entrevista, André não se refere directamente à expressão n + 3. No entanto, no final, quando analisa retrospectivamente o que fez em toda a tarefa, comenta, intrigado: "Não sei qual é a lógica de algumas letras ficarem assim, como a + 1 ou n + 3. Não percebo a lógica."
Letra como variável. No que diz respeito ao papel desempenhado pelas letras, na expressão A = c x l, André manifesta a sua estranheza, apesar de já ter trabalhado com ela no âmbito do estudo de áreas, no 1.° período deste ano lectivo:
Professora: Então e a a) (A = c x l), não te diz nada?
André: Não.
Professora: Nada? Um A, igual a c vezes l. .
André: Não, não me diz nada (...).
Professora: E porquê? Faz–te confusão?
André: É.. Faz confusão porque A... E depois vai dar c vezes /.l. Não estou a ver qual é... (interrompe a frase, não chegando a concluir o seu próprio raciocínio)
Mais uma vez, o aluno interpreta o sinal "=" como um indicador da necessidade de proceder a uma determinada operação. No entanto, o que na sua perspectiva será o "resultado obtido" consiste numa expressão literal c x l, o que não faz sentido para si. No final desta entrevista, André selecciona esta questão como uma daquelas em que sentiu maiores dificuldades, devido à presença da equação A = c x l.
6.1.2. Uso da linguagem algébrica na resolução de problemas
Depois de ler o enunciado do problema das gémeas, André analisa as expressões que lhe são dadas, procurando descobrir, a partir delas, a que poderá representar um maior número de calendários. André opta por Filipa, baseando–se na sua interpretação da expressão x + 4:
André: Sim, porque se ela está a dizer... "Nesse caso... E nesse caso, o número de calendários que eu já tenho pode ser representado pela expressão x + 4", somado ficava 4x. (pausa)
Professora: E tu achas que o 4x era maior do que o 2x, é isso?
André: (acena a cabeça, dizendo que sim)
A redução de x + 4 a 4x mostra que André tem dificuldade em aceitar a falta de fechamento das expressões algébricas. No entanto, o aluno parece não ter a certeza de que a resposta que deu seja válida. Quando é questionado sobre a possibilidade de encontrar outro processo para responder à questão, afirma sentir necessidade de conhecer o número de calendários e não consegue desenvolver outra estratégia que lhe dê maior convicção:
Professora: Tens a certeza do que estás a dizer?
André: Não, não tenho a certeza (pausa).
Professora: Hum, e se tu não tivesses a certeza, tinhas alguma forma de confirmar aquilo que estás a dizer?
André: Só se eu soubesse o número de calendários.
O aluno não tenta imaginar o que sucederia para quaisquer valores concretos que a letra pudesse representar, nem as alterações que isso provocaria em ambas as expressões algébricas. Deste modo, evidencia o facto de não conseguir utilizar a letra como variável, nomeadamente em situações problemáticas como esta.
6.2. Desempenho depois da unidade de ensino
6.2.1. Interpretação da linguagem algébrica
Letra como incógnita. Ao referir–se ao papel de a na equação a +1 = 24=, André começa por se concentrar na expressão algébrica do 1.° membro, a +1:
André: Aqui, a + 1, acho também que é a mesma coisa só que por ter o resultado já temos que saber qual é.
Professora: Não percebi...
André: O a também podia ser qualquer número, só que como é mais um igual a vinte e quatro, é como se tivéssemos de descobrir qual é o número que tem a.
Olhando apenas para a expressão algébrica a + 1 mostra compreender que a pode assumir qualquer valor. No entanto, a inclusão da expressão numa equação faz com que considere a possibilidade de determinar um valor específico para a. André aponta novamente 23 como solução, descobrindo o valor intuitivamente e sugerindo que esta equação até é "fácil demais". À semelhança do que fez nesta equação, tenta descobrir uma solução para 2x + x + 4x x1, utilizando um método informal. Por ser uma equação de tipo algébrico esta tarefa torna–se mais complexa. Quando é questionado sobre se é capaz de descobrir o valor de x, o aluno afirma:
André: Se me dessem assim a conta se calhar não.
Professora: Não?
André: Se me dessem só assim a conta para descobrir o número de x.
Professora: Ah, sim, mas se te deixassem resolver (formalmente)?
André: Sim.
André resolve a equação com recurso às regras práticas e revela que consegue efectuar correctamente procedimentos que desconhecia na 1.ª entrevista:
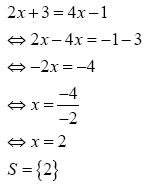
Constata–se que André resolve correctamente esta equação. A sua explicação permite compreender que utiliza as regras práticas que incluem a transposição de termos de um membro para o outro para separar os termos com incógnita dos termos independentes:
André: Então, é: deixo o 2x e passo o 4x para o primeiro termo. ..
Professora: Membro.
André: Membro, é isso. E fica...
Professora: Porquê? Estás a tentar fazer o quê?
André: Porque é positivo e fica negative. Que é para juntar os que têm letras com letras e assim. Depois aqui é a somar... Somar, fazer as contas, não é.
Professora: Fazer as contas.
André: E depois aqui é x igual a... –4 sobre –2.
Professora: Porquê?
André: Então, temos aqui um número. Fica x = –4 e depois passa o –2 cá para
baixo. Professora: Cá para baixo?? (...) É que eu não estou a perceber... Mas porquê?
André: Porque eu acho que é assim.
Na parte final, perante a equação –2x = –4, André determina correctamente o valor de x, quando divide –4 por –2. Contudo, não consegue explicar o processo que utiliza, referindo que não se recorda das razões que justificam. Neste ponto evidencia o facto de ter utilizado um processo de resolução memorizado, sem conhecer a sua justificação, não revelando uma compreensão plena da resolução de equações do 1.° grau que utiliza habitualmente.
Salienta–se, mais uma vez, o facto de ter deixado de cometer um dos seus erros iniciais mais frequentes, que consistia na adição de termos não semelhantes, procurando simplificar expressões como 2n + 3 e a + 1. Nesta entrevista, quando a letra é utilizada como incógnita, André não manifesta qualquer reacção negativa. O mesmo sucede quando esta desempenha o papel de número generalizado.
Letra como número generalizado. Embora continue a utilizar o termo "incógnita" com muita frequência, mesmo quando esta designação não se adequa à situação em causa, André reconhece claramente os momentos em que a letra pode expressar uma generalização. É o que sucede relativamente a expressões a que anteriormente afirmava não atribuir significado, como a +1 ou n + 3 . Nesta fase, André vê 3n + 3 como um número ao qual são adicionadas 3 unidades:
André: Aqui, n + 3, o n é que está a substituir um número.
Professora: Um número?
André: Sim.
Professora: Um número, como?
André: Uma incógnita, pode ser? O n é uma incógnita.
Professora: Um número qualquer ou um número em particular?
André: Não, aqui pode ser um número qualquer.
Professora: Pode ser um número qualquer?
André: Sim, mais 3.
No que toca a n2, André reconhece também essa possibilidade, afirmando sem hesitar que "O n2 é n x n ." Em seguida acrescenta: "Pode ser um número qualquer, um número qualquer vezes ele". Embora também reconheça o papel de número generalizado em expressões como 2x, é relativamente ao significado desta expressão que André revela maior insegurança:
Professora: E no 2x significava o quê?
André: Era 2x. Era x mais x.
Professora: Era x + x?
André: Hum, hum.
Professora: Hum, hum. Ou então?
André: Dois vezes x.
Professora: Diz?
André: Dois vezes x. (hesitante)
Questionado sobre se considera a hipótese de descobrir um valor único para x, André refere que isso pode suceder, mas apenas "dependendo de qual for a conta", expressão através da qual procura referir–se à situação em que 2x constitui o 1.° membro de uma equação.
Apesar das diversas imprecisões existentes na sua linguagem, é notório que o aluno aceita o papel da letra enquanto incógnita e número generalizado, encarando as expressões de um modo menos dramático do que acontecia inicialmente. O ponto onde evidencia dificuldades mais acentuadas está nas expressões que incluem mais do que uma letra. A sua reacção negativa imediata, leva a que não procure explicar o que pensa com suficiente empenho, agindo como se pretendesse passar rapidamente a outra questão na entrevista. Questionado pela professora sobre o significado que atribui a a(b + c) =ab + ac, gera–se o seguinte diálogo:
Professora: E a seguir, na alínea e), tantas letras, o que é que essas letras simbolizam?
André: Chatices.
Professora: Hum, hum.
André: É difícil.
Professora: Isso que está aí escrito é verdade?
André: Acho que sim.
Professora: Achas que sim?
André: Eu acho que sim.
Professora: Porquê?
André: Não sei.
Professora: Mas não significa nada para ti?
André: Porque, se tivesse só isto (aponta para o primeiro membro) e tivesse eu que completar, eu não sabia fazer.
Professora: Não sabias fazer?
André: Acho que não.
Professora: Hum.
André: Mas acho que é, não sei. Ou acho também que está mal... Não sei.
Professora: Estás a responder um bocadinho à toa...
André: Como é b + c não sei porque é que está aqui ab + bc ou se podia estar também a + bc. Ó stora, eu não sei isso das letras.
Inicialmente, o aluno parece reconhecer a validade da expressão, mas o seu discurso reforça o facto de sentir que não consegue aplicar a propriedade distributiva, principalmente quando dispõe apenas de símbolos literais.
Letra como variável. A sua reacção negativa perante expressões com mais do que uma letra é também visível quando se refere a A = c x l:
André: Esta aqui não sei (aponta para a a) ).
Professora: Essa aí não sabes, hum... Porque é que não sabes?
André: É só letras.
A = c x l é a expressão que se encontra na alínea a) da questão referente à interpretação da linguagem algébrica. Por este motivo, assim que a observa, profere estas palavras de modo imediato e procura passar para a expressão seguinte, evitando novas perguntas, por parte da professora. Não há qualquer evidência de que o aluno interprete a simbologia no seu papel de variável.
6.2.2. Uso da linguagem algébrica na resolução de problemas
Quando inicia a sua análise da corrida de Rita e Miguel, André começa por fazer uma interpretação correcta dos dados fornecidos e do modo como esta se deu: Rita partiu com um avanço de 200 metros mas "o Miguel é mais rápido e chega primeiro à meta". A propósito da resolução deste problema, André procura no gráfico o instante em que Rita e Miguel se cruzam, isto é, o ponto onde se dá a "ultrapassagem":
Professora: E em que instante é que eles se vão cruzar?
André: (observa o gráfico) É nos 700 metros, acho eu... 800.
Professora: Instante, é o tempo em que eles...
André: 800.
Professora: Tempo, tempo!
André: Ah, é 200 ou 200 e pouco.
Professora: Ah, então não sei... (com alguma reserva)
Perante esta leitura despreocupada do gráfico, André apercebe–se de que a sua resposta não é suficientemente precisa, uma vez que a professora evidencia algumas reservas. André justifica, em seguida, que "as barras estão um bocado grossas", referindo–se ao reduzido detalhe que consegue extrair do gráfico. Continuando a analisá–lo, centra a sua atenção nos 2000 metros onde ambos os alunos chegam, em instantes distintos. Quando é questionado sobre a eventual ocorrência de um cruzamento a 2000 metros do ponto de partida, responde: "Que eu saiba não, pelo gráfico." Volta então a centrar–se nos 200 metros que leu anteriormente e procura efectuar aritmeticamente o cálculo das imagens que lhe correspondem, através de cada uma das funções, explicando que está a tentar "fazer as contas, sem olhar para o gráfico":
Professora: Quais contas?
André: Eram as contas daqui: 200 x 4 dá 800; 3 x.. Dá, é isso!
Professora: É isso, o quê? Continuo sem entender.
André: Então, 200 x 4 dá 800. E 3 x 200 + 200 dá 800. Ficavam na mesma distância ao mesmo tempo.
Em seguida, André quando procura organizar a sua resposta escrita, reflecte sobre a sua resolução e hesita, criticando–a:
André: Eu descubro, mas a stora está a pedir a justificação, se eu escrevo como é quefizas contas...
Professora: Sim, mas as tuas contas justificam perfeitamente.
André: Da maneira como eu vou explicar, a stora... Acho que não era a justificação correcta.
O aluno considera não ter explicado convenientemente a obtenção do valor 200 que observou no gráfico. Na continuação do diálogo descreve como teria procedido se não dispusesse dessa representação, no enunciado da questão:
Professora: Mas a tua pergunta tem lógica. E se tu não tivesses o gráfico, depois como é que fazias? O gráfico deu–te uma ideia, não é, do 200. E depois essa parte convencia–te, 200 x 4 e 3 x 200 + 200 dá 800. Mas se tu não tivesses o gráfico, como é que tu chegavas a esse 200?
André: Se calhar via qual era o que estava mais perto... o tempo e a distância em que estavam mais perto um do outro e depois tentava ver.
Nesta fase, André refere–se à determinação do valor obtido pela expressão, num processo de tentativas, no qual procuraria que as distâncias produzidas para cada um dos dois corredores fossem cada vez mais próximas uma da outra. Tentando averiguar se André conseguiria formular uma equação que lhe permitisse determinar o valor 200, tal como fez Sofia, a professora continua a questioná–lo:
Professora: E se fosse a partir desta expressão, tu não eras capaz de arranjar uma forma de descobrir quando é que elas seriam iguais?
André: Acho que é a mesma coisa que fazer isto (refere–se aos cálculos que efectuou e que entretanto escreveu na sua folha)
André utiliza as expressões algébricas, avaliando–as em casos concretos e interpretando–as como a tradução dos procedimentos que deve efectuar. A partir da substituição de x por um valor concreto, é capaz de avaliar o valor produzido por cada uma delas. Parece, assim, aceitar a falta de fechamento das expressões algébricas, embora não revele a capacidade de se servir da Álgebra como instrumento na resolução de problemas.
7. DISCUSSÃO: OS PERCURSOS DE SOFIA E ANDRÉ
Antes da unidade de ensino, Sofia encara a letra apenas como incógnita. Deste modo, quando se depara com as expressões algébricas incluídas na questão 1, exprime imediatamente a necessidade de descobrir o valor que as letras representam embora isso só faça sentido no caso das equações do 1.° grau. A aluna não interpreta a letra como número generalizado e revela dificuldades em encará–la como variável. Na questão 2, a sua resposta baseia–se, sobretudo, na sua intuição (incorrecta) sobre os efeitos das operações de adição e multiplicação, decorrente das suas experiências anteriores em Aritmética. Não reconhece que as expressões podem tomar valores distintos, dependendo dos valores de x, evidenciando, novamente, dificuldades com a noção de variável. Além disso, não revela capacidade de usar outros processos, aritméticos ou algébricos, para retirar conclusões sobre a situação, interpretando as expressões de um modo precipitado. Revela, ainda, dificuldades quanto ao significado de algumas das expressões, nomeadamente ao confundir 2x com x2. Na resolução de equações do 1.° grau manifesta comportamentos distintos, dependendo do seu grau de dificuldade. Consegue resolver a equação de tipo aritmético por um processo intuitivo, mostrando compreender a noção de equação e reconhecer se um número é (ou não) solução, por substituição. No entanto, nesta fase, não consegue resolver a equação do tipo algébrico. Revela, neste ponto, ter contactado com o processo de resolução de equações no ano anterior e mostra–se preocupada por não se recordar como fazê–lo.
A vivência da unidade de ensino proporciona a Sofia diversas oportunidades de aprendizagem. O trabalho que desenvolve com sequências de números e funções leva–a a efectuar generalizações, que formula inicialmente em linguagem corrente. As discussões gerais com toda a turma, permitem–lhe reflectir sobre o uso da linguagem algébrica, que adopta, de uma forma progressiva ao longo da unidade. A resolução de tarefas de natureza investigativa proporciona–lhe a oportunidade para explorar situações que envolvem variação, construindo as suas próprias estratégias, conjecturando e refutando conjecturas. Durante toda a unidade, a aluna revela a preocupação de usar a simbologia algébrica com compreensão, procurando explicitar, em cada caso, o significado que lhe atribui.
Depois da leccionação desta unidade, Sofia consegue distinguir claramente os diferentes papéis que as letras podem assumir, passando a reconhecer, com clareza, o papel da letra enquanto instrumento que permite expressar generalizações. Quanto ao papel da letra como variável, revela também uma noção mais completa reconhecendo a dependência entre variáveis. Além disso, revela a capacidade de utilizar a linguagem algébrica na resolução de problemas, recorrendo à Álgebra como instrumento. A ideia que evidencia na primeira entrevista, de que a utilização das letras, em Matemática, tem como único propósito a representação de uma incógnita, dá lugar a uma visão mais dinâmica e multifacetada da simbologia algébrica. Após a unidade de ensino, quando a aluna foca a sua atenção numa equação onde a letra desempenha o papel de incógnita, continua a procurar imediatamente resolvê–la mas mostra que o consegue fazer por métodos intuitivos e formais. O facto de ter aplicado com rapidez um processo de resolução da equação leva–a a cometer um ou outro erro de eliminação. No entanto, o seu sentido crítico leva–a a olhar de novo para o seu trabalho, revelando capacidade de corrigir o erro que cometeu e verificar se o valor obtido é solução. Revela igualmente fortes progressos na compreensão do significado das expressões algébricas. O trabalho realizado nesta unidade ajuda–a a recordar o que tinha estudado em anos anteriores e posteriormente esquecido e a atribuir significado às expressões algébricas.
Embora seja uma aluna habituada a atingir classificações superiores à maior parte dos colegas, na disciplina de Matemática, Sofia mostra–se retraída, na primeira entrevista, quando as tarefas propostas não se enquadram nos moldes a que está habituada ou apelam a conhecimentos anteriores. Receando falhar, não arrisca na exploração das situações e na construção de novo conhecimento sobre elas. Na segunda entrevista continua a revelar timidez, traço marcante da sua personalidade, mas procura "experimentar" e criticar o que vai obtendo. Embora pareça ter, por vezes, alguma falta de segurança, evidencia uma maior capacidade de se envolver na resolução das tarefas.
Pelo seu lado, André, na primeira entrevista, começa por se mostrar intimidado pela linguagem algébrica. Quando consegue ultrapassar essa primeira reacção, atribui às letras, em geral, o papel de incógnitas. Não as interpreta como números generalizados, a não ser quando se refere a a(b + c) =ab + ac , caso em que admite a possibilidade de que as letras representem quaisquer números. Manifesta também dificuldades na interpretação da letra como variável nas duas situações desta entrevista que lhe fazem apelo: a interpretação de A = c x l (Questão 1) e a resolução do problema (Questão 2). Nesta última situação, a sua argumentação não é válida porque se baseia na transformação indevida da expressão x + 4 em 4x. O aluno lamenta não conhecer o número de calendários, mas não explora os diferentes valores que as expressões algébricas podem produzir, dependendo do valor x, em que Joana terá pensado. Mesmo não tendo a certeza quanto à validade do raciocínio que efectua a propósito das expressões algébricas, não consegue desenvolver estratégias alternativas para ganhar maior convicção. No seu discurso são também evidentes algumas incorrecções ao trabalhar com expressões algébricas: a identificação de um monómio como 2x com um número com dois algarismos começado por 2; a não aceitação do fechamento das expressões algébricas do tipo ax + b e a atribuição aos sinais "=" e "+" de um papel idêntico ao que têm em Aritmética, levando–o à adição indevida de termos não semelhantes. André mostra que compreende o que é uma equação do 1.° grau e sabe verificar, por substituição, se um número é, ou não, sua solução. Resolve intuitivamente uma equação de tipo aritmético mas não consegue resolver uma equação de tipo algébrico, porque, mais uma vez, vêm ao de cima as suas dificuldades em trabalhar com expressões algébricas.
Durante a unidade de ensino, André envolve–se com entusiasmo na realização das tarefas, ao contrário do que sucedia anteriormente em Matemática, onde, em geral, não revelava qualquer interesse pelas actividades propostas. A natureza da primeira tarefa proposta, aparentemente desligada de uma linguagem mais formal, levou o aluno a envolver–se na sua resolução. A partir desse momento, viveu com entusiasmo a maior parte das tarefas propostas, dado o seu carácter desafiador. Ao longo do tempo, a relação de André com a simbologia parece melhorar significativamente. Observa–se que o recurso à linguagem algébrica é menos frequente no seu desempenho do que no de Sofia e que, em alguns momentos da unidade de ensino evidencia dificuldades e desempenhos menos conseguidos. Salienta–se todavia que, para este aluno, o trabalho progressivo com a simbologia, inicialmente associada à observação de regularidades e à generalização, parece ter sido um contributo importante da vivência da unidade de ensino.
Verifica–se, na segunda entrevista, que o aluno progride claramente no seu sentido do símbolo, alargando o conjunto de expressões às quais consegue atribuir significado. A reacção negativa que manifesta na primeira entrevista perante a linguagem algébrica atenua–se, embora continue a sentir–se incomodado perante expressões com várias letras. No que diz respeito à clarificação do significado das expressões algébricas, manifesta também importantes progressos, aceitando a sua existência própria e libertando–se dos erros que cometia anteriormente. Este aspecto reflecte–se no seu desempenho na resolução de equações do 1.° grau. Em casos simples, utiliza métodos formais e informais com correcção mas não consegue explicar o porquê do que está a fazer. Parece valorizar mais o facto de conseguir obter rapidamente a solução da equação e responder à questão com sucesso do que compreender as razões que justificam os procedimentos que efectua. Na resolução de problemas que envolvem linguagem algébrica, encontra o valor pretendido por observação do gráfico e mostra aritmeticamente que este se adequa à situação. O facto de ter determinado o valor 200 com base no gráfico e de não ter explicado convenientemente de onde surgiu este valor leva–o a pensar que a sua resposta pode estar incompleta. Ainda revela dificuldades em operar estruturalmente com as expressões algébricas e não recorre à formulação de equações como instrumento para a resolução de problemas. No entanto, regista–se uma evolução substancial em relação à primeira entrevista, uma vez que aceita considerar um valor particular para x e tem consciência de que os seus diferentes valores podem gerar alterações nos valores obtidos em cada uma das expressões.
8. CONCLUSÃO
Sofia e André são dois alunos com características nitidamente contrastantes: a sua idade, o seu percurso escolar, a relação que mantêm com a escola e, em particular, com a disciplina de Matemática. No entanto, na primeira entrevista ambos revelam dificuldades na interpretação da linguagem algébrica. Ambos mostram interpretar preferencialmente a letra como incógnita e sentem a necessidade de descobrir o seu valor. Relativamente à compreensão da linguagem algébrica e à resolução de equações do 1.° grau, as dificuldades de Sofia prendem–se essencialmente com o facto de se sentir inibida por não se recordar do que aprendeu a esse respeito, não procurando utilizar os seus próprios processos de raciocínio. André revela dificuldades mais acentuadas e manifesta um receio generalizado sempre que se encontra perante a linguagem algébrica. É evidente a influência das experiências anteriores vividas por estes alunos no âmbito da Álgebra, que geraram um sentimento de incomodidade na actividade que são chamados a desenvolver, principalmente na primeira entrevista.
Tal como referem Kieran (1992) e Küchemann (1981), a interpretação da letra como número generalizado e a construção do conceito de variável são dois dos aspectos mais complexos para os alunos. No entanto, a resolução de tarefas com carácter exploratório e investigativo e a sua discussão aprofundada na aula parecem ter contribuído fortemente para a construção de uma visão mais ampla sobre o papel da simbologia e as suas diferentes utilizações: Sofia vai mais além, aceitando o papel da letra como incógnita, número generalizado e, pelo menos parcialmente, como variável; André, que parte de uma situação mais desfavorável, não progride tão rapidamente, mas é notável a forma como progressivamente deixa de cometer certos erros e alarga o leque de expressões algébricas a que consegue atribuir significado.
Desde a primeira entrevista, os alunos revelam compreender o que é uma equação, conseguindo identificar se um número é ou não sua solução. Sofia consegue recordar até alguns aspectos do método que aprendeu para a sua resolução formal. No entanto, isso não impede que, na primeira entrevista, ambos não conseguissem resolver equações do tipo algébrico. Após a unidade de ensino ambos os alunos continuam a resolver intuitivamente as equações mais simples e procuram usar as regras práticas mais frequentes para rapidamente obterem uma solução. Sofia supera os erros que comete pelo modo como verifica e analisa cuidadosamente o seu trabalho. Por seu lado, a compreensão de expressões algébricas permitiu a André melhorar o seu desempenho neste domínio. Em ambos os alunos são igualmente visíveis progressos na resolução de equações do 1.° grau.
No que se refere à resolução de problemas envolvendo a linguagem algébrica, Sofia e André também registam significativa evolução. Na situação inicial fazem considerações sobre a situação das gémeas sem se envolverem num processo de experimentação e particularização. Na segunda entrevista, os alunos mostram melhor desempenho, evidenciando a capacidade de adoptar estratégias que lhes permitem tirar conclusões sobre a situação proposta. Os conhecimentos de Sofia sobre os efeitos das operações de multiplicação e adição dão lugar à formulação de uma equação que traduz o problema em causa e que lhe permite determinar a solução pretendida. Por seu lado, André articula as diferentes representações da relação funcional, descobrindo a solução e provando a sua validade. Ambos os alunos reconhecem que as expressões algébricas podem tomar valores distintos consoante o valor de x, revelando–se também mais à vontade para desenvolverem o seu próprio raciocínio, explorando as situações propostas e confiando nas suas potencialidades para definir novas estratégias de actuação.
A resolução de tarefas com carácter exploratório e investigativo, envolvendo relações funcionais, e a sua discussão parecem assim ter contribuído de forma assinalável para o desenvolvimento de um significado mais rico da linguagem algébrica, nas suas diferentes utilizações, por parte dos alunos, promovendo o desenvolvimento do seu sentido do símbolo e a evolução do seu pensamento algébrico. As dificuldades que ocasionalmente continuam a manifestar comprovam, no entanto, que a compreensão dos fundamentos da Álgebra é um processo lento, que não se esgota num só ano de escolaridade.
REFERÊNCIAS
Arcavi, A. (1994). Symbol sense: Informal sense–making in formal mathematics. For the Learning of Mathematics, 14(3), 24–35. [ Links ]
Arcavi, A. (2006). El desarrollo y el uso del sentido de los símbolos. In I. Vale, T. Pimentel, A. Barbosa, L. Fonseca, L. Santos & P. Canavarro (Eds.), Números e Álgebra na aprendizagem da matemática e na formação de professores (pp. 29–47). Caminha: SEM–SPCE. [ Links ]
Bogdan, R. C., & Biklen, S. K. (1994). Investigação qualitativa em educação. Porto: Porto Editora. [ Links ]
Booth, L. R. (1984). Algebra: Children's strategies and errors. Windsor: Nfer–Nelson. [ Links ]
Booth, L. R. (1988). Children's difficulties in beginning algebra. In A.F. Coxford & A.P. Schulte (Eds.), The ideas of algebra, K–12: 1988 Yearbook (pp. 20–32). Reston, VA: NCTM. [ Links ]
Denzin, N. K., & Lincoln, Y. S. (1994). Introduction: entering the field of qualitative research. In N. K. Denzin, & Y. S. Lincoln (Edits.), Handbook of qualitative research (pp. 1–17). Londres: Sage. [ Links ]
Driscoll, M. (1999). Fostering algebraic thinking: A guide for teachers, grades 6–10. Portsmouth, NH: Heinemann. [ Links ]
English, L., & Warren, E. (1998). Introducing the variable through pattern exploration. Mathematics Teacher, 91(1), 166–70. [ Links ]
Filloy, E., & Rojano, T. (1989). Solving equations: The transition from arithmetic to algebra. For the Learning of Mathematics, 9(2), 19–25. [ Links ]
Kaput, J. (1999). Teaching and learning a new algebra. In E. Fennema & T. Romberg (Eds.), Mathematics classrooms that promote understanding (pp. 133–155). Mahwah, NJ: Erlbaum. [ Links ]
Kieran, C. (1992). The learning and teaching of school algebra. In D.A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 390–419). New York, NY: Macmillan. [ Links ]
Küchemann, D. (1981). Algebra. In K.M. Hart (Ed.) Children's understanding of mathematics: 11–16 (pp. 102–119). London: Murray. [ Links ]
MacGregor, M., & Stacey, K. (1997). Students' understanding of algebraic notation: 11–15. Educational Studies in Mathematics, 33(1), 1–19. [ Links ]
Matos, A. (2007). Explorando relações funcionais no 8."ano de escolaridade: Um estudo sobre o desenvolvimento do pensamento algébrico (Dissertação de Mestrado, Universidade de Lisboa, disponível em http://ia.fc.ul.pt). [ Links ]
ME–DGEBS (1991). Programa de Matemática: Plano de organização do ensino–aprendizagem (3.° ciclo do ensino básico). Lisboa: Ministério da Educação, Direcção–Geral dos Ensinos Básico e Secundário. [ Links ]
NCTM (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: NCTM. [ Links ]
NCTM (2000). Principles and standards for school mathematics. Reston, VA: NCTM. [ Links ]
Oliveira, H., Segurado, I., Ponte, J. P, & Cunha, M. (1999). Investigações matemáticas na sala de aula: Um projecto colaborativo. (Acedido de http://ia.fc.ul.pt/textos/p_121-131.PDF em 24– 03–2008) [ Links ]
Ponte, J. P. (2002). Investigar a nossa própria prática. In GTI (Org.), Reflectir e investigar sobre a prática profissional (pp. 5–28). Lisboa: APM. [ Links ]
Ponte, J. P. (2004). Problemas e investigaciones en la actividad matemática de los alumnos. In J. Giménez, L. Santos & J. P. da Ponte (Eds.), La actividad matemática en el aula (pp. 25–34). Barcelona: Gráo. [ Links ]
Ponte, J. P. (2006). Estudos de caso em educação matemática. BOLEMA, 25, 105–132. [ Links ]
Ponte, J. P. (2007). Investigations and explorations in the mathematics classroom. ZDM, 39(5–6), 419–430. [ Links ]
Ponte, J. P., Brocardo, J., & Oliveira, H. (2003). Investigações matemáticas na sala de aula. Belo Horizonte: Autêntica. [ Links ]
Rojano, T. (1996). The role of problems and problem solving in the development of algebra. In N. Bednarz, C. Kieran & L. Lee (Eds.), Approaches to algebra: perspectives for research and teaching (pp. 55–62). Dordrecht: Kluwer. [ Links ]
Schoenfeld, A. H., & Arcavi, A. (1988). On the meaning of variable. Mathematics Teacher, 81(6), 420–427. [ Links ]
Sfard, A., & Linchevski, L. (1994). The gains and piftalls of reification: The case of algebra. Educational Studies in Mathematics, 26, 191–228. [ Links ]
Ursini, S., & Trigueros, M. (2001). A model for the uses of variable in elementary algebra. In M. van den Heuvel–Panhuizen (Ed.), Proceedings of the 25th Conference of the International Group for the Psychology of Mathematics Education (vol. 4, pp. 327–334). Utrecht: Utrecht University. [ Links ]
Usiskin, Z. (1988). Conceptions of school algebra and uses of variables. In A. F. Coxford & A. P. Schulte (Eds.), The ideas of algebra, K–12 (pp. 8–19). Reston, VA: NCTM. [ Links ]
Yin, R. (1984). Case study research: design and methods. Newbury Park, CA: Sage. [ Links ]
NOTA
1 Para uma descrição mais detalhada consultar Matos (2007). regresar
2) Na escala de 1 (mínimo) a 5 (máximo), 1 e 2 são consideradas classificações insatisfatórias e 3, 4 e 5 satisfatórias. regresar
3) Fórmula usualmente associada, em Portugal, ao cálculo da área de um rectângulo (Área = comprimento x largura). regresar