Artículos

 

A Search for a Constructivist Approach for Understanding the Uncountable Set P(N)

 

Cindy Stenger*, Kirk Weller**, Ilana Arnon***, Ed Dubinsky****, Draga Vidakovic*****

 

* University of North Alabama, USA; clstenger@una.edu

** University of Michigan – Flint, USA; wellerk@umflint.edu

*** Center for Educational Technology, Tel–Aviv, Israel; ILanaA@cet.ac.il

**** Florida International University, USA; edd@math.kent.edu; eddub@mindspring.com

***** Georgia State University, USA; matdnv@langate.gsu.edu; draga@gsu.edu

 

RESUMEN

En el presente estudio nos preguntamos si los individuos construyen estructuras mentales para el conjunto P(N) que da significado a la expresión "todos los subconjuntos de N". Los aportes de nuestra investigación en relación con esta pregunta tienen dos vertientes. Primeramente, identificamos las perspectivas constructivistas que han sido o podrían haber sido utilizadas para describir los mecanismos de pensamiento acerca de los conjuntos infinitos, en particular el conjunto de los números naturales. Segundo, para determinar si estos mecanismos de pensamiento de los individuos acerca del conjunto P(N) pueden ser interpretados en términos de una o más de las perspectivas consideradas, analizamos la forma de pensar de ocho matemáticos. Mas allá de las concepciones negativas, o sea, de lo que P(N) no es, los resultados de nuestro análisis nos hicieron dudar sobre si la comprensión de los individuos del conjunto P(N) se extiende más allá de la definición formal. Hablamos de las posibles implicaciones de nuestros descubrimientos e indicamos futuros temas de investigación que podrían surgir de este estudio.

PALABRAS CLAVE: Conjuntos no numerables, APOE, metáfora, conjunto potencia, números naturales, imágenes mentales.

 

ABSTRACT

This study considers the question of whether individuals build mental structures for the set P(N) that give meaning to the phrase, "all subsets of N." The contributions of our research concerning this question are two–fold. First, we identified constructivist perspectives that have been, or could be used to describe thinking about infinite sets, specifically, the set of natural numbers N. Second, to determine whether individuals' thinking about the set P(N) can be interpreted in terms of one or more of the perspectives we considered, we analyzed the thinking of eight mathematicians. Beyond negative conceptions, that is, what P(N) is not, the results of our analysis cast doubt on whether individual understanding of the set P(N) extends beyond the formal definition. We discuss the possible implications of our findings, and indicate further research arising from this study.

KEY WORDS: Uncountable sets, APOS, metaphor, power set, natural numbers, mental images.

 

RESUMO

No presente estudo nos preguntamos se os indivíduos constroem estruturas mentais para o conjunto P(N) que dá significado a expressão "todos os subconjuntos de N ". Os aportes de nossa investigação em relação a esta pregunta tem duas vertentes. Primeiramente, indentificamos as perspectivas construtivistas que seriam ou poderiam ter sido utilizadas para descobrir os mecanismos de pensamento acerca dos conjuntos infinitos, em particular o conjunto dos números naturais. Segundo, para determinar se esses mecanismos de pensamento dos indivíduos em relação ao conjunto P(N) podem ser interpretados em termos de uma ou mais das perspectivas consideradas, analisamos a forma de pensar de oito matemáticos. Além das concepções negativas, isto é, de que P(N) não é, os resultados de nossas análises trouzeram a dúvida sobre se os indivíduos compreendem o conjunto P(N) além da definição formal. Falamos das possíveis implicações de nossas descobertas e indicamos futuros temas de investigação que poderão surgir deste estudo.

PALAVRAS CHAVE: Conjuntos não enumeráveis, APOE, metáfora, conjunto potência, números naturais, imagens mentais.

 

RÉSUMÉ

Dans cette étude nous nous demandons si les individus construisent des structures mentales spécifiques pour l'ensemble P(N) (<<ensemble des sous–ensembles de N>>). Nous décrivons ici deux des principaux apports de notre recherche en relation à cette question. Nous identifions tout d'abord les perspectives constructivistes utilisées ou potentiellement utilisables pour décrire les mécanismes de la pensée à propos des ensembles infinis, et en particulier l'ensemble des entiers naturels. Ensuite, pour déterminer si ces mécanismes de pensée des individus sur l'ensemble P(N) peuvent être interprétés en termes d'une ou plusieurs des perspectives considérées, nous analysons la forme de penser de huit mathématiciens. Au–delà des conceptions négatives, c'est–à–dire les approches de P(N) essentiellement par ce qu'il n'est pas, les résultats de notre analyse laissent à penser que la compréhension des individus de l'ensemble P(N) n'est va pas au delà de la définition formelle. Nous exposons enfin les possibles implications de nos résultats et nous soulignons de futurs sujets de recherche que cette étude peut dégager.

MOTS CLÉS: Ensembles non dénombrables, APOE, métaphore, l'ensemble des parties, entiers naturels, images mentales.

 

1. INTRODUCTION

Uncountable infinity is ubiquitous, both explicitly and implicitly, in the undergraduate mathematics curriculum. Explicitly, undergraduate mathematics majors study uncountable sets in Introduction to Proof or Transition courses and again in Analysis courses and upper division courses on set theory. Implicitly, students must work with uncountable sets in Calculus courses as they study functions, limits, and Riemann sums, often defined over uncountable domains.

Participation in these courses and in many other situations in the field of mathematics should lead to constructions of new mental structures for dealing with uncountable sets. This has been true since G. Cantor began the development of the mathematical theory of infinite sets in the latter part of the 19th century. In these situations, the learner must grapple with the profound idea that there are different levels of infinity, proofs of uncountability, the continuum hypothesis, the fact that 2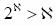 K for any cardinal number K and the relationship between ordinal and cardinal numbers. If our students are to understand, appreciate, and even further the development of these ideas, they must have an understanding of both countable and uncountable infinite sets.

Nevertheless, mathematics textbooks regularly define uncountable as not countable. For a set A, one can show that any injective function f : A 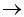P(A) from a set A to its power set P(A) cannot be surjective (see, for example, Chartrand, Polimeni, & Zhang, 2007). Applied to the set of natural numbers N, it follows that no bijective function can be defined between N and its power set P(N). Therefore, the uncountability of the set P(N) is rooted in its not being countable. It is not surprising then that students and even some mathematicians do not have a description of what P(N) is and try to find one by generalizing from properties of finite sets or countable infinite sets. Although knowing what something "is not" is a valuable part of conceptual understanding, most specialists in mathematics education, as well as many mathematicians, would deem an exclusively "negative" view of a concept as insufficient.

One way logicians try to construct an uncountable set, for example P(N), the power set of the natural numbers N, is to build a binary tree. The construction involves an iterative process, where any given step can be described recursively. However, no subset of N arises by completing a particular step of the process, nor is any subset constructed by determining the resultant state of the process (to use the language of Lakoff and Núñez, 2000). To construct a subset of N, one must first complete the tree (mentally speaking) and then traverse a particular path. No systematic procedure, iterative or otherwise, has been devised for constructing all the paths through the tree. Thus, the binary tree does not enable an individual to make explicit the meaning of the phrase all subsets of N .

This begs the question of whether some concepts in mathematics, such as uncountability, are exclusively formal. In terms of the notions of concept image and concept definition (Tall and Vinner, 1981), the concept image of the set P(N), would, if purely formal, be essentially void. According to Vinner (1991), this is an insufficient basis for understanding. He writes: "To know by heart a concept definition does not guarantee understanding of the concept. To understand ... means to have a concept image" (p. 69). Thus, from a constructivist perspective, conceptual understanding cannot rest exclusively on knowledge of the formal definition. In reality, one's concept image is never completely void; the words of a formal mathematical definition would, at the very least, evoke certain images, connect with previous experiences, or suggest informal descriptions. The issue, then, is the degree to which one's concept image informs the meaning of the concept definition. For the set P(N), the question is whether one can identify mental structures that offer insight into the meaning of what "all subsets of N " is, as opposed to what it is not.

The answer to this question does not appear in the current literature. Although literature on the learning of concepts of infinity is vast (for a partial list of relevant sources, see Dubinsky, Weller, McDonald, & Brown, 2005a, 2005b), most studies concern the comparison of infinite sets (e.g., Tall, 1980; Tirosh, 1999; Tsamir, 1999), the contradictory nature of infinity concepts (e.g., Fischbein, Tirosh, & Hess, 1979; Moreno & Waldegg, 1991; Tirosh, 1991), or historical/epistemological obstacles encountered in the conceptualization of infinite sets (e.g., Sierpinska & Viwegier, 1989; Jahnke, 2001).

Few authors have tried to elaborate mental structures an individual or group of individuals might use in developing concepts of countable sets. Exceptions include Lakoff and Núñez (2000), Tall (2001), Dubinsky et al. (2005a, 2005b), Stenger, Vidakovic, and Weller (2005), and Brown, McDonald, and Weller (in press). Moreover, no source of which we are aware considers the development of mental structures for uncountable sets such as P(N).

Cantor (1941) struggled against the fact that no one had mental structures for any infinite sets. His work led to the development of such mental structures for countable sets. Our research set out to find mental structures that give meaning to the concept of P(N), a meaning that goes beyond the formal definition. Dubinsky et al. (2005b) remark that most discussions of infinite processes in the literature, such as those found in Aristotle's writings (according to Moore, 1999) and recently in Tirosh's study (Tirosh, 1999) all involve iteration. Dubinsky et al. (2005b) propose that this might explain some difficulties that even contemporary students have with concepts of infinity. For example, some teachers of calculus feel that of the two formulations of the limit concept:

For all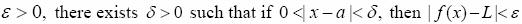

and

For all 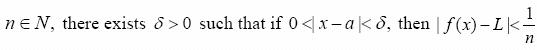students tend to find the second easier to understand than the first. The authors suggest that this might be because the students can understand the meaning of "For all n" as an iterative process, whereas no such process is apparent regarding "For all ε > 0 ". The authors suggest that if there is no apparent mental process underlying one's conception of a set, as may be the case with uncountable sets, the meaning of "all" is not entirely clear.

So we asked our question in a slightly different way. Does the literature include constructivist perspectives that might describe the development of mental structures for uncountable sets such as P(N) ? We found several candidates. Though not exhaustive, our list is representative. The perspectives cover a range of activities, such as visualization, imaging, intuition, metaphor, language, and reflective abstraction. These perspectives either have been, or could be, used to describe thinking about countable sets (in our case, the set of natural numbers N). This raises the question of whether any of these perspectives could be extended to explain individual thinking about the uncountable set P(N). To offer at least a tentative answer, we conducted interviews with eight mathematicians and examined whether they constructed mental structures for P(N) that support the formal definition. Although we did not consider every possible constructivist perspective, those we considered encompassed our subjects' responses to the following queries: "Describe your thinking about the set N," and "Describe your thinking about the set P(N)."

Before proceeding, we make several additional points. First, this report is only a preliminary investigation of P(N). Our conclusions are tentative, and our interpretations are not absolute.

The second point involves the meaning of the terms constructivism and mental structure. Although universal agreement on all aspects of the meaning of constructivism eludes the mathematical and mathematical education communities, it is generally considered that constructivism includes the notion that learning mathematics involves the construction of mathematical concepts in the minds of individuals, groups of individuals, or societies of individuals¹. This does not mean that mathematical concepts are directly constructed. Rather, a learner constructs certain structures in her or his mind to make sense of mathematical problem situations. Thus, we offer the following, not so much as a precise definition, but rather a framework for the perspectives used in our analysis.

A mental structure is any relatively stable (although capable of development) structure (i.e., something constructed in one's mind) that an individual uses to make sense of mathematical situations. A source for a mental structure is a description of where that structure comes from. A mental mechanism is a means by which that structure might develop in the mind(s) of an individual or a group of individuals.

The last point concerns the significance of this study. Specifically, why is a purely formal definition of a concept insufficient, at least for students? In a study of 70 mathematicians' thinking styles, and the social, intuitive, and aesthetic aspects of their learning, Burton (2001) found that her subjects valued meaningful, connected, and insightful explanations in their own work. On the other hand, she associated current disillusionment, both in school and university mathematics teaching, with a lack of meaning, connection, and insight. Many teachers of mathematics, interested in helping their students to build mental structures to make sense of formal mathematical ideas, share this constructivist viewpoint.

In consideration of the issues just mentioned and the perspectives that guided our analysis, we pose the following research question: Did our subjects appear to build mental structures for the uncountable set P(N) that give meaning to the phrase "all subsets of N "?

 

2. RELATED LITERATURE: PERSPECTIVES USED IN OUR ANALYSIS

In this section, we briefly describe perspectives that might be relevant to our research question. We examine how each perspective explains, or could be used to explain, thinking about infinity. We do not discuss here how each perspective might, or might not, explain individual thinking about P(N), as this is the goal of the section on data analysis.

 

2.1. Visualization

In our search through the literature on visualization, we concentrated on Presmeg (1985, 1986, 1998), Fischbein (1987), Zimmermann and Cunningham (1991), Dreyfus (1991, 1995), and Wheatly (1991), as well as references listed in those articles. According to these authors, a visual image can be used to organize one's mathematical thinking. Thus, it serves as a mental structure. In the view of some authors (e.g., Rodd, 2000), an individual constructs "spatial mental schemes" that are used as mathematical warrants. According to others (e.g., Kidron, 2003), visual activities, including computerized visualization, enhance the understanding of formal mathematics. Still, others (e.g., Zazkis, Dubinsky, & Dautermann, 1996) report that visual images contribute to analytic understandings, and vice–versa. In any case, the sources of visual images are the perceptual reports to an individual's brain of that which is physically visualized, and the mental mechanisms are the operations for converting perceptions to mental images.

Although visualization could be incorporated in the next perspective on mental images (see Piaget & Inhelder, 1971)², we have chosen to consider visualization separately and only in the case where the source is a direct physical perception (or the memory of one).

In our review of the literature on visualization, we did not find any investigations on the use of visual image as a mental structure for countable sets. On one hand, this is not entirely unexpected. An infinite phenomenon cannot be directly visualized because the physical operation of perceptual mechanisms is necessarily finite.

On the other hand, perceptual reports are interpreted by the mind, and, as Zazkis et al. (1996) found, visual and analytic thinking develop in tandem. Thus, one could imagine a learner visualizing a finite phenomenon and extending, in her or his mind, the finite phenomenon to an infinite one. This could lead to an understanding of a mathematical concept related to infinity. In a sense, a start in this direction has been made by Tirosh (1999) and Tsamir (1999), who considered the effect on students' understandings of the cardinalities of certain countable sets when (the initial terms of) these sets were presented either vertically or horizontally.

 

2.2. Mental images

Davis and Maher (1997) assert that mathematical concepts arise from mental images that are rooted in experiences (see also Hadamard, 1945; Aspinwall, Shaw, & Presmeg, 1997; Goldenberg, 1988; Sfard, 1997). Higher level concepts are developed by modifying old images or creating new ones based on existing images. In this way, new knowledge is constructed from previous knowledge. Thus, mental images are mental structures. The sources of mental images consist of experiences and previously constructed images, and the mental mechanisms are the processes used to transform those experiences into images or to create new images. More sophisticated mathematical concepts arise by developing more sophisticated human experiences, such as notational systems representing mathematical operations. Although the literature on mental images does not specifically mention the development of infinite sets, one could conjecture that mental images for such sets might be created by associating a notational system to the process of counting or set formation.

 

2.3. Intuitive insights

Fischbein et al. (1979) characterize intuition as knowledge that is "direct, global, and self–evident" (p. 5). According to Hersh (1997), intuition arises through the examination and manipulation of existing mental or physical objects. At an elementary level, this entails transformation of physical objects. At a more advanced level, one transforms mental objects in an effort to solve mathematical problems. In either case, the experience of transforming objects, whether physical or mental, creates what Hersh calls a mental trace, a mental structure that enables an individual to achieve new insights that often lead to the formation of new mathematical structures. Once developed, the individual seeks to identify the properties of these new objects. At this point, the individual uses mathematical proof to verify and to understand the properties identified. The sources for intuition are the experiences that originate from repeated examination and manipulation of physical and/or mental objects. The transformation of experience serves as a mental mechanism that leads to the formation of a mental trace.

Subconscious reflection, when applied to this mental structure, serves as a mental mechanism from which new insight, or intuition, arises. The new intuition, through further reflection and/or transformation, may lead to the creation of new mental objects or new intuitions.

In the case of the natural numbers, according to Hersh, the concept of counting is achieved by manipulating concrete objects. One becomes aware of the infinitude of the natural numbers by realizing that they can never be completely counted. Specifically, no matter what number is named, one can name a higher number. This is the basis of the successor function, which leads to a conception of N as a single structure.

 

2.4. Semiotics

In their research on language and mathematics, Cobb, Boufi, McClain, and Whitenack (1997), Cobb, Yackel, and McClain (2000), Sfard (1998), and Tall et al. (2001) discuss the interplay between mental processes and mental objects, structures that underlie the formation of mathematical conceptions. Tall et al. (2001) explain that symbols serve as pivots between process and object. Sfard (1998) asserts that mathematical objects do not exist without the use of signifiers. Cobb, Boufi, et al. (1997), Cobb, Yackel, et al. (2000), and Sfard (1998) consider classroom discourse and symbolization as mental mechanisms that support reflective shifts in discourse between mental structures such as processes and objects.

Many authors, such as Vygotsky (1981), Ernest (1997, 1998), and Rotman (1988, 1993, 2000), consider mathematics to be a language. Mathematical concepts are expressed in an individual's mind in terms of that language, considered by Chomsky (2006), among others, to be a mental structure. The source of the semiotic perspective is social discourse about mathematical situations, based on the idea that language is also a mental mechanism that molds thought (Vygotsky, 1978). Rotman (1988, 1993, 2000) also notes that symbols embody thought. He refers to the creative power of discourse and verbal exchange of thought, both oral and written. Specifically, mathematical learning involves the interplay of symbols, signs, proof, and mathematical objects within the social experiences of the individual learner. Similarly, Ernest (1997, 1998) asserts that language enables the formulation of mathematical ideas.

Given that social experiences occur within a finite context, Rotman (1993) believes that infinite sets should be discarded from mathematics because they are physically unrealizable. Tall (2005), on the other hand, sees semiotics playing an important role in one's understanding of infinity. For instance, he explains that the "potentially infinite processes of sequences, series, and the calculus" take their toll on students who do not have semiotic resources from which to draw since one can never reach a limit in one's lifetime. Despite this view, he does not offer an explicit description for the development of mental structures for infinite sets via symbolism.

Beyond Tall, no explicit theory or discussion within the semiotics literature seems to relate to the development of mental structures for infinite sets. Obviously such a development could not be based on the strictly finitist interpretation of Rotman. Yet, others who believe that such a development is possible would need to determine how the use of language, symbols, and/or signs might be extended to help learners understand infinite processes that are not physically realizable.

 

2.5. Metaphors

Although there are many variations on the use of metaphors in the development of mathematical understanding (e.g., Fischbein, 2001; Sfard, 1994), we shall focus on the notion of conceptual metaphors discussed by Lakoff and Núñez (2000), since they explicitly apply the mental structure of metaphor to infinite sets. In general, they define conceptual metaphors as "grounded, inference–preserving, cross–domain mappings" in which individuals "use the inferential structure of one conceptual domain to reason about another" (p. 6). Thus, metaphorical thinking involves the formulation of new situations in terms of more familiar contexts. In this way, the learner constructs new concepts. The sources for such thinking are the original situations that give rise to metaphors as mental structures. The "cross–domain mappings" serve as the mental mechanisms.

According to Lakoff and Núñez, many infinity concepts involve application of the Basic Metaphor of Infinity (BMI). With this mental structure, the individual imposes on an unending process, conceptualized iteratively, a unique, final resultant state. In this way, an individual thinks of an unending process in terms of a finite process, which necessarily has a last term. For the countable set N, an individual begins with an initial state (Step 0), the empty set. Step 1 consists of taking the union of the set {1} with the empty set. In general, the process is described recursively: For an arbitrary step n, one forms the set {1,2,..,n} by taking the union of the set {1,2,...,n –1} with the set {n}. Through application of the BMI, the individual imposes on the unending process a unique final state, in this case, the set N .

 

2.6. APOS Theory

Actions, processes, objects and schemas are all mental structures (e.g., Asiala et al., 1996; Dubinsky & McDonald, 2001). The sources for actions are external stimuli that specify a transformation of objects; for processes the sources are actions which are interiorized to processes; for objects the sources are processes which are encapsulated into objects; and for schemas the sources are previously constructed actions, process, objects, and schemas that are developed in stages called a triad (Piaget & Garcia, 1989; Cooley, Trigueros, & Baker, in press), and organized into a coherent whole. The mental mechanisms are operations such as interiorization, encapsulation, coordination (composition), and reversal. Recent studies by Dubinsky et al. (2005a, 2005b) have investigated how this perspective can be used to explain mathematical situations involving infinity, particularly the relationship between potential and actual infinity. These authors suggest that "potential infinity is the conception of the infinite as a process," and that "actual infinity is the mental object obtained through encapsulation of that process" (p. 346).

In an empirical study on infinite iteration, Brown et al. (in press) offer a description of the mental construction of infinite iterative processes (an instance of potential infinity) and their encapsulations (an instance of actual infinity). To construct mentally the natural numbers N, an individual might begin, as with metaphors, by performing a small number of iterations, for instance, writing or speaking about a sequence of finite sets such as {1}, {1,2}, {1,2,3}. These actions are then interiorized into a finite mental process. To obtain the first n counting numbers, one adds 1 to n–\, and adjoins the resulting natural number n to the set {1,2,...,n–1}. Coordination of multiple instantiations of this finite process leads to construction of an infinite iterative process. Here, the similarity with metaphors ends. Once the process is viewed as complete (i.e., an understanding that each step yields a set of the form {1,2,...,n}), and as a totality (i.e., an ability to see all of the steps in the process as a single, atemporal operation), the process may be encapsulated as the result of an action, or attempted action, being applied to it. In the case of infinite iteration, this might be an action of evaluation, for instance, "What do I have?" or "What comes next?" The former action involves accumulation: the object that arises from the encapsulation consists of the totality of objects produced by each step of the process. The latter action is extensive: encapsulation leads to construction of a successor object that appears "next". In some instances, both actions may yield the same object. In others, different objects may arise. In either case, the resulting object "stands outside" the process; it is not produced by completion of any step. For this reason, Brown et al. (in press) refer to the object obtained by encapsulating an infinite iterative process as a transcendent object.

 

2.7. Mathematical formalism

According to Dubinsky (2000), formalism guides the development of mental structures in some mathematical situations. That is, one uses the syntax of a formal statement in a conscious manner to direct specific constructions of actions, processes, objects, and schemas. In other words, the formal statement of the concept motivates the development of certain mental structures. MacLane (1981) asserts that mathematics consists of applying rigor and deduction to ordinary human experiences so as to uncover hidden properties. Tall (2001) concurs, stating that "we reflect on our perceptions to create new cognitive images within our personal cognitive structures" (p. 220). For each of these perspectives, formalism is a mental mechanism that leads to the development of certain mental structures. MacLane (1986) suggests that the set N (among other mathematical entities) arises from the human activities of counting and listing. One then applies the rigor of Peano's Postulates to prove the standard arithmetic properties for N. In a similar vein, Tall (2001) asserts that individuals begin with a concept image of the set of natural numbers, and then apply Peano's Postulates as a formalism, which, he argues, leads to more subtle visual imagery (see also Zazkis et al., 1996).

 

3. METHODOLOGY

In exploring the mental structures individuals might build for the set P(N), we discussed the issue with eight mathematicians. The eight subjects represented diverse mathematical interests, with one logician among the group. Subjects were asked two questions, "What is your conception of the natural numbers N ?", and "What is your conception of the power set of the natural numbers, P(N) ?" For the set N, we did not expect to find anything new. Questions about N served two purposes: to determine how the selected perspectives could be used to explain individual thinking about infinite sets; and to serve as a baseline for the analysis of our subjects' thinking about P(N). For both questions, the interviewers first posed the question, and allowed each subject to describe her or his thinking. The interviewers asked follow–up questions to clarify a subject's responses, or to probe further into a subject's thinking. With the exception of one interview, conducted as an email discussion, each interview lasted about one hour, was audio–taped, transcribed verbatim, and then checked for accuracy.

Following the steps of data analysis set forth in Asiala et al. (1996), we scripted each of the transcripts. In the script, the interview was organized into a two–column format, where the first column contained the original transcript, and the second short statements used to sketch interview passages. Then, we prepared a table of contents to formulate a list of issues, identifying instances where a given perspective might apply. Two of the authors reviewed each interview, noting evidence of thinking that aligned with a particular perspective. Evidence consisted of identifying specific phrases that reflected the construction, attempted construction, or use of mental structures associated with a particular perspective. We also looked for, but did not find, any evidence of perspectives other than those we selected for study in this paper. The two reviewers negotiated differences and shared their findings with the entire team. This approach served two purposes: triangulation of results and reliability. In the presentation of the data, the reader will note that there is not always a sharp distinction between different perspectives. Thus, we do not assert that our subjects' statements reflect a single perspective exclusively. Rather, we are interested in whether a given perspective might be used to describe a subject's thinking about N and/or P(N). Specifically, did the subject give evidence of evoking, constructing, or trying to construct, a mental structure for the set P(N) that would infuse the formal definition with greater meaning?

 

4. ANALYSIS OF THE DATA

Eight subjects, Claudia, Cecil, Doris, Ian, Kathryn, Marcus, Quinn, and Ranae³, participated in the study. For each perspective, we summarize the subjects' thinking, and present representative excerpts to illustrate our claims. As noted earlier, none of the results for the set N is new. We included an analysis of this set to determine the applicability of a given perspective, and to serve as a baseline for our analysis of P(N), the main focus of our investigation.

 

4.1 Visualization

For the set N, six of the eight mathematicians described the set N using a visual representation. For instance, Claudia, Ian, Doris, Marcus, and Quinn referred to the number line. The following excerpt from Marcus, in response to the question of how he thinks about N, is representative:

Marcus: I guess I just think about the real number line. I always see that ole' one up above the board, back when I was in grade school, that's just what I think of, obviously the right hand side.

This finite visual image was a likely source for development of his mental structure of N . He builds N by successively adding one at each step:

Marcus: I've got the number 1 ... and I guess I just interpret it in terms of the operation of addition. I think of one plus one, one plus one plus one, and so forth ... that's about the way I think of it.

As noted earlier, a direct visual perception cannot record an infinite phenomenon. To construct the set N, Marcus' visual representation evoked a process of finite enumeration that, when extended, indicated successive additions of 1, ad infinitum. Thus, the visual representation served as a source for the formation of an iterative process, a mechanism Marcus used to build a mental structure for the set N .

Unlike N, none of the mathematicians in our study recounted direct physical visualizations as sources for P(N). For instance, no subject referred to the real line as an infinite set of points to which each element of P(N) corresponds.

 

4.2 Mental images

All but one of the eight subjects described a mental image for an initial finite segment of the set N . For instance, Ranae reveals an image of N as a sequence of numerals:

Ranae: ... my mental image ... is just starting to see the list of them. I mean like the sequence of numbers ... 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, whatever.

Similarly, Cecil starts with a visual image of falling dominoes that serves as a source for his mental image of N as a "bundle of stuff":

Cecil: Uhh ... dominoes ... but that's pretty much all. It's just ... uh ... and sort of in your mind, the successor function. You've gotta start and you go from one place to another. ... When you're all done you sort of back off and say OK there's this big set of things and given any point you can move to any other point and they're ordered uh, but uh, in some other situations you want to think of them as just a bundle of stuff that you can get around in.

For Cecil, falling dominoes indicated enumeration, the basis of the successor function. The successor function served as a mental mechanism that conjured an image of N as "a bundle of stuff," a totality where "given any point you can move to another point."

Four of the eight subjects offered mental images of P(N). For instance, Kathryn saw P(N) as "very, very big, in some sense unknowable." Similarly, Doris saw P(N) as a "quagmire":

Doris: Yeah, so as soon as you said that, I'm like oh! yes, that's the ... I really think I just, as far as how I conceive of it, it's just the definition, so I'm just looking at all the subsets, it's just this quagmire of subsets [both laugh]. As far as a mental image, that's what I've got.

Ian used his remembered experience with tree structures, likely obtained from physical images, or in writing computer programs, to construct a mental structure represented mathematically as a recursive process. However, the process he describes only yields finite subsets of N .

Ian: Well, let's see, I guess I would do it recursively in sort of ... think of a tree process I suppose. I would have a set with one up through k whatever k is. You have a start, and so then I would throw, go up one level and throw in k + 1, so now you'd have one plus k through one. And then I would go down a level putting k + 1 together with everything that was in the original set from one to k .

At each recursive level k, Ian built the power set of the set {1. ,2,...,k} Although this process yields all of the finite elements of P(N), no infinite elements of P(N) arise. Ian eventually realizes this, and sees that something more is needed. Part of his difficulty stems from his belief that an infinite process can never be finished in one's mind⁴.

I: Could you talk a little more about the finishing of this process? What does it mean at least to you mentally to finish this up, to get everything?

Ian: Means really nothing to me. I would never finish it. This tree can get just as high as you need it to get. You give me a finite place you want it to reach and I can reach that. And that finite place can be as large as you want to make it but it would never finish. I really don't know; don't have much of a concept of finishing that as such at all.

I: But go back to the set of natural numbers. Do you not have a concept of finishing that process and therefore you really can't have the set of natural numbers?

Ian: I have no real concept of finishing that process either. Again, natural numbers ... those things ... there's no end to it, so I can build you ... I can give you the set, list physically the elements of the set as high as you want me to go and if you want me to go higher, I'll go higher. But no, there's no sense to me at least of finishing listing the set of natural numbers or just of the set of natural numbers. I think of as being endless. There is no finishing to them.

For Ian, the mental image of a tree is consistent with, and may contribute to, his belief that an infinite set cannot be created. Just as the tree would never be complete, the mental structure he attempted to build for P(N) would never be complete.

For Doris and Kathryn, their vague images may have helped them to see "all" as an immense, seemingly indescribable collection. However, neither image led to formation of a mental structure, nor did their images offer a precise sense of the difference in magnitude between the two sets N and P(N). For the set N, mental images served as sources for the development of iterative processes (e.g., Cecil) that inspired use of the successor function, a mechanism leading to a view of the natural numbers as a totality. In contrast, mental images for)P(N) did not serve as sources for the development of mental structures. For example, Doris' view of P(N) as a "quagmire" left her with "just the definition."

 

4.3. Intuitive insights

According to Hersh (1997), the "fundamental intuition of the natural numbers" is a "shared concept, an idea held in common after manipulating coins, bricks, buttons, and pebbles" (p. 65). In describing their thinking about N, seven of the eight subjects mentioned counting or manipulating physical objects. This "shared concept" was a common source, motivating the development of mental mechanisms, that is, ways of conceiving the endless nature of enumeration. For instance, Claudia described N as "the collection of things 1, 2, 3, and I could keep counting as long as I wanted to"; Cecil thought of N as "the description of a process"; and Quinn saw N as a progression that "continues and there is no end." These types of intuitions appeared to inspire more formal descriptions of infinite enumeration, such as "the successor function" (Cecil), or an infinite sequence of repeated additions of 1 (Claudia, Marcus, Ranae). Further reflection on the process of successively adding 1 led to an intuitive view of N as a complete mental structure. According to Claudia, such intuitions precede one's ability to think of N more formally:

Claudia: Somehow you have to know in advance what the integers are before you can take the union over all the finite truncations of the natural numbers.

I: Why do you need to know in advance what they are? Claudia: It's that I don't know what the collection of all those finite segments of the natural numbers is unless I know what the set of natural numbers is.

I: OK, so what I hear you say is that you don't see intuitively how you get from the formation of all these finite sets to the whole set.

Claudia: I don't see how I can do that without having an intuitive picture of the whole set.

For our subjects, counting and manipulating physical objects served as a source for intuitive conceptions that eventually led to the development of structures such as the successor function. These more formal structures were used as mental mechanisms to develop mental structures to inform conceptions of what N is.

Our subjects' intuitions regarding the set P(N) were just the opposite, rooted in experiences of what P(N) is not. This certainly seemed to be the case for Doris, whose repeated efforts to enumerate the set of all subsets of N ultimately failed:

Doris: I used to love when I was young sitting there and trying to list out all the subsets of some finite set, and I could just see myself doing this with the natural numbers, and I could see that I wouldn't get done, and I knew that.

I: Yeah, I know what you mean, I did that too.

Doris: And I'm not sure at what point, I know it was pretty late along the line, when I realized that even if I did keep doing that, that when I was done, I would have missed some or something.

When asked to describe P(N), several subjects (Claudia, Ian, Ranae, and Marcus) attempted to construct iterative processes to obtain P(N). Their use of iteration likely arose from prior experiences with countable collections where iterative processes abound. However, as Claudia realized, "I'd end up with the set of all finite subsets." Her insight, spontaneous and not the result of any deductive or inductive reasoning, suggests intuitive thinking. This intuition helped her to see the error in her construction.

Cecil invoked another familiar intuition regarding uncountable sets. When asked to describe a construction for P(N), he quickly rejected the possibility. Repeated experiences with countable processes, rendering only countable collections, helped formulate an intuition that uncountable sets cannot be obtained from countable processes:

I: In the same spirit as the process that constructed a single infinite set ... Could we step it up one more level so that it could be used to construct all of the subsets of N ?

Cecil: Back in the old days, there's this little part that says the power set has a higher cardinality than the set you started with, and therefore, I'm pretty sure I can't prove it anytime soon (laughter). Given a long time, I might be able to, but the power set is of higher cardinality. If you're countable here, you're not going to be countable there.

For the set N, repeated experiences with counting served as a source for intuitions regarding the unending nature of enumeration. This resulted in development of more formal mechanisms. For most of the subjects, seeing the set N as a completed structure arose from infinite application of the successor function, or a process of repeatedly adding 1. Intuitions underlying the set P(N) worked differently. On the basis of unsuccessful attempts to list the subsets of N, Doris concluded that the elements of P(N) cannot be listed. Prior knowledge about the uncountability of P(N) informed Cecil's belief that P(N) cannot be constructed iteratively. Experiences with iterative processes led several of the subjects to realize the futility of their attempts to construct P(N). None generated an intuition from which a stable mental structure for P(N) arose. As Kathryn pointed out, "I think of P(N) as ... in some sense unknowable." This begs the question: Are intuitions of P(N) necessarily rooted in terms of what P(N) is not?

 

4.4. Semiotics

Three of the eight subjects used symbol and language in ways suggested by the semiotics perspective. As a list, Ranae claimed that no one can see all of the natural numbers at once. In accordance with Sfard's (1998) description, Ranae used a signifier, the letter N, to see the totality of the natural numbers:

Ranae: In an abstract way we can see all of them [the natural numbers] at once with capital N, that's it, you know? That's kind of like the embodiment of them. So you see that big N and that is the natural numbers and ... and so you're seeing the set of natural numbers.

For Ranae, the symbol N served as a mental mechanism for construction of a mental structure for the set of all natural numbers. The list of numerals appeared to be a source for her thinking.

For Doris, the list of the first few natural numbers served as a pivot between process and object.

I: So, you said one comma two comma three comma, etcetera...

Doris: That's what I said.

I: What does that mean, "etcetera"?

Doris: Oh, I just see more numbers.

I: How far?

Doris: Depends on how far I look.

I: As far as you want to?

Doris: Oh, probably [both laugh].

I: Okay, then, how do you get from that description to the set of all natural numbers?

Doris: Oh no, that's the set of all natural numbers.

With the list as symbol, Doris could pivot, as Tall et al. (2001) suggest, between the process of writing out the list as far as she wished, and the set of all natural numbers as an object.

Our subjects did not construct P(N) as a mental structure using the semiotics perspective. For example, Ian generated subsets of N recursively by listing the elements of the power set P({l,2,...,n}) for successive values of n. However, this process only yields the finite subsets of N. Although Doris discussed difficulties her students encountered with P(N), she focused on the manner in which symbol notation for sets (e.g., braces { }) distracts rather than helps students who have difficulty understanding the concept of set:

Doris: The students aren't clear about sets in the first place and you start stumbling over the notation and somehow those braces appear.

For several of our subjects, symbolization served as a mental mechanism that supported reflective shifts in discourse that contributed to construction of the set N as a mental structure. The excerpts tell a different story for )P(N: none of our subjects used semiotics in ways suggested by the semiotics perspective to construct a mental structure for this set.

 

4.5. Metaphors and APOS Theory

We consider these two perspectives together, in part because of similarities in the transition from finite to infinite iteration, but, more importantly, to highlight differences. When considering the transition from finite to infinite iteration in the countably infinite case, the BMI and APOS Theory appear similar.

For instance, the following excerpts from Claudia, Ranae, and Quinn could be interpreted using either perspective:

Claudia: I can start with the set containing just 1 and then I can start with the set containing 1 and its successor 2, and now I'm going to make some kind of informal application of an inductive scheme.

Ranae: I mean like whatever the first number that I have I add one to it, you know given any number down the line add one to it you get the next one.

Quinn: Any repetitive thing that you see that you can do forever, you rarely continue with it. You usually stop and say, I can do this as long as necessary for me to have more numbers.

Claudia's use of the phrase "inductive scheme," Ranae's comment that "given any number down the line add one to it," and Quinn's description of the construction as a "repetitive thing that you see that you can do forever," exemplify a transition from finite to infinite iteration. According to APOS Theory, this transition occurs by application of the mental mechanisms of interiorization and coordination. Specifically, the actions of performing the first few steps are interiorized into a mental process, and then multiple instantiations of that process (with different initial and terminal points) are coordinated to form an infinite iterative process. For instance, interiorization and coordination lead to development of an inductive scheme. According to Lakoff and Núñez (2000), the mental mechanism of the BMI facilitates the transition. After construction of the initial state, and the first step arising from the initial state, one constructs an infinite process that produces any intermediate state from its predecessor. Claudia's inductive scheme could be interpreted as a process that yields any intermediate state. At this point, the similarities end. Yet, the distinction is very subtle. In the case of the BMI, the final resultant state arises by metaphorically conceptualizing the infinite process as if it were a process with a last term. In the case of APOS Theory, the resultant state arises through encapsulation, which occurs as one applies an action to the process as a completed whole. Of the five subjects who gave evidence of constructing N by iteration, none appeared to think of N metaphorically. For instance, Claudia and Ranae refer to specific actions:

I: What I understood you said is that you form the singleton 1, {1,2}, {1,2,3 } and you continue with that and then after you've built all of those ...

Claudia: Then I take the union.

Ranae: The limit of this sequence [she is referring to {1}, {1,2}, {1,2,3}, ...] would be the natural numbers ... you know, if you are looking at it as a sequence of sets.

Claudia encapsulates her iterative process in response to the action of taking the union. Ranae also makes an encapsulation, but thinks in terms of a limit. In her interview, Doris, who sees N as "all of it being there," creates a unifying structure that encompasses the objects produced by each step. In each of these cases, the resultant state, the set N, transcends any step of the process from which it arises. Thus, APOS Theory seems to explain more readily how the subjects built mental structures for N .

For P(N), as with the other perspectives considered thus far, the situation was far different. Although several subjects used iterative processes in their attempts to build mental structures for P(N), none was successful. In fact, the subjects described processes whose final resultant states were only the finite subsets of N. The following excerpt from Claudia's interview represents one such example:

Claudia: I could take the empty set, then I could look at all the singletons, then I could look at all the doubletons, is that the right? I: Two element sets. Claudia: Two element sets, then I could look at all the three element sets.

I: And if you did that forever?

Claudia: I would end up with ... No I would not end up with all the subsets, because the set of all even integers is a subset but I'm not gonna pick that one up as a finite subset.

Ranae, possessing only an action structure (in terms of APOS), resorts to "hand waving" in her attempt to describe the elements of P(N):

Ranae: Um ... so you take ... it isn't like you can just add one to it. Well the trouble is though there's other subsets than these so ... I mean because there's also {}2,3 and there's also {3,4} and there's also {6,7} and there's also {}21,29

Ranae: You know, I was only thinking of finite subsets though ... to be honest ... and see ... I can't, unless I take a class that's called "infinite" and don't bother with its cardinality or anything like that. If I just take all the ... I have all the ones that are finite, take care of them by the way I was just telling you and then just have this one big class that's infinite and there would probably be an infinite number of those and, but could I really do that with an iterative process? ... Yeah, I know it. It isn't going to be possible. Well, why isn't it? Because if I can do the natural numbers, I'm not sure how I would do that unless I just ... plunked them all in there and sort of did some hand waving.

Cecil begins with the action of forming small finite sets of natural numbers. He tries to extend this to an iterative process but realizes that his description fails to yield infinite subsets of N.

Cecil: No. The set of all subsets. Ahh, you start to build it but then almost immediately, back off because it's ... there's a process that you could go through. OK, here's {1}, and here's {2} and {3}. Those are all going to be in there, then {1,2} will be in there and {1,2,3} will be in there and I'm always ... at the beginning. I haven't really looked at ... I haven't thought about this before ... infinite subsets, I'm still ... I'm caught back here at finite subsets but I haven't said ... and all the odd numbers are a subset of ... and all the even numbers are a subset, and multiples of three are a subset and just the idea that, boy, it's a whopper and, uh, I know how to form ... you know if somebody gives me one of these sets I can say whether it's a subset or not.

Claudia and Ranae tried to construct iterative processes where, for each step n, one lists all of the subsets of that cardinality. Cecil made a similar attempt, but was less successful. Ian, as noted in the section on Mental Images, constructed the power set P({1,2,...,n}) for each step n. Like Claudia, Ranae, and Cecil, his construction only yielded the finite elements of P(N). However, unlike Claudia, Ranae, and Cecil, Ian demonstrated reluctance throughout his interview to see any infinite process as complete, whether building a mental structure for N, or attempting to build a mental structure for P(N).

One subject, Kathryn, alluded to encapsulation. In the excerpt below, she talks about a "giant leap past recursion":

Kathryn: Think to talk about P(N) in its entirety you have to make a kind of giant leap past recursion. Even to talk about one non–defined object of P(N) needs such a leap, but maybe not such a large one, since the relevant axiom there is countable choice, which is much more limited ontologically than the power set axiom.

Like the other subjects, though, she does not describe any process structure to which the mechanism of encapsulation could be applied. Thus, we cannot say what mental structures she may have constructed.

For the set N, our subjects did what an APOS analysis calls for. They started with actions, a source for a finite iterative process, which they constructed using the mechanism of interiorization. They applied actions to a completed infinite process and encapsulated that process to yield N as the transcendent object. While the BMI could be used to explain the construction of an infinite iterative process, APOS Theory appeared to align more closely with the subjects' tendencies to apply actions to the process structures they formed.

For P(N), none of the subjects successfully constructed mental structures for the set P(N). Several tried to construct iterative processes, but they soon realized the futility of their attempts. Kathryn noted that P(N) might be a giant step past recursion, but her insight did not help her to build a mental structure for the set P(N).

 

4.6. Mathematical formalism

Several of our subjects referred to formal definitions and theorems in their attempts to create meaning for the set N. As an illustration, we include below an excerpt from Quinn, who offers an informal definition of the natural numbers N, and then suggests use of the Peano Postulates or the successor function to construct the entire set.

Quinn: A string of discretely placed dots on the line that continue. I don't try to envision the end of the line.

I: Right, and how would you think about actually constructing, enumerating the natural numbers? How would you sort of get them?

Quinn: I'm not sure, if you mean something like the Peano Postulates.

I: If I said to you, so what are the natural numbers?

Quinn: I guess I would just say the numbers that people learned to count with in their earliest years, 1, 2, 3, and so forth.

I: Ahh, yeah. That's the point I was trying to get, 1, 2, 3 and so forth. So if you thought of putting that all together you might start with nothing, with the empty set, and you might throw in 1 and what would you do next? Quinn: Throw in a successor, and then a successor, and so forth.

I: Right, and what does that have to do with the natural numbers? Quinn: Well, I think what we are creating are the natural numbers.

Quinn used the number line, a visual perception, to elicit a sequence of numerals, a mental image, to serve as a source for construction of the set of natural numbers. He then coordinated the process of finite enumeration with a formal structure, in this case, Peano's Postulates, to see the natural numbers in their totality. Two other subjects applied formalism in similar ways.

They started with some version of counting or successively adding 1, and then applied rigorous mathematical mechanisms such as induction or recursion to construct the set N .

This situation contrasted sharply with what we found for P(N). Most of the subjects attempted to list subsets, generally starting with small subsets and then increasing cardinality. After realizing that such processes would only yield the finite subsets of N, several participants made references to the use of formalism. For example, Kathryn referred to the ZFC axioms, while Quinn suggested the Schroeder–Bernstein theorem (which, we note, is not about P(N).

Despite several attempts, no one described any mathematical structure that would obtain the set of all of the subsets of N . Kathryn came closest:

Kathryn: The intuition that you should be able to talk about all subsets of N came much earlier than the binary tree, out of a kind of naive philosophical intuition and not out of any formality. That is, P(N) should exist, because if you can talk about one subset you should be able to talk about all of them. And, of course, backing up the naive intuition, one of the ZFC axioms is that if X is a set, so is P(X).

Kathryn starts with subsets of N as a source for her thinking and, as Tall (2001) suggests, proposes formalization in an axiomatic system as a mechanism to establish the existence of P(N). However, her application of this ZFC axiom did not lead to any knowledge about the structure of P(N). Similarly, Quinn alludes to formal ideas as the basis for his thinking about P(N), but he is not able to construct or recall any formal structures that inform his understanding.

Quinn: Even when I was trying to get the full thing organized in my mind, I think I tended to think in terms of classical results and things that had been shown and which sets were larger than which other sets. And the Schroeder–Bernstein theorem comes in here somewhere. Don't ask me to quote it right now, but I remember thinking that it gave certain organization to my thinking process.

I: So you used some of the formal results of mathematics.

Quinn: Yeah, exactly. Without that impetus, I can't imagine that I ever would have actually sat down and really thought about the set of all subsets of anything.

I: But now that you have that impetus, you know those theorems or at least you did. Can you think about all of the subsets of the natural numbers?

Quinn: Well, I said as a theoretical construct, I know that, you know it's another one of those things where you can give examples until you are weary of the process and withdraw [laughter].

Quinn's reference to Schroeder–Bernstein concerns the cardinality of infinite sets, so application of this theorem certainly would not lead to a rigorous formulation of the structure of P(N). Nevertheless, use of Schroeder–Bernstein gives evidence of Quinn's attempt to apply formal ideas to describe P(N), something MacLane (1986) and Tall (2001) propose.

Doris also refers to use of formalism. After disclosing that her only experience with P(N) was restricted to cardinality issues, she notes that her perception of P(N) is reduced to "just the definition."

Doris: The main time that I would deal with the power set of the natural numbers is when I'm dealing with cardinality. So the first thing I'd think of is the cardinality of it, which is bigger, and that whole question.

I: The uncountability?

Doris: Yeah, so as soon as you said that, I'm like oh! yes, that's the ... I really think I just ... as far as how I conceive of it, it's just the definition.

Despite an emphasis on formalism, Doris did not build a mental structure to derive meaning from the formalism in a manner suggested by Dubinsky (2000). Instead, she only saw a "quagmire."

Again, the subjects' thinking about N contrasted with their thinking about P(N). For N, several of the subjects appeared to build mental structures using formalism in ways predicted by MacLane (1986) and Tall (2001). For P(N), the attempts to use formalism failed. In particular, Doris, who mentioned the definition, made no attempt to apply the mechanisms of APOS Theory, as Dubinsky (2000) suggests, to build a mental structure for the set.

 

5. DISCUSSION AND CONCLUSION

Our research question considered the issue, unaddressed in the literature, of whether individual understanding of the uncountable set P(N) can be described using a constructivist perspective. Specifically, do individuals construct mental structures for the set P(N) that both amplify the meaning of the formal definition and go beyond the mere assertion that P(N) is not countable? To help answer this question, we asked eight mathematicians to explain their thinking about P(N). We analyzed their responses using different perspectives. We deemed these perspectives constructivist, because we could identify certain mental structures, sources from which those structures develop, and mechanisms that lead to their development. Our definition of the term 'mental structure' was not precise. Instead, it provided a framework for consideration of the perspectives used in the analysis. The list of perspectives was not exhaustive, but representative; it covered a wide range of cognitive activities, and encompassed all of our subjects' responses. Furthermore, each perspective either has been, or could possibly be, applied to explain individual thinking about countable sets, in this instance, the set of natural numbers N. Even though the set N was not the focus of our investigation, we reported our subjects' thinking about N to serve as a baseline, or backdrop, for our analysis of P(N). The data illustrated a sharp contrast. For the set N, our subjects evoked, or built, mental structures for N. Each subject's thinking could be described using one or more of the perspectives we considered.

For P(N), the situation was just the opposite. Although our subjects made valiant attempts to build mental structures, in support of Burton's (2001) finding that mathematicians value meaningful, connected, and insightful explanations, their attempts were unsuccessful. Their responses were generally limited to vague mental images, intuitions of what P(N) is not, failed attempts to construct processes, and misapplications or incomplete applications of formalism. These results, especially in contrast to what was reported for N, indicate strong support for the following empirical claim: until further advances can be made in our understanding of P(N), absence of evidence of mental structures for P(N) is evidence of absence of those structures. In particular, explanations for the meaning of the word "all" in an uncountable context, beyond the assertion that it is non–iterative, did not arise.

In summary of the perspectives, no subject offered evidence of a visual perception to which other mental mechanisms could be applied to build a mental structure for P(N). On one hand, this was not surprising. As Lakoff and Núñez (2000) note, on–going processes, even if continuous, are conceived iteratively. Yet, no purely iterative image could give rise to an uncountable entity. On the other hand, the real line is a visual representation of an uncountable set that corresponds with P(N). However, it is not clear how an image of the real line would give greater meaning to the word "all."

At least two mental images arose in descriptions of P(N). Doris referred to P(N) as a "quagmire," and Kathryn stated that P(N) was "very, very big, in some sense unknowable." Both images suggest "larger than countable," but neither would likely motivate new experiences that would inspire development of new images that would make more precise the meaning of "all" in the formal definition.

Intuitions develop through repeated experiences that leave mental traces. Our subjects repeatedly used iteration in their attempts to build mental structures for )P(N. Although their attempts failed, spontaneous realizations of the futility of their approaches abounded. Yet, these intuitions informed a notion of what P(N) is not; they did not serve as sources for mental structures for P(N).

Several subjects tried to apply formalism. Doris and Quinn's attempts were unsuccessful. Kathryn quoted one of the ZFC axioms, but the axiom to which she referred, only establishes the existence of the set P(N) (given the assumption that N is a set). Mathematically, establishment of existence is crucial. From a constructivist perspective, it is insufficient.

When asked to describe the set P(N), six of the eight subjects listed elements, and four of the eight actually tried to construct iterative processes. The processes were of two types: to each step n, either the subject assigned all subsets of cardinality n, or the subject constructed the power set P({1. ,2,. ..,n}) For either case, one only obtains the finite elements of P(N). Each subject realized this, but none could make further progress. All of their attempts, at least in terms of the transition from finite to infinite iteration, could be interpreted either by APOS Theory, or the Basic Metaphor of Infinity.

An important finding is that our subjects did not appear to reconceptualize resultant states metaphorically. For the set N, the subjects applied actions to iterative processes. This supports research conducted by Brown et al. (in press), who discovered that their students needed to apply actions to iterative processes in order to correctly construct resultant states. Various reviewers (e.g, Dubinsky, 1999; Gold, 2001; Madden, 2001) have objected to some of the metaphors Lakoff and Núñez use to explain mathematical thinking. Schiralli and Sinclair (2003) concur. They explain that Lakoff and Núñez' method of mathematical idea analysis supplies plausible, humanistic explanations for the origin of conventional mathematical ideas but is insufficient to describe the formation of personal conceptions that constitute the realm of ideational mathematics, the realm of individual mental structures that individuals form to understand mathematical concepts. Our findings support this claim. However, this does not mean that our subjects did not give evidence of metaphorical thinking. Their attempts to construct P(N) iteratively reflected a tendency to reconceptualize uncountable entities as countable ones. This supports Lakoff and Núñez' assertion that human beings tend to think of infinite entities, even continuous ones, as repeated processes. From Tall's (1992) perspective, iteration may be a cognitive root for the mental development of uncountable structures, or, to use the language of this report, a source for the construction of mental structures for P(N).

In the case of APOS Theory, mental construction of P(N), as with any mathematical entity, requires an appropriate process mental structure and a desired action on that process that will lead to encapsulation and construction of P(N) as the transcendent object. In the case of one aspect of countable infinity, infinite iterative processes, that question has been addressed by prior research. Brown et al. (in press) offered an empirically–based, APOS theoretical description of the mental construction of infinite iterative processes and their states at infinity. The authors describe how individuals use the mental mechanisms of interiorization and coordination to construct an iterative process, and detail how the mechanism of encapsulation leads to the mental construction of the state at infinity, which is conceived as a transcendent object. Whether APOS Theory can be extended to describe the cognition of problem solving situations involving uncountable infinity remains an open question requiring further empirical research. However, the subjects' tendencies to construct iterative processes to build a mental structure for P(N), although not successful, could be a starting point. In our future research, we will analyze the iterative constructions that seemed natural to our subjects and try to find ways of enhancing them so that they do lead to a process whose encapsulation will be P(N). The problem is to find the steps that will pass beyond the finite subsets of N to include infinite subsets. One promising direction we will explore is to look at the various Computer Science algorithms for traversing trees. Although these are all designed for finite trees, one or more of them might have useful extensions to a process for an infinite tree.

As we search for a process whose encapsulation is P(N), we will continue to observe students and mathematicians to see if our sample is typical or if there are mental processes appropriate for P(N)in the minds of mathematicians and students. We will consider that an individual has a mental structure for P(N) when he or she can give an explanation of this set that goes beyond its formal definition, or explain the meaning of "all" in terms other than synonyms. We will also be able to observe a mental structure (or lack thereof) when an individual is working with mathematical situations that involve P(N) such as in proving that it is uncountable, or showing it has the same cardinality as the set of real numbers.

This study also raised the question of the general applicability of constructivism. As constructivists ourselves, we believe that individuals build mental structures to make sense of mathematical situations. This study has not changed our belief, but it does raise the question of whether certain mathematical concepts defy a constructivist interpretation. Even when faced with pure formalism, Dubinsky (2000) argues that individuals make certain mental constructions to make sense of purely formal notions. Our subjects made such attempts for P(N), but no one was successful. Thus, the results of this study cast some doubt on the claim made by Dubinsky (2000). Only further empirical research can determine whether this is in fact the case.

For some concepts, those principally studied by research mathematicians, determination of underlying mental structures may not be as crucial. For the set P(N) though, the situation is different because it is a topic of study in the undergraduate curriculum. If the most that a mathematician can communicate to her or his students about the meaning of P(N) is that it consists of all subsets of N, without further elaboration of the meaning of "all," then it is hard to see how students can develop conceptions of uncountable sets such as P(N) that go beyond empty formalism. As we indicated in the Introduction, Burton (2001) notes that current disillusionment with mathematics teaching arises from a lack of meaningful explanations. We agree and note that in order to provide such explanations for infinite sets, the teacher, indeed the mathematical professional, needs to identify or develop meaningful connections for countable and uncountable sets. While this may have been done for the former, this report shows that this has not yet been accomplished for the latter.

 

REFERENCES

Asiala, M., Brown, A., DeVries, D., Dubinsky, E., Mathews, D., & Thomas, K. (1996). A framework for research and curriculum development in undergraduate mathematics education. In J. Kaput, A.H. Schoenfeld, & E. Dubinsky (Eds.), Research in collegiate mathematics education II (pp. 1–32). Providence: American Mathematical Society.        [ Links ]

Aspinwall, L., Shaw, K.L., & Presmeg, N.C. (1997). Uncontrollable mental imagery: Graphical connections between a function and its derivative. Educational Studies in Mathematics, 33(3), 301–317.        [ Links ]

Brown, A., McDonald, M., & Weller, K. (in press). Step by step: Infinite iterative processes and actual infinity. In F. Hitt, D. Holton, & P. Thompson (Eds.), Research in collegiate mathematics education VII. Providence: American Mathematical Society.        [ Links ]

Burton, L. (2001). Research mathematicians as learners – and what mathematics education can learn from them. British Education Research Journal, 27(5), 589–599.         [ Links ]

Cantor, G. (1941). The theory of transfinite numbers (Phillip E. B. Jourdain, Trans.). La Salle, IL: Open Court Publishing.         [ Links ]

Chartrand, G., Polimeni, A., & Zhang, P. (2007). Mathematical Proofs: A transition to advanced mathematics (2nd ed.). Boston: Addison–Wesley.        [ Links ]

Chomsky, N. (2006). Language and mind (3rd ed.). New York: Cambridge University Press.         [ Links ]

Cobb, P., Boufi, A., McClain, K., & Whitenack, J. (1997). Reflective discourse and collective reflection. Journal for Research in Mathematics Education, 28(3), 258–277.         [ Links ]

Cobb, P., Yackel, E., & McClain, K. (Eds.). (2000). Symbolizing and communicating in mathematics classrooms: Perspectives on discourse, tools, and instructional design. Mahwah, NJ: Lawrence Erlbaum Associates.         [ Links ]

Cooley, L., Trigueros, M., & Baker, B. (in press). Schema thematization: A framework and an example. Journal for Research in Mathematics Education.         [ Links ]

Davis, R. B. & Maher, C. A. (1997). How students think: The role of representations. In L. D. English (Ed.), Mathematical reasoning: Analogies, metaphors and images (pp. 93–115). Mahwah, NJ: Lawrence Erlbaum Associates.         [ Links ]

Dreyfus, T. (1991). On the status of visual reasoning in mathematics and mathematics education. In F. Furinghetti (Ed.), Proceedings of the 15th Annual Conference of the International Group for the Psychology of Mathematics Education (Volume 1, pp. 33–48). Assisi, Italy.         [ Links ]

Dreyfus, T. (1995). Imagery for diagrams. In R. Sutherland and J. Mason (Eds.), Exploiting mental imagery with computers in mathematics education (pp. 3–19). Berlin: Springer.         [ Links ]

Dubinsky, E. (1999). Mathematical reasoning: Analogies, metaphors, and images. Notices of the AMS, 46(5), 555–559.        [ Links ]

Dubinsky, E. (2000). Meaning and formalism in mathematics. International Journal of Computers for Mathematical Learning, 5(3), 211–240.         [ Links ]

Dubinsky, E. & McDonald, M. (2001). APOS: A constructivist theory of learning in undergraduate mathematics education research. In Derek Holton et al. (Eds.), The teaching and learning of mathematics at university level: An ICMI study (pp. 273–280). Netherlands: Kluwer.         [ Links ]

Dubinsky, E., Weller, K., McDonald, M., & Brown, A. (2005a). Some historical issues and paradoxes regarding the concept of infinity: An APOS analysis: Part I. Educational Studies in Mathematics, 58(3), 335 – 359.         [ Links ]

Dubinsky, E., Weller, K., McDonald, M., & Brown, A. (2005b). Some historical issues and paradoxes regarding the concept of infinity: Part II. Educational Studies in Mathematics, 60 (2), 253–266.         [ Links ]

Ernest, P. (1997). Social constructivism as a philosophy of mathematics. Albany, New York: State University of New York Press.         [ Links ]

Ernest, P. (1998). The relation between personal and public knowledge from an epistemological perspective. In F. Seeger, J. Voight, and U. Waschescio, (Eds.), The culture of the mathematics classroom (pp. 245–268). Cambridge: Cambridge University Press.         [ Links ]

Fischbein, E. (1987). Intuition in science and mathematics. Dordrecht: Kluwer.         [ Links ]

Fischbein, E. (2001). Tacit models of infinity. Educational Studies in Mathematics, 48 (2/3), 309– 329.         [ Links ]

Fischbein E., Tirosh D., & Hess P. (1979). The intuition of infinity. Educational Studies in Mathematics, 10(1), 491–512.         [ Links ]

Gold, B. (2001). Where mathematics comes from: How the embodied mind brings mathematics into being. Read this! The MAA Online book review column. Retrieved September 1, 2005 at http://www.maa.org/reviews/wheremath.html.        [ Links ]

Goldenberg E. P. (1988). Mathematics, metaphors and human factors: Mathematical, technical and pedagogical challenges in the educational use of graphical representation of functions. Journal of Mathematical Behavior, 7(2), 135–173.        [ Links ]

Hadamard, J. (1945). The Psychology of invention in the mathematical field. New York: Princeton University Press.        [ Links ]

Hersh, R. (1997). What is mathematics really? New York: Oxford University Press.         [ Links ]

Jahnke, H. (2001). Cantor's cardinal and ordinal infinities: An epistemological and didactic view. Educational Studies in Mathematics, 48(2/3), 175–197.         [ Links ]

Kidron, I. (2003). Polynomial approximations of functions: Historical perspectives and new tools. International Journal of Computers for Mathematical Learning, 8 (3), 299–331.         [ Links ]

Lakoff G. & Núñez, R. (2000). Where mathematics comes from. New York: Basic Books.         [ Links ]

Madden, J. (2001). Where mathematics comes from: How the embodied mind brings mathematics into being. Notices of the AMS, 48 (10), 1182–1188.         [ Links ]

MacLane, S. (1981). Mathematical models: A sketch for the philosophy of mathematics. The American Mathematical Monthly, 88 (7), 462–472.        [ Links ]

MacLane, S. (1986). Mathematics, form, and function. New York: Springer–Verlag.         [ Links ]

Moore, A.W.: 1999, The Infinite (2nd ed.). London: Routledge & Paul.         [ Links ]

Moreno, L. E. & Waldegg, G. (1991). The conceptual evolution of actual infinity. Educational Studies in Mathematics, 22 (3), 211–231.         [ Links ]

Piaget, J. & Garcia, R. (1989). Psychogenesis and the history of science. New York: Columbia University Press.        [ Links ]

Piaget, J. & Inhelder, B. (1971). Mental imagery in the child (P.A. Chilton, Trans., original work published in 1966). London: Routledge & Kegan Paul.         [ Links ]

Presmeg, N.C. (1985). The role of visually mediated processes in high school mathematics: A Classroom investigation. Unpublished doctoral dissertation, University of Cambridge.         [ Links ]

Presmeg, N.C. (1986). Visualisation in high school mathematics. For the Learning of Mathematics, 6 (3), 42–48.        [ Links ]

Presmeg, N. C. (1998). A semiotic analysis of students' own cultural mathematics. Research Forum Report. In A. Olivier & K. Newstead (Eds.), Proceedings of the 22n^d Conference of the International Group for the Psychology of Mathematics Education (Volume 1, pp. 136–151). Stellenbosch, South Africa.         [ Links ]

Rodd, M. M. (2000). On mathematical warrants: Proof does not always warrant, and a warrant may be other than proof. Mathematical Thinking and Learning, 2 (3), 221–244.         [ Links ]

Rotman, B. (1988). Toward a semiotics of mathematics. Semiotica, 72 (1/2), 1–35.         [ Links ]

Rotman, B. (1993). Taking God out of mathematics and putting the body back in: An essay in corporeal semiotics. Stanford, CA: Stanford University Press.         [ Links ]

Rotman, B. (2000). Mathematics as sign: Writing, imagining, counting. Stanford, CA: Stanford University Press.        [ Links ]

Schiralli M. & and Sinclair, N. (2003). A constructive response to "Where Mathematics Comes From". Educational Studies in Mathematics, 52 (1), 79–91.         [ Links ]

Sfard, A. (1994). Reification as the birth of metaphor. For the Learning of Mathematics, 14 (1), 44– 55.         [ Links ]

Sfard, A. (1997). A commentary: On metaphorical roots of conceptual growth. In L. English (Ed.), Mathematical reasoning: Analogies, metaphors, and images (pp. 339–371). Mahwah, NJ: Lawrence Erlbaum Associates.         [ Links ]

Sfard, A. (1998). Symbolizing mathematical reality into being or how mathematical discourse and mathematical objects create each other. In P. Cobb, K. E. Yackel, & K. McClain (Eds.), Symbolizing and Communicating: Perspectives on mathematical discourse, tools, and instructional design (pp. 37–98). Mahwah, NJ: Lawrence Erlbaum Associates.        [ Links ]

Sierpinska, A. & Viwegier, M. (1989). How and when attitudes towards mathematics and infinity become constituted into obstacles in students. Proceedings of the 13th Annual Meeting for the Psychology of Mathematics Education (Volume 3, pp. 166–173). Paris.         [ Links ]

Stenger, C., Vidakovic, D., & Weller, K. (2005, February). Students' conceptions of infinite iteration: A follow–up study. Paper presented at the SIGMAA on RUME conference, Phoenix, AZ.         [ Links ]

Tall, D. (1980). The notion of infinite measuring number and its relevance in the intuition of infinity. Educational Studies in Mathematics, 11(3), 271–284.         [ Links ]

Tall, D. (1992). The transition to advanced mathematical thinking: Functions, limits, infinity, and proof. In D.A. Grouws (Ed.), Handbook of Research on Mathematics Teaching and Learning (pp. 495–511). New York: MacMillan.         [ Links ]

Tall, D. (2001). Conceptual and formal infinities. Educational Studies in Mathematics, 48 (2/3), 199–238.         [ Links ]

Tall, D. O, Gray, E M., Bin Ali, M., Crowley, L., DeMarois, P., McGowen, M., Pitta, D., Pinto, M., Thomas, M., & Yusof, Y. (2001). Symbols and the bifurcation between procedural and conceptual thinking. Canadian Journal of Science, Mathematics and Technology Education, 1(1), 81–104.         [ Links ]

Tall, D. (2005, July). A theory of mathematical growth through embodiment, symbolism, and proof. Paper presented at the International Colloquium on Mathematical Learning from early Childhood to Adulthood (Organized by the Centre de Recherche sur 'lEnsiegnement des Mathematiques), Nivelles, Belgium.         [ Links ]

Tall, D. O. & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in mathematics, 12 (2), 151 – 169.         [ Links ]

Tirosh, D. (1991). The role of students' intuitions of infinity in teaching the Cantorian theory. In D. Tall (Ed.), Advanced Mathematical Thinking (pp. 199–214). Dordrecht: Kluwer.         [ Links ]

Tirosh, D. (1999). Finite and infinite sets: Definitions and intuitions. International Journal of Mathematical Education in Science & Technology, 30 (3), 341–349.         [ Links ]

Tsamir, P. (1999). The transition from comparison of finite to the comparison of infinite sets: Teaching prospective teachers. Educational Studies in Mathematics, 38 (1/3), 209–234.         [ Links ]

Vidakovic, D. (1997). Learning the concept of inverse function in a group versus individual environment. In E. Dubinsky, D. Mathews, & B. Reynolds (Eds.), Readings in cooperative learning (MAA Notes No. 44, pp.175–195). Washington, D.C.: Mathematical Association of America.         [ Links ]

Vidakovic, D. & Martin, B. (2004). Small–group searches for mathematical proofs and individual reconstructions of mathematical concepts. Journal of Mathematical Behavior, 23 (4), 465–492.         [ Links ]

Vinner, S. (1991). The role of definitions in the teaching and learning of mathematics. In D. O. Tall (Ed.), Advanced Mathematical Thinking (pp. 65–81). Dordrecht: Kluwer.         [ Links ]

Vygotsky, L.S. (1978). Mind in Society: The development of higher psychological processes. Cambridge, MA: Harvard University Press.         [ Links ]

Vygotsky, L. S. (1981). The development of higher mental functions. In J. V. Wertsch (Ed.), The concept of activity in Soviet psychology (pp. 144–188). Armonk, N. Y.: Sharpe.         [ Links ]

Weller, K., Clark, J., Dubinsky, E., Loch, S., McDonald, M., & Merkovsky, R. (2003). Student performance and attitudes in courses based on APOS Theory and the ACE Teaching Cycle. In A. Selden, E. Dubinsky, G. Harel, & F. Hitt (Eds.), Research in collegiate mathematics education V (pp. 97–131). Providence: American Mathematical Society.         [ Links ]

Wheatly, G. (1991). Enhancing mathematics learning through imagery. Arithmetic Teacher, 39 (1), 34–36.        [ Links ]

Zazkis, R., Dubinsky, E., & Dautermann, J. (1996). Coordinating Visual and Analytic Strategies: A study of students' understanding of the group D₄ . Journal for Research in Mathematics Education, 27 (4), 435–457.        [ Links ]

Zimmerman, W. & Cunningham, S. (Eds.) (1991). Visualization in teaching and learning mathematics (MAA Notes No. 19). Washington, D.C.: Mathematical Association of America.        [ Links ]

 

NOTES

¹ We include groups and societies of individuals to reflect the fact that in our work we look for mental structures and their sources both in individuals (e.g., Weller et al, 2003) and in social interactions (e.g., Vidakovic, 1997; Vidakovic & Martin, 2004). regresar

² Piaget distinguishes between reproductive and anticipatory imagery. Reproductive imagery refers to reproducing in one's mind that which has already been encountered. Anticipatory imagery refers to that which is not perceived by the senses. regresar

³ Pseudonyms have been used for all of the interview subjects. regresar

⁴ In the excerpts, "I" denotes the interviewer, although various interviews were conducted by different members of the RUMEC (Research in Undergraduate Mathematics Education Community) infinity research team. The research team includes the authors of this paper plus Michael McDonald and Anne Brown. regresar