Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.10 no.3 Ciudad de México nov. 2007
Artículos
INTUICIÓN, RIGOR Y RESOLUCIÓN DE PROBLEMAS DE OPTIMIZACIÓN
Intuition, rigor and resolution of optimization problems
Uldarico Malaspina
Pontificia Universidad Católica del Perú, Perú. E–mail: umalasp@pucp.edu.pe
RESUMEN
En este artículo analizamos cualitativa y cuantitativamente las soluciones de 38 estudiantes de ingeniería a dos problemas de optimización. Ocupamos un protocolo ad hoc y las herramientas teóricas configuración epistémica y configuración cognitiva, propuestas por el enfoque ontosemiótico del conocimiento matemático. Los resultados indican que hay deficiencias en el uso de lenguaje formalizado, procedimientos, proposiciones y argumentos, así como una inadecuada interacción entre intuición, formalización y rigor.
PALABRAS CLAVE: Problemas de optimización, rigor, intuición, formalización, configuración epistémica, configuración cognitiva.
ABSTRACT
In this article we make a qualitative and quantitative analysis of the solutions of 38 engineering students to two optimization problems. We use an ad hoc protocol and epistemic configuration and cognitive configuration theoretic tools, proposed by the ontosemiotic approach of mathematical knowledge. The results indicate deficiencies in the use of formalized language, procedures, proposals and arguments, as well as an inadequate interaction between intuition, formalization and rigor.
KEY WORDS: Optimization problems, rigor, intuition, formalization, epistemic configuration, cognitive configuration.
RESUMO
Neste artigo analisamos qualitativa e quantitativamente as soluções de 38 estudantes de engenharia dos problemas de otimização. Utilizamos um protocolo ad hoc e as ferramentas teóricas configuração epistémica e configuração cognitiva, propostas pelo enfoque ontosemiótico do conhecimento matemático. Os resultados indicam que as deficiências no uso de linguagem formalizado, procedimentos, proposições e argumentos, assim como uma inadequada interação entre intuição, formalização e rigor.
PALAVRAS CHAVE: Problemas de otimização, rigor, intuição, formalização, configuração epistémica, configuração cognitiva.
RÉSUMÉ
Dans cet article nous analysons de manière qualitative et quantitativement les solutions de 38 étudiants d'ingénierie à deux problèmes d'optimisation. Nous avons employé un protocole ad hoc et les outils techniques configurations épistémique et configuration cognitive, proposées par l'approche ontosémiotique de la connaissance mathématique. Les résultats montrent que existent déficiences dans l'usage de : langage formel, procédures, propositions et arguments et une interaction inapproprié entre l'intuition, la formalisation et la rigueur.
MOTS CLÉS: problèmes d'optimisation, rigueur, intuition, formalisation, configuration épistémique, configuration cognitive.
1. INTRODUCCIÓN
Con frecuencia, en la vida cotidiana estamos resolviendo muchos problemas de optimización. Por ejemplo, buscamos el mejor camino para ir de un lugar a otro –no necesariamente el más corto–, tratamos de hacer la mejor elección al hacer una compra, buscamos la mejor ubicación cuando vamos a un cine o a un teatro, tratamos de enseñar lo mejor posible, escogemos al mejor candidato (o al menos malo) en una elección. Evidentemente, en ninguno de estos casos usamos matemática formalizada para encontrar lo que nos proponemos, pues afrontamos los problemas con los criterios que nos dan la experiencia y la intuición, aunque no necesariamente hallemos la solución óptima.
Asimismo, en las ciencias naturales y sociales se dan problemas de optimización, ya sea en situaciones prácticas o como parte de un modelo matemático. Por ejemplo, la teoría económica neoclásica tiene como elementos fundamentales la maximización de la función de utilidad del consumidor y la minimización de costos del productor; mientras que en la física se plantean los problemas de maximización de la entropía y minimización de la energía. En tales casos, se deben tratar los problemas con rigor y cuidado.
En la matemática misma hay gran variedad de problemas de optimización. Muchos de ellos han surgido de la realidad y han sido resueltos en forma rigurosa, aportando no sólo la solución misma, sino también métodos y hasta teorías. Ponemos como ejemplos el antiguo problema isoperimétrico, el cual consiste en hallar entre todas las curvas cerradas del plano, de un perímetro dado, la que encierra una región de área máxima; obtener valores extremos de funciones continuas, o determinar una superficie de revolución que encuentre la mínima resistencia al desplazarse en algún medio resistente.
Problemas de tal índole generalmente son estudiados en carreras científicas en las universidades. Así, vemos cómo una actividad mental e intuitiva que se practica permanentemente en la vida diaria –independientemente del grado de éxito que se obtenga– es conocida y tratada de manera formal y rigurosa en los primeros cursos del nivel universitario, o aparece como introducción en cursos de cálculo diferencial para estudiantes de 16 ó 17 años. Consideramos que esto ofrece una muestra de que la enseñanza de las matemáticas no siempre aprovecha las potencialidades que se van generando al resolver problemas concretos de la vida diaria; más aún cuando hay y es posible crear muchísimas situaciones atractivas y lúdicas, donde la dificultad principal radica en obtener un valor máximo o mínimo. Ante ellas, los estudiantes de primaria y secundaria pueden ejercitar su intuición y capacidades de conjeturar, demostrar o rechazar sus conjeturas, y otras vinculadas con el pensamiento matemático que fortalecen el pensamiento científico, tan necesario y útil en la sociedad del conocimiento y la información en que estamos inmersos. En Malaspina (2005) se presentan algunos problemas de optimización adaptables a diversos niveles educativos.
Por otra parte, durante nuestra experiencia didáctica en la universidad hemos observado que jóvenes que ya han estudiado los capítulos de máximos y mínimos en los cursos de cálculo diferencial, al resolver los problemas usan casi mecánicamente los criterios conocidos de la primera y segunda derivada. Sin embargo, no han desarrollado una actitud científica que conjugue la intuición, la conjetura, la formalización y el rigor ante otros problemas de optimización, donde la dificultad no radique en obtener el valor óptimo de una función continua definida en un intervalo cerrado y acotado. En la Figura 1 ilustramos las relaciones entre la intuición, la habilidad para hacer conjeturas y la formalización y el rigor, que consideramos se deberían estimular al resolver problemas en general, y de manera especial los de optimización.
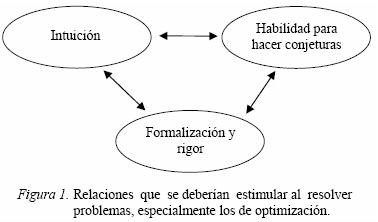
En el presente trabajo ponemos especial atención a las relaciones entre la intuición y la formalización y el rigor, que han sido motivo de estudios y debates en diversos campos de la matemática y diferentes ámbitos académicos. Tenemos, por ejemplo, el libro Conflicts between generalization, rigor and intuition. Number concepts underlying the development of analysis in 17th–19th century France and Germany (Schubring, 2005); la conferencia plenaria Intuition and rigor in mathematics education, anunciada para el Symposium on the Occasion of the 100th Anniversary of ICMI, que se celebrará en Roma en marzo del 2008, y los artículos de Cohn (1995), Roldán y Crobeiro (2001). En el último artículo, las autoras afirman que "hacer matemática significa entonces intuir y formalizar. De modo que intuición y formalización son conceptos indisolublemente unidos, siendo así que entrenar la intuición en matemáticas significa a la vez entrenar la capacidad de concientizar dicha capacidad, para poder formalizar los resultados" (p. 135).
Consideramos que un problema importante en la didáctica de la matemática es lograr que los aprendizajes que van acumulando los estudiantes potencien su intuición y capacidad de resolver problemas. En ese marco, nos planteamos la siguiente pregunta: ¿En qué medida la formalización y el rigor que se inducen en las clases de matemáticas en los primeros ciclos universitarios, particularmente en un curso de cálculo diferencial, potencian la intuición de los estudiantes al resolver problemas de optimización?
A fin de aportar elementos para dar algunas respuestas a esta pregunta, profundizar investigaciones y hacer propuestas, en este artículo indagamos acerca del uso de la intuición, de la formalización y el rigor en la resolución de problemas de optimización. Usamos las configuraciones epistémicas y cognitivas del Enfoque Ontosemiótico –EOS– del Conocimiento Matemático (Godino, Batanero y Font, 2007) para examinar cualitativamente las soluciones de 38 estudiantes de ingeniería a dos problemas, y registramos la información con un protocolo ad hoc.
De manera específica, proponemos analizar:
– La presencia o ausencia de conceptos, proposiciones y procedimientos, así como sus vínculos con la obtención de respuestas correctas al resolver los problemas de optimización planteados.
– Las argumentaciones y los nexos de ellas con el uso de lenguaje formalizado y la obtención de respuestas correctas a los problemas planteados.
– Si los alumnos consideran la justificación del carácter de óptimo de la respuesta que alcanzan en cada problema.
– En qué medida el uso del lenguaje formal contribuye a una argumentación adecuada.
– En qué medida quienes obtuvieron una respuesta correcta usaron un lenguaje formal y justificaron que tal respuesta tiene el carácter de óptimo.
El presente trabajo forma parte de una investigación más amplia, que plantea como algunas de sus hipótesis a ser trabajadas a las siguientes:
– Las formalizaciones y el rigor que se usan en las clases de matemáticas en los primeros ciclos universitarios, particularmente en cursos de cálculo diferencial, no hacen un aporte fuerte al desarrollo de la intuición para resolver problemas no rutinarios de optimización.
– Una deficiencia en la formación científica de los estudiantes de segundo o tercer ciclo universitario radica en que no usan adecuadamente lenguaje formalizado, proposiciones, procedimientos y argumentos cuando resuelven problemas de optimización.
En el segundo apartado de este trabajo expondremos el marco conceptual, precisando lo que entendemos por problema, problema de optimización y formalización, así como el rigor y la intuición al resolver un problema. Presentaremos también, de manera muy resumida, lo que son las configuraciones epistémica y cognitiva en el EOS. En la tercera parte daremos los enunciados de los problemas que propusimos a los estudiantes, y explicitaremos las configuraciones epistémicas de los problemas propuestos con base en las soluciones expertas de un destacado alumno que cursa el tercer ciclo universitario. En la cuarta sección describiremos la metodología, en la quinta mostraremos los resultados, y en la sexta enunciaremos algunas conclusiones, haremos algunas propuestas y daremos algunas pistas para profundizar en el análisis de los resultados.
2. MARCO CONCEPTUAL
Estamos asumiendo un sentido amplio de lo que significa problema, al concebirlo como toda situación que requiera analizar la información, establecer relaciones lógicas y obtener conclusiones. Además, vemos al problema de optimización como aquel cuyo objetivo fundamental es la obtención de un valor máximo o mínimo de una determinada variable, teniendo en cuenta las restricciones del caso; la obtención de una estrategia o conjunto de pasos que constituyen la mejor elección para obtener determinado fin, o que el valor óptimo o la mejor estrategia no existen. Esta manera de considerar los problemas de optimización incluye los casos de variaciones continuas (los valores que pueden tomar las variables son todos los elementos de un intervalo de números reales) y variaciones discretas (los valores que pueden tomar las variables son todos los de un subconjunto de los números enteros). Otra forma de enunciar los problemas consiste en pedir la demostración de que determinado valor (o estrategia) es el óptimo (o la óptima) para una determinada situación.
Ahora bien, los problemas de máximo y mínimo que usualmente se plantean en el cálculo diferencial atañen a la optimización, pues definen funciones de variables continuas, aunque no todos requieren de manera indispensable el uso del cálculo diferencial. También quedan incluidos problemas como el que aparece en el conocido juego de las Torres de Hanoi, al determinar el menor número de movimientos con los que se pueden trasladar, por ejemplo, los cuatro discos de una varilla a otra.
Sobre la intuición en matemáticas, recordamos que algunas maneras de entenderla han sido las siguientes: 1) la intuición es algo opuesto a lo riguroso; 2) lo intuitivo es visual; 3) la intuición nos permite conocer la verdad de algo, sin necesitar demostración alguna; 4) la intuición nos da una perspectiva holística o integradora (entendido como contrario a detallado o analítico). Un punto de vista sobre la intuición que puede alcanzar un alto grado de consenso es el siguiente: idea que posee dos propiedades fundamentales, a) inmediatez (evidencia intrínseca) y b) certeza (sin necesidad de demostración). La intuición nos hace sentir seguros de la verdad de lo que afirmamos y hace que consideremos innecesaria su demostración rigurosa. Con base en este último enfoque, siguiendo a Fischbein (1994), entederemos por intuición:
A special type of cognition characterized by self–evidence and immediacy: an intuitive cognition appears subjectively to the individual as directly acceptable, without the need for an extrinsic justification– a formal proof or empirical support (p. 200).
En este sentido, si un participante da una respuesta correcta a un problema, sin dar explicaciones a los pasos, consideramos que su solución es intuitiva; sin embargo, las intuiciones no se revelan únicamente en las respuestas correctas, ya que también se encuentran en afirmaciones consistentes y encaminadas a una respuesta correcta. Ahora bien, hay una formalización en la resolución de un problema de optimización si el participante ocupa ecuaciones, define funciones y aplica teoremas o resultados matemáticos; usa gráficos, diagramas o cuadros, o bien establece una notación para un manejo sistemático de la información o de las operaciones que considera necesario hacer. Es pertinente recordar lo que Dubinsky (2000) dice acerca del formalismo en matemáticas: "By formalism, I am referring to sets of symbols, put together according to certain rules of syntax or organization, intended to represent mathematical objects and operations" (p. 224).
Acerca del rigor, en forma usual se ha vinculado su estudio a la prueba o demostración. En tal sentido, al examinar el rigor en la solución de un problema consideramos a ésta como la prueba o demostración de los resultados (parciales y final) que se obtienen. Una solución rigurosa de un problema de optimización deberá mostrar buen uso de argumentos, con secuencias lógicas en sus afirmaciones y, en particular, con una justificación que el resultado es óptimo.
Estas ideas de problema, intuición, formalización y rigor se pueden tratar de manera integrada mediante ciertos constructos que propone el enfoque ontosemiótico de la cognición e instrucción matemática (Font y Godino, 2006; D'Amore y Godino, 2007; Godino, Font, Contreras y Wilhelmi, 2006; Godino, Batanero y Font, 2007; Ramos y Font, 2006; Godino, Font y Wilhelmí, 2006), en especial los de configuración epistémica y configuración cognitiva.
El EOS considera que es necesario contemplar una ontología formada por los siguientes elementos:
1. Lenguaje (términos, expresiones, notaciones, gráficos) en sus diversos registros (escrito, oral, gestual).
2. Situaciones–problemas (aplicaciones intra o extramatemáticas, ejercicios).
3. Conceptos–definición (introducidos mediante definiciones o descripciones), como recta, punto, número, media, función.
4. Proposiciones (enunciados sobre conceptos).
5. Procedimientos (algoritmos, operaciones, técnicas de cálculo).
6. Argumentos (enunciados usados para validar o explicar las proposiciones y procedimientos, deductivos o de otro tipo).
Estos seis tipos de objetos se articulan formando configuraciones epistémicas (Figura 2), si adoptamos un punto de vista institucional, o cognitivas si adoptamos un punto de vista personal. El análisis de dichas configuraciones nos informa sobre la anatomía de la actividad matemática.
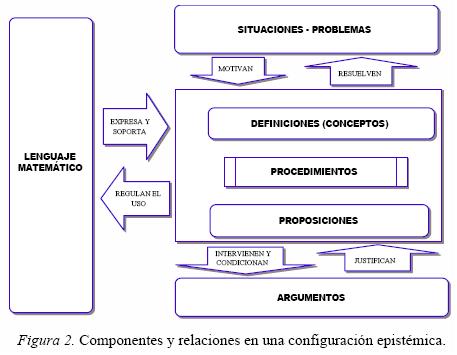
Estas herramientas teóricas ya se han empezado a utilizar para el análisis de la resolución de problemas, como muestra la tesis doctoral de Gusmao (2006).
Si además de la estructura se buscara analizar el funcionamiento (cómo interactúan los objetos) en una perspectiva temporal y dinámica, sería necesario recurrir a otra herramienta teórica del EOS –aún en elaboración–: la de los procesos, que exponen Font, Contreras y Rubio (2007). Dichos autores señalan que en el EOS no se intenta dar, de entrada, una definición de proceso debido a que hay muchas clases diferentes de procesos. Se puede hablar de proceso como secuencia de prácticas, o bien de procesos cognitivos, metacognitivos, de instrucción, de cambio, sociales, etc. Son procesos muy diferentes en los que, quizás, la única característica común a muchos de ellos sea el factor tiempo y, en menor medida, el de secuencia en la que cada miembro toma parte en la determinación del siguiente. Por tanto, el EOS, en lugar de ofrecer una definición general de proceso, ha optado por seleccionar una lista de los procesos que se consideran importantes en la actividad matemática, sin pretender incluir en ella a todos". Los procesos son: algoritmización, argumentación, enunciación, definición, comunicación, problematización, particularización, generalización, materialización, idealización, reificación, descomposición, significación, representación, institucionalización y personalización. En relación con la resolución de problemas, aclaran:
La resolución de problemas, y de manera más general la modelización, debe ser considerada más bien como hiperprocesos matemáticos, al implicar configuraciones complejas de los procesos matemáticos primarios (establecimiento de conexiones entre los objetos y generalización de técnicas, reglas y justificaciones). La realización efectiva de los procesos de estudio requiere, además, la de las secuencias de prácticas de planificación, control y evaluación (supervisión) que conllevan procesos metacognitivos (Godino, Batanero y Font, 2006, p. 9)1
El artículo citado hace una síntesis sobre el estado de desarrollo actual del EOS, donde se refiere la incorporación de determinados procesos matemáticos al marco teórico. Por ello, transcribimos el esquema con el que muestran una parte de las diferentes nociones teóricas propuestas por el EOS (Figura 3). Los autores dicen que:

En este enfoque la actividad matemática ocupa el lugar central y se modeliza en términos de sistema de prácticas operativas y discursivas. De estas prácticas emergen los distintos tipos de objetos matemáticos, que están relacionados entre sí formando configuraciones epistémicas (hexágono). Por último, los objetos que intervienen en las prácticas matemáticas y los emergentes de las mismas, según el juego de lenguaje en que participan, pueden ser considerados desde las cinco facetas o dimensiones duales (decágono). Tanto las dualidades como los objetos se pueden analizar desde la perspectiva proceso–producto, lo cual nos lleva a los procesos que se recogen en la figura (Font, Contreras y Rubio, 2007, pp. 2–3).
La respuesta dominante en las instituciones universitarias, ante la crisis de fundamentos en los finales del siglo XIX, consistió en sustentar toda la matemática en los números naturales y éstos en la teoría de conjuntos axiomatizada por Zermelo –con axiomas ad hoc que impidan la aparición de las contradicciones conocidas, mas conservando en lo posible la riqueza y agilidad de la teoría intuitiva de conjuntos. Tal solución, llamada normalmente formalismo contemporáneo o conjuntismo, es descendiente del formalismo hilbertiano, pero no se apega de manera exacta.
Este tipo de formalismo (Mosterín, 1980) plantea que en la evolución y desarrollo de las teorías matemáticas hay que considerar como mínimo tres estadios sucesivos, que corresponden a tres diferentes niveles de precisión y rigor en el concepto de prueba. En el primer estadio, llamado informal o ingenuo, se prueban los enunciados de la teoría, pero no se dice ni de dónde parte la prueba ni cuáles son los procedimientos admisibles para probar. El segundo estadio, denominado axiomático, determina el punto de partida de la prueba, elige ciertos enunciados de la teoría como axiomas y exige que todos los demás sean probados a partir de ellos, aunque sigue sin explicitarse cuáles son los procedimientos, reglas o medios de prueba admisibles. En el tercer y último estadio, llamado formalizado, el concepto de prueba está completamente precisado y explicitado, tanto en lo que respecta al punto de partida de la prueba como a los medios de prueba permitidos. El tercer estadio es más propio de los lógicos que de los matemáticos, mientras que los dos primeros son los propiamente matemáticos.
En esta investigación nos hemos situado en el primer estadio (informal o ingenuo). Por tanto, consideramos que un alumno muestra rigor cuando hace algún tipo de prueba, lo cual se puede ver como un intento de dar una justificación correspondiente al primero de los tres niveles que se han comentado en el desarrollo de las teorías matemáticas. Si la investigación se hubiera realizado con universitarios que estudian matemáticas puras, el rigor exigido podría ser el segundo nivel. Desde el primer nivel de rigor se puede hacer una gradación, según el tipo de prueba que haya efectuado el alumno (por ejemplo, ausencia de prueba, un razonamiento mediante un ejemplo, un ejemplo cuidadosamente seleccionado o un ejemplo genérico, o bien un razonamiento lógico a partir de proposiciones conocidas, inducción completa, etc.).
Si realizamos las configuraciones cognitivas de las soluciones de los estudiantes, las examinamos y comparamos con la configuración epistémica de referencia que adoptamos para cada problema, encontraremos información valiosa que responde a los objetivos específicos planteados y da elementos para hacer conjeturas sobre las relaciones entre rigor, formalización e intuición. Así, los resultados correctos sin explicitar procedimientos, proposiciones ni dar argumentos revelarían una presencia fuerte de lo intuitivo, mientras que usar proposiciones y procedimientos formales sin llegar a una respuesta correcta o constituir una secuencia argumentativa correcta –que culmine en la justificación del carácter de óptimo para el resultado– daría poco aporte a lo intuitivo, formal y riguroso que normalmente debería tener un curso de cálculo diferencial para estudiantes de ingeniería.
3. PROBLEMAS PROPUESTOS Y CONFIGURACIONES EPISTÉMICAS
Para el estudio empírico propusimos a los alumnos los problemas que incluye el Cuadro I. En el primero hay que considerar variaciones continuas y podría resolverse recurriendo al cálculo diferencial –aunque no necesariamente–, y en el segundo a variaciones discretas.

Como cada problema puede tener más de una configuración epistémica de referencia, dependiendo entre otros aspectos del nivel y del contexto en que se aplique, en esta investigación tuvimos en cuenta las soluciones de un destacado alumno universitario de tercer ciclo, ganador de medallas en olimpiadas matemáticas de ámbito internacional. Por ello, en lugar de partir de las soluciones de un profesor preferimos examinar, entre varios expertos, los modos en que enfoca los problemas un estudiante con habilidades matemáticas reconocidas, de edad y nivel académico similares a los que tienen los alumnos contemplados en el estudio. Sus primeras soluciones a los problemas fueron correctas, pero se juzgaron como muy originales o singulares al analizarlas con los otros expertos. Estuvimos de acuerdo en que muy pocos o ninguno de los alumnos los resolvería de esa manera, por lo cual se le pidió al sobresaliente estudiante que desarrollara otras soluciones, que fueron aceptadas como válidas por los otros expertos y adoptadas como referentes para hacer las correspondientes configuraciones epistémicas.
3.1. Análisis epistémico del problema 1, con variaciones continuas
Cabe precisar que las variables en este problema son: un ángulo entre los lados del paralelogramo y las longitudes de estos lados, con sus restricciones correspondientes.
3.2. Análisis epistémico del problema 2, con variaciones discretas
Cabe precisar que en este problema la variable es el número de pasos para llegar a 25, partiendo de 11. Además, en el EOS las proposiciones consideradas no necesariamente tienen que ser conocimientos previos; también se consideran a las proposiciones que resultan en el proceso de resolución del problema y podrían estar explícitas o implícitas en las soluciones desarrolladas.
4. METODOLOGÍA
La metodología empleada tomó en cuenta cuatro ejes o dimensiones que, en el enfoque ontosemiótico, se designan como el foco, el fin, la generalizabilidad y el nivel de la investigación. El foco fue epistémico (configuraciones epistémicas institucionales) y, sobre todo, cognitivo (configuraciones cognitivas de los alumnos). El fin concernió, sobre todo, a la descripción de significados personales de los alumnos, mediante el estudio de sus configuraciones cognitivas. El nivel de generalizabilidad tuvo carácter exploratorio ya que no se pretende generalizar los resultados a otros contextos o poblaciones, mientras que el nivel de análisis fue puntual, debido a que se pretendió investigar hechos y fenómenos ligados al estudio de una cuestión matemática específica en un contexto determinado.
Propusimos dos problemas de optimización, uno con variables continuas y otro con variable discreta, a 38 alumnos que cursaban el segundo o tercer ciclo universitario en sus estudios de diversas especialidades de ingeniería. Todos estaban matriculados en el curso electivo Matemática Recreativa y habían aprobado un curso de Matemática Básica y otro de Cálculo 1. Algunos estaban estudiando Cálculo 2 y otros ya estaban en Cálculo 3. Se les pidió que resolvieran los problemas individualmente y escribieran en la hoja que se les entregó todos sus cálculos, diagramas o dibujos, tanto los preliminares como los definitivos.
Las soluciones individuales fueron examinadas una a una, teniendo como referencia la configuración epistémica elaborada para cada problema. Se usó un protocolo ad hoc para registrar la información (ver Anexos I y II), prestando atención fundamentalmente a los procedimientos y argumentaciones; entre éstas, a la argumentación sobre el carácter de óptimo del resultado obtenido, propia de las soluciones rigurosas de problemas de optimización.

El análisis de nuestros datos está enmarcado por un proceso de triangulación de opinión de expertos, lo cual permite un estudio más cuidadoso y fino de los datos, al no dejar que prevalezcan sólo las primeras impresiones del investigador. Después de elaborada una primera versión del análisis, ésta fue sometida a la apreciación de expertos tanto en el EOS como en la resolución de problemas, tratando de refinarla.
Para procesar las soluciones de los alumnos, nos planteamos las siguientes preguntas: ¿Halla lo pedido? ¿Qué procedimiento sigue? ¿Argumenta por qué el valor obtenido es óptimo? Y usamos el siguiente protocolo:

5. RESULTADOS
Si bien hay muchas maneras de interrelacionar la información que se consigue al ocupar el protocolo, para esta investigación consideramos importante destacar cuatro casos con ítems de observación comunes a los problemas. Tengamos en cuenta que el Problema 1 es de variables continuas (VC) y el Problema 2 es de variable discreta (VD):
I. Casos en los que mostraron sólo sus resultados (ausencia de argumentos y de procedimientos). Examinamos los subcasos de respuestas correctas y presentamos los porcentajes correspondientes (Figura 4).
II. Casos en los que presentaron formalizaciones (uso de lenguaje formalizado). Examinamos los subcasos de respuestas correctas (IIa) y también –independientemente de la corrección de sus respuestas– los subcasos en que justificaron si el resultado obtenido es óptimo (IIb), con el uso de argumentos. Mostramos los porcentajes correspondientes (Figuras 5 y 6).
III. Casos en los que hallaron lo pedido en el problema. Examinamos los subcasos de formalización (IIIa), con uso de lenguaje formalizado, y también –independientemente de que hayan formalizado o no– los subcasos de justificación de que el resultado obtenido es óptimo (IIIb), con el manejo de argumentos. (Figuras 7 y 8).
IV. Casos en los que intentaron justificar que los resultados obtenidos son óptimos (uso de argumentos). Examinamos los subcasos de explicación correcta y presentamos los porcentajes correspondientes (Figura 9).
Con base en las configuraciones epistémicas que dimos a conocer en los Cuadros 2 y 3, elaboramos configuraciones cognitivas de las soluciones de los estudiantes, correspondientes a cada caso. Mostramos algunas de ellas como representativas de sus similares.


Estos casos llaman nuestra atención porque los alumnos simplemente escribieron una respuesta. No hay procedimientos ni argumentos; tampoco se puede percibir qué proposiciones han usado. Esto revela que, ante la tarea de resolver el problema, se quedan en una conjetura o una aproximación intuitiva. Y al ser alumnos que han aprobado un curso de cálculo diferencial, podemos afirmar que existe una débil influencia de su enseñanza y aprendizaje para ir más allá de una solución intuitiva. Es oportuno recordar lo que nos dice Fischbein: "The educational problem is to develop new, adequate, intuitive interpretations as far as possible, together with developing the formal structures of logical reasoning" (1994, p. 211).
La Figura 4 presenta en qué proporción las respuestas son correctas, con el propósito de tener una información sobre la calidad de la conjetura y la aproximación intuitiva a los problemas. Vemos que en el problema de variable discreta el porcentaje de los que muestran sólo su resultado es menor que en el problema de variable continua; sin embargo, el porcentaje de los que dan una respuesta correcta (72,7 %) es mayor que en el problema de variable continua (57,1 %). Por ello, podríamos decir que para el problema de variable discreta hay una aproximación intuitiva mejor que para el de variable continua, o que el grado de efectividad de la intuición fue mayor al tratar de resolver el problema de variable discreta.
A continuación mostramos una solución del problema de variación continua, ubicada en este caso, y su correspondiente configuración cognitiva:
Alumno 29
Problema con VC (sólo muestra su resultado y la respuesta es correcta).

Configuración cognitiva:

La ausencia de procedimientos, proposiciones y argumentos explícitos resulta clara, y la diferencia con la configuración epistémica de referencia es muy grande.
Como ya dijimos, el criterio de formalización es bastante amplio, y tratándose de jóvenes del segundo o tercer ciclo universitario –entre 17 y 18 años– no somos especialmente exigentes; sin embargo, distinguimos los que sólo escriben algunos números o dibujan sólo un paralelogramo de aquéllos que usan expresiones algebraicas, ecuaciones, notación funcional, teoremas, diagramas o notaciones propias.
Por los bajos porcentajes de casos en que hay formalizaciones, sobre todo en el problema de variable discreta, podemos señalar que hay deficiencias en el manejo formal de argumentos, procedimientos y proposiciones como las descritas en el análisis epistémico de los problemas; esto se confirma al observar que no es muy alto el porcentaje de los que llegan a una respuesta correcta empleando formalizaciones. Cuantitativamente, podríamos decir que las deficiencias son mas serias al resolver el problema con variación discreta (Figura 5), pero cabe destacar las soluciones de este problema con formalizaciones, respuesta correcta y aproximación a una argumentación sobre el carácter de óptimo de la solución hallada. A continuación mostramos una de estas pocas soluciones del problema discreto y su correspondiente configuración cognitiva, que tiene bastante en común con la configuración epistémica de referencia.
Alumno 6
Problema con VD (formaliza y da respuesta correcta).

Configuración cognitiva:

Otra mirada a los casos con formalizaciones es observar si justificaron o no que la solución –independientemente de que sea correcta o no– resulta un máximo o un mínimo, según el problema (Figura 6).
Una de las ventajas de las formalizaciones radica en que contribuyen a una exposición rigurosa de las ideas, la cual se percibe en la interrelación clara y ordenada de conceptos, proposiciones, argumentos y procedimientos. La solución correcta a un problema de optimización debería incluir la justificación de que el resultado obtenido es óptimo, pero vemos que hay un porcentaje considerable de alumnos que no lo hacen, sobre todo en el problema con variable discreta, a pesar de que formalizan. Esto nos lleva a afirmar que se requiere prestar más atención a la formación en el pensamiento riguroso y al uso adecuado de la formalización.
Resulta ilustrativo mostrar una solución del problema de variación continua en la que se usa lenguaje formalizado, pero la respuesta es incorrecta y no hay justificación de que sea óptima (en rigor, no podría haberla por ser incorrecta la respuesta; sin embargo, precisamente por no buscar una justificación la búsqueda formal termina en un caso particular no óptimo).
Alumno 6
Problema de VC (formaliza, pero no concluye correctamente).

Configuración cognitiva (Parte 1):

Configuración cognitiva (Parte 2):

El estudiante concluye, de manera equivocada, que el paralelogramo de área máxima buscado es un rectángulo cuyos lados miden 6 y 8 unidades. No obstante, podemos constatar que hay similitudes entre la configuración epistémica de referencia y la configuración cognitiva de su solución, por lo cual el estudiante llega, formalmente, muy cerca de la solución correcta, al igual que otros estudiantes que no formalizaron. Por casos como estos nos preguntamos si el rigor y las formalizaciones que se inducen en los cursos de matemáticas están realmente complementando la intuición.
Los resultados que presentamos en las Figuras 7 y 8 indican también que hay deficiencias formativas en la formalización y la actitud científica para canalizar adecuadamente las conjeturas y aproximaciones intuitivas a los problemas. No son muchos los alumnos que hallaron una respuesta correcta usando lenguaje formal, sobre todo en el problema con variable discreta, y pocos los que, al llegar a ella, justificaron –argumentaron correctamente– que cumple con la característica de ser el óptimo. Cabe destacar que muy pocos estudiantes encontraron lo pedido formalizando y justificando que lo obtenido es óptimo: 7,9 % en el problema de variación continua y 5,3 % en el de variación discreta. Sólo un estudiante (2,6 %) aplicó este procedimiento en ambos problemas. A continuación, mostramos sus soluciones, pero no transcribimos sus configuraciones cognitivas debido a su gran similitud con las configuraciones epistémicas de referencia.
Alumno 3
Problema con VC (halla lo pedido, formaliza y justifica que su resultado es óptimo).

Alumno 3
Problema con VD (halla lo pedido, formaliza y justifica que su resultado es óptimo).

Pocos alumnos intentaron justificar que sus resultados eran óptimos y, de ellos, una cantidad mínima realmente justificaron (dieron una explicación correcta). En el problema de variación discreta y otros con carácter lúdico, muchos consideraron suficiente llegar a una solución que parecía convincente, lo cual muestra las deficiencias en el pensamiento riguroso y el uso de lenguaje formalizado y de argumentos para demostrar la validez de resultados. Por otra parte, hemos encontrado casos donde parece que el uso de lenguaje algebraico para formalizar y la búsqueda de justificaciones formales los alejan de una mirada más natural de la situación planteada, sobre todo al resolver el problema con variación discreta. A modo de ilustración, transcribimos una solución y su configuración cognitiva.
Alumno 27
Problema con VD (formaliza e intenta justificar que su resultado es óptimo).

Configuración cognitiva

Se percibe que en este alumno hay un empleo de lenguaje formalizado y una intención de ser riguroso, quizás influenciado por los cursos universitarios de matemática ya aprobados, pero tal actitud no está complementando una reacción natural ante este problema de ubicarlo en un contexto aritmético y tantear algunos pasos. No llega a percibir que su ecuación no está formalizando o modelizando la situación planteada. Si bien es cierto que cuando a y b son no negativos y cumplen que 2a — 3b =14=, entonces el mínimo valor de a + b es 7 (con a = 7 y b = 0); al aplicar 7 veces el paso multiplicar por 2, partiendo del número 11, no llegará al 25. Recordemos que una de las proposiciones en la configuración epistémica de referencia es que con sólo multiplicaciones por dos no se puede llegar a 25, partiendo de 11. Una proposición casi obvia e intuible por el alumno, mas no la aplica para verificar su respuesta obtenida formalmente.
6. CONCLUSIONES Y PERSPECTIVAS
Como resumen sobre los resultados de esta investigación, la primera conclusión a la que llegamos es que se perciben deficiencias en el uso de proposiciones, procedimientos y argumentos al resolver los problemas de optimización propuestos. Hay casos en los que no se muestran explícitamente, como se nota en la Figura 4 y en la configuración cognitiva de la solución que hace el alumno 29; en otros se muestra el uso de lenguaje formalizado, pero no llegan a una respuesta correcta, como puede observarse en la Figura 5, en la configuración cognitiva de la solución del problema de variación continua, que hizo el alumno 6, y en la correspondiente a la solución del problema con variación discreta, realizada por el alumno 27.
La segunda conclusión es que una deficiencia específica de argumentación al resolver los problemas de optimización propuestos radica en la poca presencia de justificación de que el resultado es óptimo, lo cual se vuelve más notorio al resolver el problema de variable discreta (Figuras 6 y 9).
La tercera conclusión es que se perciben capacidades para intuir las respuestas correctas a los problemas propuestos, mas no han sido fortalecidas con experiencias previas en el empleo adecuado de argumentos, procedimientos, proposiciones y lenguaje formalizado, como se observa en las Figuras 4, 7 y 8.
Como conclusión más general, queremos resaltar que el uso de herramientas teóricas propuestas por el EOS, como la configuración epistémica y la configuración cognitiva, permite un estudio integrado de las nociones de problema, intuición, rigor y formalización.
El trabajo desarrollado y las deficiencias identificadas abren perspectivas para seguir investigando y hacer propuestas que contribuyan a que no continúen presentándose este tipo de deficiencias. Así, consideramos que es muy importante investigar profundamente, por una parte, en la mejor manera de orientar el aprendizaje del cálculo diferencial (muy especialmente el capítulo de máximos y mínimos); por otra, en la forma más adecuada de introducir desde la primaria problemas de optimización, con el propósito de potenciar las capacidades naturales de resolver intuitivamente diversos problemas de optimización que se presentan en la vida diaria.
Más específicamente:
– Debemos prestar más atención a educar en la formalización y el rigor, como una actitud científica que complementa la intuición. Sería conveniente planificar, para las sesiones de resolución de problemas, configuraciones epistémicas en las que el tipo de argumentación considerada como válida fuese cada vez más exigente. En particular, resulta necesario hacer una profunda investigación sobre la presencia de este enfoque en la enseñanza y aprendizaje de máximos y mínimos en el cálculo diferencial, así como su influencia en la justificación del carácter de óptimo de la solución encontrada, sobre todo en problemas cuyas variables no son continuas.
– Debemos contribuir a potenciar la intuición optimizadora que se genera al buscar situaciones óptimas en la vida diaria, educando en la formalización y el rigor desde la educación primaria, usando problemas adecuados de optimización.
Otra línea de trabajo para profundizar en esta investigación concierne a examinar los procesos considerados en el EOS. La estrecha interrelación entre ellos abre un amplio panorama de estudio, parte del cual podría hacerse siguiendo la técnica que muestra la Figura 3 y ubicar el proceso que se desea estudiar en el centro del hexágono, a fin de relacionarlo con los procesos de comunicación, enunciación, definición, argumentación y algoritmización, y luego colocarlo en el centro del decágono para analizarlo en el marco de las diversas facetas duales (Font, Contreras y Rubio, 2007).
También sería útil continuar el análisis cualitativo y cuantitativo de las soluciones hechas por los alumnos en esta investigación, pues a partir del mismo protocolo se pueden descubrir diversos niveles en la resolución de los problemas trabajados y buscar formas de concretar las propuestas planteadas en los párrafos anteriores. Si examinamos globalmente los cuadros presentados en los Anexos I y II, consideramos que pueden distinguirse hasta nueve niveles, de menor a mayor, siendo el nivel cero el de los que no se involucran en el problema, mientras que los otros ocho los describimos resumidamente en el Cuadro V.

El Cuadro VI resume el número de alumnos que se encuentra en cada nivel, según cada problema, y da elementos para considerar agrupaciones de niveles:
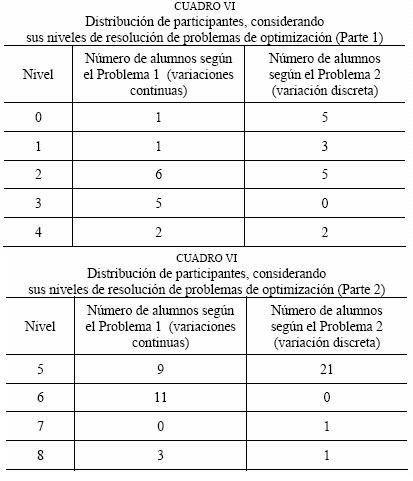
Finalmente, este tipo de estudios también puede ser complementado y profundizado al ahondar en otros problemas matemáticos; comparar soluciones individuales y soluciones hechas en grupo; hacer configuraciones epistémicas, tomando como referencia análisis hechos entre varios expertos y con alumnos ganadores de medallas en olimpiadas matemáticas internacionales, que tienen gran experiencia en resolver problemas, y ocupar configuraciones metacognitivas.
REFERENCIAS BIBLIOGRÁFICAS
Cohn, R. (1995). Entrenando la intuición. Siglo XXI. Perspectivas de la Educación desde América Latina, 2. [ Links ]
D'Amore, B. y Godino, J. D. (2007). El enfoque ontosemiótico como un desarrollo de la teoría antropológica en didáctica de la matemática. Revista Latinoamericana de Investigación en Matemática Educativa 10 (2), 191–218. [ Links ]
Dubinsky, E. (2000). Meaning and formalism in mathematics. International Journal of Computers for Mathematical Learning 5 (3), 211–240. [ Links ]
Fischbein, E. (1994). Intuition in science and mathematics. Holland: Reidel Publishing Company. [ Links ]
Font, V. y Godino, J. D. (2006). La noción de configuración epistémica como herramienta de análisis de textos matemáticos: su uso en la formación de profesores. Educaço Matematica Pesquisa 8 (1), 67–98. [ Links ]
Font, V.; Contreras, A. y Rubio, N. (2007). Procesos en matemáticas. Una mirada desde un enfoque ontosemiótico. Conferencia especial en la XXI Reunión Latinoamericana de Matemática Educativa (RELME). Maracaibo, Venezuela. [ Links ]
Godino, J. D. (2002). Un enfoque ontológico y semiótico de la cognición matemática. Recherches en Didactique des Mathématiques 22 (2–3), 237–284. [ Links ]
Godino, J. D.; Font, V. y Wilhelmi, M. R. (2006). Análisis ontosemiótico de una lección sobre la suma y la resta. Revista Latinoamericana de Investigación en Matemática Educativa (Número Especial), 131–155. [ Links ]
Godino, J. D.; Font, V.; Contreras, A. y Wilhelmi, M.R. (2006). Una visión de la didáctica francesa desde el enfoque ontosemiótico de la cognición e instrucción matemática. Revista Latinoamericana de Investigación en Matemática Educativa 9 (1), 117–150. [ Links ]
Godino, J. D.; Batanero, C. y Font, V. (2007). The onto–semiotic approach to research in mathematics education, ZDM. The International Journal on Mathematics Education 39 (1–2), 127–135. [ Links ]
Gusmao, T. R. S. (2006). Los procesos metacognitivos en la comprensión de las prácticas de los estudiantes cuando resuelven problemas matemáticos: una perspectiva ontosemiótica. Tesis de doctorado, Universidad de Santiago de Compostela. [ Links ]
Malaspina, U. (2005). Motivation and development of mathematical thinking using optimization problems. In A. Gagatsis (Ed.), Proceedings of the 4th Mediterranean Conference on Mathematics Education (Vol. II, pp 491– 500), Palermo, Italy. [ Links ]
Mosterin, J. (1980). Teoría axiomática de conjuntos. Barcelona, España: Ariel. [ Links ]
Ramos, A. B. y Font, V. (2006). Contesto e contestualizzazione nell'insegnamento e nell'apprendimento della matematica. Una prospettiva ontosemiotica. La Matematica e la Sua Sidattica 20 (4), 535–556. [ Links ]
Roldán, R. y Cribeiro, J. (2001) Entrenando la intuición en la matemática superior. Revista Ciencias Matemáticas 19 (2), 133–141. [ Links ]
Schubring, G. (2005). Conflicts between generalization, rigor and intuition. Number concepts underlying the development of analysis in 17th–19th century France and Germany. New York, USA: Springer. [ Links ]
1 Godino, J. D.; Batanero, C. y Font, V. (2006). Un enfoque ontosemiótico del conocimiento y la instrucción matemática. Departamento de Didáctica de la Matemática. Universidad de Granada, España. [Una versión resumida de este trabajo es el artículo Godino, J. D., Batanero, C. y Font, V. (2007). The onto–semiotic approach to research in mathematics education. ZDM. The International Journal on Mathematics Education 39 (1–2), 127–135 ]. regresar




















