Artículos

 

Concepciones de la transformación lineal en contexto geométrico

 

Concepts of linear transformation in a geometric context

 

Juan Gabriel Molina*, Asuman Oktaç**

 

* Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada–IPN. México, D. F. México; Email: jmolinaz@ipn.mx

** Departamento de Matemática Educativa, Centro de Investigación y de Estudios Avanzados–IPN, México, D.F., México; Email: oktac@cinvestav.mx Página de internet: http://www.matedu.cinvestav.mx/aoktac.html

 

Recepción: Abril, 07, 2006
Aceptación: Noviembre 24, 2006.

 

RESUMEN

Basándonos en la teoría de Fischbein (1987) sobre la intuición y los modelos intuitivos, en este trabajo nos enfocamos a identificar aquellos modelos intuitivos que pudieran tener algunos estudiantes con respecto a la transformación lineal en contexto geométrico. Para lograr tal propósito, diseñamos una entrevista; luego de aplicarla y analizarla, hallamos que todos los alumnos encuestados pensaban la transformación lineal en términos de ejemplos prototipo o modelos. Asimismo, hicieron patente que contaban con un universo de transformaciones lineales, como expansiones, contracciones, reflexiones, rotaciones y combinaciones de éstas. Los matices de los modelos cambiaban de acuerdo con los estudiantes y por las propiedades que asignaban a sus representaciones.

PALABRAS CLAVE: Transformaciones lineales, álgebra lineal, modelos intuitivos, intuición.

 

ABSTRACT

Referring to the theory of intuitions and intuitive models of Fischbein (1987), we focus our attention in identifying those intuitive models that some students might have with respect to linear transformations in a geometrical context. In order to achieve our goal we designed an interview; after applying and analyzing it we found that all the students that we interviewed were thinking about the linear transformation in terms of prototypical examples or models. Students seemed to have a universe of linear transformations that consisted in expansions, contractions, reflections, rotations and combinations of these. The nuances of these models were changing depending on the student and the properties that they were assigning to their representations.

KEYWORDS: Linear transformations, linear algebra, intuitive models, intuition.

 

RESUMO

Baseando–nos na teoria de Fischbein (1987) sobre a intuição e os modelos intuitivos, nesse trabalho nos focalizamos a identificar aqueles modelos intuitivos que podem ter alguns estudantes com respeito à transformação linear no contexto geométrico. Para alcançar tal propósito, planejamos uma entrevista; logo depois de aplicá–la e analisá–la, fizemos com que todos os alunos pesquisados pensassem a transformação linear em termos de exemplos protótipos ou modelos. Da mesma maneira, fizeram patente que contavam com um universo de transformações lineares, como expansões, contrações, reflexões, rotações e combinações dessas transformações lineares. Os detalhes dos modelos trocaram dependendo dos estudantes e das propriedades que assinalavam as suas representações.

PALAVRAS CHAVE: Transformações lineares, álgebra linear, modelos intuitivos, intuição.

 

RÉSUMÉ

En prenant en compte la théorie de Fischbein (1987) sur l'intuition et les modèles intuitifs, dans ce travail nous cherchons à identifier ces modèles intuitifs qui pourraient se trouver dans quelques étudiants en rapport à la transformation linéaire en contexte géométrique. Pour arriver a ce propos là, nous avons conçu un entretien. Après l'avoir appliqué et analysé, nous avons trouvé que tous les élèves avaient pensé la transformation linéaire en termes d'exemples prototypes ou de modèles. De même, l'analyse a montré que les étudiants avaient un univers de transformations linéaires, restreint aux expansions, contractions, réflexions, rotations et combinaisons de celles–ci. Les modèles changent sensiblement par rapport aux étudiants et les propriétés qu'ils donnaient à leurs représentations.

MOTS CLÉS: Transformations linéaires, algèbre linéaire, modèles intuitifs, intuition.

 

1. INTRODUCCIÓN

1.1. Acerca de la pertinencia de la investigación

Durante el proceso en que los estudiantes aprenden conceptos matemáticos, les asocian significados que construyen. En muchos casos, dichos significados se relacionan con la experiencia anterior y la intuición de los alumnos, y difieren de la interpretación teórica que la matemática les asigna. Consideramos que el conocimiento de los modelos mentales utilizados por los alumnos para elaborar estos significados intuitivos es muy importante, ya que proporcionan elementos a los investigadores y profesores para ser tomados en cuenta al investigar el fenómeno enseñanza–aprendizaje de la matemática escolar.

Nuestra investigación se centra en el Álgebra Lineal (AL). Tal interés se debe en parte a las dificultades conceptuales que esta rama representa para los estudiantes, y por su importancia en el currículo escolar. Por ejemplo, en México gran parte de las carreras, incluyendo las que involucran tecnología –como los diferentes tipos de ingenierías o licenciaturas– incluyen en su programa de estudios al menos un curso de AL.

Un rasgo característico del AL es el alto nivel de abstracción en sus conceptos. Las investigaciones muestran que esta situación hace que los estudiantes tengan dificultades para entenderla, lo cual se puede expresar bajo la forma de automatismos o interpretaciones personales que en muchos casos difieren de la interpretación que el AL pretende comunicar y, en algunos casos, obstaculizan su entendimiento (Sierpinska, 1996).

 

1.2. Objetivo de la investigación

En nuestro trabajo hemos planteado como objetivo identificar aquellos modelos intuitivos –en el sentido de Fischbein, 1987– que los estudiantes pudieran tener acerca de la transformación lineal (TL) en contexto geométrico. Aclaramos que no pretendemos decir que los modelos que se reporten estarán presentes en todos los estudiantes; más bien nos interesa observar de qué manera la existencia de algunos modelos geométricos influye en el aprendizaje del concepto de transformación lineal.

Las siguientes consideraciones ayudarán a poner en contexto al lector de nuestra investigación y a destacarla:

El estudiante tiende a olvidar las propiedades formales y tiende a mantener en mente aquellas impuestas por un modelo intuitivo. La explicación parece ser muy simple: las propiedades impuestas por el modelo concreto constituyen una estructura coherente, mientras las propiedades formales aparecen, al menos a primera vista, más bien como una colección arbitraria (Fischbein, 1989, p.10, traducción nuestra).

Es necesario conocer tales concepciones para definir sus consecuencias en el entendimiento de los conceptos.

Coincidimos con Fischbein (1989) cuando comenta que las concepciones de los estudiantes se pueden modificar (y orientarse en beneficio del aprendizaje de los estudiantes). Un primer paso para definir la estrategia que hará tal cambio es identificar los modelos tácitos en los estudiantes con respecto al concepto matemático de interés. En el caso de nuestra investigación, atenderemos el concepto de transformación lineal.

En la investigación trabajamos con situaciones geométricas en para poder identificar aquellos modelos geométricos que puedan influir la comprensión del concepto TL. La razón por la cual nos inclinamos a utilizar representaciones geométricas es porque asumimos que:

(...) nosotros inventamos, entendemos recurriendo básicamente a representaciones concretas, que son mediadoras entre significados abstractos y el transcurso de alguna actividad concreta. Esto podría ser ciertamente una afirmación trivial. Lo que no es trivial es que muchas veces los substitutos concretos no sólo inspiran a estimular el proceso de razonamiento, sino de hecho controlan su curso (Fischbein, 1989, traducción nuestra).

La conjetura central que tomamos en nuestra investigación es que algunos estudiantes pueden asociar la idea de movimiento a la TL. Para facilitar el análisis, identificamos tres tipos de movimientos:

 

a. Movimientos geométricos simples: Ciertos movimientos asociados a transformaciones lineales; por ejemplo, una TL de expansión o de contracción, una TL de rotación o una TL de reflexión.

a. Combinación de movimientos geométricos simples: Nos referimos a las combinaciones que los estudiantes puedan realizar con los movimientos simples, por ejemplo, la composición de una rotación y una expansión.

b. Transformaciones difíciles o imposibles de describir con movimientos geométricos simples o combinación de éstos: Es el caso de la TL de trasquilado, la cual requiere de interpretaciones algebraicas para ser aceptada como TL, o bien otras transformaciones como

 

La hipótesis consiste en que algunos estudiantes pueden asociar geométricamente una TL con los casos (a) y (b), y la existencia de una TL puede rechazarse geométricamente si representa el caso (c). Si esto es cierto, las consecuencias que se presenten acerca de la enseñanza y el aprendizaje de tal concepto son de mayor importancia.

Bagni (2000) observa que los estudiantes tienen una tendencia a generalizar las reglas algebraicas, particularmente las que están relacionadas con la linealidad. Sobre este fenómeno, comenta:

Las situaciones previamente descritas muestran que una regla 'simple' a menudo se ve como natural y reconfortante. Por lo tanto, desde un punto de vista afectivo también, algunos estudiantes son llevados a aplicarla a muchos casos, sin controles particulares. Desde luego, esto puede causar errores peligrosos. (Bagni, 2000, traducción nuestra).

El mismo fenómeno fue detectado por Matz (1982), quien clasificó este tipo de errores como los que se generan por la elección incorrecta de una técnica de extrapolación.

 

2. MARCO TEÓRICO: LA INTUICIÓN Y LOS MODELOS INTUITIVOS

2.1. La intuición

A continuación, discutiremos algunas ideas del trabajo de Fischbein (1987; 1989) acerca de la intuición y los modelos intuitivos, mostrando la relación que guarda con nuestra investigación.

Fischbein dice que las personas tenemos necesidad de entrar en un estado de convencimiento acerca de los conceptos matemáticos con los que nos encontramos; es decir, tener certeza de ellos. Ese estado de convencimiento es mediado por la intuición, a través de modelos intuitivos. Con respecto a la intuición, Fischbein señala que este término no tiene definición única, sino debemos entenderlo como aquellas ideas que se aceptan como ciertas al ser evidentes por sí mismas, no requieren de argumentación para que sean aceptadas.

La intuición no es la principal fuente de conocimientos evidentes y verdaderos, pero parece serlo porque su papel es exactamente crear aparición de certeza, conferir a distintas interpretaciones o representaciones un carácter de certeza intrínseca e incuestionable (Fischbein, 1987, p. 12, traducción nuestra).

Fischbein (1987) hace una delineación minuciosa de la intuición, discutiendo los rasgos característicos que pueden tener las nociones intuitivas. Cabe aclarar que no pretendemos en este trabajo hacer una categorización usando estas propiedades detalladamente; sólo nos serviremos de ellas cuando las podemos identificar claramente en las respuestas de los estudiantes. A continuación, resumimos las características tomadas en cuenta por Fischbein:

Evidencia. Las ideas intuitivas se aceptan como ciertas por sí mismas; no necesitan de argumentos para convencer de su certeza. Por ejemplo, si arrojamos una moneda al aire, no necesitamos argumentar para convencer a una persona que la moneda caerá.

Certeza. Las nociones intuitivas se aceptan como creencias intrínsecas. Las características de ser evidente y segura están relacionadas estrechamente, pero no aluden a la misma propiedad. Por ejemplo, el teorema de Pitágoras no es evidente por sí mismo, pero después de su demostración e instrucción escolarizada nos convencemos de su certeza.

Perseverancia. Las ideas intuitivas son nociones que pueden influir en nuestro pensamiento a lo largo de la vida. Aún cuando ya hayamos adquirido un grado avanzado de educación formal, se mantienen en nosotros.

Un ejemplo es el modelo tácito denominado entrada–salida (Fischbein, 1989), que consiste en lo siguiente: Cuando a un niño de primaria se le presenta una expresión como 3 = 3, puede interpretar que 6–3 = 3 o que 7–4 =3. De manera semejante, cuando se le muestra una situación como 4 + 5 = 3 + 6, puede dar la respuesta "después del igual va una respuesta, no otro problema" (Kieran, 1981, referido en Fischbein, 1989).

Lo que ocurre con los niños es que perciben que de un lado de la igualdad hay un proceso y en el otro su resultado. Por otra parte, cuando se les pide a estudiantes de secundaria que simplifiquen la expresión 2a + 5b, anotan 2a+5b= 7ab ; sin embargo, nunca suelen escribir 7ab=2a+5b . Si ahora consideramos a estudiantes universitarios y les pedimos que encuentren el equivalente de , intuitivamente aceptan que = 0.33333... . Asimismo, se mostrarían reacios a aceptar que 0.33333... es igual a ; para ellos siempre faltaría una fracción pequeñísima para considerarlo igual o que tal expresión tendería a .

Fischbein apunta que cada uno de los casos es generado por el mismo modelo intuitivo tácito, que denomina entrada–salida. De un lado de la igualdad, los estudiantes ven un proceso y del otro un resultado como 0.3333..., que se prolonga indefinidamente, es un proceso que nunca termina. Por ello, para estos estudiantes 0.333... nunca será igual a .

El punto que nos interesa resaltar de este ejemplo reside en que los estudiantes universitarios, de quienes se puede pensar que tienen cierta madurez en cuanto al razonamiento matemático, llevan consigo concepciones intuitivas que les acompañan de por vida, y podrían obstaculizar su entendimiento de conceptos matemáticos.

Coerción. Las nociones intuitivas se imponen en el individuo como representaciones o interpretaciones absolutas y únicas. Además, se oponen al conocimiento formal, lo cual provoca el efecto de que ciertos conceptos matemáticos sean considerados como inaceptables. Por ejemplo, la idea intuitiva de que "la suma infinita de términos es infinita" podría ser un obstáculo para aceptar la convergencia de series.

Estatus de teoría. Este rasgo de ciertas intuiciones tiene el efecto de que, al aceptar intuitivamente una frase, también admitimos su generalidad y universalidad, pero a través de una pieza de información muy particular, como alguna analogía o diagrama.

Extrapolación. Las nociones intuitivas pueden extrapolarse de un dominio a otro; por ejemplo, cuando un estudiante aplica las propiedades de los conjuntos finitos a los infinitos. Esta situación se refleja cuando los alumnos rechazan la posibilidad de establecer una relación unívoca entre el conjunto de los números pares positivos y el de los números naturales (Fischbein, 1987, p. 49).

Globalidad. Las nociones intuitivas tienen un carácter general, unitario o explicativo de un fenómeno o concepto. Así, cuando nos formamos una noción intuitiva de cierto fenómeno llega en forma íntegra, completa. Por ejemplo, si nos mostraran la fotografía de un amigo no llegaría a nuestra mente información sobre sus ojos, pelo, forma de vestir y luego reconoceríamos quien es. La información se daría en un solo instante, íntegra. De inmediato sabríamos de quien se trata, sin tener que enfocarnos en detalles. Así, este rasgo de las nociones intuitivas hace que tengamos una idea general de ciertos fenómenos.

Implicidad. Este rasgo de las nociones intuitivas consiste en que los sujetos que las portan son inconscientes de ellas. En nuestro trabajo se pone énfasis especial en tal característica.

 

2.2. Los modelos intuitivos

La delimitación que es fundamental para dar sentido a este trabajo es la referente a qué se entiende por modelo intuitivo y cómo influye en la cognición, ya que pretendemos identificar los modelos intuitivos que los estudiantes pueden tener sobre el concepto de transformación lineal.

Para Fischbein, los modelos intuitivos son nociones intuitivamente aceptables que se desempeñan como un sustituto de nociones intuitivamente inaceptables:

Los modelos representan una herramienta esencial para moldear o para darle forma a las cogniciones intuitivamente inaceptables. Cada vez que una persona se tiene que enfrentar con una noción que es intuitivamente inaceptable, tiende a producir (algunas veces deliberadamente, otras inconscientemente) substitutos de esa noción que son intuitivamente más accesibles. Tales sustitutos son comúnmente llamados modelos intuitivos (Fischbein, 1987, p.121, traducción y énfasis nuestros).

Con respecto a los modelos, Fischbein entiende un modelo en el sentido de Gentner (1983):

Generalmente hablando, un sistema B representa un modelo de un sistema A si, en la base de un cierto isomorfismo, una descripción o una solución producida en términos de A puede ser reflejada consistentemente en términos de B y viceversa (Gentner, 1983, citado en Fischbein, 1987, p.121).

En su trabajo, Fischbein hace una categorización más amplia acerca de los modelos; sin embargo, para nuestros fines, sólo retomaremos las siguientes clasificaciones:

 

a). Modelos explícitos y modelos implícitos (o tácitos)

En esta clasificación se distingue entre los modelos explícitos y los implícitos. Los modelos explícitos se construyen o escogen en forma consciente para facilitar que se llegue a una solución. Por ejemplo, si consideramos alguna función que da información sobre el volumen de un recipiente en términos de alguno de sus lados, esta función nos ayudaría a encontrar las dimensiones que debería tener tal lado para que el recipiente contenga el mayor volumen posible.

Un modelo es implícito o tácito cuando el sujeto no está consciente de su influencia o alcance. Esta distinción jugará un papel importante en nuestra investigación.

 

b). Modelos analógicos y paradigmáticos

Otra clasificación que propone Fischbein es la que divide los modelos en dos tipos: analógicos y paradigmáticos.

Se considera que dos entidades están en relación de analogía si hay algunas similitudes sistemáticas entre ellas, que podría asignar una persona para poder asumir la existencia de otras similitudes. En el caso de los modelos analógicos, el modelo y el original pertenecen a dos sistemas conceptuales distintos. En el caso del modelo paradigmático, el original consiste en una cierta clase de entidades, mientras que el modelo es suministrado por un ejemplar o una subclase de la categoría mencionada.

Uno puede establecer una analogía entre la corriente eléctrica y el flujo de un líquido a través de un tubo muy fino...

Cuando se le pide a un niño que identifique el estado de la materia de un polvo, usualmente podría estar confundido al aprender que el polvo es un sólido. Para él, un sólido debería tener todas las propiedades de un objeto compacto, incluyendo su compactibilidad, como una pieza de metal o de madera (Fischbein, 1987, p.122, traducción nuestra).

Un rasgo de los modelos paradigmáticos es que estos objetos pertenecen a la clase que se quiere representar; asimismo, tienen rasgos comunes (y especiales) a la clase completa. Por ejemplo, "agua" actúa como modelo para los líquidos, en el sentido de que, para que algo se considere líquido debe comportarse como agua (Fischbein, 1987, p. 122).

 

2.2.1. Sobre el papel de los modelos intuitivos tácitos

Como hemos explicado, el objetivo de nuestro trabajo es identificar los modelos intuitivos que los estudiantes relacionan con el concepto TL. Por ello, un punto relevante para nuestro trabajo, en virtud de que destaca el papel de los modelos intuitivos en nuestro pensamiento, es el siguiente:

(...) Los modelos tácitos o intuitivos (ambos, paradigmáticos y analógicos) juegan un rol fundamental en cualquier proceso de razonamiento productivo. No puede existir una actividad de razonamiento productivo sin eventos productivos que consisten en globalización, concretización, extrapolación, etc. Los modelos intuitivos son genuinamente benéficos con respecto a todos estos aspectos. Un modelo ofrece a quien resuelve un sustituto del original, que por medio de sus cualidades es mejor adaptado a la naturaleza del pensamiento humano que el original. Nosotros pensamos mejor con lo perceptible, con lo prácticamente manipulable, con lo familiar, con lo que se le puede controlar su comportamiento, con la validez implícita, que con lo abstracto, lo que no se puede representar, lo incierto, lo infinito (Fischbein, 1987, p.122, traducción nuestra).

Linchevski y Vinner (1988, citados en Fischbein, 1989, p. 10) dicen que hay varias concepciones erróneas en los estudiantes respecto al concepto de conjunto. Por ejemplo, consideran que los elementos de un conjunto deben poseer una cierta propiedad explícita común y piensan que un conjunto tiene que estar compuesto por más de un elemento. Si el modelo intuitivo que sustituye el concepto de conjunto es el de la colección de objetos, concepciones erróneas son previsibles:

El modelo intuitivo manipula detrás de escena el significado, el uso, las propiedades del concepto formalmente establecido. El modelo intuitivo parece ser más fuerte que el concepto formal. El estudiante tiende a olvidar las propiedades formales y tiende a mantener en mente aquellas impuestas por un modelo. La explicación parece ser muy simple: las propiedades impuestas por el modelo concreto constituyen una estructura coherente, mientras que las propiedades formales aparecen, al menos a primera vista, mas bien como una colección arbitraria (Fischbein, 1989).

Para los fines de nuestra investigación es importante determinar qué modelos intuitivos tienen los estudiantes sobre la TL, ya que inciden de manera fundamental en sus razonamientos productivos y marcan sus concepciones: "lo que un individuo puede aprender, y cómo lo aprende, depende de los modelos con que cuenta" (Papert, 1981, p. 13).

En Fischbein (1989) se explica, entre otras cosas, que los modelos tácitos en los estudiantes no son inalterables. Es decir, con una intervención apropiada se pueden modificar para afectar benéficamente su entendimiento de los conceptos matemáticos en los estudiantes. Dentro de sus conclusiones, a manera de sugerencia, Fischbein indica que un primer paso en la definición de la estrategia para lograr ese cambio es identificar los modelos tácitos en los estudiantes sobre el concepto matemático de interés. En nuestro caso, nos enfocamos en el concepto de transformación lineal.

En general, respecto a los modelos intuitivos, Fischbein resume:

Un modelo tiene que ser autoconsistente y al mismo tiempo consistente, por un lado, con el original; por otro lado, con las características de la cognición humana. Esta situación impone en los modelos un número de contrastes que no pueden ser fácilmente llenados en forma simultánea por la misma actividad mental. Un buen modelo tiene que ser una entidad autónoma, pero al mismo tiempo tiene que ser un mediador confiable entre la situación original y la actividad intelectual de quien está resolviendo. Consecuentemente, la mayoría de nuestros modelos tácitos intuitivos son mediadores imperfectos, llevando algunas veces a interpretaciones incorrectas e incompletas (Fischbein, 1987, p. 125, traducción y énfasis nuestros).

 

2.3. La transformación lineal y los modelos tácitos

A continuación, discutiremos algunos aspectos de nuestra investigación y mostraremos la relación que guarda con los modelos tácitos.

Como habíamos dicho anteriormente, "cada vez que una persona se tiene que enfrentar con una noción que es intuitivamente inaceptable tiende a producir (algunas veces deliberadamente, otras inconscientemente) substitutos de esa noción que son intuitivamente más accesibles" (Fischbein, 1987, p. 121, traducción nuestra).

Pensamos que el carácter abstracto del AL con frecuencia obliga a los estudiantes a buscar substitutos que les ayuden a convertir las nociones del AL en ideas aceptables intuitivamente. En los comienzos de la investigación propusimos la hipótesis de que los estudiantes podrían relacionar la transformación lineal en con ideas que involucran al movimiento; tal planteamiento está respaldado por nuestro marco teórico, pues una característica de los modelos intuitivos es "su simplicidad, su cualidad elemental, incluso se podría decir su carácter trivial. Estos substitutos implícitos adquieren su rol privilegiado en el proceso de razonamiento, sólo porque ellos son simples, económicos y directamente representables en términos de acciones" (Fischbein, 1989).

En este caso, la construcción de un modelo intuitivo tal vez no se base tanto en la inaceptabilidad de la teoría matemática, sino en la necesidad inconsciente de reducir el nivel de abstracción que posee el concepto. Nuestra idea se basa en que las representaciones geométricas de la TL tratadas en clase o libros de texto podrían ser las responsables de tal asociación, aunado a la dificultad de una interpretación inmediata visual de las propiedades analíticas del concepto.

Otro factor radica en la necesidad de los estudiantes por reducir los conceptos a algo conocido para ellos y que tenga nombre; en tal sentido, el movimiento es ideal para sus fines, al ser un fenómeno que percibimos todos los días. Por ejemplo, sabemos que todo cambia de lugar moviéndose. Si en la clase de álgebra lineal ejemplificamos a un estudiante una transformación lineal de rotación, mostrando un vector x (en , por ejemplo) y el vector x', que es imagen de x bajo esa TL, invitamos al estudiante a pensar que la TL giró el vector x, y el medio por el cual las cosas giran o cambian de lugar es el movimiento; además, que "un modelo intuitivo es, por su naturaleza, de tipo sensorial. Puede ser percibido, representado o manipulado como cualquier otra realidad concreta" (Fischbein, 1987, p. 121). Entonces, los estudiantes pueden asociar las transformaciones lineales con los movimientos simples y combinaciones de ellos, o bien sustituirlas con estos movimientos.

Sierpinska (2000) comenta que los estudiantes tienden a pensar las transformaciones lineales en términos de ejemplos prototipo como rotaciones, proyecciones y trasquilados. Nuestra conjetura es que el modelo intuitivo resulta aún más simple que esto, pues consiste en los movimientos que pueden visualizarse fácilmente.

Por otra parte, una consecuencia de que un estudiante recurra a modelos intuitivos paradigmáticos para entender la TL es que sus modelos no sean óptimos (o insuficientes en número) para representar el concepto, ya que no abarcan la totalidad de rasgos, y en el estudiante se podría dar la situación de que elija una representación que contenga propiedades que no sean compatibles con el concepto, o carezca de algunas. Este último caso, que el modelo intuitivo del estudiante carezca de ciertos rasgos de la TL, podría producir que el estudiante excluya de la clase TL algunos elementos pertenecientes a ella. Recordemos que "la mayoría los modelos tácitos o intuitivos son mediadores imperfectos, llevando algunas veces a interpretaciones incorrectas e incompletas" (Fischbein, 1987, p. 125, traducción nuestra).

Finalizamos esta sección con una cita de Pinker: "Gracias a los gráficos, captamos las matemáticas con nuestros ojos y con los ojos de la mente. Las funciones son formas (lineal, plano, empinado, cruce, suave). Y operarlas es garabatear en imágenes mentales (rotando, extrapolando, rellenando, trazando)" (Pinker, 1997, p. 359, traducción nuestra).

 

3. CONSIDERACIONES METODOLÓGICAS

En seguida, comentaremos aspectos metodológicos sobre nuestra investigación.

 

Los estudiantes

Se aplicó la entrevista de manera individual a cinco estudiantes que habían terminado una licenciatura en la Enseñanza de la Matemática, donde habían llevado uno o dos cursos de álgebra lineal. Al momento de ser entrevistados estaban inscritos en el programa de maestría en Matemática Educativa de un centro de investigación. Como la identificación sobre los posibles modelos de los estudiantes dependía mucho de lo que verbalmente comentaran durante la entrevista y del nivel de articulación y reflexión que mostraran en sus respuestas, decidimos entrevistar a alumnos de maestría en nuestra disciplina, ya que tenían cierta formación para colaborar en la investigación y explicitar sus pensamientos. Además, serían capaces de reflexionar sobre sus propias respuestas durante la entrevista, lo cual daría más elementos para elaborar nuestro análisis.

Ahora bien, los resultados que obtuvimos confirmaron tal supuesto. Los estudiantes mencionados estaban tomando un curso que involucraba el uso de tecnología como recurso para la enseñanza del AL, con el software Cabri Geomètre. En el curso aún no habían abordado las transformaciones lineales. Antes de la aplicación de la entrevista se les informó que trataría sobre transformaciones lineales, sin darles detalles. Aquí nos referimos a ellos con los sobrenombres Fabi, Gris, Sara, Hermes y Naye. Su edad variaba entre los 23 y 26 años.

 

El espacio físico

El lugar donde se aplicó la entrevista fue el Laboratorio de Didáctica y Cognición del Área de Educación Superior, en el Departamento de Matemática Educativa del Cinvestav–IPN. Se grabó cada una de las entrevistas en video (con cámara aérea fija) y audio (con caseteras normales).

 

Forma de aplicación

La entrevista se aplicó en forma individual. Cada una de las preguntas se planteó una a una a los estudiantes, conforme las iban contestando, y disponían de hojas y plumones, en el caso de que los necesitaran. Cuando tenían dificultades para expresar sus ideas, el entrevistador iniciaba una interacción verbal con ellos mediante preguntas, teniendo cuidado de no sugerir la respuesta.

El método que seguimos consistió en:

Diseño de la entrevista. Con base en nuestras consideraciones teóricas y objetivos, se planteó una serie de preguntas enfocadas a indagar en los estudiantes sus nociones sobre la TL en contexto geométrico.

Análisis a priori. Una vez definidas las preguntas, se precisó un análisis a priori detallado sobre cada una de ellas, en el que se discutió su propósito y las posibles respuestas que podrían aparecer (Molina, 2004).

Aplicación de la entrevista. Se entrevistó a cuatro estudiantes en forma individual; la información se registró con una cámara de video aérea, una estándar y una grabadora de audio.

Análisis a posteriori. Se hizo un análisis a posteriori minucioso de la aplicación por individuo, obteniendo conclusiones de acuerdo con nuestras consideraciones teóricas.

 

3.1. La entrevista

A continuación presentamos cada una de las preguntas que fueron realizadas durante la entrevista:

 

Preguntas abiertas

a) ¿Qué entiendes por transformación lineal?

b) Propón un ejemplo de una transformación lineal y argumenta porqué es lineal.

c) Propón un ejemplo de una transformación no lineal y argumenta porqué es no lineal.

d) ¿Qué significa lineal en la transformación lineal?

 

Preguntas que involucran la TL

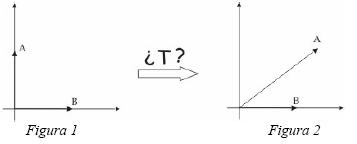
Para cada uno de los casos que se muestran a continuación diga si es posible que exista una transformación lineal que convierta los vectores de la Figura 1 en los vectores de la Figura 2. Argumente por qué.

 

3.2. Aspectos concernientes al diseño de la entrevista y su relación con los modelos intuitivos

En este apartado discutiremos cómo las consideraciones teóricas acerca de los modelos intuitivos de Fischbein (1989) nos guiaron para diseñar las preguntas de la entrevista. Como las nociones intuitivas suelen representarse mediante aquellos objetos que podemos ver, manipular y controlar su comportamiento, dichas consideraciones teóricas guiaron en un primer momento la elección del formato que acompañaría a las preguntas de la entrevista.

Al principio, la decisión de utilizar el contexto geométrico en el planteamiento de varias preguntas se fundamenta en que estas representaciones son concretas y median para acceder a significados abstractos y manipulables, lo cual facilita operar con ellas (al ser visuales ayudan a formar en la mente la imagen de un concepto abstracto). De igual manera, ayudan a los estudiantes a evocar sus ideas intuitivas acerca de la TL.

Dividimos estas preguntas en dos categorías: en la primera involucramos transformaciones lineales que son comúnmente discutidas en libros de texto o en cursos de álgebra lineal (podría ser una novedad el estilo de la pregunta, que se complementa con gráficos y la variedad del número de vectores que intervienen); en la otra incluimos transformaciones lineales poco usuales en los libros de texto que, desde nuestro punto de vista, harían que los estudiantes manipularan objetos y externaran construcciones que nos permitirían especular sobre sus posibles nociones intuitivas de la TL.

En segunda instancia, sin restarle importancia, las preguntas abiertas acerca de la transformación lineal fueron guiadas por nuestro marco teórico en el sentido de que no pedían una definición formal (ello, desde nuestro punto de vista, no refleja si los estudiantes en verdad entienden lo que definen, o no dan elementos para averiguar qué ideas intuitivas asocian al concepto). Las preguntas abiertas se diseñaron con la intención de hacer que los estudiantes contestaran en términos de lo que entendían acerca de la TL para darnos una idea sobre las nociones intuitivas que asocian al concepto.

Como un rasgo de las ideas intuitivas es que perseveran, pueden influir en nuestro pensamiento a lo largo de nuestra vida; aún cuando ya hayamos adquirido un grado avanzado de educación formal, se mantienen en nosotros. Las preguntas abiertas las pueden hacer palpables.

Ahora bien, cada una de las preguntas de la segunda parte que involucran transformaciones lineales y representaciones geométricas atiende un aspecto diferente para observar lo intuitivo en los estudiantes. Por ejemplo, el inciso e) pretende averiguar si el intercambio de dos vectores se considera como un movimiento simple, y se fija en el resultado si el estudiante identifica la transformación resultante como lineal o si su modelo intuitivo coincide con los movimientos simples.

El inciso h) tiene el propósito de observar si el estudiante acepta la identidad como una transformación, ya que no involucra un movimiento. En el l), uno de los vectores de la Figura 1 "queda igual" y el otro "se mueve", lo cual hace difícilexplicar el efecto geométrico que tiene la transformación en todo el plano. Aquí, nos interesa ver si el estudiante lo rechaza como una TL, argumentando que "el movimiento que hace un vector tiene que ser igual para el otro vector".

 

4. PRINCIPALES RESULTADOS

Ilustraremos los resultados principales de nuestra investigación y, de manera conjunta, mostraremos la evidencia que respalda nuestras observaciones para establecer una discusión sobre ellas.

 

4.1. La TL como movimientos simples y combinaciones de éstos

El resultado principal que reportamos es que sí se verificó nuestra hipótesis: los modelos intuitivos detectados en todos los estudiantes sobre la TL son una serie de casos particulares de transformaciones lineales. Estas transformaciones lineales se conocen en el ambiente escolar como expansiones, contracciones, reflexiones, rotaciones y composiciones de éstos. Los estudiantes, con el conjunto anterior de transformaciones lineales en como universo, al enfrentarse a las preguntas que las involucran, en la mayoría de los casos determinan si la transformación es lineal; en caso de que no forme parte de su universo, es excluida de la clase TL. Para justificar lo antes dicho, comentaremos algunos casos donde se refleja esta situación.

 

El caso de Hermes

En el transcurso de la entrevista este alumno contestó con desenvoltura y correctamente cada uno de los casos que se le venían planteando, mostrando facilidad para transitar entre las representaciones gráficas y las algebraicas. Sin embargo, cuando llegó al inciso l) tuvo dificultades. La pregunta que acompañaba al gráfico del inciso fue:

¿Podría existir una transformación lineal que convierta los vectores de la Figura 1 en los vectores de la Figura 2? Argumente ¿por qué?

Inciso 1 (H158 – H189)¹

De entrada, Hermes niega la existencia de la TL. Con seguridad, afirma:

H159: No, ésta no, porque está dejando fijo a B y este, está transformando a, A (señala la Figura 2), y pues no.

Resulta importante lo repentina y contundente de la reacción de Hermes al negar la posible existencia de la TL porque dos rasgos de la intuición son su evidencia y certeza. Quien experimenta tales nociones no siente necesidad de argumentos para aceptarlas como ciertas y Hermes parecía estar muy seguro de su respuesta; entonces, intervenimos para pedirle que agregara detalles a su explicación. Como respuesta, Hermes intentó dar una justificación algebraica que respaldara su afirmación; no la consiguió, pero mantuvo su postura. A continuación, pasamos a la siguiente pregunta del inciso m):

Hermes estaba en profundas meditaciones. Repentinamente, tomó la hoja en la que estaba plasmado el caso anterior, el inciso l), y a continuación desarrolló un elaborado argumento a favor de la existencia de la TL, recurriendo a ideas tocantes a los vectores base de una transformación. Aquí nos interesa resaltar que con mucha seguridad cambió de postura, y mostró que en el caso del inciso l) sí podría haber una transformación lineal y lo mismo ocurriría en el inciso m). Cuando Hermes descubrió que sí podría existir la TL, nos explicó los rasgos que él consideraba de la transformación lineal y en cuáles se apoyaba para argumentar:

H181: (Fragmento):... Pues tendría que cambiar de opinión en varias de esas, pero (... )

E182: Mjm, ¿en cuáles tendrías que cambiar de opinión?

H183: Pues en un montón, sí porque estaba yo pensando, considerando transformaciones solamente por rotación y por escala y no o sea, no necesariamente, de hecho ésta va a ser una transformación... transformación lineal, además.

Posiblemente lo que condujo inicialmente a Hermes a concluir la no existencia de la TL fue que pensaba en la transformación lineal como una función que tiene el mismo simple efecto geométrico en todos los vectores del plano (expande todos, contrae todos, rota todos); cuando nota que el vector B se mantiene constante, interpreta que la transformación no afectó a un vector, entonces concluye que no es una TL. En otras palabras, Hermes tiene en mente ciertos modelos intuitivos acerca de cómo se comportan las transformaciones lineales, de tal forma que cuando se enfrenta a una situación que no encaja dentro de su universo de modelos rechaza la existencia de la transformación lineal, como en el inciso l).

Hermes pensaba la transformación lineal en términos de movimientos geométricos simples: la expansión, compresión, la rotación y combinaciones de ellos. Cuando abordó el inciso m), detectó una transformación lineal que tenía un comportamiento que consideraba imposible en ellas, un vector se contraía y otro se expandía; ante ello, cambió de postura. Esta observación la respaldamos con el diálogo H109 –fragmento al final del párrafo acerca del inciso m) – y en H183, aunque en este caso su argumento se basa en el no cumplimiento de la propiedad de la multiplicación por un escalar.

H109: Porque como están alineados, deberían de cumplir este, esto deberían de cumplir (señala A = λB, T A=λT B ), a esto, si se cumple esto, eso se debe cumplir y veo que, que no... pues, un vector se estira y el otro se encoge, eso es lo que veo que no se puede.

Como discutimos en los párrafos anteriores, al inicio Hermes se mostró reacio en aceptar la existencia de la TL. Su firme reacción de no admitir su existencia y en no poder argumentarla podría ser la manifestación de que la intuición influye en él. Por otra parte, su cambio de postura tras observar el caso siguiente es un ejemplo de cómo una noción intuitiva puede ser modificada cuando otro modelo intuitivo entra en juego. Al reflexionar sobre la pregunta, lo que era implícito se le volvió explícito (fragmento 183), lo cual permitió el cambio en su postura. La cuestión planteada en el inciso m) tiene un formato diferente a las anteriores; esto también podría tener el efecto de evocar modelos mentales de otra naturaleza en Hermes (uno con figuras que le llevaría a afirmar que sí es una TL, porque tal vez lo asocia con la fórmula que cumple las propiedades). Él logra percibir en el inciso m) que si los lados que determinan la Figura 1 representan vectores, ocurría algo semejante a lo propuesto en el inciso l): una TL que afecta en forma diferente a los vectores. Por consiguiente, deduce que en tal caso sí podría existir.

 

El caso de Naye

Esta estudiante respondió correctamente y sin dificultad las preguntas de la entrevista, hasta que llegó al inciso l). Lo que hizo es interesante por dos motivos: primero, en su intervención se aprecia lo que interpretamos como su esfuerzo para que la transformación embone dentro de su universo de modelos; segundo, recurre a modelos intuitivos para convencerse de la existencia de tal transformación lineal; asimismo, imaginar el plano como algo flexible (diálogo N155) imaginar que la hoja de papel es el plano (diálogo, N157). En el diálogo N163 sugiere que se establezca una analogía con las funciones parciales y, por otra parte, muestra que tal transformación lineal no está presente dentro de sus modelos. En el comentario N153 evoca al movimiento y en el N175 refleja las consideraciones que utiliza para determinar si las transformaciones eran lineales o no; es decir, expresa su universo de modelos intuitivos en torno a la TL. A continuación, incluimos un fragmento de su entrevista:

E152: OK, bueno, ¿qué me podrías decir de la siguiente figura? ¿En este caso podrá existir una transformación lineal que nos convierta los vectores que tenemos en la Figura 1 a éstos?

 

N153: (...)Blo mantiene al parecer igual y A se mueve, o sea, lo transforma (... )

E154: ¿Qué te hacen pensar?

N155: (...) Estoy pensando que tal vez sí se pueda, o sea, estoy pensando en el plano como algo flexible que voy a estirar hacia un lado; entonces, todos los vectores caerían en otro espacio vectorial (... )

E156: A ver, ¿cómo está eso del plano que estiras?

N157: Haz de cuenta que esta hoja es flexible. Este es mi plano, x y y, lo puedo estirar de manera que éste quede un poco más inclinado (Figura 1), o sea en esta posición (Figura 2). Si fuera una hoja flexible, o sea, forman el paralelogramo, e, tomar, éste, para el cuadrado (dibuja en la Figura 1) y estirarlo para que quede de esta forma (dibuja en la Figura 2).

(Dibuja en las figuras):

E158: Ajá.

N159: La suma quedaría también ahí mismo, con la multiplicación por escalares no sé que pasaría. Supongo que también se cumple nuevamente si tomamos el estiramiento como transformación lineal. No... aquí no puedo aplicar la rotación y multiplicar por escalares porque no estoy rotando este vector, el B, pero tengo la idea de que puedo estirar. Me hace pensar que sí podría tener una transformación lineal que me llevara de aquí para aquí.

E160: ¿Entonces dices que si tuvieras qué? ¿La fórmula que te los estirara y dejara en esa posición?

N161: Sí, yo creo que sí, eso sería la transformación lineal.

E162: Ajá, ¿en qué más piensas?

N163: No recuerdo si la transformación lineal se puede hacer como funciones parciales, o sea... estos vectores no me los toques y todos los demás sí; no, no recuerdo.

E164: O sea, estás considerando aplicar a un vector nada más, ¿o a qué te refieres?

N165: Que transformara todos los vectores del plano, excepto los que sean sobre el eje x, pero no recuerdo si eso es una transformación lineal.

E166: Te refieres a una fórmula que deje constantes ciertos vectores y que otros los modifique, ¿en qué más piensas?

N167: Si tuviera que decir que sí o que no, diría que sí. O sea, que sí existe alguna transformación lineal, aunque me estoy contradiciendo tal vez con alguna de por ahí porque aquí sería... tal vez multiplicar este por algún escalar, pero este no.

E168: Mjm... ¿Qué te hace pensar que este sería multiplicado por un escalar y este no?

N169: Nada que ver, ¿no?

E170: No, nada más porque me interesa saber.

N171: No, porque por un escalar sería hacia arriba, pero es que yo pensaba otra vez en la rotación y en la multiplicación por un escalar. Entonces no, no tiene nada que ver. .. Yo creo que sí, sería la fórmula que haría que los vectores se estiren, pero el B es el que me (...)

E172: Te causa conflicto.

N173: Sí.

E174: ¿Cómo crees que debería estar para que no tuvieras ese conflicto?

N175: Tal vez rotado como está este y estirado, o sea, rotado y multiplicado por un escalar. Enseguida sería como el caso anterior, es rotar y multiplicar, entonces sí existe una transformación lineal. Ahora, no sé si el estiramiento, como te dije, se puede considerar una transformación lineal.

En el caso de Fabi algo semejante ocurrió cuando buscaba ciertos rasgos para decidir si se trataba de una TL. Ella podría estar pensando términos de sus modelos y que la situación embonara en este grupo, del inciso i):

E208: A ver, ¿qué me dices de la siguiente?

F209: A, pues aquí sería la misma x ..., pues sí, en el anterior que era cambiar. Aquí sería la misma x , y sólo pues solo cambiaría el sentido de la y. Ah, no, no, no, espérame, no son iguales. Sí, pensé que este era la y, como que la, como que cambiabas el (...). La B sí podría decir que es el reflejo, acá, está B sería el reflejo de ésta (señala la B en la Figura 1 y luego a la B en la Figura 2), pero la A no estaría segura de si sería el reflejo, entonces no lo veo claramente, pero (...) No, de hecho no es el reflejo (...) Ahora (...) alguna transformación, no, aquí sí no, no le veo (..) no le veo (..) no le veo relación porque en los anteriores sí, como que le buscaba alguna relación. No sé si era algún reflejo o sí cumplían alguna, se dice,. .. patrones, regularidad, ¿no?, como que repetían algo, pero aquí sí me....

E210: ¿Y ese algo que se repetía? ¿Me podrías hablar un poquito más acerca de eso, del patrón que buscabas para decir si era o no era?

F211: A ok. Bueno, como que, cumplían,... cumplían,... o sea, a ver, espérame. Esta yo te podría decir que sí, sí se podría hacer, pero a los dos juntos los bajo para acá, o sea, en el sentido de que les aplico alguna transformación que haga que B baje, que todo el sistema A y B se rote, ¿me entiendes?, y quede de esta forma. A y B (...) algo, algo así, lo, lo, le busco algún patrón, o sea, agarré estos dos, A y B, y los giré para acá ((con las manos simula tomar los vectores y girarlos)). Entonces sí podría haber alguna transformación, a todas digo que sí, jaja.

La simulación de Fabi de tomar los vectores y girarlos refleja que está pensando en la transformación como movimientos (diálogo F211). Está claramente buscando un movimiento simple que pudiera explicar el cambio en ambos vectores.

En el siguiente fragmento, Gris reflexiona acerca de cómo ha pensado la TL y deja ver la presencia de sus modelos: las transformaciones lineales que expanden y contraen:

G147: Es que nada más estoy pensando como si las transformaciones fueran multiplicar un, una componente por un escalar (escribe ), por decir. No (...), pero no siempre va a ser eso, una transformación lineal no siempre va a ser de este tipo, o sea, el simple multiplicar por un escalar,... y eso sí como que me, crea, me causa un poco de conflicto con lo que estoy tomando como una transformación lineal para mostrar nada más el aumento o la disminución de los vectores. Entonces, supongo que me lleva a pensar que sí podría existir,... o sea, si me voy con eso, de simplemente el aumento y disminución de los vectores, de las longitudes x, y, sus componentes, pues sí, ¿no? Pero igual puede ser una transformación lineal no sólo de este tipo, sino que hay otras formas de transformación lineal.

En el siguiente fragmento Sara, al comentar las operaciones que ha estado utilizando, muestra que ha estado pensando la TL como expansiones o contracciones:

S109: Entonces siento que las operaciones que voy a hacer, como (...) estoy manejando nada más, producto y no sé, tal vez suma, entonces pues yo digo que sí es una transformación lineal.

Los modelos mencionados anteriormente se perciben en todos los estudiantes entrevistados, aún en aquellos que podían transitar con desenvoltura en contextos geométricos y algebraicos (los casos de Naye y Hermes). La situación que creemos buscaba identificar la percepción geométrica del cumplimiento de las dos propiedades de la transformación lineal era: para cualquier escalar k y cualesquiera vectores

Constatamos que los estudiantes no habían reflexionado acerca de esta relación geométrica–analítica y el modelo geométrico que llevaban de la TL era aquella función que giraba o expandía los vectores en cuestión. Algunos pensaban en una combinación de estos movimientos como una posibilidad. El problema más revelador de este fenómeno fue el inciso l): aun en el caso de Naye (quien logró una interpretación geométrica en términos de un movimiento del plano) identificamos el modelo intuitivo de los movimientos.

 

4.2. La TL como la transformación de un vector en particular, y no como una función que transforma todo el plano

Aunque no lo habíamos planteado como objetivo de nuestra investigación, los resultados de la entrevista nos llevaron a observar otro fenómeno importante: varios estudiantes (Gris, Fabi y Sara) consideraban la TL como la transformación de un vector en particular, y no como una función que transforma todo el plano. Esta situación se dejó ver claramente con Gris. Posiblemente el hecho de que en varios libros de texto y que en la clase de álgebra lineal se suelan tratar ejemplos gráficos de TL donde se involucra sólo un vector y su imagen bajo cierta transformación lineal (por ejemplo, Grossman, 1996; Hitt², 2002) es el causante del conflicto de Gris, al enfrentarse a una situación que involucre dos vectores. A continuación, mostraremos fragmentos de la entrevista que nos revelan el impacto que tuvo en Gris involucrar dos vectores, y preguntar por la existencia de una misma transformación lineal que convierta los vectores de la Figura 1 en los de la Figura 2. Estos fragmentos fueron tomados de diferentes secciones de la entrevista; en ellos se refleja fuertemente la dificultad que le representaba a Gris pensar en una única transformación lineal cuando intervenía más de un vector en la pregunta:

G14: ¿Aplicando una transformación lineal? A ver si entendí.

G16: Una transformación lineal que me convierta estos vectores en éstos, ¿no? (..)

G23: Sí, ok, aquí ¿a los dos les tendría que aplicar una transformación lineal?

G27: Para convertirlo a este segundo vector... sí, ahí sí. Lo que pasa es que no entiendo si a los dos al mismo tiempo les voy aplicar la transformación lineal y obtener estos dos resultados simultáneos.

G31: ¿Una misma para los dos?

G37: Una para este y una para este, podría ser, ajá, sí.

G52: ¿Juntos?

G54: O sea, ¿tomándolos, A y B al mismo tiempo, o sea, la misma transformación lineal?

G60: ¿Una misma?

G70: ¿Si existe igual una transformación lineal para estos tres vectores?

G72: Volvemos a lo mismo, ¿la misma transformación lineal para los tres?

Gris pretendía aplicar una transformación a cada vector involucrado en la Figura 1 para mapearlo a la Figura 2. Sin embargo, aun cuando se le explicaba que se pedía preguntaba por una y solo una TL, volvía a preguntarlo. A continuación, mostramos fragmentos con Fabi y Sara en donde manifiestan problemas semejantes:

 

Fabi:

E148: ¿Qué te produce conflicto cuando son dos vectores?

F149: Ah, ok, lo que pasa es que para la transformación, me limito mucho a un vector. Yo le aplico una operación y lo puedo pasar a otro, a otro tipo de vector ¿no?, por ejemplo... e, hacerlo más inclinado, más pegado al eje x.

Sara, en el inciso l), está explicando porqué podría existir la transformación lineal, se entera de que se pregunta por una transformación lineal para los dos vectores:

E168: ¿Cuál sería la transformación que a los vectores de esta figura nos los va a llevar aquí?

S169: ¿A la transformación de los dos? (con asombro)

E170: Sí, estamos considerando a toda la figura, buscamos una transformación que al aplicarse a todos los elementos de esta figura, a este vector y a este vector, nos los convierta en esos vectores de aquí.

S171: Ah, ya, pensé que era por partes (...) mm (...) Ay, pues no veo, o sea lo que pasa es que (...) o sea, yo veo (...) por separado ¿no?, B no se mueve, entonces es la identidad, pero la A si lo muevo A entonces pasa esto, entonces (...) mm (...) no veo cómo como mover A (Figura 1). O sea, veo que si muevo A voy a mover B, o lo contrario; o sea, no se puede mover B, sólo A. Entonces, pues no (..) y si voy a aplicar esto pues se van a mover los dos.

 

4.3. Con respecto al adjetivo "lineal" en el término transformación lineal

Respecto al adjetivo lineal en el término transformación lineal, en las entrevistas con los estudiantes se observaron las siguientes ideas asociadas al concepto: Fabi lo relacionó con vectores; Naye y Sara lo vincularon con líneas rectas; Hermes con que "la transformación lineal transforma líneas rectas en líneas rectas", y Gris con "el orden en que deberán efectuarse operaciones". Notamos que en todos los casos la linealidad es relacionada con una situación concreta y es un ejemplo que muestra cómo los individuos involucrados en la entrevista producen substitutos intuitivamente más accesibles de la noción linealidad, reemplazando al concepto formal, que define cuándo un operador es lineal o vive junto a esta noción.

Esta podría ser la razón por la que en la mayoría de los estudiantes la linealidad en la TL no tiene importancia, se olvida o pasa desapercibida. Las condiciones que debe cumplir la transformación para que sea lineal se pierden con el paso del tiempo (en la mayoría de los casos), carecen de significado o son reemplazadas por nociones intuitivas que no están relacionadas con el concepto que especifica cuándo un operador es lineal. A continuación, presentamos fragmentos de entrevistas al respecto:

 

Gris

G12: Transformación lineal (...) lineal en el sentido de que va a seguir un orden, podría ser, porque por ejemplo, no puedo regresar a decirte que, que sea porque es una ecuación lineal, porque podría ser el caso como, que acá fuera x², entonces,. .. este, tal vez por eso... o sea, me imagino... significa, lineal porque vas a seguir estos pasos en esta dirección para llegar a, a la transformación o al resultado final. Eso se me viene a la mente así como nada más, una simple palabra, linealidad.

 

Sara

S20: A transformación lineal... O sea, lineal es de recta ¿no?, un vector es un pedacito de recta; vaya, entonces, si a este vector (indica el vector (1,2) de S14) yo le aplico esta operación (señala la fórmula de S12), entonces yo voy a obtener una transformación lineal.

 

Naye

N33: Sí, ya, ya tengo una que no es lineal, la cuadrática. Pensando en lineal como línea recta, la cuadrática no, no no separa sumas.

 

Hermes

H20: Ah, porque (...) no, no sé, sería como cuando,... tal vez porque cuando transformas, le aplicas la transformación a todos los puntos de una línea, vuelve a ser una línea. Podría ser por eso, pero específicamente porqué, no.

 

4.4. La noción de espacio vectorial

Cuando preguntamos a los estudiantes qué entendían por transformación lineal, la mayoría no involucró la noción de espacio vectorial en sus respuestas; sólo Naye y Hermes sí lo hicieron. Tal situación podría ser un indicativo de que con el paso del tiempo la noción de espacio vectorial se pierde en los estudiantes.

 

4.5. La noción geométrica del movimiento de un vector llevada al contexto aritmético

Como habíamos mencionado en el apartado 4.1, los libros de texto suelen representar las transformaciones lineales mediante dos vectores: uno original y otro como su imagen. En estos casos, matemáticamente hablando, habría un número infinito de posibilidades para una TL que mapee el primer vector en el segundo. Sin embargo, debido a que la mayoría de los ejemplos representa a las transformaciones lineales prototipo como rotaciones o reflexiones, el estudiante puede quedar con la impresión de que toda TL puede expresarse algebraicamente por medio de la multiplicación de las componentes del vector (x, y) por escalares. Veamos el siguiente ejemplo:

T (x,y) Representa la imagen bajo una transformación del vector (x,y)³

Una consecuencia de esta concepción es que podría constituir un obstáculo en los estudiantes para que puedan argumentar la posible existencia de una TL que involucre más de un vector. Como evidencia de esto, se pueden considerar las dificultades que tuvieron Gris, Fabi y Sara cuando se les aclaró que se preguntaba por una y sólo una TL que mapeara a todos los vectores de la Figura 1 en los de la Figura 2. Esta idea puede volverse una noción intuitiva que refleja la característica estatus de teoría, discutida en nuestro marco teórico.

 

4.6. Con respecto al movimiento

En algunos fragmentos transcritos anteriormente se observa cómo los estudiantes asocian el movimiento a las transformaciones lineales y lo manejan en sus argumentos; es decir, cada uno de sus modelos está constituido por movimientos geométricos que relacionan con sus prototipos de transformaciones lineales.

La noción intuitiva que da forma o que hace intuitivamente aceptables a estos modelos en los estudiantes es la idea de movimiento. Si en la clase de álgebra lineal el profesor ejemplifica una TL de rotación con un vector y al mostrar su rotación nos dice que "la transformación hace que el vector gire", es natural que involucremos la idea de movimiento. El movimiento es algo que percibimos todos los días de nuestra vida; por ejemplo, "si vamos caminando y nos topamos con una calle, y observamos del otro lado a una persona que va caminando en la misma dirección que nosotros, es natural que supongamos que atravesó la calle moviéndose, no que se desapareció en nuestro lado de la calle y apareció en el extremo opuesto"⁴.

Lo mismo ocurre si nos dicen que un vector ha girado: a los objetos los giramos moviéndolos. De ahí que sea natural asociar el movimiento a la TL porque el estudiante percibe la imagen de un vector u objeto bajo una transformación no como algo estático relacionado con el vector original, sino como resultado de un movimiento; un proceso donde tal vez pierda el vector original. Mostramos algunos ejemplos en los que aparece el movimiento en los argumentos de los estudiantes:

 

Fabi: inciso a)

E54: Entonces, en la Figura 1 tenemos los siguientes vectores.

F55: Éstos, ¿no?

E56: Ajá (...) Ahora, hay algo aquí (se le señala la flecha) y en la Figura 2 tenemos (...) Entonces, la pregunta es ¿si crees que podría existir una transformación lineal que convierta estos vectores en éstos?

F57: En éstos.

E58: Mjm.

F59: Mmm, a ver (...) que yo pueda hacer que este vector se mueva un poco, ¿no?, o sea,

gire, así lo estoy viendo.

 

Sara: inciso g)

S127: Lo único, según yo, lo que veo acá, es que, este vector, bueno está para, en el segundo cuadrante en el plano cartesiano. Lo que haces es girarlos ¿no?, o reflejarlos conforme, perdón, con respecto al eje y (hace movimientos con el plumón en la mano indicando la reflexión), donde ese vector B que está en el segundo cuadrante lo cambias al primero. Entonces, lo que cambia,... ¿no puedo rayar tu dibujo, verdad?

 

5. COMENTARIOS FINALES Y SUGERENCIAS DIDÁCTICAS

La aplicación de las entrevistas dio evidencia que, con el paso del tiempo, el concepto de la transformación lineal se va degradando y sólo persiste la idea de la transformación. Por ello, consideramos que es pertinente investigar sobre diseños didácticos que pongan énfasis en la otra parte, la linealidad, con el propósito de reducir la degradación del concepto. Encontramos relevante la siguiente cita de Pinker:

Filósofos dicen que el significado de un término tipo–natural viene de la intuición de un rasgo o esencia que los miembros comparten el uno con el otro y con los primeros ejemplos apodados con el término (Pinker, 1997, p. 323).

El término transformación lineal por sí mismo significa un cambio de forma. En los casos factibles de trabajar representaciones geométricas se da una concordancia entre lo que ocurre geométricamente y la idea asociada al nombre del concepto. Esto tiene como consecuencia que se ponga un velo sobre el concepto transformación lineal –en varios casos, lleva al estudiante a pensar en que la transformación lineal es el vector transformado–, ocultando quién es en realidad la transformación lineal, lo cual hace que los estudiantes se enfoquen en los objetos involucrados (por ejemplo, los vectores) y no en el proceso implícito (la TL). Sierpinska (2000) afirma que algunos diseños de aprendizaje pueden particularmente motivar esta idea en los estudiantes. Por lo anterior, es importante realizar investigaciones que se enfoquen en el diseño de situaciones didácticas donde se conduzca a los estudiantes a distinguir quién es el objeto y qué el proceso cuando trabajen la TL.

Aunque las transformaciones no lineales sean un tema ajeno al álgebra lineal, es relevante para la enseñanza de las transformaciones lineales enfatizar en ellas. Posiblemente convenga abordar la transformación antes que la TL y establecer el vínculo con la noción de función abordada en cálculo.

La investigación que llevamos a cabo mostró que los estudiantes relacionan el término transformación lineal con líneas rectas y a éstas con el grado de las expresiones algebraicas. Al parecer, algunos estudiantes tienen la idea de que si un objeto es una línea curva, no puede ser resultado de una TL; tal observación la formulamos con base en sus comentarios y en el ejemplo que sugieren como transformación no lineal: la función cuadrática. Por ello, conviene buscar una forma para romper esta concepción.

Cuando se aborden las transformaciones lineales en , es pertinente para los fines didácticos reparar en las condiciones que sus fórmulas algebraicas deben cumplir, a fin de evitar que los estudiantes tomen a fórmulas como T x, y= αx + p, βy + q representantes de una TL.

Otra recomendación con fines didácticos es que cuando se trabajen las transformaciones lineales se utilicen distintas dimensiones, por ejemplo, de , ya que podría ayudar al estudiante a percibir que las transformaciones lineales pueden representar situaciones diferentes a movimientos simples.

Creemos importante ahondar en las implicaciones didácticas que tendría la inclusión de figuras geométricas en la clase de álgebra lineal. El propósito es utilizarlas para involucrar a los estudiantes en actividades de predicción de efectos geométricos en ciertas transformaciones aplicadas a ciertas figuras, o en sentido inverso, dadas las figuras bajo cierta transformación, cuestionar al estudiante sobre la transformación lineal involucrada. Como mencionamos cuando discutíamos lo ocurrido con Hermes en el inciso m), utilizar figuras geométricas en podría ser benéfico para ilustrar maneras en que la TL puede afectar a vectores y, con ello, aumentar el universo de movimientos geométricos que los estudiantes asocien a la transformación lineal.

Esta investigación contesta algunas preguntas que nos habíamos hecho y deja la puerta abierta para investigaciones a seguir respecto al aprendizaje de las transformaciones lineales.

 

AGRADECIMIENTOS.

Este trabajo forma parte del proyecto de investigación Conacyt 2002–C01–41726S.

 

REFERENCIAS BIBLIOGRÁFICAS

Bagni, G. (2000). "Simple" rules and general rules in some high school students' mistakes. Journal für Mathematik Didaktik 21 (2), 124–138.         [ Links ]

Fischbein, E. (1987). Intuition in science and mathematics: an educational approach. Holland: Reidel.         [ Links ]

Fischbein, E. (1989). Tacit models and mathematical reasoning. For Learning of Mathematics 9, 9– 14.         [ Links ]

Gentner, D. (1983). Structure–mapping: a thoretical framework for analogy. Cognitive Science 7, 155–170.        [ Links ]

Grossman, S. (1996). Álgebra lineal. México: McGraw–Hill.         [ Links ]

Hitt, F. (2002). Álgebra lineal. México: Pearson Educación.         [ Links ]

Kieran, C. (1981). Concepts associated with the equality symbol. Educational Studies in Mathematics 12, 317–326.         [ Links ]

Linchevski, L. & Vinner, S. (1988). The naive concept of sets in elementary teachers. En A. Borbas (Ed.), Proceedings of the Twelfth Annual Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 471–478). Veszprem, Hungría: PME.         [ Links ]

Matz (1982). Towards a process model for high school algebra errors. En D. Sleeman & J.S. Brown (Eds.), Intelligent Tutoring Systems (pp. 25–50). London: Academic Press, Inc.         [ Links ]

Molina, J. G. (2004). Las concepciones que los estudiantes tienen sobre la transformación lineal en contexto geométrico. Tesis de maestría, Cinvestav, México.        [ Links ]

Papert, S. (1981). Desafío a la mente. Buenos Aires, Argentina: Ediciones Galápago.         [ Links ]

Pinker, S. (1997). How the mind works. New York: USA: Norton & Company Inc.         [ Links ]

Sierpinska, A. (1996). Problems related to the design of the teaching and learning process in linear algebra. Artículo presentado en la Research Conference in Collegiate Mathematics Education. USA: Central Michigan University.         [ Links ]

Sierpinska, A. (2000). On some aspects of student's thinking in linear algebra. In J. L. Dorier (Ed.), On the Teaching of Linear Algebra (pp. 209–246). Holland: Kluwer.        [ Links ]

 

NOTAS.

¹ La letra H indica la intervención de Hermes, la E refiere a la intervención del entrevistador y los números, atañe al diálogo dentro de la entrevista en la que ocurre la discusión. El símbolo "(...)" indica momentos donde el estudiante se mantenía en silencio. regresar

² Este autor aborda la transformación previo a la transformación lineal, situación que creemos es benéfica para fines didácticos; sin embargo, en sus ejemplos de transformaciones involucra únicamente un vector. regresar

³ Tomado de Grossman, 1996, p. 465. regresar

⁴ Mario Sánchez, comunicación personal. regresar