Las supersuperficies en el aprendizaje de la geometría

 

Mercedes A. Anido ¹ Roberto López ¹ Héctor E. Rubio Scola ¹

 

¹ Facultad de Ciencias Exactas Ingeniería y Agrimensura Universidad Nacional de Rosario Argentina E–mail: anidom@fceia.unr.edu.ar

¹ Facultad de Ciencias Exactas Ingeniería y Agrimensura Universidad Nacional de Rosario Argentina E–mail: rolopez@fceia.unr.edu.ar

¹ Facultad de Ciencias Exactas Ingeniería y Agrimensura Universidad Nacional de Rosario Argentina E–mail: erubio@fceia.unr.edu.ar

 

Fecha de recepción: Febrero del 2006
Fecha de aceptación: Septiembre de 2006

 

RESUMEN

En este trabajo se busca fundamentar y describir una propuesta sobre el "ambiente de aprendizaje" que se crea cuando se utiliza una herramienta C.A.S., en este caso el Scilab, en la enseñanza de la relación entre la ecuación de una superficie y su representación en el espacio. El computador se utiliza como una herramienta del aprendizaje. Se han elegido superficies cuyo estudio ha surgido a partir de la representación computacional: las supercuádricas y los supertoros. Se propone una forma general de obtención de las gráficas, la que a partir de las ecuaciones paramétricas de las cuádricas hace posible la obtención de una gran variedad de familias de superficies. Esto es especialmente interesante como metodología que estimula el libre juego creativo del alumno, la exploración de potenciales propiedades y el afianzamiento del conocimiento de las cuádricas.

PALABRAS CLAVE: Supercónicas,supersuperficies,supercuádricas, pensamiento visual, ingeniería didáctica.

 

ABSTRACT

In this work is sought to support and to describe a proposal on the <<learning environment>> that is created when a C.A.S tool is utilized, in this case the Scilab, in the teaching of the relation between the equation of a surface and its representation in the space. The computer is used as a learning tool. Surfaces have elected whose study has arisen from the computational representation: the superquadric and the supertorus. A general form to obtaining the graphics is proposed, the one that from the parametric equations of the quadrics makes possible the obtaining of a great variety of surfaces families. This is especially interesting as methodology that stimulates the free creative play of the student, the exploration of potential properties and the consolidation of the knowledge of the quadrics.

KEY WORDS: Superconics, supersurfaces, superquadrics, visual thinking, didactic engineering.

 

RESUMO

Neste trabalho procura–se basear e descrever uma proposta sobre o <<meio da aprendizagem>> que se cria quando uma ferramenta C.A.S. é utlizada, neste caso o Scilab, no ensino da relação entre equação de uma superfície e sua representação no espaço. O computador é usado como uma ferramenta da aprendizagem. Foram escolhidas superfícies cujo estudo surgiu da representação computacional: as superquádricas e os supertoros. É proposto uma foma geral para obtenção dos gráficos. A partir das equações paramétricas das quádricas é possível a obtenção de uma variedade grande de famílias das superfícies. Isto é especialmente interessante como uma metodologia que estimula o jogo criativo livre do estudante, a exploração de potenciais e o reforço do conhecimento das quádricas.

PALAVRAS CHAVE: Super–cônicas, super–superfícies, super–quádricas, pensamento visual, engenharia didática.

 

RÉSUMÉ

Dans ce travail, on cherche à établir et à décrire une proposition sur "l'ambiance d'apprentissage" qui se crée lorsqu'on utilise un outil CAS, dans ce cas le Scilab, dans l'enseignement de la relation entre l'équation de la surface et sa représentation dans l'espace. L'ordinateur s'utilise comme un outil pour l'apprentissage. Plusieurs surfaces dont l'étude a surgit à partir de la représentation par ordinateur, ont été choisies : les superquadriques et les supertores. On propose une façon générale pour obtenir les graphiques, celle qui, à partir des équations paramétriques des quadriques, rend possible l'obtention d'une grande variété de familles de surfaces. Ceci est particulièrement intéressant comme méthodologie qui stimule le libre jeu de l'élève, l'exploration de propriétés potentielles et la consolidation de la connaissance des quadriques.

MOTS CLÉS:Superconiques, supersurfaces, superquadriques, pensée visuelle, ingénierie didactique.

 

1. INTRODUCCIÓN

En este trabajo se fundamenta y describe una experiencia de carácter exploratorio sobre el ambiente de aprendizaje que se crea cuando es usada una herramienta C. A. S. (Computer Algebraic System), en este caso el Scilab, para la enseñanza del concepto de superficie en el espacio. El computador se emplea como herramienta del aprendizaje, en el sentido de Jonassen (1995), quien la concibe como una "herramienta cognitiva en un proceso de aprendizaje que comprometa activamente al que aprenda y que genere su comprensión y concepción de la información, más que la reproducción del conocimiento del profesor".

Una herramienta cognitiva es todo aquel instrumento del que pueden servirse las personas para amplificar su capacidad de comprender y operar en el mundo. Tal cualidad no es intrínseca a un instrumento. En el caso de la computadora, no es por sí sola un medio cognitivo; para que llegue a serlo tiene que ser utilizada dentro de un cierto dominio conceptual, de manera que ayude al usuario a comprenderlo mejor y actuar con mayor eficacia en él. Si consideramos a la geometría como un dominio conceptual, el empleo de la computadora como herramienta cognitiva en la enseñanza y aprendizaje significa que se aplica en formas que faciliten la comprensión y operación en tal dominio (Mosquera, 1996).

En la enseñanza de la geometría, que debe producir la formación adecuada de un alumno universitario, las herramientas computacionales no deben ser simples fingertip tools (Jonassen, 1995) que mecanicen el trabajo, sin una real compresión del mismo. Se debería educar en el desarrollo del pensamiento formal y, al mismo tiempo, proporcionar una visión unificada entre la geometría y sus aplicaciones, compenetrados con la idea que, para la parte operativa, la computadora es la que nos da la solución, siempre y cuando quien la use sepa lo que quiere y entienda lo que le ofrece como resultado.

La teoría del aprendizaje y de la tecnología para el aprendizaje está en el medio de la revolución científica. Los modelos constructivistas del aprendizaje se preocupan de crear ambientes donde el alumno participe activamente en la compresión del mundo externo y refleje sus interpretaciones; aquí, la función de las herramientas cognitivas es guiar al alumno en la organización y representación del conocimiento. Cuando el estudiante trabaja con tecnología computacional, en lugar de ser controlado por ella, debe ser estimulado a aprovechar las posibilidades del computador para potenciar su pensamiento.

En la enseñanza de la geometría elemental se ha tomado plena conciencia de esta idea. Por ello, se promueve el uso de desarrollo de software educacional que desde su diseño constituya una real herramienta cognitiva que tome direcciones a distintos niveles, como el Cabri y el Sketchpad. Sin embargo, ¿es posible sólo con las herramientas C.A.S. –de las que se dispone con distintas versiones, en forma generalizada, en casi todos los laboratorios de las universidades– dinamizar el aprendizaje de la geometría analítica?

El vínculo entre las representaciones analíticas y gráficas en algunas superficies no convencionales es un tema de interés formativo en cualquier facultad de ingeniería. La existencia de software que nuclea modelado por sólidas y superficies complejas, las cuales se complementan con una diversidad de módulos que cubren casi la totalidad de las materias técnicas de las carreras de ingeniería, requiere más que nunca de la base del conocimiento geométrico. En cualquier tema, la inadecuada compresión de los fundamentos geométricos y su relación con las expresiones analíticas puede ser para un alumno causa de futuras frustraciones.

La tarea de los arquitectos diseñadores e ingenieros es inseparable de la colección de leyes y elementos geométricos que idealizan el espacio de tres dimensiones, una noción de representación abstracta que tenemos sobre nuestro lugar de vida y donde cada objeto conocido está ubicado. Por su parte, las restricciones geométricas son los invariantes universales de las cuales depende todo diseño real. La construcción que hace el alumno de conceptos tan abstractos como el de las superficies implicadas en el diseño suponer que una comprensión de la geometría le ayudará a comprender mejor el mundo y a operar en él de manera más efectiva.

 

2. EL PROBLEMA DE INVESTIGACIÓN

En el primer año de la Facultad de Ingeniería, la comprensión sobre la relación bidireccional entre una ecuación dada en el espacio de tres dimensiones y la superficie que la representa ha sido siempre considerado como un tema difícil. La relación entre la movilidad de los parámetros de las ecuaciones y la variación de las formas que se obtienen es un elemento de significado importante para la construcción del concepto.

Aunque la posibilidad de una representación gráfica por computadora abre perspectivas en este campo, plantea las siguientes interrogantes: ¿Hasta qué punto la ventaja de una inmediata visualización en un determinado dominio facilita la comprensión sobre la generación de una superficie, o sobre la relación que guarda con la ecuación que la representa algebraicamente? Conocida la posibilidad de rotación o traslación o de variación del dominio, ¿cómo la utiliza el alumno? ¿Trata de optimizar la visualización? ¿Juega con secciones con distintos planos? ¿Explora? ¿Induce propiedades? ¿Trata de demostrarlas? ¿O debe proponérselo el docente? (Por ejemplo, ¿explora las secciones de un hiperboloide de una hoja al alejarse de un eje de simetría, el plano de sección? ¿Trata de justificar analíticamente lo que visualiza en la pantalla?) ¿El alumno inventa superficies? ¿Las analiza? ¿El ambiente computacional estimula la exploración del conocimiento por el alumno? ¿Lo interesa? ¿Hace significativo el aprendizaje del tema? ¿O solo actúa como un observador pasivo? ¿Qué situaciones didácticas dispara la herramienta computacional? ¿Es suficientemente formativa la inducción y verificación de propiedades cuando su proceso demostrativo está más allá de los conocimientos y tiempos posibles a ser asignados en un currículum de matemática básica?

 

3. OBJETIVOS DE LA INVESTIGACIÓN QUE SE PRESENTA

En este trabajo, se busca indagar en un caso (relativo a un tema vinculado) la validez de algunos supuestos cuya confirmación puede constituir un aporte al problema didáctico que plantea la construcción del concepto ecuación de una superficie. Se considera que:

• La rapidez de respuesta del ordenador favorece el proceso de inducción y el descubrimiento de posibles propiedades o la inmediata verificación de su no existencia, por el análisis de múltiples ejemplos.

• La aparición de situaciones problemáticas en la pantalla, como los resultados no esperados, también invitaría al alumno a un trabajo de profundización teórica y autoexigencia de procesos demostrativos. En el caso de la representación gráfica de la ecuación de una curva o superficie, el medio computacional permite con inmediatez observar en la representación gráfica la influencia de cambios efectuados en los valores de los parámetros de la expresión analítica. Y si se sigue un criterio determinado en ese libre juego, explorar la posibilidad de existencia de una propiedad.

¿Cuál sería, en tal proceso, el aporte del medio computacional, adecuadamente utilizado, al aprendizaje y al pensamiento matemático? Promovería un aprendizaje de la matemática en el sentido de Polya: "Las matemáticas son consideradas como una ciencia demostrativa; este es sólo uno de sus aspectos. Hay que combinar observaciones, seguir analogías y probar una y otra vez. El resultado de la labor demostrativa del matemático es el razonamiento demostrativo, la prueba; pero ésta a su vez es construida mediante el razonamiento plausible, mediante la intuición. Si el aprendizaje de las matemáticas refleja en algún grado la invención de esta ciencia, debe haber en él un lugar para la intuición, para la inferencia plausible." En dicho sentido de aprendizaje valoramos a la herramienta computacional, por el trabajo matemático que puede inducir. Además, el concepto de herramienta cognitiva, al que hemos hecho referencia, implicaría formar también al alumno en una autoexigencia posterior de procesos justificativos (la necesidad de demostración debería quedar por lo menos planteada).

 

4. METODOLOGÍA DE LA INVESTIGACIÓN

La ingeniería didáctica ha sido el soporte teórico y andamiaje de nuestra construcción didáctica y de investigación. A continuación, sintetizamos las ideas esenciales sobre este método de enseñanza e investigación, propuesto por Michèle Artigue (1990).

La noción de ingeniería didáctica surge en la didáctica de las matemáticas a comienzos de los ochenta. Se denominó con dicho término a una forma de trabajo didáctico equiparable con la del ingeniero, quien para realizar un proyecto determinado se basa en los conocimientos científicos de su dominio y acepta someterse a un control de tipo científico. Tal concepción está ligada a la aproximación cognitiva que se ha desarrollado alrededor de los trabajos de Vergnaud en el área de la teoría de los campos conceptuales, así como a través de las insituaciones didácticas de Brousseau y los obstáculos que clasifica. Brousseau señala que "la didáctica no consiste en ofrecer un modelo para la enseñanza, sino en producir un campo de cuestiones que permita poner a prueba cualquier situación de enseñanza, corregir y mejorar las que se han producido y formular interrogantes sobre lo que sucede" (1988).

Una característica importante de esta teoría es que considera a los fenómenos de enseñanza–aprendizaje bajo un enfoque sistémico. Chevallard (1998) describe el sistema didáctico en sentido estricto, formado esencialmente por tres subsistemas: profesor, alumno y saber enseñado. El saber a enseñar conforma el objeto de diseño de nuestra ingeniería didáctica, ya que el docente propone y organiza una serie de situaciones, jugando con diversas restricciones (variables didácticas); establece las diferentes fases (investigación, formulación, validación, institucionalización); maneja la comunicación en la clase; brinda, llegado el momento, elementos convencionales del saber; el alumno intenta, busca, hace hipótesis, propone soluciones, las confronta con sus compañeros, las defiende: el saber es considerado con su propia lógica; el problema es medio de aprendizaje.

Esta concepción no sólo propicia y crea un ámbito para que el alumno explicite sus creencias o preconceptos, sino también permite detectar los errores, dificultades y obstáculos de los cuales devienen. Tales son los puntos de partida para la construcción del conocimiento.

La metodología de la investigación didáctica se caracteriza, en comparación con otros tipos de investigación basados en la experimentación en clase, por el registro donde se ubica y por la forma de validación a la cual está asociado. De hecho, las investigaciones que recurren a la experimentación en clase se sitúan por lo general dentro de un enfoque comparativo con validación externa, que está basada en la comparación estadística del rendimiento de grupos experimentales y control.

Este no es el caso de la ingeniería didáctica, pues se ubica en el registro del estudio de casos y tiene una validación interna, sustentada en la confrontación entre el análisis a priori y el a posteriori (Artigue, 1995), donde se fundamenta en esencia la validación de los supuestos formulados en los objetivos de la investigación. La especificidad del estudio de casos reside en que permite concentrarse en una situación particular e identificar los distintos procesos interactivos que lo conforman, los cuales pueden permanecer ocultos en estudios de índole más general.

Artigue (1995) lleva a cabo la descripción de la metodología de la ingeniería didáctica por medio de una distinción temporal de su proceso experimental. Delimita este proceso en cuatro fases:

1. Análisis preliminar.

2. Concepción y análisis a priori de las situaciones didácticas de la ingeniería.

3. Experimentación.

4. Análisis a posteriori y evaluación.

 

5. ALGUNOS ANÁLISIS PRELIMINARES

5.1. Los fundamentos de la geometría y la enseñanza de la geometría en la universidad

La geometría ha crecido rápidamente desde su tradicional lugar, en el que ofrecía una descripción matemática sobre los variados aspectos del espacio físico, pues ahora incluye disciplinas como convexidad (poliedros), teoría de grafos, nudos, tiling y geometría computacional, etc. (ICMI, 1995). Este rápido crecimiento ha sido acompañado por amplias aplicaciones en robótica, procesamiento de imágenes o computación gráfica, de ahí que los enormes desarrollos pongan desafíos a los educadores matemáticos para integrar estas áreas emergentes a la geometría tradicional, como el uso de sistemas de software tendentes a ayudar en la visualización y las exploraciones geométricas.

¿Qué es la geometría y cuál rol desempeña en la enseñanza de la matemática básica de la universidad? ¿Por qué se enseña?

Por más de 2000 años, la geometría euclídea ha jugado un rol central en la enseñanza–aprendizaje de la matemática para la ingeniería, al ser un modelo privilegiado del espacio físico. Si bien la geometría liga realidad y formalización –esto último como teoría deductiva– en los últimos años parece haber perdido su papel importante en la formación matemática por diversas razones, entre las que podemos mencionar su excesiva algebrización, que ha hecho perder el sentido intuitivo de las proposiciones de partida; que limita el uso del computador a una simple visualización en pantalla, o que ha hecho perder la riqueza de un aprendizaje fruto de situaciones problematizadoras.

La geometría analítica como lenguaje algebraico de la geometría euclídea ha sido un extraordinario motor de desarrollo para casi todas las ciencias de la ingeniería, mas exige una compresión constante del significado físico o geométrico de sus ecuaciones.

¿Cómo hacer que se establezcan sistemáticamente lazos entre la teoría general abstracta y su contrapartida intuitiva y visual, de tal manera que las herramientas informáticas sirvan para un conocimiento significativo de la geometría? ¿Cómo introducir y aprovechar la herramienta computacional, sin perder el rol fundamentalmente formativo del pensamiento de la geometría? Por otra parte, ¿cómo evitar que, en la geometría analítica, el formalismo algebraico inhiba la intuición geométrica? Al respecto, se debería cuidar especialmente la fase inicial de traducción de un problema geométrico en lenguaje algebraico y la fase final de interpretación del resultado obtenido, en lugar de atender sólo a la fase intermedia, a la cual sólo le concierne una correcta manipulación de formulación algebraica. Como estamos viviendo en una sociedad donde los aspectos visuales son más dominantes, una formación universitaria adecuada —sobre todo en carreras que hacen de la matemática una asignatura instrumental— debería incluir la solución de problemas articulados entre sí, exploraciones abiertas a la discusión, análisis de modelos concretos en tres dimensiones.

Respecto a nuestra propuesta metodológica, es importante la posición epistemológica de dos geómetras italianos, Fano Terracini y Federico Enriques, a quienes consideramos como precursores de algunas corrientes actuales. Terracini (1941) señala que la geometría, desde épocas remotas, está bajo el influjo de dos poderosas fuerzas: por una parte, las necesidades que crean las aplicaciones, por otra, la libertad del espíritu humano, que puede crear por sí mismo, arbitrariamente, el objeto de estudio matemático. Las fuerzas exteriores suministran los primeros puntos de partida y las interiores tienen que someterlos a una elaboración, que decanta en una teoría general y abstracta.

Al observar cómo se formaron los primeros conceptos de la teoría de superficies, se nota que originariamente las superficies sólo eran concebidas como contenedoras de cuerpos sólidos; todavía Euler hace referencia a la superficiebus corporum. La desvinculación del soporte material recién la hizo Gauss en su obra Disquisiciones generales acerca de las superficies curvas, en la que concibe a las superficies no como el límite de un sólido, sino como un sólido cuyas dimensiones están desvanecidas. Si Terracini nos remarca con admiración el paso de casi un siglo entre la obtención de la ecuación de una curva plana y la de una superficie en el espacio, ¿cómo nos podemos extrañar de las dificultades que tienen los alumnos al construir un concepto que a los matemáticos les llevó siglos?

Para el Dr. Federico Enriques, nuestra representación intuitiva del espacio surge primero de los conceptos particulares y sube por abstracciones sucesivas a los conceptos más generales. No decimos por esto que los conceptos más generales, cuando son intuitivos, tienen menor grado de evidencia en comparación con los conceptos particulares; sin embargo, su evidencia está en relación con un estado más progresivo de la mente, en el que se ejercita una facultad de representación más abstracta. Así, desde el punto de vista intuitivo, la generalidad de los conceptos que se pueden considerar como fundamentales en la geometría tienen un límite en nuestra capacidad de representación de lo abstracto. Incluso aun cuando la lógica pueda ayudar al proceso de abstracción constructivo de los conceptos, no sustituye por sí sola a las asociaciones psicológicas que constituyen este mismo proceso. Si no se quiere una abstracción ilusoria, hay que educar la capacidad representativa de lo abstracto, recurriendo también a medios experimentales (Enriques at al, 1948).

En la búsqueda de los aspectos formativos tocantes a la enseñanza de la geometría en el nivel universitario, deberíamos tratar de extender a este nivel las preguntas dominantes que el Dr. Vinicio Villani (1994, 1995) hace al respecto de la enseñanza preuniversitaria: ¿Qué se entiende por geometría? ¿Qué rol se atribuye a la definición? ¿Es necesaria una memorización recitada o basta una conceptualización implícita? ¿Qué rol se atribuye a la conjetura, a la argumentación y a la demostración? ¿Qué rol formativo tiene cada una de estas actividades? ¿Qué auxilios didácticos y tecnológicos utilizar y con qué finalidad? ¿Los distintos tipos de software que se usan para el trazado de curvas o la representación tridimensional favorecen el proceso de conceptualización y sistematización del conocimiento geométrico? ¿Hasta qué punto la propiedad de una figura geométrica que resista todas las posibilidades de deformación visualizables en pantalla nos exime de la necesidad de demostrarla? ¿Qué aspectos debo priorizar en mi enseñanza: el sintético, el analítico o utilizar el álgebra vectorial? ¿La teoría debe preceder a la práctica o surgir partir de ésta? ¿Qué cosa es para mí un bello problema de geometría? ¿Qué contenidos geométricos debo actualizar?

El estudio de la Geometría, según Villani (1994), puede y debe contribuir a capacitar en:

• Reconstruir mentalmente la imagen de un objeto tridimensional a partir de su diseño.

• A usar, según sea la circunstancia, lenguajes de distintos tipos: verbal, gráfico, algebraico, simbólico y saber pasar de uno a otro.

• Clasificar objetos, de acuerdo con uno o más atributos.

• Razonar (incluso fuera del ámbito geométrico) en el modo hipotético deductivo en vista a operar con ciertos conceptos, o tomar decisiones racionales en la vida cotidiana, social y profesional sobre la base de datos de los hechos a disposición.

Como respuesta al cuestionamiento sobre el valor del conocimiento matemático adquirido por visualización, Miguel de Guzmán (1996) dice que la visualización en matemática es común, abstraíble y queda sometida a una elaboración racional, simbólica, que nos permite manejar más claramente la estructura subyacente a tales percepciones. Desarrollar el pensamiento visual y favorecer las habilidades de visualización son dos objetivos clave en la educación geométrica. Por ello, hay que aclarar bien lo que se entiende por pensamiento visual y visualización, pues a menudo se confunden en una sinonimia limitante o se relacionan con las simples imágenes que a menudo ilustran el discurso geométrico.

El pensamiento visual incluye la habilidad de visualizar, pero va más allá, ya que puede incluir aspectos como el reconocimiento rápido de determinantes formas o categorías, la manipulación automática de determinados códigos, etc. Explorar, seleccionar, simplificar, abstraer, analizar, comparar, completar, resolver, combinar son verbos que caracterizan a parcelas del pensamiento visual (Alsina, 1997). "El pensamiento visual –afirma Marjorie Senechal, citada por Alsina et al. (1988)–, si se explota convenientemente, puede revolucionar la forma de hacer geometría y de enseñarla". Alsina y sus colaboradores también señalan que la exploración espacial mediante el uso de ordenadores es un claro ejemplo de cómo se ha revolucionado la aproximación docente a las estructuras tridimensionales y cómo se han abierto nuevas fronteras de investigación sobre el efecto en el aprendizaje.

 

5. 2. El tema matemático. ¿Con qué criterio se ha elegido el saber a enseñar?

La repetición de tareas, de bajo orden cognitivo, no promueve un aprendizaje significativo en los estudiantes. Por el contrario, cuando la computadora es utilizada como herramienta cognitiva en la enseñanza y aprendizaje de la matemática, se les plantea a los estudiantes situaciones problemáticas de alto orden cognitivo, que van más allá de la simple ejecución de operaciones aritméticas y de la mera repetición de conceptos y algoritmos (Mosquera, 1996).

Para seguir esta idea, se ha buscado explorar las posibilidades que ofrece una utilización adecuada de las herramientas computacionales para facilitar la comprensión de los conceptos geométricos y ampliar los contenidos tradicionales relativos a cónicas y cuádricas.

En tal sentido, se ha propuesto el estudio de una familia de superficies, cuya representación es posible a partir de la introducción de las herramientas computacionales, motivando a que el alumno conjeture las propiedades y las demuestre (Anido y Rubio, 1999). En 1981, Barr y Franklin (Bar, 1981; Franklin y Barr, 1981) introdujeron una familia de superficies llamadas supercuádricas, apoyándose en el llamado producto esférico de superelipses y superhipérbolas, ya tratadas en 1979 por I. D. Faux y M. J. Pratt (1979), aunque D. L. Flanagan y O. V. Hefner las habían mencionado en 1967. También Alain H. Barr creó el concepto de supertoros.

 

Las supercuádricas posibles de ser representadas y estudiadas con los recursos de la computación gráfica (Anido y Villalonga, 1989) son utilizadas a nivel de diseño industrial hace más de dos décadas. ¿Cuáles son sus aplicaciones?

En el momento actual, hay sistemas de diseño y manufactura con núcleos de modelado de sólidos en tres dimensiones de alta performance, que se emplean para diseñar piezas y conjuntos. Debido a que utilizan recursos para la definición de sólidos, generan a su vez todas las superficies que éstos definen, permitiendo el dimensional automático de las piezas con sus restricciones. Así, puede disponerse de la información de la masa, volumen y áreas de los sólidos diseñados. Existen distintos programas que no sólo manejan el núcleo del modelado, sino también resuelven el análisis lineal de las solicitaciones mecánicas de las piezas, simulaciones mecánicas y de movimiento entre componentes, con base en la ecuación de la superficie.

Ahora bien, ¿cuál es la importancia, en el campo de la investigación didáctica, de este tema? Resulta especialmente apto para mostrar, en la concepción y el análisis apriori de una ingeniería didáctica, el campo de conocimientos geométricos que se puede generar con el apoyo de una herramienta computacional usada en forma adecuada. Pero, sobre todo, porque las supersuperficies:

 

5.3. Algunas definiciones: supercónicas, supercuadrádas y supertoros

Definición de supercónicas: Curvas obtenidas al modificar las ecuaciones paramétricas de las cónicas por la elevación a exponentes racionales positivos de todas las funciones trigonométricas de sus expresiones paramétricas.

De esta manera, podemos conseguir, por ejemplo, superelipses y superhipérbolas, cuyas expresiones paramétricas son las siguientes:

Superelipses:

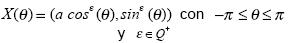
Superhipérbolas:

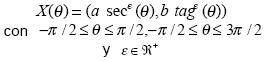
Definición de producto esférico: Dadas dos curvas en el plano representadas por sus respectivas curvas paramétricas:

Llamamos producto esférico de dos curvas a la siguiente superficie:

Definición de supercuádricas: Son las superficies obtenidas al hacer el producto esférico de dos supercónicas.

Superelipsoides:

Superhiperboloides de una hoja:

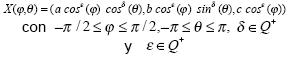
Superhiperboloides de dos hojas:

Superparaboloide elíptico:

Fuera ya de las supercuádricas, otro tipo de supersuperficies que nos interesa estudiar son los supertoros, definidos por las siguientes expresiones paramétricas:

Supertoro:

 

6 CONCEPCIÓN Y ANÁLISIS A PRIORI

El estudio de las supercuádricas no ha sido incorporado aún a los programas de geometría analítica en las facultades de ingeniería de la universidad. Su obtención a partir de una generalización de las ecuaciones de las cuádricas es fácil y la riqueza de formas a que dan lugar, con los recursos de rotación y cambio de unidades del software matemático para la representación geométrica, es infinita (ver Figura 1).

Se espera en este trabajo que pueda conseguirse la representación a partir de sus ecuaciones paramétricas. Éstas se podrían considerar como una generalización de las ecuaciones paramétricas de las cuádricas, donde son afectadas las funciones trigonométricas que aparecen con exponentes que producen, para cada valor, deformaciones análogas, las cuales a su vez inducen la categorización de las superficies generadas en distintas familias.

En algunos casos emergerá una especie de aristas en el sentido de los meridianos, de los paralelos o de ambos; en otros, una superficie reglada. Se espera que sean útiles para comprender la relación entre la forma y su representación algebraica; que cobren un especial interés para el libre juego del alumno en la búsqueda de nuevas formas (situaciones de acción) y la exploración de potenciales propiedades (situaciones de formulación y justificación), así como al afianzamiento del conocimiento de las cuádricas. Además, es fácil y posible incursionar en la representación (no utilizada comúnmente en los núcleos de modelado) del superhiperboloide de dos hojas y el superparaboloide elíptico (Figura 2).

 

Mediante la experimentación numérica y gráfica, y por la observación de sus meridianos y paralelos, se pueden inducir propiedades de reglaje que luego son demostradas analíticamente. Se ha esperado que el trabajo en el laboratorio lleve a la confirmación de los supuestos iniciales, expresados en la sección 3.

 

6.1. Las selecciones del profesor: propuesta de un problema .

A partir de las ecuaciones paramétricas de las cuádricas y de la previa presentación de las supercónicas se plantea, como desafío, la exploración de nuevas formas geométricas vinculadas a dichas superficies y la indagación de propiedades generales.

 

Este problema, en forma análoga a lo que ya han hecho en el estudio de las superficies cuádricas, requiere la consideración de distintos casos.

Por ejemplo, la ecuación paramétrica de una elipsoide en un caso particular es:

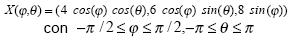
Un primer problema derivado del problema general es:

 

Se pide que y sean racionales y positivos. Para cada valor de los parámetros se obtiene una ecuación.

¿Cómo se respondería a un problema de este tipo sin herramientas computacionales de cálculo y representación, en tiempos razonables? Es aquí donde se impone la representación computacional (Figura 1) como una nueva metodología para estudiar la geometría analítica.

 

6.2 La elección de la herramienta computacional

Una de las herramientas computacionales posibles para la representación es el Scilab, una herramienta C. A. S. desarrollada en el Instituto Nacional de Investigaciones en Informática y Automática de Francia (INRIA), como parte del proyecto Métala (Bunks et al., 1999). Este software, diseñado con el fin de ofrecer una poderosa herramienta de cálculo a los expertos en matemática aplicada, es un sistema totalmente interactivo que da una gran comodidad para la visualización de las soluciones obtenidas, sea gráfica o alfanumérica. Asimismo, puede manipular la mayor parte de los objetos estándar de la matemática aplicada, como vectores, matrices, polinomios, matrices polinomiales reales o complejas. Al ser un sistema totalmente abierto, le permite al usuario definir nuevas funciones, crear nuevas tipos de variables y definir sus propias operaciones. También cabe destacar que, en el contexto social de las universidades estatales argentinas, Scilab tiene una distribución gratuita y se encuentra disponible para diversos sistemas operativos tal como Unix, Linux o Windows/98/NT.

 

7. EL DESARROLLO DE LA EXPERIENCIA EN EL LABORATORIO

Con carácter exploratorio se ha trabajado con un grupo de alumnos de la asignatura Álgebra y Geometría Analítica de la Facultad de Ciencias Exactas, Ingeniería y Agrimensura de la Universidad Nacional de Rosario, Argentina, quienes ya han aprobado las evaluaciones parciales correspondientes a los temas de cónicas y cuádricas. De igual manera, estudiaron en una clase previa, dada en el laboratorio, la generación de las supercónicas. En este trabajo se describen algunas etapas del estudio exploratorio de las supercuádricas.

Los alumnos obtienen fácilmente la representación del elipsoide que se observa en la Figura 1 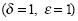. El docente les pide que, en un trabajo de relación entre las ecuaciones y la gráfica, imaginen cómo recorrer el elipsoide por los paralelos.

Ahora bien, los alumnos saben que si se deja φ constante, la coordenada z también es constante. Dicha coordenada mide la distancia al plano xy, o sea, la distancia al plano del ecuador en un elipsoide como el de la Figura 1. Esto equivale a imaginar el elipsoide seccionado por un plano cuya intersección nos da un paralelo de forma elíptica. Se plantean las siguientes preguntas:

¿ Cómo podríamos movernos recorriendo los paralelos?

Para cada φ constante, al variar el ángulo θ se recorre un paralelo.

Se observa que todo el elipsoide puede pensarse que está generado por elipses, los cuales constituyen los paralelos. En respuesta a la consigna del problema derivado, los mismos alumnos se preguntan:

¿Qué le ocurrirá a un paralelo elíptico si afectó a las funciones trigonométricas del ángulo θ que, como vimos, rige el recorrido de la elipse en su ecuación paramétrica, con un valor del exponente mayor que 2?

Ellos ya han visto en el trabajo previo sobre las superelipses en el plano que esos valores producen cúspides en la forma de la elipse Por ejemplo, para un valor del exponente igual a 3, en cada paralelo aparecerán cuatro cúspides. También han trabajado en análisis matemático las funciones paramétricas que se representan por astroides.

¿Qué puede significar en toda la superficie la aparición de infinitas cúspides en sus paralelos?

Los alumnos conjeturan que surgen las cuatro aristas que pueden mediante la computadora.

¿Cómo nos podríamos mover, en forma análoga, recorriendo los meridianos?

Si ahora consideramos θ constante, al variar φ se puede imaginar que un punto recorre una mitad de un meridiano, formando una elipse. Tal razonamiento intuitivo está facilitado por el conocimiento que el alumno tiene de las coordenadas esféricas.

¿Que ocurrirá cuando afectamos ahora, con el exponente 3, las funciones trigonométricas del ángulo φ que genera las elipses meridianos?

Se anticipa la generación de cuatro cúspides en cada meridiano.

¿Cómo incidirá en la superficie del elipsoide?

Las cúspides de los meridianos se ubican en el "ecuador" y en los "polos", como se observa en las figuras correspondientes (Figura 1, caso .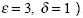

Las supersuperficies son graficadas mediante paralelos y meridianos. En la Figura 1 se muestra el elipsoide del ejemplo y los respectivos superelipsoides que resultan cuando toman determinados valores. La Figura 2 representa un hiperboloide de una hoja y sus respectivos superhiperboloides de una hoja. Se añaden además graficaciones de un paraboloide elíptico y los superparaboloides elípticos asociados. En la Figura 3 aparece un hiperboloide de dos hojas y sus deformaciones, y en la Figura 4 un toro con los supertoros correspondientes.

En un trabajo de sistemática experimentación numérica y gráfica, la observación de regularidades tocantes a determinados valores de e y S en distintas supercuádricas lleva a la inducción de las siguientes propiedades:

 

Las supersuperficies regladas

De la observación en pantalla han surgido propiedades relativas al carácter reglado de las superficies que se obtienen con ecuaciones paramétricas afectadas con exponente igual a 2. La demostración pudo plantearse como un problema de validación relativamente fácil.

La simplicidad de recursos que se necesitan hace la demostración posible para el alumno.

 

8. ANÁLISIS A POSTERIORI Y EVALUACIÓN DIDÁCTICA

Se ha buscado detectar situaciones adidácticas de acción, formulación y validación, en el sentido de Brousseau, que surjan a partir de la relación de los alumnos con los contenidos y el medio. Estas situaciones serían, de acuerdo con nuestro criterio de observación dirigida, los indicadores de un aprendizaje significativo caracterizado por Ausubel como aprendizaje por descubrimiento, e ilustrado por el mismo en un ejemplo sobre la generalización de una propiedad de los triángulos (Ausubel y Robinson, 1969).

Brousseau llama situación adidáctica "a una situación matemática específica de un conocimiento concreto que, por sí misma, sin apelar a razones didácticas y en ausencia de toda indicación intencional, permite o provoca un cambio de estrategia por el alumno".

La situación adidáctica es una parte de la situación más amplia, a la que Brousseau denomina situación didáctica, que comprende las relaciones establecidas explícita o implícitamente entre los alumnos, un cierto medio (incluyendo instrumentos y objetos) y el profesor, con el objetivo de que los alumnos aprendan el conocimiento matemático. Se trata de una serie de intervenciones del profesor sobre el par alumno–medio, destinadas a hacer funcionar las situaciones adidácticas y los aprendizajes que provocan. La evolución de una situación didáctica requiere, por tanto, la intervención constante, la acción mantenida y la vigilancia del profesor." (Chevallard et al., 1997).

¿Cómo se las caracteriza?

Situaciones adidácticas de acción

Una buena situación de acción debe permitir al alumno juzgar el resultado de su acción y ajustarla sin la intervención del profesor, gracias a la retroacción por parte del medio de la situación. Las informaciones que le devuelve la situación son percibidas por el alumno como sanciones o refuerzos de su acción.

En una situación de acción se produce un diálogo entre el alumno y la situación. Tal dialéctica de la acción le permite construir mejor su modelo implícito, pues tiene reacciones que no puede todavía formular, probar, ni mucho menos organizar en una teoría. En todo caso, la situación adidáctica provoca un aprendizaje por adaptación, según la teoría de Piaget (Chevallard et al., 1997).

Situaciones adidácticas de formulación

Con el fin de que el alumno pueda explicitar su modelo implícito y que esta formulación tenga sentido para él, es necesario que pueda utilizarla a fin de que obtenga o haga obtener a alguien un resultado. En unas situaciones adidácticas de formulación, el alumno intercambia información con una o varias personas, o bien comunica lo que ha encontrado a un interlocutor o a un grupo de alumnos, que le devuelve la información (Chevallard et al., 1997).

Situaciones adidácticas de validación

En la dialéctica de la validación, el alumno debe demostrar porqué el modelo que ha creado es válido. Sin embargo, para que construya una demostración y tenga sentido para él tiene que construirla en una situación, llamada de validación, donde necesita convencer a otra persona. Una situación adidáctica de validación da la ocasión de someter el mensaje matemático –modelo explícito de la situación– como una aseveración a un interlocutor (oponente). El oponente puede solicitar explicaciones suplementarias, rechazar las que no comprende o aquellas con las que no está de acuerdo, dando sus argumentos (Chevallard et al., 1997).

¿Qué situaciones adidácticas se observan en el laboratorio?

Con respecto al modo de apropiación de los contenidos por parte de los alumnos, es posible distinguir tres momentos estrechamente vinculados entre sí:

Primer momento: La curiosidad suscitada por el impacto visual de las primeras imágenes actúa en principio como fuente de motivación En este momento predominan las situaciones adidácticas de acción, donde los alumnos interactúan con la computadora.

Segundo momento: Tiene lugar a partir del diálogo, la discusión y el intercambio de información entre pares de alumnos frente al computador, con intervenciones ocasionales de las docentes y compañeros de otros grupos. Predominan las situaciones adidácticas de formulación, en las que ocurren los primeros intentos para interpretar, identificar y definir lo que se observa en la pantalla, es decir, las respuestas que devuelve la computadora.

Tercer momento: Pueden distinguirse situaciones adidácticas de validación a medida que transcurren las clases de laboratorio, ya que los alumnos utilizan nociones analíticas previas relativas a las secciones cónicas, superficies cuádricas y conceptos incluso del análisis matemático, que atañen al comportamiento de determinadas funciones para explicar al compañero o al docente ciertas deformaciones.

La aparición de un nuevo conocimiento, o de alguna respuesta inesperada por parte de la PC, genera un conflicto cognitivo en los alumnos que no puede ser resuelto mediante estrategias del tipo ensayo–error. Eso se debe a la función conceptualizadora del diálogo, que obliga a los alumnos a analizar y reflexionar sobre sus acciones para poder argumentar con racionalidad la pertinencia de sus decisiones en la solución dada al problema (Anido et al., 2000).

Otro rasgo a destacar en el proceso de aprendizaje es que la modalidad de trabajo adoptada, donde el énfasis está puesto en la exploración, la experimentación o la investigación antes que en la respuesta correcta, permite que los alumnos utilicen el error no como sinónimo de fracaso, sino como otro punto de partida para nuevas problematizaciones y reflexiones, en el que las posibilidades y consecuencias muchas veces son desconocidas incluso para las docentes.

Si centramos nuestra mirada en el rol docente, aparece como fundamental en el proceso de apropiación de los conocimientos por parte de los alumnos. De los datos obtenidos podemos deducir que la intervención de las docentes tiende principalmente a provocar el conflicto cognitivo en los alumnos, mediante la problematización de los contenidos. Para ello, se basan en el uso del interrogatorio didáctico, la pregunta y repregunta, el cuestionamiento de las estrategias, la contradicción y la duda, con el fin de lograr el análisis y la reflexión por parte de los alumnos. Resulta interesante observar la alternancia de situaciones didácticas en las que las docentes conceptualizan lo trabajado por los alumnos (instancia de institucionalización) con el desarrollo de situaciones adidácticas, donde se evidencia la tensión que genera la demanda de los alumnos para obtener respuestas puntuales y la no–intervención deliberada de los profesores.

En esta línea de acción pueden puntualizarse ciertas escogencias didácticas, como el encuadre de la tarea o la aclaración de las consignas dadas. El tema resulta propicio para transformar las respuestas del computador al accionar de los alumnos y sus interpretaciones en un saber que, con la ayuda del docente, constituya un conocimiento de carácter universal. Dichas intervenciones del docente obran a manera de andamiaje en la orientación y comprensión del trabajo con la PC, así como en la relación y reorganización de los nuevos conocimientos asimilados por los alumnos.

La disposición de dos alumnos frente al computador ha facilitado no sólo el diálogo entre los integrantes de un mismo equipo, sino además ha propiciado un clima áulico distendido que favorece la realización de la tarea. Resulta evidente una construcción social del conocimiento, donde el aprendizaje es mejor entendido en un proceso de diálogo y socialización (Bredo, 1994). Sin embargo, la restricción de esta modalidad didáctica estriba en la dificultad que enfrentaron las docentes durante la atención simultánea de múltiples grupos con necesidades y ritmos de aprendizaje diferentes.

Ahora bien, las posibilidades gráficas y visuales tienen una apreciable influencia en las formas de aprender de los educandos, al cumplir diferentes funciones:

• Función motivadora: Mediante el impacto y la riqueza de las imágenes (color, volumen, etc.)

• Función problematizadora: Al permitir la creación de nuevas figuras y relaciones espaciales, abriendo paso a numerosas experimentaciones e interrogantes.

• Función facilitadora de un aprendizaje significativo: Como vía de familiarización con los diversos objetos matemáticos, a través de la identificación, comparación, interpretación, aproximación y comprensión por analogía de sus representaciones.

Pudo notarse en el desarrollo del trabajo hecho por los alumnos el rol de herramienta cognitiva asignado a la computadora, ya sea a nivel de los alumnos o de las docentes, en el sentido de que se tendió en forma explícita hacia un uso racional y crítico de la misma, ya que se reflexionó continuamente acerca de sus alcances y limitaciones, ventajas y desventajas. Esto puede ser señalado en el progresivo aprovechamiento de esta herramienta en el transcurso de las etapas de trabajo.

¿Qué evaluación podemos hacer en relación a las predicciones del análisis a priori?

El análisis a posteriori confirmó las conjeturas formuladas en el análisis a priori sobre el trabajo matemático de los alumnos.

• Las imágenes que aparecen en la pantalla despiertan en los alumnos la curiosidad e inducen la investigación de nuevas formas, debido al juego matemático creativo que se facilita por la inmediata representación computarizada de las ecuaciones surgidas de la variación de los parámetros. Se intuyen nuevas imágenes que luego son materializadas en la pantalla del computador. En las situaciones adidácticas de acción se induce naturalmente una clasificación de las formas, según los valores de los parámetros; hay una partición de las familias en subfamilias y una clasificación que da lugar a la formulación de las condiciones que definen subfamilias. Algunos alumnos relacionaron las formas de meridianos y paralelos con las curvas asteroides presentadas como ejemplos de puntos cuspidales en análisis matemático.

• Se promueve naturalmente un estudio gráfico de familias de superficies, inducción de definiciones a partir de ejemplos, relación de ecuaciones con gráficas, reconocimiento de ejemplos de gráficas de un cierto tipo e interpretación del papel de los parámetros presentes en ecuaciones, específicamente los efectos de cambios de parámetros sobre la forma gráfica.

• Se generaliza, en el sentido de generalización de Polya, el concepto de cuádricas a supercuadricas, constituyéndose las primeras en un caso particular de una familia de superficies mucho más amplia, con infinitas nuevas formas. Polya (1954) sugiere dos tipos de generalizaciones, cuando dice: "Nosotros generalizamos cuando pasamos de la concepción de triángulos a la de polígonos con arbitrario número de lados. Nosotros generalizamos también cuando pasamos del estudio de funciones trigonométricas con ángulo agudo a funciones trigonométricas con ángulo irrestricto". La complejidad de una generalización depende del concepto que será generalizado y de su representación. En nuestro caso, el pasaje de las ecuaciones paramétricas de una cuádrica, donde el exponente de las funciones trigonométricas vale uno, a una expresión más general, donde puede tomar como valor números racionales, se puede considerar como una generalización de las cuádricas a una familia de superficies: las supercuádricas. Se consigue así una organización jerárquica y piramidal que constituye lo que Ausubel llama estructura cognitiva (Ausubel et al., 1987).

• Se obtienen las ecuaciones y representaciones computarizadas del superparaboloide y del hiperboloide de dos hojas, no difundidos, que consideramos pueden ser un aporte a los estudios en el tema.

• La ingeniería didáctica que desarrollamos muestra la diversidad y movilidad de los cuadros definidos por Douady (1995) que entran en juego. La aparición de los distintos cuadros (geométrico, algebraico, computacional, de cálculo) hace cumplir una condición necesaria de un buen problema que, según Douady, debe requerir al menos de dos cuadros. Los alumnos trabajan con verdaderas ventanas conceptuales, concebidas como "conjunto de partes de cuadros que un estudiante hace interactuar o combina para estudiar el problema al cual se somete".

Esas ventanas abarcan conocimientos relativos a álgebra, geometría, trigonometría, cálculo, computación (sistemas de ecuaciones paramétricas, funciones trigonométricas, análisis de dominio de las funciones implícitas vinculadas campo real y al campo de los números complejos, límite, curvas astroides que se estudian aisladas en el análisis matemático, y que se constituyen en meridianos o paralelos en las supersuperficies representadas). Douady agrega: "Para un estudiante determinado, la ventana evoluciona en el transcurso del trabajo con relación a las preguntas y los métodos que su conocimiento le sugieren. Las ventanas constituyen el sustento de los juegos de cuadros" (1993).

 

9. CONCLUSIONES

En este trabajo se ha descrito sólo una primera puesta en escena, con carácter exploratorio, de una ingeniería didáctica en un tema que podría ser incorporado a los contenidos curriculares de la matemática básica en las carreras de ingeniería, arquitectura o diseño. No obstante, desde la confrontación entre las conjeturas expresadas en el análisis previo y el análisis a posteriori surge un posible aporte a la validación de los supuestos formulados en los objetivos de la investigación que debe ser continuada y profundizada.

Se ha buscado, en esencia, aproximar respuestas al campo de cuestiones que integran el problema de investigación, al indagar en la potencialidad de la representación computarizada para comprender la relación entre una superficie y su gráfica, algo muy difícil para el alumno en la primera etapa de su formación matemática. La potencia de una herramienta C. A. S. en cuanto a la rapidez de respuesta del ordenador ha permitido la obtención y estudio computarizado de múltiples familias de curvas y superficies de interés en una facultad de ingeniería para el diseño constructivo e industrial.

También se han manifestado:

• Razonamientos basados en la intuición geométrica que lleven al desarrollo de un pensamiento anticipativo.

• Abstracciones por analogía y generalizaciones (razonamientos plausibles e intuición).

• Ampliación de la estructura cognitiva del alumno por la construcción de generalizaciones que conducen desde las cuádricas a las supercuádricas.

• El estímulo del pensamiento visual, en el sentido de Alsina (1997), en cuanto a las abstracciones que exige entender cómo se provocan, desde las expresiones analíticas, deformaciones en objetos ya abstractos, como las superficies cuádricas y tóricas.

• Una partición en familias y subfamilias originada por la clasificación de supersuperficies de acuerdo con los rangos de variación de los parámetros. Esto encuadraría en las tareas recomendadas como trabajo matemático de aprendizaje significativo por Tall (1985), quien considera a familias de este tipo como sistema genérico organizacional que provoca procesos cognitivos complejos en el aprendizaje.

Se suma a esto otra conclusión no menos importante: el tratamiento computacional por el alumno de las supersuperficies le devela o refuerza el conocimiento de la belleza de la matemática y de su poder para generar belleza.

 

10. AGRADECIMIENTOS

Este trabajo forma parte de estudios realizados en el marco del Programa 2–ECO–3, La formación matemática en carreras no matemáticas, perteneciente a la Universidad Nacional de Rosario, Argentina. Dicho programa incluye a los siguientes proyectos vinculados con la temática del trabajo y que actualmente son financiados por la Secretaría de Ciencia y Técnica de la Universidad Nacional de Rosario:

• ECO–17, La ingeniería didáctica en el diseño y seguimiento de unidades curriculares.

• ING–74, La elaboración y evaluación de los materiales curriculares para la matemática básica de carreras de ingeniería.

• La enseñanza de la matemática con herramientas computacionales, que lleva a cabo el Consejo de Investigaciones de la Universidad Nacional de Rosario (CIUNR).

Se trabajó en el laboratorio provisto por el proyecto FOMEC. No. 615– UNR, La enseñanza de la matemática con herramientas Computacionales, auspiciado por el Fondo para el Mejoramiento de la Calidad de Enseñanza de la Secretaría de Políticas Universitarias, dependencia del Ministerio de Cultura y Educación de Argentina.

 

BIBLIOGRAFÍA

Alsina, C.; Burges, C. y Fortuny, J. M. (1988). Invitación a la didáctica de la geometría. Madrid, España: Síntesis.        [ Links ]

Alsina Catalá, C.; Fortuni Aymemí, J. y Pérez Gómez, R. (1997). Geometría analítica. Madrid, España: Síntesis.        [ Links ]

Alsina Catalá, C.; Fortuni Aymemí, J.; Pérez Gómez, R. (1997). ¿Por qué geometría?. Madrid, España: Síntesis.        [ Links ]

Anido, M.; (2002) Una propuesta de incorporación de herramienta computacional a la enseñanza de la matemática en la universidad. Evaluación de experiencias. Tesis de doctorado, UNED, España.        [ Links ]

Anido, M.; Có, P.; Del Sastre, M.; Medina, L. y Panella, E. (2000). Una ingeniería didáctica diseñada alrededor del concepto de cónicas y superficies. Anales del IX Encuentro Nacional Sobre Enseñanza de la Matemática en Carreras de Ingeniería (EMCI), 32–66. Entre Ríos, Argentina: Universidad Tecnológica Nacional de Entre Ríos, Argentina–Facultad Regional Concepción del Uruguay.        [ Links ]

Anido, M. y Villalonga, M. (1989). Supersuperficies. La supersuperficie de Boy. Publicación del Congreso Internacional Computadoras en Educación (pp. 88–101). Mendoza, Argentina: Universidad de Mendoza.        [ Links ]

Anido, M. y Rubio, H. (1999). Un ejemplo de aprendizaje en el sentido de Polya. Revista Latinoamericana de Investigación en Matemática Educativa 2 (3), 5–17.        [ Links ]

Artigue, M. (1990). Ingénierie didactique. Recherches en Didactique des Mathématiques 9 (3), 281–307.        [ Links ]

Artigue, M. (1995). El lugar de la didáctica en la formación de profesores. En M. Artigue, M. Douday, R. I. Moreno y P. Gómez, (Eds.), Ingeniería didáctica en educación matemática. (pp. 7–33). Bogotá, Colombia: Grupo Editorial Iberoamericano.        [ Links ]

Ausubel, D. P.; Novack, J. D. y Hanesiam, H. (1987). Psicología educativa. Un punto de vista cognoscitivo. México: Trillas.        [ Links ]

Ausubel, D. P. y Robinson, F. G. (1969). School learning. An introduction in educational psychology. London, Great Britain: Holt, Rinehart & Winston.        [ Links ]

Barr, A. H. (1981). Superquadrics and angle–preserving transformations. I.E.E.E. Computer Graphics and Applications, 1 (1), 11–23.        [ Links ]

Bredo, E. (1994). Reconstructing educational psychology: situated cognition and Dewey an pragmation. Educational Psychologist, 29 (1), 23–35.        [ Links ]

Brousseau, G. (1988) Los diferentes roles del maestro. Buenos Aires, Argentina: UQAM.        [ Links ]

Bunks, C.; Chancelier, J. P.; Delebecque, F.; Gómez, C. (Ed.); Goursat, M.; Nikoukhah, R. & Steer, S. (1999). Engineering and scientific computing with Scilab. Boston, USA: Birkhäuser.        [ Links ]

Chevallard, Y.; Bosch, M. y Gascón, J. (1997) Estudiar matemática. Barcelona, España: ICE–Horsori.        [ Links ]

Chevallard, Y. (1988). La transposition didactique, du savoir savant an savoir enseigné. Grenoble, France: La Pensée Sauvage.        [ Links ]

De Guzmán, M. (1996). El rincón de la pizarra. Ensayos de visualización en análisis matemático. Madrid, España: Pirámide.        [ Links ]

Douady, R. (1993). L'Ingenierie Didactique. Un moyen pour l'enseignant d'organiser les rapports entre l'enseignement et l'apprentissage.Cahier de DIDIREM IREM 19. Paris: Université Paris VII.        [ Links ]

Douady, R. (1995). La ingeniería didáctica y la evolución de su relación con el conocimiento. En M. Artigue, R. Douady, I Moreno, y P. Gómez (Eds.), Ingeniería didáctica en educación matemática. (pp. 34–56; 61–97). Bogotá, Colombia: Grupo Editorial Iberoamericano.        [ Links ]

Enriques, F.; Amaldi, V.; Guarducci, A.; Vitali, G. y Vailati, G. (1948). Fundamentos de la Geometría. (pp.15–55). Buenos Aires, Argentina: Iberoamericana.        [ Links ]

Faux, A. H. y Pratt, M. J. (1979). Computational geometry for design and manufacture, New York, USA: Wiley Press.        [ Links ]

Flanagan, D. L. y Hefner, O. V. (1967). Surface moulding new tool for the engineer. Aeronautics and Astronautics, 58–62.        [ Links ]

Franklin, W. R. y Barr, A. H. (1981). Faster calculation of superquadrics shapes. Computer graphics and applications. IEEE CG & A, 41–47.        [ Links ]

Jonassen, D. H. (1995). Computers as cogniteve tools: learning with technology. And not from technology. Journal of Computing in Higher Education, 6 (2), 40–73.        [ Links ]

Mosquera, J. C. (1996). La informática y el proceso de investigación matemático en la escuela. Educación Matemática, 8 (1), 14–21.        [ Links ]

Polya, G. (1954). Induction and Analogy in Mathematics. Princeton University        [ Links ]

Tall, D. (1985). Using computer graphics programs as generic organisers for the concepts image of differentiation. Proceedings of PME, 9 (1), 105–110.        [ Links ]

Terracini, A. (1941). Orígenes de algunos conceptos geométricos. Publicaciones del Instituto de Matemática, Universidad Nacional del Litoral, Argentina 3 (6), 158–199.        [ Links ]

Villani, V. (1995). "Le transformazione Geometriche Nella Scuola Secondaria Superiore". L'insegnamiento della Matemática e delle Scienze Integrate, 18A–18B, (6), 669–688.        [ Links ]

Villani, V. (1994). L'insegnamiento preuniversitario della geometría: molte domante, qualache risposta. L'insegnamiento della matematica e delle scienze integrate, 17A–17B (5), 439–458.        [ Links ]

Villani, V. (1994). L'insegnamiento della geometría nei nuovi programmi della scuola italiana. L'insegnamiento della matematica e delle scienze integrate, 17A–17B (6), 663–674.        [ Links ]