Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.9 no.2 Ciudad de México jul. 2006
¿Cómo diseñar el sistema de evaluación del aprendizaje en la enseñanza de las matemáticas?
Olga Pérez 1
1 Departamento de Matemáticas, Universidad de Camagüey, Cuba. E mail: olguitapg@yahoo.com
Fecha de recepción: Diciembre de 2003
Fecha de aceptación: Abril de 2006.
RESUMEN
En este trabajo se exponen los principales resultados de la tesis doctoral de la autora. Se ofrece una metodología para diseñar el sistema de evaluación en las matemáticas, considerando a la evaluación como una función del sistema de dirección del proceso enseñanza–aprendizaje; además, se definen los principios y regularidades para desarrollar la evaluación en las matemáticas. La metodología propuesta se aplicó a la materia Cálculo Integral para Ingeniería Eléctrica de la Universidad de Camagüey, Cuba, habiéndose realizado una experimentación que abarcó dos cursos escolares. Se demostró que con dicha metodología es posible aumentar la dedicación de los alumnos al estudio, el rendimiento académico y su calidad. Para determinar qué indicadores permiten probar la dedicación de los alumnos al estudio se efectuó una validación mediante el criterio de expertos.
PALABRAS CLAVE: Evaluación, aprendizaje, matemática, integrales.
ABSTRACT
In this work the main results of the doctoral thesis of the author are exposed. A methodology to design the evaluation system in mathematics is offered, considering to the evaluation as a function of the direction system of the teaching–learning process; besides, the principles and regularities for develop the evaluation in mathematics are defined. The proposed methodology was applied to the Integral Calculus course for electrical engineering of the University of Camagüey, Cuba, having carried out an experimentation that covered two school courses. It was shown that with this methodology it is possible to growth up the dedication of the students to the study, the academic performance and its quality. To determine which indicators permit to test the dedication of the students to the study, it was performed a validation by means of the criterion of experts.
KEYWORDS: Evaluation, learning, mathematics, integrals.
RÉSUMÉ
Dans ce travail s'exposent les principaux résultats de la thèse de doctorat de l'auteur. Une méthodologie est offerte afin de concevoir le système d'évaluation dans les mathématiques, qui considère l'évaluation comme une fonction du système de direction du processus enseignement–apprentissage; de plus, les principes et les régularités pour développer l'évaluation dans les mathématiques sont définis. La méthodologie proposée a été appliquée au Calcul Intégral pour les études d'Ingénieur Électrique de l'Université de Camagüey, au Cuba, ayant effectué une expérimentation qui comprenait deux années scolaires. Il fut démontré qu'avec une telle méthodologie il est possible d'augmenter la dévouement des élèves à l'étude, la performance académique et sa qualité. Afin de déterminer quels sont les indicateurs qui permettent de prouver le dévouement des élèves á l'étude, une validation s'est effectuée grâce au critère d'experts.
MOTS CLÉS : Évaluation, apprentissage, mathématiques, intégrales.
RESUMO
Este trabalho apresenta os principais resultados da tese de doutorado da autora. É oferecida uma metodologia para planejar um sistema de avaliação de matemática, considerando a avaliação como uma função do sistema de direção do processo ensino–aprendizagem; além de definir os princípios e regularidades para desenvolver a avaliação em matemática. A metodologia foi implementada em Cálculo Integral para Engenharia Elétrica da Universidade de Camagüey, Cuba, em experimentação que envolveu dois cursos escolares. Resultou que com tal metodologia é possível aumentar a dedicação dos alunos ao estudo, o rendimento acadêmico e sua qualidade. Para determinar quais indicadores permitiram provar a dedicação dos alunos ao estudo foi realizada uma validação mediante o critério de expertos.
PALAVRAS CHAVE: Avaliação, aprendizagem, matemática, integrais.
MARCO TEÓRICO
Aunque en este trabajo nos referiremos a la evaluación en las matemáticas, iniciaremos nuestro estudio teórico caracterizando al sistema de dirección del proceso enseñanza–aprendizaje (Pérez, 2000), ya que consideraremos a la evaluación como una de las funciones de dicho sistema, pero le damos un diferente matiz en la planificación y organización del proceso enseñanza–aprendizaje, con base en la teoría de la formación por etapas de las acciones mentales (Pérez, 2000; Talízina, 1992).
Las características fundamentales que integran el sistema de dirección del proceso enseñanza–aprendizaje son las siguientes:
1. Equifinalidad: Al enseñar podemos obtener los mismos resultados finales a partir de diferentes condiciones iniciales y a través de métodos variados. Es decir, no siempre las características del grupo de alumnos son las mismas y los métodos y medios para enseñar pueden ser muy variados; sin embargo, podemos obtener los mismos resultados. Por tanto, rechazamos la idea de que si el grupo de alumnos inicialmente tiene deficiencias, entonces obtendremos malos resultados evaluativos.
2. Entropía: Propiedad de este sistema que indica que la dirección del proceso enseñanza–aprendizaje se va por encima de las características individuales y colectivas de los alumnos; de ahí que el alumno, por lo general, apela a diversos recursos para lograr aprobar los exámenes y la asignatura. En este sentido, se dice que el sistema adquiere entropía negativa; es decir, el sistema de dirección puede funcionar y culminar la enseñanza de forma exitosa desde el punto de vista docente, mas el aspecto educativo no se cumple, con el cual surgen dificultades en la formación de los alumnos y disminuye la calidad de los resultados obtenidos. Tal situación hace que el sistema se sobrecargue y aparezca una ruptura entre la dirección de los aspectos docentes y los educativos, produciéndose una interacción negativa, pues el proceso continúa y los aspectos negativos no se superaron.
3. Sinergia: Implica que el funcionamiento interrelacionado de todos los elementos del proceso enseñanza–aprendizaje permite obtener mejores resultados que los alcanzados cuando dichos elementos actúan aisladamente. El logro de un efecto sinérgico positivo depende de la capacidad que tenga el maestro para que el proceso aproveche el potencial de dichas interacciones.
Las funciones del sistema de dirección en el proceso enseñanza–aprendizaje comprenden cuatro aspectos (Pérez, 2000)2:
Planificación: Es la función mediante la cual se proyecta el desarrollo del proceso, por lo que implica la precisión de los objetivos, el contenido, el sistema de tareas a desarrollar, los problemas, así como los métodos y medios de enseñanza para toda la asignatura y para cada una de las unidades que la componen. Aquí debe evidenciarse la combinación adecuada de diferentes tareas para el desarrollo de habilidades y se debe propiciar la asimilación consciente de los contenidos (Gagné, 1976).
Organización: Tiene como objetivo establecer un orden interno coherente en el proceso enseñanza–aprendizaje que permita su funcionamiento como una unidad, de ahí que le incumba la estructuración y el ordenamiento interno de los componentes personales del proceso (profesor–alumno) y los elementos del contenido de las asignaturas (conocimiento, habilidades, hábitos y valores). Ello propicia que se logren los objetivos propuestos de manera más eficiente; por tanto, la organización del proceso supone dotarlo de una estructura que le permita coordinar e integrar el sistema de tareas que se debe planificar.
Cabe señalar que en esta organización coexisten dos tipos de estructura: formal e informal. La formal es la que se hace teniendo en cuenta el sistema de tareas planificadas antes de comenzar a impartir las clases, mientras que la relación de las tareas no planificadas, que surgen atendiendo a las diferencias individuales de los alumnos, atañe a la informal. Debido a que ambas estructuras mantienen una continua interrelación que produce interdependencias, generalmente es imposible establecer una separación entre ellas.
Por otra parte, es necesario que la estructura formal sea sometida a las modificaciones oportunas para adaptarla a las condiciones cambiantes del grupo de estudiantes y de cada alumno en particular, de manera que se puedan incorporar a la estructura formal aquellos elementos de la informal que sean convenientes.
Gerencia: Se produce a través de la dinámica del proceso enseñanza–aprendizaje, y consiste en tomar decisiones para que el sistema se dirija en el sentido del cumplimiento de los objetivos. En la gerencia del proceso, la evaluación debe unir en forma interrelacionada dos aspectos: rectificar los objetivos aún no alcanzados y alcanzar nuevos objetivos, ya que el proceso enseñanza–aprendizaje es irreversible en su esencia.
Evaluación: Como consecuencia de la naturaleza abierta del proceso enseñanza–aprendizaje, es el complemento lógico de la planificación. Sus características dependen y, a la vez, influyen en la organización. La misión de la evaluación consiste en lograr que el sistema se mantenga dentro de una trayectoria previamente definida, por lo cual introduce las correcciones necesarias para evitar las desviaciones que se vayan produciendo, a fin de convertir en autorregulable el proceso enseñanza–aprendizaje. Asimismo, debe estar dirigida tanto al proceso de enseñanza como al de aprendizaje, lo cual supone, por un lado, el conocimiento de los aspectos didácticos y psicológicos que intervienen en el proceso, por otro, la búsqueda de sinergia entre las diferentes actividades del mismo (Baquero, R. 1997).
Desde este marco, la evaluación es cualitativa y cuantitativa. Además, está conformada por los diferentes sistemas de comunicación que caracterizan la relación alumno–maestro, donde cada maestro debe ser un activo investigador. Ésta es una necesidad definida por las propias exigencias de la enseñanza, que demanda el estudio integral del alumno, al igual que el análisis racional de las oportunidades y amenazas que se presentan –ya sea con relación a otras materias que cursa el alumno o al propio grupo de estudiantes–y de las fortalezas y debilidades del grupo y de cada estudiante en particular. A esto se le denomina gerencia del proceso, que conlleva a una evaluación sistemática y rigurosa en busca de los aspectos positivos y negativos y de una compatibilidad entre ambos (Carretero, 1993).
Todo ello induce a ver a la gerencia como interpretación de la evaluación y considerar a esta última como un proceso progresivo dentro del cual el profesor va obteniendo diversos indicadores sobre el proceso de asimilación de los alumnos. Cada uno de estos indicadores debe incidir en el proceso enseñanza–aprendizaje, sobre la base de un efecto sinérgico favorable (Álvarez, 2001).
Esta organización cualitativa de la evaluación del aprendizaje no rechaza la utilización de instrumentos evaluativos (como técnicas cuantitativas); también incluye la información que producen dentro de una lógica cualitativa. Por tanto, no trata de minimizar lo cuantitativo, sino que lo cualitativo y lo cuantitativo se fundan en busca de la calidad.
Ahora bien, la concepción y el diseño de la estrategia a seguir implica que se adecuen los elementos organizacionales de los sistemas de planificación y de evaluación, pero esto a la vez se halla condicionado por dichos elementos, ya que soportan la futura realización de la estrategia que el maestro se trace para la dirección (Martín, 1996).
Por otra parte, en este sistema es necesaria la búsqueda de un equilibrio global, referido a la sistematización entre su concepción e implementación, entre los aspectos psicosociales, cognoscitivos y educativos (Vigotsky, 1978), así como entre el enfoque y la metodología seguida para la dirección, donde la exigencia de sistematización de rigor y formalización debida a la complejidad del proceso no debe implicar una eventual rigidez (Pérez Gómez, 1993).
Luego, la búsqueda de la flexibilidad y capacidad de adaptación de la evaluación a las características del proceso sólo se puede encauzar mediante un enfoque contingente, el cual indica que no existirá una evaluación mejor que otra o un instrumento mejor que otro, sino que esto depende del grupo, el momento y circunstancia en que se desarrolla el proceso. Por tanto, deberá recoger en su seno las exigencias de una adaptación rápida y activa del proceso a la evolución del grupo (Morin, 2000).
Hasta aquí podemos concluir que la evaluación debe orientarse hacia lo que falta para el logro de los objetivos, no a si se cumplen o no. Como concreción del estudio teórico, se precisa el concepto de evaluación (Pérez, 2000) y las exigencias para que la evaluación del aprendizaje genere un efecto sinérgico.
Concepto de la evaluación del aprendizaje
La evaluación del aprendizaje es una función del sistema de dirección del proceso enseñanza–aprendizaje mediante el cual el profesor y los alumnos concientizan el grado de desarrollo de los alumnos y qué les falta aún para la consecución3 de los objetivos de aprendizaje.
Para esto, debemos considerar las exigencias para el logro del efecto sinérgico (Pérez, 2000):
1. Evaluación del proceso de ascensión al objetivo, no sólo el objetivo.
2. Evaluación bajo la consideración que el estado del estudiante puede cambiar.
3. Evaluación flexible estratégica, o sea, que exista la posibilidad siempre de mejorar una calificación.
4. Evaluación transparente para lograr identidad de valoración en los sujetos implicados.
5. Evaluación dirigida a las particularidades de los alumnos.
6. Evaluación de los procesos metacognoscitivos.
PRINCIPIOS PARA LA EVALUACIÓN DEL APRENDIZAJE EN MATEMÁTICAS (Pérez, 2000)
Principio 1. Búsqueda del efecto sinérgico resultante: La evaluación necesita aprovechar el potencial de estar presente en las interrelacciones de todos los elementos que intervienen en el proceso, a fin de lograr su funcionamiento exitoso.
Ahora bien, en la búsqueda del efecto sinérgico se debe manifestar la relación tareas–autopreparación–evaluación mediante el uso del libro de texto. Se debe garantizar, además, el sistema para evaluar cada unidad de la materia que se enseña, con la definición de los indicadores necesarios. Para ello, es importante precisar una planificación a largo plazo de las actividades de la evaluación y su adecuada distribución en el tiempo, evitando la existencia de periodos picos o descargados para el alumno, el desinterés de alumnos deficientes y la confianza excesiva en los alumnos talento.
Principio 2. Independencia de la(s) habilidad(es) a evaluar: En la resolución de las tareas matemáticas pueden estar involucradas varias habilidades. Por ejemplo, al trabajar en un problema el alumno debe tener la habilidad de modelarlo y resolverlo, mientras que el maestro debe tener bien claro qué habilidad quiere evaluar en ese momento: ¿modelar el problema o su resolución después de modelado? Aquí es muy importante el diseño de la tarea porque propicia el desarrollo de dicha habilidad y que en su evaluación no interfieran otras habilidades. Es por eso que para poder diseñar un sistema de evaluación se necesita tomar como punto de partida el sistema de tareas.
Principio 3. Control de las operaciones (habilidades) antes del producto final: Generalmente, en matemáticas el profesor presenta un contenido y evalúa desde un inicio los resultados finales de la tarea en cuestión. Por ejemplo, el maestro explica cómo calcular integrales indefinidas y las tareas iniciales que orientan al alumno son las de calcular integrales. Sin embargo, para que el alumno desarrolle la habilidad de calcular una integral indefinida, primero debe desarrollar las tocantes a identificar las características del integrando y a seleccionar el método más adecuado en cada caso, entre otras. De ahí que el maestro tenga que diseñar su sistema de tareas de forma que le permita controlar estas habilidades, antes de comprobar si el alumno calcula dicha integral (Martín, 1996).
Es por eso que en muchas ocasiones los maestros suelen decir: ¡El alumno Pedro no sabe calcular integrales indefinidas!, pero si les preguntamos cuál es la dificultad esencial que tiene este alumno, no pueden precisarla. O, por el contrario, si Pedro se acerca a su maestro y le dice que tiene dudas en el cálculo de la integral indefinida, el maestro le vuelve a explicar todo y orienta el cálculo de otro grupo de integrales, sin poder guiar adecuadamente a Pedro (Perrenoud, 2001).
Luego, se debe tener en cuenta que la asimilación de un contenido por el alumno involucra conocimientos básicos, así como habilidades lógicas, las propias de la matemática, las docentes, etc. Por esto, resulta necesario controlarlas con el fin de conocer la responsabilidad en el logro o no del objetivo; además, no es posible evaluar un objetivo sin que se hayan controlado antes las operaciones que lo conforman. Toda la evaluación está antecedida por controles; la evaluación no es el único elemento para dirigir un proceso de aprendizaje.
Este principio reviste mucha importancia, ya que en las matemáticas hay una tendencia entre muchos maestros de dirigir el proceso sólo a través de las evaluaciones, sin la realización de controles; es decir, se evalúa cuando ya no hay remedio de rectificar el proceso. Tal situación provoca que la evaluación pierda su calidad de función en el sistema de dirección del proceso docente–educativo. Se requiere determinar los indicadores necesarios para la evaluación, así como el diseño de un sistema de tareas que propicie el control por operaciones antes del producto final.
Principio 4. Coincidencia del maestro que evalúa con el maestro que desarrolló el proceso enseñanza–aprendizaje: El conocimiento que el profesor tiene sobre el desarrollo de sus alumnos es una condición necesaria para realizar su valoración. Si el maestro no conoce las características de los alumnos, así como de la continuidad y congruencia de todos los indicadores obtenidos en el sistema de evaluación, ésta queda reducida al dato que se obtiene con la aplicación de un instrumento, con lo que ésta es la vía principal para conseguir información. Por tanto, no es posible valorar el aprendizaje de los alumnos independientemente del conocimiento que de éste se tiene; hay que tener información sobre el proceso de aprendizaje y de su situación integral, del estado de necesidades de los alumnos y de los objetivos planteados.
El principio garantiza además el acercamiento que debe existir entre la valoración del alumno y la del maestro. Si la autovaloración que el alumno realiza de su trabajo no se contradice con la valoración del maestro, entonces se propicia el desarrollo de la independencia cognoscitiva del alumno. Esto es imposible si la dirección del proceso está a cargo de un maestro y la evaluación, en determinado momento, la desarrolla otro. Por tanto, la evaluación no es acreditación.
Principio 5. Unicidad valorativa en la evaluación: Este principio ha surgido de las irregularidades encontradas. Señala que la valoración del maestro debe estar en equilibrio con la valoración del alumno evaluado, y define que el acto evaluativo no termina con dar una calificación –por muy buena que sea–, sino cuando el alumno y el maestro estén convencidos de las deficiencias e insuficiencias en la consecución del objetivo. Es necesario determinar no sólo lo que hemos alcanzado sino, con base en las ideas de Vigotsky, ¿qué falta para llegar al objetivo propuesto? (a esto se le denomina zona de desarrollo próximo).
REGULARIDADES DE LA EVALUACIÓN DEL APRENDIZAJE EN MATEMÁTICAS
Todo el razonamiento efectuado anteriormente, los principios declarados y los resultados obtenidos en la fase de experimentación (la cual se expondrá más adelante) conducen a la necesidad de enunciar un conjunto de reglas y normativas, devenidas en regularidades (Pérez, 2000) que lleven al desarrollo de la evaluación del aprendizaje. Esto, conjuntamente con una metodología para el diseño de sistemas de evaluación, ayudará a materializar el aparato teórico.
Regularidad 1. El método de comprobación de la veracidad es la base de la autoevaluación: Los alumnos capaces de hacer una adecuada autoevaluación sobre el desarrollo de sus tareas crean un método propio para comprobar los límites de veracidad de sus respuestas; sin embargo, generalmente los alumnos se apropian de dichos métodos a través del maestro.
Regularidad 2. La evaluación es más efectiva cuando el criterio para ir a exámenes finales es cualitativo: El criterio de pase al examen final lo debe dar el maestro, no una suma cuantitativa de evaluaciones (aunque es la base para que el profesor decida), pues así los alumnos presentan sus exámenes bajo un estado psicológico más favorable, sobre todo los deficientes.
Regularidad 3. La discusión grupal sobre el resultado de las evaluaciones es una vía insustituible de aprendizaje.
Regularidad 4: Los diferentes instrumentos utilizados para desarrollar la evaluación del aprendizaje dejan de ser un fin en sí mismos: Estos instrumentos son la vía para obtener indicadores cuyo sentido va a depender de la interacción entre diferentes factores que tienen lugar en cada momento de la actividad cognoscitiva. Con ello, dejan de ser un fin en sí mismos para convertirse en un momento que expresa la continuidad del sistema general donde se desarrollan; es decir, se relacionan estrechamente a lo largo de todo el proceso.
Si el instrumento se considera como la vía para obtener indicadores cuyo sentido resulta de la información que brindan en integridad con toda la información anterior, entonces el estudiante aumenta su trabajo independiente, el desarrollo de tareas colectivas y su valoración. En este sentido, el alumno conoce que la información que el profesor recoge del instrumento no es fundamental, ya que también incide su participación activa en todo el proceso.
Por tanto, el carácter cualitativo de la evaluación del aprendizaje no se definirá por el carácter cualitativo de los instrumentos utilizados, sino por toda la información obtenida. Esto lleva a afirmar que el valor de cada examen no estará en su concepción, sino en su capacidad de poder brindar información compatible con otros instrumentos ya aplicados. Así, toda la evaluación se deberá organizar en una relación de congruencia y continuidad de forma individualizada, donde puede ocurrir que, al configurarse la información para el tratamiento diferenciado de los estudiantes, sea necesario aplicar nuevos instrumentos.
La esencia de un resultado no es inherente a él, sino al de diferentes interpretaciones que se van integrando en diferentes niveles, con lo que su sentido se va constituyendo en momentos diferentes del proceso de evaluación (Hernández, 1998).
PREMISAS FUNDAMENTALES PARA EL DESARROLLO DE LA EVALUACIÓN DEL APRENDIZAJE EN LAS MATEMÁTICAS
Con base en lo anterior, donde ha sido descrito el fundamento teórico de la evaluación del aprendizaje en las matemáticas, resumiremos en tres premisas (Pérez, 2000) los aspectos que se deben considerar para desarrollar la evaluación del aprendizaje en las matemáticas. Éstas se expresan de acuerdo con tres variables fundamentales e independientes.
1. Una concepción de la evaluación que busque un equilibrio en su significación, tanto para los alumnos como para los maestros. Esto presupone:
a) Evaluación centrada en el alumno y sus particularidades.
b) Concebir la evaluación hasta la metacognición y aún hasta la metavaloración, considerando que la evaluación termina cuando los sujetos implicados constatan lo que falta para cumplir el objetivo.
2. La evaluación del sistema de dirección del proceso docente–educativo como elemento para el logro de un efecto sinérgico. Esto presupone:
a) Evaluar el proceso de ascensión al objetivo y no sólo el objetivo, determinando lo que falta para lograrlo.
b) Evaluación flexible estratégica, que siempre permite la posibilidad de mejorar una calificación.
c) Evaluación de la comprobación de la veracidad en los resultados.
3. La evaluación debe estar basada en un sistema de tareas. Esto presupone:
a) Evaluar a través de las unidades que comprenden las clases.
b) Controlar las etapas de asimilación (Vigotsky, 1979) en la consecución del objetivo final.
c) Tener en cuenta hacia dónde dirigir el control en las etapas de asimilación, según la teoría de la formación por etapas de las acciones mentales, que se puede consultar en Pérez (2000) y Talízina (1992).
¿CÓMO DEBE EL MAESTRO DISEÑAR EL SISTEMA DE EVALUACIÓN DEL APRENDIZAJE EN LA ENSEÑANZA DE LAS MATEMÁTICAS?
Hasta aquí queda claro, por una parte, que si consideramos a la evaluación como una función de la dirección del proceso enseñanza–aprendizaje, estará presente desde que se concibe cómo se desarrollará tal proceso (planificación, organización y ejecución); por otra, que no es lo mismo evaluación y exámenes.
De acuerdo con la tercera premisa, se sugiere evaluar a través de las unidades temáticas de cada semestre. Por tanto, cuando el maestro diseñe su sistema de evaluación no debe limitarse a precisar el número de exámenes que aplicará en el semestre; esta nueva concepción sugiere que el sistema de evaluación debe estar conformado por los sistemas de evaluación de cada una de las unidades que integran la materia; éstos, a su vez, están constituidos por un sistema de tareas (Chamoso, 2001).
En esta propuesta, el diseño utiliza a la unidad como célula organizativa de toda la materia, por lo cual en las primeras cinco etapas propuestas nos referiremos a la unidad. La cuarta etapa reafirma la utilización en la evaluación del sistema de tareas, mientras que la quinta y la sexta manifiestan la evaluación en forma general, dirigida a comprobar la identidad del resultado con el objetivo. Además, la metodología requiere que se defina una planificación estratégica de toda la materia (Molina, 1998), cuya esencia sea el análisis racional de las relaciones entre los elementos que intervienen en el proceso para que el sistema esté en equilibrio y se logren las funciones a él asignadas.
Las etapas para el diseño son:
1. Análisis de los objetivos.
2. Estructuración del contenido de la unidad.
3. Determinación de las cadenas de clases.
4. Diseño del sistema de tareas de la unidad.
5. Diseño del sistema de evaluación de la unidad.
6. Diseño del sistema de evaluación de la materia.
¿ Qué hacer en cada etapa ?
1. En los objetivos debe analizarse:
• Cuáles son los conocimientos, habilidades, hábitos y valores que exigen (el contenido de la enseñanza).
• El nivel de asimilación de los contenidos, lo cual atañe a si se quiere que el alumno llegue sólo a familiarizarse con los contenidos, que los reproduzcan, que puedan resolver problemas (nivel productivo) o que llegue al nivel creativo. Al precisar el nivel de asimilación podemos orientar adecuadamente el proceso enseñanza–aprendizaje.
• El nivel de profundidad de los contenidos, que está estrechamente relacionado con los métodos de la ciencia que se utilizarán. Si el objetivo dice que el alumno calcule integrales indefinidas, entonces cada maestro impartirá los métodos de cálculo que estime convenientes; luego, el nivel de profundidad precisará en el objetivo los métodos y los tipos de funciones que se considerarán en el integrando, entre otros aspectos, o sea, los métodos de la ciencia a emplear.
Este análisis permite saber lo que vamos a evaluar en la unidad y en la materia, así como el contenido de dicha evaluación.
2. La estructuración del contenido de cada unidad.
En esta etapa se deben deslindar las bases orientadoras de la acción (Talízina, 1992) con que trabajará el alumno. Su importancia radica en que el contenido refleja la lógica de la ciencia; la evaluación, la lógica del proceso enseñanza–aprendizaje. Por tanto, la organización del contenido busca la unidad entre la lógica del proceso enseñanza–aprendizaje, la de la ciencia y la de la asimilación de los alumnos, mientras que la evaluación tiene que ser la expresión de dicha unidad.
El desarrollo del proceso (organización), la lógica de la matemática como ciencia y la lógica de cómo una persona asimila no pueden ir por separado porque sería un tormento para el alumno. Se debe prestar mucha atención a cómo se va a estructurar el contenido para lograr esta unidad, pues influye en el alumno tanto en lo cognitivo como en lo afectivo y, por ende, en la formación de su personalidad.
3. Determinación de las cadenas de clases
Debido a que los tipos de clases en las matemáticas están caracterizados por los tipos de habilidades que en ella se desarrollan, la evaluación queda condicionada a este aspecto y adopta su forma, como expresión del objetivo a alcanzar en la unidad. Ahora bien, en el diseño de esta cadena no sólo se debe considerar la autopreparación que el estudiante necesita llevar a cabo entre clase y clase, sino también que en cada clase no se evalúa lo mismo, ya que esto depende de la relación entre la etapa de asimilación y los objetivos de la unidad.
Para el diseño de una cadena hay que tener en cuenta los diferentes tipos de clases que abarcará: conferencias (C), clases prácticas (CP), laboratorios (L) y seminarios (S), además de la autopreparación (AP). Los tipos de clases y el orden de la cadena se definirán considerando el tránsito por cada una de las etapas del proceso de asimilación (Talízina, 1992) y los niveles de asimilación del contenido (Pérez, 2000).

4. Diseño del sistema de tareas de la unidad
Esta etapa es esencial para el diseño del sistema de evaluación, pues en la tarea se manifiestan todos los elementos y leyes del proceso enseñanza–aprendizaje, con lo que se hace potencial el efecto sinérgico y el cumplimiento de las funciones de la evaluación para mantener el equilibrio del proceso.
Al hacer el diseño del sistema de tareas se debe relacionar, en cada cadena de clases, la etapa de asimilación para la que se diseña dicha tarea; de este análisis tienen que surgir las tareas específicas para cada actividad.
5. Diseño del sistema de evaluación de la unidad
Para el diseño del sistema de evaluación, se tomará como base la siguiente cadena de clases, muy típica en la enseñanza de las matemáticas:
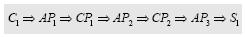
El diseño, que puede servir como modelo para cualquier unidad de clases de las matemáticas, consiste en precisar hacia dónde dirigir la evaluación en cada una de las clases y de la autopreparación, teniendo en cuenta el tránsito por las etapas de asimilación y los niveles de asimilación del contenido. Su explicación detallada se muestra a continuación:
Diseño del sistema de evaluación de la unidad
C1: Conferencia donde se debe cumplir la motivación e introducción del nuevo contenido, que se designa como Base Orientadora de la Acción (BOA). Aquí, la evaluación debe orientarse a:
• Motivar al alumno.
• Valorar si los alumnos describen los elementos de la BOA.
AP1 Es la autopreparación que forma al estudiante para las acciones externas materializadas; la evaluación debe estar dirigida a:
• Valorar si los alumnos aplican la BOA.
• Valorar si los alumnos identifican en la BOA las diferentes acciones y sus operaciones.
• Realizar la valoración por operaciones de la BOA.
CP1: Primera clase práctica, que debe estar dirigida al tránsito por la etapa de las acciones externas materializadas. A la evaluación le compete:
• Realizar el control por operaciones e introducir gradualmente el control del producto final de las acciones.
• Valorar si las acciones se desarrollan desplegadas.
• Valorar el grado de despliegue de las acciones.
AP2: Tránsito de la etapa de las acciones materiales externas a la del lenguaje externo, que debe ser conducido por la segunda autopreparación. Concierne a la evaluación:
• Valorar si se justifica cada operación desarrollada.
• Valorar si el alumno puede resolver la tarea por varios métodos, justificando cada caso.
• Conducir al alumno a que varíe algunas magnitudes del problema en cuestión para valorar si puede justificar los cambios que se producen en su resolución.
• Introducir gradualmente el control del producto final.
CP2: Consiste en la etapa del lenguaje externo, que debe cumplirse en esta clase práctica. La evaluación debe estar dirigida a:
• Valorar que se justifique cada una de las operaciones.
• Valorar que se concientice el grado de despliegue.
• Valorar la comprobación de las respuestas obtenidas, en forma externa.
• Valorar, en caso de que se reduzca el grado de despliegue, si se mutilan acciones.
• Valorar si se desarrollan las acciones por diferentes métodos.
• Controlar el producto final de forma externa.
AP3: Es la tercera autopreparación, que debe propiciar el tránsito a la etapa del lenguaje interno. La evaluación se debe circunscribir a valorar:
• Si el grado de despliegue de las acciones es cada vez menor.
• Si se justifica la reducción de las operaciones.
• Si no se mutilan acciones en la resolución de los problemas presentados.
• Si se es capaz de iniciar la resolución de problemas por etapas intermedias de todo el proceso de resolución.
S1: Seminario que debe propiciar el tránsito a la etapa del lenguaje interno, donde la evaluación tiene que valorar:
• Si se concientiza el grado de despliegue y se tiende a reducir de forma externa, incluyendo la realización de algunas operaciones de forma interna.
• Si se comprueban las respuestas de forma interna.
• Si se dominan las acciones esenciales de los conceptos de forma interna.
• El control del producto final de forma interna.
6. Diseño del sistema de evaluación de la materia
Esta etapa requiere ser valorada como una planificación estratégica donde se aprecien, de manera sistemática, las debilidades y fortalezas de la materia, así como las oportunidades y amenazas que presenta el desarrollo de todo el proceso enseñanza–aprendizaje.
El diseño del sistema de evaluación de la materia inicia con un estudio sobre la relación que hay entre los objetivos de cada unidad y los de la materia. Tal análisis nos permite conocer, de acuerdo con los niveles de asimilación y profundidad de los objetivos de la materia, el grado de ejercitación necesario de las habilidades implicadas, que pueden ser de adquisición, fijación y solidificación. Los grados de ejercitación se necesitan precisar desde el inicio de la materia, ya que es imposible lograr la fijación o la solidificación de una habilidad en el propio desarrollo de la unidad donde se imparte el contenido relacionado con ella.
El grado de ejercitación de una habilidad en una materia nos indica el nivel de repetición con el que debe tratarse en la evaluación. Por ejemplo, el cálculo de la integral indefinida es una habilidad a desarrollarse en la primera unidad, pero para lograr su solidificación se considera necesario evaluarla en otras tres unidades, independientemente de que éstas no tengan como objetivo su desarrollo, ya que esa habilidad es la base para el desarrollo de los temas.
Por tanto, los niveles de repetición de una habilidad en el sistema de evaluación están estrechamente relacionados con su grado de ejercitación –adquisición, fijación y solidificación–, lo cual se muestra en el Cuadro 2:

Posteriormente, con una matriz de carga se precisan los objetivos4 a evaluar en cada unidad (véase Cuadro 3), de acuerdo con el nivel de profundidad de los objetivos y el grado de ejercitación que se requiere. Además, la matriz de carga permite decidir en cada unidad qué objetivos de otras unidades deben ser evaluados y qué grado de ejercitación debe ser valorado para cada uno de ellos. Un ejemplo es la materia Cálculo Integral para Ingeniería Eléctrica de la Universidad de Camagüey, Cuba, que contiene nueve unidades.
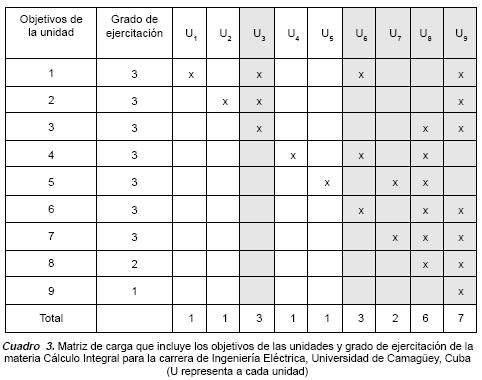
El análisis de esta matriz de carga permite inferir que en la unidad 3 deben evaluarse tres objetivos temáticos, pero el grado de ejercitación a valorar en cada uno de ellos no es el mismo, mientras que en las unidades 1 y 2 sólo se evalúan sus objetivos temáticos, y un análisis similar ocurre en las unidades 4 y 5. Las columnas sombreadas indican las unidades que deben evaluar objetivos de otras unidades.
Por otro lado, se puede observar que los objetivos de las unidades 1 a la 7 exigen el grado de ejercitación tres, lo cual indica que la habilidad debe llegar a solidificarse en el alumno. Por ejemplo, para lograr la solidificación del objetivo de la unidad número 1 se tiene que evaluar en las unidades 1, 3, 6 y 9.
Cuando se explicó el diseño de la cadena de clases, quedó claro que la evaluación debe estar dirigida hasta valorar la etapa de las acciones internas, bajo los principios de la evaluación aquí definidos. Entonces, en el tema donde se precise evaluar varios objetivos de diferentes unidades, para los diferentes niveles de ejercitación hay que definir trabajos de control parcial (exámenes), como es el caso de las unidades 3, 6, 7, 8 y 9. Las columnas están sombreadas para indicar que en dichas unidades se deben aplicar exámenes.
También cabe destacar que si en el objetivo de una unidad el grado de ejercitación requerido es de solidificación, esa unidad no puede ser la última en desarrollarse. Por tanto, hay que revisar la organización del contenido, pues es imposible evaluar la solidificación de una habilidad en la unidad donde se adquiere.
FASE DE APLICACIÓN DE LA PROPUESTA
Ésta es una fase de generalización y perfeccionamiento de nuestra investigación, la cual se experimentó en la materia Cálculo Integral para Ingeniería Eléctrica de la Universidad de Camagüey, Cuba, bajo condiciones naturales (Lewin, 1992; Elliot, 1994), según la metodología propuesta de seis etapas.
Etapa No. 1. Análisis de los objetivos
Los objetivos fundamentales de esta materia (Calderón, 1994) son los siguientes:
1. Caracterizar e interpretar los conceptos de la teoría del cálculo integral mediante problemas teóricos y prácticos que conduzcan a un modelo matemático, interrelacionando, diferenciando y calculando los diferentes tipos de integral e interpretando matemática, física y técnicamente los resultados obtenidos, seleccionando el modelo integral y, en ocasiones, modelando la función a integrar con el uso de tablas y de las nuevas tecnologías, a un nivel productivo.
2. Contribuir a la formación de la concepción científica del mundo mediante la comprensión de los conceptos de integrales, que desarrollen hábitos de proceder reflexivamente y de evaluar los resultados de su trabajo, al igual que la utilización de diversa literatura. Contribuir a la capacidad de razonamiento y de pensar lógicamente, así como a la formación computacional de los estudiantes.
A partir de estos objetivos generales, para cumplir con el principio de la independencia de la habilidad a evaluar, se determinaron las habilidades a desarrollar por los alumnos:
• Identificar los diferentes tipos de integrales a partir de las características esenciales del concepto: tipo de función y del dominio de integración.
• Aplicar las propiedades de la integral.
• Calcular las integrales definidas utilizando los teoremas fundamentales, propiedades y métodos de integración.
• Determinar la convergencia o divergencia de una integral impropia.
• Calcular las integrales múltiples, de línea y de superficie reduciéndolas a una integral definida mediante integrales iteradas, parametrizaciones o utilizando los teoremas de Green, Gauss–Ostrogradski o Stokes.
• Calcular magnitudes geométricas y del electromagnetismo empleando el modelo integral adecuado y, en ocasiones, la función a integrar.
• Modelar problemas e interpretar matemática, física y técnicamente los resultados obtenidos, seleccionando el modelo integral y, en ocasiones, modelando la función a integrar.
Etapa No. 2. Estructuración del contenido de la unidad
El diseño de la asignatura se basó en el método estructural–funcional, considerando como invariante de estos contenidos la suma de Riemann cuando la norma de la partición tiende a cero. Desde el punto de vista de las habilidades a desarrollar, para propiciar el pensamiento lógico de los alumnos seleccionamos como habilidades generalizadoras la identificación y la clasificación; una para la teoría y otra para la práctica.
La habilidad de clasificación ofrece a los alumnos la posibilidad de ubicar técnicamente cada uno de los objetos analizados. Éste es un proceso general en la teoría del cálculo integral, ya que ante cada problema el alumno debe hacer un análisis teórico para clasificar el tipo de integral a utilizar, valorando el cumplimiento de las condiciones suficientes y si es posible calcularlas por los métodos estudiados.
Para estructurar el contenido con la utilización de estas invariantes, se recurrió a las siguientes Bases Orientadoras de la Acción (BOA):
I. BOA para definir las integrales, donde cada nueva integral se introduce con la siguiente lógica:
• Establecer las características de la región y de la función.
• Definir conjunto contenido nulo, partición y norma de la partición.
• Selección de un punto arbitrario en cada elemento de la partición.
• Formación de la suma integral.
• Paso al límite de la suma cuando la norma de la partición tiende a cero.
Esta BOA se utilizó de manera que, independientemente del dominio y de la función, plantea un límite que, si existe, es considerado como el resultado de una cierta operación que se realiza sobre una función f definida y acotada sobre el dominio D). A ésta se le denomina operación de integración, según Riemann, mientras que el resultado, llamado integral, revela la esencia de la integral como proceso de aproximación.
II. BOA para el desarrollo de la teoría:
• Establecer la condición necesaria y suficiente para la integrabilidad de una función.
• Instaurar la relación entre la continuidad y la integrabilidad de la región de integración.
• Propiedades de las integrales.
III. BOA para la práctica:
• Identificar las características de la región de integración.
• Distinguir las características del integrando.
Para que estas BOA realmente contribuyan al cumplimiento de los efectos instructivos y educativos de la evaluación, deben formarse cuando se desarrolle la unidad correspondiente a integrales definidas y ser retomadas dentro del mismo tema en diversas formas (clases prácticas, extraclases, seminarios, etc.). De este modo, al ir definiendo los demás tipos de integrales mediante su uso, se podrá lograr una mayor interacción con los alumnos, quienes ganarán en independencia y tendrán más motivación en el desarrollo de la teoría, lo cual propiciará el desarrollo de su autovaloración. La tercera BOA, que se emplea para el cálculo, le permite al alumno identificar y clasificar cada tipo de integral, si cumple o no las condiciones; de esta forma le indica la vía a seguir para calcularla.
Al tener en cuenta lo anterior, el contenido se estructuró con un orden que definió las nueve unidades de la materia:
1. Integrales indefinidas.
2. Integrales definidas.
3. Integrales de líneas.
4. Curvas, sólidos, proyecciones y sistema de coordenadas.
5. Integrales dobles.
6. Integrales triples.
7. Integrales de superficie.
8. Teoremas de Stokes, divergencia y Green.
9. Aplicaciones de las integrales.
Para el cálculo de primitivas en las integrales indefinidas se siguió un proceso general (ver Anexo), el cual permitió que la evaluación no estuviera dirigida a valorar si se dominaba cada método en específico, sino el proceso general para integrar. A fin de lograr esto, el tema se diseñó utilizando el proceso general de integración, mientras que la evaluación iba dirigida a valorar si se hacían diferencias entre las diferentes técnicas de reexpresión del integrando y las posibles formas de integrar (en este último punto se puso énfasis en las generalidades).
Por ejemplo, una de las técnicas de reexpresión del integrando es el cambio de variables. Aquí, se valoraron las operaciones que incluía esta acción: definir qué sustitución se hará, calcular el diferencial de la variable a sustituir, y sustituir la variable y el diferencial en la integral. Lo que quedaba por hacer para calcular dicha integral atañía al cuarto paso del proceso general de integración, donde la solución general debía corresponder con la variable inicial que se le dio al alumno en la integral que estaba calculando. Dicha cuestión no estaba contenida en las fases del método, sino concernía la autovaloración que el alumno hacía de la respuesta obtenida.
En las integrales definidas se impartió el contenido de forma tal que fueran clasificadas en propias e impropias, pero no se dio una clase sobre las impropias y otra sobre las propias. Así, desde el principio se pudo valorar si el alumno clasificaba una integral definida en propia o impropia y la justificación de su respuesta.
Al definir las integrales de líneas, se consideró que, entre las características de la región de integración, debía precisarse que la curva tenía que estar dada en forma paramétrica y no incluir esto en el método de cálculo. Después, se le haría ver al alumno que el método para calcular integrales de líneas es el método del cambio de variables, un asunto que debe comprender para advertir la sistematicidad de lo que estudia y no como un método diferente o nuevo.
En la unidad 4, tocante a geometría, se valoró el desarrollo de habilidades en el análisis de la regularidad de una región; en determinar si un sólido era de revolución o no; en conocer las superficies típicas de cada sistema de coordenadas; en representar –planos, y en estudiar la variación de las variables en correspondencia con el sistema de coordenadas más conveniente según las superficies típicas, todo esto junto con la representación de sólidos.
Debido a que estos aspectos, al ser vistos tradicionalmente en integrales dobles y triples, ha hecho que se pierda su esencia al aplicarlos en los elementos geométricos, consideramos tratarlos como una unidad independiente, pues con su valoración en esta unidad se propició el trabajo de las integrales múltiples y de superficie.
Para esta unidad de geometría se utilizó la siguiente BOA para analizar la variación de las variables, que contribuyó a vincular la lógica de la estructuración del contenido con la del proceso de desarrollo del alumno:
1. Identificar las superficies que componen la región.
2. Determinar si es, o no, un sólido de revolución.
3. Elegir el sistema de coordenadas más conveniente.
4. Determinar la regularidad de la región
5. Determinar la variación de las variables.
Con la utilización de esta BOA, se consideró importante valorar en el cuarto punto el desarrollo de habilidades en la utilización del – plano5 para determinar la variación de las variables, por ser el método que utilizarán los alumnos posteriormente al determinar los límites de integración en las integrales triples.
En las integrales dobles y triples, para plantear las iteradas se siguió la BOA:
1. Determinar la variación de las variables.
2. Plantear las iteradas.
En este caso, el segundo paso quedó totalmente simplificado con el tratamiento que se le dio en geometría a la determinación de la variación de las variables, donde el alumno, sin saberlo, ya estaba dando los límites de integración de una integral triple. Nótese que el primer paso era precisamente la BOA de la unidad de geometría para analizar la variación de las variables; por tanto, el proceso de evaluación de dicha unidad debía tener un efecto sinérgico positivo para desarrollar exitosamente la unidad de integrales triples y dobles.
Asimismo, era importante que en esta unidad se aprovechara el significado geométrico que tenía el Jacobiano, al ser la razón de proporcionalidad de área o volumen en la transformación de coordenadas.
Las integrales de superficies, a pesar de que tienen su secuencia lógica en cuanto a las regiones de integración, desvían al estudiante de los procedimientos de cálculo de las dobles y triples. Por ello, las propusimos al final.
Para la conferencia de los teoremas de la unidad 8, que relacionan los diferentes tipos de integrales, se partió de problemas concretos a fin de que, mediante su análisis –similar a la demostración de cada teorema– se llegara a los enunciados de dichos teoremas, terminando por resolver los problemas planteados.
Y por último, aunque al definir cada tipo de integral también se hacía necesario definir las aplicaciones más inmediatas a ellas, propiamente las que caracterizaban cada tipo de integral, había un grupo de aplicaciones comunes a todas que variaban según la región de integración (masa, centroide, momento, etc.), las cuales debieron ser tratadas; de igual manera, se atendió a la relación entre el cálculo de longitud de arco por definidas y líneas y otros.
Por tanto, el enfoque dado a la evaluación para las aplicaciones estuvo dirigido a que el alumno fuera capaz de seleccionar correctamente el modelo integral más conveniente para resolver un determinado problema, así como identificar los casos donde pudiera distinguirse más de un modelo integral, haciendo hincapié en los rasgos esenciales para la selección correcta. Estas aplicaciones, más comunes, se propuso vincularlas al trabajo investigativo de los alumnos, donde mediante búsquedas parciales las estudiaran y establecieran sus relaciones para que posteriormente enfrentaran la resolución de problemas.
Otro de los elementos que se consideró en las aplicaciones fue usar la estructura estable (Pérez, 2000), de carácter general de la integral, sobre el cálculo de magnitudes físicas y geométricas. Esto llevó al estudiante a valorar que, cuando el integrando está formado por diferenciales de una magnitud o por valores puntuales de ésta mediante el diferencial de la magnitud, la integral representa el valor de esa magnitud en los límites de integración dados. Tratar las aplicaciones de la integral de esta forma permite dirigir la evaluación sobre las aplicaciones a sus elementos esenciales.
De forma general, en la estructuración del contenido se propuso utilizar racionalmente las BOA particulares para cada tipo de integrales, de forma que se pudieran establecer las articulaciones entre ellas, utilizando términos comunes.
Concerniente a los tipos de clases, se realizaron actividades integradoras en el tema de aplicaciones y después de éste, con el objetivo de evaluar la interrelación de los contenidos, de el nivel de generalización y de profundización. Dichas actividades, que se efectuaron en las modalidades de taller, seminarios y mesas redondas, propiciaron la revisión de una amplia bibliografía de cálculo integral y la discusión sobre los enfoques que diversos autores le dan a este contenido.
En resumen, la evaluación contempló la valoración de:
• Invariante general:
• Habilidades generalizadoras: Identificación y clasificación.
• Bases orientadoras de las acciones (generales): Para definir integrales, para el desarrollo de la teoría, para la práctica y para el proceso general de integración.
• Bases orientadoras de las acciones (particulares): Comprendió los métodos del cambio de variables, de descomposición de una fracción racional en fracciones simples y de integración por partes, el uso de las tablas de integración y la determinación de la variación de variables en el plano o el espacio, en cualquiera de los sistemas de coordenadas.
• Acción esencial de la asignatura: Transformar cada integral a una integral definida.
• Acciones esenciales a desarrollar: Determinar si una integral definida es propia o impropia; si la función dada no es integrable; parametrizar curvas; establecer la variación de variables en el plano o el espacio, en cualesquiera de los sistemas de coordenadas, así como identificar, en una integral de superficie, sobre qué proyecciones es posible precisar la variación de las variables para los límites de integración de la integral doble a obtener.
• Acciones esenciales generales: Identificar si una función es integrable o no, clasificar a qué tipo de integral corresponde y transformar cada integral en una integral definida.
Estas acciones esenciales generales y particulares le permitirán al profesor encaminar el trabajo de evaluación en la etapa de las acciones externas materializadas y la de las acciones externas.
Etapa No. 3. Determinación de las cadenas de clases
Por razones de espacio, en este artículo sólo mostraremos cómo se diseñó la cadena de clases de la unidad correspondiente a integrales indefinidas, que incluyó una conferencia y tres clases prácticas.
Etapa No. 4. Diseño del sistema de tareas de la unidad
Aquí consideramos relevante la utilización del proceso general de integración porque permite darle un enfoque sistémico al tema, siendo más fácil para el aprendizaje y la evaluación. El enfoque que se presenta en los textos para calcular integrales hace pensar en que deben aprenderse "muchos" métodos, sin que exista un hilo conductor entre ellos. Por tal motivo, dirigimos nuestros esfuerzos a que hubiera la lógica de la ciencia, de la asimilación y del contenido, y que la evaluación buscara la unidad de esa lógica.
Antes de diseñar el sistema de tareas, determinamos la BOA para el proceso general de integración con el fin de identificar qué acciones tenía involucradas; después elaboramos una tarjeta de estudio (Anexo 1) que reflejó el proceso general de integración. Los alumnos la utilizaron en las primeras etapas del proceso de asimilación, mientras que la evaluación se orientó a que los alumnos valoraran el proceso general de integral y el tratamiento que le dan los autores, clasificando varios métodos. A partir de esto, se les indicó a los alumnos que hicieran un trabajo de búsqueda bibliográfica donde tuvieran que valorar esta situación. El sistema de tarea que se conformó fue el siguiente:
• Dado un grupo de integrales indefinidas:
a) Identificar el modelo del integrando.
b) Identificar en cuál de ellas se puede, reexpresar el integrando, aplicando las propiedades de la integral indefinida.
c) Calcular. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Dado un grupo de integrales indefinidas:
a) Identificar el modelo del integrando f (x) y g (x).
b) Identificar en cuál de ellas se puede reexpresar el integrando utilizando completamiento de cuadrados, simplificación de fracciones, multiplicando y dividiendo por el conjugado pitagórico o descomponiendo fracciones racionales en fracciones simples.
c) Calcular cada caso. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Dado un grupo de integrales indefinidas:
a) Identificar las que tengan en el modelo del integrando una función de la forma F(g(x))g'(x).
b) ldentificar f (x) y g (x).
c) Clasificar la fórmula de las tablas de integrales inmediatas con la que se puede calcular.
d) Calcular.
• Dado un grupo de integrales indefinidas:
a) Identificar las que tengan en el modelo del integrando una función de la forma u dv .
b) Identificar quién es u y quién dv .
c) Aplicar la fórmula de integración por partes.
d) Calcular. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Dado un grupo de integrales indefinidas:
a) Identificar las que tengan en el modelo del integrando una función racional.
b) Identificar si la fracción racional es propia o impropia.
c) Descomponer la fracción racional en fracciones simples.
d) Calcular la integral. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Dado un grupo de integrales indefinidas:
a) Identificar en cuáles de ellas es necesario hacer sustitución y/o cambio de variables.
b) Indicar qué sustitución o cambio de variables se haría.
c) Calcular la integral. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Dado un grupo de integrales indefinidas:
a) Identificar en cuáles de ellas es necesario completar el diferencial para obtener una integral inmediata generalizada.
b) Completar el diferencial.
c) Calcular. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Dado un grupo de integrales indefinidas:
a) Identificar el modelo del integrando.
b) Reexpresar el integrando.
c) Integrar. Si utiliza las tablas de integrales, especifique que fórmula empleó.
• Tareas con las características anteriores, pero exigiendo la justificación de las acciones realizadas.
• Calcular un grupo de integrales indefinidas.
• Dado un grupo de ecuaciones diferenciales:
a) Transformar, si es necesario, la ecuación a la forma M(x)dx+N(y)=0 .
b) Calcular en la forma
• Resolver un grupo de ecuaciones diferenciales, con condiciones iniciales dadas.
• Las demás tareas estarán referidas a la resolución de problemas sobre diversas aplicaciones de la integral indefinida.
Etapa No. 5 Diseño del sistema de evaluación de la unidad
Con este primer grupo de tareas es posible dirigir la evaluación, en las primeras clases prácticas y la autopreparación, a que valore el desarrollo práctico de cada una de las operaciones involucradas en el proceso general de integración. Así, en la etapa materializada el alumno se enfrenta a este grupo de tareas con la tarjeta de estudio, donde aparecen todos los elementos esenciales del proceso de integración y los modelos de las acciones a ejecutar, lo cual permite valorar si se asimila la BOA dada a un nivel reproductivo.
Posteriormente, en la etapa del lenguaje externo la evaluación se basa en un sistema de tareas con estas mismas características, pero encaminado fundamentalmente a ejercitar el racionamiento teórico, de forma que la acción se transforma de la lógica de la acción a la lógica del concepto, donde el alumno pueda justificar lo que hizo y porqué. Dicha etapa también puede retomar las tareas realizadas anteriormente –donde se orienta cada operación a desarrollar– y analizar en cada una las integrales que no correspondían con las que se había pedido calcular, explicando el procedimiento seguido en cada caso.
En lo concerniente a la etapa del lenguaje interno, la evaluación se basó en tareas concretas para el cálculo de integrales, sin especificar en su enunciado las posibles acciones a realizar.
Obsérvese que las tareas descritas enfatizan en las acciones esenciales a desarrollar: identificación y clasificación. Por tanto, en el proceso de asimilación de este contenido resulta importante evaluar si el alumno sabe identificar el modelo del integrando y si clasifica la(s) técnica(s) para reexpresar el integrando, así como la fórmula para calcular la integral.
En razón de que ésta es una unidad básica fundamental dentro del cálculo integral y de la disciplina matemática para Ingeniería Eléctrica, la evaluación parcial debe estar dirigida a las acciones esenciales de identificación y clasificación, al igual que a la asimilación del proceso general de integración.
Etapa No. 6. Diseño del sistema de evaluación de la materia
Para analizar el diseño del sistema de evaluación de la materia, se determinó el grado de ejercitación que requería cada objetivo temático, en correspondencia con su nivel de asimilación y de profundidad, mientras que para ahondar en la matriz de carga (ver Cuadro 3) se tuvo en cuenta, por una parte, la interrelación entre los diferentes temas; por otra, que muchas habilidades contenidas en algunos objetivos de las unidades constituían acciones u operaciones para los objetivos de otras unidades. En este caso, se tomó a dichos elementos como base para definir el grado de ejercitación que requería cada tema.
Del estudio de esta matriz, se planteó que en el sistema de evaluación general de la materia había que aplicar exámenes parciales en las unidades 3, 6, 7, 8 y 9. Por ejemplo, en la unidad 7, tocante a integrales de superficies, el examen tendrá que orientarse al cálculo de este tipo de integrales y de las dobles; sin embargo, los aspectos del tema de geometría, de las integrales definidas e indefinidas que involucra el cálculo de la integral de superficie no deberán tener un alto grado de dificultad, pues no son habilidades esenciales a evaluar. Con esto, se pone de manifiesto el principio de la independencia de la habilidad a medir.
Para la evaluación final, el alumno deberá saber cuáles son los objetivos fundamentales que se tendrán en cuenta, los cuales serán dados en función de la solución de problemas. En este caso, se orientó a lo siguiente:
• Caracterizar los conceptos y propiedades e interpretación geométrica de los diferentes tipos de integrales.
• Establecer las relaciones entre los diferentes tipos de integrales, desde el punto de vista del cálculo, aplicaciones y teoría.
• Modelar y resolver problemas que conduzcan a ecuaciones diferenciales de variables separables, donde se interprete la integral indefinida como operación inversa a la derivación.
• Identificar si una función es integrable en una región de integración dada, clasificando el tipo de integrales.
• Resolver problemas sobre área, trabajo, longitud de una curva, volumen, flujo de un fluido, masa, momentos, centros de gravedad y centroides, entre otros.
VALIDACIÓN EXPERIMENTAL DE LOS RESULTADOS
Aquí, partimos de la siguiente hipótesis: Si se diseña un sistema de evaluación del aprendizaje fundamentado en el modelo teórico que concibe a la evaluación del aprendizaje como una función del sistema de dirección del proceso enseñanza–aprendizaje, cumpliéndose sus principios y regularidades, y considerando que la evaluación esté referida a un sistema de tareas en función de las etapas del proceso de asimilación, entonces se logrará aumentar la dedicación de los alumnos al estudio, el rendimiento académico y su calidad.
Después, se llevó a cabo una validación, sustentada en el criterio de expertos, con el objetivo de determinar los indicadores para determinar la variable independiente adecuada dedicación al estudio.
Para aplicar el criterio de los expertos sobre la base de los aspectos teóricos y metodológicos propuestos en torno a la evaluación del aprendizaje, se eligió una muestra de 12 especialistas, partiendo de un rango mínimo de competencia que se obtuvo al determinar un coeficiente de competencia según el uso del método DELPHI, aplicado como determinación perspectiva de la operacionalización de una variable y sus posibles dimensiones.
La muestra de expertos se seleccionó teniendo en cuenta los siguientes indicadores: años de experiencia docente, competencia, creatividad, disposición a partir de la encuesta, capacidad de análisis, pensamiento y vínculo con la enseñanza de la materia, en este caso las matemáticas. Respecto a la confección de los indicadores a medir en el test aplicado a los expertos contextualizados, se atendieron a los siguientes aspectos:
• Concreción del modelo teórico que se propone.
• La evaluación como función del sistema de dirección, que dé equilibrio a los elementos del proceso enseñanza–aprendizaje y logre la sinergia del proceso.
• La evaluación basada en un sistema de tareas a nivel de tema.
Todos estos aspectos presuponen que se logrará una adecuada dedicación al estudio por los estudiantes.
Al determinar la matriz de rango en cada pregunta del test, se apreciaron las siguientes técnicas estadísticas:
• Grado de concordancia de los expertos para el conjunto de todas las preguntas, utilizando el coeficiente de concordancia de Kendall.
• La concordancia entre medidas de grupos de expertos, empleando el coeficiente de rango par de Spearman.
• Determinación de la categoría o grado de adecuación más frecuentes, según la opinión de los expertos en cada pregunta.
Sobre la base de la apreciación de las técnicas anteriores, se constató que el coeficiente de concordancia de Kendall en cada pregunta arrojó resultados por encima de δ=0,82 (P<0,05) lo cual evidenció un alto grado de concordancia en los criterios emitidos por los expertos. Resultados similares se obtuvieron con el coeficiente de Spearman.
La categoría o grado de adecuación más frecuente fue el de ADECUADO, por lo cual consideramos que los indicadores uso de la bibliografía en calidad y cantidad, horas de estudio, presentación de trabajos en jornadas científicas estudiantiles, calidad de las tareas extraclases e interés por la materia resultaron pertinentes para validar el modelo teórico y la metodología de evaluación del aprendizaje que se propone en este trabajo.
Para el experimento se realizó un estudio longitudinal y prospectivo, donde la variable independiente fue manipulada por el investigador; de este modo, tanto el grupo de control como el experimental se abordaron en el siguiente período (Ander–Egg, 1993).
La muestra incluyó a 169 alumnos, divididos en dos grupos: uno de control y otro experimental:
• Grupo de control: Cálculo integral para el primer año de Ingeniería Eléctrica, Universidad de Camagüey, Cuba, cursos 92–93 y 93–94.
• Grupo experimental: Cálculo integral para el primer año de Ingeniería Eléctrica, Universidad de Camagüey, Cuba, cursos 95–96 y 96–97.
Un total de 169 alumnos pertenecían al grupo de control y 59 al experimental.
ANÁLISIS DE LOS RESULTADOS
Para el procesamiento estadístico se utilizó Microsoft Excel y Systat. El primero sirvió para introducir los datos; el segundo, para procesarlos.
En el análisis sobre las notas del examen final, se utilizó la prueba de X 2 para dos muestras independientes de la estadística no paramétrica. Además, se efectuaron varias comparaciones entre los cursos de control y los experimentales; la última se hizo entre los dos grupos experimentales para ver si existían diferencias significativas entre sus resultados.
Las calificaciones se consideraron como 5 (excelente), 4 (bien), 3 (regular) y 2 (mal).
Comparación 1
Grupo de control: curso 93–94
Grupo experimental: curso 95–96
H0: No hubo diferencia significativa entre la proporción de alumnos con calificaciones de 4 y 5 entre el curso 93–94 y el 95–96.
H1: El grupo del curso 95–96 tuvo una mayor proporción de alumnos con calificaciones de 4 y 5 que el del curso 93–94.
Sea α =0.05 y el número total de alumnos de la muestra 79.
En este caso, X 2 = 9.09 y la probabilidad de ocurrencia conforme a H0 para de X 2 > 9.09 con grado de libertad 1 fue p < 0.0005. En vista de que esta p fue mucho menor que α =0.05, se rechazó H0 y se aceptó H1, por lo cual se concluyó que hubo una mayor proporción de alumnos con calificaciones de 4 y 5 en el curso 95–96.
Comparación 2
Grupo de control: curso 93–94
Grupo experimental: curso 96–97
H0: No hubo diferencia significativa entre la proporción de alumnos con calificaciones de 4 y 5 entre el curso 93–94 y el 96–97.
H1: El grupo del curso 96–97 tuvo una mayor proporción de alumnos con calificaciones de 4 y 5 que el del curso 93–94.
Sea α =0.05 y el número total de alumnos de la muestra 76.
En este caso, X 2 = 13.55 y la probabilidad de ocurrencia conforme a H0 para de X 2 > 13.55 con grado de libertad 1 fue p < 0.0005. En vista de que esta p fue mucho menor que α =0.05, se rechazó H0, en un nivel de significación de 0.001, y se aceptó H1, por lo que se concluyó que hubo una mayor proporción de alumnos con calificaciones de 4 y 5 en el curso 96–97.
Comparación 3
Grupo de control: curso 92–93
Grupo experimental: curso 96–97
H0: No hubo diferencia significativa entre la proporción de alumnos con calificaciones de 4 y 5 entre el curso 92–93 y el 96–97.
H1: El grupo del curso 96–97 tuvo una mayor proporción de alumnos con calificaciones de 4 y 5 que el del curso 92–93.
Sea α =0.05 y el número total de alumnos de la muestra 90.
En este caso, X 2 = 8.55 y la probabilidad de ocurrencia conforme a H0 para de X 2 > 8.55 con grado de libertad 1 fue p < 0.0005. Como esta p fue mucho menor que α =0.05, se rechazó H0, en un nivel de significación de 0.001, y se aceptó H1, por lo que se concluyó que hubo una mayor proporción de alumnos con calificaciones de 4 y 5 en el curso 96–97.
Comparación 4
Grupo de control: curso 92–93
Grupo experimental: curso 95–96
H0: No hubo diferencia significativa entre la proporción de alumnos con calificaciones de 4 y 5 entre el curso 92–93 y el 95–96.
H1: El grupo del curso 95–96 presentó una mayor proporción de alumnos con calificaciones de 4 y 5 que el del curso 92–93.
Sea α =0.05 y el número total de estudiantes de la muestra 93.
En este caso, X 2 = 3.78 y la probabilidad de ocurrencia conforme a H0 para de X 2 > 3.78 con grado de libertad 1 fue p < 0.0005. En vista de que esta p fue mucho menor que α =0.05, se rechazó H0, en un nivel de significación de 0.001, y se aceptó H1, concluyéndose que hubo una mayor proporción de alumnos con calificaciones de 4 y 5 en el curso 95–96.
Comparación 5
Grupo experimental: curso 96–97
Grupo experimental: curso 95–96
H0: No hubo diferencia significativa entre la proporción de alumnos con calificaciones de 4 y 5 entre el curso 96–97 y el 95–96.
H1: El grupo del curso 96–97 tuvo una mayor proporción de alumnos con calificaciones de 4 y 5 que el del curso 95–96.
Sea α =0.05 y el número total de alumnos de la muestra 59.
En este caso, X 2 = 0.47 y la probabilidad de ocurrencia conforme a H0 para de X 2 > 0.47 con grado de libertad 1 fue p < 0.15. Por ello, se aceptó H0, pues esta p es mayor que α =0.05, concluyéndose que no hubo diferencias significativas entre la proporción de alumnos con calificaciones de 4 y 5 en ambos cursos.
CONCLUSIONES
Estadísticamente se comprobó, por un lado, que los resultados del examen final de la materia siempre fueron mejores en los grupos donde se aplicó la metodología; por otro, que no hubo una diferencia significativa entre los dos cursos donde se aplicó la metodología, a pesar de que eran grupos diferentes.
Con base en la distribución porcentual de los diferentes cursos, al considerar la participación de alumnos en jornadas científicas para estudiantes, pudo comprobarse que en los cursos donde no se aplicó la metodología hubo una participación fue de 3.2% y 4.16%, mientras que cuando se aplicó los porcentajes de participación aumentaron al 93.5% y 100%. Por ello, concluimos que la participación en trabajos científicos estudiantiles fue mejor en el grupo experimental.
La asistencia al Centro de Gestión de Información fue mejor en los grupos experimentales, ya que el 93.5% y el 100% de los alumnos asistió más de dos veces semanales, mientras que en los grupos de control sólo asistieron el 3.2% y el 6.25%.
En los grupos de control, el 96.7% y 93.7% estudiaron la materia utilizando el libro de texto, mientras que en los experimentales el 93.5% y 92.9 % utilizaron más de cuatro libros relacionados con cálculo integral. Esto nos permitió concluir que el uso de la bibliografía fue significativo cuando se aplicó la metodología.
Por último, se comprobó que el número de horas de estudio semanales en la mayoría de los alumnos de los grupos experimentales aumentó más de 20 horas (67.8% y 85.71 %); sin embargo, esto no sucedió en el grupo de control (3.2% y 2.1%).
A partir de los resultados expuestos, se pudo concluir que con la aplicación de la metodología:
• Se obtienen mejores resultados en la evaluación final de la materia.
• Se logra la participación de los alumnos en jornadas científicas para estudiantes, con trabajos de búsqueda parcial.
• Se aumenta el número de horas de estudio semanales y la asistencia al Centro de Gestión de Información.
• Se logra un mejor uso de la bibliografía relacionada con el tema de estudio.
De igual manera, aumentó la dedicación de los alumnos al estudio, el rendimiento académico y su calidad, lo cual consistió en el objetivo fundamental de nuestra investigación.
Tras haber realizado este experimento, la metodología ha sido aplicada a otras materias de matemáticas en la Universidad de Camagüey, Cuba, con efectos similares.
Los resultados de este trabajo, que merecieron el Premio Provincial de la Academia de Ciencias de Cuba en el año 2001, se han utilizado como material docente en las materias de Didáctica de las Matemáticas correspondientes a las maestrías en Ciencias de la Educación y en Enseñanza de las Matemáticas, de la Universidad de Camagüey, Cuba, así como en la maestría en Ciencias de la Educación de la Universidad Autónoma de Nuevo León, México.
BIBLIOGRAFÍA
Alcalá, M. (1996). Enseñanza de la matemática y niveles operatorios. En Actas de las VIII Jornadas para el Aprendizaje y la Enseñanza de las Matemáticas, JAEM (pp. 51–56). Salamanca, España: Sociedad Castellano–Leonesa de Profesorado de Matemáticas (Burgos). [ Links ]
Álvarez, J. (2001). Evaluar para conocer, examinar para excluir. Madrid, España: Morata. [ Links ]
Ander–Egg, E. (1993). Técnicas de investigación social. México: McGraw–Hill. [ Links ]
Asiala, M., Brown, A., DeVries, D., Dubinsky, E., Mathews, D. y Thomas, K. (1996). A framework for research and curriculum development in undergraduate mathematics education. En Jim Kaput, Alan H. Schoenfeld & Ed Dubinsky (Eds.), Research in Collegiate Mathematics Education II (pp. 1–32). USA: American Mathematical Society. [ Links ]
Aznárez, M. (1977, mayo). Ni ogro, ni aburridas. El País Semanal. Madrid, España. [ Links ]
Baquero, R. (1997). Vigotsky y el aprendizaje escolar. Buenos Aires, Argentina: Aique. [ Links ]
Berger, P. (1978). La construcción social de la realidad. Buenos Aires, Argentina: Amorrortu. [ Links ]
Buendía, L., Clas, P. y Hernández, F. (1998). Métodos de investigación en psicopedagogía. Madrid, España: McGraw–Hill. [ Links ]
Cabañas, M. G. (2000). Los problemas... ¿Cómo enseño a resolverlos? México: Grupo Editorial Iberoamérica. [ Links ]
Calderón, R. (1994). Perfeccionamiento de la enseñanza del cálculo integral en Ingeniería Mecánica (informe de investigación). La Habana, Cuba: Instituto Superior Politécnico José Antonio Echeverría. [ Links ]
Carretero, M. (1993). Constructivismo y educación. Buenos Aires, Argentina: Aique. [ Links ]
Chamoso, J. (2001). ¿Hacia unas nuevas matemáticas? Salamanca, España: Universidad de Salamanca. [ Links ]
De la Peña, J. (2002). Algunos problemas de la educación en matemáticas en México. México: Siglo XXI–UNAM. [ Links ]
Delgado, J. R. (1999). La resolución de problemas matemáticos. Dos aspectos fundamentales para lograr su eficiencia: la estructuración sistémica de los contenidos de estudio y el desarrollo de habilidades generales matemáticas. Tesis de doctorado, Instituto Superior Politécnico José Antonio Echeverría, La Habana, Cuba. [ Links ]
Díaz, F., Barriga, A. y Hernández, G. (2001). Estrategias docentes para un aprendizaje significativo. Interpretación constructivista. México: McGraw–Hill. [ Links ]
Dubinsky, E. (1995). Assessment in one learning theory based approach to teaching. En Bonnie Gold, Sandra Z. Keith & William A. Marion (Eds.), Assessment Practices in Undergraduate Mathematics (pp. 229–244). USA: The Mathematical Association of America. [ Links ]
Dubinsky, E. (1991). Reflective abstraction in advanced mathematical thinking. En David Tall (Ed.), Advanced Mathematical Thinking (pp. 95–126). Kluwer, Holand: Kluwer Academic Publishers. [ Links ]
Dubinsky, E. & Tall, D. (1991). Advanced mathematical thinking and the computer. En David Tall (Ed.), Advanced Mathematical Thinking (pp. 231–250). Kluwer, Holand: Kluwer Academic Publishers. [ Links ]
Elliot, J. (1994). La investigación–acción en la educación. Madrid, España: Morata. [ Links ]
Gagné, M. R. (1976). Principios para la planificación de la enseñanza. México: Diana. [ Links ]
Gimeno, J. (2001). Educar y convivir en la cultura global. Madrid, España: Morata. [ Links ]
Goldin–Meadow, S. (2003). Gestos oyendo: cómo nuestras manos nos ayudan a pensar. Cambridge, USA: Harvard University Press (en prensa). [ Links ]
Goldin–Meadow, S., et al. (1999). Lo que las manos del adulto le dicen a la mente del estudiante sobre matemática. El Periódico de Psicología Educativa, 91, 720–730. [ Links ]
Guevara Niebla, G. (1991, junio). México: ¿un país de reprobados? Nexos (pp. 33–44), México. [ Links ]
Hernández, H. (1998). Vigosky y la estructuración del conocimiento matemático en cuestiones de didáctica de la matemática. Rosario, Argentina: Homo Sapiens Ediciones. [ Links ]
Lewin, K. (1992). La investigación–acción y los problemas de las minorías. En AA.VV., La investigación–acción participativa. Inicio y desarrollo (pp. 13–25). Madrid, España: Ed. Popular, Biblioteca de Educación de Adultos, 6. [ Links ]
Lewin, K. (1992). La investigación acción participativa. Madrid. [ Links ]
Martín, M. (1996). Planeación, administración y evaluación de la educación. México: ITESM. [ Links ]
Molina B., Z. (1998). Planeamiento didáctico. San José, Costa Rica: EUNED. [ Links ]
Moll, L. (1990). Introduction to the book Vigotsky and education. Cambridge, USA: Cambridge University Press. [ Links ]
Morin, E. (2000). Los siete saberes necesarios para la educación del futuro. París, Francia: UNESCO. [ Links ]
Ochoa, R. (1999). Evaluación pedagógica y cognición. Bogotá, Colombia: McGraw–Hill. [ Links ]
Ochoa, R. (1994). Hacia una pedagogía del conocimiento. Bogotá, Colombia: McGraw–Hill. [ Links ]
Ovide, M. (1998). Pedagogía y universidad. Rosario, Argentina: Homo Sapiens Ediciones. [ Links ]
Pérez, O. L. (2000). La evaluación del aprendizaje como elemento del sistema de dirección del proceso de enseñanza aprendizaje en la enseñanza de las matemáticas para ciencias técnicas. Tesis de doctorado, Universidad de Camagüey, Cuba. [ Links ]
Pérez Gómez, A. I. (1993). Comprender y transformar la enseñanza. Madrid, España: Morata. [ Links ]
Perrenoud, (2001). La construcción del éxito y del fracaso escolar. Madrid, España: Morata. [ Links ]
Pozo, J. (2000). La psicología cognitiva y la educación científica. Madrid: España: Facultad de Psicología, Universidad Autónoma de Madrid. [ Links ]
Pozo, J. (1999). La solución de problemas. Buenos Aires, Argentina: Santillana. [ Links ]
Pozo, J. (1997). La crisis de la educación científica. ¿Volver a lo básico o volver al constructivismo?. Alambique. Didáctica de las Ciencias Experimentales, 14, 91–104. [ Links ]
Roger, C. (1975). Libertad y creatividad en la educación. Buenos Aires, Argentina: Paidós. [ Links ]
Rosas, S. (2001). Piaget, Vigostky y Maturana. Constructivismo a tres voces. Buenos Aires, Argentina: Aique. [ Links ]
Salinas, J. (1997). Enseñanza flexible, aprendizaje abierto. Las redes como herramientas para la formación. Edutec, 10. Obtenido de http://www.uib.es/depart/gte/revelec10.html. [ Links ]
Santos Trigo, Luz M. (1994). La resolución de problemas en el aprendizaje de las matemáticas. México: Departamento de Matemática Educativa, Cinvestav (Cuadernos de Investigación, 28). [ Links ]
Schoenfeld, A. (1992). Learning to think mathematically: problem solving, metacognition and sense making in mathematics. En D. Grouws (Ed.), Handbook for Research on Matematics Teaching and Learning (pp. 334–370). New York, USA: Macmillan. [ Links ]
Schoenfeld, A. (1985). La enseñanza de la matemática a debate. Madrid, España: Ministerio de Educación y Ciencia. [ Links ]
Shuell, T. J. (2001). Learning theories and educational paradigms. En N. J. Smelser & P. B. Baltes (Eds.), International Encyclopedia of the Social and Behavioral Sciences (Vol. 13, pp. 8613–8620). Amsterdam, Holland: Elsevier. [ Links ]
Stenhouse, L. (1987). La investigación como base de la enseñanza. Madrid, España: Morata. [ Links ]
Talízina, N. F. (1992). La formación de la actividad cognoscitiva de los estudiantes. México: Ángeles. [ Links ]
Vigotsky, L. (1978). Mind in society: the development of higher psychological processes. Cambridge, USA: Harvard University Press (versión en español: El desarrollo de los procesos psicológicos superiores (trad. Silvia Furió)). Barcelona, España: Crítica. [ Links ]
2 Queremos precisar que, aunque clasificamos en cuatro funciones la dirección del proceso enseñanza–aprendizaje en una materia, hay una constante interacción entre ellas, por lo cual su separación es prácticamente inexistente.
3 Obsérvese que se destaca "en la consecución de los objetivos", lo que no debe confundirse con "el logro de los objetivos", como tradicionalmente se describe en los conceptos dados por diversos autores sobre evaluación.
4 Los objetivos de la asignatura y las unidades temáticas se describen en la fase de aplicación de la propuesta.
5 El θ – plano es empleado en el libro de texto para Ingeniería en Cuba sobre integrales múltiples, cuando se integra sobre una región que representa un sólido de revolución, en coordenadas cilíndricas o esféricas.
ANEXO PROCESO GENERAL DE INTEGRACIÓN
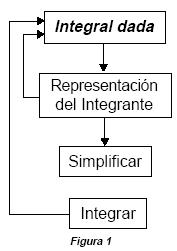
Técnicas para reexpresar el integrando
1. Aplicar las propiedades de las integrales.
2. Desarrollar y simplificar algebraicamente el integrando, utilizando:
• Completamiento de cuadrados.
• Simplificación de fracciones.
• Descomponer fracciones racionales en fracciones simples.
• Multiplicar y dividir por el conjugado pitagórico.
3. Completamiento del diferencial.
4. Sustitución yo cambio de variables.
El integrando puede estar dado por una función del tipo:
• Elemental.
• F(g(x))g(x).
• Racional.
• u dv .
• Con primitivas no elementales.
Las posibles formas de integrar son:
• Uso de colección de integrales inmediatas.
• Uso de las integrales inmediatas generalizadas.
• Método de integración por partes.
• Uso de las tablas de integrales.