Servicios Personalizados
Revista
Articulo
Indicadores
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.9 no.2 Ciudad de México jul. 2006
Una conceptualización de límite para el aprendizaje inicial de análisis matemático en la universidad
Sonsoles Blázquez 1 Tomás Ortega 1 Stella Gatica 2 Julio Benegas 2
1 Departamento de Análisis Matemático y Didáctica de la Matemática, Universidad de Valladolid, España. E–mail: ortega@am.uva.es
2 Facultad de Ingeniería y Ciencias Económico–Sociales, Universidad Nacional de San Luis, Villa Mercedes, Argentina. E–mail: nimberti@fices.unsl.edu.ar
Fecha de recepción: Febrero de 2005
Fecha de aceptación: Abril de 2006
RESUMEN
En el presente trabajo se contrasta la conceptualización métrica de límite, dada por Weierstrass, que se utiliza tradicionalmente en la docencia, con su conceptualización como aproximación óptima, dada por Blázquez y Ortega (2002), para establecer cuál de las dos es más sencilla y apropiada para la docencia–aprendizaje inicial de tal noción. Se describe el análisis hecho a los datos proporcionados por dos trabajos de exploración y, finalmente, se enuncian sus conclusiones, corroborando que la segunda conceptualización es más sencilla que la primera y, por tanto, la más apropiada para los aprendizajes iniciales 3.
PALABRAS CLAVE: Límite, conceptualización, métrica, aproximación óptima, proceso, docencia, aprendizaje, representación.
ABSTRACT
In the present work is contrasted the metric conceptualization of limit, given by Weierstrass, that is utilized traditionally in the teaching, with its conceptualization as optimum approximation, given by Blázquez and Ortega (2002), to establish which of the two is simpler and appropriate for the initial teaching–learning of such notion. It is described the analysis of the data provided by two exploration works and, finally, its conclusions are enunciated, corroborating that the second conceptualization is simpler than the first one and, therefore, the most appropriate for the initial learning.
KEYWORDS: Limit, conceptualization, metric, approximation, optimum process, teaching, learning, representation.
RÉSUMÉ
Dans ce travail, la conceptualisation métrique de limite, donnée par Weierstrass et qui s'utilise traditionnellement dans l'enseignement, est contrastée avec sa conceptualisation comme approximation optimale, donnée par Blázquez et Ortega (2002), afin d'établir laquelle des deux est la plus simple et appropriée pour l'enseingement–apprentissage initial de cette notion. L'analyse faite aux données obtenues grâce à deux travaux d'exploration est décrite, et, finalement, ses conclusions sont énumérées, corroborant ainsi que la seconde conceptualisation est plus simple que la première et, pour autant, la plus appropriée pour les apprentissages initiaux.
MOTS CLÉS : Limite, conceptualisation, métrique, approximation, optimale, processus, enseignement, apprentissage, représentation.
RESUMO
Neste trabalho é comparado o conceito de métrica de limite, dada por Weierstrass, que se utiliza tradicionalmente na docência, com seu conceito como aproximação ótima, dada por Blázquez y Ortega (2002), para estabelecer qual delas é mais simples e apropriada para o ensino e aprendizagem inicial de tal noção. É apresentado a análise feita dos dados proporcionados por dois trabalhos de pesquisa e, finalmente, se enunciam suas conclusões, corroborando que o segundo conceito é mais simples que o primeiro e, portanto, a mais apropriada para a aprendizagem inicial.
PALAVRAS CHAVE: Limite, conceituar, métrica, aproximação, ótima, proceso, docência, aprendizagem, representação.
INTRODUCCIÓN
Esta investigación forma parte de un proyecto mucho más amplio, que da continuidad a los trabajos de Blázquez y Ortega (1997, 1999, 2000, 2001a, 2001b y 2002), sobre todo a este último, donde se establece una nueva conceptualización de límite funcional (definición que surge en el proceso de formación del concepto) basada en la idea de aproximación óptima, que no requiere del formalismo presente en la conceptualización métrica de Weierstrass. Ni estos trabajos ni los que sirvieron como punto de partida para los estudios de Blázquez y Ortega (Tall y Vinner, 1981; Cornu, 1983; Robinet, 1983; Sierpinska, 1985 y 1987; Sánchez, 1997; entre otros) tratan de esclarecer cuál de estas dos conceptualizaciones es la más sencilla y, en consecuencia, la que puede ser más adecuada para que se utilice en los currículos de educación secundaria y en el primer curso de las carreras de ingeniería o similares.
Por tanto, el objetivo fundamental de esta investigación, que ocupa una metodología cualitativa, es conocer si la conceptualización métrica de límite funcional es más fácil o más difícil que la de límite funcional como aproximación óptima. Con base en la labor de Blázquez y Ortega, así como en el trabajo experimental que se está desarrollando con alumnos de Ingeniería, se hicieron dos exploraciones de aula para llegar a dicho objetivo.
La primera exploración se llevó a cabo en la Universidad Nacional de San Luis (Argentina) con estudiantes de la Facultad de Ingeniería de Villa Mercedes, mientras que la segunda en la Universidad de Valladolid (España) con los estudiantes del Curso de Aptitud Pedagógica (CAP). Los alumnos habían egresado de las licenciaturas en Matemáticas, Física, Ingenierías, Estadística y Económicas–Empresariales, y durante su formación universitaria, de cinco años, recibieron una amplia formación matemática; por tanto, sus respuestas debían tener un rango de validez destacado. En la primera exploración se trabajó sobre las propias conceptualizaciones, y en la segunda se confrontaron ambas mediante las correspondientes demostraciones que surgen al aplicarlas para establecer el teorema del signo y el de unicidad del límite.
Los documentos producidos en una y otra experimentación se analizan en el marco teórico de Duval, donde se considera al concepto de sistema semiótico como un sistema de representación que puede ser un registro de representación si permite tres actividades cognitivas:
• La presencia de una representación identificable como una representación de un registro dado.
• El tratamiento de una representación, que es la transformación de la representación dentro del mismo registro donde ha sido formada.
• La conversión de una representación, que consiste en la transformación de la representación en otra de otro registro, en la que se conserva la totalidad o parte del significado de la representación inicial. Tal actividad cognitiva es diferente e independiente a la del tratamiento.
Según Duval (1998, pp. 15–21), para comprender un concepto es necesaria la coordinación de los diferentes registros de representación, pues con uno solo (mono–registro) no se obtiene la comprensión integral del concepto. Sin embargo, la conversión entre registros no se realiza en forma espontánea, a menos que se trate de representaciones congruentes entre el registro de partida y el de llegada.
Esta teoría plantea que la comprensión integral de un concepto se encuentra basada en la coordinación de al menos dos registros de representación; tal coordinación se pone de manifiesto por medio del uso rápido y la espontaneidad de la conversión cognitiva, logrando articulaciones entre diferentes registros de representación semiótica. En palabras del propio Duval:
En los sujetos, una representación puede funcionar verdaderamente como representación, es decir, darle acceso al objeto representado, sólo cuando se cumplen dos condiciones: que dispongan de al menos dos sistemas semióticos diferentes para producir la representación de un objeto, de una representación, de un proceso... y que puedan convertir "espontáneamente" de un sistema semiótico a otro las representaciones producidas, sin siquiera notarlo.
Nosotros atenderemos a la espontaneidad y dejaremos tiempo para que los alumnos piensen las respuestas. Así está reflejado en las entrevistas grabadas, donde ciertas intervenciones hacen referencia a períodos de pensamiento de los alumnos.
De acuerdo con este marco teórico, el principal objetivo de la entrevista consistió en averiguar hasta qué punto los alumnos entendían ambas conceptualizaciones, por lo cual tuvieron que explicar sus interpretaciones en el paso al registro gráfico. Aunque estamos hablando de dos definiciones, hay una correspondencia asociativa entre sus unidades significantes elementales, que se establecerá después y, a tenor de la evolución del concepto, no debe ser obvia. Nosotros pensamos que las dificultades de aprendizaje que presentan estas unidades para los alumnos pueden ser indicadores de la dificultad de cada definición.
LA CONCEPTUALIZACIÓN
Una revisión histórica del concepto de límite, siguiendo las investigaciones de Cornu (1983) y Robinet (1983), nos permite considerar tres etapas que se diferencian básicamente por la idea de límite que subyace en ellas. Ahora bien, en la evolución del concepto se distingue la necesidad de explicitarlo y formalizarlo, que se utiliza de manera implícita desde la época griega, y no llega a su forma actual hasta el siglo XIX, en parte para validar algunos resultados obtenidos y en parte para demostrar otros más generales.
Etapa 1. Hasta los métodos infinitesimales
En esta etapa no es posible hablar de límite de funciones, pero sí aparece implícito en algunos métodos para resolver, básicamente, problemas cinemáticos y de tangentes, determinación de extremos y cálculo de cuadraturas. Sin pretender mencionar a todos los autores, destacamos las siguientes aportaciones: el método de exhausción de Eudoxo de Cnido (360 a. C.); las cuadraturas de Arquímedes (siglo III a. C.); el estudio de las series numéricas de Nicole de Oresme, alrededor de 1360; los métodos para el cálculo de tangentes de extremos de Fermat (1601–1665); el de las tangentes de Barrow (1630–1677); el de los infinitésimos de Kepler (1571–1630), y el de los indivisibles de Cavalieri (1598–1647), con el se puede dar por terminado este período.
Etapa 2. La supremacía del cálculo
Este período inicia en la segunda mitad del siglo XVII y se extiende al XVIII. Los matemáticos de esta época se esfuerzan en el tratamiento de procesos infinitos y, siguiendo el nuevo cálculo creado por Newton (1642–1727) y Leibniz (1646–1716), consiguen separar este cálculo de la geometría, aunque no aciertan a separar los métodos analíticos de los algebraicos. De las aportaciones relacionadas con el concepto de límite, sobresalen los descubrimientos de Newton (1712) sobre series infinitas, fluxiones y diferencias, así como los trabajos de Leibniz sobre el cálculo diferencial y series infinitas. Boyer (1999, pp. 500–501), en la sección 1 del libro I que conforma el tratado Philosophiae naturalis principia matematica, señala que Newton, al intentar definir el límite de una función, postula dos lemas:
Lema I: Cantidades, y la razón de cantidades, que en cualquier intervalo finito de tiempo convergen continuamente a la igualdad, y que antes del final de dicho tiempo se aproximan una a la otra más que cualquier diferencia dada, se hacen finalmente iguales.
Lema VII: La razón última del arco, cuerda y tangente, cualquiera de ellos respecto de cualquier otro, es la razón de igualdad.
Jaques Bernoulli (1654–1705) y Jean Bernoulli (1667–1748) continúan la obra de Leibniz; Jean descubre la regla de L'Hospital y la serie de Taylor, publicada por Brook Taylor en 1715. Leonhard Euler (1707–1883) integra el cálculo diferencial de Leibniz y la teoría de las fluxiones, dando lugar al "análisis" como área de la matemática que estudia los procesos infinitos. Él basa su obra en el concepto de función y, afirma Boyer (1999, p. 558), siguiendo la formulación de Leibniz, define a la función como cualquier expresión analítica, finita o infinita, formada con la cantidad variable y números o cantidades constantes.
Sin duda, el desarrollo del nuevo cálculo propició que D'Alembert (1717–1783), oponiéndose a Leibniz y Euler, pensara que la notación de las diferenciales tenía que ser sustentada por algo con mayor fundamento que el desvanecimiento de cantidades. D'Alembert interpreta las razones primeras y últimas de Newton como límites; según Boyer (1999, p. 567), postula:
Una cantidad es el límite de otra cantidad variable, si la segunda puede aproximarse a la primera hasta diferir de ella en menos que cualquier cantidad dada (sin llegar nunca a coincidir con ella).
Etapa 3. Aritmetización del análisis
Durante esta época, en la búsqueda de una fundamentación se intenta reconstruir el análisis sobre la base de conceptos aritméticos, surgen nuevos problemas en la propia matemática y en la física, y la enseñanza de las matemáticas en Francia pasa a ser obligatoria tanto en la Escuela Normal Superior como en la Politécnica. Los matemáticos se ven obligados a enseñar y, por ende, a escribir manuales de matemáticas que tengan bases rigurosas.
Hay que esperar hasta el Cours d'analyse de l'École Polytechnique, de Augustine Louis Cauchy (1821) para que surja una nueva definición que, si bien es totalmente subjetiva, supone un avance respecto a la dada por D'Alembert:
Cuando los sucesivos valores que toma una variable se aproximan indefinidamente a un valor fijo, de manera que terminan por diferir de él en tan poco como queramos, este último valor se llama el límite de todos los demás.
C. Boyer menciona que Heine, en 1872, escribe una nueva definición, atribuida a Karl Weierstrass (1815–1897), que elimina el subjetivismo de la definición de Cauchy:
Si, dado cualquier ε , existe un η0, tal que para 0 < η < η0 , la diferencia f(xo ± η) – L es menor en valor absoluto que ε, entonces se dice que L es el límite de f(x) para x = xo (Boyer, 1999, p. 696).
En el siglo pasado se sustituye la ηde Weierstrass por δ, notación que en la actualidad se suele considerar en todos los manuales de Análisis Matemático, aunque desde un análisis didáctico se descubren variaciones bastante notorias (sobre ellas estamos trabajando). La siguiente definición está tomada de Michael Spivak (1981, p. 110):
La función f tiende hacia el límite 1 en a significa: para todo ε > 0 existe algún δ > 0 tal que, para todo x, si 0 < x–a < δ, entonces f(x) – l < ε.
Otra variante consiste en escribir la primera desigualdad como un entorno reducido de radio δ centrado en a, y la segunda como un entorno de radio ε centrado en l. Definiciones parecidas pueden verse en otros autores, como Apostol (1989); Courant y Robbins (1964); García y otros (1993); Larson, Hostetler y Edwards (1998); Linés (1983); Rudin (1980); Thomas y Finney (1998). Sin embargo, ninguno postula una definición igual a la que se describe a continuación y, como es lógico, no se utiliza nada similar para establecer las propiedades de los límites. El Anexo 2 muestra un par de ejemplos de aplicación pero, siguiendo este modelo, no creemos que los posesores puedan tener dificultades para probar todas las propiedades que suelen instaurarse en el primer curso de análisis matemático de la mayor parte de las titulaciones universitarias.
Se puede hablar de una cuarta etapa, en el siglo XX, que tiene como característica la generalización a otros espacios matemáticos. Esto permitiría afirmar que la concepción de límite es topológica y, como es lógico, en dichos espacios la formulación es diferente.
La evolución de la noción de límite y las variaciones que ha tenido en el desarrollo de la matemática pone de manifiesto lo difícil que ha resultado su conceptualización. Ahora bien, todas estas conceptualizaciones surgen desde la propia matemática, no desde la didáctica. Van orientadas hacia el rigor matemático y su formalismo sintáctico ha incrementado con el avance de la matemática; sin embargo, no tienen en cuenta los aprendizajes de los alumnos.
La conceptualización con la que trabajamos, surgida de la Didáctica de la Matemática, enlaza las concepciones de D'Alembert y Cauchy, aportando rigor a la primera y eliminando el subjetivismo de la segunda. Por otra parte, debe quedar claro que en ningún caso tratamos de deslegitimar a ninguna conceptualización de límite, sólo hacemos un análisis sobre los aprendizajes de los alumnos, utilizando tanto la definición métrica de Weierstrass como la que formularon Blázquez y Ortega (2002), que referimos brevemente a continuación.
El punto de partida se encuentra en las ideas básicas de aproximación y de tendencia, que se pueden esbozar numéricamente como sigue: 1, 1.1, 1.11, 1.111, ... es una sucesión que se aproxima a 100, mas es evidente que no tiende a 100; sin embargo, la misma sucesión se aproxima a 10/9 y tiende a 10/9. La diferencia estriba en que, en el primer caso, fijada una aproximación de 100, por ejemplo 2, no se mejora por los términos de la sucesión; sin embargo, en el segundo caso, fijada una aproximación arbitraria de 10/9, distinta de 10/9, es posible encontrar un término de la sucesión que, a partir de él, todos los que le siguen están más próximos a 10/9 que la aproximación establecida.
Esta reflexión permite definir los límites secuencial y funcional, evitando el formalismo –pero no el rigor–, el subjetivismo de Cauchy y el supuesto impersonalismo de Heine; los dos últimos están todavía presentes en los manuales. Las definiciones de límite secuencial y límite funcional que proponen Blázquez y Ortega son:
L es el límite de una sucesión si para cualquier aproximación K de L, K ≠ L , existe un término de la sucesión tal que todos los que siguen están más próximos a L que a K.
El límite de la función f en x=a es L si para cualquier aproximación K de L, K ≠ L , existe una aproximación H de a, H ≠ a , tal que las imágenes de todos los puntos que están más cerca de a que H están más próximas a L que a K.
Esto equivale a decir que:
El límite de la función f en x=a es L si para cualquier aproximación K de L, K ≠ L, existe un entorno reducido de a, tal que las imágenes de todos sus puntos están más próximas a L que K.
Si se emplea la significación de tendencias establecida antes, el límite de la función / en x=a es L si cuando x tiende a a sus imágenes f(x) tienden a L.
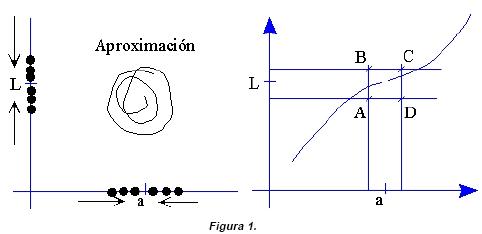
Esto se refleja de forma directa en el gráfico de la izquierda, mientras que el de la derecha representa las dos primeras acepciones: cualquier aproximación a L (distinta de L) determina una banda horizontal que contiene a L, y cualquier aproximación a a (distinta de a) define otra banda vertical que contiene a a y recíprocamente. Por tanto, fijada una banda horizontal que contiene a L, existe una banda horizontal que contiene a a, tal que la gráfica de la función tiene que atravesar el rectángulo ADCB exclusivamente por los segmentos AB y CD. Resulta evidente que esta representación no está ligada al gráfico de la función y que se puede dibujar después o no.
Sin renunciar a trabajar la definición métrica de Weierstrass, que dependerá del tipo de formación matemática que se persiga, Blázquez (1999) indica la conveniencia de hacerlo después de que los alumnos hayan asimilado la conceptualización como aproximación óptima. Desde otra perspectiva, si ambas definiciones hacen referencia al mismo concepto y son sus representaciones, ambas tienen que ser equivalentes; de hecho lo son, como muestra la correspondencia asociativa entre las unidades significantes elementales que las constituyen:

PRIMER ANÁLISIS
Una vez que se examinaron los documentos producidos por los alumnos de ingeniería durante el curso 2003, en el marco metodológico de la investigación–acción (Elliot, 1997; Kemmis y McTaggart, 1988), se constató que sus respuestas a las tareas de traducción entre ambas definiciones, ya en el segundo ciclo, fueron bastante precarias y no eran excesivamente concordantes con otras que habían dado antes sobre aproximaciones, cotas de error, y caracterizaciones de intervalos determinados por aproximaciones y por desigualdades de valores absolutos. Por esta razón, el equipo investigador creyó conveniente hacer unas entrevistas para que los alumnos explicaran sus dificultades.
De este modo, al finalizar el curso se aplicaron tres entrevistas semiestructuradas a tres parejas de alumnos de Análisis Matemático I, correspondiente a Ingeniería en Alimentos. Las entrevistas versaron sobre los siguientes contenidos: idea intuitiva de límite funcional, concepto de aproximación y mejorar la aproximación, tendencia de una variable, definición de límite como aproximación óptima y definición métrica de límite. Todas se grabaron en audio y se transcribieron para efectuar su análisis.
Las entrevistas fueron realizadas por la profesora responsable del curso, quien también es investigadora, ya que sólo ella cumplía los requisitos enunciados por Blázquez, Ibañes y Ortega (2004) sobre la investigación en curso; de ellos, resaltamos los siguientes:
• Es especialista en los contenidos matemáticos y sabe cómo se han desarrollado los conceptos en el aula.
• Ha analizado las producciones de los alumnos, sobre las que se ha hecho el análisis y las correspondientes reflexiones.
• Conoce las hipótesis de trabajo de la investigación y el estado de la misma.
• Conoce las actitudes los alumnos, su comportamiento en el aula, la facilidad de palabra, etc.
• Sabe cuáles son las apreciaciones controvertidas de los alumnos que van a ser entrevistados en torno a los contenidos que son objeto de la investigación.
La elección de las tres parejas se llevó a cabo después de analizar las respuestas dadas por los estudiantes en cuestionarios anteriores.
De las tres entrevistas, la más interesante fue la que se hizo a Gustavo y a Jéssica, ya que mantuvo dos planteamientos diferentes. Por una parte, trató de indagar las ideas que tenían los alumnos sobre cada uno de los contenidos anteriores, sus dificultades y preferencias; por otra, la profesora–investigadora intentó cerciorarse de que los alumnos llegaban a entender cada uno de los contenidos. La entrevista a cada una de las partes terminó cuando la profesora–investigadora tuvo la seguridad de que los entrevistados llegaron a expresar el concepto correspondiente (de hecho, se produjo un aprendizaje social). Las tres entrevistas fueron revisadas por el director de la investigación y el análisis se hizo conjuntamente.
La entrevista a Gustavo y a Jessica presentó 315 intervenciones, que se distribuyeron de la siguiente forma:
• Para la idea intuitiva de límite, 14: 7 de la profesora y 7 de los alumnos.
• Para el concepto de aproximación y mejorar la aproximación, 15: 6 de la profesora y 7 de los alumnos.
• Para el de tendencia de una variable, 12: 6 de la profesora y 6 de los alumnos.
• Para la definición de límite como aproximación óptima, 29: 14 de la profesora y 15 de los alumnos.
• Para la definición métrica, 246: 122 de la profesora y 124 de los alumnos.
Por razones de espacio, sólo mostramos algunas intervenciones de la entrevista, a partir de las cuales se desprenden las siguientes reflexiones: la primera indicación, acerca de la mayor o menor dificultad que pueden presentar ambas conceptualizaciones para los alumnos, viene dada por el número de intervenciones hasta que los entrevistados llegan a expresar la correspondiente conceptualización, ya que es un reflejo del esfuerzo que necesitan para el aprendizaje.
Con tal criterio, de los cinco tópicos abordados en la entrevista, el más sencillo fue el de tendencia de una variable, seguido del tocante a idea intuitiva de límite y el de aproximación y mejorar la aproximación, mientras que los más difíciles correspondieron a definición de límite como aproximación óptima y definición métrica de límite. Este último resultó muy complicado, ya que tal indicador requiere entre tres y cuatro intervenciones de los tópicos anteriores.
Referente a la conceptualización como aproximación óptima, durante la entrevista se percibió que estos alumnos tuvieron serias dificultades para interpretar mejorar cualquier aproximación distinta del propio límite y, en principio, consideraron que es suficiente que se aproxime, pero son insignificantes en comparación con las que se descubren en la conceptualización métrica. En ésta, destacan las asociadas al formalismo de la escritura, las de interpretación del simbolismo algebraico relacionado a la función valor absoluto y a las desigualdades –descritas en las secuencias de la entrevista que se reproducen–, las de la implicación de pertenencia o inclusión, la confusión de los papeles de 8 y . Además, creemos que son considerables las de dependencia de e respecto de S ,en mayor grado, y respecto del punto y de la función, en menor, aunque aquí no están tratadas.
A lo largo de la entrevista afloraron las dificultades asociadas a la semántica del estatus conceptual y a los procesos de pensamiento matemático que, según Socas (1997, pp. 127–133) "se ponen de manifiesto en la naturaleza lógica de las matemáticas y en las rupturas que se dan necesariamente en relación con los modos de pensamiento matemático". En primer lugar, si ya es conflictiva la interpretación de la función valor absoluto y hay dificultades semánticas del estatus conceptual, al asociarla con las desigualdades implícitas en la conceptualización, el problema resulta aún mayor y surgen las rupturas que se detectaron en las entrevistas. En segundo lugar, la traducción de estas desigualdades simbólicas a los intervalos asociados y su correspondiente expresión verbal son dificultades añadidas, de ahí que vuelvan a producirse nuevas rupturas en los modos de pensamiento matemático.
Tal situación se manifiesta en la siguiente secuencia de la entrevista sobre la desigualdad f(x) – L < ε , y que transcurre considerando al soporte gráfico como la representación que coordina las traducciones entre los sistemas simbólico, verbal y gráfico. Las intervenciones se indican con G (Gustavo), J (Jéssica) y P (Profesora):
81. J: Bueno, épsilon sería... tendremos un épsilon acá y un épsilon acá. Esto es épsilon más, menos L y épsilon más L.
Y continúa con las siguientes intervenciones, que no son las últimas al respecto:
117. G: Para mí, el épsilon está de ¿ hasta el punto que yo tomo del entorno, o sea, éste sería el épsilon...
118. P: Bien (comentario: Gustavo marca bien el épsilon) ¿Te das cuenta, Jéssica?
119. J: Sí.
120. P: Épsilon es la distancia que va de acá hasta acá, y es la misma que va de acá hasta acá. Entonces, si a este L le sumas épsilon te queda L más épsilon...
121. J: Sí.
122. P: ¿Y éste de acá?
123. J: Épsilon menos L.
124. P: ¿Épsilon menos L?
125. J: No, más, porque si esto es épsilon...
126. P: Esto es épsilon, ¿no? Gustavo dijo que es épsilon, que es lo mismo que esto que está acá. Bueno, si a este punto, L, le sumo épsilon obtengo este otro (Y lo señala).
127. J: ¡Bien! Y a L le resto épsilon.
128. P: ¡Ajá! Si a L le resto épsilon, ¿qué punto es?
129. J: Épsilon, épsilon menos L.
130. P: L menos épsilon, ¿está bien? Al revés, L menos épsilon.
131. J: ¡Claro! Esto es épsilon más L4...
132. P: Esto es L más épsilon y esto es L menos épsilon, ¿te das cuenta de la diferencia?
133. J: Sí.
Sin embargo, esta dificultad persiste, como indica la siguiente intervención, que se produce después:
277. J: También delta menos a5.
En el caso de 0 < x–a < δ hay que añadir la dificultad que supone la interpretación de entorno reducido, que no es tan simple como puede parecer, a tenor de la reincidencia de Jéssica en sus intervenciones. Al tocarse este tema, Jéssica afirma que la notación anterior expresa dicho entorno, mas esto no basta, ya que para que realmente comprenda su significado debe saber el papel que juega cada elemento de la expresión.
142. P: ¿El centro de qué?
143. J: Del entorno.
144. P: Muy bien. ¿De qué entorno?
145. J: Reducido.
La profesora–investigadora quiere indagar si realmente Jéssica hace una interpretación correcta de su significado, o sólo parafrasea a Gustavo. Efectivamente, las sospechas acerca de las dificultades asociadas a este concepto se confirman en las intervenciones siguientes, que tienen su desenlace hasta la 195. Transcribimos las últimas:
185. J: Ahí voy a tener igual a cero.
186. P: Entonces, ¿cuál es el caso en que valor absoluto de x menos a es cero? ¿Cuándo qué?
187. J: Cuando el valor de x sea mayor que a6.
188. P: No, mayor no.
189. J: Igual que a.
190. P: Igual que a, ¿está bien? Si yo pongo acá cero igual, la única posibilidad es que x tiene que ser igual a a.
191. J: Hum..., hum...
192. P: Si yo ahora pongo cero menor que valor absoluto de x menos a, ¿qué pasa?
193. J: Cero menor que valor absoluto de x menos a....
194. P: Tengo que sacar este caso.
195. J: Tengo que exceptuar, por eso, no tengo igual porque exceptúo este caso en que a sea igual a x.
Debido a las enormes dificultades holísticas identificadas en los procesos de pensamiento matemático que tienen los alumnos sobre el formalismo de la definición métrica, asociadas a las unidades significantes del valor absoluto, la profesora–investigadora optó por no tratar en la entrevista la dependencia de δ respecto del punto, ni respecto de la función, ni respecto de ε, cuyos aprendizajes están siendo investigados en la actualidad. Sin embargo, cabe resaltar que tales obstáculos no aparecieron en la secuencia de la entrevista que correspondió a la definición de límite como aproximación óptima –que no se reproduce en este trabajo–, pues los alumnos explicaron la significación de las unidades significantes con cierta elocuencia.
SEGUNDO ANÁLISIS
En este segundo trabajo se pretendía conocer hasta qué punto los alumnos del Curso de Aptitud Pedagógica (CAP) eran capaces de aplicar conceptualizaciones para demostrar dos teoremas sencillos: el del signo y el de unicidad (ver Anexos 1 y 2). Con tal fin, se dio un test a un grupo de egresados de la Universidad de Valladolid, pensando que durante sus estudios sólo habían ocupado la conceptualización métrica; dicho supuesto fue confirmado por las respuestas que escribieron en el test. Por esa razón, se les ofrecieron dos ejemplos de aproximación, como hechos incuestionables, que podían aplicar: que 0 es una aproximación de cualquier número y que un punto interior a un segmento es una aproximación de sus extremos.
Este pequeño test constó de dos fases: en la primera, sin ninguna ayuda externa, los alumnos tenían que demostrar el teorema del signo y el de unicidad, aplicando las dos conceptualizaciones, mientras que en la segunda debían explicar la dificultad de estas demostraciones.
Para poder valorar la validez de las respuestas emitidas, describiremos la composición del aula y la dinámica de la prueba. La especialidad de matemáticas del CAP, de la Universidad de Valladolid, fue cursada por 49 alumnos de varias licenciaturas: 12 alumnos eran licenciados en Matemáticas (11 hicieron el test), 22 en Ingeniería (1 de ellos no respondió el test), 4 en Física, 8 en Estadística, 2 en Empresariales y 1 en Económicas.
En España, el CAP es un requisito necesario para poder ingresar al cuerpo de profesores de educación secundaria. Si bien los egresados de la licenciatura en Matemáticas pueden ser los más adecuados para opositar, también pueden aplicar los de otras carreras. Por tanto, hay que contemplar a estos titulados como posibles candidatos, ya que de no hacerlo se caería en una visión sesgada por contemplar sólo una parte de los posibles profesores de educación secundaria.
Para la primera fase se les distribuyó el test a los alumnos (Anexo 1) y se les dio tiempo hasta que lo terminaran (bien porque lo hicieron entero, o porque no sabían qué hacer). Luego, el profesor escribió en la pizarra dos demostraciones de cada uno de los teoremas, donde aplicó las dos conceptualizaciones y utilizó los registros simbólico–algebraico, gráfico y verbal (en el Anexo 2 sólo se reproducen los correspondientes a la conceptualización como aproximación óptima, pues las demostraciones derivadas de la definición métrica aparecen en cualquier manual). A continuación, se les pidió a los alumnos que compararan en cada caso las dos pruebas y escribieran cuál les parecía más sencilla y porqué.
De los 48 alumnos presentes en el aula, 47 respondieron el test. La Tabla 1 muestra sus resultados globales, considerando las dos fases.
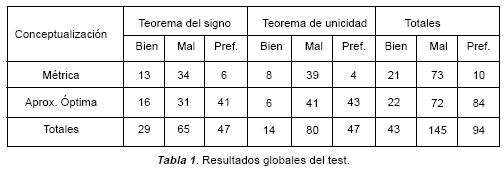
De entrada, llamó nuestra atención el porcentaje tan alto de titulados que no fueron capaces de aplicar las conceptualizaciones para hacer las demostraciones propuestas, sobre todo al utilizar la definición métrica, ya que la debieron haber aprendido y empleado durante su formación universitaria. Sólo el 27.66% hizo la demostración del primer teorema aplicando la conceptualización métrica, mientras que el 17.02% realizó la prueba del segundo teorema, utilizando la misma definición.
Los resultados positivos globales fueron ligeramente mejores cuando se aplicó la segunda conceptualización (22 resultados positivos frente a 21), aunque en el segundo teorema fueron peores. Esto se debió a que los alumnos no habían recibido ninguna instrucción acerca de la segunda conceptualización, no la conocían y, por tanto, nunca la habían aplicado para comprobar. La única referencia que tenían de ella fue la indicación sobre aproximaciones que figuró en el test, y creemos que tal situación habla por sí sola en favor de esta definición en forma incuestionable.
Respecto a las posiciones que mostraron los egresados sobre las posibles dificultades para aplicar una u otra conceptualización en cada una de las demostraciones, fue claro que los titulados piensan que son más sencillas las aplicaciones de la conceptualización de aproximación óptima. Hubo una mayoría del 87.23% para la demostración del primer teorema y del 91.49% para la del segundo.
En la Tabla 2 se han distribuido por carreras las respuestas positivas en las pruebas de ambos teoremas y sus preferencias. Los mejores resultados al aplicar la conceptualización métrica corresponden a los licenciados en Matemáticas, siendo el 72.73% en ambos teoremas, pero no sucede lo mismo al trabajar con la definición como aproximación óptima (54.55% y 18.18% en el primer y segundo teorema, respectivamente).
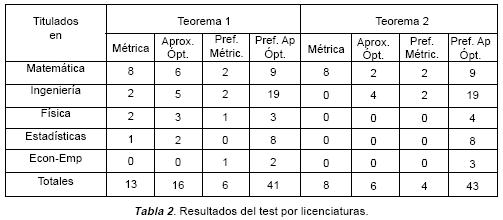
Resulta evidente que en esta licenciatura se hace un estudio más formalista que en otras, donde se invierten los porcentajes. Por ejemplo, los licenciados en Física, al aplicar la definición como aproximación óptima en el primer teorema, alcanzaron el 75%, mientras que el 18.18% de los titulados en Ingeniería aplica bien la definición como aproximación óptima para demostrar el segundo teorema, alcanzando el mismo porcentaje que los matemáticos.
En cuanto al criterio sobre la sencillez de aplicación, todos los egresados opinaron que son más sencillas las demostraciones que se derivan de aplicar la conceptualización de aproximación óptima: 87.23% frente a 12.76% para el primer teorema, y 91.49% frente a 8.51% para el segundo.
Las declaraciones indicadas por los egresados sobre qué demostraciones eran más sencillas tienen su fundamento en las justificaciones que dieron. Su análisis nos va a esclarecer en qué se fijan para afirmar que las demostraciones basadas en las aplicaciones de la conceptualización de límite como aproximación óptima son más sencillas que las establecidas en la definición métrica, y cuáles son las razones para afirmar lo contrario. A continuación, describiremos estas consideraciones:
Para 16 alumnos, las demostraciones que se derivan de la conceptualización como aproximación óptima son más sencillas porque carecen de formalismo o son menos formales. El 21.28% de los alumnos opinan lo mismo, pero opinan que estas demostraciones son más intuitivas o tienen más sentido común. Así por ejemplo, Yolanda, licenciada en Matemáticas, afirma:
Siempre es más fácil la conceptualización como aproximación óptima porque no usa formalismos, sino más la intuición y el sentido común.
Un 25.53% de los egresados argumentó que son más sencillas porque se entienden mejor o porque son más claras o menos farragosas, mientras que un 27.66% resaltó la mayor sencillez de estas demostraciones porque son más fáciles de entender. Como ejemplos, citamos los siguientes:
La segunda demostración es menos formal, por tanto, menos farragosa para los alumnos y aunque su nivel de razonamiento va en aumento, ven mejor lo menos formal. La primera lleva mucho más formalismo y suele ser más complicada de entender (Ruth, ingeniera agrónoma).
Me han sorprendido mucho las demostraciones basadas en la aproximación óptima por no estar acostumbrado a ellas, supongo que para los alumnos de enseñanza secundaria lo vean más claro de esta forma (José Javier, licenciado en Estadística).
Hacer las demostraciones sin formalismo me resulta más fácil de entender (Rosa María, licenciada en Matemáticas).
Como es natural, algunos licenciados justificaron su elección, señalando más de una razón:
La segunda es más fácil de entender, pues exige tener menos conocimientos teóricos. Es mucho más fácil de seguir por los alumnos y más fácil de aplicar (Luis Alberto, ingeniero industrial).
La segunda es mucho más sencilla porque se entiende mucho mejor y no usa tecnicismos que los alumnos no van a entender. Es mucho más cercana a la inteligencia de los alumnos (Olga, licenciada en Estadística).
Otros egresados afirmaron que estas demostraciones son más sencillas por alguna de las siguientes causas: porque el razonamiento es más sencillo, porque no es necesario tener soltura con el lenguaje matemático, porque son más explicativas o fáciles de explicar, o bien porque se puede imaginar la solución.
Es mejor trabajar la segunda porque aplica los conceptos directamente, sin tener que usar el lenguaje formal de las matemáticas (Juan Carlos, licenciado en Físicas).
Un grupo se refirió indistintamente a la conceptualización de límite como aproximación óptima y a las demostraciones que aplican esta conceptualización, y aseguró que son más sencillas por estas razones: tiene el mismo rigor, es más visual y no introduce otros conceptos. Finalmente, otro grupo numeroso de alumnos, que se fijó exclusivamente en la conceptualización, dijo que es más sencilla porque es más útil y eficaz, requiere menos capacidad de abstracción, no se olvida fácilmente o es más ventajosa por su facilidad de aplicación.
En resumen, la mayor parte de los egresados dijo que es más sencilla la conceptualización basada en la aproximación óptima, argumentando razones muy diferentes que, sin duda, pueden considerarse como rasgos característicos facilitadores del aprendizaje de la conceptualización.
Ya se ha dado cuenta de que muy pocos alumnos afirmaron que las demostraciones basadas en la conceptualización métrica son las más sencillas. La mayor parte de estos licenciados (sólo representan el 12.76% del total) esgrimió como única razón que este ha sido el único procedimiento que han utilizado durante su carrera y es al que están habituados. Por ejemplo, María Teresa, ingeniera en Telecomunicaciones, señala:
Para mí es más sencilla la conceptualización métrica, ya que todas las demostraciones estudiadas hasta ahora han sido de ese modo.
Una matemática, Isabel, indicó que es menos abstracta. A nuestro juicio, esta declaración es totalmente errónea y sólo merece una consideración testimonial.
Finalmente, algunos egresados emitieron juicios de valor contrarios al aprendizaje de la definición métrica. Por ejemplo, Rosario, ingeniera de Telecomunicaciones, asevera:
La definición métrica se aprende de memoria y se olvida fácilmente.
Por su parte, Yolanda, egresada en Matemáticas, apunta:
Para poder usar la conceptualización métrica hace falta tener ya una soltura con el lenguaje matemático.
En definitiva, muy pocos egresados opinaron que la conceptualización métrica es más sencilla. La única razón que presentan se basa en el hábito de la costumbre, ya que el resto de sus argumentos son negativos.
CONCLUSIONES
Tras el análisis de la entrevista quedó claro que para los alumnos de Ingeniería la conceptualización como aproximación óptima, aunque tiene su mayor dificultad en la interpretación de "mejorar cualquier aproximación", son menores que los problemas de la conceptualización métrica, ya que su formalismo les impide entender el significado y se enfrentan a mayores obstáculos al interpretar las desigualdades de los valores absolutos.
Por otra parte, los egresados comprenden mejor la conceptualización basada en la aproximación óptima que en la métrica. Además, creen que es más útil y eficaz; que requiere de menos capacidad de abstracción; que no se olvida tan fácilmente; que es más ventajosa por su facilidad de aplicación, y que los alumnos la entenderían mejor.
En el caso de la conceptualización como aproximación óptima, los egresados tuvieron serias dificultades para interpretar "mejorar cualquier aproximación distinta del propio límite" y, en principio, consideran que "es suficiente que se aproxime". Sin embargo, estos problemas son insignificantes respecto a los que se descubren en la conceptualización métrica, como los asociados al formalismo de la escritura, la interpretación del simbolismo algebraico vinculado a la función valor absoluto y a las desigualdades, la implicación de pertenencia o inclusión, la confusión de los papeles de δ y ε. De igual manera, creemos que también son considerables los problemas de dependencia de δ respecto de ε, en mayor grado, y respecto del punto y de la función, en menor medida, aunque aquí no están tratados.
Los alumnos del CAP también opinaron que la aplicación de la conceptualización como aproximación óptima para explicar los teoremas es más útil, que sus demostraciones son más sencillas, más intuitivas o tienen más sentido común, además de que se entienden mejor. Y justifican estas preferencias porque las demostraciones por aproximación óptima son más claras o menos farragosas; carecen de formalismo o son menos formales; el razonamiento resulta más sencillo; no es necesario tener soltura con el lenguaje matemático; son más explicativas o más fáciles de explicar; se puede imaginar su solución; tienen el mismo rigor; son más visuales o porque no introducen otros conceptos.
En resumen, la conceptualización basada en la aproximación óptima debe ser más apta para los aprendizajes iniciales universitarios de análisis matemático que la conceptualización métrica. Las razones que se han indicado pueden considerarse como rasgos característicos facilitadores del aprendizaje de la primera conceptualización, en oposición a las dificultades asociadas al formalismo de la definición métrica.
Por otra parte, se percibe una mayor defensa de la conceptualización métrica en los egresados que más la han utilizado y, en primera instancia, parece que se produce el efecto túnel, lo cual nos lleva a pensar que el profesorado será más reacio a utilizar esta conceptualización. Tal problemática no se ha investigado, es un problema abierto y deberá ser tratado en el futuro.
BIBLIOGRAFÍA
Apostol, T. (1989). Análisis matemático. Barcelona, España: Reverté. [ Links ]
Blázquez, S. (1999). Noción de límite en matemáticas aplicadas a las ciencias sociales. Tesis de doctorado, Universidad de Valladolid, España. [ Links ]
Blázquez, S., Ibañes, M. y Ortega, T. (2004). Debates y entrevistas. Texto presentado en el XVI Simposio Iberoamericano de Enseñanza Matemática. Castellón de la Plana, España (pendiente de publicación). [ Links ]
Blázquez, S. y Ortega, T. (2002). Nueva definición de límite funcional. UNO, 30, 67–82. [ Links ]
Blázquez, S. y Ortega, T. (2001b). Rupturas en la comprensión del concepto de límite en alumnos de bachillerato. Aula 10, 117–133. [ Links ]
Blázquez, S. y Ortega, T. (2001a). Los sistemas de representación en la enseñanza del límite. Revista Latinoamericana de Investigación en Matemática Educativa, 4 (3), 219–236. [ Links ]
Blázquez, S. y Ortega, T. (2000). El concepto de límite en la educación secundaria. En Cantoral, R. (Ed.), El futuro del cálculo infinitesimal (pp. 331–354). México: Grupo Editorial Iberoamérica. [ Links ]
Blázquez, S. y Ortega, T. (1999). Didáctica del análisis en matemáticas aplicadas a las ciencias sociales. Concepto de límite. En Tomás Ortega (Ed.), Temas controvertidos en Educación Matemática ESO y Bachillerato (pp. 121–154). Valladolid, España: Universidad de Valladolid. [ Links ]
Blázquez, S. y Ortega, T. (1997). Las sucesiones como aproximación didáctica a los conceptos de función y límite funcional. En Actas de las VIII Jornadas para el Aprendizaje y la Enseñanza de las Matemáticas (pp. 303–306). Salamanca, España: Sociedad Castellano–Leonesa de Profesorado de Matemáticas (Burgos). [ Links ]
Boyer, C. B. (1999). Historia de la matemática. Madrid, España: Alianza Editorial. [ Links ]
Cauchy, A. (1821). Cours d'Analyse de l'Ecole Royale Politechnyque (Premier Partie. Analyse Algébrique). Sevilla, España: SAEM Thales (edición facsímil). [ Links ]
Cornu, B. (1983). Apprentissage de la notion de limite: conceptions et obstacles. Thèse de 3ème Cycle, Mathématiques, Université I de Grenoble, France. [ Links ]
Duval, R. (1998). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. En F. Hitt (Ed.), Investigaciones en Matemática Educativa II (pp. 173–201). Cinvestav, México. [ Links ]
Elliot, J. (1997). La investigación–acción en educación. Madrid, España: Morata. [ Links ]
García, A., García, F., Gutiérrez, A., López, A., Rodríguez, G. y De la Villa, A. (1993). Teoría y problemas de análisis matemático en una variable. Madrid, España: CLAGSA. [ Links ]
Kemmis y McTaggart (1988). Cómo planificar la investigación–acción. Barcelona, España: Alertes. [ Links ]
Larson R.; Hostetler, R. y Edwards, B. (1998). Cálculo y Geometría Analítica (Vol. 1). Madrid, España: McGraw–Hill. [ Links ]
Linés, E. (1983). Principios de análisis matemático. Barcelona, España: Reverté. [ Links ]
Newton, I. (1711). ANÁLISYS per Quantitatum SERIES, FLUXIONES ac DIFFERENTIAS: cum Enumeratione Linearum TERTII ORDINIS. LONDINI: Ex Officina Pearsononiana. Anno M.DCCXII (editado por SEAM Thales y la Real Sociedad Matemática Española. Sevilla, España: 2003). [ Links ]
Robinet, J. (1983). Un experience de ingenierie didactique sur la notion de limite de fonction. Recherches en Didactique des Mathématiques, 4 (3), 223–292. [ Links ]
Rudin, W. (1980). Análisis funcional. Barcelona, España: Reverté. [ Links ]
Sánchez, C. (1997). Estudio estadístico sobre el proceso enseñanza–aprendizaje de la noción de límite de una función. Tesis de doctorado, Departamento de Estadística e Investigación Operativa, Universidad de Granada, España. [ Links ]
Sierpinska, A. (1987). Humanities students and epistemological obstacles related to limits. Educational Studies in Mathematics, 18 (4), 371–397. [ Links ]
Sierpinska, A. (1985). Obstacles epistemologiques relatifs a la notion de limite. Recherches en Didactique des Mathématiques, 6 (1), 5–67. [ Links ]
Socas, M. (1997). Dificultades, obstáculos y errores en el aprendizaje de las matemáticas en educación secundaria. En Luis Rico (Coord.), La educación matemática en enseñanza secundaria (pp. 125–154). Barcelona, España: ICE/Horsori, Universitat Autónoma de Barcelona. [ Links ]
Spivak, M. (1981): Calculus. Cálculo Infinitesimal. Barcelona, España: Reverté. [ Links ]
Tall, D. y Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12 (2), 151–169. [ Links ]
Thomas, G. y Finney, R. (1998). Cálculo con geometría analítica. Buenos Aires, Argentina: Adison–Wesley Iberoamericana. [ Links ]
3 Parte de la presente investigación está sufragada por una beca del Banco Río para Proyectos de Investigación Científica para el Perfeccionamiento Docente, concedida al proyecto Enseñanza de conceptos de análisis matemático en cursos de ingeniería (Argentina).
4 Considera ε – L y ε + L , en lugar de L – ε y L + ε. Intercambia la aritmética entre L y ε no las distingue porque no capta la significación de la desigualdad del valor absoluto, y su error persiste.
5 Sigue el mismo error de intercambio de la aritmética, en este caso entre δ y a.
6 Se evidencia que la interpretación del entorno reducido es una dificultad añadida al simbolismo 0 < x–a < δ.
Apellidos y nombre: Licenciatura:
Ejemplos de aproximaciones: 0 es una aproximación de cualquier valor. El punto medio de un segmento es una aproximación de sus extremos.
Conceptualizaciones de límite de una función en un punto.
Conceptualización métrica: L es el límite de la función / en el punto a si se verifica que 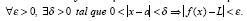
Conceptualización como aproximación óptima: L es el límite de la función / en el punto x=a si se verifica que para cualquier aproximación K de L, K ≠ L existe un entorno reducido de a tal que las imágenes de todos sus puntos mejoran dicha aproximación.
Demostrar los dos teoremas que se enuncian a continuación utilizando las dos conceptualizaciones.
Teorema 1: Si el límite, L, de una función en un punto, x=a, es positivo, existe un entorno reducido de a en el que la función es positiva.
1. Demostración utilizando la primera conceptualización.
2. Demostración utilizando la segunda conceptualización.
Teorema 2. El límite de una función en un punto, si existe, es único.
3. Demostración utilizando la primera conceptualización.
4. Demostración utilizando la segunda conceptualización.
Demostración del primer teorema. Por ser L > 0 el límite en x=a, considerando que 0 es una aproximación de L, existirá un entorno reducido de a tal que la imagen de todos sus puntos mejorará dicha aproximación y, por tanto, todas sus imágenes serán positivas.
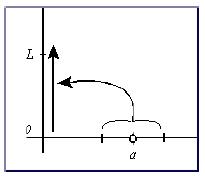
La explicación verbal utiliza el soporte gráfico de la Figura 2.
Una conceptualización de límite para el aprendizaje inicial de análisis matemático en la universidad 209
Demostración del segundo teorema.
Considerando que tuviera dos límites L y L' diferentes en x = a. En el supuesto de que L < L' , como el punto medio, M=(L+L') / 2, es una aproximación de L y de L' , aplicando la conceptualización, existe un entorno reducido de a tal que las imágenes de todos sus puntos mejoran dicha aproximación (tanto a L como a L') y, por tanto, todas esas imágenes tienen que ser mayores y menores que M. En consecuencia, es falso que L < L'. Análogamente, también resultaría ser falso que L' < L y, en consecuencia, L=L'.
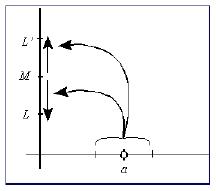
La explicación verbal utiliza el soporte gráfico y se atiende individualmente a cada uno de los supuestos límites, con un entorno reducido para cada uno. El menor de ellos serviría para los dos.














