Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Revista latinoamericana de investigación en matemática educativa
versión On-line ISSN 2007-6819versión impresa ISSN 1665-2436
Relime vol.9 no.1 Ciudad de México mar. 2006
Análisis institucional a propósito de la noción de completitud del conjunto de los números reales
Analía Bergé 1
Research Assistant Professor Mathematics & Statistics Concordia University Montreal, Canada E–mail: aberge@mathstat.concordia.ca
Recepción: Febrero de 2005
Aceptación: Enero de 2006
RESUMEN
En este artículo se presenta un estudio longitudinal a lo largo de cuatro cursos de los estudios universitarios en matemática. El análisis de los problemas y ejercicios destinados a los alumnos permite describir una organización matemática particular alrededor de la noción completitud del conjunto de los números reales e hipotetizar sobre la adquisición de conocimientos de los alumnos en este tema, que es considerado como un exponente del pasaje del cálculo al análisis matemático.
PALABRAS CLAVE: Números reales, completitud, análisis institucional, praxeologías, organización matemática.
ABSTRACT
This paper presents a longitudinal study of four undergraduate mathematics courses. The analysis of problems and exercises given in the outlines of the courses, allows us to describe a particular mathematical organization of the notion of completeness of the set of real numbers. It allows us also to make a hypothesis about the acquisition of knowledge of this topic, which is considered as an example of the passing from Calculus to Mathematical Analysis.
KEY WORDS: Real numbers, completeness, institutional analysis, praxeologies, mathematical organization.
RESUMO
Neste artigo apresentamos um estudo longitudinal ao comprido de quatro cursos dos estudos universitários em matemática. O análise dos problemas e exercícios destinados aos alunos permite descrever uma organização matematica particular em torno a la noção completude do conjunto dos números reais, e fazer hipóteses sob la aquisição de conhecimentos dos alunos neste tema que e considerado como um expoente da passagem do Cálculo ao Análise.
PALAVRAS CHAVE: Números reais, completude, analise institucional, praxeologías, organização matematica.
RÉSUMÉ
Dans cet article nous présentons une étude longitudinale au long de quatre cours universitaires en mathématiques. L'analyse des problèmes et exercises destinés aux étudiants permet de décrire une organisation mathématique particulière autour de la notion complétude de l'ensemble des nombres réels et de faire des hypothèses sur l'acquisition des connaissances des étudiants à ce sujet, qui est considéré comme une exemple du passage du Calcul à l'Analyse Mathematique.
MOST CLÉS: Nombres réels, completude, analyse institutionnelle, praxeologies, organisation mathématique.
INTRODUCCIÓN
Este artículo forma parte de un trabajo de investigación en Didáctica de la Matemática; de manera más precisa, atañe al dominio del Análisis Matemático. Hemos elegido como contenido el conjunto de los números reales y su completitud por dos motivos. Por un lado, admite un estudio didáctico longitudinal, ya que es enseñado en diferentes materias del nivel universitario con distintos niveles de profundidad. Por otro, la completitud del conjunto de los números reales aparece en problemas que están en el corazón del análisis matemático y refleja principios generales de este campo, como ser la determinación de un elemento mediante un encaje, la definición de un elemento por ser el límite de otros que satisfacen determinada condición, la realización de extremos, entre otros. Un estudio didáctico sobre esta noción puede, entonces, otorgarnos elementos para comprender la adquisición por parte de los alumnos de una gama más amplia de conocimientos.
Así, presentamos un análisis institucional diseñado a propósito de la noción conjunto de los números reales y su completitud y la institución primeros años de la licenciatura y profesorado universitario en matemática. Debido a que un estudio de esta índole necesariamente involucra una institución en particular, se ha tomado como referencia las carreras de Licenciatura en Matemática y Profesorado en Matemática de la Universidad de Buenos Aires (UBA), Argentina. Si bien este es un análisis local, posee una estructura y plantea preguntas que pueden ser importadas a otras instituciones e incluso a otros contenidos matemáticos.
Hemos enmarcado este estudio en los trabajos de Y. Chevallard (1998) y de A. Robert (1998) entre otros autores –sobre lo cual abundaremos en la sección 1–, así como en un modelo cognitivo a priori de la completitud, denominado panorama cognitivo, que detallaremos en la sección 2.
Los objetivos de este artículo son:
• Analizar las oportunidades que tiene un alumno de la Licenciatura en Matemática o del Profesorado en Matemática de enfrentarse a situaciones que involucren a la completitud del conjunto IR en los primeros años de su formación
• Ponerlas en relación con el panorama cognitivo y hacer una hipótesis sobre la posible adquisición de conocimiento por parte de los alumnos.
Exponemos nuestras preguntas en la sección 3, llevamos a cabo el análisis de ejercicios de diferentes cursos en las secciones 4, 5, 6 y 7, y presentamos nuestras síntesis y conclusiones en las secciones 8 y 9.
1. REFERENCIAS TEÓRICAS I
1.1. Praxeologías
La completitud de IR como un tópico de la matemática "vive" en mayor o menor medida en las materias de algunas instituciones y en las concepciones de los profesores o de los alumnos. Dejemos por un momento a las personas de lado y reparemos en las siguientes preguntas: ¿Cómo vive este campo en las instituciones? ¿Qué distancia guarda este saber designado para ser enseñado en una o varias materias con el "saber sabio"? ¿A qué recortes y modificaciones se someten estos saberes a fin de volverse "aptos" para ser enseñados? ¿En qué sentido se modifican las respuestas a estas preguntas al cambiar de institución? Estas y otras cuestiones son tratadas de manera general por Chevallard en la teoría de la transposición didáctica (Chevallard, 1997), donde especialmente distingue las nociones de saber sabio, saber a enseñar y saber enseñado como elementos de la transposición didáctica de un saber.
El análisis que haremos en este capítulo, el cual –en pocas palabras– podríamos decir que abarca el estudio de cómo vive la completitud en la formación de un alumno de la licenciatura en Matemática en la UBA desde la oferta de esa institución, sólo se centra en una transposición posible y, por tanto, está regida por las condiciones institucionales que la delimitan. Para clarificar a qué aludimos cuando hablamos de condiciones institucionales, nos remitimos a los términos primitivos de la teoría antropológica (Chevallard, 1992), objeto, persona e institución, los cuales se caracterizan por las relaciones que establecen entre ellos.
En principio, todo es objeto. Los sujetos y las instituciones son objetos particulares. Un objeto existe si una persona o una institución lo reconocen como existente para sí. Tal reconocimiento lo expresamos mediante la relación que se instaura entre ellos, dando lugar a las nociones rapport personal (de una persona a un objeto) y rapport institucional (de una institución a un objeto). Así, tomamos como axioma la afirmación de que un objeto existe si al menos una persona o una institución tiene un rapport hacia él. Definimos que una persona o una institución conocen a un objeto si tienen un rapport hacia él; luego, un objeto existe si existe una persona o una institución que lo conocen.
Una persona tiene aprendizaje con relación a un objeto cuando su rapport hacia él cambia, e incluso puede aprender si la institución no tiene esa intención; por ejemplo, si no es una institución de enseñanza. Los rapports personales se construyen con las personas miradas como sujetos de instituciones; un objeto vive para un sujeto ligado a las restricciones del rapport institucional hacia ese objeto, pero una persona está vinculada a muchas instituciones. De hecho, Chevallard plantea axiomáticamente que una persona es el emergente de un complejo de sujeciones institucionales y tiene un rapport personal hacia un objeto, como producto de su pertenencia o su paso por varias instituciones.
En nuestro caso, ahondaremos en las sujeciones institucionales hacia la completitud a las que está ligado un sujeto cuando es alumno de la carrera de Matemática o del Profesorado Universitario en la Universidad de Buenos Aires, a través de cuatro cursos diferentes. Cada uno de ellos ha sido pensado como una institución diferente, tomando como primera hipótesis el hecho de que cada uno tiene un rapport institucionalpropio hacia la completitud.
Un aspecto de dichas sujeciones está dado por el conjunto de tareas propuestas a un alumno (en su carácter de sujeto de cada institución) con relación a la completitud. Sin embargo, la teoría antropológica considera que resulta insuficiente observar y analizar el conjunto de tareas, por lo cual también estudia las praxeologías. Yves Chevallard (1998) describe las praxeologías en términos de tareas – tareas, tipo de tareas y género de tareas–, técnicas, tecnologías y teorías. Las nociones de tarea y tipo de tarea suponen algo preciso; por ejemplo, "demostrar que una sucesión dada es convergente" es una tarea, "demostrar que una sucesión es convergente" concierne a un tipo de tarea, "demostrar" a secas no lo es, atañe a un género de tareas. Para Chevallard:
(..) tareas, tipo de tareas, géneros de tareas no son datos de la naturaleza: son "artefactos", "obras", constructos institucionales cuya reconstrucción en tal institución, por ejemplo, en tal clase, es un problema que pertenece completamente a la didáctica y es su objeto específico (Chevallard, 1998, p. 92, traducción libre).
En un tipo de tarea, las actividades que se realizan para su concreción reciben el nombre de técnicas. Así, para el tipo de tarea "demostrar que una sucesión es convergente" una posible técnica consiste en "mostrar que es monótona y acotada y usar el resultado teórico que asegura la existencia del límite", "mostrar que es posible acotarla superiormente e inferiormente por dos sucesiones que tengan el mismo límite y usar el resultado teórico que asegura la convergencia al mismo límite", o procurar usar "los criterios de D'Alembert o de Cauchy2"si corresponde, entre otras. Los algoritmos matemáticos son casos particulares de técnicas matemáticas.
Ahora bien, en una institución dada, de las técnicas posibles para un tipo de tarea hay una o pocas técnicas institucionalmente reconocidas, quedando excluidas otras que tal vez pertenecen a otras instituciones. Tal exclusión va de la mano de la ilusión de naturalidad con la que son vistas las técnicas reconocidas por los actores de la institución.
Los discursos que describen, explican y justifican racionalmente las técnicas constituyen la tecnología, la cual varía entre las instituciones. Así, cierta racionalidad desde una institución puede verse como poco racional desde otra; además, la tecnología evoluciona dentro de una misma institución. Los argumentos que permiten justificar racionalmente las afirmaciones tecnológicas conforman la teoría, que toma con relación a la tecnología el papel que la tecnología asume respecto a la técnica y, a la vez, organiza y estructura los conocimientos en juego. El rapport institucional hacia un objeto, en función de una posición institucional, está modelado por el conjunto de tareas que deben realizar las personas que ocupan tal posición, a través de técnicas determinadas.
Dado un objeto, que puede ser un tema de estudio, como la completitud del conjunto IR, tiene sentido estudiar las praxeologías construidas por una institución (en nuestro caso puede ser un curso, una guía de ejercicios, inclusive un problema en particular). Un conjunto organizado, que está estructurado por praxeologías, integra una organización matemática, mientras que la organización didáctica consiste en la manera de llevar a cabo la organización matemática. Con base en estas nociones generales introducidas por Chevallard, describiremos y analizaremos la organización matemática respecto a la completitud de IR a través de distintas materias en las que aparece este concepto, las cuales son consideradas en este estudio como distintas instituciones.
1.2. Funcionamiento de los conocimientos a nivel técnico, disponible, movilizable
A. Robert (1998) hace una categorización sobre la puesta en funcionamiento de conocimientos en tres niveles, la cual utilizaremos también como marco de referencia para el análisis praxeológico. Esos niveles son: 1) el técnico (a grandes rasgos, corresponde a puestas de funcionamiento bajo indicación, o haciendo aplicaciones inmediatas de teoremas o fórmulas; no se debe confundir con el sentido que toma la palabra técnico en el enfoque de Chevallard); 2) el movilizable (propio de un trabajo también indicado, pero que sobrepasa la simple aplicación de una propiedad, tal vez requiriendo de la yuxtaposición de saberes o de su articulación) y 3) el disponible (comprende al trabajo autónomo, sin indicaciones, y a la capacidad de articular la teoría para la resolución). Robert plantea, entre otras hipótesis, que no se puede alcanzar cierto nivel de conceptualización si solamente se plantean tareas técnicas entre las tareas de ese nivel.
Robert establece los nives de su categorización para estudiar el modo en que los alumnos ponen a funcionar los conocimientos. Nosotros los tomaremos para estudiar el modo en que la institución dispone las tareas que tienen que realizar los alumnos. Una tarea puede estar formulada de modo que, aún usando la misma técnica de resolución, ponga a funcionar el conocimiento a nivel técnico (por ejemplo, si no hay elecciones), movilizable (si hay algunas indicaciones) o disponible (si está formulada de modo tal que el alumno tiene muchas decisiones a su cargo). Esas son consideraciones que tomaremos en cuenta al analizar las tareas.
Distintas técnicas para la concreción de una tarea también pueden revelar los niveles de funcionamiento. En nuestro ejemplo anterior, centrándonos en un alumno de las primeras materias, la aplicación directa de un criterio de convergencia de sucesiones, utilizado casi como un algoritmo, revela un funcionamiento más ligado al nivel técnico, mientras que la acotación por otras dos sucesiones es seguramente más cercano al disponible o al movilizable, si está indicado.
Vemos aquí una distinción entre la aplicación de un método y la de un algoritmo. El primero suele dejar una mayor cantidad de decisiones a cargo del alumno, y es importante considerar allí la posición del sujeto. Probablemente un alumno de las primeras materias puede aplicar fácilmente los criterios, mas tiene dificultades para emplear el método de acotar o no se le va a ocurrir intentar acotar, aunque para un sujeto con alto nivel de autonomía ambas resoluciones pueden estar en el mismo nivel de disponibilidad. Tales observaciones las tomaremos en cuenta en el análisis praxeológico.
1.3. La problematización de lo que se percibe como evidente, la validación de ciertas afirmaciones
En algunos momentos de su formación, los alumnos tienen como tarea demostrar propiedades o resultados que han podido usar como válidos o como herramientas, sin necesidad de comprobarlos. Ellos se sorprenden si deben demostrar que a.0 = 0, la validez de algún algoritmo que venían empleando en materias anteriores (por ejemplo, los criterios de convergencia de sucesiones, mencionados en la sección 1.1), escribir formalmente algo que pueden ver en un dibujo (como que el limx 1 / x = 0), o bien imaginar mentalmente ("si f.IR
1 / x = 0), o bien imaginar mentalmente ("si f.IR 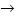 IR es continua y verifica limx
IR es continua y verifica limx f(x) = + ∞ y limx
f(x) = + ∞ y limx f(x) = – ∞ entonces es suryectiva"). Durante las horas de consulta circulan las preguntas del estilo: "¿esto te lo demuestro?", "¿qué puedo tomar como válido, hasta dónde tengo que demostrar?", "esto se ve, es obvio, no entiendo qué quieres que demuestre", "¿de dónde parto para demostrar esto?" Preguntas que muestran, por un lado, que el género de tarea no es claro para los alumnos; por otro, una cierta idea de que las demostraciones se hacen "para el docente".
f(x) = – ∞ entonces es suryectiva"). Durante las horas de consulta circulan las preguntas del estilo: "¿esto te lo demuestro?", "¿qué puedo tomar como válido, hasta dónde tengo que demostrar?", "esto se ve, es obvio, no entiendo qué quieres que demuestre", "¿de dónde parto para demostrar esto?" Preguntas que muestran, por un lado, que el género de tarea no es claro para los alumnos; por otro, una cierta idea de que las demostraciones se hacen "para el docente".
Las tareas de esta índole exigen que los alumnos pongan en práctica de nuevas técnicas, otro manejo tecnológico o un conocimiento teórico mayor, pero fundamentalmente que acepten la tarea como genuina. Esto se halla un poco ligado a considerar cierto tipo de validación –siguiendo la terminología introducida por Balacheff (1987)–, llamado pruebas intelectuales. Balacheff ha distinguido las pruebas pragmáticas de las intelectuales, al señalar que las primeras recurren a la acción para establecer la verdad de una proposición y están en cierta forma ligadas a lo empírico, mientras que las segundas se separan de la acción y se apoyan en argumentos más generales.
Dicho tema, que podríamos a grosso modo titular "pasaje de lo práctico a lo teórico" fue abordado en varias investigaciones didácticas en geometría; la marca de tal pasaje estaba dada por la exigencia de la producción de demostraciones. Como en algunas se muestra que la ruptura entre las tareas ligadas a la producción de figuras con regla y compás y las deductivas se genera a partir de un cambio de contrato didáctico, podemos pensar que estamos en presencia del mismo fenómeno en los comienzos del trabajo en el análisis a nivel superior.
Aceptar la necesidad de demostrar lo que parece evidente o perceptible tiene que ver con cierto posicionamiento interno, con la adhesión a un criterio teórico y con la reflexión, además de que en cierto sentido permanece abierta la cuestión de cómo favorecer esa reflexión desde la enseñanza. En los ochenta, las investigaciones didácticas sobre las demostraciones en geometría parecían poner de relevancia sólo el aspecto "convencer" de las pruebas; sin embargo, las pruebas cumplen otros papeles fundamentales, especialmente decidir –ya sea la veracidad o falsedad de una conjetura– y explicar, dar cuenta de ciertas afirmaciones.
Respecto al caso de demostrar aquello que parece evidente, claramente no son los aspectos "convencer" ni "decidir" los que se ponen en juego, sino más bien la comprensión y la búsqueda de razones. Podemos hallar algunos antecedentes en torno a la problemática de demostrar lo que parece evidente en el análisis histórico–epistemológico sobre el conjunto de los números reales y la completitud, presentado por Bergé y Sessa (2003). Allí, se afirma que las primeras explicitaciones de las propiedades con las que debía contar un dominio completo eran atribuidas al dominio numérico, sin haber una discusión sobre su validez; fue el deseo de fundamentar tales propiedades lo que dio lugar a las construcciones de Cantor y Dedekind. También se pone de relevancia el carácter variable de la validación, pues argumentos suficientemente válidos en cierto momento se vuelven insuficientes en otro.
En nuestro análisis consideraremos la presencia de tareas relacionadas con probar lo que parece evidente al poner la mirada, por una parte, en el modo en que está introducida esa problemática (en caso de que lo esté), por otra, en el papel que juega la representación de IR en la recta.
1.4. Un análisis de las potencialidades
El estudio praxeológico nos permite acceder a una organización matemática, pero no determinar si los sujetos, al resolver las tareas, se dedican a afinar sus técnicas de demostración (más generalmente, de acción) o si consiguen hacer una reflexión sobre sus acciones. Ahora bien, el objetivo perseguido al nivel de la reflexión por un docente que elabora las tareas es tal vez muy distante de aquello que es perceptible por el alumno a través de la lectura de las guías de tareas (trabajos prácticos). La reflexión que haga o no un alumno al concretar la resolución de las tareas no es detectada por el estudio praxeológico; empero, nos permite dar cuenta sobre las potencialidades de las tareas, pensando en qué sentido aportan a esa reflexión, si es que lo hacen.
1.5. Cálculo–análisis
El pasaje de lo pragmático a lo intelectual ha tenido su correlato en la enseñanza del análisis matemático. Circula una idea, que se nota en el diseño de la licenciatura en matemática de varias universidades, de enseñar primero cálculo elemental y después cálculo superior o análisis a secas. Al cálculo elemental le corresponde la parte más algebrizada del análisis, así como la más algorítmica; el análisis demanda otros modos de razonamiento y de técnicas que le son propias, como la acotación o la aproximación, incluso sobre las mismas nociones que pueblan el cálculo elemental.
Tal recorrido se puede ver en los programas y en los prefacios de los textos. Elon Lages Lima –un matemático brasileño cuyos textos son muy preciados sobre todo en Latinoamérica– dice en el prefacio de su obra Curso de análise, Vol. 13:
Esta es la primera parte de un Curso de Análisis. En ella se estudian las funciones reales de una variable real. La teoría es presentada desde el comienzo. No se hace uso de resultados que no estén establecidos en el texto. Todos los conceptos introducidos son ampliamente ilustrados por medio de ejemplos. A pesar de eso, es conveniente que los lectores de este libro posean una experiencia equivalente a dos semestres de Cálculo [ traducción libre]
Por su parte, Serge Lang, en el prefacio de su obra Introducción al Análisis Matemático4, expresa:
Este libro está diseñado para emplearse como texto para un primer curso de Análisis. Aunque en términos lógicos es completo en sí mismo, presupone la madurez matemática que adquieren los estudiantes que han cursado ya dos años de cálculo (...). Ahora el énfasis se desplaza de los aspectos computacionales del cálculo, a los teóricos: demostraciones de teoremas acerca de funciones continuas, trazado de curvas como x2.e–x, x.log x, x1/x, que usualmente se consideran demasiado difíciles para cursos más elementales y otros temas análogos.
Estos autores, al igual que muchos otros, reconocen una ruptura entre cálculo y análisis. Pero, ¿cuáles serían los elementos que describen y componen esa ruptura? Con una mirada didáctica identificamos el requerimiento de Lima y Lang de que se posean conocimientos de cálculo para el estudio del análisis, diciendo que el cálculo se establece como un medio5 para el análisis, donde quedarían ubicadas las fundamentaciones más profundas y muchas demostraciones. Por tanto, el estudio de la completitud se sitúa más en el análisis que en el cálculo porque lo que le da sentido es la necesidad de fundamentar.
La entrada al análisis es vista por algunos autores como el caso particular de un problema más global: el del ingreso a un nuevo dominio matemático. La tesis de Maschietto (2002) ofrece una completa síntesis de los resultados de investigaciones didácticas en lo referido a la transición álgebra/análisis. Una característica central del trabajo en análisis que Maschietto indica, y sobre la cual desarrolla su trabajo, es la introducción del punto de vista local. En efecto, un tratamiento local está en el corazón del análisis: cobra importancia aquello que sucede en un entorno de un elemento del dominio en cuestión, sin importar tanto lo que pase a nivel global e incluso a nivel puntual. La completitud no es una cuestión puntual ni completamente global.
2. REFERENCIAS TEÓRICAS II: EL PANORAMA COGNITIVO PARA IR
Robert (1998) menciona distintas herramientas para analizar los contenidos a enseñar. De ellas, repararemos especialmente en la dimensión de los niveles de conceptualización, que permite describir imbricaciones sucesivas para una misma noción. Aquí, se trata de armar las fases intermedias de estabilidad en la evolución de un cierto campo conceptual, con una organización coherente que contenga los objetos matemáticos presentados de cierta forma, los teoremas sobre los objetos, los métodos asociados a esos teoremas y los problemas que los alumnos pueden resolver con los teoremas del nivel considerado.
Si tomamos como referencia los niveles de conceptualización, el análisis histórico–epistemológico y nuestra propia experiencia docente, es posible que imaginemos seis ejes o dimensiones útiles para obtener un panorama sobre la conceptualización de la continuidad y la completitud de IR. Los distintos estados para cada eje, vistos globalmente, constituyen para nosotros un modelo a priori –tanto como insumo para un estudio institucional como para interpretar respuestas de los alumnos– que cumple el papel de hacer observables ciertos fenómenos. En ese sentido, su validación está dada exclusivamente por su fertilidad explicativa.
Hemos pensado los ejes ligados tanto a la disponibilidad técnica de un sujeto teórico acerca de tales nociones (primer eje) como al grado de reflexión de un sujeto teórico sobre el carácter de herramienta y de objeto de la completitud, sobre la necesidad de incluirla como una condición en la definición de IR, sobre la fundamentación que se lleva a cabo en torno a estas nociones, sobre la utilización flexible de los distintos aspectos de la completitud y sobre su visión acerca de las construcciones de IR (los otros cinco ejes). Asimismo, hemos considerado un estado inicial teórico, común a los ejes. En lo que resta de esta sección, describiremos el estado inicial y los ejes.
2.1. El estado inicial
El estado inicial corresponde a una visión sobre la completitud intuitiva, no problematizada, dada por el carácter preconstruido6 de las formas de la completitud que puedan aparecer. Un sujeto opera como si las propiedades se verificasen naturalmente y hace uso de ciertos resultados, sin preocuparse por su fundamentación; además, hay una naturalización de las herramientas para producir conocimiento, ya que la justificación es algo externo al sujeto, su interés se centra en la utilización de dichas herramientas.
Con respecto a la completitud, a este nivel ciertas propiedades de los objetos geométricos (por ejemplo, la continuidad natural de la recta) son transferidas al dominio numérico. Aunque este estado admite muchas posibles variantes, para nuestro trabajo las hemos englobado en uno solo. En tal sentido, es un estado inicial teórico donde pueden convivir varias concepciones contradictorias.
Tareas como las aplicaciones simples para determinar la existencia de raíces o determinar la existencia de límite de sucesiones monótonas acotadas, examinando respectivamente las hipótesis del teorema de Bolzano o las condiciones de monotonía y acotación en las sucesiones, son acordes al estado inicial.
Otra tarea que asociamos a dicho nivel es la de hallar supremos e ínfimos de ciertos conjuntos sencillos, donde el supremo e ínfimo aparecen en el rol de cotas óptimas de conjuntos accesibles por una representación en la recta, lo cual fortalece su naturalización.
A partir de este estado inicial, consideramos seis ejes que describimos a continuación.
2.2. Los ejes del panorama cognitivo
A continuación presentaremos los seis ejes, retomando para cada uno el estado inicial, al igual que describiremos algunos estados intermedios, los cuales no deben tomarse como un "camino" que ha de seguirse.
2.2.1. Disponibilidad técnica
Tomamos como variable el grado de dominio técnico y teórico que tiene un sujeto alrededor de la completitud y la continuidad. Podemos pensar en una organización teórica de esa disponibilidad por medio de los siguientes niveles, a sabiendas de que hay muchos subniveles intermedios que no describiremos aquí:
• Un nivel inicial, al cual hemos hecho referencia, que en este eje vemos plasmado en saber hacer uso de los teoremas de Bolzano y de la existencia de límites en aplicaciones simples, o bien en determinar supremos o ínfimos de conjuntos sencillos accesibles mediante una representación en aplicaciones simples.
• Un nivel en el que el sujeto encuentra la demostración de teoremas como el de Bolzano o la existencia de límite de sucesiones monótonas y acotadas, y puede reproducirlas si maneja explícitamente en esas demostraciones u otras tareas alguna versión del axioma de completitud; por ejemplo, el de supremo. Un sujeto en esta posición ve a las demás caracterizaciones como teoremas, no como posibles equivalentes. Las tareas acordes con este nivel son la demostración de los teoremas ya mencionados; asimismo, le corresponde la adquisición de técnicas para la manipulación de los objetos ligados a la versión de la completitud que se utiliza, como la demostración de la equivalencia entre las distintas caracterizaciones del supremo.
• Un nivel en el que un sujeto encuentra varias formas equivalentes de expresar la completitud de IR, donde habría una subcategorización en función de los enunciados disponibles para ese sujeto. Cada una de las caracterizaciones sobre la completitud involucra distintos objetos y la destreza en su manipulación hace que, a este nivel, la disponibilidad técnica se presente como un cierto dominio en la utilización de sucesiones, de sucesiones de Cauchy, de encajes de intervalos, de las distintas caracterizaciones del supremo, cortaduras, etc.
• Un nivel en el que un sujeto, además de que puede observar la completitud desde el contexto de espacios más generales, es consciente de que ciertas formas de expresión sobre la completitud en IR se generalizan para espacios métricos, mientras que otras ponen en juego propiedades específicas de IR, relacionadas fundamentalmente al hecho de que éste es ordenado.
2.2.2. Instrumentalidad / objetivación
A partir de las categorías de R. Douady (1986), este eje valora la medida en que la completitud se percibe como herramienta y como objeto de estudio. Si bien en el estado inicial no hay una identificación de la completitud como herramienta ni como objeto, pues sólo se utiliza en su carácter de preconstruido, en un estado más avanzado es percibida como una herramienta que posibilita definir números o entes bajo ciertas condiciones –las distancias de un punto a un conjunto o entre dos conjuntos, o la demostración de la existencia de un elemento mediante un encaje–, así como probar que ciertos extremos se realizan, ciertas distancias se realizan, etc.
En un estado más avanzado aún, la completitud es apreciada como una herramienta en el contexto de espacios más generales. Como objeto, hay distintos niveles de objetivación que están dados por la diferenciación de IR con Q en primer lugar, ya que se reconoce a la completitud como un atributo adicional al de la densidad del orden y a IR como algo más que la simple yuxtaposición de los racionales y los irracionales. Dentro de un nivel más alto, se distingue a la completitud como una propiedad de IR en alguna de sus formas; por ejemplo, el axioma de supremo. Y en un nivel más alto aún, es vista como un objeto de estudio en el marco del estudio de espacios más generales.
Ahora bien, en la explicitación de la completitud como instrumento y como objeto también notamos dos instancias: la declarativa o discursiva y la que se actualiza en el trabajo matemático, lo cual posibilita su uso técnico.
2.2.3. Necesidad
Este eje valora en qué medida un sujeto comprende la necesidad de considerar la completitud –en alguna versión– para definir a IR. En el estado inicial un sujeto no percibe la necesidad de explicitar la completitud porque es una propiedad transparente; si en algún grado la aprecia, parece verificarse naturalmente. Sin embargo, a cierto nivel de este eje un sujeto deja de ver como transparente a la completitud; incorpora un grado de problematización sobre esa cuestión y toma a la teoría como objeto de estudio.
En un nivel más alto, el sujeto puede ver a la completitud como una condición necesaria; tal hecho se encuentra ligado a comprender que el trabajo en análisis que se ha venido desarrollando descansa en esas condiciones, las cuales se aseguran para el dominio de trabajo. De modo más transversal, un sujeto que percibe como necesario incluir un axioma para el desarrollo de una teoría ha hecho una reflexión sobre los modos de reorganización de los saberes matemáticos.
2.2.4. Validación y fundamentación
Este eje considera dos aspectos: por una parte, en qué medida un sujeto concibe la necesidad de fundamentar en matemática; por otra, distingue el tipo de validación llevada a cabo (dichos aspectos no se presentan en el nivel inicial porque la fundamentación es algo externo al sujeto, que hace uso de resultados y teoremas sin tomar a su cargo su validación).
Con respecto al tipo de validación, puede tener un soporte empírico, apoyada en la visualización de una representación. En un nivel más avanzado de este eje, un sujeto argumenta las afirmaciones matemáticas y distingue una validación empírica de una que exige la movilización de otras herramientas matemáticas. La noción matemática de completitud, que a cierto nivel admite un soporte empírico, es sumamente particularmente fértil para distinguir entre los tipos de validación.
2.2.5. Flexibilidad
Este eje valora la capacidad de un sujeto para percibir las diferentes expresiones de la completitud como equivalentes y para saber utilizar una u otra, según la ocasión. No lo incluimos en el estado inicial que diseñamos para poner en común a todos los ejes, pues no se trabajan las equivalencias de la completitud a ese nivel; su aprendizaje se realiza después de un par de semestres de cálculo. Los distintos estados del eje están dados por los diferentes enunciados de los que se disponga y por su uso, de acuerdo con las tareas a realizar.
2.2.6. Posición frente a las construcciones de IR.
Este eje valora la comprensión que puede tener un sujeto, tanto acerca del sentido de que IR sea construido a partir de Q como del rol de modelo que puede adquirir esa construcción con relación a la definición axiomática. Tampoco lo consideramos en el estado inicial común a los ejes porque el aprendizaje de las construcciones se efectúa después de dos semestres de cálculo. Comprender la necesidad o el sentido de las construcciones de IR requiere pensar las condiciones que necesita un conjunto a fin de ser un buen dominio para el análisis o para desarrollar otras teorías, como en el caso de la completación de espacios métricos.
Podemos pensar que un sujeto que se plantea tales cuestiones comprende mejor la propiedad de un conjunto de ser completo. Un sujeto que puede percibir el rol de modelo que juega la construcción para un sistema de axiomas es alguien que ha hecho una reflexión acerca de la consistencia de las teorías matemáticas. Los distintos estados que asume un sujeto sobre este eje son el "valor cero" (si no conoce las construcciones), el nivel intermedio (si sabe algunas construcciones y puede percibirlas como modelos para la definición axiomática) y el nivel correspondiente a entender que tales construcciones fueron la respuesta de los matemáticos a la necesidad de conocer cuál era el dominio numérico con el que venían trabajando desde hacía varios siglos.
2.3 Estructura multidimensional
Un sujeto puede estar convencido de que es necesario demostrar los teoremas y comprender que el axioma de completitud permite definir ciertos números, pero no haber adquirido la destreza para demostrar teoremas con la completitud.
Asimismo, un sujeto puede saber demostrar esos teoremas e incluso demostrar las equivalencias (teniendo un estado alto en el eje de disponibilidad técnica), sin que esto le requiera necesariamente que haga una reflexión sobre su reutilización o su potencia, o sin que sepa en qué problema le conviene emplear una u otra caracterización de la completitud, conservando un valor bajo en el eje de flexibilidad.
También es posible que un sujeto, aunque sepa reproducir las construcciones y el teorema de completación, permanezca en un estadio bajo en los ejes de necesidad, fundamentación e instrumentación. El crecimiento cognitivo no es necesariamente uniforme; un sujeto puede estar avanzado en un eje y no en otros.
La separación de estos ejes es en cierto modo ficticia, pero resulta útil para poder pensar globalmente distintos valores en cada uno, como un modelo donde cierto estado de conceptualización es visto como una 6–upla dada por algún valor para cada eje.
A continuación, presentaremos las preguntas que guían el análisis de nuestra investigación.
3. ORGANIZACIÓN INSTITUCIONAL. HIPÓTESIS A PRIORI. PREGUNTAS PARA EL ANÁLISIS
Haremos un análisis praxeológico sobre el tema de estudio, Completitud del conjunto de los números reales en la institución Primeros años de la Licenciatura en Matemática y Profesorado Universitario de Matemática de la Universidad de Buenos Aires (UBA), donde consideraremos cuatro cursos. El primero, Análisis Matemático, forma parte del primer año que llevan los alumnos de la UBA, denominado Ciclo Básico Común (CBC); los otros tres, Análisis I, Complementos de Análisis II y Cálculo Avanzado, dependen del Departamento de Matemática de la Facultad de Ciencias Exactas y Naturales de la UBA. Al terminar el estudio, deseamos poder caracterizar a qué categoría o categorías del panorama cognitivo potencialmente aportan las tareas que tienen a cargo los alumnos en cada curso.
Algunas preguntas o ítems que van a guiarnos en nuestro estudio praxeológico al interior de cada curso son:
• ¿Qué tipo de apariciones hace la completitud en las tareas y en las técnicas? ¿Cómo aparece y cómo se usa?
• ¿Qué técnicas se utilizan en la resolución de las tareas? ¿Cuánta tecnología y teoría requieren esas técnicas? ¿Se trata de técnicas que consisten en la aplicación aislada de un teorema o propiedades? En el caso de la utilización de propiedades, ¿"es llamada" desde la formulación de la tarea o permanece implícita? ¿En qué medida es necesario para desplegar la técnica el proceso de demostración de las propiedades o teoremas? ¿En qué medida solamente el enunciado de los mismos?
Con respecto al género de tareas y a su formulación, tendremos en cuenta si favorecen un funcionamiento del conocimiento más a nivel técnico ("hallar", "resolver", "calcular", ítems aislados), movilizable ("demostrar usando tal resultado", varios ítems secuenciados) o disponible ("estudiar", "analizar", "demostrar", etc.). Procuraremos identificar los momentos en los que las técnicas usadas se vuelven insuficientes, así como los puntos de equilibrio, continuidades, rupturas y falsas continuidades.
Referente al grado de problematización de aquello que parece evidente u observable, veremos si hay tareas que involucren un trabajo de demostración de propiedades o resultados "observables", "evidentes". Asimismo, en qué medida hay una problematización y hasta qué punto las representaciones utilizadas condicionan las tareas que se proponen y si se presenta una evolución en tal dirección:
• ¿Qué elementos de las tareas serían indicadores de reflexión? ¿Qué discurso explicativo acompaña a las tareas? ¿Qué reflexiones podrían hacerse sobre ellas? ¿En qué sentido aportan a la reflexión sobre el hecho de que IR sea definido mediante un conjunto de axiomas?
• ¿Qué elementos de la ruptura cálculo–análisis se hacen presentes en las prácticas? Si hay elementos que introduzcan el punto de vista local, ¿cuáles son y cómo hacen ese proceso? ¿Qué elementos tiene el alumno para validar? ¿Qué criterios de validez favorece la realización de estas prácticas?
• ¿En qué medida las tareas contribuyen a hacer evolucionar los ejes introducidos en el panorama cognitivo?
En las secciones siguientes, analizaremos las praxeologías de las materias mencionadas. Hemos elegido la opción de pasar materia por materia. La primera parte es posiblemente un poco monótona, ya que analizamos ejercicio por ejercicio, pero presentamos una síntesis para algunas de las materias y las retomamos en forma global al final, a fin de ponerlas en relación con el panorama cognitivo.
4. ANÁLISIS MATEMÁTICO DEL CICLO BÁSICO COMÚN (CBC)
4.1 Las guías de trabajos prácticos
Esta materia tiene una duración cuatrimestral y su carga horaria es de nueve horas semanales (tres encuentros de tres horas teórico–prácticas). Consiste en un primer curso de Cálculo en una variable y su guía de trabajos incluye una práctica titulada Números reales, donde aparecen por primera vez las tareas vinculadas a la completitud. Los materiales para analizar son los enunciados de los ejercicios de la guía y la planificación docente oficial.
La guía de trabajos prácticos titulada Números reales comprende doce ejercicios en los que distinguimos tres tipos de tareas: representar subconjuntos de IR en la recta, demostrar la irracionalidad, y determinar supremos e ínfimos, máximos y mínimos de ciertos subconjuntos de IR con diferentes exigencias de justificación, según el caso. El objetivo de la guía parece ser que apunta a poder describir los conjuntos de IR y adquirir familiaridad con las nociones de supremo e ínfimo.
La noción de supremo surgió en la matemática cuando se volvió necesario nombrar o determinar a ese número, en el contexto de funciones continuas definidas en un intervalo o de sucesiones cuya convergencia parecía evidente –monótonas acotadas–; su existencia quedó garantizada una vez que IR estuvo bien definido. Más allá de las situaciones históricas a partir de las cuales se le identificó como una noción de la matemática, un matemático actual utiliza el supremo esencialmente para definir un número con determinados atributos.
En este trabajo práctico de Números reales, las nociones de supremo e ínfimo aparecen antes del tratamiento de límite y del de funciones continuas en intervalos, así como del trabajo correspondiente al análisis. Se muestran como un fin en sí mismo, en buena medida despojados de su función de herramienta y su "utilidad" a ese nivel podría ser la de constituir cotas óptimas si el conjunto no tiene máximo o mínimo. Desde nuestro punto de vista, esto es el efecto de la elección de una transposición que privilegia el recorte del saber en porciones que permiten la ejercitación y la evaluación, aunque se separe de la instrumentalidad de los conceptos.
Hay un primer grupo de cuatro ejercicios donde se pide representar en la recta algunos números, las soluciones de ciertas inecuaciones, las intersecciones y uniones de algunos intervalos de IR y ciertos conjuntos discretos, uno de ellos infinito. Con ello, se da un lugar importante a la representación de subconjuntos de IR en la recta, que es tomada en forma natural, sin ser problematizada. La cuestión de la representación pasa por estas prácticas sin una reflexión acerca de qué es la recta, cuáles son sus propiedades, si es posible determinar o no un "lugar" en la recta para cada número real, etc.
Un segundo grupo de ejercicios los podemos englobar en la tarea de hallar supremos, ínfimos, máximos y mínimos. En ellos hay un fraccionamiento de las tareas en subtareas que parecen tener como objetivo "ayudar" a obtener las respuestas. Por otra parte, va creciendo la exigencia de justificación, admitiéndose en un comienzo respuestas más intuitivas, ligadas al registro gráfico, para ir avanzando a formas más precisas y un poco menos asociadas a la visualización, casi al final de este grupo de ejercicios.
En uno de los ejercicios el tipo de tarea es encontrar, si existen, el supremo y el ínfimo para ciertos subconjuntos reales y analizar si son máximos o mínimos, lo cual indica la pérdida de sentido sobre la noción de supremo. La tarea se presenta fraccionada, ayudada por dos subtareas: la primera consiste en determinar si ciertos números son cota, la segunda en decidir si los subconjuntos son acotados. Un primer nivel de respuesta puede darse apoyándose fuertemente en la representación que se tiene de los subconjuntos en la recta, una tarea instalada en la primera parte de la práctica. En particular, casi todos los subconjuntos de este ejercicio son análogos a los que hay que representar en la recta, planteados en la primera parte de la guía. Además, todos los supremos e ínfimos cuando existen son números enteros, salvo un mínimo que da  , lo cual facilita su identificación a partir de la representación.
, lo cual facilita su identificación a partir de la representación.
Los ejercicios posteriores solicitan cierta justificación de los resultados obtenidos antes. Uno de ellos pide mostrar que 1 es cota superior del conjunto formado por los cocientes de naturales n / (n+1), así como exhibir un elemento del conjunto entre 0,9 y 1 y otro del conjunto entre 0,99 y 1. La palabra mostrar en este enunciado indica que hay que hacer algo más que encontrar, lo cual se pedía en el ejercicio anterior. A pesar de que con este ejercicio se avanza un poco en la justificación, el trabajo queda inconcluso, pues no se llega a justificar que 1 es el supremo. El trabajo podría extenderse hasta mostrar que es posible encontrar elementos del conjunto tan cercanos a 1 como se quiera, pero esto se hace en el siguiente ejercicio. La relación entre ambos ejercicios no se explicita en los enunciados; dicha tarea deberá realizarla el docente o quedará para el trabajo personal de los alumnos.
La tarea en otro ejercicio consiste en justificar que el ínf  y también se encuentra subdividida en dos subtareas. La primera es numérica y puede hacerse por tanteo o despejando; esto último abre el camino para la tarea principal. El hecho de que el conjunto esté dado por una expresión de tipo homográfica permite operar y demostrar lo que se pide sin necesidad de utilizar técnicas más analíticas, como el paso al límite.
y también se encuentra subdividida en dos subtareas. La primera es numérica y puede hacerse por tanteo o despejando; esto último abre el camino para la tarea principal. El hecho de que el conjunto esté dado por una expresión de tipo homográfica permite operar y demostrar lo que se pide sin necesidad de utilizar técnicas más analíticas, como el paso al límite.
Además, en este ejercicio se menciona la arquimedianidad, que en el contexto de la representación se vuelve transparente; parece no haber algo nuevo por demostrar7.
Estos dos ejercicios sirven para acrecentar las destrezas a la hora de demostrar, pero no para enriquecer los sentidos sobre el supremo. Cambia el tipo de tarea al pasar al ejercicio siguiente, pues ya no hay que justificar, sino "ordenar de menor a mayor". Asimismo, es una tarea ligada al aspecto "descriptivo" del supremo y se muestra un cambio fuerte con el tipo de tareas que se venía desplegando, ya que la dificultad en las demostraciones iba creciendo y, de golpe, desaparece.
En el último ejercicio de esta guía la tarea es determinar los supremos, ínfimos, máximos y mínimos en tres subconjuntos (uno del dominio y dos de la imagen) de una función cuadrática. Algo que distingue este ejercicio de los anteriores es que no tiene subtareas cuya resolución contribuya a la resolución de la tarea principal; tal vez por eso se ubica en el último lugar, mostrando una mayor autonomía. La técnica, en el caso del primer ejercicio, está dada por factorear y escribir el conjunto como unión de intervalos y dar las respuestas a partir de su determinación. Para resolver los otros a este nivel, se asume que la imagen de un intervalo por una función continua constituye un intervalo. Hallar la imagen de una cuadrática o de una cuadrática restringida a un intervalo es un ejercicio que los alumnos han realizado en prácticas anteriores.
El esquema que parece seguir esta guía de trabajos prácticos es comenzar por la presentación del supremo y las pequeñas aplicaciones, seguir con una parte más teórica y finalizar con aplicaciones un poco más complicadas que las anteriores, más autónomas, sin subtareas.
Con respecto a otros temas ligados a guías de trabajos prácticos posteriores (Sucesiones y Límites y continuidad), algunos tópicos en los que se relacionan las sucesiones y las funciones continuas con la completitud, y que en algún sentido están presentes en el trabajo en esta materia, son el hecho de que la convergencia de sucesiones monótonas acotadas sólo se asegura en un dominio completo, que vale el teorema de Bolzano para funciones continuas definidas en intervalos y las funciones continuas sobre intervalos cerrados reales alcanzan sus extremos.
Aquí, las tareas consisten en hallar límites de sucesiones que pueden ser mostradas como monótonas y acotadas, hallar las soluciones de ciertas ecuaciones que se enmarcan en las hipótesis del teorema de Bolzano, o encontrar intervalos donde se garantiza la existencia de una raíz. En tales prácticas, los teoremas son resultados fuertes que sirven para asegurar la convergencia o la existencia de raíces; por eso no hay terreno para problematizar la completitud.
4.2. La guía del docente
Entre los materiales que hemos analizado con respecto a esta materia, contamos con una "guía del docente", la cual consiste en una planificación clase por clase, elaborada por la cátedra de esta materia, y muestra el rapport institucional que se ha concebido sobre este tema. Dicha guía señala que es la intención de esta institución trabajar durante dos clases este tema. La primera comprenderá la representación en la recta, demostrar que  2 no es racional (destacando que la prueba se da por el absurdo, ya que será una técnica muy usada), mencionar la densidad, dar los axiomas de cuerpo ordenado, así como hacer notar que los reales y los racionales no se distinguen por esos axiomas. En la segunda clase, la planificación indica dar el axioma de completitud en su versión del supremo y destacar que no se cumple en Q, enunciar el principio de Arquímedes y usarlo para resolver el ejercicio donde hay que justificar que inf
2 no es racional (destacando que la prueba se da por el absurdo, ya que será una técnica muy usada), mencionar la densidad, dar los axiomas de cuerpo ordenado, así como hacer notar que los reales y los racionales no se distinguen por esos axiomas. En la segunda clase, la planificación indica dar el axioma de completitud en su versión del supremo y destacar que no se cumple en Q, enunciar el principio de Arquímedes y usarlo para resolver el ejercicio donde hay que justificar que inf  al igual que discutir con los alumnos distintos ejemplos en los que el supremo o ínfimo pertenezcan o no al conjunto. ¿Qué lugar ocupa el supremo para los alumnos a partir de estas tareas? ¿Es posible verlo como una herramienta útil y necesaria?
al igual que discutir con los alumnos distintos ejemplos en los que el supremo o ínfimo pertenezcan o no al conjunto. ¿Qué lugar ocupa el supremo para los alumnos a partir de estas tareas? ¿Es posible verlo como una herramienta útil y necesaria?
Sin embargo, el tipo de tarea deja al supremo y al ínfimo del lado de describir los conjuntos. ¿Qué valor agrega en relación con la caracterización de IR discutir si el supremo es o no un máximo? ¿Qué estatuto –es algo útil, accesorio o innecesario– puede tener para los alumnos el principio de Arquímedes en el contexto de representaciones desplegado a partir de los primeros ejercicios? El análisis de las tareas indica que no hay un correlato entre la guía docente y la de ejercicios, ya que la intención de distinguir a IR de Q, enunciada en la guía docente, no se ve plasmada en ejercicios que aborden dicha cuestión.
Con respecto a la relación entre sucesiones y completitud, la planificación incluye que sea enunciado, sin demostración, tanto el teorema que asegura la existencia del límite de sucesiones monótonas y acotadas como el que afirma que, de toda sucesión acotada, puede extraerse una subsucesión convergente. Los alumnos tienen a disposición un apunte teórico oficial de la materia en el que pueden encontrar las demostraciones, que se apoyan en el axioma del supremo. En lo tocante a la relación entre funciones continuas y completitud, se incluye en la planificación el teorema de Bolzano, destacando que en su demostración se utiliza el axioma de supremo.
De este modo, la completitud permanece encapsulada en estos tres teoremas. Los alumnos pueden avanzar en las prácticas sin aludir a la completitud porque prevalecen estos resultados, que son vistos como muy potentes. Si bien en la demostración del teorema de Bolzano se destaca que se emplea el axioma del supremo, eso queda en un lugar que "vive poco" para los alumnos, parece necesario sólo para el docente, no para ellos, por lo cual queda limitado al momento de la demostración. El tipo de tareas propuestas y la presencia de resultados que son vistos como instrumentos para resolver esas tareas hace que el rapport personal hacia la completitud en esta materia esté más ligado a las representaciones, a las nociones de cotas y extremos, permaneciendo en un nivel más bien nominal.
4.3. Síntesis de análisis del CBC
En los ejercicios que analizamos se hacen presentes las cotas, los supremos, los ínfimos y los extremos –máximos y mínimos–como instrumentos para describir y comprender un poco más la naturaleza de los subconjuntos de IR, mientras que el trabajo se desarrolla mayoritariamente con un apoyo fuerte en las representaciones. La problemática de demostrar lo que parece evidente hace pequeñas apariciones, pero el fraccionamiento de esta tarea en subtareas hace que no se despliegue. El supremo y el ínfimo se muestran como nociones en sí mismas, no vinculadas a otros objetos matemáticos, de modo que se desligan de las situaciones en las que son necesarios para definir números, reduciéndose considerablemente su sentido instrumental.
El axioma de completitud hace una aparición en esta materia, pero parece algo necesario para el docente, no para los alumnos. El análisis que hicimos nos permite ubicarla dentro del estado inicial señalado en el panorama cognitivo.
5. ANÁLISIS I DE CIENCIAS EXACTAS
Esta es una de las primeras materias que cursan los alumnos en la Facultad de Ciencias Exactas, a continuación del CBC. Se encuentra organizada en 10 horas semanales, 4 de teoría, donde se introducen los temas, se dan las definiciones y se demuestran los teoremas (las clases están a cargo del profesor) y 6 de práctica, durante las cuales se resuelven problemas en el pizarrón, habitualmente la mitad del tiempo (eso depende del docente ) y se responden consultas personales. Estas clases son impartidas por docentes auxiliares, quienes normalmente son estudiantes del doctorado, recientes doctores o alumnos avanzados de licenciatura.
La completitud del conjunto IR está vinculada con las siguientes unidades del programa: Sucesiones, Series Numéricas y Teoremas sobre funciones continuas. Los materiales de los que disponemos para analizar son los enunciados de los ejercicios que necesitan hacer los alumnos, las notas tomadas por dos alumnos distintos sobre la primera clase teórica de la materia –relacionada con el tema de la completitud– y dos entrevistas hechas a dos docentes de clases prácticas.
5.1 Breve descripción de las dos primeras clases teóricas
Las notas de las clases teóricas indican que en la primera sesión empezó con tres definiciones: 1) cota superior de un subconjunto de IR, 2) máximo y 3) supremo de un subconjunto de IR acotado superiormente, como la menor cota superior. Quedó demostrado que cuando el supremo existe es único y se enunció como axioma que todo conjunto no vacío, acotado superiormente, tiene supremo. También se especificaron las nociones de cota inferior e ínfimo, así como se expresó y demostró el primer teorema: todo conjunto acotado inferiormente y no vacío tiene ínfimo. La justificación, muy detallada, se basó en el axioma dado anteriormente, considerando el conjunto de los opuestos aditivos. Cuando el tema cambió a sucesiones, se proporcionó la definición de límite de una sucesión, se expuso el álgebra de límites (sin demostración), se puntualizó qué es la sucesión creciente y la acotada, y se comprobó con todo detalle, usando el axioma, que toda sucesión creciente y acotada converge al supremo.
En la segunda clase teórica se definieron las nociones de intervalo real abierto, conjunto abierto y clausura de un conjunto. Se puntualizó que el conjunto cerrado es aquel que coincide con su clausura, se demostró que un conjunto es abierto si y sólo si su complemento es cerrado, al igual que se enunció y argumentó en forma detallada el teorema dado un conjunto y un elemento de su clausura, existe una sucesión contenida en el conjunto que converge a ese elemento. Asimismo, se especificó el límite funcional y la continuidad puntual de una función real, y se probó la equivalencia con la definición de función continua en un punto por sucesiones.
Estas notas señalan que, en relación con los temas de completitud vistos en Análisis del CBC, los alumnos cuentan con los mismos elementos teóricos, las mismas definiciones y la misma versión del axioma de completitud, aunque con mucho mayor detalle y formalidad en su exposición y estructuración. Hasta aquí no hay contenidos nuevos respecto a la completitud, ni la explicitación de situaciones en la que sea una herramienta necesaria.
5.2. La primera guía de trabajos prácticos de Análisis I de Exactas
En cuanto a la completitud o a IR, las tareas de la primera práctica consisten en representar ciertos subconjuntos de IR, mostrar que algunos conjuntos no están acotados, calcular supremos, ínfimos, máximos y mínimos –en algunos casos argumentar que lo son–, analizar la existencia del límite en determinadas sucesiones (monótonas y acotadas), demostrar la validez de los criterios de D'Alembert y Cauchy, así como probar que el conjunto de los racionales cuyo cuadrado es menor a 2 no tiene máximo ni supremo en Q.
A excepción de las últimas dos tareas, todas las anteriores figuraban en la práctica de Análisis I CBC, y sus ítems podrían haber estado en la práctica de dicha materia. El tipo de tarea que necesitan realizar los alumnos con relación al tema muestra una gran similitud con los anteriores; sin embargo, las técnicas de resolución que se espera para las tareas son diferentes porque en esta materia hay que demostrar, las pruebas deben ser pruebas formales y se esperan resoluciones distintas de las que había en la institución anterior, aunque los contenidos y situaciones en las que se despliegan sean los mismos.
Tomemos el ejercicio donde se pide mostrar que el conjunto formado por los cuadrados de los naturales no está acotado superiormente. Si esta tarea hubiera estado en la práctica de Análisis del CBC (hay otros análogos), su justificación podría basarse en una representación, o bien tomar como punto de partida que IN no está acotado y usar, por ejemplo, que n2 > n. No obstante, a este nivel se espera otro tipo de resolución. Los dos docentes de prácticas entrevistados respondieron por separado que esperan de este ítem una prueba formal, utilizando arquimedianidad: dado un número M cualquiera, es posible exhibir un elemento del conjunto en cuestión mayor que M. Una posibilidad es considerar un n > M (por la arquimedianidad) y emplear que para los naturales n2 > n , de donde n2>M. Otra posibilidad es atender al número  M y tomar un número natural n mayor que
M y tomar un número natural n mayor que  M ; aquí se requiere también de la completitud para justificar la existencia de la raíz de M. Lo que cambia respecto a la resolución posible para el CBC es qué versión de la arquimedianidad se toma como punto de partida, su explicitación y cómo se escribe. Ahora bien, ¿cómo se negocia, si es que sucede, esta diferencia con los alumnos, más aún cuando el tipo de tarea es la misma?
M ; aquí se requiere también de la completitud para justificar la existencia de la raíz de M. Lo que cambia respecto a la resolución posible para el CBC es qué versión de la arquimedianidad se toma como punto de partida, su explicitación y cómo se escribe. Ahora bien, ¿cómo se negocia, si es que sucede, esta diferencia con los alumnos, más aún cuando el tipo de tarea es la misma?
El tipo de tarea que hay en el siguiente ejercicio es calcular supremos, ínfimos, máximos y mínimos –si existen– de ciertos subconjuntos de IR y probar que lo son. Uno de los conjuntos es finito, mientras que los otros son infinitos y discretos (forman el rango de una sucesión). La representación y la escritura por extensión de los conjuntos, al igual que la manipulación algebraica, pueden ser un medio de conjeturar los valores buscados. El conocimiento sobre sucesiones de monotonía y límites, que han aprendido los alumnos en la materia anterior, posibilita nuevas técnicas8.
Como ellos cuentan con más herramientas para la resolución podrían acceder a problemas donde el supremo y el ínfimo se pongan en juego, con un carácter más próximo al instrumental; sin embargo, esas nociones siguen teniendo el mismo sentido de la materia anterior en tareas que sólo parecen existir en el contexto de estos cursos.
La tarea de otro ejercicio pide demostrar que el conjunto no tiene máximo ni supremo en Q. Esta actividad marca una ruptura en dos sentidos. Hasta ahora, todos los conjuntos acotados tenían supremo en el conjunto en que estaban definidos, IR. Por otra parte, el supremo cumple otro papel, lo cual permite pensar en alguna diferencia entre Q e IR. Hay varias técnicas de resolución para esta tarea, según lo que se decida tomar como punto de partida. Mencionamos algunas:
no tiene máximo ni supremo en Q. Esta actividad marca una ruptura en dos sentidos. Hasta ahora, todos los conjuntos acotados tenían supremo en el conjunto en que estaban definidos, IR. Por otra parte, el supremo cumple otro papel, lo cual permite pensar en alguna diferencia entre Q e IR. Hay varias técnicas de resolución para esta tarea, según lo que se decida tomar como punto de partida. Mencionamos algunas:
1)Partir de un elemento m del conjunto, esto es, m2<2, m racional y, por ejemplo, buscar un natural n, tal que (m + l / n)2<2. Así, uno se asegura que m + 1 / n es racional. Si se acota superiormente 1 / n2 con 1/ n y m con 2, se obtiene una condición de tipo n>5 / (2–m2), que asegura que siempre va a haber un racional mayor.
2)Pensar al conjunto como un subconjunto más de IR; esto es, el conjunto de los m en Q, tales que (–
2) <m<
2 , y aplicar los resultados que han sido desarrollados en la clase teórica. Este subconjunto tiene supremo y se puede demostrar que es
2 de varias maneras: una de ellas es por el absurdo, usando la densidad de Q en IR, y demostrar finalmente que el supremo no está en Q. Como esto puede no resultar interesante a los alumnos, pueden hacer la analogía con un caso que ya conocen: el de los conjuntos que tienen supremo y no máximo. En el enunciado no hay elementos que generen una reflexión acerca de que el axioma deja de ser válido si solamente se piensa en Q. Desde ese punto de vista, el ejercicio no tendrá una significación particular para los alumnos.
3)Usar la menor cantidad posible de conocimientos iniciales. Esa fue la opción que tomó uno de los docentes consultados. En la entrevista, él dijo: "Yo lo hice en el pizarrón y a la clase siguiente vinieron muchos a preguntarme detalles de la demostración, a mí y a los otros ayudantes. Al hacerlo, asumí que no sabíamos nada, ni siquiera que entre dos racionales hay un irracional, ni que hay un racional; supuse que no conocíamos ningún resultado sobre densidad. Construimos todo a mano. Solo usé que puedo elegir un racional positivo entre cero y otro número racional, por ejemplo, dividiendo por dos. A la clase siguiente los alumnos preguntaban: "¿me puedes decir por favor qué tengo que demostrar y qué no?, ¿qué es obvio y qué no? Por ejemplo, en el ejercicio 4, ¿se asume que 2 es un irracional? La idea es que no, pero... ¿porqué no, si eso ya lo sabemos?"
En toda demostración hay algo que se asume; en este caso, como hemos visto, se puede empezar por otros puntos iniciales. Las cosas que el docente no quiere asumir como punto de partida no son nuevas; las dos resoluciones alternativas que hemos expuesto lo indican. Él tal vez desea mostrar que hay que demostrar en esta materia y utiliza el ejercicio con tal fin, tomando una posición algo extremista para marcar la ruptura de contrato y alcanzar el objetivo de movilizar en dirección a la actividad de demostrar.
La tarea de otro ejercicio es hallar supremos e ínfimos de ciertos subconjuntos de IR. Aquí, los ítems son algebraicamente más complejos que los del CBC, pero podrían haber estado en esa práctica. Con los conocimientos que han adquirido los alumnos en la materia anterior (límites, especialmente, y distintas técnicas para determinar crecimiento o decrecimiento) se amplía su campo de elecciones de técnicas con relación a este tipo de tarea, mas no añade nuevos usos de la noción de supremo, ya que la tarea sigue siendo la misma que en la asignatura anterior.
Hay dos ejercicios donde se solicita estudiar la convergencia de las siguientes dos sucesiones: xn=(1–1/2)(1–1/4)... (1–1/2n) y xn =2/1.3/3.4/5.5/7... (n+1)/(2n–1). Aunque pueden servir como un principio para observar que un número real queda dado por una sucesión, su resolución podría quedar reducida a comprobar la existencia de límite. En los ejercicios de este tipo, el docente tiene oportunidad de hacer un verdadero aporte sobre una cuestión que, de otro modo, permanecería solapada. Técnicamente es fácil, con respecto a las sucesiones de ejercicios anteriores, ver que son monótonas y acotadas; como el límite puede no ser un número conocido, lo identificamos con la sucesión.
Esta actividad muestra que el enunciado aislado de un ejercicio no permite más que analizar su "potencialidad", que puede ser muy distante de lo que los alumnos hagan o de lo que relice el docente en clase.
5.3.La segunda guía de trabajos prácticos de Análisis I de Exactas.
La segunda guía es una práctica sobre funciones y continuidad de funciones. Los temas, en su totalidad, están dentro de los que se estudiaron en Análisis I del CBC, salvo la aparición de la f(x) = [x], o parte entera de x. Los primeros ejercicios de esta guía son similares a los del CBC en su grado de dificultad y tipo de tareas, pues consisten en graficar, sustituir y hallar el dominio natural, actividades más ligadas a "resolver", no tanto a fundamentar, y podríamos afirmar que son típicas del cálculo elemental. Por ejemplo, la noción de dominio se pierde en la búsqueda de condiciones que requieren de un tratamiento de tipo algebraico, del mismo modo que las sustituciones. Hay un grupo de ejercicios que presenta tareas nuevas respecto a los ejercicios de Análisis del CBC, ya que se pide probar ciertos límites por definición y demostrar una doble desigualdad que se usará para comprobar la existencia del límite limx 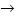 + ∞(1+1/x)x. x resto son cálculos de límites y análisis de continuidad, con una complejidad algebraica mayor que la que había en la materia anterior.
+ ∞(1+1/x)x. x resto son cálculos de límites y análisis de continuidad, con una complejidad algebraica mayor que la que había en la materia anterior.
Hay un ejercicio donde el tipo de tarea consiste en demostrar una propiedad que se ve como evidente al representar la situación. Se demanda comprobar que si f:IR 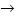 IR es continua y verifica lim x
IR es continua y verifica lim x 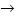 + ∞f(x) = + ∞ y limx
+ ∞f(x) = + ∞ y limx 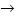 + ∞ f(x) = – ∞, entonces f debe ser suryectiva. Es un resultado "visualizable", "esperable", mas exige que se movilicen bastantes elementos para su demostración. Es necesario trabajar con la definición de límite para ver si se cumplen las condiciones del teorema de Bolzano9.
+ ∞ f(x) = – ∞, entonces f debe ser suryectiva. Es un resultado "visualizable", "esperable", mas exige que se movilicen bastantes elementos para su demostración. Es necesario trabajar con la definición de límite para ver si se cumplen las condiciones del teorema de Bolzano9.
Lo mismo sucede con los ejercicios 18, 19 y 2010, que obligan a escribir y utilizar con precisión y detalle la definición de límite o la de supremo e ínfimo. Hay un salto importante en el tipo de práctica que se espera por parte de los alumnos y la clase de argumentos que deben utilizar, en comparación con los ejercicios anteriores de esta misma guía. Sobre dichas actividades transcribimos una pequeña parte de la entrevista a un docente (A es el entrevistador y D1 el docente entrevistado).
• A: El ejercicio 17 c, el 18 y el 19 se tratan de resultados que son visibles, creíbles y complicados de explicar y escribir. ¿Notaste si eso les trajo problemas a tus alumnos?
• D1: Sí, muchísimos problemas. De hecho, no saben escribir nada. Ese día se me rebelaron, me decían: ¿por qué hay que escribir esto, si es obvio que es así?
• A: ¿Y qué les contestaste?
• D1: En general, el argumento que doy es que si bien la intuición es buena y ofrece algo en lo que apoyarse, no es una verdad absoluta. Yo hablo mucho de la intuición en clase; no es que haga todo formal, pero les propongo escribir lo que uno intuye. Y les digo que tengan cuidado porque a veces lo que se intuye es equivocado. Da igual, no los convenzo ni un poco... Por ejemplo, el 18 les parece más que obvio... y yo les pregunto ¿por qué es obvio? ¿Por qué no puede pasar que la imagen se escape para más arriba? Esa clase estuvo buenísima. Uno me dijo que si se escapara para arriba tendría un pedazo decreciente. Les dije, escribamos eso, y salió. Pero en el parcial tomamos uno por el estilo, e igual escribieron "obviamente" en la resolución.
Una vez me pasó que una chica me vino a consultar un ejercicio de este tipo. Me vino a preguntar si estaba bien como lo había resuelto y me lo mostró: había escrito el enunciado y había concluido escribiendo exactamente lo que había que probar. A ella le pareció que estaba entonces probado... Yo la miraba, no sabía qué decirle... en fin. Yo les digo para este tipo de ejercicios tenemos la única herramienta es el teorema de valor medio; hay que poner paso a paso cosas que sean solamente despejes y en algún momento usar el teorema. Pero en el ejercicio que pusimos de eso en el examen sucedió lo mismo: la mitad de los alumnos no lo hicieron.
El docente plantea la cuestión de si saben o no escribir, que se puede ampliar a si reconocen o no la necesidad/legitimidad de demostrar. Más que escribir o no escribir, el asunto es poder argumentar con elementos que formen parte de un corpus aceptado de conocimientos; en este caso, el teorema es una parte de ese corpus, y la argumentación podría no ser escrita.
En la entrevista al otro docente (D2 ), opinó sobre este grupo de ejercicios:
•D2: Y en las aplicaciones de Bolzano tienen muchas dificultades con esto. Aquí tienen que aplicar demostraciones, aquí hay que darles, "machacarles".
•A: Yo de eso quería preguntarte especialmente porque, por ejemplo, el 17c se ve, pero probarlo da trabajo...
•D2: Claro, ellos lo ven con el dibujo, pero cuando pedimos que lo demuestren usando la definición de límite, eso les cuesta mucho.
•A: ¿Les sorprende que hay que demostrar algo que se ve?
•D2: Les cuesta... Dicen: "esto es tan evidente, ¿pero cómo lo escribo?" Y te vienen a preguntar "¿así está bien escrito o hace falta más? O te dicen: "dime cuánto quieres que escriba", o "¿te convence esto?"
•A: ¿Y qué esperas por parte de ellos?
•D2: Una demostración formal, que usen las definiciones de límite.
Este fragmento muestra que hay una dificultad para los alumnos y un salto entre lo que espera el docente que realicen y lo que ellos creen que deben hacer.
Ambos partes de las entrevistas indican que enseñar a demostrar aquello que parece evidente resulta una tarea muy difícil. El método que propone el docente D1 es identificar (no se sabe muy bien cómo) que en este tipo de ejercicio se debe usar el teorema y resolverlo haciendo sólo despejes algebraicos y emplear el teorema en algún momento, con la ilusión aparente de poder algoritmizar una tarea que no nos parece algoritmizable. Mientras que el docente D2 propone la repetición ("machacarles").
5.4. Síntesis de Análisis I de Exactas
En estas guías no hay contenidos nuevos sobre la completitud con respecto a la materia Análisis I del CBC, salvo tal vez que se explicita que no está asegurada la existencia de supremo e ínfimo en Q. Hay una decisión tomada de entrar a los reales por la vía del axioma del supremo. El tipo de tareas a partir de las cuales se aborda la noción de supremo no añade nuevos contenidos a los vistos en la materia anterior, aunque son algebraicamente un poco más complicados. No obstante, dichos contenidos forman el contexto donde se despliegan cuestiones y técnicas que sí son nuevas: la pertinencia de acordar qué se demuestra y qué no, el hecho de reducir un problema a un caso anterior, poner en juego la necesidad de definir y la conveniencia de contar con un sistema de axiomas como punto de partida.
De igual manera, acotar, hacer acotaciones intermedias para facilitar las cuentas y las condiciones respecto a la variable en cuestión, comprender el sentido de poner condiciones para las variables, comprender que para probar una implicación (por ejemplo, la definición de límite) se plantea el consecuente y se recortan unas condiciones sobre la variable a fin de que valga. Aunque todos esos elementos no se desprenden automáticamente de la resolución de los problemas, dichas habilidades pueden ser tomadas o no; esto depende del grado de reflexión del alumno, del docente, de las interacciones entre los alumnos, etc. En relación con la completitud, no hay ejercicios que hagan necesaria la explicitación de ese atributo de IR.
Hay un cambio importante en las exigencias para validar las afirmaciones. El fragmento de la entrevista a un docente sobre algunos ejercicios de la primera práctica muestra que los alumnos no comprenden las razones de este cambio, el cual no es evidente en la medida que no se planean nuevas tareas a los alumnos. Las pruebas apoyadas en representaciones o en ciertos supuestos "ingenuos" (por ejemplo, el conjunto IN no está acotado) ya no son aceptadas como legítimas porque los docentes esperan mayor formalismo en las demostraciones. Las tareas no están presentadas con subtareas que las fraccionan; sin embargo, los ejercicios se parecen bastante a los de la materia anterior. Con base en nuestro marco teórico, esas diferencias son esencialmente contractuales, pues parecería que los alumnos asumen estos cambios en las demostraciones más debido a que el docente se los exige que por ser algo interesante para ellos, desde el punto de vista matemático.
El estudio praxeológico nos permite concluir que no hay un cambio significativo con la materia anterior en términos del tipo de tareas. La teoría –que sustenta las técnicas y las tecnologías– es la misma, pero las técnicas son diferentes porque se exige una validación o fundamentación no empírica. Además, hay una estabilidad dada por la aparición de la completitud encapsulada en los teoremas. En términos del panorama cognitivo, creemos que hay elementos para ubicar a un sujeto que aprueba los ejercicios prácticos de esta materia en el estado inicial. Un alumno que prepara su examen final evoluciona en el eje de validación, debido a que usa en forma explícita el axioma para probar los teoremas.
6. COMPLEMENTOS DE ANÁLISIS II
La materia Complementos de Análisis II es complementaria del curso Análisis II. Su carga horaria es de cinco horas semanales, dos teóricas y tres prácticas. Los temas del programa son: números reales como cuerpo ordenado completo, sucesiones y series en IR, completación por cortaduras del cuerpo racional, definición alternativa del cuerpo IR con sucesiones de Cauchy racionales, nociones básicas de topología en IR" y funciones de variación acotada e integral de Riemann–Stieljes.
La primera tarea que deben resolver los alumnos es probar cuatro afirmaciones relacionadas entre sí, a partir de cuatro premisas. Entre los primeros ejercicios, hay por lo menos uno que consiste en demostrar la equivalencia entre ciertos enunciados; otros tienen como objetivo conjeturar propiedades y demostrarlas, muchas de ellas respecto al supremo y al ínfimo. Esto marca una diferencia con las materias anteriores en dos sentidos: por un lado, el juego deductivo es tomado como objeto de estudio; por otro, la demostración cobra el sentido de validar una conjetura.
En las clases teóricas se definió a IR como el conjunto de cortaduras racionales y se mostró que así definido cumple tanto el axioma de supremo como el teorema de encaje de intervalos; asimismo, que toda sucesión de Cauchy converge. El supremo tiene en esta materia un rol más cercano al de objeto, en comparación con las dos materias anteriores, y cumple la función de definir ciertos números (distancias, especialmente). Ahora bien, el rol de objeto lo identificamos a partir de la manipulación que se hace de esa noción en ejercicios que podríamos denominar "aritmética de supremos e ínfimos": demostrar las relaciones entre sup A e inf A con sup(–A) e inf(–A), y entre sup (c.A), inf (c.A) y c.supA c.inf A, al igual que encontrar y probar la relación entre sup A, sup B y sup (A+B). Hay actividades que demandan hallar supremos y demostrar que lo son, pero se presenta previamente un ejercicio donde hay que demostrar la equivalencia entre tres distintas caracterizaciones de supremo. Esto no añade nuevos sentidos al supremo, pero sí abre el panorama de técnicas al momento de demostrar que tal candidato es el supremo.
La primera aparición del supremo y del ínfimo en la guía, con un uso instrumental, se da en la segunda práctica, al definirse tanto la distancia entre un punto y un conjunto como entre dos conjuntos. Un buen manejo operatorio de tales nociones es necesario para probar, por ejemplo, la desigualdad triangular para esas distancias.
Desde el punto de vista del análisis praxeológico, la teoría es la misma que en las materias anteriores, pero el conjunto de tareas, técnicas y tecnologías es diferente, ya que el supremo tiene un rol más cercano al de objeto y se ha instalado el estilo de justificar formalmente las afirmaciones. Eso hace que no exista un soporte en las representaciones sobre la recta.
No hay en esta práctica "aplicaciones" de la completitud, excepto en el caso de una sucesión monótona creciente, mientras que las tareas, indicadas de manera escasa, corresponderían al nivel movilizable, según la categorización de Robert (1998). La aritmética de supremos marca un terreno de estabilidad, con un nivel diferente de conceptualización del que había en las otras materias, e interpretamos que una ruptura ocurre en el momento en que se utilizan los supremos y los ínfimos para definir distancias, debido a que se hace explícito el rol de herramienta de dichas nociones.
Si se toma en cuenta el panorama cognitivo, interpretamos que el tipo de tareas planteadas a los alumnos de esta materia favorece la evolución en el eje de instrumentalidad/objetivación y también en el de disponibilidad técnica.
7. CÁLCULO AVANZADO
Los temas que contempla el programa de la materia Cálculo Avanzado son: números reales, cardinalidad, espacios métricos, sucesiones y series en el campo complejo, rudimentos de la teoría de espacios normados y diferenciación en espacios euclideanos; la completitud, ahora de espacios más generales y no sólo de IR, forma parte de los temas a estudiar. Las limitaciones de un espacio no completo, además de las potencialidades y alcances de un espacio completo, pueden ser comprendidas y cobran mayor sentido en espacios más generales, como los que se estudian en esta materia.
Referente a los materiales que tenemos para analizar, consisten en las guías de trabajos prácticos del año 2003. El tipo de tarea que hay en las prácticas es demostrar, mostrar, probar, enunciar y probar, analizar, armar ejemplos que cumplan tal o cual condición y demostrar la equivalencia entre enunciados; la mayoría corresponde a un tipo de trabajo bastante autónomo. Hay dos partes de la práctica en las que se estudia la completitud: una al comienzo de la primera práctica, cuando aparece un ejercicio que trata específicamente sobre la completitud de IR, que vamos a analizar a continuación; la otra se da en el estudio de espacios métricos completos.
7.1. Enunciados equivalentes sobre la completitud
En la primera guía de trabajos prácticos hay un ejercicio que toma a la completitud de IR como objeto de estudio. Su enunciado es:
Mostrar que en un cuerpo totalmente ordenado arquimediano son equivalentes las afirmaciones siguientes:
i) Toda sucesión acotada tiene una subsucesión convergente
ii) Toda sucesión de Cauchy es convergente
iii) Si (In)n>1 es un encaje de intervalos cuyas longitudes tienden a cero, entonces existe un único
iv) Todo conjunto acotado superiormente y no vacío tiene supremo
v) Toda sucesión monótona y acotada tiene límite
Las afirmaciones son equivalentes en un cuerpo ordenado arquimediano, en el sentido de que poseen el mismo valor de verdad: si los elementos de un cuerpo ordenado arquimediano satisfacen una de esas afirmaciones, satisfacen entonces las otras. Si no se añade la hipótesis de arquimedianidad, las afirmaciones dejan de ser equivalentes. Ahora bien, si un cuerpo ordenado satisface además las afirmaciones i), iv) o v), entonces también satisface ser arquimediano, mientras que la arquimedianidad no se deduce de las afirmaciones ii) ni iii). De hecho, una adaptación de estas últimas dos caracterizaciones sirve también para expresar la completitud de espacios no necesariamente ordenados.
Este ejercicio muestra distintos aspectos de la completitud de IR que, en principio, no parecen ligados entre sí. Asimismo, permite "observar la completitud", tomarla como objeto de estudio y potencialmente hace que los alumnos interpreten que cada uno de esos enunciados son expresiones de la completitud. Lo anterior nos hace ubicar a esta materia en otro nivel de conceptualización respecto a la completitud; empero, eso depende en cierto modo de la reflexión que se haga sobre este ejercicio. Eventualmente, podría sólo servir para mejorar las técnicas en demostrar, sin que se haga evolucionar al alumno en otros ejes de racionalidad.
También este ejercicio favorece la relación de aspectos que habitualmente parecen "estancos", lo cual posibilita la imbricación de herramientas y condiciones que, en principio, parecen no estar relacionadas unas con otras.
Resulta interesante hacer las demostraciones de todas implicaciones posibles; por ejemplo, ¿qué elementos se ponen en juego al tomar como punto de partida a cada uno de los enunciados? Partir de i) lleva a armar sucesiones y subsucesiones convenientes a partir de un encaje o de un conjunto acotado, a preguntarse si una sucesión de Cauchy es una sucesión acotada para poder usar la hipótesis, o si a partir de que una sucesión monótona tiene una subsucesión convergente se puede deducir la convergencia de la sucesión original. Partir de ii) lleva a construir sucesiones o subsucesiones de Cauchy a partir de una sucesión acotada, de un encaje de intervalos, de un conjunto acotado o de una sucesión monótona y acotada para poder usar la hipótesis.
Partir de iii) lleva a construir encajes convenientes en todos los casos. En algunos casos tal vez implica pasar por alguno de los otros enunciados; por ejemplo, para probar ii) una manera es usar que toda sucesión de Cauchy es acotada, y recurrir al argumento que se empleó para probar i) a partir de iii), a fin de obtener una subsucesión convergente de la sucesión de Cauchy, lo cual conduce a plantear preguntas sobre las sucesiones de Cauchy. Partir de iv) para demostrar v) o iii) implica tomar los conjuntos formados por la sucesión monótona o por los extremos inferiores o superiores del encaje, así como sus respectivos supremos e ínfimos, pero para demostrar i) o ii) se requiere de otra construcción que no fue utilizada hasta ahora, de modo que la existencia de supremo permita construir una subsucesión convergente11. Partir de v) hace necesario pensar cómo extraer subsucesiones o sucesiones monótonas de una sucesión acotada, de una sucesión de Cauchy, de un encaje de intervalos o de un conjunto superiormente acotado.
En todos los casos hay que usar la definición de límite como algo necesario, construir una subsucesión tomando con precisión los subíndices y, de manera más general, elaborar un objeto que cumpla con ciertas condiciones.
Las situaciones de este tipo hacen que los alumnos se formulen preguntas que están en condiciones de abordar y vean como resultados necesarios a las demostraciones que, muchas veces, aparecen como ejercicios recortados en las guías o en los textos. Por otra parte, la demostración de la equivalencia entre enunciados es un ejercicio interesante porque no pone al alumno a "adivinar" el teorema que debe usar (eso forma parte de los datos), sino generar las condiciones para poder usar en cada caso la hipótesis12. En relación con el panorama cognitivo, este tipo de tarea favorece un crecimiento en los ejes de disponibilidad técnica y flexibilidad, pero su concreción no necesariamente conduce a evolucionar en los otros ejes.
7.2. Espacios métricos completos
En esta materia se define la completitud de un espacio métrico mediante la convergencia de sus sucesiones de Cauchy. La práctica de Espacios métricos contiene una sección titulada Completitud, cuyos siete ejercicios abarcan tres aspectos: "poner a punto" un cierto manejo de las sucesiones de Cauchy; hacer explícitas ciertas propiedades y la caracterización de los espacios completos, y mostrar que algunos espacios en particular son espacios completos. Uno de los ejercicios del segundo grupo consiste en demostrar que la completitud es equivalente a que valga el teorema de Cantor. Las técnicas son las mismas que en el ejercicio analizado en 7.1; para ambas implicaciones hay que construir un encaje conveniente y una sucesión de Cauchy para poder usar las hipótesis.
Hasta que los alumnos no apliquen esos espacios para hacer otras cosas (como desarrollar tópicos de análisis), los alcances de la completitud o las limitaciones de un espacio no completo no se pondrán de manifiesto. Tras desarrollar la teoría de espacios métricos, en esta materia se tratan temas de análisis en IRn, con lo que los espacios más generales no se "usan" como dominio de trabajo. Es en materias posteriores (por ejemplo, Análisis Funcional) donde tal vez se empleen los atributos de un espacio completo para desarrollar ciertos tópicos de Análisis.
El estudio de la completitud de espacios más generales puede llevar a un sujeto –aunque no necesariamente– a evolucionar en el eje de disponibilidad técnica, en el sentido que ha sido señalado en el panorama cognitivo: observar la completitud de IR desde una posición más general, tomando consciencia de que algunas formas con las que se expresa la completitud se generalizan, mientras otras ponen en juego propiedades específicas de IR, sobre todo las ligadas al hecho de ser ordenado. No va de suyo que el estudio de espacios métricos generales y el del teorema de completación favorezca la evolución del eje de posición frente a las construcciones, siendo posible que se limite a hacer crecer solamente los aspectos más técnicos.
En la siguiente sección haremos una mirada global al conjunto de tareas relacionadas con la completitud.
8. ORGANIZACIÓN MATEMÁTICA ALREDEDOR DE LA COMPLETITUD
Ya mencionamos en la sección 1 que Chevallard se refiere a la organización matemática como un conjunto organizado, estructurado de praxeologías. En el siguiente cuadro 13,14,15sintetizamos la organización matemática alrededor de la completitud, con una columna para tareas, una para técnicas, una para tecnologías, una para teorías y una en la que señalamos los ejes del panorama cognitivo que cada problema contribuye potencialmente a hacer evolucionar. Los distintos tonos de sombreado corresponden a los cuatro diferentes cursos.
9. SÍNTESIS Y CONCLUSIONES
Lo que hemos analizado a lo largo de este artículo nos permite afirmar que, en las dos primeras materias estudiadas, la completitud vive encapsulada en teoremas fuertes –criterios de convergencia de sucesiones, el teorema de Bolzano– cuya utilización hace que los alumnos no se vean confrontados con la completitud como problema. Un atributo de la completitud en dichas materias es la existencia de supremo, que hace su aparición en función de describir mejor los subconjuntos y no en situaciones de definir ciertos números, quedando así reducido su aspecto instrumental. Esa tarea, que para su resolución muchas veces se apoya en la representación en la recta, para nosotros constituye un primer nivel de estabilidad alrededor de esta noción, el cual fue identificado con el estado inicial del panorama cognitivo descrito en la sección 2.
Un poco más adelante se presentan como objeto de estudio ciertos elementos ligados a la completitud y a la construcción de un dominio completo, como cortaduras, encajes de intervalos y sucesiones de Cauchy. En particular, las prácticas de la materia Complementos de Análisis II contienen tareas destinadas a hacer efectiva una cierta manipulación del supremo, mediante la equivalencia entre sus caracterizaciones y la aritmética de supremos. Esto no necesariamente le agrega sentido a esa noción, ni a la completitud de IR, pero prepara el terreno para un uso que tal vez constituye una ruptura con respecto a los usos anteriores, que atañían a definir distancias. Probar la equivalencia entre los distintos enunciados de la completitud de IR (una de las primeras tareas que deben llevar a cabo los alumnos de Cálculo Avanzado) abre la posibilidad de relacionar e imbricar distintos atributos de la completitud y comprender ciertas características de un dominio completo, además de otorgar un entrenamiento en probar resultados equivalentes con técnicas similares, en el caso de espacios más generales.
El siguiente cuadro de doble entrada muestra para cada materia, en términos cuantitativos, la proporción de tareas que aportan potencialmente a hacer evolucionar cada eje del panorama cognitivo. Los denominadores de las fracciones representan la cantidad de tareas de cada materia. Por ejemplo, el 2/5 en el cuadro correspondiente a cálculo avanzado y flexibilidad expresa que 2 de 5 tareas de Cálculo Avanzado hacen potencialmente evolucionar el eje de flexibilidad.
Una primera rápida lectura del cuadro indica que tres ejes quedan débiles desde la oferta de la institución: necesidad, flexibilidad y posición frente a las construcciones. El eje de flexibilidad requiere de mucha disponibilidad técnica, lo cual restringe sus posibilidades a una sola materia, que es la de Cálculo Avanzado; de ese modo nos explicamos su baja aparición en el cuadro. Las proporciones correspondientes a los otros ejes muestran que esas cuestiones no son tomadas a cargo por la institución.
Hacemos la siguiente interpretación sobre el tratamiento que tiene la noción de completitud en las cuatro materias. Aunque se ponen de relevancia nuevos aspectos del mismo objeto con distinto tratamiento, que responde a nuevas preguntas cada vez, éstas no se explicitan en la oferta institucional y los alumnos no entienden porqué ni para qué tienen que lidiar con estas demostraciones y propiedades sobre objetos que les resultan conocidos, habida cuenta de los tratamientos anteriores, que resultaban suficientes. Tal vez el fracaso en el pasaje del Cálculo al Análisis pueda explicarse porque los alumnos no se plantean espontáneamente las nuevas preguntas que, por otro lado, son difíciles de elaborar. En ese sentido, la institución tiene una posición privilegiada, que no está explotando al máximo nivel.
10. REFERENCIAS BIBLIOGRÁFICAS
Balacheff, N. (1987). Processus de preuve et situations de validation. Educational Studies in Mathematics 18 (2), 147–176. [ Links ]
Bergé, A. y Sessa, C. (2003). Completitud y continuidad revisadas a través de 23 siglos. Aportes a una investigación didáctica. Revista Latinoamericana de Investigación en Matemática Educativa 6 (3), 163–197. [ Links ]
Chevallard, Y. (1992). Concepts fondamentaux de la didactique: perspectives apportées par un approche anthropologique. Recherches en Didactique des Mathématiques 12 (1), 73–112. [ Links ]
Chevallard, Y. (1997). La transposcion didactica. Del saber sabio al saber enseñado. Argentina: Aique Grupo Editor S.A. [ Links ]
Chevallard, Y. (1998). Analyse des pratiques enseignantes et Didactique des Mathématiques: l'approche antropologique. En Actes de l'École d'été de la Rochelle, 91–118. [ Links ]
Douady, R. (1986). Jeu de cadres et dialectique outil–objet. Recherches en Didactique des Matehématiques 7 (2), 5–32. [ Links ]
Maschietto, M. 2002. L'enseignement de l'analyse au lycée: les débuts du jeu global/local dans l'environnement de calculatrices. Thèse doctorale, Université Paris VII. [ Links ]
Robert, A. (1998). Outils d'analyse des contenus mathématiques à enseigner au lycée et a l'université. Recherches en Didactique des Mathématiques 18 (2), 139–190. [ Links ]
Robert, A. y Robinet, J. (1996). Prise en compte du méta en Didactique des Mathematiques. Recherches en Didactique des Mathématiques 16 (2), 145–176. [ Links ]
2 Criterio de D'Alembert: si (an)nεN es una sucesión de números positivos tales que el cociente an+1/an converge a un número l<1, entonces la sucesión an converge a 0. Criterio de Cauchy: si (an)nεNes una sucesión de números positivos tales que  converge a un número l<1 , entonces la sucesión an converge a 0.
converge a un número l<1 , entonces la sucesión an converge a 0.
3 Lima, Elon Lage s (1992). Curso de análise (volume 1). Rio de Janeiro, Brasil: Instituto de Matemática Pura e Aplicada–CNPq–Projeto Euclides.
4 Lang, Serge (1990). Introducción al Análisis Matemático. Addison–Wesley Iberoamericana.
5 Usamos la palabra medio para referirnos a la noción de milieu, que fue introducida por Brousseau, y posteriormente ha sido precisada y reformulada. Utilizamos aquí medio en una versión más próxima a la de Chevallard: lo pensamos como un sistema de saberes y conocimientos preparado para permitir la formulación y la validación de las producciones. En el caso de los alumnos, es un sistema de conocimientos con el que pueden interactuar al menos parcialmente, sin intervención del profesor.
6 Tomamos la idea de preconstrucción de Chevallard (1997): objetos preconstruidos son aquellos cuya existencia se presenta como evidente, en un contexto que elude el cuestionamiento, con una idea o una representación que no permite operar ni hacer demostraciones. Interpretamos la idea de Chevallard en el sentido de que con estos objetos preconstruidos no se puede operar ni hacer demostraciones que involucren a esa noción en su carácter de objeto.
7 La arquimedianidad es un postulado indispensable en el conjunto de axiomas que presentó Hilbert para definir a IR, sin embargo, si se utiliza otro axioma de completitud, por ejemplo, el de supremo, la arquimedianidad se obtiene como consecuencia. En el marco de las representaciones resulta obvia.
8 Por ejemplo, en el caso del inciso (d), el conjunto es  . La desigualdad 2n /(7n–3)>(2n+2)/(7n+4) muestra algebraicamente que an > an+l ; esto es, la sucesión es decreciente, luego el límite (2/7) es el ínfimo y el supremo se alcanza en n=1 (o sea, es un máximo). Una técnica más analítica para ver que es decreciente es considerar la función 2x /(7x–3), para x >1 y comprobar que la derivada es negativa.
. La desigualdad 2n /(7n–3)>(2n+2)/(7n+4) muestra algebraicamente que an > an+l ; esto es, la sucesión es decreciente, luego el límite (2/7) es el ínfimo y el supremo se alcanza en n=1 (o sea, es un máximo). Una técnica más analítica para ver que es decreciente es considerar la función 2x /(7x–3), para x >1 y comprobar que la derivada es negativa.
9 La versión del teorema de Bolzano que se suele enseñaren este curso es: Sea f:[a,b] IR continua. Si f(a)<d<f(b),entonces existe c ε (a,b), tal que f(c) = d.
IR continua. Si f(a)<d<f(b),entonces existe c ε (a,b), tal que f(c) = d.
10 Ejercicio 18: Sea f continua y estrictamente creciente en la semirrecta [a, +∞), talque limx  + ∞ f(x)= M. Probar que Im(f) = [f(a),M). Mostrar con un ejemplo que si sólo se pide que/sea creciente, entonces puede ser Im(f) ≠ [f(a),M Ejercicio 19: Sea f:(a,b):
+ ∞ f(x)= M. Probar que Im(f) = [f(a),M). Mostrar con un ejemplo que si sólo se pide que/sea creciente, entonces puede ser Im(f) ≠ [f(a),M Ejercicio 19: Sea f:(a,b):  IR estrictamente creciente y continua, que limx
IR estrictamente creciente y continua, que limx  + a f(x)= c y limx
+ a f(x)= c y limx  + b f(x)= d .Probar (a)Im(f) = (c, d); (b) Existe f–1 (c,d)
+ b f(x)= d .Probar (a)Im(f) = (c, d); (b) Existe f–1 (c,d)  (a,b)y es continua; (c) limx
(a,b)y es continua; (c) limx  + c f(x)= a y limx
+ c f(x)= a y limx  + d f(x) = b; (d) Encontrar contraejemplos si (i) f no es continua, (ii) f no es creciente. Ejercicio 20: Sea f:(a,b):
+ d f(x) = b; (d) Encontrar contraejemplos si (i) f no es continua, (ii) f no es creciente. Ejercicio 20: Sea f:(a,b): IR continua y sean T =supx ε(a,b)f(x) y B = inf x ε(a,b) f(x). Demostrar que f:(a,b)
IR continua y sean T =supx ε(a,b)f(x) y B = inf x ε(a,b) f(x). Demostrar que f:(a,b) (B,T) es suryectiva.
(B,T) es suryectiva.
11 En efecto, tomar el supremo al rango de la sucesión (an) no sirve para encontrar una subsucesión convergente. Es interesante " sacarse de encima" los términos de la sucesión que son puntos aislados; de hecho, nos interesa "pescar" algún punto de acumulación. Una construcción posible es considerar los conjuntos  y sus respectivos supremos αk , que existen por hipótesis. Esos supremos forman una sucesión decreciente debido a la relación de inclusión de los conjuntos Ak ; el rango de esa sucesión es un conjunto inferiormente acotado, tiene un ínfimo x y no resulta difícil mostrar que x = limx
y sus respectivos supremos αk , que existen por hipótesis. Esos supremos forman una sucesión decreciente debido a la relación de inclusión de los conjuntos Ak ; el rango de esa sucesión es un conjunto inferiormente acotado, tiene un ínfimo x y no resulta difícil mostrar que x = limx  + ∞ α(x)Se construye una subsucesión ank de an , de modo que cada ank difiera en menos de 1/k de cada αk . Esa subsucesión converge a x.
+ ∞ α(x)Se construye una subsucesión ank de an , de modo que cada ank difiera en menos de 1/k de cada αk . Esa subsucesión converge a x.
12 Esta consideración nos parece interesante para un docente porque permite identificar qué tipo de habilidad se evalúa.
13 En este caso puede realizarse por la elección que se ha hecho de los números irracionales (no podría usarse la misma técnica si el número elegido fuera π)
14 En este caso puede realizarse porque los supremos e ínfimos en cuestión son todos números enteros salvo uno, que da 
15 El enunciado de este ejercicio está en el Anexo IV.3.















