Artículos

 

Estimación del valor en riesgo en la Bolsa Mexicana de Valores usando modelos de heteroscedasticidad condicional y teoría de valores extremos

 

Value-at-Risk-Estimation in the Mexican Stock Exchange Using Conditional Heteroscedasticity Models and Theory of Extreme Values

 

Alejandro Iván Aguirre Salado*, Humberto Vaquera Huerta**, Martha Elva Ramírez Guzmán***, José René Valdez Lazalde**** y Carlos Arturo Aguirre Salado*****

 

* Posgrado en Estadística. aleaguirre84@colpos.mx.

** Profesor investigador titular, Posgrado Forestal. hvaquera@colpos.mx.

*** Profesora investigadora titular, Posgrado en Estadística. martharg@colpos.mx.

**** Profesor investigador titular, Posgrado Forestal, Colegio de Posgraduados, Campus Montecillo, Texcoco, Estado de México. valdez@colpos.mx.

***** Profesor investigador, Facultad de Ingeniería, Universidad Autónoma de San Luis Potosí. San Luis Potosí, México. carlos.aguirre@uaslp.mx.

 

Fecha de recepción: 18 de abril de 2010;
Fecha de aceptación: 30 de enero de 2012.

 

Resumen

Se propone una metodología para la estimación del valor en riesgo (VaR) del índice de precios y cotizaciones (IPC) de la Bolsa Mexicana de Valores mediante el uso combinado de modelos autorregresivos y medias móviles (ARMA); tres diferentes modelos de la familia ARCH, de los cuales uno es simétrico (GARCH) y dos asimétricos (GJR-GARCH y EGARCH); y la teoría de valores extremos. Los modelos ARMA se usaron para obtener residuales no correlacionados que sirvieron de base para el análisis de valores extremos. Los modelos GARCH, GJR-GARCH y EGARCH, al incluir en el modelo las volatilidades pasadas, son particularmente útiles tanto en periodos de inestabilidad como de calma. Más aún, los modelos asimétricos GJR-GARCH y EGARCH modelan de manera distinta el impacto de los shocks positivos y negativos del mercado. Todo esto surge de la necesidad de calcular la pérdida máxima que puede tener el IPC en un cierto nivel de confiabilidad y en un periodo de tiempo dado, mediante modelos más eficientes que estimen la volatilidad de manera dinámica. En forma paralela se usó el método RiskMetrics a manera de comparación para la metodología propuesta. Se concluye que la metodología de los modelos de heteroscedasticidad condicional con teoría de valores extremos para la estimación del valor en riesgo presentó un desempeño mejor que el método RiskMetrics; particularmente el modelo EGARCH presentó menos violaciones del VaR, pero en general los tres modelos de la familia ARCH funcionaron de manera adecuada y generaron estimaciones más pequeñas comparadas con las de RiskMetrics, evaluadas en el mismo nivel de error y de confiabilidad mediante la prueba de proporción de fallas de Kupiec.

Palabras clave: ARMA, VaR, GARCH, EVT, riesgo financiero.

 

Abstract

This work proposes an approach for estimating value at risk (VaR) of the Mexican stock exchange index (IPC) by using a combination of the autoregressive moving average models (ARMA); three different models of the ARCH family, one symmetric (GARCH) and two asymmetric (GJR-GARCH and EGARCH); and the extreme value theory (EVT). The ARMA models were initially used to obtain uncorrelated residuals, which were later used for the analysis of extreme values. The GARCH, EGARCH and GJR-GARCH models, by including past volatility, are particularly useful both in instability and calm periods. Moreover, the asymmetric models GJR-GARCH and EGARCH handle differently the impact of positive and negative shocks in the market. The importance of the IPC in the Mexican economy raises the need to study its variations, particularly its downward movement; so, we propose to use VaR to calculate the maximum loss that IPC may have, at a certain level of reliability, in a given period of time, using more efficient models to dynamically quantify volatility. The RiskMetrics approach was parallelly used as a way to compare the methodology proposed. The results indicate that the ARMA-GARCH-EVT methodology showed a better performance than RiskMetrics, because of the simultaneous adjustment of ARMA-GARCH models for returns and variances respectively. Although estimates of the EGARCH models had fewer violations of VaR, the estimates of the three models used for volatility were more accurate than the others, evaluated at the same error and reliability levels through the Kupiec Likelihood Ratio test.

Keywords: ARMA, VaR, GARCH, EVT, financial risk.

Clasificación JEL: A23, C13, C22, C32, E37, F37, G12 y G11.

 

Introducción

El valor en riesgo (VaR por sus siglas en inglés-value at risk) se define como la pérdida máxima que puede sufrir un activo (y en su caso más general un portafolio, el cual está formado por un conjunto de activos) en un cierto nivel de confiabilidad α. En términos estadísticos se define como el 1 - α-ésimo cuantil de la distribución de las pérdidas de un activo (Bhattacharyya y Ritolia, 2008).

El VaR surge como un método para estimar el riesgo con técnicas estadísticas tradicionales ya empleadas en otros campos de la investigación, por ejemplo el uso de la teoría de valores extremos en la toma de decisiones en ingeniería (Chryssolouris et al, 1994); para estimar la corrosión marina del acero en el largo plazo (Melchers, 2008); en la estimación del ozono urbano (Reyes et al, 2009), entre otros. Formalmente, el VaR estima la pérdida máxima sobre un horizonte de tiempo dado, en condiciones normales del mercado, en un nivel de confiabilidad dado (Fernández, 2003). Por ejemplo, un banco puede decir que el VaR diario para su portafolio es de 15 millones de dólares al 99 por ciento de confiabilidad. Esto significa que en uno de cien casos, en condiciones normales de mercado, sus pérdidas serán superiores a los 15 millones (Christoffersen, 2003).

El manejo del riesgo y el desarrollo del VaR tiene sus orígenes en los famosos desastres financieros ocurridos a comienzos de los años noventa que provocaron enormes pérdidas, como el caso del Orange County en Estados Unidos, con una pérdida de 1.81 billones de dólares, el Barings en Inglaterra, con 1.33 billones de dólares, el Metallgesellschaft en Alemania, con 1.34 billones de dólares, y el Daiwa en Japón, que perdió 1.1 billones de dólares, entre otros más. Estos desastres demuestran que sin la debida supervisión y manejo del riesgo se pueden perder billones de dólares en un periodo de tiempo relativamente corto (Crouhy et al., 2000).

Durante los últimos años se han multiplicado las pérdidas ocasionadas por los derivados, que son instrumentos financieros empleados para realizar coberturas en operaciones de compra y venta de acciones. De 1987 a 1998 estas pérdidas han sumado cerca de 28 billones de dólares; comparados con los 90 trillones de dólares del mercado representan 0.03 por ciento del total (Jorion, 2000).

Para el caso de México, la crisis financiera de 1995, provocada por el abuso de la política cambiaría, sirvió para bajar y estabilizar la inflación de 160 por ciento en 1987 a 7 por ciento en 1994. Sin embargo, el déficit de la cuenta corriente comenzó a crecer a medida que la inflación bajaba. Su financiamiento reposó en los flujos de capitales externos, que sirvieron para financiar la inversión y el consumo, y por medio de esto generar el auge crediticio, que sirvió como antecedente de la crisis bancaria (Millán-Valenzuela, 1999).

Generalmente, las series financieras presentan distribuciones de colas pesadas (Gencay y Selcuk, 2004). Para el modelado de estas colas se han propuesto la distribución log-normal, la distribución generalizada del error, y mezclas de la distribución normal (Boothe y Glassman, 1987).

Sin embargo, para la asignación de probabilidades a los cuantiles en el cálculo del valor en riesgo es más conveniente el modelado paramétrico de las colas de la distribución de los retornos, en lugar de ajustar una distribución a la muestra entera (Gencay y Selcuk, 2004). Una buena aproximación a estos modelos lo constituye la teoría del valor extremo.

Existen numerosas metodologías para el cálculo del VaR, entre las que sugieren usar las colas de una distribución a los valores extremos (Embrechts, 2000). McNeil (1999) propone el uso del análisis de valores extremos (EVT, por sus siglas en inglés-extreme value theory) en el cálculo del VaR, y la pérdida esperada (ES) para el manejo de riesgos de mercado, operacional y de crédito, entre otros. Glasserman et al. (2000) analizan el uso de la simulación Montecarlo. El uso del VaR mediante modelos GARCH con EVT es empleado por Gencay y Selcuk en 2004 en nueve economías emergentes, mientras que Bhattacharyya y Ritolia lo emplean en 2008 para el caso del principal índice de la India.

A la fecha se han desarrollado numerosas metodologías para medir el VaR en mercados emergentes (Dimitrakopoulos et al., 2010), entre las cuales se ha propuesto utilizar modelos de heteroscedasticidad condicional, valores extremos, o la combinación de ambas (Gencay y Selcuk, 2004); sin embargo, se ha desestimado el hecho de que la metodología de valores extremos requiere de observaciones no correlacionadas (Bhattacharyya y Ritolia, 2008). Es por ello que se propone utilizar adicionalmente modelos ARMA para eliminar dichas correlaciones.

Para evaluar la eficiencia y la validez del método propuesto en este trabajo, el mismo se comparó con la metodología RiskMetrics (desarrollada por la compañía J. P. Morgan en octubre de 1994), también conocida como el método de suavizamiento exponencial. Dicha metodología consiste en un promedio de las volatilidades a lo largo del tiempo, y actualmente es la metodología estándar para la medición del riesgo financiero.

 

I. Modelos de volatilidad y teoría de valores extremos

I.1. Modelos de volatilidad

La volatilidad se define como la varianza condicional de los retornos de los activos, y es un factor importante en la valoración de opciones y el mercado financiero (Tsay 2002). Aunque las correlaciones de los retornos de los activos son pequeñas, los cuadrados correspondientes son altos, siendo lo más apropiado para su estimación el empleo de modelos de series de tiempo (Bhattacharyya y Ritolia, 2008).

Los modelos más usados para explicar estos casos son los de volatilidad dinámica, de la forma:

donde r_t es el retorno en el tiempo t, μ_t es la media esperada para el retorno en el tiempo t, σ_t es la volatilidad en el tiempo t, y Z_t es la parte estocástica del modelo y depende de los residuales (Bhattacharyya y Ritolia, 2008).

I.1.1. Modelos de heteroscedasticidad condicional

Engle (1982) introdujo los primeros modelos sistemáticos para la volatilidad. El modelo propuesto fue conocido como ARCH(q), el cual se describe a continuación:

Donde r_t es el retorno, μ_t es la media esperada de los retornos, ε_t es el error de predicción, σ_t² es la varianza condicional en el tiempo t, z_t es una variable aleatoria con media cero y varianza unitaria, y finalmente las a's son los coeficientes del modelo ARCH(q).

Posteriormente, Bollerslev (1986) amplió estos modelos al añadir a la ecuación de la varianza las estimaciones de la misma en periodos anteriores; estos modelos fueron conocidos como modelos autorregresivos generalizados de heteroscedasticidad condicional, el GARCH(p,q):

Donde α₀ > 0, α₁ > 0, para i = 1 ,..., q, y b_¡ > 0 para j = 1,..., p. Además, se debe cumplir que 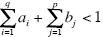para que la varianza incondicional de ε_t sea finita.

Si observamos el modelo GARCH(1,1) se puede apreciar que la volatilidad en el tiempo t depende de la volatilidad en el tiempo t-1, por lo que se deduce que estos modelos son apropiados para agrupaciones de periodos, con altas o bajas varianzas.

I.1.1.1. Modelos EGARCH. Los modelos EGARCH fueron introducidos por Nelson (1991). Bollerslev y Mikkelsen (1996) propusieron la siguiente reformulación:

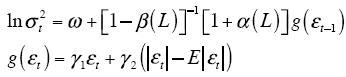
E |ε_t| depende de las suposiciones hechas sobre la distribución de ε_t. Para la distribución normal

Para ia distribución t-student tenemos que

I.1.1.2. Modelos GJR-GARCH. Estos modelos fueron propuestos por Glosten, Jagannathan y Runkle (1993). Su versión generalizada es la siguiente:

Donde S_t^– es una variable dummy que toma el valor de 1 si ε_t < 0 y 0 si ε_t > 0.

En estos modelos el impacto de los errores ε_t² sobre la varianza condicional σ_t² es diferente cuando ε_t es positivo o negativo. Los modelos tARCH de Zakoian (1994) son muy similares a los modelos GJR-GARCH; la única diferencia es que utilizan la desviación estándar condicional en lugar de la varianza condicional.

I.1.2. Estimación en modelos de heteroscedasticidad condicional

La estimación más común se hace por el método de máxima verosimilitud (Tsay, 2002). En este caso, la función de máxima verosimilitud para un modelo ARCH(m) es como sigue:

Donde α = (α₀, α₁,...,α_m)' y f (ε₁,..., ε_m | α) son la densidad conjunta de ε_i ,..., ε_m. Generalmente esta última expresión es muy complicada y simplemente se utiliza la función de verosimilitud condicional:

El logaritmo de la verosimilitud es:

Y finalmente, como 2π no contiene parámetros, se tiene que:

En algunos casos sucede que z_t tiene una distribución de colas pesadas, tal como la distribución t de student o la distribución de errores generalizada (GED por sus siglas en inglés). Para el caso de la distribución t de student con v grados de libertad la varianza será v/ v- 2, y para v>2 se tiene que . (Recuérdese que z_t tiene distribución con media cero y varianza unitaria.) Por lo tanto, la función de densidad de ε_t es:

Donde Γ (x) es la función gamma evaluada en x:

Si recordamos que ε_t = z_t σ_t se tiene que la función de verosimilitud condicional es:

Donde v>2, por lo que el logaritmo de la verosimilitud es:

La ecuación anterior se aplica cuando los grados de libertad son especificados, y generalmente se utilizan valores para v de entre 3 y 6 grados (Angelidis et al., 2004).

Si se desea estimar conjuntamente los grados con los parámetros de los modelos se utiliza la siguiente log-verosimilitud:

Adicionalmente se puede utilizar una distribución más general de colas pesadas conocida como la distribución de errores generalizada (Nelson, 1991), cuya función de densidad es:

y λ es el parámetro de qué tan pesada o delgada es la cola; así:

Nótese que cuando v = 2 z_t se distribuye normal estándar. Para v< 2 esta distribución tiene colas más pesadas que la distribución normal; por ejemplo, si v= 1 entonces z_t sigue una distribución doble exponencial, y para v>2 esta distribución tiene colas más delgadas.

La función de log-verosimilitud para este caso es:

En general, se tiene que la función de log-verosimilitud puede escribirse en términos de la función de densidad de z_t en la siguiente forma (Angelidis et al., 2004):

donde D(z_t; v) es la función de densidad de z_t.

I.2. Teoría de valores extremos (EVT)

Una alternativa al uso de los cuantiles de la distribución de los retornos para calcular el VaR, es el uso de la distribución de los valores extremos de los retornos para modelar exclusivamente los valores extremos y usar los cuantiles de esta distribución para obtener una mejor estimación del valor en riesgo. En este contexto, la teoría de los valores extremos juega un rol importante para encontrar la distribución de los valores máximos de una serie de datos (Finkenstadt y Rootzen, 2001).

I.2.1. Metodologías para encontrar los valores extremos de una serie

El primero es el llamado máximo por bloques, donde se dividen las series de tiempo en secciones de igual tamaño y se escoge el valor más grande dentro de cada bloque. La ventaja de este método es que se escogen valores sobre todo el conjunto de datos; sin embargo, se pueden omitir los siguientes valores extremos dentro del mismo bloque que posiblemente sean mayores que el máximo dentro de otro bloque.

I.2.1.1. Máximos por bloques. Fisher y Tippet (1928) y más tarde Gnedenko (1943) demostraron que las únicas distribuciones límite para modelar los valores extremos son las siguientes:

Donde α > 0 se denomina el parámetro de forma para las familias Fréchet y Weibull. Este grupo de funciones se conoce como las distribuciones del valor extremo.

En términos prácticos, para la estimación de los máximos en bloques el método es como sigue: (1) se seleccionan los máximos dentro de cada bloque, (2) se elige una distribución a priori del tipo G (x) anterior, y finalmente (3) se estiman los parámetros por máxima verosimilitud.

Para evitar la selección de una función a priori se utiliza la expresión dada por Von Mises (1936) y Jenkinson (1955), conocida como la distribución generalizada de los valores extremos, GEV (del inglés Generalized Extreme Value distribution):

donde 1 + εx > 0. El parámetro ξ se conoce como el índice de cola y está relacionado con la forma de la distribución. La distribución Fréchet puede obtenerse a partir de la GEV al fijar ξ = α^-1; para la distribución Weibull se tiene que ξ = - α^-1 y para la Gumbell ξ = 0.

De lo anterior se observa que es posible realizar la estimación en la metodología de máximos por bloques si se aplica el método de máxima verosimilitud a la distribución GEV.

I.2.1.2. El método de picos sobre umbral (POT). El método de picos sobre umbral (POT, por sus siglas en inglés) selecciona los valores más grandes que sobrepasan un umbral; así, la mayor parte de los resultados de este método se basa en la distribución de los excesos sobre dicho umbral.

Supóngase que se tiene una variable R con función de distribución F_R; la función condicional de R, dado que es mayor que un umbral u, se conoce como la distribución de los excesos de R, F_R,u, y está dada por:

donde 0 < y < R_u-u, y R_u, corresponde al extremo superior de la variable aleatoria.

En la búsqueda de la distribución de los excesos existe el siguiente teorema (Balkema y De Hann, 1974; Pickands, 1975).

Para una gran clase de funciones de distribución, la distribución de los excesos de R, F_R,u para valores grandes de u, es aproximadamente igual a:

donde ξ ∈R β = σ + ξ (u - μ), ξ y β se conocen como los parámetros de forma y escala, y G_{ξ, β} se conoce como la distribución generalizada de Pareto (GDP por sus siglas en inglés) (Pickands, 1975).

Según el valor del parámetro ξ de la GPD se obtienen tres tipos de funciones de distribución. Si ξ > 0, la GPD es una distribución de Pareto con parámetros α = 1/ξ, k = β / ξ, para valores y > 0. Para ξ = 0 la GPD corresponde a una distribución exponencial con parámetro 1 / β y y > 0. Finalmente, si ξ < 0, las GPD toman la forma de una distribución tipo Pareto II, la cual está definida en el rango 0 <y < β/ξ.

I.2.1.2.1. Métodos para la selección del umbral"u". Un método para estimar el valor de u consiste en utilizar el valor esperado de los excesos, definido como:

Donde r₍₁₎, r₍₂₎, son las observaciones mayores que ; <r_max y r_max corresponden a la observación más grande de la muestra. A partir de ese estimador de la media de los excesos se analiza la tendencia de la gráfica de las parejas ordenadas (, ê ()). Si G_ξ,β es una aproximación válida de F_Ru para un umbral dado u*, el gráfico de la media de los excesos debe ser aproximadamente lineal alrededor de u*, lo cual permite seleccionar intervalos a partir de los cuales seleccionar el umbral u.

I.3. Cálculo del valor en riesgo mediante el uso de valores extremos

Sea R_t una serie de tiempo estrictamente estacionaria que representa las pérdidas de un activo; nótese que la función de excesos de pérdida de R_t es:

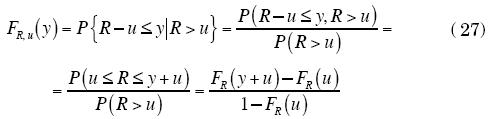
Sea x = y + u si la distribución de los máximos de R converge a la distribución generalizada de los extremos H_ε (x); entonces, la distribución de los excesos "y" converge a una distribución generalizada de Pareto G_ξ,β (y) y se tiene que:

Al reemplazar este resultado en la ecuación anterior tenemos:

Si se conoce la función de distribución F_R el cálculo del VaR sólo requiere el cálculo de los parámetros de su distribución y encontrar el cuantil 1 -α de dicha distribución. Sin embargo, esta función generalmente se desconoce, por lo que se utiliza el resultado anterior, donde F_R depende de F_R (u) y de G_ξ,β (x-u).

Si usamos como estimador de F_R(u) su función de distribución empírica, se llega al siguiente resultado (Byström-Hans, 2004):

Entonces, dada la definición de valor en riesgo se tiene:

y al despejar para el valor en riesgo tenemos finalmente la expresión siguiente:

donde ξ ∈ R β = σ + ξ (u - μ). Aquí ξ es el parámetro de forma y β el de escala, y se calculan por máxima verosimilitud.¹

 

II. Datos y metodología

II. 1. Obtención y preparación de los datos de estudio

Se obtuvo la serie del índice de precios y cotizaciones de la Bolsa Mexicana de Valores del periodo comprendido entre el 27 de febrero de 2009 y el 26 de febrero de 2010. Dicho periodo coincidió con la etapa final de la crisis financiera global de octubre de 2008, durante la cual se vivieron periodos con mucha volatilidad, y en el que el manejo del riesgo se convirtió en una de las principales herramientas para evitar las enormes pérdidas características de esos periodos.

Para cada uno de los valores de la serie se calculó el retorno logarítmico en la siguiente forma:

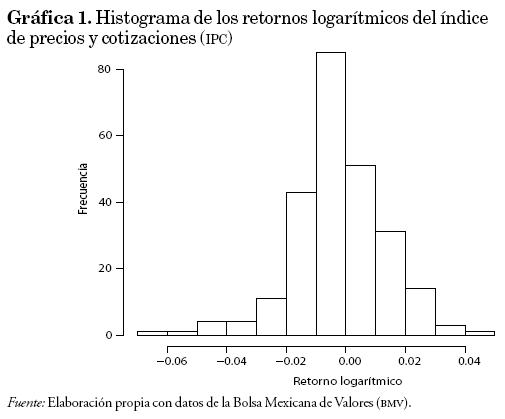
Donde P_t representa el valor del índice en el tiempo t. Conviene aclarar que la serie de los retornos logarítmicos es aproximadamente igual a la serie de las ganancias (retorno simple). Finalmente, como debemos obtener la serie de las pérdidas, simplemente cambiamos de signo la serie anterior. En la gráfica 1 se puede observar el histograma de los retornos logarítmicos de la serie.

II.2. Modelado de la media y la varianza de los residuales

Para modelar la media de los retornos se utilizó un modelo de series temporales, se ajustaron modelos de medias móviles y autorregresivos, y se escogió el modelo que minimizó el criterio de información de Akaike y que cumplió con las pruebas de Ljung-Box sobre la no correlación de los residuales (Tsay, 2002). Simultáneamente se ajustó el modelo GARCH(p,q) con el menor número de parámetros y que modeló correctamente las varianzas condicionales de los retornos.

Para lo anterior Francq y Zakoian (2004) sugieren minimizar la siguiente función de Quasi-verosimilitud con respectó a los parámetros de la serie ARMA y GARCH simultáneamente.

donde son procesos definidos recursivamente por:

Para el caso de este trabajo se utilizó el programa Oxmetrics, el cual calcula los parámetros del modelo ARMA para la media y GARCH para la varianza de manera simultánea (véase Ara Introduction to OxMetrics 6 de Doornik, 2009).

II. 3.VaR mediante modelos GARCH y teoría de valores extremos

Al utilizar únicamente los modelos GARCH para las colas pesadas, típicas en los retornos financieros, se pueden subestimar los valores extremos de estas series. Por otro lado, para poder utilizar la teoría de los valores extremos para modelar los máximos de la serie de los retornos financieros, se requiere que dicha serie no esté correlacionada, lo cual en la práctica generalmente no sucede.

Los resultados obtenidos en teoría de valores extremos asumen que las series son independientes e idénticamente distribuidas. Sin embargo, normalmente las distribuciones de los retornos presentan autocorrelaciones; ante esta situación, Bhattacharyya y Ritolia (2008) propusieron realizar un análisis de valores extremos a los residuales estandarizados de una serie ARIMA-GARCH, y con este resultado calcular el VaR de los retornos como sigue:

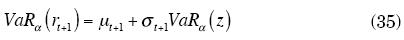
Donde VaR_a (z) es el VaR calculado a los residuales estandarizados del modelo ajustado a los retornos.

II.4. Pérdida esperada (Expected Shortfall-ES)

El Expected Shortfall indica cuál es el valor esperado de la pérdida, dado que esta es superior al VaR; es una medida desarrollada por Artzner et al. (1998) definida como:

El cálculo del ES para una distribución continua se define como:

Donde U representa el extremo superior de los retornos, y F_R (•) y f_R (•) corresponden a la función de distribución y de densidad de los retornos, respectivamente.

Para el caso de un modelo de Valores Extremos (Bhattacharyya y Ritolia, 2008), se obtiene que el ES puede estimarse como:

Donde ξ ∈ R β = σ + ξ (u - μ). Aquí ξ es el parámetro de forma y β el de escala de la distribución generalizada de Pareto.²

II.5. Ajuste del modelo

II.5.1.Comparación histórica o Backtest

Esta prueba se utiliza para probar el ajuste del modelo, así como para comparar entre distintos modelos. El Backtest asume que el número de fallas o número de datos históricos que caen fuera de los límites del VaR tiene una distribución binomial con p = 1 - α. La prueba se basa en el estadístico de Kupiec (Finkenstadt-Rootzen, 2001):

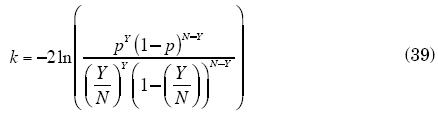
Donde Y es el número de fallas, N el número total de datos y p = 1 - α (α es el utilizado para calcular VaR_α).

El estadístico k es una prueba de razón de verosimilitudes que tiene una distribución asintóticamente χ₁².

Alternativamente se puede obtener la estimación directa a partir de la distribución binomial; se calcula el intervalo de confianza para Y como (y₁, y₂), tal que P (Y < y₁) = P (Y > y₂) = 1 -α'/2 = 0.025 y Y ~ BIN(N, p). Aquí Y es el número de fallas, N el número total de datos y p = 1 - α. Si el número de fallas Y observado cae dentro del intervalo anterior, entonces se acepta que la hipótesis 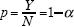y el modelo son adecuados.

 

III. Resultados y discusión

Es normal que existan correlaciones en las series financieras que pueden ser modeladas con series temporales. Para el caso del índice de precios y cotizaciones de la Bolsa Mexicana de Valores esta situación se verificó al realizar las pruebas de Ljung-box. De igual manera, al examinar las funciones de autocorrelacion muestral y autocorrelacion parcial muestral se observó que es posible ajustar un modelo ARMA a la serie de los retornos para modelar las correlaciones existentes.

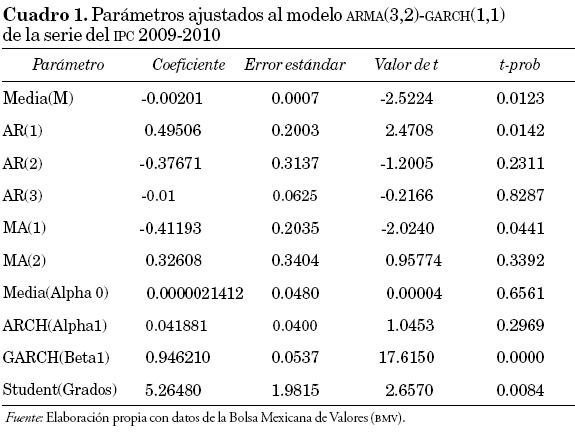
Al realizar el ajuste de varios modelos ARMA a los retornos financieros y revisar sus correspondientes criterios de información de Akaike, se encontró que el modelo ARMA (3,2) fue el que obtuvo el mínimo valor. En este sentido, se ajustaron modelos autorregresivos de orden menor o igual a 3 conjuntamente con modelos de medias móviles de orden menor o igual a 2 para revisar el número de fallas en las que dichos modelos incurren.

Al aplicar la prueba de Jarque-Bera a los residuales (Tsay 2002), para el caso del modelo ARMA (3,2) se encontró un valor para el estadístico de 30.74, que al ser comparado con una χ₂² se obtiene un P-value igual a 2e-7, por lo que evidentemente se rechaza la hipótesis nula de que los residuales siguen una distribución normal.

Debido a lo anterior, para modelar los residuales se utilizaron los modelos ARCH (1), GARCH (1,1), EGARCH(1,1) y GJR-GARCH (1,1) con distribución t-student. En cada caso se realizó un estudio de los valores extremos a los residuales estudentizados para encontrar las medidas de valor en riesgo utilizando la metodología del cálculo del VaR mediante modelos GARCH con teoría de valores extremos.

Para el caso de los modelos EGARCH, el modelo ajustado fue:

Mientras que el modelo GJR-GARCH

El VaR calculado con el modelo EGARCH presentó 12 fallas (recuérdese que se produce una falla si el valor real del retorno sobrepasa el valor en riesgo estimado) correspondientes a un p-value de 1 en la prueba de Kupiec, dos fallas menos que el calculado con los modelos GJR-GARCH y GARCH, en los cuales el p-value es de 0.5129234. (Recuérdese que la hipótesis nula -el promedio de fallas es igual a 5 por ciento- en este caso no se rechaza.)

La medida de comparación para evaluar cada modelo fue el número de fallas que se obtuvieron, así como el grado de ajuste de los parámetros a través de sus correspondientes pruebas de t.

El modelo RiskMetrics obtenido y ajustado para los retornos fue el siguiente:

Los resultados se muestran en la gráfica 2, donde se comparan los tres modelos ARCH, el modelo RiskMetrics y dos modelos no dinámicos (Bootstrap y EVT).

Comparamos los modelos GARCH, GJR-GARCH y EGARCH (con un total de 14 fallas como máximo en el cálculo del VaR) con el modelo de RiskMetrics (que si bien obtuvo un número de fallas inferior, sus estimaciones del valor en riesgo son más grandes). Al realizar la prueba de ajuste de Kupiec se encontró que todos los modelos tienen un promedio de fallas de 5 por ciento con una confiabilidad de 95 por ciento, lo que indica que el modelo está dentro de los límites fijados para la estimación del valor en riesgo, que en este caso fue de 5 por ciento. Se encontró también que el VaR calculado con valores extremos (0.02253312) fue más pequeño que el encontrado por el método de Bootstrap de simulaciones históricas (0.02623782). La misma situación se verificó con el cálculo de la pérdida esperada.

Respecto al análisis de la pérdida esperada, observamos resultados similares a los obtenidos por el VaR; en este caso el ES_0.95 sigue siendo menor para el caso del ARMA (3,2)-GARCH (1,1)-EVT que el obtenido con el modelo RiskMetrics. La gráfica 3 nos muestra la pérdida esperada para la serie completa del IPC.

Para el modelado de la volatilidad se probaron los modelos ARCH (1) y los modelos GARCH (1,1), y se encontró que el valor en riesgo utilizando los modelos ARCH presenta estimaciones demasiado elevadas y poco conservadoras que sobreestiman el valor de la máxima pérdida posible. Por otra parte, el número de fallas en las que incurren es similar al de los modelos GARCH. Lo anterior puede observarse en la gráfica 4, en la que se muestra el valor del VaR calculado con diferentes modelos ARMA para la media y con el modelo ARCH (1) para la volatilidad. Finalmente, debido a lo anterior se hace evidente la eficiencia de las estimaciones en un modelo GARCH, comparadas con las de los modelos ARCH.

De manera similar, en la gráfica 5 se muestra el valor en riesgo calculado con diferentes modelos ARMA para la media y con el modelo GARCH (1,1) para la volatilidad. Se observa que el número de fallas no disminuye significativamente al variar el modelo para la media; sin embargo, al utilizar el modelo GARCH para la volatilidad disminuye considerablemente la magnitud de la estimación del valor en riesgo, aunque el número promedio de fallas se incrementa ligeramente (14 en comparación con las ocho del modelo ARCH).

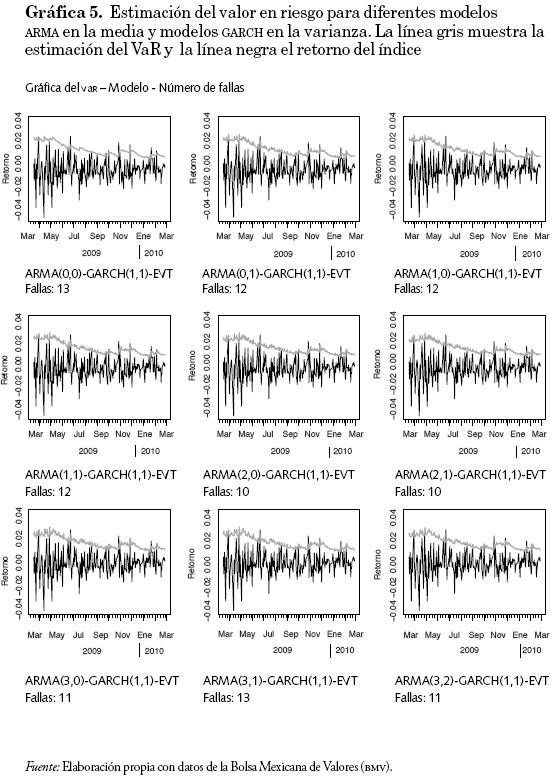
Por otra parte, se realizó el cálculo del valor en riesgo por el método de RiskMetrics, con el objetivo de poder tener un punto de referencia y comparación para nuestro modelo ARMA-GARCH-EVT.

Los resultados se muestran en la gráfica 2, donde se observa que el modelo RiskMetrics presenta un total de siete fallas en el cálculo del VaR, valor muy por debajo del número de fallas máximo para considerar adecuado el modelo.

Durante la revisión de los coeficientes del modelo ajustado RiskMetrics se observó que, a excepción de las medias, el resto de los coeficientes fueron significativamente diferentes de cero, derivado de que la metodología recomienda un valor para el coeficiente λ de 0.94 para datos diarios.

Se ajustó también el valor en riesgo y la pérdida esperada por el método de valores extremos y por el método de bootstrap de simulaciones históricas, con el fin de obtener un comparativo de los métodos dinámicos contra los métodos estáticos. En este caso se observa que tanto el VaR como el ES son más pequeños si se calculan por el método de valores extremos que si se calculan por el de bootstrap.

Finalmente, se ajustó un modelo para la serie diaria del IPC correspondiente al periodo del 1 de enero de 2000 al 26 de febrero de 2010, con un total de 2245 observaciones. Se encontró que el mejor modelo ajustado fue un ARMA(1,1)-GARCH(1,1)-EVT; los parámetros ajustados se muestran en el cuadro 2. Debido a la cantidad de datos empleados se encontraron problemas en la estimación de los modelos asimétricos; sin embargo, dada la similitud en los resultados anteriores entre los modelos ARCH empleados, es suficiente con ajustar el modelo GARCH y realizar las comparaciones con el RiskMetrics bajo distintas condiciones de mercado.

Al analizar el estadístico de Kupiec para probar el ajuste de los modelos se encontró que ambos ajustaron correctamente un valor en riesgo al 95 por ciento, con 145 fallas para el modelo RiskMetrics (p-value 0.1118) contra 137 fallas del modelo ARMA(1,1)-GARCH(1,1)-EVT (p-value 0.3758). En la gráfica 6 también se puede observar el periodo de la crisis mundial de 2008, donde se nota un incremento de la volatilidad del índice; además se observa un buen desempeño en el ajuste del VaR, debido principalmente a que ambos modelos incluyen en sus ecuaciones las volatilidades pasadas. Esta propiedad de los modelos GARCH se adapta particularmente bien a las condiciones reales del mercado, donde a periodos de inestabilidad le siguen periodos de inestabilidad, y a periodos de calma le siguen periodos de calma.

En las gráficas 6 y 7 se puede observar claramente la superioridad de los métodos dinámicos en el cálculo de las medidas de riesgo con respecto a los métodos estáticos. Y dentro de los métodos dinámicos se muestra la ventaja del modelo propuesto, donde las estimaciones son más pequeñas que en el RiskMetrics (con el mismo nivel de confiabilidad en la prueba del ajuste de fallas de Kupiec, α =0.05).

De manera similar se calculó la pérdida esperada para la serie del IPC 2000-2010; los resultados se muestran en la gráfica 7. Se puede observar que los resultados son similares en ambos casos, con ciertas regiones donde la pérdida esperada del modelo ARMA-GARCH se encuentra por debajo del modelo RiskMetrics. En la misma gráfica se puede observar, al igual que en el caso del VaR, un adecuado desempeño del ES durante el periodo de la crisis económica de 2008, propiciado en gran parte por la propiedad de los modelos GARCH de actualizar la varianza presente con base en las anteriores.

 

IV. Conclusiones

El número de fallas obtenidas con la metodología RiskMetrics fue menor en comparación con los modelos GARCH, GJR-GARCH y EGARCH; sin embargo, se observó que sus estimaciones en general son más grandes que las de este último. Del análisis de los datos se observó que ambos métodos son muy similares, ya que la diferencia en el número de fallas de ambos modelos no fue significativa, es decir, de las 250 observaciones probadas se encontró un promedio de 12 fallas, lo cual es un valor aceptable.

Por otra parte, ya que el modelo RiskMetrics es un caso particular de los modelos GARCH, presentó ciertas limitaciones en su uso, en particular si la serie de los retornos estaba correlacionada.

El uso de los modelos ARMA mejoró el pronóstico del VaR con respecto al RiskMetrics debido principalmente a que el pronóstico de la media se incluye en el cálculo del VaR. Por otra parte se eliminan las correlaciones de los residuales, generando así las condiciones necesarias para el análisis de los valores extremos.

Como se observó en el presente artículo, al variar el tamaño de la serie de datos generalmente se cambia el modelo ARMA de la serie, por lo que se recomienda usar una cantidad de datos que represente de forma conservadora la tendencia de la serie. Conforme se emplean series con datos más antiguos, el modelo podría sesgarse y no representar la tendencia actual de la serie.

Al comparar los modelos asimétricos GARCH y ARCH se observó que GARCH tuvo las estimaciones más precisas respecto a ARCH. GARCH indica que la máxima pérdida del índice de precios y cotizaciones es ligeramente superior a 5 por ciento, en contraste con el modelo ARCH que presenta una pérdida máxima del índice de precios y cotizaciones de cerca de 10 por ciento. Se encontró también, con base en la prueba de Kupiec, que ambos modelos no violaron el VaR ajustado en más de 5 por ciento del total de las observaciones (P-value de 0.51).

Por otra parte, se observó que a inicios del periodo estudiado se presentó una considerable volatilidad, la cual coincide con la parte final de la crisis de octubre de 2008. Para el caso de los modelos, en este periodo de tiempo se encontró que RiskMetrics presentó más fallas en comparación con GARCH, GJR-GARCH y EGARCH. Por otra parte, en los periodos de poca volatilidad se observó que estos modelos presentaron estimaciones más precisas que RiskMetrics, como se observa en el periodo de julio 2009 a febrero 2010.

Finalmente, se concluye que la metodología del cálculo del valor en riesgo mediante modelos de heteroscedasticidad condicional con teoría de valores extremos presentó mejor desempeño comparada con la metodología RiskMetrics.

Con respecto a las medidas de riesgo obtenidas por EVT y Bootstrap, se observa que se obtuvieron mejores resultados con el primer método (EVT), y, al ser estos métodos estáticos, se encontró un desempeño relativamente pobre en comparación con los métodos dinámicos, sobre todo en periodos de inestabilidad económica.

Se propone que el modelo ARMA-(GARCH-EGARCH-GJR-GARCH)-EVT para estimar el valor en riesgo se implemente para (1) informar a los analistas financieros y a las empresas sobre el riesgo presente en las operaciones financieras que realizan, y (2) fijar posiciones límite para corredores y casas de bolsa, ya que el valor en riesgo funciona como punto de referencia de diversos instrumentos financieros.

 

Referencias bibliográficas

Angelidis, T.,A. Benos y S. Degiannakisb (2004), "The Use of GARCH Models in VaR Estimation", Statistical Methodology, 1, pp. 105-128.         [ Links ]

Artzner, P., F. Delbaen, J. M. Eber y D. Heath (1998), "Coherent Measures of Risk", mathematical Finance, 9 (3), pp. 203-228.         [ Links ]

Balkema, A. A. y L. De Haan (1974), "Residual Lifetime at Great Age", Annals of Probability, 2, pp. 792-804.         [ Links ]

Bhattacharyya, M. y G. Ritolia (2008), "Conditional VaR Using EVT-Towards a Plane Margin Scheme", International Review of Financial Analysis, 17, pp. 382-395.         [ Links ]

Bollerslev, T. (1986), "Generalized Autoregressive Conditional Heteroske-dasticity", Journal of Econometrics, 31, pp. 307-327.         [ Links ]

Bollerslev, T. y Hans 0. Mikkelsen (1996), "Modeling and Pricing Long-Memory in Stock Market Volatility", Journal of Econometrics, 73 (1), pp. 151-184.         [ Links ]

Boothe, P. y P. D. Glassman (1987), "The Statistical Distribution of Exchange Rates", Journal of International Economics, 22, pp. 297-319.         [ Links ]

Byström-Hans, N. E. (2004), "Managing Extreme Risks in Tranquil and Volatile Markets Using Conditional Extreme Value Theory", International Review of Financial Analysis, 13, pp. 133-152.         [ Links ]

Christoffersen, P. (2003), Elements of Financial Risk Management, San Diego, Elsevier Science, 214 pp.         [ Links ]

Chryssolouris, G., V. Subramanian y L. Moshin (1994), "Use of Extreme Value Theory in Engineering Decision Making", Journal of Manufacturing Systems, 13 (4), pp. 302-312.         [ Links ]

Crouhy, M., D. Galai y R. Mark (2000), Risk Management, Nueva York, McGraw-Hill, 752 pp.         [ Links ]

Dimitrakopoulos D. N, M. G. Kavussanos y S. I. Spyrou (2010), "Value at Risk Models for Volatile Emerging Market Equity Portfolios", The Quarterly Review of Economics and Finance, 50 (4), pp. 515-526.         [ Links ]

Doornik, J. A. (2009), Ara Introduction to Oxmetrics 6, Londres, Timberlake Consultants Press, 249 pp.         [ Links ]

Embrechts, P. (2000), "Extreme Value Theory: Potentials and Limitations as an Integrated Risk Management Tool", Derivatives Use, Trading & Regulation, 6 (1), pp. 449-456.         [ Links ]

Engle, R. F. (1982), "Autoregressive Conditional Heteroskedasticity with Estimates of the Variance of United Kingdom Inflation", Econometrica, 50, pp. 987-1008.         [ Links ]

Fernández, V. (2003), "Extreme Value Theory: Value at Risk and Returns Dependence around the World", documento de trabajo 161, Universidad de Chile, Centro de Economía Aplicada.         [ Links ]

Finkenstadt, B. y H. Rootzen (2001), Extreme Values in Finance, Telecommunications, and the Environmental, Boca Raton, Florida, CRC Press LLC, 405 pp.         [ Links ]

Fisher, R. y L. Tippett (1928), "Limiting Forms of the Frequency Distribution of the Largest or Smallest Member of a Sample", Proceedings of the Cambridge Philosophical Society, 24, pp. 180-190.         [ Links ]

Francq, C. y J. M. Zakoian (2004), "Maximum Likelihood Estimation of Pure GARCH and ARMA-GARCH Processes", Bernoulli, 10 (4), pp. 605-637.         [ Links ]

Gencay, R. y F. Selcuk (2004), "Extreme Value Theory and Value at Risk: Relative Performance in Emerging Markets", International Journal of Forecasting, 20, pp. 287-303.         [ Links ]

Glasserman P., P. Heidelberger y P. Shahabuddin (2000), "Efficient Monte Carlo Methods for Value-at-Risk", Risk Management Report 2000.         [ Links ]

Glosten, L. R., R. Jagannathan y D. Runkle (1993), "On the Relation between the Expected value and the Volatility of the Nominal Excess Return on Stocks". Journal of Finance, 48, pp. 1779-1801.         [ Links ]

Gnedenko, B. V. (1943), "Sur la Distribution Limite du Terme Maximum d'une Série Aléatoire", Annals of Mathematics, 44, pp. 423-453.         [ Links ]

Jenkinson, A. F (1955), "The Frequency Distribution of the Annual Maximum (or Minimum) Values of Meteorological Elements", Quarterly Journal of the Royal Meteorological Society, 81 (348), pp. 158-171.         [ Links ]

Jorion, P. (2000), Value at Risk: The New Benchmark for Managing Financial Risk, 2a. ed., Nueva York, McGraw-Hill, 544 pp.         [ Links ]

McNeil, A. J. (1999), "Extreme Value Theory for Risk Managers", Internal Modeling and CAD II, RISK Books, 93-113.         [ Links ]

Melchers, R. E. (2008), "Extreme Value Statistics and Long-term Marine Pitting Corrosion of Steel", Probabilistic Engineering Mechanics, 23 (4), pp. 482- 488.         [ Links ]

Millán-Valenzuela, H. (1999), "Las causas de la crisis financiera en México: Economia", Sociedady Territorio, 2 (5), pp. 25-66.         [ Links ]

Nelson, D. (1991), "Conditional Heterocedasticity in Asset Returns: A New Approach"', Econometrica, 59, pp. 347-370.         [ Links ]

Pickands, III, J. (1975), "Statistical Inference Using Extreme Order Statistics", The annals of Statistics, 3 (1), pp. 119-131.         [ Links ]

Reyes, H. J., H. Vaquera, y J. A. Villasenor (2009), "Estimation of Trends in High Urban Ozone Levels Using the Quantiles of (GEV)", Environme-trics, 21 (3), pp. 1-15.         [ Links ]

Tsay, R. S. (2002), Analysis of Financial Time Series, Nueva York, John Wiley and Sons, Inc., 448 pp.         [ Links ]

Von Mises, R. (1936), "La distribution de la plus grande de n valeurs", Bulletin of the American Mathematical Society, 2, pp. 271-294.         [ Links ]

Zakoian, J. M. (1994), "Threshold Heteroscedastic Models", Journal of Economic Dynamics and Control, 18, pp. 931-955.         [ Links ]

 

NOTAS

¹ Recuérdese que los máximos obtenidos por el método de picos sobre umbral a los residuales estandarizados del modelo ARMA-GARCH ajustado a los retornos, tienen una distribución generalizada de Pareto.

² Recuérdese que los máximos obtenidos por el método de picos sobre umbral a los residuales estandarizados del modelo ARMA-GARCH ajustado a los retornos, tienen una distribución generalizada de Pareto.