Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Economía mexicana. Nueva época
versión impresa ISSN 1665-2045
Econ. mex. Nueva época vol.20 no.1 Ciudad de México ene. 2011
Artículos
¿Ha ampliado la liberalización comercial la desigualdad económica entre los estados mexicanos? Un análisis desde la perspectiva econométrico–espacial
Has Trade Liberalization Increased Economic Inequality among the Mexican States? An Analysis from a Spatial Econometric Perspective
Vicente Germán–Soto y José Luis Escobedo Sagaz*
* Catedráticos–investigadores, Facultad de Economía, Universidad Autónoma de Coahuila, Unidad Camporredondo, Edificio "E", Planta Baja C.P. 25280, Saltillo, Coah. México, tel. (844) 412 87 82, fax (844) 410 26 79. vicentegerman@uadec.edu.mx, lanzas_ 98@yahoo.com.mx
Fecha de recepción: 8 de septiembre de 2008;
Fecha de aceptación: 17 de diciembre de 2009.
Resumen
Actualmente se debate si la liberalización comercial ha ampliado o no la desigualdad económica, tanto entre países como entre regiones. Este trabajo analiza la desigualdad económica entre los estados mexicanos mediante la convergencia y las técnicas de econometría espacial. Los resultados señalan una asociación positiva en la relación espacio–convergencia que disminuye en la etapa más reciente. Estimamos la dirección y la magnitud de esta relación, y encontramos que la caída en la convergencia coincide con la mayor apertura comercial del país. Además, la dependencia espacial estimada señala la persistencia de un cluster de ingresos bajos en el sur del país, que puede ser especialmente preocupante.
Palabras clave: liberalización comercial, desigualdad de ingresos, econometría espacial, crecimiento económico, México.
Abstract
What are the empirical effects of trade liberalization? This question is debated nowadays, in both an international and a regional scope. This work analyzes the economic inequality among Mexican states by means of a convergence methodology and spatial econometrics techniques. Results indicate a positive association between spatial autocorrelation and convergence, which has been diminishing during recent years. We also estimate the magnitude and direction of this relationship, and find that the lack of convergence agrees with trade openness in the country. Spatial dependence indexes point out a consistent low income cluster in the South of the country, which is worrying.
Keywords: trade liberalization, income inequality, spatial econometrics, economic growth, Mexico.
Clasificación JEL: C31, N96, O18, R12.
Introducción
Un hecho estilizado de la teoría económica es que cuando una economía abre sus mercados a la libre competencia ésta incrementa los niveles de producción y de bienestar para la sociedad. Generalmente se obtienen resultados en esa dirección debido a que la mayor competencia que generan los libres mercados hace que los precios de los bienes y servicios desciendan a niveles cada vez más competitivos. Con ello se logra que el consumo llegue a estratos de la población con menores niveles de ingreso. En teoría, y desde un punto de vista global, el bienestar de la población debe mejorar a medida que las estructuras de mercado se asemejan más a uno de competencia perfecta.
En México, los niveles de competencia entre las empresas se han incrementado desde que inició el proceso de apertura externa.1 Después de 20 años de libre comercio con Norteamérica y el mundo, ha habido un mejoramiento, en términos macroeconómicos, de los niveles competitivos de los mercados. Sin embargo, ¿qué tanto se han beneficiado las esferas microeconómicas de la economía nacional?, ¿estarán mejor los consumidores ahora que antes de la liberalización comercial?, ¿qué tan competitivas se han vuelto nuestras empresas? Aunque es difícil responder todas y cada una de estas preguntas, es posible derivar algunas inferencias, especialmente desde una perspectiva más agregada. Por ejemplo, al concentrarnos en los efectos a nivel de entidad federativa podemos formarnos una idea de los impactos de la apertura externa en los niveles de ingreso de sus habitantes.
El libre comercio ha significado un aumento de la producción nacional, la inversión y la generación de empleos; sin embargo, ha impuesto una disyuntiva a la economía mexicana: elegir entre aumentar el crecimiento económico (es decir, aumentar la producción o el tamaño del pastel) o distribuir en forma equitativa los beneficios derivados de una mayor producción (es decir, cómo repartir el pastel). Muy comúnmente estos dos objetivos no son del todo compatibles, y requieren la aplicación de políticas que busquen equilibrar el desarrollo regional.
Al igual que en México, en el plano internacional ha habido mucho interés (principalmente en las últimas décadas) por saber si un mayor crecimiento económico (eficiencia) se ha traducido en mayor igualdad de ingresos (equidad); es decir, si los países menos favorecidos se han beneficiado de ese mayor crecimiento económico, o si por el contrario prevalecen situaciones de empeoramiento a pesar del mayor dinamismo de las economías.
Esta disyuntiva entre buscar mayor eficiencia o mejorar la equidad ha sido abordada por los economistas en los últimos años en términos del análisis de las tendencias empíricas hacia la convergencia, y ha sido motivo de largos y controvertidos debates académicos. Muchos trabajos de la teoría del crecimiento (principalmente en estudios a nivel de países) se han centrado, casi de manera exclusiva, en la discusión de si las economías están o no en proceso de convergencia —véanse, por ejemplo, algunos trabajos clásicos como Barro (1991), Barro y Sala–i–Martin (1992a y 1992b), Mankiw, Romer y Weil (1992), Chatterji (1992), Quah (1993), Islam (1995), Crafts (1999), y Dinopoulos y Thompson (2000), entre otros—. Un factor relevante para la convergencia ha sido el papel del espacio en los procesos económicos —inicialmente sugerido en los trabajos de Fingleton (1999a y 1999b), y Rey y Montouri (1999), entre otros—. Particularmente en las áreas regionales, la dimensión espacial es un elemento importante cuando se estudian las fuentes de la desigualdad de ingresos.
Si un conjunto de economías está en convergencia, en términos de ingreso, significa que los beneficios del crecimiento económico los aprovechan tanto las economías de mayores ingresos como las más rezagadas, de tal manera que la economía global aumenta los niveles de bienestar. Una metodología que recientemente se ha explorado, tanto a nivel de países como de regiones, es la denominada como σ y β convergencia. En México, algunas contribuciones con esta metodología son los trabajos de Esquivel (1999), Messmacher (2000), Cermeño (2001) y Chiquiar (2005), entre otros. Mediante el análisis de un periodo de tiempo relativamente largo, en todos esos trabajos la velocidad de la convergencia estimada ha cambiado de signo en el periodo más reciente, lo que parece sugerir que la liberalización comercial desempeña un papel clave en este proceso. También hay contribuciones que abordan el tema de la convergencia desde diferentes perspectivas. Dos ejemplos son los trabajos de Aroca, Bosch y Maloney (2005), donde se emplean técnicas espaciales para analizar el vínculo entre divergencia de ingresos y liberalización comercial, y los trabajos de Carrion–i–Silvestre y Germán–Soto (2007 y 2009), que usan técnicas de series de tiempo en variables de la producción per cápita para analizar el proceso estocástico de la convergencia regional mexicana. Los autores concluyen que tal proceso no puede entenderse si no se considera el cambio estructural de los años ochenta.
El presente trabajo se incrusta en el marco de la literatura del crecimiento económico, empleando técnicas de análisis espacial de los datos para ampliar la evidencia sobre el vínculo entre convergencia y liberalización comercial. Específicamente nos basamos en el análisis anual del correlograma de la I de Moran (con indicadores globales y locales) y en ecuaciones de convergencia β para examinar cómo se han desempeñado las conductas regionales de crecimiento e ingreso en dos diferentes etapas de la economía mexicana: antes y después de la liberalización comercial. Estudios previos dentro de esta línea de investigación han abordado la misma problemática en el caso de las regiones de Estados Unidos (Rey y Montouri, 1999) y en las regiones mexicanas (Aroca, Bosch y Maloney, 2005). Sin embargo, nuestra aportación descansa en ejercicios claramente diferenciados. Primero, a diferencia del trabajo de Rey y Montouri (1999), empleamos ecuaciones de convergencia condicional, un asunto que en el caso mexicano es relevante debido a que la heterogeneidad es mayor en las economías estatales de México.2 Segundo, la evidencia reportada en el trabajo de Aroca, Bosch y Maloney (2005) se desarrolla mediante la combinación de indicadores espaciales con estimadores de densidad de Kernel para examinar el reordenamiento de los niveles de ingreso per cápita de los estados mexicanos; en nuestro caso, basamos la evidencia empírica en ecuaciones de regresión condicional (con técnicas de la econometría espacial) que controlan por diferencias regionales.3 Tercero, Aroca, Bosch y Maloney (2005) abordan el periodo comprendido entre 1970 y 2002, con datos de cada cinco años, mientras que nuestro trabajo abarca un periodo más amplio (1940–2005) y utiliza una base de datos diferente con periodicidad anual. Como consecuencia de las distintas técnicas de análisis, bases de datos y periodicidad, será interesante comparar las conclusiones alcanzadas en ambos trabajos.
En términos de los resultados empíricos, encontramos una asociación positiva entre convergencia y dependencia espacial que llevó a una disminución de la dispersión de ingresos regionales en México en torno a 1.75 por ciento anual durante 1940–2005; una tasa muy similar a la obtenida en muchos otros países, y muy cercana también a la tasa reportada en otros trabajos previos sobre el desempeño mexicano.4 Al considerar un cambio estructural en la economía mexicana a mediados de los años ochenta, observamos que el proceso de convergencia no fue uniforme: estimamos para el periodo 1940–1985 una tasa de disipación de las disparidades en torno a 3.7 por ciento, mientras que en la etapa más reciente (1985–2005) las estimaciones indican la formación de una tendencia hacia la divergencia, acompañada por un descenso importante de los indicadores de dependencia espacial. Para apoyar estas conclusiones hemos construido un indicador de apertura comercial que sugiere que ésta se halla relacionada con la menor igualdad de ingresos registrada entre los estados en la etapa más reciente.
También encontramos que los efectos espaciales (de elevada significación) subrayan la formación de un cluster de ingresos bajos entre los estados del sur del país. Este hallazgo resulta interesante para el gobierno, los planeadores de política económica regional y el conjunto de la sociedad, ya que es un indicativo de que el modelo de crecimiento económico mexicano, con una orientación muy marcada hacia el exterior y una disminución acelerada del gasto público, no sólo no ha logrado reducir las diferencias económicas entre las regiones del país, sino que parece acentuarlas. De este resultado se infiere que es urgente atender y diseñar objetivos de política económica que busquen atenuar los desequilibrios regionales, que observen más atención en las regiones que presentan mayor rezago, y que no sólo se planteen objetivos de mayor crecimiento macroeconómico como metas prioritarias.
La estructura del artículo es como sigue. En la primera sección llevamos a cabo un análisis exploratorio y presentamos la ecuación de convergencia clásica. En la segunda exponemos la metodología de la convergencia con dependencia espacial, describimos la base de datos y comentamos los principales resultados. A la luz de los resultados obtenidos, en la sección III analizamos la relación entre los procesos de liberalización comercial y de convergencia. Finalmente, la sección IV destaca algunas conclusiones.
I. Análisis exploratorio y la ecuación de convergencia clásica
1.1. Análisis exploratorio
Antes de presentar la metodología y los resultados del análisis, es conveniente situar la geografía política de los estados mexicanos y su relación con los niveles de producción per cápita para entender el desempeño regional de los últimos años. El mapa 1 muestra que los resultados recientes del crecimiento regional de México coinciden con la distribución geográfica en el mapa: en la diversidad mexicana coexisten un sur pobre y atrasado junto a un centro y norte relativamente prósperos. En el mapa 1 los tonos más oscuros representan las entidades federativas con mayor productividad al final del periodo. En general, se observa que en el centro y norte del país prevalecen las tonalidades más intensas, contrariamente a las más claras que dominan en la parte sur. Notables excepciones a la conducta descrita son los desempeños mostrados por Campeche y Quintana Roo, ya que las extracciones de petróleo, en el primero, elevan artificialmente los niveles de productividad, mientras que las inversiones en infraestructura y servicios turísticos de los últimos años explican el sesgo producido en el segundo estado.
Con base en la visualización ofrecida por el mapa 1 (y desde un punto de vista informal), el resultado del desempeño regional mexicano en la actualidad ha sido uno de gran desigualdad de ingresos. Sin embargo, para investigar si esta conducta ha prevalecido en el largo plazo tendremos que hacer uso de herramientas más formales.
1.2. La ecuación de la convergencia clásica
Esta metodología predice que en el largo plazo las diferencias en ingresos per cápita de un conjunto de economías tenderán a desaparecer, por lo que se le conoce como la teoría de la convergencia, y ha sido probada en diferentes niveles geográficos, como por ejemplo para conjuntos de países, para regiones de un mismo país o para conjuntos de regiones de varios países.5 El enfoque clásico de la convergencia está basado en dos hipótesis: la convergencia σ y la convergencia β (Barro y Sala–i–Martin, 1992a). La primera hipótesis apoya sus predicciones de convergencia en el análisis de la dispersión de ingresos en el largo plazo, mientras que la segunda estima una ecuación de regresión entre tasas de crecimiento y niveles iniciales de producción per cápita. En términos más formales, las ecuaciones (1) y (2) caracterizan estas dos hipótesis. Para el caso de la convergencia σ tenemos:

donde yi,t0 es el ingreso per cápita de la región i en el año t, N es el número de regiones, T es el número de periodos, y la media del conjunto de datos viene determinada por la expresión:
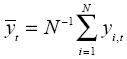
La evolución gráfica de σt en el tiempo, con una tendencia de la dispersión de ingresos a disminuir, suele interpretarse como evidencia a favor de la convergencia σ.
En cambio, las regresiones de convergencia β tienen la siguiente estructura:

donde yi,t0 es el nivel inicial de producto per cápita del i–ésimo estado, y yi,t0+T corresponde al nivel final de producto per cápita. En la especificación (2) el parámetro β tiene el siguiente valor: 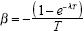 donde a su vez el valor del parámetro λ nos da un aproximado de la velocidad de la convergencia. Finalmente, ε es un término de error aleatorio. El parámetro de interés es λ, ya que su valor indica la presencia o no de un proceso de convergencia. Si λ es positivo y significativo implica que los estados con mayores niveles de producción per cápita crecieron a menores tasas anuales que aquellos estados con menores niveles de producto, y ello se interpreta como evidencia de que la brecha relativa (y, en este caso, absoluta) entre estados se cierra mediante un proceso de convergencia. Cuando λ es negativo constituye evidencia de que los estados más ricos crecieron a tasas anuales mayores, y no se presenta convergencia alguna.
donde a su vez el valor del parámetro λ nos da un aproximado de la velocidad de la convergencia. Finalmente, ε es un término de error aleatorio. El parámetro de interés es λ, ya que su valor indica la presencia o no de un proceso de convergencia. Si λ es positivo y significativo implica que los estados con mayores niveles de producción per cápita crecieron a menores tasas anuales que aquellos estados con menores niveles de producto, y ello se interpreta como evidencia de que la brecha relativa (y, en este caso, absoluta) entre estados se cierra mediante un proceso de convergencia. Cuando λ es negativo constituye evidencia de que los estados más ricos crecieron a tasas anuales mayores, y no se presenta convergencia alguna.
Aunque la ecuación (2) ha sido objeto de amplia investigación empírica, puede llegar a ser bastante restrictiva si las diferencias estructurales de las economías son importantes (diferentes estados estacionarios); una propiedad que bien puede compartir el conjunto de entidades mexicanas, dada su heterogeneidad (véase el mapa 1, como ejemplo). Esta limitante de la ecuación (2) se ha enfatizado mucho en los estudios internacionales. Además, Mankiw, Romer y Weil (1992) consideran que las economías tienden en realidad a sus respectivos estados estacionarios y no a uno en común, como pronostica la convergencia absoluta. En este caso, la ecuación que debe ser objeto de investigación empírica presenta el formato siguiente:

donde el vector Xi,t0 busca controlar por diferencias en los niveles de producto per cápita del estado estacionario.
La ecuación (3) permite capturar las diferentes tendencias hacia el estado estacionario del conjunto de economías; sin embargo, no considera la autocorrelación espacial (externalidades regionales producidas por la difusión de tecnologías o el comercio, entre otros factores), es decir, los efectos que el crecimiento de una región puede tener en el desempeño económico de sus regiones vecinas. Debido a que se ha demostrado que este fenómeno puede ser importante en los procesos de crecimiento económico, debemos contemplar este factor en el presente estudio.
II. Dependencia espacial y convergencia regional: metodología, datos y resultados
II. 1. Repaso teórico y empírico
La localización espacial y las conexiones vecinales de las regiones (autocorrelación espacial) pueden ser factores determinantes en los procesos del desarrollo regional. Desde esta perspectiva, la autocorrelación espacial puede definirse como la coincidencia de valores similares en localidades similares (véase Anselin, 1988a), de tal manera que lo que ocurre en una región tiene consecuencias también en las regiones vecinas. La autocorrelación espacial puede ser positiva, cuando valores elevados o bajos de una variable tienden a concentrarse en determinado espacio, o negativa, cuando las áreas geográficas tienden a estar rodeadas de vecinos con valores muy desiguales.
Dentro de este creciente cuerpo teórico, algunos trabajos pioneros realizados para países desarrollados como los de Fingleton (1999a y 1999b), Rey y Montouri (1999), López–Bazo et al. (1999), y Florax y Nijkamp (2005), entre otros, han observado que el uso de datos localizados espacialmente (como el PIB per cápita de regiones o países) puede dar lugar a estimaciones sesgadas de los modelos tradicionales de convergencia. Las interrelaciones halladas para conjuntos de países y regiones parecen indicar que el desempeño económico de una determinada región no depende exclusivamente de sus variables fundamentales, sino también de la dinámica de desarrollo de las regiones a las que se encuentra geográfica y económicamente unida.
Así por ejemplo, Fingleton (1999a) revela la existencia de una importante autocorrelación y heterogeneidad espacial en las ecuaciones de convergencia de las economías europeas. Paralelamente, López–Bazo et al. (1999) dan cuenta de un elevado grado de dependencia espacial en el PIB per cápita para una muestra de regiones europeas, mediante el uso de indicadores globales y locales de la dependencia espacial. De forma similar, fuertes patrones de autocorrelación espacial y global fueron reportados en los ingresos regionales de EUA durante el periodo 1929–1994 por Rey y Montouri (1999). Resultados muy similares se obtuvieron en Magalhães, Hewings y Azzoni (2005) para los estados de Brasil durante el periodo 1970–1995, y también para el caso mexicano en el trabajo de Aroca, Bosch y Maloney (2005) durante 1970–2002.
Más recientemente, el análisis económico espacial vinculado a los procesos convergentes de las economías evoluciona en torno a la consideración de distintos elementos teórico–metodológicos para los que aún no se tiene evidencia concluyente. Por ejemplo, una línea que se trabaja es cómo neutralizar el posible problema de endogeneidad en las variables de control del modelo. Mella–Márquez y Chasco–Yrigoyen (2006) adelantan una posible solución al problema en el caso español.6 Los autores tratan el caso en el que las variables explicativas endógenas podrían estar correlacionadas con los términos de error, invalidando de esta manera las estimaciones estándar (y la inferencia estadística asociada). Ellos recomiendan realizar estimaciones a través de métodos de variables instrumentales. Por otro lado, un refinamiento adicional al modelo original de convergencia usa una estructura bayesiana para probar convergencia regional, principalmente cuando existen problemas relacionados con la presencia de heterogeneidad y observaciones atípicas en muestras regionales (Erthur, Le Gallo y LeSage, 2007).
Otra línea de investigación se concentra en ofrecer alternativas a la forma de identificar la dependencia espacial en los modelos econométricos. No ha habido acuerdo al respecto, y prevalecen dos formas como las principales: los modelos de error y retardo espacial, con el primero como el más importante, de acuerdo con la evidencia empírica. Sin embargo, los resultados de diversos trabajos recientes sugieren que ello puede deberse a una forma de modelación mal especificada. Por ejemplo, López–Bazo, Vayá y Artis (2004), y Fingleton y López–Bazo (2006), consideran que los contrastes de dependencia espacial llevan a esta conclusión, cuando en la práctica la difusión de externalidades entre las economías es la más obvia (es decir, la forma de retardo espacial). Para evitar el sesgo producido por los contrastes tradicionales, los autores proponen analizar el crecimiento con un modelo Durbin espacial que incluya externalidades tecnológicas. El modelo Durbin espacial es la forma reducida de un modelo con dependencia seccional cruzada en los errores, y se puede usar como un enfoque más general en la selección de modelos. Esta idea se explora en Mur y Angulo (2006), donde se analiza el papel que desempeña el modelo Durbin espacial para especificar un modelo econométrico espacial. Aunque atractivo para el caso de las regiones europeas (conformado por un gran número de observaciones), este enfoque puede resultar muy restrictivo en el caso mexicano, ya que es más demandante en términos de datos, una de las limitaciones que enfrentamos al usar estadísticos espaciales.
II.2. Base de datos
Con el fin de probar la hipótesis de la convergencia y dar una idea del papel del espacio geográfico entre los estados mexicanos, usamos una base de datos anual durante 1940–2005. Esta base de datos se construyó a partir de la información sobre producción estatal publicada por el Instituto Nacional de Estadística y Geografía (INEGI) para el periodo 1993–2005, así como de la base de datos publicada en Germán–Soto (2005) para el periodo comprendido entre 1940 y 1992. Con la información recabada sobre producto estatal construimos la variable producción per cápita, misma que se emplea en este trabajo al dividir las cifras de producto por la población estatal, estimada por el Consejo Nacional de Población (Conapo).7
Por otro lado, y con el fin de ofrecer estimaciones de la convergencia condicional (en un modelo que contempla el papel de la dependencia espacial), hacemos uso de una serie de variables control para las que existe información oficial a nivel de los estados: 1) esperanza de vida (construida como años de vida promedio de la población de cada estado al nacimiento); 2) índice de natalidad (construido como el número de nacimientos por cada mil habitantes), y 3) porcentaje de población económicamente activa de la población total. Estas variables fueron consideradas como el valor promedio de cada subperiodo, y su elección responde al criterio de disponibilidad de la información.8 Las fuentes de información para este conjunto adicional de variables fueron el INEGI (1999) para el periodo comprendido entre 1940 y 1995, y el Conapo (2001) y el INEGI (2006) para el periodo temporal más reciente.
II. 3. Especificaciones teóricas y resultados
En el análisis de datos espaciales suelen seguirse dos fases básicas: una primera conocida en la literatura como exploratoria (o uso de indicadores globales y locales de asociación espacial), y una segunda conocida como confirmatoria (o uso de un conjunto de estadísticos obtenidos a través de un modelo de regresión), cuando los contrastes globales y locales han identificado la presencia de autocorrelación espacial en los datos. De esta manera, podemos abordar la relación espacio–convergencia desde una perspectiva exploratoria (usamos el criterio de convergencia σ con los instrumentos de autocorrelación global y local) y desde un análisis confirmatorio (el criterio de convergencia β condicional en un modelo con datos georreferenciados). En las secciones siguientes presentamos las especificaciones teóricas y los resultados.
II.3.1. La convergencia σ y la autocorrelación espacial global
El papel del espacio resulta incuestionable cuando la probabilidad de atraer un nivel mayor de desarrollo económico es mayor para las áreas pobres rodeadas de áreas ricas que para las áreas pobres rodeadas de áreas pobres. Es por ello que parece atractiva la idea de considerar la variable geográfica en los modelos de convergencia.
En esta sección usamos diversas herramientas diseñadas para detectar autocorrelación espacial; sin embargo, el análisis lo llevamos a cabo con el estadístico I de Moran (1948).9 Al seguir el análisis de Rey y Montouri (1999), en la gráfica 1 reportamos dos curvas de la distribución regional de ingresos: la curva de dispersión basada en el coeficiente de variación (esto es, convergencia σ), y otra más que mide la evolución de la autocorrelación espacial de los ingresos estatales para el mismo periodo (el estadístico I de Moran).

Las ecuaciones de estimación empírica que dieron origen a estas dos curvas son la ecuación (1), para el caso de la convergencia σ, y la expresión dada en (4), para el estadístico I de Moran, que mide la autocorrelación espacial:
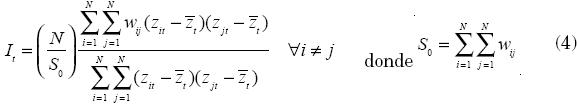
El estadístico presentado en la ecuación (4) se describe de la siguiente manera:10 wij es un elemento de la matriz binaria de contactos espaciales W, de tal forma que wij = 1 si los estados i y j comparten una frontera común, y toma el valor de cero en cualquier otro caso; zit y zjt representan el valor de los ingresos de las regiones i y j respectivamente, en el año t (medidas en logaritmos naturales); 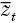 es el valor promedio en el año t; N es el número de observaciones; y S0 es un factor que se usa para dar una escala a la matriz W.
es el valor promedio en el año t; N es el número de observaciones; y S0 es un factor que se usa para dar una escala a la matriz W.
El papel de la matriz de contactos espaciales W es introducir la noción de "vecindad" para cada estado, y se define como "... una matriz cuadrada no estocástica cuyos elementos wij reflejan la intensidad de la interdependencia existente entre cada par de regiones i y j" (Moreno y Vayá, 2000, p. 23). En términos más formales presenta la siguiente estructura:

En esta forma, los resultados básicos con el contraste I de Moran se reportan en el cuadro 1. Como se puede apreciar, hay evidencia de dependencia espacial en el PIB per cápita, dado que los coeficientes estimados son estadísticamente significativos al 1 por ciento en casi todos los años del periodo. Sin embargo, en los años de mayor volatilidad económica (véase 1976 a 1989 y para los años 1995 y 1996)11 hay pérdida de significación del contraste I de Moran, aunque son todavía estadísticamente válidos al 5 por ciento de significancia.
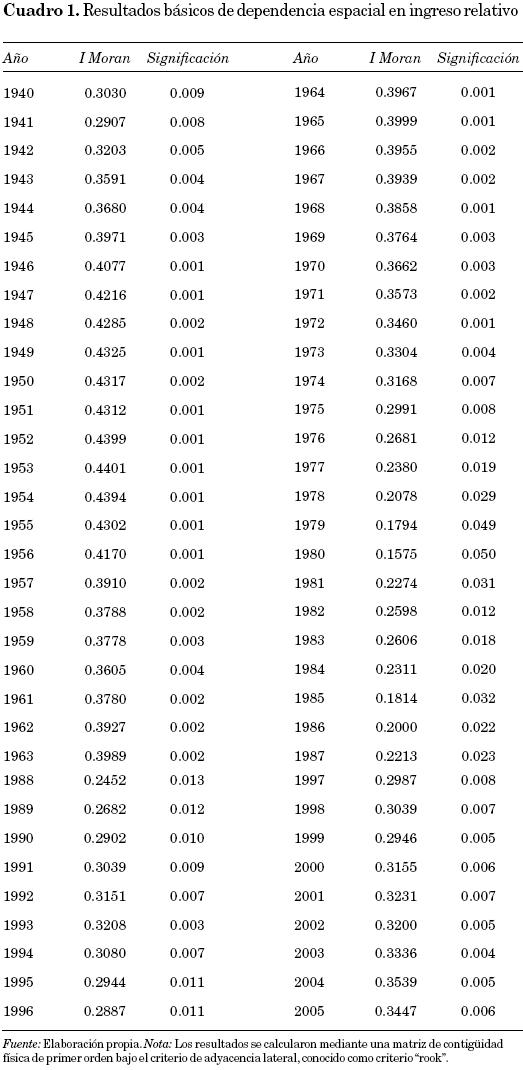
Un análisis comparativo de la evolución temporal entre la autocorrelación espacial y la dispersión de ingresos puede ayudarnos a entender la relación existente entre estas dos variables en el caso mexicano. En la gráfica 1 se observa que no hay una relación claramente definida, aunque desde los años ochenta tanto la dispersión como la dependencia espacial parecen ir en ascenso. Además, la relación se torna especialmente imprecisa en esa década.
El coeficiente de correlación entre las variables puede ser de gran utilidad para entender el comportamiento que se muestra en la gráfica 1. Para el periodo global (66 años), el coeficiente de correlación (calculado en cerca de 0.57) indica una relación positiva entre ambas variables; sin embargo, y debido a que esta conducta no fue uniforme a lo largo del periodo, hemos realizado estimaciones para diferentes subperiodos. Si consideramos la etapa entre 1940 y 1985, la correlación aumenta hasta cerca de 0.64, un resultado que es indicativo de que a mayor tasa de convergencia hubo mayor dependencia espacial. Por otro lado, se estima una relación negativa para el subperiodo 1985–2005, al calcularse una correlación de –0.19; sin embargo, este resultado puede hallarse afectado por el periodo particularmente inestable que prevaleció en los años ochenta. En particular, el coeficiente de correlación para el periodo posterior a la inestabilidad económica (por ejemplo 1990–2005) indica una relación positiva entre ambas variables, aunque con una intensidad relativamente menor, al estimarse en cerca de 0.26. En este caso, la menor asociación entre las variables espacio–convergencia parece hallarse en el aumento en las diferencias de ingreso. Desde un punto de vista global y de largo plazo las variables tienden a moverse en la misma dirección: mayor convergencia se asocia con mayor dependencia espacial.
Para efectos de ilustración, calculamos otro instrumento útil en el análisis del grado de la dependencia espacial de una variable: el diagrama de dispersión de Moran. Este diagrama está basado en los resultados estimados con la ecuación (4). La gráfica 2 presenta los resultados para cuatro años de la muestra.12 Cada representación contiene un diagrama de dispersión de Moran con los ingresos estandarizados de un estado contra su retardo espacial (también estandarizado). El retardo espacial de un estado es un promedio ponderado de los ingresos de sus estados vecinos, estimado a través de una matriz de contactos.

Cada diagrama de dispersión contiene cuatro cuadrantes que definen cuatro tipos de asociación espacial local entre un estado y sus vecinos:13(AA) un estado de ingresos altos con vecinos de ingresos altos (cuadrante I); (BA) un estado de ingresos bajos rodeado de vecinos de ingresos elevados (cuadrante II); (BB) un estado de ingresos bajos rodeado de vecinos también con ingresos bajos (cuadrante III), y (AB) un estado de ingresos elevados junto a vecinos de ingresos bajos (cuadrante IV). Los cuadrantes I y III constituyen formas positivas de la dependencia espacial, mientras que los cuadrantes II y IV representan patrones negativos.
Como se puede observar en la gráfica 2, hay un acomodo de las observaciones en torno a una tendencia positiva entre ingresos relativos, lo que invita a pensar en la presencia de un patrón de dependencia espacial. Estos esquemas (obtenidos con la I de Moran global) nos dan una idea de la presencia de la autocorrelación espacial; sin embargo, hasta el momento sólo constituyen evidencia en forma conjunta para el total de la muestra. Por lo tanto, si queremos estudiar la presencia de clusters regionales que presentan una concentración de valores elevados o bajos, tendremos entonces que revisar contrastes locales.
II.3.2. La convergencia σ y la autocorrelación espacial local
Los contrastes globales no son sensibles a situaciones donde pueda prevalecer inestabilidad importante en la distribución espacial de la variable.
Por ejemplo, no permiten captar situaciones donde se formen agrupaciones de regiones que concentren valores más elevados o bajos de lo que cabría esperar ante una distribución homogénea, es decir, no permiten valorar la posible formación de clusters regionales. Para ello se han desarrollado herramientas de detección de la dependencia local, como la Ii de Moran y la Gi(d) de Getis y Ord (1992), basadas en los contrastes tradicionales. El contraste local de Moran, en este caso, se define de la siguiente manera para el i–ésimo estado (Moreno y Vayá, 2000):

donde Ji es el conjunto de regiones vecinas a i.
En el mapa 2 reproducimos los estadísticos locales de Moran para una muestra de cuatro años. Como se aprecia, hay dos resultados consistentes. Primero, entre 1940 y 2005 la evolución de ingresos regionales en México ha sido en torno a dos clusters: uno de estados ricos en el norte del país, y otro de estados pobres en el sur del país. Estos resultados dan una idea del grado de polarización de ingresos imperante entre los estados mexicanos. Es notable la presencia del cluster de ingresos bajos dibujado en el sur del país, ya que en tres estados resulta significativo al 5 por ciento en todos los años del periodo: Guerrero (GRO), Oaxaca (OAX) y Puebla (PUE).

Los resultados con el estadístico I de Moran local para todos los años del periodo se resumen en el cuadro 2. En la tercera columna reportamos el número de años (de un total de 66) para los cuales el estadístico local proporciona indicios de la formación de clusters, mediante un nivel de significancia de 5 por ciento. Este nivel de significancia está basado en un bootstrap de 999 permutaciones sobre los estados vecinos para cada observación. También reportamos el número de años en los que el índice local de Moran resulta significativo en cada uno de los cuatro cuadrantes del diagrama de dispersión.

Los resultados del cuadro 2 indican que el patrón local de asociación espacial tiende a reflejar la trayectoria global de asociación espacial positiva entre los ingresos per cápita de una región y sus vecinos (véase la gráfica 2), ya que 82 por ciento de los indicadores locales que son significativos pertenece ya sea al cuadrante I o III del diagrama de dispersión, lo cual refleja la formación de los clusters AA y BB, respectivamente. Sin embargo, la mayor parte de la evidencia se concentra en el cuadrante III, con 70 por ciento del total de los indicadores significativos (véase la suma total de 414 en el cuadro 2), mientras que el cuadrante I aporta poco más de 12 por ciento.
Además, a lo largo de los 66 años el único cluster persistente es el del cuadrante III, es decir, el de ingresos bajos, y tres de esos estados son consistentes en todos los años del periodo: Guerrero, Oaxaca y Puebla.14 El primero con 65 años significativos de los 66 posibles, el segundo con 46 y el tercero con los 66 años. Los resultados de la columna C–III proporcionan suficiente evidencia de que el cluster de esos estados (en el sur del país) no es producto de la casualidad.
II.3.3. La convergencia β condicional y la dependencia espacial
El análisis econométrico estándar considera implícitamente el supuesto de que los términos de error desde cada individuo son independientes en la ecuación (3). Si expresamos el término de error en términos vectoriales tenemos:

donde I es la matriz identidad. Sin embargo, la econometría espacial considera que este supuesto puede ser bastante restrictivo en un contexto de corte transversal, donde las relaciones económicas entre los estados vecinos pueden llevar a diferentes formas de dependencia espacial. Con el fin de dar validez a este supuesto, se han desarrollado diversas propuestas que consideran el hecho de que los errores pueden ser no esféricos. Dos modelos de mayor uso con este fin son los modelos de error espacial y de retardo espacial.
A. El modelo de error espacial
Esta especificación examina si la dependencia espacial funciona como un mecanismo de error, en el cual los errores de regresión de los diferentes individuos pueden mostrar covarianza espacial (Anselin, 1988b). Para cualquier momento t el término de error es:

con γ como el coeficiente de error espacial. Al despejar, se obtiene:

donde A = (I–γW)–1 y ut ~N(0, σ2I). En este caso, el término de error original tiene la siguiente matriz de covarianzas no esférica:

En la medida en que cada individuo i tenga una conectividad diferente, es decir, que el peso espacial sea relevante, entonces las covarianzas en (8) serán diferentes. El uso de mínimos cuadrados ordinarios (MCO), ante la presencia de errores no esféricos, produciría estimaciones insesgadas del parámetro de la convergencia (y del intercepto), pero una estimación sesgada de los parámetros de la varianza. Esto significa que la inferencia basada en MCO no puede ser la adecuada si los efectos espaciales son significativos. Por lo tanto, la inferencia sobre el proceso de convergencia debe basarse en un modelo de error espacial estimado por métodos de máxima verosimilitud.
Al sustituir (7) en (3), la ecuación de investigación empírica de la convergencia con el término de error espacial adquiere la siguiente forma (volvemos ahora a la forma lineal de las ecuaciones):
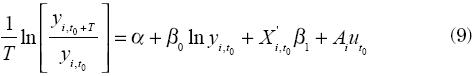
donde Ai representa la fila i–ésima de la matriz A = (I–γW)–1. A partir de la ecuación (9) es evidente que una perturbación aleatoria introducida en uno de los estados no sólo afectará la tasa de crecimiento en ese estado, sino que también impactará las tasas de crecimiento de los demás estados del sistema, vecinos y no vecinos, a través de la estructura de covarianza del error que se recoge en la matriz A.
B. El modelo de retardo espacial
En este caso se considera que la dependencia espacial se crea por la interacción presente entre los estados. De acuerdo con esto, se agrega una variable dependiente con un retardo espacial en el lado derecho de la ecuación (3), tal y como se expresa en la ecuación (10):
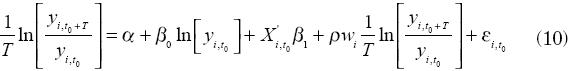
donde p es el coeficiente del retardo espacial, wi la i–ésima fila de la matriz W, y los demás términos son como se definieron previamente. Desde esta perspectiva, el valor esperado de la tasa de crecimiento del ingreso estatal no solamente se explica por el efecto producido por las variables con las que se relaciona (incluido su nivel inicial de ingresos), sino que también se encuentra afectada por impactos producidos en otros estados con los que tiene relación (Rey y Montouri, 1999).
II.3.4. Resultados de la relación convergencia condicional–dependencia espacial
A. Regresiones MCO y diagnósticos
Los supuestos de MCO (normalidad, homoscedasticidad y no autocorrelación) no necesariamente se satisfacen cuando se trata de datos espaciales. En particular, existe la posibilidad de que los errores o las variables muestren dependencia espacial. Con el fin de evaluar esta posibilidad, en el modelo de regresión hemos estimado la ecuación de convergencia condicional por MCO. El conjunto de resultados, así como los diagnósticos de regresión, se muestran en el cuadro 3.

En general, en las tres muestras de datos las estimaciones del coeficiente β resultan altamente significativas y tienen el signo esperado, aunque se aprecian algunos problemas de significación en las variables usadas como control. El primer conjunto de diagnósticos pertenece a las pruebas de multicolinealidad y normalidad de los residuos. En las tres muestras el número estimado de multicolinealidad (1.28, 1.38 y 1.19) está por debajo del límite aceptable de 20 (véase Anselin, 1992), por lo que no se espera que surjan problemas derivados de esta fuente. Por otro lado, la prueba Jarque–Bera indica que la regresión del periodo 1940–1985 presenta algunos problemas de normalidad en los errores, aunque en las otras dos regresiones el supuesto de normalidad sí se satisface.
Debido a que no se encontraron problemas de falta de normalidad en las regresiones 1940–2005 y 1985–2005, la prueba Breusch–Pagan se selecciona por el paquete estadístico SpaceStat para el diagnóstico de heteros–cedasticidad. En cambio, en la regresión 1940–1985, donde se rechazó la falta de normalidad, se estima la prueba Koenker–Bassett. Cuando hay poca información sobre la forma de la heteroscedasticidad, la prueba White es la más apropiada. Sin embargo, con las tres pruebas hay un amplio consenso sobre la no existencia de problemas potenciales desde esta fuente, aunque la prueba White admite que la regresión 1985–2005 puede presentar, aunque débilmente (en 10 por ciento pero no en 5 por ciento), problemas de heteroscedasticidad.
Un último grupo de diagnósticos corresponde a la dependencia espacial. No hay un resultado claro sobre esta variable entre el conjunto de pruebas implementadas. En general, las pruebas I de Moran y Multiplicador de Lagrange del modelo de error espacial concluyen que la dependencia espacial es significativa en las regresiones 1940–1985 y 1985–2005, mientras que las pruebas Multiplicador de Lagrange y su correspondiente versión robusta del modelo de retardo espacial estiman significación en las regresiones 1940–2005 y 1940–1985. La última de las pruebas de este diagnóstico, la prueba SARMA, también concluye en esta dirección.
B. Regresiones por máxima verosimilitud
El cuadro 4 presenta los resultados de estimación del modelo de retardo espacial. Además de las estimaciones de los coeficientes estructurales, también se muestran los resultados de diagnóstico de la heteroscedasticidad y la dependencia espacial. Encontramos una elevada significación de las variables control usadas en el modelo, pero sobre todo del coeficiente que estima la velocidad de la convergencia para las regresiones 1940–2005 y 1940–1985. La falta de significación en la tercera de las regresiones puede ser atribuible a la falta de normalidad en los errores anticipada por los estadísticos de este modelo desde el cuadro 3, ya que la estimación por máxima verosimilitud se basa en el supuesto de normalidad de los errores. Sin embargo, el parámetro p asociado con la variable dependiente espacialmente rezagada no resulta significativo en ninguna de las regresiones; además, el criterio de información de Akaike (AIC) tiene un valor muy similar al obtenido en el modelo de la regresión estándar, por lo que se puede concluir que la implementación de este modelo no produce mejoras sustanciales respecto a su versión estándar.

La prueba Breusch–Pagan espacial confirma la no existencia de problemas de heteroscedasticidad en ninguna de las regresiones. Sin embargo, el conjunto de estadísticos que prueban dependencia espacial no validan el modelo de retardo espacial. En particular, los resultados no satisfacen la siguiente condición:15

por lo que es poco probable que el coeficiente autorregresivo desde cada regresión sea significativo.16
Las estimaciones del cuadro 5 señalan la presencia de autocorrelación en forma de error espacial. Al basarnos en el criterio de información de Akaike, las estimaciones del modelo de error espacial observan mejoras sustanciales respecto a los otros dos modelos en las tres regresiones ensayadas. Además, los coeficientes estimados son altamente significativos (incluyendo el parámetro γ), principalmente en las dos primeras regresiones. Este resultado confirma el patrón de dependencia espacial reportado en secciones previas con indicadores de autocorrelación global y local.
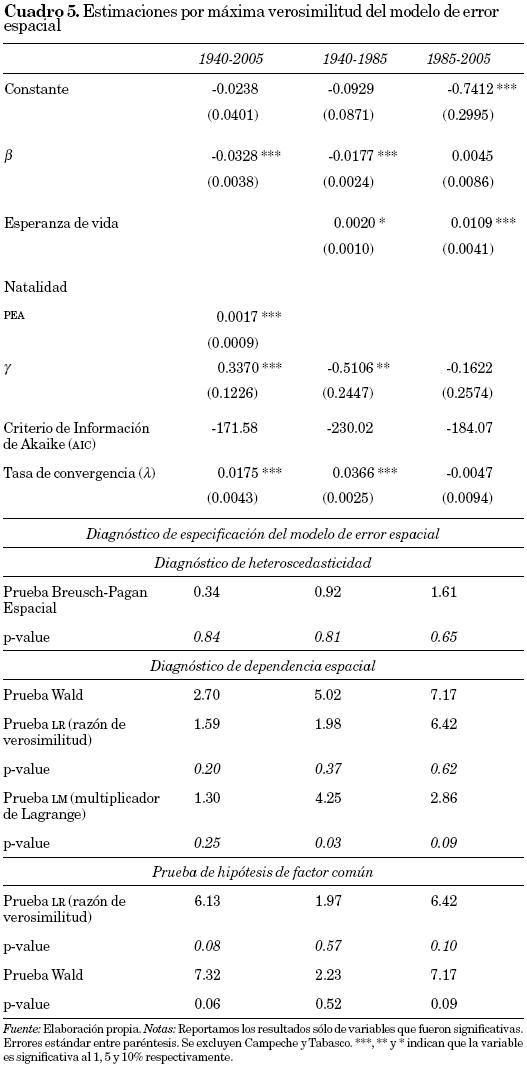
En ninguna de las regresiones se aprecian problemas de heteroscedasticidad, y los estadísticos de dependencia espacial satisfacen la condición (11) en dos de las ecuaciones (la estimación del periodo 1940–1985 no satisface esta condición). Sin embargo, los resultados de las pruebas LR y WALD sobre la hipótesis de factor común están en la dirección correcta, ya que en todos los casos logran satisfacer la condición WALD LR. Además, ninguna de estas pruebas es altamente significativa (todas estiman una probabilidad mayor a 5 por ciento), lo cual indica que no existen inconsistencias en la especificación del modelo.17
C. Análisis de la convergencia regional
Un análisis comparativo de las tasas de convergencia estimadas por el conjunto de regresiones que comprendieron hasta el año 1940 y la regresión estimada para el periodo posterior a 1985 permite concluir en dos sentidos: primero, las tasas de convergencia regional se han desdibujado a medida que se ha consolidado el proceso de apertura comercial; y segundo, la dependencia espacial se constituye en un elemento clave del proceso de convergencia regional, la cual también disminuyó su intensidad en la medida en que las relaciones comerciales de las economías estatales se volcaron hacia el exterior.
De acuerdo con las estimaciones del modelo de error espacial, la tendencia hacia la convergencia en términos de producto per cápita se registró a una velocidad de 1.75 por ciento durante 1940–2005, mientras que para el periodo 1940–1985 esta velocidad se estimó en 3.6 por ciento. En general, las diferencias entre ambos periodos se esperaban, dada la evidencia empírica previa (véanse, por ejemplo, Esquivel, 1999; Messmacher, 2000, y Chiquiar, 2005, entre otros), donde se documentó que el periodo de convergencia terminaba por los años ochenta, aproximadamente. Para el periodo más reciente, sin embargo, las estimaciones reportaron una tasa no ya de convergencia, sino de divergencia, aunque ésta resultó con un coeficiente pequeño y no significativo.
En general, la economía mexicana registró tasas espectaculares de crecimiento económico durante 1940–1975 (Villarreal, 1988) aproximadamente, una etapa que dio mayor impulso al crecimiento interno, lo cual permitió aumentar el tamaño de la tarta económica. Esto favoreció las relaciones económicas entre los estados y, como consecuencia, llevó a que se distribuyeran los recursos de ese mayor crecimiento. Dado el agotamiento de este modelo, al caer el crecimiento a tasas negativas durante varios años (sobre todo durante los ochenta), la apertura al mercado externo ha privilegiado el aumento de la producción (actuar con eficiencia); sin embargo, al parecer no ha habido una distribución justa de los rendimientos de ese mayor crecimiento (actuar con equidad).
III. Liberalización comercial y convergencia regional
¿Por qué suponemos que el proceso de liberalización comercial ha tenido implicaciones importantes en aumentar la desigualdad regional en México? Desde la recesión de 1982, ocurrida como crisis de deuda externa, el gobierno mexicano emprendió un proceso de liberalización al relajar los aranceles y las cuotas de importación de muchos productos. Este proceso se aceleró posteriormente en 1986 (con la incorporación del país al GATT) y en 1994 (con la entrada en vigor del Tratado de Libre Comercio de América del Norte). Después de 40 años de ser prácticamente una economía cerrada al exterior, la economía mexicana pasó a ser, en poco tiempo, una economía abierta. Una de las principales razones que justificaron el abandono del proteccionismo fue el bajo nivel de exportaciones (Lustig, Borthsworth y Lawrence, 1992).
El Fondo Monetario Internacional y el Banco Mundial recomendaron (no sólo a México sino a los países en desarrollo en general) una nueva estrategia de recuperación y crecimiento basada en las exportaciones. Entre las estrategias se incluyeron: liberalización comercial, depreciación del tipo de cambio, privatización de empresas estatales y reducción del gasto público, entre otras (Sachs, 1988, p. 77).
Aunque las estrategias de crecimiento basadas en exportaciones tuvieron mucho éxito en países de Asia, en el caso de México no queda claro el impacto de la apertura económica en algunas variables macroeconómicas, tales como la producción, el empleo y la desigualdad de ingresos. En este trabajo encontramos que la desigualdad de ingresos se ha incrementado, y una posible causa apunta al proceso de apertura económica que se ha seguido.
Desde que el gobierno mexicano decidió orientar la política comercial hacia el exterior, se ha incrementado la producción nacional; sin embargo, gran parte de ese aumento se ha reducido a compras entre grandes empresas con actividades de ensamble de mercancías en territorio mexicano. Este esquema se conoce en México como maquila, y al tratarse de actividades de ensamble, básicamente, ha reducido la generación de valor y ha roto las relaciones de abastecimiento de insumos entre estados industrializados y no industrializados, ya que ahora las mayores compras de los estados industriales son con empresas del extranjero.
Es difícil reducir a un número el grado y la intensidad de la apertura comercial, pero, con el propósito de comparar su evolución con el proceso de convergencia, nos apoyamos en un indicador muy socorrido en análisis de apertura comercial: el cociente que resulta de dividir las exportaciones e importaciones entre la producción. El indicador así construido lo relacionamos con el proceso de convergencia desde 1940. Los datos para exportaciones e importaciones se tomaron del INEGI (1999 y véase página web para años más recientes: www.inegi.gob.mx) y se hallan en miles de dólares. La gráfica 3 ofrece información visual sobre la intensidad y la evolución de estas dos variables.
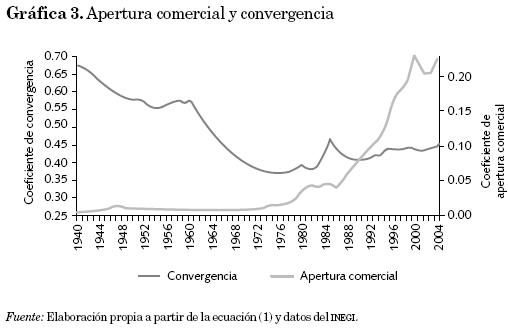
Como se observa, la medida de apertura comercial registró poca variación desde inicios del periodo hasta los años ochenta, al tiempo que la desigualdad de ingresos (medida por el coeficiente de variación) cayó paulatinamente a niveles cada vez más bajos. A mitad de los años ochenta se produce un cambio significativo en la tendencia de la apertura comercial, al registrar en años sucesivos un crecimiento exponencial; mientras tanto, el proceso convergente no sólo se detiene, sino que parece cambiar a uno de divergencia. Asimismo, la dependencia espacial ha caído en forma importante en relación con los niveles alcanzados hasta antes de 1980.
IV. Conclusiones
En economía parece difícil conciliar entre objetivos principales que en el largo plazo pueden resultar contradictorios. Algunas veces la inercia de la política económica se carga más hacia uno de ellos, lo que lleva a que, al tratar de aumentar la eficiencia, olvidemos la equidad, y no se obtenga un claro equilibrio de fuerzas.
En este trabajo hemos aplicado el enfoque de la convergencia condicional y la dependencia espacial para tener una idea de los resultados de crecimiento y desigualdad. Las relaciones espaciales (o vecinales) entre las economías estatales deben verse como parte del proceso de crecimiento; ignorarlas puede invalidar los instrumentos tradicionalmente utilizados, ya que éstos asumen independencia y homogeneidad entre las economías analizadas. Específicamente, el desempeño económico de una determinada región no depende exclusivamente de sus variables fundamentales, sino también de la dinámica de desarrollo de las regiones a las que se encuentra geográfica y económicamente unida.
En términos empíricos, encontramos que la convergencia regional de ingresos en México ha sido un proceso más bien lento, ya que mediante variables control y medidas de dependencia espacial en una ecuación de regresión se estimaron tasas de convergencia de alrededor de 1.75 por ciento durante 1940–2005. Encontramos, además, que esta tendencia no fue uniforme, y que la disipación de las diferencias estatales per cápita parece haberse detenido desde 1985. Las estimaciones de la velocidad de convergencia para dos diferentes subperiodos fluctuaron entre 3.6 por ciento para 1940–1985 y divergencia para 1985–2005.
Por otro lado, los efectos espaciales resultaron altamente significativos y dieron una idea de la formación de un cluster consistente de ingresos bajos entre los estados del sur del país, mientras que el cluster de ingresos elevados se distribuye entre los estados del centro y norte del país. Este resultado parece coincidir con las ideas planteadas por muchos otros autores sobre la convergencia de clubes (véanse Chatterji, 1992, y Quah, 1993, entre otros). En general, nuestros resultados coinciden ampliamente con los hallados por Aroca, Bosch y Maloney (2005). Por ejemplo, en ambos trabajos se destaca el aumento de la divergencia y la consistencia del cluster de ingresos bajos entre los estados del sur en la etapa más reciente. Sin embargo, hay algunas diferencias bien establecidas, como por ejemplo el hecho de que el cluster de ingresos elevados no sólo se restringe a los estados fronterizos (Aroca, Bosch y Maloney, 2005, p. 376) sino que también se expande a algunos estados del centro y del golfo, como Jalisco, Querétaro y Veracruz (véanse los resultados del cuadrante IV en el cuadro 2). Este resultado parece más consistente con el patrón geográfico que presenta el país en la actualidad: centro y norte parecen crecer, mientras que el sur se rezaga (véase el mapa 1). Desde esta perspectiva es posible tener conclusiones más reales sobre la dinámica regional mexicana: estados del centro, del norte y de la frontera se están distanciando de los estados geográficamente pertenecientes al sur, principalmente desde que la apertura comercial tuvo lugar. Además, este distanciamiento parece responder tanto a un aumento de la actividad económica en los estados del centro y del norte, como a una reducción del desempeño económico de los estados del sur.
Los resultados obtenidos con esta investigación son de gran utilidad para el gobierno, los planeadores de política económica regional y el conjunto de la sociedad, ya que sugieren que el proceso de apertura externa está concentrando los beneficios derivados del comercio externo principalmente hacia aquellas regiones mejor preparadas para aprovechar las ventajas de la inversión extranjera y del comercio. Analizar las ganancias derivadas del proceso de apertura comercial y los cambios en el comercio entre regiones industriales y no industriales puede ser una línea de trabajo que continúe esta investigación, ya que la apertura puede estar favoreciendo a los estados con mayor vocación industrial o inhibiendo el crecimiento en los estados donde las actividades primarias, como la agricultura, tienen un peso importante en la producción total.
Referencias bibliográficas
Anselin, L. (1988a), Spatial Econometrics: Methods and Models, The Netherlands, Kluwer Academic Publishers. [ Links ]
–––––––––– (1988b), "Lagrange Multiplier Test Diagnostic for Spatial Dependence and Spatial Heterogeneity", Geographical Analysis, 20 (1), pp. 1–17. [ Links ]
–––––––––– (1992), SpaceStat Tutorial: A Workbook for Using SpaceStat in the Analysis of Spatial Data, Urbana, University of Illinois. [ Links ]
Aroca, P., M. Bosch y W. F. Maloney (2005), "Spatial Dimensions of Trade Liberalization and Economic Convergence: Mexico 1985–2002", The World Bank Economic Review, 19 (3), pp. 345–378. [ Links ]
Barro, R. J. (1991), "Economic Growth in a Cross Section of Countries", Quarterly Journal of Economics, 106 (2), pp. 407–443. [ Links ]
Barro, R. J. y X. Sala–i–Martin (1992a), "Convergence", Journal of Political Economy, 100 (2), pp. 223–251. [ Links ]
–––––––––– (1992b), "Regional Growth and Migration: A Japan–US Comparison", Journal of the Japanese and International Economies, 6, pp. 312–346. [ Links ]
Carrion–i–Silvestre, J. L. y V. Germán–Soto (2007), "Stochastic Convergence amongst Mexican States", Regional Studies, 41 (4), pp. 531–541. [ Links ]
–––––––––– (2009), "Panel Data Stochastic Convergence Analysis of the Mexican Regions", Empirical Economics, 37 (2), pp. 303–327. [ Links ]
Cermeño, R. (2001), "Decrecimiento y convergencia de los estados mexicanos: Un análisis de panel", El Trimestre Económico, 68 (4), pp. 603–629. [ Links ]
Chatterji, M. (1992), "Convergent Clubs and Endogenous Growth", Oxford Review of Economic Policy, 8 (4), pp. 57–59. [ Links ]
Chiquiar, D. (2005), "Why Mexico's Regional Income Convergence Broke Down", Journal of Development Economics, 77, pp. 257–275. [ Links ]
Conapo (Consejo Nacional de Población) (1998), La situación demográfica de México, México, Conapo. [ Links ]
–––––––––– (2001), Cuadernos de salud reproductiva, República Mexicana, México, Conapo. [ Links ]
Crafts, N. (1999), "Economic Growth in the Twentieth Century", Oxford Review of Economic Policy, 15 (4), pp. 18–34. [ Links ]
De la Fuente, A. (1997), "The Empirics of Growth and Convergence: A Selective Review" , Journal of Economics Dynamics & Control, 21, pp. 23–73. [ Links ]
Dinopoulos, E. y P. Thompson (2000), "Endogenous Growth in a Cross–section of Countries", Journal of International Economics, 51, pp. 335–362. [ Links ]
Erthur, C., J. Le Gallo y J. P. LeSage (2007), "Local versus Global Convergence in Europe: A Bayesian Spatial Econometric Approach", Review of Regional Studies, 37 (1), pp. 82–108. [ Links ]
Esquivel, G. (1999), "Convergencia regional en México, 1940–1995", El Trimestre Económico, 66 (4), pp. 725–761. [ Links ]
Fingleton, B. (1999a): "Spurious Spatial Regression: Some Monte Carlo Results with Spatial Unit Roots and Spatial Cointegration", Journal of Regional Science, 39 (1), pp. 1–19. [ Links ]
–––––––––– (1999b), "Estimates of Time to Economic Convergence: An Analysis of Regions of the European Union", International Regional Science Review, 22 (1), pp. 5–34. [ Links ]
Fingleton, B. y E. López–Bazo (2006), "Empirical Growth Models with Spatial Effects",Papers in Regional Science, 85 (2), pp. 178–198. [ Links ]
Florax, R. J. G. M. y P. Nijkamp (2005), "Misspecification in Linear Spatial Regression Models", Tinbergen Institute Discussion Paper No. TI 2003–081/3. [ Links ]
Germán–Soto, V. (2005), "Generación del producto interno bruto mexicano por entidad federativa, 1940–1992", El Trimestre Económico, 72 (3), pp. 617–653. [ Links ]
Getis, A. y J. Ord (1992), "The Analysis of Spatial Association by Use of Distance Statistics", Geographical Analysis, 24, pp. 189–206. [ Links ]
INEGI (Instituto Nacional de Estadística y Geografía) (1999), Estadísticas históricas de México, Aguascalientes, INEGI. [ Links ]
–––––––––– (2002), Censos económicos, 1999, Aguascalientes, INEGI. [ Links ]
–––––––––– (2006), Censos económicos, 2004, Aguascalientes, INEGI. [ Links ]
Islam, N. (1995), "Growth Empirics: A Panel Data Approach", Quarterly Journal of Economics, 110 (4), pp. 1127–1170. [ Links ]
López–Bazo, E., E. Vayá, A. J. Mora y J. Suriñach (1999), "Regional Economic Dynamics and Convergence in the European Union", The Annals of Regional Science, 33, pp. 343–370. [ Links ]
López–Bazo, E., E. Vayá y M. Artís (2004), "Regional Externalities and Growth: Evidence from European Regions", Journal of Regional Science, 44 (1), pp. 43–73. [ Links ]
Lustig, N., B. Borthsworth y R. Lawrence (1992), North American Free Trade, Washington, The Brookings Institution. [ Links ]
Magalhães, A., G. J. D. Hewings y C. R. Azzoni (2005), "Spatial Dependence and Regional Convergence in Brazil", Investigaciones Regionales, 6, pp. 5–20. [ Links ]
Mankiw, N. G., D. Romer y D. N. Weil (1992), "A Contribution to the Empirics of Economic Growth", Quarterly Journal of Economics, 107 (2), pp. 407–437. [ Links ]
Mella–Márquez, J. M. y C. Chasco–Yrigoyen (2006), "Urban Growth and Territorial Dynamics: A Spatial–Econometric Dynamics of Spain", en A. Reggiani y P. Nijkamp (eds.), Spatial Dynamics, Networks and Modelling, Cheltenham, Edward Elgar Publishing, pp. 325–366. [ Links ]
Messmacher, M. (2000), "Desigualdad regional en México: El efecto del TLCAN y otras reformas estructurales", documento de trabajo 2000–4, Banco de México. [ Links ]
Moran, P. A. P. (1948), "The Interpretation of Statistical Maps", Journal of the Royal Statistical Society Series B, 10 (2), pp. 243–251. [ Links ]
Moreno, R. y E. Vayá (2000), Técnicas econométricas para el tratamiento de datos espaciales: La econometría espacial, Barcelona, Universitat de Barcelona. [ Links ]
Mur, J. y A. Angulo (2006), "The Spatial Durbin Model and the Common Factor Tests", Spatial Economic Analysis, 1 (2), pp. 207–226. [ Links ]
Quah, D. T. (1993), "Empirical Cross–Section Dynamics in Economic Growth", European Economic Review, 37 (2–3), pp. 426–434. [ Links ]
Rey, S. J. y B. D. Montouri (1999), "US Regional Income Convergence: A Spatial Econometric Perspective", Regional Studies, 33 (2), pp. 143–156. [ Links ]
Sachs, J. (1988), "Políticas comerciales y de tipo de cambio en programas de ajuste orientados al crecimiento", Estudios Económicos, 3 (1), pp. 77–108. [ Links ]
Villarreal, R. (1988), "El desarrollo industrial de México: Una perspectiva histórica", en Instituto Nacional de Estudios Históricos de las Revoluciones de México (INEHRM) y Fondo de Cultura Económica (FCE) (eds.), México: 75 años de revolución, México, FCE, pp. 257–339. [ Links ]
Este trabajo forma parte del proyecto "El impacto de los flujos de inversión extranjera en el crecimiento y desigualdad regional de México", beca F–PROMEP–36/Rev–03. V. Germán–Soto agradece a la Secretaría de Educación Pública y a la Universidad Autónoma de Coahuila por el apoyo financiero recibido.
1 Los inicios de este proceso se pueden situar desde mediados de los años ochenta, con el ingreso de México al Acuerdo General de Aranceles y Comercio (GATT), hoy Organización Mundial del Comercio (OMC), y la paulatina relajación de los controles externos de la economía.
2 Rey y Montouri (1999) estiman ecuaciones de convergencia absoluta, ya que al parecer no fue necesario condicionar el modelo a las diferencias estructurales de los estados de Estados Unidos.
3 En el estudio de Aroca, Bosch y Maloney (2005) el uso de un estimador de Kernel permite controlar por esas diferencias.
4 Una velocidad de convergencia en torno a 2 por ciento parece que ha sido una constante en los estudios del crecimiento económico. Los primeros trabajos que exploraron este fenómeno, como los de Barro y Sala–i–Martin (1992a, 1992b), indistintamente concluyeron en esa cifra. De la Fuente (1997) documenta una gran cantidad de trabajos que concluyen en tasas similares de 2 por ciento.
5 Como ejemplos, véase la literatura citada en la introducción de este trabajo.
6 Agradecemos a un dictaminador la sugerencia de esta cita bibliográfica.
7 Las fuentes de información de este conjunto de variables fueron INEGI (1999), también disponible en: www.inegi.gob.mx; Conapo (1998), también disponible en www.conapo.gob.mx; y los Censos Económicos publicados por el INEGI (2002 y 2006).
8 También ensayamos con otras variables, como densidad de población, tasa de alfabetización y tasa de fertilidad, pero al ser no significativas optamos por excluirlas del modelo.
9 Los resultados fueron bastante similares con otros estadísticos, como la C de Geary o la G de Getis y Ord. La I de Moran tiene la ventaja de que puede calcularse en GeoDa, un paquete especializado en análisis espacial de datos.
10 Todos los cálculos se realizaron en SpaceStat y GeoDa. Ambos constituyen programas de econometría espacial creados por Luc Anselin. Mientras que el primero ha sido el tradicionalmente usado en estudios de dependencia espacial, el segundo ha sido recientemente diseñado y se encuentra disponible en su página web: http://geodacenter.asu.edu/software/downloads.
11 Durante estos años hubo recurrentes crisis económicas y financieras en el país, por ejemplo en 1976, 1982, 1987 y 1994–1995.
12 Tanto la gráfica 2 como el mapa 2, presentada más adelante, fueron reproducidas con el paquete GeoDa.
13 Los cuadrantes se leen desde la posición noreste (AA: I) y girando hacia la izquierda, en contra de las manecillas del reloj.
14 Aunque muy al final del periodo se suman otros dos estados: Chiapas y Veracruz.
15 En inglés, WALD = prueba Wald; LR = razón de verosimilitud y LM = multiplicador de Lagrange.
16 El valor de la prueba Wald (del cuadro 4) se calcula como el valor de la prueba t del coeficiente p elevado al cuadrado. El valor de la prueba LM es el estimado en el cuadro 3.
17 Como notan Fingleton y López–Bazo (2006), esta decisión puede estar contaminada por el sesgo de especificación de los contrastes; sin embargo, en el caso que estudiamos no es posible instrumentar la sugerencia que ellos proponen, ya que nuestras observaciones son más bien limitadas. Además, los resultados con ambos modelos apuntan en la misma dirección sobre las conclusiones respecto a la liberalización y la convergencia regional.














