Artículos

 

Redistribution as a Local Public Good Subject to Congestion

 

Jaume Sempere*

 

* Profesor-investigador de tiempo completo en el Centro de Estudios Económicos (CEE) de El Colegio de México. Camino al Ajusco 20, Col. Pedregal de Sta. Teresa, 10740 México, D.F., México. jsempe@colmex.mx.

 

Fecha de recepción: 25 de octubre de 2004.
Fecha de aceptación: 28 de agosto de 2007.

 

Abstract

When analyzing migration policies, second best redistribution becomes a local public good subject to congestion. The remedial policy consists of a kind of second best finance for that good.

Keywords: migration, gains from trade.

 

Resumen

Cuando analizamos las políticas migratorias, la redistribución del ingreso mediante impuestos indirectos se convierte en un bien público local sujeto a congestión. La solucion a este problema pasa por diseñar una financiación adecuada para este bien público.

Palabras clave: emigracion, ganancias de comercio.

JEL Classification: F22, F13, D61.

 

Introduction

As surveyed in Borjas (2002), important us policy measures regarding immigration have been inspired by the concerns that migrants can become public charges, as well as to avoid the us public welfare to become an immigration magnet (consider, for instance, the 1891 us Congress legislation concerning entry of persons likely to become public charges, or even the 1994 Proposition 187 in California).

In a more theoretical framework, Wildasin (1994) shows how income redistribution policies by a host country distort migration decisions, and may make all inhabitants of the host country worse off when freeing migration. (See Myers and Papageorgiou, 2000; Razin and Sadka, 1995; Wellisch and Wildasin, 1996; Wellisch and Walz 1998; and also Wildasin, 1998; for related topics.) Also, Brecher and Choudhri (1990) discuss the problems of using a redistribution mechanism based on indirect taxation (as the mechanism that Dixit and Norman, 1980, use for proving gains from trade)¹ in order to attain a Pareto gain from freeing factor markets. These two papers take a host country point of view.

In this paper we analyze the policies needed in order to achieve Pareto gains from freeing international migration, when countries are using income redistribution policies. In order to achieve a deeper understanding of the problems, and also consider the origin country point of view, I base my presentation in the discussion of a very simple model.

The basic intuition of the negative results in Brecher and Choudhri (1990) and Wildasin (1994) is that subsidies can attract more migrants than is efficient. These additional migrants represent a cost for the fiscal system. The per-head cost of redistribution increases whenever the proportion of those receiving net subsidies increases. For certain levels and types of migration, the increase in the per-head cost of making the redistribution, and the distortion in the allocation of workers in the world, can make it impossible to obtain Pareto gains from freeing migration. I will show that, in addition, migration not only may increase the fiscal cost of redistribution in the host country, but also may increase that cost in the origin country.

Here, income redistribution is a kind of local public good subject to congestion. Hammond and Sempere (2006) analyzed the gains from migration in economies with local public goods subject to congestion. The variation in the demographic composition could change the average cost of provision of those goods. Then, free migration could result in changes in costs of provision of the local public goods (or reductions in the quality of these) exceeding the efficiency gains from migration. The solution proposed was to introduce residence charges that were function of the congestion characteristics² and the migration plan³ of each individual.

In the model that I present here, these residence charges would actually operate as Pigou taxes on migration; i. e. as devices to make migrants internalize the higher cost of redistribution caused by their presence in the host country and their absence in the origin country. With these taxes, migrants bear the cost of the fiscal externality caused on the origin and host countries by the marginal migrant. I show that the internalization of the fiscal externality by migrants is enough to make Pareto gains from freeing migration feasible again. Therefore, these type of taxes could be the appropriate remedy for the problems analyzed in Brecher and Choudhri (1990) and Wildasin (1994).

We finally extend the model to consider cases in which governments cannot use the first best Pigouvian scheme, and thus have to tax all migrants at the same rate. If those taxes make migrants bear the average fiscal redistributive cost caused by the average marginal migrant, achieving Pareto gains from free migration is feasible, despite the distortion caused in the allocation of workers among countries. The only information required for obtaining a Pareto gain is aggregate information regarding prices, wages and profits, and also whether a person is a migrant or not.

The paper is organized as follows: Section I presents a model where Pareto gains from freeing migration are possible with lump sum redistribution. Section II shows the impossibility of obtaining Pareto gains from free migration in the same example, when Dixit-Norman redistribution is used. Section III shows how a system of Pigouvian taxes on migration can make, together with the Dixit-Norman scheme, Pareto gains from freeing migration feasible again. Section IV analyzes the same issue, but with more than one type of migrant, when non-discriminatory taxation of migrants has to be used. Section V concludes the paper with some final remarks.

 

I. A simple model with Pareto gains from migration with lump sum transfers

Given that we focus our discussion on the problems in using the Dixit-Norman compensatory mechanism, we present a simple model (based on Wildasin, 1994) in which, as trivial efficiency gains from freeing migration will appear, the only issue is the redistribution of the efficiency gains from migration.

Assume that there are two regions, 1 and 2. Let 1 be the normalized world population of mobile workers. The proportion of the world population of mobile workers living in each region in the allocation without migration (referred to from now on as the status quo) is P1 and P2, respectively. We assume that each worker supplies inelastically a unit of labor. We assume that P₁ < P₂ so region 2 is more populated than 1 in the status quo. We also assume the absence of any kind of migration costs.⁴

There is a single firm in each region producing a homogeneous commodity using labor as the only input. We assume that both regions share the same technology. For simplicity, we assume that each regional firm is owned by the status quo set of workers in its region, but they cannot physically transport their part of the firm with them if they migrate. However, they would receive their share of the profits (net of taxes) wherever they live. We also assume that the number of shares in a regional firm owned by each worker is not the same for all its owners.⁵ We assume that the only source of non-labor income is distributed profits. This implies that the income distribution in the status quo coincides with the distribution of shares of the firms.⁶

We assume that the technology is represented by the production function f(l) = 2l=^½ Where l is the proportion of the world population working in the corresponding region once migration is liberalized.⁷

We assume perfect competition, so that wages equal marginal productivity of labor. Our assumption on the population sizes in the status quo implies that

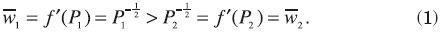
Thus, if we free migration, region 1 will receive an inflow of immigrants from region 2. This inflow will stop when wages are equalized between regions. Given the structure of our model, this inflow will stop when both regions have the same number of workers. Thus (P₂ - P₁) / 2 workers will migrate from region 2 to region 1. The new equilibrium is an efficient allocation in which marginal productivity of labor is equalized among regions.

Increasing the size of the labor force will decrease wages in region 1. The decrease in wages in region 1 is

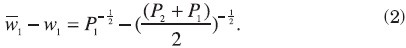
That is, the difference between status quo wages and market wages with free migration.

However, profits will increase in the amount

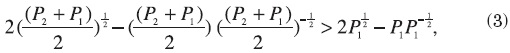
where the sum of the left hand side of the inequality represents profits (production less wages paid) with free migration, and the sum of the right hand side terms represents profits in the status quo.

This could be rewritten as

So, given that (p₂ + p₁ ) / 2 > p₁) , profits are larger with free migration than in the status quo.

It can be shown that the aggregate gains in profits are larger than the aggregate losses in wages P₁ (w₁ - w₁) for the status quo workers in region 1. There would be a Pareto gain in region 1 if all its status quo workers owned the same share of the firm. However, if they own different proportions of the firm, and we look for a pareto gain, a system of lump sum transfers would be required to redistribute the gains from migration. This system must tax workers with larger shares in the regional firm, and subsidize workers with no shares or few enough shares, as the increase in their dividends is not enough to compensate the decrease in their wage income.

In region 2 the situation would be opposite, as aggregate wages would increase and aggregate profits decrease. By symmetry with the situation in region 1, the wage increase would not be enough to compensate the decrease in profits. However, it is easy to show that the net aggregate gains in region 1 are large enough to compensate the net aggregate losses in region 2. The intuition is that the free migration equilibrium is first best optimal and, without any distortion, the pareto frontier with free migration must dominate the pareto frontier without free migration.

achieving the pareto gain would require knowledge of the shares of the firms owned by each worker. Feasibility of the lump sum transfer system would also require interregional transfers from region 1 to region 2. These transfers can take two forms. The first is pure intergovernmental transfers that make feasible the compensation of losers in region 2 by the government in that region. The second is the possibility that region 2 can tax all its status quo inhabitants, independently of where they are working in the new equilibrium. This could make region 2 gain from freeing migration, by sharing with all its actual inhabitants the gains in wages obtained by its migrants.

 

II. Equilibrium with Dixit-Norman compensation

This section analyzes the possibility of using a redistribution mechanism based on taxes on prices and on profits, in order to obtain a pareto gain from freeing migration. That is, following Dixit and Norman (1980,1986), we analyze the feasibility of using the tax system to freeze wages and profits at status quo levels, and obtain a positive net fiscal revenue in the free migration economy. Given that all consumers would face the same budget constraint as in the status quo, none is worse off. The existence of a positive fiscal revenue out of this policy makes possible that, through the appropriate redistribution of the fiscal revenue, some consumers are made better off and a Pareto gain is achieved. Clearly, this redistribution mechanism is informationally less demanding than the mechanism sketched in the last section, because it uses only aggregate information about the economy, instead of individual information about individual ownership.

We now assume that the government in region 1 subsidizes free migration wages received by workers, so that wages remain as in the status quo. Assume, to start with, that government 2 does not do so. Then the equilibrium migration condition is

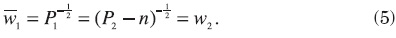
The equilibrium level of migration is in this case n = P₂ - P₁. It is twice the first best level of migration. The population living and working in region 1 is P₁ + n = P₂. The difference between this and the first best level of migration is the migration fiscally induced by the redistributive policy. The total subsidy in wages amounts to

That is, the unit subsidy in wages times the workers receiving it. The increase in aggregate profits due to migration (that could be taxed away and used to subsidize wages) is

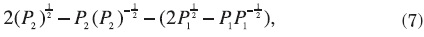
where the sum of the first two terms are profits (production less wages paid) in the free migration equilibrium, and the sum of the last two are profits in the status quo. notice that the firm in region 1 is paying the market wage (when there are P2 workers), whereas workers receive subsidized wages. The previous expression can be rewritten as

Thus the net revenue of the public sector is

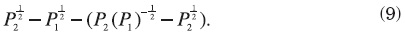
It is straightforward to show that it is negative. The subsidy in wages grows more than the increase in profits because of the fiscally induced migration. This makes unfeasible the use of the Dixit-Norman compensatory mechanism. This coincides with the results obtained in Wildasin (1994) (in fact, this is a particular case of Wildasin's model) and with the results of Brecher and Choudhri (1990) for a small country. With a similar argument it could be shown that it is not feasible for region 2 to freeze wages (and so obtain a positive revenue out of commodity taxation, as market wages rise in that region) and profits (in this case, by using the positive revenue in commodity taxation to subsidize the negative profits) at status quo levels.

If both regions freeze wages at their status quo levels, the result is even worse. Given that, independently of migration, the difference in wages will persist (and given that there are no migration costs) all mobile workers will try to move to region 1. All production will inefficiently be made in region 1, and the production level in region 2 will equal zero. With no other policy action, there is an impossibility of obtaining pareto gains from freeing migration with the redistribution mechanism discussed in this section. In a more complex model, migration costs and attachment to specific locations would set a bound to the migration flow. However, unless migration costs are high enough to prevent any migration at all, the problems caused by fiscally induced migration would persist.

 

III. A Pigou tax on the fiscal externality

As shown in the previous section, the second best redistribution of the gains from migration is a local public good subject to congestion. Increasing the proportion of the inhabitants receiving the subsidy increases the per-head cost of provision. This increase is large enough to transform the efficiency gains from migration into fiscal losses.

The solution that we are going to analyze consists in charging a tax on all actual workers in a given region, and paying back this tax to those that were in that region in the status quo (to ensure feasibility of the status quo allocation). obviously, this would be equivalent to a system of taxes on migrants, who are the ones that are not refunded their taxes. Thus, in the remainder of the paper we will refer to them as migration taxes. Those could be interpreted as the pigouvian solution to the fiscal externality that appeared in the previous section.

The taxes on migration that would correct for the fiscal externality in region 1 are those that charge all migrants with the fiscal externality caused by the marginal migrant. That is, the subsidy on the wage of the marginal migrant, t_t = w₁— (P₁ + n)^-½. To start with, we assume that only country 1 sets corrective taxes. Then, the equilibrium migration condition is

Substitution of t₁ gives

This implies that migrants to region 1 are financing the fiscal externality caused by them. However, there are still too many migrants with respect to the optimal allocation. This is because the redistributive policy of region 2 is distorting the migration decision. notice that the migration equilibrium condition means that regions are simply exchanging population, but migrants are contributing to finance the compensatory policies in region 1. In this inefficient allocation the fiscal cost of freezing wages in region 1 is

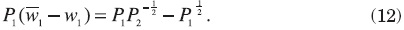
and the fiscal revenue from freezing profits is

It is easy to show that the balance is positive.

In the absence of further policy measures, the government in region 2 obtains a positive revenue out of freezing wages

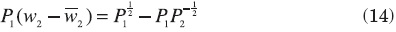
and a negative revenue from freezing profits

It is easy to show that the balance is negative. In our simple and symmetric model (and given that the compensatory policy implies that regions only exchange populations) the fiscal surplus in region 1 just equals the deficit of region 2. A system of interregional lump sum transfers would make the status quo allocation feasible for both regions. However, strict Pareto gains are not feasible in this case.

To achieve a strict Pareto gain, additional policy measures have to be taken. The required policy has to compensate for the excessive migration that the redistributive policy in region 2 causes. This is equivalent to a tax on migrants, charging them for the fiscal externality in region 2. The tax amounts to the contribution to the tax on wages in region 2 by a marginal non-migrant, t₂ — (P₂ — n)^-½ —w₂ . Then, the migration equilibrium condition is

or equivalently,

which implies an efficient distribution of population.

 

IV. The more than one type case

In the simple economy with just one type of worker of the previous sections, achieving an efficient allocation of population amounts to establishing a system of redistribution by nationality. We are indirectly excluding migrants from the subsidy in wages in region 1, and making them participate in the tax on wages in region 2. There are no problems of incentive compatibility other than the possible illegal migration (i. e. evasion of the tax on migrants) that could be induced, if taxes on migrants in both regions are high enough.

In a more sophisticated model where the fiscal externality depends on the type of migrant that we are considering, differential taxation of migration would be needed to fully internalize the fiscal externality. The contribution of this section is to analyze whether aggregate information about wages and profits (necessary to implement the Dixit-Norman compensatory mechanism), and information about who the migrants are, is enough to achieve a Pareto gain from freeing migration.

If the relevant characteristics are not easily observed, incentive constraints would exclude discriminatory taxation of migrants. Then migration decisions will be distorted, and different kind of inefficiencies will appear. However, in the following example we will show that despite this additional inefficiency, Pareto gains from freeing migration could be achieved.

consider now a slightly more complicated model, with two types of mobile workers in each region. Let j (for j = a,b) be the superindex denoting the type, and Pf the proportion of workers of type j (for j = a,b) in region i (for i = 1,2). We assume that P/ >P/, so region 2 has more workers of each type than region 1. As before, this will determine the direction of migration flows. Assume also that each worker will supply inelastically a unit of labor. The production function in region 2 will be very similar to the one before,

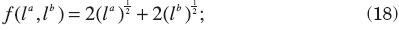
so both labor types obtain the same wage. Assume instead that the production function in region 1 has the form

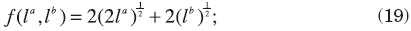
so labor of type a is twice as productive as labor of type b in region 1. This could happen because of unmodelled differences in infrastructure between the two regions. I introduce this asymmetry between the regions' technology, because this will imply a difference between labor types that will result in a distortion in the allocation, if we treat both types equally. The objective of this section is to show the possibility of Pareto gains, despite the inefficiency introduced by this distortion.

In the status quo allocation, wages are larger in region 1 than in region 2 for both types of labor. If there is the possibility of free migration, then the migration equilibrium condition without public intervention implies

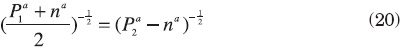
for type a, and

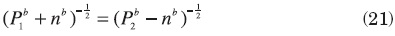
for type b. Solving these equations gives the equilibrium levels of migration for each type. As before, this is an efficient allocation, and Pareto gains from freeing migration could be obtained if appropriate lump sum transfers were available.

Assume now that government 1 wants to use a Dixit-Norman kind of redistribution mechanism together with corrective migration taxes, as those discussed in section 3, but cannot distinguish among the different types of workers, so that it charges the same tax to all of them. Assume also that, for simplicity, government does not try to redistribute. Also assume that the tax charges the fiscal externality caused by the average marginal migrant, so

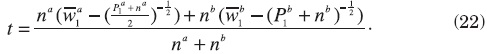
This, together with the migration equilibrium conditions

and

determines the new equilibrium.

It is easy to see that the presence of the same tax for both types of labor induces too much migration of type b and too little of type a, with respect to the efficient allocation. Therefore, the new allocation is not efficient. However, notice that all migrants are financing the tax externality caused by them (and in average they are obtaining the wages they would, without public intervention). Following straightforwardly the argument in section 3, in the new equilibrium all the status quo workers in region 1 have their wages frozen at the status quo level, and profits plus immigration taxes are at least enough to finance the necessary subsidy in wages. This implies that the first region is obtaining a Pareto gain from freeing migration. A similar argument as in section 3 could be used to analyze the case of region 2.

 

V. Final remarks

We have presented a simple example in which Pareto gains from freeing migration are possible, when governments can use lump sum taxation. When this type of non-distortionary taxation is not feasible, a Dixit-Norman compensatory mechanism based on taxing wages and dividends could be used. However, without other policy measures, this type of mechanism distorts migration flows, and the distortion can be such that the gains from migration turn out to be losses, because of the resulting increase in the fiscal cost of implementing the compensatory policies.

Efficient allocation of workers among regions requires a kind of Pigou taxes on migration that make migrants internalize the fiscal externalities. This type of taxes is, in fact, equivalent to a system of nationality-based Dixit-Norman compensatory mechanism. However, apart from information about prices and profits, its feasibility requires the knowledge of the type of migrant. This could be infeasible in practice, because of incentive constraints.

If governments cannot use migration taxes that discriminate for different types of migrants, the required policy consists of a single tax on all migrants that makes migrants, on average, bear the cost of the fiscal externality they cause. This does not lead to an efficient allocation of labor among regions. However, Pareto gains from freeing migration flows are possible in our example, if a Dixit-Norman compensatory mechanism, complemented with this tax, is used to redistribute the aggregate efficiency gains.

 

References

Borjas, G. (2002), "Welfare reform and Immigrant Participation in Welfare Programs", International Migration Review 36, pp. 1093-1123.         [ Links ]

Brecher, R. and E. Choudhri (1990), "Gains from International Factor Movements without Lump Sum Compensation: Taxation by Location Versus Nationality", Canadian Journal of Economics 23, pp. 44-59.         [ Links ]

Dixit, A. and V. Norman (1980), Theory of International Trade, Welwyn, Herts., James Nisbet.         [ Links ]

---------- (1986), "Gains from Trade without Lump-Sum Compensation", Journal of International Economics 21, pp. 99-110.         [ Links ]

Hammond, P. J. and J. Sempere (2006), "Migration with Local Public Goods and the Gains from Changing Places", Stanford university, Department of Economics, working paper 1-06.         [ Links ]

Myers, G. and Y. Papageorgiou (2000), "Immigration Control and the Welfare State", Journal of Public Economics 75, pp. 183-207.         [ Links ]

Razin, A. and E. Sadka (1995), "Restricting Migration: Wage Rigidity and Income Redistribution", American Economic Review 85 (Papers and Proceedings), pp. 312-316.         [ Links ]

Wellisch, D. and U. Walz (1998), "Why Do Rich Countries Prefer Free Trade over Free Migration? The Role of the Modern Welfare State", European Economic Review 42, pp. 1595-1612.         [ Links ]

Wellisch, D. and D. Wildasin (1996), "Decentralized Income Redistribution and Immigration", European Economic Review 40, pp. 187-217.         [ Links ]

Wildasin, D. (1994), "Income Redistribution and Migration", Canadian Journal of Economics 27, pp. 637-656.         [ Links ]

---------- (1998), "Factor Mobility and Redistributive Policy: Local and International Perspectives", in P. Sorensen (ed.), Public Finance in a Changing World, London, MacMillan Press, pp. 151-191.         [ Links ]

 

Notas

Acknowledgements: This paper has been highly motivated by joint research with Peter Hammond on migration and other supply-side policies. A preliminary version of this paper was presented at the conference "The political economy of migration". Helpful comments from the participants are acknowledged. The comments of Subir Chattopadhyay and Dragan Filipovich and an anonymous referee are also gratefully acknowledged.

¹ Dixit and Norman show that, when freeing trade, freezing wages and other prices (using indirect taxation) at status quo levels make it possible to obtain a positive net fiscal revenue that can be used to improve all consumers.

² Congestion characteristics are those relevant for the determination of the needs for consuming certain public goods. Thus, they determine the consumption (and so the level of congestion induced) of those goods.

³ Migration plans are vectors that specify where individuals plan to reside in different dated-events.

⁴ This would imply that all migration is unregulated (and therefore legal). Illegal migration would have an implicit cost.

⁵ Assuming that all status quo workers in each region own the same number of shares of the regional firm would eliminate the problem of redistribution within regions.

⁶ We leave this income distribution unspecified. Specifying a given income distribution would have allowed to compute exact gains and losses for each individual. However, this would have been at the cost of a more complicated notation, without adding more insight to the results.

⁷ More general production functions would give the same qualitative results, as far as they present decreasing returns to labor. This simple formulation is used in order to obtain closed form solutions.