En el contexto de la demostración geométrica tradicional basada en diagramas, el ‘método de superposición’ es perfectamente identificado.1 En general, se describe a través del uso singular de la figura o el diagrama. Así lo hace Robin Hartshorne, destacando su ajenidad a la estructura proposicional del sistema euclidiano y la peculiar operación diagramática que supone:
Hay otra situación en la que Euclides usa un método que no es explícitamente autorizado por sus axiomas. Nada en los Postulados o las Nociones Comunes dice que podemos tomar una figura y moverla a otra posición. A esto lo llamamos el método de superposición. (Hartshorne, 2000: 33)
Heath subraya el movimiento, es decir, la específica y característica movilización de la figura asociada al método: “La fraseología de las proposiciones, por ejemplo I.4 y I.8, en las que Euclides emplea el método indicado, no deja lugar a dudas de que consideraba una figura como realmente movida y colocada sobre la otra” (1908: 225). Luego de ilustrar su énfasis evocando la demostración del teorema I.4 de los Elementos, agrega:
Al mismo tiempo, está claro que a Euclides no le gusta el método y lo evita siempre que puede, por ejemplo, en I.26, donde prueba la igualdad de dos triángulos que tienen dos ángulos respectivamente iguales a dos ángulos del otro y un lado de uno igual al lado correspondiente del otro. (Heath, 1908: 225)
Este autor señala que tal renuencia euclidiana no encuentra respaldo en objeciones explícitas planteadas por los “geómetras antiguos” (Heath, 1908: 225); siguiendo esta idea, Paolo Mancosu advierte que no se encuentran críticas a la legitimidad del método hasta mediados del siglo XVI. Sus comentarios en relación con las objeciones de Peletier y Candalla parecen ubicar la disconformidad de estos en la singular intervención diagramática, en especial, en la apelación al “movimiento”; un punto principal consiste en el cuestionamiento a su carácter más “mecánico” que propiamente “geométrico” (Mancosu, 1996: 28 y ss.). Algunas de las defensas ante tales críticas, referidas por Mancosu, parecen centrarse en vindicar el carácter “intelectual” y no “mecánico” de la superposición. Así cita este autor el siguiente pasaje de Clavius (respondiendo a Peletier):
Puesto que él no parece haber entendido de manera satisfactoria cómo los geómetras usan esa superposición. Porque no quieren que esa superposición se realice en la realidad (pues eso sería algo mecánico), sino sólo en el pensamiento y en la mente, que es tarea de la razón y del intelecto. (Mancosu, 1996: 30)
En consecuencia, tanto quienes atacan el método de superposición, como quienes lo defienden, parecen concentrarse en la contribución diagramática: para objetarla o para vindicarla. Ese énfasis se encuentra plenamente justificado. Pero ¿cuál es precisamente el papel del diagrama en dicho método? Asumiré que el estilo deductivo euclidiano apela (desde el punto de vista expresivo) a la conjunción de los componentes visual y verbal, resultando relevante tal formato comunicacional, desde el punto de vista inferencial. El diagrama representa así (actuando de manera cooperativa con el lenguaje) un recurso protagónico de la demostración. Luego debe estudiarse su contribución no insularmente, sino en interacción con su contrapartida textual o lingüística. El propósito de esta nota es, prestando especial atención a tal pertinente heterogeneidad, examinar en detalle el método de superposición. Desde esta perspectiva, al estudiar cómo Euclides emplea tal método (en I.4, I.8 y III.24) sobresalen dos rasgos: a) un uso inferencialmente original y preeminente del diagrama “contrabalanceado” por la contribución lingüística, y b) una conciencia precisa de los límites deductivos de esta articulación y su mitigación (sistemática) por el recurso a una estrategia demostrativa complementaria, a saber, la reducción al absurdo. El advertir estos rasgos quizá permita en el futuro elaborar (bajo una nueva luz) una respuesta a la cuestión de la solidez de dicho método que haga justicia a la práctica euclidiana.
El itinerario expositivo es el siguiente. En los apartados 1, 2 y 3 se reproducen y estudian, respectivamente, I.4, I.8 y III.24 -únicos ejemplos (como es conocido) de uso del método por parte de Euclides en Elementos-. Este examen comparativo arroja como resultado la identificación de una estrategia inferencial heterogénea compartida y definida. En el apartado 4 se razona tal método atendiendo a su dimensión constructiva y, en especial, a la articulación de esta con la Noción Común 4 (NC4). Finalmente, el último apartado sugiere un problema: comprender la robustez normativa del método en términos de la práctica euclidiana. La respuesta quizá podría surgir de esta descripción atenta a su sofisticado equilibrio expresivo e inferencial.
1
Probablemente la lectora, el lector posea una intuición razonablemente precisa de aquello que se quiere captar a través de la noción de “heterogeneidad inferencial”, en el contexto de la demostración basada en diagramas.2 No obstante, una aproximación más precisa a dicho concepto resultará beneficiosa para los exámenes siguientes. Por “heterogeneidad expresiva” se entiende la concurrencia de medios expresivos visuales y lingüísticos a los fines comunicacionales. En el contexto específico de la demostración matemática, tal heterogeneidad puede constituirse en un recurso esencial desde el punto de vista deductivo, en tales casos, se habla de “heterogeneidad inferencial”.3 Nótese que, consecuentemente, tal predicado no debiera aplicarse (en forma aislada) ni a la expresión de la demostración, ni a su estructura.4 El foco correspondería que se centrara en la articulación o el vínculo. Desde este ángulo, la comprensión de la demostración (qua inferencia) auspicia una atención decidida a la inteligencia de aquellos planos. Así, al análisis de grano fino estructural (reconocido desde siempre como valioso en términos epistémicos), se agrega ahora el discernimiento de la trama expresiva, vindicada como relevante en términos cognitivos. En particular, fenómenos como la interacción gráfico-verbal reclaman aquí una atención cuidadosa. Sin embargo, esta atención a la dimensión comunicativa o mediática no desdibuja la preocupación bidimensional central: la articulación expresión/estructura. El examen de las demostraciones específicas que siguen refleja esta sensibilidad metodológica.
A continuación, reproduciré la demostración de I.4 y discutiré la aplicación del método de superposición con cierto detalle. El teorema en cuestión dice:5
Si dos triángulos tienen dos lados del uno iguales a dos lados del otro y tienen iguales los ángulos comprendidos por las rectas iguales, tendrán también las respectivas bases iguales, y un triángulo será igual al otro, y los ángulos restantes, a saber: los subtendidos por lados iguales, serán también iguales respectivamente.
La demostración es como sigue:
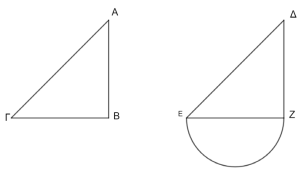
Sean ΑΒΓ, ΔΕΖ, dos triángulos que tienen los dos lados ΑΒ, ΑΓ iguales a ΔΕ, ΔΖ, respectivamente, es decir ΑΒ a ΔΕ y ΑΓ a ΔΖ, y el ángulo ΒΑΓ igual al ángulo ΕΔΖ.
Digo que también la base ΒΓ es igual a la base ΕΖ y que el triángulo ΑΒΓ será igual al triángulo ΔΕΖ y los ángulos restantes, subtendidos por los lados iguales, serán también iguales respectivamente, es decir, el (ángulo) ΑΒΓ (igual) al (ángulo) ΔΕΖ, y el (ángulo) ΑΓΒ (igual) al (ángulo) ΔΖΕ.
Pues si se aplica el triángulo ΑΒΓ al triángulo ΔΕΖ y el punto Α se coloca sobre el punto Δ y la recta ΑΒ sobre la recta ΔΕ, coincidirá también el punto Β sobre el punto Ε por ser igual ΑΒ a ΔΕ; al coincidir también ΑΒ con ΔΕ, la recta ΑΓ coincidirá también con ΔΖ por ser igual el ángulo ΒΑΓ al ΕΔΖ; de modo que también el punto Γ coincidirá con el punto Ζ por ser igual a su vez ΑΓ a ΔΖ. Pero también el punto Β había coincidido con el punto Ε; de modo que la base ΒΓ coincidirá con la base ΕΖ [pues si habiendo coincidido el punto Β con el punto Ε y el punto Γ con el punto Ζ, no coindice la base ΒΓ con la base ΕΖ, dos rectas encerrarán un espacio; lo cual es imposible. Por tanto, coincidirá la base ΒΓ con la base ΕΖ] y será igual a ella [NC4]; de modo que también el triángulo entero ΑΒΓ coincidirá con el triángulo entero ΔΕΖ y será igual a él, y los ángulos restantes coincidirán con los ángulos restantes y serán iguales a ellos, el (ángulo) ΑΒΓ al (ángulo) ΔΕΖ y el (ángulo) ΑΓΒ al (ángulo) ΔΖΕ.
Por consiguiente, si dos triángulos tienen dos lados del uno iguales a dos lados del otro y tienen iguales los ángulos comprendidos por las rectas iguales, tendrán también las respectivas bases iguales y un triángulo será igual al otro, y los ángulos restantes, a saber: los subtendidos por lados iguales, serán también iguales, respectivamente. (Que es lo que había que demostrar.)
En el análisis de la prueba se distinguen cuatro etapas o momentos. El primero se caracteriza por la peculiaridad del entramado heterogéneo, donde el diagrama es manipulado en forma abstracta, a los efectos de respaldar las primeras aserciones de coincidencia. La descripción de la acción de superponer o aplicar el triángulo ΑΒΓ al triángulo ΔΕΖ, el punto A sobre el punto Δ y la recta AB sobre la recta ΔΕ apela a una suerte de dinámica diagramática. Por supuesto, esta expresión es una metáfora, pero permite captar bien dos ideas fundamentales: el recurso descripto (en forma heterogénea) refiere a la manipulación diagramática (no al diagrama estático), y la dinámica ocurre (desde un punto de vista fenomenológico) no en el plano físico, sino mental o abstracto. En ella, el protagonismo de la figura resulta notorio, pero el papel del texto (que introduce la dinámica y sus alcances precisos) deviene así mismo esencial. Esta articulación texto-diagrama forma parte de la originalidad expresiva de esta modalidad heterogénea; los diagramas correspondientes a ambos triángulos no son explotados inferencialmente apelando a propiedades de su presentación “estática” (como, por ejemplo, cuando se usa el diagrama para respaldar la aserción de que una figura es parte de otra), sino para apoyar a la operación mental de “traslación” o “aplicación” de uno sobre el otro, es decir, a cierta “dinámica” abstracta que obra cooperativamente desde el texto. En este primer momento, al diagrama le corresponde un cierto trabajo inferencial particular (por supuesto, no en solitario): legitimar la coincidencia de A sobre el punto Δ y la recta AB sobre la recta ΔΕ. Su aporte consiste en la especificación precisa del significado secuenciado (vía lingüística) del “hacer coincidir” general; tal especificación es suficientemente informativa como para permitir el desarrollo adecuado de la trama demostrativa en este estilo comunicacional. El diagrama colabora así en la delimitación de una posibilidad específica, de un movimiento particular de la figura en cuestión. Podría describirse con mayor detalle el papel del diagrama (reparando en el carácter condicional del aserto euclídeo) más que justificando (al modo tradicional, un paso), legitimando o respaldando de manera informativa una posibilidad, a los efectos de explotarla inferencialmente.6 Imagínese la lectora o el lector la comprensión de la prueba en ausencia de los diagramas, sin interacción heterogénea.
En seguida, se abre una segunda etapa, donde la trama demostrativa combina lo que aquí denominamos “premisas de coincidencia” y “premisas de igualdad”, con el fin de respaldar aserciones de coincidencia. Esta estrategia demanda, en la justificación de la coincidencia, un respaldo que excede el recurso diagramático: las premisas de igualdad involucradas no se pueden justificar por esa vía. Estudiemos tal estrategia en detalle. Para respaldar la coincidencia del punto B con el E no es suficiente apelar al diagrama: se requiere una “premisa de igualdad”. Así, en la trama demostrativa euclidiana, tal coincidencia resultará de las relaciones que respalda la operación diagramática más la igualdad de ΑΒ y ΔΕ. La igualdad de los segmentos (fundada lingüísticamente) más las “premisas de coincidencia” (fundadas en el diagrama) permiten respaldar (de manera heterogénea) la conclusión de la coincidencia del punto B con el E. Visto desde otro ángulo: tampoco la premisa de igualdad sola permite alcanzar la conclusión de coincidencia; conviene retener este aspecto. La combinación de recursos gráficos y lingüísticos otorga al método de superposición una regimentación que el acento exclusivo en su originalidad visual no permite apreciar con facilidad.
Un esquema cooperativo semejante se repite en la demostración de la coincidencia de las rectas ΑΓ y ΔΖ. La premisa de coincidencia será, en este caso, la coincidencia de ΑΒ con ΔΕ -información extraída de la operación diagramática-. La premisa de igualdad resulta aquí la igualdad de los ángulos ΒΑΓ y ΕΔΖ -información, obviamente, extraída del texto-. Es decir, ni la premisa de coincidencia, ni la de igualdad por sí solas permiten la conclusión.
Repárese ahora en la tercera instancia del esquema, la conclusión: el punto Γ coincidirá con el Ζ. La justificación se conforma con la premisa de coincidencia (ΑΓ coincide con ΔΖ) más la premisa de igualdad (ΑΓ es igual a ΔΖ). Advierta, la lectora/el lector, que siguiendo el texto, no basta la coincidencia de ΑΓ con ΑΖ para mostrar la coincidencia de los puntos, por ello interviene la premisa de igualdad, asimismo tampoco es suficiente la premisa de igualdad, para el éxito inferencial se requiere la premisa de coincidencia (previamente demostrada).
Se puede aislar ahora la estrategia común al “bloque” compuesto por estos tres procesos argumentales. Examinados desde el punto de vista puramente expresivo, resalta la movilización de recursos heterogéneos. Si se los examina desde el punto de vista argumentativo, tal heterogeneidad expresiva se revela elocuentemente inferencial. El punto de arribo: conclusión de coincidencia. ¿Cuáles son sus premisas? Premisa(s) de coincidencia (cuyo respaldo involucra el diagrama) + premisa de igualdad (de justificación textual).
Ahora ingresamos en una tercera etapa, cuya característica fundamental consiste en apelar a la estrategia del absurdo, exhibiendo la limitación de las premisas de coincidencia (por sí solas) para respaldar la aserción de coincidencia requerida. Llegados a este punto de la trama demostrativa euclidiana, aparece una novedad interesante: se ha probado que coinciden los puntos B y E, así como Γ y Z, es decir, dos premisas de coincidencia. Se trata de demostrar la conclusión siguiente: BΓ coincide con EZ. Si se aplica el esquema característico del bloque inmediatamente anterior, se enfrenta un problema: falta la premisa de igualdad. Por supuesto, si se supiera que BΓ y EZ son iguales, la dificultad estaría solucionada: una estrategia análoga a las anteriores permitiría arribar a la conclusión deseada de coincidencia. Pero no es el caso. ¿Cómo sortear esta limitación? La interpolación ofrece la respuesta: una argumentación por el absurdo.7 A partir de asumir que no coinciden, se desemboca en el absurdo que representa el diagrama, a saber: que “dos rectas encierren un espacio”. Independientemente de la fuente que permite aseverar esta imposibilidad, el tránsito discursivo explícito desde la suposición a esta última cláusula se apoya de manera inequívoca en la información diagramática (aunque de nuevo tampoco en forma exclusiva). Esta argumentación permitiría afirmar luego la coincidencia entre BΓ y EZ. Se cierra así este tercer tramo de la demostración, que apela significativamente a la reducción al absurdo.
La cuarta y última etapa se define por el protagonismo de NC4: la noción común legitima el pasaje directo de la aserción de coincidencia a la de igualdad. En primer término, dada la coincidencia entre BΓ y EZ, vía NC4, se llega al primer resultado del teorema: que las “respectivas bases” son iguales. Adviértase que se tiene la coincidencia de los triángulos y aplicando NC4, se obtiene que son iguales; y la coincidencia de los ángulos, y aplicando NC4, se llega a la igualdad de los mismos.
2
Antes de analizar el segundo ejemplo, revisaré la demostración de I.7, pues su resultado posee un papel decisivo en la prueba de I.8 y el tipo de control argumental que exhibe (apelando en forma decisiva a la extracción de información co-exacta del diagrama) permite apreciar mejor los mecanismos de control en obra.
El teorema I.7 afirma
No se podrán levantar sobre la misma recta otras dos rectas iguales respectivamente a dos rectas dadas, de modo que se encuentren en dos puntos distintos por el mismo lado y con los mismos extremos que las rectas dadas.
La demostración parte de la suposición de la negación de lo que se pretende demostrar. Es decir, sería posible levantar las dos rectas AΔ y ΔB iguales respectivamente a las rectas AΓ, ΓB que se encuentren en Γ y Δ distintos, por el mismo lado. Así ΓA será igual a ΔA y ΓB igual a ΔB y se traza ΓΔ:
Como AΓ es igual a ΔA, AΓΔ es igual a AΔΓ (son ángulos de la base de un triángulo isósceles) pero, como informa el diagrama, ΔΓB está incluido en AΓΔ y, dado que este último ángulo es igual a AΔΓ, AΔΓ es mayor que ΔΓB. Luego ΓΔB es mayor, como informa el diagrama, AΔΓ y, dado que AΔΓ es mayor que ΔΓB, por lo tanto, ΓΔB es mayor que ΔΓB. Pero como ΓB y ΔB son iguales, ΔΓB y ΓΔB son iguales (nuevamente por I.5). Pero entonces se tiene que ΓΔB y ΔΓB son iguales y ΓΔB es mayor que ΔΓB, lo cual es absurdo. Por lo que queda probado lo que se pretendía.
Se ha subrayado la contribución del diagrama a la economía heterogénea inferencial; se trata de la intensa explotación de las relaciones parte-todo, captadas en el diagrama -atribuciones con tal fundamento son, paradigmáticamente, aquellas que Kenneth Manders denomina “co-exactas”-. Se pide a la lectora, el lector que guarde esta observación para el momento de evaluar el tipo de control que gobierna el uso del método de superposición -dado el papel central que I.7 juega en la demostración de I.8.
Ahora sí, me concentraré en dicho teorema:
Si dos triángulos tienen dos lados del uno iguales respectivamente a dos lados del otro y tienen también iguales sus bases respectivas, también tendrán iguales los ángulos comprendidos por las rectas iguales.
La demostración es la siguiente:
Sean ΑΒΓ, ΔΕΖ dos triángulos que tienen los dos lados ΑΒ, ΑΓ iguales, respectivamente, a ΔΕ, ΔΖ, (es decir) el lado ΑΒ al lado ΔΕ y el lado ΑΓ al lado ΔΖ; y tengan también la base ΒΓ igual a la base ΕΖ.
Digo que el ángulo ΒΑΓ es también igual al ángulo ΕΔΖ.
Pues si se aplica el triángulo ΑΒΓ al triángulo ΔΕΖ y se pone el punto Β sobre el punto Ε y la recta ΒΓ sobre la recta ΕΖ, coincidirá también el punto Γ con el punto Ζ por ser igual ΒΓ a ΕΖ; y al coincidir ΒΓ con ΕΖ coincidirán también ΒΑ, ΓΑ con ΕΔ, ΔΖ.
Pues si coincide la base ΒΓ con la base ΕΖ y los lados ΒΑ, ΑΓ no coinciden con los lados ΕΔ, ΔΖ sino que se desvían como ΕΗ, ΗΖ, podrán ser construidas sobre una misma recta otras dos rectas iguales respectivamente a dos rectas dadas que se encuentren en puntos distintos por el mismo lado y con los mismos extremos. Pero no pueden construirse [I, 7]; por tanto, no es posible que, aplicada la base ΒΓ a la base ΕΖ, no coincidan los lados ΒΑ, ΑΓ con los lados ΕΔ, ΔΖ. Luego coincidirán; de modo que también el ángulo ΒΑΓ coincidirá con el ángulo ΕΔΖ y será igual a él.
Por consiguiente, si dos triángulos tienen dos lados del uno iguales respectivamente a dos lados del otro y tienen las bases respectivas iguales, también tendrán iguales los ángulos comprendidos por las rectas iguales. Q. E. D.8
Quizá cause sorpresa la similitud estructural del comienzo de la demostración. Se trata de aplicar o hacer coincidir el triángulo ΑΒΓ con el ΔΕΖ, el punto B con el Ε y la recta ΒΓ con la ΕΖ, exactamente de forma análoga a la operación diagramática que caracteriza el comienzo de la demostración de I.4. Se podría agregar la misma observación que en I.4 acerca de la complicidad heterogénea: el respaldo diagramático al antecedente (por supuesto, no en solitario) supone especificar una posibilidad de aplicación de un triángulo sobre el otro, segmentado por la intervención lingüística, y, este es el punto más importante, de modo inferencialmente rico, para demostrar el condicional relevante, es decir, el primer bloque antes identificado. Nótese que pueden hacerse los mismos comentarios aquí respecto a los planos expresivo e inferencial que los antes efectuados.
Ahora el segundo bloque. Al igual que en I.4 la coincidencia de los puntos (Γ y Ζ, en este caso) no puede respaldarse exclusivamente por las premisas de coincidencia arriba identificadas; es necesaria una premisa de igualdad, a saber: ΒΓ es igual a ΕΖ. Conclusión: la coincidencia de Γ y Z. Premisa de coincidencia (entre segmentos) más premisa de igualdad (entre segmentos) permiten afirmar coincidencia (entre puntos). En el análisis de I.4 y I.8, el acento se ubica en el complemento o fortalecimiento de la premisa de coincidencia (de justificación esencialmente diagramática) por parte de la premisa de igualdad (de justificación lingüística) para resaltar el efecto de “control” o “balance” lingüístico sobre la contribución diagramática. Sin embargo, de modo análogo a lo señalado en I.4, también se llama la atención sobre otro aspecto de especial importancia: la insuficiencia de la premisa de igualdad para, por sí sola, arribar a la conclusión pretendida. Así culmina el segundo bloque.
En la tercera etapa hay un punto desafiante: ¿cómo respaldar las dos aserciones de coincidencia requeridas? Para justificar la coincidencia de ΒΑ con ΕΔ y ΓΑ con ΔΖ, puede conjeturarse una estrategia que apele a determinadas premisas de coincidencia e igualdad. Pero, obviamente, no se cuenta con esa información. De nuevo, la respuesta, ante la ausencia de premisas que puedan permitir el tránsito a las conclusiones de coincidencia, es estructuralmente la misma que en el caso de I.4: la reducción al absurdo. Aquí la hipótesis del absurdo es exactamente (podría decirse) la hipótesis de la demostración por absurdo de I.7. Se advertirá que la figura que retrata tal hipótesis en I.8 es la misma (salvo diferencias inesenciales) que sirve a la demostración de I.7. En pocas palabras: la demostración de I.7 (cuya prueba exhibe una manifiesta naturaleza heterogénea) resuelve la dificultad.
Un punto interesante a resaltar es la necesidad de asegurar la coincidencia (y la igualdad por NC4) de los “extremos” relevantes, a los efectos de aplicar I.7, y este trabajo lo hace prolijamente el método de superposición. Se puede concluir así la coincidencia de BA con EΔ y ΓA con ΔZ. Puesto que de manera respectiva coinciden estos lados, se pasa a la coincidencia de los ángulos correspondientes, es decir: BAΓ y ΓΔZ. Este tránsito parece desmentir los desarrollos previos; una suerte de “memoria demostrativa” colabora en la comprensión del punto: la coincidencia de lados permite arribar de forma directa a la de los ángulos, pero este resultado se desencadena apoyándose en una premisa de igualdad provista lingüísticamente (la de las bases de los triángulos en cuestión).
En la cuarta etapa, ya que coinciden los ángulos, se pasa vía NC4 a la igualdad correspondiente, es decir: el ángulo BAΓ es igual al ΓΔZ. La aplicación de NC4 no aparece explícita en el texto de Euclides, pero esto es frecuente. Así, la demostración de I.8 (al igual que la de I.4) observa la secuencia de las cuatro etapas examinadas.
3
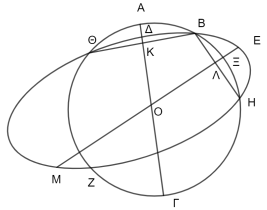
Conforme se avanza en la lectura de los Elementos, las demostraciones suelen sustentarse en una arquitectura sofisticada de resultados previos; un análisis como el presentado aquí no obliga a una reconstrucción exhaustiva de tal red, pero se beneficia de examinar los nodos esenciales. En este sentido, parece razonable retratar algunos de los apoyos fundamentales que sostienen la demostración del teorema III.24 (en particular, la reducción al absurdo que alberga) vía el diagrama siguiente:
Por supuesto, no se trata de captar la totalidad de la red, por ejemplo, ella incluye III.5, pues juegan un papel protagónico en la prueba de III.10, así como I.16, esencial en la demostración por absurdo que permite probar III.23. No obstante, una revisión rápida de las demostraciones de III.10 y III.23 permite apreciar el tipo de control que balancea (al igual que en los casos estelares discutidos en los apartados 1 y 2) la apelación diagramática.
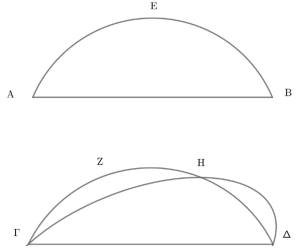
El teorema III.10 expresa:
Un círculo no corta a otro círculo en más de dos puntos.
Su demostración incluye la figura siguiente:
La prueba es por absurdo. Sean ABΓ y ΔEZ los círculos en cuestión; supóngase los puntos B, H, Z, Θ son aquellos en que se cortan tales círculos. Usando el Porisma de III.1, ya que en ABΓ la recta AΓ divide en partes iguales la recta BΘ formando ángulos rectos, el centro de ABΓ está en AΓ. Como en el mismo círculo, la recta NΞ divide en partes iguales la recta BH formando ángulos rectos, por el Porisma de III.1, el centro de ABΓ está en NΞ. Luego tal centro está en NΞ y en AΓ, es decir, es O. De igual modo, se demuestra que O es el centro de ΔEZ. Así se tendría que el mismo punto (O) es el centro de los dos círculos que se cortan. Pero esto es absurdo, por III.5.
Esta demostración es inferencialmente heterogénea y, en consecuencia, tal será la naturaleza del control que impondrá, así como respeta el diagrama (en la dinámica referida) la división del trabajo propuesta por Manders. Observaciones semejantes pueden formularse sobre III.23. Tal teorema afirma que:
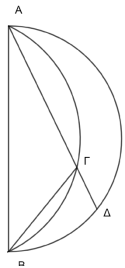
Sobre la misma recta no se podrán construir dos segmentos circulares semejantes y desiguales en el mismo lado.
Su demostración incluye la figura siguiente:
De nuevo, la demostración es por absurdo. Si fuera posible, sean los segmentos circulares semejantes y desiguales AΓΒ y AΔΒ construidos sobre la recta AB. Como AΓΒ y AΔΒ son semejantes, por definición, admiten ángulos iguales. Luego los ángulos AΓΒ y AΔΒ serán iguales, es decir, el ángulo externo será igual al interno, pero esto es absurdo por I.16.
Finalmente, el teorema III.24 afirma que:
Los segmentos circulares semejantes que están sobre rectas iguales son iguales entre sí.
La demostración es la siguiente:
Estén, pues, sobre las rectas iguales ΑΒ, ΓΔ los segmentos circulares semejantes ΑΕΒ, ΓΖΔ.
Digo que el segmento ΑΕΒ es igual al segmento ΓΖΔ.
Pues si se aplica el segmento ΑΕΒ al (segmento) ΓΖΔ y se pone el punto A sobre el punto Γ y la recta ΑΒ sobre la (recta) ΓΔ, el punto Β coincidirá también con el punto Δ por ser igual ΑΒ a ΓΔ; y habiendo coincidido ΑΒ con ΓΔ coincidirá también el segmento ΑΕΒ con el (segmento) ΓΖΔ. Porque si la recta ΑΒ coincide con la (recta) ΓΔ pero el segmento ΑΕΒ no coincide con el (segmento) ΓΖΔ, o bien caerá dentro de él o fuera; o se desviará como el (segmento) ΓΗΔ, y un círculo cortará a otro círculo en más de dos puntos: lo cual es imposible [III, 10]. Por tanto, no es posible que coincidiendo la recta ΑΒ con la recta ΓΔ no coincida también el segmento ΑΕΒ con el segmento ΓΖΔ; luego coincidirá con él y será igual a él.
Por consiguiente, segmentos circulares semejantes que están sobre rectas iguales son iguales entre sí. Q. E. D.
Al igual que en los dos casos examinados, el punto de partida consiste en respaldar diagramáticamente las premisas de coincidencia, a saber: aplicar o hacer coincidir el segmento AEB con el ΓΖΔ, el punto A con el Γ y la recta AB con ΓΔ. Al igual que en los casos de I.4 y I.8 podría catalogarse el aporte diagramático (en la cooperación heterogénea) como contribuyendo a especificar, de modo inferencialmente relevante, una posibilidad particular de la superposición como operación abstracta, capaz de respaldar el condicional relevante (primera etapa). La conclusión que afirma la coincidencia de B con Δ, como en los casos anteriores, requiere sumar a las premisas de coincidencia, la de igualdad: en este caso, ΑΒ es igual a ΓΔ. Así mismo: ni premisas de coincidencia, ni premisa de igualdad, aisladamente, permiten resolver el desafío. Ésta es la segunda etapa. De nuevo, para demostrar la coincidencia del segmento ΑΕΒ con el ΓΖΔ, no basta la coincidencia de AB con ΓΔ ni la igualdad es suficiente. El problema es solucionado con el mismo expediente, a saber: demostración por reducción al absurdo. Si no coincidieran los segmentos, AEB caerá dentro o fuera de ΓΖΔ o se desviará como el segmento ΓΗΔ.9
Las dos primeras alternativas son eliminadas por III.23 y la tercera por III.10. Esta división establecida por Heath precisa cómo opera la refutación de las consecuencias de la hipótesis del absurdo; en el texto de la demostración, se introdujeron dos modificaciones al original, siguiendo a este autor, para beneficiar la comprensión del desarrollo de la prueba. Dado este formato de la reducción al absurdo y el papel protagónico de III.10 y III.23, las observaciones destinadas a sus respectivas pruebas permiten apreciar con claridad meridiana cómo nuevamente la apelación a aquella estrategia demostrativa cumple un papel análogo a los casos anteriores. Como se me ha sugerido, existe una suerte de in crescendo en la complejidad de las demostraciones por el absurdo movilizadas en cada caso de la aplicación del método, pero este rasgo no altera la identidad de la función cumplida. En todos los casos, aquella estrategia funciona como el balance imprescindible para lograr la conclusión de coincidencia.
Debido a que las tres alternativas son absurdas, la demostración culmina afirmando la coincidencia de los segmentos circulares semejantes (tercera etapa). Finalmente, sólo resta la aplicación de NC4 a aquella premisa de coincidencia para obtener la igualdad requerida por el teorema: AEB es igual a ΓΖΔ (cuarta etapa).
4
Una observación relevante acerca del método de superposición en Euclides es que quizá pueda interpretarse desde dos perspectivas distintas (aunque fuertemente relacionadas).10 Como se ha hecho aquí, desde un ángulo inferencial, procurando discernir cómo contribuye singularmente a la economía deductiva de la demostración euclidiana. Más concretamente: cómo opera en términos inferenciales. Pero también resulta relevante examinarlo desde otro ángulo: cómo opera en términos constructivos. En este accionar constructivo, quizá podría aproximarse a un tipo o modalidad de recurso protagónico en la dinámica euclidiana, a saber: los postulados. En particular, permitiendo una operación diagramática análoga a las que habilitan los tres primeros postulados. Estos afirman:
Postúlese el trazar una línea recta desde un punto cualquiera hasta un punto cualquiera.
Y el prolongar continuamente una recta finita en línea recta.
Y el describir un círculo con cualquier centro y distancia.
En un sentido muy natural, el recurso a la superposición habilita operaciones diagramáticas tales como aplicar o superponer una figura sobre otra. Esta contribución constructiva aparece como característica definitoria de los postulados. Proclo escribe:
Sin embargo, así como un problema difiere de un teorema, un postulado difiere de un axioma, aunque ambos no estén demostrados; uno se asume porque es fácil de construir, el otro se acepta porque es fácil de conocer. Ésta es la base sobre la cual Geminus distingue postulado de axioma. (Proclus, 1970: 142)
No obstante, la licencia que este supuesto postulado (implícito) autorizaría exhibe una notoria peculiaridad si se lo compara con los antes citados: la construcción diagramática envuelta en el método de superposición no ocurre en forma gráficamente explícita, es decir, no existe ningún esfuerzo expresivo gráfico por captar ni el resultado, ni el proceso de superposición. Dadas las dos figuras, la intervención lingüística es la responsable de promover la operación de superposición. Aunque no es comunicada a través de una modificación gráfica del diagrama, su contenido obviamente es visual. Como se dijo antes, se trata de una operación abstracta o mental. Pero más relevante, aquella licencia exhibe otra singularidad: como su estudio detallado revela, su implementación entreteje en forma original las dos dinámicas (constructiva e inferencial), haciendo difícil predicar la facilidad (referida por Proclo) de la aludida construcción. Dicho en forma directa: la coincidencia es laboriosamente establecida.
La consecuencia sobresaliente de introducir esta discusión, sin embargo, no es laudar una respuesta categórica sobre la proximidad del permiso dado por el método con un postulado; su aporte consiste en realzar la dimensión constructiva de esta estrategia demostrativa y refinar así su descripción, captando la combinación original de aquellas dos dinámicas. Luego, la secuencia de implementación del método de superposición (discutida antes de manera detallada) podría describirse como una operación constructiva-inferencial, que culminaría con una o más conclusiones de coincidencia estelares, seguida de una operación netamente inferencial (que involucra a la NC4).
NC4 interviene así en el paso final de un sofisticado proceso. Dicha noción, como se recuerda, pertenece a la lista de cinco nociones comunes que (siguiendo a Heiberg) se atribuyen a Euclides:
NC1) Las cosas iguales a una misma cosa son también iguales entre sí.
NC2) Y si se añaden cosas iguales a cosas iguales, los totales son iguales.
NC3) Y si de cosas iguales se quitan cosas iguales, los restos son iguales.
NC4) Y las cosas que coinciden entre sí son iguales entre sí.
NC5) Y el todo es mayor que la parte.
En una reciente y notable contribución, Vincenzo de Risi ofrece poderosas razones para considerar que NC4 (así como NC5) no pertenece al conjunto original de las nociones comunes euclidianas, perseverando creativamente en una interpretación que cuenta con ilustres defensores; así, por ejemplo, Paul Tannery escribe (siendo 7 y 8, precisamente, las correspondientes a 4 y 5 de la lista anterior): “Las tres primeras nociones comunes fueron las únicas reconocidas por Heron, y este hecho, a pesar del apoyo que Proclo presta a las nociones 7-8, socava singularmente la autoridad de todas las demás” (1912: 52).
Pero, más relevante para los fines de este trabajo, para de Risi NC4-NC5 (a diferencia de NC1-NC3) poseen una suerte de caracterización estructural compartida, en virtud de desempeñar un papel análogo:
Esta noción común, que establece que las figuras congruentes son iguales, se usa para pasar de la superposición a la igualdad de contenido: la superposición se da intuitivamente, la igualdad debe establecerse proposicionalmente. En este sentido, NC4 juega el mismo papel epistémico que NC5 en tanto permite pasar de un procedimiento visual no proposicional (superposición y coincidencia) a un enunciado proposicional sobre propiedades exactas (igualdad). (De Risi, 2020)
Se podría decir que NC4 constituye una suerte de puente entre dos mundos: el del medio expresivo y el de las relaciones matemáticas relevantes. Coincidencia pertenece al primero; igualdad, al segundo. El carácter profundamente heterogéneo del método de superposición (como se describe aquí) se encuentra en perfecta concordancia con este rasgo estructural de NC4. Podría pensarse que ese rasgo estructural de la noción común ilustra o refleja la naturaleza profunda del método, como aquí lo interpreto. En tal sentido, no debiera sorprender que la elucidación detallada de sus diversas implementaciones contribuye a iluminar una cuestión relevante referida a la característica lógica de NC4.
Pareciera existir una coincidencia muy amplia en relación con la asunción implícita, por parte de Euclides, de la conversa de NC4. Es decir, NC4 debería leerse, más que como condicional, como equivalencia. Heath escribe:
Sobre la Noción Común 4, Tannery observa que tiene un carácter indiscutiblemente geométrico y, por lo tanto, debería haber sido excluida de las Nociones Comunes; de nuevo, es difícil ver por qué no va acompañada de su conversa, en todo caso para las líneas rectas (y, podría añadirse, también para los ángulos), de la que Euclides hace uso en I.4. (Heath, 1908: 225, énfasis mío)
Asimismo de Risi, quien argumenta en contra de la autenticidad de NC4, también parece inclinarse en ese sentido.11
En estas proposiciones, Euclides no hace referencia explícita a NC4 en la forma en que lo conocemos, sino que emplea diferentes expresiones para transmitir la idea de que las figuras coincidentes son iguales. En Elementos I.4, Euclides simplemente afirma, de paso, que “la base BC coincidirá con la base EF y será igual a ella”, y esta oración no parece una inferencia de un principio general sobre congruencia e igualdad. En la misma proposición Euclides también asume tácitamente, del mismo modo, las proposiciones inversas de que, si dos ángulos o dos segmentos son iguales, coincidirán al superponerse: “el punto B coincidirá también con E, porque AB es igual a DE”; y “la recta AC también coincidirá con DF, porque el ángulo BAC es igual al ángulo EDF”. Sin embargo, estos dos principios no se expresan como nociones comunes en los Elementos y la uniformidad del lenguaje en los tres casos sugiere fuertemente una interpretación epistemológica uniforme: Euclides no estaba empleando aquí ninguna inferencia a partir de axiomas y más bien respaldó un enfoque no axiomático de la relación entre congruencia e igualdad, moviéndose libremente entre las dos nociones. (De Risi, 2020, énfasis mío)
Si se entiende NC4 como se formula en la cita, parece evidente, a la luz del análisis de los tres casos examinados, que Euclides nunca usa la conversa de NC4. La demostración de la coincidencia reclama, además de la premisa de igualdad, alguna premisa de coincidencia; no hay pues un pasaje expedito, inmediato, directo desde igualdad a coincidencia. En ese sentido, Euclides no parece moverse libremente en las dos direcciones. Por supuesto, sí hay un tránsito expedito, directo (en los tres casos estudiados) de coincidencia a igualdad. Ese movimiento es autorizado en forma rigurosa y precisa por NC4.12
5
La importancia del método de superposición en la arquitectura de los Elementos es indiscutible; en palabras de Heath: “Pero viendo cuánto de los Elementos depende de I.4, directa o indirectamente, difícilmente se puede considerar que el método tenga, en Euclides, sólo una importancia subordinada; por el contrario, es fundamental” (1908: 225).
Ahora bien, dadas las críticas modernas y las estrategias posteriores de su eliminación vía axiomática, puede emerger una legítima inquietud: ¿es normativamente fiable este método? La estabilidad de los resultados obtenidos en el contexto euclidiano sugiere una respuesta positiva.
Hartshorne, luego de apuntar que el método implica la posibilidad de trasladar figuras de una ubicación a otra en el plano sin alterar lados y ángulos, expone una respuesta conocida. En primer lugar, se debe precisar tales asunciones a través de una caracterización de movimiento rígido. Éste se entendería como una transformación uno a uno de los puntos del plano en sí mismo que preserva rectas y lleva de segmentos y ángulos a segmentos y ángulos congruentes. Para captar el método de superposición se debe asumir la posibilidad de traslaciones, rotaciones y simetrías. Así, ejemplifica Hartshorne, puede definirse una traslación desde el punto <0, 0> a <a, b> por
y una rotación del ángulo α alrededor del origen por
El autor arriba a la siguiente conclusión:
[…] podemos justificar fácilmente el uso del método de superposición en el plano cartesiano real, pero ya que no hay coordenadas ni números reales en la geometría de Euclides, debemos considerar su uso del método de superposición como un postulado o axioma adicional no declarado. (Hartshorne, 2000: 34)
¿Es esta una respuesta a la cuestión inicial? Sí y no. La diferencia entre la cuestión planteada y el problema atendido por Hartshorne es que su preocupación reside en la posibilidad de legitimar (con recursos más recientes) las operaciones respaldadas en principio por el método original. El punto relativamente disimulado en tal estrategia es que, entre una y otra versión del procedimiento, hay un decisivo momento intermedio: el de la precisión o elucidación de la práctica metodológica original. Dicho de otro modo: si se entiende el método de superposición euclidiano en los términos de Hartshorne, es decir, luego de su operación de precisión o refinamiento, la legitimidad se encuentra fuera de discusión.13 Pero, ¿y el método original, de naturaleza heterogénea e ínsito en una práctica matemática que, obviamente, no cuenta con los recursos de control inferencial usados en la respuesta de Hartshorne? La cuestión de comprender el éxito y estabilidad de la geometría euclidiana en sus términos originales ha sido explícitamente propuesta y abordada por Manders (1996, 2008a y 2008b). Sugiero que la descripción ofrecida del método de superposición podría alentar un tratamiento particular, si aceptamos el reto de develar sus criterios normativos específicos. Espero enfrentar tal problema en un trabajo futuro.











 nueva página del texto (beta)
nueva página del texto (beta)