Introducción
El objetivo de este trabajo es presentar una metodología que simula la expansión de la mancha urbana, aplicando una variación espacial de las Cadenas de Markov (CM). Esta metodología se pone a prueba con métricas de bondad de ajuste que sirven para valorar la precisión de la simulación realizada, es decir, utiliza indicadores que miden qué tan parecidos son los resultados del modelo respecto a lo que ocurre en la realidad. En este trabajo se utilizan cuatro métricas de bondad de ajuste: el Índice Kappa de Cohen, el Índice de Jaccard, la dimensión fractal y la entropía de Shannon. Si el modelo replica aceptablemente la realidad, entonces puede utilizarse como un instrumento que genere información relevante sobre el futuro del crecimiento de la ciudad (Mandelbrot, 1983; Batty y Longley, 1994; Unibazo y Suazo, 2009).
Las Cadenas de Markov espaciales simulan los estados de un sistema en un tiempo determinado, a partir de dos estados precedentes en el espacio, esto significa que la modelización no tiene en cuenta las variables explicativas y descriptivas, sino que se basa exclusivamente en el análisis de la dinámica interna del sistema; en nuestro caso, corresponde al crecimiento de la mancha urbana y en muchos trabajos se refiere a la evolución del cambio de usos del suelo.
Se trata de un procedimiento en tiempo discreto, donde el valor en el tiempo t1 depende de los valores de los tiempos t0 y t (i.e. cadena marko-viana de segundo orden). El algoritmo compara/cuenta los datos de dos mapas en base raster, donde el suelo ocupado se codifica como uno y el no ocupado como cero (i.e. mapas de la mancha urbana de la ciudad de Toluca en 2003 y 2017), estos datos estiman y configuran una matriz de probabilidad de transición. La predicción se materializa en un mapa de la ciudad de Toluca de 2031, en el que se observa suelo ocupado y suelo no ocupado a nivel de pixel, que expresa la probabilidad de cambiar o pertenecer en la categoría analizada (i.e. categoría binaria).
El resultado será una serie de mapas binarios de probabilidad para el tiempo t1, proyección desde t. Para ello se considera el número de unidades temporales (e.g. años en nuestro caso, que definen la información con la que contamos) transcurridos entre t0 y t, asumiendo que es una evolución lineal. En el caso de la Zona Metropolitana de Toluca se ha proyectado a 2031 a partir de los años 2003 y 2017. Al tener las proyecciones de la zona metropolitana se realiza un análisis con indicadores de bondad de ajuste que valoren la similitud de los resultados del modelo de Cadenas de Markov espaciales con la realidad observada, para tener un indicador de precisión del modelo.
El estudio se centra en la Zona Metropolitana de Toluca, Estado de México, la cual ha experimentado un crecimiento considerable de la población en los últimos años, afectando significativamente la tasa de expansión urbana en el área y llevándola a considerarse como una ciudad millonaria (i.e. ciudad que rebasa el millón de habitantes) con una población actual de aproximadamente 1,846,602 habitantes (Inegi, 2015). La población está restringida dentro de un área de 2,957.4 La presión urbana y el impacto en los recursos naturales de esta región requiere monitorear y planificar el manejo de la tierra, el desarrollo urbano, entre otras muchas cuestiones.
Se aplica un enfoque analítico de Ciencias Sociales Espacialmente Integradas (Garrocho, 2016), el cual integra modelos matemáticos, tecnológicos (e.g. fotos de satélite, Sistemas de Información Geográfica), desarrollos informáticos automatizados (e.g. programas had-hoc) y una visión espacial para analizar procesos sociales, en este caso: la expansión de la mancha urbana en la Zona Metropolitana de Toluca para el periodo 2003-2017 y su posible evolución a 2031.
La metodología utilizada en este trabajo es novedosa, ya que se avanza al hacer las CM a escala de pixeles. Existen antecedentes recientes como Rey (2001), quien propone las Cadenas de Markov espaciales con incorporación de la interacción espacial entre regiones. En México destaca el trabajo de Valdivia-López (2008), que busca la dinámica intradistribucional a nivel municipal por medio de Cadenas de Markov espaciales, en este escrito no se utilizan regiones para realizar la metodología, se propone una interacción entre pixeles, que es la base de cualquier imagen o mapa.
Muchas de las investigaciones apuntan a la utilización de modelos que unen CM, autómatas celulares (AC) y SIG, como es el caso del uso de la tierra (Overmars y Verburg, 2006; Kamusoko et al., 2009; Han et al., 2009), en modelos de distribución en el crecimiento de la mancha urbana (Arsanjani et al., 2011; Mahiny y Clarke, 2012; Estoque y Murayama, 2012; Vaz et al., 2012; He et al., 2013; Arsanjani et al., 2013; Valdivia y Linares, 2013). Las CM determinan la potencial transición de los estados en el vecindario, mientras que los AC controlan el cambio espacial a través de las reglas globales, considerando la configuración del vecindario y los SIG que muestran los mapas de entrada/salida del modelo (Liu et al., 2007; He et al., 2008). En este trabajo se unen las CM y SIG dejando de lado a los AC, ya que sólo se utiliza una regla local aleatoria de crecimiento; con lo anterior se genera un modelo de Cadenas de Markov espaciales que es robusto en el tiempo y en el espacio.
Estrategia de presentación
El objetivo de este trabajo es metodológico: consiste en mostrar cómo se realiza la proyección espacio-temporal de las Cadenas de Markov espaciales. No se pretende, de ningún modo, proponer correcciones al método markoviano tradicional, sino un método nuevo de modelización y proyección del crecimiento de la mancha urbana, robusto en el espacio y en el tiempo.
El trabajo se divide en cuatro apartados: una breve explicación del método de Cadenas de Markov; la metodología que se aplica en este trabajo, sus fortalezas y debilidades, se explica la regla de difusión aleatoria, que es una aportación de este trabajo, además, se detallan las medidas de bondad de ajuste utilizadas para comparar la exactitud/inexactitud de las Cadenas de Markov espaciales que se proponen. Cada métrica que se utiliza se orienta a cómo se realiza la proyección del crecimiento de la mancha urbana con el modelo: i) Índice Kappa de Cohen: compara los mapas y muestra estadísticamente qué tan parecidos son; ii) Índice de Jaccard: expresa el grado en que los mapas son semejantes en la posición y en el estado del pixel; iii) Dimensión fractal es una medida de cuánto está fragmentada la mancha urbana, en este escrito se toma la dimensión como una medida de crecimiento y iv) Entropía de Shannon: indica la dispersión máxima posible en la que una variable se distribuye en el espacio, esto muestra qué tan bien se distribuyen los pixeles con el método propuesto. Estas dos primeras secciones son claves por el carácter metodológico del artículo. En el apartado 4, se pone a prueba el diseño el modelo de Cadenas de Markov espaciales, se estiman las medidas de bondad de ajuste y se analizan los resultados. Finalmente, en el último apartado se sintetizan los principales hallazgos, las aportaciones y las limitaciones así como las ventajas de las Cadenas de Markov espaciales.
1. Cadenas de Markov
Las CM muestran la transición de un estado a otro dentro de un número finito de posibles estados (Quah, 1993, 1996; Garrocho y Jiménez, 2018). Es el método más útil para modelar procesos estocásticos y de evolución probabilística, cuando se conoce solamente la situación presente. El crecimiento de la mancha urbana y otros muchos procesos que podemos observar en el tiempo son modelados mediante procesos estocásticos, como cualquier colección de variables aleatorias {X(t)} que dependen del tiempo t (Valdivia-López, 2008; Garrocho y Jiménez, 2018).
Un proceso estocástico (X) tiene la propiedad markoviana si la condicional de cualquier evento futuro t1 es independiente del evento pasado, sólo depende del estado actual del proceso. En este caso el proceso no tiene memoria. Si para todos los enteros n≥ 0 y todos los estados i0, i1,…, in-1, i, j, entonces se aplica la ecuación (1).
Se menciona que el proceso está en el estado i al tiempo n. Sea {Xn}n ≥ 0 un proceso estocástico discreto con espacio de estados E = {i, j, k,…}.
Dado que el sistema se encuentra en el estado i en el momento t, deberá encontrarse en alguno de los estados en t+n, donde la probabilidad de transición depende no sólo de los estados sino también del instante en el cual se efectúa la transición (i.e. la probabilidad es independiente del tiempo). Por lo que para todo i y n deberá cumplirse la ecuación (2), llamadas propiedades de Markov para todas las variables i, j (Yin y Zhang, 2010).
Donde pij es la matriz de transición, en nuestro caso la matriz de cambios de estado (i.e. cambio de espacio vacío a espacio ocupado), donde i es la clasificación inicial del espacio en 2003 y j la clasificación en 2017. La suma de los valores de las filas de la matriz debe ser igual a la unidad, para todos y cada uno de los estados “actuales”. Además, como se trata de probabilidades condicionales, deben ser no negativas.
La metodología expuesta da cuenta de la situación probabilística de cambio temporal, pero no espacial, por lo tanto, se utilizan la imagen en t, para aplicar la probabilidad de transición y se le agrega una regla de difusión aleatoria que ubica espacialmente los pixeles que tienen mayor probabilidad de cambio en cada categoría. Con este procedimiento la probabilidad de cambio es mayor de acuerdo con el contacto con cada pixel (e.g. contacto con vecinos cercanos). De esta manera se generan la metodología de Cadenas de Markov espaciales que se sustenta bien en el tiempo y en el espacio.
2. Metodología
Una proyección en el territorio es la generación de eventos en el futuro, que puede ser representada en un mapa. En los modelos tradicionales de proyección, los estados de equilibrio futuros se obtienen a partir de información pasada. En las Cadenas de Markov espaciales se realizan con información o, en nuestro caso, con información georreferenciada (i.e. mapas) en tiempo actual (Zapata et al. 2009).
Trabajar con información georreferenciada nos da la posibilidad de mostrar los datos en términos espaciales, fáciles de comprender y con mayor exactitud. Este tipo de información se maneja a través de SIG, que permiten interactuar con la información y realizar múltiples análisis generando resultados precisos. La capacidad de análisis que se realiza con un SIG es la diferencia entre los programas de visualización de datos y la de visualización de mapas (Mas et al., 2009).
En un SIG existen dos modelos de datos básicos estandarizados: i. El modelo Vectorial representa la información a través de figuras geométricas, con las que se representan fenómenos discretos con limite definido. La información que se asocia con formas geométricas (i.e. líneas y polígonos) se encuentra almacenada en filas en la tabla de atributos. ii. El modelo raster representa las características geográficas usando celdas discretas organizadas en una malla rectangular (i.e. los pixeles del mapa). La información la traduce en una matriz bidimensional de pixeles, referenciada a partir de la esquina inferior izquierda, y cada celda o pixel posee datos asociados (Zapata et al., 2009; Chávez y Garrocho, 2018).
Disponer de información georreferenciada en un SIG no basta para realizar cálculos matemáticos complejos, como los que requieren las Cadenas de Markov espaciales. Es necesario disponer de herramientas robustas que permitan realizar desarrollos automatizados de diversos modelos y métricas de análisis espacial, operando de forma amistosa con SIG. En nuestro caso nos apoyamos en la Estación de Inteligencia Territorial de El Colegio Mexiquense: CHRISTALLER® (Chávez y Garrocho, 2018).
CHRISTALLER® es una herramienta de computación que conjunta SIG, matemáticas especializadas y programación orientada a objetos (e.g Python), que ha permitido modelar el crecimiento urbano de manera efectiva y eficiente. Una alternativa en la cual se ha trabajado es el modelado con AC, que constituye un posible enfoque para la proyección del crecimiento urbano mediante la simulación de procesos espaciales como sistemas dinámicos discretos, pero no tan efectivos en el tiempo (Alkhe-der y Shan, 2005; Jiménez et al., 2018).
Una alternativa que solventa el problema del tiempo al utilizar AC son las CM, los dos modelos realizan proyecciones del crecimiento de la mancha urbana y sólo se necesitan los datos o mapas binarios actuales para realizar una proyección. Al utilizar SIG se facilita la obtención de mapas en formato Raster. Para este trabajo se codifica/filtra el mapa raster con unos en el suelo ocupado y ceros en el suelo no ocupado en la mancha urbana de la ciudad en estudio.
Las imágenes de satélite utilizadas fueron filtradas por la Unidad de Informática de El Colegio Mexiquense, A.C., dentro del proyecto CRISTALLER®. La precisión del modelo es alta y se expresa por medio de las técnicas de bondad de ajuste. El mapa base raster tiene muchos atributos dentro del pixel, entre ellas está la cobertura de cada uno, la georreferenciación del área por cada pixel, entre otras. En este trabajo se realiza un filtrado binario de la localización de las zonas que contiene el área de interés. Filtrar las imágenes obtenidas del satélite Landsat permite determinar en el mapa el área ocupada y el área no ocupada, con lo cual se convierte en un mapa binario, lleno de ceros y unos.
Se cuenta con los mapas de la zona urbana de la ciudad de Toluca en los años 2003 y 2017. El mapa de 2003 binario son los datos en el tiempo t0 y los datos del mapa 2017 binario es el tiempo t. Con esta información se realiza un conteo de ceros y unos, que se agrupan para generar una matriz de transición (P), de las Cadenas de Markov para tener una proyección en el tiempo t1. Con el cálculo de esta matriz Pn se tienen las mediciones en el tiempo, los cuales se llevan a un análisis espacial (Buzai, 2007).
Cuando se utilizan Cadenas de Markov espaciales para realizar proyecciones, se usan reglas de contigüidades para expresar el crecimiento o cambio en los estados en la matriz de transición (i.e. primera ley de la Geografía). La regla establece que un pixel tiene mayor probabilidad de cambiar de categoría o estado por el contacto con un pixel vecino. Por tanto, es más probable que no se convierta en esa categoría de un pixel que está más lejano (Rey, 2001; Buzai, 2007; Araya y Cabral, 2010).
Como se ha mencionado, el desarrollo de los procesos los realizamos con la ayuda de CHRISTALLER®. Los datos de entrada consisten en dos mapas binarios en diferente tiempo (e.g. mapa en t0 y el mapa en t). A partir de esta información se realizó un conteo binario que sentó las bases para generar una matriz de transición. Con la metodología de Cadenas de Markov espaciales se obtuvo una nueva matriz de transición que es la proyección de los datos con la que se realizó la simulación espacial. Se tomaron los valores que cambiaron de cero a uno así como los que permanecieron en uno y se aplicó una regla de difusión aleatoria en el mapa en t, que genera el nuevo mapa en el tiempo t1.
Se menciona en muchos trabajos que el modelo Cadenas de Markov espaciales es un derivado de los AC. A pesar de que las CM utilizan algunos elementos de los AC (i.e. la reja bidimensional, las vecindades), para este trabajo no se utilizó la regla de transición que recorre toda la reticular bidimensional, se utilizó una regla que realiza recorridos locales y no globales. Por tanto, se puede decir que no es un derivado sino un modelo con su propia autonomía.
3. Ejemplo de distribución de pixeles con las Cadenas de Markov espaciales
En esta subsección se plantea una metodología específica “paso a paso” de la regla de difusión que se utiliza. Es decir, para facilitar la compresión de la propuesta metodológica, se presentan ejemplos de cómo se realiza la distribución de pixeles con la proyección de Cadenas de Markov espaciales.
Caso 1
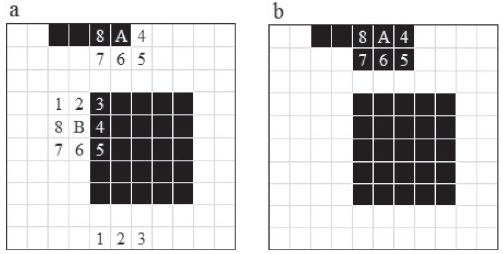
El primer caso trata de una mancha contenida en el centro (Figura 1a). Esta imagen muestra una cuadrícula de dimensiones 10x10 (i.e. tiene 10 cuadros de ancho y 10 cuadros de altura). La multiplicación de los cuadros (ancho/altura) nos otorga un plano de dimensión de 100 cuadros; cada cuadro para nuestro caso representa un pixel binario (i.e. cuadro en color negro, representa un pixel con valor uno y cuadro en color blanco, representa un pixel en cero).
La distribución de los pixeles después de haber obtenido la proyección con Cadenas de Markov espaciales se hace de la siguiente forma: con la ayuda de las aplicaciones de CHRISTALLER® se realiza una selección aleatoria de un pixel en lo ancho y largo de la imagen. Posteriormente, a los ocho vecinos cercanos (i.e. a los que rodean al pixel) se les cambia el valor (i.e. si el pixel está en valor cero cambia a valor uno). Al terminar de cambiar el valor de aquéllos se realiza otra selección aleatoria de otro pixel, hasta agotar los pixeles que cambiaron de cero a uno o que se mantienen en uno.
Al tomar la metodología de la distribución de los pixeles para nuestro ejemplo mostramos una cuadrícula con 25 cuadros en color negro y 75 cuadros en color blanco (Figura 1a). La primera selección aleatoria nos otorga una ubicación (4,2) que es el cuadro que denominamos como A (i.e. cuatro cuadros de ancho y dos de altura), el conteo de los cuadros se realiza de la esquina superior izquierda que es el inicio. Se identifican los ocho cuadros cercanos al cuadro A (i.e. vecinos cercanos) y se enumeran del uno al ocho. Observamos que los cuadros 1, 2, 3, 4, 7 y 8 están color blanco, mientras que los cuadros 5 y 6 están en color negro. Por lo tanto, los cuadros en color blanco cambian a cuadros en color negro y los cuadros que ya están en color negro se rescribe el color (i.e. se toma en cuenta esta reescritura con el objetivo de bajar el conteo de cuadros negros o pixeles con valor uno, generados por la CM). Todo el cambio que ha sucedido se muestra en la Figura 1b.
Quedan cuadros negros en la proyección de Cadenas de Markov, por lo tanto, se realiza otra selección aleatoria y tenemos el cuadro marcado como B, con coordenadas (7, 8). Se numeran los cuadros cercanos del uno a ocho y se obtiene el resultado. Realizados los dos procesos, ahora tenemos 36 cuadros en color negro y 64 en color blanco. Lo anterior da muestra de un crecimiento de la mancha. Además de una disminución de los cuadros que cambiaron de color blanco al negro que se calcularon con CM, esto es, al encontrar los puntos que fueron seleccionados en forma aleatoria, deben cambiar 16 cuadros a color negro y no solamente 11 (Figura 1b). Los cinco cuadros de diferencia son los cuadros rescritos color negro, el impacto sólo se observa en los cálculos de la CM, que es mínimo.
Caso 2
En el siguiente ejemplo se observan dos manchas en la cuadrícula, una de mayor tamaño que la otra (Figura 2a).
En este ejemplo se realiza una selección aleatoria del punto A, (Figura 2a), este punto con coordenadas (8,8) es un punto que no tiene vecinos cercanos o cuadros en color negro. Es un cuadro en color blanco y por lo tanto sus ocho vecinos cercanos son cuadros en color blanco, cuando sucede este caso (i.e. un área no poblada, cuadros en color blanco) se desprecia este punto y se selecciona otro punto en forma aleatoria (Figura 2b) el punto A desaparece.
Ahora realizamos una búsqueda del punto B, sus vecinos cercanos se numeran de uno a ocho y los cuadros en color blanco que son vecinos cercanos cambian de color (i.e. los cuadros 3, 4 y 5 cambian a color negro) (Figura 2b). Los cuadros 1, 2, 6, 7 y 8 se reescriben en color negro.
Se realiza otra selección aleatoria para bajar el número de cuadros en color negro. Encontramos el punto C con coordenadas (8, 3). Se numeran los vecinos cercanos, aunque estén de color blanco y no tengan vecinos cercanos en color negro como se muestra en la Figura 2a. En este caso no son necesarios los vecinos en color negro y sólo se toma en cuenta el cuadro negro marcado como C. Esta es una aportación del programa de difusión aleatoria que se realizó, se considera que si existe una mancha pequeña tiende aumentar de tamaño, es un crecimiento espacio-temporal. Como se observa en la Figura 2b.
En este ejemplo se seleccionan tres puntos aleatorios, por lo tanto suponemos que la imagen tiene mayor cobertura en cuadros negros, pero no es así. Lo que se busca es mostrar qué hace el programa cuando se encuentra un cuadro/pixel en color blanco y un cuadro/pixel en color negro. El programa sólo toma en cuenta dónde se posiciona el punto aleatorio para determinar si hay expansión o no.
Caso 3
En este ejemplo se muestra cuando la mancha de cuadros negros esta en las fronteras de la imagen y además qué sucede si un punto tiene coordenadas justo en la frontera de la mancha, como se muestra en la Figura 3a.
En ésta, se selecciona el punto A que está en la frontera de la imagen, se numeran los ocho vecinos, como se observa en la figura. Observamos que el punto A esta en la parte superior y los vecinos del 1 a 3 no se toman en cuenta y desaparecen como se muestra en la Figura 3b.
En este ejemplo solamente se cambió de color a cinco vecinos cercanos y tres desaparecieron o no se tomaron en cuenta.
Se encuentra el cuadro/punto B, que es un cuadro en color blanco por lo tanto no se toma en cuenta para hacer cambio de color a los vecinos cercanos. Existen tres vecinos cercanos de color negro al punto B, como se muestra en la Figura 3a. Este cuadro no se toma en cuenta para hacer cambio de color por restricción del programa de expansión de la mancha (Figura 3b).
Podemos concluir que las reglas de expansión/difusión que se programaron se basan en lo siguiente:
1) Se selecciona un punto en la retícula en una forma aleatoria.
2) Si el punto encontrado es un pixel/cuadro en color negro, los ocho vecinos cercanos (i.e. los vecinos que rodean al punto encontrado) se convierten en pixeles/cuadros a color negro.
3) Se puede reescribir el pixel/cuadro que ya tiene color negro. Con esto se realiza una disminución en el excedente de pixeles/cuadros que generan las CM, si es el caso.
4) Si el punto encontrado es un pixel/cuadro en color blanco, no se considera y se realiza una nueva búsqueda aleatoria hasta completar el excedente que genera la CM.
Esta idea de regla de difusión aleatoria es creada en este trabajo para determinar el proceso de vecindad inmediata de cada pixel o punto en el territorio, ya que se parte de la suposición de que lo que ocurre en un pixel incide con fuerza en lo que ocurre en otros inmediatos a ése.
En muchos estudios se ha utilizado un modelo de agregación limitada que es muy similar a la regla de difusión aleatoria, en el cual los pixeles urbanos (i.e. para nuestro caso pixeles en color negro) se difunden aleatoriamente sobre un campo probabilístico hasta juntarse con algún otro pixel urbano que ya existe o está en espera de crecer y por lo tanto son pegados al lugar donde se produce la expansión, calculando las nuevas probabilidades sobre las cuales se difundirán los siguientes pixeles urbanos (Batty, 1991; Batty y Longley, 1994; Makse et al., 1995; Buzai, 2007).
3.1. Validación del método
Para la validación del método es necesario comparar los mapas reales con los simulados. Es decir, comparar los resultados generados por la técnica propuesta con los datos reales, para decidir qué tan adecuado es el modelo que produce resultados cercanos a la realidad o al menos razonablemente cercanos. La comparación no es sencilla y es imprescindible adoptar métodos o técnicas que permitan mejorar los procedimientos de comparación (Congalton, 1991; Pascual et al., 2010; Araya y Cabral, 2010).
Comparar dos mapas, uno real que representa el tiempo “t” y otro simulado con el modelo que representa el tiempo “t1”, es una forma aceptable de medir la igualdad, en mayor o menor grado. Para ello se presentan dos técnicas que permiten medir la igualdad/similitud de dos mapas y de esa manera establecer la validez del modelo. Además, se introducen dos técnicas que miden el crecimiento/contracción de la mancha urbana, que es algo novedoso para este tipo de trabajos (Pascual et al., 2010; Jiménez et al., 2018).
3.1.1. Índice Kappa de Cohen
El Índice Kappa de Cohen (k) es una medida de comparación de mapas que ajusta el efecto del azar. En este trabajo, entre mapas de categorías binarias, el resultado k puede tomar valores entre -1.0 y +1.0 y se interpreta de manera parecida al índice de correlación de Pearson: mientras más cercano a +1.0, mayor es el grado de concordancia entre los mapas, si es cercano a -1.0, mayor es el grado de discordancia; un valor alrededor de 0.0 indica ausencia de similitud entre los mapas. El resultado del índice de Kappa de Cohen nos muestra el efecto del azar y es posible saber si sus resultados son estadísticamente significativos (López-de-Ullibarri y Pita-Fernández, 1999; Abraira, 2001; Viera, 2005).
Donde P 0 es la proporción de igualdad observada, Pe es la proporción de igualdad esperada y 1 - Pe representa la igualdad o concordancia máxima. Entonces, el numerador del Índice de Kappa de Cohen expresa la proporción de igualdad observada menos la esperada, en tanto que el denominador es la diferencia entre la igualdad total y la proporción esperada. Si este valor es igual a 1.0, estaríamos frente a una situación en que la igualdad entre los mapas es perfecta (100% de igualdad), cuando el valor es 0.0 los mapas tienen un parecido de cero (e.g. no se parecen en nada), y si el valor es -1.0 un mapa sería el inverso del otro (Viera, 2005; Jiménez et al., 2018).
Viera (2005) propone una guía de umbrales como los que se presentan en el Cuadro 1. La interpretación de los k es una cuestión subjetiva y no existe acuerdo general. Sin embargo, esta guía se acepta cuando el número de pixeles que componen las imágenes es elevado, como es nuestro caso, que consideramos casi 4.0 millones de pixeles. Por lo tanto, aquí utilizaremos los umbrales interpretativos de k que se muestran en el cuadro 1 (Jiménez et al., 2018).
Cuadro 1 Interpretación del Índice de Kappa de Cohen
| Indice Kappa | Estimación del grado de Igualdad |
|---|---|
| <0 | No igualdad |
| 0.0-0.2 | Insignificante |
| 0.2-0.4 | Bajo |
| 0.4-0.6 | Moderado |
| 0.6-0.8 | Bueno |
| 0.8-1.0 | Muy bueno |
Fuente: elaboración propia, con base en Viera (2005).
3.1.2. Índice de Jaccard
El Índice de Similitud de Jaccard (Ij) expresa el grado en el que dos imágenes (e.g. mapas) son semejantes (Reyes y Torres-Florez, 2009). El intervalo de valores para el índice de Jaccard va de 0.0, cuando la desigualdad entre los mapas es total, hasta 1.0, cuando dos mapas tienen la misma medida de concordancia-posición. El índice se obtiene con la ecuación (4).
El Índice de Jaccard es sencillo de analizar desde la teoría de conjuntos. En el conjunto A, los objetos que se encuentren en su dominio se nombran T21. En el conjunto B, los objetos que se encuentran en su dominio se les etiqueta T12. Los objetos que se encuentre en la unión de los dos conjuntos (i.e. A U B) se les califica como T11. Todo lo que este fuera de los estos lo etiquetamos como T22. Para más detalles y ejemplos ver Jiménez et al., 2018.
El Índice de Jaccard (e.g. ecuación 4) calcula dos aspectos clave para la comparación de mapas: la igualdad de los datos raster y su posición en el mapa. Los resultados obtenidos en este trabajo tienen una significancia de 0.85, de acuerdo con el Cuadro 1, son muy buenos resultados. Para el Índice Kappa y el Índice Jaccard se utiliza el Cuadro 1 para dar significancia a los resultados.
3.1.3. Dimensión fractal
Los fractales fueron introducidos por Mandelbrot (1983), un estudio de estructuras irregulares y fragmentadas que se presentan en diferentes escalas (e.g. como las costas o las montañas). La aparición de una estructura a diferentes escalas se denomina autosimilitud, ya que cada una de las partes, cualquiera que sea su grado de acercamiento, presenta semejanza a la figura original. Si tomamos un objeto lo observamos y lo analizamos con diferentes niveles de aproximación, las características geométricas se preservan y este es un aspecto sumamente importante para describir y analizar fractales.
El grado de irregularidad y fragmentación de los objetos que aparecen en la naturaleza (e.g. en este trabajo mapas) es posible medirla con la dimensión fractal (D). Es un valor que se expresa desde un punto de vista geométrico. Al medir objetos irregulares genera un valor no-entero (e.g. es un numero fraccionario). En el espacio euclideano están bien definidos los valores como D =0 (punto), D =1 (línea), D =2 (plano bidimensional) y D =3 (volumen) (Shen, 2002).
Con la dimensión en la cual se trabaja se puede considerar que la dimensión fractal también es una dimensión de crecimiento, ya que D =1 es una línea y D =2 es un plano totalmente lleno de puntos o un plano sólido. Por lo tanto, la dimensión fractal que se utiliza está contenida entre uno y dos. Si la métrica se acerca a uno podemos decir que tiene disminución de puntos (i.e. decreció la proyección del modelo). En otro caso, si la medida está cerca de dos, podemos decir que tiene muchos puntos, está casi lleno (i.e. creció la proyección del modelo).
La dimensión euclídeana de un objeto relaciona la unidad de medida utilizada con el valor geométrico medido N(L)=(1/L)D, donde 1/L corresponde a la escala, que son las divisiones que se hacen en el plano (i.e. tomar la imagen a nivel de pixel). El cálculo de D se basa en la correspondiente medición del número de pixeles en color negro que cubren determinado conjunto (línea, superficie o volumen), N(L) en función de la escala. El cálculo es sólo válido en el rango en el que la relación entre N(L) y 1/L que es una relación potencial, y está bien definida mediante la ecuación (5).
A esta relación potencial se le denomina método de conteo de cajas o pixeles (box counting), que miden el crecimiento o contracción de la mancha urbana. Al utilizar el concepto de fractal se han encontrado muchos objetos fractales en distintos sistemas naturales (sistemas irregulares y fragmentados), así como en los sistemas sociales y en estructuras socioespaciales (Goodchild y Mark, 1987). Con esto podemos distinguir entre fractales perfectamente autosimilares (generados a través de procesos de iteración en forma regularmente determinada) y fractales cuya autosimilitud es básicamente estadística (no-determinísticos o generados a través de un proceso estocástico) (Buzai, 2007).
3.1.4. Entropía de Shannon
La entropía es un concepto que se ha utilizado para describir la estructura y el comportamiento de diferentes sistemas (Batty, 2012). En este trabajo se propone la aplicación de la medida de entropía en la expansión urbana para determinar la concentración y dispersión espacial (Yeh y Xia, 2001; Sudhira et al., 2004; Sun et al., 2007).
La entropía de Shannon indica la proporción de la dispersión máxima posible en la que una variable se distribuye entre categorías o zonas espaciales. Es decir, tiene un valor de 1.0, la variable que está distribuida uniformemente entre todas las zonas, y si se acerca a 0.0, la variable se concentra en un pequeño número de zonas (Cabral et al., 2013). Se expresa mediante la ecuación (6).
donde En es la entropía relativa, p(xi) es la probabilidad de que la variable x se encuentre en una de las zonas, clases o categorías.
El cálculo de entropía de Shannon es un índice de expansión urbana que utiliza datos obtenidos de forma remota (e.g. con SIG), puede identificar y caracterizar eficientemente el grado de concentración espacial o dispersión en un área específica (Yeh y Xia, 2001; Araya y Cabral, 2010).
El valor de la entropía nos lleva a señalar que, para todas las dimensiones de los sistemas urbanos, hay un rango de valores en los que ésta podría tolerarse sin comprometer su eficiencia o su resiliencia. Si la entropía tiene un valor cercano a cero, el área urbana es demasiado uniforme, por lo tanto, vulnerable a cambios o desastres. Si la entropía tiene un valor cercano a uno, el sistema urbano no podrá asignar eficientemente los recursos necesarios para que el sistema funcione (Batty, 2012; Cabral et al., 2013).
Por lo tanto, la entropía debe mantenerse dentro de un rango definido por el valor mínimo, por arriba del cual el sistema se vuelve vulnerable e inestable, y en el valor máximo, por debajo del cual el sistema se vuelve insostenible; determinar umbrales óptimos puede ser muy útil para las administraciones urbanas, ya que proporciona información valiosa sobre funcionamiento de los sistemas urbanos (Araya y Cabral, 2010; Cabral et al., 2013).
Las métricas de bondad de ajuste presentadas en esta sección se calculan con la Estación de Inteligencia Territorial: CHRISTALLER®.
4. Resultados
La clasificación del espacio ocupado y vacío da una muestra del crecimiento de la mancha urbana en un periodo de tiempo determinado. Las CM permiten conocer las probabilidades de que los pixeles se mantengan en una u otra clasificación de espacio ocupado o vacío. Una forma sencilla y eficiente de discretizar las categorías es codificar/filtrar como 1 al espacio ocupado y 0 al espacio vacío. En la Tabla 1 se presentan los estados o categorías en que se clasifica el espacio urbano de cada ciudad.1 Los Vectores Iniciales Totales (x0) se construyeron a partir del conteo de pixeles binarios en cada categoría por año, en relación con el total (Tabla 1).
Tabla 1 Vectores de estado inicial, 2003-2017
| Ciudad | Toluca | ||
|---|---|---|---|
| 1 | 0 | Total | |
| 2003 | 736 513 | 2 946 179 | 3 682 692 |
| % | 20.0 | 80.0 | 100 |
| 2017 | 1220632 | 2 462 060 | 3 682 692 |
| % | 33.1 | 66.9 | 100 |
Fuente: elaboración propia con datos generados por CHRISTALLER®.
Los vectores de estado iniciales muestran el incremento o cambio de estado de pixeles en 2003 y 2017. Los que permanecen en 1 pasaron de 736,513 a 1,220,632 (un incremento de 11.1%) y los que permanecieron en 0 bajaron de 2,946,179 a 2,462,060 (una disminución de 13.1%). En total, en la ciudad de Toluca, los pixeles que cambiaron su estado, es decir: la mancha urbana que se modifica o crece, son 484,119 en 14 años (un aumento de 13.1%).
4.1. Matriz de transición: 2003-2017
Una manera para observar los cambios al interior de la distribución a lo largo del tiempo son las CM, donde el insumo principal son las matrices de probabilidades de transición, que representan la probabilidad de estar en un estado Pn en el periodo t1, a partir de la distribución en el periodo t (Modica y Poggiolini, 2012).
La construcción de la matriz de transición para 2003-2017 se genera por un conteo de cambios entre las dos categorías de pixeles de un año a otro. Basta consultar las aplicaciones de CHRISTALLER® y ordenar la información como se muestra en el Tabla 2.
Tabla 2 Matriz de transición 2003-2017
| 2017 | n | |||
|---|---|---|---|---|
| 0 | 1 | |||
| 2003 | 0 | 80 % | 20 % | 2 946 179 |
| 1 | 15 % | 85 % | 736 513 | |
| 3 682 692 | ||||
Fuente: elaboración propia, conteo realizado con la ayuda de CHRISTALLER®
La Tabla 2 muestra que en 14 años, al medir el crecimiento de ciudades, permanecen 2,349,918 pixeles, 80% en cero (suelo que no ha sido ocupado). Existe una transición de cero a uno (cambio a suelo ocupado) 596,261, 20%. Cambio de uno a cero 112,142, 15%, suelo que se convirtió en no ocupado y finalmente suelo que permanece en el estatus de suelo ocupado 624,371, 85%. Por tanto, puede inferirse que existe una cantidad grande de suelo que no ha sido ocupado o cambiado de estatus.
4.2. Segundo estado de transición: 2017-2031
La Tabla 3 es la nueva matriz de transición que es una proyección de datos binarios que estarán presentes en el mapa 2017-2031 de Toluca y que mantuvieron las condiciones para el conteo.
Tabla 3 Matriz de proyección, 2017-2031
| 2031 | n1 | |||
|---|---|---|---|---|
| 0 | 1 | |||
| 2017 | 0 | 67% | 33% | 1 972 089 |
| 1 | 25% | 75% | 1 710 603 | |
| 3 682 692 | ||||
Fuente: elaboración propia, conteo realizado con la ayuda de CHRISTALLER®.
El principal cambio en el periodo 2003-2017 es que, 3,249,918 pixeles que se encontraban en la categoría de suelo no ocupado (i.e. pixeles en cero que permanecen en cero), equivalían a 80% del total. La proyección mostrada en la Tabla 3 indica que para 2031 la probabilidad de que los pixeles permanezcan en esa categoría se reduce a 67%. La probabilidad de transitar de valor de cero a uno subiría de 20% a 33% y la de pasar de valor uno a cero van de 15% a 25%. En síntesis, la proyección sugiere una redistribución progresiva importante de condiciones para vivir/trabajar, por lo tanto existe mayor suelo ocupado que vacío.
4.3. Resultados del modelo de expansión urbana con Cadenas de Markov espaciales
El área de estudio de este trabajo es la Zona Metropolitana de Toluca, para el periodo 2003-2017 (Figuras 4a y 4b), esta ciudad se sitúa en el centro de la república mexicana. Las imágenes satelitales que utilizamos como referencia para los resultados del modelo de Cadenas de Markov espaciales se obtuvieron de los satélites Landsat 5 y 8. La situación en 2003 para la ciudad de Toluca se muestra en la Figura 4a, esta imagen satelital de 2003, junto con la imagen de 2017 (Figura 4b), son los mapas con los cuales se realiza la matriz de transición utilizada y los datos de entrada para la herramienta en CHRISTALLER®.
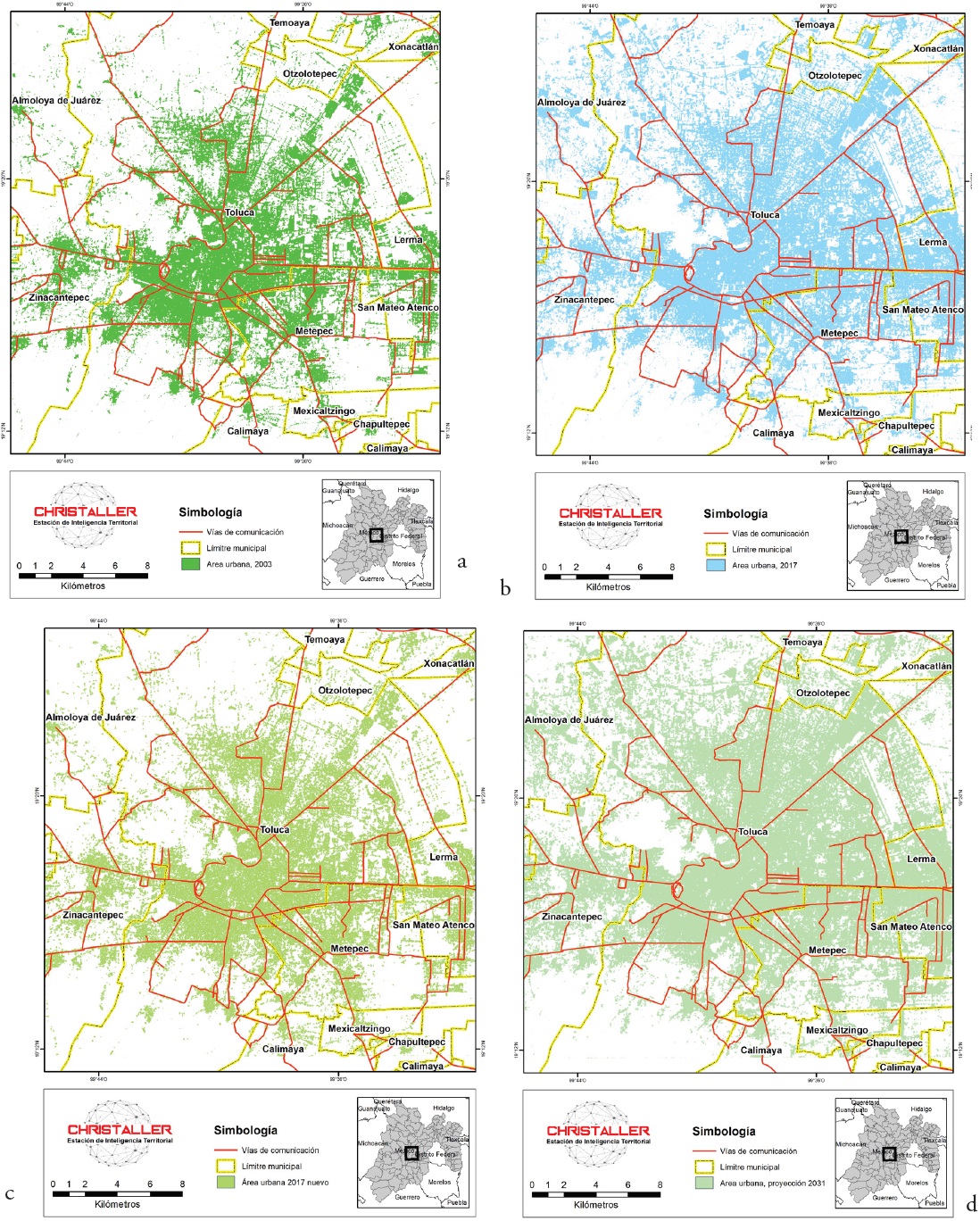
Fuente: elaboración propia con base en LandSat.
Figura 4 Mapas de Satélite y Proyecciones del Valle de Toluca
Con el uso de herramientas de CHRISTALLER® se estiman los indicadores de comparación, de crecimiento y de distribución, lo que valida la regla aleatoria de crecimiento utilizada en las Cadenas de Markov espaciales, ello muestra qué tan efectiva es la metodología en la expansión de la mancha urbana en la ciudad de Toluca en el periodo de experimentación.
Para realizar un banco de pruebas del modelo es necesario hacer una proyección utilizando como referencia el mapa de Toluca en 2003 para bosquejar el mapa en 2017 y así realizar la comparación con el mapa real de 2017. La Figura 4c muestra la simulación del crecimiento de la mancha urbana para 2017 con la regla de difusión aleatoria, que es una aportación al modelo. Para realizar la difusión o expansión se toman los valores de la Tabla 2, que es la matriz de transición, de la cual solamente se consideran los valores que cambian de cero a uno, 596,261 pixeles y los que permanecieron en uno, 624,371 pixeles: un total de 1,220,632 pixeles que van a cambiar en el mapa de 2003.
Con la proyección de la ciudad de Toluca para 2017, realizada con la regla de difusión aleatoria, podemos observar qué tan eficiente es el método distribución de pixeles. Como se mencionó, el valor máximo de los índices Kappa de Cohen y Jaccard es 1.0. El Índice Kappa de Cohen para Toluca es 0.78, lo cual indica que la regla de difusión es buena en el proceso de expansión de la mancha urbana.
El Índice de Jaccard muestra resultados aún más alentadores para la regla de difusión aleatoria. Toluca registró un Jaccard de 0.85, lo que indica una alta capacidad de la regla para distribuir los pixeles en el mapa con una alta eficiencia. Los valores de los indicadores de comparación son buenos, la regla nos permite distribuir los pixeles con menor incertidumbre en la expansión de la mancha urbana para el valle de Toluca en un periodo de catorce años. Esta regla de difusión aleatoria podría ser un instrumento importante para los planificadores urbanos.
Se calcula la dimensión fractal para determinar cuánto creció la mancha urbana mostrando resultados muy buenos (Tabla 4). Las diferencias de crecimiento entre la imagen satelital de 2017 y la proyección utilizando el modelo de Cadenas de Markov espaciales realizado por CHRISTALLER® registra una variación de menos de una décima, con lo cual se puede considerar muy buen ajuste.
Tabla 4 Resultados de la dimensión fractal y de la entropía de Shannon
| Toluca | 2003 | 2017 | Proyección 2017 | Proyección 2031 | Clasificación |
|---|---|---|---|---|---|
| Dimensión Fractal | 1.74 | 1.85 | 1.79 | 1.92 | Buena |
| Entropía de Shannon | 0.72 | 0.91 | 0.89 | 0.99 | Buena |
Fuente: elaboración propia, con la ayuda de CHRISTALLER®.
En la Tabla 4 se muestra el índice de la entropía de Shannon para la ciudad de Toluca, como se mencionó, el valor máximo del índice es 1.0. El índice de entropía muestra una distribución uniforme de la concentración de los pixeles en la zona metropolitana. Con esto se muestra un crecimiento de la mancha urbana.
El índice de entropía de Shannon para Toluca en 2003-2017 y la proyección 2017 indica una buena distribución de pixeles con una diferencia de casi una décima, lo cual indica que la mancha urbana está creciendo de una forma adecuada (e.g. no crece en una zona, si no en todas las zonas del mapa). En la proyección realizada por el modelo de Cadenas de Markov espaciales al calcular la entropía existe un resultado muy cercano a uno: esto es muy interesante, porque, aparentemente, la velocidad de crecimiento de la mancha urbana es elevada, por lo tanto, el valor indica que está muy bien distribuido el crecimiento, esto es una conjetura que debe probarse considerando más ciudades.
Los archivos e imágenes utilizados son masivos de alta complejidad, pero CHRISTALLER® fue capaz de manejar toda esta información. Las imágenes satelitales de la ciudad de Toluca contienen alrededor de cuatro millones de pixeles. Considerando la magnitud de la información, la complejidad de los cálculos, la utilización de la regla de difusión aleatoria, la estimación iterativa de los índices de comparación/expansión urbana y la generación automática del mapa de simulación, podemos considerar que el desempeño en el modelo de Cadenas de Markov espaciales realizado por CHRISTALLER® es muy rápido y eficiente en la proyección. En promedio, CHRISTALLER® requiere un minuto para generar los resultados y las proyecciones de la ciudad, lo que se traduce como buenos resultados en la aplicación.
Con la certeza de que el modelo propuesto de Cadenas de Markov espaciales es muy eficiente y tiene muy buenos resultados, podemos generar una proyección de la ciudad de Toluca para 2031, Figura 4d. En este mapa se muestra un equilibrio en los valores que cambiaron de uno a cero y al inverso, por tanto, se puede decir que en un periodo de 14 años la velocidad de crecimiento de la ciudad de Toluca bajó, pero falta verificar este resultado con pruebas que no se discuten en este trabajo. Cabe mencionar que matemáticamente esta aseveración es posible, pero geográficamente es más difícil que ocurra. Por ello, en este trabajo el cambio de los pixeles con valor de uno a cero no se toma en cuenta y se desprecia.
En la Figura 5 se puede ver a simple vista el crecimiento de la mancha urbana. Responde bien al patrón básico generado por la regla de difusión aleatoria utilizada en este trabajo. Los mapas de área urbana de la ciudad de Toluca en 2003 y 2017 se superponen dándole dos tonalidades de gris en el mapa de la Figura 5, se puede decir que es área construida en 14 años, captada por la foto de satélite. Las nuevas zonas urbanas generada por Cadenas de Markov espaciales en el mapa son los pixeles en color negro, un producto de la simulación.
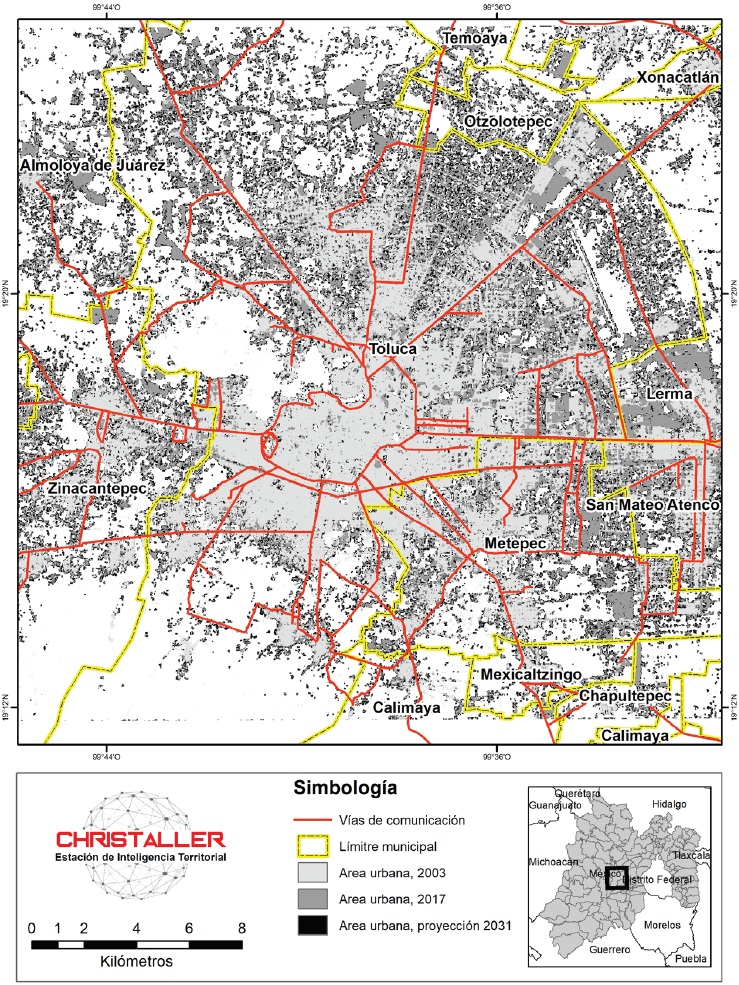
Fuente: elaboración propia con CHRISTALLER®.
Figura 5 Toluca: mapa de comparación visual de Toluca en el crecimiento 2003-2031, uso del modelo de Cadenas de Markov espaciales
Lo destacable en la imagen de proyección de Toluca (Figura 4d) y en el mapa de comparación visual (Figura 5) son las zonas que restringe el modelo utilizado, con una inspección visual podemos darnos cuenta que hay tres zonas que mantienen su fisonomía casi sin modificaciones hasta 2031: el centro de la ciudad de Toluca se observa una zona que se mantiene en 28 años y es el cerro de la Teresona, por sus elevaciones es difícil construir en ese lugar y existen otras restricciones, en la segunda zona donde no se ve un crecimiento acelerado es la del volcán (i.e. el Nevado de Toluca) que está en la parte baja-izquierda de la imagen, es un territorio denominado parque nacional y no se puede construir, en la zona de Lerma, que tiene terrenos destinados al aeropuerto de Toluca, lo mismo donde se impide la construcción (Figuras 4d y 5, vista de frente en la parte derecha casi en el centro).
Con la técnica de Cadenas de Markov espaciales se muestra que las nuevas áreas serían más compactas y cercanas a zonas construidas. La comparación fue realizada por CHRISTALLER®; es evidente que, al usar los mapas, mejora mucho el acuerdo entre los mapas reales y simulados (Figura 5). Comparar los mapas de crecimiento urbano engaña mucho al observador, pero se realiza un esfuerzo para saltar este obstáculo en el programa que se desarrolló (i.e. hacer que los mapas hablen), como se muestra en la Figura 5.
La comparación visual mostró cómo el modelo elaborado con Cadenas de Markov espaciales en el crecimiento de la mancha urbana responde al patrón básico que ocurre en la realidad, pero mostrando un crecimiento mayor y más compacto. Además, con este modelo, el nuevo crecimiento de la mancha urbana se adhiere a construcciones ya existentes y nuevas urbanizaciones aisladas desaparecen por falta de vecindad o por restricciones de espacio para construir (Figuras 4d y 5).
Conclusiones
En este trabajo se adoptó una técnica innovadora para explorar el crecimiento de la mancha urbana en la ciudad de Toluca: Cadenas de Markov espaciales. El objetivo fue mostrar cómo funciona esta técnica de crecimiento-proyección tomando como ejemplo la Zona Metropolitana de Toluca, que se puede decir tiene una velocidad de crecimiento muy elevada por ser una ciudad millonaria con relación a sus habitantes. Los resultados muestran que el enfoque de análisis con Cadenas de Markov espaciales ofrece información valiosa y una visión alterna al enfoque tradicional de crecimiento con regiones, se enfoca principalmente en el crecimiento de la mancha urbana con pixeles en mapas binarios en base rasters.
En las Cadenas de Markov espaciales lo más destacable es su análisis espacio-temporal, que es muy difícil de encontrar en técnicas que proyectan mapas o que realizan crecimiento en estos. El poder que tienen las Cadenas de Markov es el tiempo, es lo que se aprovecha para sólo agregar el espacio con una regla de difusión aleatoria en la distribución. Se generan proyecciones a lo largo de 14 años, a partir de los mapas de la ciudad disponibles.
La unión de un sistema de información geográfica con Cadenas de Markov espaciales nos lleva de la mano para generar una herramienta en la plataforma de simulación llamada CHRISTALLER® (Estación de Inteligencia Territorial de El Colegio Mexiquense). Este software automatiza los procesos de análisis y genera una herramienta de interés que se puede utilizar en diferentes áreas del conocimiento.
Las técnicas de comparación de mapas y la comparación-posición de la mancha urbana nos lleva a utilizar comparadores estadísticos, como son el Índice Kappa de Cohen y el Índice de Jaccard; los resultados fueron muy alentadores y muy precisos; además, lo mostrado en la Figura 5, donde se realiza una comparación visual entre mapas, muestra la dinámica de cambio de la mancha urbana a lo largo de 28 años y las zonas que se restringen en el mismo periodo. La comparación de los mapas y la generación de índices demuestran qué tan eficiente es el modelo, sin embargo, la verdadera variable en la cual no se puede tener control es en la obtención de los mapas para el análisis, todo depende de que tenga las mismas condiciones de captura en la toma, pero esto no se puede lograr fácilmente. Para superar este obstáculo se genera un umbral de índice que dependerá de la investigación en proceso (i.e. bueno o malo dependiendo del criterio del investigador).
Los procedimientos de comparación de mapas llevaron a explorar técnicas poco utilizadas en la investigación cartográfica: la dimensión fractal y la entropía de Shannon, cuyo uso ha sido una contribución importante para mostrar el crecimiento-difusión de la mancha urbana.
Con los resultados mostrados por las Cadenas de Markov espaciales y los SIG, podemos decir que es posible construir un modelo predictivo. La proyección de los datos se realiza con Cadenas de Markov, técnica ya comprobada en mucha literatura que brinda una proyección en años determinados (i.e. todo depende de la construcción de la matriz de transición); para generar la proyección en el espacio se agrega una regla nombrada regla de difusión aleatoria para volver las Cadenas de Markov espaciales.
Se puede llegar a la conclusión de que la combinación de herramientas matemáticas y SIG en los trabajos de análisis, supervisión y control de los fenómenos urbanos conforman una herramienta de gran valor, sobre todo si se cuenta con los recursos necesarios. Si se dispone de mapas o imágenes de buena resolución, tanto espacial como temporal, se puede extraer una información muy precisa para procesarla con mucha fiabilidad mediante el uso de SIG. Estos datos, cuanto mayor es su precisión facilitan en gran medida la obtención de índices y muestran una proyección correcta de las ciudades en estudio.











 nova página do texto(beta)
nova página do texto(beta)